Ising Model of Cardiac Thin Filament Activation with Nearest-Neighbor Cooperative Interactions

Abstract

We have developed a model of cardiac thin filament activation using an Ising model approach from equilibrium statistical physics. This model explicitly represents nearest-neighbor interactions between 26 troponin/tropomyosin units along a one-dimensional array that represents the cardiac thin filament. With transition rates chosen to match experimental data, the results show that the resulting force-pCa (F-pCa) relations are similar to Hill functions with asymmetries, as seen in experimental data. Specifically, Hill plots showing (log(F/(1-F)) vs. log [Ca]) reveal a steeper slope below the half activation point (Ca₅₀) compared with above. Parameter variation studies show interplay of parameters that affect the apparent cooperativity and asymmetry in the F-pCa relations. The model also predicts that Ca binding is uncooperative for low [Ca], becomes steeper near Ca₅₀, and becomes uncooperative again at higher [Ca]. The steepness near Ca₅₀ mirrors the steep F-pCa as a result of thermodynamic considerations. The model also predicts that the correlation between troponin/tropomyosin units along the one-dimensional array quickly decays at high and low [Ca], but near Ca₅₀, high correlation occurs across the whole array. This work provides a simple model that can account for the steepness and shape of F-pCa relations that other models fail to reproduce.

INTRODUCTION

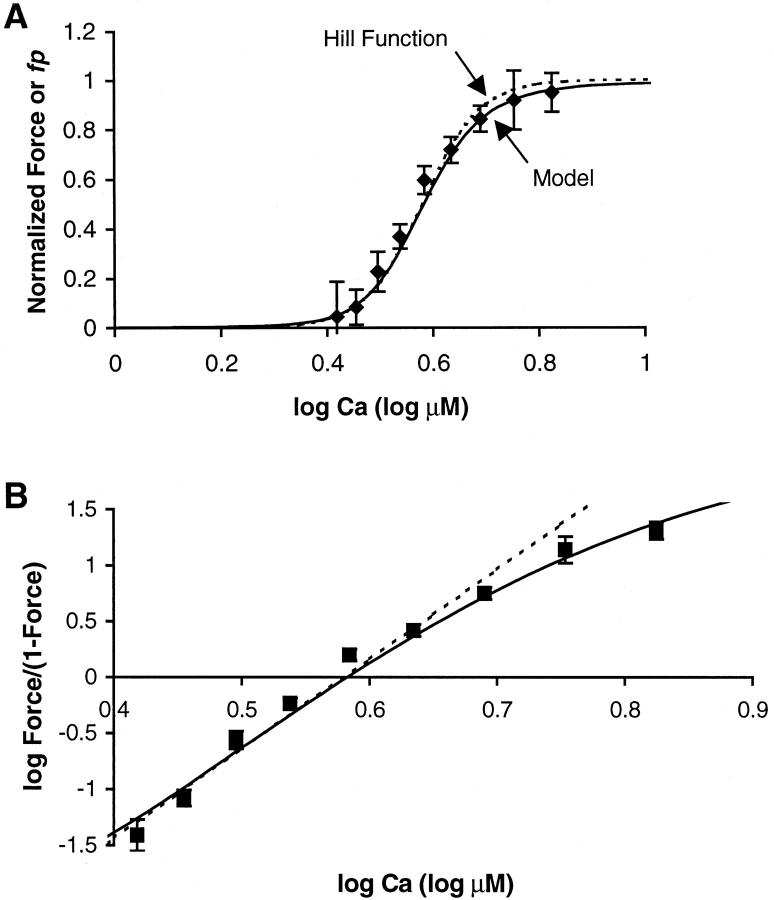
Cardiac muscle exhibits high sensitivity to calcium (Ca) so that during each heartbeat, relatively small changes in free cytosolic [Ca] produce large changes in developed force. A protocol to characterize Ca sensitivity is to measure steady-state force as a function of activator calcium, known as a Force-pCa (F-pCa) relationship as shown in Fig. 1 A (diamonds). Typical for cardiac muscle, the data can be approximately fit by a Hill function given by

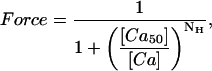(1)

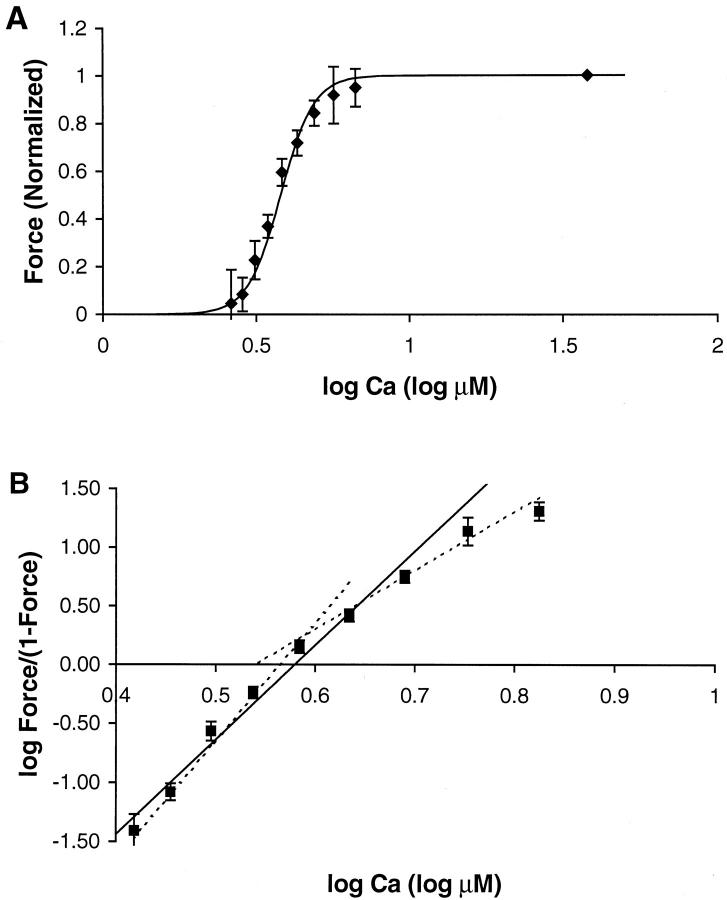
where [Ca] is the free Ca concentration, [Ca₅₀] is the Ca concentration producing half maximal force, and N_H is the Hill coefficient. The solid trace in Fig. 1 A is a Hill function fit to the experimental data with N_H equal to 8. A more precise method to characterize this coefficient is a Hill plot where log (Force/(1−Force)) is plotted as a function of log [Ca], as shown in Fig. 1 B. For a true Hill function (solid trace), a straight line is found where the slope is the Hill coefficient and the zero crossing corresponds to [Ca₅₀]. In contrast, the experimental data are better fit by two slopes (dotted traces) where the initial slope is 10 and the final slope is 5. Hence, the apparent cooperativity is greater below [Ca₅₀] than above. Similar results have been reported elsewhere for cardiac and skeletal muscle (Brandt et al., 1980; Moss et al., 1985, 1983; Sweitzer and Moss, 1990).

FIGURE 1.

Experimentally measured F-pCa relation from cardiac muscle from rat. The muscle is skinned (the sarcolemma is removed) to allow for precise control of activator [Ca] level, and the sarcomere length is maintained at 2.05 μm via feedback control. The data are similar to that from a previous publication that provides a complete description of the methods (Dobesh, 2001). (A) Data are plotted as normalized force (Force) vs. the log of activator [Ca] in μM (i.e., 1.0 corresponds to 10 μM). The symbols show the mean of the data, and the error bars show the standard error. The solid trace data are fit using a Hill function with [Ca₅₀] = 3.8 and N_H = 8. (B) Data from A are replotted using a Hill plot with log (Force/(1−Force)) plotted as function of log [Ca]. The solid trace shows the true Hill function which produces a single straight line in the Hill plot (slope = N_H and zero crossing = log[Ca₅₀]). In contrast, the experimental data are not fit by a single straight line but are more closely fit by two straight lines with slopes equal to 10 and 5 (dashed traces). Note that the errors bars show the standard error computed after transforming the raw data points individually using log (Force/(1−Force)). Because this transformation is nonlinear, the standard error reported in A may differ from that in B. Hence, the fit to the experimental data may fall within the error bars in A but not B.

In cardiac muscle, the force generating actin-myosin interactions are sterically controlled by troponin, a protein complex with a single regulatory binding site for Ca (Dotson and Putkey, 1993). A single binding site should theoretically produce a single Hill coefficient equal to 1, hence the high local slopes of the experimental Hill plot are indicative of cooperative behavior. However, the exact source of the cooperativity is still under much debate with many proposed mechanisms (Razumova et al., 2000; Rice et al., 1999). For example, cross-bridges are thought to increase the affinity of troponin for Ca so that Ca sensitivity should increase with developed force (Guth and Potter, 1987; Hofmann and Fuchs, 1987). Experimental evidence also shows cooperativity between neighboring cross-bridges so that an attached cross-bridge may facilitate binding of nearby cross-bridges. One possible mechanism is that strongly bound cross-bridges hold the tropomyosin in permissive conformation to facilitate attachment of nearby cross-bridges. For example, in vitro studies suggest that binding of isolated myosin heads can produce activation of the thin filament even in the absence of Ca (Bremel and Weber, 1972; Swartz and Moss, 1992; Trybus and Taylor, 1980). Also, the forces from a bound cross-bridge may produce significant realignment of actin-binding sites along compliant thick and thin filaments to increase the binding of nearby cross-bridges (Daniel et al., 1998). Another proposed cooperative mechanism involves end-to-end interactions of the regulatory troponin/tropomyosin (T/T) units along the thin filament. The T/T units overlap by several residues, a feature thought to mediate end-to-end interactions that increase apparent cooperativity (Johnson and Smillie, 1977; Pan et al., 1989).

There have been many attempts to model cardiac myofilaments based on one or more of the cooperative mechanisms given above (Dobrunz et al., 1995; Landesberg and Sideman, 1994; Razumova et al., 2000; Rice et al., 1999; Zou and Phillips, 1994). Unfortunately, many of the modeling efforts are hampered by the paucity of direct experiment estimates of the cooperative mechanisms, especially with regard to nearest-neighbor cooperative effects (Razumova et al., 2000; Rice et al., 1999). Moreover, the models fail to reproduce basic cooperative behavior as characterized by F-pCa relations. Specifically, the models have failed to provide a framework to understand why F-pCa relations are closely approximated by Hill functions and why Hill plots show two slopes. This work seeks to address these issues by proposing a model of cardiac thin filament activation using an Ising model approach from equilibrium statistical physics. Similar Ising models published previously have focused on simulating cooperative binding of S1 myosin heads to skeletal muscle, a related but critically different manifestation of thin filament cooperative behavior (Hill et al., 1980; Tobacman and Butters, 2000).

METHODS

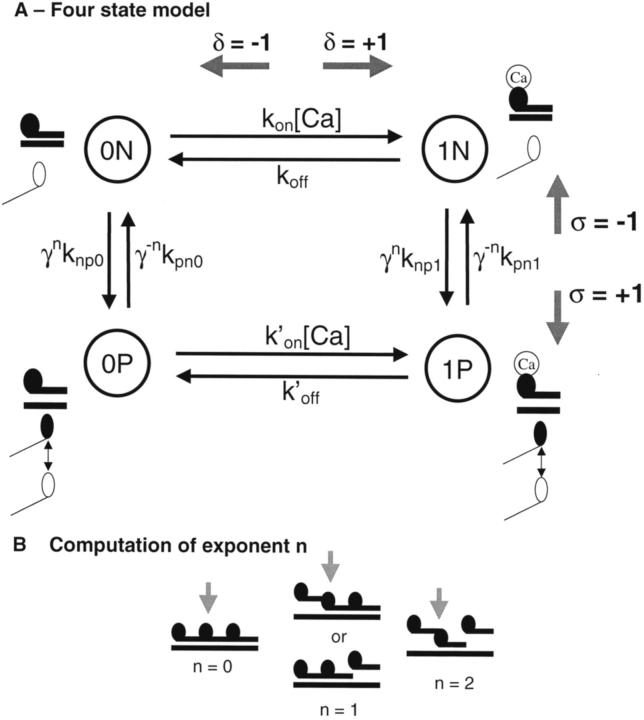
The model is developed using a 4-state Markov model of a T/T unit as shown in Fig. 2 A. We assume troponin binds a Ca ion on a single regulatory site as appropriate for cardiac myofilaments. The two right states have Ca bound to troponin, inasmuch as the two left states have no Ca bound. The T/T unit is assumed to be in either a nonpermissive state that prevents cross-bridge binding or a permissive state that allows cross-bridges to cycle to generate force. The nonpermissive conformations are shown as the two upper states in Fig. 2 A, whereas permissive conformations are the two lower states. Note that cross-bridges are not explicitly represented but are assumed to cycle and generate force whenever the T/T unit becomes permissive. Each 4-state model represents one of 26 T/T units (Brandt et al., 1987) in a one-dimensional linear array to represent the thin filament. The ends of the array are assumed to connect (referred to as periodic boundary conditions) so that every unit has two neighbors.

FIGURE 2.

The model assumes 26 equivalent T/T units that are situated end-to-end along the thin filament. (A) Each T/T unit can be represented by a 4-state Markov model with transition rates between the states as shown. The states are coded with 0x or 1x to represent no Ca or Ca bound, respectively, to the single regulatory site on cardiac troponin. The units are coded with xN and xP to represent states that are in the nonpermissive and permissive conformations, respectively. Cross-bridges are not explicitly represented but are assumed to bind and generate force when units become permissive. The transition rates are shown for Ca binding are given by k_on[Ca] and k_off for the nonpermissive states and k′_on[Ca] and k′_off for the permissive states. The transition rate from a nonpermissive to a permissive state depends both on a base rate and a cooperativity term. The base rates are the k_npx and k_pnx where x is 0 or 1 depending on whether or not Ca is bound. The base rates are modified by cooperativity terms γⁿ and γ⁻ⁿ where n is the number of neighboring units in the permissive conformation (see B). The model can be solved in steady state using an Ising approach where each T/T unit is assumed to have two spins, δ and σ. The δ spin can take on values −1 for no Ca bound and +1 for Ca bound, and the σ spin can take on values −1 for nonpermissive and +1 for permissive. (B) The nearest-neighbor dependencies appear as exponents on γ terms that are computed on the number of neighboring units in the permissive conformation. The exponent n can take on the values of 0 for no permissive neighbors, 1 for a single permissive neighbor, and 2 when both neighbors are permissive. The whole model consists of 26 T/T units along the thin filament where the first and last units are assumed to be connected so that all units have two neighbors.

Ca binding is assumed to follow simple first-order kinetics. The forward rate is assumed to be diffusion limited and independent of the permissive state so that k_on = k′_on. The reverse rate is assumed to depend on the permissive state of the T/T unit. The model assumes k_off > k′_off in agreement with experimental evidence that the affinity of troponin for Ca increases when activated in the presence of cycling cross-bridges. The relationship between k_off and k′_off is set by a parameter μ > 1 such that the following relations hold:

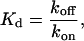(2)

(3)

Many researchers have assumed that the steep F-Ca relations in cardiac muscle result from end-to-end interactions of T/T units along the thin filament. The model implements such a cooperative mechanism by making the rates between nonpermissive and permissive states depend on the states of the two nearest-neighbor T/T units. The nearest-neighbor interactions are set by a parameter γ whose physical interpretation will be discussed momentarily. The neighbor dependencies appear as exponents on γ that are computed by the number of neighboring units in the permissive conformation as shown in Fig. 2 B. The exponent n can take on the values of 0 for no permissive neighbors, 1 for a single permissive neighbor, and 2 for both neighbors permissive. The net effect of the γⁿ terms is to increase the nonpermissive to permissive transition rates when the neighbors are also permissive. Similarly the γ⁻ⁿ terms decrease the reverse rates from permissive to nonpermissive states. Therefore an individual T/T unit is more likely to make the transition to permissive when its neighbors are permissive. Likewise, an individual T/T unit is more likely to make the transition to nonpermissive when its neighbors are nonpermissive. Hence, the γⁿ and γ⁻ⁿ terms promote uniformity along the thin filament so that T/T units tend to take the permissive states of their neighbors.

The physical interpretation of γ comes from the neighbor-induced change in the transition energy barrier between nonpermissive and permissive states. More specifically, one can write

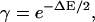(4)

where ΔE is the change in the free energy difference induced by either neighboring T/T being in the permissive state.

Although the γⁿ and γ⁻ⁿ terms set the cooperative effects, the base rate for transitions between nonpermissive and permissive states must still be defined. The base rates are set as follows for nonpermissive to permissive transitions:

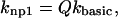(5)

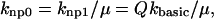(6)

where k_basic is a rate in units of s⁻¹ and Q is a coefficient that is assumed to be larger than 1 for this model of the thin filament. The rationale of this construction will be considered momentarily. Note that without Ca bound to the T/T unit, transition rate from nonpermissive to permissive is slower by the factor μ defined above. Hence the relaxed, nonpermissive state is favored when no Ca is bound. The opposite is also true, and Ca binding to the T/T unit promotes activation. Also by choosing the factor μ defined above, the system will satisfy microscopic reversibility for any choice of n. Hence, the product of rates in the clockwise direction will equal the product in the counterclockwise direction in Fig. 2 A. A similar construction has been used elsewhere (Dobrunz et al., 1995). Note that μ has a dual role by both inhibiting the transitions to permissive when no Ca is bound and enhancing binding of Ca when the unit is permissive. The net effect of increasing μ is to augment the bias toward nonpermissive at low [Ca] and permissive at high [Ca].

The base rate for transition rates from the permissive to the nonpermissive state is assumed to be independent of whether Ca is bound (i.e., k_np0 = k_np1). However, we choose to use γ to determine these rates with the following relation:

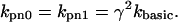(7)

To understand the rational of this construction, consider some specific thin filament configurations. First, assume that the thin filament is completely in the nonpermissive state so that n will be 0 for all units and

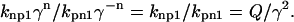(8)

Assuming that γ² ≫ Q > 1, then nonpermissive states are highly favored, and the thin filament will be close to fully relaxed. Now consider when the thin filament is fully activated, then n will be 2 for all units so that

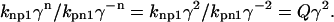(9)

For the same assumption that 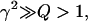then permissive states are highly favored, and the thin filament will be close to fully activated.

Now consider when the thin filament is in a state where half the units are in the permissive conformation and the other half are in the nonpermissive conformation. This corresponds to a half-maximum force in terms of conventional muscle physiology. In this situation, n will not be 1 for all units, but we will make this approximation for the moment and compute

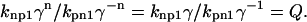(10)

Assuming that Q > 1, then permissive states are favored over nonpermissive states. The parameter Q can be considered a bias term to tip the system toward fully permissive as Ca levels increase. As Q increases, the system tends to activate more easily, and the fraction of permissive units will approach 1 at high Ca. Conversely, as Q decreases toward 1, the fraction of permissive units will approach 0.5 at high Ca.

The model construction and rates as defined correspond best to ideas developed from experimental characterizations of muscle physiology. The system can be implemented in a straightforward fashion using Monte Carlo techniques. We can assume 26 T/T units in a one-dimensional linear array to represent the thin filament. At each time step, the exponent n must be computed for each of the units, and we assume that the ends are wrapped so that unit 1 and unit 26 are connected. The state of each T/T is then updated considering the transition rates as defined in Fig. 2 A, and the system can be evolved forward in time.

However the same model can also be solved in equilibrium conditions using an Ising approach. To do this, we recast the system so that each T/T unit has two spins, δ and σ. The δ spin can take on values −1 for no Ca bound and +1 for Ca bound. The σ spin can take on values −1 for nonpermissive and +1 for permissive. Comparing to the states represented in Fig. 2 A, the δ spin corresponds to the left-to-right direction, and the σ spin corresponds to the top-to-bottom direction. Assuming each of the T/T is one of four states the complete thin filament model has 4^N = 4²⁶ configurations. The probability associated with any configuration is computed using

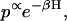(11)

where the energy H is computed as

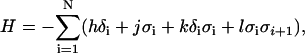(12)

and h, j, k, and l are constants that are determined from the rates in Fig. 2 A. The constants h and j correspond to magnetic fields applied in the δ spin and σ spin directions, respectively. A coupling term k exists to couple changes in the δ spin and σ spin directions. Intuitively, this forces the Ca binding transition to affect the nonpermissive to permissive transition. A coupling term l exists so that neighboring units will tend to align in σ spin direction. Intuitively, this produces an energetic penalty when one unit is nonpermissive and the next unit is permissive, or vice-versa. Hence the lowest energy is obtained when the neighboring units are either both nonpermissive or both permissive.

The partition function of the system is

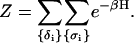(13)

A more convenient form of the partition function can be computed using the transfer matrix formalism (Plischke and Bergersen, 1989) with

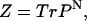(14)

where Tr is the trace of a matrix and

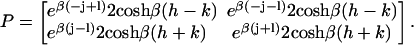(15)

By computing eigenvalues (λ₁ and λ₂) of P, the partition function can be rewritten as

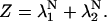(16)

The eigenvalues will be derived as functions of the model parameters later. For now, the eigenvalues can be used to derive the mean spins in the δ and σ directions as follows:

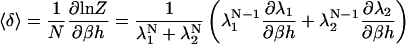(17)

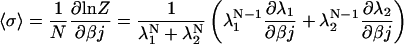(18)

To convert from the Ising approach to the kinetic model of Fig. 2, we use the principle of detailed balance, according to which 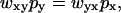where w_xy is the transition probability per unit time for converting state y to state x, and p_x is the equilibrium probability of state x. Using that the kinetics rate constant k_xy linking state x to y is proportional to the transition probability per unit time w_xy, detailed balance yields

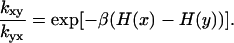(19)

Here we have used that the probability of state x in the Ising model is given by the Gibbs distribution of Eq. 12, with the energy function H corresponding to that state. Notice that in Eq. 19, the left side refers to the kinetic model, whereas the right side refers to the Ising model. Thus we can recast the kinetic parameters described earlier in terms of the Ising model parameters.

As an example, let us consider the transition between the state x = 1N (δ = 1, σ = −1) and y = 0N (δ = −1, σ = −1). The left side in Eq. 19 yields k_on[Ca]/k_off or using Eq. 2, [Ca]/K_d = Ca. The difference in energy between these two states is H(x) − H(y) = 2(k−h). Thus, from Eq. 19,

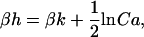(20)

where Ca = [Ca]/K_d, the free [Ca] normalized by K_d, the binding constant for troponin in the nonpermissive conformation. Using similar arguments, it can be shown that

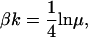(21)

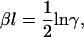(22)

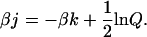(23)

Given that the Ising approach solves for equilibrium, then only the ratios of rates actually need to be considered. Hence K_d is used instead of k_on and k_off, and k_basic becomes unimportant as it appears in both forward and reverse rates for the nonpermissive to permissive transition rates. Inasmuch as only the ratios of rates actually need to be considered, we constructed the model in Fig. 2 based on individual forward and reverse rates for two reasons. First, some of the rates could be estimated from experimental data. Hence, the individual rates are more closely aligned with physiologist's views of the system. Second, the model in Fig. 2 may be extended to nonequilibrium conditions using Monte Carlo methods. Although not considered in this paper, the rates provided here produce reasonable results in this application.

For any overlap or thick and thin filaments, there is a maximal amount of steady-state force that occurs for large, saturating [Ca] levels. Although we lack direct experimental evidence, we assume that this situation corresponds to all T/T units in the permissive conformation (permissive fraction equals 1) to allow for maximal actin-myosin interactions. Hence a permissive fraction equal to 1 will recruit all potential cross-bridges that can cycle so that normalized force will also be equal to 1. At the other extreme of low [Ca], the fraction of permissive units will equal 0, and no cross-bridges will be cycling to produce a normalized force equal to 0. For intermediate values of [Ca], we assume that the fraction of permissive units translates into the fraction of recruited, cycling cross-bridges, and hence also the fraction of normalized force. For example, if the permissive fraction is 0.3, then we assume 30% of potential cross-bridges are cycling and generating force, and the normalized force equals 0.3.

RESULTS

Computing force and Ca-binding relations

A primary goal of this study is to understand the role of nearest neighbor cooperativity in producing steep F-pCa relation in cardiac muscle. In steady state, the fraction of cycling cross-bridges should be determined primarily by the activation state of the thin filament (i.e., the fraction of permissive T/T units will be the same as the fraction of cycling cross-bridges) if filament overlap is not considered, as done in this model. If one makes this assumption that normalized force is equal to the fraction of permissive units (see Methods), then an analytic solution for force can be derived using the Ising model. As shown in Fig. 2, the state of each of the 26 T/T units is either nonpermissive (σ = −1) or permissive (σ = +1). Hence, the average σ spin for the whole system, denoted by 〈σ〉, will take values between −1 and 1. Then the fraction of permissive units, fp, can be computed using

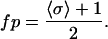(24A)

The equation for 〈σ〉 is derived using the eigenvalues of P as described in the Methods section to yield

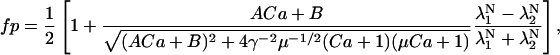(24B)

where

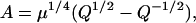(25)

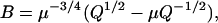(26)

and

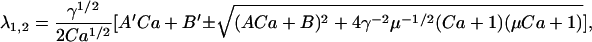(27)

where

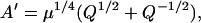(28)

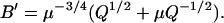(29)

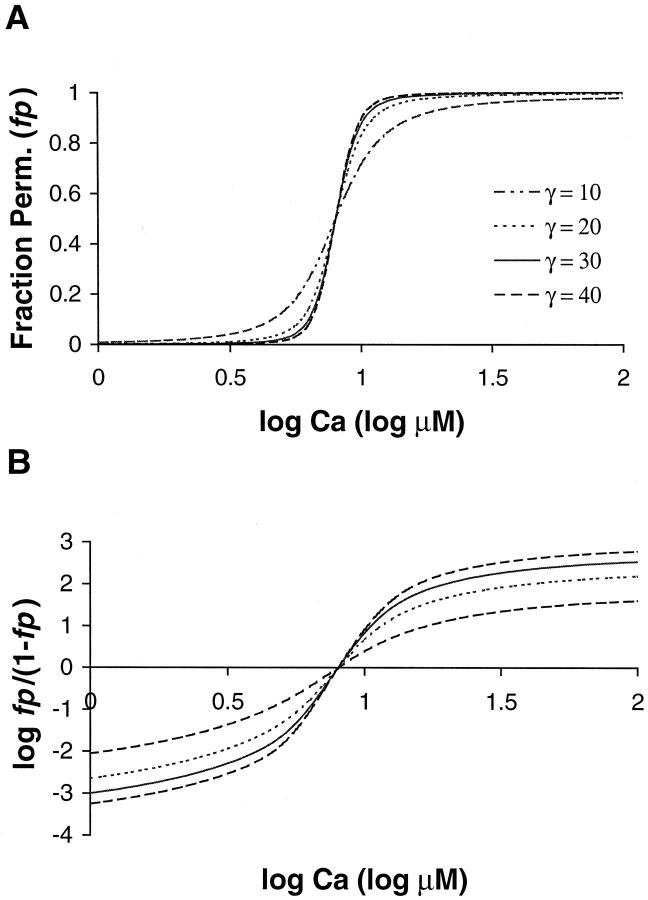
In the equations above, Ca is a nondimensional variable computed by normalizing free [Ca] by K_d. One must simply vary free [Ca] and compute fp as shown above to generate the relations shown in Fig. 3 A. Data are shown for γ set to 10, 20, 30, and 40; all other parameters remain the same (K_d = 10 μM, μ = 10, Q = 2). The results show increasing steepness as γ is raised to larger values. The steepness can be quantified using a Hill plot shown in Fig. 3 B. The Hill plot shows log (fp/(1−fp)) as function of log [Ca] where fp is the fraction of permissive units from Fig. 3 A. The slope of the Hill plot reports the apparent cooperativity in the system at any value of [Ca].

FIGURE 3.

Model results are shown for four values of γ. (A) The fraction of permissive units (fp) is plotted vs. log [Ca]. These plots can be compared to the F-pCa relation in Fig. 1 if one assumes that force is proportional to the fraction of permissive units. The values of γ are 10, 20, 30, and 40 as labeled, whereas the other parameters were fixed (K_d = 10 μM, μ = 15, and Q = 2). As γ increases, the steepness also increases indicating higher apparent cooperativity. (B) Apparent cooperativity is assessed using a Hill plot showing log (fp/(1−fp)) as a function of log [Ca]. The traces are sigmoidal and not linear; hence, the model does not produce true Hill functions. The slope is close to maximal near [Ca₅₀] (corresponding to the zero crossing) and decreases to either side. The N_H50 values (the slope at Ca₅₀) point are 4.4 for γ = 10, 7.7 for γ = 20, 9.4 for γ = 30, and 10.3 for γ = 40.

As shown in Fig. 2, the state of each of the 26 T/T units has either Ca unbound (δ = −1) or Ca bound (δ = +1). The average δ spin for the whole system, denoted by 〈δ〉, will take values between −1 and 1. Then the fraction of T/T units with Ca bound can be computed using

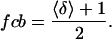(30)

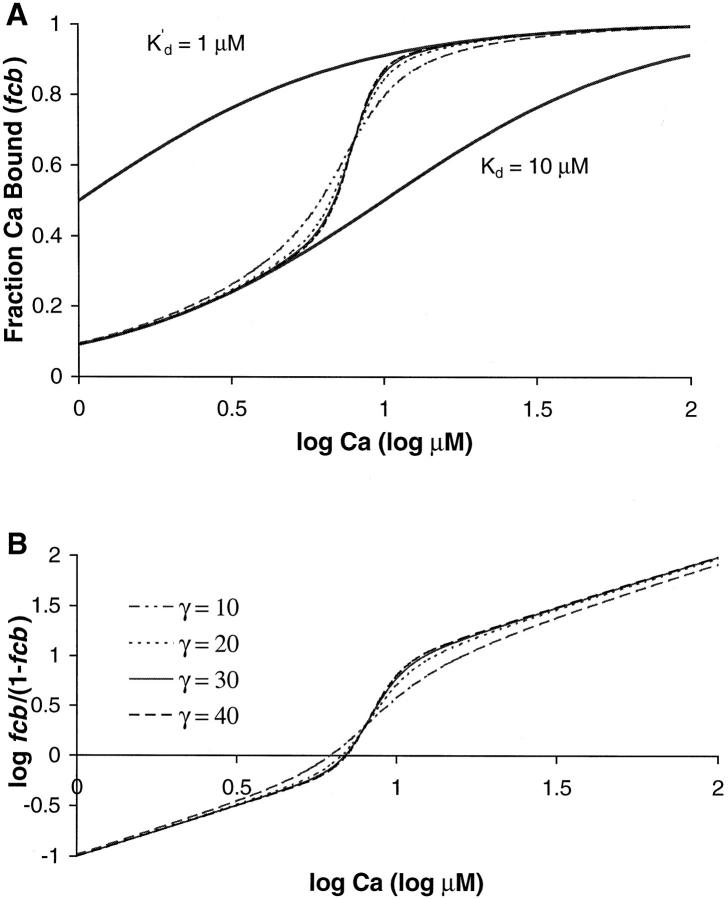
The Ca binding curves in Fig. 4 are produced for the same parameters and values of γ as in Fig. 3. Fig. 4 A included two additional traces that illustrate predicted binding curves for simple buffers with K_d = 10 μM and K′_d = 1 μM. The model results show that the Ca binding initially resembles the lower curve for the simple buffer corresponding to K_d = 10 μM. However as a greater fraction of units become permissive, the model Ca binding becomes steeper and switches to the upper curve for the simple buffer corresponding to K′_d = 1 μM. In the model, K′_d/μ = K_d so that binding of Ca first follows a curve determined by K_d and then switches to a curve determined by K_d and μ. The switch between the curves follows the highly cooperative fp curves. Hence, the apparent cooperativity of Ca binding is greatly increased during the transition phase. The switch is most clearly seen in the Hill plots of fcb shown in Fig. 4 B. In these plots, the slope is initially 1 reflecting the uncooperative binding at low [Ca]. Near the transition region, the slope gets larger indicating the higher apparent cooperativity near the Ca₅₀ point. At even larger [Ca], the slope again returns to 1 as the binding again is uncooperative.

FIGURE 4.

Model results are shown for four values of γ. (A) The fraction of unit with Ca bound (fcb) is plotted vs. log [Ca]. The four data traces are from the same simulation as those in Fig. 3. In the lower [Ca] range, the fcb initially resembles the lower thick trace that shows the Ca binding curve for a simple buffer with a dissociation constant = 10 μM. In the upper [Ca] range, the fcb resembles the upper thick trace that shows the Ca binding curve for a simple buffer with a dissociation constant = 1 μM. The transition between the curves reflects the highly cooperative fp curves shown in Fig. 3. (B) Apparent cooperativity is assessed using a Hill plot showing log (fcb/(1−fcb)) as a function of log [Ca]. The slope is initially 1 reflecting the uncooperative binding at low [Ca]. Near the transition region, the slope gets larger indicating the higher apparent cooperativity near the [Ca₅₀] point. At even larger [Ca], the slope again returns to 1 as the binding again is uncooperative. The slope is largest near [Ca₅₀] point (corresponding to the zero crossing in Fig. 3 B). For the cases shown, the slope is 2.9 for γ = 10, 4.2 for γ = 20, 4.8 for γ = 30, and 5.1 for γ = 40.

Returning to Fig. 3, the model fp curves can be compared to Force-pCa relations reported for real muscle. The comparison to real F-pCa relations becomes important when one attempts to narrow the range of parameters for the myofilament model. Real cardiac muscle shows steep F-pCa relations with Hill coefficients in the range of 7–10. We will determine the apparent cooperativity at the point where half the T/T units are permissive. This point, referred to the Ca₅₀ point, can be found by the zero crossings in the Hill plots as shown in Fig. 3 B. The Ca₅₀ point can be determined analytically using the expression,

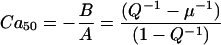(31)

where the concentration is normalized by K_d. The value of actual calcium concentration ([Ca₅₀]) that corresponds to 50% force can be calculated as

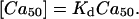(32)

Note that the Ca₅₀ point does not depend on γ. The slope of the Hill plot at the Ca₅₀ point, referred to as N_H50, can be computed analytically as

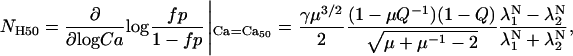(33)

where γ, Q, and μ are defined as before and λ₁ and λ₂ are the two eigenvalues of P from Eqs. 15 and 27.

Study of parameter space

Fig. 5 shows N_H50 as a function of γ and Q at three levels of μ. The parameter γ is varied between 5 and 45 in increments of 2.5, whereas the parameter Q is varied between 1.25 and 3 in increments of 0.25. The lines show isoclines of N_H50 as labeled with an increment of 2 between adjacent lines. The three panels show results for μ = 5 (A), 10 (B), and 15 (C). The results show that N_H50 is a monotonically increasing function of γ. Initially the increase is a linear function of γ as might be predicted by the first γ term in Eq. 33. However as γ increases, the growth slows as evidenced by widening isoclines. The decreased growth results from the 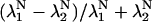term. This term is nearly 1 for small values of γ, because the larger eigenvalue (λ₁) dominates with N = 26 in this model. However, as γ increases, the two eigenvalues become nearly equal at the Ca₅₀ point. In this case, the term is <1, and the net effect is to reduce N_H50. Hence, the growth becomes less than linear with respect to γ.

FIGURE 5.

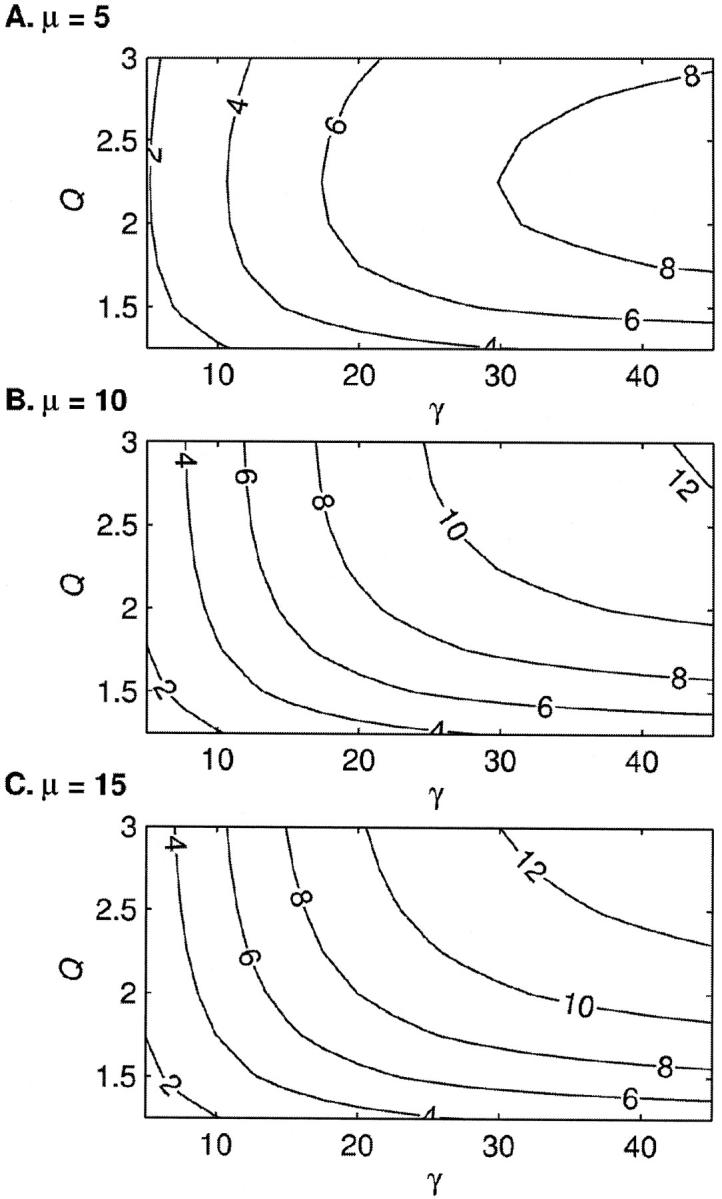
The Hill coefficient at half activation, N_H50, is plotted as a function of γ and Q at three levels of μ. The parameter γ is varied between 5 and 45 in increments of 2.5, whereas the parameter Q is varied between 1.25 and 3 in increments of 0.25. The contour lines show the isoclines for levels as labeled and increase with an increment of 2. Results for μ = 5 (A), 10 (B), and 15 (C). In general, N_H50 is an increasing function of γ, μ, and Q. However, for the μ = 5 case, the dependence on Q is nonmonotonic, a feature investigated further in Fig. 6 (see text for details).

The effects of parameter Q are more complicated. For large μ, N_H50 is a monotonically increasing function of Q (see Fig. 5, B and C). However, for μ = 5, the apparent cooperativity is a nonmonotonic function of Q (see Fig. 5 A). This effect is further explored in Fig. 6. Fig. 6 A shows the model fp relations for Q = 1.25, 1.5, 2.0, and 3.0. The other parameters are fixed values (K_d = 10 μM, μ = 5, γ = 20). The parameter Q affects the value of fp at extremely large and small values of [Ca]. With Q ≫1, the plateau fp approaches 1 at large, saturating values of [Ca]. The effect can be most easily seen in the Hill plots with log (fp/(1−fp)) plotted as a function of log [Ca] in Fig. 6 B. For example, with Q = 3, the Hill plot approaches 2.72 which corresponds to a plateau fp = 0.998. In contrast, for the smallest value shown, Q = 1.25, the Hill plot only approaches 1.29 which corresponds to a plateau fp = 0.951. The opposite relation occurs for low values of [Ca]. In this regime, low Q produces a very small fp whereas a larger Q promotes a larger fp, indicating more activation at low values of [Ca].

FIGURE 6.

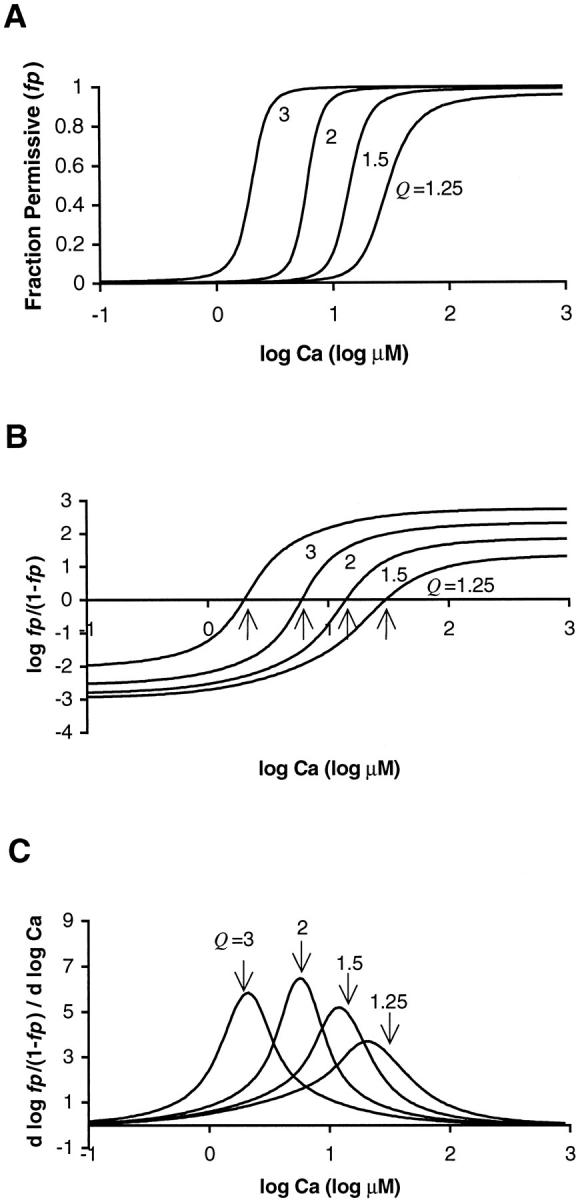
The plots illustrate the effects of variation of parameter Q. (A) fp relations are shown for Q = 1.25, 1.5, 2.0, and 3.0. The other parameters were fixed values (K_d = 10 μM, μ = 5, γ = 20). The parameter Q affects the value of fp at extremely large and small values of [Ca]. With a large value of Q, the plateau fp approach 1 at high, saturating values of [Ca]. (B) Hill plots show log (fp/(1−fp)) plotted as function of log [Ca]. The data are the same as in A. The arrows indicate the zero crossings that correspond to the [Ca₅₀]. (C) Slope of the Hill plots from B is also plotted. The slope reports the apparent cooperativity at different levels of [Ca]. In general larger Q values produce more activation at low [Ca]. The value of parameter Q also affects the symmetry of the fp relations. See that the peaks of the slopes do not always line up with the [Ca₅₀] points, as indicated by the arrows drawn at the same [Ca] as the zero crossings in B. Hence, the N_H50 value that reports the Hill coefficient at half activation does not always report the maximum slope of the corresponding Hill plot.

Besides affecting the saturating level of fp, Q also affects the symmetry of the fp relations. This effect can be seen in the Hill plots in Fig. 6 B, but for additional clarity, the slopes of the Hill plots are also plotted in Fig. 6 C. Larger Q values produce more activation at low [Ca]. This increased activation at low [Ca] has the side effect of causing the peak apparent cooperativity to shift to higher values of [Ca], sometimes occurring above the Ca₅₀ point. For example, the data for Q = 3 show a peak apparent cooperativity which is slightly above the Ca₅₀ point (compare the location of the arrows for the Q = 3 traces in B and C). Because of this type of asymmetry, the N_H50 values (as reported in Fig. 5) may not correspond to the maximum slope of the corresponding Hill plot. For Q near 2, the fp relations become closer to symmetric, and the peak slope of the Hill plots is close to the Ca₅₀ point. As Q is reduced to 1.5 and 1.25, the Hill plots become less symmetric. Now the peak apparent cooperativity occurs below the Ca₅₀ point (compare the location of the arrows for the Q = 1.25 traces in B and C). Note that the Ca₅₀ refers to the true fp = 0.5 point, not the point of half-maximum force point that could be obtained if the fp values were renormalized to the measured plateau level at saturating [Ca]. See also that the peak slope of the Hill plots falls below Ca₅₀ point as Q is reduced toward 1. This observation is important because real muscle shows greater apparent cooperativity below vs. above Ca₅₀, as seen in Fig. 1 B.

Given the analysis above, the roles of parameters γ, μ, and Q should be clearer. The parameter γ plays an important role is setting the apparent cooperativity, but does not affect the Ca₅₀ point. The parameter Q sets the plateau levels of the fp relations at the extremes of high and low [Ca] and affects the symmetry and apparent cooperativity in the transition regions. Recall that μ has a dual role by both inhibiting the transitions to permissive when no Ca is bound and enhancing binding of Ca when the unit is permissive. Hence, the most obvious effect of increasing μ is to shift Ca₅₀ leftward. Another effect of increasing μ is to augment the bias toward nonpermissive at low [Ca] and permissive at high [Ca]. Hence, increasing μ will also augment cooperativity and increase the difference in the plateau levels of the fp relations at the extremes of high and low [Ca] (data not shown). The model actually contains one other parameter K_d. However, changing K_d alone produces a trivial change of translating the fp relations and fcb relations to left or right without affecting the shape or apparent cooperativity. Note that N, the T/T units in thin filament, is a fixed parameter equal to 26 for all of the simulations presented in this paper. The choice of N = 26 is consistent with experiment estimates, but the exact value of this parameter does strongly effect results as long as N is large (>20). Hence we chose a fixed value for N to reduce dimensionality of the parameter space to be characterized.

Correlation between units

The model is constructed so that the σ spins of neighboring T/T units will tend to align. This effect is quantified by computing ρ(i), the correlation of a reference unit (0) with another unit (i) in the one-dimensional array. The value of ρ(i) can be calculated as follows:

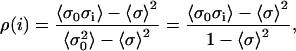(34)

where 〈σ〉 is the mean spin computed across the whole ensemble as calculated by Eq. 18. The correlation term 〈σ₀σ_i〉 is the correlation of the spin of the reference T/T unit (the 0^th T/T unit) and the i^th T/T unit away along the thin filament model. This value can be calculated as

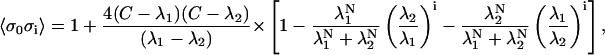(35)

where

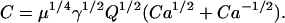(36)

Hence, the value of ρ(i) is both a function of [Ca] and of the model parameters. For all parameter choices, ρ(0) = 1 and ρ(i) = ρ(−i).

Fig. 7 shows the calculated values of ρ(i) for two sets of parameter variations. In Fig. 7 A, all model parameters are fixed (corresponding to the γ = 20 trace in Fig. 3), and the Ca level is set to three fixed values (log [Ca μM] = 0.4, 0.9, and 1.5). The middle level corresponds to Ca₅₀, and values near Ca₅₀ produce high correlation between units for separation as large as 12. Hence, units are correlated for distances that correspond to half the distance of the 26 T/T unit system. At higher or lower Ca levels, the correlation level decreases more rapidly with separation and is not a strong function of γ. Similar plots with γ = 10, 30, or 40 produce barely perceptible changes at the high or low Ca levels (data not shown). However, near Ca₅₀, the dependence of correlation on γ is more pronounced as shown Fig. 7 B. Here, γ is varied whereas other parameters are fixed (corresponding to data in Fig. 3), and the Ca level is set to Ca₅₀. Under these conditions, the correlation is clearly dependent on γ. For all separations above 0 (that always yield 1), the correlation is found to be a monotonically increasing function of γ.

FIGURE 7.

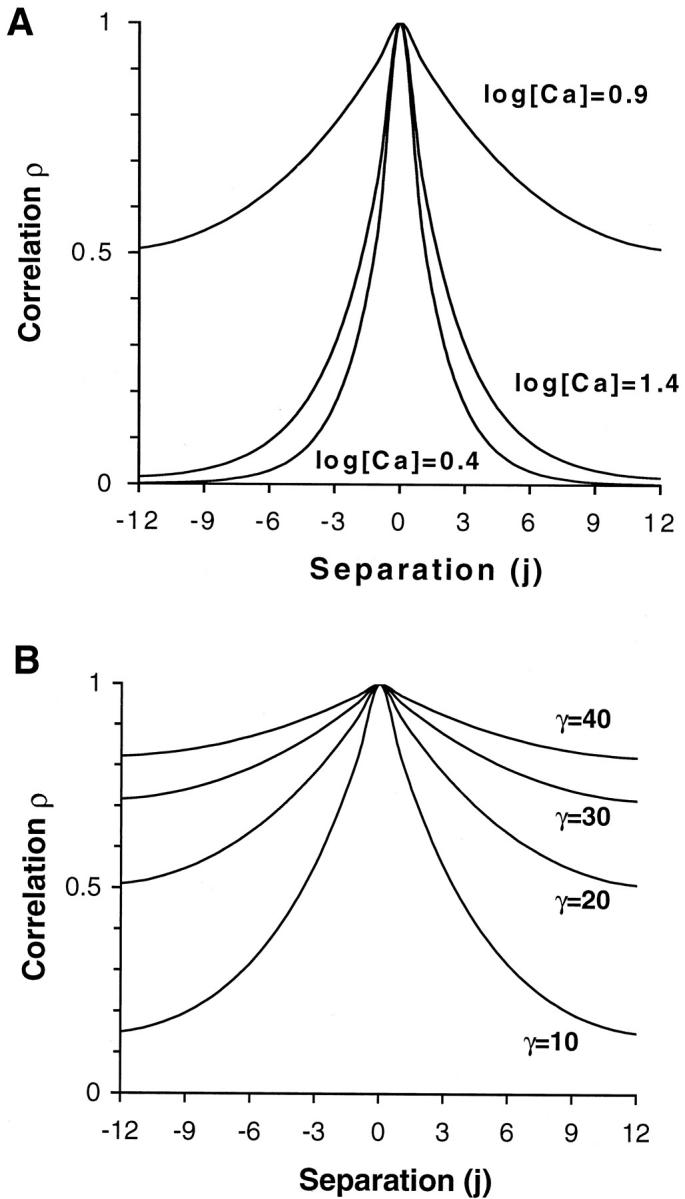
Correlation ρ(i) computed for two sets of parameter variations where i is the number of units from the point of reference. (A) Ca level is set to three fixed values (log ([Ca] / 1 μM) = 0.4, 0.9, and 1.5) whereas other model parameters are fixed (K_d = 10 μM, μ = 15, Q = 2, and γ = 20). The correlation is equal to 1 at i = 0 and decreases in either direction. The correlation falls most rapidly at high or low [Ca] whereas values near Ca₅₀ produced correlation between units for separation as large as 12. (B) The parameter γ is set at four values whereas the parameters are fixed (K_d = 10 μM, μ = 15, Q = 2, and [Ca] = [Ca₅₀]). Near [Ca₅₀], the correlation falls off more slowly as γ is increased. At [Ca] values much smaller or larger than [Ca₅₀] where normalized force is closer to 0 or 1, respectively, the falloff of correlation is not as strongly dependent on γ (data not shown).

Fitting experimental F-pCa relations

A primary goal of this work is to explore if a model with explicit nearest neighbor cooperativity could reproduce experimentally observed F-pCa relations in cardiac muscle. To this end, we attempt to reproduce the data shown in Fig. 1 using the model with appropriate choices for parameters. For the model, the fraction of permissive units (fp) is compared to normalized force in the experimental data. The model results (solid trace) are shown in Fig. 8 A on the same axis with the experimental data (symbols) and a true Hill function (dashed trace) for comparison. The model results are similar to the Hill function but are lower above Ca₅₀, as is also seen in the experimental data. To further quantify the apparent cooperativity, the data are also shown as Hill plot in Fig. 8 B. In the Hill plots, the model results show different slopes above and below Ca₅₀, although the transition is not as sharp as in the experimental data (compare to Fig. 1 B.). Moreover, the initial slope below Ca₅₀ is ∼8 for the model, whereas the experimental data can fit with a line with slope = 10 (compare to Fig. 1 B.).

FIGURE 8.

The model is used to fit the experimentally determined F-pCa relation from Fig. 1. (A) The fraction of permissive units (fp, solid trace) from the model is compared to normalized force in the experimental data from Fig. 1. The plot also shows a true Hill function (dashed trace) for comparison. The model results are similar to the Hill function but are lower above Ca₅₀, as is also seen in the experimental data. (B) Data is replotted using Hill plots where both log (fp/(1−fp)) and log (Force/(1−Force)) are plotted as a function of log of activator [Ca] in μM. In the Hill plots, the model results show different slopes above and below Ca₅₀, although the transition is not as sharp as for the experimental data (compare to Fig. 1 B). Moreover, the initial slope below Ca₅₀ is ∼8 for the model, whereas the experimental data can fit with a line with slope = 10. Model parameters are K_d = 2.125, μ = 15, γ = 40, and Q = 1.5. See text for the method of choosing the parameters. Note that the errors bars show the standard error computed after transforming the raw data points individually using log (Force/(1−Force)). Because this transformation is nonlinear, the standard error reported in A may differ from that in B. Hence, the fit to the experimental data may fall within the error bars in A but not B.

The model has essentially four free parameters that are chosen with the following considerations. The Ca binding constant, K_d, is adjusted to 2.125 which gives the proper Ca₅₀ value; changing this parameter makes a trivial change of shifting the traces left or right on the abscissa. The value of μ is set to 15 as this seems to be roughly in line with experimental results that show that troponin binds Ca more strongly when cross-bridges are cycling. For example, Guth and Potter (1987) estimated an increase of >10-fold, and the modeling studies by Landesberg and Sideman (1994) suggest an ∼13-fold increase using the data of Hofmann and Fuchs (1987). Inasmuch as our model does not explicitly consider cross-bridges, the permissive state in the model is assumed to represent this situation where the T/T unit is activated and cross-bridges are cycling. With K_d and μ set, the remaining parameters were chosen as follows. A relatively large value of γ = 40 is chosen to produce a high apparent cooperativity (see Figs. 3 and 5). A relatively low value of Q = 1.5 is chosen to produce a larger disparity in apparent cooperativity below vs. above Ca₅₀ (see Fig. 6).

Note that there is an important tradeoff between γ and Q. As γ increases, the overall apparent cooperativity goes up, but a side effect is that the slopes above and below Ca₅₀ become essentially the same. The effects of lowering Q are roughly the opposite, lowering overall apparent cooperativity but increasing the difference in the slopes above and below Ca₅₀. Given that no experimental estimate exists for γ and Q, we could, in principle, choose values we need. The final choice, shown in Fig. 8, represents a reasonable compromise with γ and Q balanced to give high apparent cooperativity and a breakpoint near Ca₅₀. This compromise was found through trial and error, so a slightly better fit to the experimental data might be accomplished through other means. Even so, our experience with the parameter variation studies suggests that any improvements will be marginal given the essential tradeoff between γ and Q.

DISCUSSION

Cooperative mechanisms

The work here has focused on nearest-neighbor interactions between adjacent T/T units. Considerable evidence suggests the importance of this mechanism. For example, partial extraction of as little as 5% of troponin C is seen to alter F-pCa relations in skeletal muscle (Brandt et al., 1987). This finding led the researchers to propose that all the regulatory proteins shift in concert so that at any given time, the whole thin filament is on or off. Although our model does not completely support this point of view, our model does show similar behavior with respect to the Ca dependence of correlation. Near Ca₅₀, correlation functions are near 1 for up to half the distance of the network with γ = 40, the value needed to reproduce experimental F-pCa relations (Fig. 7 B). Hence, near Ca₅₀, the T/T units show high correlation across the whole 26 unit system. However, for low or high Ca, the correlation functions are much reduced (Fig. 7 B), showing that the correlation of units across the thin filament is a function of activator Ca level in this model. One interpretation of this result is that the spread of activation will also be a function of activator Ca level. Murray and Weber (1980) first suggested that Ca level could modulate the number of actin monomers activated by the binding of Ca to troponin. Their experiments with regulated actin and S1 heads showed a greatly slowed onset of ATPase activity at low Ca, suggesting that few actin monomers were activated as compared to higher levels of Ca.

The modeling work here suggests that nearest-neighbor interactions between adjacent T/T units are sufficient to explain steep F-pCa relations. However, the construction of the model may be able to accommodate other proposed cooperative mechanisms as well. For instance, cycling cross-bridges are known to increase the affinity of troponin for Ca. In our model, the transition from nonpermissive to permissive is assumed to increase the affinity of T/T units for Ca by a factor of μ (see Eq. 3). Recall from the Methods section that the term μ is required for the model to satisfy microscopic reversibility. Hence, the change in Ca affinity is concomitant to the end-to-end cooperative mechanism. Another proposed cooperative mechanism is interactions between neighboring cross-bridges. In our model, cross-bridges are not explicitly represented but are assumed to cycle and generate force whenever T/T units become permissive. Given that neighboring T/T units are coupled and their activity is correlated (see Fig. 7), then one can extrapolate this to suggest that the activity on neighboring cross-bridges would be correlated as a secondary effect of direct neighbor interactions of the T/T units. Hence, the same cooperative behavior could potentially have different manifestations that appear as separate phenomena depending on whether one is considering cross-bridges, regulatory proteins, or both in combination. Further study with refined versions of the model is required before more definitive arguments can be made as to how many proposed cooperative mechanisms can be accommodated. Finally, cooperative behavior has been proposed where the attachment of one cross-bridge pulls the neighboring cross-bridges into register, thereby increasing their probability of attachment (Daniel et al., 1998). Our model could not account for this type of cooperativity as cross-bridges are not explicitly represented here.

Model limitations

Statistician George Box (1976) is quoted as saying, “all models are wrong, but some are useful.” Likewise, the purpose of this study is to develop a relatively simple, but useful model of thin filament activation. This model has only four parameters with straightforward physical interpretations, and the parameter space can be well characterized, a feature that is often not possible with more sophisticated models. The model's ability to reproduce experimental data F-pCa relation suggests that some “main ingredients” of cooperative behaviors have been captured by our model. However, like most simple models, we have made abstractions that are inconsistent with known experimental data. For example, the basic model construction is around a functional unit of troponin and tropomyosin spanning seven actin monomers. This functional unit concept has a long history dating back to the work of Hill and co-workers (1980). Such a construction may be inconsistent with many known features of muscle (e.g., see model critique discussed in Razumova et al. (2000)). Some recent work has even argued that the system of overlapping troponins is more closely approximated by a continuous chain rather than discrete functional units spanning seven actin monomers (Tobacman and Butters, 2000). Although we admit many potential inconsistencies with experimental data, we focus on the most pertinent limitations in the following discussion.

An obvious limitation is that the model lacks explicit cross-bridge interactions. We assume that steady-state force is proportional to the fraction of permissive T/T units in the model—a reasonable, but not completely defensible position. The presence of cross-bridges is thought to produce several important changes to thin filament. For example, strongly bound myosin heads appear to move troponin to a more lateral position on the F-actin helical backbone of the thin filament (e.g., Lehman et al., 2001). Also, data from reconstituted thin filaments suggest that the presence of one or two strongly bound myosin heads can “trap” the thin filament in an activated state even after Ca has dissociated (Bremel and Weber, 1972; Swartz and Moss, 1992; Trybus and Taylor, 1980). Hence, real thin filament is regulated not only by Ca as in this model, but attached cross-bridges should also play an important role. Although future versions of the thin filament model could in principle contain cycling cross-bridges, significant modification may be necessary. For example, the model in Fig. 2 is constructed assuming detailed balance because no energy is added to the system. By including cycling cross-bridges that hydrolyze ATP, such an assumption cannot be made, so the number of parameters to be defined is necessarily increased.

Another limitation is in the number of states represented. In the model, T/T units are assumed to be in one of four states as shown in Fig. 2. This number of states with simple Eyring-type transition rates is a tremendous simplification for this system of large proteins with potentially complex biomolecular interactions. For example, troponin and tropomyosin form large protein complexes with multiple points of interactions with each other and the F-actin helical backbone (e.g., Lehman et al., 2001). In regards to blocking actin-myosin interactions, the model assumes only two positions, nonpermissive and permissive. However, most experimental studies suggest at least three functional positions for tropomyosin, referred to as blocked, closed, and open (McKillop and Geeves, 1993). The first two states allow only detached or weakly bound cross-bridges, whereas the open state allows strongly bound cross-bridges. It is tempting to consider that the permissive state in our model corresponds to open whereas the nonpermissive state corresponds to blocked and closed. However, regulatory proteins and cross-bridges appear to be highly interactive; hence, the assumption that T/T units act simply as an “on-off switch” to allow cross-bridges to cycle is a simplifying assumption. We envision that inclusion of three position states of the T/T units would also require explicit cycling cross-bridges to produce a meaningful model. This level of detail is a potential refinement to the current model but is beyond the scope of this modeling study.

In the model presented here, the end units were assumed to be continuously wrapped so that T/T unit 1 communicates with T/T unit 26. The assumption of periodic boundary conditions is required to use transfer matrix formalism to solve the Ising model (Eqs. 14–16). In a real thin filament, no such wrapping is present. However, to implement this nonperiodic boundary condition, a Monte Carlo approach must be employed. Preliminary work suggests that this effect will be nonnegligible. For example, assume that unit 1 and unit 26 only have a single neighbor and n can be either 0 or 1, but not 2 (see Fig. 2). This feature will tend to reduce activation in these two units and across the whole system as well. Recall from Fig. 7 B, that the correlations near Ca₅₀ could be quite high even at distances up to half the network. The repressing effect of nonperiodic boundary conditions is not noticeable at low [Ca] where activation is essentially 0 already, but repression of force is more noticeable as [Ca] and activation levels rise. The overall effect is similar to a low value of Q, producing a greater disparity in apparent cooperativity below Ca₅₀ compared to above. The effect of unwrapping the ends may provide an additional mechanism to contribute to the breakpoint in Hill plots, but this mechanism will require further study with a Monte Carlo implementation of the model.

Comparison with previous modeling efforts

There is a long history of modeling cooperativity in the myofilament with models ranging from very simple to very complex. Most of these previous studies fall into three main classes. The first class of models are cooperative actin-myosin models that have focused on the cooperativity in the attachment of S1 myosin to native or reconstituted thin filaments. The initial work in this area was by Hill et al. (1980) who laid the framework and methodologies to incorporate nearest-neighbor interactions like those in this study. In these studies, the concentration of S1 myosin heads is varied while monitoring the binding to regulated thin filaments. The S1 binding curves show cooperative behavior that is undoubtedly related to the cooperativity seen in F-pCa relations. However, these are critically different phenomena, and direct comparison of model results is not possible.

Many previously published models fail to reproduce F-pCa relationships that show high apparent cooperativity throughout the whole range from 0 to maximum force. This failure is likely inherent to the model construction in which the cooperative effects are computed using a mean field approximation instead of considering the explicit spatial distribution of states as done in this study. For example, the model here sets transition rates as a function of n, the number of permissive neighbors. Assume instead that n is a function of the mean number of permissive units in the ensemble and is applied to the transition rates of all units. In this case, only the total number of permissive units is considered and not the spatial location of the units on the one-dimensional array. With this mean field approximation, the system can be represented by four states instead of 4²⁶ states, a tremendous reduction. However, the apparent cooperativity is critically altered. Now cooperative interactions are generated as a function of the mean number of permissive units, so local effects are not considered. The net effect is that at low [Ca], the mean number of permissive units is low, so cooperative effects are also low in this regime. As the [Ca] rises near Ca₅₀, the mean number of permissive units changes most rapidly so cooperative effects tend to be strongest here. At the higher [Ca], most all units are already permissive, so cooperative effects are also low in this regime. The net effect is simulated F-pCa relations that show high apparent cooperativity around Ca₅₀, but noticeably reduced cooperativity at high and low [Ca] (see Razumova et al., 2000; Rice et al., 1999).

Other modeling approaches have not used the mean field approximation and have generally met with better success in reproducing F-pCa relations. For example, a Monte Carlo model incorporating end-to-end and other cooperative mechanisms (Zou and Phillips, 1994) can simulate steep F-pCa relations. Hunter et al. (2000) recently reported on a myofilament model based on the work of Hill and co-workers using a statistical weight matrix approach (similar to the Ising model approach given here). The focus of this study was simulating the effect of sarcomere length on Ca sensitivity, an important effect not considered here. The published work most similar to the current study is from Dobrunz et al. (1995) that considered a model with a nearest-neighbor cooperativity very similar to that in Fig. 2. However, instead of using an Ising approach, the simulations were carried out by assuming nine T/T units in a continuously wrapped chain and tracking the occupancy of all 4⁹ possible conformations. Although this approach does reproduce F-pCa relations similar to experimental data, the results did not provide closed form solutions or parameter variation studies. Our preliminary work with this model suggested another potential problem. When recasting the model in the format of Fig. 2, Dobrunz and co-workers has μ set to 1000. Such a large value can inhibit proper relaxation under dynamic simulations such as twitches. Once a T/T unit becomes activated, Ca is tightly bound and is very slow to come off so that relaxation is impaired (unpublished result).

Future Directions

The model presented shows tremendous promise in simulating cooperative myofilament responses although this study is restricted to steady-state responses. Unlike other models, F-pCa relations can be reproduced with a relatively simple formulation based on a biophysical foundation. Continuing in the realm of steady-state responses, additional studies could consider the effects of sarcomere length that are known to strongly affect F-pCa relations by a mechanism that is still unresolved. Such a modeling effort would likely require additional parameters to consider the sarcomere geometry and perhaps explicit cross-bridge dynamics. With such changes, future work could also consider dynamic responses as well. The cooperative mechanisms thought to play a role in steep F-pCa relations are presumably critical for shaping twitch dynamics. As found in previous modeling studies, consideration of dynamic responses may provide important clues to the cooperative mechanisms that shape myofilament responses (Razumova et al., 2000; Rice et al., 1999).