Hydration-Driven Transport of Deformable Lipid Vesicles through Fine Pores and the Skin Barrier

Abstract

We studied aggregate transport through semipermeable, nano-porous barriers experimentally and theoretically. By measuring and modeling the effect of hydration gradient across such barriers, spontaneous transbarrier transport of suitable lipid aggregates in vesicular form was proven to be driven by partial aggregate dehydration at the application site. By generalizing the Onsager transport model we derived a set of equations that rationalize all pertinent observations. Dehydration-induced vesicle motion starts with a lag time. This corresponds to the time needed to reach the limiting vesicle hydration; both are proportional to the starting excess water volume and decrease with increasing relative humidity at application site. The rate of transbarrier transport is insensitive to these parameters but increases with vesicle deformability and volume exchange capability. Both these properties depend on membrane composition. Reversible demixing of bilayer components is the cause of nonlinear bilayer characteristics and also potentially affects the effective membrane hydrophilicity. High hydrophilicity of vesicle surface and extreme aggregate shape adaptability together are necessary for successful material transport across the skin. This demonstrates the significance of basic biophysical investigations for better understanding of biological systems and for the practical use of artificial, nature-inspired carriers in drug delivery.

INTRODUCTION

Mechanical properties of lipid bilayers and their role in nature, especially at the level of cells (Needham and Evans, 1988), have been studied extensively (Lipowsky, 1991). For example, membrane elastomechanics has been found to regulate the filterability of human red blood cells (Tuvia et al., 1992) and cell capping (Gaub, 1989), affect fusion (Cevc and Richardsen, 1999), intercellular trafficking (Jülicher and Lipowsky, 1993), and the stability of lipid vesicle suspensions (Gompper and Goos, 1995; Helfrich, 1973), and to be involved in membrane recognition and protein binding (Cevc, 1995a), etc.

With an eye on applications, high-bilayer deformability was invoked to explain the behavior of lipid vesicles in suspensions (Lipowsky, 1991) or a shearing field (Diat et al., 1993), and inside a pore (Gompper and Kroll, 1995). Suspension stability depends on vesicle elastomechanics as well (Evans and Parsegian, 1986). Bilayer elastomechanics was furthermore concluded to influence the outcome of structural (Safinya et al., 1986) and rheologic (Hoffmann and Ulbricht, 1998) lipid suspension characterizations. More examples could be given.

High membrane elasticity was moreover suggested to be crucial for pushing a vesicle through a pore smaller than the average aggregate diameter (Gompper and Kroll, 1995; Cevc, 1995b). This was argued to be of paramount importance for the success of the noninvasive, carrier-mediated material transport across the skin (Cevc, 1995b, 1996). Indeed, all successful transcutaneous carriers excel through their highly adaptable membrane (Cevc, 1996; Van den Bergh et al., 1999); conventional liposomes (Schreier and Bouwstra, 1994, Zellmer et al., 1995) or mixed lipid micelles (van Kuijk-Meuwissen et al., 1998a,b), which are nearly inelastic, cannot penetrate the skin barrier.

Vesicle responsiveness to external transcutaneous gradients was proposed to be another key to successful carrier-based transdermal drug delivery. This sensitivity arguably increases with aggregation number for a given vesicle (Cevc, 1996). Moreover, vesicles applied on the skin under occlusion (Cevc and Blume, 1992) remain on body surface. Fully hydrated vesicle must be pushed across the skin by strong transbarrier electrical potential (Gebauer, 1998) or pressure (Cevc, 1996). Alternatively, at least partial vesicle drying must be induced (Cevc and Blume, 1992).

Combination of strong vesicle deformability and of transcutaneous nonchemical—e.g., hydration—gradient is thus essential for achieving spontaneous vesicle transport through the skin. This was demonstrated indirectly in recent years in numerous transdermal drug delivery studies (Cevc, 1995b; Cevc et al., 1996; 1998). To provide more direct evidence we now designed and performed a series of dedicated experiments addressing specifically this question. We tackled individually different aspects of hydration-driven aggregate transport through a semipermeable, nano-porous barrier and its independence of aggregate concentration. Specifically, we collected data characterizing the sensitivity of transbarrier flux to: 1) aggregate size and concentration; 2) aggregate bilayer rigidity; and 3) transbarrier hydration gradient. To quantify the results we used a simple phenomenological model, which is briefly introduced in the following section and in greater detail in Appendices. A preliminary version of this model was published in Cevc (1996).

In the first part of theoretical discussion we focus on transbarrier transport phenomenology and explore the role of solvent efflux. The reason for this is that such efflux was repeatedly invoked to discount the importance of hydrotaxis on the skin. Subsequently, we discuss and calculate barrier resistance to transport of different aggregates using experimental data to provide direct evidence for hydration-driven transport across an artificial skin-model barrier as well as the skin.

Modeling transport across a semipermeable barrier

The skin has been optimized through evolution to become an excellent (semipermeable) barrier. This organ is nearly refractory to all but the smallest molecules (Christophers et al., 1989); if it was not, we would die because of poisoning or dehydration. Hydrophilic molecules have especially great difficulty overcoming the skin barrier, whose resistance increases quasiexponentially with oil-water partition coefficient (Potts and Guy, 1992). But even lipophilic molecules, including many drugs, diffuse through the skin only if they are quite small. This is due to the exponentially decaying rate of transcutaneous transport with increasing permeant mass (Potts and Guy, 1992), which reflects an approximately exponential increase in the work needed to insert a molecule into the skin.

Molecular diffusion across the skin is thus improved by the skin permeation enhancers, which support partitioning and/or diffusivity of small molecules into the skin by fluidizing cutaneous lipids (Hadgraft and Guy, 1989). In contrast, the skin lipid fluidization offers little help for the molecules that are heavier than ∼400 Da. The reason is that such substances have great difficulty to find space in intercellular lipid matrix in the skin. Common phospholipids with a molecular mass above 700, consequently, do not cross the skin in significant quantity. Skin permeation enhancers make no practical difference in this respect.

Transcutaneous water transport involves hydrophilic, ∼0.4-nm wide intercellular pores in the skin (Aguiella et al., 1994). Appreciably wider, ∼20-nm large pores are generated in the skin by external electroosmotic pressure (Pikal, 1990) or by the organ-penetrating particles pushed into the skin with high enough force (Cevc, 1996; Schätzlein and Cevc, 1998). We therefore used artificial semipermeable barriers with 20- to 30-nm pores to characterize partially confined aggregate transport.

To interpret quantitatively the various—including nondiffusive—contributions to transcutaneous flux of material, it is necessary to understand, and differentiate, their background.

Transport drivers

Transport is driven by free energy difference between the original x = 0 and destination x = d_s sites. An unequal chemical potential and activity of the transported entity (= transportant) on either barrier side, and the finite resulting transbarrier osmotic pressure difference ΔΠ, are the two best-known consequences of this. In the context of this work, a transportant is typically an aggregate in vesicular form.

Transportant concentration gradient across a barrier is frequently assumed to be the sole origin of transbarrier osmotic pressure or solvent activity difference. In reality, other activity differences may also be important. Contributions from the nonpermeating solutes j or from an extrinsic relative water pressure difference over an open boundary are but two examples. Total osmotic pressure difference, as sensed by transportant m, is thus written as

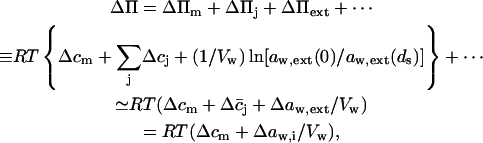(1)

where c and a values give concentrations and activities, respectively. Overline indicates an average value. More detailed explanation, derivations, and definitions are given in Appendices A and C.

Effects of aggregation on transport drivers

Let us assume that all n_a molecules in an aggregate respond to an external gradient as if they were dissolved. Limiting aggregate solubility, c_limit(n_a), then decreases with aggregation number: c_limit(n_a) ≤ c_limit(1)/n_a. Transportant-dependent osmotic pressure difference changes in parallel.

Aggregate sensitivity to an external activity gradient follows the opposite trend. For example, a transportant partly dehydrates if water activity around a transportant is diminished. In contrast, when this water activity increases, transportant-water association becomes more favorable and transportant may bind more water. (Exceptions are the situations in which a transportant has already reached its solubility limit, owing to interaggregate interactions, e.g., due to Van der Waals attraction.)

Total change in the osmotic pressure sensed by an aggregate with diameter r_v consisting of n_a molecules is given by:

(2)

This explains why relatively large aggregates have greater potential to cross semipermeable barriers than smaller entities under the influence of transportant-independent gradient, such as osmotic pressure. The proviso is that the resulting free energy change exceeds the activation energy for aggregate motion across a barrier (see Discussion).

Barrier resistance and transport activation energy

Barrier resistance grows exponentially with transport activation energy. This energy typically increases with transportant size or aggregation number, in the latter case with some power of n_a. The resulting negative effect of transportant size or aggregation number increase on barrier resistance must be compensated by raising driving pressure, if transport is to continue. Minimization, or even reversal, of such resistance is a key to success. To achieve such a goal, one must understand transportant motion through, and aggregate adaptation to, a pore—and vice versa.

Activation energy for molecular insertion into a barrier increases logarithmically with the inversed partition coefficient of an inserted molecule m:

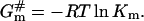(3)

Energetic cost of forcing a vesicle into a narrow pore, in the simplest approximation, is related to the ease of elastic membrane deformation. To calculate the work of such deformation, one can use the classical Helfrich model (Helfrich, 1973). Free energy change associated with a vesicle entering a pore is then found to be proportional to the change in relative surface area of a vesicle and to vesicle membrane elasticity modulus k_c (Cevc, 1995b). More precise bilayer elasticity description suggests a different power but gives a qualitatively similar picture (Gompper and Goos, 1995).

A vesicle unable to adjust rapidly to the changes resulting from aggregate shape transformations must break, at least locally and temporarily. The main reasons for this are variability in inner-to-outer bilayer area ratio or in vesicle volume. The work needed for such change is proportional to the square of bilayer breaking (poration) tension divided by an effective lateral bilayer compressibility modulus and by surface density of molecules; the latter is given by the inverse value of molecular area (Needham and Evans, 1988). As such area is only a little sensitive to a changing aggregation number/vesicle size ratio, the ease of membrane poration is mainly governed by the pertinent tension-to-modulus ratio.

To describe pore penetration by an ultraadaptable vesicle, the low membrane elasticity modulus k_c (Leibler, 1986) and the low bilayer breaking tension γ_break (G. Cevc, D. Gebauer, A. Schätzlein, and U. Vierl, unpublished results) of such a vesicle must be allowed for. This is due to the role that these parameters together play in determining the effective aggregate shape adaptability.

A convenient approach is to introduce into theoretical models composition- and stress-dependent relative membrane rigidity and membrane tension functions, 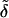and δ, respectively. These functions then scale the energy of a complex bilayer relative to the corresponding conservative elastic and breaking energy of a simple membrane. In the first approximation this yields:

(4)

Better, but also more complex, approximations are described in Gompper and Goos (1995). For r_pore/r_v ≤ 1, the elastic term normally prevails. Membrane-breaking energy may become dominant. Phosphatidylcholine vesicles with 100-nm diameter thus switch between the two regimes when pore size is ∼100 nm. For ultraadjustable mixed lipid vesicles with a similar -and δ -value, the situation is not much different.

Molar free energy of noninteracting water-binding aggregates depends on ambient water activity. If water activity on both barrier sides is different, to the effect of causing at least partial aggregate de- or rehydration on one barrier side, the difference will cause aggregate motion through a barrier. The underlying hydration free energy change that drives such motion is proportional to maximum hydration free energy and to water activity difference:

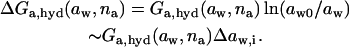Most ultraadaptable bilayers have arguably soft and relatively thick interfaces. (De)-Hydration free energy of an individual aggregate with such properties is given approximately by

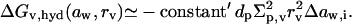(5)

as is explained in Appendix B. Hydration energy of a vesicle (a ≡ v) thus increases with aggregate surface area, interfacial thickness or softness, and hydrophilicity. These aggregate properties are described here through parameters r_v, d_p, and respectively.

Physical meaning of Eq. 4 is the following. Low relative rigidity of a bilayer allows energetically inexpensive elastic membrane deformation. Likewise, a small δ-value implies that lipid bilayer is easily permeabilized and relaxed by poration. Membranes with the right composition therefore adapt extremely well to/under stress, as then δ → 0. The process typically involves dynamic and reversible local adaptation of bilayer composition to local stress and/or shape changes (Cevc, 1995b). Partial bilayer component demixing, leading to the accumulation of the membrane softening surfactant and the sites with extreme local surface curvature, is one manifestation of this. Molecular or segmental motion perpendicular to bilayer surface furthermore increases interfacial thickness and effective hydrophilicity. Both have positive consequences on spontaneous transbarrier aggregate motion.

Specifically, use of differently soluble components in an aggregate tends to favor three-dimensional, aggregate-confined, molecular de/mixing in a bilayer; the proviso is that the solubility of at least one ingredient is relatively high. Using corresponding molecular mixtures therefore typically lowers the value of parameters 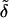and δ. In parallel, values of parameters d_p and Σ_p,v are raised. The likelihood for hydration-driven vesicle motion through a barrier then gets higher, as is explained in the following sections.

Fluxes through a barrier

Generally, transportant flux across a semipermeable barrier comprises several contributions. Each is proportional to a transbarrier chemical potential difference. For brevity, we limit our analysis to the situations in which one transportant-dependent (index m), one solvent- or water-dependent (index w), and one transportant-independent (index i) chemical potential difference (μ) plays a significant role; external hydrostatic pressure difference (p) may participate as well. This yields expressions given in Appendix A. Direct proportionality and cross-correlation factors (𝒫) in these expressions describe direct and indirect system sensitivity to said gradients, respectively.

It is reasonable to combine all transportant-independent activity changes into a single extrinsic water activity gradient (index ext). This acts on a system in thermodynamic equilibrium. The sum of products of all average concentrations and of corresponding chemical potential differences is then zero.

Water flux across a barrier with total area of pores A_pores given by the product of pore density and a single pore surface can be expressed as a function of transbarrier pressure differences p and Π, of barrier refractivity coefficient σ_m, and of different permeability constants 𝒫:

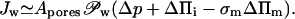(6)

Simultaneous transportant flux is given by

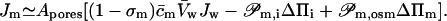(7)

All necessary definitions are given in Appendix D. Eqs. 6 and 7 suggest that the transportant-independent osmotic pressure difference plays a similar role in transbarrier transport as an external hydrostatic pressure difference.

Eqs. 6 and 7 together highlight the meaning of refractivity coefficient. This parameter measures osmotic activity of a given component on a barrier. When a barrier is totally impermeable to m, σ_m = 1; maximum possible water flux then flows through a barrier, driven by the osmotic pressure difference caused by an uneven distribution of component m. Water flux persists until concentration of m on either barrier side is equal and the corresponding osmotic pressure difference vanishes. Conversely, for a perfectly permeable barrier, σ_m = 0. Easy transportant motion through such barrier then leaves no need for the transbarrier water flow that otherwise would be induced by the transportant-dependent osmotic pressure difference.

The influence of m-independent contributions on transportant motion across a barrier depends on the sign of originating gradient(s). In one extreme case, when refractivity coefficient is unity, the transportant rich compartment is diluted by solvent flux as long as Δa_w,i < Δc_mV_m. For Δa_w,i > Δc_mV_m, however, the transportant concentration on either barrier side does not equalize. This is due to prevalence of the m-independent osmotic pressure over conventional osmotic pressure. In another limiting case, when a barrier is perfectly permeable to m, reaching certain Δa_w,i value reverses transportant flow direction. In a different range of water activity values, Δa_w,i increases transportant flux beyond the maximum value that would be driven by transbarrier transportant concentration difference alone.

Barrier permeation by a molecule

The permeability of a pore to substance m in the simplest approximation decreases exponentially with activation energy and is proportional to the effective permeant mobility/diffusivity and to partition coefficient. Pore length diminishes permeability value,

(8)

as is easily deduced from Eq. 3.

Barrier penetration by an aggregate

Barrier penetrability is governed more by the physical and elastomechanical than by the chemical properties of a transported entity. Activation energy for an aggregate crossing a fixed-size pore is thus identical to the free energy of penetrant deformation, giving for penetrability,

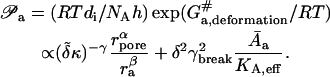(9)

The former, general expression in Eq. 9 stems directly from Eyring's theory. The more specific and linearized equation invokes also Eq. 4 and assumes that aggregate deformation energy is much smaller than thermal energy. Empirical exponents α, β, and γ have positive values of the order of 1 (Gompper and Kroll, 1995).

Transport criteria

Molecules permeate through a semipermeable barrier when the resulting molar free energy gain exceeds the work of permeant partitioning into a pore,

(10)

concluding from Eqs. 7 and 8. Barrier permeation therefore becomes easier with growing transbarrier osmotic pressure difference and/or with greater intrabarrier partition coefficient.

Aggregates penetrate a porous barrier when energetic gain is greater than energetic cost of pore and/or aggregate deformation during barrier crossing. In case of hydration-driven transport, the former energy is identical to aggregate de/hydration energy. The latter contribution is given by Eq. 4 and indirectly by Eq. 9. This means that:

We can use Eq. 19 from Appendix B to calculate vesicle hydration free energy and then limit our consideration to small water activity changes. After truncation and collection of all vesicle-related parameters on the left side, and all barrier and other parameters on the right side of equation, we then get:

(11)

The above rough criterion can be used to decide when an aggregate vesicle will cross a nano-porous barrier driven by hydration. Representative Σ_p,v values for different phospholipids and the value for constant′ of pure water can be found in Cevc and Marsh (1987).

The propensity for barrier penetration first increases linearly and then logarithmically with transbarrier water activity difference, according to Eq. 11. Enlarging pore diameter, raised to a low power, has the same effect. Pore penetration probability simultaneously grows with the thickness and, even more strongly, the hydrophilicity of vesicle surface. On the other hand, increasing bilayer deformation energy and, potentially less strongly, vesicle size decreases this likelihood.

Solvent counterflow versus barrier penetration

Variable vesicle sensitivity to a fixed transbarrier gradient partly compensates, and sometimes overcompensates, increasing transport resistance with aggregate growth. An appropriately generalized form of Eq. 7, with only the leading terms included, then becomes

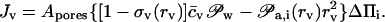(12)

(Unilamellar) Vesicle size dependency is included implicitly into reflectivity and permeability parameters.

Eq. 12 reveals that transportant flow is controlled by permeant- or penetrant-independent osmotic pressure difference, in the absence of other free energy contributions. Flow direction, consequently, can be deduced by considering relative magnitude of ratio of both right-side terms in Eq. 12:

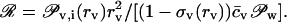When this ratio attains the value of 1, the net flow is zero; for smaller values, solvent counterflow prevails. Solvent counterflow becomes progressively unimportant when the ratio gradually exceeds the value of 1.

Negligibly small vesicle concentration difference across a barrier makes calculation of flux from Eqs. 9 and 12 particularly simple:

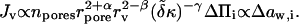(13)

Solvent flow thus plays no role as long as water activity gradient across a barrier is approximately constant: the gradient-maintaining water loss into surrounding areas in such a situation completely neutralizes water efflux across a barrier. Aggregate transport across the skin or other tight biological barriers provides an example for this. We practically checked the conclusion, and compared the result with model predictions, in a series of dedicated experiments described in the following sections.

MATERIALS AND METHODS

All solvents, buffering salts, and fluorescent labels were of analytic quality. They were purchased from Merck or Sigma (both Germany) or Molecular Probes (Eugene, OR), respectively. Depending on experimental design, 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-fluoresceine (DPPE-Fl) or diphenylhexatriene (DPH) was used.

Preparation of liposomes

Liposomes consisted of soybean phosphatidylcholine (SPC, purity >95%) and were prepared with conventional methods. In brief, an organic solution of the required lipid amount, including label, was first dried under vacuum (10 Pa) over night. The resulting lipid film was then hydrated with triethanolamine-HCl buffer (pH = 6.5, 10 mM) to prepare a 10% lipid suspension. The suspension was finally sonicated for 60 min at 4°C to obtain vesicles with desired radius. The latter was measured by photon correlation spectroscopy.

Preparation of ultraadaptable vesicles (Transfersomes^®, a trademark of IDEA AG, Munich, Germany)

In short, ultraadaptable lipid aggregates were prepared by mixing an ethanolic SPC solution with the appropriate amount of sodium cholate. This corresponded to between 1 w−% and 13 rel. w−% cholate, relative to the used phospholipid mass. The resulting lipid mixture was subsequently combined with triethanolamine-HCl buffer to yield 10 w−% total lipid concentration and pH = 7.2, which is near the apparent pK of cholate. To prepare uncharged ultraadaptable vesicles, SPC was mixed directly with the non-ionic polysorbate surfactant in buffer (pH = 6.5). The resulting suspension in either case was extruded sequentially through a series of track-etched polycarbonate filters with decreasing pore size (200 nm, 100 nm, 50 nm), to reach the final vesicle size below 70 nm, which ensures vesicle unilamellarity. The suspension was then frozen and thawed (2⋯3×) to fuse vesicles and obtain vesicle sizes greater than 500 nm. Finally, the average vesicle size was brought to specification by repeated extrusions through suitable polycarbonate filters, with the average pore size commensurate to desired final vesicle size. The final vesicle size was also confirmed to comply with the selected size by photon correlation spectroscopy. Such preparation method minimized the danger of suspension contamination with oligolamellar vesicles, which are normally present when vesicles are fractured from multilamellar vesicle suspension.

To prepare vesicles of different shape adaptability, relative concentration of the surfactant, which acts as membrane softening and destabilizing agent (cholate or polysorbate), was varied. Membrane flexibility, which is the inverse of membrane rigidity, was also checked directly by measuring the deformation of unilamellar vesicles near an adhesive lipid monolayer at the air-water interface with ellipsometry (Cevc et al., unpublished results).

Vesicle size determination

The dynamic light scattering on vesicle suspension was measured in triplicate with a Zetasizer 2C instrument (Malvern Instruments, Malvern, UK) or with an ALV (Langen, Germany) device equipped with multi-tau 5000 correlator. Cumulant and Contin analysis was used to calculate the average vesicle radius and standard deviation of the mean, always before and often after the passage through a barrier.

Penetration across an artificial barrier (the skin surrogate)

This was determined in two types of laboratory-built devices. In both, vesicle suspension was driven through a large number of pores of known size in the polymeric microporous filter. Pore diameter was chosen to be between 20 nm and 400 nm, dependent on the size of test vesicles.

In first kind of measuring device, used chiefly to assess the degree of vesicle fragmentation during barrier crossing, hydrostatic external pressure was used to push vesicle suspension through narrow pores. Transbarrier pressure difference was varied between 1 hPa and 1 MPa, as required. In a second kind of instrument, a defined hydration gradient corresponding to pressure difference between approx. 10³ MPa and 0.1 MPa was created across a barrier. This was achieved by changing relative humidity above donor compartment between RH = 20% and ∼100%. The receiver fluid was an aqueous solution with RH → 100%.

Transbarrier flux of fluorescently labeled vesicles in either case was measured as a function of time. The integrity and practically unchanged size of lipid aggregates was confirmed by the dynamic light scattering. Relative penetration capability was calculated from the standard hydrostatic-flow expression 𝒫_Tfs = j/Δp, using water permeability data (Permeation = 𝒫_Tfs/𝒫_water × 100%) to calibrate the results of the first kind of measurement. When hydration pressure was used, the values were not normalized.

HPLC was sometimes done before and after experiments to control the degree of filtration.

Penetration through the skin

This was assessed by measuring the appearance of rhodamine label, covalently attached to DPPE molecules in vesicle bilayers, in the receiver fluid of a Franz cell. The latter contained ∼250-μm-thick human skin preparation, not older than 24 h, and was kept at physiological skin surface temperature (32°C). Label, and thus vesicle, concentration in the receiver fluid was calculated from the fluorescence intensity data measured in real-time with a Perkin-Elmer LS5 spectrometer. Ultradeformable vesicle flux was first determined relative to the values measured with conventional phosphatidylcholine liposomes over a long period of time. In later experiments, absolute flux values were derived using fluorescence intensity versus labeled vesicle concentration calibration curve for the purpose.

The preservation of vesicles in the suspension on the skin during transport was checked by electron microscopy and by lateral electric conductivity measurements. The latter also provided approximate value for the limiting hydration of the most frequently used ultradeformable vesicles on the skin, c_w,min ∼40%. Although this value is rather low it is compatible with a tight packing of deformed, but reasonably hydrated vesicles.

RESULTS

The focus of our work was on hydration-driven transport. We therefore first determined the amount of water bound to different vesicle membranes using gravimetric method. Subsequently, we measured the transbarrier flow of corresponding vesicles as a function of lipid bilayer composition, membrane elasticity, and tension strength. We also studied the effects of changing pressure difference across a barrier, relative vesicle size, and suspension concentration.

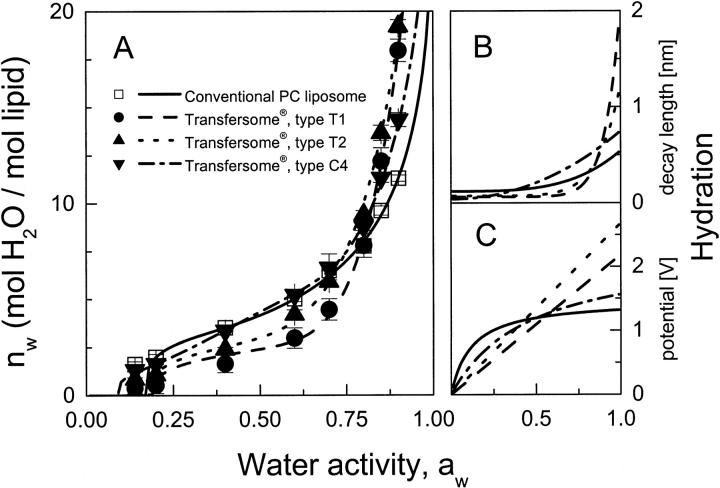
Fig. 1 illustrates the results of water adsorption experiments and thus highlights effective hydrophilicity of various lipid membranes. Simple phosphatidylcholine bilayers, in the low water activity range, are as attractive for water as one of the tested mixed lipid bilayers. The other two types of mixed bilayer, which contain a nonionic membrane softening agent, for a_w ≤ 0.6, are less hydrophilic. The situation changes for a_w ≥ 0.8. In this water activity range, all the tested mixed lipid bilayers bind more water than phosphatidylcholine, in some cases up to ∼100%.

FIGURE 1.

Water adsorption isotherms of phosphatidylcholine (multi)bilayers and of highly flexible mixed lipid membranes consisting of SPC and sodium cholate at room temperature (A). Effective hydration decay length (B) and surface hydration potential (C) as a function of water activity in the system.

Limiting hydration of the tested mixed lipid vesicles on the skin under nonocclusive conditions is around 40 w−%. Under such conditions, relative molar concentration of water on the skin surface is estimated to be near 30/1, the precise value depending on individual vesicle suspension. This corresponds to rather tight vesicle packing but is not incompatible with persistence of the highly deformed unilamellar vesicles.

The nonlocal electrostatic model of hydration, described in Appendix B, sheds some light on the phenomenon of enhanced water uptake by soft membranes. Quantitative adsorption isotherm analysis done within the framework of such a model (Fig. 1, B and C) implies that the softening of lipid bilayers goes in parallel with bilayer-water interface softening, which supports solvent binding. The increase in effective hydration decay length indicated in Fig. 1 B for the mixed lipid bilayers in comparison with pure phosphatidylcholine indicates this. Fig. 1 C illustrates the concurrent change in surface hydration potential of different tested lipid bilayers, which reflects increasing exposure of polar lipid headgroups in the interfacial region with increasing bilayer hydration. Similar observations were made in previous studies (Cevc and Marsh, 1987; Cevc, 1995a; Cevc et al., 1995).

The available data do not allow precise quantification of the effect, owing to the difficulty of getting accurate results in the range of high water activity (Rand and Parsegian, 1989). They leave no doubt, however, that membrane softening agents tend to increase bilayer propensity to bind water.

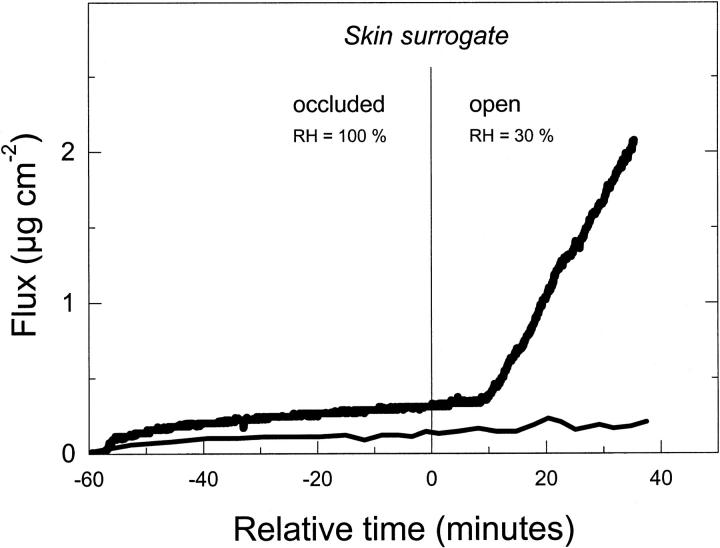
Fig. 2 illustrates typical flow measurement results. Under occlusion, no significant transport across a barrier is observed with any of test formulations. This is strictly true for the period t > 20 min, at which time the mixed lipid micelles and other relatively small aggregates labeled with DPH have already diffused across a barrier; consequently, the early transbarrier flux for a suspension of highly deformable vesicles containing surfactants is ∼2× higher than that measured with liposomes. After elimination of occlusion at t = 60 min the flux of liposomes is similarly low for t ≥ 60 min. In contrast, the ultraadaptable mixed lipid vesicles then begin to move through a barrier in significant quantity ∼10 min after hydration gradient establishment. The measured label in ultraadaptable vesicle flux corresponds to ∼3 μg lipid h⁻¹ cm⁻² barrier (or ∼8 g lipid h⁻¹ per square centimeter of pore surface) and persists for at least 60 min.

FIGURE 2.

Temporal dependence of vesicle transport across a nano-porous membrane (r_pore = 30 nm) as a function of transbarrier water activity gradient (occlusion versus nonocclusion).

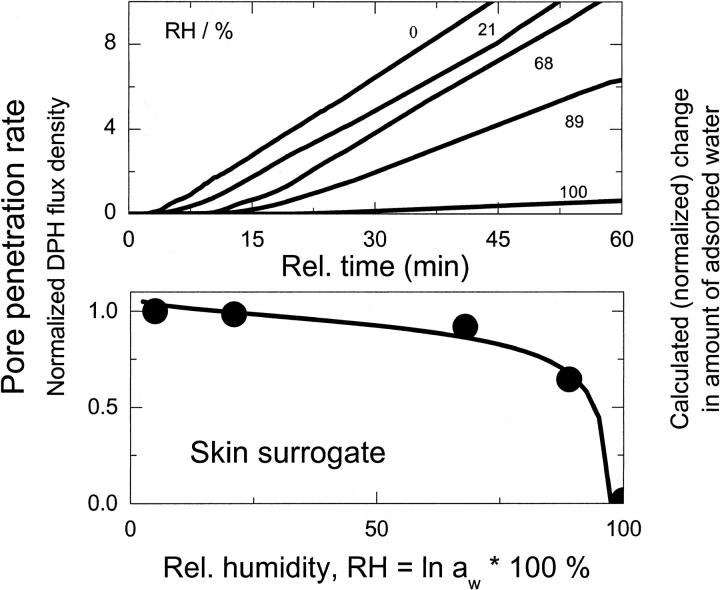
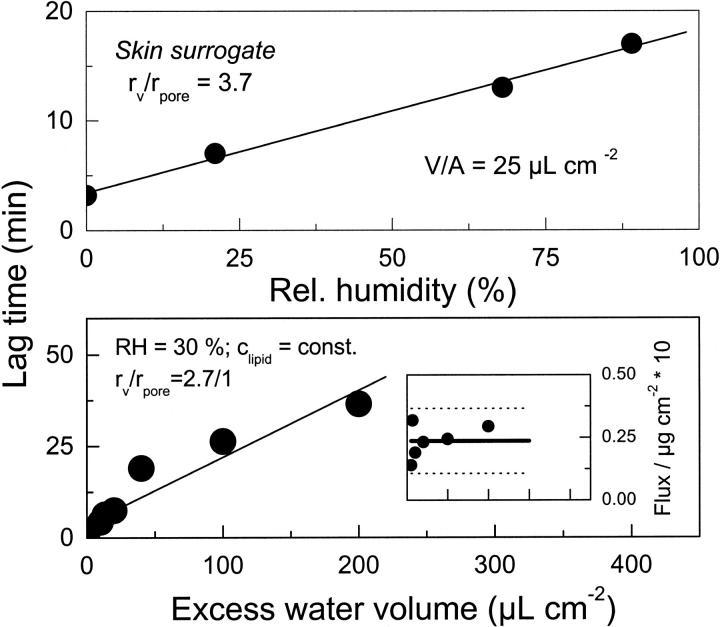
The measured flux of ultraadaptable vesicles changes with transbarrier humidity, that is, with osmotic pressure difference. Increasing water activity gradient across a barrier always promotes transbarrier motion of ultraadaptable vesicles. We studied the dependency by varying relative humidity in donor compartment while keeping water activity in receiver compartment constant. The results are shown in Fig. 3. Original measured data are given in upper panel. The derived transbarrier flux density is shown in lower panel as bullets. Increasing water activity at donor side diminishes transbarrier water activity gradient. This is seen first to diminish transbarrier flux very rapidly and then more gradually (lower panel, Fig. 3), as one would expect on the basis of water adsorption model (curve). The original data also reveal that increasing water activity at donor side prolongs the lag time between suspension application and onset of vesicle flow through a barrier.

FIGURE 3.

Effect of transbarrier water humidity or activity gradient on transport of highly deformable vesicles across a barrier with narrow pores (r_v/r_pore = 2.7). Upper panel gives the flux as a function of time; lower panel provides the corresponding barrier penetrability values (flux derivative, bullets) and water adsorption isotherm for a comparable lipid membrane (curve).

Changing applied water volume while keeping applied lipid amount constant has a similar effect: greater volume prolongs the lag time for transport onset, as is obvious from Fig. 4 (upper panel), and from Fig. 5. Such change does not influence significantly the average flux across a barrier, however (Fig. 4, lower panel; and Fig. 5, lower panel, inset).

FIGURE 4.

Effect of changing excess water volume on the flux of ultraadaptable vesicles across a barrier with small pores (r_v/r_pore = 2.7) as a function of time. Dashed lines give 95% confidence limit.

FIGURE 5.

Lag time for penetration of ultraadaptable mixed lipid vesicles across a nano-porous barrier as a function of water activity gradient (upper panel; derived from Fig. 3) or of excess water volume in donor compartment (lower panel). Inset illustrates the insensitivity of flux for the latter data set and is derived from Fig. 4. Lines are results of linear fits to the data; dashed lines give 95% confidence limits.

More quantitative analysis of lag-time sensitivity suggests that relative vesicle size may be important, but much less so than applied water volume (Fig. 5, lower panel) or relative humidity on donor side (Fig. 5, upper panel). Good correlation (R = 0.99) between experimental data (bullets) and results of linear approximation (line) suggests that the delayed onset of vesicle transport is controlled by the time required to dry excess water at donor site. The conclusion is substantiated by proportionality between the excess water volume and the lag time for transbarrier transport, shown in Fig. 5 (lower panel; R = 0.95).

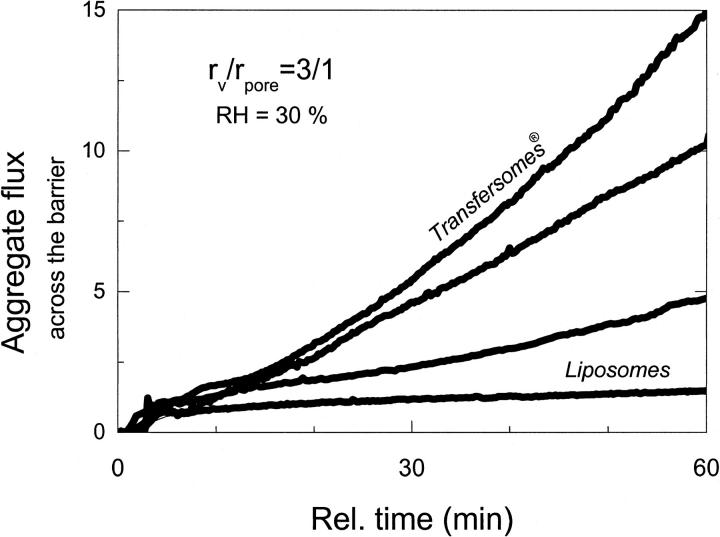
Figs. 6 and 7 illustrate effects of vesicle bilayer rigidity on vesicle suspension flux across a barrier. The former picture gives an impression about the test suspension flux changes with time after elimination of occlusion. The latter figure quantitates the dependency and also provides information on vesicle size effects.

FIGURE 6.

Control of transbarrier flux by changing vesicle shape adaptability by changing the composition of mixed lipid bilayers, under conditions of constant relative penetrant size (r_v/r_pore = 3) and transbarrier water activity gradient (RH = 30%).

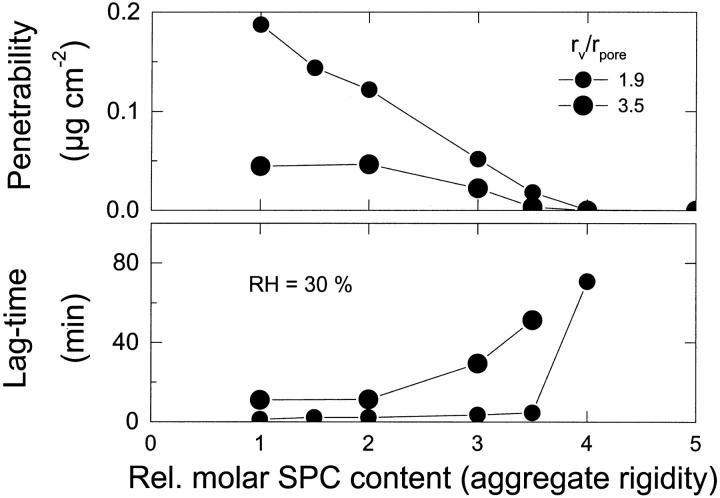
FIGURE 7.

Effect of vesicle size and adaptability, changed by varying lipid bilayer composition, on the penetrability of a barrier to large vesicles (upper panel) or on lag time for transbarrier transport (lower panel), measured at 30% relative humidity.

Data scrutiny reveals a strongly nonlinear functional dependence (Fig. 7). This is indicative of unusual rheological behavior of the system, which resembles non-Newtonian flux versus pressure dependence reported for highly deformable vesicles in Cevc et al. (1998). In either case, the observed suspension flux characteristics reflect changes in bilayer properties; most importantly, variations in bilayer rigidity. Ellipsometric measurements reveal that the mixed phosphatidylcholine/surfactant bilayer rigidity is always lower than that of pure phosphatidylcholine bilayers, by up to a factor of 10 in the tested composition range. More specifically, we found bilayer rigidity to decrease nonlinearly, in a concave fashion, with decreasing relative phosphatidylcholine concentration in the bilayer. This resembles qualitatively the features seen in Fig. 7.

In other words, relatively rigid vesicles, with a low relative surfactant concentration, cannot traverse a semipermeable barrier in significant quantity; in contrast, vesicles with the right relative concentration of membrane softening agent overcome the barrier with ease (compare to Fig. 7). To emphasize this dependency, the data in Figs. 7 and 8 are given in composition, rather than in the less well-defined rigidity, terms.

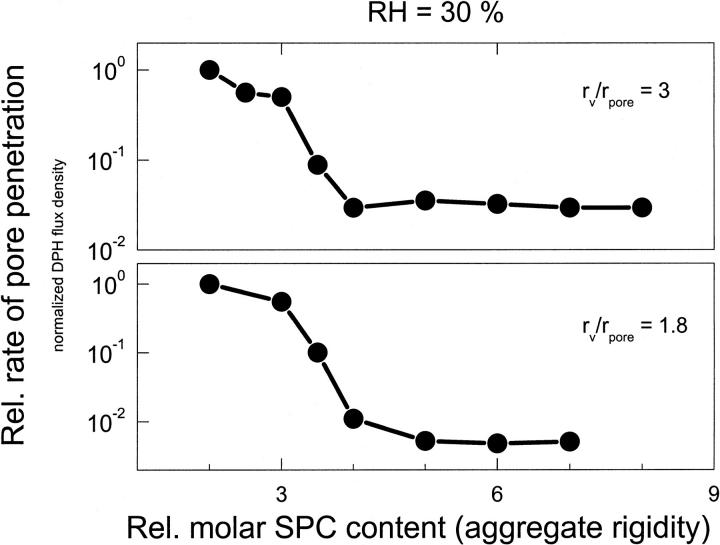
FIGURE 8.

Effect of vesicle adaptability, varied by changing bilayer composition, on the normalized transport of relatively large (r_v/r_pore = 3; upper panel) and small (r_v/r_pore = 1.8; lower panel) vesicles across a barrier with 30-nm pores, measured at 30% relative humidity. (Values in horizontal range are not significantly different from the lower detection limit.)

The situation is less clear for the vesicles with relatively low ratio r_v/r_pore = 1.9, indicating the limit of test validity. (The probable reason is partial overlap of vesicle and pore size distributions, which is greater for the more deformable vesicles with strongly fluctuating shape and effective size.)

Relatively large mixed lipid vesicles cross a semipermeable barrier with approximately constant and high efficacy. The proviso is that vesicle bilayer flexibility (i.e., inverse rigidity) and poration ability are both high. They must be high enough to make the aggregate sufficiently adaptable. The transport lag time for small aggregates is less sensitive to the vesicle shape adaptability, but this is not generally the case (compare to Fig. 7, lower panel).

When a mixed-lipid membrane rigidity increases above a certain limit, the observed lag time gets rapidly longer and pore penetration ability (penetrability) of vesicles is essentially zero. We previously argued that this happens when the elastic bilayer energy significantly exceeds thermal energy. To confirm the phenomenon we repeated experiments over a wider range of vesicle rigidities using two slightly different aggregate sizes. The results are given in Fig. 8 and corroborate the statement. The data also reveal some vesicle size dependence: not unreasonably, relatively small aggregates cross the barrier even when they are more rigid, arguably as long as the work of deformation for small and large aggregates is comparably low.

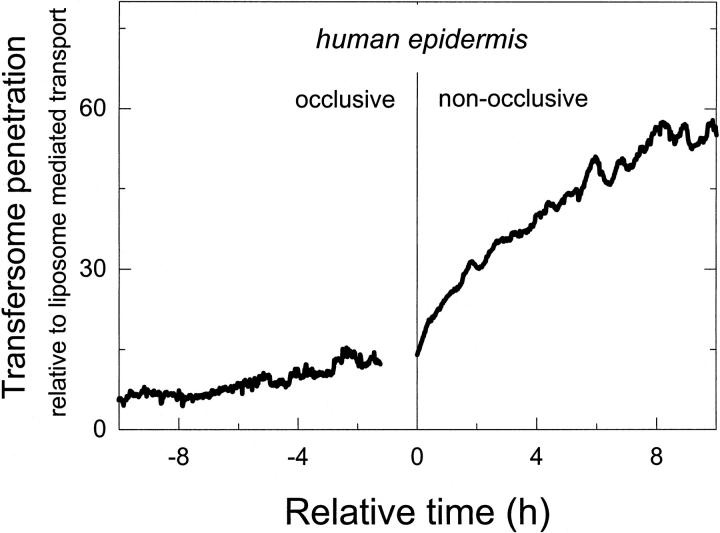
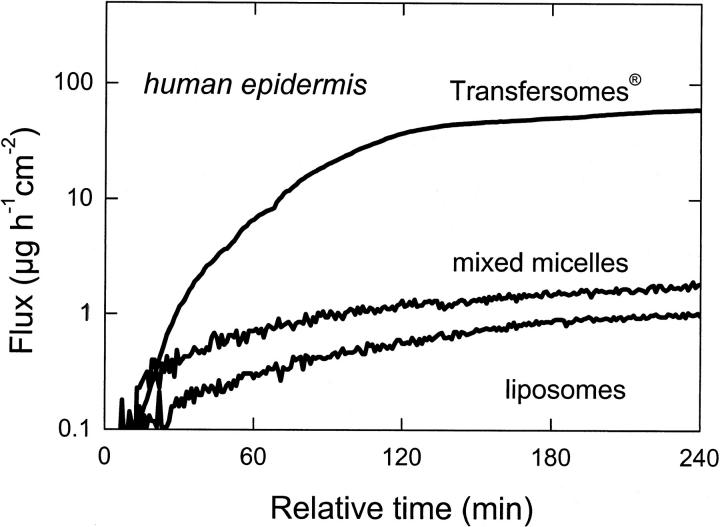
We measured qualitatively similar transport data for artificial membranes and the skin (compare to Fig. 9): vesicle transport under occlusive conditions was much less efficient than on open skin, with a naturally occurring transcutaneous water activity gradient (Warner et al., 1988). On the other hand, the flux of highly deformable vesicles across the skin was much higher than for conventional, more rigid lipid vesicles or for the mixed-lipid micelles (compare to Fig. 10). This indicates that transport across surrogate and mammalian skin obeys similar rules. The theory outlined in this work is thus applicable in either case.

FIGURE 9.

Vesicle-mediated transport of fluorescent label DPH across intact, excised skin as a function of time, driven by transcutaneous water activity gradient.

FIGURE 10.

Transport of various lipid aggregates across nonoccluded human skin.

DISCUSSION

Spontaneous transport of certain lipid aggregates across a semipermeable barrier in contact with air is of great practical value. For example, such transport is useful for staining the skin for the high-resolution microscopic investigations and for drug delivery into human body (Schätzlein and Cevc, 1998). We previously hypothesized that a combination of high membrane elasticity and hydrophilicity with a naturally occurring transbarrier water activity gradient is responsible for this. Here we provide extensive experimental evidence for the claim, obtained with an artificial semipermeable barrier, and put data into the framework of a phenomenological theoretical model that is useful for further system optimization.

Representative flux data measured with a semipermeable barrier with 30-nm pores are illustrated in Fig. 2. They reveal size exclusion similar to that described for the skin. The 30-nm pores in such a skin surrogate model are larger than the size of individual molecules and smaller than typical heteromolecular aggregates. The pores therefore permit transbarrier diffusion of individual small entities under occlusion. The diffusive transport of small fluorescent entities through the skin model rapidly comes to a standstill, however. In our test system, this happens after ∼20 min, when the pool of dissolved molecules and of small molecular aggregates at donor side is exhausted. The kinetics of the process is approximately exponential, as one would expect on the basis of the time-dependent version of Eq. 7.

Transbarrier transport is insignificant after the cessation of molecular diffusion, when only aggregates with r_a > r_pore are left on an occluded barrier. This means that σ_a = 1 (compare to Eq. 7). Accordingly, and in agreement with Eqs. 7 and 18, aggregates should stand a much poorer chance to cross the skin than individual molecules. The reason for this is that untreated skin with contains even narrower pores than the skin surrogate with 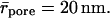Several groups have nevertheless tested lipid aggregates of various kinds (liposomes, see Mezei, 1988 and Weiner et al., 1989; niosomes, Hofland et al., 1995 and Schreier and Bouwstra, 1994; micelles, van Kuijk-Meuwissen et al., 1998a,b; and Transfersomes^®, Cevc, 1996; Cevc et al., 1998) on the skin. Epicutaneously applied labels and drugs in such aggregates were found typically on and in the organ (Zellmer et al., 1995; Van den Bergh et al., 1999). The calculated efficiency of delivery was typically found to be below 0.5%. This is close to total area of shunts in the skin, such as hair follicles and imperfect junctions between corneocyte clusters. Several authors therefore concluded—in agreement with implications of Eq. 7—that transfollicular and transshunt transport is mainly responsible for conventional lipid aggregate transport into the skin (Lieb et al., 1992; Cevc, 1996). This explains why conventional aggregates rarely, if ever, cross intercellular junctions in the skin (Bouwstra et al., 2001).

Eqs. 15 and 16 imply that a change of osmotic pressure/water activity on one barrier side should increase transbarrier water, as well as transportant, flux. Figs. 2–5, and 10, confirm that aggregate transport rate indeed decreases with diminishing transbarrier water activity gradient. Transport rate falls to zero for 100% relative humidity at the donor side, that is, for a_w = 0. (The curve in Fig. 3 is calculated from the water adsorption isotherm given in Fig. 1 and confirms the proportionality between transport rate and penetrant dis/ability to attract or keep water.)

Concluding from Eq. 11, the unbound water concentration at the site of aggregate application must fall below 1 − c_w,min if penetrant transport across a semipermeable barrier is to commence. Changing total lipid concentration in the range c > 1 − c_w,min consequently does not affect lipid aggregate transport across a semipermeable barrier. Data given in Fig. 4 confirm the prediction. The same results also corroborate the assumption that transbarrier lipid diffusion from a suspension of relatively large lipid aggregates is negligibly small.

The lag time for vesicle transport through a barrier is experimentally found to be relatively insensitive to aggregate composition. This is in agreement with Eq. 12 (see Fig. 8). The constancy of penetrant flux therefore mirrors a linear relationship between J_m ≡ J_a ≡ J_vesicle and Δa_w,i. The linear relationship between this lag time and the applied excess water volume is in line with the second term in Eq. 12.

According to Eq. 9, the penetrability of a barrier to an aggregate should change with penetrant deformability. Fig. 6 confirms this to be the case. Figs. 6 and 7 together, furthermore, suggest that 𝒫_aggregate,w is not a simple function of aggregate composition. Rather than this, 𝒫_aggregate,w value depends on subtle interplay between system ingredients.

Also according to Eq. 9, aggregate transport should be sensitive to penetrant and pore size mismatch. Experimental evidence for this is given, e.g., in Cevc et al. (unpublished results). The data reveal that larger ultraadaptable vesicles have greater difficulty in crossing a “confining pore” than smaller aggregates. The dependency is relatively weak, however. The observed effect is chiefly caused by the friction in a pore, which is approximately proportional to the deformed aggregate length. In contrast, vesicles with a conventional, less deformable membrane exhibit a strongly nonlinear size dependency and a cutoff at r_v > 1.5r_pore (see Cevc et al., unpublished results).

Intercellular spaces in the skin are filled by lipids that are mainly in a crystalline phase. The residual “free space” is so sparse that even water molecules only manage to cross the skin at the rate of 400 μg cm⁻² h⁻¹ (Potts and Francoeur, 1990). Larger molecules pass the skin at an even smaller, often practically negligible, rate (Potts and Guy, 1992).

Hydration free energy of all hydrophilic surfaces is negative. In thermodynamic equilibrium this energy is minimum: G_a,hyd0(a_w) ≤ 0. Free energy difference caused by a partial surface dehydration ΔG_a,hyd(a_w) is therefore always positive. This is the reason why hydrophilic aggregates applied on a semipermeable barrier separating two compartments with different water content sometimes migrate through the barrier spontaneously. In so doing they seek to attain sufficient, or maximum, hydration. The resulting spontaneous transbarrier aggregate motion increases with transportant surface hydrophilicity, as one would expect on the basis of Eqs. 11 and 9.

For commonly used phospholipids, such as phosphatidylcholine, ΔG_a,hyd0(a_w) ≤ 60 RT, or some 30 kJ/mole or less (Cevc and Marsh, 1987). Owing to the strong spatial variability of bilayer free energy, this translates into very large (de)hydration pressures reaching 10³ MPa upon (nearly) complete lipid dehydration (Rand and Parsegian, 1989). Lipid headgroup and bilayer flexibility increases the value because of the fluctuation-enhanced water uptake and the extra repulsion between lipid bilayers (Cevc et al., 1995). The relatively steep and high water adsorption isotherms of ultraflexible mixed lipid bilayers, compared with the fluid phosphatidylcholine bilayers (compare to Fig. 1), are in agreement with the supposition.

All aggregates capable of crossing semipermeable barriers with normally confining pores have a highly flexible membrane. This also holds true for skin crossing by ultraadaptable vesicles (Transfersomes). We were the first to argue that this is due to capability of such aggregates to deform and fit into pores in the skin, widened by penetrants into sufficiently broad hydrophilic channels. Indirect evidence for this is the successful delivery of peptides and proteins across animal and human skin by means of nonocclusively applied ultraadaptable vesicles. Examples include insulin (Cevc et al., 1998) and other macromolecules (Cevc, 1996) but also transcutaneously transported antigens and adjuvants for noninvasive immunization (Paul et al., 1995; Paul and Cevc, 1995).

In conclusion, we propose a detailed phenomenological model of aggregate transport across semipermeable barriers. This model can describe and predict the skin penetration by aggregates of different deformability. We have shown experimentally that motion of sufficiently adaptable aggregates through otherwise confining pores in a barrier is driven by exogenous transbarrier gradients, such as the penetrant-concentration independent water activity gradient. The much smaller aggregate concentration gradient was concluded to be unimportant. We furthermore confirmed that water flux does not affect significantly penetrant motion through a barrier. The provision is that sufficient water activity gradient is maintained across transport obstacle. Lag time for hydration-driven aggregate penetration is prolonged by water outflow; however, such flow affects the necessary aggregate dehydration process. In contrast, the rate of vesicle transport through a barrier is nonlinearly and strongly sensitive to aggregate deformability and to the relative size of a penetrant. Starting aggregate or water concentration plays a minor role in the respect. This is due to the dominance of penetrant deformability over barrier penetrability and also may reflect changes in water binding/release by (mixed) lipid bilayers. The flow of ultraadaptable vesicles across surrogate and natural skin has similar characteristics.

Our findings collectively vindicate the claim that ultraadaptable vesicles have special ability to penetrate artificial and natural semipermeable barriers. Lipid diffusion from such vesicles across the skin is practically irrelevant in comparison with the penetration-based ultraadaptable vesicle motion through a barrier. We believe that this also holds true for other lipid-induced changes in barrier properties, which were experimentally precluded in this work by using an artificial skin model. It is equally improbable that such effects have influenced the results of previous studies with ultraadaptable vesicles on the skin.

APPENDIX A: MODELING TRANSBARRIER TRANSPORT

Material transport is driven by free energy G or chemical potential μ difference between two sides of a barrier. This reflects unequal activity of a transported substance—or shortly: a transportant—on both barrier sides (x = 0, x = d_s), and creates a transbarrier osmotic pressure gradient ΔΠ.

Transbarrier concentration difference (Δc_m) of transportant (index m) is often taken to be the only reason for material locomotion. If so, the transport driving (osmotic pressure) gradient is given by: ΔΠ_m ≡ RT(c_m(0) − c_m(d_s) ≡ RTΔc_m > 0. The associated solvent activity difference across a barrier Δa_w(Δc_w) ≡ Δa_w can also be used to express this pressure ΔΠ_m = Δa_w RT/V_w.

In a better approximation one also considers the water activity differences other than those originating from uneven transportant distribution in the studied system. Contributions of nonpermeating solutes j, of low relative water pressure near an open boundary a_w,ext = ln(p_w/p_w0), of electrical potential difference across the barrier, etc., are then included. Any externally applied pressure Δp that is felt directly by transportant or solvent molecules also must be added to osmotic pressure difference.

The effective osmotic pressure difference across a barrier in more general approximation, according to the equation given in the main text body, is given by

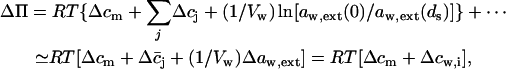(14)

where a_w,ext(0)−a_w,ext(d_s) = Δa_w,ext and Assuming that we get . Further relying on the fact that solutes contribute only little to total system volume, we can define and use c_w is water concentration and V_w is the partial molar volume of water.

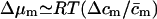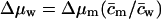The term in Eq. 14 thus includes all water activity—and thus free energy—changes that are independent of m and its concentration. This is indicated by index i. Similar expressions can also written in terms of chemical potential differences, e.g., using and with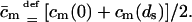

In the spirit of Onsager approach we assume that flux of m across a semipermeable barrier increases linearly with transbarrier permeant concentration and chemical potential difference and with the transportant independent water-potential differences:

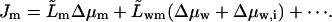(15)

The concurrent transbarrier water flux, which depends on external pressure difference Δp as well, is given by

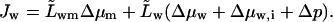(16)

We assumed 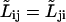and have written to simplify equations.

We lumped all the transportant-independent activity changes together into a single water activity gradient, Δμ_w,i. This implies , and leads to

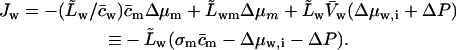(17)

Refractivity coefficient, 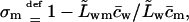serves here as another auxiliary parameter.

From Eq. 16 we can express water potential gradient in terms of transbarrier flow, 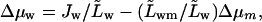to get to the most compact version of the transportant flow equation

(18)

in which 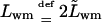and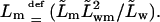

It is furthermore customary to replace proportionality factors L… by the corresponding permeability constants and and to use (osmotic) pressure in place of chemical potential difference. This leads to Eqs. 6 and 7 (given in the main text body), that are equivalent to Eqs. 17 and 18. All these results clearly reveal that transportant independent osmotic pressure difference plays a similar role in transport equations as externally applied potential or hydrostatic pressure differences. This means that transbarrier water activity/potential difference serves as a battery driving hydrophilic entities across a barrier.

APPENDIX B: AGGREGATE DE/HYDRATION FREE ENERGY

The cause for hydration-dependent pore penetration is the lowering of aggregate hydration energy after barrier crossing. This is equivalent to a transbarrier hydration pressure associated with corresponding hydration free energy change. To evaluate such energy change one can argue as follows.

Aggregates of hydrophilic molecules generally shed water below saturating water activity value and attract, as well as are attracted by, water molecules above such value. Both trends are approximately proportional to aggregation number. Hydration energy can therefore be obtained by integrating water adsorption isotherm of the corresponding molecular assembly (Cevc and Marsh, 1987).

The simplest theoretical possibility to estimate maximum hydration free energy of an aggregate is to multiply the hydration energy of a single molecule with aggregation number and aggregate concentration (Cevc, 1996).

Molecular parameterizations of hydration phenomena trace negative hydration energy of hydrophilic molecules to direct, e.g., H-bond-mediated water binding to the polar residues on a molecule and/or to water polarization in the short- and long-range molecular electrostatics field. Nonlocal electrostatics is suitable for describing both phenomena with a focus on the effects of (interfacial) water structure.

The hydration relevant properties of hydrophilic molecules are captured within the framework of nonlocal electrostatic approach by using local surface electrostatic excess charge density (with total surface density Σ_p,v) and total surface charge density (Σ_el,v) as main molecular polarity parameters (Cevc and Marsh, 1987). Water properties, in the first approximation, are described by static ε and high frequency ε_∞ dielectric constant and of water correlations decay length Λ_hyd. ε₀ is dielectric permittivity of free space. Surface density of hydration free energy is then derived to be

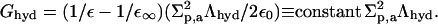To get molar hydration free energy, this value is multiplied with the molar exposed surface area N_aA. The corresponding value for an aggregate is obtained through multiplication with n_aA.

A change in aggregate molar hydration energy as a function of water activity and aggregation number is given by

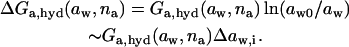In terms of surface hydrophilicity parameter Σ_p,a of an aggregate, and of water correlations length, the result reads (Cevc and Marsh, 1987):

Allowing for interfacial thickness and swelling effects (Cevc et al., 1995), which effectively prolong the reach of hydration, gives

(19)

where d_p is the decay length of interfacial hydrophilicity profile and s ≤ 0.5 is a measure of interfacial softness. Their ratio, in the limiting case (Cevc, 1995a), defines an effective decay length of (surface) hydration, illustrated in Fig. 1 B. The product to a constant, corresponds to bilayer hydration potential, illustrated in Fig. 1 C. To get the hydration energy of an individual penetrant, ΔG_a,hyd(a_w,n_a) is divided by the molar aggregate concentration c_a. To replace variable n_a with aggregate radius, the relationship 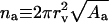is used.

In a relevant limiting case, interfacial width is much larger than the intrinsic decay length of intermolecular correlations in pure water, 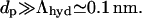The interface is then typically soft. Interfacial thickness in such a situation becomes the chief determinant of the range of hydration phenomena (Cevc et al., 1995). This justifies introduction of an asymptotic version of Eq. 19 in the form of Eq. 5 (given in the main text). Implicit in this result are the relations 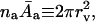constant′ = constant/2π. Also considered is the fact that bilayer rigidity is not very important from the energetic point of view. This permits the neglect of long-range surface undulations (Evans and Parsegian, 1986).

Interfacial thickness obviously affects the results of so-called hydration force measurements between (multi)bilayers. A particularly clear example are lamellar phases of long-headed, nonionic surfactants in water (Lyle and Tiddy, 1986).

APPENDIX C: USEFUL RELATIONS, APPROXIMATIONS, AND DEFINITIONS

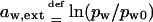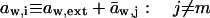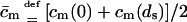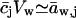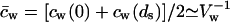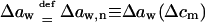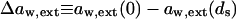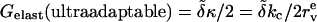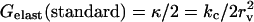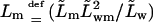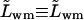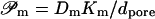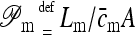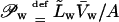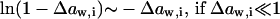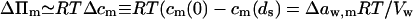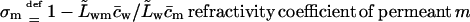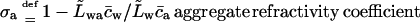APPENDIX D: LIST OF ABBREVIATIONS

a

used as index indicates an aggregate, especially a barrier penetrating aggregate (penetrant)

A

barrier area

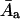
average molecular area in an aggregate

A_pores

total pores area in a barrier

a_w0

water activity value at saturation

a_w,i

transportant independent contribution to water activity

a_w,ext

external water activity (at an ambient site far from the open barrier boundary)

c_a

aggregate concentration (in moles)

average permeant concentration

c_w

water concentration (in moles)

c_w,i

concentration of transportant unaffected (independent) water

d_i

the (relative) size of entry/exit site

D_m

diffusivity of permeant m in a pore

d_p

decay length of the interfacial hydrophilicity profile

d_pore

pore length

G

free energy

G_a,hyd

the molar free energy of aggregate hydration

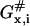
activation free energy for barrier crossing by x

G_{bilayer surface}

free energy of a lipid layer surface

h

Planck's constant

j

solute incapable of crossing a barrier

J

flux across a barrier

K

partition coefficient of permeant m

K_A

isothermal lateral bilayer compressibility modulus

K_A,eff

effective lateral bilayer compressibility modulus

k_c

membrane elasticity modulus

K_m

partition coefficient of solute m

proportionality factor between the corresponding flux contribution and transbarrier chemical potential difference of permeant

L_m

proportionality factor between the corresponding flux contribution and transbarrier permeant chemical potential difference in an alternative version of equation

proportionality factor between the corresponding flux contribution and transbarrier chemical potential difference of water

proportionality factors of cross-correlation terms in flux equation

L_wm

proportionality factor of cross-correlation terms in an alternative form of flux equation

m

permeant, i.e., a barrier permeating solute

n_a

aggregation number

N_A

Avogadro's constant

n_pores

number of pores per unit area (pores density) in a barrier

𝒫

permeability constant

𝒫_a,i

barrier penetrability to a vesicle, corresponding to P_m,i in case of permeation

𝒫_m

barrier permeability to species m in the contribution to the flux driven by m-dependent osmotic pressure difference

𝒫_m,i

barrier permeability to species m associated with the flux driven by osmotic pressure difference independent of m

𝒫_w/p_w0

relative water pressure

𝒫_w

barrier permeability to water

r_a

aggregate radius

r_v

vesicle radius

r_pore

pore radius

RT

thermal energy

S

interfacial softness parameter

x = 0

original site, or donor side, of the studied semipermeable barrier

x = d_s

receiver side, or destination site, of the studied semi permeable barrier

V_m

partial molar volume of species m

V_w

partial molar volume of water

stress- or deformation-dependent elasticity renormalization factor

(stress, composition

relative membrane rigidity function

Δa_w

permeant caused water activity difference across a barrier

Δa_w,ext

solution independent (external) water activity difference across a barrier

Δa_w,i

permeant independent water activity difference across a barrier

Δc_m

permeant concentration difference (gradient) across a barrier

ΔG_a,hyd(a_w)

energetic gain of vesicle hydration

ΔG_elast

energy cost of penetrant's elastic deformation

Δ𝒫

external hydrostatic pressure acting on a barrier

ΔΠ

transbarrier osmotic pressure difference (gradient)

ΔΠ_ext

extrinsic transbarrier osmotic pressure difference

ΔΠL_i

total transportant independent osmotic pressure difference across a barrier

ΔΠ_m

DP-permeant-caused osmotic pressure difference across a barrier

Δμ_m

transbarrier chemical potential difference of permeant

Δμ_w

permeant dependent transbarrier water activity difference

Δμ_w,i

permeant/transportant independent transbarrier water activity difference

κ

elastic energy

the range of hydration, or water correlations decay length

μ

chemical potential

v

fraction of barrier surface covered by pores

σ_m

refractivity coefficient

Σ_p,a

average surface hydrophilicity parameter