Structural Proton Diffusion along Lipid Bilayers

Abstract

For H⁺ transport between protein pumps, lateral diffusion along membrane surfaces represents the most efficient pathway. Along lipid bilayers, we measured a diffusion coefficient of 5.8 × 10⁻⁵ cm² s⁻¹. It is too large to be accounted for by vehicle diffusion, considering proton transport by acid carriers. Such a speed of migration is accomplished only by the Grotthuss mechanism involving the chemical exchange of hydrogen nuclei between hydrogen-bonded water molecules on the membrane surface, and the subsequent reorganization of the hydrogen-bonded network. Reconstitution of H⁺-binding sites on the membrane surface decreased the velocity of H⁺ diffusion. In the absence of immobile buffers, structural (Grotthuss) diffusion occurred over a distance of 100 μm as shown by microelectrode aided measurements of the spatial proton distribution in the immediate membrane vicinity and spatially resolved fluorescence measurements of interfacial pH. The efficiency of the anomalously fast lateral diffusion decreased gradually with an increase in mobile buffer concentration suggesting that structural diffusion is physiologically important for distances of ∼10 nm.

INTRODUCTION

Proton pumping plays a key role in important processes as diverse as cellular respiration in mitochondria and bacteria where it is required for the reduction of O₂ to water (Ruitenberg et al., 2002), the light-driven production of ATP (Steinberg-Yfrach et al., 1998; Sacksteder et al., 2000) and acid secretion in epithelia (Brown et al., 1988; Breton et al., 1996). There is intense interest in experiments which reveal, at the molecular level, how protons are drawn through proteins (Chen et al., 2000) and how protons that have been pumped across membranes reach another membrane protein that utilizes the established pH gradient. In case of purple membranes, protons can efficiently diffuse along the membrane surface (Heberle et al., 1994; Alexiev et al., 1995). This two-dimensional migration occurs with a surface diffusion coefficient, D_s, about five times smaller than that of bulk water at room temperature (Lechner et al., 1994a). The protons are delayed on the proteinous surface due to the high density of proton-binding sites that form a concentrated layer of an undilutable buffer (Gutman and Nachliel, 1997). Between the membrane bound buffer molecules, the protonic charge may be transported: i), via molecular diffusion of an acidic carrier (e.g. H₃O⁺) or ii), via structural (Grotthuss) diffusion, by which the protonic charge is displaced along a network of hydrogen-bonded water molecules. Proton diffusion according to the Grotthuss mechanism occurs much faster than molecular diffusion because it is uncoupled from the self-diffusion of its mass (Kreuer, 1996). Thus, D_s may serve as a criterion to conclusively show structural diffusion. There had been several attempts to visualize fast H⁺ surface migration. The first experiments were carried out under monolayers in a Langmuir trough (Teissie et al., 1985). However, the authors failed to calculate D_s. Additionally, the monolayer result has been disputed, with arguments that convection may contribute to the H⁺ transfer observed and that the contribution of the buffer as a carrier of acidity has been ignored (Gutman and Nachliel, 1995). The latter is true also for a recent monolayer study using an electrochemical microscope (Slevin and Unwin, 2000). When repeated taking buffer contributions into account, a small D_s resulted (Zhang and Unwin, 2002). In addition, possible polarization effects due to large external steady state electrical fields have been neglected. Polarization artifacts were also claimed (Gutman and Nachliel, 1995) to bias D_s values derived from the incremental conductivity of an aqueous phase arising due to monolayer spreading over its surface (Sakurai and Kawamura, 1987; Morgan et al., 1988).

Using two independent experimental approaches, we now demonstrate structural proton diffusion along the surface of lipid membranes. In diluted buffer, proton surface migration may occur over very large distances (100 μm). For physiological buffer concentrations, we estimated a travel distance of 10 nm. This result suggests that fast structural diffusion along biological membranes allows proton transport between a proton source and a proton sink.

MATERIALS AND METHODS

Planar membranes

Planar bilayer lipid membranes (BLM) were formed (Mueller et al., 1963) from diphytanoyl-phosphatidyl-choline (DPhPC, Avanti Polar Lipids, Alabaster, AL) dissolved at 20 mg/ml in n-decane (Merck, Darmstadt, Germany). They were spread across a circular hole (0.2 or 1.1 mm in diameter for fluorescence and microelectrode experiments, respectively) in a diaphragm separating two aqueous phases of a Teflon chamber. The aqueous salt solutions (Merck) were buffered with Tris (Fluka, Buchs, Switzerland) or CAPSO (Sigma, Dreisenhofen, Germany). During the steady state experiments, they were agitated by magnetic stirrer bars.

Steady-state experiments

In the immediate vicinity of the vertically mounted BLM, the spatial distributions of two different ions were monitored simultaneously. Therefore, a double-barreled microelectrode sensitive to both H⁺ and Ca²⁺, and a reference electrode were placed at the trans side of the BLM (Pohl et al., 1998). Ion sensitivity of the double-barreled microelectrodes was achieved by filling one barrel with the Hydrogen Ionophore IIa cocktail (Amman, 1986) and the other with the Calcium Ionophore IIa cocktail (both Fluka). Tip diameter of the electrodes was 3 μm.

The setup for simultaneous membrane conductivity and microelectrode measurements (Fig. 1 A) has been described elsewhere (Pohl et al., 2001). In brief, current-voltage relationships were measured by a patch-clamp amplifier (model EPC9, HEKA, Germany). Voltage sampling from the microelectrodes was performed by two electrometers (Model 617, Keithley Instruments Inc., Cleveland, OH) connected via an IEEE-interface to a personal computer. Continuous motion of the microelectrode perpendicular to the surface of the lipid bilayer was handled by a hydraulic microdrive manipulator (Narishige, Tokyo, Japan). Touching the membrane was indicated by a steep potential change (Antonenko and Bulychev, 1991). Inasmuch as the motion velocity of the electrode was known (2 μm s⁻¹), its position relative to the membrane could be determined at any instant of the experiment. Electrodes with a 90% rise time below 0.6 s were selected. Artifacts due to a very slow electrode movement are therefore unlikely. Nevertheless, possible effects of time resolution or distortion of the unstirred layer were tested by making measurements while moving the microelectrode toward and away from the bilayer. Because no hysteresis was found, it could be assumed that an electrode of appropriate time resolution was driven at a rate that is slow relative to the rate at which any electrode induced disturbance of the unstirred layer reaches a “stationary” state. The accuracy of the distance measurements was estimated to be ±5 μm.

FIGURE 1.

(A) A microelectrode (ME) consisting of pH- and Ca²⁺-sensitive barrels was moved at 2 μm/s perpendicular to the lipid plane formed by the bilayer itself, the torus, and the lipid on the Teflon support. (B) Representative experimental records induced by 2.5 μM A23187 in the presence of a 2:0.2 mM transmembrane [Ca²⁺] gradient (bulk solution: 1 mM Tris, 1 mM Mes, 100 mM choline chloride, pH 7). After touching the membrane, the electrode was withdrawn to a distance of 20 μm. Switching the transmembrane potential from 0 to +150 and then −150 mV revealed no effect, suggesting that the Ca²⁺/2H⁺ exchange is electroneutral.

Kinetic measurements

Membrane-intercalated N-(fluorescein-5-thiocarbamoyl)-1,2-dihexadecanoyl-sn-glycerol-3-phosphoethanolamine, triethylammonium salt (fluorescein DHPE, Molecular Probes, Eugene, OR) has been used to measure the pH adjacent to bilayer surface. The fluorescein DHPE/DPhPC ratio was 0.01–0.05. The hydrophobic caged proton (6,7-dimethoxycoumarin-4-yl)methyl diethyl phosphate was synthesized in analogy to (7-methoxycoumarin-4-yl)methyl diethyl phosphate (Schade et al., 1999) by reaction of diethyl phosphoric acid chloride with 6,7-dimethoxy-4-(hydroxymethyl) coumarin. Fluorescence excitation was realized by a 150-W xenon lamp that via a monochromator was attached to an inverse microscope (20× objective). For fluorescence detection from the horizontally mounted BLM, a photodiode connected to a current amplifier (EPC9) was used. Photocleavage of the caged proton by a xenon flash lamp (all TILL Photonics, Grafelin, Germany) yields 4-(hydroxymethyl)-6,7-dimethoxycoumarin, a diethyl phosphate anion, and a proton that results in a rapid drop in pH.

A photoactivatable version of fluorescein (fluorescein bis-(5-carboxymethoxy-2-nitrobenzyl) ether, dipotassium salt, CMNB-caged fluorescein; Molecular Probes) allowed visualization of bulk diffusion. Both in the cases of proton and fluorescein diffusion, flash and detection areas were separated by a system of diaphragms (Fig. 2 A).

FIGURE 2.

(A) pH and [Ca²⁺] profiles indicating identical transmembrane Ca²⁺ and H⁺ flux densities in the membrane center. (B) From the lipid covering the Teflon support, a significant H⁺ release but no Ca²⁺ release (zero first derivative at the interface) was measured. (C) The interfacial pH and [Ca²⁺] shifts at distance d from the membrane center relative to the respective values at d = 0. Increasing of Tris concentration from 1 mM (circles) to 36 mM (squares) restricted proton release to the lipid bilayer. Bulk solution: 100 mM choline chloride, 4 μM A23187, pH 7.0. CaCl₂-concentration gradient: 20:0.1 mM.

Monte Carlo simulations

Adjacent to a membrane there is usually a stagnant layer that acts as an additional diffusion barrier. Within this so called unstirred layer, transport is thought to be rate limited by diffusion (Barry and Diamond, 1984). It was simulated in a conventional way using a cubic spatial (Cartesian) grid with integer nodes. Grid lines were separated by distance b. In the direction parallel to the membrane (X and Y coordinates), the random walk domain was infinite. Perpendicular to the membrane, random walk was limited to the size δ of the unstirred layer, i.e., |Z| ≥ N × b = δ, with N being an integer. The H⁺ was placed at random within the bilayer area (x, y < r, z = 0, where r is radius of the bilayer). With rate constants k₁, …, and k₆, the tracer then hopped, respectively, to one of six neighboring nodes. During the random walk, the time spent in a node and the probabilities to reach the ith neighbor were equal to 1/(k₁ + … + k₆) and k_i/(k₁ + … + k₆), respectively. With respect to the position of the node, the rate constants k₁, …, k₆ were set equal to rate constants k_s and k_b at the membrane surface (N = 0) and in the bulk (|N| > 0), or to H⁺ adsorption and desorption rates, k_a (movement from |N| = 1 to |N| = 0) and k_d (movement from |N| = 0 to |N| = 1).

Random walk of the tracer was terminated after reaching either Z = δ or a prescribed time limit. Long runs (10⁷ time steps) were used to compile kinetic histograms of tracer appearance in the observation area. To evaluate the statistical error, several independent runs were made. The absolute value of the grid parameter b was chosen so that the ratio b² × k_B/6 yielded D = 4.4 × 10⁻⁶ cm²/s for tracer diffusion in the bulk. To obtain theoretical pH profiles for 0 < z < 50 μm, the number of visits in predefined points of a grid plane perpendicular to the membrane were integrated over a given time interval.

RESULTS

Steady-state experiments

Performing an electroneutral exchange of one Ca²⁺ for two H⁺, the ionophore A23187 induces steady state transmembrane Ca²⁺ and H⁺ fluxes (Kolber and Haynes, 1981; Pohl et al., 1990). Their densities, j_Ca and j_p, respectively, are equal to the respective flux densities measured in the immediate membrane vicinity according to mass conservation. j_Ca is calculated from its concentration gradient at the membrane water interface:

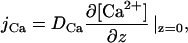(1)

where D_Ca is the aqueous diffusion coefficient of Ca²⁺. j_p results from the combined contributions of hydrogen ion (j_H), hydroxyl ion (j_OH), and buffer (j_BH) fluxes through the unstirred layers (Borisova et al., 1974; Pohl et al., 1998):

(2)

where D_H, D_OH, D_b, δ_H, δ_OH, and δ_b are aqueous diffusion coefficients and individual unstirred layer (USL) thicknesses of H⁺, OH⁻, and buffer, respectively. β is the buffer capacity of aqueous solutions. Under our conditions (β > 0.1 mM, pH 7, δ_H = 3 δ_b), Eq. 2 is simplified to:

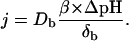(3)

Consequently, pH profiles measured with microelectrodes are determined by buffer diffusion rather than H⁺ diffusion (Pohl et al., 1998). Both Ca²⁺ concentration and pH were measured as a function of the distance, z, to the membrane while moving a double-barreled (both Ca²⁺ and H⁺ sensitive) microelectrode toward and away from the bilayer (Pohl et al., 1998) (Fig. 1 A). Because i), A23187 did not increase membrane conductivity (1 ± 0.1 nS cm⁻²) and ii), neither near-membrane [Ca²⁺] nor pH were affected by a transmembrane potential (Fig. 1 B), it was concluded that deviations from the electrically silent exchange of one Ca²⁺ for two H⁺ (Pohl et al., 1990) did not occur. Nevertheless, in the vicinity of the membrane center j_P/j_Ca was <2 (Fig. 2 A), suggesting that some of the H⁺ ions were not delivered to the aqueous phase after being transported across the membrane. Rather, H⁺ migrated laterally along the lipid surface and reached the aqueous phase at some distance, d, from the membrane center. Accordingly, H⁺ liberation may have occurred not only from the bilayer part of the lipid (d < r), but also from the membrane torus or from the lipid covering the Teflon support (d > r) (Fig. 1 A). In contrast, Ca²⁺ release was restricted to d < r. Experimental proof for lateral H⁺ migration was obtained in two ways:

1. j_Ca calculated from the [Ca²⁺] profiles (Eq. 1) was zero for d > r (Fig. 2 B). In contrast, j_P was different from zero as revealed by the non-zero first derivative of the simultaneously measured pH profile (Fig. 2 B). Because a carrier-mediated H⁺ transport across the Teflon septum is easily ruled out, lateral H⁺ migration remains as the sole origin for j_P. Unfortunately, Eq. 3 cannot be used for an accurate calculation of j_P in this case because buffer diffusion parallel to the membrane biases the result. Precise microelectrode based flux measurements are possible only in the very center of the membrane (Pohl et al., 1997; Pohl et al., 1998) where the concentration does not depend on the space coordinates parallel to the membrane (Levich, 1962; Pedley, 1983).

2. To conclusively demonstrate lateral H⁺ diffusion along the membrane surface, the H⁺ desorption rate was varied by increasing the buffer concentration from 1 to 36 mM. Due to an increased probability of a collisional H⁺ transfer from the membrane surface to buffer molecules, j_P was zero for d > r indicating a complete inhibition of migration along the membrane surface (Fig. 2 C). A j_P/j_Ca ratio equal to two in the membrane center confirmed the result.

To investigate the molecular mechanism of H⁺ surface diffusion, Monte Carlo simulations were undertaken. The parameters k_s, k_d, and k_a were varied to fit the theoretical to the experimental pH profile in the interval z < 50 μm. A k_a/k_d ratio > 2 produced satisfactory results. This result is in agreement with earlier experiments on planar membranes, indicating the existence of a kinetic barrier for proton transfer from the bilayer surface to bulk water (Antonenko et al., 1993). Similarly, molecular dynamics simulations suggested that the energy barrier for H⁺ transport from the membrane surface back into an unbuffered bulk solution is higher than the energy barrier for the H⁺ adsorption to the membrane surface (Smondyrev and Voth, 2002). It was possible to fit our data with k_s/k_b > 1 as well as with k_s/k_b < 1 suggesting that two-dimensional diffusion has not to be fast. Slow two-dimensional diffusion has been observed for example on the surface of a purple membrane (Heberle et al., 1994; Lechner et al., 1994b). Thus, steady-state microelectrode experiments provide evidence for a two-dimensional H⁺ diffusion along the bilayer surface but they do not allow vehicle diffusion to be distinguished from structural diffusion.

Kinetic experiments

To determine the velocity of H⁺ diffusion, kinetic experiments were carried out. Fast proton liberation in a small rectangular area on the bilayer surface was achieved by flash photolysis of a hydrophobic caged compound (Fig. 3 A). H⁺ migration over a variable distance s to a region of interest was visualized as a change in fluorescence intensity of a lipid bound pH-sensitive dye. Similarly, the velocity of vehicle bulk diffusion was assessed by uncaging fluorescein, which has a size close to buffer molecules. For s = 70 μm, the fluorescence peak was recorded 0.45 s after H⁺ flash liberation. The respective time τ_max that fluorescein required to travel the same distance was equal to 9 s. Thus, H⁺ diffusion is much faster than fluorescein diffusion (Fig. 3 B). If release and detection areas were point-like, the H⁺ and fluorescein bulk diffusion coefficients (D = s²/6τ_max) were, respectively, on the order of 10⁻⁴ and 10⁻⁶ cm²/s. The latter is reasonable for vehicle bulk diffusion, whereas the former would be consistent only with surface diffusion. τ_max of H⁺ diffusion increased linear with both s² (Fig. 4) and the buffer concentration (Fig. 5). Using the assumption about point-like dimensions again, the surface diffusion coefficient, D_s, was estimated to be about s²/4τ_max = 8.3 × 10⁻⁵ cm² s⁻¹ at infinite buffer dilution (Fig. 5). Exact calculations were undertaken by the Monte Carlo simulation algorithm already described. A satisfactory fit to experimental fluorescence kinetics was achieved with D_s = 5.8 × 10⁻⁵ cm² s⁻¹ (compare also Fig. 3). k_a/k_d decreased from 10 to 1 with an increase in buffer concentration from 0.1 to 0.9 mM. Thus, D_s exceeded D_b by an order of magnitude. Even if the buffer molecules were able to carry H⁺ by two-dimensional diffusion, their D_s of 8 × 10⁻⁶ cm² s⁻¹ would be too small. Substitution of buffer molecules by the fastest acid carriers available, i.e., by H₃O⁺ or OH⁻ (D_s = 3 × 10⁻⁵ cm² s⁻¹) revealed the same result. Inasmuch as vehicle diffusion cannot account for the high migration velocity, structural diffusion has to be considered.

FIGURE 3.

(A) Using a set of diaphragms, two regions of the membrane (large circle) were selected that were exposed to the UV flash or used for fluorescence measurements. (B) Different kinetics of flash triggered fluorescence changes at a distance s = 70 μm between both regions in the case of 1 mM caged H⁺ (blue) or 1 mM caged fluorescein (green) corresponding, respectively, to two-dimensional surface diffusion (D_s = 5.8 × 10⁻⁵ cm²/s) and three-dimensional bulk diffusion (D_b = 2.8 × 10⁻⁶ cm²/s). In the former case fluorescence was collected from fluorescein labeled lipids (5%) incorporated into the membrane. Bulk solution: 100 mM NaCl, 0.1 (for H⁺) or 1 mM (for fluorescein) 1 mM CAPSO. The fit of the Monte Carlo simulations to the experimental data is shown by red triangles.

FIGURE 4.

Kinetics of pH changes in an observation area on the membrane surface as a function of its distance s to the area of proton release. The maximum of fluorescence (i.e., the peak of the surface proton concentration in the observation area) appeared with a delay τ_max after proton uncaging. τ_max was a linear function of s². In this plot, the shades of gray of the circles correspond to the shade of gray of representative experimental traces recorded at s = 60, 77, 100, and 125 μm. For clarity, the experimental records corresponding to the triangles are omitted.

FIGURE 5.

Mobile buffer concentration determined the kinetics of pH changes in the observation area that was located on the membrane surface at a distance of 73 μm to the area of proton release. τ_max was a linear function of the buffer concentration. From the regression, a rough estimate of D_s (s²/4τ_max = 8.3 × 10⁻⁵ cm² s⁻¹) at infinite buffer dilution can be made, if it is assumed that H⁺ release and observation areas are point like. The shades of gray of the circles correspond to the shades of gray of representative experimental traces recorded for 0.1, 0.5, and 0.9 mM CAPSO (pH 9.0). For clarity, the experimental records corresponding to the empty circles are omitted.

H⁺ acceptors on the membrane surface lower the efficiency of lateral H⁺ migration. Incorporation of A23187, for example, lowers D_s to 2.0 × 10⁻⁵ cm² s⁻¹ (Fig. 6). Addition of Ca²⁺ that competes with H⁺ for binding to the ionophore reversed the effect, i.e., D_s increased again to the value that was measured without A23187. The Ca²⁺ effect was due to an interaction with A23187 because in the absence of the ionophore, Ca²⁺ did not alter D_s.

FIGURE 6.

Effect of A23187 on the kinetics of pH changes in an observation area (s = 73 μm) on the membrane surface. Addition of 10 μM A23187 to the bathing solution (100 mM NaCl, 100 μM CAPSO) resulted in a retarded appearance of the fluorescence peak. Fitting the theoretical time course calculated by the Monte Carlo algorithm to the experimental data revealed a D_s of 2.0 × 10⁻⁵ cm² s⁻¹. Subsequent addition of 100 μM Ca²⁺ that competed with H⁺ for binding to A23187 reversed the effect (D_s = 5.8 × 10⁻⁵ cm² s⁻¹).

DISCUSSION

The present work demonstrates Grotthuss diffusion along the membrane surface. In a nearly buffer depleted medium, Grotthuss diffusion enables the protonic charge to travel ∼100 μm. In contrast to earlier studies showing long-range H⁺ surface migration, for example, between gramicidin channels in a bilayer (Antonenko and Pohl, 1998), transport by acid carriers has been excluded as a possible transport mechanism.

So far, convincing evidence for H⁺ transfers along hydrogen bond chains has been presented for much shorter distances. For example, the H⁺ conductivity of gramicidin A channels is due to structural diffusion. In contrast to water and cations that are transported throughout most of the channel length by a single-file process (Finkelstein and Andersen, 1981), the H⁺ can pass other molecules within the channel. Being able to jump along a continuous row of water molecules inside the channel, the protonic charges move across the channel independent from water molecules as revealed by electroosmotic and streaming potential experiments (Levitt et al., 1978). The isolated knowledge of the experimentally determined H⁺ diffusion coefficient (0.34 × 10⁻⁵ cm² s⁻¹) (Pomes and Roux, 1996; Gutman and Nachliel, 1997), does not allow to conclude that Grotthuss diffusion is involved. That is, the lateral H⁺ diffusion coefficient is expected to be higher than the H⁺ diffusion coefficient in bulk water (9.3 × 10⁻⁵ cm² s⁻¹) (Pines et al., 1988). According to molecular dynamics simulations, it is indeed 40 times higher (Schumaker et al., 2000). The limiting step is not the movement across the channel but H⁺ entry or exit. The H⁺ exits the channel, leaving water molecules partially aligned. The dipole moment of the water chain must then turn to become receptive to another proton (Schumaker et al., 2001).

In the presence of more than one water chain on the membrane surface, this restriction is not longer rate limiting. Because different H⁺ may enter different water chains, the protonic charge moves faster on the membrane surface than across a transmembrane channel. Being only 10 times faster than carrier diffusion in the bulk, lateral H⁺ migration is not consistent with a totally concerted mechanism of translocation along extended water chains. Rather, proton transfer on the membrane surface results from the random alignment of neighboring water molecules and subsequent rapid hydrogen-bond length fluctuations. The observation that lateral H⁺ diffusion (D_s = 5.8 × 10⁻⁵ cm² s⁻¹) is slightly slower than bulk diffusion in pure water (9.3 × 10⁻⁵ cm² s⁻¹) agrees well with the prediction that ordering of water in the solvation layer of membranes should lower the H⁺ diffusivity (Gutman and Nachliel, 1997). Because the reduction is rather small, it may be assumed that the net displacement of charge due to continual interconversion between covalent and hydrogen bonds occurs on the membrane surface with nearly the same time constant as in water, i.e., within picoseconds (Tuckerman et al., 1995). This processes is rapid relative to H⁺ uptake (0.01 pS) by most buffers (Gutman and Nachliel, 1995). Thus, fast H⁺ delivery to the membrane by transfer through buffer molecules (Mitchell, 1961) and by water hydrolysis (Nachliel et al., 1987; Kasianowicz et al., 1987; Kasianowicz and Bezrukov, 1995) is consistent with the passage of H⁺ between a source and sink by the Grotthuss mechanism.

Phenomenologically, this conclusion is in line with reports about lateral H⁺ migration at the water-Langmuir film interface (Morgan et al., 1988; Leite et al., 1998). However, quantitatively, a D_s of 5.8 × 10⁻⁵ cm² s⁻¹ contradicts the possibility of ever detecting monolayer conductance. Because the conducting layer is extremely thin, it would only be possible to measure the incremental conductance due to the monolayer if D_s was five orders of magnitude larger (Shapovalov and Ilichev, 1992). Thus, our data support monolayer studies that failed to visualize proton surface conductance (Menger et al., 1989; Shapovalov and Ilichev, 1992).

In contrast with a monolayer study reporting long range lateral H⁺ conduction in the presence of concentrated buffers (Gabriel et al., 1994), we have found that the effective distance that a H⁺ can migrate on the membrane, depends on the buffer concentration of the solutions (Figs. 2 and 5). The experimentally observed k_a/k_d decreased by factor of 10 with the increase of buffer concentration by the same factor was theoretically predicted (Georgievskii et al., 2002a,b). With respect to this dependency, the observed D_s yields an estimated travel distance of ∼10 nm at b = 30 mM. The shortening of the travel distance from 100 μm to several nanometers is in agreement with a phenomenological model of coupled proton surface-bulk diffusion (Georgievskii et al., 2002a,b). Fixed (i.e., membrane bound) buffers also tend to decrease the H⁺ migration velocity (Fig. 6). This observation suggests that structural H⁺ diffusion between interfacial proteinous binding sites occurs, although the macroscopically observed D_s is much smaller than expected for Grotthuss diffusion (Heberle et al., 1994; Lechner et al., 1994a). Even if structural diffusion is limited to a distance of 10 nm, it may be of physiological importance because it provides a potentially efficient pathway for proton transfer between neighboring proteins compared with the alternative modes of transport involving acidic vehicles and/or desorption and diffusion through bulk solution. Transport along water wires on the membrane surface agrees well with models for the relay of H⁺ to reactive centers of proteins by buried water molecules (Gottschalk et al., 2001; Lanyi and Luecke, 2001). Thus, internal water molecules may exchange their protons with water molecules on the membrane surface, building up the proton-conducting pathway.