Abstract
The contiguous inhibitory and regulatory regions of troponin I in the heterotrimeric troponin complex play a critical role in Ca2+ activation of striated muscle. Knowledge of the structure of this critical region within the complex will enhance efforts toward understanding regulatory mechanisms. Toward this goal, we have used simulated annealing to study the structure of the inhibitory and regulatory regions of cardiac muscle troponin I in the calcium-saturated complex formed between cardiac troponin C and cardiac troponin I. We have incorporated distances determined experimentally by Förster resonance energy transfer in the full-length complex, rather than using peptides derived from cTnI. For these models, we assume a helix-loop-helix conformation for the inhibitory region. We have found several structures that satisfy the experimental constraints fairly well. Although it is not possible to eliminate any of these models at this time, future studies with additional experimental restraints will yield insights on the mechanisms of calcium regulation in cardiac muscle.
INTRODUCTION
Muscle contraction is regulated by a group of proteins called the troponin complex located on the thin filament (Farah and Reinach, 1995). Intact troponin is composed of three subunits: troponin T (TnT), troponin C (TnC), and troponin I (TnI). TnT connects the troponin complex to tropomyosin located on the surface of the actin filament. The conformation of TnC is sensitive to calcium concentration, allowing for regulation of muscle contraction. TnI inhibits contraction in inactive muscle by blocking the interaction of myosin and actin required for muscle contraction. In contracting muscle, Ca2+ binds to the N-terminal region of TnC, exposing a hydrophobic patch on TnC to which TnI binds (Herzberg and James, 1985; Herzberg and James, 1988; Houdusse et al., 1997). The binding of TnI to the TnC hydrophobic patch relieves the inhibition of actin-myosin interaction, allowing for activation of actomyosin ATPase and force development. No high-resolution structure for the intact troponin complex has been determined.
The conformation and biochemistry of TnC have been extensively studied. Fast skeletal TnC (sTnC) has four EF-hand calcium-binding motifs (Herzberg and James, 1985; Sundaralingam et al., 1985; Lewit-Bentley and Rety, 2000). Two are located near the N-terminus (sites I and II) and are unoccupied in relaxed muscle, but are bound to calcium in active muscle. These sites are low affinity (Ka ≈ 105 M−1) that bind calcium specifically (Potter and Gergely, 1975). The cardiac isoform of TnC (cTnC) lacks a functional site I due to nonconservative mutations. The C-terminal region of TnC contains two high affinity EF-hand motifs (sites III and IV) that can bind Mg2+ and Ca2+ competitively (Ka for Mg2+ ≈ 103 M−1; Ka for Ca2+ ≈ 107 M−1) (Potter and Gergely, 1975). Sites III and IV bind Ca2+ in both relaxed and active muscle. The crystal structure of sTnC has been determined in both the 2-Ca2+ (Herzberg and James, 1988) and 4-Ca2+ states (Houdusse et al., 1997). Skeletal TnC is a dumbbell-shaped molecule with an N-terminal globular domain containing sites I and II, connected by an approximately 20 residue solvent-exposed α-helix to a C-terminal globular domain containing sites III and IV. A rather open conformation for the N-terminal domain is found in 4-Ca2+ sTnC, in which the B and C helices move away from the A and D helices. As a consequence of the lack of a functional site I in cTnC, the N-terminal domain of 3-Ca2+ cTnC has a closed conformation (Sia et al., 1997) similar to that found in 2-Ca2+ sTnC (Herzberg and James, 1988). However, Förster resonance energy transfer (FRET) measurements demonstrated a Ca2+-induced open conformation in the N-domain for cTnC in the presence of bound cTnI (Dong et al., 1999). When bound to synthetic peptides containing the regulatory region of TnI (cTnI 149-165; sTnI 115-131), an open configuration has been observed for both cTnC (Li et al., 1999) and sTnC (McKay et al., 1997). The open TnC N-terminal conformation found in these structures and in 4-Ca2+ sTnC (Houdusse et al., 1997) agrees well with the FRET results.
The segment of sTnI that is responsible for the inhibition of muscle contraction has been identified as sTnI 96-116 (Syska et al., 1976). The corresponding region of cTnI is cTnI 130-149. The inhibitory region of TnI interacts with actin in relaxed muscle but not in contracting muscle, as demonstrated using affinity chromatography (Syska et al., 1976). Ca2+ activation of muscle results from the binding of the cation to the N-domain of TnC and is accompanied by a Ca2+-dependent interaction of the regulatory region of TnI (sTnI 115-129, cTnI 150-165) with an exposed hydrophobic patch in the Ca2+-induced open N-domain of TnC. This Ca2+-dependent interaction, which triggers other molecular interactions ultimately leading to the activated state of muscle, is facilitated by the breaking of the inhibitory region from actin. Details of these interactions are not well understood.
The structures of the intact binary (TnC/TnI) and ternary complexes (TnC/TnI/TnT) are unknown. However, there have been several high-resolution studies of segments of TnI in complex with TnC (McKay et al., 1997; Li et al., 1999; Vassylyev et al., 1998). There have also been many low-resolution studies of the intact complexes. The skeletal binary complex has been shown to have an extended conformation by neutron diffraction (Olah et al., 1994). A second, but substantially different, model for the complex within the trimeric troponin has also been reported on the basis of neutron scattering data (Stone et al., 1988). A model for the skeletal TnC/TnI complex in the calcium-saturated state has been created based on a variety of low-resolution data, as well as the sTnC crystal structures and some high-resolution TnC-TnI fragment structures (Tung et al., 2000).
FRET is a powerful experimental method for the determination of difference in intersite distances in biomolecular systems (Cheung, 1991; Stryer, 1978). In the FRET technique, the amount of excitation energy transferred from an energy donor to an acceptor is measured (Förster, 1965). The efficiency of transfer is proportional to the inverse sixth power of the donor and the acceptor separation and is very sensitive to small changes in the separation. The distances derived from FRET can be used to determine structures at low resolution. This has been done for a number of proteins including chloroplast coupling factor 1 (Richter et al., 1985), actomyosin (Botts et al., 1989), and the actin monomer and filament (O'Donoghue et al., 1992). Nucleic acid models have also been successfully constructed using this method (Tuschl et al., 1994). In the absence of complete high resolution structures, FRET provides a database for construction of low resolution structures. Such structures are useful in providing mechanistic insights on the function of the system.
Here we report models of the complex formed between Ca2+-loaded cTnC and cTnI based on intermolecular and intramolecular distances derived from FRET in the inhibitory and regulatory regions of cTnI. The FRET distances were obtained with full-length binary complex as well as fully reconstituted ternary complex (Dong et al., 2000; Dong et al., 2001). These regions of cTnI in troponin are of special interest because they play important roles in the mechanisms of Ca2+ activation and regulation (Dong et al., 2001).
METHODS AND MATERIALS
Protein preparations
Native cTnC has two cysteines in positions 35 and 84. In this study, we used seven cTnC mutants each containing a single cysteine: C35S, C84S, C35S/C84S/N51C, C35S/C84S/S89C, C35S/C84S/E94C, C35S/C84S/T127/S, and C35S/C84S/M159C. These mutants were generated from a cDNA encoding TnC of chicken slow muscle isolated from a λgt10 cDNA library as previously outlined and using a polymerase chain reaction (PCR) kit (Dong et al., 1999). Wild-type and mutant proteins were expressed in E. coli strain BL21(DE3) under isopropyl-1-thio-β-d-galactopyranoside induction, and the expressed proteins were separated from a phenyl-Sepharose CL-B4 column containing Ca2+. cTnC bound to the column was eluted by a buffer containing EDTA. A mouse cDNA clone of cTnI was used to generate wild-type and single-cysteine mutants. The mutant clone construction, protein expression in E. coli BL21(DE3), and protein purification and characterization were carried out as in our previous work (Dong et al., 1997a). Four single-cysteine cTnI mutants (C81S/C98I/Q131C, C81S/C98I/R146C, C81S/C98I/A152C, and C81S/C98I/L160/C) were generated in which the two endogenous Cys81 and Cys98 were changed to Ser and Ile, respectively. In our previous studies, the cTnC mutants containing single cysteines in positions 35, 51, 84, and 89 were found to have Ca2+ affinities that were within the normal range of affinities for native/wild-type cTnC. In complexes with native cTnI, the Ca2+ affinities were 10-fold enhanced, as expected. The cTnI mutants when reconstituted into binary complexes with cTnC enhanced Ca2+ affinities by a factor of 8–10.
The single cysteines in cTnC mutants were labeled with MIANS [2-(4′-maleimidylanilino)naphthalene-6-sulfonic acid] as donor of FRET and the cysteines in cTnI mutants were labeled with DDPM [N-(4-dimethylamino-3,5-dinitrophenyl)maleimide] serving as FRET acceptor. The labeling of both cTnC and cTnI mutants was done under denatured conditions and the labeled proteins were subsequently renatured, following the general procedures as in previous studies ( Dong et al. 1997a). The degree of donor labeling was >95%, and the degree of labeling of acceptor was slightly greater than that of donor labeling for a given pair of donor-labeled cTnC and acceptor-labeled cTnI. Complexes formed between donor-labeled cTnC and acceptor-labeled cTnI were prepared by incubating the donor-labeled protein with an excess of the acceptor-labeled protein in 6 M urea, followed by a stepwise dialysis to remove urea and decrease [KCl] to 0.1 M (Dong et al., 1997b).
FRET measurements
We used FRET to calculate the distribution of distances between donor site on cTnC and acceptor site on cTnI, as previously described (Dong et al., 1997a; She et al., 1988). Donor fluorescence intensity decays were measured in the time domain with an IBH 5000 photon-counting lifetime system equipped with a stable nanosecond flash lamp operated at 40 kHz in 0.5 atm of hydrogen. The measurements were carried out at 20°C with samples in 100 mM KCl, 1 mM EGTA, 50 mM MOPS at pH 7.2, and in the presence of either Mg2+ (5 mM) or Mg2+ (5 mM) plus Ca2+ (0.1 mM). Donor excitation was isolated with a 350-nm three-cavity interference filter, and the emission was isolated with a Corning 3-73 cutoff filter. The decay data were used to recover the distribution of distances (Dong et al., 1997a) based on the assumption of a Gaussian distribution (Lakowicz et al., 1988).
cTnC conformation modeling
X-PLOR (Brünger, 1992) was used for all molecular modeling and simulation. The CHARMM forcefield (version 22) (Brooks et al., 1983) was used, with additional modifications as described.
A model for 3-Ca2+ cTnC in the cTnC/cTnI complex was constructed and used in subsequent modeling. Because the relative orientations of the two globular domains of cTnC have not been determined at high resolution, a homology model for bovine cTnC was created using the 2-Ca2+ sTnC crystal structure (Herzberg and James, 1988) as a template. However, the N-terminal region conformation for cTnC 1-81 was then altered so as to duplicate the cTnC N-terminal conformation derived for the N-terminal cTnC/cTnI 149-165 complex determined by NMR spectroscopy (Li et al., 1999).
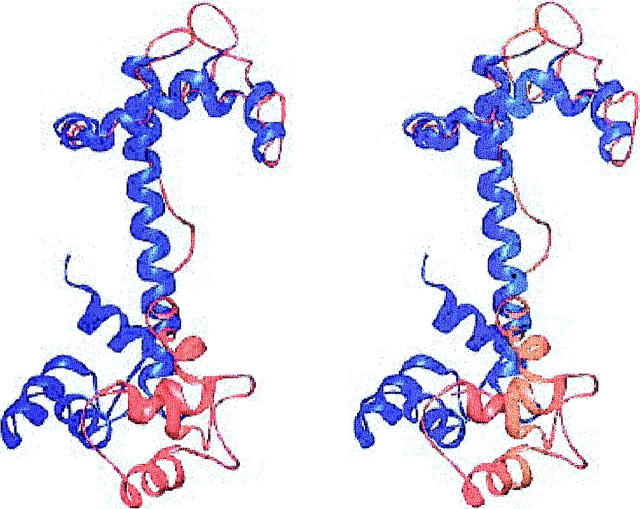
For comparison, a series of models was also constructed with another set of relative orientations of the two domains of cTnC. In this TnC structure, the relative orientations of the N-terminal domain determined by NMR dipolar couplings (Dvoretsky et al., 2002) was used. As with the above sTnC homology model, the conformation of cTnC 1-81 was altered to that observed in the N-terminal cTnC/cTnI 149-165 high-resolution NMR structure (Li et al., 1999). The superposition of the dipolar coupling and homology models of cTnC is shown in Fig. 1.
FIGURE 1.
Stereoview of the superposition of the dipolar coupling (blue) and sTnC homology orientation (red) models for cTnC. The structures were aligned using cTnC 1-81. Generated with Ribbons (Carson, 1998).
Starting structure of cTnI 129-160 conformation
For both possible cTnC models used, a series of 100 different random starting structures was generated for cTnI. For each cTnI atom, an x coordinate was assigned randomly, and similarly for the y and z coordinates. Every coordinate of every atom was assigned completely randomly, with no relationship to any other coordinate. The starting conformation of cTnI 149-160 was taken from the N-terminal cTnC/cTnI 149-165 NMR structure (Li et al., 1999). One hundred different completely random conformations were generated for cTnI 129-148, for both the homology model orientation and dipolar coupling orientation cTnC models.
Simulated annealing using FRET distance restraints
Each of the 100 random structures was used as a starting conformation for a simulated annealing (SA) molecular dynamics run, followed by energy minimization, with FRET derived distance restraints. During the SA and minimization, the FRET determined distances shown in Table 1 were incorporated as harmonically restrained bonds in a manner analogous to the use of nuclear Overhauser effect distance restraints derived from NMR experiments. Force constants for these bonds were determined from the half-widths of the distributions (full-width at half maximum) of the FRET distances, using the following equation.
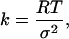 |
(1) |
where k is the bond force constant, RT is thermal energy at 300 K (0.596 kcal/mol) and σ2 is the standard deviation of the experimental distance distribution determined by FRET (σ2 = half-width/2.35) (Lakowicz et al., 1988). For the FRET restraints the interprobe distances were approximated by bonds between the C-α atoms of restrained residues. In addition, all bonded terms from the CHARMM all-atom forcefield were used during SA, except that no terms for nonbonded forces (van der Waals or electrostatics) were used. This protocol is similar in spirit to that used for developing three-dimensional models using NOE distance restraints.
TABLE 1.
Interresidue FRET distances used to construct the cTnC/cTnI 129-160 models*
| Residues | FRET distance (Å) | Half-width (Å) | Model§ distance (Å) |
|---|---|---|---|
| cTnC 35 - cTnI 131 | 30.2 | 2.9 | 30.8 |
| cTnC 35 - cTnI 146 | 27.0 | 4.1 | 28.4 |
| cTnC 35 - cTnI 152 | 24.5 | 4.2 | 18.9 |
| cTnC 35 - cTnI 160 | 26.4 | 2.7 | 27.0 |
| cTnC 51 - cTnI 131 | 21.2 | 4.8 | 18.6 |
| cTnC 51 - cTnI 146 | 30.5 | 6.4 | 17.8 |
| cTnC 51 - cTnI 152 | 20.8 | 6.5 | 15.9 |
| cTnC 51 - cTnI 160 | 23.7 | 5.8 | 22.8 |
| cTnC 84 - cTnI 131 | 24.3 | 6.9 | 31.8 |
| cTnC 84 - cTnI 146 | 23.5 | 4.0 | 25.3 |
| cTnC 84 - cTnI 152 | 21.4 | 5.2 | 21.1 |
| cTnC 84 - cTnI 160 | 24.7 | 4.4 | 27.9 |
| cTnC 89 - cTnI 131 | 26.5 | 5.2 | 27.7 |
| cTnC 89 - cTnI 146 | 24.3 | 4.3 | 20.2 |
| cTnC 89 - cTnI 152 | 23.0 | 2.5 | 21.2 |
| cTnC 89 - cTnI 160 | 24.8 | 5.2 | 25.1 |
| cTnC 94 - cTnI 131 | 26.0 | 3.0 | 27.7 |
| cTnC 94 - cTnI 146 | 24.3 | 4.1 | 20.2 |
| cTnC 94 - cTnI 152 | 25.6 | 3.0 | 26.6 |
| cTnC 94 - cTnI 160 | 28.7 | 7.0 | 28.2 |
| cTnC 127 - cTnI 131 | 37.0 | 2.8 | 38.8 |
| cTnC 127 - cTnI 146 | 28.4 | 3.7 | 37.2 |
| cTnC 127 - cTnI 152 | 33.0 | 3.1 | 37.9 |
| cTnC 127 - cTnI 160 | 37.1 | 5.0 | 44.0 |
| cTnC 159 - cTnI 131 | 26.6 | 3.5 | 26.1 |
| cTnC 159 - cTnI 146 | 25.5 | 3.8 | 22.2 |
| cTnC 159 - cTnI 152 | 26.4 | 4.8 | 22.9 |
| cTnC 159 - cTnI 160 | 29.7 | 5.0 | 28.6 |
| cTnI 129 - cTnI 152† | 28.4 | 6.9 | 20.9 |
| cTnC 35 - cTnC 111‡ | 46.7 | 6.6 |
These are interresidue distances between cTnC and cTnI in which the cTnC regulatory N-domain is saturated with Ca2+. The distance is the mean distance of the distribution of the distances, and the half-width is the full width at half-maximum height of the distribution.
taken from Dong et al., 2001.
taken from Dong et al., 2000.
inter-C-α distance measured from one structure of homology model.
The SA calculations allowed for the creation of many different structures for cTnI, which were then further refined with minimization. No term for van der Waals energy or electrostatics was used during SA, to permit extensive refolding of the molecules during refinement while guaranteeing that the cTnI residues could satisfy bonded energy terms and the FRET restraints. (Nonbonded interactions were included in final refinement, as described below.) The conformations of cTnC and of cTnI 152-160 were held fixed during SA. The conformation of cTnC was allowed to vary during the final minimization in which van der Waals were included, however. An α-helical secondary structure for cTnI 129-137 and 146-160 was enforced, as indicated by secondary structure for mouse cTnI 129-160 predicted by GORIV (Garnier et al., 1996):
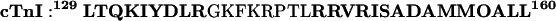 |
The regions shown in boldface are predicted to be helical, whereas the rest of the sequence (138-145) is predicted to be in a coil conformation. The helical structure of these regions was enforced by the use of a harmonic energy term for the (i, i + 1, i + 2, i + 3) C-α pseudo-dihedrals in the segments, with a minimum at a pseudo-dihedral value of +49°, the value for an ideal α-helix (Smith et al., 1997). The restraints for alpha helicity are required because of the high temperatures used during simulated annealing. During SA, a uniform mass of 50 amu was used for all atoms to use a 10 fs timestep. Before the introduction of FRET and secondary structure distance restraints, a 1000-step conjugate gradient minimization was conducted to satisfy the other bonded-energy terms of the forcefield. Then the FRET and secondary structure restraints were applied. After a preliminary 1000-step conjugate gradient energy minimization, each conformation was heated to 10000 K over a period of 50 ps. The structures were then cooled from 1000 K to 100 K over a period of 100 ps. Visual inspection and energetic analysis confirmed that this was sufficient to generate numerous structures, which satisfied all bonded terms, including secondary structure restraints and FRET restraints. This process resulted in a collection of 100 structures for the complex for each cTnC starting structure. Each cooled structure was minimized using conjugate-gradient methods for 2075 steps. This was sufficient to relieve bad van der Waals contacts, and any further minimization resulted in only very minor changes in the structures. During the final minimization, the van der Waals term was turned on, as were the pseudo-dihedral-based secondary structure restraints and the inter-C-α FRET distance restraints. The conformations of all cTnI and cTnC residues were allowed to vary during the final minimization.
The 100 final cTnI structures generated using SA and energy minimization for each given cTnC conformation were analyzed using conformational clustering based on root mean square distance (RMSD). For each cTnC structure, the generated cTnI structures were ordered by FRET distance restraint energy. The 10 cTnI structures for each cTnC structure with the lowest energies were then selected as low-energy structures. The RMSD between each low-energy structure and all other structures generated using the cTnC conformation was determined. During the RMSD calculation, only those cTnI α carbons from residues with FRET distance restraints were included. This emphasized the locations of the restrained residues during clustering. Two structures were included in the same cluster if they both had an RMSD of 5.5 Å or less to the same low-energy conformation. If any two groups shared one or more structures, then they were combined. Using this approach, three low-energy families of structures were identified for the sTnC homology model conformation of cTnC. Similarly, two low-energy families of structures were determined for the conformation of cTnC suggested by NMR dipolar couplings.
RESULTS
FRET distances
A total of 28 intermolecular distances between cTnC and cTnI were determined, in the presence of Mg2+ alone and in both Mg2+ and Ca2+. Several of these distances were previously reported in a preliminary study and were refined in the present work. The distances determined in the presence of bound Ca2+ (Mg2+ + Ca2+) and the half-widths of the distributions of the distances are listed in Table 1. Under these conditions, all three Ca2+ sites of cTnC were saturated. Although the individual cysteine residues modified with the donor probe in cTnC mutants were distributed along the length of the polypeptide, the four cysteines of cTnI mutants labeled with the acceptor were clustered within the contiguous inhibitory and regulatory regions (residues 130-165). FRET distances were determined between each of the seven cTnC sites and each of the four cTnI sites. These distances provided a large set of FRET restraints for modeling the structure of the complex cTnC-cTnI in the inhibitory/regulatory region. Two previously published intramolecular distances, one in the cTnI inhibitory region (between residues 129 and 52) and one between the two domains of cTnC (between residues 35 and 111), were used as additional restraints and are included in Table 1.
Resonance energy transfer rates may be affected by several factors, and these have been extensively discussed and tested. The effect of the donor-acceptor orientation factor κ2 in the estimation of mean distances and the distribution of distances is complex, because no theoretical models are available to describe the distribution of distances between two sites in proteins. Wu and Brand (1992) provided a detailed analysis, based on simulations and experimental results, of several factors that can modify an apparent distribution of distances. We used the dynamic averaged value of 2/3 for κ2 to calculate the Förster distance Ro. This use is justified in the calculation of mean intersite distances provided that the value of Ro is in the vicinity of or smaller than the mean distance. This requirement was met in the present study for most of the estimated distances as the individually determined Ro values were in the range 25–27 Å, close to or smaller than the recovered mean distances (Table 1). The experimental uncertainty in the determination of Ro was estimated using the standard procedure for propagation of random error and was in the range of 1–2 Å. This error is also typical for a large number of systems which we have studied in the past. Simulations by Wu and Brand also showed that the shape of the distribution of distances is better defined when Ro is close to or longer than the mean distance (Wu and Brand, 1992). The shape of a distance distribution should not depend upon Ro, but an apparent distance distribution containing a contribution from a large orientation distribution is expected to depend upon Ro and has an asymmetric shape. The FRET intensity decay data from the latter systems cannot be fitted with symmetric probability functions. In our systems, FRET data obtained from all donor-acceptor pair could be fitted with a Gaussian. Although the existence of a κ2 distribution cannot be ruled out, it is reasonable to assume that the recovered apparent distributions approximate the actual distance distributions.
Compact cTnI 129-160 structure
The dipolar coupling and homology based orientations for cTnC resulted in rather similar low-energy families of cTnI structure. Therefore, the families of low-energy models generated using both of these orientations are discussed together below.
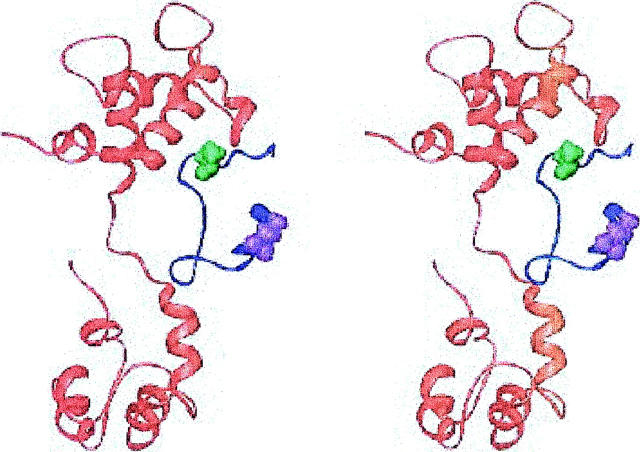
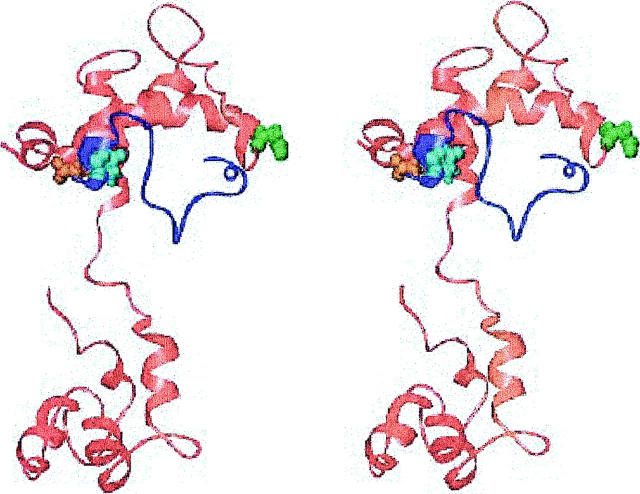
The structure of the lowest FRET restraint energy conformation, generated using the homology model of cTnC, is shown in Fig. 2. The largest deviation of inter-C-α distances from the FRET interprobe distances is for the distance between cTnI 129 and cTnI 152, which are 10.5 Å too close in this structure. In this family of structures, the inhibitory region of cTnI does not contact cTnC, in agreement with NMR chemical shift and relaxation time measurements (Abbott et al., 2001).
FIGURE 2.
Stereoview of the lowest energy structure from the compact cTnI 129-160 family of models, with the TnC homology-based orientation. The cTnC is shown in red, cTnI in blue, cTnI 129 in violet, and cTnI 152 in green. Generated with Ribbons (Carson, 1998).
This structure brings cTnI 129 and cTnI 152 too close together, within the context of the inter-C-α approximation, resulting in rather compact conformations for cTnI 129-160. Based on this FRET interprobe distance, Dong and co-workers argued for a more extended conformation for this segment of cTnI (Dong et al., 2001).
A similar family of cTnI conformations was found among the low-energy families of structures generated using the dipolar coupling derived model for cTnC. The superposition of the lowest energy member of this family from the dipolar coupling cTnC models and of the lowest energy structure from the compact family of structures built with the homology orientation of cTnC is shown in Fig. 3. Only residues 1-94 of cTnC are shown in this figure. Although these two cTnI conformations are somewhat different, they are quite similar. In particular, they are both compact configurations, with similar disagreements with the FRET distances. In the structure with the dipolar-coupling conformation of cTnC examined here, the only interresidue distance that disagrees with FRET data by more than 8 Å is cTnI 129-cTnI 152. This distance is about 9 Å too short in the model, similar to the results for the lowest energy homology model compact cTnI 129-160 structure.
FIGURE 3.
Stereoview of the structure of the lowest energy compact cTnI 129-160 model built with a homology-based orientation of cTnC, and a similar conformation from the dipolar coupling orientation models. The structure of cTnI 1-94 is in red, cTnI from the homology model structure in blue, and a similar dipolar coupling model cTnI conformation in green. cTnI 129 is in violet, cTnI 152 in orange. Generated with Ribbons (Carson, 1998).
Structures with the cTnI inhibitory region located near the central helix
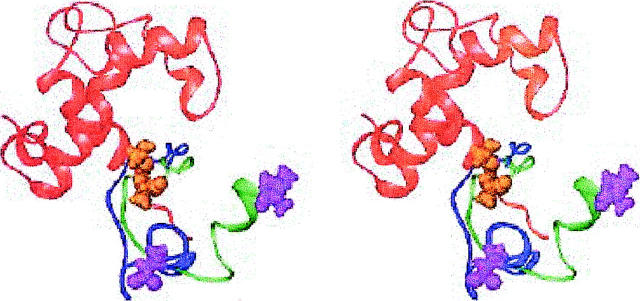
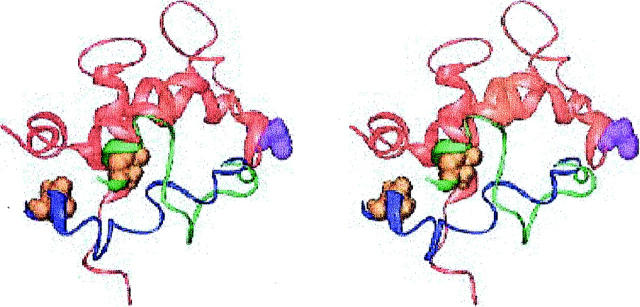
The lowest energy structure of another family is shown in Fig. 4. All of the FRET derived distance restraints can be satisfied within 6.5 Å in this family. The cTnI segment around residues 139-140 closely approaches the central helix of cTnC. However, NMR evidence (Abbott et al., 2001) suggests no interactions (or perhaps very weak ones) between the inhibitory region of cTnI and the central helix of cTnC. A structure from this family with a higher energy (but still one of the ten lowest energy structures) with fewer interactions with the central helix is also shown. This structure indicates that minor modifications can be made to improve the agreement of this region with the NMR data.
FIGURE 4.
Stereoview of the lowest energy cTnI model with the regulatory region located near the cTnC central helix (blue). This structure was generated using g homology model orientation for cTnC. Also shown is the cTnI conformation from another member of this family (green). cTnI 139 is space filling in both conformations. cTnC is shown in red. Generated with Ribbons (Carson, 1998).
Structures with cTnI located near the N-terminus of cTnC
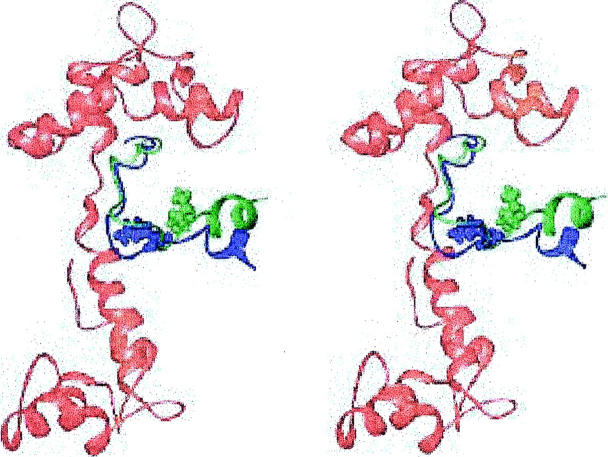
Shown in Fig. 5 is the lowest energy structure of another family. In this structure, the distance between cTnC 51 and cTnI 131 is about 9 Å too long. These residues are indicated in Fig. 5. Another area of concern in this family is that the inhibitory region around cTnI 131 and cTnC 15 are in contact. NMR methods have been used to show that there are no significant interactions between the inhibitory region of cTnI and the N-terminal region of cTnI, although there may be weak ones (Abbott et al., 2001).
FIGURE 5.
Stereoview of the lowest energy structure with the inhibitory region of cTnI located near the cTnC N-terminus, and the homology orientation for cTnC. cTnC is in red, cTnI in dark blue. cTnC 51 is space filling and green, cTnC 15 is space filling and orange, cTnI 131 is space filling and cyan. Generated with Ribbons (Carson, 1998).
Similar low-energy families of structures were generated using the dipolar coupling derived model for cTnC. The superposition of the lowest energy member of this family from the dipolar coupling cTnC models and of the lowest energy homology model structure with cTnI 129-160 located near the N-terminus of cTnC is shown in Fig. 6. Only residues 1-94 of cTnC are shown in this figure. Although these two cTnI conformations are somewhat different, they are quite similar. In particular, the inhibitory region of cTnI interacts with the B-helix of cTnC in both models, with similar disagreements with the FRET distances. In the structure with the dipolar-coupling conformation of cTnC examined here, the only interresidue distance that disagrees with FRET measurements by more than 8 Å is cTnC 51-cTnI 131. This distance is about 9 Å too long in the model, similar to the results for the lowest energy homology model structure with cTnI 129-160 located near the cTnC N-terminus.
FIGURE 6.
Stereoview of the lowest energy cTnI 129-160 model with the inhibitory region of cTnI near the cTnC N-terminus, generated using a homology-based orientation of cTnI (cTnI in green). Also shown is a similar structure from the dipolar-coupling models (cTnI in dark blue). cTnI 131 is orange and space filling in both models. cTnC 1-94 is in red, with cTnC 51 space filling and violet. Generated with Ribbons (Carson, 1998).
DISCUSSION
In this work, we have used simulated annealing methods to construct models for the complex formed between Ca2+-saturated cTnC and cTnI 129-160 (the inhibitory region and the bulk of the regulatory regions). The models were specifically constructed to satisfy distances derived using thirty FRET distances. The FRET experiments were conducted using the intact binary or ternary complexes. A helix-loop-helix orientation for the cTnI regulatory region was assumed, on the basis of secondary structure prediction. Probe lengths were not explicitly included, but rather the FRET distances were incorporated as inter-C-α restraints.
Several families of cTnI conformations with low FRET restraint energies were identified. Surprisingly, somewhat different orientations of cTnC resulted in very similar low-energy families of structures. Although the modeling methods used here are by necessity approximate, they are capable of generating several possible structures for the inhibitory and regulatory regions of cTnI for further experimental testing. By beginning from many different possible structures, we greatly improve sampling of possible structures.
None of these models should be eliminated without further testing of these structures. Each can be further tested in future experimental work. All of them show fairly good agreement with the FRET data, within the limits of the approximations made. These approximations include the assumptions of rapid and isotropic probe rotation (κ2 = 2/3) and the neglect of explicit probe lengths in the simulations. Structures belonging to each of these families also appeared repeatedly during the modeling.
If the true conformation of cTnI 129-160 is similar to that observed in the rather compact family of cTnI129-160 model structures, then cTnI 129 and 152 should be fairly close (20 Å) in the calcium-saturated state of the troponin complex. Therefore, these residues should only be ∼10 Å from each other in the 2-Ca2+ form of the complex, because the distance observed between these residues increases by ∼9 Å upon calcium saturation according to FRET (Dong et al., 2001). This would result in a quite compact structure for the inhibitory region.
A low-energy family of structures with the cTnI inhibitory structure located near the central helix of cTnC also appeared. This family shows the best agreement with the FRET distances, assuming that our approximations are valid. Slight modifications to this structure result in inhibitory region conformations that should interact, at most, weakly with the central helix of cTnC, in agreement with NMR studies (Abbott et al., 2001).
A structure in which the regulatory region is near the N-terminal regulatory domain of cTnC is also possible. Interaction between the inhibitory region of cTnI and the regulatory N-domain of cTnC has been observed with NMR (Abbott et al., 2001), but the interaction appears to be weak (Abbott et al., 2001) compared to the well-known regulatory region-cTnC interaction (Li et al., 1999). This structure would suggest that cTnI 131 should be close to cTnC 15. This hypothesis could be tested experimentally. Indeed, cross-linking between sTnC 21 and sTnI 96-134 (homologous to cTnI 130-168) has been reported (Leszyk et al., 1998).
A model of the complex formed between skeletal TnI and TnC fully saturated with Ca2+ was recently reported showing proximities between the two proteins over a large segment of the TnI (Tung et al., 2000). In this model, the inhibitory region (residues 95-114, corresponding to cTnI 129-148) was modeled as a flexible β-hairpin in which the sharp turn was very close to the C-domain of TnC. This structural feature is not compatible with our models. Although some structural differences in the inhibitory region of TnI in the complex can be expected between the two isoforms of TnI, FRET distances are not consistent with a β-hairpin in the cardiac TnC-TnI complex.
We have identified a number of possible arrangements for the inhibitory and regulatory regions of cTnI in the intact Ca2+-saturated cTnC-cTnI complex. In these models the inhibitory region is modeled as a helix-loop-helix motif. These structures agree reasonably well with FRET distances and will help guide future studies of these regions of the cardiac troponin complex. The present models are confined to a small, but critical, segment that plays a key role in activation and regulation of cardiac muscle. Refinement of the models with additional experimental restraints and inclusion of a longer cTnI segment will provide insights from a low-resolution structure suitable for investigation of regulatory events.
Acknowledgments
This work was supported by grants from National Institutes of Health (HL52508 to H. C. C. and RR12255 to S. C. H. and C. L. Brooks, III).
References
- Abbott, M. B., W. J. Dong, A. Dvoretsky, B. DaGue, R. M. Caprioli, H. C. Cheung, and P. R. Rosevear. 2001. Modulation of cardiac troponin C-cardiac troponin I regulatory interactions by the amino-terminus of cardiac troponin-I. Biochemistry. 40:5992–6001. [DOI] [PubMed] [Google Scholar]
- Botts, J., J. F. Thomason, and M. F. Morales. 1989. On the origin and transmission of force in actomyosin subfragment 1. Proc. Natl. Acad. Sci. USA. 86:2204–2208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaqminathan, and M. Karplus. 1983. CHARMM: A program for macromolecular energy, minimization and dynamics calculations. J. Comp. Chem. 4:187–217. [Google Scholar]
- Brünger, A. 1992. X-PLOR, Version 3.1: A System for X-Ray Crystallography and NMR. Yale University Press, New Haven.
- Carson, M. 1998. Ribbons 2.0. J. Appl. Crystallogr. 24:958–961. [Google Scholar]
- Cheung, H. C. 1991. Resonance energy transfer. In Topics in Fluorescence Spectroscopy. J. Lakowizc, editor. Plenum Press, New York. 121–171.
- Dong, W. J., M. Chandra, J. Xing, M. She, R. J. Solaro, and H. C. Cheung. 1997a. Phosphorylation-induced distance change in a cardiac muscle troponin I mutant. Biochemistry. 36:6754–6761. [DOI] [PubMed] [Google Scholar]
- Dong, W. J., C. K. Wang, A. M. Gordon, and H. C. Cheung. 1997b. Disparate fluorescence properties of 2-[4'-(iodoacetamido)anilino]naphthalene-6-sulfonic acid attached to Cys-84 and Cys-35 of troponin C in cardiac muscle troponin. Biophys. J. 72:850–857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong, W. J., J. Xing, M. Villain, M. Hellinger, J. M. Robinson, M. Chandra, R. J. Solaro, P. K. Umeda, and H. C. Cheung. 1999. Conformation of the regulatory domain of cardiac muscle troponin-C in its complex with cardiac troponin-I. J. Biol. Chem. 274:31382–31390. [DOI] [PubMed] [Google Scholar]
- Dong, W. J., J. M. Robinson, J. Xing, P. K. Umeda, and H. C. Cheung. 2000. An interdomain distance in cardiac troponin C determined by fluorescence spectroscopy. Protein Sci. 9:280–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong, W. J., J. Xing, J. M. Robinson, and H. C. Cheung. 2001. Ca2+ induces an extended conformation of the inhibitory region of troponin I in cardiac muscle troponin. J. Mol. Biol. 314:51–61. [DOI] [PubMed] [Google Scholar]
- Dvoretsky, A., E. M. Abusamhadneh, J. W. Howarth, and P. R. Rosevear. 2002. Solution structure of calcium saturated cardiac troponin C bound to cardiac troponin I. J. Biol. Chem. 277:38565–38570. [DOI] [PubMed] [Google Scholar]
- Farah, C. S., and F. C. Reinach. 1995. The troponin complex and regulation of muscle contraction. FASEB J. 9:755–767. [DOI] [PubMed] [Google Scholar]
- Förster, Th. 1965. Istanbul Lectures, Part III: action of light and organic crystals. In Modern Quantum Chemistry, Vol. 3. O. Sinanoglu, editor. Academic Press, New York. 93–137.
- Garnier, J., J. F. Gibrat, and B. Robson. 1996. GOR method for predicting protein secondary structure from amino acid sequence. Methods Enzymol. 266:540–553. [DOI] [PubMed] [Google Scholar]
- Herzberg, O., and M. N. James. 1985. Structure of the calcium regulatory muscle protein troponin-C at 2.8 Å resolution. Nature. 313:653–659. [DOI] [PubMed] [Google Scholar]
- Herzberg, O., and M. N. James. 1988. Refined crystal structure of troponin C from turkey skeletal muscle at 2.0 Å resolution. J. Mol. Biol. 203:761–779. [DOI] [PubMed] [Google Scholar]
- Houdusse, A., M. L. Love, R. Dominguez, Z. Grabarek, and C. Cohen. 1997. Structures of four Ca2+-bound troponin C at 2.0 Å resolution: further insights into the Ca2+ switch in the calmodulin superfamily. Structure. 5:1695–1711. [DOI] [PubMed] [Google Scholar]
- Lakowicz, J. R., I. Gryczynski, H. C. Cheung, C. K. Wang, M. L. Johnson, and N. Joshi. 1988. Distance distributions in proteins recovered by using frequency-domain fluorometry. Applications to troponin I and its complex with troponin C. Biochemistry. 27:9149–9160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leszyk, J., T. Tao, L. M. Nuwaysir, and J. Gergely. 1998. Identification of the photocrosslinking sites in troponin-I with 4- maleimidobenzophenone labelled mutant troponin-Cs having single cysteines at positions 158 and 21. J. Muscle Res. Cell Motil. 19:479–490. [DOI] [PubMed] [Google Scholar]
- Lewit-Bentley, A., and S. Rety. 2000. EF-hand calcium-binding proteins. Curr. Opin. Struct. Biol. 10:637–643. [DOI] [PubMed] [Google Scholar]
- Li, M. X., L. Spyracopoulos, and B. D. Sykes. 1999. Binding of cardiac troponin-I147-163 induces a structural opening in human cardiac troponin-C. Biochemistry. 38:8289–8298. [DOI] [PubMed] [Google Scholar]
- McKay, R. T., B. P. Tripet, R. S. Hodges, and B. D. Sykes. 1997. Interaction of the second binding region of troponin I with the regulatory domain of skeletal muscle troponin C as determined by NMR spectroscopy. J. Biol. Chem. 272:28494–28500. [DOI] [PubMed] [Google Scholar]
- O'Donoghue, S. I., B. D. Hambly, and C. G. dos Remedios. 1992. Models of the actin monomer and filament from fluorescence resonance-energy transfer. Eur. J. Biochem. 205:591–601. [DOI] [PubMed] [Google Scholar]
- Olah, G. A., S. E. Rokop, C. L. Wang, S. L. Blechner, and J. Trewhella. 1994. Troponin I encompasses an extended troponin C in the Ca2+-bound complex: a small angle X-ray and neutron scattering study. Biochemistry. 33:8233–8239. [DOI] [PubMed] [Google Scholar]
- Potter, J. D., and J. Gergely. 1975. The calcium and magnesium binding sites on troponin and their role in the regulation of myofibrillar adenosine triphosphatase. J. Biol. Chem. 250:4628–4633. [PubMed] [Google Scholar]
- Richter, M. L., B. Snyder, R. E. McCarty, and G. G. Hammes. 1985. Binding stoichiometry and structural mapping of the epsilon polypeptide of chloroplast coupling factor 1. Biochemistry 24:5755–5763. [DOI] [PubMed] [Google Scholar]
- She, M., J. Xing, W.-J. Dong, P. K. Umeda, and H. C. Cheung. 1988. Calcium binding to the regulatory domain of skeletal muscle troponin C induces a highly constrained open conformation. J. Mol. Biol. 281:445–452. [DOI] [PubMed] [Google Scholar]
- Sia, S. K., M. X. Li, L. Spyracopoulos, S. M. Gagne, W. Liu, J. A. Putkey, and B. D. Sykes. 1997. Structure of cardiac muscle troponin C unexpectedly reveals a closed regulatory domain. J. Biol. Chem. 272:18216–18221. [DOI] [PubMed] [Google Scholar]
- Smith, P. E., H. D. Blatt, and B. M. Pettitt. 1997. A simple two-dimensional representation for the common secondary structural elements of polypeptides and proteins. Proteins. 27:227–234. [PubMed] [Google Scholar]
- Stone, D. B., P. A. Timmins, D. K. Schneider, I. Krylova, C. H. I. Ramos, F. C. Reinach, and R. A. Mendelson. 1988. The effect of regulatory Ca2+ on the in situ structures of troponin C and troponin I: a neutron scattering study. J. Mol. Biol. 281:689–704. [DOI] [PubMed] [Google Scholar]
- Stryer, L. 1978. Fluorescence energy transfer as a spectroscopic ruler. Annu. Rev. Biochem. 47:819–846. [DOI] [PubMed] [Google Scholar]
- Sundaralingam, M., M. Bergstrom, G. Strasburg, P. Rowchowdhury, M. Greaser, and B.-C. Wang. 1985. Molecular structure of troponin C from chicken skeletal muscle at 3 Å resolution. Science. 227:945–948. [DOI] [PubMed] [Google Scholar]
- Syska, H., J. M. Wilkinson, R. J. Grand, and S. V. Perry. 1976. The relationship between biological activity and primary structure of troponin I from white skeletal muscle of the rabbit. Biochem. J. 153:375–387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tung, C. S., M. E. Wall, S. C. Gallagher, and J. Trewhella. 2000. A model of troponin-I in complex with troponin-C using hybrid experimental data: the inhibitory region is a beta-hairpin. Protein Sci. 9:1312–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuschl, T., C. Gohlke, T. M. Jovin, E. Westhof, and F. Eckstein. 1994. A three-dimensional model for the hammerhead ribozyme based on fluorescence measurements. Science. 266:785–789. [DOI] [PubMed] [Google Scholar]
- Vassylyev, D. G., S. Takeda, S. Wakatsuki, K. Maeda, and Y. Maeda. 1998. Crystal structure of troponin C in complex with troponin I fragment at 2.3-Å resolution. Proc. Natl. Acad. Sci. USA. 95:4847–4852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, P., and L. Brand. 1992. Orientation factor in steady-state and time-resolved resonance energy transfer measurements. Biochemistry. 31:7939–7949. [DOI] [PubMed] [Google Scholar]