An X-Ray Diffraction Study on Early Structural Changes in Skeletal Muscle Contraction

Abstract

Structural changes in frog skeletal muscle were studied using x-ray diffraction with a time resolution of 0.53–1.02 ms after a single electrical stimulus at 8°C. Tension began to drop at 6 ms (latency relaxation), reached a minimum at 8 ms, and then twitch tension developed. The intensity of the meridional reflection at 1/38.5 nm⁻¹, from troponin molecules on the thin filament, began to increase at 4–5 ms and reached a maximum at ∼12 ms. The meridional reflections based on the myosin 43-nm repeat began to decrease when the tension began to develop. The peak position of the third-order myosin meridional reflection began to shift toward the higher angle at ∼5 ms, reached a maximum shift (0.02%) at 10 ms, and then moved toward the lower angle. The intensity of the second actin layer line at 1/18 nm⁻¹ in the axial direction, which was measured at 12°C, began to rise at 5 ms, whereas the latency relaxation started at 3.5 ms. These results suggest that 1), the Ca²⁺-induced structural changes in the thin filament and a structural change in the thick filament have already taken place during latency relaxation; and 2), the Ca²⁺ regulation of the thin filament is highly cooperative.

INTRODUCTION

Physiological contraction of skeletal muscle is initiated by an action potential in the transverse tubules. A voltage sensor in the transverse tubules (dihydropyridine receptor) causes a conformational change of the calcium channel (ryanodine receptor) in the sarcoplasmic reticulum, which is located close to the Z-line in frog skeletal muscle. This results in calcium release into cytoplasm. The released calcium diffuses into myofibrils and binds to troponin molecules on the thin filament. The troponin-tropomyosin complex, which inhibits interaction between actin and myosin in the absence of calcium, undergoes a structural change upon binding calcium and allows the actin-myosin interaction. Then muscle contraction takes place.

X-ray diffraction from skeletal muscle provides structural information about proteins in myofibrils. Intensity changes in the early phase of contraction have been reported for the reflections that arise from the axial periodic arrangement of troponin molecules in the thin filament (Maéda et al., 1992), for those that arise from the helical structure of the thin filament (Kress et al., 1986), and for myosin and troponin-related reflections (Martin-Fernandez et al., 1994). However, precise comparisons of the time courses of the intensity changes and tension developments were limited by the available x-ray flux. Also, the temporal relationship between the intensity changes of other weaker reflections and tension development has not been determined with sufficient resolution, because the x-ray flux to make such a study was not available.

The “high flux” beamline (BL40XU) at the SPring-8 third-generation synchrotron radiation facility is designed to obtain the highest possible x-ray flux, 1 × 10¹⁵ photons/s at 12 keV, for small-angle scattering experiments (Inoue et al., 2001). Thus, it is most suited for muscle-diffraction experiments with high time resolutions. I used this beamline to elucidate an accurate relationship between structural changes in muscle proteins and tension development. The results were compared with calcium binding to troponin, which was deduced from experiments using calcium indicators (Baylor and Hollingworth, 2000).

MATERIALS AND METHODS

X-ray diffraction techniques

X-ray diffraction experiments were made using the BL40XU system (Hara et al., 2001; Inoue et al., 2001) at the SPring-8 third-generation synchrotron radiation facility (Harima, Hyogo, Japan). The ring current was 100–70 mA. The specimen-to-detector distance was 2.8 m. The x-ray energy was either 10.5 or 15.0 keV. A combination of Ni and Rh coatings of the two focusing mirrors was used. The energy bandwidth was ∼2% at 10.5 keV and 3% at 15.0 keV. At 10.5 keV, the flux without attenuation was 8 × 10¹⁴ cps. However, it was reduced approximately fourfold by an aluminum absorber to avoid radiation damage. Thus, the flux was ∼2 × 10¹⁴ cps. When the equatorial reflections were measured, the intensity was further reduced by approximately sixfold to avoid saturation of the detector. Experiments on the first and second actin layer lines were made with 15.0-keV x rays, for which the full flux was 6 × 10¹⁴ cps. Because these layer lines are at a larger angle than other reflections, it was necessary to use shorter wavelength (higher energy) x rays to record them with the detector and camera length used in this experiment. At 15.0 keV, no attenuation was used, because the radiation damage was not severe. Also, because only very weak actin layer lines were measured, there was no problem of detector saturation. Thus, the x-ray flux was 6 × 10¹⁴ cps. The size of the beam was adjusted to 0.25 mm horizontally and 0.15 mm vertically (full width at half-maximum) at the specimen in all experiments.

X-ray diffraction patterns were recorded using an x-ray image intensifier (model V5445P, Hamamatsu Photonics, Hamamatsu, Japan; Amemiya et al., 1995) coupled with a fast charge-couple device (CCD) camera (model C7770, Hamamatsu Photonics). This camera has three CCD chips that are exposed and read out alternatively to achieve a high frame rate. It can record 290 frames/s with a full frame of 640 × 480 pixels in 10 bits. The frame rate can be further increased by reducing the number of vertical pixels. In the current study, each frame had either 640 × 144 or 640 × 72 pixels, so that the frame rate was 980 or 1887 frames/s (1.02 or 0.53 ms/frame, respectively). The camera was rotated by 90° so that the vertical direction of the CCD (with a variable number of pixels) was parallel to the equator of the muscle-diffraction pattern, and the horizontal direction (with 640 pixels) was parallel to the meridian. At an x-ray energy of 10.5 keV, the two sides of the meridian and one side of the equator can be recorded with 640 × 144 pixels (Fig. 1), and only the two sides of the meridian can be recorded with 640 × 72 pixels. To record the first and second actin layer lines, the detector was shifted by ∼0.25 nm⁻¹ along the equator so that the strongest part of the second layer line could be recorded. The use of fast-decay phosphor (P46) reduced the persistence in the image intensifier to a negligible level (<1%) at the time resolution of the present study. The signals from the three CCDs were processed by different amplifiers. Because the basal (dark) levels of the signals from the three CCDs were different, a dark image was recorded by each CCD and subtracted from each frame. Also, because the gain of the preamplifier for each CCD was different, a correction (<6%) was made for the detector response. Even after this correction, a regular three-frame variation of intensity sometimes remained (for example, see Fig. 3 D).

FIGURE 1.

An x-ray diffraction pattern from a frog sartorius muscle in a resting state. This image was obtained by adding those from 10 exposures on different parts of 1 muscle. Total exposure time was 10.2 ms, x-ray energy was 10.5 keV, and specimen-to-detector distance was 2.8 m. The images were aligned before addition by using the two 14.3-nm meridional reflection peaks as a guide. The top horizontal arrow indicates the 14.3-nm meridional reflection from the thick filament. The lower horizontal arrow indicates the 44.1-nm meridional reflection from C-protein. The short vertical arrow indicates the equatorial (1,0) reflection.

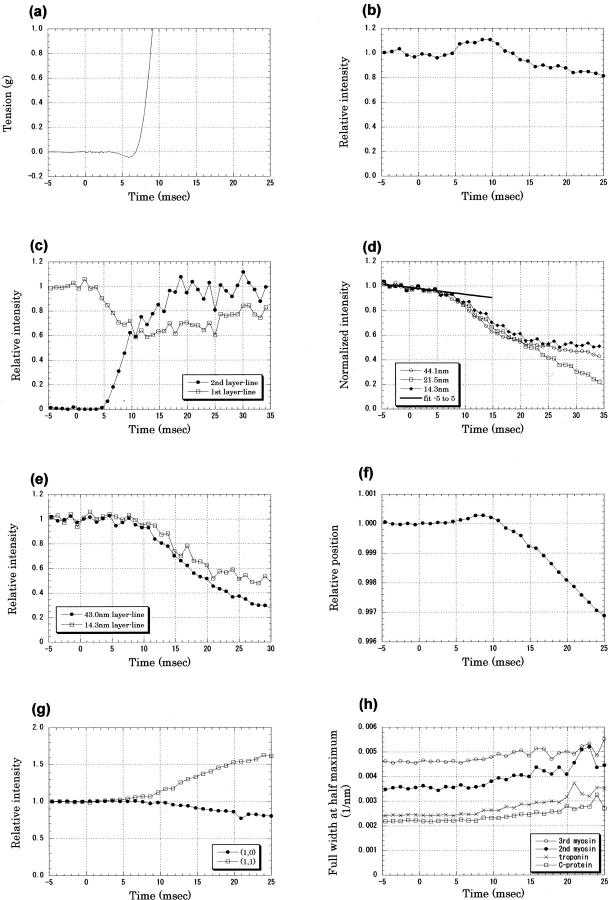
FIGURE 3.

Tension and x-ray diffraction intensities recorded in the early phase of twitch of frog sartorius muscle at 12°C. The x-ray data were recorded with a time resolution of 1.02 ms; results from 13 muscles, each of which was made to contract ∼10 times, were averaged. Intensity was normalized by an average of those before the stimulus. (A) Tension. A 1-ms stimulus was given at time 0. This trace is an average of 18 twitches of 9 muscles. (B) Intensity change of the troponin reflection at 1/38.5 nm⁻¹ after an electrical stimulus at time 0. The averaged intensity before the stimulus was 54,000 photons. Mean ± SD (n = 12) <0.01 before the stimulus and <0.05 in 0–25 ms. (C) Intensity changes of the first and second actin layer lines at 1/36 and 1/18 nm⁻¹, respectively. The intensity of the first layer line was normalized with that before the stimulus, whereas that of the second layer line was normalized by the intensity at 30–35 ms. The averaged intensity of the first layer line before the stimulus was 74,000 photons, and that of the second layer line at 30–35 ms was 59,000 photons. Mean ± SD (n = 11) for the second layer line, <0.01 both before the stimulus and in 0–25 ms; for the first layer line, <0.04 before the stimulus and <0.11 in 0–25 ms. (D) Intensity changes of the meridional reflections from the thick filament, a reflection from C-protein at 1/44.1 nm⁻¹, the second myosin reflection at 1/21.5 nm⁻¹, and the third myosin reflection at 1/14.3 nm⁻¹. The line was fitted to the slow intensity decrease of the C-protein reflection between −5 and 5 ms. The averaged intensities before the stimulus were 130,000, 55,000, and 124,000 photons for the three reflections, respectively. Means ± SD (n = 12) for the three reflections were <0.01 before the stimulus and <0.04 in 0–25 ms. (E) Intensity changes of myosin layer lines: the first layer line at 1/43 nm⁻¹ and the (1,0) sampling peak of the third layer line at 1/14.3 nm⁻¹. The averaged intensities before the stimulus were 53,000 and 9000 photons for the first and third layer lines, respectively. Mean ± SD (n = 12) for the 43-nm layer line, <0.01 before the stimulus and <0.04 in 0–25 ms; for the 14.3-nm layer line, <0.03 before the stimulus and <0.05 in 0–25 ms. (F) The position of the third-order meridional reflection from the thick filament, which was calculated from the center of gravity of five data points around the peak. The distance from the direct beam was normalized by the value before the stimulus. An increase indicates a shift toward the higher angle. Mean ± SD (n = 12) <0.0003 before the stimulus and <0.0012 in 0–25 ms. (G) Intensity changes of the equatorial reflections: the (1,0) reflection and the (1,1) reflection. The averaged intensities before the stimulus were 432,000 and 198,000 photons for the (1,0) and (1,1) reflections, respectively. Mean ± SD (n = 12) for the (1,0) reflection, <0.001 before the stimulus and <0.06 in 0–25 ms; for the (1,1) reflection, <0.03 before the stimulus and <0.11 in 0–25 ms. (H) Lateral width (full width at half-maximum) of the meridional reflections: the third-order myosin reflection at 1/14.3 nm⁻¹, the second-order myosin reflection at 1/21.5 nm⁻¹, the troponin reflection at 1/38.5 nm⁻¹, and the C-protein reflection at 1/44.1 nm⁻¹. Mean ± SD (n = 12) for the 14.3-nm reflection, <0.0001 nm⁻¹ before the stimulus and <0.0005 nm⁻¹ in 0–25 ms; for the 21.5-nm reflection, <0.0001 nm⁻¹ before the stimulus and <0.0006 nm⁻¹ in 0–25 ms; for the 38.5-nm reflection, <0.00005 nm⁻¹ before the stimulus and <0.0006 nm⁻¹ in 0–25 ms; and for the 44.1-nm reflection, <0.00004 nm⁻¹ before the stimulus and <0.0005 nm⁻¹ in 0–25 ms.

Muscle preparation

The specimen was a sartorius muscle of a small (body length, 6–8 cm) bullfrog (Rana catesbeiana). The frog was decapitated and quickly pithed, and the sartorius muscles were dissected. The muscle was mounted vertically in a specimen chamber through which Ringer solution containing 115 mM NaCl, 2.5 mM KCl, 1.8 mM CaCl₂, 3.0 mM Hepes (pH adjusted to 7.2 at 25°C) was circulated. The temperature was either 8 or 12°C. To avoid radiation damage, the specimen chamber was moved downward at a speed of 100 mm/s during an x-ray exposure. The specimen chamber had a pair of electrodes (made of silver plates), which were placed along the two sides of the muscle to induce field stimulation. The muscle was stimulated with a single supramaximal electric pulse of 1 ms duration. Tension was measured by one of the following two transducers. One was a semiconductor gauge with high sensitivity (model AE801, AME, Horten, Norway) and a resonant frequency of ∼2 kHz, which was used to measure latency relaxation. The other was a strain-gauge transducer (model UT-100, Minebea, Tokyo, Japan) with a resonant frequency of 300 Hz, which was mainly used to measure the peak twitch tension. Tension signal was recorded digitally with a sampling rate of 20 kHz. Because a small tension change was difficult to measure when the specimen was moving, latency relaxation was measured separately before and after x-ray experiments without moving the specimen chamber.

The muscle was stretched so that the sarcomere length was ∼2.5 μm in the resting state when measured with laser diffraction. The maximum twitch tension depended on the size of the muscle, ranging from 20 to 50 g. The resting tension was ∼3% of the peak twitch tension. The time-to-peak was ∼60 ms at 12°C. Stretching a muscle made it easier to measure the latency relaxation. Also, stretch made the muscle fibers straight so that the intensity of the meridional reflections did not change when the muscle was moved vertically in the x-ray beam. The intensities of the meridional reflections were affected by the tilt of the fiber axis in the plane defined by the fiber axis and the x-ray beam, because a sharp meridional diffraction spot moves in and out of the Ewald sphere when the fiber axis is tilted in this plane. Thus, at a shorter length, muscle fibers tended to be wavy, and the intensities of meridional reflections often varied erratically from frame to frame when the muscle was moved vertically (see Harford and Squire (1997) for this effect).

The data recording on each muscle was repeated 10–15 times with the same vertical translation. No significant deterioration of twitch tension was noticed. After each data recording, the specimen was moved sideways by 0.5 mm so that the same part of the muscle was not irradiated by x rays twice. No sign of radiation damage was observed under a light microscope after an experiment.

Data processing

Each x-ray diffraction pattern was rotated by using the two diffraction spots of the third-order myosin meridional reflection on either side of the equator as axis guides. Images of the same frame number were summed over experiments on each muscle (Fig. 1). Quadrant averaging was also done. A meridional intensity profile was obtained by integrating the intensity in the lateral region of 0–0.0051 nm⁻¹ (Fig. 2 A). Then, for the second to sixth myosin meridional reflections, background was subtracted by linearly connecting the regions on the two sides of the reflection (Fig. 2 A). The area above the background was taken as the integrated intensity. A lateral region of 0.022–0.058 nm⁻¹ was used for integration of the first myosin layer line, and 0.018–0.039 nm⁻¹ was used for the (1,0) sampling of the third myosin layer line. The equatorial intensity distribution was obtained by integrating the region within 0.0064 nm⁻¹ from the equator. The intensity was normalized by that before a stimulus, and the results were averaged over different muscles. The x rays used in the present experiment had an energy bandwidth of ∼3% with an asymmetric energy profile, which has a longer tail toward lower energies (Inoue et al., 2001). Thus, a peak profile of a meridional reflection had a tail toward the wider angle. This made it inappropriate to use the center of gravity of an intensity peak for its position. Therefore, the position was obtained by calculating the center of gravity of only five data points around the peak after a linear background subtraction. Although the positions of the three CCD chips were adjusted to one-third of the pixel size, the spacing changes measured in the present study were much smaller. Thus, it was necessary to correct for the misalignment of the three CCD chips. Even after this was done, the data points sometimes showed a tendency to cluster in three points (for example, see Fig. 4 E).

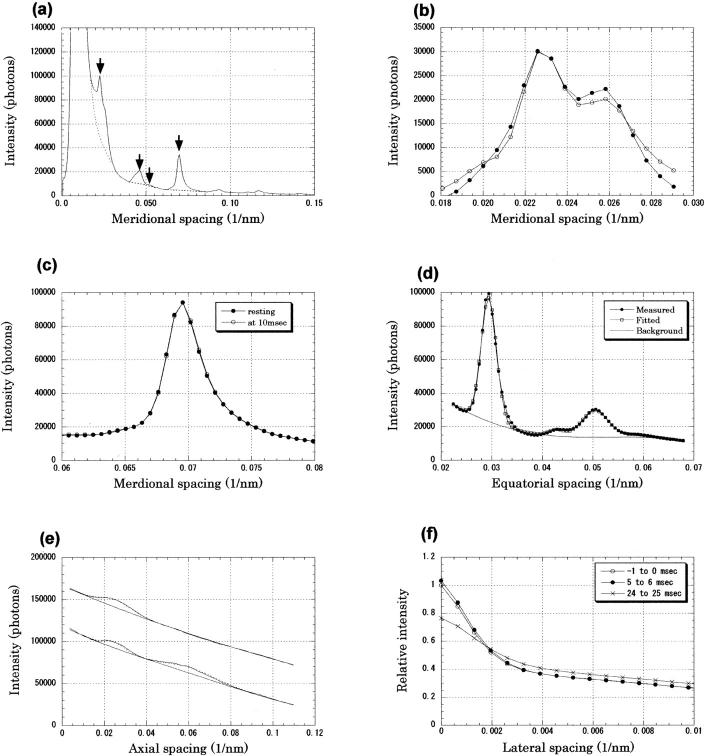
FIGURE 2.

(A) Intensity profile along the meridian; same data as in Fig. 1. Intensity was integrated within 0.0051 nm⁻¹ from the meridian. Arrows indicate (from left) 44.1-nm C-protein reflection, 21.5-nm second-order myosin reflection, 19-nm second-order troponin reflection, and 14.3-nm third-order myosin reflection. (B) Intensity profile in the region containing the C-protein and troponin reflections. The intensity distribution after background subtraction (•) and that obtained by the fitting procedure assuming three peaks at 1/44.1, 1/38.5, and 1/46 nm⁻¹ (○) are plotted. (C) Intensity profile along the meridian around the third-order myosin meridional reflection. Background is not subtracted. The profiles before the stimulus (resting) and 10–11 ms after the start of the stimulus are plotted. Temperature was 8°C. The intensity at 10–11 ms was higher on the high-angle side and lower on the low- angle side, which shows a shift of the peak toward the higher angle. The x-ray energy was 10.5 keV. This is an average of results from 10 contractions of 1 muscle. (D) Equatorial intensity profile in a resting state. A measured profile, a fitted profile, and a background are shown. The profile was fitted with a fourth-order polynomial background with four peaks: (1,0), (1,1), (2,0), and Z-line reflections. (E) Intensity distribution in the region of the first and second actin layer lines (0.19–0.29 nm⁻¹ in the equatorial direction) recorded with 15.0-keV x rays at 12°C. Upper profile is the intensity distribution before the muscle was stimulated, and lower profile is that at 14 ms after the beginning of the stimulus. For clarity, the lower profile was shifted vertically by 50,000 photons. The peak at ∼1/40 nm⁻¹ is the first layer line, whereas that at 1/18 nm⁻¹ (in the 14-ms trace only) is the second layer line. The observed profile (continuous line), fitted peaks (dotted line), and fitted background are shown. (F) Lateral intensity profile of the troponin reflection at 1/38.5 nm⁻¹ in three frames: in 1 ms before the beginning of the stimulus), in 5–6 and 24–25 ms after the beginning of the stimulus at 12°C. Profiles are averages over 129 contractions of 11 muscles that were normalized by the meridional intensity before the stimulus as unity.

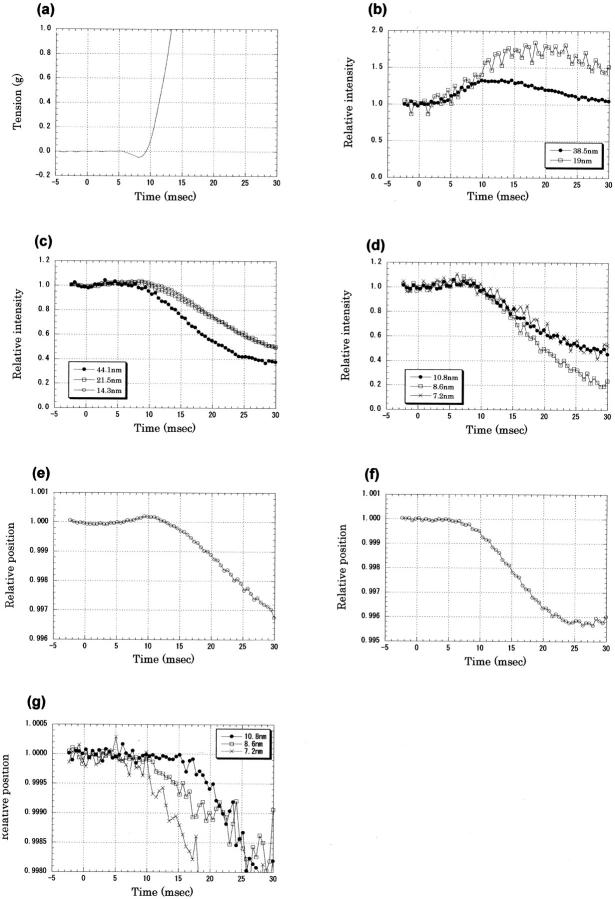
FIGURE 4.

Tension and x-ray diffraction intensities recorded in the early phase of twitch of frog sartorius muscles at 8°C. The x-ray data were recorded with a time resolution of 0.53 ms from 13 muscles, each of which was contracted 6–10 times. The intensity was normalized by the average of data points before the stimulus. (A) Tension recording in the early phase of twitch of frog sartorius muscles at 8°C. A 1-ms stimulus was given at time 0. This is an average of 28 contractions of 14 muscles. (B) Intensity changes of the first and second troponin reflections at 1/38.5 and 1/19 nm⁻¹ after an electrical stimulus at time 0. The averaged intensity before the stimulus was 160,000 for the first-order and 2000 photons for the second-order reflections. Mean ± SD (n = 14) for the 38.5-nm reflection, <0.06 both before the stimulus and in 0–30 ms; for the 19-nm reflection, <0.06 before the stimulus and <0.24 in 0–30 ms. (C) Intensity changes of the meridional reflections from the thick filament: a reflection from C-protein at 1/44.1 nm⁻¹, the second-order myosin reflection at 1/21.5 nm⁻¹, and the third-order myosin reflection at 1/14.3 nm⁻¹. The averaged intensities before the stimulus were 346,000, 180,000 and 372,000 photons for the three reflections, respectively. Mean ± SD (n = 14) for the C-protein reflection was <0.01 before the stimulus and <0.05 in 0–30 ms; for the second- and third-order myosin reflections, <0.01 before the stimulus and <0.04 in 0–30 ms. (D) Intensity changes of the higher-order meridional reflections from the thick filament: the fourth-order myosin reflection at 1/10.8 nm⁻¹, the fifth-order myosin reflection at 1/8.6 nm⁻¹, and the sixth-order myosin reflection at 1/7.2 nm⁻¹. The averaged intensities before the stimulus were 29,000, 33,000, and 1,2000 photons for the three reflections, respectively. Mean ± SD (n = 14) for the fourth-order reflection, <0.01 before the stimulus and <0.04 in 0–30 ms; for the fifth-order reflection, <0.02 before the stimulus and <0.06 in 0–30 ms; and for the sixth-order reflection, <0.05 before the stimulus and <0.12 in 0–30 ms. (E) The position of the third-order meridional reflection from the thick filament, which was calculated from the center of gravity of five data points around the peak. The distance from the direct beam, normalized by the resting value, is plotted. An increase indicates a shift toward the higher angle. Mean ± SD (n = 14) <0.00003 before the stimulus and <0.0002 in 0–30 ms. (F) The position of the second-order meridional reflection from the thick filament, which was calculated from the center of gravity of five data points around the peak. Mean ± SD (n = 14) <0.00009 before the stimulus and <0.0002 in 0–30 ms. (G) The positions of the fourth- (10.8 nm), fifth- (8.6 nm), and sixth- (7.2 nm) order meridional reflections from the thick filament, which were calculated from the center of gravity of five data points around the peak. Mean ± SD (n = 14) for the fourth-order reflection, <0.0001 before the stimulus and <0.0003 in 0–30 ms; for the fifth-order reflection, <0.00004 before the stimulus and <0.0003 in 0–30 ms; and for the sixth-order reflection, <0.0002 before the stimulus and <0.0010 in 0–30 ms.

To measure the intensities of the meridional reflections from C-protein and troponin at ∼1/44.1 and 1/38.5 nm⁻¹, respectively (Rome et al., 1973a,b), a fitting procedure was used. The intensity profile was fitted with a sum of three peaks and a fourth-order polynomial background (Fig. 2, A and B) using a modified Levenberg-Marquardt algorithm (subroutine UNLSF in the IMSL library, Visual Numerics, Inc., San Ramon, CA). The highest points of the peaks were fixed at 1/46, 1/44.1, and 1/38.5 nm⁻¹. The first small peak at 1/46 nm⁻¹ actually consisted of two or more meridional reflections of an unknown origin (Huxley and Brown, 1967). The troponin and C-protein reflections were also split into two peaks but could not be resolved in the present study. For the profile fitting, the intensity profile of the meridional reflection at 1/14.3 nm⁻¹ was obtained by using a linear background subtraction. It was then converted to the energy profile via normalization by the distance between the peak position and the direct beam. The profiles of the 46-, 44.1-, and 38.5-nm reflections were expected to be broader than that of the 14.3-nm reflection because of the vertical beam size (∼0.2 mm at the detector) and the spatial resolution of the x-ray detector (∼0.3 mm). The observed profile was expected to be a convolution of the intrinsic width of the reflection with the energy spread, beam size, and spatial resolution. To simulate this, the profile obtained from the 14.3-nm⁻¹ reflection was broadened to fit the peaks of the three reflections. Broadening of 200% gave the most satisfactory result. The fit was generally good enough to separate contributions from the three reflections (Fig. 2 B).

The lateral width of a meridional reflection was obtained in a 1-pixel axial section (parallel to the equator) that passed through the peak of the reflection (Fig. 2 F). The axial width of the section (1 pixel) corresponds to a meridional spacing of 0.00065 nm⁻¹. The background was removed by linearly extrapolating the intensity distribution in the region of 0.005–0.010 nm⁻¹ to the meridian. A full width at half-maximum was obtained by interpolation between data points. The beam size and the spatial resolution of the detector (see the previous paragraph) accounted for 1–2 pixels (∼0.001 nm⁻¹) of the width.

The intensities of the (1,0), (1,1), and (2,0) equatorial reflections from the hexagonal lattice of the thick and thin filaments and a reflection from the square lattice of the thin filaments (Yu et al., 1977) were also measured using a fitting procedure. The entire equatorial intensity profile was fitted with a fourth-order polynomial background curve plus four reflection peaks (Fig. 2 D). Because the width of the reflections (corresponding to an energy width of ∼10%) was larger than the beam energy spread (2%), peaks were fitted with Gaussian functions.

The intensities of the first and second actin layer lines (at 1/36 and 1/18 nm⁻¹ axially, respectively) were also measured by fitting a fourth-order polynomial background plus two peaks (Fig. 2 E). The profiles of the peaks were assumed to be a Gaussian function with a 50% larger width on the high-angle side. For the second-order layer line, which had an intensity that increased after a stimulus, the intensity was not normalized by the resting intensity but was normalized between zero and peak values (Fig. 3 C).

RESULTS

Experiments at 12°C

Tension

At 12°C, muscle tension began to drop 3.5 ms after the onset of the stimulus (Fig. 3 A). This phenomenon is known as the latency relaxation (Sandow, 1944). The tension then began to rise, crossed the resting level at 7 ms, and developed quickly to reach the maximum twitch tension. The size of the latency relaxation was variable from muscle to muscle but was in the range of 0.05–0.1 g, which was 1/500 to 1/1000 of the peak twitch tension, in agreement with the previous reports (Sandow, 1944; Abbott and Ritchie, 1951).

Reflections from the thin filament

The intensity of the first troponin meridional reflection (at 1/38.5 nm⁻¹) began to rise at ∼5 ms after the onset of the stimulus (Fig. 3 B). It reached a maximum of ∼110% of its resting intensity at ∼9 ms and then decreased. The lateral width of the reflection was 0.0024 nm⁻¹ in the resting state (Fig. 3 H). When the muscle developed tension, the width increased (Fig. 2 F) and reached ∼0.0033 nm⁻¹ at 25 ms after the stimulus.

Maéda et al. (1992) argued that the intensity decrease of this reflection in the late phase was due to the binding of myosin heads to the thin filaments. In their measurement using a position-sensitive linear detector, the lateral intensity profile of the troponin reflection did not change when tension developed. However, in the present result (Fig. 2 F), it increased by nearly 50%. Because the net integrated intensity of a meridional reflection is proportional to the observed intensity multiplied by its radial width (Huxley et al., 1982), most of the intensity decrease in the late phase can be accounted for by this broadening. Martin-Fernandez et al. (1994) measured the meridional intensity changes in frog striated muscle in the early phase of contraction at 8°C with a time resolution of 4 ms. They explained the intensity changes in terms of four types of time courses: K₁ is due to thin-filament activation; K₂ is due to an order-disorder transition, during which the register between the filaments is lost; K₃ is due to formation of an actin-myosin complex; and K₄ is due to a change in the axial orientation of the myosin heads. Martin-Fernandez and colleagues found that the time course of the troponin reflection could be explained by combining the first three time courses. This interpretation is supported by the present observation.

The intensity of the second-order layer line from the actin-tropomyosin helix at 1/18 nm⁻¹ axially and ∼1/4 nm⁻¹ laterally was measured with 15.0-keV x rays. It also began to increase 5 ms after the beginning of the stimulus (Fig. 3 C). It reached a maximum at 20 ms. This result is similar to that reported by Kress et al. (1986) at a 2-ms time resolution.

The intensity of the outer region of the first actin layer line at 1/36 nm⁻¹ is known to decrease on contraction (Yagi, 1991). This layer line overlaps with the first myosin layer line at 1/43 nm⁻¹. When the intensity was integrated in this region (0.19–0.29 nm⁻¹ laterally), it was found to start to decrease 4 ms after the stimulus (Fig. 3 C). This change is earlier than that of the myosin layer line that was measured in an inner region (see Reflections from the thick filament), which suggests that the decrease represents the intensity change of the first actin layer line. The apparent axial peak position of the layer line moved from 1/41 to 1/43 nm⁻¹ in 5–15 ms after the stimulus (data not shown), which also suggests that the first layer-line intensity decreased.

Reflections from the thick filament

The intensities of the second- (at 1/21.5 nm⁻¹) and third- (at 1/14.3 nm⁻¹) order meridional reflections from the thick filament and the reflection from the C-protein (at 1/44.1 nm⁻¹) showed a tendency to decrease before the tension began to develop (Fig. 3 D). In each data set from one contraction experiment, the intensity either increased or decreased, with the maximum size of the change being up to 10%. It could be averaged out after summing a large amount of data, but with 100–150 data sets, the averaging was incomplete and resulted in a small change of intensity that either decreased or increased (see Experiments at 8°C). A possible cause of this gradual intensity change is the variation in muscle thickness along the muscle axis. Because the x-ray beam was passed through a different part of the muscle in each frame, variation in muscle thickness along the muscle fiber affected the observed intensity. The thickness of the muscle was <1 mm, so the number of fibers in depth was ∼10. The beam size was just 0.25 mm in width, which is only twice as large as the fiber diameter. Thus, because the fibers were not aligned perfectly parallel to the vertical translation, the number of fibers in the beam varied considerably during the vertical movement. This could cause an intensity change of 10%. Another possible reason for the gradual intensity change is a tilt of the fiber axis toward the x-ray beam (for its effect, see Methods). Because the gradual intensity change was not very striking in the equatorial reflections (see Equatorial reflections), changes in the sampling of the sharp meridional spots by the Ewald sphere may account for a part of it.

When the gradual intensity decrease was extrapolated (Fig. 3 D), the intensities of these reflections seemed to deviate at 5–8 ms after the beginning of the stimulus. The lateral widths of these three meridional reflections began to increase when the tension developed at 7–8 ms after the beginning of the stimulus (Fig. 3 H). The widths increased by 20–30% at 25 ms. This observation is consistent with the conclusion reached by Martin-Fernandez et al. (1994) that the intensity decrease of the myosin meridional reflections is partially due to loss of the axial register of the thick filaments (their time course K₂; see Reflections from the thin filament).

The intensities of the first- and third-order myosin layer lines at 1/43 and 1/14.34 nm⁻¹, respectively, also began to decrease at ∼8 ms after the beginning of the stimulus (Fig. 3 E).

The third-order myosin meridional reflection is known to shift toward the lower angle on contraction (Huxley and Brown, 1967). However, before this took place, the peak began to shift slightly toward the higher angle at 4 ms after the start of the stimulus and reached a maximum shift (0.03%) at ∼8 ms (Fig. 3 F). Then it began to move toward the lower angle. A similar result was obtained when the center of gravity of the entire profile of the reflection (not just the five points around the peak) was used as the peak position (data not shown). Although this reflection consists of two or three peaks (Huxley and Brown, 1967), they were not resolved in the present study.

Equatorial reflections

The intensity of the (1,0) equatorial reflection began to decrease at 8–10 ms after the start of the stimulus (Fig. 3 G). On the other hand, the intensity of the (1,1) reflection seemed to increase earlier, at ∼5 ms.

Experiments at 8°C

These experiments were made at higher time resolution (0.53 ms) and at lower temperature (8°C), where the contraction is slower, to clarify the time courses of meridional reflections. Because the size of a frame was only 640 × 72 pixels, the equatorial reflections were not measured. As there was not a problem of detector saturation on the equator, a higher flux was used than in the experiments at 12°C, and weaker reflections were measured.

Tension

The muscle tension began to drop 6 ms after the onset of the stimulus (Fig. 4 A). It then began to rise, crossed the resting level at 9 ms, and developed quickly. Thus, the mechanical response was slower by ∼2 ms at 8°C than at 12°C.

Reflections from troponin and C-protein

The intensity of the first troponin meridional reflection began to rise at 4–5 ms after the onset of the stimulus (Fig. 4 B). It reached a maximum of ∼130% of its resting intensity at ∼12 ms and then decreased. The increase was larger than at 12°C. This may be because the rise was shorter at 12°C.

The intensity of the second-order troponin meridional reflection at 1/19 nm⁻¹ also began to increase ∼5 ms after the beginning of the stimulus. It reached a maximum (70% higher than the resting intensity) at 15–20 ms and then began to decrease. Although the exact point of the start of the intensity change is difficult to define because of the scatter of data points, back-extrapolation of the slope of the intensity change gives 4 ms as the point of increase.

Reflections from the thick filament

The intensity of the meridional reflection from C-protein began to decrease slightly at 5 ms and then dropped rapidly after 10 ms (Fig. 4 C). The small, gradual decrease between 5 and 10 ms may not represent a true intensity change, because the intensity increase of the troponin reflection, which overlaps with the C-protein reflection, may affect the intensity measurement during this period.

The intensities of the second- (at 1/21.5 nm⁻¹), third- (at 1/14.3 nm⁻¹), fourth- (at 1/10.8 nm⁻¹), fifth- (at 1/86 nm⁻¹), and sixth- (at 1/7.2 nm⁻¹) order meridional reflections from the thick filament all began to decrease 8 ms after the start of the stimulus (Fig. 4, C and D). This is consistent with the observation by Piazzesi et al. (1999) that was made on single frog fibers at 4°C with a time resolution of 5 ms that all myosin reflections had the same latency as force development. The second-order reflection actually consists of several peaks (Huxley and Brown, 1967), and the fifth-order reflection has a peak on its small-angle side. These reflections were not resolved in the present study. In all meridional reflections, there was a gradual increase before the intensities began to decrease. Its possible causes are discussed (see Experiments at 12°C).

As was the case at 12°C, the position of the third-order myosin reflection began to shift toward the higher angle 5 ms after the stimulus and reached a maximum shift (0.02%) at ∼10 ms (Fig. 4 E). It then began to move toward the smaller angle. The peak position of the second-order myosin meridional reflection began to shift toward the smaller angle at ∼5 ms and continued to move afterward in the same direction (Fig. 4 F). Martin-Fernandez et al. (1994) found that the intensity of the low-angle half of this reflection decreased with a time course corresponding to that of a myosin-actin interaction (K₃; see Reflections from the thin filament), whereas the high-angle half decreased faster with a time course corresponding to an order/disorder transition (K₂). The different time courses in different parts of the reflection may contribute to the apparent shift of the reflection. Measurements on other meridional reflections (the fourth, fifth, and sixth) did not show an early shift toward the higher angle that was observed with the third-order reflection (Fig. 4 G). Although all of these reflections are actually composed of several peaks, they were not separated in the present experiment. It is possible that the shifts of peaks that were observed here were actually caused by relative intensity changes of closely separated peaks.

DISCUSSION

The present study is the first to investigate structural changes of muscle proteins in the early stage of contraction at a time resolution better than 1 ms using x-ray diffraction. To compare the structural changes with the rapid elevation of the cytoplasmic Ca²⁺ concentration, it is essential to measure the structural changes at this time resolution. It is also important to define the onset of force development. The latency relaxation can be used as a mark of transition from a resting to an active state of the contractile system (Sandow, 1944).

Structural change of troponin molecules

The earliest intensity changes observed in the present experiment were found in 1) the troponin meridional reflections, and 2) the actin layer lines. The intensity increase of the troponin reflections has been interpreted to be due to a structural change of troponin molecules upon Ca²⁺ binding, whereas their intensity decrease in the later phase was due to the binding of myosin heads to the thin filament (Maéda et al., 1992) or, additionally, the order/disorder transition of filaments (Martin-Fernandez et al., 1994). The intensity changes of the actin layer lines have been interpreted to be due to the shift of tropomyosin on the actin helix (Parry and Squire, 1973; Kress et al., 1986; Yagi and Matsubara, 1989). A recent report suggests that the intensities of the actin layer lines are also affected by a structural change in troponin molecules (Narita et al., 2001). The early change in the equatorial (1,1) intensity (Fig. 3 G) may also be due to a conformational change in the thin filament.

The concentration change of the intracellular Ca²⁺ in the early phase of contraction of frog muscle has been studied extensively by Baylor and colleagues (see, for a review, Baylor and Hollingworth, 2000). They measured changes in the Ca²⁺ concentration using various fluorescent dyes and calculated the time course of Ca²⁺ binding to troponin (Baylor and Hollingworth, 1998). Taking the diffusion of Ca²⁺ from the Z-line to the M-line into account, they concluded that Ca²⁺ binding begins at 1–2 ms after the onset of a stimulus, and most troponin molecules in the thin filament have bound Ca²⁺ at 4 ms. Although their experiments were made at a higher temperature (16°C) than in the present study (8 or 12°C), most troponin molecules were expected to have bound Ca²⁺ at 4 ms in the present experiments. The binding constant of troponin that they employed in their calculation was 0.885 × 10⁸ M⁻¹·s⁻¹, and the dissociation constant was 115 s⁻¹. These are close to the values reported for the actin-tropomyosin-troponin complex by Rosenfeld and Taylor (1985), who used fluorescence-labeled troponin I for the measurement. Thus, a considerable fraction of troponin molecules should have undergone a structural change at 4 ms, whereas the present results show that the conformation of troponin only began to change at 4 ms at 8 and 12°C. Although the exact latency is difficult to measure because of the scatter of data, it is certain that the x-ray intensity change at 4 ms did not exceed 20% of the maximum change.

The slow time course of the conformational change of troponin shows that the binding of Ca²⁺ did not immediately change the conformation of troponin molecules. It also indicates that the intensity change of the troponin meridional reflection was associated not with the Ca²⁺ binding itself, but with the conformational change of troponin that took place later. One plausible explanation that has been discussed by Kress et al. (1986) is that the conformational change is highly cooperative so that it takes place only when most of the troponin molecules on one thin filament have bound Ca²⁺. Because Ca²⁺ is released near the Z-line and diffuses toward the M-line, Ca²⁺ concentration at the tip of the thin filament increases slowly (Hollingworth et al., 2000). The calculated rise in the Ca²⁺ concentration near the M-line began at 3 ms and reached a maximum at ∼8 ms (Baylor and Hollingworth, 2000). This is similar to the intensity changes of the troponin reflection and the second actin layer line. The presence of the clear 3-ms latency before the x-ray intensity changed supports this idea. If the entire thin filament is regulated as a single unit (Brandt et al., 1987), the slow structural change of troponin molecules observed in the present study may be accounted for.

Structural change in the thick filament

The present study shows the presence of early apparent spacing changes of the meridional reflections from the thick filament. The shift of the second- and third-order myosin meridional reflections began to take place at 5–6 ms after the start of the stimulus, when the intensities of the meridional reflections from the thick filament had not begun to change (Fig. 4, C and D). The apparent spacing change of the third-order reflection was biphasic in that it was directed initially toward the higher angle (shorter spacing) and then toward the smaller angle (longer spacing). Because the tension initially goes down in latency relaxation and then develops, the directions of the apparent spacing changes were the same as what would be expected if the tension were stretching the thick filament. However, although the first apparent spacing change was ∼2–3% of the second change, the latency relaxation was <1% of the peak tension. Thus, the size of the first change was not proportional to the tension. The apparent spacing changes of the second- and higher-order reflections also began simultaneously as the latency relaxation but continued monophasically toward the smaller angle. These different behaviors of the apparent spacing changes suggest that they are not simply related to the tension development.

Because the apparent spacing changes take place before the intensities begin to change, it is unlikely that they are artifacts due to changes in the peak height. On the other hand, intensities of reflections from the thin filament had already started to change at 6 ms. Because the separation of reflections is not good in the present experiments due to the low energy resolution, it is necessary to consider possible artifacts. For instance, overlap of an actin or troponin reflection with the myosin meridional reflections might affect the spacing measurement. However, as the apparent spacing was measured by using only the strongest part of the reflections, it is unlikely that a slight overlap with a neighboring reflection would affect the spacing measurement. Also, no strong reflections are expected to arise from the thin filament on the low-angle side of the second- and third-order myosin meridional reflections.

A meridional intensity profile from resting skeletal muscles of vertebrates has many fine peaks (Huxley and Brown, 1967; Haselgrove, 1975; Malinchik and Lednev, 1992; Yagi et al., 1996; Linari et al., 2000). This is because the intensity distribution of the meridian is sampled by interference between the two symmetric halves of the thick filament across the M-line (Rome et al., 1973a; Linari et al., 2000). In the present results, the directions of the early shift of the peak positions were not fixed: the third order moved toward the higher angle whereas the second order moved toward the smaller angle. This phenomenon is likely to be caused by a small change in the interference pattern. A similar phenomenon has been reported by Huxley et al. (1994), who found that the amount of shifts of the meridional reflections from the thick filament upon contraction was considerably variable, although all shifts were toward the smaller angle.

In the present study, because the meridional intensity profile itself was not observed with high spatial resolution, it is difficult to assess the precise nature of the interference change. However, it is certain that a structural change takes place in the thick filament even before the tension begins to develop. Thus, it is suggested that Ca²⁺ directly affects the structure of the thick filament. Although one of two light chains of a myosin head can bind Ca²⁺, its binding site is occupied by Mg²⁺ in the resting state and can be replaced only very slowly by Ca²⁺ (Bagshaw and Reed, 1977).

It is interesting to note that the spacing change begins simultaneously with the latency relaxation. The resting tension of skeletal muscle is borne by titin (or connectin) molecules (Wang et al., 1991; Maruyama, 1997), which are bound to the thick filaments. Thus, it can be speculated that Ca²⁺ binds to titin and causes a structural change in the thick filament that lowers the resting tension. A possible candidate for the Ca²⁺ binding site on titin is the PEVK region, which is located in the N2-line of the sarcomere (Tatsumi et al., 2001). A structural change in this region may extend the titin molecule and lead to a drop in the resting tension and a structural change in the thick filament.