Abstract
In oxygenic photosynthesis, water is oxidized at a protein-cofactor complex comprising four Mn atoms and, presumably, one calcium. Using multilayers of Photosystem II membrane particles, we investigated the time course of the disassembly of the Mn complex initiated by a temperature jump from 25°C to 47°C and terminated by rapid cooling after distinct heating periods. We monitored polarographically the oxygen-evolution activity, the amount of the YDox radical and of released Mn2+ by EPR spectroscopy, and the structure of the Mn complex by x-ray absorption spectroscopy (XAS, EXAFS). Using a novel approach to analyze time-resolved EXAFS data, we identify three distinct phases of the disassembly process: (1) Loss of the oxygen-evolution activity and reduction of YDox occur simultaneously (k1 = 1.0 min−1). EXAFS spectra reveal the concomitant loss of an absorber-backscatterer interaction between heavy atoms separated by ∼3.3 Å, possibly related to Ca release. (2) Subsequently, two Mn(III) or Mn(IV) ions seemingly separated by ∼2.7 Å in the native complex are reduced to Mn(II) and released (k2 = 0.18 min−1). The x-ray absorption spectroscopy data is highly suggestive that the two unreleased Mn ions form a di-μ-oxo bridged Mn(III)2 complex. (3) Finally, the tightly-bound Mn2(μ-O)2 unit is slowly reduced and released (k3 = 0.014 min−1).
INTRODUCTION
The molecular basis of photosynthetic water oxidation has remained one of the major enigmas in bioenergetics research. The cleavage of bound water molecules to molecular oxygen and four protons is accomplished by the Photosystem II (PSII) protein-cofactor complex embedded in the thylakoid membrane of higher plants, green algae, and cyanobacteria. PSII functions as a water-plastoquinone oxidoreductase. It mediates the light-driven transfer of electrons from water at the lumenal side to a pool of plastoquinone molecules at the stromal side of the photoenzyme. The oxidation of two bound water molecules to molecular oxygen is catalyzed by a metal center at the lumenal side of PSII which contains four Mn atoms and, presumably, one calcium as well as one chloride ion as essential cofactors (Debus, 1992; Haumann and Junge, 1999; Dau et al., 2001; Robblee et al., 2001). Water oxidation proceeds through a light-driven cycle consisting of five increasingly oxidized redox states of the metal center, Si (i = 0–4, i represents the number of stored oxidizing equivalents; Kok et al., 1970). The S1-state is stable in the dark. Three polypeptides of 17, 23, and 33 kDa, denoted as extrinsic proteins, are bound at the lumenal side of PSII. They shield the Mn complex against the bulk water and play a role in establishing the binding properties of the metal ions (for review see Seidler, 1996).
Recently the molecular structure of PSII has been resolved by means of protein crystallography at a resolution of 3.8 Å (Zouni et al., 2001). Electron densities of heavy atoms have been identified and attributed to four Mn atoms. Structural details of the metal center, however, remain invisible. Detailed information on the Mn complex in various states is needed to understand the bioinorganic chemistry involved in photosynthetic water oxidation.
EXAFS spectroscopy can yield information on the structure of metal centers in metalloenzymes of noncrystalline samples, often at a higher resolution (with respect to the distances between atoms) than protein crystallography (Teo, 1986; Yachandra and Klein, 1996; Scott, 2000; Dau et al., 2001). The application of this technique to PSII has produced several tentative (and more or less detailed) structural models of the Mn complex (Yachandra et al., 1993; DeRose et al., 1994; Penner-Hahn, 1999; Dau et al., 2001; Robblee et al., 2001). Several models comprise two di-μ-oxo bridged Mn-dimers (two Mn2(μ-O)2 units), both lying about in the membrane plane (George et al., 1989; Mukerji et al., 1994; Dau et al., 1995; Schiller et al., 1998). (The μ indicates a bridging position between two metal ions; di-μ-oxo indicates the presence of two parallel oxygen bridges.) Models with three di-μ-oxo bridges between Mn atoms have also been discussed (Penner-Hahn, 1999; Robblee et al., 2001). PSII samples with a partly reduced Mn complex due to treatment with external electron donors have been studied by EXAFS spectroscopy (Riggs et al., 1992, 1993; Riggs-Gelasco et al., 1996b). Calcium has been proposed to be at a distance of ∼3.3 Å to Mn (Latimer et al., 1995, 1998; Cinco et al., 1998). However, this result was not reproduced by other authors (Riggs-Gelasco et al., 1996a).
It has been known for a long time that heating of PSII to moderate temperatures, which leaves the overall protein structure largely intact, inactivates oxygen evolution (Cheniae and Martin, 1966; Yamashita and Butler, 1968; Shutilova et al., 1995). Heat inactivation of oxygen evolution has been shown to be coupled to the unbinding of the three extrinsic polypeptides with molecular masses of 17, 23, and 33 kDa in the case of plant PSII (Franzen and Andreasson, 1984; Nash et al., 1985; Enami et al., 1994, 1998). Assaying the Mn content of heated PSII by atomic absorption spectroscopy, EPR, and NMR, the release of Mn from its binding site has been observed (Nash et al., 1985; Coleman et al., 1988; Enami et al., 1994, 1998). In the absence of the extrinsic proteins, the release of Mn has been proposed to be the consequence of its reduction to Mn2+ by external reductants, namely by OH− ions, in a reaction which may involve the production of peroxide (Thompson et al., 1989, Yocum, 1992).
In this work we employed moderate heating of PSII (temperature jump to 47°C) to achieve a relatively slow and stepwise disassembly of the Mn complex of PSII. The states of the Mn complex reached after increasing periods of heating were investigated by oxygen polarography, EPR spectroscopy, and, in particular, by x-ray absorption spectroscopy. We use a (novel) joint-fit approach to analyze simultaneously EXAFS spectra of the intact and the partially disassembled Mn complex at various times after the heat jump. The simultaneous simulation of these EXAFS spectra reduces the number of independent fit parameters per spectrum, thereby increasing the reliability of the obtained structural parameters. Based on the thus-obtained fit results, we develop a consistent kinetic and structural model which describes the stepwise disintegration of the Mn complex. The intact Mn complex in its S1 state seems to contain two di-μ-oxo bridges between high-valent Mn. One interesting intermediate formed within only 10 min of heating is a binuclear Mn unit with two Mn(III) ions separated by ∼2.7 Å and connected by one di-μ-oxo bridge.
MATERIALS AND METHODS
PSII membrane particles
PSII-enriched membrane particles were prepared from market spinach as described elsewhere (Iuzzolino et al., 1998; Schiller and Dau, 2000). The oxygen-evolution activity of the preparations under saturating continuous white-light illumination was 1200–1400 μmol O2 mg−1Chl h−1 at 28°C. This high activity is mainly attributable to the use of 1 M of betaine as a stabilizing cosolute in all preparation and assay media (Murata et al., 1992; Lee et al., 1997; Schiller and Dau, 2000). PSII membranes were stored at a chlorophyll concentration of ∼2.5 mg/ml at −80°C until use.
XAS and EPR samples
The same PSII samples were used for both x-ray absorption and EPR measurements. They were prepared as described elsewhere (Schiller et al., 1998; Iuzzolino et al., 1998). For the heating experiments of this work, frozen PSII membranes were thawed for 30 min on ice and washed in a betaine-free buffer containing 10 mM NaCl, 5 mM CaCl2, and 25 mM MES-NaOH, pH 6 (buffer A). The resuspended pellet was filled into small acrylic-glass frames (outer dimensions of 20 × 4 × 1 mm) with a Kapton foil covering the bottom, and the frames were centrifuged at 48,000 × g for 15 min in a swing-out rotor. The centrifugation tubes with the pellet were then filled with buffer A and further centrifuged at 128,000 × g for 100 min. After centrifugation, the obtained PSII multilayers (thickness ∼400 μm) were dried for 6 h at 4°C in darkness (at 90% humidity) and then stored in liquid nitrogen. Each sample contained ∼0.5 mg of chlorophyll and Mn at a concentration of ∼1 mM. Noteworthily, the mechanical and geometrical properties of the thus-obtained samples allowed us to carry out first the heat treatment and then the EPR and EXAFS measurements on the same sample. For EPR measurements, the frames of acrylic-glass backed by Kapton tape and filled with PSII membrane particles were put on rods of acrylic-glass and inserted into the cavity of the spectrometer.
Heat treatment
Frozen PSII multilayer samples were thawed for 1 min at room temperature. Samples were enclosed in Eppendorf cups and exposed to 47°C for 0–180 min by immersion in a digitally controlled thermostated water bath. Immediately after the heat treatment, the PSII multilayers were again rapidly frozen (within less then 5 s) in liquid nitrogen (freeze-quench procedure for XAS and EPR samples). For the activity assay, the samples were not frozen in liquid nitrogen, but rapidly put on ice, resuspended (sample temperature always close to 0°C), and then immediately used for the polarographic measurements. This procedure of heating was the result of extensive variation of heating temperature and time followed by characterization of the heated samples by chlorophyll fluorescence measurements (see Pospíšil and Dau, 2000). At 47°C and for the indicated heating times, the inhibition of oxygen evolution in betaine-free samples was slow enough to be resolved.
Rate of oxygen evolution
Oxygen evolution measurements were carried out with PSII multilayers which were resuspended on ice (immediately after the heat treatment as described above) in a medium containing 10 mM NaCl, 5 mM CaCl2, 1 M betaine, and 25 mM Mes-NaOH, pH 6. Oxygen evolution was assayed using a Clark-type electrode under saturating continuous white-light illumination at 28°C using a chlorophyll concentration of 5 μg/ml, and 0.25 mM DCBQ plus 1 mM K3[Fe(CN)6] as artificial electron acceptors.
EPR measurements
EPR measurements with PSII multilayer samples were performed using an x-band EPR spectrometer (9.1 GHz, Bruker ESP 300E, Oxford, UK). EPR spectra were collected at 20 K using a helium cryostat. Data acquisition was carried out with the ESP 300 software of the spectrometer. For further experimental conditions, see figure legends.
X-ray absorption measurements
X-ray absorption measurements were carried out at the undulator beamline ID 26 of the European Synchrotron Radiation Facility (ESRF) in Grenoble, France. Manganese x-ray absorption spectra were measured by monitoring the excited x-ray fluorescence. The spectra were collected by scanning with an Si220 crystal monochromator, at 20 K, using a helium cryostat. The excitation angle between the electric field vector of the x-ray beam and the normal to the surface of the PSII multilayers was 55° (magic angle, Dittmer and Dau, 1998). x-ray fluorescence was detected perpendicular to the incident beam by a PIN photodiode (22-mm diameter, Eurisys Measures). A chromium filter was mounted between sample and photodiode to suppress scattered x-rays. A full x-ray absorption spectrum was recorded within only 8 s (scan range: 6500–7000 eV). Four separate spots and four scans per spot were taken on each sample. By controlling the Mn K-edge position we ensured that radiation damage (Dau et al., 1997) of the samples was negligible (the shift of the Mn K-edge was less than 0.2 eV after four scans on the same spot, meaning that ∼95% of Mn remained in its initial oxidation state). Energy calibration was facilitated by the simultaneous monitoring of the narrow pre-edge peak of a KMnO4 standard. For further details, see Meinke et al. (2000).
Data evaluation
Each XAS spectrum represents the average of ∼45−50 individual scans to improve the signal-to-noise ratio. After subtraction of the pre-edge background, the averaged spectra were normalized as described elsewhere (Schiller et al., 1998; Meinke et al., 2000). The Mn K-edge energy was determined using the integral method described in Dittmer et al. (1998), a method which is similar, but not identical to, the method-of-moments introduced by Alp et al. (1989). The energy scale of the EXAFS data was transformed to a wavevector scale (k-scale) using an energy threshold (E0) of 6546 eV. Phase functions for different elements in the various shells of backscatters were calculated using FEFF (version 7; see Mustre de Leon et al., 1991). For simulation and curve-fitting of EXAFS data, the EXAFS amplitude reduction factor (S02) was chosen to be 0.85; the used energy threshold (E0) was 6546 eV; data for k = 2.2 to 11.8 A−1 corresponding to energies ranging from 25 to 540 eV above the energy threshold were simulated. The k3-weighted EXAFS spectra were subjected to a least-squares curve-fit procedure using the in-house software SimX (Dittmer, 1999). For further details, see figure captions and text of the article presented here.
To judge the fit quality, the Fourier-filtered R-factor was used (denoted as RF). The RF value was obtained by calculation of the standard EXAFS R-factor for experimental and simulated data previously filtered by Fourier-isolation using a rectangular window ranging from 1.3 to 3.6 Å. The RF depends neither on the fit quality outside of the considered R-range nor on the number of k-space data points chosen during the transition from energy to wavevector scale. It should be noted that Fourier-filtering was employed only for calculation of the RF-value (after curve-fitting); for curve-fitting itself, exclusively unfiltered k-spectra had been used.
The rate constants that describe the various effects of heating on the Mn complex of PSII multilayers were determined by least-squares curve-fitting. The rate constants that are shown in Table 1 represent the mean values of the individual rates obtained from the simulations of the various effects of heating. The following equations were applied: a single exponential decay (plus offset; Eq. 1); a fast rising reaction (k2) preceded by an even faster process (k1) plus a slower exponential rise (plus offset; Eq. 2); a consecutive decay reaction plus a slower exponential decay (plus offset; Eq. 3); a consecutive reaction (Eq. 4); and a triple exponential decay (plus offset; Eq. 5; see results section for further details).
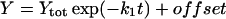 |
(1) |
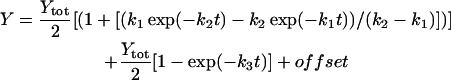 |
(2) |
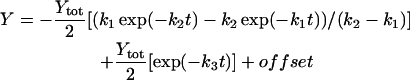 |
(3) |
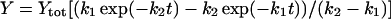 |
(4) |
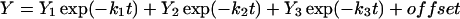 |
(5) |
TABLE 1.
Rate constants and relative amplitudes describing the response to a temperature jump
| Relative amplitude of ki-component
|
||||
|---|---|---|---|---|
| Equation no. | k1 1.0 ± 0.2* min−1 | k2 0.18 ± 0.04* min−1 | k3 0.014 ± 0.005* min−1 | |
| Decay of 02 evolution activity | 1 | 88% | – | – |
| TyrDox reduction | 1 | 95% | – | – |
| Mn2+ formation | 2 | p.r. | 50% | 50% |
| Downshift of Mn | 5 | 17% | 50% | 33% |
| K-edge energy | ||||
| Increase of ∼2.7 Å Mn-Mn distance | 1 | p.r. | 100% | – |
| Change of coordination no. | ||||
| NI | 3 | p.r. | 50% | 50% |
| NII | 2 | p.r. | 50% | 50% |
| NIII | 3 | p.r. | 50% | 50% |
| NIV | 4 | p.r. | 100% | – |
| NV | 1 | 100% | – | – |
| NVI | 3 | p.r. | 50% | 50% |
RESULTS
Previously frozen multilayers of PSII membrane particles were thawed for 1 min at room temperature. Then, these samples were suddenly exposed to a temperature of 47°C; and the processes initiated by this temperature jump were stopped by rapid cooling after heating times ranging from 0 to 180 min. This protocol facilitates the detailed analysis of the time course (or kinetics) of the heat-induced changes at the Mn complex by oxygen polarography, EPR spectroscopy, and x-ray absorption spectroscopy.
Oxygen polarography
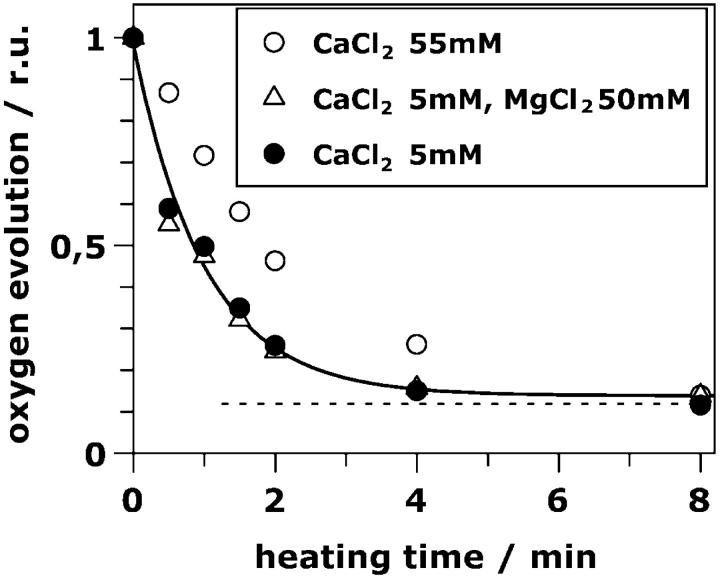
The rate of oxygen evolution of PSII particles exposed to saturating continuous light was investigated (Fig. 1). Using standard salt concentrations (5 mM CaCl2, solid circles, Fig. 1), already after 2 min of heating almost total inactivation is observed. The decay of the oxygen-evolution activity is well described by a single exponential with a rate constant of 1 min−1 (Fig. 1, solid line, see also Table 1). A small residual rate of oxygen evolution is observed even after long heating times (Fig. 1, dotted line). This offset was absent when only ferricyanide was used as an artificial electron acceptor (no DCBQ, high concentrations of K3[Fe(CN)6], results not shown). This behavior might be related to the production of hydrogen peroxide in centers where the Mn complex is partly disassembled (Schröder and Akerlund, 1986; Klimov et al., 1993).)
FIGURE 1.
Relative oxygen-evolution activity of resuspended PSII samples previously exposed to 47°C for various time periods. Oxygen evolution was measured in the presence of 5 mM CaCl2 (solid circles), 5 mM CaCl2 plus 50 mM MgCl2 (open triangles) and 55 mM CaCl2 (open circles). Additionally all media contained 15 mM NaCl, 1 M betaine, 20 mM MES-NaOH, pH 6, and 1 mM K3[Fe(CN)6] plus 0.25 mM DCBQ as electron acceptors. (Solid line), Single exponential decay with a rate constant of 1 min−1. (Dotted line), The small offset value discussed in the body of the text.
It has been shown that a temperature increase induces the rapid release of the so-called extrinsic polypeptides (MW of 17, 23, and 33 kD) from the PSII protein complex (Franzen and Andreasson, 1984; Nash et al., 1985; Enami et al., 1994) with a half-time close to 1 min. This half-time matches the deactivation half-time of our heated samples. Note that in the samples which were used for the experiments discussed here, no stabilizing cosolute like glycine betaine was present. In the presence of betaine, the extrinsic polypeptides are significantly more tightly bound (Murata et al., 1992; Lee et al., 1997) and the heat-induced loss of PSII activity is drastically slowed down (data not shown). We conclude that, most likely, the heat-induced deactivation process is coupled to the release of the extrinsic polypeptides of PSII.
The affinity of PSII for calcium binding is significantly reduced in PSII depleted of the extrinsic polypeptides (Ghanotakis et al., 1984; Seidler, 1996). In their absence, calcium at high concentration is required to retain oxygen-evolution activity at a reduced rate (in saturating light, 15–50% of the rate detectable in the presence of extrinsic polypeptides; Mei and Yocum, 1991; Andreasson et al., 1995). We also measured the oxygen-evolution activity in the presence of 55 mM of CaCl2 (instead of 5 mM). Under these high-calcium conditions, the loss of oxygen evolution is retarded (Fig. 1, open circles). The use of 50 mM of MgCl2 plus 5 mM of Ca2+, however, does not retard the deactivation (Fig. 1, triangles). This observation is suggestive that the heat-induced loss of the oxygen-evolution activity is indeed closely related to the release of the extrinsic polypeptides and, consequently, of calcium.
EPR spectroscopy
The heat-induced changes in the magnitude of two EPR signals were monitored (Fig. 2 A). In PSII the Tyr-161 of the D2 protein, which is not actively involved in the PSII electron transfer chain, mostly is present as a radical, the YDox radical (Debus et al., 1988; Vermaas et al., 1988). The YDox radical gives rise to a narrow EPR signal centered at g = 2 (see Miller and Brudvig, 1991). Reduction of the YDox radical necessarily results in the disappearance of the associated EPR signal. The amplitude of the YDox signal rapidly decreased with heating time and was close to zero after ∼2 min (Fig. 2 A, inset). After longer heating times a small underlying radical signal (centered at g = 2) of unknown origin remained. The decrease of the YDox signal (Fig. 2 A, dots) is well described by a single exponential with the same rate constant as observed for the loss of oxygen evolution, namely 1.0 min−1 (Fig. 2 A, line; the offset—dotted line—is attributable to the small underlying radical signal already mentioned above).
FIGURE 2.
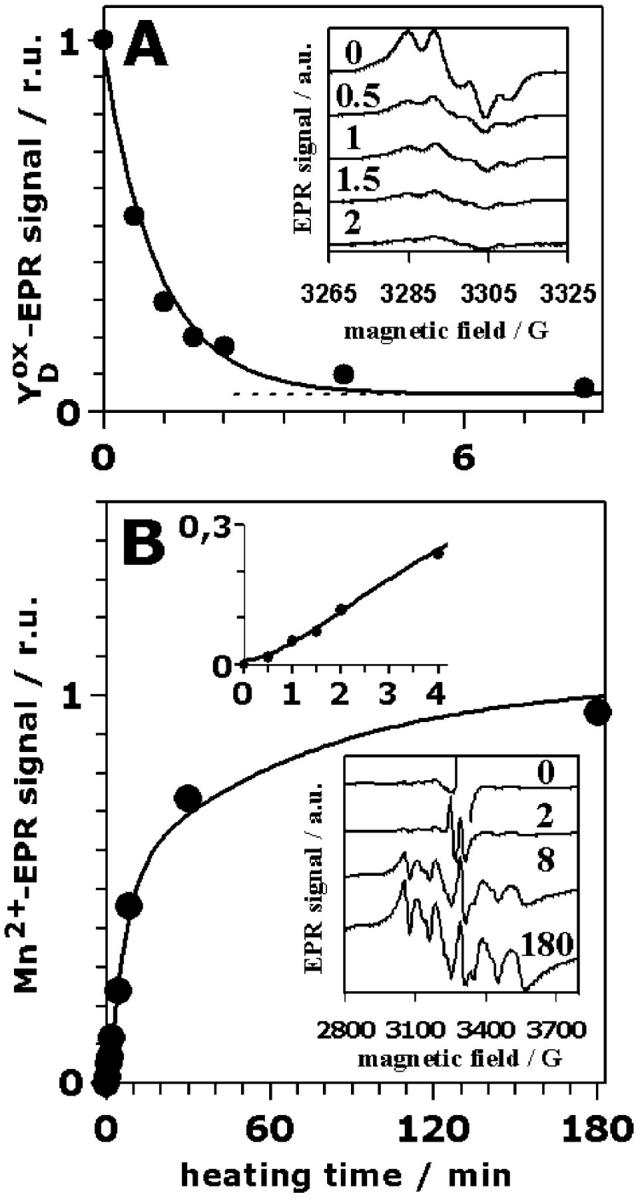
Relative amplitudes of EPR signals of PSII multilayers as function of the heating time: (A), YDox and (B), hexaquo-Mn2+. The data points represent the average of the analysis of three different samples. (A) The given amplitudes of the YDox signal correspond to the height of the first low-field maximum (see inset). The solid line was calculated using a mono-exponential decay with a rate constant of 1 min−1 and a small offset (dotted line). (Inset), EPR spectra of oxidized tyrosine YDox heated for the indicated time periods (in min) (EPR measurements at 20 K; microwave power of 2 μW; field modulation by 2.6 G at 100 kHz). (B) The amplitudes of the EPR spectra due to hexaquo Mn2+ were calculated as the sum of the amplitudes of the six lines (see inset) after normalization of the whole spectra on the amplitudes of the rhombic iron signal (∼g = 4, not shown). (Solid line), Calculated using the parameters listed in Table 1. (Top inset), EPR signal magnitude (solid circles) using an expanded time scale to show the sigmoidicity (lag-phase behavior) which is well reproduced by the simulations (solid line). (Bottom inset), EPR spectra of Mn2+ ligated by six water molecules (the hexaquo-Mn2+ six-line signal) at the indicated heating times. (EPR measurements at 20 K; microwave power of 300 μW; field modulation by 20 G at 12.5 kHz).
Manganese released from its binding site, the so-called free manganese, is typically present in the form of an Mn2+ symmetrically coordinated by six water molecules. This [Mn(H2O)6]2+ complex gives rise to a characteristic six-line EPR signal (Yocum et al., 1981; Miller and Brudvig, 1991). Therefore, the Mn2+ EPR signal was employed to monitor the release of Mn from its binding site subsequently to its reduction (Fig. 2 B). Almost no Mn2+ EPR signal was observed in the control (Fig. 2 B, inset, 0 min). For increasing heating times, the signal gradually develops; it reaches its maximal amplitude not before 180 min (Fig. 2 B, inset, 180 min). The increase in the Mn2+ EPR signal magnitude is clearly biphasic (Fig. 2 B, dots). The biphasic increase is preceded by a lag phase (see top inset in Fig. 2 B). The amplitudes of the fast and slow rising component are of equal magnitude (as revealed by curve-fitting) meaning that two of the four protein-bound Mn are released more than ten times faster than the second Mn pair. A similarly biphasic formation of Mn2+ in heated PSII has been previously reported (Coleman et al., 1988; Enami et al., 1994). A satisfying description of the data points in Fig. 2 B was obtained assuming that Mn2+ is released in a consecutive reaction, meaning that a reaction characterized by a rate constant of ∼1 min−1 precedes the fast Mn release. The curve in Fig. 2 B was calculated using Eq. 2 and rate constants of 1 min−1 (preceding process), 0.18 min−1 (fast Mn release) and 0.014 min−1 (slow Mn release) and equal amplitudes of the fast and slow release components (Table 1).
EXAFS spectra of intact PSII
The structural rearrangements of the Mn ligand environment as induced by the heat jump were investigated using x-ray absorption spectroscopy (XAS). Spectra were collected near (edge region) and above the Mn K-edge (EXAFS region).
EXAFS spectra are related to the superposition of the wave functions describing electrons released by the x-ray absorbing atom (the absorber, here Mn) and electron-backscattering at the nearby atoms (the backscatterers) of the first few coordination spheres (Stern, 1988; Teo, 1986). Therefore, EXAFS spectra are determined by the nuclear coordinates of the atoms in the vicinity of the absorber. As usually done, after normalization and background removal the energy scale was transformed to wavevector- or k-scale, and the EXAFS oscillations were weighted with k3. Exclusively such k3-weighted EXAFS spectra as well as the amplitude of the corresponding Fourier transformations (FT) are shown and discussed in the following.
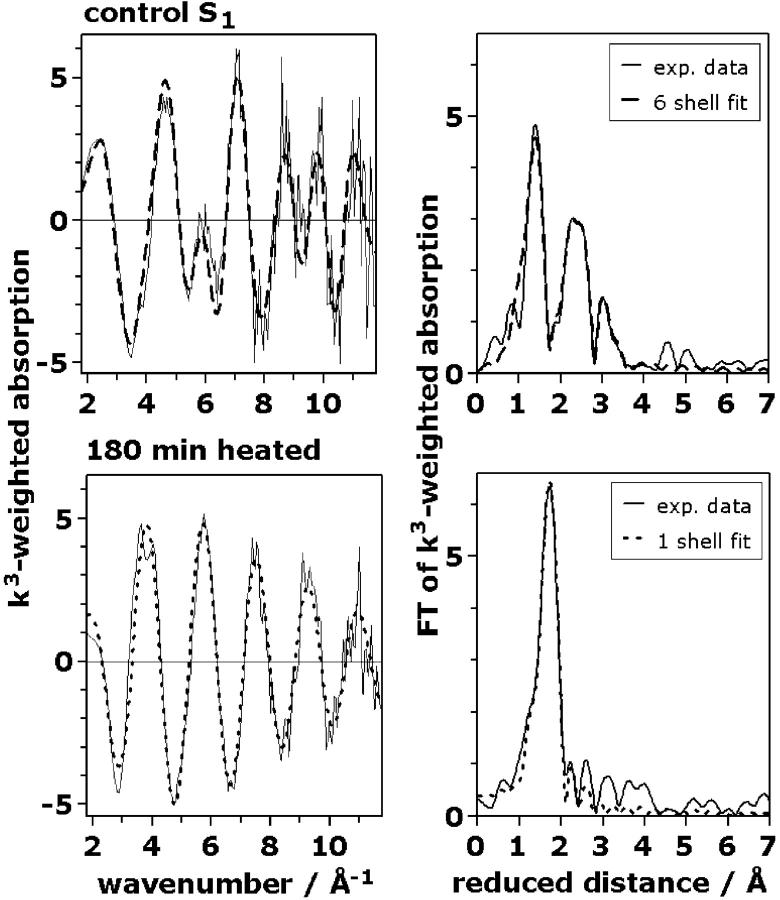
Fig. 3 (left column, thin lines) shows spectra of the unheated (control) PSII (upper row) and after 180 min of heating at 47°C (lower row). Visual inspection immediately reveals that the k-space EXAFS oscillations differ strongly. The right column of Fig. 3 shows the respective FTs. In unheated PSII three major peaks are visible (right, upper row), whereas only one major peak is present after 180 min of heating (right, lower row). The Fourier-transformed EXAFS spectra are shown because they facilitate a rough qualitative analysis of the EXAFS data. These FTs are related to the radial electron-density distribution around the absorbing Mn ions. Often, each peak in the FT represents one distinct shell of backscattering atoms at a mean absorber-ligand distance which is by ∼0.5 Å greater than the FT-peak position. However, the contributions of different backscatterers with closely spaced distances may give rise to interference phenomena leading to a counterintuitive behavior of the FT. (This holds in particular for regions of the FT where the amplitude is close to zero.) To extract quantitative structural information, exclusively k3-weighted EXAFS spectra were simulated (curve-fit); FTs were not involved in the fit approach used.
FIGURE 3.
EXAFS spectra of the Mn in PSII multiplayer preparations exposed for 0 min (intact PSII control, upper row) and 180 min (hexaquo Mn2+-state, lower row) to 47°C. (Left column), k3-weighted EXAFS spectra in the k-space; (right column), the respective Fourier transforms. The FTs were calculated for data points ranging from 25–540 eV using an energy threshold of E0 = 6546 eV. Control PSII (upper row): (solid line), experimental spectrum; (dashed line), a fit with six shells of backscatterers (fit no. 8, Table 2). PSII heated for 180 min (lower row): (solid line), experimental spectrum; (dashed line), a fit with a single shell of oxygen backscatterers.
In Table 2, simulation parameters for the EXAFS spectrum of the unheated PSII in its S1 state are shown; the used simulation approaches are discussed in the following. It is commonly assumed that, in the S1 state, the four Mn ions are present as five- or six-coordinate Mn(III) and Mn(IV). (The presence of any tetrahedrally coordinated Mn is not only unlikely from a chemical viewpoint, but also in conflict with the small magnitude observed for the XAS pre-edge feature.) To reduce the number of independent parameters, we did not use the number of ligands in the first Mn coordination sphere as a fit parameter, but fixed this number to a value of between 5 and 6 (i.e., 5.5).
TABLE 2.
Parameters obtained by alternative EXAFS-simulation approaches for the intact Mn complex
| Mn-O (N)
|
Mn-O (N)
|
Mn-Mn
|
Mn-Mn
|
Mn-Ca (Mn)
|
Mn-O (N/C)
|
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample | Fit no. | nfree | NI | RI [Å] |
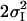 [Å2] [Å2] |
NII | RII [Å] |
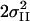 [Å2] [Å2] |
NIII | RIII [Å] |
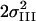 [Å2] [Å2] |
NIV | RIV [Å] |
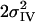 [Å2] [Å2] |
NV | RV [Å] |
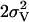 [Å2] [Å2] |
NVI | RVI [Å] |
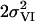 [Å2] [Å2] |
RF [%] | 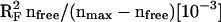 |
| PS II in S1-state | 1 | 8 | 5.5* | 1.86 | 0.029 | 1.30 | 2.71 | 0.005 | 3.4 | 3.62 | 0.007 | 17.8 | 63 | |||||||||
| 2 | 8 | 5.5* | 1.86 | 0.029 | 1.19 | 2.71 | 0.005 | 1.4 | 3.66 | 0.014 | 20.6 | 85 | ||||||||||
| 3 | 8 | 5.5* | 1.86 | 0.029 | 1.22 | 2.71 | 0.005 | 1.2 | 3.19 | 0.026 | 25.5 | 130 | ||||||||||
| 4 | 9 | 4.9† | 1.86 | 0.021 | 0.6† | 2.16‡ | 0.014‡ | 1.21 | 2.71 | 0.005 | 3.2 | 3.62 | 0.006 | 9.8 | 22 | |||||||
| 5 | 9 | 4.9† | 1.86 | 0.021 | 0.6† | 2.16‡ | 0.014‡ | 1.17 | 2.71 | 0.005 | 1.1 | 3.67 | 0.010 | 12.4 | 35 | |||||||
| 6 | 9 | 4.9† | 1.86 | 0.021 | 0.6† | 2.16‡ | 0.014‡ | 0.99 | 2.71 | 0.005 | 1.2 | 3.19 | 0.026 | 19.2 | 84 | |||||||
| 7 | 10 | 4.9† | 1.86 | 0.021 | 0.6† | 2.16‡ | 0.014‡ | 1.0* | 2.71 | 0.004 | 1.0* | 3.13 | 0.032 | 2.9 | 3.62 | 0.007 | 8.0 | 17 | ||||
| 8 | 10 | 4.9† | 1.86 | 0.021 | 0.6† | 2.16‡ | 0.014‡ | 1.0* | 2.71 | 0.005 | 0.5* | 3.07 | 0.004* | 0.5* | 3.29 | 0.004* | 3.0 | 3.63 | 0.008 | 5.2 | 7 | |
| 180 min heated | 9 | 3 | 6.2 | 2.16 | 0.014 | 16.2 | 32 | |||||||||||||||
In the last row, the fit results obtained for the fully disassembled state (180 min of heating) are shown. EXAFS phase functions were calculated for the absorber-backscatterer combinations shown in the first row; the elements given in parenthesis could also contribute to the respective backscattering shell. Meaning of symbols: Ni, apparent coordination number (per Mn); Ri, mean distance; 2σi2, Debye-Waller parameter; nFree, number of independently varied parameters, RF, filtered R-factor calculated for FT distances ranging from 1.2 to 3.6 Å as a measure for the fit quality (represents deviations in percent). The parameter in the last row represents the so-called goodness of fit, a quadratic error which is corrected for the increase in fit-quality due to an increased number of variable simulation parameters (Teo, 1986; nmax = 16, see text).
Simulation parameters which were fixed (no variation by the curve-fit algorithm).
In fit 4-8, NI and NII were variable, but coupled to yield a sum of 5.5.
RII and 2σII2 were determined from a fit of the spectrum obtained after 180 min of heating and fixed in the fits of the control spectrum.
In Table 2, the first three rows of parameters stem from a simple and conservative approach (three shells of backscattering atoms) which results in a low fit quality (RF ≈ 20%). One reason for this low fit quality is an inappropriate representation of the ligand distances in the first Mn coordination sphere by a single Gaussian distribution function (σ = 0.12 Å) centered at 1.86 Å (for a more detailed discussion, see Penner-Hahn, 1999). Using a more complex, pronouncedly asymmetric distribution function (4–8 in Table 2, sum of two Gaussian distributions with fixed amplitude ratio of 5: 0.5), we obtain a reduction of RF by up to 50% (1–3 versus 4–6). Presently, for the unheated PSII a clearcut assignment of the Mn ligands at ∼2.16 Å to a particular ligand species is not feasible; a putative chloride ligand and/or small amounts of released Mn might contribute.
The fit approaches 1–3 as well as 4–6, demonstrating that there is a minimum of the error sum for backscattering atoms ∼3.2 Å and ∼3.6 Å as already noted previously (Penner-Hahn, 1999; Meinke et al., 2000). We assume that a distinct number of heavy backscatterers (Mn, Ca) ∼3.2 Å and several light backscatterers (O, N, C) ∼3.6 Å determine the EXAFS spectra. Particularly good fits are obtained using simulation approach 8, which involves six absorber-backscatterer distances.
Not only the considerations outlined above lead us to a simulation approach involving six distinct absorber-backscatterer distances. Only a six-shell approach facilitates satisfying joint-fit simulations of both, the heating response of the PSII Mn complex (as shown below) and of EXAFS data collected at various detection angles on partially oriented samples (not shown, see Haumann et al., 2001).
In approach 6, we determine a value for NIII of 0.99. In approach 8, NIII is fixed to a value of 1.0 (corresponding to two 2.7 Å Mn-Mn vectors per Mn4-complex). For NIII fixed to a value of 1.5 (three Mn-Mn vectors), RF was found to increase significantly to 8.9% (and 2σ2III to 0.01 Å2). If NIII was allowed to vary, NIII and 2σ2-III refined to 0.98 and 0.005 Å2, respectively. These observations are suggestive that there are two 2.7 Å Mn-Mn vectors per Mn4-complex. However, the analysis presented in Table 2 should not obscure that the NIII-value of almost exactly one is obtained only if backscattering atoms at ∼2.0 Å and 3.2 Å are explicitly considered in the simulation approach. A similar reduction in the NIII-value due to the inclusion of additional backscattering shells already has been described previously, and it was correctly concluded that these additional shells are difficult or impossible to resolve by fully unbiased fits (meaning without constraints) of individual EXAFS spectra (DeRose et al., 1994; Riggs-Gelasco et al., 1996b; Penner-Hahn, 1999). In Table 2, the existence of well-defined minima in the error-sum was ensured by using constraints (fixed values of some Ni and σi). In the simulations of the time dependence discussed below, six shells of backscatterers became resolvable by virtue of the used joint-fit approach.
To emphasize that the choice of the simulation approach affects the absolute value obtained for NIII and to demonstrate that central conclusions of this work do not rely on the use of the complex six-shell approach, in the following, curve-fit results obtained for a three-shell simulation are also presented.
The used simulation approach of the EXAFS spectrum obtained after 180 min of heating (attributable to Mn2+) is particularly simple. The main peak in the FT (Fig. 3, 180 min) is well described by using a single shell of light atoms (O) at a distance of 2.16 Å to Mn. The coordination number of this shell was found to be close to 6 (Table 2). These results are expected for Mn2+ ions symmetrically coordinated by six water molecules. Some small peaks in the FT in the region above 2 Å, however, remain unexplained. Similar peaks were also observed in the EXAFS spectrum of an aqueous solution of MnCl2 (data not shown). We interpret the small peaks in the FT above 2 Å (Fig. 3, right, 180 min) as representing distances between Mn2+ and atoms of an hydration environment consisting of water and the macromolecules (polypeptides and lipids) present in the used PSII preparation. In the following, these weak long-distance contributions to the EXAFS spectra of the released aqueous Mn2+ are neglected.
Time dependence of EXAFS spectra
Fig. 4 shows EXAFS spectra of eight PSII samples exposed to 47°C for distinct time periods ranging from 0 to 180 min. In the control (no heating), three FT peaks are visible. With increasing heating time, the peak magnitudes become gradually diminished, and one new peak corresponding to the aqueous Mn2+ (Mn-OH2 distance of ∼2.2 Å) becomes prominent.
FIGURE 4.
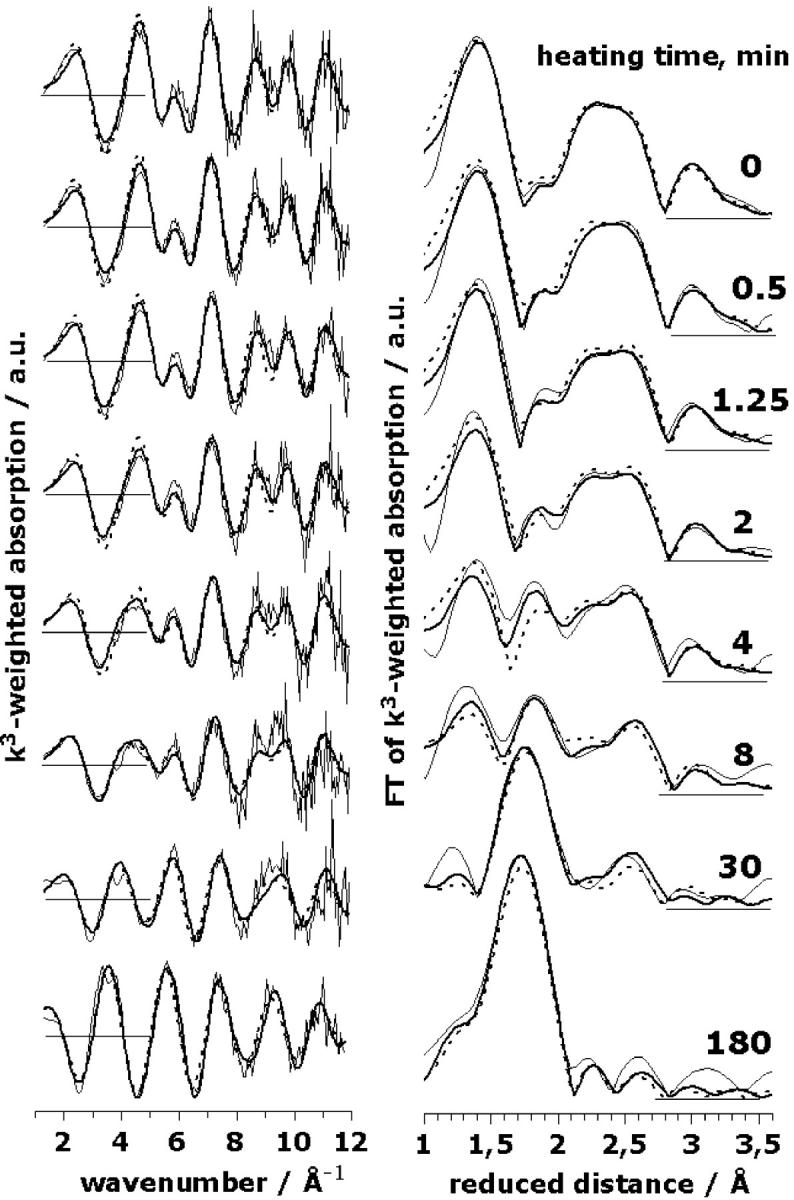
A series of EXAFS spectra for PSII heated for the indicated time periods. (Left panel), k3-weighted EXAFS spectra; (right panel), the respective Fourier transforms (FT parameters as in Fig. 3). (Thin lines), Experimental spectra; (thick lines), the results of a simultaneous fit (joint-fit) of all spectra with six shells of backscatterers; (dashed lines), simulations of the spectra based on the model discussed in the text. The structural parameters used for the shown simulations are given in Table 3 and Fig. 5.
In the following we consider three shells of light atoms (O/N/C) and three shells of heavy atoms (Mn/Ca) as discussed in the context of Table 2 (approach 8). Curve-fitting was performed under the assumption that the observed variations in the EXAFS spectra can be modeled by changes in the coordination numbers. This assumption is confirmed, a posteriori, by the good agreement between experimental and calculated spectra, and the consistency of the fit results. We used an EXAFS joint-fit approach (Dittmer, 1999; Dau et al., 1999). A joint fit of several related spectroscopic data sets (Hansen et al., 1987) has also been termed global data analysis (Roelofs et al., 1992). This means that the eight EXAFS spectra, representing eight different heating times, were fitted simultaneously by parameter variations and minimization of a common error-sum. Some fit parameters (namely the coordination numbers, Ni) were allowed to vary independently, whereas for other parameters (namely the distances, Ri, and the Debye-Waller parameters, σi) the fit approach enforces identical values of corresponding parameters in all eight spectra. Fig. 4 facilitates the comparison of the calculated spectra resulting from this fit approach (thick lines) and the experimental spectra (thin lines).
The simulation parameters are listed in Table 3 (for further details on the restraints and variations applied in the fit procedure, see Table 3 legend); the coordination numbers as a function of the heating time are shown in Fig. 5 (solid circles). The 1RF-value, which represents the averaged deviation between eight calculated and eight measured spectra (see Materials and Methods), was reasonably low (∼11%). Other simulation approaches differing in the number and nature of coordination shells again yielded significantly higher RF-values (>15%; e.g., the three-shell approach corresponding to the open circles in Fig. 5) and/or erratic time courses of the apparent coordination numbers (not shown). These findings represent a particular important justification for the use of the six-shell simulation approach. Noteworthily, the six distances determined by the joint-fit of the eight EXAFS spectra are within 0.01 Å, identical to the distances obtained by curve-fitting of the single spectrum of the unheated PSII for the constrained six-shell approach denoted as 8 in Table 2.
TABLE 3.
Results of a joint-fit of the eight EXAFS spectra obtained for eight distinct heating periods ranging from 0 to 180 min
| Shell I | Distance vector | Coordination number/per Mn Ni | Distance/Å Ri | Debye-Waller parameter/Å2 2 σi2 |
|---|---|---|---|---|
| I | Mn–O/N | 3.92 ± 0.82* (5.5)† 3.44§ | 1.853 ± 0.003* 1.853§ | 0.0186 ± 0.0050* (0.0276)† 0.0156§ |
| II | Mn–O | 0.31 ± 0.35* (0.0) 0.06§ | 2.164 ± 0.002* 2.163§ | 0.0124 ± 0.0020* 0.0110§ |
| 6.21‡ ± 0.40* (6.0) | ||||
| III | Mn–Mn | 1.02 ± 0.06* (1.0) 1.23§ | 2.709 ± 0.002* 2.715§ | 0.0046 ± 0.0020* 0.0065§ |
| IV | Mn–Mn | 0.43 ± 0.18* (0.5) | 3.083 ± 0.020* | 0.0027 ± 0.0025 |
| V | Mn–Ca/Mn | 0.45 ± 0.14* (0.5) | 3.295 ± 0.020* | 0.0027 ± 0.0025 |
| VI | Mn–O/N/C | 2.86 ± 0.55* (3.0) | 3.637 ± 0.010* | 0.0080 ± 0.0025 |
The values of Ri and σi of the eight spectra were coupled to yield equal numbers in all spectra (joint-fit approach); in addition the values of σIV and σV were fixed (no variation during the individual fit session). The averaged RF value of the eight spectra was 11%. The shown Ni values refer to the intact Mn complex of PSII (no heating, 0 min) and, for shell II, also to the state resulting from 180 min of heat exposure; the resulting Ni for the other heating periods are shown in Fig. 5 (solid circles).
Indicated is the range of values obtained for variations in the values of σIV and σV (σIV = σV = 0.0002, 0.0027, 0.0052) and in the k-weighting (either k2- or k3-weighting for all three values of σIV and σV). This range represents the robustness of the fit with respect to variations in details of the fit approach, but not a confidence interval.
The values in parentheses were used for the calculation of the model spectra shown in Fig. 4.
Coordination number as obtained for samples exposed to 180 min of heating.
Results of a three-shell simulation of the eight spectra (Fig. 5, open circles); Ri and 2σ2 were coupled to yield identical values for all eight spectra; RF was 25.0%.
FIGURE 5.
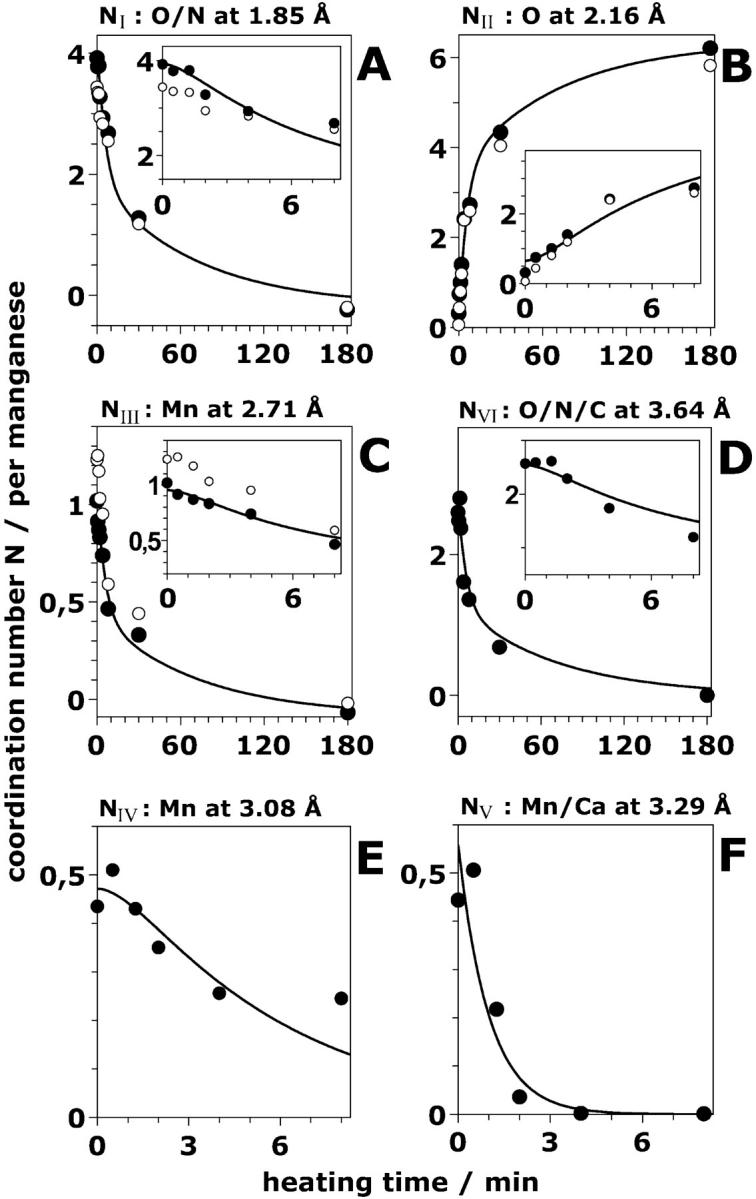
Time dependence of the six Ni, the apparent coordination numbers per Mn atom of the Mn4-complex. The Ni (solid circle) were obtained by a least-squares joint-fit procedure of the experimental EXAFS spectra (shown in Fig. 4) with six shells of backscatterers (for the respective distances, Ri, and further details, see Table 3). The open circles represent the apparent coordination numbers obtained for an alternative three-shell simulation. The data points at each heating time represent the mean value of the coordination numbers obtained by the variations described in the legend of Table 3. The solid lines were calculated using a consecutive reaction scheme with rate constants k1, k2, and k3 of 1.0, 0.18, and 0.014 min−1, respectively (see Table 1). The insets show the data points at short heating times on an expanded time scale. Note the lag phase apparent in the insets.
Assuming noise-free data and in the absence of systematic errors, the maximal number of allowable fit parameters, nmax, per EXAFS spectrum can be estimated according to nmax = 2 Δk ΔR/π, where Δk and ΔR denote the k-range of the experimental data and the relevant R-range of the Fourier-transformed data, respectively (estimate on basis of the sampling theorem, degrees of freedom in Brillouin, 1962). For k ranging from 1.5 to 11.8 Å−1 and R ranging from 1.0 to 3.5 Å, nmax equals 16. In the simulations of the intact PSII (nfree = 10, see Table 2), we stayed clearly below this upper limit, because most Ni (apparent coordination numbers) were fixed to yield chemically reasonable values. However, simulations of the EXAFS spectra collected at various distinct times after the heat jump need to involve variable Ni. When simulating individual EXAFS spectra using all six coordination numbers as variable parameters, the number of fit parameters is close to nmax, and numerically significant fit results were not obtained (at least not for the EXAFS oscillations which correspond to distances greater than 3 Å). For the joint-fit of the eight EXAFS spectra, nmax equals 128 (8 × 16) and by the coupling of fit parameters (meaning identical values for distances and Debye-Waller parameters in all eight spectra) we could stay clearly below this upper limit (58 variable parameters were used). Noteworthily, there is no general theory to determine the actual number of acceptable fit parameters. (This holds in particular for the joint-fit approach.) The nmax-estimate on basis of the sampling theorem provides only an absolute upper limit; and a number of variable parameters, nfree, smaller than nmax, do not ensure the significance and uniqueness of the fit result. However, empirically we find that by using the joint-fit approach the significance of the fit results is largely improved.
Inspection of Fig. 5 reveals that the number of light atoms ∼1.85 Å, which represent the direct ligands to Mn in the intact complex, decreases in a biphasic manner (with increasing heat-exposure time, Fig. 5 A); a complementary biphasic increase of a coordination shell of O-atoms at a distance of ∼2.16 Å to Mn is observed (Fig. 5 B). This biphasic increase matches the increase of the six-line EPR signal attributed to Mn2+ (Fig. 2 B). Thus, we attribute the 2.16 Å FT peak to Mn2+ coordinated by six water molecules. Mn2+ is produced with a fast phase accounting for the release of two Mn atoms from their binding site and in a slower reaction accounting for the remaining two Mn atoms.
Two further shells of atoms exhibit a similar biphasic behavior, namely the O/N shell at ∼3.6 Å (Fig. 5 D) and the Mn-Mn distance at ∼2.7 Å (Fig. 5 C). The latter is commonly attributed to two di-μ-oxo bridged Mn pairs (see Discussion). Seemingly, one pair is “destroyed” rapidly by the heating procedure, resulting in a decrease of the 2.7 Å Mn-Mn coordination number from N ∼1 (1.02) to N ∼0.5. The second di-μ-oxo bridged Mn pair is clearly more stable. Noteworthily, a similar biphasic decrease in the number of Mn-Mn vectors of ∼2.7-Å length is obtained if only three shells of backscatterers are considered (Table 3,§). The initial value of NIII, however, is larger than the value obtained for the six-shell approach, namely 1.23 (Table 3), but for both approaches the coordination number is almost halved at 8 min after the temperature increase.
The coordination number of the O/N shell at ∼3.6 Å is also found to be reduced by ∼50% after the release of the first Mn pair (Fig. 5 D). In the binuclear Mn complex, no EXAFS interactions between heavy atoms, except the 2.7 Å vector between the two Mn atoms, were detected (see below). Thus, the decay of the coordination number of the shell at ∼3.6 Å which parallels the release of the first Mn pair strongly supports our assignment of this shell to light atoms. A 3.6-Å coordination shell of light backscatterers to Mn above 3 Å has also been observed in PSII samples which contained only two Mn atoms because of the depletion of the other two Mn atoms by a biochemical treatment (Dörner et al., 1998). We note that multiple scattering paths involving the central Mn and its ligands in the first coordination sphere might also contribute to the 3.6-Å EXAFS oscillations (unpublished results).
The shell at 3.1 Å attributed to a Mn-Mn interaction exhibits a different kinetic behavior. Its coordination number decreases to ∼0 (Fig. 5 E) concomitantly with the release of the first two Mn atoms within ∼10 min. This observation is readily explained if we assume that the Mn-Mn vector at 3.1 Å connects one Mn atom of the loosely bound pair with one Mn of the more stable pair. Consequently, after the release of the first pair from its binding site, this distance is no longer detectable in the EXAFS spectra.
The coordination number of the 3.3 Å shell, which we attribute to a heavy atom, decreases particularly rapidly (the decrease was well described by a single exponential). It was close to zero after only 2 min of heating (Fig. 5 F). The coordination number of this shell seems to be ∼0.5 in the intact PSII (Table 3). For further details, see Discussion section.
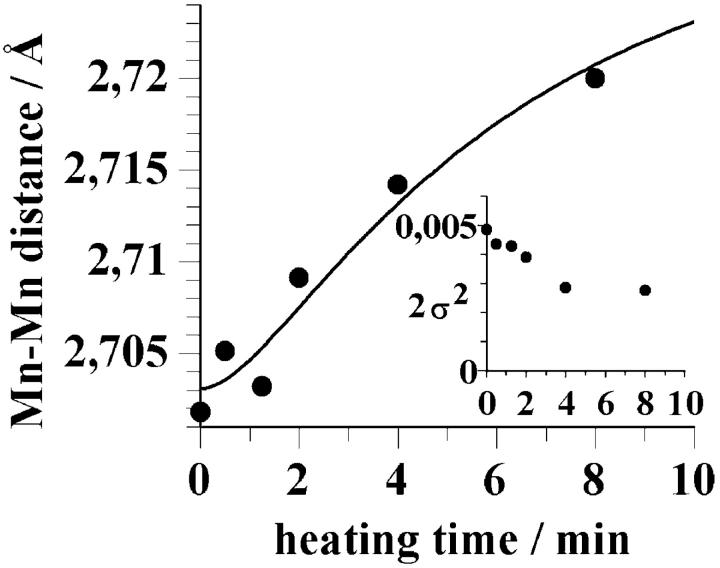
The average distance of the two shortest Mn-Mn vectors that results from the joint simulation of the EXAFS spectra is 2.71 Å. This value was obtained when the distance parameter had been coupled to equal values during the joint fit. When the distance between these Mn atoms and the Debye-Waller parameter are allowed to vary independently, we observe a small increase of this Mn-Mn distance for heating times ranging from 0 to 8 min (Fig. 6); the Debye-Waller parameter seems to decrease (inset in Fig. 6). A fit of the data points in Fig. 6 with the same consecutive reaction that accounted for the loss of the first Mn-Mn interaction (see Fig. 5 C) yielded a total change by only 0.02–0.03 Å (Fig. 6, line).
FIGURE 6.
The mean distance between the Mn atoms separated by ∼2.7 Å as function of the heating time. The distances were obtained using the joint-fit approach described in the legend of Table 3, but allowing for independent variations of RIII and 2σIII2. The line was calculated according to Eq. 4 (see also Table 1). (Inset), The Debye-Waller parameter as function of heating time.
In summary, in response to a temperature jump all four Mn atoms are released from their binding site, finally leading to four [Mn(H2O)6]2+ complexes. One of two di-μ-oxo bridged Mn pairs is rapidly lost (k2 = 0.18 min−1), whereas the second Mn pair (Mn-Mn distance of ∼2.73 Å) is much more firmly bound (k3 = 0.014 min−1). The reduction and release of any bound Mn is preceded by the rapid loss of a Mn-Ca/Mn vector at 3.3 Å (k1 = 1.0 min−1) due to the release of one Ca ion or, less likely, due to the increase of a Mn-Mn distance from 3.3 Å to >4 Å (which would render it invisible in the EXAFS spectra).
Kinetic model for the disassembly of the Mn complex
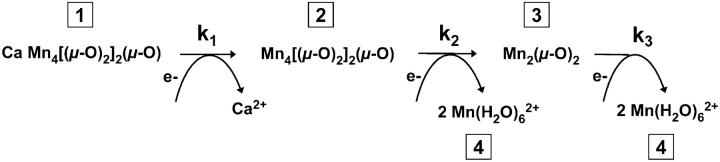
We searched for a kinetic model that accurately describes the release of Mn/Ca from their binding sites and the concomitant formation of Mn2+. The model involves three rate constants: k1, k2, and k3 (Table 1, Scheme 1). (1) The k1 reaction accounts for the loss of oxygen evolution (Fig. 1), for the reduction of YDox (Fig. 2 A) and for the rapid loss of the 3.3 Å vector (Fig. 5 F). The kinetics of these reactions are all described by the same rate constant, namely of k1 (= 1 min−1). (2) The k2 reaction accounts for the fast Mn release resulting from the loss of the first Mn dimer (Fig. 5, A, C–E) and for the concomitant formation of Mn2+ (Fig. 5 B). These processes are well described by k2 (= 0.18 min−1). (3) The k3 reaction describes the slow reduction (Fig. 2 B) and release (Fig. 5 B) of the second Mn dimer (k3 = 0.014 min−1). We furthermore assumed (on the basis of the EPR and EXAFS data) that the k1 process is not coupled to Mn release, but that the k2 and k3 processes account for the release of two Mn (per PSII) each. (All offset values introduced for fine adjustment of the simulation curves were small.) The simulation curves that resulted from this approach are shown in Fig. 5 (solid lines). The time dependence of all six coordination numbers is reasonably well described by using only the above three kinetic components. The assumption of a kinetic component (k1) that precedes the release of Mn facilitates the reproduction of the apparent lag-phase behavior.
SCHEME 1.
Kinetic-structural model for the stepwise disassembly of the Mn complex in response to a temperature jump. Four species (or states) of Mn complexes are involved (marked by the numbers in squares); the rate constants for transitions between these species are k1, k2, and k3.
The rate constants that are coupled to the formation of the resolvable intermediate states of the Mn complex after a heat jump seemingly represent the rate-limiting steps. We cannot rule out that additional short-lived intermediates occur during the disassembly of the Mn complex. Because their decay rate exceeds their formation rate, such short-lived intermediates necessarily remain invisible.
We calculated the EXAFS spectra for different heating times on basis of the rate constants of the described kinetic model using a chemically reasonable set of coordination numbers of the six shells of atoms (Table 3, figures in parenthesis) and the distances and Debye-Waller parameters shown in Table 3. The obtained EXAFS spectra are shown in Fig. 4 as dotted lines. For all heat exposure periods, the experimental spectra are reasonably well reproduced, thus confirming the underlying kinetic and structural assumptions.
Changes in the Mn oxidation state
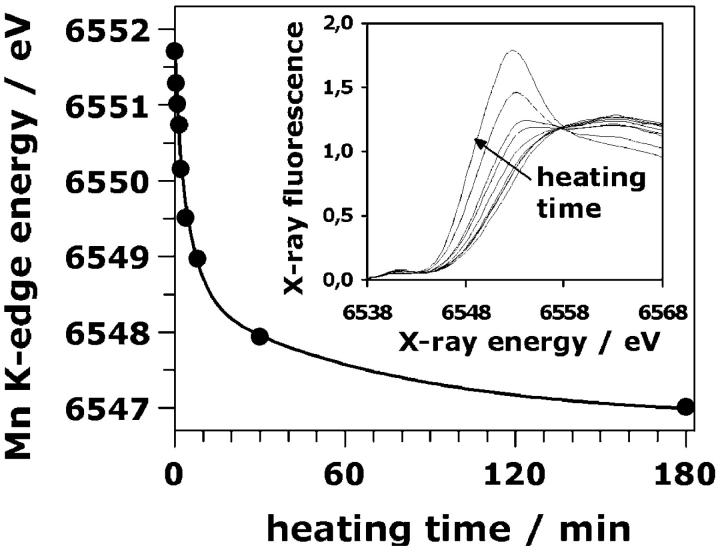
The position of the Mn K-edge on the energy scale has been found to be related to the Mn oxidation state (Kirby et al., 1981a, Penner-Hahn et al., 1990; Sauer et al., 1992; Dittmer et al., 1998; Iuzzolino et al., 1998, and references therein); typically a downshift of the edge position by 0.5–1.0 eV is observed for a decrease in the average oxidation state by 0.25 (reduction by a single electron per four Mn ions). We monitored the reduction of Mn by recording XAS edge spectra at the Mn K-edge. The inset of Fig. 7 shows edge spectra for various heat exposure times. The spectrum obtained after 180 min greatly differs from the one of the control; the clearly visible peak at ∼6554 eV is typical for Mn(II).
FIGURE 7.
The Mn K-edge energy as function of the heating time. The K-edge position was determined from edge spectra using the integral method of Dittmer and Dau (1998). The line was calculated using a triple exponential decay plus offset (see Table 1). The K-edge energy decreased by ∼4.5 eV after 180 min of heating. (Inset), Mn K-edge spectra of PSII samples heated for 0, 1, 1.5, 2, 4, 8, 30, and 180 min (from right to left; see arrow).
From the edge spectra, the position of the Mn K-edge was determined by the integral method described elsewhere (Dittmer et al., 1998). In the control, the Mn K-edge was found at an x-ray energy of ∼6551.7 eV. This value decreases by a total of 4.6 eV down to 6547.1 eV indicating the conversion of essentially all high-valent Mn ions into Mn(II) (compare Dittmer et al., 1998). The Mn K-edge energies are plotted as function of the heating time in Fig. 7 (dots); there is no lag phase. We simulated the reduction of Mn with the same three rate constants (of 1.0, 0.18, and 0.014 min−1) used above to model the loss of Mn/Ca from their binding sites (see Table 1). The best simulation of the data points in Fig. 7 was obtained using Eq. 5 (triple exponential decay) and edge shifts of 0.8 eV, 2.3 eV, and 1.5 eV (solid line in Fig. 7). Each of the three steps of the disassembly process seems to be coupled to Mn reduction by 1–3 electrons.
DISCUSSION
Analysis of the time dependence of EXAFS spectra
Using a freeze-quench approach, we carried out the first time-resolved EXAFS investigation on the PSII Mn complex. In this particular case the required time-resolution had been conveniently low (∼30 s). However, with respect to data analysis the encountered problems and benefits are mostly the same as they will be for any time-resolved EXAFS investigation. (First steps toward time-resolved XAS at the PSII manganese complex with a time resolution in the ms range are reported elsewhere; Haumann et al., 2002a,b.)
At most times a mixture of different states is present and the spectra constitute a linear superposition of the spectra of the individual states. On a first glance, this constitutes a major problem because the resulting complexity of the EXAFS spectra hampers a meaningful simulation of the individual spectra (too many involved backscatterer shells). We dealt with that problem by using a special joint-fit approach which is based on the assumption that a single set of absorber-backscatterer distances can facilitate an adequate description of all the collected EXAFS spectra. A similar joint-fit approach has been applied successfully to a set of EXAFS spectra obtained for various enzyme-substrate stoichiometries (Dau et al., 1999).
Guided by the experimentally determined time courses (Figs. 1, 2, 4, and 7), a kinetic model was constructed where the rate-limiting steps are described by first-order rate constants (k1, k2, and k3 in Scheme 1). We simulated the time courses of the six coordination numbers as well as the time course of supplementary signals (being the activity loss, the disappearance of the TyrD radical and the occurrence of Mn(H2O)62+ as detected by EPR spectroscopy, and the x-ray edge position) using the same set of rate constants (k1 = 1.0 min−1, k2 = 0.18 min−1, and k3 = 0.014 min−1) for each time course.
These simulations provide not only rate-constant values, but they allow us to deduce likely coordination numbers (and thereby structural models) associated with each of the four pure states of the kinetic model. Finally, to verify the adequacy of the deduced kinetic-structural model (Scheme 1, values in parenthesis in Table 3), we simulated the complete set of EXAFS spectra without introducing any additional variables (dashed lines in Fig. 4).
In summary, the used global analysis involves: (1) a joint-fit of the EXAFS spectra collected at various times, (2) the description of several signals (11 time courses, 6 × Ni plus five supplementary signals) with the same set of rate constants, and (3) the construction of a kinetic-structural model (Scheme 1). By this global analysis the following has been achieved: (i) determination of the reaction sequence (construction of a kinetic model); (ii) determination of the rate-constant values of the rate-limiting steps; and (iii) structural characterization of the initial, two intermediate, and one final state.
Furthermore, the joint-fit of EXAFS spectra facilitates the resolution of otherwise (more or less) hidden subshells. Specifically, we found that in the distance range 3.0–3.7 Å, three different backscatterer shells are needed to describe adequately the EXAFS spectra. The EXAFS in this distance range mostly has been interpreted in terms of one or maximally two backscatterer shells (George et al., 1989; Penner-Hahn et al., 1990; MacLachlan et al., 1992; Yachandra et al., 1993; DeRose et al., 1994; Meinke et al., 2000). Conflicting results have been obtained with respect to the presence of Ca or Mn and the metal-to-metal distance (3.3 Å versus 3.7 Å; MacLachlan et al., 1992, 1994; Latimer et al., 1995, 1998; Riggs-Gelasco et al., 1996a). Furthermore, the orientation of a 3.3-Å Mn-Mn vector determined by LD-EXAFS (George et al., 1989; Mukerji et al., 1994; Yachandra et al., 1993) seems to be in conflict with the recent crystallographic results (Zouni et al., 2001). The difficulty to resolve three distinct shells certainly is one aspect of the ongoing controversies.
The 2.7 Å Mn-Mn vector
One basic and undisputed feature of the intact Mn complex is the presence of short Mn-Mn distances of ∼2.7 Å that have been attributed to di-μ2-oxo bridged Mn pairs (Kirby et al., 1981b; Yachandra et al., 1986; George et al., 1989; Penner-Hahn et al., 1990; Riggs-Gelasco et al., 1996a; MacLachlan et al., 1992; Schiller et al., 1998, Meinke et al., 2000) by comparison with multinuclear Mn model compounds (Wieghardt, 1989; Christou, 1989; Pecoraro, 1992; Armstrong, 1992; Larson and Pecoraro, 1992). In these model compounds, Mn-Mn distances ranging from 2.65 to 2.75 Å are exclusively found for Mn(III) or Mn(IV) ions connected by di-μ2-oxo bridges, whereas the involvement of μ3-oxo bridges is found to result in distances clearly exceeding 2.75 Å. It certainly is not excluded that relevant structural motifs have remained unexplored by model chemistry. Nonetheless, because there is no evidence that any alternative structural motifs can result in Mn-Mn distances close to 2.7 Å, in the following it is assumed that the 2.7-Å Mn-Mn distances found in the intact and partially disassembled complex are indicative of di-μ2-oxo bridged pairs of Mn ions. This assumption is in good agreement with our results on the disassembly process discussed further below.
Based on the analysis of Fourier-filtered EXAFS data or on simulations of unfiltered spectra involving a low number of backscattering shells, mostly values for N2.7Å close to 1.25 have been obtained, suggesting that there are either two (N2.7Å = 1.0) or three (N2.7Å = 1.5) Mn-Mn vectors of 2.7-Å length per Mn4-complex (MacLachlan et al., 1992; DeRose et al., 1994, Riggs-Gelasco et al., 1996a, Penner-Hahn, 1999; Robblee et al., 2001; see also Fits 1–3 in Table 2 and open circles in Fig. 5). Using more complex simulation approaches which explicitly take into account the mostly undisputed presence of backscattering atoms at ∼2.0–2.2 Å (O or N) and ∼3.2 Å (Mn or Ca), we consistently determine N2.7Å-values close to one (Tables 2 and 3, Fig. 5 plus further fit results which are not shown). This finding represents evidence in favor of the presence of exactly two Mn-Mn vectors of 2.7-Å length, but only if the use of more complex simulation approaches (meaning more backscatterer shells plus constraints to ensure the uniqueness of the fit results) is indeed appropriate. We found that the use of more complex approaches is required: 1) to obtain reasonably good simulations of the first-sphere EXAFS oscillations and to avoid unreasonably low values for the number of atoms in the first coordination sphere of manganese, 2) to account for the presence of Mn-Mn or Mn-Ca distances ∼3.2 Å, 3) to describe appropriately the linear dichroism in the EXAFS spectra of partially oriented PSII samples (Schiller et al., 1998; Haumann et al., 2001), and 4) to account for the temporal changes in the EXAFS as they are induced by a temperature jump (Figs. 4 and 5).
In summary, we certainly cannot exclude the presence of three Mn-Mn vectors of 2.7-Å length, but we consider the presence of exactly two Mn-Mn vectors of 2.7-Å length to be the more likely alternative. In the following discussion, the existence of two Mn-Mn vectors of 2.7-Å length per Mn4-complex is assumed, suggesting the presence of two pairs of di-μ-oxo-bridged Mn ions in the intact manganese complex in its S1-state. The results of the disassembly experiments discussed below are compatible with this notion.
Stepwise disassembly of the Mn complex
Typically, in intact organisms and in biological buffer systems the thermodynamically favored state of Mn is Mn(II) (at pH 6.5). The assembly of the photosynthetic Mn complex involves not only the chelating effect of the protein matrix, but also the light-driven Mn(II) oxidation by the Tyr-Z radical. This photoactivation (Ananyev et al., 2001) results in the tetranuclear Mn complex of PSII being mostly in its S1-state. For example, in PSII preparations at 4°C, complete reversal of the high-valent Mn ions (oxidation states III and IV) of the assembled complex to the thermodynamically favored hydrated Mn(II) requires several days and is difficult to separate fully unambiguously from chlorophyll and protein degradation. Here we used moderate heating to accelerate the Mn reduction and release processes. Interestingly, we find that the disintegration or disassembly process involves several distinct intermediates as discussed in the following.
First step—Ca release
The activity loss, the TyrD-radical disappearance, and the loss of the putative Mn/Ca shell at 3.3 Å, all three processes are characterized by the same rate constant, i.e., k1 = 1 min−1. The activity loss is significantly and specifically reduced by using high concentrations of Ca in the assay buffer. As already concluded above, most likely the k1 processes are related to the release of the extrinsic polypeptides and, consequentially, of Ca (see Results section).
It is still unclear whether calcium is close to the Mn atoms of the oxygen-evolving complex. Calcium has not been assigned in the crystallographic electron density map (Zouni et al., 2001). By EXAFS spectroscopy, conflicting results had been obtained (MacLachlan et al., 1992; MacLachlan et al., 1994; Yachandra et al., 1993; Latimer et al., 1995; Latimer et al., 1998; Riggs-Gelasco et al., 1996a). Recent experiments involving the replacement of Ca by Sr and the analysis of Sr K-edge EXAFS spectra as well as Ca-EXAFS results on the native Mn complex seem to indicate the presence of two metal atoms (e.g., Mn) at a distance of 3.3–3.6 Å from strontium (Cinco et al., 1998) or calcium (Cinco et al., 2001).
Our analysis of EXAFS spectra in control and heated PSII revealed a distance between heavy atoms of ∼3.3 Å with an apparent coordination number of ∼0.5 per Mn which is lost during the k1 phase. The loss of the 3.3 Å distance is not coupled to further structural changes of the Mn complex detectable by EXAFS spectroscopy.
We have three possibilities for assigning the 3.3 Å EXAFS oscillations: 1) one Mn-Mn vector, 2) one Ca ion at about the same distance from two Mn atoms, or 3) two Ca ions at the same distance to one Mn. The third possibility seems to be less likely because the number of essential Ca ions at the active site of PSII is, most likely, one (Ono and Inoue, 1988; Shen et al., 1988; Ädelroth et al., 1995). We tentatively assign the 3.3 Å EXAFS oscillations to backscattering by calcium which is at a distance of 3.3 Å to two Mn ions. We note that the first possibility (assignment to backscattering by a Mn ion at 3.3 Å) is not rigorously excluded, because the Ca release might cause some secondary perturbation of the structure of the Mn complex. However, taking into consideration the close relation between calcium and the k1 process as well as the Sr- and Ca-EXAFS results (Cinco et al., 1998; 2001), we consider the second possibility (i.e., backscattering by Ca at ∼3.3 Å) to be more likely.
Second step—transition to a binuclear Mn complex
The observed lag-phase behavior (Figs. 2 B and 5) and the corresponding kinetic model show that the k1 process precedes the second disassembly step. Seemingly, further disassembly steps require the foregoing release of the extrinsic polypeptides and Ca. The extrinsic polypeptides as well as Ca itself protect the Mn complex against reduction presumably by reducing the accessibility of the Mn complex to water (or water-derived species) and other small external reductants (Rashid and Carpentier, 1989; Tamura et al., 1990; Mei and Yocum, 1991; Mei and Yocum, 1992, Riggs et al., 1992; 1993; Van der Meulen et al., 2002). Therefore we assume that the increased solvent accessibility of the Mn complex facilitates further reduction and disassembly steps.
The k2 phase involves reduction of about one-half of the Mn(III, IV) ions to Mn(II). Inasmuch as the observed six-line EPR signal (Miller and Brudvig, 1991; Yocum et al., 1981) as well as the Mn-ligand distances are typically observed for released Mn(II), we assume that the Mn(II) ions are no longer present at their original binding site. For the remaining two Mn ions, the EXAFS results allow formulation of an essentially unambiguous structural model. The distance between the two remaining Mn ions is 2.73 Å; this Mn-Mn distance is highly suggestive of a di-μ-oxo bridged Mn2 unit. The reduction in the value of the Debye-Waller parameter (2σ2) upon the transition toward the di-μ-oxo bridged Mn2 unit is suggestive that a specific Mn2 unit remains bound to the PSII protein matrix.
The structure of the Mn complex treated with exogenous reductants, namely NH2OH and hydroquinone, has been studied by EXAFS (Riggs et al., 1992; 1993; Riggs-Gelasco et al., 1996a); evidence for the presence of only one Mn2(μ-O)2 unit in some of the “super-reduced” states has been obtained (in contrast to two Mn2(μ-O)2 units in the S1-state). Noteworthily, the artificially reduced Mn complex mostly did not loose its capability to evolve oxygen (Mei and Yocum, 1991; 1992), whereas the partially disassembled complex is catalytically inactive (Fig. 1). Thus, in Riggs et al. (1992; 1993) and Riggs-Gelasco et al. (1996b), strong artificial reductants were used to create super-reduced states of the otherwise mostly intact Mn4 complex, whereas we investigated intermediates of the thermally activated disassembly process (which is likely to proceed permanently, albeit at low rates, in intact organisms). We note that, despite similarities, the Mn4 complex in super-reduced states is not directly related to the Mn2 intermediate of the disassembly process.
In the following we will discuss three scenarios on the relation between the intact PSII manganese complex and the Mn2(μ-O)2 intermediate of the disassembly process.
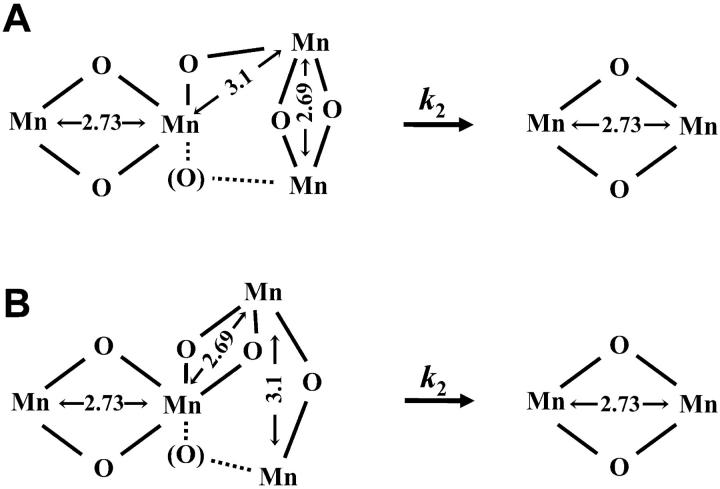
The intact complex consists of two di-μ-oxo bridged Mn-dimers with one Mn ion of the first dimer connected to Mn of the second dimer by a mono-μ-oxo bridge, but also a funnel or T-type arrangement where one Mn of the second dimer, connected by two di-μ-oxo bridges to the two Mn ions of the first dimer, is not excluded (see Scheme 2 A). In the first Mn dimer, the Mn-Mn distance is ∼2.7 Å (e.g., R1 = 2.69 Å); in the second dimer it is longer (e.g., R2 = 2.73 Å) as indicated by linear dichroism EXAFS results (Mukerji et al., 1994; Schiller et al., 1998; Dittmer, 1999). This distance heterogeneity contributes to the σ, the Debye-Waller parameter, according to: σ2 = σ122 + σintr2, with σ12 = 2 (R2−R1) and σintr being the intrinsic Debye-Waller parameter related to a homogenous, approximately Gaussian-type distance distribution. Upon release of one Mn pair, σ decreases (σ12 = 0) and the Mn-Mn distance of the remaining pair is 2.73 Å. Furthermore, due to the disappearance of the inter-dimer mono-μ-oxo bridges, the 3.1 Å-EXAFS distance also disappears. The described scenario is in good agreement with the EXAFS data.
The second scenario involves a trimer-monomer arrangement in the intact complex meaning a Mn3((μ-O)2)2 unit connected by a mono-μ-oxo bridge to the fourth Mn ion (see Scheme 2 B). One special feature of the Mn3((μ-O)2)2 unit is the presence of four μ-oxo ligands at the central Mn. It has been found that in synthetic models this situation results in elongation of the 2.7 Å distance, a phenomenon presumably explainable by a trans effect of μ-oxo ligands at the central Mn (Philouze et al., 1994). This means that, already, the presence of a di-μ-oxo bridge with R < 2.71 Å (e.g., 2.68 Å as discussed above) is not supportive of a trimer-monomer model. Furthermore, upon release of one Mn of the trimer unit, the previously elongated Mn-Mn distance of the remaining di-μ-oxo bridged dimer should shrink. Instead, we find an identical or even increased Mn-Mn distance. Thus, the trimer-monomer scenario involves two problematic assumptions: (i) the release of one Mn from the trimer unit does not destabilize the remaining Mn2(μ-O)2 unit; and (ii) the release does not affect the Mn-Mn distance of the remaining unit even though the number of μ-oxo ligands at the intermediate unit becomes reduced from four to two.
The third scenario involves complete destabilization of the tetranuclear complex and formation of a new Mn2(μ-O)2 unit that had not been present in the intact complex. We will discuss two problematic aspects of this scenario involving (i) kinetic considerations and (ii) a template effect of the protein matrix. (i) The mostly entropically driven transition to the Mn(II) state is slow because the initial and the two intermediate states are kinetically relatively stable. This means that significant energy barriers prevent rapid disintegration. These barriers (mostly) represent the energy needed to break bonds of the protein-bound Mn complex. After the breaking of these bonds, the system could move rapidly energetically downhill toward the finally stable Mn(II) state. In the scenario discussed here, however, it would need to move more efficiently (meaning more rapidly) toward a new Mn2(μ-O)2 structure that is energetically less favored than the final Mn(II) state. (ii) The structure of the intact Mn complex certainly is determined by the protein environment, which acts as a template for the formation of the complex. The relatively high stability of the slowly disintegrating Mn2(μ-O)2 unit structure is only explainable by a particularly strong template effect. Taking into consideration this strong template effect, it is likely that the Mn2(μ-O)2 unit of the partially disassembled complex is also present in the intact complex. In other words, it is difficult to imagine that the same protein matrix should enforce different Mn2(μ-O)2 units in the intact and the partially assembled complex.
SCHEME 2.
Two alternative models for the transition from the tetranuclear Mn complex to a binuclear complex. Only bridging oxides are depicted; the presence of the bridging oxygens in parenthesis is not excluded. The Mn-Mn distances are given in Å. In the tetranuclear complex, one Mn-Mn distance of a di-μ-oxo bridged Mn pair is smaller than 2.71 Å (e.g., 2.69 Å), whereas the other one is greater than 2.71 Å (e.g., 2.73 Å). (A) Dimers-of-dimers model; (B) trimer-monomer model for the tetranuclear complex. The depicted arrangements are compatible with the electron density information obtained by protein crystallography (at 3.8-Å resolution; Zouni et al., 2001).
Taking into consideration the still-limited insights into the chemistry of protein-bound multinuclear Mn complexes, it is impossible for us to rule out any of the three alternative scenarios. In the light of the EXAFS results presented here, we presently consider the most straightforward first scenario (dimer of Mn2(μ-O)2-dimers in the intact complex, single dimer in the Mn2-complex) to be more likely than the second or third one.
By analysis and simulations of the various EPR (and ENDOR) spectra measured for the PSII manganese complex in its S2 state, it has been repeatedly attempted to determine spin-exchange coupling constants, Jij, and to evaluate alternative structural models in the light of the obtained sets of Jij values (for references and reviews see Hasegawa et al., 1999a; Peloquin and Britt, 2001; Carrell et al., 2002). At present, the unambiguous determination of a unique set of coupling constants cannot be achieved, but some types of exchange coupling schemes have been excluded. On these grounds, all recent investigations involving advanced EPR simulations have consistently lead to the conclusion that a linear version of the dimer-of-dimers model as well as the originally proposed C-shape arrangement (Yachandra et al., 1993) are unlikely structural motifs for the PSII manganese complex in its S2 state (Hasegawa et al., 1999a; Peloquin and Britt, 2001; Carrell et al., 2002). However, none of these simulations allow it to exclude models of the dimer-of-dimers type definitively. The dimer-of-dimer topology corresponds to “minor solutions” of the EPR simulations which require relaxing of some assumptions (range of coupling constants for a given structural motif; see Peloquin and Britt, 2001).
Comparing the first and second scenarios in the light of the EPR results, we find that according to Peloquin and Britt (2001) the trimer-monomer structure of Scheme 2 B represents the clearly more appropriate model, whereas according to Carrell et al. (2002) the funnel-type dimer-of-dimers model shown in Scheme 2 A is favored. (Carrell et al. also consider cubane/butterfly structures to be good candidates, but these structures are essentially impossible to reconcile with the EXAFS results.) The funnel-model of Carrell et al. (2002) corresponds to Scheme 2 A, if the second interdimer mono-μ-oxo bridge, which is depicted using dotted lines for bond representation, is assumed to be present. The existence of this μ-oxo-bridge is neither implied nor excluded by the presently available EXAFS data. Therefore, in Scheme 2 A this bridge is depicted using dotted lines. If this second mono-μ-oxo bridge is absent, alternative bridging motifs need to be present (e.g., μ-carboxylate bridge, bridging chloride, and hydrogen bonds between terminally coordinated water species) to ensure a structure of the complex which is compatible with the crystallographically determined electron density. The funnel model implied by Scheme 2 A seems to be compatible with one of the possible coupling schemes of Hasegawa et al. (1999a,b).
In conclusion, it would be premature to rule out any of the structural motifs hinted at in Scheme 2. The dimer-of-dimers model depicted in Scheme 2 A, which differs from the one originally proposed by Yachandra et al. (1993), facilitates a particularly straightforward interpretation of the results presented here (first scenario), but it is not uniquely implied by the EXAFS data. For the intermediate dinuclear manganese complex, however, clear evidence has been obtained that it is an Mn2(μ-O)2 complex.
Acknowledgments
The competent work of the technicians S. Feite, J.C. Collet-Fenetrier, and L. Leclerc (European Synchrotron Radiation Facility, Grenoble) is gratefully acknowledged.
We thank the Deutsche Forschungsgemeinschaft (SFB 498, project C6) and the German Bundesministerium für Bildung und Forschung (grants 05SN8RMA/2 and 05KS1KEA/6) for financial support. P.P. thanks the Alexander von Humboldt-Stiftung for financial support.
Abbreviations used: Ca, calcium; DCBQ, 2,6-dichloro-p-benzoquinone; EPR, electron paramagnetic resonance spectroscopy; FT, Fourier transform; EXAFS, extended x-ray absorption fine structure; LD, linear dichroism spectroscopy on unidirectionally oriented samples; MES, 2-(n-morpholino)ethanesulfonic acid; Mn, manganese; MW, molecular weight; NMR, nuclear magnetic resonance; P680, primary donor of PSII; PSII, Photosystem II; QA, bound plastoquinone on subunit D1 of PSII; Si, oxidation states of the Mn complex; YD, Tyr-161 of subunit D2 of PSII; XALDS, x-ray absorption linear dichroism spectroscopy; XAS, x-ray absorption spectroscopy.
References
- Alp, E. E., G. L. Goodman, L. Soderholm, S. M. Mini, M. Ramanathan, G. K. Shenoy, and A. S. Bommannavart. 1989. A new approach to determining the charge distribution in copper compounds. J. Phys. Cond. Matter. 1:6463–6468. [Google Scholar]
- Ananyev, G. M., G. C. Dismukes, C. Vasko, and G. C. Dismukes. 2001. The inorganic biochemistry of photosynthetic oxygen evolution/water oxidation. Biochim. Biophys. Acta. 1503:52–68. [DOI] [PubMed] [Google Scholar]
- Andreasson, L. E., I. Vass, and S. Styring. 1995. Calcium ion depletion modifies the electron transfer on both donor and acceptor sides in Photosystem II from spinach. Biochim. Biophys. Acta. 1230:155–164. [Google Scholar]
- Ädelroth, P., K. Lindberg, and L. E. Andreasson. 1995. Studies of Ca2+ binding in spinach Photosystem II using 45Ca2+. Biochemistry. 34:9021–9027. [DOI] [PubMed] [Google Scholar]
- Armstrong, W. H. 1992. Polynuclear manganese complexes as models for the Photosystem II water oxidation catalyst. In Manganese Redox Enzymes. V.L. Pecoraro, editor. VCH, New York. 261–286.
- Brillouin, L. 1962. Science and Information Theory. Academic Press, New York.
- Carrell, T. G., A. M. Tyryshkin, and G. C. Dismukes. 2002. An evaluation of structural models for the photosynthetic water-oxidizing complex derived from spectroscopic and x-ray diffraction signatures. J. Biol. Inorg. Chem. 7:2–22. [DOI] [PubMed] [Google Scholar]
- Cheniae, G., and L. F. Martin. 1966. Studies on the function of manganese in photosynthesis. Brookhaven Symp. Biol. 19:406–417. [PubMed] [Google Scholar]
- Christou, G. 1989. Manganese carboxylate chemistry and its biological relevance. Acc. Chem. Res. 22:328–335. [Google Scholar]
- Cinco, R. M., J. H. Robblee, A. Rompel, C. Fernandez, V. K. Yachandra, K. Sauer, and M. P. Klein. 1998. Strontium EXAFS reveals the proximity of calcium to the manganese cluster of oxygen-evolving Photosystem II. J. Phys. Chem. B. 102:8248–8256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cinco, R. M., J. H. Robblee, J. Messinger, C. Fernandez, K. L. McFarlane, K. Sauer, and V. K. Yachandra. 2001. Ca cofactor of the water-oxidation complex: evidence for a Mn/Ca heteronuclear cluster. In PS2001 Proceedings. CSIRO Publishing, Collingwood, Australia. S10–004, 1–6.
- Coleman, W., J. Govindjee, and H. S. Gutowsky. 1988. The effect of chloride on the thermal inactivation of oxygen evolution. Photosynth. Res. 16:261–276. [DOI] [PubMed] [Google Scholar]
- Dau, H., J. C. Andrews, T. A. Roeloffs, M. J. Latimer, W. Liang, V. K. Yachandra, K. Sauer, and M. P. Klein. 1995. Structural consequences of ammonia binding to the manganese center of the photosynthetic oxygen-evolving complex: an x-ray absorption spectroscopy study of isotropic and oriented Photosystem II particles. Biochemistry. 34:5274–5287. [DOI] [PubMed] [Google Scholar]
- Dau, H., J. Dittmer, L. Iuzzolino, H. Schiller, W. Dörner, L. Heinze, V. A. Sole, and H.-F. Nolting. 1997. X-ray absorption linear dichroism spectroscopy (XALDS) on the Photosystem II manganese complex: radiation damage and S1-state K-edge spectra. J. Phys. IV. 7:607–610. [Google Scholar]
- Dau, H., J. Dittmer, M. Epple, J. Hanss, E. Kiss, D. Rehder, C. Schultze, and H. Vilter. 1999. Bromine K-edge EXAFS studies of bromide binding to bromoperoxidase from Ascophyllum nodosum. FEBS Lett. 457:237–240. [DOI] [PubMed] [Google Scholar]
- Dau, H., L. Iuzzolino, and J. Dittmer. 2001. The tetra-manganese complex during its redox cycle—x-ray absorption results and mechanistic implications. Biochim. Biophys. Acta. 1503:24–39. [DOI] [PubMed] [Google Scholar]
- Debus, R. J. 1992. The manganese and calcium ions of photosynthetic oxygen evolution. Biochim. Biophys. Acta. 1102:269–352. [DOI] [PubMed] [Google Scholar]
- Debus, R. J., B. A. Barry, G. T. Babcock, and L. McIntosh. 1988. Site-directed mutagenesis identifies a tyrosine radical involved in the photosynthetic oxygen-evolving system. Proc. Natl. Acad. Sci. USA. 85:427–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeRose, V. J., L. Mukerji, M. J. Latimer, V. K. Yachandra, K. Sauer, and M. P. Klein. 1994. Comparison of the manganese oxygen-evolving complex in Photosystem II of spinach and Synechococcus sp. with multinuclear manganese model compounds by x-ray absorption spectroscopy. J. Am. Chem. Soc. 116:5239–5249. [Google Scholar]
- Dittmer, J. 1999. Linear dichroismus-röntgenabsorptionsspektroskopie zum katalytischen zyklus des wasserspaltenden mangankomplexes der photosynthese in theorie und experiment. Ph.D. Thesis, Christian-Albrechts-Universität, Kiel, Germany.
- Dittmer, J., and H. Dau. 1998. Theory of the linear dichroism in the extended x-ray absorption fine structure (EXAFS) of partially vectorially-ordered systems. J. Phys. Chem. 102:8196–8200. [Google Scholar]
- Dittmer, J., L. Iuzzolino, W. Dörner, H.-F. Nolting, W. Meyer-Klaucke, and H. Dau. 1998. In Photosynthesis: Mechanisms and Effects, Vol. II. G. Garab, editor. Kluwer Academic Publishers, Dordrecht, The Netherlands. 1339–1342.
- Dörner, W., J. Dittmer, L. Iuzzolino, W. Meyer-Klaucke, and H. Dau. 1998. A new method for determination of the edge position of x-ray absorption spectra. In Photosynthesis: Mechanisms and Effects, Vol. II. G. Garab, editor. Kluwer Academic Publishers, Dordrecht, The Netherlands. 1343–1346.
- Enami, I., M. Kamo, H. Ohta, S. Takahashi, T. Miura, M. Kusayanagi, S. Tanabe, A. Kamei, A. Motoki, M. Hirano, T. Tomo, and K. Satoh. 1998. Intramolecular cross-linking of the extrinsic 33-kDa protein leads to loss of oxygen evolution but not its ability of binding to Photosystem II and stabilization of the manganese cluster. J. Biol. Chem. 273:4629–4634. [DOI] [PubMed] [Google Scholar]
- Enami, I., M. Kitamura, T. Tomo, Y. Isokawa, H. Ohta, and S. Katoh. 1994. Is the primary cause of thermal inactivation of oxygen evolution in spinach PS II membranes release of the extrinsic 33 kDa protein or Mn? Biochim. Biophys. Acta. 1186:52–58. [Google Scholar]
- Franzen, L. G., and L. E. Andreasson. 1984. Studies on manganese binding by selective solubilization of Photosystem II polypeptides. Biochim. Biophys. Acta. 765:166–170. [Google Scholar]
- George, G. N., R. C. Prince, and S. P. Cramer. 1989. The manganese site of photosynthetic water-splitting enzyme. Science. 234:789–791. [DOI] [PubMed] [Google Scholar]
- Ghanotakis, D. F., J. N. Topper, G. T. Babcock, and C. F. Yocum. 1984. Water-soluble 17 and 23 kDa polypeptides restore oxygen evolution activity by creating a high-affinity binding site for calcium on the oxidizing side of Photosystem II. FEBS Lett. 170:169–173. [Google Scholar]
- Hansen, U.-P., J. Kolbowski, and H. Dau. 1987. Relationship between photosynthesis and plasmalemma transport. J. Exp. Bot. 38:1965–1981. [Google Scholar]
- Hasegawa, K., T. Ono, Y. Inoue, and M. Kusunoki. 1999a. How to evaluate the structure of a tetranuclear Mn cluster from magnetic and EXAFS data: case of the S2-state Mn-cluster in Photosystem II. Bull. Chem. Soc. Jpn. 72:1013–1023. [Google Scholar]
- Hasegawa, K., T. Ono, Y. Inoue, and M. Kusunoki. 1999b. Spin-exchange interactions in the S2-state manganese tetramer in photosynthetic oxygen-evolving complex deduced from g = 2 multiline EPR signal. Chem. Phys. Lett. 300:9–19. [Google Scholar]
- Haumann, M., and W. Junge. 1999. Photosynthetic water oxidation: a simplex-scheme of its partial reactions. Biochim. Biophys. Acta. 1411:121–133. [DOI] [PubMed] [Google Scholar]
- Haumann, M., M. Grabolle, M. Werthammer, L. Iuzzolino, J. Dittmer, W. Meyer-Klaucke, T. Neisius, and H. Dau. 2001. The manganese complex of Photosystem II: a structural model for the S1, S2, and S3 oxidation states derived from linear dichroism EXAFS spectroscopy at 20 K and at room temperature. In PS2001 Proceedings. CSIRO Publishing, Collingwood, Australia. S10–013, 1–5.
- Haumann, M., M. Grabolle, T. Neisius, and H. Dau. 2002a. The first room-temperature x-ray absorption spectra of higher oxidation states of the tetra-manganese complex of Photosystem II. FEBS Lett. 512:116–120. [DOI] [PubMed] [Google Scholar]
- Haumann, M., P. Pospíšil, M. Grabolle, C. Müller, P. Liebisch, A. V. Solé, T. Neisius, J. Dittmer, L. Iuzzolino, and H. Dau. 2002b. First steps towards time-resolved BioXAS at room temperature-state transitions of the manganese complex of oxygenic photosynthesis. J. Synchrotron Rad. 9:304–308. [DOI] [PubMed] [Google Scholar]
- Iuzzolino, L., J. Dittmer, W. Dörner, W. Meyer-Klaucke, and H. Dau. 1998. X-ray absorption spectroscopy on layered photosystem II membrane particles suggests manganese-centered oxidation of the oxygen-evolving complex for the S0-S1, S1-S2, and S2-S3 transitions of the water oxidizing complex. Biochemistry. 37:17112–17119. [DOI] [PubMed] [Google Scholar]
- Kirby, J. A., A. S. Robertson, J. P. Smith, A. C. Thompson, S. R. Cooper, and M. P. Klein. 1981a. State of manganese in the photosynthetic apparatus. 2. X-ray absorption edge studies on manganese in photosynthetic membranes. J. Am. Chem. Soc. 103:5529–5537. [Google Scholar]
- Kirby, J. A., D. B. Goodin, T. Wydrzynski, A. S. Robertson, and M. P. Klein. 1981b. State of manganese in the photosynthetic apparatus. 1. Extended x-ray absorption fine structure studies on chloroplast and di-μ-oxo-bridged dimanganese model compounds. J. Am. Chem. Soc. 103:5537–5542. [Google Scholar]
- Klimov, V. V., G. Ananyev, O. Zastryzhnaya, T. Wydrzynski, and G. Renger. 1993. Photoproduction of hydrogen peroxide in Photosystem II membrane fragments: a comparison of four signals. Photosynth. Res. 38:409–416. [DOI] [PubMed] [Google Scholar]
- Kok, B., B. Forbush, and M. McGloin. 1970. Cooperation of charges in photosynthetic O2 evolution. I. A linear four-step mechanism. Photochem. Photobiol. 11:457–475. [DOI] [PubMed] [Google Scholar]
- Larson, E. J., and V. L. Pecoraro. 1992. Introduction to manganese enzymes. In Manganese Redox Enzymes. V. L. Pecoraro, editor. VCH, Weinheim, Germany. 1–28.
- Latimer, M. J., V. J. DeRose, L. Mukerji, V. K. Yachandra, K. Sauer, and M. P. Klein. 1995. Evidence for the proximity of calcium to the manganese cluster of Photosystem II: determination by x-ray absorption spectroscopy. Biochemistry. 34:10898–10909. [DOI] [PubMed] [Google Scholar]
- Latimer, M. J., V. J. DeRose, V. K. Yachandra, K. Sauer, and M. P. Klein. 1998. Structural effects of calcium depletion on the manganese cluster of Photosystem II: determination by x-ray absorption spectroscopy. J. Phys. Chem. B. 102:8257–8265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, C. B., H. Hayashi, and B. Y. Moon. 1997. Stabilization by glycinebetaine of photosynthetic oxygen evolution by thylakoid membranes from Synechococcus PCC7002. Mol. Cells. 7:296–299. [PubMed] [Google Scholar]
- MacLachlan, D. J., B. J. Hallahan, S. V. Ruffle, J. H. Nugent, M. C. W. Evans, R. W. Strange, and S. S. Hasnain. 1992. An EXAFS study of the manganese O2-evolving complex in purified Photosystem II membrane fractions. The S1 and S2 states. Biochem. J. 285:569–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacLachlan, D. J., J. H. A. Nugent, P. J. Bratt, and M. C. W. Evans. 1994. The effects of calcium depletion on the O2-evolving complex in spinach PS II: the S1, S2 and S3 states and the role of the 17 kDa and 23 kDa extrinsic polypeptides. Biochim. Biophys. Acta. 1186:186–200. [Google Scholar]
- Mei, R., and C. F. Yocum. 1991. Calcium retards NH2OH inhibition of O2 evolution activity by stabilization of Mn2+ binding to Photosystem II. Biochemistry. 30:7836–7842. [DOI] [PubMed] [Google Scholar]
- Mei, R., and C. F. Yocum. 1992. Comparative properties of hydroquinone and hydroxylamine reduction of the calcium-stabilized oxygen-evolving complex of Photosystem II: reductant-dependent manganese(2+) formation and activity inhibition. Biochemistry. 31:8449–8454. [DOI] [PubMed] [Google Scholar]
- Meinke, C., A. V. Solé, P. Pospíšil, and H. Dau. 2000. Does the structure of the water-oxidizing Photosystem II-manganese complex at room temperature differ from its low-temperature structure? A comparative x-ray absorption study. Biochemistry. 39:7033–7040. [DOI] [PubMed] [Google Scholar]
- Miller, A.-F., and G. W. Brudvig. 1991. A guide to electron paramagnetic resonance spectroscopy of Photosystem II membranes. Biochim. Biophys. Acta. 1056:1–18. [DOI] [PubMed] [Google Scholar]
- Mukerji, I., J. C. Andrews, V. J. DeRose, M. J. Latimer, V. K. Yachandra, K. Sauer, and M. P. Klein. 1994. Orientation of the oxygen-evolving manganese complex in a Photosystem II membrane preparation: an x-ray absorption spectroscopy study. Biochemistry. 33:9712–9721. [DOI] [PubMed] [Google Scholar]
- Murata, N., P. Mohanty, H. Hayashi, and G. C. Papageorgiou. 1992. Glycinebetaine stabilizes the association of extrinsic proteins with the photosynthetic oxygen-evolving complex. FEBS Lett. 296:187–189. [DOI] [PubMed] [Google Scholar]
- Mustre de Leon, J., J. Rehr, S. I. Zabinsky, and R. C. Albers. 1991. Ab initio curved-wave x-ray-absorption fine structure. Phys. Rev. B. 44:4146–4156. [DOI] [PubMed] [Google Scholar]
- Nash, D., M. Miyao, and N. Murata. 1985. Heat inactivation of oxygen evolution in Photosystem II particles and its acceleration by chloride depletion and exogenous manganese. Biochim. Biophys. Acta. 807:127–133. [Google Scholar]
- Ono, T., and Y. Inoue. 1988. Discrete extraction of the Ca atom functional for O2 evolution in higher plant Photosystem II by a simple low pH treatment. FEBS Lett. 227:147–152. [Google Scholar]
- Peloquin, J. M., K. A. Campbell, D. W. Randall, M. A. Evanchik, V. L. Pecoraro, W. Armstrong, and R. D. Britt. 2000. 55Mn ENDOR of the S2-state multiline EPR signal of Photosystem II: implications on the structure of the tetranuclear Mn cluster. J. Am. Chem. Soc. 122:10926–10942. [Google Scholar]
- Peloquin, J. M., and R. D. Britt. 2001. EPR/ENDOR characterization of the physical and electronic structure of the OEC Mn cluster. Biochim. Biophys. Acta. 1503:96–111. [DOI] [PubMed] [Google Scholar]
- Pecoraro, V. L. 1992. Structurally diverse manganese coordination complexes: from voodoo to oxygenic Photosynthesis. In Manganese Redox Enzymes. V.L. Pecoraro, editor. VCH, New York. 197–231.
- Penner-Hahn, J. E. 1999. Structural characterization of the Mn site in the photosynthetic oxygen-evolving complex. In Metal Sites in Proteins and Models. Redox Centres. H. A. O. Hill, P. J. Sadler, and A. J. Thomson, editors. Springer Verlag, Heidelberg, Germany. 1–36.
- Penner-Hahn, J. E., R. M. Fronko, V. L. Pecoraro, C. F. Yocum, S. D. Betts, and N. R. Bowlby. 1990. Structural characterization of the manganese sites in the photosynthetic oxygen-evolving complex using x-ray absorption spectroscopy. J. Am. Chem. Soc. 112:2549–2557. [Google Scholar]
- Philouze, C., G. Blondin, J. Girerd, J. Guilhem, C. Pascard, and L. Doris. 1994. Aqueous chemistry of high-valent manganese. Structure, magnetic, and redox properties of a new type of Mn-Oxo cluster, [Mn4IVO4(bpy)6]4+: relevance to the oxygen evolving center in plants. J. Am. Chem. Soc. 116:8557–8565. [Google Scholar]
- Pospíšil, P., and H. Dau. 2000. Chlorophyll fluorescence transients of Photosystem II membrane particles as a tool for studying photosynthetic oxygen evolution. Photosynth. Res. 65:41–52. [DOI] [PubMed] [Google Scholar]
- Rashid, A., and R. Carpentier. 1989. CaCl2 inhibition of H2O2 electron donation to Photosystem II in submembrane preparations depleted in extrinsic polypeptides. FEBS Lett. 258:331–334. [Google Scholar]
- Riggs, P. J., C. F. Yocum, J. E. Penner-Hahn, and R. Mei. 1992. Reduced derivatives of the manganese cluster in the photosynthetic oxygen-evolving complex. J. Am. Chem. Soc. 114:10650–10651. [Google Scholar]
- Riggs, P. J., R. Mei, C. F. Yocum, and J. E. Penner-Hahn. 1993. Characterization of the manganese site in the photosynthetic oxygen evolving complex: the effect of hydroxylamine and hydroquinone on the x-ray absorption spectra. Jpn. J. Appl. Phys. 32:527–529. [Google Scholar]
- Riggs-Gelasco, P. J., R. Mei, D. F. Ghanotakis, C. F. Yocum, and J. E. Penner-Hahn. 1996a. Reduced derivatives of the Mn cluster in the oxygen-evolving complex of Photosystem II: an EXAFS study. J. Am. Chem. Soc. 118:2400–2410. [Google Scholar]
- Riggs-Gelasco, P. J., R. Mei, C. F. Yocum, and J. E. Penner-Hahn. 1996b. X-ray absorption spectroscopy of calcium-substituted derivatives of the oxygen-evolving complex of Photosystem II. J. Am. Chem. Soc. 118:2387–2399. [Google Scholar]
- Robblee, J., R. Cinco, and V. K. Yachandra. 2001. X-ray spectroscopy based structure of the Mn cluster and mechanism of photosynthetic oxygen evolution. Biochim. Biophys. Acta. 1503:7–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roelofs, T. A., C. H. Lee, and A. R. Holzwarth. 1992. Global target analysis of picosecond chlorophyll fluorescence kinetics from pea chloroplasts. A new approach to the characterization of the primary processes in Photosystem II α- and β-units. Biophys. J. 61:1147–1163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sauer, K., V. K. Yachandra, R. D. Britt, and M. P. Klein. 1992. The photosynthetic water oxidation complex studied by EPR and x-ray absorption spectroscopy. In Manganese Redox Enzymes. V. L. Pecoraro, editor. VCH, New York. 141–175.
- Schiller, H., and H. Dau. 2000. Preparation protocols for high-activity Photosystem II membrane particles of green algae and higher plants, pH-dependence of oxygen evolution and comparison of the S2-state multiline signal by x-band EPR spectroscopy. J. Photochem. Photobiol. 55:138–144. [DOI] [PubMed] [Google Scholar]
- Schiller, H., J. Dittmer, L. Iuzzolino, W. Dörner, W. Meyer-Klaucke, V. A. Solé, and H. Dau. 1998. Structure and orientation of the oxygen-evolving manganese complex of green algae and higher plants investigated by x-ray absorption linear dichroism spectroscopy on oriented Photosystem II membrane particles. Biochemistry. 37:7340–7350. [DOI] [PubMed] [Google Scholar]
- Schröder, W. P., and H. E. Akerlund. 1986. H2O2 accessibility to the Photosystem II donor side in protein-depleted inside-out thylakoids measured as flash induced oxygen production. Biochim. Biophys. Acta. 848:359–363. [Google Scholar]
- Scott, R. A. 2000. X-ray absorption spectroscopy. In Physical Methods in Bioinorganic Chemistry—Spectroscopy and Magnetism. L. Que, Jr., editor. University Science Books, Sausalito, CA. 465–504.
- Seidler, A. 1996. The extrinsic polypeptides of Photosystem II. Biochim. Biophys. Acta. 1277:35–60. [DOI] [PubMed] [Google Scholar]
- Shen, J. R., K. Satoh, and S. Katoh. 1988. Isolation of an oxygen-evolving photosystem II containing only one tightly bound calcium atom from a chlorophyll b-deficient mutant of rice. Biochim. Biophys. Acta. 936:386–394. [Google Scholar]
- Shutilova, N., G. Semenova, V. V. Klimov, and V. Shnyrov. 1995. Temperature induced functional and structural transformations of the Photosystem II oxygen evolving complex in spinach subchloroplast preparations. Biochem. Mol. Biol. Int. 35:1233–1243. [PubMed] [Google Scholar]
- Stern, E. A. 1988. Theory of EXFAS. In X-Ray Absorption. D. C. Koningsberger and R. Prins, editors. John Wiley and Sons, New York. 3–52.
- Tamura, N., H. Inoue, and Y. Inoue. 1990. Inactivation of the water-oxidizing complex by exogenous reductants in PS II membranes depleted of extrinsic proteins. Plant Cell Physiol. 31:469–477. [Google Scholar]
- Teo, B. K. 1986. EXAFS: Basic Principles and Data Analysis. Springer Verlag, Berlin, Germany.
- Thompson, L. K., R. Blaylock, J. M. Sturtevant, and G. W. Brudvig. 1989. Molecular basis of the heat denaturation of photosystem II. Biochemistry. 28:6686–6695. [DOI] [PubMed] [Google Scholar]
- Van der Meulen, K. A., A. Hobson, and C. F. Yocum. 2002. Calcium depletion modifies the structure of the photosystem II O2-evolving complex. Biochemistry. 41:958–966. [DOI] [PubMed] [Google Scholar]
- Vermaas, W. F. J., A. W. Rutherford, and Ö. Hansson. 1988. Site-directed mutagenesis in photosystem II of the cyanobacterium Synechocystis sp. PCC 6803: donor D is a tyrosine residue in the D2 protein. Proc. Natl. Acad. Sci. USA. 85:8477–8481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wieghardt, K. 1989. Die aktiven Zentren in manganhaltigen Metalproteinen und anorganische Modellkomplexe. Angew. Chem. 101:1179–1198. [Google Scholar]
- Yachandra, V. K., V. J. DeRose, M. J. Latimer, I. Mukerji, K. Sauer, and M. P. Klein. 1993. Where plants make oxygen: a structural model for the photosynthetic oxygen-evolving manganese cluster. Science. 260:675–679. [DOI] [PubMed] [Google Scholar]
- Yachandra, V. K., R. D. Guiles, A. E. McDermott, R. D. Britt, S. L. Dexheimer, K. Sauer, and M. P. Klein. 1986. The state of manganese in the photosynthetic apparatus. 4. Structure of the manganese complex in Photosystem II studied using EXAFS spectroscopy. The S1 state of the oxygen-evolving Photosystem II complex from spinach. Biochim. Biophys. Acta. 850:324–332. [Google Scholar]
- Yachandra, V. K., and M. P. Klein. 1996. X-ray absorption spectroscopy: determination of transition metal site structures in photosynthesis. In Biophysical Techniques in Photosynthesis. J. Amesz, and A. J. Hoff, editors. Kluwer Academic Publishers, Dordrecht, The Netherlands. 337–354.
- Yamashita, T., and W. L. Butler. 1968. Inhibition of chloroplasts by UV-irradiation and heat treatment. Plant Physiol. 43:2037–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yocum, C. F. 1992. The calcium and chloride requirements for photosynthetic water oxidation. In Manganese Redox Enzymes. V.L. Pecoraro, editor. VCH, New York. 71–83.
- Yocum, C. F., C. T. Yerkes, R. E. Blankenship, R. R. Sharp, and G. T. Babcock. 1981. Stoichiometry, inhibitor sensitivity, and organization of manganese associated with photosynthetic oxygen evolution. Proc. Natl. Acad. Sci. USA. 78:7507–7511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zouni, A., H.-T. Witt, J. Kern, P. Fromme, N. Krauß, W. Saenger, and P. Orth. 2001. Crystal structure of photosystem II from Synechococcus elongatus at 3.8 A resolution. Nature. 409:739–743. [DOI] [PubMed] [Google Scholar]