Abstract
Sphingomyelin is enriched within lipid microdomains of the cell membrane termed lipid rafts. These microdomains play a part in regulating a variety of cellular events. Computer simulations of the hydrogen-bonding properties of sphingolipids, believed to be central to the organization of these domains, can delineate the possible molecular interactions that underlie this lipid structure. We have therefore used molecular dynamics simulations to unravel the hydrogen-bonding behavior of palmitoylsphingomyelin (PSM). A series of eight simulations of 3 ns each of a single PSM molecule in water showed that the sphingosine OH and NH groups can form hydrogen bonds with the phosphate oxygens of their own polar head, in agreement with NMR data. Simulations of PSM in a bilayer assembly were carried out for 8 ns with three different force field parameterizations. The major physico-chemical parameters of the simulated bilayer agree with those established experimentally. The sphingosine OH group was mainly involved in intramolecular hydrogen bonds, in contrast to the almost exclusive intermolecular hydrogen bonds formed by the amide NH moiety. During the bilayer simulations the intermolecular hydrogen bonds among lipids formed a dynamic network characterized by the presence of hydrogen-bonded lipid clusters of up to nine PSM molecules.
INTRODUCTION
Our view of the structural organization of biological membranes has recently evolved. The fluid-mosaic model of Singer-Nicolson (1972), which envisaged a uniform fluid lipid matrix, has been revised by recent findings that describe the existence of submicrometer scale domains in cell plasma membranes (Simons and Ikonen, 1997). These microdomains (or lipid rafts), created by the partitioning of cholesterol and sphingolipids into a liquid-ordered phase, in turn partition proteins between the fluid membrane and their own liquid-ordered phase. This property enables rafts to play a critical role in many functional properties of the surface membrane, including cell signaling, adhesion, and migration (Simons and Toomre, 2000). There is considerable current interest in how the associative properties of membrane lipids, and in particular the sphingolipids combining with cholesterol, allow their sorting into different microdomains on the cell surface (Anderson and Jacobson, 2002). The nature of the specific interaction of cholesterol with sphingolipids is unclear (Radhakrishnan et al., 2000), yet it is believed to give rise to the special properties of these microdomains (Brown and London, 2000).
The enigmatic properties of sphingolipids were noted by their discoverer, who named them in honor of The Sphinx (Thudicum, 1884). Sphingolipids and their metabolites are involved in many vital biological processes including differentiation, cellular senescence, apoptosis, and proliferation (Ohanian and Ohanian, 2001). They consist of long-chain amino alcohols (sphingosine or dihydrosphingosine) linked by an amide bond to a fatty acid (Fig. 1). They have several properties that distinguish them from the common glycerophospholipids (Brown, 1998). One is the fact that they can be glycosylated. This modification provides great structural diversity used in cell and pathogen recognition (Campbell et al., 2001) and a potential for an extensive hydrogen-bonding network above the cell surface, linking together glycosphingolipids and other components of rafts such as the carbohydrate chain of GPI-anchors (Boggs, 1987).
FIGURE 1.
Hydrogen-bonded conformations of palmitoylsphingomyelin: the seven conformations were used as starting conformers for MD simulations. For the sake of clarity, only the polar head of each PSM molecule is reported in the figure. The atom numbering of PSM is shown on the left side of the figure. A dashed line indicates intramolecular hydrogen bonds.
We have modeled sphingomyelin, the most common sphingolipid in mammalian cells (Voet and Voet, 1995), by means of molecular dynamics (MD) simulations. Natural sphingomyelin is heterogeneous in terms of its amide-linked fatty acid. We have chosen to simulate one of the most experimentally studied sphingomyelins: palmitoylsphingomyelin (PSM) (Fig. 1). The enantiomeric configuration of our model was the same as natural PSM in which the carbon atoms C2 and C3 are in the 2S, 2R configuration (Shapiro and Flowers, 1962). The distinctive propensity of sphingolipids for hydrogen-bond formation, provided by the OH and NH groups at the interface of the nonpolar hydrocarbon chains with the polar headgroups, is the focus of this study. This structural property is important both for the interaction of PSM within a bilayer assembly and for the signaling role that sphingolipid metabolites have in the cytoplasm (Ohanian and Ohanian, 2001). The OH group of PSM can act both as hydrogen-bond donor and acceptor whereas its amidic group can act as hydrogen-bond donor. These properties markedly contrast with the two carbonyl groups (acceptor only) found in the interfacial region of glycerophospholipids and are believed to be important for the sphingolipid-cholesterol interaction within lipid rafts (Brown, 1998). An insight into the nature of the forces that stabilize these intra- and intermolecular forces within a bilayer is of fundamental importance to the understanding of their role in forming the distinctive interfacial environment of lipid rafts.
We therefore decided to simulate the stability of different conformations of PSM in water and to analyze their hydrogen-bonding capacity. The behavior of PSM within a bilayer has subsequently been addressed.
METHODS
Software and force field parameterization
MD simulations were carried out with the GROMACS software (Berendsen et al., 1995). Two systems were analyzed: a single PSM lipid molecule in water (2864 atoms) and a fully hydrated PSM bilayer formed by 128 molecules of PSM (29,400 atoms). The single-molecule starting structures were built with the biopolymer module of the InsightII graphic program purchased from Accelrys (San Diego, CA). By means of this method a set of seven conformers (A–G) was generated (Fig. 1). The criteria for defining a conformer were based solely upon the type of intramolecular hydrogen bonds that characterized the analyzed conformations irrespective of other geometrical parameters.
The bilayer starting assembly was generated by modifying the equilibrated dipalmitoylphosphatidylcholine (DPPC) bilayer downloaded from the database at http://indigo1.biop.ox.ac.uk/tieleman/download.html (file “lipid.itp”). Three different force fields were examined.
Force Field 1 (FF1): a combination of the standard GROMACS parameters plus modified parameters (Tieleman and Berendsen, 1996) for Lennard-Jones interactions between the CH2/CH3 and water oxygens that were increased so as to accurately simulate a decane-water interface (Van Buuren et al., 1993), used with SPC/E parameters for water. Polar head: atom types CH3, NL, CH2, OS, P, and OM were used as defined in the ffgmx.atp file of GROMACS. Partial charges, angles, and dihedrals were adopted from the DPPC topology of Tieleman (http://indigo1.biop.ox.ac.uk/tieleman/download.html, file “dppc.itp”). Interfacial region: The partial charges of the OH group and peptidic moiety were adopted from the side chain of serine and from the peptidic bond as described in the file ffgmx.rtp of GROMACS. Atom types OA, HO, N, H, C, O, CH1, and CH2 were used. Lipid tails: Atom types CP2 and CP3 were used and an improper dihedral was used to keep the sphingomyelin trans double bond planar.
Force Field 2 (FF2): The second force field (FF2) was identical to FF1 but used in combination with the SPC water model. It had the same atom types, bonded and nonbonded parameters, as FF1.
Force Field 3 (FF3): This third force field was a further adaptation of the GROMOS set (http://indigo1.biop.ox.ac.uk/tieleman/download.html, file “lipid.itp”) optimized to reproduce the density of pentadecane in water, and found to give optimal simulation of a DPPC bilayer (Berger et al., 1997; Marrink et al., 1998, Tieleman et al., 1999); it was used here with the SPC water model. This force field is a mixture of lipid-optimized parameters and parameters from the GROMOS software (van Gunsteren and Berendsen, 1988). GROMOS parameters were taken from ffgmxnb.itp, lipid parameters from Berger (Berger et al., 1997). Polar head: same parameters and atom types as defined in the DPPC topology by Tieleman (http://indigo1.biop.ox.ac.uk/tieleman/download.html, file “dppc.itp”). Interfacial region: atom types, partial charges, angles and dihedrals as in the DPPC topology by Tieleman except for the OH and peptidic group specific to sphingomyelin. For these two functional groups the partial charges and atom types were the same as in the PSM1 topology (serine side chain and peptidic bond from GROMACS). Lipid tails: All the dihedrals, angles, and atom types were the same as defined by Tieleman in the DPPC topology. An improper dihedral was used to keep the trans double bond planar.
Although the SPC model has been preferred because of its more accurate chemical potential (Tieleman and Berendsen, 1996; Marrink et al., 1998), the tighter lipid-packing density provided by the SPC/E model proved instructive regarding the effect of packing density upon hydrogen-bond formation in a bilayer, and has been included here. For the sake of clarity the differences between the nonbonded parameters among the three force fields are reported in Table 1.
TABLE 1.
The two different sets of Lennard-Jones parameters for the CH2/CH3-OW, CH2–CH2, and CH3–CH3 interactions
| Force field | Nonbonded interaction | 10−3 × C61/2* | 10−3 × C121/2* |
|---|---|---|---|
| FF1 and FF2 | CH2-OW | 1.2910 | 0.04334 |
| CH3-OW | 1.4167 | 0.04745 | |
| CH2-CH2 | 1.1350 | 0.06863 | |
| CH3-CH3 | 1.3046 | 0.08268 | |
| FF3 | CH2-OW | 2.7934 | 0.06280 |
| CH3-OW | 3.0885 | 0.06933 | |
| CH2-CH2 | 1.5050 | 0.07664 | |
| CH3-CH3 | 1.8398 | 0.09369 |
Parameter C61/2 in [kJmol−1 nm6]1/2 and C121/2 in 10−3 × [kJmol−1 nm12]1/2.
MD simulations were carried out at constant temperature and pressure (NPT ensemble). A constant pressure of 1 bar was applied independently in each direction with a coupling constant of 1.0 ps, and the simulated systems were allowed to adjust their volume to an optimum value. Temperature was controlled by coupling to a temperature bath with a coupling constant of 0.1 ps. The time step was 2 fs and bond lengths were constrained by the LINCS algorithm (Hess et al., 1997).
Long-range interactions were treated with a twin-range cutoff, set to 2.0 nm for the electrostatic interactions and 1.0 nm for the van der Waals interactions.
Trajectories were computed on a PC Linux cluster. The optimal computational speed was obtained with four processors connected by a message-passing interface. The single PSM molecule was simulated in explicit water at 288 K up to 3 ns with the FF1 parameters. The PSM bilayer was simulated at 325 K for 8 ns with FF1, FF2, and FF3.
The bonded and nonbonded energies (Coulombic and van der Waals interactions) of each sphingomyelin conformer were computed by analyzing the last 0.5 ns of each trajectory.
Lifetimes and donor-acceptor distances of the hydrogen bonds were estimated by averaging the results of three different trajectories with different starting configurations. Hydrogen bonds were detected by analyzing the trajectories with the program g_hbond of the GROMACS software (Berendsen et al., 1995). A proton-acceptor distance cutoff of 0.25 nm and a hydrogen-acceptor-donor angle cutoff of ±90 degrees were used for defining the hydrogen bonds (Baker and Hubbard, 1984). The lifetime of a hydrogen bond was computed by summing up all the hydrogen-bond occurrences throughout the simulation time. Analysis programs were written for assessing water-bridged hydrogen bonds.
Bilayer equilibration
A PSM bilayer formed by 128 lipids and 3400 water molecules was equilibrated (68 wt.% fraction water). A high degree of hydration is expected to better reproduce a biological membrane (Tieleman and Berendsen, 1996). The bilayer was simulated at 325 K to reproduce a liquid crystalline phase (Bar et al., 1997). There was a drift in box size and potential energy during the first 0.3 ns of simulation. This first part of the trajectory was discarded for all the subsequent time-averaged computations. After this initial drift the box size remained constant and the area per lipid group was 56.5 ± 0.1 Å2 with FF1 parameters; 57.3 ± 0.1 Å2 with FF2 parameters; and 59.9 ± 0.1 Å2 with FF3 parameters.
RESULTS AND DISCUSSION
Single PSM molecule in water
Conformations A–G (Fig. 1) were used as starting conformations for 0.1 ns of MD simulation with atomic position restraints. The FF2 parameterization was used. During this simulation water molecules were allowed to equilibrate around the PSM molecule. The coordinates of each conformer and solvent that were generated at the end of the restrained simulation were used for a 3-ns simulation at 288 K without position restraints.
We analyzed the data to determine the hydrogen-bond lifetimes and geometries of the individual PSM conformations (Table 2) and their nonbonded energies together with the proper dihedral energies (Table 3). The other components of the bonded energies (angle, improper dihedrals) showed <3% difference between the different conformers, with very large standard deviations, and are not shown. Only one PSM conformer (conformer A), in which the phosphate esteric oxygen O1 was coordinated with the OH group, remained almost completely stable throughout the 3-ns simulation (Table 2). The dynamics of the hydrogen bonds of conformations A, C, and G were different. The hydrogen bond between the NH group and the oxygen O1 (in conformations C and G) broke and reformed several times during the trajectory. The hydrogen bond between the NH group and the oxygen O1 of conformer G was formed for 25% of the simulation, breaking and reforming 110 times over 3 ns. On the other hand, the hydrogen bond between the OH group and the oxygen O1 (conformer A) broke only five times over 3 ns and stayed formed for 99.6% of the simulation time.
TABLE 2.
Lifetimes and equilibrium distances (± SD) of the sphingomyelin hydrogen-bonded conformations. The nomenclature Φ6 and Φ7 indicate how many atoms are involved in a cycle upon hydrogen-bonding formation
| Donor-acceptor distance [Å]
|
Donor-acceptor angle [°]
|
|||||||
|---|---|---|---|---|---|---|---|---|
| Conformer | Lifetime [ns] | Number of times reformed | Φ5 | Φ6 | Φ7 | Φ5 | Φ6 | Φ7 |
| A | 2.990 (±0.006) | 5 (±3) | 1.5 (±0.4) | 20 (±25) | ||||
| B | 0.720 (±0.060) | 16 (±5) | 1.7 (±0.4) | 24 (±19) | ||||
| C | 0.615 (±0.100) | 95 (±12) | 2.4 (±0.2) | 76 (±8) | ||||
| D | 0.060 (±0.025) | 0 | 2.1 (±0.2) | 34 (±18) | ||||
| E | 0.009 (±0.003) | 0 | 1.5 (±0.4) | 2.3 (±0.4) | 21 (±11) | 50 (±15) | ||
| F | 0.0045 (±0.004) | 0 | 1.5 (±0.4) | 2.1 (±0.2) | 26 (±20) | 30 (±17) | ||
| G | 0.750 (±0.091) | 110* (±15) | 2.5 (±0.2) | 1.5 (±0.4) | 76 (±8) | 22 (±20) | ||
This value was evaluated by summing the number of times that both the NH–O1 and OH–O1 hydrogen bonds were reformed.
TABLE 3.
Coulombic, Lennard-Jones, and proper dihedral energies (± SD) for the hydrogen-bonded conformations of sphingomyelin described in the text. Energies were averaged over the lifetimes of the conformers. Temperature was 288 K, and pressure 1 bar
| Hydrogen-bonded conformation | Coulombic energy [kJ/mol] | Lennard-Jones interactions [kJ/mol] | Coulombic interactions with water [kJ/mol] | Proper dihedrals [kJ/mol] | Total energy [kJ/mol] |
|---|---|---|---|---|---|
| A | −600 (±51) | −10 (±15) | −660 (±120) | 26 (±7) | −1244 (±193) |
| B | −600 (±70) | −50 (±15) | −660 (±110) | 29 (±6) | −1281 (±201) |
| C | −540 (±47) | −40 (±10) | −670 (±60) | 25 (±7) | −1225 (±124) |
| D | −600 (±33) | −40 (±15) | −600 (±90) | 31 (±7) | −1209 (±145) |
| E | −600 (±20) | −26 (±16) | −530 (±80) | 32 (±5) | −1124 (±121) |
| F | −620 (±50) | −40 (±15) | −630 (±130) | 35 (±8) | −1255 (±203) |
| G | −600 (±52) | −30 (±17) | −610 (±63) | 25 (±6) | −1215 (±138) |
| G* | −620 (±43) | −45 (±15) | −610 (±120) | 26 (±6) | −1249 (±184) |
When O1 was hydrogen-bonded with the OH group, the resulting hydrogen-bond distance was the shortest observed (1.5 Å) and completed a stable six-atom cycle (Φ6) wherever it occurred (conformers A, E–G; Table 2). The intramolecular hydrogen bond formed by O1 with the NH group was longer (2.4Å) and formed a five-atom cycle (Table 2), with a dihedral energy particularly favorable (Table 3). When the NH moiety was hydrogen-bonded with the phosphate anionic oxygen (conformations D and E) or with the phosphate esteric oxygen O″1 (conformation B), calculated lifetimes were much shorter (Table 2). Adopting the force field FF3 did not change the conformation lifetimes.
Intramolecular and intermolecular (with water) Coulombic interactions contributed nearly equally to the total nonbonding energy of all seven conformers; Lennard-Jones interactions were <4% of the total, suggesting very little interaction between the two lipid chains of sphingomyelin in water. The least stable conformer (E) had the highest energy by a considerable margin (85 kJ/mole), but the small variations in computed energies of the other conformations (all six fell within 72 kJ/mole) did not directly correlate with their relative stability (compare Tables 2 and 3).
The energy values reported refer to the entire molecule, not just for the intramolecular hydrogen bonds that define each conformer; contributions from the rest of the molecule and especially variability in its interactions with water result in a high variation in the energy values (note the high standard deviations) and somewhat mask the contribution of the intramolecular hydrogen bonds. However, some trends are evident.
The importance of water as a competing hydrogen-bonding partner can be seen in the two conformers (D, E) that have the least favorable energetic interaction with water (Table 2). For each conformer, sequestering the phosphate anionic oxygens in an intramolecular interaction is at the expense of a hydrogen bond formed with the surrounding network of water molecules. The analysis showed that the phosphate anionic oxygens of conformer D had, on average, 1.7 hydrogen-bonded water molecules during the conformer lifetime. This number increased to 2.6 when the hydrogen bond between the NH group and the anionic oxygen was disrupted. Conformer E behaved similarly: the number of water molecules hydrogen bonded to the phosphate anionic oxygens increased from 1.0 to an average of 2.3 after disruption of the intramolecular hydrogen bond. In contrast, in the other conformers (which did not involve bonding an anionic oxygen intramolecularly to the NH group) formation of intramolecular hydrogen bonds did not alter the number of bonds formed with water.
Intermolecular bonding to water, along with intramolecular Lennard-Jones interactions, appeared also to dominate the energy profile of conformer B, which has intermediate stability (lifetime 0.61 ns; Table 2). In this conformer the NH group hydrogen bonds to the phosphate esteric oxygen O″1; formation of a second hydrogen bond between the OH group and esteric oxygen O1 produces conformer F with a much shorter half-life probably due to the unfavorable dihedral potential (Table 3).
To obtain a further insight into the energetically favored conformers of sphingomyelin in water, we analyzed the last 0.5 ns of the single molecule trajectories. Inasmuch as the seven trajectories started from different initial conformers they could probe the energy landscape better than a single trajectory. The time evolution of the nonbonded energy of the different conformers is shown in Fig. 2. Occasionally during the simulated time some of the hydrogen bonds characteristic of the starting conformer were broken and hydrogen bonds typical of other conformers were formed for short time intervals. The hydrogen bond between the OH group and the phosphate esteric oxygen O1 (conformer A in Fig. 1) was present throughout the final 0.5 ns of all trajectories even if the interaction was not present in the starting configuration. The nonbonded energies for the five trajectories starting from conformers B–F showed several recognizable minima along their time course (Fig. 2). The conformers belonging to these transient minima were isolated from the trajectory and the intramolecular hydrogen bonds analyzed. Minima that presented a conformer different to the starting conformer are circled in Fig. 2. A new conformer (G*) was found in the minimum belonging to the trajectory that started from conformer E. This new conformer is characterized by the simultaneous presence of three hydrogen bonds: two found in conformer G (NH and OH group coordinated to the oxygen O1) and the third was the one typical of conformer B (NH group coordinated to oxygen O″1). The hydrogen bonds angles and donor-acceptor distances for the three intramolecular hydrogen bonds of G* were identical to the geometries of conformer B and G (Table 2). The almost ubiquitous presence of conformer A within the minima further suggests that the intramolecular hydrogen bond between the sphingosine OH and the oxygen O1 is the one of the dominant noncovalent interactions of PSM.
FIGURE 2.
Time evolution of the intramolecular nonbonded energies (Coulombic and Lennard-Jones) during the last 0.5 ns of simulation for the sphingomyelin conformers. Conformers at energy minima were isolated from the trajectory and analyzed with respect to their intramolecular hydrogen-bonding. The minima that showed a PSM conformation different from the starting conformer are circled.
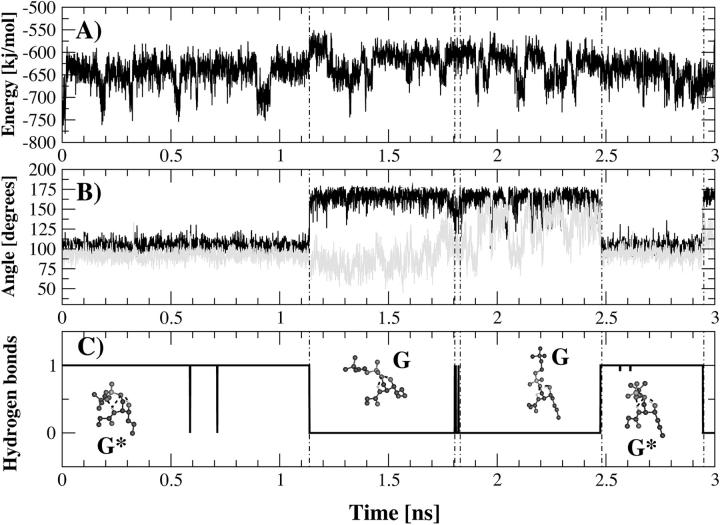
The isolated conformers were then energy-minimized and the nonbonded energies were computed. Conformer G* had an intramolecular nonbonded energy and an intramolecular Coulombic energy that were, on average, respectively 30 kJ/mol and 60 kJ/mol lower than the other conformers. Conformer G* was then used as a starting conformer for a 3-ns simulation at 288 K. During the first 1.1 ns of simulation, the hydrogen bonds characteristic of conformers A, B, and C remained stable. After this initial phase the hydrogen bond between the NH group and the phosphate esteric oxygen O″1 broke for 1.3 ns and then reformed during the last 0.6 ns of trajectory. This hydrogen bond is disrupted and reformed because of a rotation around the dihedral angle defined by the phosphorus, the oxygen O1, and the carbons C1 and C2 (i.e., a rotation around the O1–C1 bond). As shown in Fig. 3 there is a strict correlation between this dihedral and the formation-disruption of the hydrogen bond between NH group and the oxygen O″1. The dihedral transition (from 104° to 156°) increased the distance between the NH group and the phosphate esteric oxygen O″1, resulting in disruption of the hydrogen bond. When this occurred, a second dihedral transition took place around the dihedral angle defined by the atoms O″1, phosphorus, O1 and C1 (Fig. 3). A rotation of 40° (from 90° to 130°) around the P–O1 bond, together with the previous dihedral transition, moved the polar head into an upright position with respect to the lipid tails. The driving force that caused the equilibrium to shift from conformer G* to G was to be found in the Coulombic interaction with water. The analysis of electrostatic interactions between PSM and water throughout the trajectory indicated that 73 kJ/mol were gained during the transition from G* to G. This result suggests that when the polar head is an upright position the electrostatic interactions with water are optimized.
FIGURE 3.
Time course of intramolecular nonbonded energy (A), dihedral transitions (B), and hydrogen-bond formation (C) for the 3-ns simulations at 288 K of conformer G*. The analyzed dihedral angles are defined by the phosphorus atom, the oxygen atom O2, and the carbon atoms C1 and C2 (in black) and by the oxygen atom O″1, phosphorus atom, oxygen atom O1, and carbon atom C1 (in gray). The conformations that PSM adopts along the trajectory (G and G*) are shown in the lowest panel. The formation of a hydrogen bond between the NH group and the phosphate esteric oxygen atom O″1 is correlated to the dihedral angle transitions (Fig. 3 C).
Our study benefits from the detailed NMR analysis by Talbott (Talbott et al., 2000) of the hydrogen-bonding properties of PSM in solution and in reverse micelles and from the molecular mechanics simulations of phosphosphingolipids by DuPré and Yappert (1999). For fully hydrated PSM below its critical micelle concentration, NMR implicated both the sphingosine NH and OH groups in intramolecular hydrogen bonding. The NH group was suggested to interact with either of the esteric oxygens (O1 or O″1; our conformers C and G or B and F respectively) or an anionic oxygen (our conformers D and E). Our analysis suggests that of these possible interactions, those with the esteric oxygens are considerably more stable inasmuch as the anionic oxygens will preferably form a hydrogen bond with a molecule of water; and that intramolecular interaction with O1 (conformer C) is more stable than with O″1 (conformer B). The OH group was suggested (Talbott et al., 2000) to form a very stable hydrogen bond with the O1 esteric oxygen, protected from forming intermolecular bonds by the kink in the sphingosine chain introduced by the adjacent trans double bond between C4/C5. Our simulations of the single molecule confirmed the unusual stability of this bond, which was formed in every case when trajectories were started from conformers in which it was not initially present.
SPHINGOMYELIN BILAYER
Physico-chemical properties
A hydrated bilayer formed by 128 PSM lipids was built, equilibrated, and simulated to analyze the hydrogen-bonding behavior of PSM in the liquid crystalline phase in a bilayer.
Order parameters of the lipid tails were computed from the trajectory and compared to experimental values determined by NMR on deuterated sphingolipids (Fig. 4). The deuterium order parameters profiles of the n-palmitoyl chain reproduce well, with all the three sets of parameters, the experimental values determined for the corresponding positions of n-stearoyl chain of galactosyl ceramide (Morrow et al., 1993) in fluid phase. Our results for the deuterium order parameters at position 2 next to the headgroup falls within the experimental range of 0.18–0.24 determined for small n-alkyl chains within lipid aggregates (Pope et al., 1984; Seelig and Niederberger, 1974; Söderman et al., 1988). The largest differences were found for the first three atoms closest to the water-bilayer interface for which the simulated order values were lower than the experimental values (Fig. 4). A similar difference in order parameters was seen in MD simulations of a DPPC bilayer (Tieleman and Berendsen, 1996), possibly because NMR does not measure the same instantaneous order parameters that are obtained from simulations (Petrache et al., 1999). Subtle deficiencies in the hydrocarbon chain potential and/or long time-scale “wobble” motions could also contribute to the observed differences (Tu et al., 1995).
FIGURE 4.
Deuterium order parameters for the simulated PSM bilayer. Values were averaged over time. Solid black circles are for the experimental values for the corresponding positions of n-stearoyl chain of galactosyl ceramide, gray triangles are for the n-palmitoyl chain simulated with the FF1 parameters, dark gray circles are for the FF2 parameters, and black squares for the FF3 parameters.
The cross-sectional area per lipid of the simulated bilayers equilibrated at 56.5 Å2 (FF1), 57.3 Å2 (FF2), and 59.9 Å2 (FF3). Two values are found for the cross-sectional area of palmitoylsphingomyelin in liquid crystalline bilayers in the literature: 64.3 Å2 (Maulik et al., 1986) and 47.0 Å2 (Maulik and Shipley, 1996) per molecule. Measurements on PSM monolayers at a surface pressure that mimics that found in biomembranes suggest a cross-sectional area of 55 Å2 (Li et al., 2001). As pointed out recently (Nagle and Tristam-Nagle, 2000), experimental determination of the physical parameters of bilayers, and in particular the area/lipid, is subject to a relatively high level of uncertainty, arising both from variations in experimental methods and from the models used to interpret the data; 25% divergence in values from essentially the same data are not uncommon (Nagle, 1993). The values given by our simulations describe the packing density of PSM in a liquid crystalline state well within the range of experimental values. FF1 and FF2 have a more repulsive Lennard-Jones potential for the interactions between the CH2/CH3 and water oxygens than FF3 (Table 1). This increased hydrophobicity compensates for the less attractive Lennard-Jones potential among the CH2 and CH3 groups (Table 1) and yields a lower area per lipid. Moreover, the SPC/E water model (FF1) increases the packing density by screening more efficiently the headgroup charges than the SPC water model because of its increased polarity (Tieleman and Berendsen, 1996).
The parameters that describe the simulated bilayer thickness (Table 4) agree well with the experimental results (Maulik et al., 1986; Maulik and Shipley, 1996). The interfacial width, which is defined as the distance over which the water density drops from 90% to 10% of the bulk value, was evaluated after bilayer equilibration. Its thickness was 1.0 nm for FF1 and FF2 and 1.1 nm with FF3 parameters, in agreement with value found for DPPC bilayers (Tieleman and Berendsen, 1996). The magnitude of this parameter suggests that water can penetrate into the bilayer to reach the OH and NH functional groups. The possible insertion of water molecules in the hydrogen bonds was therefore taken into account when analyzing the trajectories.
TABLE 4.
Comparison between x-ray scattering data and simulated values for the bilayer thickness; mean value (± SD)
| Parameter | Experimental | FF1 | FF2 | FF3 |
|---|---|---|---|---|
| Lamellar repeat [Å] | 65.9 | 65.0 (±0.1) | 65.0 (±0.1) | 66.7 (±0.1) |
| Phosphate- Phosphate distance [Å] | 42.0, 36.5 | 36.0 (±0.1) | 36.0 (±0.1) | 38.5 (±0.2) |
| Area per lipid [Å2] | 47.0,* 55.0,† 64.3‡ | 56.5 | 57.3 | 59.9 |
From Maulik and Shipley, 1996; data for a PSM bilayer.
From Li et al., 2000; data for a PSM monolayer.
From Maulik et al., 1986; data for a PSM bilayer.
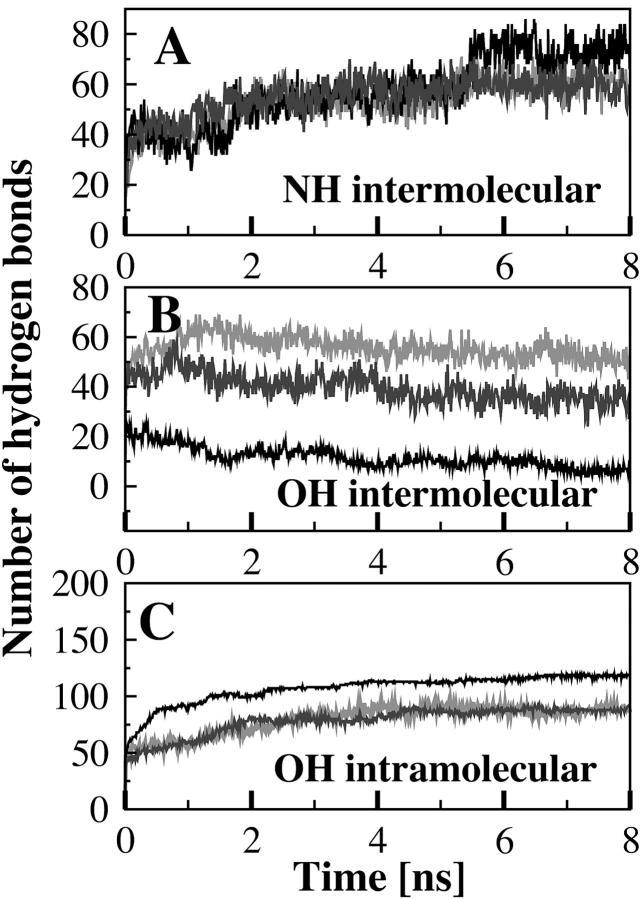
Our simulations of PSM in a lipid bilayer reproduced both the primary intermolecular bonding propensity of the NH group and dominant intramolecular bonding (Fig. 5 A) propensity of the OH group (Fig. 5 C). Inasmuch as this is the first MD simulation of a sphingolipid in a bilayer, it is worth noting that our simulated bilayer reproduced accurately many of the known features of PSM bilayers. These include the dominance of Coulombic over Lennard-Jones interactions in determining the total lipid energy (Boggs, 1987), the lamellar repeat and phosphate-phosphate distance (Maulik et al., 1986; Maulik and Shipley, 1996), interfacial region, and order parameters (Egberts and Berendsen, 1988).
FIGURE 5.
Time evolution of the intermolecular hydrogen bonds formed between the NH group as proton donor (A), the intermolecular hydrogen bonds formed by the OH group as proton donor (B), and the intramolecular hydrogen bonds formed by the OH group of palmitoylsphingomyelin with the esteric oxygen O1 (C). Data obtained with the FF1 parameters are in gray, with the FF2 parameters in dark gray and the FF3 parameters in black.
The hydrogen-bonding network
In Table 5 the type and number of conformers that were present during the last nanosecond of simulation are reported. Overall, the OH group remained primarily involved in the stable intramolecular hydrogen bond formed with the phosphate esteric oxygen O1 (conformer A, Table 5; and Fig. 5 C), as for the single hydrated molecule of PSM; in contrast, the NH group formed very few intramolecular hydrogen bonds (conformers B–G; Table 5) although it was the prime contributor to intermolecular hydrogen bonds within the bilayer (Fig. 5 A). During the last nanosecond of simulation using the FF1 parameters, the sphingomyelin NH group was on average involved in 61 ± 4 intermolecular hydrogen bonds (Fig. 5 A), of which 15 were bridged by a water molecule, but only 16 intramolecular hydrogen bonds were formed (Table 5). When the FF2 parameters were used the sphingomyelin NH group was on average involved in 59 ± 5 intermolecular hydrogen bonds (Fig. 5 A) of which 11 were bridged by a water molecule. Only 18 lipids presented an intramolecular hydrogen bond (conformers B–G*, Table 5). Using the FF3 parameters the number of intermolecular hydrogen bonds (73 ± 5) was slightly bigger, with 22 bridged by water (Fig. 5 A), in contrast to only 15 lipids that formed intramolecular hydrogen bonds through the NH group (Table 5).
TABLE 5.
Number of intramolecularly hydrogen-bonded conformers (±SD) within the PSM bilayer as a function of time. The number of occurrences for each conformer is reported for the last nanosecond of simulation
| Conformation | FF1 | FF2 | FF3 |
|---|---|---|---|
| A | 88 (±2) | 88 (±1) | 118 (±2) |
| B | 1 (±1) | 4 (±1) | 3 (±1) |
| C | 5 (±1) | 3 (±1) | 3 (±1) |
| D | 1 (±1) | 2 (±1) | 1 (±1) |
| E | 1 (±1) | 0 | 0 |
| F | 1 (±1) | 3 (±1) | 3 (±1) |
| G | 5 (±1) | 3 (±1) | 2 (±1) |
| G* | 2 (±1) | 3 (±1) | 3 (±1) |
The hydrogen-bonding behavior of the NH and OH groups as a function of the packing density confirms what has been found experimentally (Talbott et al., 2000). Above the critical micelle concentration, in the NMR study sphingomyelin formed reverse micelles (Talbott et al., 2000) in which the lipid-lipid contacts must approximate those present in a bilayer. In this preparation the sphingosine NH group was found to be particularly susceptible to forming intermolecular hydrogen bonds, whereas the OH group remained primarily bonded intramolecularly, reflecting its steric protection by the C4/C5 double bond. Only at higher lipid concentrations (>50 mM) did this OH contribute to intermolecular hydrogen bonds (Talbott et al., 2000). The greater importance of the NH compared to the OH group in intermolecular bonding is also apparent in studies where the effect of chemical modification of each group upon the interaction of PSM with cholesterol has been studied (Kan et al., 1991, Gronberg et al., 1991). The simulations also demonstrated the stability of conformer G in which the esteric oxygen O1 bonded simultaneously with the sphingosine OH and NH groups; and of conformer G* in which the NH group simultaneously formed an additional bond with the O″1 oxygen.
Although the difference in physical dimensions of the bilayer measured after simulations using the different sets of parameters were relatively modest (Table 4), the increasingly lower packing density found on progressing from FF1 to FF3 produced a major difference in the involvement of the OH group in intermolecular hydrogen bonding, and thus on the extent of the hydrogen-bonded network created. During the last nanosecond of simulation with FF3 parameters, 118 out of 128 lipids involved their OH group in an intramolecular hydrogen bond (conformer A) and only six formed intermolecular hydrogen bonds via this group acting as proton donor (Fig. 5, B and C). In contrast, the number of lipids adopting conformation A over the last nanosecond of simulation was only 88 ± 2 with the FF1 parameters, but the number forming intermolecular hydrogen bonds directly with other PSM molecules was 29, and 52 ± 3 if the insertion of water was taken into account (Fig. 7 B). The FF2 parameters gave rise to an intermediate behavior inasmuch as the number of lipids adopting conformation A was the same as with FF1 (88 ± 1) but only 22 intermolecular hydrogen bonds were directly formed by the OH group acting as a proton donor. This number increased to 35 ± 4 if bridging by a water molecule was taken into account.
FIGURE 7.

Sideview (A) and topview (B) of the simulated PSM bilayer in the liquid crystalline state. The frame was isolated from the MD trajectory obtained with the FF1 parameters (at 8 ns). A hydrogen-bonded cluster formed by eight lipids is shown as a solid line. Dashed black lines indicate the intermolecular hydrogen bonds. In (C) the residue PSM 59 from the cluster is represented together with all the intermolecular hydrogen bonds it formed. For the lipid-water-lipid hydrogen bonds only the bridging waters are reproduced. The donors and acceptors of the surrounding lipids that participated in direct lipid-lipid hydrogen bonds with PSM 59 are depicted as spheres.
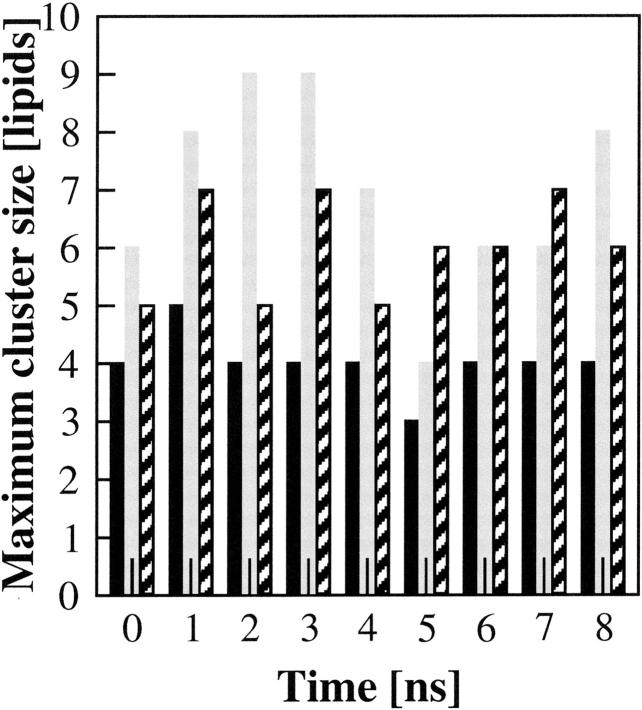
The increased potential under FF1 parameterization for PSM molecules to form hydrogen bonds through both their NH and OH groups resulted in a clear difference in the number of lipid molecules that were bridged by an intermolecular hydrogen bond, at any point in time. Fig. 6 shows that, under FF1 parameters, the maximum number of bridged lipids in the bilayer changed dynamically between four and nine over the 8 ns of simulation, with an average value of 7 ± 1.5. The larger area per lipid induced by the FF2 parameters decreased the cluster size to an average value of 6 ± 0.8. With the FF3 parameters, giving the largest area per lipid, the average maximum number of PSM molecules linked by hydrogen bonds of 4 ± 0.5. Fig. 7 shows, in both a cross-section of bilayer and from above, the cluster of eight PSM molecules linked by hydrogen-bonding in the last nanosecond of simulation with FF1 parameters.
FIGURE 6.
Size of the maximum hydrogen-bonded clusters of lipids within the simulated PSM bilayer in the liquid crystalline phase as a function of time. The cluster size for the MD simulations with the FF1 parameters is indicated in gray, the bars for the FF2 parameters are patterned, and the bars for the FF3 parameters are in black.
In Fig. 7 C a PSM lipid (PSM 59) that formed seven intermolecular hydrogen bonds is shown: four hydrogen bonds were bridged by a water molecule and three were made directly with the surrounding lipids. This is the maximum possible number of hydrogen bonds that a single molecule of PSM can form.
A detailed analysis of the percentage of lipids forming from four to seven intermolecular hydrogen bonds was therefore performed. In Fig. 8 this percentage is reported as a function of time for the last nanosecond of simulation for FF1 and FF3 that had the smallest and largest area per lipid respectively. All the possible hydrogen-bonding donors and acceptors were taken into account (i.e., phosphate oxygens and interfacial groups), as were hydrogen bonds formed directly and via one intermediate water molecule. These extensively hydrogen-bonded PSM molecules are the key contributors to a hydrogen-bonded network, and differ between the parameter sets (Fig. 8). When only direct lipid-lipid interactions were considered, the hydrogen-bond propensity (i.e., the proportion of lipids at any one time forming at least one interlipid hydrogen bond) was 73.4%, 70.1%, and 51.9% for FF1, FF2, and FF3, respectively. The force field parameterization did not have any major influence on the percentage of lipids making from one to three intermolecular hydrogen bonds.
FIGURE 8.
Time evolution of the number of intermolecular hydrogen bonds formed by PSM in a bilayer assembly. The percentage of lipids making four, five, six, and seven intermolecular hydrogen bonds is indicated by bars colored in black, white, dark gray, and gray respectively. (A) refers to the trajectory simulated with the FF1 parameters, and (B) to the FF3.
The fact that a substantial proportion (20–40%) of PSM in a bilayer form, not one (via NH group) or even two (adding the OH group) intermolecular hydrogen bonds, but up to four or seven hydrogen bonds by using the full range of donor/acceptors available in the interfacial and headgroups regions, was unexpected. However, sphingolipid-rich membranes show properties, such as much slower rates of lipid and protein diffusion (Morrot et al., 1986; Cribier et al., 1990; el Hage Chahine et al., 1993; Dietrich et al., 2002), compatible with a strong sphingolipid-bonded network being established. Even phosphatidylcholine, generally considered to have limited capability for intermolecular hydrogen bonding, has been found by MD simulations to form an extensive hydrogen-bonded network via bridging water molecules (Pasenkiewicz-Gierula et al., 1997).
The FF1 parameters gave the smallest cross-sectional area per lipid (56.5 Å2); that given by FF2 and FF3 were 0.8 Å2 and 3.4 Å2 (or 1.4% and 6.0%) larger. Compared to differences in experimental determination of this parameter, the differences in the simulated values appear to be quite minor. However, they amount to 0.89 Å and 1.85 Å in each dimension for FF2 and FF3 respectively, sufficient to account for the dramatic effect on hydrogen-bond formation that was found. At the tighter PSM packing obtained with FF1 or FF2, the sphingosine OH group started to participate appreciably (41% of PSM molecules for FF1 and 26% for FF2, rather than 8% for FF3) in intermolecular hydrogen-bonding, contributing not only its own hydrogen as a donor, but freeing up the O1 esteric oxygen as acceptor. Overall, twice as many PSM molecules (24% versus 44%) formed four to seven intermolecular hydrogen bonds at the higher packing density. The effect of the slightly higher packing density is perhaps most clearly seen in the maximal size of hydrogen-bonded clusters: with the FF3 parameter set, the maximal cluster was a relatively stable four PSM molecules; at the higher densities (FF1), it was nine (FF1) or seven (FF2), although these clearly formed and dissociated over the nanosecond time scale so that the average size of the largest cluster was seven or six PSM molecules for FF1 and two over the 8 ns of simulation.
Whereas differences in packing density of PSM in this critical region for hydrogen-bond formation have been achieved in this study by varying the simulation parameters, in biological membranes similar increases in packing density are achieved by increasing the chain length of the acyl chain (Li et al., 2001). Inasmuch as longer fatty acids than palmitate are normally present on cellular sphingomyelin in biological membranes (Brown, 1998), our simulation with all three parameter sets possibly underestimates the full propensity for intersphingolipid hydrogen-bonding on the cell surface. It will be of interest to determine the effect of cholesterol upon this hydrogen-bonded network.
CONCLUSIONS
The hydrogen-bonding properties of sphingomyelin in water, as a single molecule and assembled into a bilayer, have been studied using MD simulations. In agreement with NMR data (Talbott et al., 2000), our study of the single PSM molecule found that the interfacial NH and OH moieties of sphingomyelin were extensively involved in forming intramolecular hydrogen bonds with oxygens of the phosphate headgroup. In particular, hydrogen bonds formed with the proximal (O1) esteric oxygen by both the NH and OH groups were stable throughout the 3 ns of simulation, as was the conformer in which both hydrogen bonds existed simultaneously. Of the two hydrogen-bond donors to O1 oxygen, the OH group appeared to be more favored as it was formed when trajectories were initiated from less stable conformers. In addition, a bond that formed between the NH and the distal esteric oxygen (O″1) was also relatively stable (lifetime 0.610 ns), and could coexist with simultaneous bonding to the proximal O1 from both NH and OH groups.
Electrostatic interactions between PSM and surrounding water were a major determinant of the intramolecular bonding of this lipid. The molecules of water that surrounded the phosphate directly competed with (and so destabilized) intramolecular hydrogen bonds involving the phosphate anionic oxygens. Similarly, interactions of the polar head with water were important in tuning the interactions of the sphingosine NH with the distal phosphate oxygen (O″1).
Extension of the MD simulation to a bilayer formed by 128 PSM lipids in the liquid crystalline state showed a marked change in the hydrogen-bonding properties of PSM. Over 48% of the sphingosine NH groups, and 40% of the OH groups, became involved in intermolecular hydrogen-bonding, so that dynamic arrays of up to nine PSM molecules, interlinked by hydrogen-bonding, formed, dissociated, and reformed over the 8-ns simulation. The extent of hydrogen-bond formation was found to be very sensitive to changes in the packing density of PSM, approximately halving if the area/lipid increased by 6% (by using weaker values for Lennard-Jones interactions). Overall, the study adds detail to our understanding of the hydrogen-bonding pattern of sphingomyelin in solution, and emphasizes the potential of the hydrogen-bonding capability of this lipid in forming multimeric lipid assemblies in the bilayer.
Acknowledgments
E.M. thanks Dr. J. Kleinjung, Dr. D.P. Tieleman, and Prof. P. Quinn for helpful discussions, and gives special thanks to Dr. J. Heringa, who established contacts with the Mathematical Biology Division.
This work was supported by the European Network on Sphingolipids Synthesis and Organization, contract number HPRN-CT-2000-00077; the authors have also benefited from discussions with other members of the network.
References
- Anderson, R. G., and K. Jacobson. 2002. A role for lipid shells in targeting proteins to caveolae, rafts, and other lipid domains. Science. 296:1821–1825. [DOI] [PubMed] [Google Scholar]
- Baker, E. N., and R. E. Hubbard. 1984. Hydrogen bonding in globular proteins. Prog. Biophys. Mol. Biol. 44:97–179. [DOI] [PubMed] [Google Scholar]
- Bar, L. K., Y. Barenholz, and T. E. Thompson. 1997. Effect of sphingomyelin composition on the phase structure of phosphatidylcholine-sphingomyelin bilayers. Biochemistry. 36:2507–2516. [DOI] [PubMed] [Google Scholar]
- Berendsen, H. J. C., D. van der Spoel, and R. van Drunen. 1995. GROMACS: A message passing parallel molecular dynamics implementation. Comp. Phys. Commun. 95:43–56. [Google Scholar]
- Berger, O., O. Edholm, and F. Jahnig. 1997. Molecular dynamics simulations of a fully hydrated bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 72:2002–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boggs, J. M. 1987. Lipid intermolecular hydrogen bonding: influence on structural organization and membrane function. Biochim. Biophys. Acta. 906:353–404. [DOI] [PubMed] [Google Scholar]
- Brown, R. E. 1998. Sphingolipid organization in biomembranes: what physical studies of model membranes reveal. J. Cell Sci. 111:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown, D. A., and E. London. 2000. Structure and function of sphingolipid and cholesterol-rich membrane rafts. J. Biol. Chem. 275:17221–17224. [DOI] [PubMed] [Google Scholar]
- Campbell, S. M., S. M. Crowe, and J. Mak. 2001. Lipid rafts and HIV-1: from viral entry to assembly of progeny virions. J. Clin. Virol. 22:217–227. [DOI] [PubMed] [Google Scholar]
- Cribier, S., G. Morrot, J. M. Neumann, and P. F. Devaux. 1990. Lateral diffusion of erythrocyte phospholipids in model membranes comparison between inner and outer leaflet components. Eur. Biophys. J. 18:33–41. [DOI] [PubMed] [Google Scholar]
- Dietrich, C., B. Yang, T. Fujiwara, A. Kusumi, and K. Jacobson. 2002. Relationship of lipid rafts to transient confinement zones detected by single particle tracking. Biophys. J. 82:274–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DuPré, D., and M. C. Yappert. 1999. Conformational simulation of phosphosphingolipids by molecular mechanics. Theochem. 467:115–133. [Google Scholar]
- Egberts, E., and H. J. C. Berendsen. 1988. Molecular dynamics simulation of a smectic liquid crystal with atomic detail. J. Chem. Phys. 89:3718–3732. [Google Scholar]
- El Hage Chahine, J. M., S. Cribier, and P. F. Devaux. 1993. Phospholipid transmembrane domains and lateral diffusion in fibroblasts. Proc. Natl. Acad. Sci. USA. 90:447–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gronberg, L., Z. S. Ruan, R. Bittman, and J. P. Slotte. 1991. Interaction of cholesterol with synthetic sphingomyelin derivatives in mixed monolayers. Biochemistry. 30:10746–10754. [DOI] [PubMed] [Google Scholar]
- Hess, B., H. Bekker, H. J. C. Berendsen, and J. G. E. M. Fraaije. 1997. LINCS: a linear constraint solver for molecular simulations. J. Comp. Chem. 18:1463–1472. [Google Scholar]
- Kan, C., Z. S. Ruan, and R. Bittman. 1991. Interaction of cholesterol with sphingomyelin in bilayer membranes: evidence that the hydroxy group of sphingomyelin does not modulate the rate of cholesterol exchange between vesicles. Biochemistry. 30:7759–7766. [DOI] [PubMed] [Google Scholar]
- Li, X. M., M. M. Momsen, J. M. Smaby, H. L. Brockman, and R. E. Brown. 2001. Cholesterol decreases the interfacial elasticity and detergent solubility of sphingomyelins. Biochemistry. 40:5954–5963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrink, S. J., O. Berger, P. Tieleman, and F. Jahnig. 1998. Adhesion forces in lipid membranes. Biophys. J. 74:931–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maulik, P. R., D. Atkinson, and G. G. Shipley. 1986. X-ray scattering of vesicles of n-acyl sphingomyelins. Determination of bilayer thickness. Biophys. J. 50:1071–1077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maulik, P. R., and G. G. Shipley. 1996. N-palmitoyl sphingomyelin bilayers: structure and interactions with cholesterol and dipalmitoylphosphatidylcholine. Biochemistry. 35:8025–8034. [DOI] [PubMed] [Google Scholar]
- Morrot, G., S. Cribier, P. F. Devaux, D. Geldwerth, J. Davoust, J. F. Bureau, P. Fellman, P. Herve, and B. Frilley. 1986. Asymmetric lateral mobility of phospholipids in the human erythrocyte membrane. Proc. Natl. Acad. Sci. USA. 83:6863–6867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrow, M. R., D. Singh, D. Lu, and W. M. Grant. 1993. Glycosphingolipid acyl chain orientational order in unsaturated phosphatidylcholine bilayers. Biophys. J. 64:654–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagle, J. F. 1993. Area/lipid of bilayers from NMR. Biophys. J. 64:1476–1481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagle, J. F., and S. Tristram-Nagle. 2000. Structure of lipid bilayers. Biochim. Biophys. Acta. 1469:159–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohanian, J., and V. Ohanian. 2001. Sphingolipids in mammalian cell signalling. Cell. Mol. Life Sci. 58:2053–2068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasenkiewicz-Gierula, M., Y. Takaoka, H. Miyagawa, K. Kitamura, and A. Kusumi. 1997. Hydrogen bonding of water to phosphatidylcholine in the membrane as studied by a molecular dynamics simulation: location, geometry, and lipid-lipid bridging via hydrogen-bonded water. J. Phys. Chem. A. 101:3677–3691. [Google Scholar]
- Petrache, H. I., T. Kechuan, and J. F. Nagle. 1999. Analysis of simulated NMR order parameters for lipid bilayer structure determination. Biophys. J. 76:2479–2487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pope, J. M., L. W. Walker, and D. Dubro. 1984. On the ordering of n-alkane and n-alcohol, solutes in phospholipid bilayer model membrane systems. Chem. Phys. Lipids. 35:259–277. [Google Scholar]
- Radhakrishnan, A., T. G. Anderson, and H. M. McConnel. 2000. Condensed complexes, rafts, and the chemical activity of cholesterol in membranes. Proc. Natl. Acad. Sci. USA. 97:12422–12427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seelig, J., and W. Niederberger. 1974. Deuterium labeled lipids as structural probes in liquid crystalline bilayers. J. Am. Chem. Soc. 96:2069–2072. [Google Scholar]
- Simons, K., and E. Ikonen. 1997. Functional rafts in cell membranes. Nature. 387:569–572. [DOI] [PubMed] [Google Scholar]
- Simons, E., and D. Toomre. 2000. Lipid rafts and signal transduction. Nat. Rev. Mol. Cell Biol. 1:31–39. [DOI] [PubMed] [Google Scholar]
- Singer, S. J., and G. L. Nicolson. 1972. The fluid mosaic model of the structure of cell membranes. Science. 175:720–731. [DOI] [PubMed] [Google Scholar]
- Shapiro, D., and H. M. Flowers. 1962. Studies on sphingolipids. VII. Synthesis and organization of natural sphingomyelins. J. Am. Chem. Soc. 84:1047–1051. [Google Scholar]
- Söderman, O., G. Carlström, U. Olsson, and T. C. Wong. 1988. Nuclear magnetic resonance relaxation in micelles. J. Chem. Soc. Faraday Trans. 84:4475–4486. [Google Scholar]
- Talbott, C. M., I. Vorobyov, D. Borchman, K. G. Taylor, D. B. DuPre, and M. C. Yappert. 2000. Conformational studies of sphingolipids by NMR spectroscopy. II. Sphingomyelin. Biochim. Biophys. Acta. 1467:326–337. [DOI] [PubMed] [Google Scholar]
- Thudicum, J. L. W. 1884. In A Treatise on the Chemical Constitution of the Brain. Bailliere, Tindall and Cox, London, UK. p149.
- Tieleman, D. P., and H. J. C. Berendsen. 1996. Molecular dynamics simulations of fully hydrated DPPC with different macroscopic boundary conditions and parameters. J. Chem. Phys. 105:4871–4880. [Google Scholar]
- Tieleman, D. P., M. S. Sansom, and H. J. C. Berendsen. 1999. Alamethicin helices in a bilayer and in solution: molecular dynamics simulations. Biophys. J. 76:40–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu, K., D. J. Tobias, and M. L. Klein. 1995. Constant pressure and temperature molecular dynamics simulation of a fully hydrated liquid crystal phase dipalmitoylphosphatidylcholine bilayer. Biophys. J. 69:2558–2562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Buuren, A. R., S. J. Marrink, and H. J. C. Berendsen. 1993. A molecular dynamics study of the decane/water interface. J. Phys. Chem. 97:9206–9213. [Google Scholar]
- Van Gunsteren, W. F., and H. J. C. Berendsen. 1988. GROMOS: GROningen MOlecular Simulation Software Technical Report. Laboratory of Physical Chemistry, University of Groningen, Nijenbogh, The Netherlands.
- Voet, D., and J. G. Voet. 1995. Biochemistry, 2nd ed. Wiley, New York. pp662–726.