Folding of a Highly Conserved Diverging Turn Motif from the SH3 Domain

Abstract

Recent NMR structural characterization studies showed that a seven-residue segment (FKKGERL) from the src SH3 domain adopts the nativelike diverging type II β-turn in aqueous solution in support of the prediction based on the I-sites library of sequence structural motifs. We study the conformational variability and folding/unfolding thermodynamics of this peptide in explicit solvent using replica-exchange molecular dynamics simulations, which greatly enhances the sampling of the conformational space. This peptide samples three main free energy basins (nativelike, intermediate, and unfolded) separated by small barriers. The nativelike basin is fractionally populated (ΔG_300K = 0.4 kcal/mol) with structures that satisfy a subset of the NMR-derived constraints. The intrinsic stability of the diverging turn is examined in relationship to the nature of three specific contacts: a turn-hydrogen bond, a mainchain-to-sidechain hydrogen bond, and an end-to-end hydrophobic contact. We have carried out simulations of mutants at the highly conserved GE positions in the sequence. The mutation E5D destabilizes the isolated diverging turn motif, contrary to the observation that this mutation stabilizes the fyn SH3 domain. The G4T mutation also destabilizes the isolated diverging turn; however, the extent of destabilization is smaller than that of the reverse mutation in the drk SH3.

INTRODUCTION

The answer to the question of whether peptides adopt well-defined structures in isolation is still unknown and remains a major challenge toward understanding protein folding. Several reasons have been suggested for peptides not adopting native structures. Most emphasis is placed on the competition between local versus nonlocal interactions (Munoz and Serrano, 1996). It is generally believed that nonlocal interactions stabilize proteins in both native and denatured states and that the peptides derived from them cannot adopt native secondary structure in isolation (Yi et al., 1998). If there are sequence segments where the local interactions dominate over nonlocal interactions, then they are likely to adopt native structure in isolation. The possibility of these segments serving as folding initiation sites has inspired several studies seeking secondary structural motifs in proteins that form stable structure in solution (Dyson et al., 1992a,b; Viguera et al., 1996; Wright et al., 1988).

The majority of studies of protein segments have focused on α-helix formation in contrast to β-sheet formation. In an α-helix, the stabilization is a result of local interactions. However, residues in nonadjacent sequences take part in the formation of β-sheets (Searle, 2001) and require stabilization by tertiary interactions (Wang and Shortle, 1997). The β-hairpin structure has attracted considerable interest after the observation of significant populations of β-hairpins in several monomeric peptides (Blanco et al., 1994). Since the β-hairpin is a prototype for a simple antiparallel β-sheet, it has served also as a model system for β-sheet formation and stabilization. For example, a 16-residue β-hairpin (GB1) that forms a nativelike structure in aqueous solution has been thoroughly examined through experiment and theory (Dinner et al., 1999; Eaton et al., 2000; Garcia and Sanbonmatsu, 2001; Griffiths-Jones et al., 1999; Munoz et al., 1997; Pande and Rokhsar, 1999). It has been found that in this system nonlocal interactions play an important role in the stability of the folded structure (Griffiths-Jones et al., 1999). Although β-turns occur very frequently in proteins (Wilmot and Thornton, 1988), their role in early events in protein folding is not clear. Early theoretical studies on stability of turns were based on dipeptide systems (Tobias et al., 1990; Yang et al., 1996; Zimmerman and Scheraga, 1977). Experimental studies by Dyson et al. (1992b) on plastocyanin showed that only a small number of peptides had some tendency to form structures in isolation, and the strongest tendency was found for motifs similar to diverging β-turns.

Recent work has identified a seven-residue segment in the src SH3 domain to have the high propensity to adopt the nativelike diverging type II β-turn structure in isolation (Bystroff and Baker, 1998). The identification was based on the I-sites library of sequence-structure motifs (Bystroff and Baker, 1997). This diverging turn motif is highly conserved across the SH3 domains (Larson and Davidson, 2000). NMR structural characterization of this peptide segment in isolation confirmed the I-site prediction of the nativelike structure (Yi et al., 1998). Since this segment is capable of forming on its own, its conformation may be dominated by local interactions (Bystroff and Baker, 1998). These observations, along with the results of mutagenesis experiments, strongly support the idea that the diverging β-turn may play a role early in folding, preventing the inappropriate formation of β-hairpin and establishing the proper packing of hydrophobic sidechains between two diverging β-strands (Yi et al., 1998).

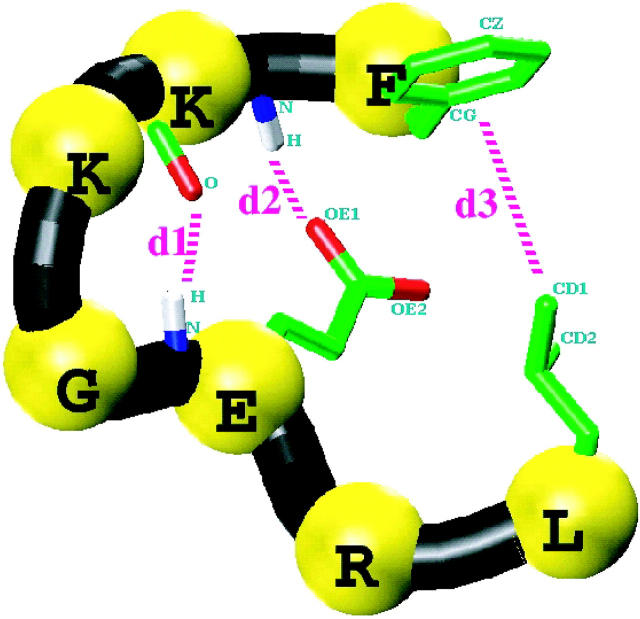
Considering the critical role which the diverging type II β-turn may play in the folding of β-sheet proteins, we have investigated the nature of local interactions in the folding of this motif. The seven-residue peptide, Phe-Lys-Lys-Gly-Glu-Arg-Leu (FKKGERL), of protein kinase c-src SH3 domain is considered. This turn structure is referred to hereafter as the SH3 peptide (Fig. 1). It is termed diverging because of the lack of backbone-backbone hydrogen bonds between the two strands. The residues KKGE define the type II β-turn. The turn is typified by three specific local contacts as shown in Fig. 1. The first contact is the mainchain-mainchain hydrogen bonding between the carbonyl oxygen of lysine at position 2 (K2) and the amide proton of E. For convenience, we termed the internuclear distance responsible for this contact, d1. The second contact, (d2), is the mainchain-sidechain hydrogen bonding between the amide proton of K2 with the sidechain carboxylate oxygen of E. The final contact, d3, is hydrophobic in nature between the sidechains of F and L, which bracket the turn. The peptide was structurally characterized using TOCSY and ROESY NMR experiments by Baker and co-workers (Yi et al., 1998). The Nuclear Overhauser Effect (NOE) intensities and J-couplings were consistent with a diverging type II β-turn and showed evidence of these three specific contacts.

FIGURE 1.

Three-dimensional schematic picture of the SH3 peptide in a nativelike type-II β-diverging turn conformation. The sequence of the peptide is Phe-Lys-Lys-Gly-Glu-Arg-Leu and only the relevant sidechains are shown. Also shown are the three specific contacts that characterize the diverging turn: d1, mainchain-mainchain hydrogenbond; d2, mainchain-sidechain hydrogen bond, and d3, end-residue sidechain hydrophobic contact. The atoms that are used to define these interactions are explicitly labeled.

In this paper, we examine the folding of the isolated SH3 peptide in water. The free energy of the solvated peptide is computed using replica–exchange molecular dynamics (REMD), in which no structural biases are imposed (Sugita and Okamoto, 1999). The replica exchange methodology provides excellent conformational sampling that cannot be achieved using a conventional molecular dynamics (MD) simulation by allowing access to regions separated by high barriers. The REMD has been applied toward the elucidation of conformational distribution and the calculation of folding transition temperature of short peptides (Garcia and Sanbonmatsu, 2001; Sanbonmatsu and Garcia, 2002). From the replica-exchange simulations, conformational distributions and structural characteristics of the SH3 peptide have been gathered at temperatures ranging from 276 to 469 K with intervals of 6–8 K. We have analyzed the conformational distribution in folded and unfolded regions. The results from the simulations are compared with those from the NMR experiments such as NOE, spin coupling of individual residues, and their temperature-dependence. We look for the existence of conformations that are consistent with the NMR measurements, especially those that satisfy the NMR-derived constraints individually rather than simultaneously.

The nature of contacts that characterize the diverging turn, the correlation between contacts, and the secondary structural distribution of the folded region are also explored. We have sought the most critical contacts for folding the turn. The free energy difference between the folded and unfolded states has been calculated from their relative populations. The contribution to the free energy from its enthalpic and entropic components is estimated. Finally, variations in SH3 domain sequences are explored using simulations of mutants with the goal of finding local interactions that would increase the stability of the turn (Martinez and Serrano, 1999; Riddle et al., 1999). The sequence GE in the diverging turn has been identified as highly conserved and mutations at these positions greatly affect the stability of the entire domain. We have carried out REMD simulations of mutants under identical conditions to the wild type to find out whether such substitutions stabilize or destabilize the peptide. First, the mutation of ASP to GLU at position 5 (E5D) is considered so that comparison can be made to the observation that this mutation stabilizes the fyn SH3 domain (Maxwell and Davidson, 1998). We also considered the mutation of GLY to THR at position 4 in the peptide sequence (G4T) similar to the sequence found in the drk SH3 domain (Mok et al., 2001).

MATERIALS AND METHODS

The highly parallel replica-exchange method incorporates molecular dynamics trajectories with a temperature-exchange Monte Carlo process to provide efficient sampling of configurational space (Sugita and Okamoto, 1999). The Monte Carlo exchange allows a peptide conformation (or a configuration) at low temperature to be swapped with a conformation at high temperature. The swapping between replicas depends on whether the potential energy gap between neighboring replicas becomes comparable to the temperature difference. The Metropolis criterion assures that the exchange satisfies the detailed balance. The REMD algorithm was incorporated into the AMBER 4.1 suite. The details of the implementation are given elsewhere (Garcia and Sanbonmatsu, 2001).

The replica-exchange MD simulations were implemented with 24 replicas, wherein each of the replicas is a system of SH3 peptides in explicit solvent at constant volume. The dimension of the solvated cubic box is 30.672 Å. The replicas were run at the following temperatures (in Kelvin): 276, 282, 288, 294, 300, 306, 313, 319, 326, 334, 341, 349, 357, 365, 374, 383, 392, 402, 412, 423, 434, 445, 457, and 469. The temperatures were chosen such as to maintain an exchange rate ∼10%. A time step of 2 fs was used and the exchange between replicas was attempted every 125 steps (0.25 ps). The generalized reaction field treatment (Hummer et al., 1994) was used for electrostatic interactions with a cutoff of 8 Å. The nonbonded pair list was updated every 10 steps. All bonds involving hydrogen were constrained using SHAKE. The system was coupled to an external heat bath with a relaxation time of 0.1 ps (Berendsen et al., 1984). Each of the replicas was simulated for 6 ns, yielding a total sampling time of 144 ns. The production run was considered to be the last 5.8 ns/replica. The x-ray structure of the diverging turn motif (FKKGERL) from the human tyrosine-protein kinase c-src SH3 domain (PDB file: 1FMK) is considered as the native structure when comparing results from the simulation. It corresponds to residues 102–108 in the PDB residue numbering scheme.

All replicas were started from extended conformations and no structural biases were imposed in the sampling. The peptide was solvated with 903 water molecules using the TIP3P model (Jorgensen et al., 1983). The PARM94 force field (Cornell et al., 1995) was used with an all-atom representation for the SH3 peptide. We have also carried out REMD simulations using the PARM96 force field (Kollman et al., 1997). The simulation conditions were identical so that direct comparison can be made with the calculations using PARM94 force field. It has been suggested that PARM96 is a better force field for β-sheets (Wang et al., 1999). Furthermore, simulation work from our group found that PARM96 prefers β-hairpin (Garcia and Sanbonmatsu, 2002). Krueger and Kollman (2001) have made free energy estimates for the SH3 peptide system utilizing different force fields. Their free energy comparisons were calculated with the MM-PBSA approach by postprocessing trajectories that were obtained with the PARM94 force field. We calculate the free energy differences of the folded and unfolded states of this peptide by performing separate REMD simulations.

Two additional replica-exchange MD simulations were carried out to study the effects of mutation on the stability of the diverging turn motif. We considered the E5D and G4T mutations of the SH3 peptide. The simulations were carried out under identical conditions to facilitate the evaluation of relative stabilities. Finally, a conventional MD simulation was carried out at constant volume and temperature. In this simulation the initial configuration of the SH3 peptide corresponds to a helical structure. The simulation was carried out for 12 ns at room temperature. It is utilized to illustrate potential sampling errors that can be encountered in short conventional MD simulations.

RESULTS AND DISCUSSION

Conformational distribution

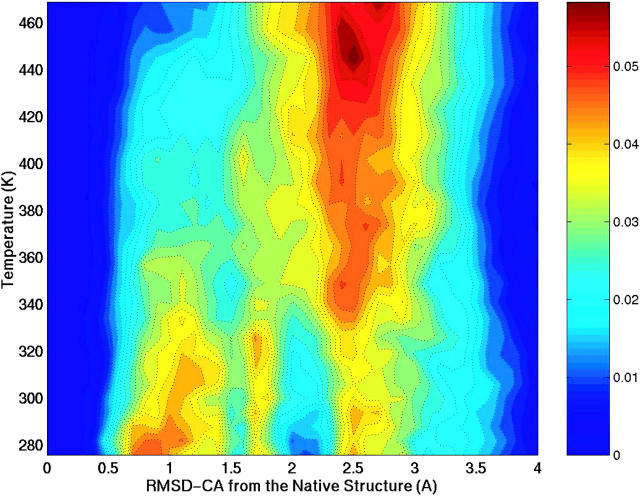
Since the SH3 peptide adopts an assortment of conformations over a wide range of temperatures, a suitable order parameter has to be considered to track those changes and differentiate the states of the peptide. Our focus is on distinguishing conformations adopted by this peptide from a nativelike diverging type II β-turn. A natural choice is the root mean square deviation of the backbone C_α atoms (RMSD-CA) from the native state (crystal structure). Fig. 2 shows the probability of conformations along this coordinate as a function of temperature. In the contour plot, red indicates the most probable (populated) conformations. Three major basins are sampled in the temperature range 276–469 K. We define these three basins as P1, P2, and P3. The first basin (P1) corresponds to conformations that deviate less than 1.5 Å RMSD-CA from the native structure. Basin P2 gathers conformations that are between 1.5 Å and 2.1 Å RMSD-CA from the native structure. The third basin, P3, corresponds to conformations that deviate the most (RMSD-CA > 2.1 Å). We classify basin P1 as folded, and basins P2 and P3 as primarily unfolded.

FIGURE 2.

Contour plot describing the conformational variability of the SH3 peptide as a function the root-mean-square-deviation of C_α atoms from the native (RMSD-CA) and temperature. The red color indicates the most probable (populated) conformations. The side bar relates the color gradient to fractional population. Three major basins are defined based on this map: P1, RMSD-CA ≤ 1.5 Å; P2, 1.5 Å <RMSD-CA ≤ 2.1 Å; and P3, RMSD-CA > 2.1 Å.

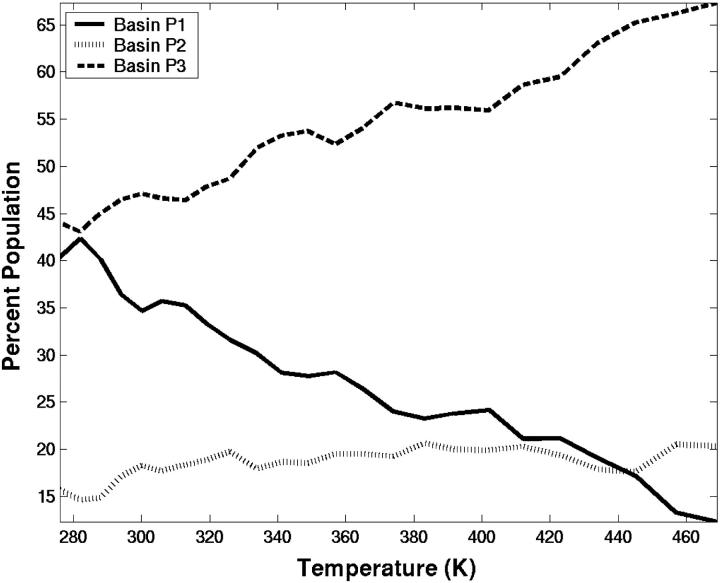
Conformations from the P1 basin closely resemble the native structure and are populated at low temperatures. With increasing temperature, the conformational preference shifts to basins P2 and P3. In the P2 region there is an increase in population near 320 K. At very high temperature, most of the conformations are found at RMSD-CA = 2.5 Å and correspond to structures that are random-coil or extended. Because this is a short peptide, the chain length limits the maximum RMSD-CA value for unfolded conformations. Fig. 3 shows the relative populations of the basins. Conformations from the unfolded basin P3 dominate the distribution at all temperatures, At 276 K, it accounts for 44% of the population. An appreciable number of conformations from the folded basin P1 are also populated at low temperatures, ∼40%. The intermediate basin P2 is populated from 15% to 20% and remains constant with increasing temperature.

FIGURE 3.

The percentage of population in each of the three basins: P1 (solid lines), P2 (dotted lines), and P3 (dashed lines). The basins are defined based on Fig. 2.

Thermodynamics of folding

The free energy of folding of the SH3 peptides is calculated from their relative population along the RMSD-CA coordinate, which is an average over many microscopic coordinates. The change in free energy, ΔG, is

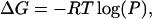(1)

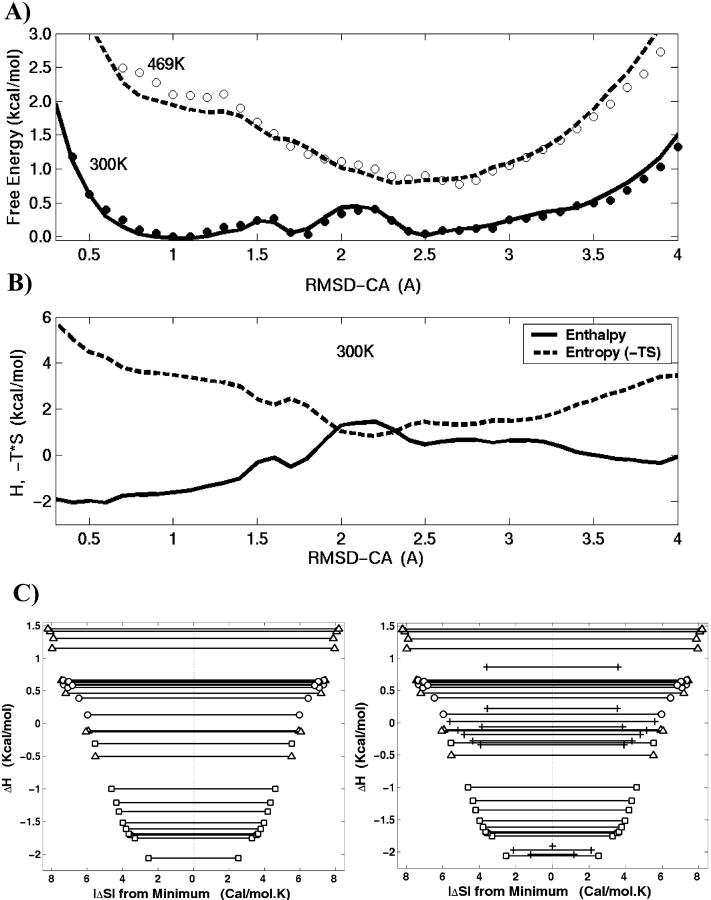
where P is probability distribution for a given RMSD-CA and R is the ideal gas constant. Fig. 4 A shows the free energy change at two different temperatures. At 300 K, the free energy surface is very shallow as minima and barriers are not high. Therefore, the ensemble at room temperature is comprised of conformations from all three basins. The lowest free energy is at RMSD-CA = 1.1 Å. Two additional minima are found within RT. The minimum at RMSD-CA = 2.5 Å is separated by a high barrier compared to the one at RMSD-CA = 1.8 Å. Also shown in the same plot is the free energy change at 469 K. At this temperature there is only one shallow minimum at RMSD-CA = 2.5 Å. It is the region where populations from the basins P2 and P3 merge at high temperature.

FIGURE 4.

(A) The free energy change at 300 K (solid lines) and 469 K (dashed lines) are plotted along the RMSD-CA coordinate. (B) The enthalpic (solid lines) and entropic (dashed lines) components of free energy at 300 K. The entropy is plotted as −TΔS. (C) The plot of entropy versus enthalpy. The width along the x-axis shows the magnitude of entropy relative to the minimum. The contributions from folded (squares), intermediate (circles), and unfolded (triangles) basins are clarified. The left figure considers the meaningful RMSD-CA range (0.5 A < RMSD-CA < 3.5 A) inasmuch as the extreme RMSD-CA values are associated with very low entropy and high numerical error. The plot on the right is given for comparison which considers the same range as the free energy plots in A and B and the extreme RMSD-CA points are marked +.

The interplay between enthalpic and entropic contributions is also explored, assuming a linear relationship between free energy and temperature (i.e., heat capacity, C_p = 0). At each point along the RMSD-CA coordinate, the temperature-dependence of ΔG is fitted to

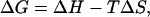(2)

where ΔH is the change in enthalpy and ΔS is the change in entropy (Hummer et al., 2000). In Fig. 4 A, the line represents the fit for Eq. 2. The free energy and its components incorporate both peptide and solvent contributions. The enthalpic and entropic components along the RMSD-CA coordinate are shown in Fig. 4 B. The entropy is plotted as −TΔS at 300 K. At low temperatures, the peptide system is stabilized by enthalpic contribution and driven toward basin P1. At high temperatures, however, entropic contributions dominate and the system is found mainly in basin P3.

The minima in enthalpy and entropy are found at low and high RMSD-CA. Small enthalpy at low RMSD-CA is expected because folded conformations minimize energetic interactions. The enthalpy of the unfolded basin (high RMSD-CA) is 2 kcal/mol higher compared to that of the folded basin (low RMSD-CA). The RMSD as an order parameter limits the number of configurations at low and high RMSD-CA values. The lowest RMSD-CA is achieved by a few conformations that resemble the nativelike structure, whereas the maximum number of conformations at very large RMSD-CA is limited by the chain length. This explains the small entropy found at the low and high RMSD-CA. A significant entropic contribution to the free energy occurs at RMSD-CA = 2.2 Å. Interestingly, the broadest distribution of the end-to-end distance is found at the same RMSD-CA.

The enthalpy and entropic contributions span a range of ∼8 kcal/mol. However, the entropy and enthalpic contributions to the free energy compensate such that the range of free energy change is only 1 kcal/mol. The inadequate compensation of a peak in the enthalpy by entropy results in a high barrier at RMSD-CA = 2 Å. Such an entropy-enthalpy compensation effect has been observed in chemical reactions (Cooper, 1999; Lumry and Rajender, 1970) and, more recently, in a hairpin peptide (Dinner et al., 1999). This compensation can be visualized in the plot of entropy versus enthalpy shown in Fig. 4 C. The plot is reminiscent of a two-dimensional projection of the funnel energy landscape where the folded conformation has small configurational entropy (near the center of the coordinate system) and low contact energy (bottom of the well). The tradeoff between entropy and enthalpy is qualitatively consistent with the folding funnel (Bryngelson et al., 1995; Nymeyer et al., 1998; Onuchic et al., 1997). However, in the folding funnel a decrease in energy is correlated to the reduction in configurational entropy, whereas we show a correlation with the total entropy. The main difference between the configurational entropy and total entropy comes from the burial of hydrophobic groups (Makhatadze and Privalov, 1995), a contribution that is not significant in a short peptide. In the calculations involving free energy changes we made the simplifying assumption that there is no temperature-dependence in ΔH and ΔS. A detailed analysis that incorporated the heat capacity, which defines the temperature-dependence of ΔH and ΔS, revealed that the heat capacity is small, in agreement with the observations of small heat capacities for peptides (Makhatadze, 1998).

A convenient way to express the conformational stability of the SH3 peptide is in terms of the difference in free energy between the unfolded and the native state. Assume that the system is in thermodynamic equilibrium; then the change in free energy for going from an unfolded state to folded state is

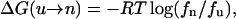(3)

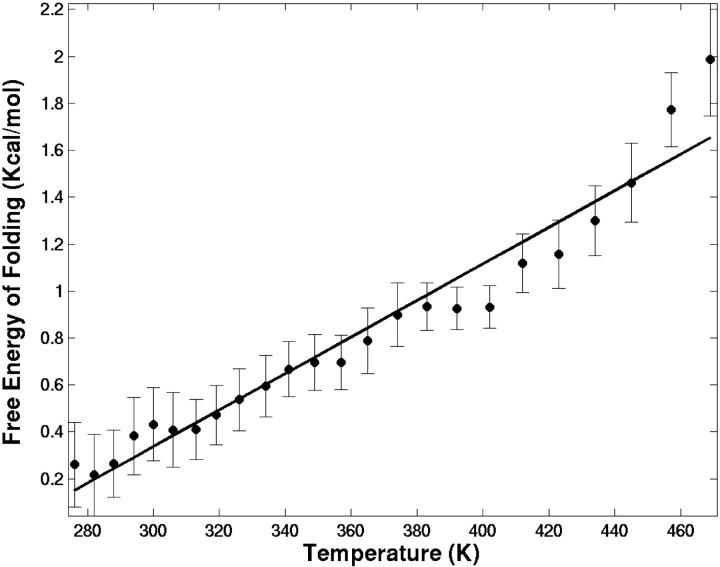
where f_n and f_u are the fractions of the peptide in folded (native) and unfolded states, respectively. We have used the cutoff of RMSD-CA = 1.5 Å for separating the folded from unfolded structures. Fig. 5 shows the free energy change for folding as a function of temperature. The melting temperature for this peptide is extrapolated to 257 K, below the lowest T simulated. At room temperature, the free energy of folding is estimated to be 0.41 ± 0.20 kcal/mol, indicating that the SH3 peptide is not stable. As temperature increases, the free energy cost for folding also goes up. Assuming a linear model, the stability of this peptide can be expressed in terms of the enthalpic and entropic contributions to the free energy change. At 300 K, the contribution from enthalpy is ΔH = −2.0 kcal/mol and the contribution from entropy is −TΔS = 2.3 kcal/mol.

FIGURE 5.

The free energy change of folding as a function of temperature. The line represents the fit to free energy using a linear model. The RMSD-CA = 1.5 A is used to separate the folded from unfolded structures. Error bar indicates the error in mean obtained from block analysis considering a block size of 2900 coordinate sets (725 ps) that is ∼14 times longer than the correlation time.

Comparison with NMR data

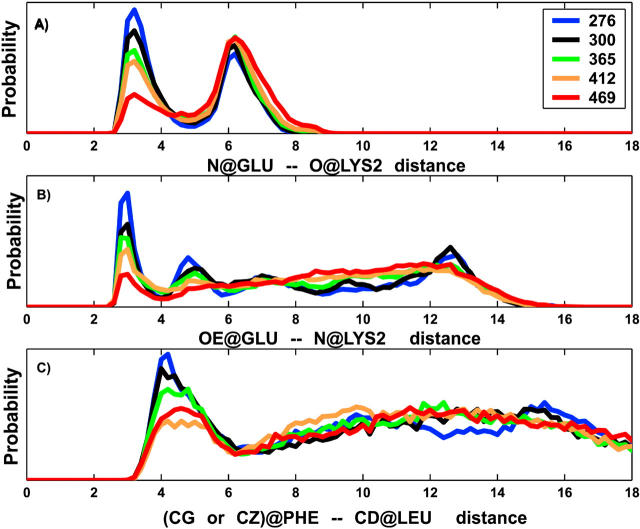
We have evaluated the temperature-dependent distribution of the three specific distances, d1, d2, and d3 (Fig. 1), that have been characterized by NMR to define the nativelike structure. The first distance, d1, is calculated as the internuclear separation between the mainchain atoms, carbonyl oxygen of K2, and amide nitrogen of E. The second distance, d2, is calculated as the internuclear separation between the mainchain amide nitrogen of K2 and carboxylate oxygens of sidechain of E. The third distance, d3, is measured between the sidechain atoms of F (CG or CZ) and L (CD1 or CD2) as marked in Fig. 1. The probability distribution of these three distances at five different temperatures is shown in Fig. 6, A–C. The distance d1 shows bimodal distributions at all temperatures. At low temperature, the first peak centered at 3.2 Å is stronger and narrower, indicating the existence of well-defined structure due to the mainchain-mainchain hydrogen bond. The second peak centered at 6.2 Å is broader and arises due to turning away of the backbone atoms. As temperature increases, the first peak loses amplitude whereas the second peak gains strength. Both peaks become broader at high temperature, but the peak positions do not shift.

FIGURE 6.

The temperature-dependent probability distribution of distances that describe the three specific interactions: mainchain-mainchain hydrogen bond (A); sidechain-sidechain hydrogen bond (B); and the end-residue sidechain hydrophobic contact (C). The pictorial representation of interactions along with the atoms considered for the internuclear distances are illustrated in Fig. 1. Only the distributions for five temperatures (276, 300, 365, 412, and 469 K) are shown.

The probability distribution of distance d2 has peaks at short and long distances at low temperatures. The closest distance peak is very sharp and centered at 3 Å. It indicates the existence of a mainchain-sidechain hydrogen bond that loses its amplitude with increasing temperature. It is followed by two broad peaks centered at 5.2 Å and 12.8 Å for temperatures below 350 K. At high temperatures, contacts at long distances show a broad distribution covering the 4 Å–16 Å range. The probability distribution of distance d3 shows a sharp peak at 4.2 Å, indicating the existence of hydrophobic contacts between the sidechains of the end residues. However, the decrease in intensity of this peak with increasing temperature is not gradual (i.e., the peak at 469 K has a higher amplitude than the peak at 412 K). At the lowest temperature, two additional broad structural peaks are observed at 10 Å and 15 Å. A Gaussian distribution centered at 12 Å is observed at higher temperatures. It resembles the behavior of an end-to-end distribution of a random peptide.

The three local contacts that characterize the turn as suggested from NMR are evident from the distribution of specific distances discussed above. In the NMR experiment a combination of chemical shift and NOE data were used to show the existence of these three specific contacts (Yi et al., 1998). In the simulations, the first peak in the probability distributions signifies the existence of conformations that satisfy these local contacts.

We have calculated the NMR spin couplings (³J_NHα) and compared them with those obtained from experiments. Their values can be related to conformations that are folded (nativelike) or highly unfolded. The ³J_NHα couplings are obtained from the dihedral angle φ using the Karplus relationship (Karplus, 1959; Pardi et al., 1984). These values are calculated at T = 15°C, closer to the temperature at which the measurements were carried out (Yi et al., 1998). Fig. 7 A shows both the measured and the calculated coupling values for residues 2–6. The agreement between experiment and calculated values is excellent for all residues, except for K2. The calculated ³J_NHα coupling of K2 is lower than expected by ∼1.4 Hz. The calculated values show a trend similar to the measured values. Experimentally, a small ³J_NHα (∼5 Hz) value for residue 3 of the peptide (K3 in our case) compared to a random coil value of 6.6 Hz (Smith et al., 1996) was shown as an indication of its participation in a β-turn (Wuthrich, 1986). Similarly, in the simulations the lowest coupling is found for K3. The temperature-dependence of ³J_NHα couplings also has been considered. Fig. 7 B shows the temperature-dependence of residues 2–6 of the peptide. As expected, ³J_NHα coupling values increase with temperature for most of the residues. The variation in the high temperature coupling constants can be related to different φ angle propensities of the residues in random coil conformation (Serrano, 1995). Residues G and E show less variation with temperature. The residue K3 shows the most sensitivity to the temperature due to the disruption of the type II turn.

FIGURE 7.

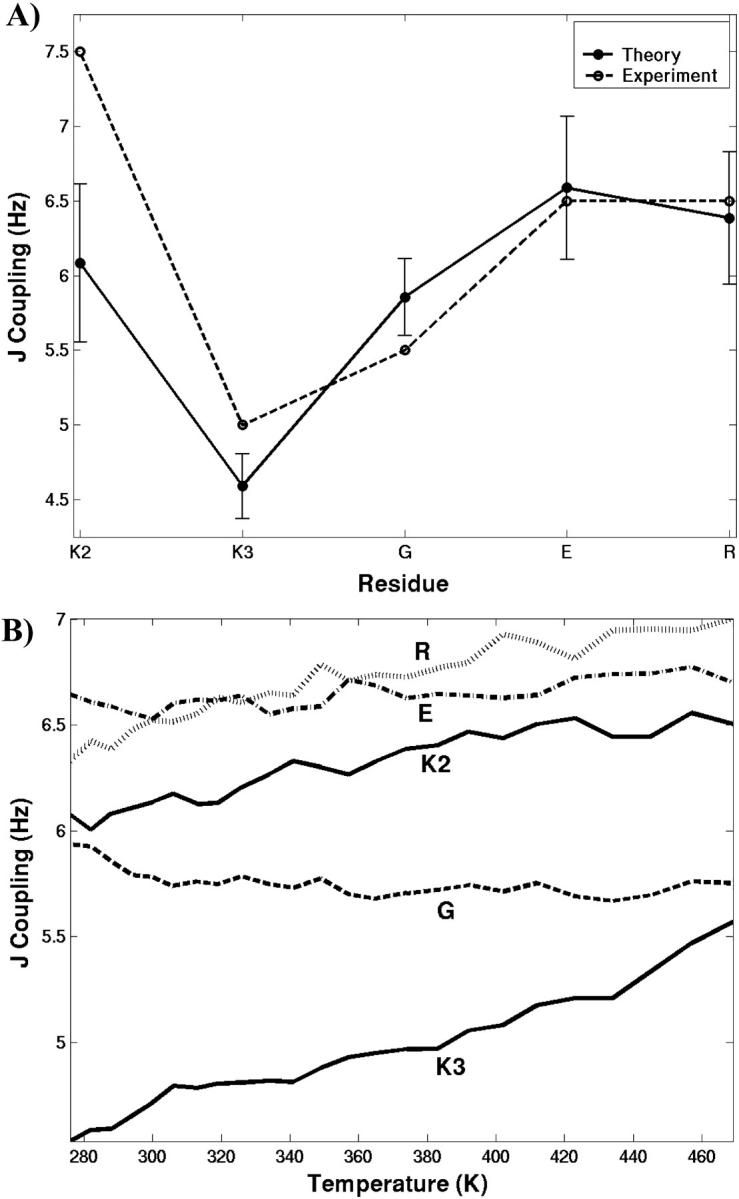
Plot (A) shows both the measured (dashed lines) and the calculated (solid lines) coupling values, ³J_NHα, for residues 2–6 of the SH3 peptide at 288 K. The error bar shows the standard deviation in mean obtained from block analysis considering a block size of 800 coordinate sets (200 ps). Plot (B) shows the temperature-dependence of ³J_NHα for the same residues.

The measured J-couplings and NOEs are the result of an ensemble and time average over a conformational distribution (Burgi et al., 2001; Choy and Forman-Kay, 2001; Daura et al., 1999; Onuchic, 1997; Stote et al., 2000). However, it is evident from thermodynamic analysis that the SH3 peptide is populated in several conformational states that are in equilibrium. Then the quantitative interpretation of NOE constraints and ³J_NHα coupling values is not straightforward, inasmuch as it requires the distribution of conformational states and their relative population. Additionally, NOE measurements do not provide insight into the frequency or correlation between the three specific contacts. The utilization of calculated ³J_NHα coupling values as a structural probe for conformational identification is also hampered because one cannot discriminate between well-known conformations with the same φ angle, such as poly-proline-II-like and helical structures (Smith et al., 1996). However, MD simulation is a valuable tool to extract such structural information at the atomic level, and to provide clarity to experimental interpretation, as shown below.

Probability distributions of contact formation

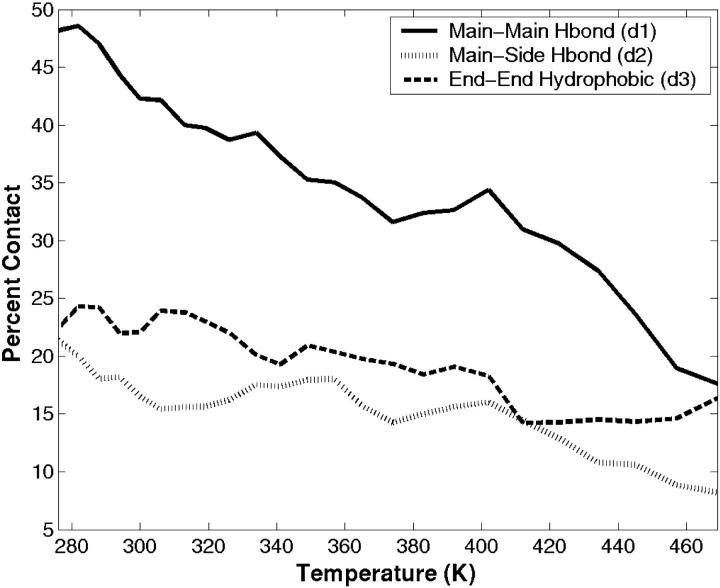
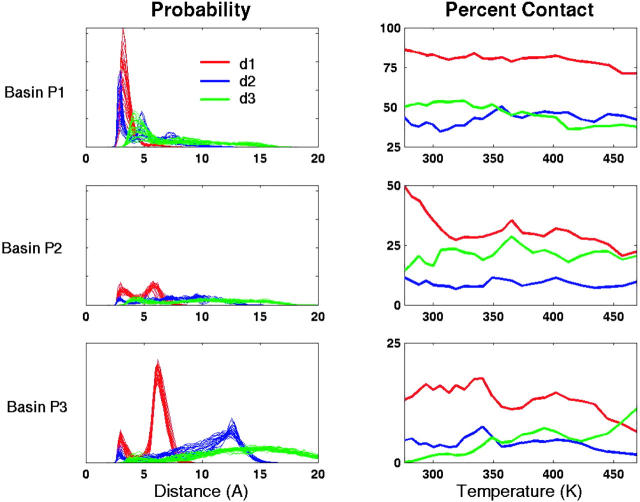
The frequency of occurrence and the strength of the three specific contacts that are observed in the internuclear distribution of distances, d1, d2, and d3, are considered in detail. From here on we use the symbols d1, d2, and d3 to mean contacts as well as distances. In this analysis, only the first peak in the internuclear distance distribution, shown in Fig. 6, is considered as an indication for the formation of a contact (either hydrogen bonding or hydrophobic). The d1 and d2 contacts are defined to form hydrogen bonding contacts when the internuclear distance is less than 4 Å. The third contact, d3, is defined to form a hydrophobic contact when the distance is less than 6 Å. These cutoff distances are chosen from the observed distributions and not from any geometrical or energetic properties inherent to these contacts. Fig. 8 shows the percentage of contacts that are formed as a function of temperature. At low temperatures, 48% of the conformations form contact d1, the mainchain-mainchain hydrogen bond. This has the highest occurrence of the three contacts. Although the population of d1 contact decays with increasing temperature (18% at 469 K), its dominance is preserved. The second contact, d2, is the least populated, with 21% and 8% at low and high temperatures, respectively. It supports the weakness of a sidechain-mainchain hydrogen bond, especially the one that is spatially in the middle between the turn and the end-to-end contact. At low temperatures, 24% of the population is found with a formed hydrophobic contact, d3.

FIGURE 8.

The percentage of specific contacts: d1 (solid lines); d2 (dotted lines); and d3 (dashed lines) that are formed as a function of temperature. The cutoff distances used to define the formation of these specific contacts are deduced from the distribution of internuclear distances plotted in Fig. 6.

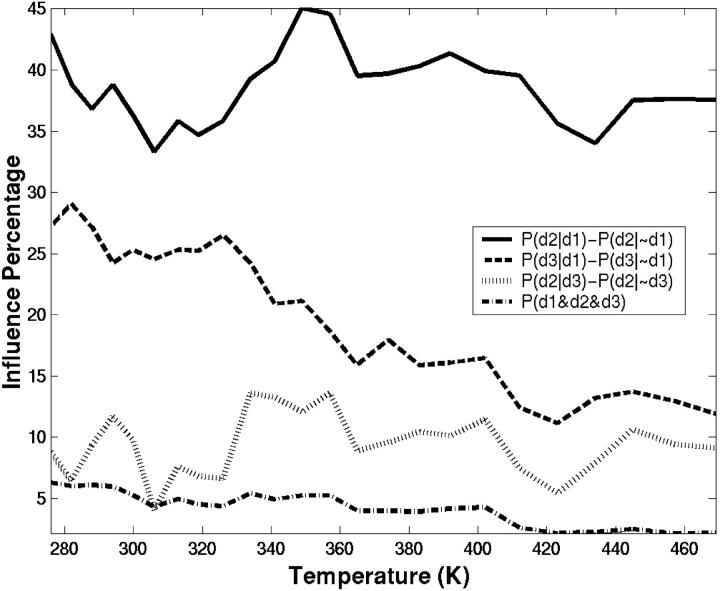
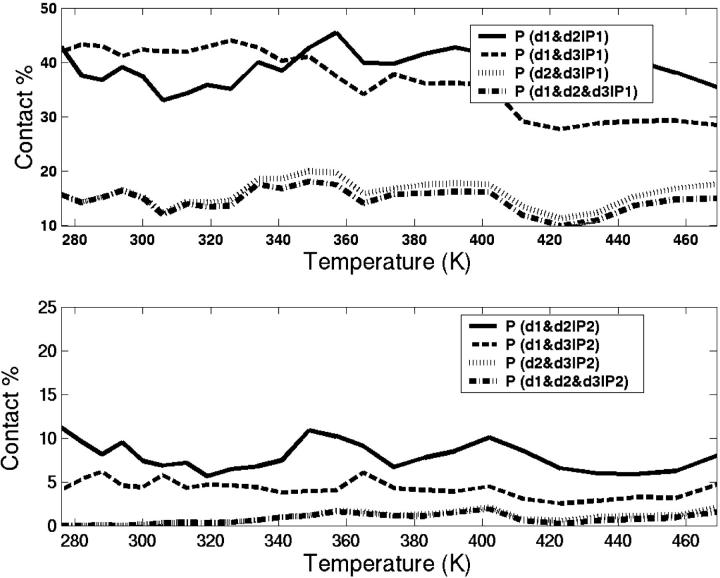
We have also explored the correlations between the three specific contacts to find out whether the formation of these contacts are independent of each other or whether they are influenced by each other. In addition, the simultaneous formation of all three contacts is also explored. Fig. 9 shows the extent of influence of specific contacts on each other. The influence is considered as the difference in conditional probability for observing one contact in the presence and absence of the other contact. For example, the solid curve shows the difference in conditional probability, [P(d2|d1) − P(d2|∼d1)], the probability of observing contact d2, given that contact d1 exists minus the probability of observing contact d2 given that d1 does not exist. The temperature-dependent correlation coefficients (not shown) track the quantities plotted in Fig. 9 fairly well. When the mainchain-mainchain hydrogen bond, d1, is already formed, the probability for observing conformers with contact d2 increases by 42%. The correlation between contacts d1 and d2 is indicated by a correlation coefficient of 0.5 at room temperature. Even though d1 and d2 contacts decrease with increasing temperatures, the influence of d1 on d2 has been maintained.

FIGURE 9.

The extent of influence (as a percentage) of specific contacts on each other. The correlation between the specific contacts d1 and d2 (solid lines), d1 and d3 (dashed lines), and d2 and d3 (dotted lines) are plotted as functions of temperature. The probability of simultaneous formation of all three contacts (dashed-dotted lines) is also given. The influence is expressed as the difference in conditional probability, P(i|j) − P(i|∼j), the probability of observing contact i, given that contact j exists minus the probability of observing contact i given that j does not exist.

The d1 contact also influences, to a lesser degree, the formation of the hydrophobic contact, d3 (correlation coefficient = 0.3). According to the plot, the probability of forming d3 contact increases by 27% when the d1 contact exists. However, this influence decays steeply with temperature. The contact d3 does not influence the formation of d2. The correlation analysis provides a coefficient below 0.1, suggesting that d2 and d3 are uncorrelated. Finally, we find only 6% of conformations satisfy all three contacts simultaneously at low temperatures. Our analysis indicates that to form d2 and d3, structure should also have the d1 contact formed. Therefore, conformations with the d1 contact have a high potential of forming a diverging turn. Consequently, a two-dimensional conformational map of RMSD-CA and internuclear distance d1 captures the essentials of the SH3 peptide folding. The folded and unfolded basins discussed above are evident in such a plot shown in Fig. 10 A. The folded region is given by the boundary [d1 < 4.5 Å] and [RMSD-CA < 1.5 Å]. The unfolded region is given by [d1 > 5 Å] and [RMSD-CA > 2.1 Å]. The intermediate region is spread over a larger area.

FIGURE 10.

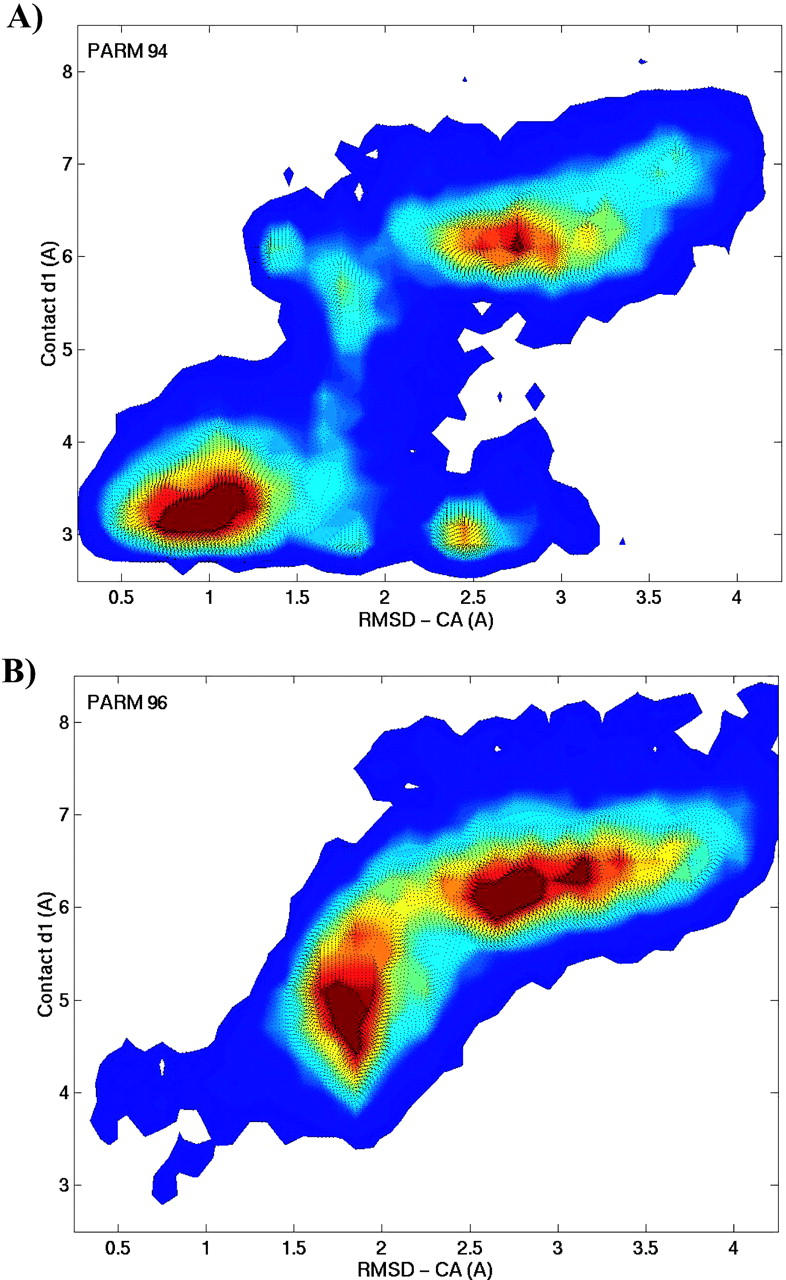
The room temperature conformational map obtained with PARM94 (A) and PARM96 (B) force fields. It is plotted as a function of RMSD-CA and contact d1 where the red color indicates high conformational probability.

Characterization of the three main conformational basins

Insight into the role of local contacts in folding can be obtained by relating the probability of occurrence and correlation of three specific contacts within the three basins P1, P2, and P3. Fig. 11 shows the probability distribution of the three specific distances and the percentage of contacts formed in the three conformational regions as a function of temperature. In the folded basin, more than 86% of conformations are found with the mainchain-mainchain hydrogen bond formed as indicated by a single sharp peak at 3.2 Å in the distance distribution. For the mainchain-sidechain contact d2, the internuclear distance distribution shows three structural peaks. The first peak corresponds to a hydrogen bond and occurs in 44% of folded conformations. Approximately 50% of folded conformations form hydrophobic contact d3, indicated by a single broad peak centered at 4 Å.

FIGURE 11.

The internuclear distance distributions of the three specific contacts: d1 (red), d2 (blue), and d3 (green); and their populations in basins P1, P2, and P3 are plotted as functions of temperature. In the distribution plots multiple lines refers to distributions at different temperatures (ranging from 276 K to 469 K). The condition for whether a contact has been formed is the same as given in Fig. 8.

The least populated basin, P2, can be considered as an intermediate with partial occupancy of stabilizing interactions. The population analysis shows that d1 is still the dominant contact in this region (50%) and the corresponding distance distribution also occupies a second peak at 5.8 Å. The conformations with the d2 contact are greatly diminished in this basin as a result of an increase in structures with the GLU sidechain turned outwards from the turn. About 29% of the conformations are found with the hydrophobic contact. In the unfolded region, basin P3, the second peak of the d1 distance dominates, indicating no significant amount of mainchain-mainchain hydrogen bonded conformers. Most of the sidechain-mainchain interactions are also weakened as indicated by the diminished peak at 3 Å in the probability distribution for the d2 distance (Fig. 11). The d3 distance shows a Gaussian distribution centered ∼15 Å, implying the lack of native hydrophobic contacts in the unfolded basin. However, at high temperatures, the hydrophobic contacts increase slightly to 11%. The increased probability of forming this hydrophobic contact may result from a stronger hydrophobic effect with an increase in temperature. The hydrophobic effect for small solutes can be related to the chemical potential of hard spheres in water, Δμ_ex. From the information theory of the hydrophobic effect (Hummer et al., 1998; 1996) we know that Δμ_ex ∼ Tρ², where ρ is the density of water. Therefore, we expect the hydrophobic effect to be stronger as T increases. However, since ρ(T) decreases with T, Δμ_ex will reach a maximum and decrease (Garde et al., 1996). In our calculations, the hydrophobic effect will be artificially stronger at higher T, since the density is kept constant.

We want to explore whether the simultaneous existence of the three specific contacts are satisfied in the folded basin. Fig. 12 shows correlations of contacts in basins P1 and P2 as a function of temperature. In the folded basin, 43% of the structures are found with both d1 and d2 contacts formed. A similar percentage is also found for structures with both d1 and d3 contacts formed. However, only 16% of the folded structures are observed with both d2 and d3 contacts formed, which are uncorrelated. Interestingly, the temperature-dependence of the simultaneous formation of all three contacts follows closely the simultaneous formation of both d2 and d3 contacts. As shown in Fig. 12, only 2% of conformers satisfy simultaneous satisfaction of all three specific contacts in P2 basin. We do not observe any significant amount of correlations between contacts in configurations from the P3 basin.

FIGURE 12.

The percentage of populations in basin P1 (a) and P2 (b) with d1 and d2 (solid lines), d1 and d3 (dashed lines), d2 and d3 (dotted lines), and d1 and d2 and d3 (dotted-dashed lines) contacts formed.

Stability of the turn with ASP instead of GLU at position 5

Our analysis of the correlation between contacts suggested that substitutions, which enhance the correlation between contacts d2 and d3, may increase the stability of the diverging turn. An ideal mutation is E5D. This mutation could lead to more stabilization because of the reduction of sidechain entropy due to its short carboxylic sidechain; however, it can still form a hydrogen bond to the backbone hydrogen from K2. Many SH3 domains are found with ASP in position 5 in the turn (Larson and Davidson, 2000). According to a sequence alignment of a large number of SH3 domains from the protein database, ASP is present in 60% of sequences compared to the 23% prevalence found for GLU (Maxwell and Davidson, 1998).

In contradiction to our expectations, we find the mutated peptide to be less stable than the wild type by 0.61 ± 0.20 kcal/mol. Predominantly, basins P2 and P3 are populated. The E5D mutation destabilizes the isolated diverging turn by diminishing the formation of the d2 contact. The formation of the d1 contact also has been diminished. We find that the sidechain carboxylic group of ASP prefers to form a hydrogen bond with the neighboring (ARG) backbone. Twenty-five percent of the conformations are found with hydrogen bonding to the ARG compared to 5% that form the d2 contact. The shorter sidechain of ASP enables it to hydrogen-bond to the neighboring ARG backbone amino hydrogen instead of the K2 backbone amide hydrogen as is the case in wild type. Such a behavior of the ASP residue has been especially well-known as a “helix-breaker” when it occurs inside a helix or as a capping amino acid at the end of helices (Harper and Rose, 1993; Huyghues-Despointes et al., 1993; Vijayakumar et al., 1999).

It has been shown experimentally that the E5D mutation stabilizes the fyn SH3 domain by 0.7 kcal/mol (Maxwell and Davidson, 1998). The mutated sequence (FKKGDRL) is similar to the diverging turn segment found in the N-terminal SH3 domain of Crk (PDB: 1CKA). The RMSD-CA analysis shows the diverging turns from the src SH3 and the crk SH3 crystal structures are structurally identical (RMSD-CA = 0.08A). In fact, the d2 contact distance is shorter in crk SH3 domain than in the src SH3. The E5D substitution may stabilize the diverging turn when it is part of the protein. It is illustrated here, however, that in isolation such a substitution leads to destabilization.

The strongest experimental evidence that supports our unexpected observation, although indirect, comes from the double mutation studies on the fyn SH3 domain. It was found that a specific nonlocal interaction between the sidechain of the residue at the position 5 of the diverging turn (Glu24) with the sidechain of a residue from the β-sheet (Ser41) contributed 0.5 kcal/mol to the stability of the domain (Maxwell and Davidson, 1998). In experiments dealing with mutations in an immunoglobulin V_k domain, Boris Stepie and co-workers were able to show that a high local propensity mutation for a type II′ β-turn in a V_k domain (A15P) was stabilizing (Niggemann and Steipe, 2000; Ohage et al., 1997). However, they found that a mutation that restored the V_k domain sequence consensus (A15L) was even more stabilizing—therefore showing that the stability of the whole protein upon mutation is greatly influenced by nonlocal interactions.

Formation of other turn structures

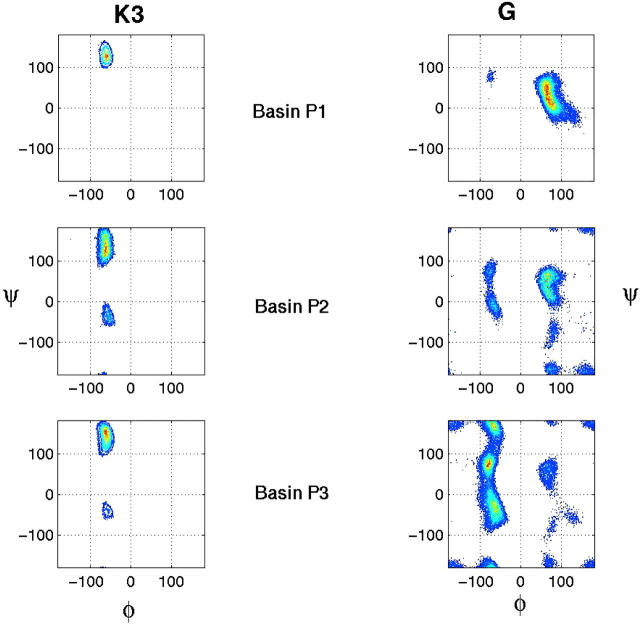
The conformational distributions were considered earlier in terms of their root-mean-square-deviation (RMSD) from native C_α atoms. Here, we investigate the propensities of the critical residues of the SH3 peptide to populate the different regions of (φ,ψ) map. The (φ,ψ) distribution for the two key residues that determine the turn, K3 and G, are considered since the diverging structure spreads the (φ,ψ) values of the remaining residues into a fairly extended region. The ideal values for a type II turn are (−60, 120) for K3 and (80, 0) for G (Wilmot and Thornton, 1988). Fig. 13 shows the (φ,ψ) map for K3 and G in the three different basins. In the folded basin P1, the (φ,ψ) values remain near the ideal type II turn values. Residue G takes a positive φ value which is critical for forming a turn. In the P2 basin, G samples a wide range of (φ,ψ) values indicating neither specific preference nor existence of strict secondary structure. The (φ,ψ) angles of K3 also sample additional areas that may correspond to regions of helical. It further confirms that basin P2 is an intermediate where several different states are sampled. In this region, the configurational entropic contribution can be significant. The P3 basin consists of conformations with long end-to-end distances where the (φ,ψ) values that can be sampled by G are restrained with respect to the φ dihedral angle.

FIGURE 13.

The Ramachandran (φ,ψ) map for K3 and G residues of the SH3 peptide in three different basins.

We examined the trajectories for conformations with several different kinds of turns and their dependence on the temperature. A structure is defined to be type II β-turn when the (φ,ψ) values for the turn residues K3 and G fall within ±30° of the ideal values, (−60, 120) and (80, 0), respectively. With this criterion, ∼18% of the population can be considered as a type II turn. We have also monitored the type I and type VI turns based on Ramachandran angles of K3 and G (Wilmot and Thornton, 1988). The type I and type II turns are two most frequently occurring β-turns in proteins which differ only in terms of the orientation of middle peptide. It has been suggested, for proteins, that conformational interchange is possible between type I and type II turns through the flip of this central peptide (Gunasekaran et al., 1998). However, we do not see evidence for that interchange in the isolated short peptide. For example, conformations that satisfy the type I turn compose less than 4% of the total population.

Formation of helical structures

The helical propensities of the SH3 peptide residues are considered here. It was suggested that the polar sidechains at positions 3 and 5 in the SH3 peptide along with the positioning of GLY residue in this sequence destabilize the formation α-helix (Yi et al., 1998). The helical content can be calculated as having three consecutive residues satisfying the following (φ,ψ) for a helix: (φ,ψ) =(−65 ± 35, −37 ± 30) (Lifson and Roig, 1961). We find the helical content of the SH3 peptide to be minimal. As expected, GLY has the lowest helical content. Recent theoretical work on the same peptide using conventional MD simulations showed that the conformations sampled depended on the initial conformations (Krueger and Kollman, 2001). In that study, the simulations that were started with helical structures never produced nativelike structures, whereas the ones that were started with nativelike structures remained as nativelike (Krueger and Kollman, 2001). The REMD simulations, considered here, provide excellent sampling such that regardless of the initial configuration, the nativelike conformations are found.

To identify the helical region in the conformational map and to illustrate the lack of sampling, a 12-ns-long conventional MD simulation of SH3 peptide was carried out at room temperature with an initial helical structure. The projection of the trajectory along the RMSD-CA coordinate is shown in color in Fig. 14 A. The black line represents the projection of the trajectory along the RMSD-CA atoms of the initial helical structure. The SH3 peptide remained helical for ∼4 ns. Then it went through a transitional region for 2 ns, before reaching the folded state. It remained folded for the rest of the simulation, ∼6 ns. The color-coding is utilized to map the time trajectory onto the two-dimensional conformational map of RMSD-CA versus internuclear distance d1 as shown in Fig. 14 B. The helical and nativelike regions can be easily located in the contour map. The helical region is confined between [d1 < 4 Å] and [2.1 Å < RMSD-CA < 3.5 Å]. The same helical region can be identified in a similar map shown earlier (Fig. 10 A), demonstrating that REMD accesses the helical conformational region at room temperature. As estimated from the free energy, the native state is stabilized over the helical state by 1.04 ± 0.18 kcal/mol at 300 K.

FIGURE 14.

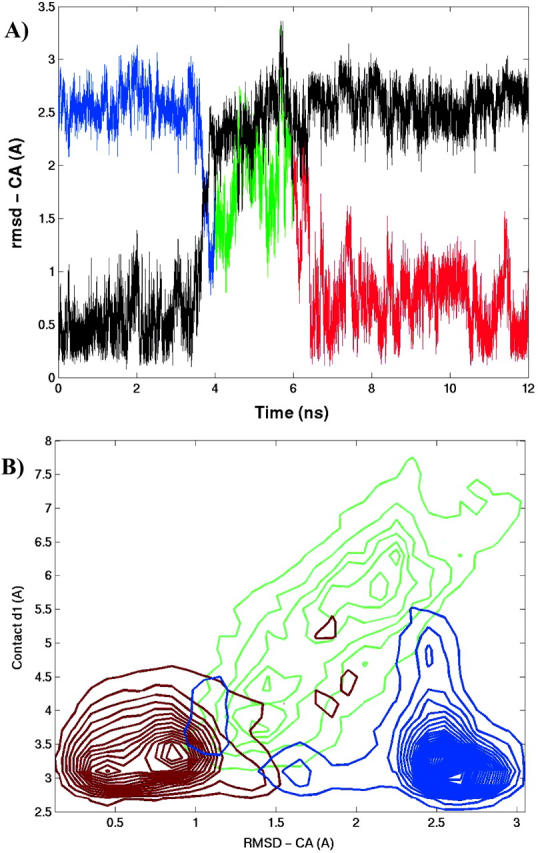
(A) The trajectory of the conventional MD simulation started with a helical configuration of the SH3 peptide at 300 K. The RMSD-CA from the helical (black) and native (color) structures is plotted. (B) The conformational map plotted as a function of RMSD-CA and contact d1. The color-coding is utilized to map the trajectory onto the conformational map. The trajectory starts helical (blue), goes through a transitional region (green), and finally proceeds to the folded state (red).

Role of GLY on the stability of the turn

We have further investigated the importance of having GLY at the fourth position in the SH3 peptide as found in many other type II turns (Wilmot and Thornton, 1988). Such a placement also allows the backbone to adopt a left-handed helical conformation. The sequence alignment on SH3 domains indicated a very high probability for GLY at this position, ∼77% (Larson and Davidson, 2000; Mok et al., 2001). The diverging turn motif from the SH3 domain of the Drosophila protein drk (drk SH3), however, has a THR instead of a GLY. The interest in the drk SH3 domain arises because it exists in equilibrium between folded and unfolded states under nondenaturing aqueous buffer conditions. NMR structural data of this domain showed signatures of diverging turn structure in the wild type (R. Pomes, Research Institute of the Hospital of the Sick Children, personal communication), whereas a single mutation of THR to GLY (T4G) resulted in strong stabilization of the domain (Mok et al., 2001).

The REMD simulation results on G4T mutant show that THR substitution hinders the formation of nativelike conformations and causes severe destabilization on the isolated peptide. According to the thermodynamic analysis, having THR instead of GLY destabilizes the diverging turn motif by 1.73 ± 0.06 kcal/mol. From the experimental measurements on drk SH3, the stabilization from the reverse mutation, T4G, was 2.5 kcal/mol (Mok et al., 2001). The NMR data on the drk SH3 suggested that in the unfolded state the diverging turn motif has non-native topology. This observation led to the speculation that THR in the sequence stabilizes the unfolded state by forming non-native conformation and that the GLY substitution disrupts the non-native residual structure in the diverging turn (Mok et al., 1999; 2001). However, the analysis of the conformational distribution of G4T mutant showed no evidence for the existence of a significant number of non-native secondary structures such as helices. We searched for FKKTERL sequence in the PDB and found that the closest sequence pattern corresponded to the sequence KKTER in horse cytochrome C (PDB: 1HRC). It occurs at the beginning of a helix and the (φ,ψ) values indicate that THR is helical (Lifson and Roig, 1961). So it is quite possible that in the presence of rest of the protein, the diverging turn motif of the drk SH3 can adopt non-native conformations such as helical.

Conformational dependence on force fields

The success of a computational study such as this often depends upon the quality of the force field. The folding of the SH3 peptide into the nativelike structure provides confidence in the force field inasmuch as it can unearth the sequence-specific secondary structure. The force field used, PARM94 (Cornell et al., 1995), is reasonable in deterring the formation of α-helical and β-hairpin structures and favoring the type II turn structure. The PARM96 (Kollman et al., 1997; Wang et al., 1999) force field was developed to correct for the overestimates of helical formation by PARM94. We have explored how the well the recent AMBER parameter set PARM96 reproduces these results. The REMD simulations with the PARM96 force field resulted in diminished formation of nativelike conformations, down to 20% of the population. Compared to the case with PARM94 (Fig. 10), the conformational distribution does not quite access the folded region [d1 < 4.5 Å] and [RMSD-CA < 1.5 Å] with PARM96 as illustrated in Fig. 10 B. In fact, the conformational distribution lies at the folding “edges” of the basin. Compared to PARM94, the nativelike and helical states are destabilized by 1.34 ± 0.16 kcal/mol and 2.88 ± 0.37 kcal/mol, respectively, at room temperature. Furthermore, with PARM96, the nativelike conformations are stabilized over helical conformations by 2.59 ± 0.21 kcal/mol, compared to 1.04 ± 0.18 kcal/mol obtained with PARM94. The above comparisons are summarized in Table 1.

TABLE 1.

Stability of wild type and mutants of isolated SH3 peptide at room temperature

	Wild type	E5D	G4T	Wild type (PARM96)
A) Stability at 300 K
ΔG (unfolded→folded)	0.41 ± 0.20	1.21 ± 0.10	2.99 ± 0.64	1.91 ± 0.12
ΔG (helical→folded)	−1.04 ± 0.18	−0.23 ± 0.24	−1.21 ± 0.01*	−2.59 ± 0.21
B) Stability relative to wild type
ΔG (folded)		0.61 ± 0.20	1.73 ± 0.06*	1.34 ± 0.16
ΔG (helical)		−0.20 ± 0.14	2.06 ± 0.11	2.88 ± 0.37

The last column corresponds to wild-type simulations run with PARM96 force field. All other simulations were run with PARM94 force field. Error bar indicates the error in mean obtained by separating the data into four blocks. (^*) indicates the error analysis done using only two blocks.

We have also compared our results with those from the parameter comparative study by Krueger and Kollman (2001) on the same peptide. As mentioned in the Methodology section, it was based on a continuum model, the Molecular Mechanical-Poisson/Boltzmann Surface Area (MM-PBSA) approach (Srinivasan et al., 1998), in contrast to the explicit solvent model considered here. Both calculations agree that the greater stability for the SH3 peptide is obtained with PARM94, and that PARM96 significantly disfavors helical structures. However, the extent of helical destabilization differs. The major discrepancy is that MM-PBSA analysis suggested that PARM94 favors the helical state over the native state by 5.3 kcal/mol and PARM96 favors the native state over helical state by 3 kcal/mol, whereas our calculations indicate that native state is preferred over helical state with both PARM94 and PARM96. These differences can be most likely attributed to lack of sampling and the inaccuracy of the implicit solvent treatment considered in the MM-PBSA study.

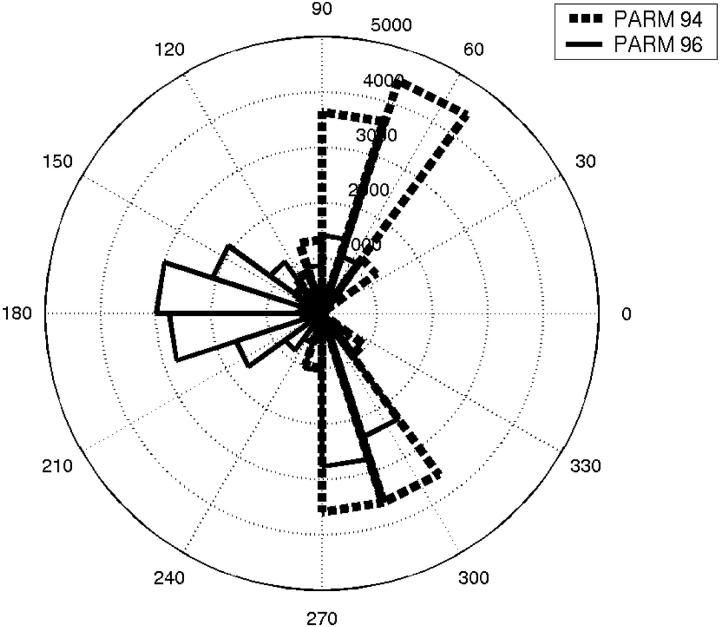
For this peptide, the only difference between PARM94 and PARM96 is in the parameters assigned to the backbone dihedrals. We identify the dihedral parameters involving GLY residue as one of the main culprits in preventing the SH3 peptide from forming nativelike structures with PARM96 force field. The angle histogram shown in Fig. 15 compares the (φ,ψ) values for GLY from simulations that used PARM94 with those of the PARM96 force field. Only the distribution at room temperature is plotted. It is evident that the (φ,ψ) distribution for GLY is different between these two parameter sets. With PARM 94, φ values for GLY are consistent with the turn structures whereas the accessibility of positive φ values is significantly more restricted with PARM96. Previous REMD studies of α-helical peptides showed that PARM96 was inadequate to model the thermodynamics of α-helical peptides (Garcia and Sanbonmatsu, 2002). The above observations cast doubt on the suitability of PARM96 to model proteins.

FIGURE 15.

The φ-dihedral angle histogram for GLY residue with PARM94 (dashed lines) and PARM96 (solid lines) force fields at 300 K.

CONCLUSIONS

The replica-exchange molecular dynamics method provided an efficient sampling of the configurational space of the SH3 peptide, enabling us to identify three main basins sampled by the peptide. We observed the existence of nativelike β-type II diverging turn conformations. We were able to categorize the three basins as conformational regions that corresponded to the folded, intermediate, and unfolded states, respectively. Conformations from the unfolded basin dominated the distribution at all temperatures. The probability of observing nativelike conformations decayed gradually with increasing temperature, with 40% at 276 K to 5% at 469 K. Thus, only a fraction of the conformations formed a type II diverging turn, indicating that the folded state of this peptide is unstable in aqueous solution.

Our results are in agreement with the observations from the proton NMR, which indicate that the type II β-turn population is partially populated (Yi et al., 1998). The three specific contacts (d1, d2, and d3) as suggested from NMR experiments were evident from the structural peaks in the distribution of specific distances obtained from the simulations. There is also good agreement between calculated and experimental J-couplings. The NMR measurements are ensemble- averaged over different structures. A conventional MD simulation is unlikely to yield adequate sampling of conformational space for the proper evaluation of such ensemble averages. The MD simulation that was started with a helical configuration of the SH3 peptide was used to illustrate the need for the conventional MD simulation to be carried over for a very long time to sample all relevant conformations. The REMD simulations, as shown here, greatly increase the effectiveness of conformational searching and can be used as a tool to interpret the NMR-derived parameters.

From the REMD simulations, we found that the conformation of the SH3 peptide in the folded basin was not unique. It was also notable that a broad distribution of conformations from both intermediate and unfolded regions also contributed to the ensemble at room temperature. We also found nativelike folded structures exist where not all the NMR-derived constraints, d1, d2, and d3, were satisfied. Only 16% of folded structures simultaneously satisfied all three contacts as interpreted by NMR observations. Most of the folded structures satisfied either individual (d1 contact) or a combination of (d1 and d2 or d1 and d3 contacts) NMR constraints. Therefore, we believe that NMR observations of these contact constraints cannot be interpreted solely in terms of existence of structures that simultaneously satisfy all three constraints.

This study also revealed general insights into the nature of local contacts that provide stability to the SH3 peptide. The mainchain-mainchain hydrogen bond contact, d1, has the highest occurrence and accounted for in 48% of conformations. The mainchain-sidechain hydrogen bond (d2) and the hydrophobic contact of the end residue sidechains (d3) occurred in ∼20% of conformations. We found that 86% of the folded conformations have contact d1 formed whereas ∼45% of conformations have either d2 or d3 contacts formed. The contacts d1 and d2 and d1 and d3 were highly correlated and can be observed simultaneously. The simultaneous formation of all three contacts was determined primarily by whether the uncorrelated contacts d2 and d3 were able to form. We conclude that the mainchain-mainchain hydrogen bond contact is critical for folding of this peptide inasmuch as it has the highest occurrence in folded structures and correlates strongly to the formation of other two contacts.

We determined the thermodynamic stability of the folded form of the SH3 peptide relative to the unfolded form. The estimated free energy of folding of the isolated diverging turn motif at 300 K was 0.41 ± 0.20 kcal/mol. Therefore, the stability of this motif inside the protein must be a consequence of the strength of various noncovalent forces that may be either electrostatic or hydrophobic in origin. We evaluated the free energy of the SH3 peptide along the RMSD-CA coordinate. The thermodynamic profile indicated a very shallow free energy surface with small barriers. At room temperature, the minimum free energy was found at RMSD-CA = 1.1 Å. The components of free energy have been decomposed to determine the factors that stabilize the peptide. The minima in enthalpy and entropy were found at low and high RMSD-CA values. Furthermore, the entropy and enthalpy contributions to the free energy compensate each other such that the range of free energy change was on the order 2 RT.

We carried out simulations of E5D and G4T mutants to explore whether the positioning of amino acids in the SH3 peptide sequence biases toward the folding of a type II diverging turn. Experimental mutational studies have shown that the substitutions at these positions greatly affect the stability of the entire SH3 domain (Maxwell and Davidson, 1998; Mok et al., 2001). Most of the SH3 domains (60%) are found with D at position 5 in the diverging turn motif. Furthermore, the E5D mutation stabilizes the fyn SH3 domain by 0.7 kcal/mol. In the REMD simulations we found the contrary; the E5D mutation destabilized the isolated diverging turn motif by 0.61 ± 0.20 kcal/mol. The second mutation G4T occurs at a position where sampling a positive φ-angle is critical for forming the turn as evidenced by a 77% probability of occurrence for G at this position in the SH3 sequence. The mutation G4T destabilized the isolated diverging turn by 1.73 ± 0.06 kcal/mol, which compares well with the value of 2.5 kcal/mol observed for the reverse mutation in the drk SH3. The latter mutation was also investigated for the existence of non-native secondary structures. Unlike the observations of diverging turns adopting non-native secondary structures in the denatured state of the drk SH3, no significant secondary structural motif was found for the G4T mutant.

Several theoretical and experimental studies suggested that the diverging turn motif considered is one of the most stable secondary structures in the native and denatured SH3 domain. Our results indicate that, when outside the network of the rest of the protein, the diverging turn motif has low stability and is fractionally populated. Furthermore, the folded state corresponds to conformations where not all the native contacts are satisfied. Such a picture of SH3 peptide based on local interactions should not eliminate any possible role the diverging turn motif may play in the overall folding of SH3 domain. Even with its low intrinsic stability, the diverging turn can behave as part of a nucleus for folding and increase the folding rate. The isolated structures that exist in non-native conformations could still facilitate the formation of secondary structures by positioning segments in favorable locations (Wang and Shortle, 1995; 1996). The lack of native contacts should not alter folding pathway. The presence of a nativelike secondary structural motif in a denatured protein does not imply that it has a high intrinsic stability. It is possible that the diverging turn motif can be stabilized by interactions from the unfolded β-strands in SH3 domain (Shortle et al., 1996; Wang and Shortle, 1997). Finally, our investigation for an optimum sequence for the diverging turn motif that would increase the intrinsic stability did not quite agree with the stability achieved for the entire domain.