Heterogeneous Presynaptic Release Probabilities: Functional Relevance for Short-Term Plasticity

Abstract

We discuss a model of presynaptic vesicle dynamics, which allows for heterogeneity in release probability among vesicles. Specifically, we explore the possibility that synaptic activity is carried by two types of vesicles; first, a readily releasable pool and, second, a reluctantly releasable pool. The pools differ regarding their probability of release and time scales on which released vesicles are replaced by new ones. Vesicles of both pools increase their release probability during repetitive stimulation according to the buildup of Ca²⁺ concentration in the terminal. These properties are modeled to fit data from the calyx of Held, a giant synapse in the auditory pathway. We demonstrate that this arrangement of two pools of releasable vesicles can account for a variety of experimentally observed patterns of synaptic depression and facilitation at this synapse. We conclude that synaptic transmission cannot be accurately described unless heterogeneity of synaptic release probability is taken into account.

INTRODUCTION

A variety of experiments indicate that single synaptic connections exhibit a broad distribution of presynaptic release probabilities. Among these are studies using minimal stimulation (Dobrunz et al., 1997), block of synaptic transmission by MK801 (Rosenmund et al., 1993; Hessler et al., 1993; Huang and Stevens, 1997), fluctuation analysis (Walmsley et al., 1988; Isaacson and Hille, 1997), styryl dyes (Murthy et al., 1997), and presynaptic voltage clamp (Burrone and Lagnado, 2000; Sakaba and Neher, 2001b). This heterogeneity of release probability is generally accepted. Nevertheless, the implications of heterogeneous release probabilities for synaptic transmission and its short-term plasticity have not received sufficient attention so far.

Based on electrophysiological recordings at the calyx of Held synapse, we demonstrate that nonuniformity in presynaptic release probabilities can influence the kinetics and steady-state activity under repetitive stimulation, and that these aspects cannot be neglected for a faithful description of the transmission process. Particularly, dynamic models of neuronal network activity will be strongly influenced by the specific way in which heterogeneity of release probability is treated.

Recently, simultaneous electrophysiological recordings from the pre- and postsynaptic compartment of the calyx of Held, a giant excitatory central synapse in the mammalian auditory pathway (Held, 1893), have become feasible and allow a direct experimental approach to presynaptic mechanisms of central synaptic transmission (Borst et al., 1995; Forsythe, 1994; see von Gersdorff and Borst, 2002, and Schneggenburger et al., 2002, for reviews). The calyx of Held synapse is a fast-excitatory, glutamate-mediated connection and contains hundreds of individual active zones, which operate in parallel when activated by an action potential (AP). We consider this synapse well suited for a modeling approach of synaptic transmission in the central nervous system because many experimental parameters have become available recently.

In an early approach to model release and recruitment of vesicles, the simple depletion model (Liley and North, 1953), every AP was assumed to deplete a pool of identical readily releasable vesicles by a constant fraction, whereas vacated sites were simultaneously replenished with a single slow time constant. Several studies of synaptic short-term depression have revealed discrepancies between the predictions of this model and experimental results (Weis et al., 1999; Wu and Borst, 1999; for a review, see Zucker and Regehr, 2002). Particularly, it was found in many types of synapses that steady-state activity was higher than predicted on the basis of the initial decay of synaptic strength. Also, it is quite evident at many synapses that release probability increases during the first two or three stimulations in a train due to facilitation. The enhanced steady-state response (relative to the prediction of the simple depletion model) was accounted for by assuming an activity-dependent, extra recruitment of readily releasable vesicles (Worden et al., 1997). Specifically, the recruitment was assumed to be enhanced by elevated Ca²⁺ concentration after presynaptic action potentials (Dittman et al., 2000; Gingrich and Byrne, 1985; Heinemann et al., 1993; Kusano and Landau, 1975; Weis et al., 1999). In agreement with this assumption, it was shown that recovery from synaptic depression is accelerated by high-frequency stimulation of the presynaptic terminal (Dittman and Regehr, 1998; Dittman et al., 2000; Stevens and Wesseling, 1998; Wang and Kaczmarek, 1998; Gomis et al., 1999). Simultaneous facilitation was allowed in the model by Dittman and Regehr (1998).

In a recent simulation of Ca²⁺ signals and release, Meinrenken et al. (2002) considered the specific case of a single class of vesicles located within an active zone at random distances from a cluster of Ca²⁺ channels. Variable distances from the Ca²⁺ source resulted in highly heterogeneous release probabilities and interesting predictions regarding facilitation and short-term depression. Recruitment of new vesicles after depletion was neglected, such that the model is accurate only for short periods of stimulation. In contrast, the study presented here focuses on longer stimulation intervals, considering two vesicle pools that differ from each other in release probability and kinetics of replenishment after depletion. A variety of experiments at the calyx of Held addressed the problem of short-term plasticity and helped to identify several synaptic mechanisms relevant for the dynamics of synaptic short-term changes (Borst et al., 1995; Forsythe, 1994, 1998; Meyer et al., 2001; Neher and Sakaba, 2001; Sakaba and Neher, 2001a,b; Schneggenburger et al., 1999; Scheuss et al., 2002; von Gersdorff et al., 1997; Wang and Kaczmarek, 1998; Weis et al., 1999; Wu and Borst, 1999). Nevertheless, no conclusive evidence is available yet as to whether heterogeneity among vesicles is positional, or intrinsic, or a combination of both, as in neuroendocrine cells (Voets et al., 1999).

About 550 active zones have been estimated in an ultrastructural analysis of the calyx of Held synapse (Sätzler et al., 2002). Depleting the pool of releasable vesicles by strong stimulation either by flash photolysis of caged calcium in the presynaptic terminal (Schneggenburger and Neher, 2000), or by direct strong presynaptic depolarization (Sakaba and Neher, 2001b) led to estimates of a total number of releasable vesicles of ∼1800–3000 vesicles. Capacitance measurements and presynaptic depolarizations yielded estimates of an even larger pool size of releasable vesicles (Sun and Wu, 2001). This number exceeds the number of ∼550 active zones by far. However, the average probability of release from single active zones is only 0.25–0.4 for a single action potential under physiological conditions (Meyer et al., 2001). A comparison of this low number with the large number of releasable vesicles demonstrates that depletion of the pool of releasable vesicles during short trains of action potentials cannot be expected, unless such depletion is restricted to a subset of more readily releasable vesicles.

Prolonged depolarization under presynaptic voltage clamp revealed two distinct components of presynaptic release, separating the releasable pool into a rapidly and slowly releasing one (Sakaba and Neher, 2001a,b). Approximately 50% of the vesicle pool could be released rapidly within a few milliseconds, whereas the second half of vesicles was released with a slower rate (Sakaba and Neher, 2001b). Slow vesicles were found to recover rapidly with a time constant of less than 1 s (τ ∼ 100 ms), independent of the stimulus pattern used (Sakaba and Neher, 2001a). Rapidly releasing vesicles recovered on a much slower timescale (τ ∼ 4 s at physiological Ca²⁺ concentrations). This recovery was even more delayed when the buildup of presynaptic Ca²⁺ concentration was lowered (τ ∼ 9.1 s in the presence of 5 mM EGTA) and accelerated up to τ < 0.5 s under elevated presynaptic Ca²⁺ concentrations (Sakaba and Neher, 2001a). The latter finding suggests that the presynaptic accumulation of Ca²⁺ after intense stimulation speeds up the recovery of the fast vesicles (Dittman and Regehr, 1998; Stevens and Wesseling, 1998; Wang and Kaczmarek, 1998). We will demonstrate that this calcium dependency of the rapidly releasing vesicles cannot fully explain the observed steady-state level during trains of stimuli. Slowly releasing vesicles seem to be particularly suited for maintaining secretion during long trains of activity due to their rapid recovery. Although their slowness prevents a major contribution to the first responses within such trains, a buildup of facilitation may increase their release probability to the point at which they contribute. It is not known, however, whether they contribute to both synchronous and asynchronous release or only to the latter. Also, it is possible that positional heterogeneity, as considered by Meinrenken et al. (2002), exists within the two pools.

The pools of slow and fast vesicles seemed to recover independently (Sakaba and Neher, 2001a), suggesting that both pools are refilled via parallel pathways. Recovery of the slowly releasing vesicles, however, is so much faster than that of rapidly releasing ones, that it would hardly influence their number, if fast releasing vesicles emerged from slowly releasing ones as a result of a maturation process. Differences in release probability between the two pools arise in our model from the assumption that a subset of specialized release sites (containing the rapidly releasing vesicles) is colocalized with a release-triggering calcium channel, the Ca²⁺ signal of which adds to that of other Ca²⁺ channels evenly distributed within the active zone. A second set of release sites (the slowly releasing ones) lack this special channel, but sense the Ca²⁺ signal of all the other channels. Differences in mean distances between calcium channels and release sites cause differences in release probability in this model. A similar scenario has been discussed in the context of fast and slowly releasing vesicles in chromaffin cells (Klingauf and Neher, 1997; Voets et al., 1999).

The two classes of vesicles, which we assume in our model should be considered as representative for the more general case of a graded distribution of vesicle properties. We will demonstrate that a heterogeneity in release probability, together with calcium-dependent enhancement of vesicle recruitment, is sufficient to explain the observed steady-state synaptic strength during repetitive activity.

The frequency dependence of the amplitudes of excitatory postsynaptic currents (EPSCs) during steady-state depression has important consequences for the transmission of information. For example, rate coding of information is impossible, once the postsynaptic current decreases as with the inverse of the stimulation frequency (Tsodyks and Markram, 1997; Markram et al., 1998a; Varela et al., 1997). Within our model the synaptic steady-state activity at the calyx of Held does not reach a 1/f-dependence for any stimulation frequency, so that synaptic steady-state activity provides a mechanism to transmit a broad range of frequencies.

MATERIALS AND METHODS

Experimental studies of the calyx of Held (Helmchen et al., 1997; Meyer et al., 2001; Sakaba and Neher, 2001a,b; Schneggenburger et al., 1999; Schneggenburger and Neher, 2000; von Gersdorff et al., 1997; Wu and Borst, 1999) constrain most of the parameters of our model (explained in detail in Selection of Model Parameters). The model was fitted to a set of experimental data taken from von Gersdorff et al. (1997) by adjusting the two free parameters, γ and p₁ (at rest). The model, fitted to the data of von Gersdorff et al. (1997), was subsequently compared to a second independent set of experimental estimates from Meyer et al. (2001). Table 1 summarizes the values which have been assigned to the model parameters.

TABLE 1.

Model parameters

Parameter	Value	Source
p1 at rest (ΔCa2+ = 0)	0.025	free parameter
p2 at rest (ΔCa2+ = 0)	0.14	(Meyer et al., 2001)
τP1	0.15 s	(Sakaba and Neher, 2001a)
τP2 at [Ca2+]gl = 0	9.1 s	(Sakaba and Neher, 2001a)
τP2 at [Ca2+]gl = 0.5 μM	3.4 s	(Sakaba and Neher, 2001a)
no. of reluct.-rel. ves. at rest	1200	(Sakaba and Neher, 2001a)
no. of readily-rel. ves. at rest	1200	(Sakaba and Neher, 2001a)
x0	0.4 μM	(Helmchen et al., 1997)
τx	0.1 s	(Helmchen et al., 1997)
[Ca2+]r	0.1 μM	(Helmchen et al., 1997)
JCa,max	2.615	(Schneggenburger et al., 1999)
EC50	2.314 mM	(Schneggenburger et al., 1999)
α(1 + η)	27 μM	(Schneggenburger and Neher, 2000)
α	10 μM	def. by Eq. 10, p1(at rest), and p2(at rest)
η	1.6926	def. by Eq. 10, p1(at rest), and p2(at rest)
γ	0.2 μM−1	free parameter
K1/2	42.5 μM	def. by Eq. 10, p1(at rest), and p2(at rest)

The computer simulations were written in C language, compiled and run on Pentium PCs. The kinetic equations for the pool occupancy of the readily releasable pool were solved numerically using a fourth-order Runge Kutta method (Press et al., 1992). Synaptic steady-state activity was studied by computing the occupancies of and the release from both pools after applying a train of 100 stimuli for a given stimulus frequency.

RESULTS

The two-pool model of vesicle recruitment

Here we start with the simplest model and consider two sorts of vesicles which differ regarding their probability of release: readily releasable vesicles (pool 2) and reluctantly releasable vesicles (pool 1). Following an AP, simultaneous release of presynaptic vesicles occurs from both pools and each pool is depleted by the fraction specified by the respective release probability. Reluctantly releasable vesicles are released with a lower probability than readily releasable vesicles. Vesicles in both pools are recruited independently of each other through parallel pathways (Fig. 1). We recognize that the assumption of two pools may be an oversimplification, inasmuch as graded release probabilities have been observed at several types of synapses (see Introduction). A two-pool model should, however, be able to highlight the influences of vesicle heterogeneity better than a graded one.

FIGURE 1.

Two-pool model of vesicle recruitment and release. Upon presynaptic stimulation vesicles are released from two different pools that differ regarding their release probability and timescales of recruitment. Reluctantly releasable vesicles (pool 1) are released with a lower release probability (p₁) than readily releasable vesicles (pool 2, release probability p₂). As indicated by the values assigned to the rate constants of refilling (see Table 1 and Eq. 5), pool 1 recovers faster from depletion than pool 2. The release probabilities of both pools, as well as the rate of recruitment 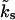into pool 2, depend on changes in the Ca²⁺ concentration.

Reluctantly releasable vesicles from pool 1 are released with the probability p₁, which is lower than the probability of release p₂ for a readily releasable vesicle from pool 2. Probabilities p₁ and p₂ may include contributions from asynchronous release (release between a given action potential and the following one), which may be important in the case of the reluctantly releasable pool.

Reluctantly releasable vesicles (pool 1) are coupled to a large reservoir of vesicles, which provides a constant influx k_r. The backflow is proportional to the number of reluctantly releasable vesicles,

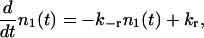(1)

so that the stationary population of pool 1 is given by 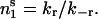We assume here that the reservoir contains an infinite number of vesicles so that the number of docked vesicles of pool 1 is not limited. As the total number of vesicles that can be released during strong stimulation at the calyx of Held (1623–3779 vesicles, Sakaba and Neher, 2001a; 3300–5200 vesicles, Sun and Wu, 2001) exceeds the number of morphologically docked vesicles per calyx terminal (<800, Sätzler et al., 2002), vesicles of pool 1 may include “visitorlike” vesicles, which temporarily dock to the membrane at places not limited to specialized release sites (see Zenisek et al., 2000, and Discussion below).

In contrast, the total number of readily releasable vesicles is limited by the total number of release sites 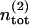available to pool 2. (Readily releasable vesicles are assumed to provide the major contribution to maximum EPSC amplitudes at the beginning of a stimulus train, which exhibit a bell-shaped dependency in a nonstationary variance analysis and indicate a finite number of release sites; Meyer et al., 2001.) Each site is either empty or occupied by a readily releasable vesicle. Transitions from the occupied to the empty state occur with constant rate k_t, whereas the recruitment rate from the empty into the occupied state,

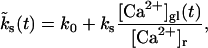(2)

contains a term k₀ to account for the recovery of pool 2 independent of Ca²⁺ and a second term that depends linearly on the intracellular global calcium concentration [Ca²⁺]_gl, relative to the basal calcium concentration [Ca²⁺]_r. In general the global Ca²⁺ concentration [Ca²⁺]_gl(t) will change in the course of a stimulus train (see Eqs. 12 and 13), which makes the rate 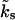in Eq. 2, time-dependent.

Note that this scenario implies a different mathematical description for readily releasable and reluctantly releasable vesicles. The finite number of release sites assigned to pool 2 limits the possible number of readily releasable vesicles. In between stimuli it increases in proportion to the number of empty release sites 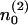and decreases in proportion to the number of release sites n₂ already occupied with readily releasable vesicles:

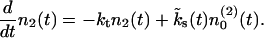(3)

As discussed above the total number 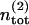of release sites assigned to pool 2 is constant, so that 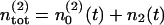holds. Once a vesicle is released, the release site immediately returns to the empty state. In contrast, the number of reluctantly releasable vesicles is neither limited by the number of available release sites nor by the number of vesicles in the infinite reserve pool.

In order to avoid computations of absolute numbers of vesicles, we express the quantities 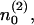n₁, and n₂ as ratios of pool occupancies. We divide n₁ and n₂ by the total number of release sites at rest, n_tot:

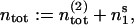and compute b₁ = n₁/n_tot and b₂ = n₂/n_tot, which denote the fraction of vesicles in pool 1 and the fraction of occupied sites in pool 2.

For constant global Ca²⁺ concentrations, i.e., [Ca²⁺]_gl = constant, the kinetic rate 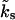is time-independent. In that case, Eqs. 1 and 3 are easily solved analytically. In the absence of presynaptic stimulation and spontaneous release events we obtain the following time evolution of the relative occupancies b₁(t,t₀) and b₂(t,t₀):

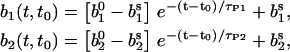(4)

where

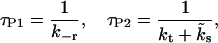(5)

denotes the two time constants of pool refilling (under constant Ca²⁺ concentrations).

The occupancies are uniquely determined by their initial values 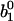and 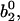and decay for long times to their stationary values 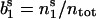and

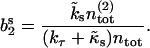(6)

For time-dependent global Ca²⁺ concentrations, the rate 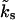is not constant. In that case the time evolution of the occupancy b₂ is given by

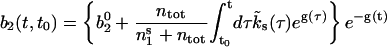(7)

with

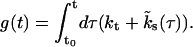These equations describe the time course of pool occupancies in between action potentials neglecting asynchronous release. Therefore, asynchronous release is considered in our calculations as part of the release associated with a given action potential (see below). This simplifies the calculations and should not lead to significant errors in the prediction of pool sizes, inasmuch as the relative changes in pool sizes due to asynchronous release are small under most physiological conditions.

It is clear from Eqs. 4 and 7 that the pool dynamics are completely determined if the initial pool occupancies, the time course of Ca²⁺ (see Eq. 13), the steady-state values, and the kinetic rates of refilling are specified. As shown below, estimates of the kinetic rates of refilling, k_t and 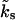, as well as the steady-state occupancies, can be obtained from experiments (Meyer et al., 2001; Sakaba and Neher, 2001a,b; Weis et al., 1999; Wu and Borst, 1999). The following paragraph explains how the occupancies immediately after release are computed. These will subsequently be used as initial values, determining the time course in between action potentials. (For practical reasons the time evolution b₂(t) is computed by directly solving the kinetic Eq. 3 numerically using a fourth-step Runge-Kutta method; Press et al., 1992.)

Resting conditions and release after a single action potential

At rest, the system is in steady state, i.e., the number of release sites occupied with vesicles from pool 1 or 2 is given by the corresponding steady-state values and 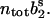An action potential (AP) at time t_AP causes release of vesicles from both pools: the number of vesicles released is proportional to the respective pool occupancy and the corresponding release probability. If we assume that the postsynaptic current is directly proportional to the number of vesicles released, the AP-generated EPSC is given by

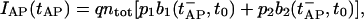(8)

with q denoting a quantal size assigned to the release of a single vesicle. Here 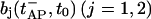denotes the pool occupancy immediately before the release of vesicles at time t = t_AP. In the presence of asynchronous release this equation has to be modified, inasmuch as p₁ and p₂ may contain some contribution of delayed release events. Delayed release events do not add to the peak EPSC, but contribute to depolarization in a nonclamped, postsynaptic neurone.

Immediately after the release of vesicles, the pool occupancy is given by

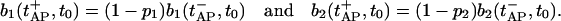If no further stimulation occurs, both pools recover toward their resting states according to Eqs. 1, 3, and 7, with initial conditions given by 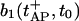and 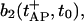respectively. These equations depend on the simultaneous changes in the global Ca²⁺ concentration (see Eq. 12) which will be discussed in the next section.

Facilitation of release probability

Although the overall short-term plasticity during stimulus trains at many synapses is a decay of EPSC amplitudes (depression), the opposite effect, i.e., the facilitation of subsequent amplitudes, has also been observed under certain conditions (Dittman et al., 2000; Schneggenburger et al., 1999). Whereas depression is widely attributed to depletion of the pool of readily releasable vesicles (postsynaptic desensitization might also contribute to synaptic short-term depression; see Scheuss et al., 2002, for a detailed discussion), the detailed mechanisms of facilitation are less well understood. A common idea, the so-called residual Calcium hypothesis (Katz and Miledi, 1968), correlates the increase in EPSC amplitudes during repetitive stimulation with the simultaneously observed rise in the global presynaptic calcium concentration. The importance of residual calcium for facilitation is well established. It is, however, still a point of debate how the residual calcium interacts with the release machinery (see Zucker and Regehr, 2002, for review).

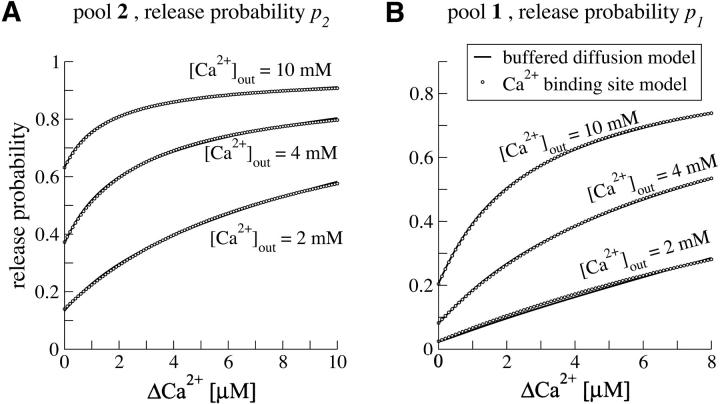
Within the frame of our model we consider facilitation to be exclusively a consequence of changes in local Ca²⁺ concentration at the release site (Felmy et al., 2003). An alternative approach attributes calcium-related facilitation of release to a high affinity Ca²⁺ binding site as part of the release apparatus, responding to global Ca²⁺ changes (Bertram et al., 1996; Dittman et al., 2000; Tang et al., 2000; Yamada and Zucker, 1992). We stress, however, that the results of our model calculations do not crucially depend on the underlying model of facilitation. We demonstrate in Appendix B that very similar changes in release probability can be obtained with both types of models depending on proper choice of model parameters (Fig. 8). In Appendix A we summarize the ideas underlying the specific facilitation model of our study.

Buffered calcium diffusion and facilitation of release

To describe release and facilitation we first take into account that at least four calcium binding sites are required to activate transmitter release (Bollmann et al., 2000; Borst and Sakmann, 1996; Dodge and Rahamimoff, 1967; Heidelberger et al., 1994; Schneggenburger and Neher, 2000). For each pool j (j = 1,2) we use a Hill equation with a fourth-order dependency of the release probability p_j on the local Ca²⁺ concentration [Ca²⁺] at a presynaptic release site of pool j,

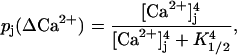(9)

with K_1/2 denoting the calcium concentration for half-maximal release. In the following we discuss the dependence of the local Ca²⁺ concentration [Ca²⁺] on the residual Ca²⁺ concentration ΔCa²⁺, which gives rise to facilitation, i.e., the dependence of p_j on ΔCa²⁺.

Local domains of high calcium concentration exist in the close vicinity of open Ca²⁺ channels or clusters of Ca²⁺ channels and are thought to play a major role in controlling the mechanisms of neurotransmitter release (Meinrenken et al., 2002; Aharon et al., 1994; Chad and Eckert, 1984; Fogelson and Zucker, 1985; Neher, 1998b; Rios and Stern, 1997; Simon and Llinas, 1985). When Ca²⁺ enters the presynaptic terminal through open channels, local Ca²⁺ microdomains build up quickly and are strongly influenced by the presence of mobile Ca²⁺ buffers (Naraghi and Neher, 1997; Neher, 1998a; Roberts, 1994). Theoretical studies point toward microdomains exhibiting Ca²⁺ concentrations as high as 100 μM (Yamada and Zucker, 1992), whereas experimental estimates point to lower local concentrations of ∼10–25 μM (Bollmann et al., 2000; Schneggenburger and Neher, 2000). Such local Ca²⁺ domains of nanometer dimensions should not be confused with global elevations of Ca²⁺ concentration of ∼0.5–1 μM, which can be measured after action potentials in experiments with Ca²⁺ indicator dyes (Takahashi et al., 1999; Helmchen et al., 1997).

We assume that the release site is well within the microdomains of several Ca²⁺ channels of a given active zone. In the presence of saturable buffers, the amplitudes of the local Ca²⁺ domains depend on the state of saturation of these buffers immediately before the action potential, which in turn depends on residual calcium, ΔCa²⁺, as depicted in Fig. 2. As explained in detail in Appendix A, the peak local Ca²⁺ concentration at a release site of pool j, [Ca²⁺]_j, can be expressed as

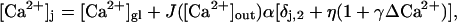(10)

where α, η, and γ are free parameters of the model. The local concentration deviates from the global Ca²⁺ concentration due to the influx of Ca²⁺ through channels, which are close enough to the release site, such that the release site is located within their microdomain. In Eq. 10, the elevation of the local Ca²⁺ signal above [Ca²⁺]_gl is a product of the flux J_Ca, a proportionality constant α, and the term in square brackets, which comprises the contributions of the different sources of Ca²⁺ (see below). The global calcium, [Ca²⁺]_gl = [Ca²⁺]_r+ΔCa²⁺, is elevated above the resting level [Ca²⁺]_r by the residual Ca²⁺ concentration, which is denoted by ΔCa²⁺ and will be discussed in the next section.

FIGURE 2.

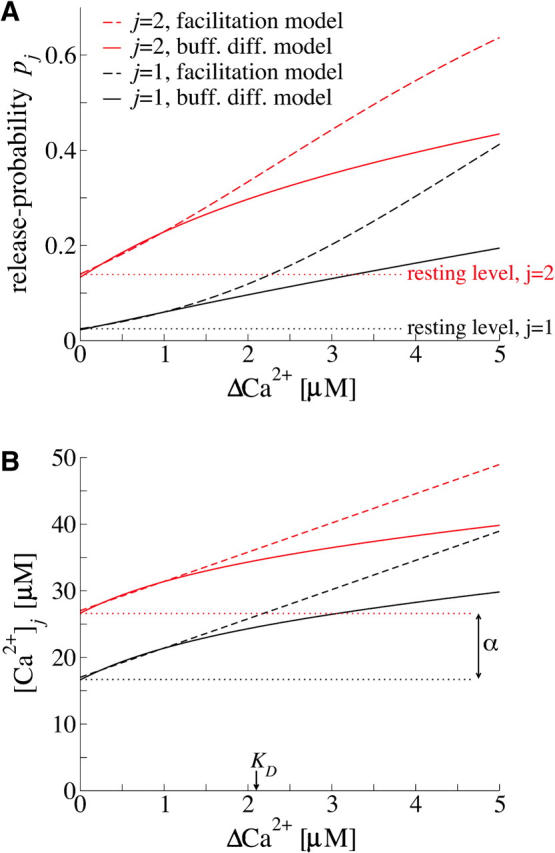
Effect of elevations in presynaptic Ca²⁺ concentration on release probability and local Ca²⁺ concentrations. (A) Dependence of the release probabilities p₁ (black lines) and p₂ (red lines) on elevations in the global calcium concentration ΔCa²⁺ as computed from the facilitation model (Eqs. 9 and 10, dashed lines) and the buffered diffusion model (Eqs. 9 and A10, solid lines; see also Appendix A). (B) Dependence of the local calcium concentration [Ca²⁺]_j (j = 1,2) triggering release from pool 1 (black lines) and pool 2 (red lines) on changes in residual calcium ΔCa²⁺ as computed from Eq. A10 (solid lines). The parameter K_D denotes the elevation in [Ca²⁺]_j (j = 1,2) for half-maximal increase in ΔCa²⁺. For ΔCa²⁺ < K_D, Eq. A10 can be approximated by the linear relation in Eq. 10 (dashed lines). The local calcium concentration [Ca²⁺]₁ (black lines) for a reluctantly releasable vesicle (pool 1) is displaced downward by the constant decrement α (see Eq. 10).

The Ca²⁺ influx J_Ca([Ca²⁺]_out) depends on the extracellular Ca²⁺ concentration (Church and Stanley, 1996; Schneggenburger et al., 1999). Measurements indicate that Ca²⁺ influx exhibits strong saturation (half-maximal Ca²⁺ influx at EC₅₀ ∼ 2.6 mM [Ca²⁺]_out) and is described by a Michaelis-Menten saturation equation (Schneggenburger et al., 1999),

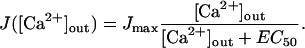(11)

Note that we use J_max and J([Ca²⁺]_out) as dimensionless quantities which describe the flux relative to the Ca²⁺ flux measured at 2 mM extracellular [Ca²⁺]_out (Schneggenburger et al., 1999).

In our model, vesicles of pool 2 are assumed to be released from a limited number of specific release sites. These release sites are believed to be embedded in regions of high density of Ca²⁺ channels (Llinas et al., 1992; Haydon et al., 1994; Borst and Sakmann, 1996) and may specifically be linked to one or several distinct Ca²⁺ channels at short distances (Bennett et al., 1992; Sheng et al., 1996; Rettig et al., 1997). Here we assume that vesicles of pool 2 have such a channel tightly linked to the release apparatus, which we assume to be located at such a short distance that Ca²⁺ buffers cannot intercept Ca²⁺ ions on their way from the channel mouth to the Ca²⁺ sensor of the release site. Vesicles of pool 1 lack such a colocalized channel. Hence, when Ca²⁺ enters the presynaptic terminal, vesicles of pool 1 and 2 are exposed to different local Ca²⁺ concentrations. The contribution of the colocalized channel (denoted by α in Eq. 10) to the local Ca²⁺ signal is only present for pool 2, as accounted for in Eq. 10 by a Kronecker symbol δ_j,₂, which has the value one for j = 2 (pool 2) and zero for j = 1 (pool 1). (Differences in the triggering local calcium signal between pool 1 and 2 could also originate from a cluster of channels specifically linked to the release sites of pool 2, with each channel at a slightly larger distance contributing a fraction of the increment α.)

This contribution is independent of the Ca²⁺ binding state of buffers and consequently independent of ΔCa²⁺. In Eq. 10 the terms in brackets (multiplied by η) are present for both types of release sites and represent the summed contribution of all the other Ca²⁺ channels at a given active zone. For these channels buffering is significant, so that the Ca²⁺ influx from these channels does depend on ΔCa²⁺. If the global Ca²⁺ concentration is close to the resting value then Ca²⁺ buffers are mainly free, and [Ca²⁺]_j ∼ α(δ_j,2 + η). The term proportional to ΔCa²⁺ (proportionality constant γ) models reduced buffering power at higher [Ca²⁺]_gl due to partial buffer saturation (see Appendix A for details).

According to Eq. 9, [Ca²⁺]_j determines the release probability p_j for pool j. Hence release depends on the extracellular Ca²⁺ concentration [Ca²⁺]_out, the global intracellular calcium concentration [Ca²⁺]_gl, and four model parameters K_1/2, α, η, and γ where α and K_1/2 are redundant for evoked release. The values for J_max and EC₅₀ have been estimated by measurements with varying concentrations of [Ca²⁺]_out (Schneggenburger et al., 1999). Note that two of the remaining four model parameters (α and η) are determined by the estimated local calcium concentration at the release site (Bollmann et al., 2000; Schneggenburger and Neher, 2000), and by the relative release probability p₁/p₂ (see Selection of Model Parameters and Fig. 2).

Calculating EPSCs evoked by a sequence of action potentials

We calculate the dynamics of the presynaptic spatially averaged Ca²⁺ concentration [Ca²⁺]_gl using the single compartment model (Neher and Augustine, 1992; Helmchen et al., 1997). In this model the time course of the free Ca²⁺ concentration is calculated by treating the presynaptic terminal as a single cell compartment within which [Ca²⁺] is rapidly equilibrated by diffusion. Furthermore it is assumed that the intracellular Ca²⁺ concentration rapidly equilibrates with the calcium buffers inside the presynaptic terminal. These assumptions are considered to hold with regard to the slow processes of vesicle recruitment, which happens in between action potentials. The Ca²⁺ influx due to an AP is modeled as an instantaneous increase of the global Ca²⁺ concentration by x₀, which elevates the global Ca²⁺ concentration by ΔCa²⁺ above resting level. The residual calcium ΔCa²⁺ is removed by Ca²⁺ pumps on a much slower time scale, denoted by τ_x. The time course of the free global calcium [Ca²⁺]_gl after an AP at time t = 0 is then given by

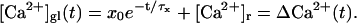(12)

The range of τ_x and x₀ has been measured experimentally for the calyx of Held (Helmchen et al., 1997) and the values adopted for our calculations are displayed in Table 1.

For repetitive presynaptic AP stimulation we assume constant Ca²⁺ influx with each AP (Borst and Sakmann, 1999), and that the globally elevated calcium concentrations add linearly (Helmchen et al., 1997; Weis et al., 1999). The increase in global residual calcium Δ⁽ⁿ⁾Ca²⁺ after a sequence of n stimuli, applied with frequency f_stim, corresponding to an interstimulus interval of Δt = 1/f_stim, is then given by (Helmchen et al., 1996)

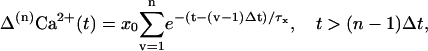(13)

where we have assumed that the first stimulus occurs at time t = 0. Computing the sum in Eq. 13 we determine the actual global residual calcium ΔCa²⁺ (t) reflecting the sequence of previous APs (see Fig. 5 D). Inserting ΔCa²⁺ (t) into Eq. 10 yields the corresponding release probabilities p₁ and p₂, which are facilitated due to previous stimulation (Fig. 5 C).

FIGURE 5.

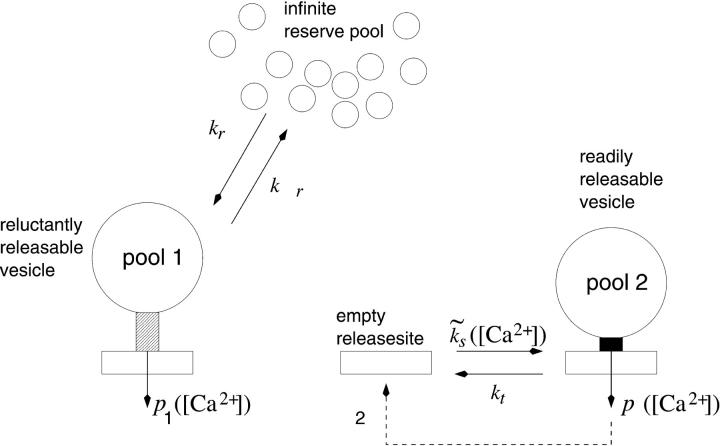
Pool dynamics during and after repetitive stimulation. Model predictions of the two-pool model during and after stimulation with 10 Hz (thick black line) and 100 Hz (black line); parameters in Table 1. (A) Occupancy in pool 1. (B) Occupancy in pool 2. The arrow indicates the Ca²⁺-enhanced recovery at the end of the stimulus train. (C) Facilitation of the release probabilities p₁ (open circles) and p₂ (solid circles). Circles indicate the release probability at the time of stimulation (larger circles for stimulation with 10 Hz). (D) Elevation in the global calcium concentration [Ca²⁺]_gl during repetitive stimulation as computed by Eq. 13. (E) Recovery after repetitive stimulation with 200 Hz (50 stimuli).

During a sequence of several APs the postsynaptic current elicited by the nth stimulus is calculated in analogy to Eq. 8 by

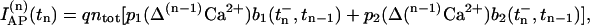(14)

where Δ⁽ⁿ⁻¹⁾Ca²⁺ denotes the change in global calcium due to the previous (n − 1) stimuli and is computed by Eq. 13. The occupancy in pool 1 immediately before release caused by the nth stimulus, 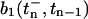, is computed from Eq. 4 with initial conditions given by the pool occupancy 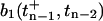immediately after the prior, (n − 1)th stimulus,

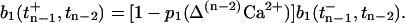(15)

Hence, successively applying Eqs. 15 and 14 enables us to calculate the postsynaptic current for a given sequence of APs.

We set the initial conditions to the resting conditions in Eq. 6 and track the effects of subsequent stimuli by updating the pool occupancies b_j (using Eqs. 4, 7, and 15) and release probabilities p_j (Eqs. 10 and 13) while progressing along the stimulus train.

Selection of model parameters

Experimental studies at the calyx of Held allow to restrict the number of free model parameters as described in the following. Recording quantal release rates on the basis of a deconvolution approach led to an estimate of the joint total number of releasable vesicles in both pools of 2000–4000 vesicles (Sakaba and Neher, 2001a,b; Schneggenburger and Neher, 2000). Capacitance measurements at the calyx of Held yielded a somewhat larger estimate of 5000 vesicles (Sun and Wu, 2001). At rest the total pool of releasable vesicles seems to be shared equally by reluctantly and readily releasable vesicles (Sakaba and Neher, 2001a,b). In the model, 1200 vesicles are attributed to each of the two vesicles pools, yielding a total number of 2400 vesicles as estimated by Neher and Sakaba (2001). The initial release probabilities of both pools are adjusted to yield a quantal content of 140–210 vesicles, as estimated by Schneggenburger et al. (1999), and Borst and Sakmann (1996), respectively. Nonstationary variance analysis of maximum EPSC amplitudes at elevated extracellular calcium concentrations exhibited a bell-shaped dependency, indicating that at least 80% of the release sites of pool 2 are occupied at rest.

Recovery of a reluctantly releasable pool was found to be independent of the intracellular Ca²⁺ concentration, and occurred with a single time constant of 0.15 s (Sakaba and Neher, 2001a,b; Wu and Borst, 1999). The time constant of replenishment into pool 2 was found to vary with changing presynaptic Ca²⁺ concentrations, ranging from τ_P2 = 9.1 s when Ca²⁺ was buffered to very low values, τ_P2 = 3.4 s for [Ca²⁺]_gl = 500 nM (Sakaba and Neher, 2001a), and τ_P2 = 4.2 s, for physiological conditions (von Gersdorff et al., 1997). On the basis of Eq. 6 (for a steady-state occupancy of 92.3%) and Eqs. 2 and 5 this leads to an estimate of the kinetic rates of k_t = 0.0028 s⁻¹, k₀ = 0.107 s⁻¹, and k_s = 0.0368 s⁻¹. Note that the rate of recovery 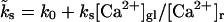exhibits a Ca²⁺-independent term k₀ which, at resting [Ca²⁺]_r, is ∼3× larger than the Ca²⁺-dependent contribution.

Parameters regarding the change of intracellular Ca²⁺ concentration (x₀ and τ_x, see Eq. 12) during trains of APs are taken from Helmchen et al. (1997) as indicated in Table 1. The values for α and η are computed from experimental estimates of the local calcium concentration close to release sites, and by the ratio p₁/p₂ of release probabilities at rest. At ΔCa²⁺ = 0, the second term of Eq. 10 simplifies to α(δ_j2 + η). For the readily releasable pool (j = 2), this term was set to 27 μM (see Fig. 2 B), close to the estimated local Ca²⁺ concentration at the release site (Schneggenburger and Neher, 2000). Using Eqs. 9 and 10 and the two values assigned to the release probabilities at rest, this yielded α = 10 μM and η = 1.6929.

Assuming that transmitter release under resting conditions is largely mediated by vesicles in pool 2, the value for p₂ is constrained by estimates of the quantal contents during a presynaptic AP (see above; Borst and Sakmann, 1996; Schneggenburger et al., 1999). The release probability p₁ at rest was set to 0.025 for all simulations. This leaves one more free model parameter, γ. This parameter γ was estimated by fitting the model to the (normalized) steady-state EPSC amplitude as function of frequency (data from Fig. 2 A in von Gersdorff et al., 1997). The fit of the model through γ was then compared to a second independent set of experimental data, the depression of EPSC amplitudes under stimulation with 10 Hz (data from Meyer et al., 2001). Note that the value found for γ predicts a slope of ∼4–5 in the relationship between [Ca²⁺]_j and ΔCa²⁺ (Fig. 2 B, dashed line). A similar slope factor would be necessary to explain the relationship between facilitation and residual Ca²⁺ in a recent experimental study (Felmy et al., 2003).

Table 1 summarizes the values which have been assigned to the model parameters.

The model in comparison to experimental data

It has been noted that the simple depletion model fails to account for the magnitude of synaptic responses during repetitive synaptic activity (Weis et al., 1999; Zucker and Regehr, 2002). Experiments in several brain regions demonstrated that an elevation of presynaptic Ca²⁺ levels accelerates the recovery from depression (Dittman and Regehr, 1998; Sakaba and Neher, 2001a; Stevens and Wesseling, 1998; Wang and Kaczmarek, 1998). Accordingly, previous theoretical work at the calyx of Held demonstrated that a Ca²⁺-dependent rate of recovery could create an activity-induced, extra recruitment of readily releasable vesicles to maintain the high synaptic activity during steady-state depression (Weis et al., 1999).

Neither Ca²⁺-enhanced recruitment nor facilitation of release can fully account for synaptic steady-state activity

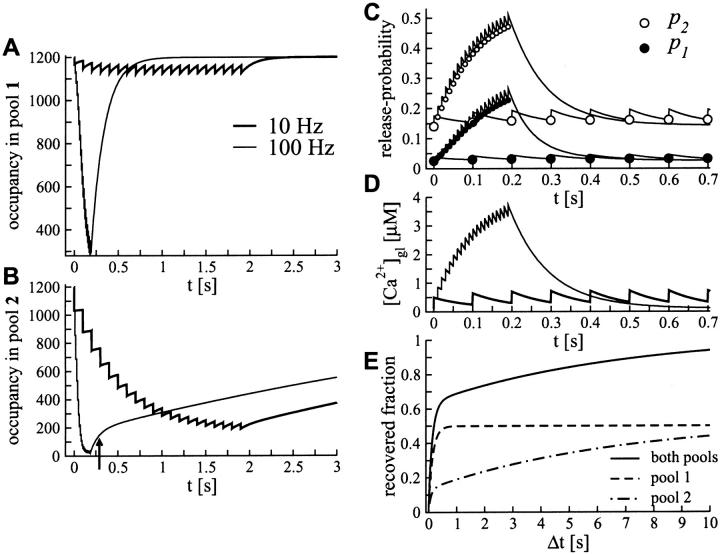
We first repeat the theoretical analysis of Weis et al. (1999) for the frequency-dependence of the (normalized) steady-state depression current (Fig. 2 B in Weis et al., 1999; see also experimental data in Fig. 3). The model of Weis et al. comprises a single pool of readily releasable vesicles and a Ca²⁺-dependent rate of recovery, but no facilitation of release. We confirmed the results of Weis et al. (1999), if we allowed the vesicle recruitment rate to be as strongly Ca²⁺ dependent as assumed in that study. Meanwhile, however, this Ca²⁺ dependence has been measured (see Selection of Model Parameters and Table 1 for details and references). Using this value, the single-pool model could not explain the experimental result for any value of p_rest (Fig. 3, triangles and squares). To illustrate this point, in Fig. 3 we show the predictions of the single-pool model for the normalized steady-state current for two values of the release probability, p_rest = 0.14 (squares) and p_rest = 0.2 (triangles). The single-pool model clearly fails to account for the steady-state activity during repetitive stimulation.

FIGURE 3.

Comparison of the single-pool model to experimental data. Steady-state EPSC amplitudes (normalized with respect to the first AP in the stimulus train) as a function of frequency. The model is compared to experiments (data taken from von Gersdorff et al., 1997) for two different release probabilities, p_rest = 0.14 (open squares) and p_rest = 0.2 (filled triangles). The parameters of the single-pool model (Weis et al., 1999) are constrained by the experimental estimates in Table 1. Lines indicate the predictions of the single-pool model after facilitation of release has been included in the model (p_rest = 0.14, solid line; p_rest = 0.2, dashed line).

In contrast to the findings of Weis et al. (1999), our analysis of the single-pool model underestimates the steady-state EPSC amplitudes—–despite a Ca²⁺-dependent recruitment rate. The reason for this is the low value of k_s = 0.0368 s⁻¹, which is constrained by the experimentally observed values from Sakaba and Neher (2001a). This yields a Ca²⁺ dependency of the recruitment rate 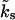, which is four times weaker than initially assumed (see k_1b = 0.15 s⁻¹ in Weis et al., 1999).

The model by Weis et al. (1999) did not account for Ca²⁺-related facilitation of release. At the calyx of Held initial release probabilities seem to be low. Hence repetitive stimulation might not completely exhaust the readily releasable pool and Ca²⁺-related facilitation of release might help to increase the steady-state activity in the model calculations. We therefore extended the single-pool model to include facilitation as described in Facilitation of Release Probability for the readily releasable pool (probability p₂ assigned to the single-pool model). Fig. 3 indicates, however, that facilitation of release hardly affects the plateau activity during steady-state depression—even if a parameter set for maximal facilitation is chosen (p_2,rest = 0.14, solid line; p_2,rest = 0.2, dashed line; rest of parameters as given in Table 1). The reason for this finding is that at higher frequencies the pool of readily releasable vesicles is strongly depleted during steady-state depression such that release is mainly determined by recruitment of new vesicles (see also Fig. 5 B). At low frequencies (<5 Hz) facilitation is not significant, because ΔCa²⁺ decays in between consecutive stimuli. From these results we conclude that an additional mechanism is necessary to maintain the high synaptic activity during steady-state depression.

Heterogeneous release probability can explain steady-state activity

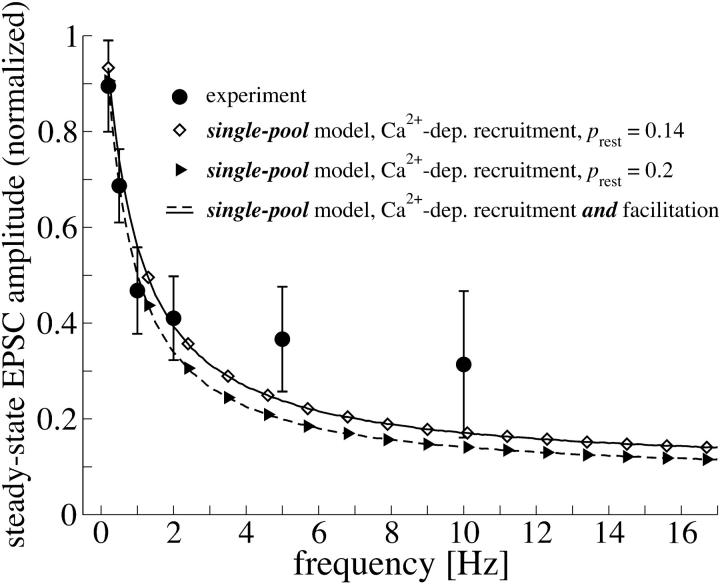
We suggest that this additional mechanism is heterogeneity of presynaptic release probability, as modeled by the two-pool model, comprising a pool of reluctantly releasable vesicles (pool 1) and a pool of readily releasable vesicles (pool 2). For the set of parameters from Table 1, the parameter γ is adjusted to fit the experimental data, giving γ = 0.2 μM⁻¹. As displayed in Fig. 4 A the two-pool model matches the experimental results and is able to explain the elevated steady-state activity. As an additional test, predictions of the model are compared to a second set of experimental data in Fig. 4 B. This data set represents the average time course of depression at 10 Hz, measured with 100 μM CTZ in n = 7 cells (see Fig. 2, Meyer et al., 2001). The predictions show reasonable agreement with the recorded depression of EPSC amplitudes during a 10-Hz stimulus train.

FIGURE 4.

Comparison of the two-pool model to experimental data. (A) Steady-state EPSC amplitudes (normalized with respect to the first AP in the stimulus train) as function of frequency (von Gersdorff et al., 1997). The two-pool model (blue solid line) was fitted to the experimental data using p₁ (at rest) and γ as fit parameters, rest of parameters constrained by experimental estimates (Table 1). The dot-dashed red line displays predictions of a two-pool model ignoring facilitation of release. The black dashed and black solid line correspond to the fits of the constrained single-pool model from Fig 3 B; depression of EPSC amplitudes during 10 Hz stimulus trains (normalized to the first EPSC; data from Meyer et al., 2001) . The prediction by the four types of models shown in A are displayed. Note that the single-pool models (black lines) tend to underestimate EPSC amplitudes during the steady-state phase of depression.

Fig. 5, A and B display the contributions of both pools of vesicles separately during repetitive stimulation with 10 and 100 Hz. It is clear from Fig. 5 B that the number of vesicles released per AP from pool 2 decreases during the stimulus train. When reaching steady activity at 10 Hz, ∼34 vesicles are released from pool 2. Pool 1 contributes 30 vesicles and provides about half of the resources for maintaining steady-state activity.

As displayed in Fig. 4 and Fig. 5 C, facilitation of release does not contribute to steady-state activity for frequencies below 10 Hz, for which the release probabilities p₁ and p₂ remain around resting level. This finding is not surprising as facilitation of release is assumed to be related to elevations in residual calcium, ΔCa²⁺, which decay with a time constant of τ_x = 100 ms.

Fig. 5, A, B, and E, show the recovery of both pools after repetitive stimulation with 100 Hz. While pool 1 still contains more than a quarter of its initial occupancy at the end of the stimulus train (occupancy of 280 vesicles after 20 stimuli), the occupancy of pool 2 reaches almost zero (occupancy of 30 vesicles at the end of the 100-Hz stimulus train). Within the first 0.5 s after stimulation, the filling state of pool 2 exhibits a rapid component of recovery (see Fig. 5 B, arrow), which reflects the Ca²⁺-enhanced extra recruitment of vesicles into pool 2. In order to compare the model to the observed accelerated recovery of pool 2 under elevated Ca²⁺ concentrations (Fig. 3 C in Sakaba and Neher, 2001a), recovery of both pools was calculated after stimulation with 200 Hz (50 stimuli). Under these conditions pool 2 is nearly empty (occupancy of 12 vesicles) and the simulated presynaptic Ca²⁺ concentration has reached high concentrations of ∼12 μM (not shown). This situation is likely to resemble the massive Ca²⁺ influx during the long-lasting depolarizing stimuli used by Sakaba and Neher (2001a,b) and Wu and Borst (1999). As displayed in Fig. 5 E our simulations yield a similar speedup in the recovery of pool 2 as observed experimentally under elevated presynaptic Ca²⁺ concentration at the end of a long-lasting depolarizing stimulus (see Fig. 3 C in Sakaba and Neher, 2001a). Furthermore, the joint recovery of both pools, as compared to the recovery of pool 2 only, compares well to Fig. 5 A in Wu and Borst (1999), where a strong depolarizing pulse was used to study the joint recovery.

DISCUSSION

Summary

We have explored a model of presynaptic vesicle dynamics comprising heterogeneous presynaptic release probabilities and Ca²⁺-related recruitment and facilitation of release. Heterogeneous release has been modeled by two discrete pools of vesicles: reluctantly releasable vesicles (pool 1), which are released with a lower release probability than the readily releasable vesicles from pool 2. These two types of vesicles do not only differ in their release probability, but also regarding the time scales of replenishment. The pool of readily releasable vesicles is quickly depleted during repetitive stimulation and the major fraction of it recovers with a slow time constant of a few seconds. Concerning the pool of reluctantly releasable vesicles the situation is different: Due to the low release probability of p₁ ∼ 0.03–0.2 every stimulus depletes this pool by only a small fraction and the pool is rapidly refilled with a time constant of a few hundred milliseconds. Hence this pool serves as a backup supply during repetitive stimulation and carries part of the steady-state activity. During stimulation with 10 Hz, for instance, reluctantly releasable vesicles contribute one-half to the steady-state amplitude. The model can account for the experimentally observed patterns of synaptic depression (and facilitation) at the calyx of Held over a wide range of stimulation frequencies. Hence we conclude that heterogeneous release in the form of two discrete pools of vesicles differing in release probability and their time scales of replenishment can provide an intrinsic dynamic mechanism to maintain synaptic activity during repetitive stimulation.

Homogeneous versus heterogeneous release probability

We demonstrated that a single-pool model that includes mechanisms of Ca²⁺-driven extra recruitment of vesicles and facilitation of release fails to explain the steady-state activity during synaptic depression, if the parameters of the model are chosen in accordance with experimental values which can be determined independently at the calyx of Held. A similar critique may also be relevant for the recently designed general model of short-term plasticity of Dittman et al. (2000). Their single-pool model was based on two different calcium-dependent mechanisms; first, facilitation of release and, second, refractory depression. The latter mechanism corresponds to the assumption of a calcium-enhanced rate of recovery as included in our model. The model of Dittman and co-workers was shown to reproduce a variety of patterns of short-term plasticity at the climbing fiber to Purkinje cell synapse, the parallel fiber to Purkinje cell synapse, and the Schaffer collateral to CA1 pyramidal cell synapse (Dittman et al., 2000). However, if the model of Dittman et al. (2000) were applied to the calyx of Held with the parameter values constrained by experiments, we expect calcium-enhanced pool recovery to fail. In particular, Dittman et al. (2000) assumed a rate of recovery which exhibits a much stronger Ca²⁺ dependency than that found at the calyx. Converting their estimate of k_max (see Eq. 3 in Dittman and Regehr, 1998, and Eq. 14 in Dittman et al., 2000) into the frame of our model would result in a value of k_s in Eq. 2 of k_s∼1 s⁻¹, which is almost two orders of magnitude larger than the value used here (k_s = 0.0368 s⁻¹), the latter being tightly constrained by the reported Ca²⁺ dependence of recovery time constants at the calyx of Held (Sakaba and Neher, 2001a). In the model of Weis et al. (1999), the parameter corresponding to k_s was ∼4× larger than the one used here (see Results). This value was needed to explain the enhanced EPSC amplitude during the steady-state phase of depression at frequencies >2 Hz (see Weis et al., 1999, their Fig. 2). Nevertheless, introducing exogenous Ca²⁺ buffers did not lead to the expected changes in recovery after 10 Hz depression (Weis et al., 1999). This agrees with our present finding that the steady-state phase of depression <10 Hz is not largely influenced by the Ca²⁺-dependent recovery of pool 2 (Fig. 3). We conclude that Ca²⁺-dependent recovery of a readily releasable vesicle pool exists at the calyx of Held (Wang and Kaczmarek, 1998; Sakaba and Neher, 2001a), but that its effect on steady-state EPSC amplitude during depression up to 10 Hz stimulus frequencies is weaker than predicted by the models of Weis et al. (1999) and Dittman et al. (2000). We suggest that at the calyx of Held heterogeneity of release probability is necessary to maintain synaptic activity during steady-state depression.

Synaptic heterogeneity of release probability has been reported from the hippocampus (Allen and Stevens, 1994; Dobrunz et al., 1997; Hessler et al., 1993; Huang and Stevens, 1997; Murthy et al., 1997; Rosenmund et al., 1993; Isaacson and Hille, 1997), and dorsal spinocerebellar tract neurons (Walmsley et al., 1988). Furthermore, at hippocampal synapses synaptic depression is not accompanied by a reduction in the frequency of spontaneous release of vesicles (Cummings et al., 1996). This finding may be consistent with our model if spontaneous release is due to release of vesicles from a reluctantly releasable pool for which a low degree of depletion may be balanced by some facilitation of release under increasing residual Ca²⁺ concentrations. Also, our model assumptions are suitable to describe properties of two types of vesicles, as observed in experiments using total internal reflection microscopy (Zenisek et al., 2000). In such investigations at nerve terminals of retinal bipolar cells a specific class of binding sites bind vesicles, called residents, for longer periods. These vesicles are released upon depolarization with higher release probability than so-called visitor vesicles that dock and undock in rapid succession and are released with low probability during stimulation.

A recent numerical simulation of the buildup and decay of Ca²⁺ microdomains at the calyx of Held (Meinrenken et al., 2002) treated all docked vesicles as intrinsically homogeneous, sensing stochastically heterogeneous Ca²⁺ signals due to randomly varying distances from clusters of Ca²⁺ channels. The influence of stochastic factors on release probability, such as numbers of open channels and geometric variations, was also the subject of detailed simulations by Quastel et al. (1992). In contrast to these studies our model may be termed a deterministic model of positional heterogeneity in release probability, referring to the fact that the two pools differ by the inclusion or lack of a specific nearby channel. We would like to point out that our model also contains some aspect of intrinsic heterogeneity, because vesicles from pool 1 and pool 2 are assumed to be replenished on largely different time scales. Other aspects of intrinsic heterogeneity, such as heterogeneity in release probability caused by different molecular properties of the release apparatus, could readily be incorporated by a reinterpretation or reformulation of the equations describing p_j (Eqs. 9 and 10; see Appendix B for detailed discussion). We also would like to stress that most likely stochastic factors within the two pools will contribute to the heterogeneity in release probability. Extensive additional experimental data, however, will be necessary to further specify the assumptions, to reduce the number of free parameters and to explore the range of validity of existing models of synaptic short-term plasticity, at the calyx of Held and in other areas of the brain.

Synaptic transmission of information

Fig. 4 A shows that the amplitude of postsynaptic currents during steady-state depression depends on the input frequency (von Gersdorff et al., 1997). This frequency-dependence of propagated presynaptic stimuli has been observed at synaptic connections in different areas of the brain (Abbott et al., 1997; Dobrunz et al., 1997; Fisher et al., 1997; Galarreta and Hestrin, 1998; Markram et al., 1998a,b; Thomson and Deuchars, 1994). In general the spike output by a neuron is assumed to be correlated with the input to that neuron, whereas the exact code by which the information is transmitted may be shaped by the frequency and specific temporal structure of the input pattern (see Dayan and Abbott, 2001, and Koch, 1999, for review). In particular it has been noted that the properties of synaptic transmission vary between specific types of neurons and these synaptic properties seem to determine the contributions of rate and temporal signals to the postsynaptic response (Tsodyks and Markram, 1997; Markram et al., 1998a; Trommershäuser and Zippelius, 2001; Varela et al., 1997). In accordance with this idea, bursting patterns have been found to be unique at individual cells and to vary over a wide frequency range (Kandel and Spencer, 1968; Larson et al., 1986; Suzuki and Smith, 1985). Let us assume that the frequency of presynaptic stimulus trains carries information and ask how the corresponding rate code is propagated to the postsynaptic side. (Here we do not address the question of how the presynaptic input relates to the generation of action potentials in the postsynaptic neuron. Instead, we focus on the question of how the postsynaptic current depends on the presynaptic stimulus protocol. In that sense, we use the term information to characterize how the postsynaptic response reflects the presynaptic input pattern.)

Previously this question was studied in the frame of a phenomenological model of synaptic transmission, defined on the basis of electrophysiological experiments in the neocortex (Tsodyks and Markram, 1997; Varela et al., 1997). The model predicted a 1/f decay in the amplitude of the steady-state depression current 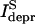for stimulation frequencies f larger than a limiting frequency f_lim (Eq. 3 in Tsodyks and Markram, 1997), such that

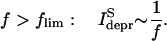(16)

Note, that a 1/f behavior of 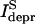implies that the average postsynaptic depolarization will not change with increasing frequency, making a rate coding of the input stimulus train impossible. Therefore the limiting frequency f_lim has been introduced to indicate the upper limit of presynaptic input rates that can be transmitted toward the postsynaptic side by a frequency-dependent code and to indicate the frequency range within which synapses are able to transmit information about the presynaptic firing rate.

Experiments at neocortical pyramidal neurons have shown the predicted 1/f behavior for a range of stimulation frequencies in between 10 and 40 Hz (Tsodyks and Markram, 1997). Variations of release probability by changes in extracellular calcium concentrations have caused a shift of f_lim (Castro-Alamancos and Connors, 1997; Dobrunz et al., 1997; Markram et al., 1998a; Tsodyks and Markram, 1997), implying that the response characteristics of a synaptic connection not only depend on the neuronal type, but also on the specific physiological conditions.

As displayed in Fig. 6 the EPSC amplitude during steady-state depression, as recorded in experiments on the calyx of Held, does not reach a 1/f behavior in the range of recorded stimulus frequencies (<10 Hz). Furthermore, our model suggests that the synaptic steady-state activity at the calyx of Held does not reach a 1/f-dependency for any range of stimulation frequencies larger than 10 Hz. We conclude that high synaptic steady-state activity provides a mechanism to transmit a broad range of frequencies. This property may be crucial for the calyx of Held, which functions as a sign-inverting relay synapse in neuronal circuits of the auditory system underlying sound localization. Our analysis suggests that at the calyx of Held a heterogeneous population of synaptic vesicles is necessary to explain the observed synaptic steady-state activity. We therefore conclude that nonuniform release probabilities at the calyx of Held and possibly in other areas of the brain may be of functional relevance for the transmission of information at synapses.

FIGURE 6.

Steady-state EPSC amplitudes as function of frequency. Predictions of the two-pool model (blue solid line, parameters as in Fig. 4) over a wide range of stimulation frequencies (amplitudes normalized with respect to the first AP in the stimulus train). Predictions of the single-pool model (dashed line) taken from Fig. 3; experimental data from von Gersdorff et al. (1997). The dot-dashed line indicates an ∼1/f-decay.

APPENDIX A: THE BUFFERED DIFFUSION MODEL: PREDICTIONS FOR FACILITATION OF TRANSMITTER RELEASE

In this appendix we briefly review previous theoretical work which provides a framework for the description of buffered Ca²⁺ diffusion and which is used to compute local calcium gradients—so-called calcium microdomains (Naraghi and Neher, 1997; Neher, 1986,1998a). These microdomains emerge around the mouths conducting calcium channels due to the interaction of calcium with endogenous mobile calcium buffers. We will show that under suitable assumptions this theory can be simplified such that within well-defined limits of model parameters, it yields a linear relation between the local calcium concentration, [Ca²⁺], at the release site and the residual calcium concentration, ΔCa²⁺.

We first consider the case that Ca²⁺ enters the presynaptic terminal through a single point source (channel) where it interacts with calcium buffers.

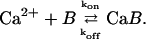(A1)

We distinguish between two different kinds of buffers. The first buffer B⁽¹⁾ has low Ca²⁺ affinity and is present in high concentration. Therefore the free concentration of this buffer, denoted by [B⁽¹⁾], does not change significantly in the vicinity of the channel, as buffer molecules taking up Ca²⁺ will rapidly be diffusionally replaced by free buffer molecules. The second buffer B⁽²⁾ is present in much lower concentration than buffer B⁽¹⁾, so that

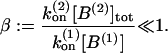(A2)

Here [B⁽²⁾]_tot denotes the total concentration of B⁽²⁾. The second buffer is assumed to have a moderately high affinity for [Ca²⁺] (dissociation constant 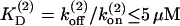) such that it partially saturates when the global calcium, [Ca²⁺]_gl, is elevated after stimulation by an amount of Ca²⁺ = [Ca²⁺]_gl−[Ca²⁺]_r above the basal concentration [Ca²⁺]_r.

The spatial distribution of the calcium concentration c(r) (r denotes the distance from the channel) obeys a reaction-diffusion equation: it reacts with both buffers according to Eq. A1 and diffuses with diffusion constant D_Ca. This equation has been solved in Neher (1998a) in linear order in β:

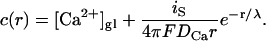(A3)

The local concentration c(r) is given by the global concentration [Ca²⁺]_gl and the influx through the channel, which decays exponentially with the distance from the channel, r. Here i_s denotes the single channel current and F is Faraday's constant. The decay length λ is dominated by the first buffer in high concentration

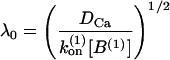(A4)

with small modifications due to the presence of the second buffer

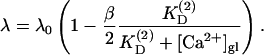(A5)

It should be noted that Eq. A3 describes the local calcium concentration in the vicinity of an open channel, which depends on the global presynaptic calcium concentration. Due to presynaptic stimulation the global calcium concentration increases above resting level by an amount of ΔCa²⁺ = [Ca²⁺]_gl−[Ca²⁺]_r, as discussed with help of a single compartment model in Eqs. 12 and 13.

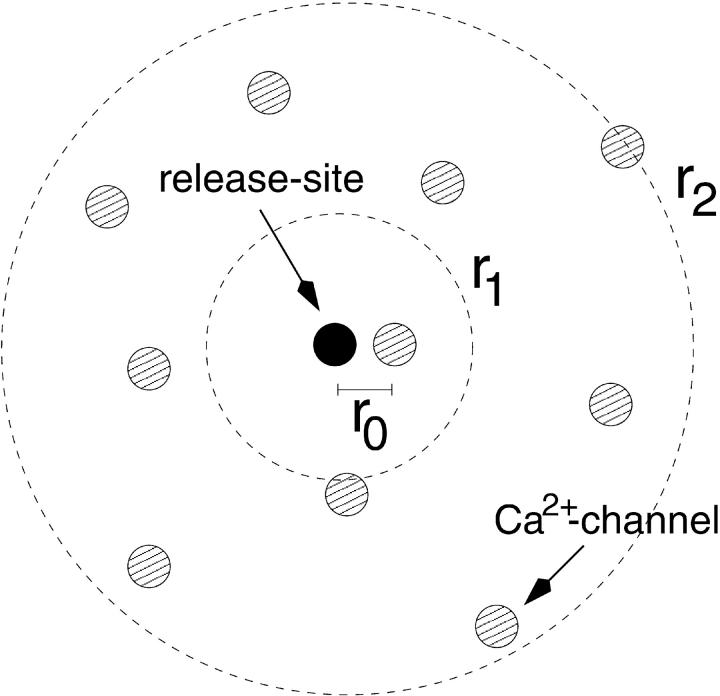
Synaptic vesicles are believed to be docked to release sites which are embedded in regions of high density of Ca²⁺ channels (Llinas et al., 1992; Haydon et al., 1994) and may specifically be linked to one or several distinct Ca²⁺ channels at short distances (Bennett et al., 1992; Sheng et al., 1996; Rettig et al., 1997). We therefore assume that the presynaptic release site is colocalized with a Ca²⁺ channel (at position r₀), and embedded in a cluster of (n−1) Ca²⁺ channels, which are distributed with a density of 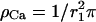(r₁ indicating the average distance between the channels) within a cluster radius of r₂ (see Fig. 7).

FIGURE 7.

Geometric configuration of Ca²⁺ channels around a release site. A single Ca²⁺ channel at distance r₀ is colocalized with the release site (black circle), which itself is surrounded by a cluster of Ca²⁺ channels (hatched circles); average area per channel 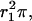cluster radius r₂ (after Fig. 1 A in Neher, 1998a).

We assume that buffer is present in the presynaptic terminal with a high concentration, such that 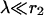and that microdomains due to individual Ca²⁺ channels add up linearly (Neher, 1998a). The assumption 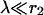implies that only Ca²⁺ channels in the vicinity of a given release site contribute significantly. This is relevant for the calyx of Held, where we assume that an active zone consists of a larger cluster of Ca²⁺ channels, into which three to six release sites are embedded (see Meinrenken et al., 2002 for an alternative scenario). If the n channels are identical and open simultaneously, the calcium concentration at the release site, c(r), is given as the sum over the individual microdomains (Eq. A3) of all n channels as

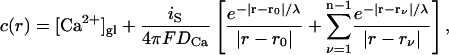with r_ν denoting the position of the νth channel. This expression simplifies, if we locate the release site at the origin, i.e., set r = 0 in the above equation.

The closest, possibly colocalized Ca²⁺ channel is at a distance r₀ from the release site and contributes most to c(r) and therefore is considered separately. For r₁ ≫ r₀ the sum is replaced by an integral (channel density 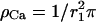), so that

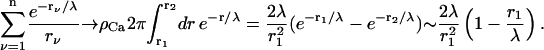In the last step we have assumed 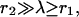so that we can neglect 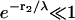and expand exp(−r₁/λ) ≈ 1 − r₁/λ. For the colocalized channel we have 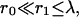so that 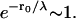With these approximations, we find for the local Ca²⁺ concentration at a release site, which is located at the origin and embedded in a region of high density of Ca²⁺ channels

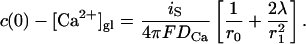(A6)

For a fixed extracellular calcium concentration [Ca²⁺]_out, the influx of Ca²⁺ is constant in time. Variations in extracellular Ca²⁺, however, are often used to experimentally manipulate the probability of release (see also Fig. 8). We include such effects of variable extracellular Ca²⁺ concentration by taking into account that the Ca²⁺ influx saturates with increasing concentration of extracellular calcium [Ca²⁺]_out (Church and Stanley, 1996; Schneggenburger et al., 1999), as described by Eq. 11.

FIGURE 8.

Comparison of the two facilitation models for varying elevations in global and extracellular Ca²⁺ concentration. The solid line corresponds to the buffered diffusion model (Eqs. 9 and A10); see Table 2 for the values assigned to the model parameters. Circles represent the fit of the calcium-binding-site model (Eq. B11) using 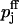and K_d,j (j = 1, 2) as fit parameters (see Table 3); equivalent initial release probabilities ( 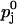for j = 1,2) assigned for both models. (A) Release probability p₂ from pool 2 as function of elevations in global calcium ΔCa²⁺. (B) Release probability p₁.

Note that the first term within the brackets of Eq. A6 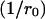represents the contribution to the microdomain of the specifically linked Ca²⁺ channel at location r₀. In our model (see Results) we assume that vesicles of pool 2 have such a channel tightly linked to the respective release apparatus, whereas vesicles of pool 1 lack such a channel. Hence the local Ca²⁺ concentration at release sites of pool 1, [Ca²⁺]₁ and of pool 2, [Ca²⁺]₂, differ by this term

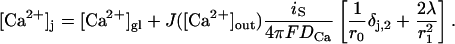(A7)

Here we have introduced the Kronecker symbol δ_j,2 = 1 for j = 2 and 0 otherwise.

Recent experimental evidence (Felmy et al., 2003) suggests that elevation of global Ca²⁺ by ∼1 μM does not lead to full saturation of an endogenous Ca²⁺ buffer in the calyx of Held. This implies 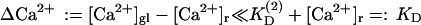(ΔCa²⁺ denoting the elevation of the global Ca²⁺ concentration above resting level [Ca²⁺]_r), so that λ can be expanded in ΔCa²⁺:

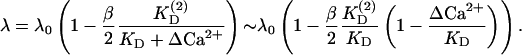(A8)

Combining Eqs. A7 and A8 and introducing the constants

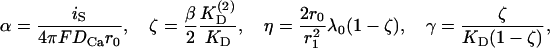we find the following functional dependence of the local Ca²⁺ concentration at a release site

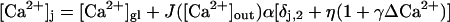(A9)

This functional form is used in the main part of the paper (see Eq. 10) with α, η, and γ considered as free parameters.

When studying highly elevated Ca²⁺ concentrations (see next section) the condition 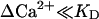does not hold. In that case Eq. A5 has to be used instead of Eq. A8. We introduce the constant 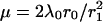and yield

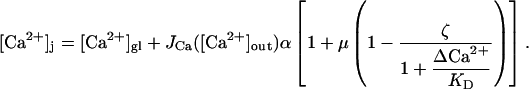(A10)

Equation A10 will be used in the following section for comparing the buffered diffusion model of facilitation to an alternative model.

APPENDIX B: COMPARISON OF TWO FACILITATION MODELS: BUFFERED DIFFUSION VERSUS CALCIUM-BINDING SITE

Here we demonstrate that our model of vesicle recruitment does not crucially depend on the specific assumptions about presynaptic facilitation of release. Although the general notion relates facilitation of release to changes in the global intracellular calcium, the question of how the residual calcium interacts with the release machinery is a matter of an ongoing debate. In our approach it is assumed that facilitation represents a change in the local Ca²⁺ signal (see Felmy et al., 2003). Different approaches have been proposed by Bertram et al. (1996), Dittman et al. (2000), Tang et al. (2000), and Yamada and Zucker (1992). In some of these models, transmitter release probability is modulated by a high affinity calcium-binding site. Here we show that in the frame of our calculations, both types of models yield very similar calcium dependency and hence facilitation characteristics of release probability.

In the work of Dittman et al. (2000) and Tang et al. (2000) it is assumed that the release of vesicles is controlled by a high affinity Ca²⁺ binding site (facilitation site), responding to global changes in residual calcium ΔCa²⁺, such that the release probabilities p_j vary according to

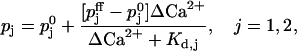(B11)

with K_d,j denoting the two dissociation constants of the facilitation sites assigned to pools 1 and 2, 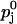the probability of release at rest, i.e., ΔCa²⁺ = 0, and 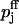at full facilitation (ΔCa²⁺ = ∞). These parameters are treated as free model parameters.

In order to compare the calcium-binding-site model to our facilitation model of buffered diffusion, the parameters μ, ζ, and K_D in Eq. A10 had to be specified. The parameters were chosen such that Eq. A10 matched the linear approximation (Eq. A10) for low values of ΔCa²⁺ (see Fig. 2 B). The values are summarized in Table 2.

TABLE 2.

Model parameters of the buffered diffusion model

Parameter	Value	Linear facil. model (Table 1)
p1 at rest (ΔCa2+ = 0)	0.025	0.025
p2 at rest (ΔCa2+ = 0)	0.14	0.14
KD	2.1 μM	≈μζ/ηγ = 3.5 μM
K1/2	42.5 μM	42.5 μM
α	10 μM	10 μM
μ	2.816	—
ζ	0.413	—

The calcium-binding-site model was then fitted to the predictions of the buffered diffusion model by assigning equivalent initial release probabilities to both models and using 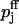and K_d,j (j = 1, 2) as fit parameters. The fitted estimates of 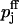and K_d,j are summarized in Table 3. Fig. 8 displays the changes in presynaptic release probability as a function of increasing residual calcium for different values of extracellular calcium concentration as predicted from each of the models. From this and the results in Table 3, it is clear that, for appropriately chosen parameters, both models come to the same predictions and do not differ within experimental accuracy.

TABLE 3.

Fit of the calcium binding site model to the buffered diffusion model. The calcium binding site model (Eq. B11) was fitted to the buffered diffusion model (Eqs. 9 and A10, parameters from Table 2) using 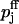(j = 1, 2) and K_D as fit parameter (101 data points per fit)

[Ca2+]out		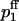Kd,1		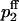Kd,2
2 mM	1	22.45 μM	0.95	8.69 μM
4 mM	0.98	7.83 μM	0.92	2.88 μM
10 mM	0.93	2.89 μM	0.95	1.63 μM

We want to emphasize two points: first, although based on different physiological mechanisms, the two approaches reveal very similar quantitative features. As displayed in Fig. 8 for a set of physiological parameters (Table 2), the two facilitation models discussed here exhibit the same dependence of both release probabilities on ΔCa²⁺ and coincide within the range of experimental verifiability. Second, due to the lack of knowledge about the physiological mechanisms involved we do not aim at a detailed analysis of the underlying mechanisms, but want to formulate a model with a minimal number of parameters. The basic assumption here only concerns the residual Calcium hypothesis (Katz and Miledi, 1968) assuming that facilitation is related to an increase in global residual Ca²⁺, which itself changes as a result of presynaptic stimulation. Fig. 8 shows that our model of vesicle dynamics is independent of the assumptions about the underlying facilitation mechanisms.

Although the calcium-binding-site approach seems to be based on less specific assumptions, it carries a larger number of free parameters: in contrast to the facilitation model based on buffered calcium diffusion it is not possible to differentiate between facilitation effects due to variations of the residual calcium or the extracellular Ca²⁺ concentration (see Eq. 10). An elevated extracellular Ca²⁺ concentration, for instance, requires a new set of estimates for 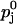and 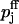for each of the vesicle pools, whereas one set of fit parameters in the buffered diffusion model (Eqs. 10 and A10) covers the whole range of Ca²⁺ dynamics.