Sperm Initiate a Ca²⁺ Wave in Frog Eggs that is More Similar to Ca²⁺ Waves Initiated by IP₃ than by Ca²⁺

Abstract

We have measured the initial propagation velocity of the sperm-induced Ca²⁺ wave in the egg of Xenopus laevis and have compared it with the initial propagation velocities of the inositol triphosphate (IP₃)-induced and Ca²⁺-induced Ca²⁺ waves. The initial mean propagation velocity of the sperm-induced wave (13 μm/s) is very similar to that of the IP₃-induced waves (12.3 μm/s) and two times faster than the mean Ca²⁺-induced wave velocity (6.6 μm/s). We have generated realistic simulations of the fertilization wave in the frog egg using a computational technique based on the finite difference method. Modeling refinements presented here include equations for the production, degradation, and diffusion of IP₃, a description for Ca²⁺ dynamics in the endoplasmic reticulum, and a highly concentrated endoplasmic reticulum in the egg cortex. We conclude that models incorporating sperm-induced IP₃ generation fit the data best and those involving the influx of either Ca²⁺ or a diffusible sperm factor fit the data poorly. This independence from Ca²⁺ influx is also supported by electrophysiological data indicating that Ca²⁺ influx is not needed to maintain open Cl⁻ channels that generate the fertilization potential.

INTRODUCTION

Fertilization triggers one or more waves of increased cytosolic calcium concentration starting at the site of sperm-egg fusion in all organisms studied. These waves generate both the fast and slow blocks to polyspermy and play an important role in releasing the egg from cell cycle arrest (Nuccitelli, 1991; Stricker, 1999; Ciapa and Chiri, 2000; Runft et al., 2002). However, the mechanism by which these waves are themselves initiated upon fertilization is not well understood. Presently there are three popular hypotheses: 1), The “calcium bomb” hypothesis proposes that upon fertilization Ca²⁺ enters the egg either from stores in the sperm itself or through channels in the sperm's plasma membrane (Jaffe, 1983). This creates a bolus of elevated calcium concentration that triggers a wave of Ca²⁺ release from the endoplasmic reticulum (ER). This wave propagates further by the self-sustaining mechanism of calcium-induced calcium release (CICR). 2), The “sperm-factor” hypothesis proposes that a diffusible activator of calcium release enters the egg from the sperm after fusion with the egg (Swann, 1990). 3), The sperm receptor hypothesis proposes that the interaction of sperm and egg membranes activates a special class of receptors on the egg surface that results in the production of inositol trisphosphate (IP₃). This second messenger opens IP₃-dependent calcium channels (IP₃ receptors or IP₃Rs) in the egg's endoplasmic reticulum to release calcium near the fertilization site. In both mammalian and amphibian eggs, integrins have been proposed as putative sperm receptors (Almeida et al., 1995; Shilling et al., 1997; Shilling et al., 1998). In the frog egg, peptides targeted to integrins on the egg surface were able to activate the calcium wave (Iwao and Fujimura, 1996; Shilling et al., 1998).

Our goal is to determine which of the above mechanisms are most likely to be responsible for triggering the fertilization Ca²⁺ wave in the Xenopus egg. We assume that different initiation mechanisms will exhibit distinctive dynamics during the initial stages of the fertilization wave. Therefore we have made accurate quantitative measurements of this dynamic behavior and have compared them with predictions made by realistic computer models that incorporate different initiation mechanisms.

MATERIALS AND METHODS

Obtaining gametes

Xenopus laevis eggs were obtained by gentle massage of ovaries of females that had been induced to ovulate by injection with 300–500 IU human chorionic gonadotropin 8–10 h before massage.

Male frogs were anesthetized in tricaine methanesulfonate (1.5 g/l) and then were decapitated and pithed. The testes were removed and stored in OR2 (82.5 mM NaCl, 2.5 mM KCl, 1.0 mM CaCl₂ 1.0 mM MgCl₂, 1.0 mM Na₂HPO₄, 5.0 mM Hepes; pH 7.8) supplemented with L15 culture media at 4°C for up to a week.

Microinjection of eggs

Mature, albino eggs were microinjected using an oil-filled line attached to a threaded syringe as previously described by Nuccitelli et al, (1993) with approximately 3 nl of 10 mM Ca-green-1-dextran (10,000 mol wt), in an intracellular injection buffer (109.0 mM KCl, 5.0 mM HEPES, 5.0 mM CaCl₂, 10 mM EGTA; pH 7.3) to yield an approximate final concentration of 60 μM inside the egg. Microinjection was conducted in a chlorobutanol solution (10% chlorobutanol in calcium-free OR2 (82.5 mM NaCl, 2.0 mM KCl, 5.0 mM HEPES, 20 mM MgCl₂, 0.1 mM EGTA; pH 7.4) to reduce the likelihood of activation of the eggs. Once injected, the eggs were held in the chlorobutanol solution for ∼1 min and were then placed in F1 solution (41.25 mM NaCl, 1.75 mM KCl, 0.5 mM NaHPO₄, 1.9 mM NaOH, 2.5 mM HEPES, 0.25 mM CaCl₂, 0.063 mM MgCl₂; pH 7.8) and the injected dye was allowed to diffuse for 1–3 h. Some eggs were also microinjected with various amounts of 1G9 in conjunction with the Calcium Green Dextran. The antibody was allowed to diffuse throughout the egg for at least 2.5 h.

Electrophysiology and Ca²⁺ influx blockers

The calcium channel blockers used were gadolinium, nickel, and cobalt. The solutions containing these blockers were all made in standard F1. The solutions prepared were 100 μM solutions of GdCl₃ and of GdCl₃·6H₂O, 1 mM solutions of NiCl₂·6H₂O, and CoCl₂·6H₂O. These were made from 10 mM stock solutions containing the appropriate channel blockers. All solutions were in the pH range of 7.30–7.8.

Glass micropipettes were made from 0.75 mm or 0.78 mm inner diameter borosilicate capillary tubing with an inner filament. Each micropipette was filled with 3M KCl and had a resistance between 4.7 and 28.2 MΩ when measured in standard F1, with the majority having resistances between 14.0 and 20.0 MΩ. A new electrode was used for each egg. Measurements were made using the GeneClamp 500 (Axon Instruments, Foster City, CA) and a chart recorder. The F1 solution was exchanged with a solution containing the appropriate calcium channel blocker immediately after fertilization had occurred through a vacuum- and gravity-driven flow system that was attached to the low volume chamber (Warner Instruments, RC-10 chamber). This low volume chamber was used to allow for quick exchange of the solutions. After the recovery period following the solution exchange, some of the eggs were removed from the chamber and placed in standard F1 where they were observed to develop through the swimming tadpole stage.

Dejellied eggs

Eggs were collected and dejellied using the 0.3% β-mercaptoethanol in 1/3 modified Ringer (MR) solution. A piece of testis was cut off and macerated in 100 μl of jelly water. It sat in the jelly water for at least 15 min before being used and was kept on ice. The jelly water-treated sperm were then centrifuged for 2 min at 2000 × g before being used to fertilize the egg to separate the sperm from the particulate matter of the testis.

Using EGTA

A stock solution of 250 mM, pH 7.83, was made in distilled water. This was diluted to 5 mM in Ca²⁺-free F1 at pH 7.82. Upon fertilization of the egg, the bath of normal F1 was exchanged for the Ca²⁺-free F1 containing the EGTA.

Fluorescence imaging

The eggs were placed on a Zeiss LSM 410 Invert Laser Scan confocal microscope for all of the experiments described here. The Zeiss LSM 410 Invert was equipped with an argon/krypton excitation laser (Zeiss, 110 V, 25 mW, 488/586 nm) and an ultraviolet laser (Coherent, 220 V, 50 mW, 351/364 nm). We used a 10× Fluar lens (Zeiss, 0.5 N.A.) for all experiments. Filters for calcium-green-1-dextran were a 510-nm dichroic for excitation and a 515–555 nm band pass for emission.

Egg activation by IP₃ injection

Eggs microinjected with fluorescent dye were dejellied using a 2% β-mercaptoethanol solution (pH 8.9), agitated for ∼1 min. The eggs were then rinsed three times in MR pH 6.5 followed by three rinses in MR pH 7.8. Eggs were placed on the confocal stage and impaled with a micropipette containing 10 μM IP₃. After determining that the impalement did not activate or otherwise damage the egg, the IP₃ was injected while recording images.

MODEL AND SIMULATIONS

Model of calcium handling

The model of calcium handling that we use here is an extension of the model used in the earlier work on fertilization waves in Xenopus by our group (Wagner et al., 1998). It is based on the assumption that the dominant handling mechanisms for intracellular Ca²⁺ are IP₃-sensitive channels and SERCA pumps in the ER. We chose parameter values to account for the experimentally observed bistability of calcium handling system and observed wave speed. The kinetic scheme of regulation of the IP₃ receptor by calcium and IP₃ is based on the De Young-Keizer model (De Young and Keizer, 1992) as simplified by Li and Rinzel (Li and Rinzel, 1994). In this scheme IP₃ works as a permissive switch. Calcium opens the channel when it binds to the activating site (fast) and causes it to close again by binding to an inhibitory site (slow). Here we have extended the earlier model by including an equation that describes the dynamics of calcium concentration within the ER. We obtain the following set of equations for calcium concentration:

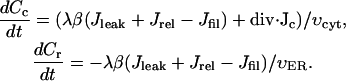(1a)

And the equation for dynamics of uninhibited channels:

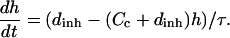(1b)

Here C_c and C_r denote cytoplasmic and ER calcium concentrations, respectively. J_rel is the rate of calcium release into the cytoplasm and J_fil is the rate at which calcium is being moved back into the ER by SERCA pumps. λ scales the density of channels and pumps in the ER membrane and β is the fraction of calcium that remains free (not bound to buffers). These rates are related to the unit of total intracellular volume. To account for the fact that only part of total egg volume is available to calcium in each compartment (the cytoplasm and the ER) we normalized the source terms in Eqs. 1a and 1b by the fractions of intracellular volume occupied by these compartments: υ_cyt and υ_ER respectively. Here we assume that υ_cyt + υ_ER = 1. J_c is the diffusion flux of Ca²⁺ in the cytoplasm. Finally, h is the fraction of channels that are not inhibited by calcium, h_∞ is its equilibrium value at a given calcium concentration, and τ is time constant of inhibition. Discussion of the specific form of these terms is provided in Appendix 1. Here we only note that most of them depend on IP₃ and Ca²⁺ concentration in a nonlinear fashion. The parameters of the calcium-handling model are given in Table 2.

TABLE 2.

Parameters of calcium handling model

dI	Dissociation constant for IP3 binding site	0.025 μM
dact	Dissociation constant for activating Ca2+ binding site	1.2 μM
dinh	Dissociation constant for inhibiting Ca2+ binding site	4.0 μM
vrel	Ca2+ release rate constant	1.0 s−1
vL	Leak rate constant	0.0005 s−1
Vmax	Maximum pump rate	0.12 μM/s
kP	Michaelis constant for the pump	0.4 μM
λ	Scaling parameter for density of pump and channels	30.0
β	Fraction of Ca2+ that is free	0.02
τ	Inhibition time constant	100 s
D0	Effective diffusion constant of Ca2+	40 μm2/s

Model of IP₃ metabolism

In this study we have integrated a realistic model of IP₃ metabolism into our simulation framework for the first time. This model is based on a mechanism in which IP₃ is generated by phospholipase C (PLC) and degraded by two parallel pathways: dephosphorylation to IP₂ by 5-phosphotase and phosphorylation to IP₄ by 3-kinase. This mechanism is based on a study of IP₃ metabolism in Xenopus oocyte (Sims and Allbritton, 1998). This study shows that under the conditions of low [IP₃] (∼100 nM) and [Ca²⁺] > 1 μM, phosphorylation is the major pathway of IP₃ removal, with a half-life time of ∼60 s. On the other hand, when the concentration of inositol trisphosphate is high (>8 μM), the second messenger is primarily removed by dephosphorylation by 5-phosphatase. At low [IP₃] and low [Ca²⁺] (<400 nM), both pathways remove approximately equal amounts of IP₃.

The Xenopus egg can also exhibit calcium wave propagation in response to other stimuli besides sperm (e.g., triggered by the injection of a bolus of calcium). Because IP₃ works as a permissive switch of calcium channels we assume that there is a background level of IP₃ present in the egg before fertilization. We have measured the total average amount of IP₃ in 20 unfertilized eggs and calculate that this would result in an average cytoplasmic concentration of around 0.3 μM (Snow et al., 1996). In our model we have used a basal IP₃ level of 0.1 μM and assume this level results from the balance between production and degradation of the second messenger in the unfertilized egg. Our model also allows for additional local production of IP₃ near the site of fertilization. Finally, IP₃ is diffusing within the cytosol. The resulting equation for IP₃ dynamics is the following:

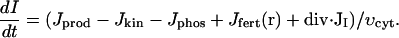(2)

Here I denotes IP₃ concentration, J_prod is the stationary rate of IP₃ production, J_kin and J_phos are rates of its degradation by kinase and phosphotase pathways respectively. J_fert(r) is the additional source of IP₃ in the vicinity of the fertilization site. The latter term is spatially dependent and quickly declines with the distance, r, from the fertilization site. Derivation and specific form of different terms in Eq. 2 are given in Appendix 2. The parameters of the IP₃ metabolism model are given in Table 3.

TABLE 3.

Parameters of IP₃ metabolism model

Vmphos	Maximum rate of 5-phosphotase	0.02 μM/s
KMphos	Michaelis constant of 5-phosphotase	30.0 μM
Vmkin1	Maximum rate of Ca2+-free form of 3-kinase	0.002 μM/s
KMkin1	Michaelis constant of Ca2+-free form of 3-kinase	2.5 μM
Vmkin2	Maximum rate of Ca2+-bound form of 3-kinase	0.007 μM/s
KMkin2	Michaelis constant of Ca2+-bound form of 3-kinase	0.4 μM
dkin	Dissociation constant of Ca2+ binding site on 3-kinase	0.1 μM
DI	IP3 diffusion constant	300 μm2/s
Iss	Basal concentration of IP3	0.12 μM
Jmax	Maximum IP3 production rate at fertilization site	0.06 M/s

Sperm-factor

Part of our modeling study investigates the hypothesis of a sperm-factor—a soluble, diffusible molecule that is capable of activating Ca²⁺ release. Little is known about the nature of this sperm-factor or about the specific mechanism by which it activates calcium release. Therefore, we assumed in our model that its mode of action is similar to that of IP₃ and it binds to the receptor and works as a permissive switch for CICR. We also assume that binding to receptors does not affect its diffusion significantly. Therefore, the sperm-factor concentration is governed by a simple diffusion equation:

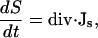(3)

where S is the concentration of the sperm-factor.

Structure of the egg

In our model we include some elements of the internal anatomy of the egg. At this stage we only consider distinct properties of the cortical region, but eventually other heterogeneities such as animal-vegetal gradients in yolk concentration will be included. Our assumptions concerning the properties of the cortical region are based upon a number of experimental observations: 1), Electron microscopy has indicated that the cortical ER becomes about twofold more concentrated in the cortex of the egg than deeper in the egg after maturation (Campanella et al., 1984; Gardiner and Grey, 1983). 2), Ca²⁺ imaging studies have indicated that the peak [Ca²⁺]_i during the wave is nearly twice as high in the cortex as it is deep in the cytoplasm (Fontanilla and Nuccitelli, 1998). This concentration difference may result from a combination of factors, including the higher density of ER containing Ca²⁺ channels and pumps involved in calcium handling in the cortical region. Our preliminary simulations with the simplified “point system” show that although increasing channel density leads to a sharper rise in calcium concentration, this factor alone is not sufficient to account for the higher peak calcium concentration as observed in the experiments. Thus, in our model we have incorporated a spatial dependence of the volume fraction taken by the ER and density of IP₃ receptors—assuming that they may be higher in the layer adjacent to the plasma membrane.

We use functions 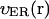and 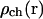to describe this dependence. Both functions remain nearly constant within the deep parts of the egg but rise exponentially near the plasma membrane. Both are scaled by the same factor ζ_ER:

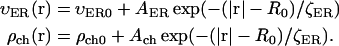Here 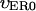and 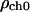are the values deep within the egg, ζ_ER = 10 μm, A_ER and A_ch are the relative maximum elevations in the ER volume fraction and channel density, R₀ is egg radius. We will also keep in mind that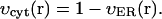

Another type of heterogeneity pertains to the diffusion of calcium. Ca²⁺ binds to a number of mobile and immobile buffers within the cell cytosol. It was shown that its diffusion under such conditions may be approximately described by a regular diffusion equation with an effective diffusion constant. This constant is ∼100 times smaller than that measured in water (Allbritton et al., 1992). As expected, the effective rate of calcium diffusion depends on types and concentrations of buffers (mobile or immobile). It is known that in the cortical region of the Xenopus egg there is a high density of cytoskeletal proteins and cortical granules, both of which serve as immobile buffers of cytosolic calcium. Therefore, we assume that these proteins may contribute to the lowering of the effective diffusion constant for calcium near the plasma membrane. In our model this spatial dependence is given by the expression:

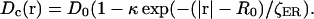Here D₀ is the effective diffusion constant for calcium deep within the egg and κ is the maximum value of the relative change in calcium diffusivity. For the sake of simplicity we assumed that this dependence is scaled by the same space factor, ζ_ER, as the ER distribution. Structural parameters of the egg are given in Table 4.

TABLE 4.

Structural parameters of the egg

υER0	ER volume fraction at the center of the egg	0.2
AER	Maximum increase in the ER volume fraction in the cortical region	0.26
ρch0	IP3Rs density at the center of the egg (arbitrary units)	1.0
Ach	Maximum elevation in the IP3Rs density in the cortical region (arbitrary units)	1.3
ζER	Width of the cortical region	10 μm
κ	Relative change in Ca2+ effective diffusion constant in the cortical region	−0.5
R0	Egg radius	500 μm

Simulations

In the course of our work we used two sets of simulations. One was done with the so-called point system model in which diffusion terms were omitted. This model was further simplified in the following ways. First, due to the conservation of the total amount of calcium in the point system, we have eliminated the equation for the ER calcium concentration. Second, in these simulations we were only interested in the first few seconds of the evolution of the system. Because IP₃ does not change significantly during this time period we treated it as a steady parameter. Such reduction allowed us to represent the system's behavior on a two-dimensional phase plane. The resulting two ordinary differential equations (ODE) were integrated using XPP software (Emertrout, http://www.math.pitt.edu/bard/xpp/xpp.html). We have chosen the Runge-Cutta method with a time step 0.05 s.

Three-dimensional calculations

For three-dimensional (3-D) calculations we have used our full model. Symmetry considerations were used to reduce the amount of computer time needed. There is not much known about the effect of animal-vegetal asymmetry on wave propagation. Thus we assumed that before fertilization the egg is spherically symmetrical. Fertilization destroys spherical symmetry but conserves rotational one with the axis coming through the site of fertilization and center of the egg. We have rewritten grad and div in cylindrical coordinates and eliminated angular dependence terms. Therefore, in terms of a required computational power our model is equivalent to a two-dimensional simulation in a semicircle although physically it represents the 3-D egg. We have used explicit forward Euler method for integrating this system. The equation solver was written in C++ using Overture framework (Brown, Henshaw: http://www.llnl.gov/CASC/Overture/). This software package also provides a generator for chimera grids and build-in capabilities for interpolating solutions between component grids. In our simulations we used a chimera grid that consists of a rectangular piece for the internal parts of the egg and a circular annulus for the periphery. Simulations were run under Linux on a 450-MHz Intel Pentium II processor. We used 0.07 s for a time step and 5 μm spatial resolution.

RESULTS

Experimental observation of fertilization waves

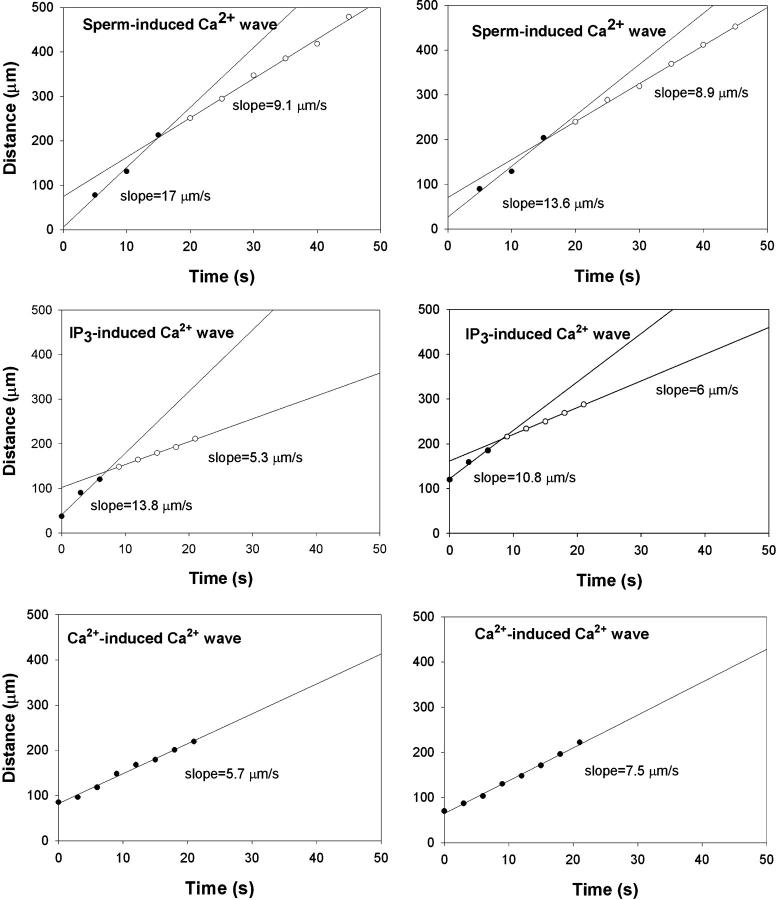
We have activated the Ca²⁺ wave in mature frog eggs by three different methods: fertilization, IP₃ injection, and inducing a Ca²⁺ leak (Fig. 1). We carefully measured the initial propagation velocity of the waves triggered by each of these stimuli (Fig. 2). We found that both the sperm-induced and IP₃-induced Ca²⁺ waves exhibited a rapid initial tangential cortical velocity (13 ± 1.2(5) and 12.3 ± 2.1(2) μm/s [mean±SE(N)], respectively) that then slowed after the first 10–15 s, whereas the Ca²⁺-triggered Ca²⁺ wave appeared to have a single, fairly slow tangential velocity (6.6 ± 0.7 μm/min [mean±SE, n = 5]). Quantification of these waves shows that after the initial fast spread, the speed of wave propagation along the cortex is only marginally higher than that of propagation through the center. We now believe that such a reduction in wave speed can be explained by a change in the mechanism from propagation driven by diffusion of IP₃ to that driven by diffusion of calcium. We discuss this further in the last section of the paper.

FIGURE 1.

Time sequence of confocal images of Ca²⁺ wave initiation using a 40-μm thick optical section. Albino Xenopus eggs were injected with calcium green-dextran and activated by sperm (top), IP₃ microinjection (middle) or Ca²⁺ leak (bottom). Arrows mark the leading edge of the Ca²⁺ wave. Both fertilization and the microinjection of IP₃ produced a Ca²⁺ wave that traveled faster during the first 10–15 s than waves triggered by a Ca²⁺ leak.

FIGURE 2.

Tangential spread of [Ca²⁺]_i wave over time. Two typical results are shown side by side for each wave type. The data for sperm-induced and IP₃-induced waves are best fit by two straight lines of different slopes or velocities. Early time points (filled circles) have a steeper slope or higher velocity than later time points (open circles). In contrast, Ca²⁺-induced Ca²⁺ wave propagation is best fit with a single straight line of lower slope or velocity (bottom two examples).

To quantify propagation of fertilization Ca²⁺ waves we measured the position of the wave front at different times. We took these measurements in two directions: 1) along the cortex, tangent to the surface and 2) in the direction along the normal to the surface at the site of fertilization. Then we plotted the tangential measurements versus time in Fig. 2 because many of these displayed two propagation rates. Initially the rate of spread of calcium release tangentially along the cortex is much faster than the speed of the subsequent wave (13 vs. 6 μm/s). In contrast, the propagation in the normal direction is somewhat delayed and slower in the first 30–50 s (3.4 ± 0.5(7) μm/s) and never displayed two slopes. The combination of these two factors gives the fertilization wave in the Xenopus egg its distinct concave shape.

One concern about these measurements of the propagation in the normal direction is that the fluorescent signal will be attenuated as it passes through the thicker cytoplasm on route toward the center of the egg. The spherical shape of the egg visualized on an inverted microscope requires that the epifluorescent signal traverse a greater amount of cytoplasm as the wave moves from the periphery toward the egg center. To determine how deep into the cytoplasm we are able to detect fluorescence, we placed the tip of a micropipette at the center of an egg and injected a 15 nl droplet of Alexa fluor 594 hydrazide (50 mM). One would predict that this amount of dye would initially form a sphere with a 150-μm radius, but in fact the dye tends to move along the outside of the glass pipette, forming a cone shape that is visible in Fig. 3 D. We were unable to detect the pipette at the center of the egg before or just after injection (Fig. 3). However, dye became visible just after injection at ∼360 μm from the edge of the egg. This would correspond to a cytoplasmic path length of 550 μm through which the fluorescent signal passed. Within 22 ± 3 (SE, N = 5) s after injection the dye became visible at the center of the optical section of the egg. Given its molecular weight of 759, its diffusion constant in water would be ∼2 × 10⁻⁶ cm²/s and the dye would be expected to diffuse by no more than 150 μm in a 20-s interval. This is an upper limit because the egg cytoplasm is much more viscous than water. Given the 600 μm radius of the egg, this observation implies that signals as deep as 450 μm from the egg's surface can be detected in our system using a very bright fluor at 50 mM. Because the injected Ca²⁺ green-dextran used was 10 mM and diffused throughout the egg to a final concentration of 100 μM, we would not expect to be able to detect the signal from this dye as deep as that from 50 mM Alexa. However, we believe that the signal we observe is representative of Ca²⁺ changes at least 300 μm below the surface. Observing a spherical egg on an inverted microscope, fluorescence from a horizontal plane passing through the center of the egg will pass through 300 μm of cytoplasm when the wave has traveled 80 μm inward from the plasma membrane. Therefore, Ca²⁺ waves propagating into the cytoplasm from the plasma membrane should be reliably detected within 80 μm of the plasma membrane. This means that our conclusion regarding the initial velocity profiles tangential and normal to the plasma membrane is reliable. It also raises the question of what we are measuring when we see the wave travel across the egg. Because we are not able to detect light emitted from cytoplasm deeper than 300 μm, we must be detecting fluorescence emitted from an outer shell of cytoplasm ∼300 μm thick.

FIGURE 3.

Microinjection of a 10 nl droplet of 50 mM Alexa fluor 594 into the center of a Xenopus egg. The dye is not visible in the center of the egg but can be detected after diffusing for 20 s.

Preliminary modeling study using a point system model

We began our modeling study by investigating the behavior of a “point system.” Such a simplified model describes a well-stirred medium with no diffusion so equations are reduced to the set of ODEs. Although one obviously cannot observe any spatial effects such as a wave in such a system, it is a very useful approximation for a preliminary study. First, it allows us to illustrate how spontaneous Ca²⁺ release can be triggered. Second, it helps to estimate the values of parameters that are needed for it, therefore reducing the number of costly simulations using a full-fledged spatial model. Here it is also convenient to treat the IP₃ concentration as a control parameter rather than as a dynamic variable. This way the model is reduced to two equations and its behavior can be easily analyzed on a phase plane.

Phase diagrams

A convenient way to represent the behavior of a two-component dynamic system is by way of a phase diagram because the state of such a system is fully defined by the values of its two dynamic variables (Fig. 4). In our case, these variables are the calcium concentration (abscissa) and the fraction of uninhibited IP₃ receptors (ordinate). As values of these variables change over time in the course of Ca²⁺ release, consecutive states of the system form a curve on this plot called a “phase trajectory” (thick lines). These trajectories are essentially parametric representations of the system's dynamics.

FIGURE 4.

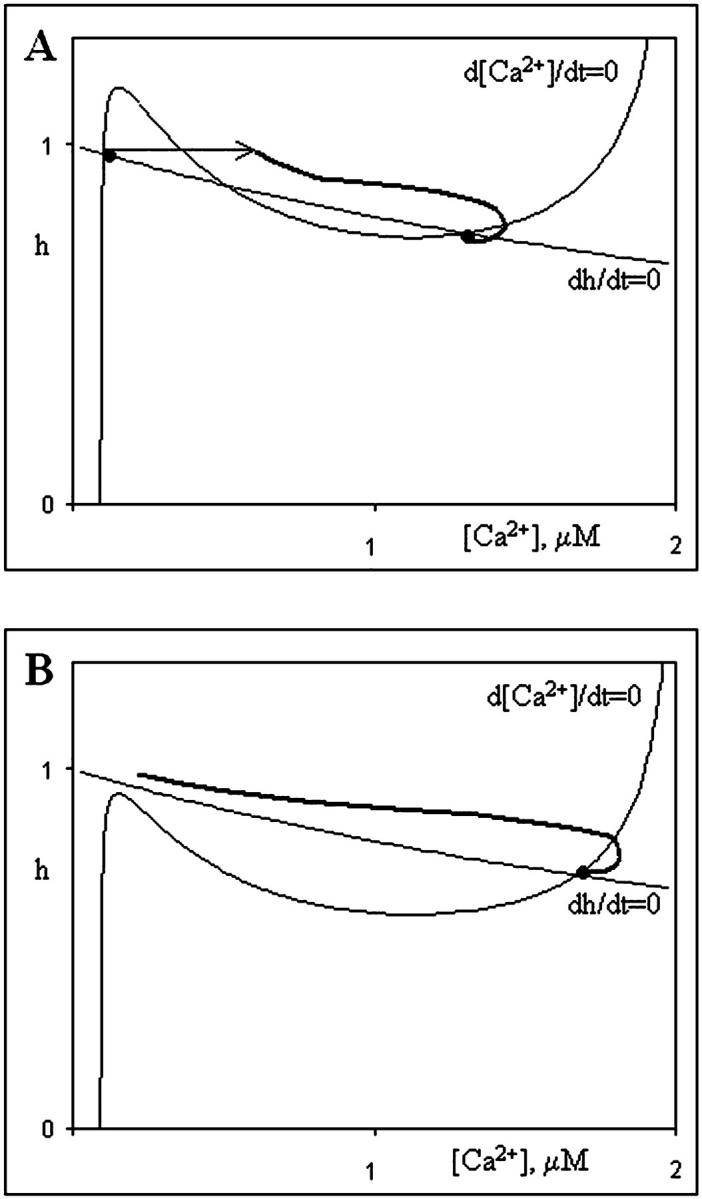
Nullclines of the simplified point system and two scenarios of wave initiation. a) Calcium release is initiated by a perturbation, such as Ca²⁺ injection. b) Shift in parameters (increase of IP₃ level) leads to the loss of low-calcium steady state. Calcium concentration inevitably rises to attain the only remaining high-calcium steady state.

An additional feature of a phase diagram is the depiction of nullclines, representing the points on the phase diagram for which the rate of change for a given variable is equal to zero because the right side of the corresponding differential equation is zero at those points. The intersection of two nullclines corresponds to a steady state where neither variable changes. Such a steady state can be either stable or unstable with respect to a small perturbation so perturbation analysis is employed to determine stability.

Fig. 4 shows phase diagrams for possible scenarios of Ca²⁺ signal initiation that correspond to different hypotheses. In this simplified system, the concentration of IP₃ is clamped at 100 nM and we draw nullclines and phase trajectories. The N-shaped curve corresponds to points where d[Ca²⁺]/dt = 0 and the monotonically decreasing curve corresponds to dh/dt = 0. In Fig. 4 A nullclines intersect at two points that correspond to steady state. Therefore the system is bistable. The first steady state corresponds to low- and the second to high-calcium concentrations. Both steady states are stable with respect to small perturbation. If a relatively large (superthreshold) perturbation is applied while the system is in the low-calcium state (Fig. 4 A, thin arrow), the calcium concentration continues to rise (thick solid line) until it reaches the high steady state value. Such a perturbation mimics an injection of external Ca²⁺ into the egg.

The other two initiation scenarios can be represented by the shift of parameters near the site of fertilization. Both the action of a putative activator and a rise in IP₃ concentration leads to a higher fraction of channels available for calcium release from the ER. The bulk effect of these changes is an increase in Ca²⁺ release flux (J_rel). In our simplified point system model they are indistinguishable. Both scenarios result in a shift of the nullclines, as shown on Fig. 4 B. The low calcium steady state is lost when the N-shaped nullcline (that corresponds to cytosolic calcium dynamics) shifts downward. In its new position it has only one intersection with the other nullcline, and the system therefore has only one steady state (high calcium). Inevitably, the Ca²⁺ concentration rises to attain this steady state (thick solid line). Our next task is to incorporate the three proposed mechanisms into our full 3-D model of the Xenopus egg.

Fertilization waves in 3-D computer simulations

We have investigated the three proposed initiation mechanisms with our 3-D model of the Xenopus egg Ca²⁺ wave. Simulation results were then compared with the experimental measurements of wave dynamics to find which of them provided the best fit.

Ca²⁺ bomb hypothesis

When we introduce a bolus of Ca²⁺ in our model that is sufficient to elevate the local concentration to a 1μM level within a semispherical area with a 10 μm radius adjacent to the boundary (Fig. 5 a), the wave retains the convex shape of the initial perturbation for a relatively long time due to the relatively slow diffusion rate of Ca²⁺. It does not spread rapidly in the cortex as IP₃ does. Only later does it develop a concave profile apparently due to heterogeneity of the egg. Comparing this model with experimental observations we find that it predicts the slower initial wave speed quite well but does not predict the overall spatial pattern, which looks quite similar to both sperm- and IP₃-induced release (Fig. 1).

FIGURE 5.

Local injection of (a) calcium (1 μM) and (b) slow diffusing sperm-factor (D = 30 μm²/s) initiate calcium waves in computer simulations. They fail, however, to reproduce fast initial spread of calcium release along the egg cortex as seen in the experiments (compare to Fig. 1, top).

Calcium channel blockers

We conducted another experimental test of the Ca²⁺ bomb hypothesis. If Ca²⁺ influx through a sperm channel is occurring after sperm-egg fusion, the blockage of Ca²⁺ channels or removal of external Ca²⁺ should reduce this influx and the local increase in [Ca²⁺]_i. Because the fertilization potential is generated by a Ca²⁺-gated Cl⁻ channel, it too should be disrupted by reducing Ca²⁺ influx. We fertilized the eggs in normal F1 medium and as soon as we could be sure that the fertilization potential had begun its upward rise, we changed the medium in the chamber holding the eggs to one containing either a Ca²⁺ channel blocker or Ca²⁺ chelator. However, we observed no change in the fertilization potential of the Xenopus egg upon addition of these channel blockers, indicating no change in Cl⁻ channel conductivity had occurred (Fig. 6; Table 1). This suggests that Ca²⁺ influx is not required for Cl⁻ channel gating as early as we could completely change the medium (ranging from 36 to 72 s after fertilization).

FIGURE 6.

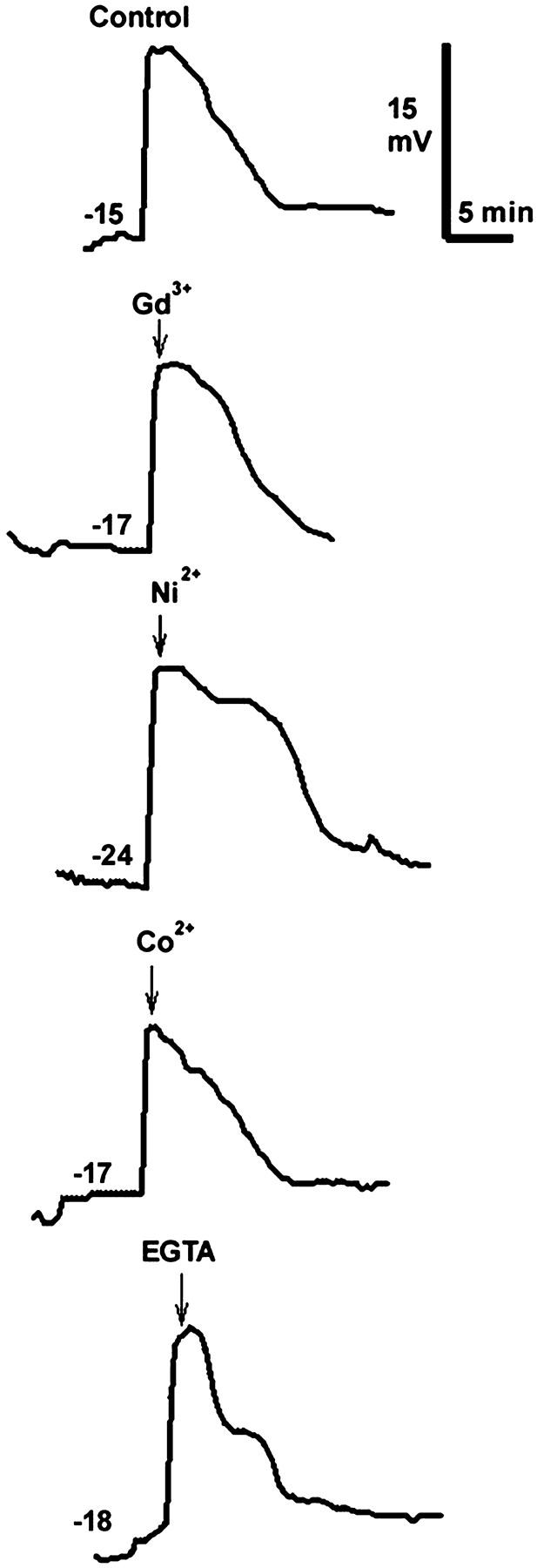
Typical fertilization potentials measured in Xenopus eggs under different conditions. The resting membrane potential (mV) before fertilization is indicated on each recording and the voltage and time scales are on the upper right. At the time indicated by each arrow, the medium containing the indicated blocker or chelator completely replaced the F1 medium in the chamber holding the egg (100 μM Gd³⁺, 1 mM Ni²⁺, and Co²⁺, 5 mM EGTA).

TABLE 1.

Timing of fertilization and medium changes

	Minutes between insemination and fertilization (mean ± SE (N))		Minutes between fertilization and medium change (mean ± SE (N))
Ion added	Jellied	Dejellied	Jellied	Dejellied
100 μM Gd3+	8.2 ± 0.8(7)	5.2 ± 0.4(3)	1.0 ± 0.2(7)	0.9 ± 0.2(3)
1 mM Ni2+	5.7 ± 0.3(6)	3.4 ± 0.8(3)	0.8 ± 0.2(6)	0.6 ± 0.07(3)
1 mM Co2+	6.5 ± 1.4(6)	6.3 ± 3.1(3)	0.8 ± 0.2(6)	1.2 ± 0 (2)
5 mM EGTA	–	4.2 ± 1.0(4)	–	1.4 ± 0.2(4)

We considered the possibility that the jelly layers might impede access of these blockers to the plasma membrane and repeated the experiments using dejellied eggs. The calcium channel blockers also had no effect on the fertilization potential of the fertilized, dejellied eggs (Table 1).

Chelating external calcium

In addition to using calcium channel blockers to test the role of external calcium on the fertilization potential of the Xenopus egg, the calcium chelator, EGTA, was used. To assure that EGTA could rapidly buffer external calcium, the jelly layer was removed from the egg's surface before impalement with the microelectrode. A procedure similar to the one above was used, with the exception of the use of 5 mM EGTA rather than calcium channel blockers during the solution change. As with the calcium channel blockers, EGTA did not change the fertilization potential of the fertilized egg (Table 1). The membrane potential trace for the EGTA trial does not deviate much from that of the control (Fig. 6).

Sperm-factor

Two popular hypotheses have been proposed for how a diffusible sperm-factor could activate eggs: 1), It could act directly as an IP₃R activator; or 2), It could act indirectly to lead to the production of IP₃, such as PLC would. When the introduction of a small spherical bolus of IP₃R activator is modeled we see yet a different predicted Ca²⁺ wave shape (Fig. 5 b). Here we introduce a bolus of the same size and position as the bolus of calcium in the previous example and the initial concentration of activator within the bolus was 10,000 times higher than its assumed affinity for the IP₃ receptor. The choice of the initial concentration can be justified as follows. Because the initial cortical spread of calcium signal extends to ∼150 μm, we assume that whatever causes it should still be effective at such a distance from the site of fertilization. On the other hand, the size of the initial bolus should be much less than the sperm size (∼15–20 μm long for Xenopus). If activator is to reach physiologically active levels within 150 μm bolus, then its initial concentration should be a few thousand times higher. Simulations show, however, that although sperm-factor was allowed to diffuse freely within the cytoplasm and its initial gradient was huge, it failed to spread fast enough to trigger fast cortical propagation observed in the experiment. We believe that the reason for this is a relatively low diffusion constant (we assumed it to be 40 μm²/s given a molecular weight of 30 kD).

The second popular hypothesis is that the sperm factor is indeed phospholipase C, which would generate IP₃ by hydrolyzing PIP₂. This mechanism could produce a wave shape similar to that resulting from IP₃ production (see below) assuming that the rate of hydrolysis were as fast as the endogenous rate in the egg. However, our model does not produce the same rapid initial tangential wave because we would expect there to be a delay between sperm-egg binding and Ca²⁺ release due to the diffusion time for PLC to get into the egg (Fig. 5 b). Therefore we think it is unlikely that this mechanism is operating in the frog egg.

IP₃ production

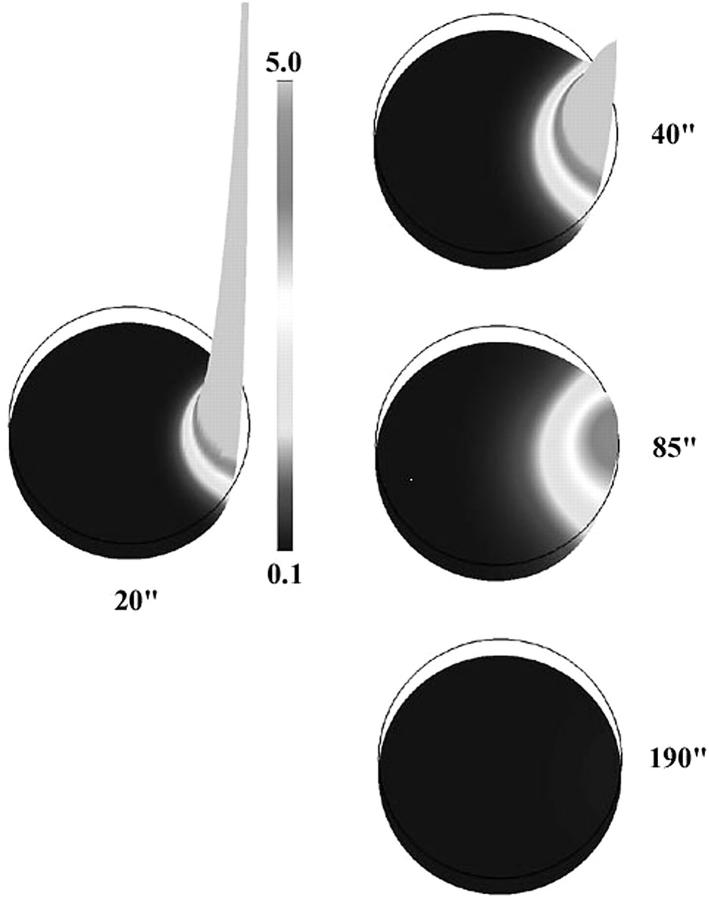
The only mechanism of the three most popular candidates that reproduces the rapid tangential cortical spread is the local production of IP₃ at the fertilization site. This allows rapid production of a gradient in [IP₃]. In our simulation IP₃ was produced for only 3 s after fertilization. The rate of production was such that the resulting concentration at the fertilization site briefly reached 1 mM (8000 times its assumed affinity to the receptor). Due to high diffusivity (D_IP3 = 300 μm²/s in our simulations) and steep initial gradient, this second messenger rapidly spreads over a larger area of the egg (Fig. 7). The combination of the elevated IP₃ level and the high density of Ca²⁺ channels in the ER concentrated in the cortical region creates conditions for the very fast spread of calcium release in a large sector of this region (Fig. 8). The initial propagation of the calcium wave here is essentially driven by fast diffusion of IP₃ rather than calcium. As we mentioned above, the latter is rather slow due to the presence of multiple calcium binding proteins in the egg cytoplasm. This release is triggered by the mechanism plotted in Fig. 4 B.

FIGURE 7.

Simulated IP₃ profile for the initiation scenario shown on Fig. 8. During first few seconds there is a very high and narrow peak of IP₃ concentration (in μM) near fertilization site. As it smoothes out due to diffusion and degradation larger area of elevated IP₃ appears (40–90 s). Eventually, IP₃ returns to its basal level (190 s).

FIGURE 8.

Computer simulations of the wave initiated by rapid production of IP₃ near fertilization site. Initial rate of production is 0.06 M/s. Production decays exponentially over 3 s and is spatially limited to a 20 μm circular area on the plasma membrane. The initiation dynamics of this wave appears to be similar to that observed in the experiment. As on Fig. 1, zero time corresponds to the moment just before the first appearance of calcium release. This appears 10 s after start of IP₃ production.

DISCUSSION

New findings

Careful analysis of the initial stages of [Ca²⁺]_i wave propagation reveals a fast initial tangential wave propagation velocity in sperm-induced and IP₃-induced but not Ca²⁺-induced waves. We have developed a refined computer model of the fertilization-induced Ca²⁺ wave in the frog egg that has a number of new features that significantly distinguish it from the model used in our previous work (Wagner et al., 1998). These features include a three-dimensional spatial domain, a dynamic equation for calcium concentration in the ER, a dynamic equation for [IP₃] that includes degradation by two different mechanisms, and finally, a heterogeneous distribution of the ER, IP₃ receptors, and calcium buffers. Using this improved model, we have generated computer simulations of these waves that are compared to quantitative experimental measurements of fertilization calcium waves. By carefully comparing the experimental data with these improved models, our simulations show that only the local production of IP₃ near the site of fertilization can reproduce the experimentally observed calcium dynamics. Therefore we suggest that this is the most likely mechanism of wave initiation.

Initial phase wave propagates faster than subsequent trigger wave

In the proposed mechanism, the fast initial cortical spread that is often observed in the experiments can be attributed to a phase wave. Such a wave takes place due to the combination of two factors. First, calcium release is enhanced within a large area by rapid spread of highly diffusive IP₃. Second, the cortical region has a high density of IP₃ receptors and therefore, is more sensitive to the increase in IP₃ level than internal parts of the egg. As a result, in a subcortical layer where these two factors overlap, the low calcium steady state disappears and calcium level inevitably rises until it reaches a high calcium steady state. The phase wave occurs because the activation of calcium release is not completely simultaneous. Due to a finite rate of IP₃ diffusion it is slightly delayed in the areas further away from fertilization. Thus, calcium elevation first starts near the fertilization site whereas the phase of the adjacent points further along the cortex is slightly shifted. This creates a fast propagating wave that is observed in the experiments and simulations. Once this wave reaches the region where the IP₃ concentration is not sufficient to trigger spontaneous release, the mode of propagation changes to a much slower trigger wave.

All of our experimental observations and modeling results support local IP₃ production as a crucial step in the initiation of fertilization calcium waves in the Xenopus egg. It is possible however that this is not the only mechanism involved. Although it appears that the calcium bolus and sperm-factor hypotheses alone cannot explain wave dynamics, it is conceivable that they operate alongside an IP₃ mechanism. One possibility, for instance, is that sperm-factor is indeed an active PLC that enhances local IP₃ production. However, recent studies of sperm-egg fusion suggest that Ca²⁺ release occurs before dye can be seen diffusing from the egg into the sperm and are inconsistent with the diffusion of sperm factor into the egg (Nuccitelli, et al., in preparation).

No support for the Ca²⁺ bomb hypothesis

The Ca²⁺ bomb hypothesis proposes that the sperm introduces sufficient Ca²⁺, either from intracellular stores or through ion channels in the sperm's plasma membrane, to trigger Ca²⁺-induced Ca²⁺ release from the ER. None of our results here supports that hypothesis. Imaging eggs activated by Ca²⁺ influx reveals very slow tangential initiation velocities that do not resemble sperm-induced waves (Figs. 1 and 2). Modeling predicts similar slow wave velocities. In addition, our measurements of the fertilization potentials in eggs exposed to Ca²⁺ channel blockers or Ca²⁺ chelators within 50 s of sperm-egg fusion show no change in the Ca²⁺-gated Cl⁻ channels. This suggests that these channels do not rely on Ca²⁺ influx for their activation. However, we cannot rule out the possibility that sufficient influx to trigger CICR occurred during the first 36 s before we could completely change the external medium to block Ca²⁺ influx.

APPENDIX 1: EQUATIONS FOR Ca²⁺ DYNAMICS

Our equations for calcium and channel dynamics are based on the De-Young-Keizer model for gating of the IP₃R by Ca²⁺ and IP₃ (De Young and Keizer, 1992) as simplified by Li and Rinzel (1994). According to this model calcium fluxes between the cytoplasm and the ER can be expressed in the following form:

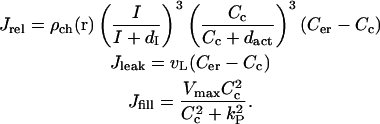(A1)

Here 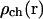is the spatially dependent density of IP₃Rs, d_I and d_act are dissociation constants for IP₃ and activating Ca²⁺ binding sites on IP₃ receptor, v_L is calcium leak rate constant, V_max and k_P are maximum pump rate and Michaelis constant for the pump respectively.

Eq. A1 is based on the assumption that the binding and dissociation of IP₃ and Ca²⁺ are fast compared to changes in calcium and IP₃ concentrations. Therefore, the fraction of receptors that has IP₃ and activating Ca²⁺ bound rapidly adjusts to its equilibrium value for current concentrations of ligands. The third power in calcium release term corresponds to the assumption that it takes three subunits of the receptor to be activated for the channel to open.

Diffusion terms in our equations require special attention. This is due to the fact that we consider heterogeneity of the egg with respect to the distribution of the ER and calcium buffers. We have assumed that the effective diffusion constant for calcium is lower near the plasma membrane where more immobile buffers are present (Eq. 5). In addition to this, calcium diffusion within the cytosol is probably more obstructed where there is more volume taken by the ER. It is not clear what is the actual dependence of the diffusion constant on the volume fraction occupied by the ER, so we will simply assume that this dependence is linear. Therefore, we can write the expression for the diffusion flux of Ca²⁺ in the egg's cytosol:

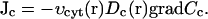(A2)

APPENDIX 2: THE MODEL OF IP₃ DYNAMICS

In our model IP₃ is generated throughout the egg at a constant rate and degraded by two pathways—phosphorylation to IP₄ by 3-kinase and dephosphorylation by 5-phosphotase. In some simulations it can also be generated locally near the site of fertilization. First, we consider degradation pathways. According to Allbritton and co-workers, phosphorylation is a major pathway at physiological levels of IP₃ (0.1–1 μM). The rate of phosphorylation also depends on calcium concentration. Here we assume that both the maximum rate and Michaelis constant of 3-kinase change upon binding Ca²⁺. Assuming also that calcium binding to the enzyme is fast compare to rate of changes in calcium concentration we arrive at the following expression for the rate of phosphorylation:

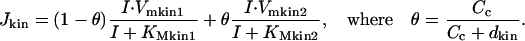(A3)

Here V_mkin1 and V_mkin2 are maximum rates of phosphorylation by calcium-free and calcium-bound forms of 3-kinase respectively, K_Mkin1 and K_Mkin2 are corresponding Michaelis constants. θ is the fraction of the kinase in calcium-bound form and d_kin is the dissociation constant of calcium binding site.

Phosphorylation of IP₃ by 5-phosphotase becomes essential at high (∼30 μM) concentrations of the second messenger and is calcium independent. In our model its rate is given by the expression:

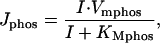(A4)

where V_mphos is the maximum rate of dephosphorylation and K_Mphos is Michaelis constant for 5-phosphotase.

The rate of constant IP₃ production is set in such a way as to equilibrate degradation reactions if both [IP₃] and [Ca²⁺] are at their basal levels. In some simulations we added the extra term for IP₃ production to account for one of the initiation mechanisms. This term is a function of the following form:

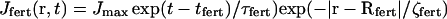(A5)

Here J_max is maximum rate of IP₃ production, t_fert is the time of fertilization and R_fert is the radius vector of fertilization point. This production term quickly declines with time (τ_fert = 2 s) and with distance from the fertilization site (ζ_fert = 10 μm).

Diffusion of IP₃ is treated in a similar way to that of calcium. Unlike calcium however, IP₃ is not buffered in the cytosol so its effective diffusion constant depends only on the cytosolic volume fraction. The diffusion flux J_I in Eq. 6 can be expressed as:

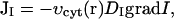(A6)

where D_I is the diffusion constant of IP₃ in cytosol.