Fluctuations and Slow Variables in Genetic Networks

Abstract

Computer simulations of large genetic networks are often extremely time consuming because, in addition to the biologically interesting translation and transcription reactions, many less interesting reactions like DNA binding and dimerizations have to be simulated. It is desirable to use the fact that the latter occur on much faster timescales than the former to eliminate the fast and uninteresting reactions and to obtain effective models of the slow reactions only. We use three examples of self-regulatory networks to show that the usual reduction methods where one obtains a system of equations of the Hill type fail to capture the fluctuations that these networks exhibit due to the small number of molecules; moreover, they may even miss describing the behavior of the average number of proteins. We identify the inclusion of fast-varying variables in the effective description as the cause for the failure of the traditional schemes. We suggest a different effective description, which entails the introduction of an additional species, not present in the original networks, that is slowly varying. We show that this description allows for a very efficient simulation of the reduced system while retaining the correct fluctuations and behavior of the full system. This approach ought to be applicable to a wide range of genetic networks.

INTRODUCTION

The machinery of biological cells consists of an enormous network of molecules interacting with each other in a complex manner. Information is processed through varying the concentrations and localization of these chemical species in response to external and internal stimuli (Bray, 1995). A lot of effort has been devoted to modeling the chemical network of a whole cell (Tomita et al., 1999; Holden, 2002) or some of its subsystems (Hasty et al., 2001) on a computer. A faithful computer model of a cell would have several advantages. On the one hand, it will enhance our understanding of cell function. In the computer model any quantity of interest can be easily observed whereas measuring the same quantity may require painfully complicated experiments in the real system. On the other hand, such a model will be of practical importance in drug development because the reaction of a cell to a putative drug can be tested immediately.

Bulk chemical reactions can be mathematically described by differential equations for the concentrations of the species involved. However, in a cell there is often only a small number of molecules of each kind, e.g., there is only one copy of the DNA for a given gene. This leads to large concentration fluctuations and therefore, the interactions among these molecules occur in a random fashion. There has been considerable recent interest in studying the effect of this intrinsic noise experimentally (Ozbudak et al., 2002; McAdams and Arkin, 1999). Issues of interest include whether such fluctuations, intrinsic to the biological system, can affect the regulation of the production of proteins, degrade the synchrony of the circadian clock, disturb precise cell signals, etc. Thus, a computer model of a cell has to not only describe the concentrations (or average number of molecules) of each species in the cell but also model the fluctuations of the actual numbers around their averages due to the intrinsic stochastic nature of the reactions. An algorithm proposed by Gillespie (1977) is now commonly used to take into account this intrinsic noise that accompanies chemical reactions in a cell.

A numerical description of a stochastic chemical network is achieved by identifying all possible reactions, measuring the reaction rates for all these reactions as well as the initial numbers of molecules of each chemical species, and then applying the Gillespie algorithm to the full set of equations to predict the temporal evolution of the system. However, the number of reactions in a network can be large; the analysis of the lysis-lysogeny pathway of E. coli infected by phage λ requires the values of over 30 reaction constants (Arkin et al., 1998). In addition to the sheer number of reactions, there is a large range of timescales that complicates simulations. Some elementary reactions like the binding or release of a transcription factor to an operator site or the dimerization of some protein occur on timescales of seconds (Arkin et al., 1998). On the other hand, the biologically more interesting reactions like transcription or translation of a gene happen on the timescale of minutes to hours. In practice, this implies that during a simulation of all reactions involved in a network hundreds to thousands of individual fast reactions have to be simulated for each slow reaction. Given that the scientific focus is typically on understanding the network on the timescale of the slow reactions, this can result in a very large computational overhead.

When the underlying biochemical reactions are known, it would be very useful to treat the fast reactions in some effective manner instead of simulating them explicitly, which is computationally time consuming. It is customary to eliminate the reactions that occur on fast timescales, and study the remaining ones on large timescales when the fast ones are in equilibrium. The price to pay is the appearance of effective rate constants known as Michaelis-Menten kinetics and Hill coefficients. In the framework of chemical rate equations, where concentration fluctuations are neglected, the replacement of fast reactions by effective rate constants for the slow reactions is exact in the limit that the timescales of the fast reactions become very short.

Recently, there has been interest in applying and finding effective descriptions of fast reactions in the presence of statistical fluctuations due to small numbers of the molecules involved (Hasty et al., 2000; Kepler and Elston, 2001; Gillespie, 2001). In the framework of small numbers of molecules it is not a priori clear if the effective description of fast reactions in terms of concentration-dependent rate constants for the slow reactions in the spirit of the Michaelis-Menten kinetics and Hill coefficients is still appropriate. Here, we want to study the following question: does the Gillespie algorithm applied to the network of reactions represented by a reduced set of equations give a correct account of fluctuations in the biochemical pathway? If the answer is yes, the stochastic treatment of biologically relevant large systems can be greatly simplified, because in most cases fast and slow reactions coexist. If the answer is no, one has to develop different techniques to eliminate fast reactions in the interest of computational efficiency.

We discuss three self-regulatory networks, two with negative feedback either through protein dimers or tetramers, the other one with positive feedback through protein dimers. We treat in detail the model where the gene product can form dimers that in turn inhibit the transcription of the gene. This model is based on the λ repressor gene cI of phage λ in E. coli, which enables one to give biologically relevant values to the 10 reaction rate constants of the full model. These networks contain fast dimerization (or tetramerization) and DNA binding as well as slow transcription and translation reactions. We find, that the DNA-binding reactions can be well described in an effective Michaelis-Menten way. Eliminating, in addition, the fast dimerization (or tetramerization) reaction leads to an effective reaction rate of the Hill type. We find however that in this case the fluctuations of the effective system are much stronger than the fluctuations of the full system. In the positive feedback case, these strong fluctuations make the system switch between two states. We point out that this misrepresentation of the fluctuations is due to the choice of variables used in the effective Hill system. If the system is to be described on slow timescales, care has to be taken that the concentrations of all species occurring in the effective description are indeed slowly varying quantities. In the case of a dimerization reaction neither the number of monomers nor the number of dimers has this property. We show how a slowly varying variable that is not the concentration of any of the species present in the original model can be introduced and that an effective description using this slowly varying variable indeed correctly reproduces the fluctuations of the full system. This way of proceeding should be applicable to much more general situations than the reactions studied in this paper.

MODELS

Our focus is identifying a correct effective description of fast reactions in genetic networks. We will study this issue using three explicit models that describe the expression of a single protein with feedback. The primary model we study describes a network with negative feedback through dimers as is found, e.g., in the control circuit for the λ repressor protein cI of phage λ in E. coli (Ptashne et al., 1980). We will take advantage of the variety of studies of this specific λ repressor system (Arkin et al., 1998; Hasty et al., 2000; Thattai and van Oudenaarden, 2001) in guiding our choice of biologically reasonable model parameters. This ensures that the problems of some effective modeling methods that we raise are not of a purely theoretical nature but actually are important in biologically relevant parameter regimes. The other two models describe positive feedback through dimers of the protein and negative feedback through tetramers of the protein, respectively.

All three models are generic and similar to those describing real genetic networks and, therefore, developing a faithful yet efficient computational description of these three models by themselves is of practical importance. The fact that our results apply to all three related but different models indicates their generality and their applicability to other genetic networks.

Negative feedback through dimers

The model with negative feedback through dimers found for the λ repressor protein cI of phage λ in E. coli is one of the models studied in (Bundschuh et al., 2003). Thus, we will here only summarize it and refer to (Bundschuh et al., 2003) for the details. The slow reactions of the model are expressed in terms of the free DNA D coding for the protein P to be regulated, the RNA polymerase R, the complex D^* of RNA polymerase bound to the promoter site on the DNA molecule, and the mRNA M. They are transcription, translation, and the decay of the mRNA and of the protein which we describe as

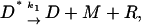(1)

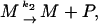(2)

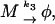(3)

and

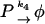(4)

with rate constants k₁, k₂, k₃, and k₄, respectively.

The fast reactions of the model are the formation of the complex between DNA and RNA polymerase

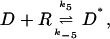(5)

the dimerization of the monomers P into the dimers P₂

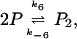(6)

and the binding of the dimer to the operator site on the DNA forming the DNA-dimer complex Q

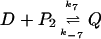(7)

that provides the negative feedback by competing with the RNA polymerase for the binding to the DNA. The forward and backward rates of these three reactions are k₅, k₋₅, k₆, k₋₆, k₇, and k₋₇, respectively. Typical values of the rate constants can be derived from the phage λ system as discussed in (Bundschuh et al., 2003). They are listed in Table 1.

TABLE 1.

Rate constants of the model with negative feedback through dimers

Constant	Rate
k1	0.0078 s−1
k2	0.043 s−1
k3	0.0039 s−1
k4	0.0007 s−1
k5	0.038 s−1 (nM)−1
k−5	0.3 s−1
k6	0.025 s−1 (nM)−1
k−6	0.5 s−1
k7	0.012 s−1 (nM)−1
k−7	0.9 s−1

These rate constants have been derived from the phage λ system in (Bundschuh et al., 2003). Although we do not intend to describe this specific system in detail, the derivation of the rates from a real system ensures that the order of magnitude of the rates is biologically reasonable.

Positive feedback through dimers

Positive feedback is achieved by letting the RNA-polymerase bind only to the DNA-dimer complex Q making the binding of the dimers and the RNA polymerase to DNA cooperative instead of competitive. In terms of the reactions this means that the DNA–RNA-polymerase complex D^* is replaced by the DNA–RNA-polymerase–protein-dimer complex Q^*. Reactions 1 and 5, which involve the complex D^* in the negative feedback case, become

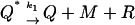(8)

and

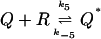(9)

where for simplicity we use the same reaction rates as in the model with negative feedback assuming similar biochemical mechanisms.

Negative feedback through tetramers

If tetramers instead of dimers are responsible for the negative feedback, the dimers P₂ in the model have to be replaced by the tetramers P₄. The two reactions 6 and 7 are replaced by

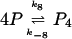(10)

and

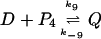(11)

where Q now represents the DNA–protein-tetramer complex with new forward and backward rates k₈, k₋₈, k₉, and k₋₉, respectively. In the absence of experimental data for these rate constants we choose k₈ = 0.000833 s⁻¹ (nM)⁻³, k₋₈ = 1.0 s⁻¹, k₉ = 0.1 s⁻¹ (nM)⁻¹, and k₋₉ = 0.9 s⁻¹ that result in a reasonable equilibrium number of protein monomers and have backward rates very similar to their counterparts in the model with negative feedback through dimers. The forward rates have additional dimensions of concentrations and are thus less likely to be conserved as we exchange tetramers for the dimers.

REVIEW OF MICHAELIS-MENTEN AND HILL KINETICS

We will now describe the traditional way of eliminating the fast reactions from the rate equations. When the number of molecules is large enough, the system is described by the concentrations of all species. We will denote the concentration of a species X by [X]. Later, we will study what happens when the number of molecules is small, and fluctuations are important. We will describe this approach explicitly for the model with negative feedback through dimers and only give the results for the other two models.

Michaelis-Menten kinetics

First, we eliminate the DNA-binding reactions Eqs. 5 and 7. Assuming therefore that they reach equilibrium on short enough timescales one can incorporate them into the transcription reaction Eq. 1. The transcription reaction Eq. 1 can be reinterpreted as an mRNA production reaction

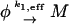(12)

with an effective rate of k_1,eff = k₁[D^*] where [D^*] is the concentration of DNA with RNA polymerase bound to the promoter. Because the RNA polymerase R and the repressor dimer P₂ compete via reactions Eqs. 5 and 7 for binding to the DNA, the concentration [D^*] of DNA with RNA polymerase bound to the promoter depends on the concentration [P₂] of repressor dimers. This dependence can be made explicit by noting that the total concentration [D] + [D^*] + [Q] of DNA in the cell is fixed at C = 1/V ≈ 1 nM where V is the cell volume. This conservation equation can be combined with the laws of mass action of reaction 5, [D][R] = K₅[D^*], and reaction 7, [D][P₂] = K₇[Q], where K₅ = k₋₅/k₅ and K₇ = k₋₇/k₇ are the equilibrium constants of promoter binding and operator binding, respectively. Eliminating [Q] and [D] from the three equations, solving them for [D^*] and multiplying by the raw rate constant k₁ of Eq. 1 yields an effective transcription rate (i.e., rate of Eq. 12)

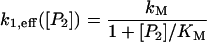(13)

with k_M = k₁C[R]/([R] + K₅) and K_M = K₇([R] + K₅)/K₅. Using the numbers given in Table 1 and the fixed concentration [R] = 30 nM of RNA polymerase (McClure, 1983) yields k_M = 0.00616 nM/s and K_M = 356 nM. An analogous derivation for the model with positive feedback through dimers yields

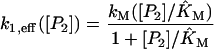(14)

with 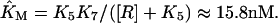For the model with negative feedback through tetramers we have

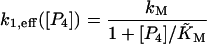(15)

with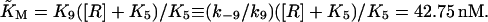

These functional forms are known as Michaelis-Menten kinetics. Thus, we will denote the effective genetic network described by the five reactions Eqs. 2–4, 6, and 12 with the effective transcription rate given by Eq. 13 and its counterparts in the other two models the “Michaelis-Menten systems”.

Hill kinetics

There is still one fast reaction remaining in the Michaelis-Menten systems, namely the dimerization reaction Eq. 6 or the tetramerization reaction Eq. 10, respectively. To eliminate it in the dimer cases we note that protein monomer and dimer molecules are in equilibrium characterized by [P]² = K₆[P₂], where K₆ = k₋₆/k₆ is the dimerization equilibrium constant. Substituting this in the effective rate given by Eq. 13 yields the effective rate

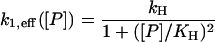(16)

with k_H = k_M and K_H = (K_MK₆)^1/2. With our choice of the rate constants these two parameters take the values k_H = 0.00616 nM/s and K_H = 84 nM. For the model with positive feedback through dimers we get

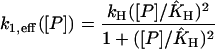(17)

with 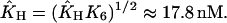In the model with negative feedback through tetramers, the equilibrium constant K₈ = k₋₈/k₈ = 1200(nM)³ of the tetramerization reaction enters and we get

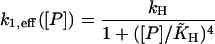(18)

with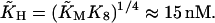

These functional forms are known as Hill kinetics with Hill parameter 2 or 4 as indicated by the square or fourth power of the protein monomer concentration in the denominator, respectively. Therefore, we will denote the effective genetic networks described by the four reactions Eqs. 2–4, and 12 with the effective transcription rate given by Eq. 16, 17, or 18, respectively, the Hill systems.

NUMERICAL COMPARISON OF FULL AND EFFECTIVE SYSTEMS

Method

To investigate the consequences of an effective description of fast reactions, we simulate the full system of reactions as well as the Michaelis-Menten and the Hill system for all three models with the Gillespie algorithm (Gillespie, 1977). The intrinsic quantities the Gillespie algorithm acts on are not the concentrations but the actual numbers of molecules of each species. Instead of rate constants k_i, all reactions are characterized in the Gillespie framework by reaction probabilities c_i per unit time and per molecule. These are related to the rate constants k_i by powers of the volume V of the system where the exponent of V depends on the reaction (Gillespie, 1977). Because the volume V of an E. coli cell can be conveniently written as V = 1 (nM)⁻¹, the actual numerical values of the reaction probabilities c_i in the Gillespie framework are identical to the numerical values of the reaction rates k_i as long as the latter are expressed in nM. At the same time concentrations measured in nM also directly correspond to the number of molecules of the respective species in an E. coli cell and equilibrium constants are converted from one system to the other by dropping or adding the unit nM. To distinguish between concentrations of a species measured in nM and the actual number of molecules of this species we will denote the concentration of species X by [X] and the number of molecules by the corresponding lower case letter x.

For all three models described by the three systems of reactions (full, Michelis-Menten, and Hill) the Gillespie algorithm was used to simulate 10,000 independent time courses of the genetic network starting with a single DNA molecule and 30 molecules of RNA polymerase (McClure, 1983). Each of the 10,000 instances was run until 50,000 s of reaction time were simulated. By observing the number of proteins p as a function of reaction time, it was ensured that the system is well in the stationary state after this time (as also suggested by the slowest characteristic time 1/k₄ ≈ 1500 s of the system.) The 10,000 independent numbers of protein monomers at the end of each run approximate the distribution P(p) of the number p of proteins in the stationary state.

Distribution of protein monomer numbers

Histograms of the distributions P(p) are shown in Fig. 1. Visual inspection of these histograms already reveals the general result: For all three models the full system and the Michaelis-Menten system produce indistinguishable distributions whereas the Hill systems consistently show distributions with much larger fluctuations than the full system. This overestimation of the fluctuations becomes especially blatant for the model with positive feedback: The model with positive feedback represents a genetic switch that can take on two distinct equilibrium values of the number of monomers. Due to the absence of a basal transcription rate in our models, one of these equilibrium values is p = 0 and the other is some positive equilibrium value p = p₁. If the protein number ever reaches p = 0 and the number of mRNA molecules vanishes at the same time, no mRNA and thus no new proteins can be produced anymore and the system remains in the state p = 0 forever. Our initial conditions are chosen in the vicinity of p₁. The simulation of the full system (and the Michaelis-Menten system) show that in none of the 10,000 independent time courses the monomer number reaches the other equilibrium value p = 0. In contrast to that, the inflated fluctuations in the Hill system drive the system away from the equilibrium value p₁ to the state p = 0 in 283 of the 10,000 independent simulations which appear as the peak at p = 0 in the corresponding histogram in Fig. 1. Because the fluctuations induce a fixed probability per unit time that the system switches from the state around p = p₁ to the state at p = 0 the fraction of independent simulations ending at p = 0 increases as longer time courses are simulated.

FIGURE 1.

Histograms of the protein monomer number distributions. The histograms show the distributions of the protein monomer number p obtained in 10,000 independent simulations of the three different models. The first row shows data for negative feedback through dimers, the second row for positive feedback through dimers, and the third row for negative feedback through tetramers. For each of the three models, the first column shows data obtained by simulating the full set of reactions, the second column shows data obtained in the Michaelis-Menten system, and the last column shows data obtained in the Hill system.

To quantify the differences in the distributions between the different systems the average number 〈p〉 of protein monomers and the Fano factor

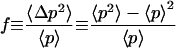(19)

which has been commonly used to characterize its fluctuations are calculated from the histograms for all three models and all three systems. In the Hill system with positive feedback the 283 simulations that resulted in p = 0 were omitted from these averages to only describe the properties of the system at the equilibrium position around p = p₁. The results are shown in Table 2. The numbers for the Fano factors confirm the qualitative picture that the Hill systems strongly overestimate the fluctuations. In addition, we emphasize that not only does the Hill approximation provide an incorrect description of the intrinsic noise it can even yield wrong average values 〈p〉 of the monomer number. This is most pronounced for the model with negative feedback through tetramers with much smaller differences for the other models. In all three models the Michaelis-Menten systems correctly reproduce the results of the full systems.

TABLE 2.

Average number of protein monomers 〈p〉 and Fano factor f characterizing the fluctuations of the number of monomers for the full set of reactions and two different effective descriptions for three different networks of a single protein with feedback

	Dimers/negative	Dimers/positive	Tetramers/negative
〈p〉
Full	62.6 ± 0.1	92.9 ± 0.1	20.81 ± 0.05
Michaelis-Menten	62.6 ± 0.1	93.1 ± 0.1	20.83 ± 0.05
Hill	62.2 ± 0.2	91.9 ± 0.3	23.9 ± 0.1
f
Full	1.44 ± 0.02	1.60 ± 0.02	1.02 ± 0.01
Michaelis-Menten	1.45 ± 0.02	1.62 ± 0.02	1.01 ± 0.01
Hill	6.33 ± 0.10	12.3 ± 0.2	3.75 ± 0.08

Intuitive explanation

Why are the fluctuations of the Hill system larger than the real fluctuations and why do even the average numbers of protein monomers differ between the Hill and the full systems? The first is a consequence of the noise reducing effect of the dimerization or tetramerization reactions. According to Bundschuh et al. (2003), the noise reduction can be understood in the model of negative feedback through dimers as follows: The source of the fluctuations is the irregular production of proteins by the translation reaction Eq. 2. In the presence of a dimerization reaction, the produced protein monomers are in an equilibrium with the protein dimers. The quantity that is changed if a new protein is produced is really the total number n = p + 2p₂ of proteins, where p denotes the number of monomers and p₂ denotes the number of dimers in the solution. For any given total number n of proteins, there is an equilibrium between the monomers and the dimers. On average we find from our simulations in the model with negative feedback through dimerization 〈n〉 ≈ 446. From the relation n = p + 2p₂ and the law of mass action p² = 20p₂ we can derive that an increase in n by one protein from its average value of 〈n〉 ≈ 446 leads to an increase in p of only 0.074 monomers. Thus, a large fluctuation in the production of proteins results in a much smaller one in the population of monomers in the presence of the dimerization reaction. The same considerations apply to the other two models. In the Hill systems the dimerization and tetramerization reactions have been eliminated. Thus, this buffering of the fluctuations cannot take place any more and the Hill systems exhibit unrealistically large fluctuations. In contrast, the Michealis-Menten system where the buffering dimerization reaction is explicitly retained, the results are in very good agreement with those for the full model.

The differences in the average number of protein monomers between the full and the Hill systems is a direct consequence of the difference in fluctuations between these two systems. The true effective transcription rate k_1,eff is the average of the instantaneous transcription rate over the distribution of protein monomers and dimers/tetramers. The derivation of the effective transcription rates k_1,eff for the Hill systems on the other hand only refers to the average numbers of protein monomers and dimers/tetramers and ignores all fluctuations, e.g., it makes use of the laws of mass action that are only correct on average but not at every given point in time. Describing a whole distribution simply by its average value is a valid approximation if the distribution is narrow. Thus, the broader distribution of the Hill systems (see Fig. 1) increase the difference between the true effective transcription rate and the effective transcription rates given by Eqs 16, 17 and 18, which can lead to a different average number of protein monomers.

Computational effort

To quantify the computational efficiency of the different systems, we count how many elementary reactions have been simulated on average in one 50,000 s time course. The numbers are given in Table 3. The table shows that the Michaelis-Menten systems use more or less the same number of elementary time steps as the full systems indicating that most of the elementary reactions simulated are attributed to the dimerization and tetramerization reactions. The Hill systems on the contrary require three to four orders of magnitude less computational effort. This makes a big difference because in our implementation of the system a 900-MHz pentium III processor can perform around 0.5 × 10⁶ elementary reactions per second. Averaging over 10,000 time courses in the Hill systems takes on the order of a few minutes. The same simulation for the full and Michaelis-Menten systems takes a few days on the same machine. This is unacceptable if these simple networks are merely a small module of more complicated genetic networks to be simulated.

TABLE 3.

Average number of elementary reactions during the simulation of 50,000 s of the full set of reactions and two different effective descriptions for three different networks of a single protein with feedback

Reactions	Dimers/negative	Dimers/positive	Tetramers/negative
Full	1 × 107	2 × 107	2 × 107
Michaelis-Menten	1 × 107	2 × 107	2 × 107
Hill	5 × 103	7 × 103	2 × 103

Consequences

Simulations of the full set of reactions of even simple genetic networks like our three models can take a considerable amount of computer time if the network contains fast reactions like dimerizations and tetramerizations. An effective description of the fast reactions by Hill systems reduces the computational effort by three to four orders of magnitude and brings it into a regime where simulations of more complex networks can be meaningfully performed. However, the Hill description yields a false estimate of the intrinsic fluctuations. This may result in an overestimation of whatever positive or negative role fluctuations may play in the functioning of the cell. Even if one is not primarily interested in the fluctuations themselves, the Hill description can yield false results. For example, in the genetic switch model with positive feedback one would be lead to the wrong conclusion that the system is instable and randomly switches from one of the two equilibrium states to the other by using the Hill description. Also, in the other systems the average number of protein monomers given by the Hill description is incorrect because the averages are themselves influenced by the fluctuations. Thus, an effective description of the Hill type has to be avoided when simulating genetic networks despite its computational efficiency.

EFFECTIVE DESCRIPTION IN TERMS OF SLOW VARIABLES

To solve the dilemma between computational efficiency and faithfulness we will now derive an effective description of the fast reactions that is as computationally efficient as the Hill description but does not sacrifice the correct description of the fluctuations of the system. We will again mainly illustrate our technique using the model with negative feedback through dimers and give only results for the other two models.

New slow variables

The key insight underlying the effective descriptions we present here is the observation that although some of the intrinsic variables of the models are evolving very rapidly, they can be combined to yield new slowly evolving variables. Reformulating the models in terms of these slowly evolving variables yields efficient yet faithful descriptions of the models.

Although we cannot give a general recipe to identify slow variables of a set of reactions, the strategy is to identify quantities that are conserved under the fast reactions. Conserved quantities arise typically if a chemical species appears in several complexes. Although the formation of these complexes is fast, the total number of the species is evolving slowly and is a prime candidate for a slow variable to be introduced for an efficient yet faithful simplification of the model.

In the model with negative feedback through dimerization one such quantity conserved under the fast reactions is the total number of DNA molecules d + d^* + q, where d is the number of free DNA molecules D, d^* is the number of DNA–RNA-polymerase complexes D^*, and q is the number of DNA–protein-dimer complexes Q. Each of the individual variables d, d^*, and q changes rapidly during the simulation but their sum is completely conserved (at a value of one) even under the slow reactions, and we have used it above to eliminate the fast DNA-binding reactions. After eliminating the three fast variables d, d^*, and q, we still have the number p of protein monomers P and the number p₂ of protein dimers P₂ that fluctuate very rapidly because the dimerization reaction can exchange pairs of monomers for a dimer on a fast timescale. Thus, an effective description involving these intrinsically fast variables is doomed to fail. A slow variable of the system is the total number of proteins independent of their presence in the form of a monomer or a dimer. Thus, we introduce a new species N that describes a protein that could be either in the monomeric or the dimeric form. The number of molecules of this species is given by n = p + 2p₂. The corresponding slow variable for the tetramerization reaction is p + 4p₄ describing the total number of proteins in either the monomeric or tetrameric form. We note that the newly introduced species is not among the species the original model is formulated in. Nevertheless, its introduction is crucial for a faithful effective description of the dimerization reaction.

The behavior of the new species N and the mRNA M are described by the new set of slow reaction equations

(20)

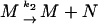(21)

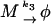(22)

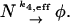(23)

The second and third of these reactions inherit their rate constants k₂ and k₃ from the corresponding original reactions Eqs. 2 and 3 respectively. The rate constants of the first and last reaction are effective rate constants related to k_1,eff([P₂]) and k₄ in the original model, which have to be reexpressed in terms of the only remaining quantity n.

Effective rates

To turn reactions 20–23 into a complete description of the original models we have to determine the effective rate constants k_1,eff and k_4,eff and provide a way to calculate the averages and fluctuations of the original variables p and p₂ from simulation results of the effective model using the variable n. Because we want to simulate the reactions 20–23 with the Gillespie algorithm it is convenient to immediately derive the effective rate constants, c_1,eff(n) and c_4,eff(n) as functions of the number n of total protein molecules. We obtain these effective rate constants by adopting a method used by Paulsson and Ehrenberg (2000). In a simple system with only two species, one of which changes in number very slowly and the other very rapidly, they obtain the effective rate for changes in the slow variable by averaging over the conditional distribution of the fast variable given the value of the slow variable. The key issue of identifying the correct slow variables does not arise in their model. Having identified the correct slow and fast variables we adopt their method to our models.

For a given number of protein molecules n, the monomer and dimer numbers p and p₂ fluctuate on a fast timescale. Their fluctuations described by a conditional distribution quantified by the probabilities f_n(p₂) to see a number p₂ = (n − p)/2 of dimers given a total number n of proteins. This conditional distribution is the crucial quantity linking the effective models to the original models. It can be determined in two different ways. In the case of the dimerization reaction it is determined by the master equation of the dimerization reaction

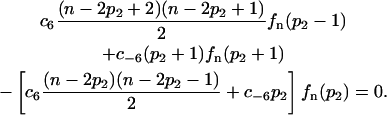(24)

Here, c₆ and c₋₆ are the reaction probabilities per unit time per molecule corresponding to the rate constants k₆ and k₋₆. This master equation can be iterated for a fixed n as a function of p₂ starting at p₂ = 0 to derive the exact distribution f_n(p₂). A similar master equation describes the tetramerization reaction. Also the latter can be iterated for a fixed n to obtain the exact probabilities 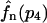to find a tetramer number p₄ = (n − p)/4 given a total number n of proteins. In the case of more complicated systems of reactions that do not allow the iteration of a master equation anymore to obtain the distribution corresponding to f_n(p₂), approximations to this distribution can be obtained by simulating the fast reactions by themselves with the Gillespie algorithm for different values of the slow variables, which are constant under the fast reactions.

In the process of connecting the effective rates to the original models we will first use the distribution function f_n(p₂) to calculate the effective rate c_4,eff of reaction 23. This reaction is derived from reaction 4. The latter occurs with a probability of c₄p per unit time if there are p monomers present where c₄ is the dimensionless version of the rate constant k₄. In the effective system, the total number of proteins n is given instead of the number p of monomers and reaction 23 occurs with a probability nc_4,eff(n) per unit time. For the two rates to be compatible, the probability per unit time with which proteins are destroyed must be the sum over all the probabilities for monomer numbers p = n − 2p₂ weighted by the probabilities to find that monomer number given the total protein number is n, i.e.,

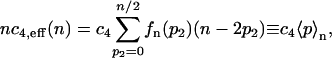(25)

where 〈p〉_n denotes the average number of monomers p given the total number of proteins n. This yields

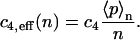(26)

This formula is correct for all three models if we remember that the averaging has to be performed over the distribution 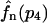for the model with negative feedback through tetramers.

In the same way the rate c_4,eff(n) is given by

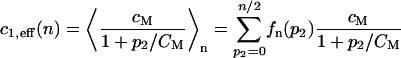(27)

for the model with negative feedback through dimerization where c_M and C_M are the dimensionless analogs of the Michaelis-Menten rate k_M and the Michaelis-Menten equilibrium constant K_M respectively. The corresponding effective rates for the other two models are obtained by taking averages over the dimensionless versions of Eqs. 14 and 15.

The effective rates c_1,eff(n) and c_4,eff(n) from Eqs. 26 and 27 can be tabulated as a function of the total number n of proteins and the Gillespie algorithm can then be applied to the four slow reactions Eqs. 20–23 using these tabulated rates. Such a simulation yields a distribution P(n) of the total number n of proteins from which the average number 〈p〉 and the Fano factor f of the monomer population has to be derived. To this end, we note that the dimerization (or tetramerization) reaction in itself for a given total number n of proteins yields an average number 〈p〉_n of monomers introduced above and the conditional average of p²

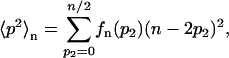(28)

where again f_n(p₂)(n − 2p₂)² has to be replaced by 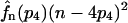for the model with tetramerization. Given tables of 〈p〉_n and 〈p²〉_n for the relevant range of protein numbers n and an estimate P(n) of the distribution of these protein numbers obtained by a simulation, we can obtain the total average protein number

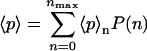(29)

and the square average

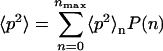(30)

and thus the Fano factor of the variables of the original system. We would expect that this scheme of averaging over the conditional distribution of the fast variable given a fixed value of the slow variable to be correct only if the fast reactions are sufficiently fast that the (conditional) steady-state distribution is reached between slow reactions. For the models we have studied our results for the effective description presented next agree very well with the full simulation. On the other hand, if the fast reactions are only marginally faster than the slow reactions the entire issue of eliminating the fast reactions and that of the validity of the Hill approximation do not arise.

Results

Using the master equations we tabulate the conditional expectation values 〈p〉_n and 〈p²〉_n and the effective rates c_1,eff(n) and c_4,eff(n) for all three models for all n up to n = 10,000. Using the tables of the two effective rates we simulate for all three models 10,000 independent time courses of reactions 20–23. As before, each individual time course covers 50,000 s of simulated time. The final number of molecules of the 10,000 independent time courses give us an estimate of the distributions P(n) for the three models. Using the tables of 〈p〉_n and 〈p²〉_n we derive the average number of monomers 〈p〉 and its Fano factor f in the way described earlier (see Effective Rates). The results are shown in Table 4. Comparison with Tables 2 and 3 show that the effective systems using slow variables correctly reproduce the average values and fluctuations of the monomer number. At the same time the effective systems require only the low computational effort of the Hill systems giving a three to four orders of magnitude advantage over the simulation of the full systems.

TABLE 4.

Average number of protein monomers, its Fano factor, and the number of elementary reactions needed to simulate 50,000 s for the effective descriptions in terms of slow variables of three different networks of a single protein with feedback

Quantity	Dimers/negative	Dimers/positive	Tetramers/negative
〈p〉	62.3 ± 0.1	93.0 ± 0.1	20.85 ± 0.05
f	1.44	1.60	1.02
Reactions	5 × 103	7 × 103	2 × 103

Another approach to fast reactions

Recently, Kepler and Elston (2001) have presented a large variety of results on mathematical approximations to the behavior of genetic networks. Before we conclude we compare our work on the dimer model with negative feedback with the results on a related model in their paper.

Kepler and Elston start from an effective description of their system in terms of the monomer concentration [P] and the mRNA concentration [M]. Assuming that our reactions 2 and 3 are always in equilibrium, they eliminate the mRNA concentration [M]. In the deterministic limit they obtain an equation for the time evolution of [P] (their equation (39)) of the form

(31)

where g([P]) contains the effects of monomer production and decay. (The form of g([p]) is more complicated than our Hill form due to their more complicated set of reactions.) In agreement with our study they find that this effective description is inadequate. In their Appendix A they suggest an improved approximation that introduces a prefactor into Eq. 31 yielding (their equation (A12))

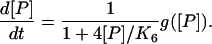(32)

For the purpose of comparison we obtain a deterministic dynamical equation, however, for the key slow variable [N], starting from the effective reactions 20–23 and eliminating the mRNA in the spirit of Kepler and Elston. The result of the form

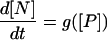(33)

can be closed by expressing [P] on the right hand side as a function of [N] as we did within the Gillespie formalism for the fluctuating variables. Instead let us express [N] in terms of [P] on the left hand side of Eq. 33 as

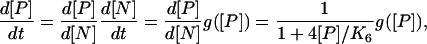(34)

where the last equality follows from [P]² = K₆[P₂] and [N] = [P] + 2[P₂]. We thus note that Kepler and Elston's additional factor is simply the derivative 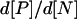consistent with our approach. However, as Kepler and Elston note their description is only valid in the parameter regime where the fluctuations of the number of protein monomers due to the equilibrium between dimers and monomers is small compared to the fluctuations due to the rest of the network. This is because they consider only macroscopic concentrations and do not refer to the microscopic fluctuations of these variables. Applying the Gillespie scheme to their effective system would correctly reproduce the fluctuations of p due to the autoregulation mechanism on long timescales but miss the short-time fluctuations of the dimerization reaction. In our full system for the model with negative feedback through dimers we evaluate the contribution to the fluctuations due to the dimerization reaction alone and find a Fano factor for the number of protein monomers of f_dim ≈ 0.9 (Bundschuh et al., 2003). Because the total Fano factor of the full system (see Table 2) is f ≈ 1.44, the fluctuations due to the dimerization reaction alone are not small compared to the fluctuations due to the rest of the network. Thus, for our biologically motivated model, Kepler and Elston's effective description cannot be applied.

CONCLUSIONS

Computational efficiency requires that in a genetic network of fast and slow reactions, the fast reactions be eliminated. This is not a straightforward matter if the reduced system of reactions is to show the same level of intrinsic fluctuations as the full system. We have investigated how this can be achieved in three biologically plausible models for gene autoregulation through feedback.

We found that the most straightforward effective description of the fast reactions known as Hill dynamics grossly overestimates the fluctuations present in the system. This overestimation affects also the average behavior of the system and depending on the model can even yield qualitatively wrong results. Thus, such an effective description should not be used. We identify the inclusion of fast-varying variables in the effective description of the system as the reason for its failure. We show how the fast reactions can be eliminated by identifying the correct slow variables and obtain a computationally very efficient model that faithfully represents not only averages but also the intrinsic fluctuations. In the case of a dimerization reaction the slow variable is the total number of proteins in the system whereas the number of monomers as well as the number of dimers are fast-varying variables, none of which is suited for a faithful effective description of the system on long timescales. This is an example showing that the correct slow variable does not have to be any of the concentrations of the species appearing in the original model. Because all three models studied show similar behavior we assume that the concept of describing a system in terms of slowly varying variables that may not be the concentrations of species in the original model is applicable to other genetic networks as well and will be helpful in enabling large-scale simulations of genetic networks.