Protein Structure and Dynamics in Nonaqueous Solvents: Insights from Molecular Dynamics Simulation Studies

Abstract

Protein structure and dynamics in nonaqueous solvents are here investigated using molecular dynamics simulation studies, by considering two model proteins (ubiquitin and cutinase) in hexane, under varying hydration conditions. Ionization of the protein groups is treated assuming “pH memory,” i.e., using the ionization states characteristic of aqueous solution. Neutralization of charged groups by counterions is done by considering a counterion for each charged group that cannot be made neutral by establishing a salt bridge with another charged group; this treatment is more physically reasonable for the nonaqueous situation, contrasting with the usual procedures. Our studies show that hydration has a profound effect on protein stability and flexibility in nonaqueous solvents. The structure becomes more nativelike with increasing values of hydration, up to a certain point, when further increases render it unstable and unfolding starts to occur. There is an optimal amount of water, ∼10% (w/w), where the protein structure and flexibility are closer to the ones found in aqueous solution. This behavior can explain the experimentally known bell-shaped dependence of enzyme catalysis on hydration, and the molecular reasons for it are examined here. Water and counterions play a fundamental and dynamic role on protein stabilization, but they also seem to be important for protein unfolding at high percentages of bound water.

INTRODUCTION

Nonaqueous enzymology is nowadays an active area of work, having matured to a point where, besides its large implications in basic protein science, it has an important impact in biotechnology, from where grew its roots. Many studies contributed to this during the last two decades (see Bell et al., 1995; Halling, 2000; Klibanov, 2001, for reviews), and now many of the factors influencing catalysis in nonaqueous solvents (mostly organic solvents) are known. Despite this large knowledge, not much is known about the exact molecular events that occur in proteins when performing catalysis under these nonphysiologic conditions.

The amount of water has been recognized as one of the main controlling factors of enzyme activity in nonaqueous media (see Bell et al., 1995; Klibanov, 2001, for reviews). Its has been early recognized (Zaks and Klibanov, 1984, 1985, 1988a,b) that the presence of water was essential for catalysis, and that the control of water was exerted by the amount of molecules bound to the enzyme and not by its percentage in the organic solvent (Zaks and Klibanov, 1988a). Additionally, the effect of water was not a simple one. For suspended subtilisin, adding water to the dry enzyme increased activity up to a certain point, but then the activity decreased again when the amount of bound water was increased further (Affleck et al., 1992); the maximum activity was for ∼10–15% (w/w) of bound water. This bell-shaped dependence was also found for subtilisin in compressed propane (Carvalho et al., 1996; Fontes et al., 1998b) and carbon dioxide (Carvalho et al., 1996); the maximum of activity was for ∼10–12% (w/w). Increased hydration was associated with increased flexibility of the enzyme (Affleck et al., 1992; Broos et al., 1995; Hutcheon et al., 2000; Partridge et al., 1998), and this effect was interpreted as if water could act as a lubricant (Zaks and Klibanov, 1988a) for the protein in contact with the organic solvent. Dry enzymes would be very rigid, but become flexible upon binding of water, making catalysis possible. The reduction of enzyme activity at higher levels of hydration was suggested (Affleck et al., 1992) to be explained by conformation changes that could alter the active site, consistent with the observation that enzymes display much more native structure in pure organic solvents than in aqueous-organic mixtures (Griebenow and Klibanov, 1996). Proteins denature in organic solvents and this does not happen in dry conditions due to their low flexibility and consequent inability to jump over the barrier from the folded to the unfolded state (Zaks and Klibanov, 1988b); i.e., they are kinetically trapped. Therefore, there seems to be a fine equilibrium between having enough water for the enzyme to have flexibility for catalysis, and not having too much water so that the enzyme does not unfold.

Counterions are another factor controlling catalysis in nonaqueous solvents. Counterion neutralization of proteins in nonaqueous media plays a much more fundamental and structural role than in water (see Halling, 2000, for a review). Although the high dielectric of water screens the electrostatic interactions, allowing opposite charges to be far apart, the low dielectric of nonaqueous media does not allow this to happen and counterions are bound to the protein to neutralize its ionizable groups.

Connected with the effect of counterions is the effect of pH on enzyme activity. In aqueous solutions enzymes show a marked dependence on pH, exhibiting a maximum of activity at a given value. The concept of pH does not apply easily to nonaqueous solutions, given the lack of availability of free protons, making the ionization equilibria of protein groups somewhat undefined. However, it was discovered (Zaks and Klibanov, 1985) that enzyme suspensions exhibited catalytical profiles that were dependent on the pH of the solution from where they were prepared, and this profile was similar to the one found in aqueous solution. Therefore, the enzyme retained “pH memory” from the media in which it was prepared. This also occurs in small model compounds containing protein functional groups (Costantino et al., 1997). The explanation of this strange behavior lies in kinetics. In nonaqueous solvents, ionizable groups would be more stable in neutral states, but they cannot reach them because there is no possibility to exchange or transfer protons (Xu and Klibanov, 1996).

The structure that a protein adopts in a nonaqueous solvent cannot be easily inferred. However, there is now a reasonable amount of structures of proteins made with crystals grown in aqueous conditions (some cross-linked afterwards) and placed in organic solvents (Allen et al., 1996; Fitzpatrick et al., 1994, 1993; Gao et al., 1999; Schmitke et al., 1997, 1998; Yennawar et al., 1995, 1994; Zhu et al., 1998). No major conformational changes were observed, when compared with the corresponding structures in water. Small side-chain rearrangements were observed, as well as the binding of organic solvent molecules in some selected places of the protein. One should stress that these crystals always contained a quantity of water bound to the protein, whose structure could be determined.

Molecular dynamics (MD) simulations using full detail have been used before to have insights on the structure and behavior of enzymes in organic solvents (Colombo et al., 1999; Hartsough and Merz, 1992, 1993; Norin et al., 1994; Peters et al., 1996; Toba et al., 1996; Zheng and Ornstein, 1996). Generally, these studies evidenced overall structural conservation, with increased electrostatic interactions (salt bridges and hydrogen bonds), and reduced flexibility of the protein, when compared with corresponding water simulations. These studies were normally made with counterions balancing the total charge, even if the presence of one counterion per unprotected charged group seems a more reasonable situation (Halling, 2000). Crystallographic water molecules were used in some simulations (Colombo et al., 1999; Hartsough and Merz, 1992, 1993; Toba et al., 1996; Zheng and Ornstein, 1996), but, as far as we are aware, only one study (Toba et al., 1996) compared two hydration conditions. Higher hydration yielded less distorted structures and higher flexibility, pointing to the lubricant power of water. However, no systematic study of hydration was performed.

Our main goal in this work is to investigate the effects of hydration on protein structure and dynamics. For that we used two model protein systems in hexane. The first is a small protein, ubiquitin from human origin, that has been used in theoretical studies many times before. The second is a medium sized enzyme, cutinase from Fusarium solani pisi, that we have used before (Fontes et al., 1998a) to rationalize enantioselectivity. Cutinase is a serine protease that, unlike other lipases, has a preformed oxyanion hole (Martinez et al., 1994). Like many enzymes, cutinase shows a clear dependence of its activity on enzyme hydration in nonaqueous solvents, having a bell-shaped curve with a maximum at a certain water activity (Fontes et al., 1998a).

In this work we perform MD simulations of ubiquitin and cutinase in hexane, considering a situation of pH memory at pH 7, and neutralizing with counterions each charged group that cannot be stabilized by an intraprotein salt bridge. Different hydration conditions (i.e., bound water) are studied, and the results show that hydration plays a fundamental role in protein structure and dynamics.

MATERIAL AND METHODS

General simulation approach of our studies

The conditions experienced by proteins when in organic solvents (or nonaqueous solvents in general) are quite different from the ones experienced in water solutions. First of all, proteins are not part of the organic solution itself, but rather in solid suspensions, solid cross-linked crystals, enclosed in inorganic matrices or adsorbed to these same matrices, in contact with the organic solvent. The simulation of such systems, that truly consist of one (more or less) solid phase containing the protein, and another liquid phase corresponding to the solvent, is not obvious. Similarly to others (Colombo et al., 1999; Hartsough and Merz, 1992, 1993; Norin et al., 1994; Peters et al., 1996; Toba et al., 1996; Zheng and Ornstein, 1996), our approach in this work was to simulate one protein molecule in a box of solvent. This most likely corresponds to a situation that is harder on the protein than the real situation, but we hope (and the results are showing) that it can capture the overall physical features of the system, presenting a degree of metastability sufficient for extrapolating its behavior to larger and more complex systems.

One of the questions that should be addressed is the ionization state of protonable residues. Here we try to mimic the experimentally characterized situation of pH memory (Zaks and Klibanov, 1985), where we can apply in the nonaqueous solution the same ionization state observed in water, and use the normal theoretical tools (Bashford and Karplus, 1990; Warshel, 1981; Yang et al., 1993) to predict it.

The neutralization of charged protein groups by counterions is another question that must be mimicked by the simulation procedure. In organic solvent the ions are most likely associated with ionizable groups at the surface of the protein (Halling, 2000). One could consider one counterion per charged group of the protein, but this number of counterions may not be needed, inasmuch as some groups of the protein can establish salt bridges among them, even if these are not present in the x-ray structure.

Setup of molecular dynamics/mechanics simulations

All molecular dynamics/mechanics simulations were done using the GROMOS96 program package and force field (Scott et al., 1999; van Gunsteren et al., 1996). Bond lengths were constrained using SHAKE (Ryckaert et al., 1977), with a geometric tolerance of 0.0001. Nonbonded interactions were calculated using a twin-range cutoff (van Gunsteren and Berendsen, 1990), with short- and long-range cutoffs of 8 Å and 14 Å, respectively. In the water simulations, the SPC water model (Hermans et al., 1984) was used, and a reaction field correction was applied to electrostatic interactions (Barker and Watts, 1973; Tironi et al., 1995), considering a dielectric constant of 54 (the dielectric constant of SPC water; Smith and van Gunsteren, 1994). Hexane was modeled using the GROMOS96 parameters for alkanes (Daura et al., 1998) and considered flexible in the simulations. This parameterization considers partial charges of zero in all CH_n atoms. Molecular dynamics simulations were performed using heat baths (Berendsen et al., 1984). Unless stated otherwise, the temperature coupling constant used is 0.1 ps. The time step used in the integration of equations of motion was 0.002 ps. Simulations were run in the canonical ensemble.

Protein structures used in the studies

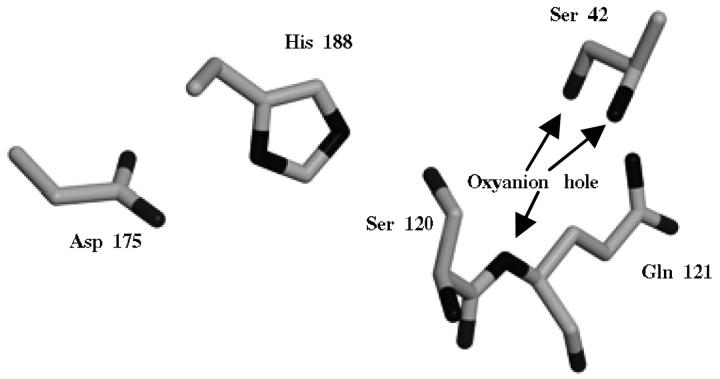
For ubiquitin, the structure from human origin was used (PDB code: 1UBQ; Vijay-Kumar et al., 1987), refined at 1.8 Å resolution. The structure of cutinase from Fusarium solani pisi refined at 1.0 Å was used (PDB code: 1CEX; Longhi et al., 1997). Due to the high resolution of the cutinase structure, there is a considerable number of side chains with alternative conformations. In the majority of the cases, the conformation with the highest occupancy was used. However, some alternative conformations for residues in the active side may be important and worth investigating (see next section on modeling protein protonation equilibrium). The catalytic Ser 120 (see Fig. 1) has two conformations, one close to the catalytic His 188 and another a bit further away. Concerted with Ser 120, there is a water molecule (Wat 526) with two alternative conformations. Asn 84 is another residue showing alternative conformations. Combinations of the alternative conformations of these two residues (Ser 120 and associated conformation for Wat 526, and Asn 84) were tested, given a total of four conformations.

FIGURE 1.

Active site of cutinase. Represented are the side chains of Asp 175, His 188, Ser 120, and Gln 121 (the last two contain the main chain between them). Arrows indicate the oxyanion hole, namely the NH groups of Gln 121 and Ser 42, and the OH group of Ser 42. The conformation A for Ser 120 is the one represented. Figure prepared with XtalView (McRee, 1992) and Raster3D (Merritt and Bacon, 1997).

Modeling protein protonation equilibrium

The calculations of the protonation equilibrium were performed using a methodology developed by us and described in detail before (Baptista and Soares, 2001). This methodology, besides treating different ionization states of ionizable groups, also considers proton tautomerism, as well as the multiconfigurational behavior of protons belonging to alcohol groups and crystallographic water molecules. Crystallographic water molecules were included in the calculation if their relative accessibility was less or equal than 50%. The MEAD package (version 2.2.0; Bashford, 1997; Bashford and Gerwert, 1992) is used to calculate electrostatic energy terms by solving the linear Poisson-Boltzmann equation. These energies are used by a Monte Carlo procedure implemented in the program PETIT (Proton and Electron TITration; Baptista et al., 1999; Baptista and Soares, 2001) to sample the ionization and proton configuration behavior at different values of pH. For details about the exact procedure used in the MEAD and PETIT calculations, see reference for Baptista and Soares (2001) and the Appendix of reference Baptista et al. (2002). The GROMOS96 (Scott et al., 1999) charges were used.

Selecting counterion positions

Our approach to find counterion positions that respect the criterion specified above is the following. First we dock positive (Na⁺) and negative (Cl⁻) ions on the x-ray structure of the protein. Each docked ion is added to the protein structure before a new docking experiment is done. Positive and negative ions are docked independently. This is a super-set of the total amount of ions needed to neutralize the ionizable groups. Other docking experiments are performed on the energy-minimized structure of the protein. This structure was obtained by energy minimization of side chains on the framework of a restrained main-chain, allowing the appearance of low-deformation salt bridges in an environment that mimics the low dielectric conditions of the organic solvent (vacuum). Counterions are docked on this structure using the same procedure specified above. This constitutes an unbiased method to find out the groups most likely to need counterions for their neutralization. The ion positions will then be chosen, based on the ion placement on the x-ray structure, for the groups that are neutralized on the docking experiments on the minimized structure. This is because we want to start with the x-ray structure conformation. This configuration is the starting point for the simulations in hexane with different hydration conditions. The same configuration will be used in the control water simulations that require ions. Simulations in water without ions were also performed.

The actual docking protocol was implemented in Autodock 2.4 (Goodsell et al., 1993; Goodsell and Olson, 1990). The GROMOS96 (Scott et al., 1999) charges were used. A distance-dependent dielectric constant was used for electrostatic interactions (Mehler and Solmajer, 1991; Solmajer and Mehler, 1991). Monte Carlo simulated annealing was used, starting with a value of RT of 10 kcal mol⁻¹, and performing 100 cycles, each where the value of RT was multiplied by 0.92 (for Na⁺) or 0.90 (for Cl⁻). The number of maximum accepted or maximum rejected Monte Carlo steps was 20,000. The translation step was initially 1.0 Å and a reduction factor of 0.9702 was applied for each cycle. Ten different runs were calculated for positioning each ion, and the lowest energy result was chosen; normally, the lowest energy solution was found many times. Four sodium ions and four chloride ions were docked on ubiquitin and ten sodium ions and ten chloride ions were docked on cutinase. These numbers correspond to the number of charged groups that cannot be compensated by establishing salt bridges at the protein surface.

The procedure described here for placing counterions finds, as expected, ion positions in close association (contacting) with the charged protein groups. If the groups are exposed, the ions dock near them, whereas if they are buried they try to find a stable position in the neighborhood. This is the case of a sodium ion needed to balance the negative charge of the catalytic Asp 175, that docks in the hydrophobic part of the active site, 7 Å distant from the nearest Asp 175 carboxyl oxygen atom. Another sodium ion docks in the active site zone, neutralizing Glu 44. Neither of these sodium ions is contacting with the catalytic triad, or the oxyanion hole.

Setup of water hydration studies

The different amounts of water hydration around the protein (to be used in the hexane simulations) were prepared as follows. Both protein structures were solvated in a truncated octahedron box of water molecules using a cubic box of water molecules equilibrated at the experimental density at 300 K and 1 bar (canonical ensemble). Crystallographic water molecules with low accessibility were included: 19 water molecules for ubiquitin and 58 water molecules for cutinase. The final number of water molecules was 4535 in the case of ubiquitin and 6112 in the case of cutinase. These systems were subjected to 6000 steps of energy minimization using the steepest descent method. For finding water molecules more firmly bound to the protein, we decided to freeze the water around the protein by doing molecular dynamics simulations at successively decreasing values of temperature of the heat bath. Random initial velocities were assigned to the systems from a Maxwell-Boltzmann distribution at 300 K. Then, 50 ps were run with all protein heteroatom positions restrained to their initial positions with a force constant of 10⁶ kJ mol⁻¹ nm⁻¹, and a temperature coupling constant of 0.01 ps. Then, six runs of 5 ps each, and using the same restraints, were successively run at temperature values of 250 K, 200 K, 150 K, 100 K, 50 K, and 0 K, each starting from the previous and using a temperature coupling constant of 0.01 ps. Finally, an energy minimization consisting in 2000 steps was run for the final structures. Water molecules were selected from this frozen system, by considering the distance to the protein. Therefore, a different number of molecules were selected to have hydration percentages (weight of water per weight of dry protein) within the range that we wanted to study: 0% (no water), 2.5%, 5.0%, 10%, 15%, 20%, and 25%. The chosen water molecules concentrate around the more hydrophilic zones of the protein, mostly around charged groups, where the ions were already placed.

Simulations in water were run using the periodic box referred to above. Random initial velocities were assigned to the systems from a Maxwell-Boltzmann distribution at 300 K and a 50-ps simulation was calculated at this temperature with a temperature coupling constant of 0.01 ps and applying position restraints to all heteroatoms of the protein (force constant 10⁶ kJ mol⁻¹ nm⁻¹). Then a further 50 ps were calculated at the same temperature with a temperature coupling constant of 0.1 ps and position restraints applied to Cα atoms only. This is to equilibrate the water around the protein and prevent large perturbations at the beginning. This final structure (and velocities) was the initial structure of the production runs.

Hexane simulations were prepared using the protein structures with different degrees of hydration as described above and considering truncated octahedron boxes with the same size as the water simulations. The number of hexane molecules was adjusted by considering the experimental density at 300 K and 1 bar, and the free space left in the box. The number of water molecules included and the number of hexane molecules are related by their relative densities in the pure liquids, i.e., hexane molecules are eliminated when more water is considered. The same protocol for initialization applied to water simulations is applied here for hexane simulations.

The question of multiple replicas

MD simulations using present-day force fields yield conformational ensembles similar to the x-ray structure. The same is not necessarily expected for simulations in organic solvent environments. The protein structure in these environments is not expected to be exactly the same as in the essentially aqueous environment captured by the x-ray structure. If we start from the x-ray conformation, we expect to have conformational changes that are associated with a certain probability to occur. Inasmuch as our simulations only consider one protein molecule at a time and are limited to time scales of the order of nanoseconds, we have realized from our initial tests that replicates were needed to study these situations quite far from the equilibrium. A unique simulation does not capture the characteristics of the ensemble that should be ideally studied. A sufficient number of replicas capture the essentials of the system in a much more realistic way, as the results presented in this work show.

RESULTS AND DISCUSSION

Protonation states at physiological pH

The pK_a calculations for ubiquitin (Table S1 of Supplementary Material) show that the most likely protonation states at pH 7 are fully deprotonated acids, fully protonated lysines and arginines, and neutral histidine. This is expected, inasmuch as all ionizable residues are exposed to the solvent. On the other hand, pK_a calculations for cutinase deserve some considerations, especially for the ionizable residues that are most responsible for the catalytic activity (see Fig. 1). Table S2 of Supplementary Material contains the results of the pK_a calculations for the four conformer combinations of catalytic Ser 120 and Asn 84. The results are quite similar for all calculations. All ionizable groups of the protein, with the exception of the catalytic histidine 188, have clear protonation states at pH 7. Notably, the aspartic acid of the catalytic triad (Asp 175) has a remarkably low pK_a between −0.32 and 0.44, evidencing that this residue is always deprotonated in serine proteases, in accordance with Warshel and co-workers (Warshel et al., 1989). The catalytic histidine 188 has a pK_a between 6.66 and 6.94, suggesting a mixed population between charged and neutral forms. Due to the specific stabilization provided by the aspartic 175 of the catalytic site, the tautomer with the proton at N^δ1 is predominant (data not shown). The existence of this proton has been demonstrated (Lau and Bruice, 1999) to be fundamental for the integrity of the active site, and for the stability of the whole protein. The protonation state chosen for the catalytic histidine residue was thus the neutral state, protonated at N^δ1.

TABLE S1.

pK_1/2 of all ionizable residues of ubiquitin

Residue	pK1/2
N-Term	8.19
Lys 6	10.20
Lys 11	11.16
Glu 16	3.84
Glu 18	3.65
Asp 21	2.74
Glu 24	4.63
Lys 27	12.09
Lys 29	11.61
Asp 32	3.82
Lys 33	10.92
Glu 34	2.72
Asp 39	2.98
Arg 42	11.62
Lys 48	10.87
Glu 51	3.80
Asp 52	1.82
Arg 54	13.30
Asp 58	3.35
Tyr 59	10.25
Lys 63	10.90
Glu 64	3.49
His 68	5.23
Arg 72	13.17
Arg 74	12.70
C-Term	3.64

TABLE S2.

pK_1/2 of all ionizable residues of cutinase

	pK1/2
Conformer choice	Ser 120 A Asn 84 A	Ser 120 A Asn 84 B	Ser 120 B Asn 84 A	Ser 120 B Asn 84 B
Residue
Arg 17	12.09	12.09	11.90	11.90
Arg 20	15.68	15.67	15.07	15.07
Asp 21	2.74	2.74	2.59	2.60
Asp 22	0.85	0.85	0.55	0.56
Asp 33	4.09	4.10	4.08	4.09
Tyr 38	13.30	13.29	12.96	12.93
Arg 40	14.81	14.84	14.72	14.73
Glu 44	1.89	1.90	1.80	1.78
Glu 60	2.73	2.73	2.28	2.27
Lys 65	11.31	11.31	10.92	10.92
Asp 66	4.07	4.08	4.01	4.01
Tyr 77	12.07	12.26	12.05	12.31
Arg 78	11.80	11.80	11.75	11.75
Asp 83	3.21	3.26	3.20	3.26
Arg 88	15.17	15.16	15.16	15.16
Arg 96	12.37	12.36	12.36	12.36
Glu 97	3.93	3.93	3.90	3.90
Lys 108	10.51	10.51	10.48	10.47
Asp 111	3.80	3.80	3.80	3.80
Tyr 119	13.71	13.67	13.70	13.65
Glu 131	3.65	3.65	3.65	3.65
Asp 132	1.83	1.83	1.82	1.83
Asp 134	3.32	3.33	3.32	3.31
Arg 138	14.02	14.01	14.01	14.01
Asp 139	3.57	3.58	3.57	3.57
Lys 140	11.54	11.54	11.54	11.55
Tyr 149	11.83	11.81	11.85	11.82
Lys 151	10.50	10.47	10.49	10.48
Arg 156	12.57	12.57	12.57	12.57
Arg 158	12.46	12.47	12.46	12.46
Tyr 162	12.75	12.77	12.76	12.76
Asp 165	2.67	2.68	2.68	2.68
Arg 166	14.77	14.76	14.76	14.76
Lys 168	10.96	10.94	10.95	10.94
Asp 175	−0.32	−0.37	−0.39	−0.44
His 188	6.94	6.85	6.73	6.66
Tyr 191	14.77	14.74	14.78	14.77
Asp 194	3.73	3.72	3.69	3.69
Arg 196	12.19	12.19	12.13	12.13
Glu 201	4.13	4.13	4.11	4.11
Glu 205	4.09	4.08	4.08	4.07
Lys 206	11.81	11.80	11.80	11.81
Arg 208	13.03	13.03	13.01	13.00
Arg 211	13.92	13.91	13.90	13.90
C-Term	3.65	3.65	3.65	3.65

The N-terminus was not considered in the calculation because there are 16 residues missing and this part of the protein is better considered as neutral, i.e., NH₂. A and B in the conformer choice refer to the highest and lowest occupancy conformers, respectively. The four possible combinations of conformers for Ser 120 and Asn 84 (see Material and Methods) are analyzed.

Analysis of control water simulations

To compare the results obtained in organic solvent, control water simulations were performed. When setting up these simulations, the first choice was to try to maintain the conditions as similar as possible to the conditions used in the hexane simulations, including the amount of counterions introduced and their positioning. However, simulations without counterions were also made for both proteins. Table 1 contains some of the analysis performed for these simulations. The simulations were considered sufficiently stable after 2 ns, and a period of 2 ns after was used to calculate average quantities. In the case of ubiquitin in water with ions, the 2 ns averaging period was considered after 3 ns of simulation instead, due to minor drift in the root mean square (r.m.s.) deviation. All simulations show reasonable values of r.m.s. deviation from the x-ray structure (highest value is 0.20 nm), showing that the simulation conditions are reproducing the correct physics of the system. Ubiquitin presents lower values of r.m.s. deviation than cutinase, but in the former the C-terminal tail was eliminated in the analysis.

TABLE 1.

Comparative analysis of water MD simulations

Simulation	r.m.s.d. from x-ray Cα atoms (nm)	r.m.s.d. from water MD* Cα atoms (nm)	r.m.s. fluc tuations all atoms (nm)	Number of persistent H-bonds‖	Radius of gyration (nm)	Total area (Å2)	Hydrophilic area†(Å2)	Hydrophobic area†(Å2)	Ratio hydrophobic/ hydrophilic area	Conserved secondary structure relative to x-ray structure %	Conserved secondary structure relative to water MD* %	r.m.s.d. from x-ray active site‡ (nm)
Cutinase in water (2–4 ns)	0.14		0.100	130	1.501	8360	3527	4833	1.370	84		0.08
Cutinase in water and ions #1 (2–4 ns)	0.18	0.18	0.100	120	1.506	8324	3468	4856	1.400	88	95	0.12
Cutinase in water and ions #2 (2–4 ns)	0.20	0.17	0.100	123	1.519	8767	3844	4923	1.281	83	91	0.08
Ubiquitin in water (2–4 ns)	0.09§		0.102§	48	1.084§	4529	2108	2420	1.148	84
Ubiquitin in water and ions (3–5 ns)	0.10§	0.09§	0.114§	39	1.086§	4596	2190	2407	1.099	84	95

^*This corresponds to the average (2–4 ns) protein structure obtained from the pure water MD simulation.

^†Hydrophobic atoms, C and S; hydrophilic atoms, O and N; hydrogen atoms were not considered.

^‡Active site residues considered: the side chains (including Cα) of His 188, Asp 175 and Ser 120; the NH groups of Gln 121 and Ser 42. The side chain of Ser 42 is also part of the oxyanion hole, but inasmuch as it is quite mobile, we choose not to include it.

^§The C-terminal tail of ubiquitin (residues 71–76) was not considered due to its extreme mobility.

^¶In this analysis, the regular secondary structures considered are the α-helix, the β-sheet, the 3₁₀ helix and the β-bridge (DSSP classification; Kabsch and Sander, 1983). The residues that remain in the same secondary structure class are counted.

^‖A hydrogen bond is considered to exist in one conformation if the distance between the hydrogen atom and the acceptor is less than 2.5 Å and the angle formed by donor-hydrogen-acceptor is less than 135°. The persistent hydrogen bonds are the ones that occur more than 50% of the time.

The simulations with counterions show larger deviations from the x-ray structure than the simulations in pure water. This is more evident in the case of cutinase, where we found some deviation in the active site (Table 1), being the reason why two simulations were calculated to check the reproducibility of this observation. The ions in these simulations, as is usual in water media, do not interact specifically with the protein, but their presence changes the equilibrium between internal and external forces, as evidenced by the number of internal hydrogen bonds (Table 1), which are substantially lower when ions are present (39 versus 48 in ubiquitin, and 120 and 123 versus 130 in the case of cutinase). Inclusion of ions in molecular dynamics simulations of proteins has been always a matter of debate. The ions included in the simulations do not correspond to the total charge neutralizing ions used in many protein simulations, inasmuch as both proteins have zero charge at pH 7. Because these water simulations were meant to be used as controls, these ions correspond to a direct shielding of charged groups of the protein that cannot form salt bridges. Some studies have shown that the successful simulation of some proteins is highly dependent on the presence of counterions (Ibragimova and Wade, 1998), being these, besides the charge-shielding ones (such as ours), some extra ions to reach a 0.2 M ionic strength; this study used a lattice sum method to correct long-range electrostatics. A recent study (Walser et al., 2001) using the GROMOS96 force field compared the effect of different long-range electrostatic corrections and the presence of ions on the simulation of ubiquitin crystals, finding that the inclusion of counterions (just total charge-neutralizing ones) leads to higher r.m.s. deviations from the x-ray structure, when using the same reaction field correction (Barker and Watts, 1973; Tironi et al., 1995) used here. A lattice sum method was more insensitive to the inclusion of ions, but did not perform better than the reaction field method. The method to initially place ions had a small effect on the results, which may be a consequence of the slow equilibration of the ionic atmosphere in these (Walser et al., 2001) and other simulations (Ibragimova and Wade, 1998; Pfeiffer et al., 1999). In many cases (as in this work), ions are placed near the protein, and move away from it during the simulation. Therefore, their initial placement may be one of the sources for the slow equilibration observed. It is well known that electrostatic interactions remain one of the biggest problems in molecular dynamics simulations of aqueous systems, and maybe ion inclusion in different electrostatic schemes leads to different and somewhat contradictory effects. Discussing or investigating them here is clearly outside of the scope of this work, so we decided to adopt a pragmatic approach: given that our simulation scheme resembles very closely the one found out by Walser et al. (2001) to give better results (reaction field cutoff and no ions), and given that our simulations in pure water without counterions were the most well-behaved ones, we decided to consider these as the control simulations for the studies in organic solvent. Nevertheless, the differences between simulations with and without ions were not extremely high, so the choice is not exceedingly important.

Studying different hydration conditions

To characterize protein structure and dynamics under different hydration conditions, we hydrated the x-ray structure of the proteins (with ions positioned) with increasing quantities of water, from 0% to 25%. MD simulations of 4 ns were calculated for each water content. For each condition, several replicas were run (a minimum of three and a maximum of five), by varying the initial velocities assigned to the first conformation.

Most simulations are reasonably stabilized after ∼2 ns or earlier, as judged from the r.m.s. deviation. However, there are some cases where the r.m.s. deviation is not stabilized after this period, showing considerable drift, or displaying large oscillations. Inasmuch as we are analyzing many replicas, we choose not to handle these cases in a special way. This supposes that these unstable cases will appear as outlyers and will be handled by the statistical analysis. We choose to use medians for the analysis, inasmuch as this method is less sensitive to these outlyers.

The initial distribution of water molecules is changed substantially during the course of the simulations. In the end of the simulations, there is further concentration of water molecules around charged groups and ions, which have a large tendency to capture water molecules.

Structural analysis

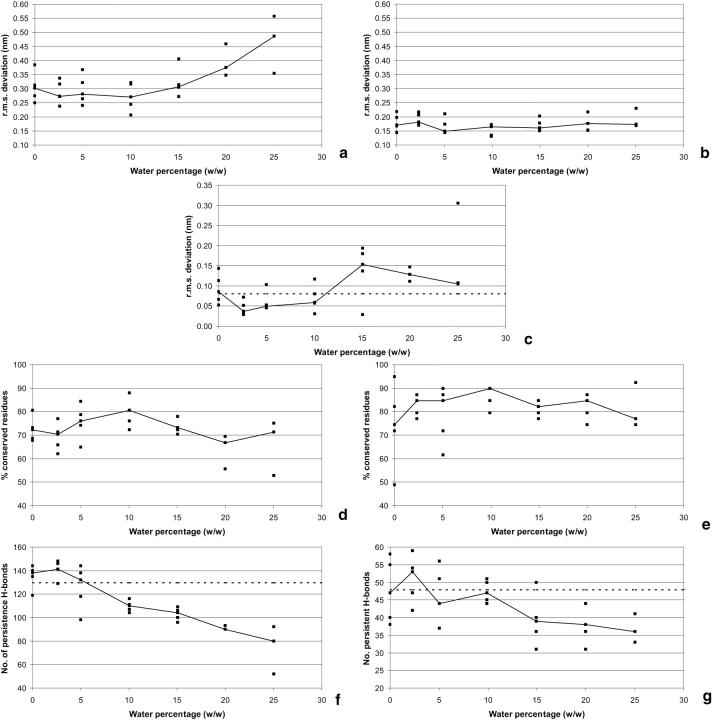
The r.m.s. deviations from the average structure of the control water simulation are presented in Fig. 2, a and b. As a general observation, it is clear that the dispersion of the results is very high in both cases, evidencing the need for the use of replicas to extract meaningful conclusions from the results. We will analyze the trends using medians instead of individual results. Another general observation is that ubiquitin is much more stable than cutinase in all conditions studied, presenting much lower values of r.m.s. deviation. This is probably due to its very compact fold.

FIGURE 2.

Structural analysis in hexane simulations with different hydration. (a), r.m.s. deviation of Cα atoms of cutinase from average structure of the control in water. (b), Same as a for ubiquitin, but the C-terminal tail (residues 71–76) is excluded. (c), r.m.s. deviation (of the 2–4 ns average) of the active site residues of cutinase, when compared with the x-ray structure. The atoms contributing for the r.m.s. deviation are specified in Footnote 3 of Table 1. The dashed line represents the average r.m.s. deviation observed in the water simulation. (d) Percentage of cutinase residues (2–4 ns average) in the same secondary structure class as in the control water simulation without counterions (using the 2–4 ns average). See Footnote 5 of Table 1 for the secondary structure types considered. (e), The same as d, but for ubiquitin. (f), Hydrogen bond analysis for cutinase (using the 2–4 ns period). See Footnote 6 of Table 1. Persistent hydrogen bonds are the ones occurring more than 50% of the time. The dashed line represents the number of hydrogen bonds observed in the corresponding water simulation. (g), Same as f, but for ubiquitin.

In both cases, the effect of hydration is a complex one. For low levels of hydration, the protein systems approach their corresponding aqueous solution structures with increasing quantities of water up to a certain point (variable, but in the range of 5–10% (w/w)) and start to deviate again for higher values of hydration. This situation is more evident in the case of cutinase, given the strong structural conservation of ubiquitin. The preservation of regular secondary structure when compared with the aqueous situation (Fig. 2, d and e) shows a clearer picture. These results are consistent with the r.m.s. deviation and point out to a maximum conservation at water percentages ∼10% (w/w). Once again ubiquitin is more stable than cutinase overall, but the pattern of variation is similar. These results are an indication that the water content is fundamental to regulate the protein structure in organic solvent situations. Absence of water makes the structure different from the one found in aqueous solution, although increasing the water content a bit allows it to acquire a more native fold. Increasing the water even more leads to unfolding and destruction, as evidenced by the high values of r.m.s. deviation. This is very clear in the case of cutinase, which reaches very high values of r.m.s. deviation and low values of secondary structure preservation. In this particular case, the α-helical content (results not shown) follows the general trend depicted on Fig. 2 d, but the β-sheet content increases above 10%, and remains constant for higher values of hydration. This is not mimicked by ubiquitin, where a less clear behavior is observed.

The hydrogen bond analysis (Fig. 2, f and g) shows results consistent with the other structural features presented so far. The number of intraprotein hydrogen bonds decreases in general with increasing water quantities, despite the fact that there may be values ∼2.5% where the number of hydrogen bonds increases. Low hydration generates a stronger pattern of intraprotein hydrogen bonds, whereas at higher hydration the water competes for these hydrogen bond donors and acceptors, leading to a reduction of the pattern of intraprotein hydrogen bonds. The dashed line, representing the number of hydrogen bonds in the pure water simulation of the proteins, intercepts the data obtained in organic solvent in the 5–10% zone, which, accordingly to the results presented in Fig. 2, a, b, d, and e, correspond to the most nativelike protein conformations.

Analysis of the radius of gyration (data not shown) reveals that this quantity increases with the water percentage, especially in the case of cutinase. Despite being observed for ubiquitin, its variation is much smaller. One very curious observation is that cutinase in hexane seems to be larger that in water, for all water percentages studied. The same does not happen for ubiquitin (similarly with other simulation studies of lipases; Norin et al., 1994; Peters et al., 1996). By visual inspection (data not shown) we could see that the larger size of cutinase in hexane does not correspond to significant solvent penetration in the structure. Instead, the loops that approach the structure in the water simulation (namely the ones surrounding the active site, especially the loop 180–188), adopt a more open conformation in hexane. The active site and the loop 180–188, are markedly hydrophobic and its closure in the water simulation may be an attempt to avoid water. Two other MD simulations of cutinase (Creveld et al., 1998; Lau and Bruice, 1999) show this zone to be quite mobile and different from the x-ray structure. Cutinase is more hydrophobic than ubiquitin, as it is suggested by its larger hydrophobic/hydrophilic ratio (see Table 1), which could make it more sensitive to hydrophobic stabilization by hexane. Visual inspection of the active site shows that hexane can enter it and possibly be a stabilizing factor in its open conformation, similar to what would be expected in the presence of a substrate. This may have potential consequences in catalysis, or at least in the accessibility of hydrophobic substrates. However, we do not perceive single hexane molecules bound to specific zones of the active site, suggesting that the interaction between hexane and the protein is fluidlike.

The different water percentages have a noticeable effect on the surface characteristics of the proteins. As expected, the hydrophobic area/hydrophilic area ratio is higher when the water content is low and decreases when the water content is increased (data not shown). In both cases, and in accordance with other simulation studies (Toba et al., 1996), this ratio is clearly higher than the one observed in the MD simulations performed in pure water, evidencing a larger exposure of hydrophobic zones in hexane.

The active site conservation along hydration is analyzed in Fig. 2 c. The behavior of the active site mimics the one observed for the whole structure, i.e., there is stabilization when water is increased from the pure hexane simulation, but this zone becomes destabilized when the water percentages are increased above 10%. The data in Fig. 2 c points to a further stabilization in the 20–25% zone, but this is not totally clear, given the high dispersion of the values and the fact that there are fewer replicas in these conditions (three, instead of five). The simulations at 2.5–10% present conformations closer to the x-ray structure than the pure water simulation, which may be due to the reduced conformational changes observed in the active site loops in hexane (see above). In any case, the active site of cutinase is remarkably conserved in these simulations, clearly suggesting that the protein still possesses catalytic capabilities under these conditions. It is interesting to analyze what is happening to the two sodium ions that were initially positioned in the active site. Whereas in the water simulations these ions move away from the protein, in hexane the situation is diverse; at low hydration they remain in the vicinity of the active site (mostly the one stabilizing Glu 44), whereas at higher hydration (above 15%), they move away. However, these ions do not interfere directly with the catalytic triad, and, in all situations, the ions have the tendency to form ion pairs.

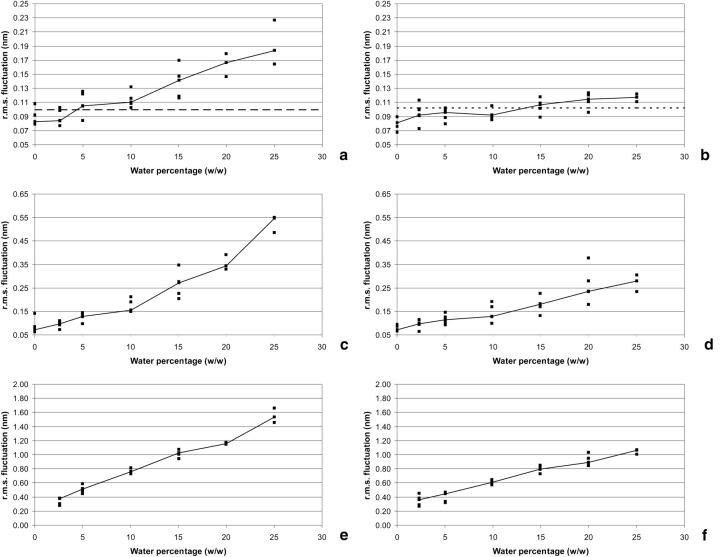
Dynamic aspects

The average r.m.s. fluctuations for the proteins in different hydration conditions (Fig. 3, a and b) evidences that the protein mobility increases substantially and consistently with increasing concentrations of water. In pure hexane the proteins have lower mobility than in pure water, but with increasing hydration, two regions of behavior are observed. In the first, that occurs up until 10% of water, each protein gains higher mobility, but reaches a plateau where its dynamics remain more of less constant. After 10%, the rate of increase is higher. In cutinase, the typical mobility of the pure water simulation is reached ∼5–10% of water, whereas in ubiquitin it is necessary to go for values ∼15% to reach the same situation, even if it is very close to it after 2.5%. Additionally, it never reaches values as high as cutinase. Therefore, despite the fact that the behavior is overall the same for the two proteins, ubiquitin displays a lower degree of sensitivity to external conditions. Overall, this increasing flexibility with increasing hydration is consistent with previous experimental (Affleck et al., 1992; Broos et al., 1995; Hutcheon et al., 2000; Partridge et al., 1998) and simulation studies (Toba et al., 1996).

FIGURE 3.

r.m.s. fluctuations analysis of hexane simulations (corresponding to the 2–4 ns period). (a), r.m.s. fluctuations for the cutinase protein atoms (all atoms). The dashed line represents the average r.m.s. fluctuation observed in the corresponding water simulation. (b), Same as a, but for ubiquitin (the C-terminal tail—residues 71–76—is not included). (c), r.m.s. fluctuations of the counterions in the cutinase simulations. (d), Same as c, but for ubiquitin. (e), r.m.s. fluctuations for water molecules in cutinase simulations. (f), Same as e, but for ubiquitin.

There seems to be two fluctuating regimes for the protein under increasing water content. Fig. 3, c (cutinase) and d (ubiquitin) show that the same seems to occur for the case of counterions. Their r.m.s. fluctuations increase with increasing water content, but the rate of increase is lower for the zone below 10% of water than for higher hydration. Surprisingly, the water r.m.s. fluctuations, depicted in Fig. 3, e (cutinase) and f (ubiquitin), seem to be similar over all hydration conditions analyzed, increasing more or less constantly with increasing hydration.

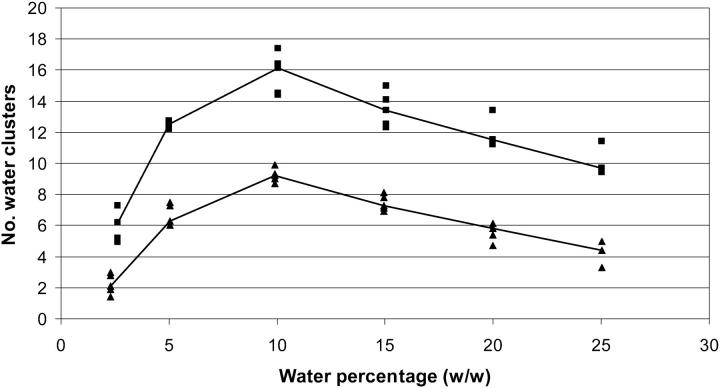
What is the reason for the two regime behavior of fluctuations? One possible answer can be found in Fig. 4, where the water clusters of more than one element (representing zones of contiguous water molecules) are analyzed. The number of clusters increases dramatically with increasing hydration, until a maximum at ∼10%, where it starts to decrease. The explanation for this is simple: the water associated with the molecular surface can increase up to a certain point forming a multitude of small clusters that remain isolated. With increasing hydration, the clusters start to fuse and become larger, thereby reducing their number. These large clusters make the protein surface more waterlike and less organic, creating conditions for higher fluctuations and higher ion diffusion. Ultimately these large water clusters provide the adequate environment for unfolding conformational changes to occur.

FIGURE 4.

Average number of water clusters (corresponding to the 2–4 ns span). These clusters are constituted by loosely interacting water molecules. The criterion used was to group water molecules whose oxygen atoms are within 5 Å of any other water oxygen of the cluster. Clusters of only one element are not considered. The results for cutinase are represented by filled squares (upper part) whereas ubiquitin results are represented by filled triangles (lower part).

A molecular view of proteins in nonaqueous solvents

Fig. 5 contains stereo representations of the final conformations (4 ns) of selected conditions, which can visually illustrate several points discussed in this work. Fig. 5 a corresponds to the pure water simulation of cutinase (without ions) used as the control situation. The conformations corresponding to 5% and 10% of water (Fig. 5, c and d) seem to be the ones more similar to the control (Fig. 5 a). The structure obtained at ∼25% of water (Fig. 5 e) is substantially different, evidencing considerable destruction of several secondary structure elements, even if many characteristics of the fold still remain intact.

FIGURE 5.

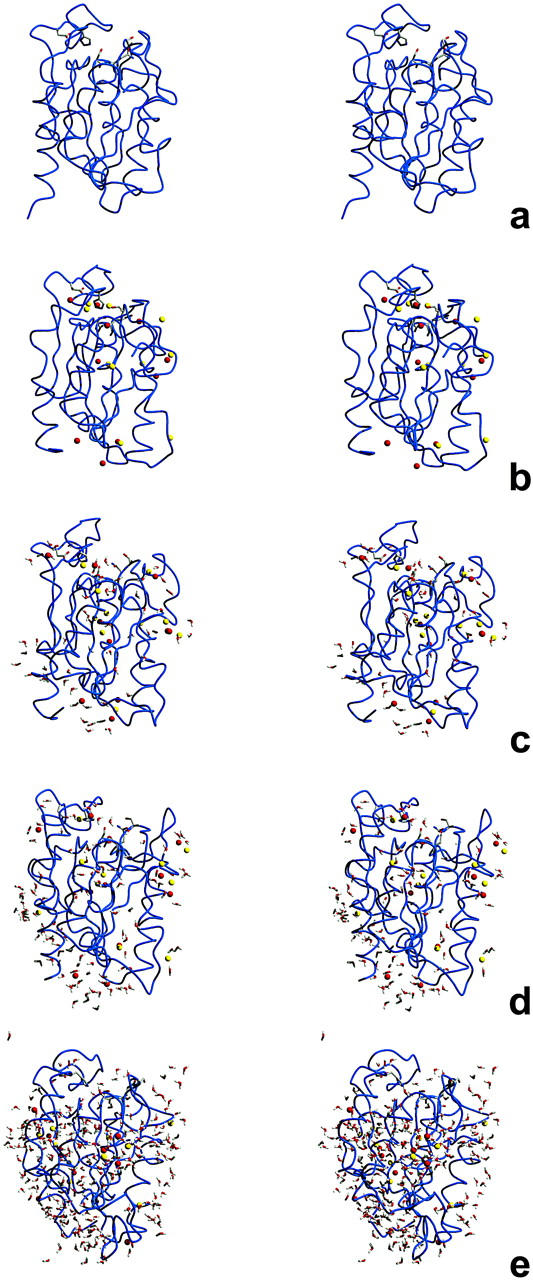
Stereo pictures of the final conformation of cutinase in several simulation conditions after 4 ns (the simulations corresponding to the median are selected here). The fold is represented by a smooth blue trace and the side chains of the active site are represented using sticks. Sodium and chloride ions are rendered using spheres, with red and yellow colors respectively. In the simulations in hexane containing water, water molecules are rendered using sticks. The figures were prepared using Molscript (Kraulis, 1991) and Raster 3D (Merritt and Bacon, 1997). Presented are simulations in pure water (a), and in hexane with ions and 0% (b), 5% (c), 10% (d), and 25% (e) of water.

In all simulations in hexane with ions, there is an absolute tendency for the ions to remain firmly associated with the protein, contrary to what happens in water, where they are most of the time dispersed in the solution (data not shown). This association contributes for reducing the protein flexibility, given that control simulations in hexane without water molecules and ions (results not shown) show higher flexibility for the protein (a median r.m.s. fluctuation of 0.100 nm when compared with a median of 0.082 nm for the corresponding simulations with ions). However, the protein is much less native when ions are not present, judging from its higher r.m.s. deviation from the control water simulation (a median of 0.38 nm).

There is some tendency for the formation of ion pairs in the hexane simulations, a situation that is highly increased when hydration is high, something very evident at ∼25% of water (Fig. 5 e), where the majority of the counterions are involved in the formation of ion pairs. This is particularly destructive, given that the protein follows these ions and experiences substantial conformational changes. Ultimately, this may be the main reason behind unfolding, or at least one of the forces leading to it. Obviously, this depends on hydration. Water is not evenly distributed (see Fig. 5, c and d), locating itself on selected zones of the protein, mostly around ions and ionizable groups; the active site is one of these places. This distribution of water around polar zones is consistent with studies using dry enzymes (Careri et al., 1980; Rupley et al., 1983, 1980), which evidenced the solvation of charged and polar groups first. The water molecules in our simulations have a marked tendency to remain associated with the protein. This tendency is absolute until high hydration, where, sometimes, water clusters or isolated water molecules temporarily detach from the protein. This can explain water migration between the solvent and the protein, a situation present in experimental conditions, where enzyme catalysis is controlled by the water activity of the solvent (Halling, 1990; Parker et al., 1995; Partridge et al., 1998). Additionally, this could also explain the well-known effect of catalytic control through ion exchange via the use of solid-state buffers (Halling et al., 1996; Harper et al., 2000; Zacharis et al., 1997). Water clusters may solvate ions and transport them between the solid phases (solid buffer and suspended or immobilized protein) through the organic solvent. In the time scale of the simulations, we could not perceive ion migration toward the hexane region, suggesting that this may be occurring in a longer time scale. This may be related with the nonpolar nature of hexane, and may be different in more polar solvents, as suggested by simulation studies (Zheng and Ornstein, 1996).

CONCLUDING REMARKS

The large number of MD simulations in organic solvent performed here clearly shows a high degree of dispersion, far superior to what is observed in water simulations. The reasons for this are not totally clear, but one possible explanation may be that we are simulating a system that is inherently unstable and is kinetically trapped (Zaks and Klibanov, 1988b). From an x-ray structure to a water simulation we do not expect to see many structural changes, inasmuch as both situations correspond to highly aqueous environments. From an x-ray structure to an organic solvent may be a totally different matter. In general, organic solvents denature proteins and metastability is the reason why this does not occur in the conditions used to do catalysis in these media. These metastabilizing factors (for example, the contact with other protein molecules) are not totally present in the models usually simulated, rendering the simulated system more unstable than the real systems. Nevertheless, as we show here, phenomenological aspects of real experiments can be captured by these simulation studies.

The control that water exerts on enzyme activity in organic solvents can be explained by our simulations. Native structure conservation is higher at an optimal value of water content (5–10% w/w; see Fig. 2), being the structure less stable in lower (including zero) or higher water contents. This is mimicked by the active site zone, which, in hexane, is even more similar to the x-ray structure than in water, suggesting that catalytic properties are intact. Water is necessary to stabilize polar groups and counterions in selected zones of the protein, including the active site (see Fig. 5). Additionally, water plays an instrumental role in rendering the protein flexible enough to perform its biological function. The 5–10% hydration zone also provides similar protein flexibility as that observed in water simulations. This hydration zone promotes the most native structure and the same physiological flexibility. Experimentally, a hydration of ∼10% (w/w) is usually the optimal zone for catalysis with suspended enzymes (Affleck et al., 1992; Carvalho et al., 1996; Fontes et al., 1998b). For cutinase, the optimal percentage of bound water was not determined, but a bell-shaped dependence of catalysis on water activity is observed (Fontes et al., 1998a). Experimental studies where enzyme activity in organic solvents is controlled by other molecular lubricants (organic molecules with similar effects as the water), also show the same picture (Griebenow et al., 2001): optimal activity coincides with the zone where the protein structure and its conformational mobility are more similar to the ones found in water.

The reasons behind unfolding (or at least destruction of some parts of the structure) under high water content are worth mentioning here. Protein destruction starts to occur when the water clusters at the surface of the protein start to collapse into larger clusters (see Fig. 4), providing a medium for ion diffusion and for the formation of ion pairs. With this (or due to this), the charged groups of the protein move to keep themselves neutral, resulting in structural changes (see Fig. 5). Water, besides acting as a lubricant providing the protein enough flexibility, can, above a certain level, lower the kinetic barrier between the folded and unfolded states. The ions also seem to play an important role in this process.

SUPPLEMENTARY MATERIAL

Tables containing the pK_1/2 values calculated for all protonatable residues of ubiquitin and cutinase. These values are obtained from protonation equilibrium calculations using continuum electrostatic and Monte Carlo sampling methods.