Abstract
Bioapatite, the main constituent of mineralized tissue in mammalian bones, is a calcium-phosphate-based mineral that is similar in structure and composition to hydroxyapatite. In this work, the crystallographic structure of bioapatite in human fetuses was investigated by synchrotron radiation x-ray diffraction (XRD) and microdiffraction (μ-XRD) techniques. Rietveld refinement analyses of XRD and μ-XRD data allow for quantitative probing of the structural modifications of bioapatite as functions of the mineralization process and gestational age.
INTRODUCTION
Bones are skeletal organs that allow body mobility and protect internal organs. In addition to mechanical functions, bones have an essential role in metabolic activity as mineral reservoirs that are able to absorb and release ions. From a histological point of view, bone consists of several organic and inorganic tissues such as fibrous and lamellar parts, cartilage, and marrow and contains vascularization, innervation, and so on. In terms of structure, bones can be considered as a dispersion of mineral particles (biominerals) embedded in an organic matrix, which forms the contiguous phase. Bioapatite, considered the major component in the mineralized part of mammalian bones, is a calcium-phosphate mineral with a structure that closely resembles hydroxyapatite (OHA), Ca10(PO4)6(OH) (Smith et al., 1983) with variable chemical composition. Bioapatite in fact is a highly accommodating mineral species that is able to store and release calcium, phosphorous, and several other ions such as Na, K, Mg, F, CO3, and OH. For this reason, bioapatite represents an important mineral reservoir for the metabolic activity of the organism (Skinner, 2000). Biochemical activity makes the mineral bone composition vary greatly, depending on the site of sampling, cellular metabolism, age, diet, and diseases. These features make it difficult to univocally establish the composition and structure of bioapatite minerals and to explain the discrepancy in results that can be found in the literature (Driessens and Verbeeck, 1990).
The apatitelike nature of the mineralized part of bone tissue was revealed many years ago by x-ray diffraction (XRD) investigations (De Jong, 1926). It is well established (Smith and Smith, 1978; Very and Baud, 1984) that bone minerals are mainly constituted by defective calcium hydroxyapatite (DOHA) with variable composition. Natural bioapatite is a highly defective/poorly crystallized structure with broad diffraction lines that prevent accurate phase or composition determination by XRD techniques; consequently, most structural models of bioapatite rely principally on chemical information (Driessens and Verbeeck, 1990). The general formula Ca10−x+ηXy(PO4)6−x(CO3)x(OH)2−x+η proposed by Skinner (2000) accounts for the possible inclusion of ions (x), the substitution of CO32− for PO43−, and the presence of calcium vacancies.
The development and maintenance of bone mineral involves complex processes and a continuous turnover of mineral and organic parts that derive from metabolic activity, aging, and disease. An understanding of the structural and chemical transformations of natural bioapatite, as well as the nature and function of the precursor materials and the role of environmental constraints in determining the structure and composition of the ultimate bone mineral, are all relevant issues from biological and medical points of view that motivate extensive research activity in the field (Posner et al., 1975; Albright and Skinner, 1987). Synthetic OHA is produced by precipitation from a calcium-phosphate-containing aqueous solution. The precipitation of synthetic OHA from the initial solution involves the formation of several intermediate calcium-phosphate phases. Amorphous calcium phosphate (ACP), which has a composition similar to whitlockite (Ca10(HPO4)(PO4)6), appears as the initial precipitate from the solution. The ability of ACP to absorb both Ca2+ and HPO42− leads to the formation of a defective apatite with the general formula Ca9(HPO4)y(PO4)6−yOHy. From a chemical point of view, the evolution of this compound results in a continuous increase in the OH− content as well as an increase in the Ca/P ratio, from Ca/P = 1.43 (in ACP) to Ca/P = 1.67 (in OHA). Several authors (Berry, 1967; Joris and Amberg, 1971) realistically hypothesized that DOHA and OHA form a solid solution with the general formula Ca10−x(HPO4)x(PO4)6−x(OH)2−x. Other works suggest the formation of intermediate phases such as octocalcium phosphate (OCP) with the formula Ca8(HPO4)2(PO4)4 · 5H2O and dicalcium phosphate dihydrate (DCPD) with formula CaHPO4 · 2H2O (Brown et al., 1979. The presence and the relative amounts of these phases are constrained by environmental parameters such as the composition of the initial solution, pH, temperature, and so on. Given the complexity of the processes involved in precipitating synthetic OHA, it is clear that understanding the mechanisms involved in the formation of natural bioapatite is an intricate task.
Ossification is the process whereby new bone is produced; it starts early in humans, during gestation, and continues after birth and throughout childhood. The early stages of mineralization of bone tissue proceed through the formation and growth of bioapatite crystallites from a precursor material (Brown et al., 1979; Termine and Posner, 1967). These stages are essential in determining the quality of the adult bone; however, several questions about the processes that are related to the evolution and growth of bone mineral during ossification still remain unanswered. Various techniques such as x-ray radiography (Bagnall et al., 1977; Bareggi et al., 1993), histology (Gray et al., 1995, Nobackar and Robertson, 1951), sonography (Filly et al., 1987; Budorick et al., 1991; Wallny et al., 1999), dual-energy absorptiometry (Panattoni et al., 1995; Braillon et al., 1992), and computed tomography (Braillon et al., 1996) have been employed to investigate the morphological development of bone and its mineral density during fetal growth. Complementary techniques such as XRD (Germine and Parsons, 1988; Bigi et al., 1997) and x-ray absorption spectroscopy (XAS; Miller et al., 1981) have been used to describe the crystalline structure of mineralized bone tissue. Nevertheless, relatively few XRD studies have been performed on human samples (Chatterji and Jeffery, 1968; Smith and Smith, 1976; Royle and Speller, 1995) and, very rarely, on human fetal bone (Oyedepo and Henshaw, 1997).
In this work, we studied the crystallographic structure of bone mineral in human fetuses at different gestational ages during the early stages of bone formation using high-quality XRD and micro-XRD (μ-XRD) measurements. Diffraction data were quantitatively analyzed using the Rietveld refinement approach (Young, 1993), which allowed us to characterize the structure of bioapatite in its early stages and to follow its modification as a function of the mineralization process.
EXPERIMENTS AND DATA ACQUISITION
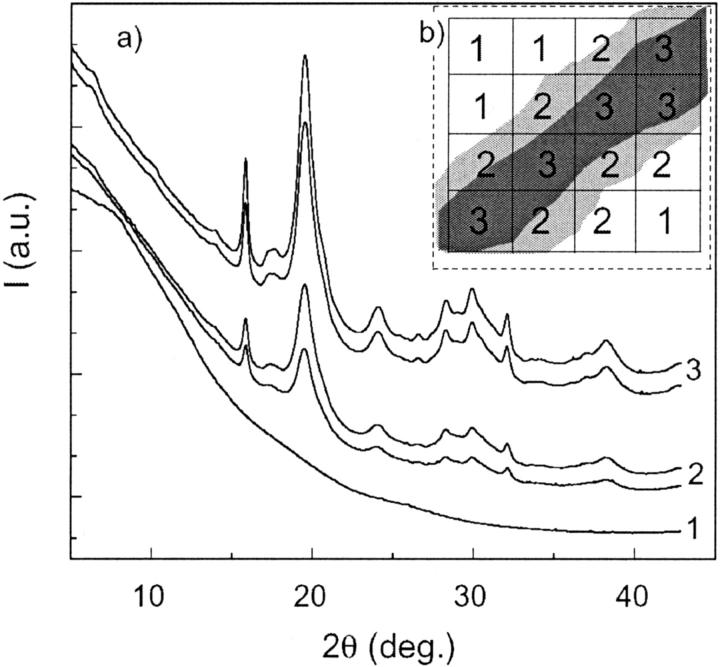
Twenty-two bone samples collected from the lumbar vertebrae of human fetuses were analyzed. All samples, which were provided by the Department of Pathology of Eduard Herriot Hospital (Lyons, France), were excised from human fetuses with no known pathologies that were prematurely deceased at different gestational ages ranging from 16 to 26 weeks. The vertebrae were stored in pure ethyl alcohol to prevent degradation. At these gestational ages, fetal vertebrae are made up of a cartilaginous template in which regions of mineralized tissue are embedded. These regions are ossification centers from which the vertebra mineralization process (endocondrial ossification) originates. Fig. 1 a shows the image of a thin (8-μm thick) slice of a vertebra horizontally excised from a 26-week-old fetus. The ossification region is characterized by a dense network of dark, fine structures (trabeculae). Fig. 1 b shows the μ-XRD patterns collected from the surrounding region (A) of the bone slice and, inside the ossification region, from a clear region (B) and from a dark trabecula (C). The evident differences between the three μ-XRD patterns A, B, and C highlight the structural variations in the different regions investigated: the μ-XRD pattern collected from a trabecula presents diffraction peaks revealing the presence of a crystallized structure, whereas the patterns corresponding to the surrounding and interstitial regions are characterized by broad halos that indicate an amorphous phase without significant traces of crystalline phases.
FIGURE 1.
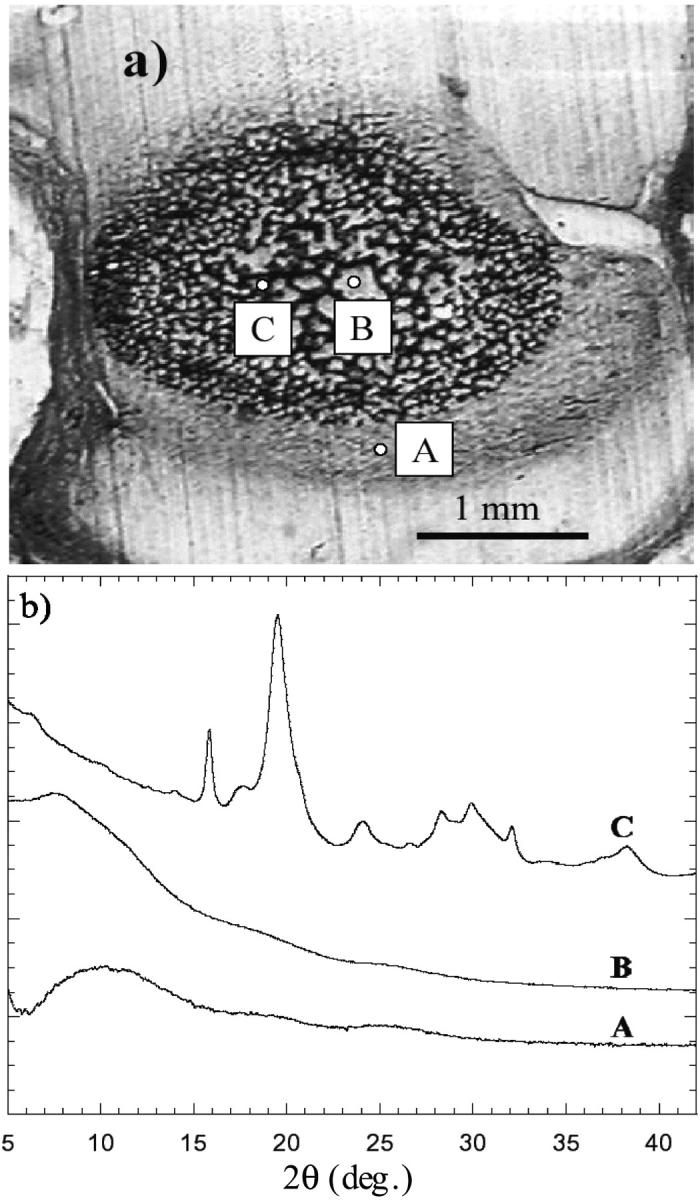
(a) Microscopic image of a thin vertebra slice excised from a 26-week-old fetus. (b) μ-XRD patterns collected from the surrounding region (A), from a clear internal region (B), and from a dark trabecula (C).
Fetal bone samples were studied using XRD to investigate the bone mineral structure as a function of fetal age, whereas the μ-XRD technique was used to examine the bone mineral structure inside the ossification center. Samples for XRD were excised from the mineralized regions of the vertebra body and crumbled by hand for a few minutes in agate mortar, and the finest particles were selected with a sieve. This procedure allows a homogeneous dispersion of particles, which is well suited for good-quality XRD patterns. For each sample, 10–20 mg of powder were enclosed in a cylindrical borosilicate capillary (inner diameter, D = 0.5 mm) and sealed under N2 to prevent degradation of organic parts. This procedure ensures minimal exposure of the samples to air. Each capillary was immersed for ∼10 min in an ultrasonic bath to compact the powders. XRD experiments were carried out on the General Italian Line for Diffraction and Absorption (GILDA) beamline (Pascarelli et al., 1996) at the European Synchrotron Radiation Facility (ESRF) in Grenoble, France. Powder diffraction patterns were collected using an angle-dispersed setup (Meneghini et al., 2001) based on a 2-D imaging plate (IP) camera (200 × 400 mm2). The beam size on the sample was 1.5 × 1 (horizontal × vertical) mm2. The beam energy chosen was 12 keV, which corresponds to a wavelength of 1.0332 Å. During the experiment, the beam energy (E) was regularly checked and proved to be within ±0.5 eV (ΔE/E < 10−4). The capillaries containing the bone powders were mounted horizontally on a goniometer head, aligned on the beam, and kept rotating during acquisition to improve the grain statistics. The IP was positioned perpendicular to the sample at a distance of 304 mm. The collection time for each diffraction pattern was 15 min. The diffraction patterns, stored in the IP latent images, were read and digitized using a BAS-2500 laser scanner with a 100 × 100 μm2 pixel size and a dynamic range of 16 bits/pixel. The parameters of the instrumental setup, namely, the sample-to-detector distance, instrumental peak broadening, and IP orthogonality, were calibrated and controlled regularly during the experiment, thereby collecting and refining the diffraction patterns of standard reference materials (LaB6: NIST SRM/RM660a; Si: NIST SRM/RM640c). A synthetic calcium hydroxyapatite (Riedel-de Haën AG, Germany) and a bone sample excised from an adult (33 year old) human vertebra were used as reference compounds.
The μ-XRD measurements were performed on the microfocus beamline ID13 (Riekel et al., 1992) at the ESRF. A thin slice (thickness ∼8 μm) of a vertebral bone from a 26-week-old fetus was investigated using a focused x-ray beam at a 0.9755-Å wavelength and with a 5-μm spot size. The sample was mounted on a goniometer head at a distance of ∼62 mm from the detector screen. Diffraction patterns were recorded using a liquid-N2-cooled charge-couple device (CCD) with an active area of 2 × 25 cm2 and were mounted perpendicular to the incident beam. The detector geometry (distance from sample, tilt of detector, center of diffraction pattern) was calibrated using a powder diffraction pattern of calibration standard Al2O3 using the program FIT2D (Hammersley et al., 1994). A microdiffraction map of a sample region was realized by translating the sample along the vertical and horizontal directions in a square area 30 × 30 μm2 wide with a mesh of 10 μm. Sixteen 2-D diffraction patterns were collected at each sample position (see Fig. 6 b).
FIGURE 6.
(a) μ-XRD patterns relative to different selected areas of the bone sample. (b) Schematic of the scanning procedure: diffractograms labeled 1 are collected from the intertrabecular region, those labeled 2 are collected from the trabecular surface, and those labeled 3 are collected from the inner region of the trabecula.
The use of area detectors such as IPs and CCDs allows diffraction patterns to be collected with high counting statistics and greatly reduced acquisition times. These characteristics were well suited to this experiment, because we were dealing with a relatively large number of weakly scattering samples, and a fast readout allowed the effects produced by sample degradation to be reduced. Moreover, the possibility of integrating a large fraction of the Debye-Scherrer rings made it possible to diminish the effect of preferred orientation in the sample.
The 2-D Debye-Scherrer rings were integrated to the equivalent of a 2θ scan and were corrected for polarization and tangent geometry using the FIT2D package. IP images were integrated along circle arcs as illustrated in Fig. 2 a. The asymmetrical “cake” integration was used to extend the reciprocal space and to avoid an additional instrumental line broadening due to the x-ray beam divergence in the horizontal plane. The μ-XRD images (Fig. 2 b) were integrated using the whole screen. XRD and μ-XRD patterns were analyzed using the Rietveld structural refinement approach as implemented in the General Structure Analysis System (GSAS) package (Larson and von Dreele, 1994).
FIGURE 2.
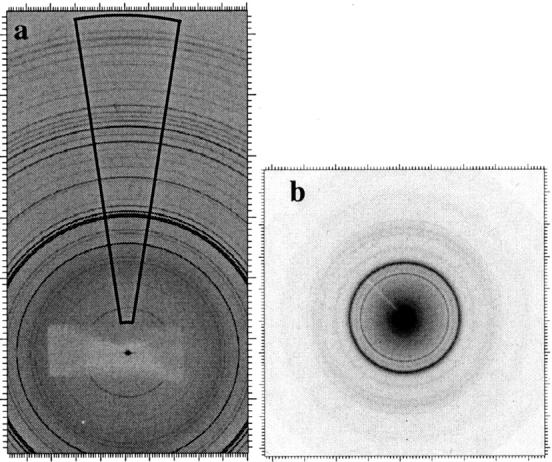
(a) Typical 2-D XRD image collected from synthetic OHA at GILDA; the area used to convert the 2-D image into the equivalent 1-D pattern is shown. (a) Typical 2-D μ-XRD image of bone bioapatite measured at ID13.
DATA ANALYSIS AND RESULTS
XRD data
Fig. 3 displays the XRD patterns of the synthetic OHA, the adult bone sample, and two fetal bone samples of 26 (A26) and 16 (A16) weeks old. The four diffraction patterns display evident similarities and point out the analogy between the structures of bone bioapatite and synthetic OHA (Posner and Diorio, 1958; Smith and Smith, 1978; Very and Baud, 1984). Detailed diffraction studies on single-crystal OHA indicate a monoclinic structure (space group P21/b) (Elliot et al., 1973; Ikoma et al., 1999). However, the hexagonal symmetry works well when dealing with powder diffraction data, and the crystal structure of synthetic OHA is usually described in space group P63/m with a hexagonal unit cell (Posner and Diorio, 1958; Kay et al., 1964; Sudarsanan and Young, 1969; Pritzkow and Rentsch, 1985). The crystallographic structure reported by Sudarsanan and Young (1969) was adopted as a structural model in the Rietveld refinement of synthetic OHA and bone bioapatite samples. Good structure refinements (Fig. 4) were obtained by varying the scale factor, background coefficients, unit-cell axes (a = b and c), and profile-function parameters. Atomic thermal factors, site occupancies, and atomic positions were kept fixed during the refinement, because the quality of the diffraction patterns was not sufficient to refine the crystal structure. The parameters that we refined are independent of peak intensities and therefore are not affected by absorption conditions and (weak) preferred orientation, which has been documented in at least some of the microfocus images.
FIGURE 3.
Experimental XRD pattern intensities (I, in arbitrary units, a.u.) relative to synthetic OHA, adult bone sample, and fetal bone samples 26 (A26) and 16 (A16) weeks old. Patterns are vertically shifted for the sake of clarity.
FIGURE 4.
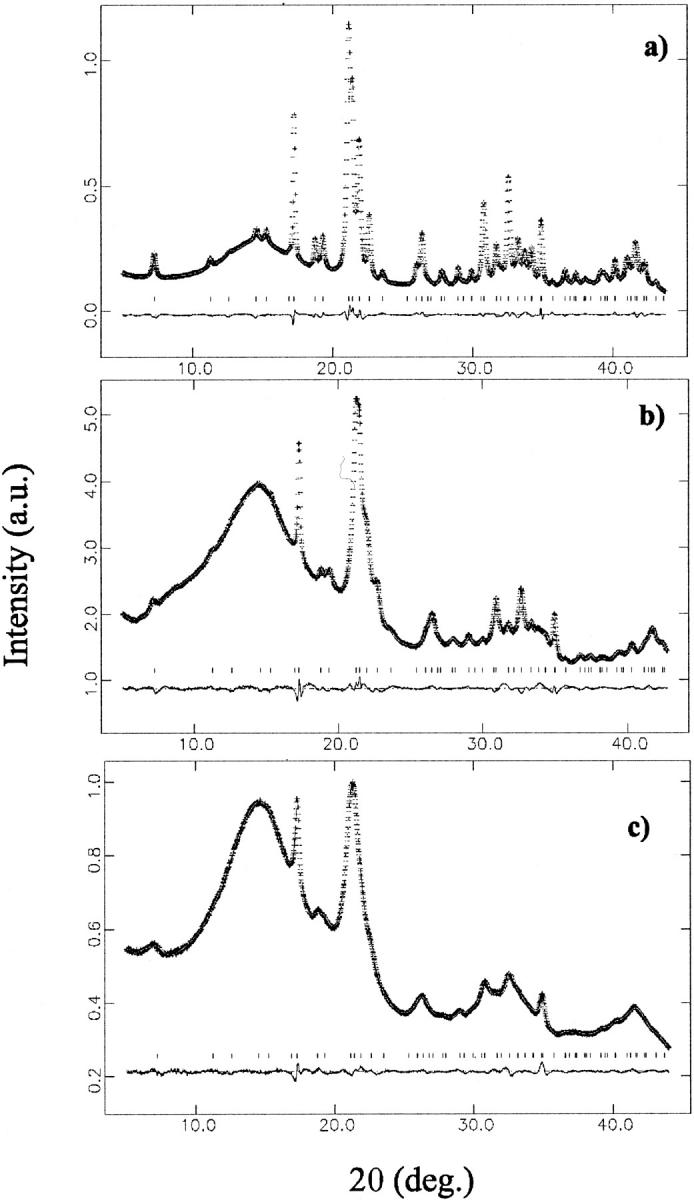
Rietveld refinement for selected samples: (a) synthetic OHA; (b) bioapatite in the adult bone sample; and (c) bioapatite in fetal bone sample (16 weeks old). Each panel reports the observed and refined data, almost indistinguishable (top trace); their difference (bottom trace), shifted for clarity; and the calculated reflection positions (middle points).
The diffraction patterns of bone samples are characterized by a quite intense background that shows a marked halo at 2θ ∼ 15°. This feature, which is present also in the synthetic OHA diffraction profile, mainly derives from the diffuse scattering contribution of the glass capillary sample holder. The background was described using a 12-term shifted-Chebishev function, and the diffraction profile was modeled by a pseudo-Voigt peak-shape function (Thompson et al., 1987) as implemented in the GSAS package.
The profiles of bone-sample patterns show signs of strong anisotropy in the peak broadening. In fact, from a close inspection of the diffraction profiles reported in Fig. 3, it is evident that the 00l reflections in adult as well as in fetal bone samples are noticeably sharper than the other reflections of the pattern. The sharper 00l reflections suggest that, as in the case of synthetic OHA, also in bioapatite crystals the coherent diffraction domains preferentially extend along the crystallographic c direction. To achieve satisfactory fits of the experimental diffraction profiles, it was necessary to employ anisotropic contributions to the peak-shape function. Fixing the anisotropic broadening axis along the 00l direction, the refined anisotropy broadening coefficient Xe (Larson and Von Dreele, 1994) assumed negative values ranging between −0.9° and −1.3° in fetal samples and became Xe ∼ −0.40° in the adult bone sample. The Xe coefficient in fetal samples shows a large dispersion of values that does not reveal a trend as a function of gestational age. However, the Xe absolute values in bone mineral are greater than those found in synthetic OHA (Xe = −0.22°), which means that the anisotropy of bone mineral is more pronounced than in hydroxyapatite, and that it is greater in younger bone mineral than in adult bone mineral.
Observing the diffraction patterns in Fig. 3, it can also be noted that the diffraction peaks of bone bioapatite are broader than the diffraction peaks of synthetic OHA. This feature clearly indicates that fetal bone bioapatite is a more poorly crystallized/highly defective material. Moreover, the diffraction lines of fetal bone samples are broader than those of adult bone, which suggests that the diffracting particles (crystallites) in the younger bone are smaller and/or more defective than in adult bones. Both crystallite size and the lattice defects concur in determining the broadening of the XRD peaks, so that the sample-related line shape can be considered as a convolution of strain- and size-related profiles. The remarkable anisotropy that characterizes the profile function of bone samples indicates either a large number of defects in the a, b plane and/or the anisotropic shape of the crystallites (coherent domains) that should be elongated along the crystallographic c direction (Carlström and Glas, 1959). Strain- and size-related contributions are different functions of the diffraction angle (Warren, 1990), so that at least in principle, it should be possible to distinguish between the two effects. However, on poorly crystallized compounds such as bone bioapatite, this is a difficult task. An attempt to determine the microstrain effect (see Appendix A) does not allow the detection of any trend as a function of age (bone maturation), and thus for the sake of simplicity, we have neglected the microstrain contribution and assumed that the peak broadening is largely caused by particle-size effects. This approximation overestimates the particle size (Appendix A) but does not affect the trend observed as a function of age (bone maturation). We have estimated the crystallite size as length along the c axis (τc) and the width of the a, b plane (τa,b) by applying the Scherrer formula:
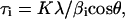 |
(1) |
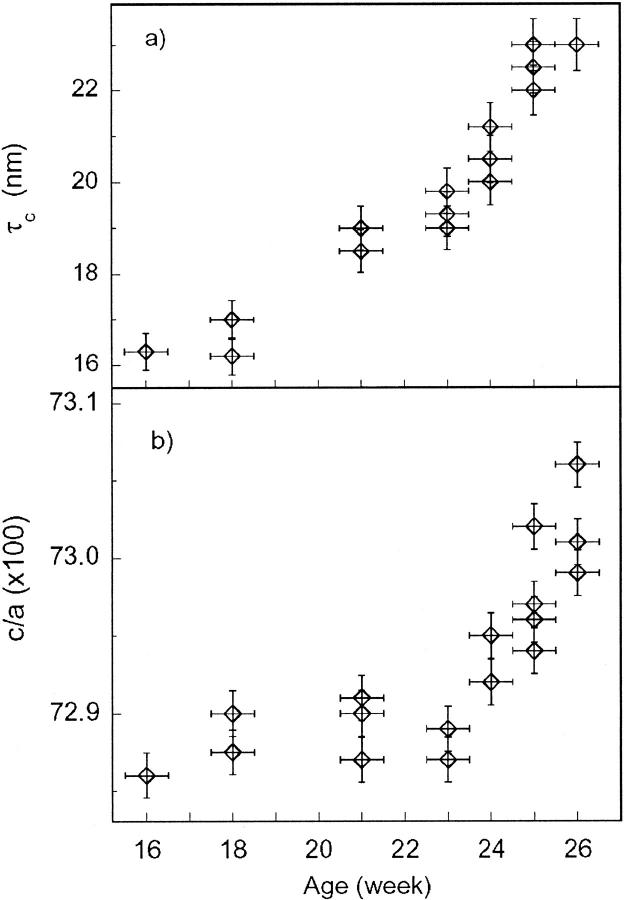
where K = 0.9 is the shape factor, λ is the x-ray wavelength, and βi = Δ2θ − βexp is the experimental full-width half-maximum (Δ2θ) of the diffraction line corresponding to the crystallographic direction i, subtracted by the instrumental broadening contribution βexp · βexp that was calculated using the relation given by Meneghini et al. (2001), which describes the angular resolution as a function of the diffraction angle using a flat-plate detector. Peak-width analysis shows that in the adult bone sample, τc ∼ 33 nm and τa,b ∼ 12 nm, and in fetal bone samples, τc ∼ 16–20 nm and τa,b ∼ 6–7 nm. The reported values are in agreement with the dimensions reported in literature (Wheeler and Leweis, 1977). The τa,b values as a function of fetal age remain constant within the experimental uncertainty. The significant finding of our data is the progressive sharpening of the diffraction peaks corresponding to the 00l crystallographic direction as a function of gestational age. Fig. 5 demonstrates the increase of τc as a function of fetal age from ∼16.5 nm for the 16-week-old sample to ∼20 nm in the 26-week-old sample and reaching 33 nm in the adult sample.
FIGURE 5.
Evolution of the bioapatite crystallite size (a) along the c axis and (b) of the c/a ratio, as a function of gestational age.
A further significant finding derives from the refinement of the unit-cell dimensions. Table 1 reports the lattice parameters refined in bone samples and synthetic hydroxyapatite. The lattice-parameter values for fetal bones were averaged for all of the investigated samples. The uncertainty of fetal lattice parameters was calculated as the variance of the whole set of XRD data. This uncertainty displays quite a large dispersion (σ ∼ 6 × 10−3) that is well above the statistical uncertainty given by GSAS (σ ∼ 1 × 10−3). This effect is only partially due to the known underestimation of the statistical error in GSAS; it is more likely a real feature that reflects the natural spread of structural parameters in natural samples. The unit cell of fetal bioapatite appears expanded with respect to the synthetic OHA (Δa/a ∼ 0.2% and Δc/c, ∼0.04%); whereas the unit cell for adult bone bioapatite is reduced with respect to the unit cell of synthetic OHA, thereby registering greater compression in the a,b hexagonal plane (Δa/a = −0.4%) and smaller shortening along the c axis (Δc/c = −0.1%). When the c/a ratios of the unit-cell parameters are compared, it can be noted that the c/a ratio in adult bone (c/a = 0.7326) is equal to the value c/a = 0.7326 that was reported by Smith and Smith (1976) for adult bone bioapatite and slightly larger than the c/a ratio in synthetic OHA that was found by us (c/a = 0.7305) and reported in literature (c/a = 0.7301; Sudarsanan and Young, 1969). Fig. 6 reports the values of the c/a ratio in fetal samples as a function of the gestational age. Despite the dispersion of values, one can notice an increasing trend of the c/a ratio as a function of bone aging. The results of XRD data analysis come in agreement with those reported previously (Nuzzo et al., 2003). However, in the present work, the Rietveld refinement approach ensures better reliability.
TABLE 1.
Refined values of the unit-cell parameters
| Sample | a = b (Å) | c (Å) |
|---|---|---|
| OHA | 9.4220 (6) | 6.8833 (5) |
| Adult | 9.3836 (9) | 6.8745 (9) |
| Fetal (XRD)* | 9.4411 (57) | 6.8862 (23) |
| Fetal (μ-XRD)† | 9.4405 (43) | 6.8766 (26) |
Numbers in parentheses indicate reported errors on last digits.
Reported values were averaged over all samples investigated by XRD.
Reported values were averaged over whole area investigated by μ-XRD.
μ-XRD data
Powder diffraction measurements on fetal bone samples highlight structural modifications as a function of gestational age. These changes, on average, reflect the modification induced by age on the overall bone mineral within the ossification region. The microdiffraction technique allows the gaining of deeper insight into structural effects of the mineralization process by the direct examination of different regions of a single structure (trabecula) inside the ossification center. The average size of a trabecula inside the ossification region is ∼50–100 μm (Nuzzo et al., 2003), thus the small (∼5 μm) spot size allows for different regions of a single trabecula to be selectively investigated. A 30 × 30-μm2 square region around a bone trabecula was probed (Fig. 6 b), and selected μ-XRD patterns are shown in Fig. 6 a. The μ-XRD patterns depict evident differences: some of them, corresponding to mineralized regions (curves labeled 2 and 3 in Fig. 6), present clearly defined diffraction peaks, whereas others, corresponding to the cartilaginous intertrabecular space (curves labeled 1 in Fig. 6), display an amorphous behavior. The μ-XRD patterns were Rietveld-refined using the same approach as for the XRD data. The average lattice parameters refined from μ-XRD data are reported in Table 1; these values are in good agreement with those resulting from XRD data refinement.
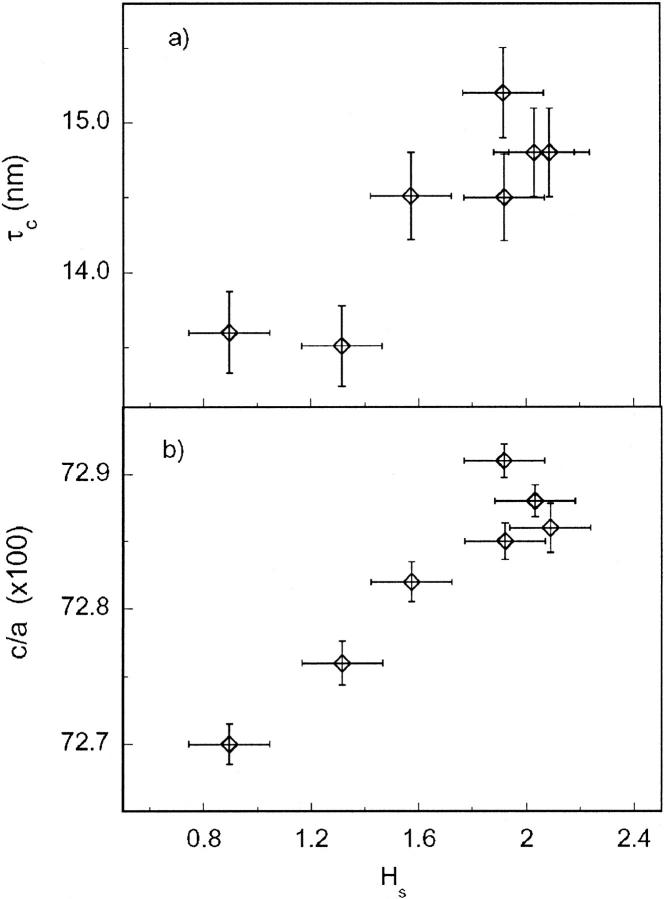
It can be noted that the μ-XRD patterns reported in Fig. 6 depict significant differences in the intensities of diffraction peaks with respect to the background. The diffractogram intensity is related to the mineral density inside the volume probed by the x-ray microbeam; consequently, weaker reflections suggest that the beam is probing a region in the vicinity of the trabecula surface, where the cartilage occupies a (large) fraction of the volume (Fig. 6 b). On the contrary, more intense patterns indicate that the beam, as expected in the inner trabecular region, probes a larger fraction of mineral particles. To quantify the variable intensity of diffraction patterns, we referred to the histogram scale factors implemented in GSAS. The histogram scale factor (Hs) is a refinable variable that is proportional to the number of unit cells of a given phase present in the sample. Fig. 7 shows the particle size (τc) and the c/a ratio as a function of Hs: both τc and the c/a ratio depict a positive trend as a function of Hs. The positive correlation between reflection intensity and particle size indicates that in the external region of the trabecular area, bioapatite presents smaller crystallites, whereas larger bioapatite crystallites occur in the inner region of the trabecula. In addition, the increasing c/a ratio from the outer to the inner region of a single trabecula confirms the tendency found analyzing the powder diffraction data of bone samples with increasing gestational age. These results suggest that the trabecular region is composed of “younger” bone particles at the surface of the trabecula, which reflects an early stage of the ossification process, whereas “older” bone particles in the inner part of the trabecula signal a more mature stage. As in the XRD data, the Xe values obtained from refining μ-XRD patterns are in the range of −0.80° to −0.90°, which documents a remarkable anisotropy of the 00l reflections. Moreover the μ-XRD images suggest a weak texture effect; however, a reliable analysis of texture is beyond the scope of the present work.
FIGURE 7.
Evolution of bioapatite crystallite size (a) along the c axis and (b) of the c/a ratio, as a function of histogram scale factor (Hs) refined by GSAS (see text for details).
DISCUSSION
The analogies between XRD patterns of synthetic OHA and adult and fetal bone samples demonstrate that the crystallographic structure of bone mineral closely resembles that of OHA. The natural bone minerals realistically consist of a mixture of defective hydroxyapatite phases with variable chemical composition. However, we obtained good Rietveld refinements using a single OHA phase as a structural model. This suggests that the average structure of bone bioapatite results from a homogeneous distribution of OHA-like phases. Moreover, the differences between the observed and calculated patterns in the Rietveld refinements do not show features that can be associated with polycrystalline phases other than OHA-like ones. Considering the high statistics of our XRD and μ-XRD data, the occurrence of polycrystalline phases other than OHA-like phases can be considered negligible in these bone samples. Unfortunately, the diffuse scattering coming from the sample holder (XRD) and the intense air scattering (μ-XRD) make it difficult to determine and quantify the presence of amorphous phases.
X-ray diffraction data show that the bone mineralization process as a function of gestational age implies average growth of bioapatite crystallites and/or the reduction of their lattice defects and strains. Microdiffraction data reveal that the overall development of bone mineral observed as a function of fetal age corresponds on a microscopic scale to the mineralization process within a developing area of the bone: μ-XRD data indicate that within the trabecular region, there are areas characterized by small and/or highly defective bioapatite crystallites, which is as expected for immature or prematurely formed mineral particles. Moving toward inner regions of a trabecular area results in a progressive enlargement of the crystallites, which is as expected for the mature mineral. Moreover, XRD and μ-XRD suggest that the lattice deformations (revealed by the increased c/a ratio) are directly related to the maturation progress of bioapatite mineral: younger bioapatite crystallites show smaller values of the c/a ratio, whereas more mature bioapatite crystallites present increasing values of the c/a ratio.
Structural changes in early-forming bioapatite mineral can offer insight into the composition of the bone mineral component during the early ossification stages. This problem has usually been addressed through compositional studies demonstrating an overall deficit of calcium with respect to phosphorus during the early stages of the ossification process in vivo as well as in vitro (Pellegrino and Biltz, 1972; Burnell et al., 1980) and in human fetuses (Oyedepo and Henshaw, 1997). The various models proposed suggest the presence of a mixture of impure OHA and calcium-phosphate phases characterized by different calcium-phosphate stoichiometry, such as ACP (Ca/P = 1.44; Termine and Posner, 1967) and OCP (Ca/P = 1.33; Brown et al., 1979). It has been also demonstrated that the calcium content in bone tissue increases as a function of gestational age (Driessens, 1990). However, the main drawback of chemical analysis lies in the difficulty in discriminating between crystalline and amorphous phases inside a single specimen. A close inspection of the low-angle region in our diffraction patterns of fetal samples reveals a systematic shift of the 100 reflections toward lower 2θ angles with respect to the 2θ100 position in synthetic OHA, which demonstrates the expansion of the unit-cell along the 100 direction. Other authors have reported a similar effect on poorly crystallized apatites (Le Geros-Zapanta, 1965; Brown et al., 1979), although these authors interpreted their findings in a different way. Brown et al. (1979) explained the lattice expansion along the 100 direction in OHA-containing precipitates as due to the presence of interlayered mixtures of OHA and OCP. However, the possibility of detecting the OCP by standard XRD analyses is impeded by the instability of the OCP phase, which rapidly hydrolyzes to produce OHA (Cheng, 1987) as well as by the occurrence of interlayer mixtures of OCP and OHA that produce superimposed and mixed diffraction peaks. The refinements of our data do not show residual features that can be related to the OCP phase, even if the reduced air exposure of the sample during preparation and measurements diminishes the probability of sample degradation. Our data thus suggest the absence of significant OCP contamination, even in the early bioapatite mineral (Fig. 4, c). Our results are consistent with the findings of other authors that interpreted the lowering of the 2θ100 position as due to compositional effects such as, for example, the inclusion of Cl− (substituting for OH−) and HPO42− (substituting for PO4) ions in apatite, which causes the lengthening of the apatite a axis (Le Geros-Zapanta, 1965).
CONCLUSIONS
XRD and μ-XRD data demonstrate that early-forming bone minerals can be described by a calcium-phosphate phase (bioapatite) whose structure closely resembles that of hexagonal OHA. The bioapatite crystallites are small and elongated along the crystallographic c axis, and they grow as bone maturation proceeds. The bone maturation process involves structural changes related to the composition of bioapatite. Our data suggest that the early-forming bone mineral is a calcium-defective deficient OHA phase. The calcium deficit is progressively reduced with bone mineral maturation.
Acknowledgments
R. H. Wenk is appreciative for hospitality at the ESRF during sabbatical leave, and to Luce Lutterotti (University Di Trento, Italy) for help with MAUD code. The authors acknowledge the help of Dr. M. Burghammer in running the ID13 beamline and the excellent technical support of F. Campolungo, V. Sciarra, V. Tullio (INFN-LNF), and F. D'Anca (INFM-OGG Grenoble) in optimizing the GILDA beamline setup.
APPENDIX A
Two-dimensional detectors such as CCDs and IPs allow for the collecting of patterns with exceptional counting statistics and reduction of the effects of preferred orientation in the sample. However, the reduced angular resolution yields larger uncertainty in the line-shape profile fitting with respect to high-resolution diffractometers. In particular, in the present case, it is difficult to distinguish between microstrain and particle-size contribution to the diffraction-line shape. In the main work, we decided to neglect the microstrain contribution. However, microstrain is expected to give a non-negligible contribution in these poorly crystallized samples, and additional justification of our approximation will provide more confidence in the systematic trends observed and described in the bulk of this paper.
Because of the wide line broadening, peak superposition, and the strong anisotropy in peak broadening, it was not possible to derive particle size and microstrain from the GSAS profile parameters. In addition, superposition and peak width also prevented the use of the Williamson-Hall method (Delhez et al., 1993) that, in the case of strong anisotropy in peak broadening (as in our case), can be applied only to reflections for which two or more orders are available. To get further insight on the size and strain contributions, we independently refined some data sets of adult and fetal bone samples using the material analysis using diffraction (MAUD) code (Lutterotti and Scardi, 1990), which allows for the specific anisotropic treatment of root-mean-square (rms) microstrain as well as crystallite size. In these refinements, the amorphous component was approximated by a silica glass (“cubic” with very small grain size). For the crystalline hydroxyapatite component lattice parameters (a, c), anisotropic crystallite size (corresponding to the average length of the columns normal to the diffracting plane) and rms microstrain were refined. Temperature factors were kept constant, whereas the atomic positions and occupancies did not vary significantly. The principal results are summarized in Table 2; the c/a ratios are in good agreement with the previous GSAS results. Moreover, the OHA crystallites appear anisotropic and larger in adult than in fetal bone as already observed. Microstrain and crystallite size are both strongly anisotropic, which suggests, as already noted, that OHA crystallites are needles extending parallel to the c axis. Interestingly the inclusion of the microstrain contribution in the profile fitting results in smaller crystallite size. However, it is noticeable that the microstrains remain almost the same in adult as in fetal bone samples without any significant trend with fetal age. This suggests that the bone maturation process mainly affects the crystallite size, whereas microstrain only weakly affects the changes in diffraction-line shape; thus this independent analysis justifies our model.
TABLE 2.
Structural parameters obtained in refining XRD patterns with MAUD Rietveld package
| Size (nm)
|
Strain (%)
|
||||
|---|---|---|---|---|---|
| Sample | c/a | τa,b | τc | Sa,b | Sc |
| Fetal | 0.7303 | 3 | 13 | 0.012 | 0.05 |
| Adult | 0.7327 | 7 | 27 | 0.011 | 0.03 |
Anisotropic crystallite size and rms microstrain were refined using the method of Lutterotti and Scardi (1990).
References
- Albright, J. A. and H. C. W. Skinner. 1987. Bone: structural organization and remodeling dynamics. In The Scientific Basis of Orthopaedics. J. A. Albright and R. Brand, editors. Appleton and Lange, Norwalk, CT. 161–198.
- Bagnall, K. M., P. F. Harris, and P. R. M. Jones. 1977. A radiographic study of the human fetal spine. 2. The sequence of development of ossification centres in the vertebral column. J. Anat. 124:791–802. [PMC free article] [PubMed] [Google Scholar]
- Bareggi, R., V. Grill, M. A. Sandreucci, G. Baldini, A. De Pol, A. Forabosco, and P. Narducci. 1993. Development pathways of vertebral centra and neural arches in human embryos and fetuses. Anat. Embryol. (Berl.) 187:139–144. [DOI] [PubMed] [Google Scholar]
- Berry, E. E. 1967. The structure and composition of some calcium-deficient apatites. J. Inorg. Nucl. Chem. 29:317–327. [Google Scholar]
- Bigi, A., G. Cojazzi, S. Panzavolta, A. Ripamonti, N. Roveri, M. Romanello, K. Noris Suarez, and L. Moro. 1997. Chemical and structural characterization of the mineral phase from cortical and trabecular bone. J. Inorg. Biochem. 68:45–51. [DOI] [PubMed] [Google Scholar]
- Braillon, P. M., A. Lapillonne, P. S. Ho, R. Bouvier, M. Bochu, and B. L. Salle. 1996. Assessment of the bone mineral density in the lumbar vertebrae of newborns by quantitative computed tomography. Skeletal Radiol. 25:711–715. [DOI] [PubMed] [Google Scholar]
- Braillon, P. M., B. L. Salle, J. Brunet, F. H. Glorieux, P. D. Delmas, and P. J. Meunier. 1992. Dual energy X-ray absorptiometry measurement of bone mineral content in newborns: validation of the technique. Pediatr. Res. 32:77–80. [DOI] [PubMed] [Google Scholar]
- Brown, W. E., L. W. Schroeder, and J. S. Ferris. 1979. Interlayering of crystalline octocalcium phosphate and hydroxyapatite. J. Phys. Chem. 83:1385–1388. [Google Scholar]
- Budorick, N. E., D. H. Pretorius, M. R. Grafe, and K. V. Lou. 1991. Ossification of the fetal spine. Radiology 181:561–565. [DOI] [PubMed] [Google Scholar]
- Burnell, J. M., E. J. Teubner, and A. G. Miller. 1980. Normal maturational changes in bone matrix, mineral, and crystal size in the rat. Calcif. Tissue Int. 31:13–19. [DOI] [PubMed] [Google Scholar]
- Carlström, D. and J. E. Glas. 1959. The size and shape of the apatite crystallite in bone as determined from line-broadening measurements on oriented specimens. Biochim. Biophys. Acta 35:46–53. [DOI] [PubMed] [Google Scholar]
- Chatterji, S. and J. W. Jeffery. 1968. Changes in structure of human bone with age. Nature 219:482–484. [DOI] [PubMed] [Google Scholar]
- Cheng, P. T. 1987. Formation of octocalcium phosphate and subsequent transformation to hydroxyapatite at low supersaturation: a model for cartilage calcification. Calcif. Tissue Int. 40:339–343. [DOI] [PubMed] [Google Scholar]
- De Jong, W. F. 1926. La substance mineral dans le os. Rec. Trav. Chim. Pays-Bas. 45:445–448. [Google Scholar]
- Delhez, R., T. H. de Keijser, J. I. Langford, D. Louer, E. J. Mittemeijer, and E. J. Sonneveld. 1993. The Rietveld method. In IUCr Monograph on Crystallography 5. R. A. Young, editor. Oxford Univ. Press, Oxford. 132–166.
- Driessens, F. C. M. and R. M. H. Verbeeck. 1990. Biominerals. CRC Press, Boca Raton, FL. 179–209.
- Elliot, J. C., P. E. Mackie, and R. A. Young. 1973. Monoclinic hydroxyapatite. Science 180:1055–1057. [DOI] [PubMed] [Google Scholar]
- Filly, R. A., G. F. Simpson, and G. Lindowski. 1987. Fetal spine morphology and maturation during the second trimester: sonographic evaluation. J. Ultrasound Med. 6:631–637. [DOI] [PubMed] [Google Scholar]
- Germine, M. and J. R. Parsons. 1988. Deconvoluted x-ray diffraction analysis of bone and mixtures of bone and particulate hydroxyapatite. J. Biomed. Mater. Res.(Suppl: Applied Biomaterials) 22:55–67. [PubMed] [Google Scholar]
- Gray, H., P. L. Williams, and L. H. Bannister. 1995. Gray's Anatomy: The Anatomical Basis of Medicine and Surgery, 38th ed. Churchill Livingstone, Edinburgh, NY.
- Hammersley, A. P., S. O. Svensson, and A. Thompson. 1994. Calibration and correction of spatial distortions in 2D detector systems. Nucl. Instrum. Methods Phys. Res. A 346:312–321. [Google Scholar]
- Ikoma, T., A. Yamazaki, S. Nakamura, and M. Akao. 1999. Preparation and structure refinement of monoclinic hydroxyapatite. J. Solid State Chem. 144:272–276. [Google Scholar]
- Joris, S. J. and C. H. Amberg. 1971. The nature of deficiency in nonstoichiometric hydroxyapatite. II. Spectroscopic studies of calcium and strontium hydroxyapatite. J. Phys. Chem. 45:157–164. [Google Scholar]
- Kay, M. I., R. A. Young, and A. S. Posner. 1964. Crystal structure of hydroxyapatite. Nature 204:1050–1052. [DOI] [PubMed] [Google Scholar]
- Larson, A. C. and R. B. Von Dreele. 1994. General Structure Analysis System (GSAS) Manual. LANSCE, MS-H805, Los Alamos National Laboratory, Los Alamos, NM.
- Le Geros-Zapanta, R. 1965. Effect of carbonate on the lattice parameters of apatite. Nature 24:403–404. [DOI] [PubMed] [Google Scholar]
- Lutterotti, L. and P. Scardi. 1990. Simultaneous structure and size-strain refinement by the Rietveld method. J. Appl. Crystallogr. 23:246–252. [Google Scholar]
- Meneghini, C., G. Artioli, A. Balerna, A. F. Gualtieri, P. Norby, and S. Mobilio. 2001. Multi purpose imaging plate camera for in-situ powder XRD at the GILDA beamline. J. Synchrotron Rad. 8:1162–1166. [Google Scholar]
- Miller, P., D. W. Hukins, J. G. Hasnainand, and P. Lagarde. 1981. Extended x-ray absorption fine structure (EXAFS) studies of the calcium ion environment in bone mineral and related calcium phosphate. Biochem. Biophys. Res. Commun. 99:102–106. [DOI] [PubMed] [Google Scholar]
- Nobackar, C. R. and G. G. Robertson. 1951. Sequence of appearance of ossification centers in human skeleton during the first five prenatal months. Am. J. Anat. 89:1–28. [DOI] [PubMed] [Google Scholar]
- Nuzzo, S., C. Meneghini, P. Braillon, R. Bouvier, S. Mobilio, and F. Peyrin. Microarchitectural and physical changes during fetal growth in human vertebral bone. J. Bone Miner. Res. 18: In press. [DOI] [PubMed]
- Oyedepo, A. C. and D. L. Henshaw. 1997. Calcification of the lumbar vertebrae during human fetal development. Calcif. Tissue Int. 61:179–182. [DOI] [PubMed] [Google Scholar]
- Panattoni, G. L., A. Sciolla, and G. C. Isaia. 1995. Densitometric studies of developing vertebral bodies. Calcif. Tissue Int. 57:74–77. [DOI] [PubMed] [Google Scholar]
- Pascarelli, S., F. Boscherini, F. D'Acapito, J. Hrdy, C. Meneghini, and S. Mobilio. 1996. X-ray optics of a dynamical sagittal focusing monochromator on the GILDA beamline at the ESRF. J. Synchrotron Rad. 3:147–155. [DOI] [PubMed] [Google Scholar]
- Pellegrino, E. D. and R. M. Biltz. 1972. Mineralization in the chick embryo. I. Monohydrogen phosphate and carbonate relationships dur-ing maturation of the bone crystal complex. Calcif. Tissue Res. 10:128–135. [DOI] [PubMed] [Google Scholar]
- Posner, A. S., F. Betts, and N. C. Blumenthal. 1975. Bone mineral composition and structure. In The Musculoskeletal System. F. C Wilson, editor. J. B. Lippincott, Philadelphia, PA.
- Posner, A. S. and A. F. Diorio. 1958. Refinement of the hydroxyapatite structure. Acta Crystallogr. 11:308–309. [Google Scholar]
- Pritzkow, W. and R. Rentsch. 1985. Structure refinement with x-ray powder diffraction data for synthetic calcium hydroxyapatite by Rietveld method. Crystal Res. Tech. 20:957–960. [Google Scholar]
- Riekel, C., P. Bösecke, and M. Sanchez del Rio. 1992. Two high-brilliance beamlines at the ESRF dedicated to microdiffraction, biological crystallography, and small-angle scattering. Rev. Sci. Instrum. 63:974–981. [Google Scholar]
- Royle, G. J. and R. D. Speller. 1995. Quantitative x-ray diffraction analysis of bone and marrow volumes in excised femoral head samples. Phys. Med. Biol. 40:1487–1498. [DOI] [PubMed] [Google Scholar]
- Skinner, H. C. W. 2000. Mineral and human health. In Environmental Mineralogy. EMU Notes in Mineralogy 2. D. J. Vaughan and R. A. Wogelius, editors. Eötvös University Press, Budapest. 383–412.
- Smith, C. B. and C. A. Smith. 1976. An x-ray diffraction investigation of age-related changes in the crystal structure of bone apatite. Calcif. Tissue Res. 22:219–226. [DOI] [PubMed] [Google Scholar]
- Smith, C. B. and C. A. Smith. 1978. Structural role of bone apatite in human femoral compacta. Acta Orthop. Scand. 49:440–444. [DOI] [PubMed] [Google Scholar]
- Smith, E. L., R. L. Hill, I. R. Lehman, R. J. Lefkowitz, P. Handler, and A. White. 1983. Principles of Biochemistry: Mammalian Biochemistry, 7th ed. McGraw-Hill Book Company, New York.
- Sudarsanan, K. and R. A. Young. 1969. Significant precision in crystal structural details: Holly Springs hydroxyapatite. Acta Crystallogr. B 25:1534–1543. [Google Scholar]
- Termine, J. D. and A. J. Posner. 1967. Amorphous/crystalline interrelationships in bone mineral. Calcif. Tissue Res. 1:8–23. [DOI] [PubMed] [Google Scholar]
- Thompson, P., D. E. Cox, and J. B. Hastings. 1987. Rietveld refinement of Debye-Scherrer synchrotron x-ray data from Al2O3. J. Appl. Crystallogr. 20:79–83. [Google Scholar]
- Very, J. M. and C. A. Baud. 1984. X-ray diffraction of calcified tissues. In Methods of Calcified Tissue Preparation. G. R. Dickson, editor. Elsevier Science Publishers, Amsterdam. 369–390.
- Wallny, T. A., R. L. Schild, R. Fimmers, U. A. Wagner, M. E. Hansmann, and O. Schmitt. 1999. The fetal spinal canal: a three-dimensional study. Ultrasound Med. Biol. 25:1329–1333. [DOI] [PubMed] [Google Scholar]
- Warren, B. E. 1990. X-ray diffraction. Dover Publications, New York.
- Wheeler, E. J. and D. Leweis. 1977. An x-ray study of the paracrystalline nature of bone apatite. Calcif. Tissue Res. 24:243–251. [DOI] [PubMed] [Google Scholar]
- Young, R. A. 1993. The Rietveld Method. Oxford University Press, Oxford.