Molecular Dynamics Simulations of Phospholipid Bilayers with Cholesterol

Abstract

To investigate the microscopic interactions between cholesterol and lipids in biological membranes, we have performed a series of molecular dynamics simulations of large membranes with different levels of cholesterol content. The simulations extend to 10 ns, and were performed with hydrated dipalmitoylphosphatidylcholine (DPPC) bilayers. The bilayers contain 1024 lipids of which 0–40% were cholesterol and the rest DPPC. The effects of cholesterol on the structure and mesoscopic dynamics of the bilayer were monitored as a function of cholesterol concentration. The main effects observed are a significant ordering of the DPPC chains (as monitored by NMR type order parameters), a reduced fraction of gauche bonds, a reduced surface area per lipid, less undulations—corresponding to an increased bending modulus for the membrane, smaller area fluctuations, and a reduced lateral diffusion of DPPC-lipids as well as cholesterols.

INTRODUCTION

Lipid bilayers play important roles in cells as barriers for maintaining concentrations and as matrices to support membrane proteins. Their physical properties have been studied extensively (Bloom et al., 1991), showing the importance of membrane dynamics to the insertion of proteins and direct transport of small molecules (Gennis, 1989).

During the last decade, realistic atomic level computer simulation has evolved as a complementary technique (Egberts and Berendsen, 1988; Heller et al., 1993) in the study of bilayers. Such methods have made substantial progress (Pastor, 1994; Tu et al., 1996; Tieleman et al., 1997; Scott, 2002) during the last few years. Available computing power has, however, restricted such simulations to fairly small systems and short timescales.

Biological membranes are neither completely rigid nor fluid, but they are characterized by a delicate balance between rigidity and fluidity. The properties of a biological membrane is governed by the detailed composition of the bilayer that contains lipids of various types and different membrane proteins. Many experimental and computational studies have concentrated on model systems consisting of a single lipid like DPPC. Such studies of simplified systems have been necessary and have increased our understanding of the properties of biological membranes. Simulation studies have now reached a stage where we can take a step forward and turn our attention to more complicated and realistic systems consisting of mixtures of different molecules. A first step is to include cholesterol into a DPPC bilayer. Cholesterol is an important lipid that occurs at various concentrations in biological membranes. One role of cholesterol is to act as a regulator of membrane fluidity. Cholesterol containing membranes have been studied using a large variety of experimental physical techniques in the last decades. See for instance the reviews of McMullen and McElhaney (1996); and Bloom et al., (1991). The general conclusions from these experimental studies seem to be that cholesterol softens the main (gel/liquid crystalline) phase transition and thus makes the high temperature liquid crystalline phase more ordered.

Fairly simplified simulations that could reproduce this effect qualitatively were done early (Scott and Kalaskar, 1989; Scott, 1991; Edholm and Nyberg, 1992). It was, however, not until quite recently that detailed molecular dynamics simulations including explicit solvent water were performed on cholesterol containing lipid bilayers. This includes studies of Robinson et al. (1995), Tu et al. (1998), Smondyrev and Berkowitz (1999, 2000, 2001), Pasenkiewicz-Gierula et al. (2000), Chiu et al. (2001a,b, 2002), and Róg and Pasenkiewicz-Gierula (2001). It is however still a problem that the many effects of the cholesterol on the bilayer dynamics occur on temporal and spatial scales previously not accessible in atomic detail computer simulations. The present study extends size to ∼1000 lipids and timescale to ∼10 ns, which is an increase of about a factor of five in size as well as time compared to most earlier work. In addition, it covers a wide range of cholesterol concentrations. Thus, we are able to show the variation with cholesterol concentration of some quantities. In addition, the fairly large number of cholesterol molecules (due to the large system size) and the length of the simulations make it possible to base conclusions on reasonably good statistics. This is important, since the DPPC molecules can adopt a range of different conformations depending on positions and orientations of the cholesterol molecules.

METHODS

Force field

The parameters of the force field employed for the simulations have been described in detail earlier (Berger et al., 1997; Lindahl and Edholm, 2000). The advantage with this force field is that it has been parameterized for lipids and long hydrocarbon chains to reproduce experimental quantities like volume/lipid (Nagle and Wiener, 1988) accurately. United atoms were used for the nonpolar CH₂/CH₃ groups in the hydrocarbon tails, reducing the number of atoms per DPPC molecule to 50 and per cholesterol to 29. Atomic charges for the DPPC molecules were taken from ab initio quantum mechanical calculations (Chiu et al., 1995). The headgroup Lennard-Jones parameters used were taken from the OPLS force field (Jorgensen and Tirado-Rives, 1988), and the tail parameters were the ones determined by Berger et al. (1997). 1,4 electrostatic interactions were reduced by a factor of two and 1,4 Lennard-Jones interactions by a factor of eight. Bond rotations in the carbon tails were modeled with Ryckaert-Bellemans dihedrals (Ryckaert and Bellemans, 1975) and the corresponding 1,4 interactions removed. For cholesterol Lennard-Jones parameters and bonded parameters were taken from GROMACS and charges of the head were distributed with +0.40 electron charges on the hydrogen, −0.54 on the oxygen, and +0.14 on the carbon to which the hydroxyl group is attached.

Initial structures

The initial structures of the systems with 5, 10, and 15% cholesterol were generated from equilibrated DPPC bilayers with 1024 DPPC molecules taken from the simulations of Lindahl and Edholm (2000). The appropriate number of DPPC molecules (52, 102, and 146) was then selected randomly (equally many in each side of the bilayer) and replaced by the same number of cholesterol molecules. The initial structure of the cholesterol molecule was taken from the crystal structure (Craven, 1979). Bad van der Waals contacts were removed by slowly growing the van der Waals parameters of the cholesterol molecule. The systems with 25 and 40% cholesterol were generated in the same way starting from equilibrated conformations with 15% cholesterol and contained 256 and 410 cholesterol molecules, respectively.

Simulations

A 1.0-nm cutoff was employed for Lennard-Jones interactions and 1.8 nm for electrostatics, with the long-range electrostatics part being updated every 10 time steps when the neighbor list was regenerated. This is the same cutoff scheme as was used successfully with the same potential parameters in Berger et al. (1997) and Lindahl and Edholm (2000) for pure DPPC systems.

All bonds were constrained using the LINCS algorithm (Hess et al., 1997) for the lipids and SETTLE (Miyamoto and Kollman, 1992) for the water. LINCS is a very robust constraint algorithm, making it possible to use 4-fs time steps. The temperature was kept at 323 K using the Nosé-Hoover coupling scheme (Nosé, 1984; Hoover, 1985). The pressure was scaled to 1 bar separately in all three coordinate directions with a time constant of 0.5 ps (Berendsen et al., 1984). This resulted in zero average surface tension. Since the coupling time constant was finite there were still significant fluctuations in pressure and surface tension, but when averaged over several nanoseconds these are negligible.

Molecular dynamics simulations of five different lipid-bilayer systems were performed for 16 ns. The first 6 ns were considered as equilibration and were not used for calculating averages. This might seem long, but it is necessary to let the DPPC molecules rearrange around the cholesterols and make sure that most equilibrium properties have converged reasonably. It is clear that different quantities come to equilibrium at different paces. The necessary equilibration time is shortest for local averages and even the total energy that is dominated by fairly short-range interactions seems to need no more than about half a ns for convergence. On the other hand, the growth of large scale undulatory modes is slow, and 6 ns is probably barley enough. Finally, at least another order of magnitude in time would be needed to observe segregation of the system into cholesterol-rich and cholesterol-poor regions if this would be thermodynamically favorable at some cholesterol to DPPC ratios. The simulated systems consisted of 1024 lipids. 5, 10, 15, 25, and 40% of the lipids were cholesterol, the rest DPPC. The hydration was set to 23 waters per lipid or in total 23,552 water molecules. For comparison at 0% cholesterol concentration, data from the simulations of Lindahl and Edholm (2000) was used. Coordinates were stored to disk every 2 ps (500 time steps). From these trajectory files various averages were calculated. Only data from the last 10 ns were used for the analysis.

A separate simulation of a much smaller system consisting of 64 DPPC molecules each hydrated with 23 waters was performed for 10 ns at a constant area of 0.546 nm²/lipid and the constant normal pressure 1 bar. This area per DPPC is close to the area per DPPC in the system with the highest cholesterol concentration. In this pure DPPC system we could calculate an average surface tension of −70 dyn/cm exerted by the system during the last 5 ns. This means that keeping the area to the value given above corresponds to applying an external surface tension of 70 dyn/cm on the system (or 35 dyn/cm on each monolayer interface).

All simulations were performed with the molecular dynamics package GROMACS (Berendsen et al., 1995; Lindahl et al., 2001; van der Spoel et al., 2001), parallelizing over 32 IBM SP2 332-Mhz Silver PowerPC (ppc604) CPUs. Every job was split onto 32 processors (8 four-processor nodes) with roughly the same number of DPPC, cholesterol, and water molecules assigned to each processor. The simulations were run at the parallel computing center, PDC, Stockholm, and proceeded at ∼24 ps per hour of wall time.

RESULTS AND DISCUSSION

Since the simulations were carried out at the constant isotropic pressure of 1 bar, the size of the simulation box was allowed to adjust independently in all three coordinate directions. The equilibrium state in the simulations corresponds therefore to one of 1 bar applied external pressure and zero surface tension. The system was allowed to adjust not only its volume (density) but also the area-to-thickness ratio. We therefore, show the total volume and total area of the system versus cholesterol concentration in Table 1. This shows that volume as well as area decreases with cholesterol concentration. For the former quantity, the decrease is almost linear, although the linear approximation is less good in the later case.

TABLE 1.

Some important quantitative results from the simulation versus cholesterol concentration

Bilayer property		0%	5%	10%	15%	25%	40%	Error
Box volume	Vbox [nm3]	1989	1945	1912	1881	1807	1708	±0.01%
Box area	Abox [nm2]	325	291	283	271	248	222	±0.1%
Box height	boxz [nm]	6.12	6.68	6.76	6.94	7.29	7.69	±0.1%
Order parameter sn1 chain	〈SCD〉2−8	−0.223	−0.229	−0.258	−0.271	−0.291	−0.292	±0.5%
Order parameter sn2 chain	〈SCD〉2−8	−0.234	−0.241	−0.274	−0.289	−0.316	−0.328	±0.5%
Gauche fraction averaged over both chains	[%]	25.5	25.1	24.6	23.9	22.3	20.9	±0.5%
DPPC tilt angle	[°]	24.10	25.02	21.08	20.06	19.43	20.25	±0.3%
Volume per DPPC	VDPPC [nm3]	1.225	1.213	1.211	1.212	1.198	1.189	±0.01%
Area per DPPC	ADPPC [nm2]	0.635	0.583	0.582	0.573	0.554	0.542	±0.1%
Area per cholesterol	Achol [nm2]	–	0.290	0.289	0.282	0.276	0.271	±0.1%
Bending modulus	kc [10−21J]	45.4	(9.26)	61.5	68.1	84.0	50.0	±25%
Lateral diffusion coefficient of DPPC	D [10−7cm2/s]	3.9	2.5	2.4	2.4	1.4	0.9	±10%
Lateral diffusion coefficient of cholesterol	D [10−7cm2/s]	–	3.3	3.7	3.2	1.8	0.8	±10%

The averages was calculated from 10 ns of simulation. Statistical errors were estimated from the difference between successive 1 ns subaverages.

Volumes

The volume decrease can easily be understood from the fact that a cholesterol molecule has a smaller volume than a DPPC-lipid. For the cholesterol-free system, we can calculate the volume of a DPPC molecule as:

(1)

A separate simulation of pure water at 323 K with the same cutoffs and other conditions as the lipid simulation shows that the volume of a water molecule V_w is 0.0312 nm³ for the present water model. Using V = 1989 nm³, N_lipid = 1024, and N_w = 23 × 1024 = 23,552 gives the volume of a DPPC molecule in the cholesterol-free system as V_DPPC = 1.225 nm³. This is about half a percent smaller than the experimental value 1.232 nm³ (Nagle and Tristram-Nagle, 2000). The volume of a cholesterol molecules in the crystal structure can be calculated from the size of the unit cell (Craven, 1979), which is 4.984 nm³ and contains eight cholesterols and eight waters. Assuming an experimental volume of 0.030 nm³ for a water molecule we then get V_chol = 0.593 nm³. If this volume and the volume of the water molecules are assumed to be constant, independent of cholesterol concentration in the simulations, we may calculate the volume of a DPPC molecule as a function of the cholesterol concentration(x = N_chol/N_lipid) from the equation:

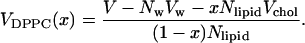(2)

Doing this, we find a slight decrease of the DPPC volume with increasing cholesterol concentration. At the highest concentration 40% we get 1.189 nm³, which corresponds to a 3% decrease of the volume compared to that in the cholesterol-free system. A support for this interpretation is found from the simulation of a pure DPPC/water system at a surface area per DPPC molecule comparable to that in the 40% cholesterol system. The volume per DPPC molecule at the lower area/lipid is ∼2% smaller than in the system at the experimental area per DPPC molecule.

One alternative explanation for the volumes could of course be that cholesterol occupies a different (larger) volume in the lipid bilayer than in the crystal structure. We can exclude this explanation with the following argument. If we assume the volumes of the DPPC molecules and the water molecules are fixed, equal to that in the cholesterol-free system, we can calculate the cholesterol volume needed to explain the box volumes in the simulations from the equation:

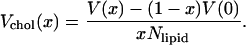(3)

Then, we obtain a value between 1.1 and 1.3 nm³ depending on x. This is twice the crystal structure value and far too large to be reasonable. The conclusion is therefore that this could not explain the volumes from the simulations. The explanation is instead that cholesterol induces a better packing of the DPPC molecules and thereby a decrease in the volume occupied by a DPPC molecule. This is an effect of that cholesterol reduces the surface area per DPPC molecule, which will be discussed in the next subsection.

Areas

It is not an obvious problem how to distribute the area of the simulation box between cholesterol and DPPC molecules. In cholesterol crystals (Craven, 1979), the area per cholesterol molecule can be calculated to be ∼0.38 nm². If we assume this area in the lipid bilayer, the remaining area becomes too small for the remaining DPPC molecules. At the highest cholesterol concentration, only 0.47 nm² remains per DPPC molecule. This is close to the area in the gel phase, although we clearly observe from the simulations that the DPPC molecules still are fairly disordered in the presence of 40% cholesterol. We can, however, come up with separate areas for the DPPC molecules and cholesterol in the following way. The average thickness of the lipid bilayer, h(x) can be calculated as:

(4)

The area occupied by a DPPC molecule in the bilayer can be written in terms of volume and thickness as:

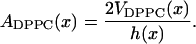(5)

This means that we can write the area per DPPC as:

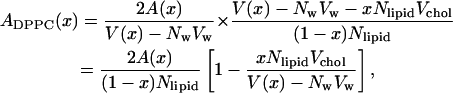(6)

using Eq. 2 for the volume and Eq. 4 for the thickness. The area per cholesterol can then be calculated from the remaining area:

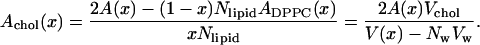(7)

This results in a separation of the total area into an area per DPPC and an area per cholesterol that is shown in Table 1. It is reassuring that the area per cholesterol is fairly independent of cholesterol concentration while the area per DPPC shows a clear decrease with increasing cholesterol concentration. For statistical reasons, the best estimate for the cholesterol area probably comes from the runs with the highest concentrations and is 0.27 nm². This result is consistent with other recent simulations (Scott, 2002; Smondyrev and Berkowitz, 2001) and with an old observation (Rothman and Engelman, 1972).

The reason why cholesterol occupies an ∼30% smaller area in a lipid bilayer than in a cholesterol crystal is that the cholesterol molecule is too short to span an entire DPPC monolayer. It becomes therefore partly buried among the DPPC molecules. This is only partially evident from the dimensions and properties of the involved molecules. The cholesterol molecule consists of a rigid ring system that has a length of ∼0.85 nm extending from the polar hydroxyl group to the start of the short chain. The chain will, if it is totally extended, span ∼0.75 nm. This makes the maximum length of the molecule 1.6 nm. With the volume 0.593 nm³, this gives an area of 0.37 nm² in fair agreement with the area calculated from the crystal dimensions. The monolayer thickness calculated from the simulations ranges from 1.9 nm up to 2.2 nm depending on cholesterol concentration. The cholesterol heads do, however, stay anchored at the level of the carbonyl groups of the DPPC molecules. The DPPC chains below the carbonyls could if they had maximal extension span ∼1.85 nm, but they are not ordered in the liquid crystalline phase and in fact they only span a distance of 1.5–1.7 nm depending on cholesterol concentration.

The electron density across the bilayer supplies information about the thickness and order of the bilayer. It can be constructed from diffraction data (Nagle and Tristram-Nagle, 2000). The profiles calculated from simulation data show the characteristic features of experimental profiles and are shown in Fig. 1. It is seen that increased cholesterol concentration thickens the bilayer, makes the dip in the center deeper, and the peaks in the headgroup regions higher.

FIGURE 1.

Electron density across the bilayer for different cholesterol concentrations.

Order parameters

The most popular quantities to characterize the order in lipid bilayers are order parameter of the type that can be measured by deuterium NMR. Such an order parameter may be defined for every CH₂ group in the chains as:

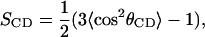(8)

where θ_CD is the angle between a CD-bond (in the experiment) or a CH-bond (in the simulation) and the membrane normal. Since we use united atoms in the simulations we have to reconstruct the CH-bond from the positions of three successive CH₂-groups assuming tetrahedral geometry of the CH₂-groups. The brackets indicate averaging over the two bonds in each CH₂-group, all the lipids and time. We have chosen to plot these order parameters versus position in the chain separately for the two chains (sn1 and sn2) of the DPPC molecules for the different cholesterol concentrations. The sn2 chain is attached to the middle carbon of the glycerol backbone and is therefore on the average positioned slightly closer to the membrane surface than the sn1 chain. The simulations show that the upper end of the sn2 chain on the average is anchored 0.15 nm closer to the membrane surface than the sn1 chain. Therefore, the order parameters, especially in the upper part of the chain are slightly larger (more negative) in the sn2 chain compared to in the sn1 chain. The CH₂ groups are numbered consecutively from 2 to 15. Number 1 would be the carbonyl carbon and number 16 the CH₃ group. The results are collected in Fig. 2. Simulations of small pure DPPC-bilayers during short times give order parameters that are in fair agreement with experiment (Seelig and Seelig, 1974) as shown for instance in Berger et al. (1997). For large systems, undulations complicate things a bit and there is a slight difference between simulated order parameters in a 64-lipid and a 1024-lipid system DPPC system. Typical for order parameter profiles of pure phospholipid bilayers is that there is a plateau region in the upper and middle part of the chains in which the order parameters vary only slightly. Then there is a drop toward zero at the end of the chain. It is seen that this behavior is not conserved at high cholesterol concentrations. Instead, the order parameter profile gets a pronounced peak in the middle of the chain. This is most pronounced for the sn1 chain.

FIGURE 2.

Calculated order parameters corresponding to NMR deuterium ones versus chain position for different cholesterol concentrations. (top for the sn1 chain and bottom for the sn2 chain.)

Deuterium order parameters have been measured by NMR for a variety of different lipids and lipid mixtures for 30 years. Among the recent studies involving cholesterol, Paré and Lafleur (1998) could be mentioned. Detailed data are found already in Stockton and Smith (1976) for egg phosphatidylcholine bilayers with perdeuterioctadecanoic acid included as NMR probe. The individual resonances were not resolved in the plateau region going from carbon 2 to 10 in their 18-unit chains. The picture is fairly consistent with the simulations. The quadrupole splitting that is proportional to the order parameter increases linearly with cholesterol concentration up to the maximal experimental concentration which is 33%. The effect is largest in the middle of the chain where there is almost a factor of 2 between the order parameters of the cholesterol-free system and that with 33% cholesterol. The effect is slightly larger in these experiments than in the present simulation. One should, however, keep in mind that the lipid composition is different and that the probe is a single chain molecule in the experiments.

It is obvious that one effect of the cholesterol is that its rigid ring system orders the hydrocarbon chains of the neighboring DPPC molecules. This is consistent with that the main effect occurs in the middle of the lipid chains that are located at the same level in the bilayer as the ring system. The effect is smaller at the end of the chains which mostly experience contact with the short cholesterol chain. The effect is also smaller in the beginning of the chain. It seems as if the possibilities to increase the order in the upper parts of the DPPC hydrocarbon chains are quite limited. An indirect effect of cholesterol that goes beyond the neighboring lipids is that the surface area of the entire lipid bilayer is reduced. Thus, cholesterol could viewed as a substance that increases the surface tension of the bilayer. One could therefore try to mimic this effect in a pure DPPC bilayer by applying a positive surface tension that reduces the area per DPPC molecule to the same value as in a system with a certain percentage cholesterol. The area in that system was adjusted to get an area per DPPC molecule of 0.546 nm², which is close to the area per DPPC molecules in the system with 40% cholesterol. This simulation was run at fixed area and a fixed normal pressure of 1 bar. This corresponds to an applied surface tension on the system of ∼70 dyn/cm. The order parameters of the sn1 chain were then calculated and are displayed together with the same order parameters for two systems at zero surface tension (the ones without cholesterol and with 40% cholesterol) in Fig. 3. It is clear that the order parameter profiles of the two pure DPPC systems are very similar in shape. The lower area per lipid results essentially just in increased order in the plateau region between hydrocarbon 2 and 10. Then the profile decays steeper for the system at lower surface area so that the order parameters end up quite close for the last group in the chain. In contrast to that the system with cholesterol starts with the same order parameter as the cholesterol-free system and experimental surface area, has an order parameter that increases and goes through a maximum in the middle of the chain. The order parameter is then ∼0.07 units larger (more negative) all the way through the entire second half of the chain. Thus, we do not have the plateau region going from hydrocarbon 2 to 10 that is characteristic for the pure DPPC system at both surface areas. Still, if one defines an average order parameter

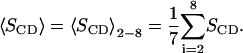(9)

This will not differ so much between the system with cholesterol and the cholesterol-free system at the same surface area per DPPC. But the reason for this is that the order parameter increases almost linearly along the chain in the system with cholesterol and the order parameters become equal between hydrocarbon 4 and 5. The effect is similar but a bit less pronounced for the sn2 chain.

FIGURE 3.

Calculated NMR order parameters for the sn1 chain versus chain position for the system with 40% cholesterol (triangles), the cholesterol-free system at surface tension zero (circles), and for a cholesterol-free system at the same surface area per DPPC molecule as the system with 40% cholesterol (squares).

Relating area and order parameters

The ordering of the hydrocarbon chains in a lipid bilayer can obviously be characterized in a number of ways. This includes deuterium order parameters, gauche fraction, and area per lipid. Obviously there is at least some correlation between these parameters. It is therefore quite natural to look for a relation by which one can calculate the parameters from each other. Berger et al., (1997) found from simulations an almost linear relation between order parameters of the NMR type and the area per lipid over a fairly narrow area interval. Petrache et al. (1999) observed similar results from simulations and suggested based on geometric modeling a simple analytical relation between order parameter and the distance traveled by the chain in the direction normal to the bilayer. This is written as a relation between the distance, D_n, traveled in the direction perpendicular to the membrane of chain segment n and the corresponding order parameter S_CDⁿ:

(10)

where D_M = 0.125 nm. This may for fixed volumes be rewritten as a relation between the area per lipid A_DPPC and an average order parameter 〈S_CD〉 for the plateau region. If this relation is inverted one may write the average order parameter as a function of the area per lipid:

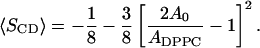(11)

The parameter A₀ is here the area of a fully ordered lipid. Despite the nonlinearity, this equation is fairly linear in the interesting area and order parameter intervals. In Fig. 4 the average order parameters of the region from carbon 2 to 8 is shown separately for the sn1 and sn2 chains versus the area per DPPC-lipid as calculated from the simulations. In the same figure, Eq. 11 is shown with the values 0.46, 0.47, and 0.48 nm² for the parameter A₀. The agreement is reasonable except for the system with 5% cholesterol, which has the same area per DPPC as the 10% system but order parameters much closer to those of the cholesterol-free system. The reason for this is that the 5% system contains one huge undulation covering the whole periodic box. This gives a smaller projected area per lipid. This also affects other properties of the system in a way that could be anticipated. The reason why we get this (single) large undulation in one case but not in any other case is not clear and could be discussed. It may be related to the initial distribution.

FIGURE 4.

The calculated average order parameters 〈S_CD〉₂₋₈ from the simulation versus the calculated area per DPPC-lipid (squares for for the sn1 chain and circles for the sn2 chain.) The lines shown are the relations obtained from the equation of Petrache et al. (1999) using the values 0.48 nm² (full line), 0.47 nm² (dashed line), and 0.46 nm² (dotted line) for the model parameter A₀.

It is, however clear that Eq. 11 gives a slightly steeper variation of the order parameter with area than the present simulations. The value 0.47 nm² for A₀ which seems to give the best fit is quite close to the experimental area per lipid in the gel phase. This is reassuring. One should, however, keep in mind the order parameter profiles especially with large amounts of cholesterol are different from those of the pure DPPC systems and that the model behind Eq. 11 is quite simple. With this in mind, the agreement is astonishingly good. (Petrache et al., 2000) have calculated the area per DPPC, DMPC, and for some other lipids from experimental NMR results using Eq. 10. They obtain a fair agreement with what is experimentally known about the area per lipid.

Dihedral angles

Another measure of lipid order is the fraction gauche dihedrals in the lipid chains. A low percentage of gauche bonds is indicative of an ordered system. The fraction of gauche bonds has been plotted in Fig. 5 versus the number of the dihedral, separately for the sn1 and sn2 chains. The dihedrals have been numbered consecutively along the chain, starting with 1 for the 1-2-3-4 dihedral with 1 being the carbonyl carbon ending with 13 for the 13-14-15-16 dihedral with 16 being the terminal CH₃ group. We observe an increasing fraction of gauche bonds toward the end of the chain. The curves do, however, oscillate strongly. The gauche fraction is larger for odd dihedrals in the sn1 chain and for even dihedrals in the sn2 chain, and the oscillations are stronger in the sn2 chain. Despite this different behavior, the average fraction of gauche bonds is virtually identical for the two chains. In Table 1, we therefore only show the average fraction versus cholesterol concentration. The difference between the two chains is as small as 0.1%. The effect of cholesterol upon the average fraction of gauche bonds is small, a reduction from 25.5% to 20.9% upon going from a cholesterol-free system to a system with 40% cholesterol. This could be compared to the area per DPPC that changes from 0.635 nm² to 0.542 nm² between the same systems, which is more than half the way down to the area of the gel phase. A closer inspection of Fig. 1 shows, however, that the change in gauche contents is more substantial in the middle of the chains. Close to the end of the chain, the gauche fraction is close to that of a system with maximum disorder (which would be 40% with the present dihedral potential) irrespective of cholesterol content. Close to the carbonyl anchoring of the chain, there are restrictions upon the dihedrals that do not allow for big changes in the gauche contents. Thus, it might be more fair to average over the central part of the chain. For dihedrals 5 to 10, we observe an average drop of the gauche contents from 24.8 to 18.6%. This change is larger but still small compared to the area change. It is also reasonable that the effect of cholesterol upon the dihedrals of the DPPC molecules is largest in the region of the rigid cholesterol rings.

FIGURE 5.

Percentage gauche bonds versus number of the dihedral. (top for the sn1 chain and bottom for the sn2 chain.)

Different ways of quantifying lipid order

The ordering effect of cholesterol can be measured using a number of different order parameters, for instance, the area per lipid, the fraction gauche bonds, or the usual deuterium NMR order parameters. Qualitatively, they all show the same change. Increased cholesterol concentration reduces gauche content and makes the NMR order parameter more negative. A quantitative analysis however shows that the effect is quite different on the different measures of order. We can define a dimensionless order parameter for each these quantities that is zero in the cholesterol-free DPPC system and one in a pure DPPC gel phase system. For the area, A we have:

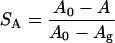(12)

with A₀ = 0.635 nm² and A_g = 0.48 nm² (the area in the gel phase). Similarly we have, assuming that the gauche fraction is zero in the gel phase and the NMR order parameter −0.5:

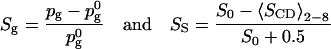(13)

with 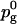= 0.255 and S₀ = −0.228. What we see then is that at 40% cholesterol concentration the area order parameter has reached 0.60, i.e. that the area has decreased by 60% of the area change necessary to bring DPPC into the gel phase. For the other order parameters, the change is much less, from 0 to S_g = 0.18 and S_S = 0.30. This indicates that even if all these three order parameters are measures of how far the system is from the gel or liquid crystalline phase, the relation between them is not simple. This is even more pronounced at lower cholesterol concentrations where the effect on the gauche content of the chains seems to even weaker, whereas the effect on the area per DPPC is much more direct.

Tilts and electrostatics

The tilt of the flat cholesterol ring system with respect to the membrane normal is easy to define. For the phospholipid molecules, we define the tilt angle as the angle between the vector from the average position of the ends of the chains (CH₃-groups) to the end of the headgroup (choline) and the membrane normal. As seen from Table 1, the tilt of the DPPC molecule decreases slightly from 24° to 25° down to ∼20° with increasing cholesterol concentration. The average tilt of the cholesterol ring system is larger and drops from 42° at 5% cholesterol down to ∼28° at 40%. The tilt in the direction perpendicular to the flat site of the ring system is small and the main part of tilt of the cholesterols occurs in the opposite direction.

The electrostatic potential across the bilayer was calculated by integrating Poisson's equation twice with the charge distribution taken from the simulations. The result is shown in Fig. 6 for a couple of cholesterol concentrations. The electrostatic potential is 600–700 mV lower in the water than in the middle of the bilayer in all cases. The variation with cholesterol concentration is probably within the size of the statistical errors. The sign of the potential is due to overpolarization from the water, an effect that already has been reported by several authors for pure phospholipid bilayers. The contribution from the cholesterol molecules to the potential across the monolayer is negligible, which is reasonable but not obvious. The cholesterol dipole is one order of magnitude smaller than the one of the phospholipid, but the outcome depends also upon the tilt. The contributions from both DPPC and water are approximately constant −4.3 V and +4.9 V independent of cholesterol concentration. The reduced total number of DPPC dipoles with increasing cholesterol concentration is compensated by a smaller area per DPPC and by a slightly increased tilt of the headgroup dipole out of the membrane plane going from 10° to 12° at zero cholesterol concentration up to ∼15° at the highest cholesterol concentrations. A small potential barrier in the headgroup region is present in the systems with cholesterol but not in the pure DPPC system. The barrier is not a direct consequence of the cholesterol molecules but follows from reduced water penetration into the headgroup region that in its turn is a consequence of the reduced area per phospholipid.

FIGURE 6.

The full electrostatic potential as a function of position perpendicular to the membrane at 0 (full line), 25 (dashed line), and 40% (dotted line) cholesterol. The bilayer is centered at 0 nm.

Undulations

Large lipid bilayers are in general not planar but the bilayer surface may on a mesoscopic scale form undulations. Most atomic scale simulations cannot cover the time and length scales to describe such motions accurately. In simulations of the present size and timescales, it is however, possible to start seeing these motions (Lindahl and Edholm, 2000). In a continuum representation, the bilayer could be described as a surface u(x,y) subject to a potential energy functional that contains two terms, one that contains the energetic cost of bending the bilayer and one the cost of increasing the water/lipid exposure (Safran, 1994):

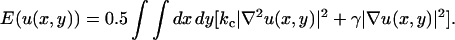(14)

This equation contains two parameters, the bending modulus k_c with dimension energy and the surface tension γ with dimension force per length unit. Statistical mechanics gives then the mean square amplitude of the undulations as a function of the length of the wave vector q as:

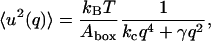(15)

where k_B is the Boltzmann constant and T the temperature. This means that the parameters k_c and γ could be determined from a plot of the mean square amplitude versus wave number. This was also done for a pure DPPC system (Lindahl and Edholm, 2000). We may, however, sum the contributions from all the undulatory modes with wave vectors that are small enough to fit into the two-dimensional periodic box and get a total mean square amplitude of the undulatory motions. In doing this, we use that surface tension was fixed to zero in the present simulations and are thus left with the first term in the denominator of Eq. 15. If the sum is calculated numerically, the approximate relation (Lindahl and Edholm, 2000):

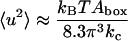(16)

is obtained. Observe, that an integral approximation gives different numerical coefficients in Eq. 16 due to errors are introduced at the low wave vector cutoff.

The bending moduli calculated for the different systems are shown in Table 1. There is a general tendency for the size of the undulations to drop with increasing cholesterol content as also can be seen from Fig. 7. We conclude that cholesterol reduces undulations and increases the bending modulus of the system. The effect is not dramatic considering that the bending moduli may differ by several orders of magnitude between lipid types, but there is a clear decrease in the undulatory amplitudes. The calculated bending modulus of the pure DPPC system compares well with experiment as noted already (Lindahl and Edholm, 2000). Still, these data are quite uncertain. The statistical error is quite large, 20–30%. The undulations also need long time to develop and come into equilibrium (as noted already in Lindahl and Edholm, 2000). There seems to be a problem with the system containing 5% cholesterol. It has a very small apparent bending modulus since one undulation covering the entire periodic box gets a very high amplitude. There may be several reasons for this.

FIGURE 7.

Molecular graphics view of the systems after 10 ns of simulation. (top) Pure DPPC, (middle) DPPC with 10% cholesterol, and (bottom) DPPC with 40% cholesterol.

The experimental bending modulus of mixtures of cholesterol and steareyl-oleyl-phosphatidylcholine(SOPC) from micropipette methods has been reported (Evans and Rawicz, 1990). Their results show an increase from 0.90 × 10⁻¹⁹ J for pure SOPC to 2.46 × 10⁻¹⁹ J for a 50:50 mixture of SOPC and cholesterol. (Duwe and Sackmann, 1990) reports similar experimental values for dimyristoylphosphatidylcholine (DMPC), 1.1 × 10⁻¹⁹ J for the pure phospholipid and 4.2 × 10⁻¹⁹ J for a mixture with 30% cholesterol. These values are for different lipids and different temperatures (but still in the liquid crystalline phase for those lipids), but illustrates the general tendency. This indicates that our results are in qualitative in agreement with experiment.

Compressibilities

In principle, we may determine the volume and an area compressibility moduli of the system from the fluctuations in volume and area of the entire system during the simulation from the equations:

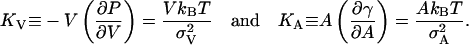(17)

Data from the simulations are shown in Table 2. The relative volume fluctuations σ_c/V are slightly less than 0.1% and quite stable. This gives values of K_V in the interval 28–48 kbar that is consistent with experimental values. See e.g. Braganza and Worcester (1986). It is more tricky with the area fluctuations, since there still is varying amounts of drift in the area even after the 6 ns equilibration. A direct application of Eq. 17 gives area compressibility moduli in the interval 100–1000 dyn/cm. To try to correct for the drift, we assume that this is linear in time and subtract a linear drift fitted in the least square sense to the area versus time. This reduces fluctuations and gives area compressibility moduli in the interval 640–2000 dyn/cm. In neither case, we get a systematic variation with cholesterol concentration. The conclusion is that we need longer simulations to able to draw good quantitative conclusions about fluctuation quantities. Anyhow, we get an area compressibility modulus that is considerably larger than the value 250–300 dyn/cm observed in a simulations of pure DPPC (Lindahl and Edholm, 2000). It is more similar to the values observed in simulations of pure DPPC bilayers in Feller and Pastor (1999). Experiments report about a fourfold increase in K_A from 144 to ∼600 dyn/cm in DMPC bilayers upon inclusion of 33–50% cholesterol (Needham et al., 1988). For another lipid (SOPC) the reported increase is smaller (Bloom et al., 1991). The present simulations reproduce the increasing area compressibility with cholesterol concentration in a qualitative sense.

TABLE 2.

Volume and surface compressibility moduli calculated from the volume and area fluctuations of the simulations

Compressibility moduli		0%	5%	10%	15%	25%	40%
KV = VkBT/σV2	kbar	–	37	33	28	48	54
KA = AkBT/σA2	dyn/cm	275	110	780	300	950	490
KA* = AkBT/σA2 (drift subtracted)	dyn/cm	–	730	1700	640	1900	1300

In the last line K_A^* is calculated from the area fluctuations obtained after the fitting and subtracting of a linear drift in time.

Lipid diffusion

The lateral diffusion coefficient, D, of the lipids was calculated from the long time mean square displacement (MSD) of the lipids versus time from the relation:

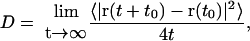(18)

where r is the vector describing the center of mass of a lipid molecule in the two membrane plane dimensions. The averaging indicated by the brackets was performed over all lipid molecules and all initial time origins t₀. As noted by Lindahl and Edholm (2001) one has, however, to take care in calculations like this. During the simulation, center of mass velocities of the entire system are removed, but there may still be some motion of the entire bilayer with respect to the center of mass of the system (that also includes the water) and some motion of the two monolayers with respect to each other. This kind of motion should be fairly small for a system of this size, but it is not completely negligible and we did take care and subtracted such motion. For the cholesterol-free system this resulted in a diffusion coefficient of 3.9 × 10⁻⁷ cm²/s. This is more than a factor three larger than the value 1.2 × 10⁻⁷ reported by Lindahl and Edholm (2001) from simulations of a much smaller 64-lipid system during 100 ns but comparable to the value 3 × 10⁻⁷ cm²/s reported by Essmann and Berkowitz (1999) from a 10-ns simulation of a fairly small system. We think that the difference compared to the 100-ns simulations partly is due to that 10 ns still is a bit short time for measuring diffusion. Still, the data in Lindahl and Edholm (2001) shows a mean square displacement that to a good approximation is linear in time over the interval 5–100 ns. The mean square displacements calculated from the cholesterol-free simulation correspond to displacements of ∼1.2 nm in the membrane plane in 10 ns. This is about two lipid-lipid distances and should be enough for coming out of the time regime characterized by rattling in a cage of surrounding lipids. One possible explanation for the difference is then that there is a finite size effect. There may be some collective diffusion of groups of lipids that is slightly faster than the diffusion of single lipids. Such a motion would only be present in a large enough system. Anyhow, the differences between the different simulations are small compared to the differences between experimental diffusion constants measured with different techniques.

The motion in the direction perpendicular to the bilayer is restricted and after some time it reaches a limiting value that is ∼0.7 nm in the cholesterol-free system. This value decreases with increasing cholesterol concentration and is only 0.3 nm in the system with 40% cholesterol. This is consistent with the decrease in area fluctuations that we observe with increasing cholesterol concentration. Since the volume fluctuations are small, thickness fluctuations have to decrease in the same way as area fluctuations.

The coefficients of diffusion for cholesterol and DPPC are shown in Table 1 and Fig. 8. We observe a decrease in the diffusion coefficient both of cholesterol and DPPC molecules with increasing cholesterol concentration. The decrease is almost a factor of four over the concentration interval covered in the present simulations. This is not a direct influence of the cholesterol molecules but an indirect effect from the ordering of the DPPC molecules and the reduced area.

FIGURE 8.

Lateral diffusion coefficient of DPPC and cholesterol versus cholesterol concentration.

Experimentally, different techniques and different lipids seem to result in quite a large spread in data on lateral diffusion. Most of the literature is, however, consistent about that cholesterol slows down the diffusion in the liquid crystalline phase (Almeida et al., 1992). The effect is small; a nonlinear variation with cholesterol concentration has been suggested and some authors see almost no effect. Vaz et al. (1985) suggests based on FRAP (fluorescence recovery after photobleaching) measurements, a decrease from between 1.6 and 0.4 × 10⁻⁷ cm²/s (depending on temperature) to between 1.3 and 0.2 × 10⁻⁷ cm²/s going from 0% to 40% cholesterol in a DMPC bilayer. Kuo and Wade (1979) report similar figures for a DPPC/ cholesterol system based on pulsed NMR measurements.

The diffusion of the DPPC molecules is slower than that of the cholesterol ones, but the difference gets smaller at higher cholesterol concentration and the coefficients of diffusion are essentially equal at the highest cholesterol concentration. Qualitatively, one can argue that the lower mass and shorter length of the cholesterol molecule should make its diffusion slower. The longer phospholipid fatty acid chains with entanglement possibilities work also in the same direction. However, a substantial part of the damping of lipid translational velocities comes from electrostatic interactions between lipid headgroups and between lipid headgroups and water. Since the headgroup of DPPC has got a much larger dipole moment than that of cholesterol, the diffusion of DPPC will more effectively slowed down by these interactions. This works in the opposite way and quantitative estimate for the total difference between the coefficients of diffusion is not easily done.

In addition, the individual lipids and the two types of lipid molecules do not move independently of each other. In fact the most DPPC molecules keep the same nearest cholesterol within the complete simulation time. Cholesterols orient themselves with their hydroxyl groups close to the carbonyl groups of the phospholipids and try to stay there. To some extent we therefore have a joint diffusion of cholesterol and DPPC that may explain the equal coefficients of diffusion at close to equal concentrations of the two lipids.

The hydrogen bonding was analyzed in the system with 25% cholesterol and 75% DPPC. Each cholesterol molecule has a polar hydroxyl group that may hydrogen bond either as a donor or acceptor. The DPPC molecules on the other hand have no polar hydrogens but plenty of atoms that can act as acceptors for hydrogen bonds. We found on the average seven hydrogen bonds per DPPC molecules to water molecules. The cholesterol molecules had on the average 0.7 hydrogen bonds to DPPC molecules and 0.6 to water molecules. The hydrogen bonding in between cholesterol molecules was negligible. The time correlation was analyzed for the hydrogen bonds as

(19)

where the variable s_i is 1 if we have a hydrogen bond, and 0 otherwise. The averaging was done over all initial times t₀ and over all hydrogen bonds, i, which existed at time t₀. This resulted in the curves in Fig. 9. It is seen that the decay is nonexponential both for the cholesterol-water and the cholesterol-DPPC hydrogen bonds. The former one is, however, essentially zero after a couple of ns and an average lifetime of the cholesterol-water hydrogen bonds can be calculated from the integral of the correlation function to ∼150 ps. The cholesterol-DPPC correlation is still 0.20 after 5 ns and the decay is algebraic (t^−0.7), which would give an infinite average lifetime if extrapolated and integrated to infinity. The conclusion is that ∼10% of the cholesterols are hydrogen bound in the same way to the same phospholipid during the entire simulation. In addition, there is a fraction of the cholesterols that just change hydrogen bonding acceptor within the same phospholipid during the simulation. This means that on the timescale of these simulations, all molecules do not move independently. Hydrogen bound pairs of molecules will of course diffuse slower than the single molecules.

FIGURE 9.

Time autocorrelation function for hydrogen bonds between cholesterol molecules and DPPC molecules (upper curve), and for hydrogen bonds between cholesterol and water (lower curve).

Another way to probe this is to monitor the time development of the mean square distance between molecules. If two different lipids undergo independent diffusion in the plane with diffusion constants D₁ and D₂ we would have

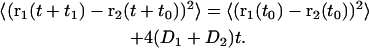(20)

We calculated this function for all cholesterol/DPPC pairs and binned the functions according to the initial distance. We found linearity in time after 1−2 ns according to the prediction but the slope was significantly smaller when the initial distance was small. The slope increased in a systematic way by almost a factor of two going from initial distances below 0.5 nm out to 2.5 nm where the slope saturated.

Finally, we tried to look for signs for a segregation process in the systems with high cholesterol concentration. We were not able find any evidence from the simulation data for segregation into cholesterol-rich and cholesterol-poor regions. Such a process may still occur but on timescales that are beyond the 10 ns that is covered in the present simulations.

CONCLUSIONS

The size of the systems simulated in this work provides a direct illustration of the molecular-level effects of cholesterol molecules intercalated in lipid bilayers. Some of the most important quantitative results are listed in Table 1, and they are in good agreement with results from chemistry and biology. Cholesterol reduces the area per phospholipid in the simulations and increases the ordering of the hydrocarbon chains, which has also been observed in experiments and other simulations. Further, the simulations provide additional less obvious information. In contrast to the area packing that would occur if a surface tension was applied to the system, we find that the change in order parameters is not uniform i.e., that the effect of the cholesterol addition depends on the depth in the bilayer. Interestingly, the quantitative “ordering” effect of the bilayer varies quite significantly between different measures such as area per lipid, NMR order parameters, and gauche contents. The present simulations are also the first ones to show the reduced membrane undulations upon cholesterol addition, and we calculate the increased area compressibility in agreement with published experimental observations.

These physiochemical effects are of great biological importance in many organisms (McMullen and McElhaney, 1996; Bloom et al., 1991). Cholesterol in bacterial membranes makes them rigid enough to survive without a real cellular wall, and the partial immobilization of lipids increases the density of the membrane interior, which reduces the water molecule permeability of the cell plasma membrane. This stiffening of the membrane is explained by a general smoothening of the transition from gel to liquid crystalline phase of the bilayer that occurs when cholesterol is added. The same smoothening will however also increase the fluidity at lower temperatures compared to a pure gel phase system. In this way the cholesterol molecules also act as a stability buffer to prevent crystallization of the bilayer at lower temperatures. Altering the amount of cholesterol in the bilayer is thus an easy and convenient way for nature to adopt the physical properties of the bilayer to the environment.

The strength of the present approach is that the parameters involved have clear physical interpretations and can be systematically tested and understood from much simpler systems. Although it is reassuring that they still accurately reproduce experimental results on advanced systems and long timescales, we should keep in mind that there are important dynamics on even longer scales. Although the systems seem to be in equilibrium after 10 ns, there may still exist processes that would need much longer time to come into equilibrium. There may for instance be slow segregation phenomena occurring over microsecond scales, which we have not yet seen any indication of in simulations.