Electrostatic Contributions to the Stability of a Thermophilic Cold Shock Protein

Abstract

The thermophilic Bacillus caldolyticus cold shock protein (Bc-Csp) differs from the mesophilic Bacillus subtilis cold shock protein B (Bs-CspB) in 11 of the 66 residues. Stability measurements of Schmid and co-workers have implicated contributions of electrostatic interactions to the thermostability. To further elucidate the physical basis of the difference in stability, previously developed theoretical methods that treat electrostatic effects in both the folded and the unfolded states were used in this paper to study the effects of mutations, ionic strength, and temperature. For 27 mutations that narrow the difference in sequence between Bc-Csp and Bs-CspB, calculated changes in unfolding free energy (ΔG) and experimental results have a correlation coefficient of 0.98. Bc-Csp appears to use destabilization of the unfolded state by unfavorable charge-charge interactions as a mechanism for increasing stability. Accounting for the effects of ionic strength and temperature on the electrostatic free energies in both the folded and the unfolded states, explanations for two important experimental observations are presented. The disparate ionic strength dependences of ΔG for Bc-Csp and Bs-CspB were attributed to the difference in the total charges (−2e and −6e, respectively). A main contribution to the much higher unfolding entropy of Bs-CspB was found to come from the less favorable electrostatic interactions in the folded state. These results should provide insight for understanding the thermostability of other thermophilic proteins.

INTRODUCTION

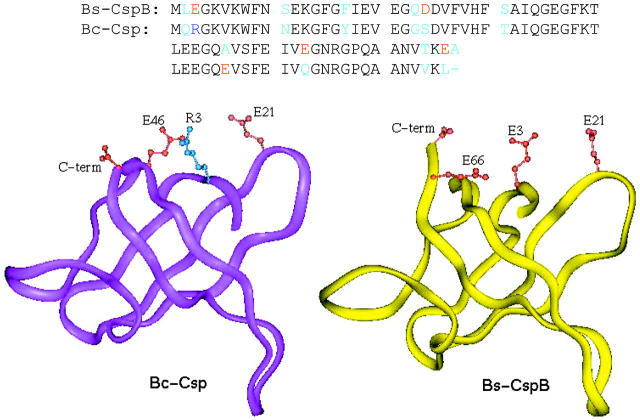
Electrostatic interactions have long been implicated in the thermostability of thermophilic proteins (Perutz and Raidt, 1975; Perutz, 1978; Vogt and Argos, 1997; Jaenicke and Bohm, 1998; Szilagyi and Zavodszky, 2000; Petsko, 2001; Zhou, 2002d). Bacillus caldolyticus cold shock protein (Bc-Csp) provides an ideal system for investigating the roles of electrostatic interactions. This protein differs from its mesophilic homolog, Bacillus subtilis cold shock protein B (Bs-CspB), in 11 of the 66 residues. Schmid and co-workers (Perl et al., 2000; Pace, 2000; Mueller et al., 2000; Perl and Schmid, 2001; Delbruck et al., 2001) have shown that the difference in stability can be accounted for by mutations (all involving charges) in just three positions: residues 3, 46, and 66. These are Arg, Glu, and Leu in Bc-Csp but are Glu, Ala, and Glu, respectively, in Bs-CspB (see Fig. 1). We have previously developed theoretical methods to treat electrostatic effects in both the folded and the unfolded states (Vijayakumar and Zhou, 2001; Zhou, 2002a; Dong and Zhou, 2002). In this paper, we use these methods to study the effects of mutations, ionic strength, and temperature to further elucidate the physical basis of the difference in stability between Bc-Csp and Bs-CspB.

FIGURE 1.

Sequence and structure comparison of Bc-Csp and Bs-CspB. In the positions where the sequences are different, neutral residues are in cyan, negatively charged residues are in red, and the positively charged R3 residue of Bc-Csp is in blue. In the structure of Bc-Csp, the distances from R3 to E21, E46, and the C-terminal are 9.8, 4.6, and 8.2 Å, respectively. The distances of E3 in Bs-CspB to E21, E66, and the C-terminal are 5.9, 4.6, and 7.1 Å, respectively.

Charged residues may form favorable interactions in the folded state, but these are accompanied by desolvation cost. In addition, a charged residue may also experience residual interactions with other charged residues in the unfolded state (Pace et al., 2000; Zhou, 2002a,b,c), and nonelectrostatic factors may contribute to the folding equilibrium. The complexities of these issues make it difficult to quantitatively predict the effects of mutations from or into a charged residue on the folding stability. We have made progress in this direction (Vijayakumar and Zhou, 2001; Zhou, 2002a; Dong and Zhou, 2002). Fig. 2 shows a comparison of calculated and experimental results for the changes in unfolding free energy by 38 charge mutations in six proteins ranging from barnase to Bs-CspB. Overall the correlation coefficient is 0.88. The results for the five mutations in Bs-CspB are encouraging. These mutations bring the sequence of Bs-CspB closer to that of the thermophilic homolog, and in agreement with experiment (Perl et al., 2000; Perl and Schmid, 2001), increases in stability were calculated in four of the mutations. Here, the calculations are expanded to converse mutations in Bc-Csp to see whether they lead to the expected decrease in stability. In particular, we found that Bc-Csp appears to use destabilization of the unfolded state by unfavorable charge-charge interactions as a mechanism for increasing stability. Sanchez-Ruiz and Makhatadze (2001) have previously obtained results that are in qualitative agreement with the experimental data for mutational effects.

FIGURE 2.

Comparison of calculated effects of 38 charge mutations on the unfolding free energies of six proteins (Vijayakumar and Zhou, 2001; Zhou, 2002a; Dong and Zhou, 2002) to experimental results.

In contrast to the effects of individual charge mutations, the effects of ionic strength and temperature are global in nature and are much less prone to errors in treating a particular local factor. These global effects can yield great insight into the contributions of electrostatic interactions to folding stability. We have shown previously that the electrostatic free energy of a molecule, calculated with the Poisson-Boltzmann (PB) equation, has a simple dependence on ionic strength (I) when I is small (Boschitsch et al., 2002):

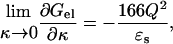(1)

where κ = (8πIe²/ɛ_sk_BT)^1/2, ɛ_s is the dielectric constant of water, and Q is the total charge on the molecule. According to Eq. 1, when κR ≪ 1 (where R is the size of the protein), regardless of the specific distribution of the charges, the electrostatic free energy decreases with ionic strength; the larger the magnitude of the total charge, the steeper the decrease. Equation 1 allows us to attribute the disparate ionic strength dependences of the unfolding free energies of Bc-Csp and Bs-CspB to the difference in their total charges, −2e and −6e.

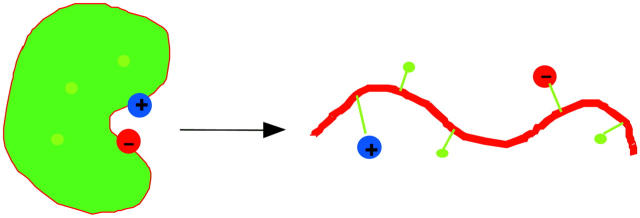
Because of the strong temperature dependence of the dielectric constant of water, electrostatic interactions are expected to contribute to the temperature dependence of the unfolding free energy (Zhou, 2002d). The favorable interactions of a charge with water molecules implies that the hydration water molecules will be organized and thus have a lower entropy than bulk water. Upon protein folding, the solute-solvent interactions will in general become less favorable (giving rise to the desolvation cost) and solvent organization will be less, resulting in an entropy gain (illustrated in Fig. 3 A). When two individually solvated charges (as in the unfolded state) are brought together in the folded state, the entropy changes will be very different depending on whether the charges have the same or opposite signs (illustrated in Fig. 3, B and C). Two like charges next to each other will reinforce each other's solvent-organizing effect, but two opposite charges next to each other will cancel each other's solvent-organizing effect. These results indicate that favorable electrostatic interactions in the folded state may contribute a loss of unfolding entropy whereas unfavorable electrostatic interactions may contribute a gain in unfolding entropy. We therefore suggest that the observed higher unfolding entropies of Bc-CspB and Bc-Csp mutants such as R3E/L66E are a result of the less favorable electrostatic interactions in the folded state (relative to Bc-Csp). In agreement with experiment, the calculated value of TΔΔS is greater than the magnitude of ΔΔG, resulting in a higher unfolding enthalpy for Bs-CspB.

FIGURE 3.

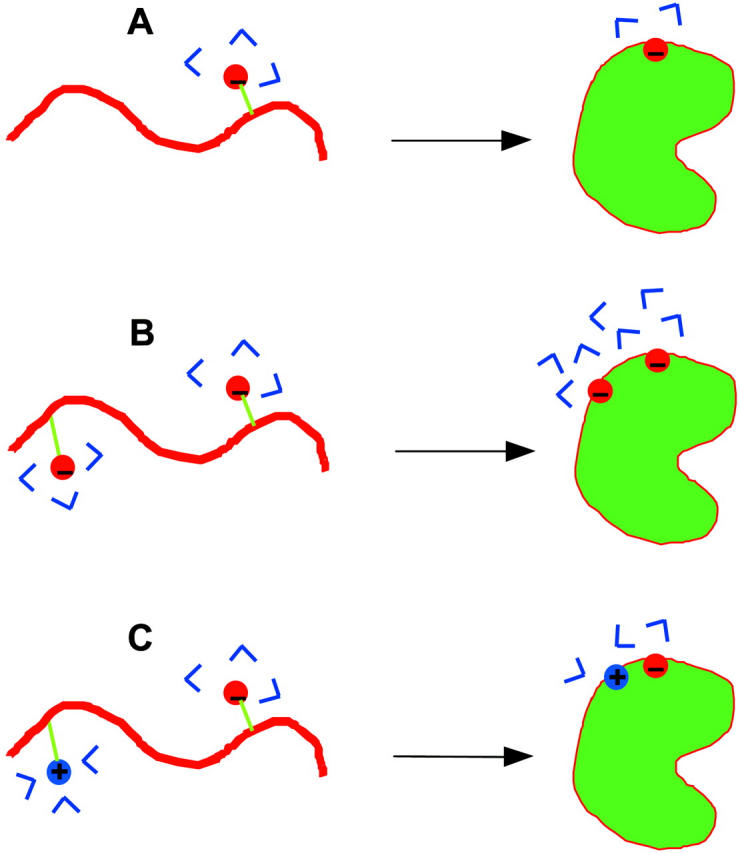
Ordering of hydration water around charges in the unfolded and folded states: (A) a single charge; (B) a pair of like charges; and (C) a pair of opposite charges.

THEORETICAL METHODS

Electrostatic model for protein unfolding

Fig. 4 illustrates the model that we have used to treat electrostatic interactions in the folded and the unfolded states (Vijayakumar and Zhou, 2001; Zhou, 2002a; Dong and Zhou, 2002). The electrostatic contribution to the unfolding free energy is

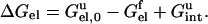(2)

In the folded state, the electrostatic free energy G_el^f is obtained by solving the PB equation, with the boundary between the low protein dielectric and the high solvent dielectric defined as the van der Waals surface of the protein. The electrostatic free energy in the unfolded state consists of two terms: a solvation term G_el,0^u, with each charged residue treated in the same way as a folded protein molecule, and a charge-charge interaction term G_int^u, calculated with a Gaussian-chain model that accounts for the sampling of residue-residue distances.

FIGURE 4.

The model for treating electrostatic interactions in the folded and unfolded states. All atoms were assigned partial charges. Circles with “+” or “−” inside represent charged residues, whereas small green circles represent other partial charges.

Modeling of mutations

When a mutation is introduced, all the three terms in Eq. 2 will be perturbed. The change in the difference of G_el,0^u and G_el^f will be called ΔΔG_el⁰. To isolate the electrostatic effect of the mutation, structural changes in the folded state were kept to a minimum. That is, only the mutated side chain was allowed to optimize its conformation within the existing environment using the program InsightII (Molecular Simulations, San Diego, CA.). The AMBER force field (Weiner et al., 1984) was used for the energy minimization. For wild-type Bc-Csp and Bs-CspB, the structures were from Protein Data Bank entries 1c9o and 1csp (Mueller et al., 2000; Schindelin et al., 1993), respectively.

The PB equation was solved by the UHBD program (Madura et al., 1995). The electrostatic potential φ was calculated first from a 100 × 100 × 100 grid with 1.5 Å spacing centered at the geometric center of the wild-type protein. This was followed by a 140 × 140 × 140 grid with 0.5 Å spacing at the same center. A final round of focusing at the CB atom of a mutated side chain was introduced on a 60 × 60 × 60 grid with 0.25 Å spacing. The electrostatic energies of the folded protein and the isolated mutation residue were calculated by

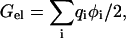(3)

where q_i are the partial charges. ΔΔG_el⁰ was obtained by taking the difference in G_el between the isolated mutation residue (modeling the unfolded state) and the folded protein and then the change in these differences by the mutation. AMBER charges and radii were used. The solvent dielectric constant was set to that of water at a particular temperature (Archer and Wang, 1990). In previous studies (Vijayakumar and Zhou, 2001; Dong and Zhou, 2002), the protein dielectric constant (ɛ_p) was set to 4. Here we also investigated the effect of varying this parameter by carrying our calculations with ɛ_p = 2, 4, and 10.

ΔΔG_el⁰ can be decomposed into a solvation term for the mutation residue, a solvation term for the rest of the folded protein, and a term representing the interactions between the mutation residue and the rest of the protein. Thus

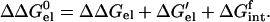(4)

The first two terms can be calculated from discharging the rest of the protein and the mutation residue, respectively. The electrostatic potential from either of these two calculations can be used to calculate ΔG_int^f. By multiplying the electrostatic potential of the mutation residue alone with the charges of other residues, ΔG_int^f can be further decomposed into contributions from interactions with individual residues.

Twenty-seven mutations of Bc-Csp and Bs-CspB were studied in three sets of solvent conditions: 1), I = 100 mM and T = 70°C; 2), I = 2.1 M and T = 70°C; and 3), I = 100 mM and T = 25°C. For calculating G_el,0^u and G_el^f, Asp, Glu, and the C-terminal were unprotonated, whereas the N-terminal, Lys, and Arg were protonated. For calculating G_int^u, the total energy of charge-charge interactions in the unfolded state (to model the effects of ionic strength and temperature), the same set of protonation states were assumed. However, for modeling the effects of charge mutations on G_int^u, sampling of protonation states were allowed (Zhou, 2002a).

Ionic strength dependence

To model the effects of ionic strength, G_el^f for the folded protein, G_el,0^u for all the charged residues, and G_int^u were calculated at I = 100, 200, 300, 400, and 500 mM.

Temperature dependence

The electrostatic contribution to the unfolding entropy was calculated as

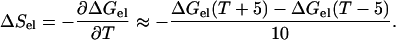(5)

It was assumed that the dielectric constant of water is the only temperature-dependent parameter.

RESULTS AND DISCUSSION

Effects of charge mutations

The calculated results on ΔΔG_el for 21 mutations on Bc-Csp and six mutations on Bs-CspB at I = 100 mM and T = 70°C are listed in Table 1. Those with ɛ_p = 4 are compared to experimental data of Schmid and co-workers (Perl and Schmid, 2001) in Fig. 5 A. The agreement slightly deteriorated when ɛ_p is decreased to 2 or increased to 10, with the root-mean deviation increasing from 0.46 kcal/mol to 0.53 and 0.48 kcal/mol, respectively. Overall, the correlation coefficient between the calculation results with ɛ_p = 4 and experimental data is 0.98. Unless otherwise noted, the results below are for ɛ_p = 4.

TABLE 1.

Effects of charge mutations on the unfolding free energies (in kcal/mol) of Bc-Csp and Bs-CspB at I = 100 mM and T = 70°C

Protein	Mutation	ΔΔGel0 (calc)*	−ΔGintu (calc)	ΔΔGel (calc)†	ΔΔG (expt)
Bc-Csp	Q2L	−0.41 (−0.49, −0.28)	0	−0.41	0.5
	R3E	−2.17 (−2.26, −1.99)	0.50	−2.67	−2.7
	R3E/E21A	−1.48 (−1.70, −1.26)	0.76	−2.24	−2.7
	R3E/E46A	−0.84 (−0.76, −0.89)	0.79	−1.63	−2.0
	R3E/L66E	−4.52 (−4.77, −4.01)	0.44	−4.96	−4.9
	R3E/E46A/L66E	−2.94 (−3.59, −2.29)	0.76	−3.70	−4.1
	R3L	−0.94 (−0.94, −0.90)	0.25	−1.19	−0.9
	R3K	−0.16 (−0.25, −0.07)	0	−0.16	−0.2
	R3A	−0.86 (−0.85, −0.83)	0.25	−1.11	−1.9
	N11S	0.43 (0.05, 0.23)	0	0.43	0.3
	Y15F	0.01 (−0.01, 0.02)	0	0.01	0
	E21A	0.10 (0, 0.16)	0.21	−0.11	−0.3
	G23Q	0.03 (0.10, 0.04)	0	0.03	−0.3
	G23Q/S24D	−0.28 (−0.15, −0.30)	−0.42	0.14	−0.1
	S24D	−0.35 (−0.28, −0.35)	−0.42	0.07	0.2
	T31S	−0.01 (0, −0.01)	0	−0.01	0.2
	E46A	−0.43 (−0.27, −0.51)	0.27	−0.70	−0.2
	E46A/L66E	0.11 (0.02, 0.29)	0.25	−0.15	−1.4
	Q53E	0.16 (0.26, 0.11)	−0.14	0.30	−0.1
	V64T	−0.17 (−0.28, −0.09)	0	−0.17	−0.3
	L66E	−0.29 (−0.42, −0.04)	−0.04	−0.25	−1.2
Bs-CspB	E3R	2.74‡ (2.87, 2.61)	−0.44	3.18	2.7
	E3L	1.75‡ (1.82, 1.62)	−0.22	1.97	1.6
	A46E	−1.01‡ (−0.45, −1.21)	−0.39	−0.62	−0.6
	E66L	2.21‡ (2.33, 1.92)	0	2.21	2.1
	E3R/E66L	3.35‡ (3.52, 3.08)	−0.46	3.81	3.4
	E3R/T64V/E66L	3.22 (3.33, 3.01)	−0.46	3.68	3.7

^*In this column, the first number was calculated with ɛ_p = 4 and the pair of numbers in parentheses were calculated with ɛ_p = 2 and 10, respectively.

^†Calculated as the sum of ΔΔG_el⁰ with ɛ_p = 4 and ΔG_int^u.

^‡These results were reported previously (Dong and Zhou, 2002).

FIGURE 5.

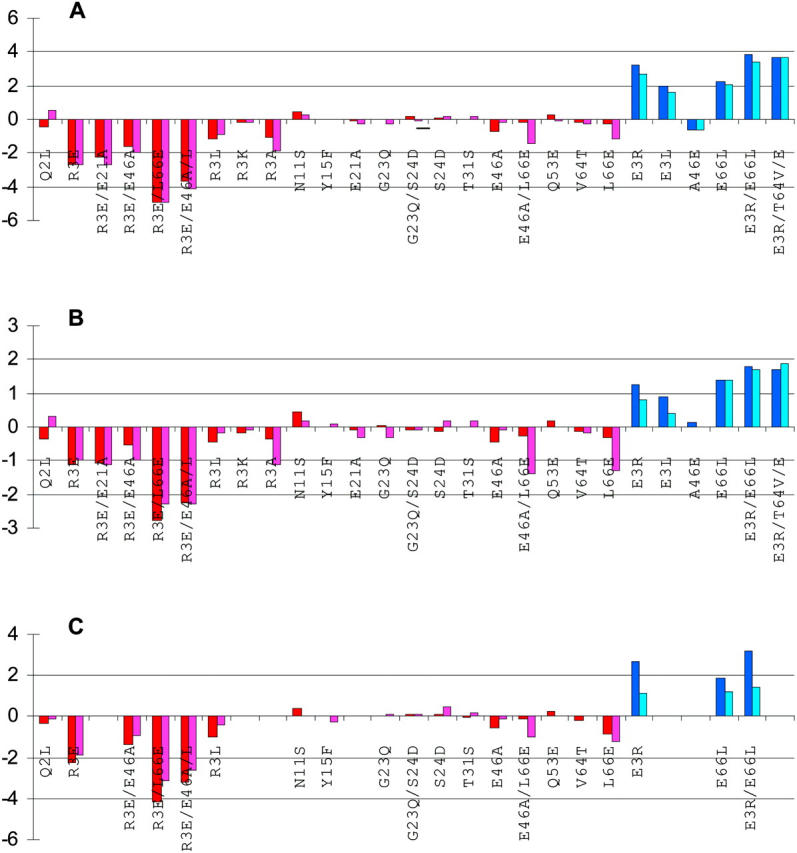
Comparison of calculated and measured effects of 27 mutations on the unfolding free energy of Bc-Csp and Bs-CspB. Calculated results for Bc-Csp and Bs-CspB are represented by red and blue bars, respectively, whereas measured results for Bc-Csp and Bs-CspB are represented by magenta and cobalt bars, respectively. (A) I = 100 mM and T = 70°C; (B) I = 2.1 M and T = 70°C; and (C) I = 100 mM and T = 25°C. The protein dielectric constant was 4 for the calculated results.

Mutations on residue R3 of Bc-Csp have the largest effects on the unfolding free energy. As replacements of R3 are made by another positive charge (K), neutral residues (L and A), and a negative charge (E), the magnitude of ΔΔG_el rises sharply. The calculated results on ΔΔG_el quantitatively reproduce the measurements of Schmid and co-workers (Perl et al., 2000; Perl and Schmid, 2001) and strongly suggest that residue R3 contributes to the stability of Bc-Csp mainly through electrostatic interactions. The measured difference in ΔΔG between the R3L and R3A mutants (−0.9 vs. −1.9 kcal/mol) suggests a nonpolar contribution as well, but this cannot be accounted for within our electrostatic model.

It is of interest to note that as much as 0.5 kcal/mol of the 2.7 kcal/mol decrease in folding stability of the R3E mutant comes from stabilizing the unfolded state. In the unfolded state, charge-charge interactions are dominated by residues close along the sequence, since these will have higher probabilities of sampling short distances (Zhou, 2002a). For unfolded Bc-Csp, R3 is in an unfavorable position because the charges immediately preceding and after it (the N-terminal and residues K5 and K7) are all positive. Mutation to E3 will change unfavorable interactions with these positive charges into favorable ones and stabilize the unfolded state.

Of the 2.2 kcal/mol of −ΔΔG_el⁰ for the R3E mutations, 0.4 kcal/mol comes from higher desolvation cost for E3 (than R3), −0.1 kcal/mol comes from the difference in solvating the rest of the protein, and 1.9 kcal/mol comes from less favorable interactions with the protein environment. In particular, interactions with E46, E21, and the C-terminal account for 1.6, 0.6, and 0.5 kcal/mol, respectively, of −ΔΔG_el⁰. These are compensated by interactions with the N-terminal and K5, which contribute 1.3 kcal/mol to ΔΔG_el⁰. Weak interactions with numerous other residues make up the remaining portion of ΔΔG_el⁰.

The above details of the various contributions to the ΔΔG_el⁰ result for R3E also help understanding the effects of additional mutations on the R3E mutant. Specifically, the R3E/E21A and R3E/E46A mutants have smaller magnitudes of ΔΔG_el⁰ (−1.5 and −0.8 kcal/mol, respectively) mainly because an unfavorable interaction (with either E21 or E46) is now absent. In contrast, in the R3E/L66E mutant, an additional unfavorable interaction is introduced, and consequently −ΔΔG_el⁰ increases to 4.5 kcal/mol. In the R3E/E46A/L66E triple mutant (which resembles Bs-CspB the most among all R3E mutants), an unfavorable interaction is removed but another is introduced, and the value of ΔΔG_el⁰, −2.94 kcal/mol, is intermediate. These results generally are in accord with experimental observations. However, there is disagreement regarding the interaction between E3 and E21. The fact that the measured ΔΔG does not change upon the additional mutation E21A on the R3E mutant suggests absence of interaction between these two residues, whereas our calculations found an interaction energy of 0.6 kcal/mol. The apparent discrepancy may indicate the limitation of our calculations in not allowing for the mutated and neighboring residues to sample different rotamers.

Our calculations show that the unfolded state is also significantly stabilized by the E21A and E46A mutations. In both cases, the immediately preceding and following charges are all negative (E19 and D25 for the former and E42, E43, and E50 for the latter). All together, residual charge-charge interactions for the R3E/E46A/L66E triple mutant account for 0.76 kcal/mol, or 20%, of the total loss of 3.7 kcal/mol in folding stability.

In agreement with experimental observations (Perl et al., 2000; Perl and Schmid, 2001), most of the other 13 mutations on Bc-Csp have marginal effects on the folding stability. The increase in stability by converse mutations on Bs-CspB have been discussed previously (Dong and Zhou, 2002).

Electrostatic interactions can be weakened by an increase in ionic strength or an increase in the dielectric constant of water brought by a decrease in temperature. Comparisons of calculated and experimental results for the effects of the mutations at I = 2.1 M and T = 70°C and at I = 100 mM and T = 25°C are displayed in Fig. 5, B and C. Again, there is reasonable overall agreement between calculation and experiment. It is of interest to note that, even at an ionic strength of 2.1 M, there are still substantial electrostatic interactions in the folded state, which may be attributed to the compactness of the protein. This finding casts doubt on attributing residual effects of charge mutations at a high ionic strength (such as 2 M) solely to a nonelectrostatic origin (such as hydrophobic interactions). At room temperature, our calculations on the effects of the mutations again indicate significant electrostatic contributions to the folding stability of Bc-Csp, but with smaller magnitudes as a result of the increase in the dielectric constant of water.

Effect of ionic strength on overall stability

The role of the total charge in the effect of ionic strength can be understood from the general result given in Eq. 1 for low ionic strengths and the specific result for a spherical protein:

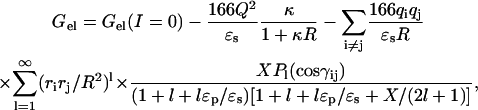(6)

where R is the radius of the protein; X = κRK_l−&1by2;(κR)/K_l+&1by2;(κR), with K_l+&1by2;(x) denoting modified Bessel functions; r_i is the radial distance of charge q_i; γ_ij is the angle between the radial vectors of charges q_i and q_j; and P_l(x) are the Legendre polynomials. Both Eq. 1 and Eq. 6 show that a dominant contribution to the ionic strength dependence of G_el is a term proportional to Q². The total charges on Bc-Csp and Bs-CspB are −2e and −6e, respectively, thus the electrostatic free energy of folded Bs-CspB is expected to decrease with ionic strength much more rapidly than that of Bc-Csp. Our calculation results conform to this expectation. From I = 100 to 500 mM, G_el decreased 1.04 kcal/mol for folded Bc-Csp but 2.53 kcal/mol for folded Bs-CspB at T = 70°C. The electrostatic free energy of the unfolded state also decreased with ionic strength. Specifically, the solvation energies of all the charged groups decreased by 2.07 kcal/mol for unfolded Bc-Csp and by 2.30 kcal/mol for unfolded Bs-CspB, and the residual charge-charge interaction energy decreased by 0.36 kcal/mol for unfolded Bc-Csp and by 0.26 kcal/mol for unfolded Bs-CspB. Taken together, ΔG_el decreased by 1.4 kcal/mol for Bc-Csp but was unchanged for Bs-CspB.

Experimentally, Perl and Schmid (2001) observed a slight decrease in the unfolding free energy from I = 100 to 500 mM for Bc-Csp and a significant increase in ΔG for Bs-CspB. For both proteins, ΔG increases from I = 500 mM to 2.1 M. The increase in stability by high ionic strengths is likely due to the Hofmeister effect of salts (Perl and Schmid, 2001; Baldwin, 1996). Our implicit assumption is that all protein variants studied here are stabilized to the same extent by the Hofmeister effect. With this assumption, we would predict that the difference in stability between Bc-Csp and Bs-CspB will decrease by 1.4 kcal/mol from I = 100 to 500 mM. This decrease is in quantitative agreement with the measurement of Schmid and co-workers.

The main source of the disparate ionic strength dependences of the unfolding free energy for Bc-Csp and Bs-CspB is the difference in the total charges. For Bs-CspB, the larger magnitude of the total charge leads to a sharper decrease with ionic strength in the electrostatic free energy of the folded state. This sharper decrease is at nearly the same pace with which the electrostatic free energy of the unfolded state varies with ionic strength, leading to an almost constant ΔG. On the other hand, Bc-Csp has a small net charge and the ionic strength dependence in the folded state is much weaker than in the unfolded state; consequently ΔG is found to decrease with ionic strength. A recent continuum model study by Dominy et al. (2002) yielded similar results and reached the same conclusion on the role of the total charge. Within the PB model, the total charge as a determinant of the ionic strength dependence of ΔG is inevitable.

Two additional pieces of evidence support the attribution of the disparate ionic strength dependences of the stabilities of Bc-Csp and Bs-CspB to the difference in the total charges. On the calculation side, the R3E/L66E mutant of Bc-Csp, with an increase of total charge from −2e to −5e is found to have the same ionic strength dependence as Bs-CspB, i.e., ΔG_el remains constant from I = 100 to 500 mM. On the experimental side, the ionic strength dependences of Bs-CspB and Bc-Csp were found to bracket a majority of the mutants with intermediate total charges (Perl and Schmid, 2001).

Contributions of electrostatic interactions to temperature dependence of ΔG

The contribution of electrostatic interactions to the unfolding entropy was calculated according to Eq. 5 from the temperature dependence of the electrostatic free energy of the folded protein and the solvation energies of the charged residues and the residual charge-charge interaction energy in the unfolded state. With ɛ_p = 4, ΔS_el was 8.7 cal/mol/K for Bc-Csp but 29.9 cal/mol/K for Bs-CspB at I = 100 mM and T = 70°C. The difference in ΔS_el is 21.2 cal/mol/K, which accounts for more than half of the measured difference of 40 cal/mol/K in the unfolding entropy (Perl and Schmid, 2001). Similarly, the change in ΔS_el by the R3E/L66E mutation is 19.4 cal/mol/K, accounting for half of the measured change of 41 cal/mol/K in the unfolding entropy. The magnitude of ΔS_el increases at ɛ_p = 2 and decreases at ɛ_p = 10. However, the differences in ΔS_el of the R3E/L66E mutant and Bs-CspB with Bc-Csp are nearly constant at ∼20 cal/mol/K.

We are now in a position to decompose the −5.0 kcal/mol calculated change in unfolding free energy by the R3EL66E mutation into entropic and enthalpic components. The entropic component TΔΔS_el is 343 × 19.4 cal/mol = 6.7 kcal/mol, and the enthalpic component is thus ΔΔH_el = ΔΔG_el + TΔΔS_el = 1.7 kca/mol. Though the calculated ΔΔH_el is much smaller than the measured change in unfolding enthalpy (which was 9.1 kcal/mol), there is qualitative agreement in that the unfolding enthalpy of the R3EL66E mutant (and by extension Bs-CspB) is higher than that of Bc-Csp. We now see that the higher unfolding enthalpy of the R3EL66E mutant is a consequence of the higher unfolding entropy, which in turn may be attributed to the less favorable electrostatic interactions in the folded protein.

Implications for other thermophilic proteins

The effects of charge mutations, ionic strength, and temperature on the folding stability report complementary information on the contributions of electrostatic interactions. The effects of charge mutations usually are dominated by the desolvation cost and interactions with nearby charged and polar groups. Both our study and the study of Dominy et al. (2002) indicate that the total charge plays a dominant role in the dependence on ionic strength. Our study further suggests that overall more favorable environments for charged residues lead to a smaller unfolding entropy.

A key to our approach is the explicit treatment of the unfolded state, which often is relegated to the status of an implicit “reference state”. Only after accounting for the temperature and ionic strength dependence of the electrostatic free energy of the unfolded state can one properly obtain information on the unfolding entropy and enthalpy and the ionic strength dependence of the unfolding free energy. Moreover, in several cases (R3, E21, and E46), the thermophilic Bc-Csp appears to use destabilization of the unfolded state as a mechanism for increasing thermostability.

It is of great interest to see whether this intriguing mechanism is used by other thermophilic proteins. In addition, the control of ionic strength dependence of protein stability by the total charge and the contribution of electrostatic interactions to the unfolding entropy suggested by the present study warrant further testing. Applications of the present approach to other thermophilic proteins, with the interrogation of experiments, should provide a more comprehensive understanding on the role of electrostatic interactions in thermostability.