Energetics and Self-Assembly of Amphipathic Peptide Pores in Lipid Membranes

Abstract

We present a theoretical study of the energetics, equilibrium size, and size distribution of membrane pores composed of electrically charged amphipathic peptides. The peptides are modeled as cylinders (mimicking α-helices) carrying different amounts of charge, with the charge being uniformly distributed over a hydrophilic face, defined by the angle subtended by polar amino acid residues. The free energy of a pore of a given radius, R, and a given number of peptides, s, is expressed as a sum of the peptides' electrostatic charging energy (calculated using Poisson-Boltzmann theory), and the lipid-perturbation energy associated with the formation of a membrane rim (which we model as being semitoroidal) in the gap between neighboring peptides. A simple phenomenological model is used to calculate the membrane perturbation energy. The balance between the opposing forces (namely, the radial free energy derivatives) associated with the electrostatic free energy that favors large R, and the membrane perturbation term that favors small R, dictates the equilibrium properties of the pore. Systematic calculations are reported for circular pores composed of various numbers of peptides, carrying different amounts of charge (1–6 elementary, positive charges) and characterized by different polar angles. We find that the optimal R's, for all (except, possibly, very weakly) charged peptides conform to the “toroidal” pore model, whereby a membrane rim larger than ∼1 nm intervenes between neighboring peptides. Only weakly charged peptides are likely to form “barrel-stave” pores where the peptides essentially touch one another. Treating pore formation as a two-dimensional self-assembly phenomenon, a simple statistical thermodynamic model is formulated and used to calculate pore size distributions. We find that the average pore size and size polydispersity increase with peptide charge and with the amphipathic polar angle. We also argue that the transition of peptides from the adsorbed to the inserted (membrane pore) state is cooperative and thus occurs rather abruptly upon a change in ambient conditions.

INTRODUCTION

Amphipathic, α-helical peptides are abundant in nature, serving as membrane permeating agents in the host defense system of many organisms. Antibiotic peptides, such as alamethicin, isolated from the Trichoderma viride fungus, the bee venom peptide melittin, the magainins of the African frog Xenopus laevis, and many others, are among the most intensively studied peptides (Hancock et al., 1995; Nicolas and Mor, 1995). Attempts to mimic nature and design novel antibacterial drugs have stimulated numerous experimental and theoretical studies of amphipathic peptides.

The distinctive structural characteristic of amphipathic helical peptides is the division of their cylindrical envelope into complementary hydrophobic and hydrophilic faces. Viewed along the helix axis, the hydrophilic face is often characterized by a well-defined polar angle, α. In many peptides, the polar face is positively charged, due to the presence of lysine and/or arginine residues.

Adsorption onto the hydrocarbon-water interface of the membrane is most likely the first stage of interaction between most amphipathic peptides and membranes. The prevailing picture of the adsorbed state is that the peptide lies parallel to the interface, pushing sideways polar lipid headgroups, with its hydrophobic sector embedded in the membrane hydrophobic core, resulting in local (and, at higher concentrations, global) thinning of the lipid bilayer, and an unfavorable elastic deformation free-energy penalty. Experiments reveal that above a certain threshold concentration of adsorbed peptides, the membrane undergoes a phase transition, whereby the peptides are inserted into the lipid bilayer to form the walls of membrane-spanning pores (He et al., 1996a; Yang et al., 2001). It has been suggested that peptide insertion takes place because the membrane perturbation in the adsorbed state is larger than in the inserted state (He et al., 1996a; Epand et al., 1995; Chen et al., 2002). An alternative theory treating the mixture of adsorbed peptides and pores (modeled as monodisperse rigid rings) according to scaled-particle theory has recently been presented by Zuckermann and Heimburg (2001). According to this theory, peptide insertion is driven by excluded area interactions between adsorbed peptides.

Although pore formation in lipid membranes is a well-established phenomenon (Ladokhin et al., 1997; Matsuzaki et al., 1997; Ludtke et al., 1996; He et al., 1996b; Bezrukov and Vodyanoy, 1993), its underlying molecular mechanisms are very partially understood. In early models, amphipathic peptides in the inserted state were depicted as lining up densely along the perimeter of a “barrel-stave” pore; their hydrophobic faces apposed to the surrounding lipid tails and their hydrophilic faces in contact with water (Boheim, 1974; Sansom, 1991). In-plane neutron-scattering measurements on lamellar phases of alamethicin-containing lipid bilayers (He et al., 1996b), combined with oriented circular dichroism studies (Huang and Wu, 1991), have confirmed the assembly of eight or nine alamethicin molecules into barrel-stave pores of radius R ≈ 9 Å.

On the other hand, various other experiments, as well as computer simulations (Lin and Baumgärtner, 2000), indicate that the barrel-stave model is often inapplicable, especially for pores composed of highly charged peptides. More explicitly, a variety of experimental studies involving membrane pores formed by melittin (net charge z_p = +6) (Matsuzaki et al., 1997), magainin (+4) (Matsuzaki et al., 1996a; Ludtke et al., 1996), and other charged peptides (Matsuzaki et al., 1996b; Yang et al., 2001) lend strong support to a different, “toroidal” pore model. Unlike in a barrel-stave pore in which the peptides are tightly packed against each other, in the toroidal pore, a lipid “spacer” region of length corresponding to several lipid headgroup diameters separates between the peptides. This model appears quite natural in view of the strong electrostatic repulsion between the highly charged peptides, which tends to increase the interpeptide spacing and hence also the pore diameter (Yang et al., 2001; Lin and Baumgärtner, 2000). The gap between peptides is most likely bridged by a bent, approximately semitoroidal lipid rim, with the polar lipid headgroups facing the aqueous pore (Weakliem et al., 1995; Bagdassarian et al., 1991) (see Fig. 2.)

FIGURE 2.

A segment of a toroidal pore, containing one peptide and its neighboring semitoroidal lipid rims.

Unlike barrel-stave pores whose circumference is uniquely prescribed by the number of their constituent (e.g., alamethicin) peptides, toroidal pores appear to exhibit variable sizes, depending on experimental conditions and method of measurement. For instance, based on neutron-scattering experiments, a radius of 22.0 Å has been reported for melittin pores (Yang et al., 2001). On the other hand, leakage measurements (of dye markers from lipid vesicles) performed at two different laboratories indicate pore radii in the range 12.5–15.0 Å (Ladokhin et al., 1997), and 6.5–12.0 Å (Matsuzaki et al., 1997), respectively. The latter set of experiments also reveals an increase in the average pore radius upon increase in peptide to lipid ratio. Finally, comparing the number of peptides per pore (in the range 4–7) with the measured pore radius, it has been concluded that the barrel-stave model is inappropriate for highly charged peptide pores (Ludtke et al., 1996; Yang et al., 2001).

Electrostatic interactions between the peptides, as well as between the peptides and membrane lipids, must play a central role in determining the mechanisms of peptide adsorption onto the membrane, insertion into the membrane, as well as the structure and size of peptide pores (Bechinger, 1997; Lin and Baumgärtner, 2000). For example, using pH-sensitive (histidine-containing) peptides, it was shown that the orientation of amphipathic peptides with respect to the membrane interface changes with the bulk pH, and hence with the amount of charge. More explicitly, under acidic conditions, in which histidine groups are positively charged and strongly repel each other, the peptides align parallel to the membrane plane, changing into a transmembrane orientation at physiological pH values (Titus et al., 1999). Another way to demonstrate the effect of electrostatic interactions between peptides in the pore state was to change the salt concentration in solution. It was shown, for example, that (alamethicin) channel life times increase substantially with ionic strength (Hall et al., 1984), consistent with earlier findings suggesting that high salt concentration stabilizes small membrane pores (Boheim, 1974). Unfortunately though, direct experimental information pertaining to the effects of electrostatic interactions on the pore state of peptides is rather scarce. A major goal of the present study is to analyze the role of electrostatic interactions in determining the structural and energetic characteristics of charged peptide pores.

The elastic deformation associated with peptide adsorption and insertion involves an energetic (membrane perturbation) penalty that depends on the nature and composition of the lipid molecules constituting the membrane. It also depends on the peptide characteristics (e.g., the hydrophilic angle or peptide length) and concentration. It is well known, for instance, that the “hydrophobic mismatch” (Bloom et al., 1991; Killian, 1998; Morein et al., 2000), measuring the difference between the peptide length and the (unperturbed) membrane thickness, plays a crucial role in determining the membrane perturbation free energy and other characteristics of the interaction between lipids and integral proteins (Huang, 1986; Harroun et al., 1999; Fattal and Ben-Shaul, 1993; Ben-Shaul, 1995; May and Ben-Shaul, 1999). Numerous theoretical studies have dealt with the interaction between integral proteins and lipid membranes. However, only few of those are directly relevant to the interaction between lipid bilayers and amphipathic peptides. The membrane perturbation energy associated with peptide adsorption has been addressed by Huang and co-workers using continuum elastic theories (Huang, 1995), as well as on the basis of simple packing considerations (Ludtke et al., 1995). More recently, changes in the membrane lateral pressure profile, reflecting changes in the embedding lipid matrix, have been invoked to explain shifts in the size distribution of alamethicin pores (Cantor, 2002). However, a detailed molecular-level theory of the membrane perturbation energy as a function of peptide structure and density and lipid properties is still lacking.

The structural, energetic, and thermodynamic characteristics of amphipathic peptide adsorption and insertion are governed by the interplay between the electrostatic and elastic interactions discussed above. Our general goal in this paper is to present a systematic analysis of this interplay, focusing on the dependence of electrostatic interactions between charged peptides on the energetic and size characteristics of peptide pores.

More explicitly, our pore formation free energy will be expressed as a sum of the peptides' electrostatic charging energy that favors pore expansion, and a “surface” (membrane perturbation) term that counterbalances this tendency. The electrostatic (charging) energy of the pores will be calculated using Poisson-Boltzmann (PB) theory. The lipid perturbation contribution to the pore free energy will be treated using a familiar phenomenological model for lipid packing in membranes and micelles (Israelachvili et al., 1976; Ben-Shaul and Gelbart, 1994), yielding a simple expression for the free energy of the semitoroidal lipid rim. Then, for a given number and type of peptides (as specified by their charge and hydrophilic angle), the equilibrium pore size is found by balancing the opposing forces corresponding to the electrostatic and membrane perturbation components of the pore's free energy. One of the major qualitative conclusions of our analysis is that, with the exception of very weakly charged peptides, the toroidal pore model is more appropriate than the barrel-stave model.

Given the equilibrium pore size and energy, we shall derive the pore size distribution using a simple statistical-thermodynamic model that treats pore formation as a two-dimensional (2D) self-assembly phenomenon. The size distribution calculations are limited to the dilute (peptide in lipid) solution regime, where interchannel interactions can be neglected. We also ignore the possible effects of interactions between inserted and adsorbed peptides. We conclude the discussion with several comments pertaining to the thermodynamic characteristics of the transition of peptides from the adsorbed to the inserted state.

THEORY

Consider a “perforated” lipid bilayer consisting of 2N_l lipid molecules (N_l per monolayer) and N_p membrane spanning peptides oriented perpendicularly to the membrane plane. The N_p-inserted peptides self-assemble into circular pores of different sizes s, such that ∑sn_s = N_p, with n_s denoting the number of pores composed of s peptides (or s-pores).

In the first part of this section we shall describe our method of calculating f_s⁰, the free energy per peptide in an (isolated, immobile) s-pore. In the second part we use f_s⁰ in a simple statistical-thermodynamic scheme for calculating the equilibrium distribution of pore sizes, {n_s^eq}.

Pore free energy

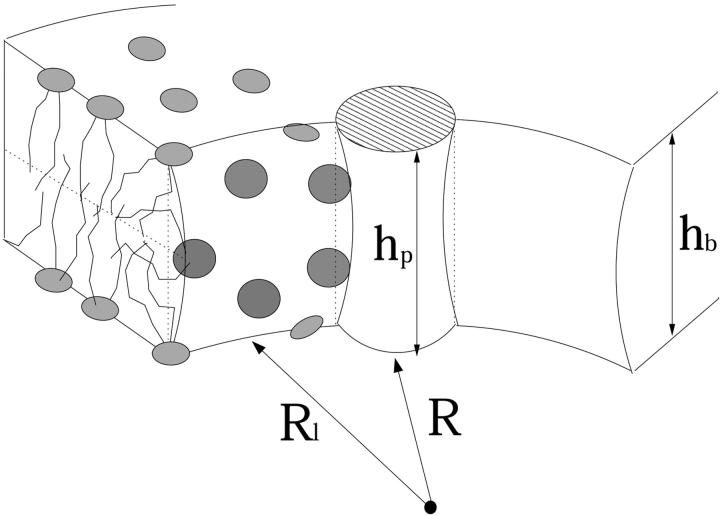
We assume that the amphipathic peptides forming the membrane pores are α-helical, and model them as cylinders of radius R_p and length h_p. (See, however, Shai, 1994; White and Wimley, 1999.) The hydrophilic face apposing the aqueous channel is assumed to subtend a well-defined angle α, carrying polar and charged residues of net total charge z_p. The complementary hydrophobic surface, of angle 2π − α, faces lipid chains of the host membrane. A schematic top view of a membrane pore, illustrating that the peptides are not necessarily in contact with each other, is shown in Fig. 1. A side-view illustration of a pore is shown in Fig. 2.

FIGURE 1.

Schematic top view of a tetrameric peptide pore. The peptide surface marked L_p is uniformly charged; L_l denotes the hydrocarbon-water interface of the lipid membrane rim.

The formation free energy of such a pore involves two major s-dependent contributions. The first, of magnitude f_s,el⁰ (R; z_p, α) per peptide, is the electrostatic (charging) energy, which depends parametrically on z_p and α, and decreases with the pore radius R owing to electrostatic repulsions between the peptides. The second term, f_s,mp⁰ (R; α), represents the membrane perturbation free energy, accounting for all changes in lipid packing associated with peptide insertion into the bilayer. This term is a sum of the elastic perturbation experienced by the lipid molecules in contact with the hydrophobic face of the peptide and (whenever the peptides are not in contact) the line energy associated with the inevitable change in lipid packing along the lipid-water contact region, (of length L_l ≠ 0 in Fig. 1). Both contributions to f_s,mp⁰ depend on the hydrophobic mismatch, measuring the difference between the length of the peptide, h_p, and the thickness of the bilayer's hydrophobic core, h_b. To simplify our analysis, we shall assume perfect hydrophobic matching, h_p = h_b, thus attributing f_s,mp⁰ entirely to the rim energy. The equilibrium radius of the pore is the value of R corresponding to the minimum of

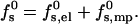(1)

Before turning to a more detailed discussion of the two terms on the right hand side of Eq. 1, it may be noted that the interplay between these opposing tendencies is analogous to that between headgroup repulsion and hydrocarbon-water surface tension in micellar aggregates of amphiphilic molecules (Israelachvili et al., 1976; Ben-Shaul and Gelbart, 1994). Actually, peptide pores may also be regarded as 2D water-in-oil microemulsion droplets, with the amphipathic peptides playing the role of surfactants (Safran, 1994).

The electrostatic free energy

The electrostatic free energy of the toroidal pore will be evaluated using PB theory. Despite its approximate character, this mean-field theory has proved successful in predicting and explaining many experimental observations pertaining to similar, spatially confined environments, e.g., DNA-cationic lipid complexes (Harries et al., 1998; Wagner et al., 2000).

Because we are not specifically concerned here with a particular amphipathic peptide, several simplifying approximations will be made to allow systematic analyses of charge and size effects. One approximation is to treat the z_p charges as randomly distributed over the hydrophilic face of the peptide, giving rise to uniform charge density σ = ez_p/h_pαR_p, with e denoting the elementary charge and R_p = 6 Å the radius of the cylindrical peptide. For highly charged peptides, say z_p ≥ 3, and typical peptide characteristics such as h_p = 30 Å and α = 2π/3, we find e/σ ≤ 120 Ų, comparable to the area spanned by thermal fluctuations of charged amino acid side chains.

The charge-smearing approximation is certainly less satisfactory for smaller z_p values. It should be mentioned, however, that we have carried out comparative electrostatic calculations for uniform versus “stripe-wise” distributions of peptide charge and found rather small differences, even for low z_p.

We approximate the electrostatic charging energy of a pore of length h_p, by the charging energy of a section of length h_p of an infinitely long pore. This approximation reduces the dimensionality of the PB equation by eliminating end effects at the pore mouths. Again, comparing the results of this calculation with numerical solutions of the three-dimensional (3D) PB equation, we found that the end effects are minor.

Finally, in most calculations we assume that a sharp boundary (the thick line in Fig. 1) separates between the low dielectric medium (ɛ_o ≈ 2) within the membrane and peptide cores and the high dielectric (ɛ_w = 80) aqueous interior of the pore. The convex regions, of length L_p along the pore contour, are the uniformly charged cylindrical peptide faces. The complementary sectors, of length L_l, are electrically neutral surfaces, marking the interface between lipids and water. This geometrical model is appropriate for toroidal pores whose constituent peptides are well separated from each other; say, d ≥ R_p = 6 Å in Fig. 1.

For small, barrel-stave, pores whose boundaries consist of tightly packed peptides, allowance should be made for a nonzero, counterion-free layer of intermediate (pore radius-dependent) dielectric constant. For these very small pores, we have carried out finite difference PB calculations (Gilson et al., 1987; Honig and Nicholls, 1995), and found enormous electrostatic formation energies for all z_p ≥ 1. We thus conclude that the barrel-stave scheme is only reasonable for very weakly charged peptides. Nevertheless, to provide an estimate of the magnitude of electrostatic repulsion of such pores, an approximate closed-form model for calculating their charging energies is described in the Appendix. The s and z_p dependencies predicted by this model are in line with the finite difference PB calculations, and the electrostatic potentials and energies are also similar. Note, however, that unless otherwise specified, all the electrostatic calculations presented in this paper are for the toroidal pore model, where L_l is at least a few molecular diameters.

Assuming that the embedding aqueous solution contains a 1:1 electrolyte of concentration n₀, the 2D PB equation for the peptide pore in Fig. 1 reads

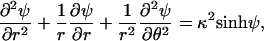(2)

with r denoting the distance of an arbitrary point from the pore's center and θ its polar angle relative to, say, the x axis; ψ = eϕ/k_BT is the reduced electrostatic potential, where ϕ is the electrostatic potential, k_B denotes Boltzmann's constant, and T the temperature. κ⁻¹ = l_D = (ɛ_wk_BT/8πn₀e²)^1/2 denotes the Debye screening length. In all calculations, we have assumed physiological salt conditions, namely n₀ = 0.1 M, and room temperature T = 300 K, corresponding to l_D ≈ 10 Å.

Our membrane pore model consists of s identical sections, as indicated in Fig. 1. By symmetry, the tangent component of the electric field must vanish at all planes emanating radially from the pore center and bisecting the L_p and L_l lines, i.e.,

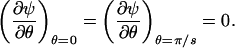(3)

Assuming that the electric field does not penetrate the hydrophobic regions (as appropriate in the “decoupling limit” (Carnie et al., 1994; Andelman, 1995)), the boundary conditions (Gauss' law) at the pore walls read,

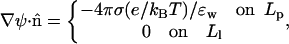(4)

with σ = ez_p/h_pαR_p denoting the charge density on the polar peptide face and ɛ_w = 80 standing for the dielectric constant of water. In the numerical calculations presented in the next section, the PB equation has been solved by a collocation method as described by Houstis et al., (1985).

The effective charge on the peptide hydrophilic face, z_p, and hence the surface charge density in Eq. 4, depend on the degree of protonation of the basic amino acid residues. More explicitly, the number of positive charges on the peptide surface may be smaller than the number of titratable amino groups, as some of them may not be protonated (Borisenko et al., 2000). Following Ninham and Parsegian (1971), it can be shown that the degree of protonation is given by 1/(1 + exp(2.3(pH − pK⁰) + ψ_s(R)), where K⁰ is the equilibrium constant for a deprotonation reaction of the type: R − NH₃⁺ → NH₂ + H⁺ of an isolated amino group in water, and ψ_s is the reduced electrostatic potential on the peptide surface. Since ψ_s depends on pore size and peptide charge, the effective charge density in Eq. 4 is not strictly constant, but rather “regulated” by the pore diameter and pH. Typical pK⁰ values for lysine and arginine residues are 10.5 and 12.0, respectively (Matthew, 1985). Our numerical solutions of the PB equation yield ψ_s(R) ≤ 6 for all (toroidal) pore sizes of interest. Thus for pH ≤ 8, all arginine residues are fully (≥95%) charged. Similarly, for pH ≤ 6.5, all lysine residues are charged. Assuming that these conditions are fulfilled, we have treated σ as independent of pore size. These conditions may not apply for small, barrel-stave pores where other assumptions (such as the charge-smearing scheme and the existence of a sharp dielectric boundary) are also questionable. For these, highly confined geometries, atomic level calculations are called for.

After solving PB equation for ψ, subject to the boundary conditions specified above, the charging free energy of the pore can be calculated using

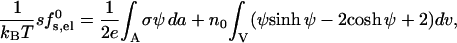(5)

with the first integral extending over the charged peptide surfaces and the second over the entire pore volume.

The charging free energy, sf⁰_s,el, includes both the “self energy” corresponding to the charging energy of the isolated peptides, and the excess (or interaction) electrostatic energy associated with the close proximity of the peptides in the pore. The excess electrostatic free energy, per peptide, is given by

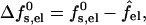(6)

with 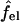denoting the charging free energy of an isolated, noninteracting peptide. This quantity may be interpreted as the electrostatic free energy per peptide in an infinitely large pore. Since the limit R → ∞ corresponds to a single peptide adsorbed on a planar lipid wall, we may also interpret 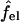as the electrostatic free energy of an isolated peptide adsorbed on the membrane surface. Note that 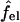depends on z_p and α.

Membrane perturbation free energy

We model the membrane rim segment (of length L_l, Fig. 2.) which separates between neighboring peptides as a section of a bent semitoroidal rim, as illustrated in Fig. 2. The lipid molecules constituting these rims are not in their ideal packing environment, which is the planar (peptide-free) lipid bilayer. The membrane perturbation free energy, f_s,mp⁰, is the excess packing free energy of the rim molecules, relative to the packing free energy (of the same number of molecules) in the planar bilayer.

The optimal rim geometry depends on the molecular characteristics of its constituent lipids, primarily their spontaneous curvature (Helfrich, 1973). Thus, for one lipid species, the optimal rim geometry might be a straight semicylindrical segment bridging between two peptides, whereas others would prefer organizing in a bent semitoroidal rim. Since the focus of this paper is not on the prediction of exact pore dimensions made of specific peptides in specific lipid bilayers, but, rather, the general characteristics of the competition between peptide repulsion and membrane-rim perturbation, we shall suffice here with a simple phenomenological model for f_s,mp⁰, as follows.

We assume that the rim is a segment of a circle (of radius R_l) of arc length L_l, and excess energy per unit length λ. Namely,

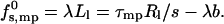(7)

To avoid additional parameters, we assume that λ is a constant, independent of the pore radius R_l (as appropriate for straight rim segments and in the limit of large R_l). In the second equality, we have introduced the radial force, τ_mp = ∂(sf_s,mp⁰)/∂R, which opposes pore expansion because of the increasing line energy. Simple geometrical considerations reveal 2πR_l = s(L_l + b), where b is a geometrical constant depending parametrically on α and R_p; implying τ_mp = 2πλ. Thus, ignoring rim curvature effects, τ_mp, like λ, is independent of s.

Clearly, the toroidal pore model is appropriate, essentially by definition, only when L_l is large enough to enable at least several lipid molecules, in the space between peptides, to bend and poke their headgroups into the aqueous interior of the pore. Since, typically, the cross-sectional area per lipid headgroup is a ≥ 50 Ų, this means that L_l should be larger than L_l ≈ 7 Å. Smaller distances, as suggested for barrel-stave pores, imply exposure of lipid hydrophobic tails to water, resulting in a much larger interfacial (water-hydrocarbon) energy. A crude estimate of this energy can be obtained as follows. The hydrocarbon-water contact area, per peptide, is L_lh_p, corresponding to interfacial energy 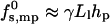, and hence 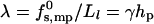, with γ ≈ 0.1 k_BT/Ų denoting the common value for lipid-water contact (Israelachvili et al., 1976). This yields λ ≈ 3 k_BT/Å or τ_mp ≈ 20 k_BT/Å. This value is much larger than the value of λ for a toroidal channel, as argued below.

An estimate of λ for the semitoroidal rim (Fig. 2) may be obtained using the “opposing forces” model for amphiphile packing in micellar aggregates (Israelachvili et al., 1976; Ben-Shaul, 1995). Using g to denote the packing free energy per lipid in a self-assembled aggregate (e.g., planar bilayer or semicylindrical rim) we express g as a sum of two contributions with opposite effects on the average area per lipid, a: i), the water-hydrocarbon surface energy, γa, which tends to minimize a; and ii), interlipid repulsion of strength c/a whose components include the spatial and/or electrostatic repulsion between lipid headgroups, as well as the (chain-conformational) entropic repulsion between the lipid tails, all favoring maximal a; c is a phenomenological constant measuring the strength of headgroup repulsion. (It may be noted that these forces operate at different planes relative to the hydrocarbon-water interface. Their balance, and the balance of their moments dictate the equilibrium area and curvature, both measured at the “neutral surface” (May and Ben-Shaul, 1999). However, we shall suffice here with a much simpler analysis, with a measured at the interface.)

The opposing forces model yields, 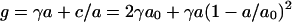, where 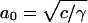is the optimal headgroup area dictated by the balance of the two opposing forces (i.e., minimal g).

Most phospholipids, owing mainly to their large (double chain) hydrophobic tail, prefer packing in the planar bilayer environment, with a = a₀ ≈ 60–70 Ų, implying g_bil = 2γa₀ for the free energy per lipid in the bilayer. The (excess) free energy per lipid in the semitoroidal rim is necessarily higher, g = g_rim − g_bil = γa_rim(1 − a_rim/a₀)², with a_rim denoting the area per molecule in the rim. Ignoring rim curvature effects, the number of lipids, per peptide, in the rim section is N_l^rim = L_lπh_p/2a_rim, and hence

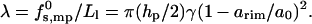(8)

Thus, according to this model, the minimal rim free energy and hence the actual value of λ depends on the ability of the lipids to pack with an area per headgroup as close as possible to a₀.

From simple geometric packing considerations it follows that the minimal area per headgroup of a single-tail amphiphile in a cylindrical micelle is 40–45 Ų, implying a_cyl^min ≅ (80–90) Ų for a double-tail lipid. Thus, in principle, the area per molecule in the rim could be as small as a_rim ≅ 85 Ų, resulting in λ ≅ 0.25 k_BT/Å for the typical bilayer value a_bil = a₀ = 70 Ų and γ = 0.12 k_BT/Ų. (It should be noted, however, that the diameter of such semitoroidal rims is somewhat larger than the membrane thickness, indicating imperfect hydrophobic matching and hence a necessary, additional, free-energy penalty associated with the seam between the cylindrical and planar regions.) Interestingly, the value λ = 0.25 k_BT/Å agrees quite closely with the prediction of a molecular-level (chain-packing) theory for the line tension corresponding to the semitoroidal lip of a planar lipid bilayer (May, 2000). Realizing that λ may vary markedly from one lipid-peptide system to another, all the calculations presented in the next section are for τ_mp = 2πλ =1 k_BT/Å, serving as our standard choice for the rim line energy. Our qualitative conclusions, pertaining, e.g., to the variation of optimal pore size with peptide charge or polar angle, are rather insensitive to variations in τ_mp. On the other hand, absolute pore sizes and energies may vary significantly with τ_mp, possibly reflecting the experimentally observed differences corresponding to different lipid membranes.

Equilibrium pore size

The circular, perfectly symmetric pore model depicted in Fig. 1 is of course an idealized structural scheme, neglecting fluctuations in pore size and shape, which are expected to increase with the average pore radius. Furthermore, as the 2D density of pores increases, interactions between them may become important, leading possibly (as in 3D micellar systems) to pore elongation and alignment. In this paper, however, we are specifically interested in low peptide concentrations where the average pore size is relatively small and interaction effects are negligible. We shall therefore assume that all s-pores are, indeed, perfectly circular and characterized by a well-defined equilibrium radius R_eq = R_eq(s; z_p, α). The value of R_eq is dictated by the balance of forces,

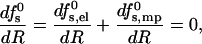(9)

with the derivatives

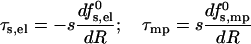(10)

representing, respectively, the radial forces acting to increase (τ_s,el > 0) and decrease (τ_mp > 0) the pore radius.

Pore size distribution

Excluding the areas corresponding to the aqueous interiors of the pores, the total surface area, A, of a lipid bilayer composed of 2N_l lipids (N_l per monolayer) and N_p membrane-spanning amphipathic peptides, is A = N_la₀ + N_pa_p. Here, a₀ = a_bil is the average area per lipid in the membrane, which we shall treat as a constant, a₀ = 70 Ų, in all calculations; a_p = πR_p² ≈ 115 Ų is the constant cross-sectional area per peptide. In a tensionless membrane, the aqueous regions will adjust their areas to the optimal pore size distribution, playing no role in determining this distribution.

The free energy of a membrane corresponding to a pore size distribution {n_s}, is given by

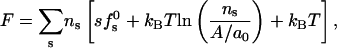(11)

with f_s⁰ denoting the free energy per peptide in a pore of size s; Eq. 1. (The use of a₀ as the unit area is discussed below.)

The equilibrium size distribution is the one that minimizes F subject to the material conservation condition,

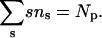(12)

Minimizing F we find

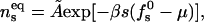(13)

with 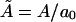denoting the membrane area measured in units of a₀ and β = 1/k_BT. The chemical potential per peptide, 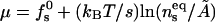is the Lagrange multiplier conjugate to the conservation constraint Eq. 12.

Size distributions are sometimes expressed in terms of the normalized weight distribution X_s = N_s/N_p = sn_s/N_p, which in our case is given by

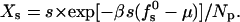(14)

For a given N_p, the normalization condition 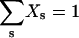enables evaluation (generally numerically) of μ for a given N_p, or vice versa.

Returning to Eq. 11, it should be noted that the choice of a₀ as the unit area is analogous to the use of a molecular volume in the 3D free energy of a self-assembling system (Safran, 1994). It should nevertheless be added that the correct choice of the right length (or area, or volume) scale is a highly nontrivial statistical-mechanical issue, as discussed for instance in the context of microemulsions (Reiss et al., 1996). In microemulsions, the natural length scale for droplet fluctuations was argued to be comparable to the diameter of a single surfactant molecule. Noting the analogy between a perforated lipid membrane and a 2D microemulsion, our use of a₀ as the unit area appears as the most natural choice. Still, since the choice of a₀ can strongly affect the calculated size distribution, we may regard a₀ as a phenomenological parameter that may be scaled by comparison to experiment. Indeed, using a₀ ≈ a_l yields reasonable agreement with available experimental results (see below).

RESULTS AND DISCUSSION

In the first part of this section, we present numerical results pertaining to the structural and energetic characteristics of isolated peptide pores, focusing on their variation with s, R, z_p and α. Pore size distributions are discussed in the second part.

Pore characteristics

The electrostatic free energies presented below were calculated using Eq. 5, following the numerical solution for ψ using PB Eq. 2. Pore free energies were calculated for a wide range of pore radii R, which, for a given s, correspond to a wide range of interpeptide distances, d. The relationship between d and R in an s-pore (see Fig. 1) is

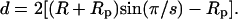(15)

Recall that our PB calculations are valid for relatively large, toroidal, pores (d ≥ 7 Å, or so). In most cases of interest, the equilibrium values of d are well above this lower limit. In the rare cases where this condition is not satisfied, the electrostatic energy will be estimated using the capacitor model (see Appendix, Eq. 17).

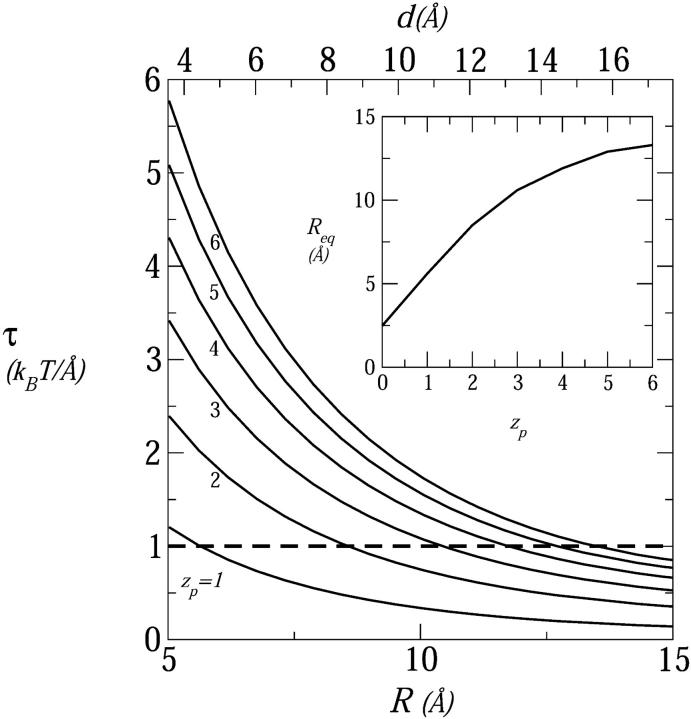
Fig. 3 shows the electrostatic repulsive force acting in a four-peptide pore, 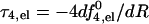, as a function of the pore radius R and the interpeptide distance, d, for peptides carrying z_p = 1,…,6 charges on their polar face, α = 120°. The equilibrium pore radius, R_eq (see inset), is dictated by the crossing point of the electrostatic force and the membrane perturbation force τ_mp. The horizontal dashed line in Fig. 3, corresponding to τ_mp = 1 k_BT/Å, represents our estimate of the radial force associated with the expansion of the semitoroidal lipid sectors, as discussed in the previous section. (Recall that semitoroidal rim formation is impossible for small interpeptide separations, d ≤ d^* ≈ 7 Å, where the membrane perturbation force is that of a barrel-stave pore, 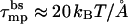; beyond the scale of Fig. 3.)

FIGURE 3.

The radial electrostatic force in a four-peptide pore as a function of the pore radius (R, bottom scale) and the interhelical separation (d, top scale) for different peptide charges, z_p = 1,…,6. The horizontal dashed line marks the attractive force resulting from the line energy of the semitoroidal lipid rim, τ_mp = 1 k_BT/Å. The crossing points of the force curves mark the equilibrium radii and are shown as a function of z_p in the inset. In these calculations, n₀ = 0.1 M and α = 120°.

As expected, R_eq (equivalently d_eq) increases with z_p, reflecting the increase in electrostatic repulsion between peptides. From Fig. 3 it is apparent that all peptides, except perhaps the most weakly charged ones (z_p = 1), conform to the toroidal pore model. This conclusion follows from the fact that the equilibrium value of the interpeptide spacing (d ≥ 10 Å already for z_p = 3) exceeds d^*, the minimum separation allowing for the formation of a low energy semitoroidal rim.

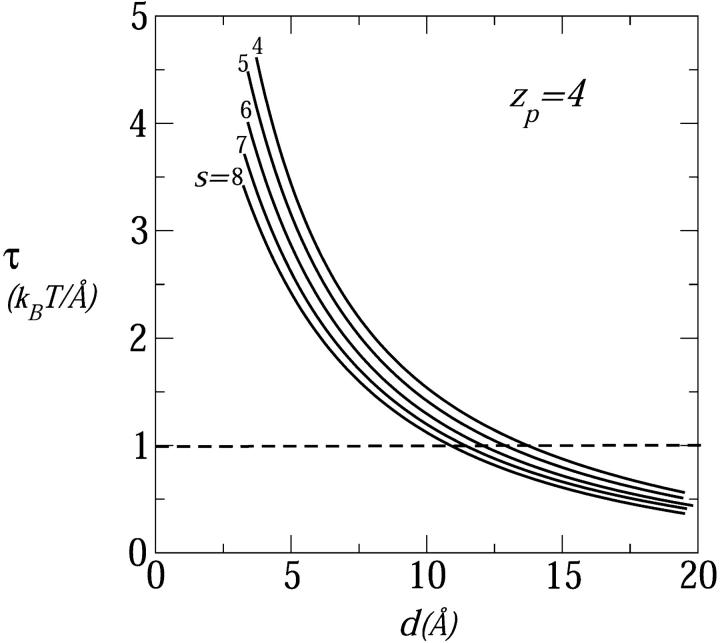
In Fig. 4 we show the electrostatic repulsion force between tetravalent (z_p = 4) peptides assembled into pores of varying sizes (s = 4–8) as a function of the interhelical distance, d. As in Fig. 3, the equilibrium separation between peptides is marked by the crossing points between these curves and the constant membrane perturbation force described by the dashed horizontal line. The equilibrium interhelical distance is seen to decrease as the number of peptides per pore increases. If interpeptide interactions were governed by nearest-neighbor repulsion we would expect a nearly constant d_eq, (nearly, and not exactly, because the interaction depends weakly on the relative peptide orientation, which depends on s).

FIGURE 4.

The electrostatic repulsive force as a function of the interhelical distance in pores composed of s = 4,…,8 peptides; all peptides carry four charges; n₀ = 0.1 M, α = 120°.

A simple qualitative explanation of the results shown in Fig. 4 can be given based on the general notion that the major source of electrostatic repulsion between like-charged surfaces is the osmotic pressure associated with counterion confinement (see, e.g., Evans and Wennerström, 1994; Parsegian and Gingell, 1972; Wagner et al., 2000). Similar, counterion osmotic pressure is the source of electrostatic repulsion in a charged cylindrical channel enclosing an aqueous electrolyte solution. Suppose the cylinder's radius R is increased while its surface charge density is kept constant. Since the number of counterions increases with the number of surface charges, and hence linearly with R, whereas their density (hence the pressure) decreases quadratically with R, the electrostatic free energy decreases with R. Obviously, increasing the aggregation number, s, of a circular peptide pore at constant d is analogous to increasing the cylinder's radius while keeping its surface charge density constant. Thus, for a given d, the radial electrostatic force decreases with s, explaining why d_eq decreases with s, as shown in Fig. 4. For large enough s, the pore walls become essentially planar, and the interhelical spacing should approach a constant value.

All pores in Fig. 4 fulfill our condition d_eq > d^* ≈ 7 Å, and may safely be classified as toroidal, consistent with the qualitative notion that this is the preferred pore geometry for multivalent peptides, (here z_p = 4 as, e.g., in magainins). Similar behavior is found for all z_p ≥ 3 peptides and even z_p = 2. The only case where our calculations suggest a possible preference for barrel-stave arrangement (d_eq ≤ 7 Å) is that of large s pores composed of weakly charged peptides, z_p = 1, as indicated in Figs. 3 and 5 .

FIGURE 5.

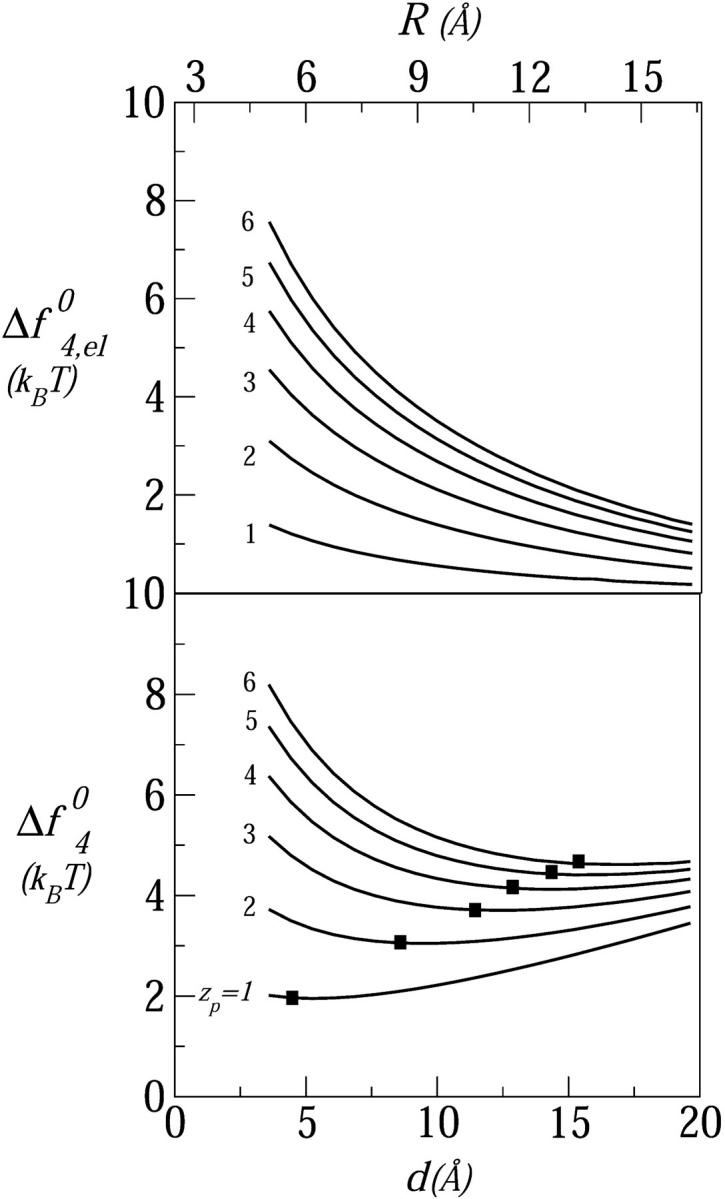
The excess free energy per peptide (relative to the adsorbed state) in a tetrameric pore, as a function of the interhelical distance and the pore radius, for six values of the peptide charge: z_p = 1,…,6. (Top panel) The electrostatic interaction free energy. (Bottom panel) The total excess free energy. The solid squares mark the equilibrium positions; the membrane perturbation force is τ_mp = 1 k_BT/Å; n₀ = 0.1 M, α = 120°.

The effect of peptide charge on the pore formation free energy is demonstrated in Fig. 5 for tetrameric pores composed of peptides carrying z_p = 1,…,6 charges. The top panel of this figure shows the excess electrostatic free energy per peptide in the pore (see Eq. 6) as a function of d. As expected, this energy increases with z_p and decreases monotonically with d, approaching zero in the limit of infinite membrane radius. The lower panel displays the total pore formation free energy, 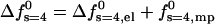, for 2πλ = τ_mp = 1 k_BT/Å. The equilibrium interpeptide spacing increases with z_p; the rate of the increase decreases with z_p.

The minima in Fig. 5 appear quite shallow, suggestive of large pore size fluctuations. It should be noted, however, that the root mean-square fluctuations in pore radius δR = [〈R²〉 − (〈R〉)²]^1/2 are determined by the total pore free energy, sf_s⁰, rather than the free-energy per peptide, f_s⁰. The root mean-square radius fluctuations can be estimated using the general expression,

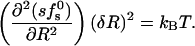(16)

From our numerical results, it follows that the δR's are actually quite small, ranging from 2 Å for z_p = 1, 2 to ≈3 Å for z_p = 6.

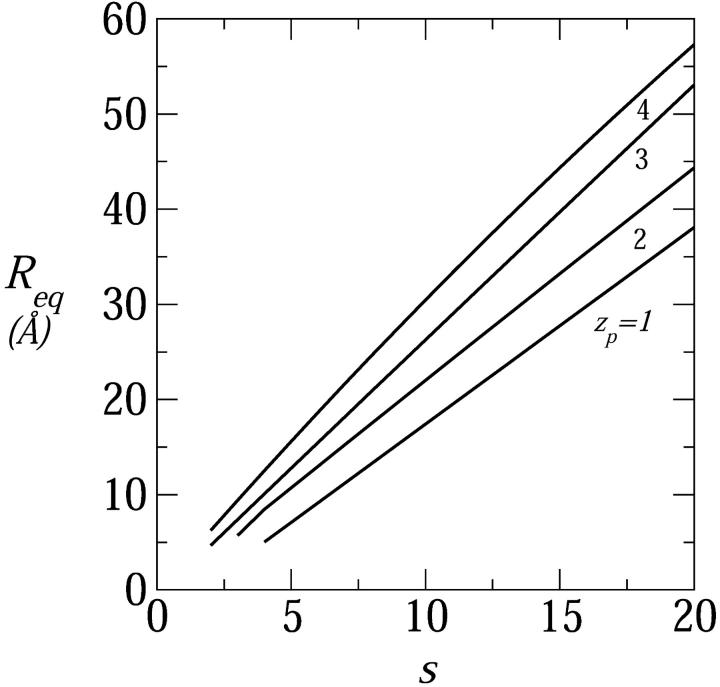
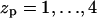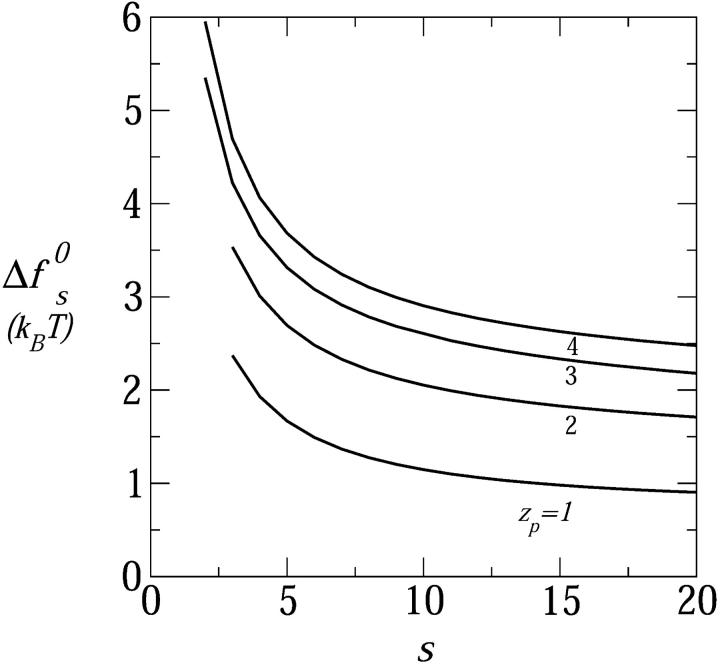
The range of equilibrium pore radii and their dependence on the peptide aggregation number is displayed in Fig. 6 for four values of the peptide charge . The corresponding values of 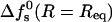are shown in Fig. 7. All cases considered in Fig. 6, except the z_p = 1 curve, correspond to the geometry of toroidal pores, i.e., their R_eq correspond to d > d^*. The equilibrium pore radii increase, nearly linearly, with s; at a rate that increases with z_p (corresponding to the increase with z_p of d_eq). Of course, pore radii on the order of 10–20 Å would allow the passage of rather large molecules across the lipid membrane. The probability that this may indeed happen depends on the pore size distribution, which depends sensitively on the pore free energies (those shown in Fig. 7), and the total concentration of inserted, transmembrane peptides. As expected, the minimal free energy per peptide decreases with s, approaching a constant value when the pore radius gets large compared to the Debye screening length, l_D, in which limit the pore walls behave as being planar. Since small pores are preferred on entropic grounds, the appearance of large multipeptide pores is improbable, despite their low energies (see below).

FIGURE 6.

The equilibrium radius of toroidal pores as a function of the peptide aggregation number, for z_p = 1,…,4; τ_mp = 1 k_BT/Å, α = 120°, n₀ = 0.1 M.

FIGURE 7.

The formation free energy, per peptide, of (equilibrium) toroidal pores as a function of the peptide aggregation number, for z_p = 1,…,4; τ_mp = 1 k_BT/Å, α = 120°, n₀ = 0.1 M.

All the calculations presented in this section correspond to the physiological salt concentration, 0.1 M. Increased salt concentrations, and hence smaller Debye lengths, result in increased screening of the Coulomb repulsion between peptides, thus favoring small pore formation. Indeed, smaller pores are known to form at high salt concentrations (Sansom, 1991).

Weakly charged peptides

Figs. 3, 5, and 6 show that the equilibrium distance between peptides in a membrane pore decreases as z_p decreases. In fact, the equilibrium interpeptide spacing in pores composed of singly charged (z_p = 1) peptides suggest their classification as barrel-stave rather than toroidal pores. For such small pores, as discussed in the previous section, the capacitor model, Eq. 17 (see Appendix), is more appropriate than the PB expression Eq. 5.

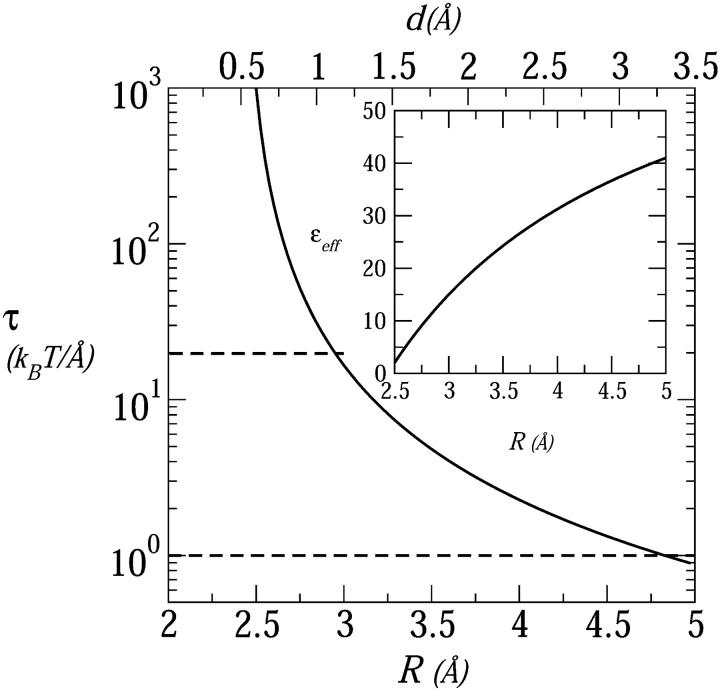
In Fig. 8 we show the electrostatic repulsion force operating in a tetrameric pore composed of z_p = 1 peptides, calculated using the capacitor model, Eq. 17. Using the membrane perturbation force corresponding to a semitoroidal lipid rim (τ_mp = 1 k_BT/Å, lower dashed line in Fig. 8) we find an equilibrium interpeptide spacing of d_eq ≈ 3.2 Å. Clearly, this spacing is too small to warrant the formation of a semitoroidal rim. That is, for such small d's, the membrane perturbation force should be calculated using the much higher value, 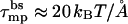(upper dashed curve in Fig. 8) corresponding to the exposure of hydrocarbon chains to water. This in turn implies an even smaller interhelical spacing, d_eq ≈ 1 Å, which may safely be regarded as corresponding to a barrel-stave pore.

FIGURE 8.

The electrostatic repulsive force in a tetrameric pore composed of weakly charged (z_p = 1) peptides. This force is the radial derivative of the electrostatic charging energy, calculated using the small-pore model, Appendix Eq. 17, with δ = 2 Å. The horizontal dashed line is τ = τ_mp^bs = 20 k_BT/Å representing the opposing force resulting from the exposure of lipid tails to water. The dashed line at τ = τ_mp^tor = 1 k_BT/Å is the force used in the toroidal model. The inset shows the effective dielectric constant used in this calculation.

There is, however, another alternative for pore formation by the z_p = 1 peptides; namely, to increase the space between them to d_eq = d^* ≈ 7 Å, thus enabling the formation of a (low energy, ≈λ_tord^*) semitoroidal rim segment. It turns out that the formation free energy of such a “minimal” toroidal pore is significantly lower than that of a small barrel-stave pore, even for z_p = 1 peptides. For instance, the energy of a tetrameric barrel-stave pore of radius R ≈ 3 Å (d = 1 Å), and 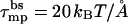to balance the electrostatic repulsion, is Δf₄⁰ ≈ 14 k_BT/peptide, compared to the energy Δf₄⁰ ≈ 2 k_BT/peptide for a toroidal pore of radius R ≈ 7 Å (d ≈ 7 Å). Increasing R (and hence d) results in a very steep reduction in the electrostatic energy, but a concomitant increase in the hydrophobic (exposure) energy corresponding to the large value of τ_mp^bs. Expansion of the pore to the minimal toroidal pore radius (R ≈ 7 Å) (thereby replacing τ_mp^bs by the much lower line energy τ_mp^tor) remains the energetically favorable solution even if 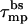were smaller by a factor of two or three. It must be emphasized, however, that our small-pore model ignores all atomic details (charge pairing for instance) that could perhaps explain the formation of barrel-stave pores by weakly charged peptides.

The effect of polar angle

The polar angle α is believed to play a key role in pore formation by amphipathic peptides (Wieprecht et al., 1997; Epand et al., 1995; Uematsu and Matsuzaki, 2000). Suppose, as suggested by Fig. 1, that the angle α indeed coincides with the lipid-water interface. Based only on purely geometric considerations, an increase in α suggests an increase in the optimal aggregation number s. Indeed, this behavior has been demonstrated experimentally by Lear et al. (1988) for pores composed of electrically neutral peptides, containing varying proportions of hydrophobic (leucine) and polar (serine) residues. Actually, if only the angle defining the hydrophilic sector were important, one should expect the optimal aggregation number to depend on α according to the simple relationship: s = 2/(1 − α/180°), yielding s = 4 for α = 90°, s = 6 for α = 120°, etc.

In reality, the dependence of the pore energy on α is far more complicated, due to additional factors such as specific (e.g., hydrogen-bonding) interpeptide and lipid-peptide interactions and, of greater and more general relevance here, electrostatic interactions. Qualitatively, electrostatic interactions tend to enhance the increase of (the optimal) s with α, due to the closer proximity of charged residues belonging to neighboring peptides. However, once the distance between peptides exceeds the Debye screening length (l_D ≈ 10 Å in our case) the electrostatic repulsion between neighboring peptides depends mainly on their total charge rather than its distribution over their polar face.

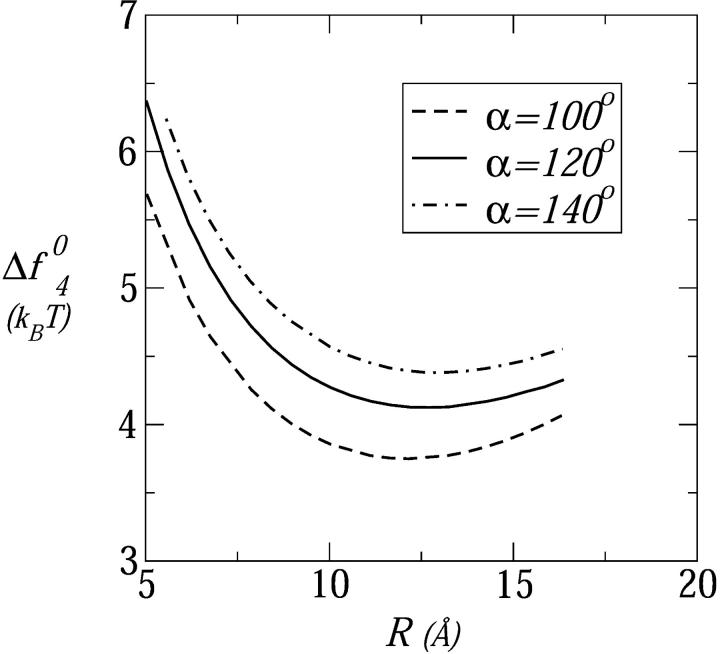
Fig. 9 shows the formation free energies of tetrameric pores composed of tetravalent peptides for three values of the polar angle: α = 100°, 120°, 140°. In all three cases the equilibrium pore size (R ≈ d ≈ 12 Å) corresponds to the toroidal structure. Consistent with the qualitative arguments above, we find that the formation free energy increases as α increases. These apparently small differences (of order 1 k_BT) are magnified in the pore size distribution, and in the probability of peptide insertion into the membrane, due to the exponential dependence of the pore populations on sΔf_s⁰, as discussed in more detail next.

FIGURE 9.

The formation free energy, per peptide, in a tetrameric pore composed of tetravalent peptides, as a function of the pore radius for three values of the polar angle: α = 100°, 120°, and 140°. Here τ_mp = 1 k_BT/Å and n₀ = 0.1 M.

Pore populations

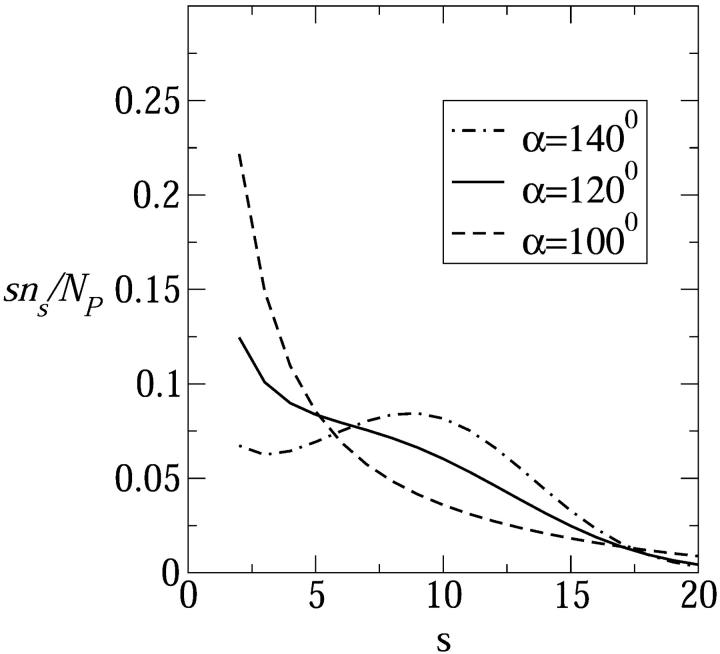
In Fig. 10 we show X_s = sn_s/N_p, the weighted size distribution of toroidal pore, for a rather low concentration of inserted peptides in the membrane, N_p/2N_l = 1/400. As expected, an increase in peptide charge z_p results in a larger average pore size and a broader size distribution. Fig. 11 shows the size distributions corresponding to tetravalent peptide pores for the three polar angles considered in Fig. 9, revealing that the average pore size indeed increases with α. In particular, the weight distribution corresponding to α = 140° exhibits a maximum at the rather large value of s = 10. It should be remembered, however, that the number of s-pores in the membrane is given by n_s rather than sn_s. Still, the α dependence of n_s revealed in Fig. 11 is consistent with various previous suggestions to regulate pore sizes and stability by tuning α (Wieprecht et al., 1997; Uematsu and Matsuzaki, 2000).

FIGURE 10.

The weight distribution of pore sizes, N_s/N_p = sn_s/N_p, corresponding to peptide charges z_p = 2,3,4. The ratio between the number of transmembrane peptides and lipid molecules in the membrane is N_p/2N_l = 1/400. Here τ_mp = 1 k_BT/Å, α = 120°, and n₀ = 0.1 M.

FIGURE 11.

Size distribution of peptide pores composed of tetravalent peptides for three values of the polar angle: α = 100°, 120°, and 140°. Other details as in Fig. 10.

Peptide insertion

It is widely accepted now that peptide insertion and pore formation occur only after the peptides have first adsorbed onto the membrane surface, and that the adsorbed state is not a metastable kinetic intermediate but, rather, a thermodynamically stable phase. Electrostatic interactions between adsorbed peptides, at least at low surface coverages, are much weaker than those between neighboring pore-forming peptides. Thus, our calculations of 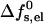should provide a reasonable estimate of the electrostatic energy cost associated with peptide insertion. These calculations indicate that the electrostatic energy associated with pore formation is typically 10–20 k_BTs per pore (see, e.g., Fig. 5), thus opposing peptide insertion and assembly into ordered pores. Pore formation is also opposed by the loss of entropy associated with the aggregation of s independent peptides into one aggregate. Thus, there must be additional mechanisms that can promote the transition from the adsorbed to the inserted state. One of these are excluded area interactions between adsorbed peptides as their coverage increases (see, e.g., Zuckermann and Heimburg, 2001). Another possible mechanism is the elastic perturbation of the lipid membrane by the adsorbed peptides, which may increase with their surface concentration to an extent favoring the smaller elastic perturbation in the inserted state (Chen et al., 2002). Yet another important mechanism of great relevance in biological systems is the favorable interaction between the intrinsic dipole of the peptides with the membrane potential. For typical membrane potentials (100 mV) and peptide dipoles (65 D) (Sansom, 1991), this interaction is on the order of several k_BTs, possibly large enough to partly or even fully overcome the insertion barrier.

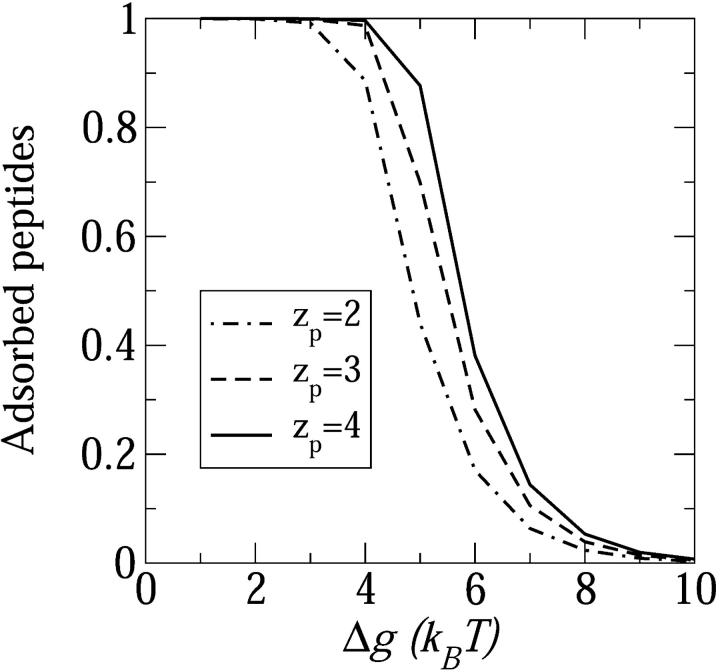
All of the above factors that can contribute to peptide insertion have been studied both experimentally and theoretically. Nevertheless, a coherent picture elucidating the synergistic action of these forces is not yet available. Notwithstanding this state of affairs, we would like to close this section with an illustrative estimate of the degree of peptide insertion into the membrane, assuming that an energetic boost, Δg per peptide, has been provided to the system to enhance peptide insertion into the membrane, so that the excess free energy per inserted peptide reduces from Δf_s⁰ to Δf_s⁰ − Δg. The origin of Δg could be the higher elastic membrane perturbation in the adsorbed as compared to the inserted state (Chen et al., 2002), excluded area interactions between densely adsorbed peptides (Zuckermann and Heimburg, 2001), the unfavorable interaction of the peptide dipole with the external field, or combination of these mechanisms. In Fig. 12 we show the fraction of adsorbed peptides as a function of Δg for three values of the peptide charge. In this particular calculation, the overall (i.e., inserted and adsorbed) peptide to lipid ratio in the adsorbed monolayer is N_p^tot/2N_l = 1/40.

FIGURE 12.

The fraction of adsorbed peptides on the membrane surface as a function of the insertion energy gain Δg (see text) for three values of the peptide charge, z_p = 2,3,4. The minimal energy required for pore formation increases with peptide charge. In this calculation N_p^tot/2N_l = 1/40, α = 120°, τ_mp = 1k_BT/Å, and n₀ = 0.1 M.

The steep change in the fraction of adsorbed peptides shown in Fig. 12 is a consequence of the cooperative nature of the pore formation process, resembling an oligomerization or micellization process (Ben-Shaul and Gelbart, 1994). For this type of processes, a change in the association equilibrium constant (through a change in temperature or in the standard reaction free energy) results in a sharp transition from “reactants” to “products” (or vice versa). The transition gets sharper, resembling a phase transition, when the cooperativity of the process (namely the average aggregation number involved) gets larger. The increase with z_p in the value of Δg corresponding to the adsorbed → inserted transition is due, of course, to the increase in the pore's electrostatic energy. Other factors that we have not specifically treated here, such as the nature and composition of the lipid membrane, which influence (differently) both the adsorbed and inserted state, may also affect the transition point, possibly drastically. The sensitivity of the transition from the adsorbed to inserted state to membrane characteristics explains, in principle, why amphipathic peptides exhibit pore formation in one membrane but not in another.

Most recently, Chen et al. (2002) have analyzed the insertion behavior of alamethicin in several lipid bilayers, finding that the transition from the adsorbed to the inserted state is sigmoidal, yet steeper than the transition predicted by a simple micellization scheme (similar to our model above). The authors attribute the enhanced transition to the fact that the elastic deformation of the lipid membrane is larger in the adsorbed state and its quadratic increase with the surface concentration of adsorbed peptides. In our model this would amount to assuming 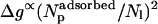, which might indeed be the case due to both elastic and excluded area interactions.

SUMMARY

Our goal in this work has been to provide a consistent analysis of the major factors affecting the energetics and sizes of membrane pores composed of charged amphipathic peptides. We found that pores composed of charged peptides conform generally to the toroidal model, whereby a finite semitoroidal membrane rim intervenes between neighboring peptides, thus largely reducing the electrostatic energy of the pore. Only very weakly charged peptides, e.g., alamethicin, may prefer the barrel-stave pore structure, where the peptides are tightly packed against each other.

We also found that the free-energy minima of the toroidal pores are rather shallow, suggesting substantial variations in pore sizes and pore aggregation numbers. Furthermore, since the membrane perturbation (rim) energy depends sensitively on the nature and composition of the lipid mixture, a given type of peptides may exhibit very different behaviors when interacting with different lipid membranes. These notions may explain the wide variety of pore sizes and insertion thresholds observed experimentally for peptides interacting with different lipid membranes. On the other hand, weakly charged (e.g., alamethicin) peptides appear to exhibit much smaller variations in size (Yang et al., 2001).

Additional conclusions from our calculations involve the role of the polar angle, the peptide charge, and the energetic barrier to peptide insertion. We found, for example, that the pore formation free energy increases with the polar angle owing to stronger electrostatic repulsion, even in toroidal pores where the peptides are well separated from each other.

Attempting to elucidate the general trends governing pore formation, we had to adopt several simplifying approximations. Among those are the assumption that the peptide charge is uniformly smeared over the helix polar face, the use of a constant (curvature independent) membrane rim energy, and the neglect of elastic membrane deformations, such as those implied by a hydrophobic mismatch between peptide and membrane thickness. The inherent limitations of our mean-field PB treatment of the electrostatic interactions, especially in small barrel-stave pores, has already been discussed in Theory. Notwithstanding all the above reservations, we believe that the qualitative behaviors predicted by our theory, especially for highly charged toroidal pores, are valid. Only atomic-level calculations can yield quantitative information concerning the structure and energetics of small, weakly charged pores.

Appendix: Small pores

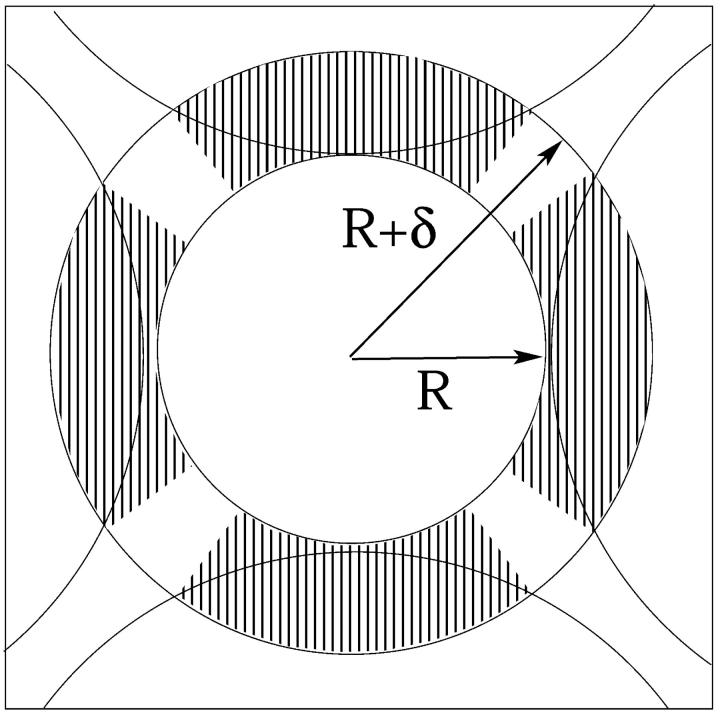
The radius R of a barrel-stave pore consisting of several tightly packed peptides is on the order of just a few molecular (water and/or counterion) diameters (see Fig. 13). The electrostatic energy of such pores is extremely sensitive to such details as the exact positions of the peptide charges and to local variations in the dielectric constant. Thus, in calculating this free energy, allowance should be made for the fact that the peptide charges are actually located slightly inside the low dielectric region, and the solvated counterions cannot really reach the surface charges. In finite difference PB calculations, these effects are often accounted for by assigning a small low-dielectric shell of width δ/2 ≈ 1 Å around every (fixed or mobile) charge in the system (Gilson et al., 1987; Honig and Nicholls, 1995). Apart from modifying the interaction between charged surfaces and mobile ions in solution, this picture suggests that the intervening space between neighboring peptides is a low dielectric medium, implying very strong electrostatic repulsion between them. In the text we argued that this repulsion is strong enough to render the small pore model illustrated in Fig. 13 highly unlikely, except perhaps for pores composed of very weakly charged peptides. To estimate the electrostatic energy of the very small pores, we shall use here a highly simplified, analytical “capacitor” model, as outlined below. The predictions of this model, especially the electrostatic potential and the magnitude of the electrostatic charging energy, show satisfactory agreement with finite difference PB calculations for the same pore geometry (Fattal, unpublished).

FIGURE 13.

Schematic representation of a small tetrameric peptide pore. The blank and shaded areas of the circular shell represent, respectively, regions of high and low dielectric constants.

The peptide charges involve some motional freedom and may therefore be modeled as forming an equipotential surface at distance R + δ from the center of the pore, with δ denoting the (average) minimal distance separating the surface charges from the mobile ion charges in solution (see Fig. 13). Note that the (peptide) charge distribution along this cylindrical equipotential surface is not uniform, owing to (azimuthal) variations in the local dielectric constant. The counterions in solution are mobile, yet because of the small pore dimensions and hence the strong repulsion between them, the counterions may be assumed to reside in another, equipotential layer at distance R from the pore's center, thus forming a concentric capacitor of gap size δ = 2 Å.

The gap is devoid of charges, and its effective dielectric constant is calculated using the following model. For R corresponding to tightly packed peptides, there is no room for water molecules to enter the R, R + δ shell, and its dielectric constant is set to ɛ = ɛ_o = 2. The volume of this shell increases with R, and we assume that the added volume is filled up by water molecules, implying an R dependence of the effective dielectric constant. The effective dielectric constant of a concentric capacitor whose gap consists of alternating azimuthal regions of different dielectric constants (as in Fig. 13) is the arithmetic average of the corresponding constants, namely, ɛ_eff(R) = ɛ_o + χ(R) (ɛ_w − ɛ_o) = 2 + 78χ(R), with χ(R) denoting the volume fraction of water in the gap. Qualitatively, the increase of ɛ_eff(R) with R (see the inset in Fig. 8) is consistent with molecular level models of the effective (“distance-dependent”) dielectric constant in confined environments (Warshel, 1979; Gilson et al., 1993).

The electrostatic charging energy per peptide according to the small pore model, 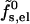, is that of the corresponding concentric capacitor, namely

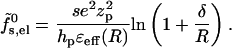(17)