Ligand-Induced Conformational Changes: Improved Predictions of Ligand Binding Conformations and Affinities

Abstract

A computational docking strategy using multiple conformations of the target protein is discussed and evaluated. A series of low molecular weight, competitive, nonpeptide protein tyrosine phosphatase inhibitors are considered for which the x-ray crystallographic structures in complex with protein tyrosine phosphatase 1B (PTP1B) are known. To obtain a quantitative measure of the impact of conformational changes induced by the inhibitors, these were docked to the active site region of various structures of PTP1B using the docking program FlexX. Firstly, the inhibitors were docked to a PTP1B crystal structure cocrystallized with a hexapeptide. The estimated binding energies for various docking modes as well as the RMS differences between the docked compounds and the crystallographic structure were calculated. In this scenario the estimated binding energies were not predictive inasmuch as docking modes with low estimated binding energies corresponded to relatively large RMS differences when aligned with the corresponding crystal structure. Secondly, the inhibitors were docked to their parent protein structures in which they were cocrystallized. In this case, there was a good correlation between low predicted binding energy and a correct docking mode. Thirdly, to improve the predictability of the docking procedure in the general case, where only a single target protein structure is known, we evaluate an approach which takes possible protein side-chain conformational changes into account. Here, side chains exposed to the active site were considered in their allowed rotamer conformations and protein models containing all possible combinations of side-chain rotamers were generated. To evaluate which of these modeled active sites is the most likely binding site conformation for a certain inhibitor, the inhibitors were docked against all active site models. The receptor rotamer model corresponding to the lowest estimated binding energy is taken as the top candidate. Using this protocol, correct inhibitor binding modes could successfully be discriminated from proposed incorrect binding modes. Moreover, the ranking of the estimated ligand binding energies was in good agreement with experimentally observed binding affinities.

INTRODUCTION

Rational structure-based ligand design is becoming more important as an increasing number of three-dimensional structures of biological targets become available. An essential element in the ligand design process is to predict reliable binding affinities for candidate ligands. This is important for at least two reasons. Firstly, it provides a means to score compounds and screen virtual compound libraries in an attempt to enhance the selection of those members, which are most likely to be active against the target of interest, and hence reduce the number of compounds to synthesize. Secondly, it can yield valuable insight into the binding determinants for the complex of interest. In a practical ligand design process, computational docking tools are applied to predict ligand binding modes as well as associated binding affinities. In that respect, low energy binding modes should resemble the experimentally observed binding mode. Otherwise, there are no well-established objective criteria to discriminate between a correct or incorrect docking mode.

During the last decades docking methods have received much attention from the scientific community. However, estimating reliable ligand binding affinities and ligand binding modes is a very challenging task. At least two fundamental prerequisites are required: 1), a reliable scoring function, and 2), a proper treatment of ligand and protein flexibility to account for induced changes in the conformation of the protein target and the ligand itself. Most docking methods are based on fairly general scoring functions to make them applicable for a wide range of systems. To reduce the degree of freedom and the size of the problem, early docking procedures treated both the ligand and the protein as rigid bodies (Kuntz et al., 1982; Sobolev et al., 1996). To improve the docking procedures, most docking approaches take ligand flexibility into account but treat the protein target as rigid (Rarey et al., 1996; Makino and Kuntz, 1998; Sobolev et al., 1996, 1997; Baxter et al., 1998; Oshiro et al., 1995). Docking simulations with a flexible target are currently not attractive given the need to obtain results for a single ligand within minutes.

Docking studies in our laboratory using different docking approaches showed that more reliable results could be obtained, when ligands (cocrystallized with a given protein) are docked back into their parent protein structures. Due to the effect of induced fit the docking methods were generally less successful when a ligand from one complex is docked to a protein-binding site derived from a complex with another ligand. This was observed to be the case, even for closely related ligands with equally good binding affinities, where small shifts in atomic positions in the binding site are induced from one ligand to the other. This suggests that one single conformation of the protein-binding site may not be sufficient to address the diversity of possible binding modes induced by different ligands. Consequently, a rigid protein-binding site can lead to errors in the identification of the correct binding mode and the assessment of reliable binding affinities.

Ligand binding can involve a wide range of induced conformational changes in the protein, such as loop or domain movements. However, in most cases changes in the protein backbone structure are negligible and in 85% of the ligand-protein complexes in the protein databank only a small number of side chains (three or less) undergo conformational changes upon ligand binding (Najmanovich et al., 2000). The root mean square displacement (RMSD) between corresponding Cα atoms deviated less than 2 Å in 88% and less than 1 Å in 75% of the cases. It is important to note that main-chain conformational changes between a protein in complex with different ligands in general has a lower RMSD as compared to the side-chain RMSD of the corresponding complexes. This suggests that ligand-induced conformational changes are more pronounced for side chains as compared to main-chain conformational changes. In many cases, the changes involve rotamer differences in protein side chains which often have χ1 close to the {t, g(+), g(−)} symmetry values of 180°, 60°, and –60° degrees. Therefore combinatorial approaches applying statistical information of conformational side-chain preferences may be very efficient.

The present study addresses a computational problem often encountered in the early phase of a drug discovery project. The fundamental question is how one can account for the diversity of binding modes induced by various ligands. The goal is to enhance the correct prediction of binding mode and binding affinity of possible drug candidates, when only one single structure of the protein target is available. Here, we demonstrate the application of a simple docking strategy. Our approach is based on producing various models using one single structure of the target protein and statistical information of side-chain conformational preferences. More precisely, χ-dihedral angles of the side chains in question are assigned discrete values from a main chain dependent rotamer library such that all possible combinations of the different rotamer states are represented. To evaluate our approach, we have used the x-ray crystallographic structure of human protein tyrosine phosphatase 1B (PTP1B) solved in complex with a hexapeptide (Protein Data Bank; entry code 1ptu) as a test case (Bernstein et al., 1997, Jia et al., 1995). We have chosen PTP1B inasmuch as it has recently received much attention due to its proposed role as a negative regulator of insulin signaling (Møller et al., 1995; Ide et al., 1994; Boylan et al., 1992; McGuire et al., 1991), and hence there exists a great interest in designing selective inhibitors for this enzyme. Inspection of this x-ray structure reveals that a few side chains flanking the active site region are important for substrate recognition. Here, we focus on the side chains of Asp48, Lys120, Asp181, and Phe182 and study the influence of conformational changes of these side chains on the binding behavior of different ligands. As we will demonstrate in the Results and Discussion section, relatively small structural changes restricted to side chains can have a significant impact on binding affinities predicted by computational docking tools.

METHODS

The reference structure

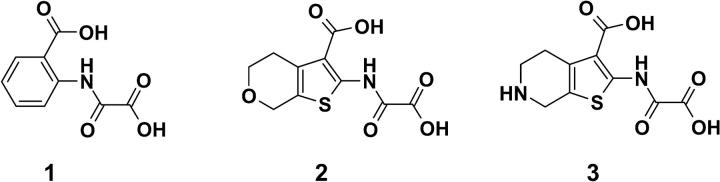
The high resolution x-ray crystallographic structure of PTP1B solved in complex with a hexapeptide DADEpYL-NH₂ (pY stands for phosphorylated tyrosine) (Jia et al., 1995) was obtained from the Protein Data Bank (Bernstein et al., 1997, entry code: 1tpu). In the following this structure is referred to as the reference structure, inasmuch as it is used for comparisons and serves as a template structure for all protein models produced by the rotamer approach. To evaluate the rotamer approach as well as the quality of the produced receptor models, three other PTP1B structures (Andersen et al., 2000; Iversen et al., 2000; pdb entry codes: 1c85, 1c87, and 1c88) solved in complex with the inhibitors 1, 2, and 3 shown in Fig. 1, were included. These structures were only used for comparison and evaluation of the approach. The PTP1B structures were superimposed onto the reference structure. The resulting positions of the superimposed inhibitors were used to measure the RMS differences to those predicted by FlexX (see Table 1).

FIGURE 1.

Chemical structures of inhibitors used in the docking experiments.

TABLE 1.

RMS to 1PTU PDB entry code	RMS (Å) of heavy atoms to the reference structure	RMS (Å) of side chains to the reference structure
1c85	0.37	0.67
1c87	0.23	0.95
1c88	0.37	0.94

RMS difference between the x-ray crystallographic structures (pdb entry codes: 1c85, 1c87 and 1c88) and the reference structure (pdb entry code: 1ptu).

Crystallographic water molecules

All crystal water molecules were removed from the reference structure with the exception of a single well-defined buried water molecule located in the binding pocket between the main chain NH of Phe182 and the scissile oxygen of pY. This water molecule (W 304) has been observed in all x-ray crystallographic structures of PTP1B in complex with different ligands. Generally, the role of crystallographically identified water molecules is difficult to interpret. Clearly, they may play an important role in the drug design process—in particular, when ligands are modified in a way that could lead to either the creation or removal of cavities large enough to accommodate water. In the present study we kept the well-defined active site water molecule, because it is involved in the catalytic process and interacts with the protein via well-defined hydrogen bonds.

Preparation of protein models

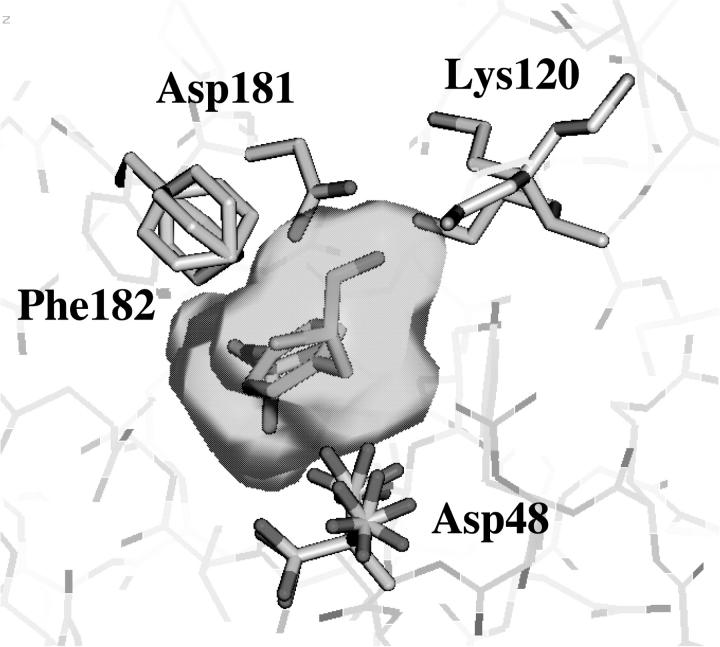
Amino acid side chains are known to adopt discrete conformations (rotamers) depending on the local protein environment (Petrella et al., 1998). Side chains exposed to the active site are assigned discrete conformations obtained from a main chain conformation dependent rotamer library such that all possible combinations of the rotamer states are represented. The four side chains considered in this study are Asp48, Lys120, Asp181, and Phe182 (see Fig. 2).

FIGURE 2.

Superposition of the 96 models used for docking.

An analysis of a main chain torsional angle dependent rotamer library within QUANTA (Accelrys Inc., San Diego) reveals that Phe182, Lys120, and Asp48 can adopt 3, 4, and 8 rotamer states, respectively. For Asp181 only one rotamer identical with the one observed in the 1ptu x-ray structure was populated. Thus a total of 3 × 4 × 8 = 96 different protein models were generated using the reference structure as a template. The 96 protein rotamer models are all identical except for the conformations of the three side chains Phe182, Lys120, and Asp48. In Fig. 2, the 96 models have been superimposed. The majority of the proposed rotamer modes could be discarded based on close contact arising when all possible combinations of the rotamer states for the selected side chains are modeled. To identify such models we simply computed the potential energy for each rotamer model after it was energy-minimized in 20 steps steepest descent minimization including all atoms using CHARMM (Brooks et al., 1983). The objective of the minimization procedure was not to relax the receptor models as such, but rather to obtain a potential energy for later comparison and evaluation. Two of the rotamer conformations of Lys120 had serious clashes with other side chains in the binding pocket. The other half of the models had acceptable conformations.

pK_a calculations

There are three charged residues in the binding pocket of PTP1B, which have been indicated to interact with a bound inhibitor. These are two Asp (48, 181) and one Lys (120) side chain. One of the questions is if the protonation state of these residues is affected by the presence of the ligand. To estimate this effect due to inhibitor binding, we used the multisite titration model introduced by Schaefer and Karplus (Schaefer et al., 1997) to calculate the ionization state of the three residues Asp48, Lys120, and Asp181. The calculations were performed in absence and in the presence of the inhibitor. Hydrogens were added using CHARMM and the protein atoms were assigned partial charges and radii from the CHARMM22 force field. A probe radius of 1.4 Å was used for molecular surface calculations. For the interior dielectric constant, we used ɛ = 20 as suggested by Antosiewicz et al. (1996) and the solvent dielectric constant was set to ɛ = 80. The ionic strength was set to 0.145 M with the ion density after a Boltzmann distribution at 300 K. Initially the potential was calculated on a 2 Å grid, and the so-called focusing technique was applied for a more accurate evaluation of the potential around the ionization sites by subsequently reducing the grid size to 1.4 Å, 0.7 Å, and 0.35 Å.

Formal charges were assigned to the ligands. The pK_a of the oxalylamide in compounds 1–3 is 2–2.5, whereas the pK_a of the other carboxylate in the compounds is close to 4. Therefore the oxygens of these carboxylates were assigned a charge of −1/2. As discussed below, the three ionizable side chains are estimated to be fully charged in the absence and the presence of the inhibitors at physiological pH.

FlexX docking

In this study we applied the FlexX docking program (Rarey et al., 1996), which uses an efficient incremental construction method (Leach and Kuntz, 1992) to optimize the interaction between a flexible ligand and a rigid binding site. In this methodology, an empirically derived scoring function, which is optimized to reproduce experimental binding affinities and binding conformations for various crystallographic resolved protein/ligand complexes, is used to predict the free energy of binding (ΔG_bind). In all docking experiments presented in this study a scoring function with default parameters was used.

RESULTS AND DISCUSSION

The paper is outlined as follows. After describing the results from the pK_a calculations the docking experiments are presented. Firstly, the set of inhibitors are docked to the structure of PTP1B originally solved in complex with the hexapeptide DADEpYL-NH₂ (pdb entry code: 1ptu) and the parent structures (i.e., the structures of PTP1B solved in complex with the corresponding inhibitor; pdb entry codes: 1c85, 1c87, and 1c88). Secondly, the inhibitors are docked to the protein models produced by the rotamer approach. Thirdly, the best protein models (i.e., those which obtained the best free energy of binding in the FlexX docking procedure for each inhibitor) are compared to the experimental structure solved in complex with the inhibitor in question.

pK_a calculations

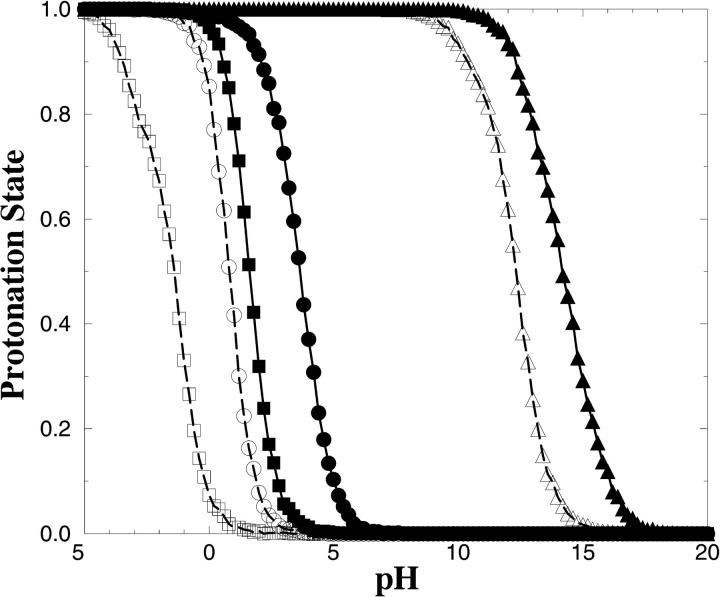
The titration curves for the ionizable active site residues Asp48, Lys120, and Asp181 are shown in Fig. 3. The curves with solid and open symbols are obtained for the enzyme in complex with an absence of an inhibitor, respectively. The pK_a values in the absence of the inhibitor are calculated to 0.8, 12.3, and −1.4 respectively, whereas the calculated pK_a values for Asp48, Lys120, and Asp181 in the presence of the inhibitor are 1.6, 14.2, and 3.7. It is not surprising that the presence of the inhibitors increases the pK_a, because the inhibitor itself is negatively charged. Our results indicate that the three side chains investigated are charged in the presence as well as absence of the inhibitors at physiological pH. Hence, in the docking experiments the three side chains are charged.

FIGURE 3.

Calculated titration curves. Open squares, circles, and triangles represent the calculated titration curves for Asp48, Lys120, and Asp181, respectively, in absence of the inhibitor. The titration curves in presence of the inhibitor are represented with solid symbols.

Docking of the ligands to their parent structures

To illustrate the shortcoming of the simplest docking experiment, we first discuss the results obtained from docking of each of the three inhibitors to their parent structures and additionally to the protein structures cocrystallized with the other inhibitors (“cross-docking”). The results of the docking experiment are shown in Table 2, together with the experimentally determined inhibition constants. The results are quantified in terms of the lowest estimated free energy of binding and the RMS difference between the predicted binding conformation and the experimental binding mode (number in parenthesis). As seen from the results in the diagonal, the docking procedure successfully identifies the correct binding mode as the lowest energy configuration, when the protein structure is derived from the complex with the inhibitor itself. Nevertheless, the docking procedure is less successful when the inhibitors are docked against the protein structures derived from complexes obtained with other inhibitors as seen from the off-diagonal results in Table 2. The cross-docking experiment shows that the assumption of a rigid protein cavity can lead to errors not only in the predicted binding affinities but also in the predicted binding modes of the inhibitors. To overcome this shortcoming, we investigate in the following a combination of FlexX and multiple protein targets produced by the rotamer approach.

TABLE 2.

X-ray structure/compounds	1c85 [kJ/mol]	1c87 [kJ/mol]	1c88 [kJ/mol]	1ptu [kJ/mol]	Exp. Ki [μM]
1	−32.8 (1.1)	−19.8 (13.5)	−33.7 (8.7)	−23.0 (17.6)	200
2	−24.4 (8.5)	−34.5 (0.9)	−31.2 (0.8)	−30.9 (3.9)	63
3	−26.4 (8.7)	−27.5 (0.8)	−37.0 (1.2)	−27.0 (20.3)	4

Results of docking inhibitors 1, 2, and 3 to their parent PTP1B crystal structures (to which they were cocrystallized) shown in bold as well as to the structures cocrystallized with the other inhibitors. The predicted free energies of binding ΔG are in [kJ/mol]. The RMS (Å) differences between the experimental and predicted ligand binding modes are given in parentheses.

Docking of ligands to the reference structure

In this section we present the docking results for each of the inhibitors obtained for the reference structure. Recall that this structure was chosen inasmuch as it has never seen the nonpeptide inhibitor and consequently, the geometry of the binding site is adapted to the bound hexapeptide. The 15 best scoring docked solutions (in terms of estimated free energy of binding) for each of the inhibitors 1, 2, and 3 are shown in Fig. 4, A–C as functions of the RMS difference between the experimental and the predicted binding modes. There is no correlation between low predicted free energy of binding (ΔG_bind) and low RMS for any of the inhibitors. For example, the lowest ΔG_bind for compound 3 is ∼−27 kJ/mol (Fig. 4 C), but the RMS difference between the predicted and the experimentally observed binding mode is 20 Å. On the other hand, the docking mode having the lowest RMSD (2.3 Å), when compared to the experimental observed binding mode, has a predicted ΔG_bind of −25 kJ/mol; i.e., 2 kJ/mol larger compared to the docking mode of the lowest energy of binding. Similar results are obtained for compound 2 shown in Fig. 4 B. Here, the binding mode with the lowest predicted ΔG_bind (∼−31 kJ/mol) has an RMS difference of 4 Å compared to the experimentally observed binding mode. For compound 1 all of the 15 best scored docking modes have relatively large RMS deviations >8 Å and the predicted free energies of binding are all within a narrow range between ∼−23.0 kJ/mol and −19.5 kJ/mol (Fig. 4 A). In this case, the inhibitor complex with the lowest free energy of binding has a RMS deviation of 8 Å, when compared to the experimentally observed binding mode. In all three cases, the complexes based on the reference structure poorly predict the correct ligand binding mode, even though the differences between the crystal structures mainly are restricted to conformational changes of a few side chains. Hence, the predicted ΔG_bind could not be used to discriminate between a correct or an incorrect binding mode.

FIGURE 4.

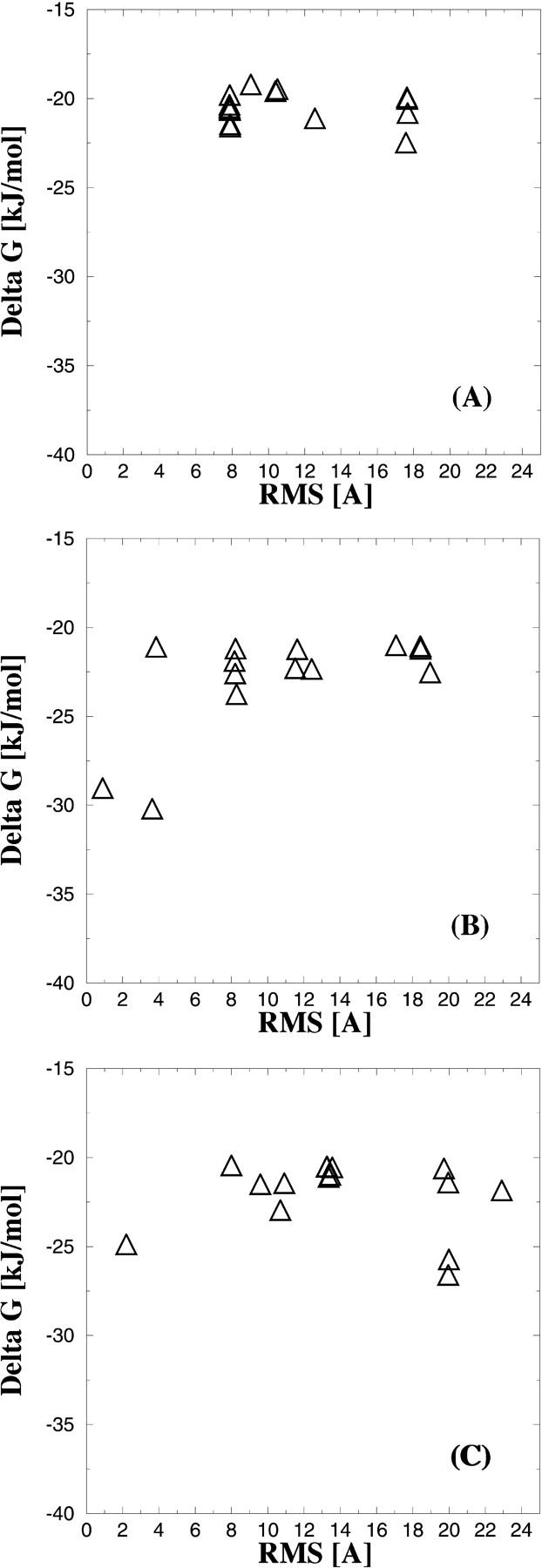
FlexX docking results obtained against the reference structure. (A) The 15 lowest predicted free energies of binding [kJ/mol] of inhibitor 1 versus the RMS difference (Å). The difference is calculated between the docked and the experimentally observed ligand binding conformation. B and C show the results obtained for the inhibitors 2 and 3, respectively.

In the following we apply the rotamer approach to side chains exposed to the active site of the reference structure. The objective is to test the robustness of the rotamer approach, i.e., to examine if a single protein structure can be modified to recognize the inhibitors 1, 2, and 3, resulting in binding modes and estimated affinities, which match experimental findings.

Docking compounds against 96 protein models

The docking results for each of the inhibitors 1, 2, and 3 to each of the 96 PTP1B models produced from the reference structure using the rotamer approach are presented below. The single best docking mode of lowest predicted free energy of binding obtained for each of the inhibitors 1, 2, and 3 against the 96 PTP1B models are shown in Fig. 5, A–C as functions of the RMS differences between the experimentally observed and the predicted binding modes. The lowest ΔG_bind values obtained among all PTP1B models for each of the compounds 1, 2, and 3 are −32.8, −34.5, and −37.0 kJ/mol, respectively, and correspond to the binding modes which have low RMS differences when compared to the experimentally observed binding modes. More importantly, in all cases these ΔG_bind values are significantly improved when compared to the docking results obtained by using the reference structure. Furthermore, the ranking of the estimated binding energies of the inhibitors correlate with the experimentally determined binding affinities (Table 2). This correlation is not unexpected, inasmuch as FlexX is based on a scoring function, which has been derived from fitting experimental data (binding constants, binding modes, etc.; Rarey et al., 1996). Hence, the scoring function indirectly includes the contribution from the unbounded state. Of course, this contribution is only exactly true for the set of ligands used in deriving the scoring function. It is difficult to estimate an absolute value for the contribution of the unbounded state of our inhibitors, but the excellent agreement between predicted binding modes and experimentally observed binding modes suggests that the scoring function also represents the class of inhibitors used in our study.

FIGURE 5.

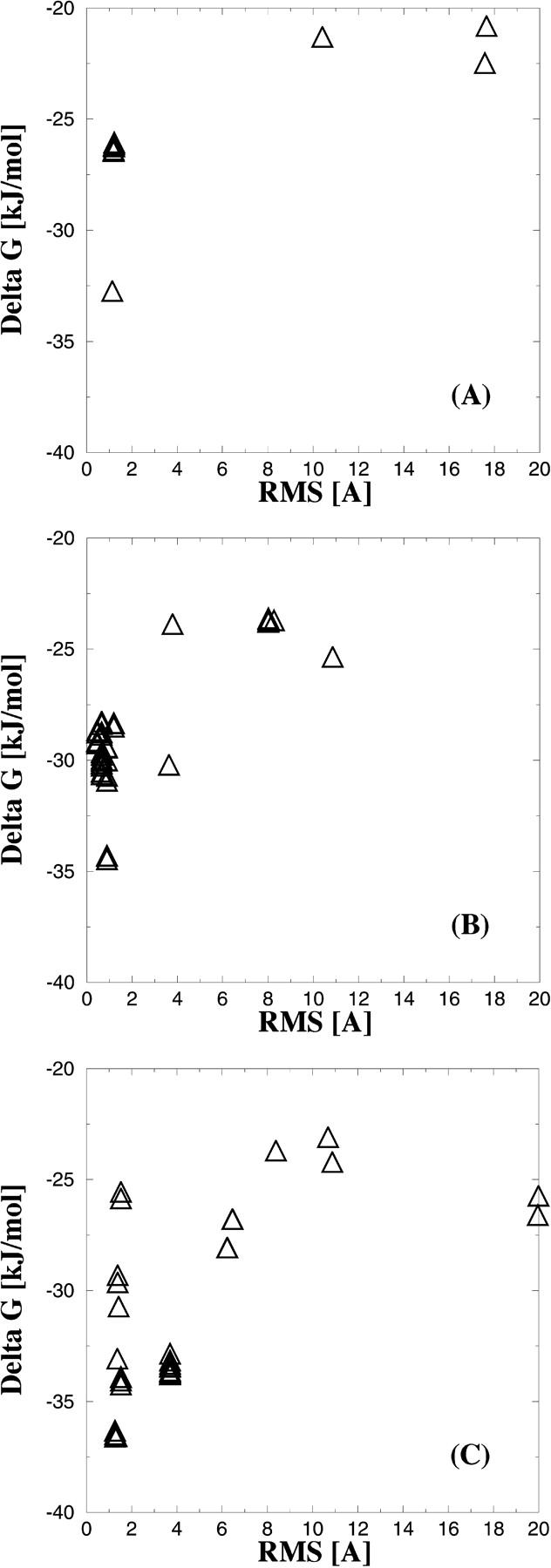
Results obtained from FlexX docking experiments against the 96 models of the PTP1B binding site. (A) Lowest free energy of binding [kJ/mol] of inhibitor 1 to each of the 96 protein models as function of the RMS difference between the docked and the experimentally observed binding mode. B and C show the results obtained for the inhibitors 2 and 3, respectively.

For compounds 1 and 3 (Fig. 5, A and C), the docking modes, which are in best agreement with experiments, also have the lowest free energy of binding. The complex with lowest estimated binding energy for compound 2 has a RMS value of ∼1 Å when compared to the experimentally observed binding mode. The docking modes with the second and third lowest predicted free energy of binding have slightly lower RMS values being close to 0.75 Å. However, we consider these docked modes to be equally good and the best solution (in terms of energy) has a significantly lower ΔG_bind of ∼5 kJ/mol compared to the docked conformation with a slightly lower RMS.

To further validate the liability of the docking procedure, we docked inhibitors 1, 2, and 3 against the rotamer models, which resulted in the overall lowest binding energy according to the results in Fig. 5. Again, the 15 best scored docking modes for the three inhibitors against the best protein model are shown in Fig. 6, A–C as a function of the RMS differences between the experimental observed and the predicted binding mode. So in contrast to the results presented in Fig. 5, the results in Fig. 6, A–C originate from one protein model. Significantly better results were obtained than in the docking procedure using the reference structure (see Fig. 4).

FIGURE 6.

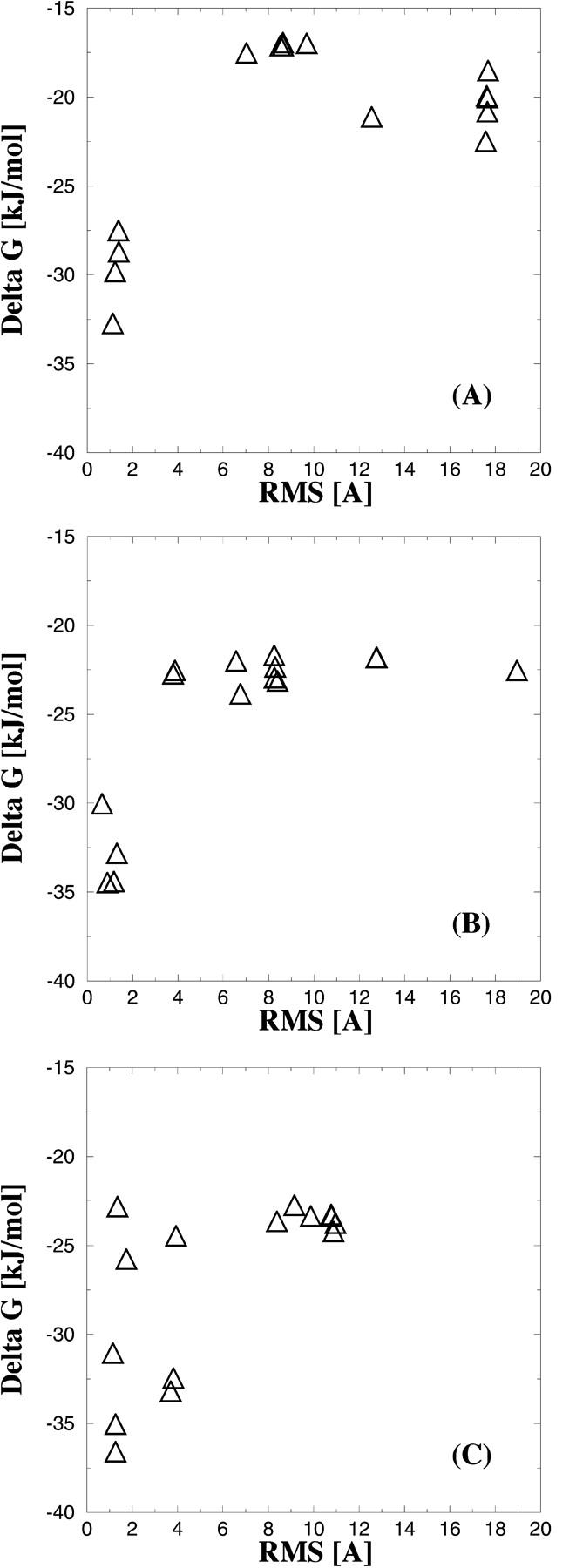
Solutions obtained by docking compounds 1, 2, or 3 to the protein model, which has the best score according to the results in Fig. 5. (A) The 15 best scored complexes [kJ/mol] for compound 1 versus the RMS difference (Å). B and C show the results obtained for the inhibitors 2 and 3, respectively.

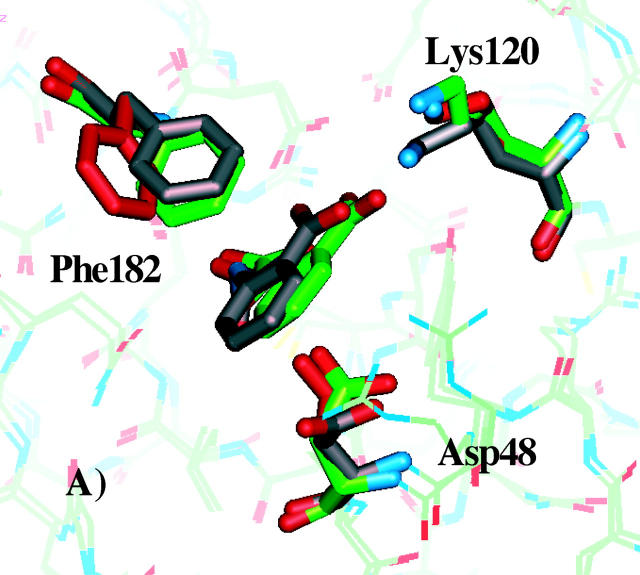
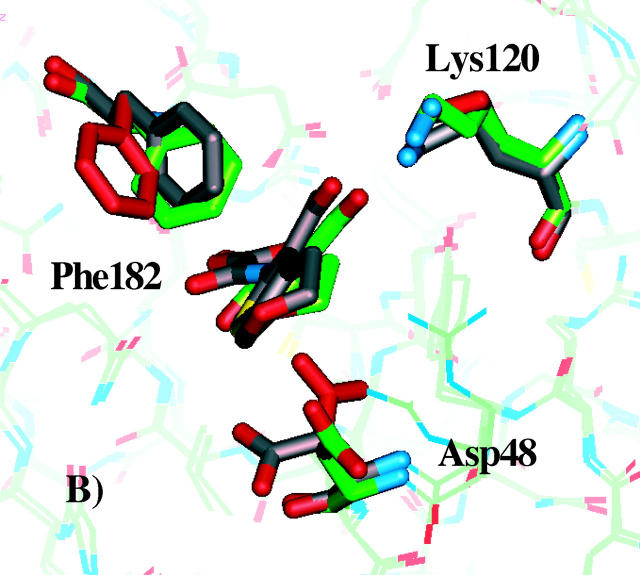
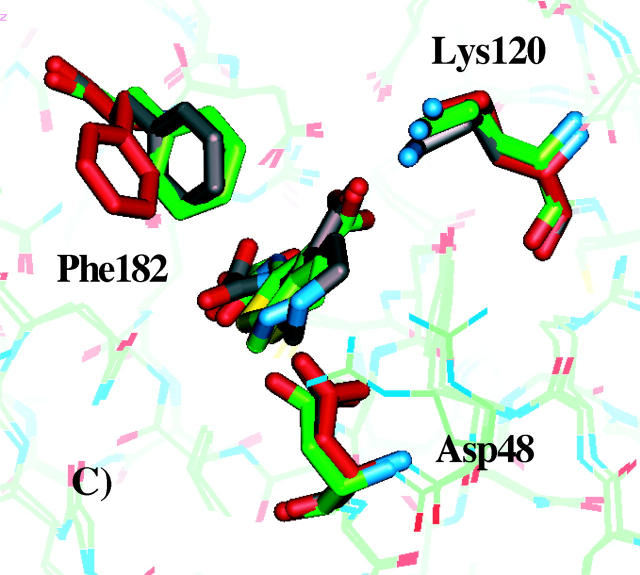
An interesting question is to what extent the three best rotamer models agree with the experimentally resolved x-ray structures of PTP1B in complex with inhibitors 1, 2, or 3. To investigate this, we superimposed the x-ray structures of PTP1B in complex with the compounds 1, 2, and 3 with the three best PTP1B rotamer models, deduced from Fig. 5. The superimposed structures are displayed in Fig. 7. Side-chain conformations of the best rotamer model and the corresponding predicted ligand binding mode are shown in gray. The crystal structures in complex with the compounds are shown in green, and side-chain conformations of the reference structure are shown in red.

FIGURE 7.

Comparison of x-ray crystallographic structures and docked modes obtained for the best PTP1B models. A–C show the structures of inhibitors 1, 2, and 3, respectively in complex with PTP1B. Side-chain conformations of the best PTP1B models and the corresponding docked inhibitor are shown in gray. The crystal structures in complex with the compounds are shown in green, and the reference side-chain conformations are shown in red.

As shown in Fig. 7 A, the side-chain conformations of Phe182 and Lys120 of the protein model, which correspond to the lowest predicted ΔG_bind, agree well with the x-ray crystallographic structure. The Asp48 side-chain conformation differs by being more exposed to the solvent. The second best model (not shown) for compound 1 has similar Asp48 and Lys120 side-chain conformations as in the experimental structure, but the benzene ring of Phe182 is rotated almost 40° from the conformation in the experimental structure. The best predicted binding mode (obtained among the 96 rotamer models) for inhibitor 2 is compared to the experimental structure in Fig. 7 B. Again, good agreement is found between the predicted Phe182 and Lys120 side-chain conformations and the experimentally observed conformations. In all the top five best models, Phe182 and Lys120 have the same conformations, whereas Asp48 in all cases are more or less exposed to solvent. Having Asp48 in a conformation identical to the one observed in the reference structure (shown in red) is prohibited due to unfavorable interactions with the pyran oxygen of the inhibitor (Iversen et al., 2000). Finally, in the case of compound 3, the side-chain conformations of Phe182, Lys120, and Asp48 are nearly identical to the experimentally observed conformations (Fig. 7 C). In the five best models, Asp48 adopts a conformation identical to the reference structure, inasmuch as the carboxylate of this side chain forms a salt bridge interaction with the basic nitrogen in compound 3, which is in good agreement with the experimental conformation (Iversen et al., 2000).

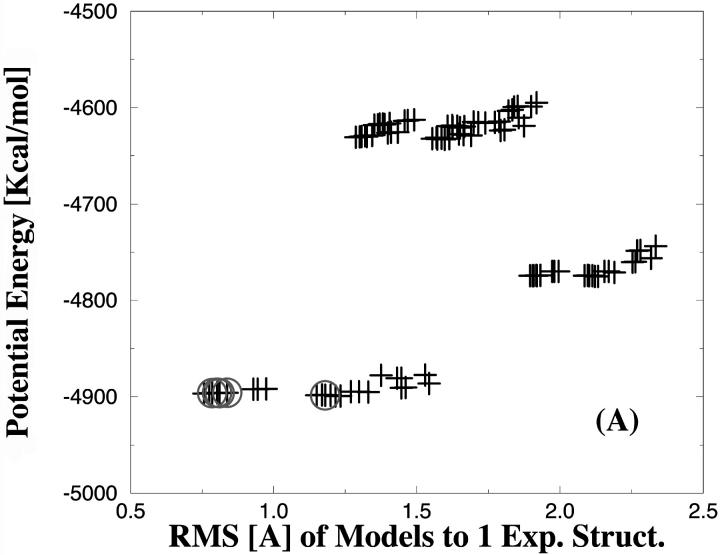
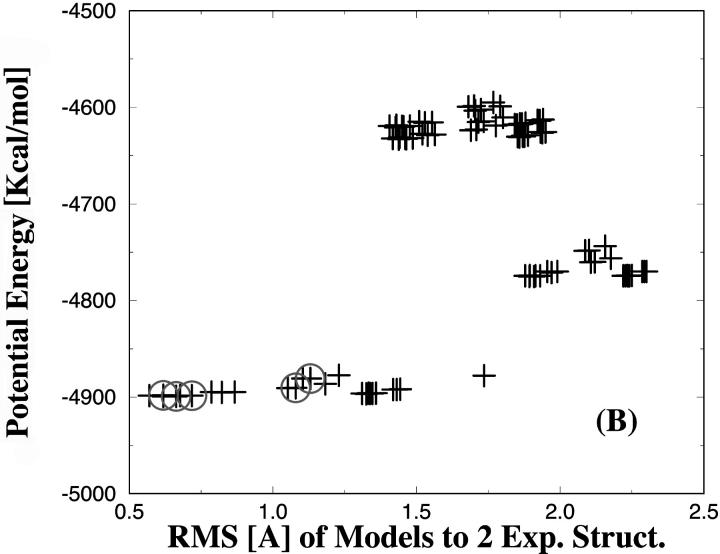
Finally, we calculated the potential energies of the 96 PTP1B models (in the absence of the compounds) and show those as a function of the side-chain RMS difference between predicted and the experimental structures in Fig. 8. This was undertaken to identify rotamer models with minor protein clashes and to elucidate if the rotamer models, which recognized the inhibitors 1, 2, and 3 with the best affinity, were among the models of low potential energy. It is important to emphasize that the models only have been minimized for a few steps as described in the Methods section. The potential energies of the PTP1B rotamer models are within the energy range of ∼−4900 to −4600 kcal/mol. The 96 models cluster into different regions with respect to potential energy. Models with low potential energy are generally closer to the experimental structures as shown in Fig. 8. The circles indicate the five models, which were predicted to have the best (i.e., lowest) ΔG_bind. In all cases, the five best ranked protein models belong to the cluster of lowest potential energy. Rotamer models with significant protein clashes should of course be discarded in the first step and not be considered in the docking procedure. However, we used all rotamer models in this study to ensure that the inhibitors would recognize feasible models, i.e., low energy protein models.

FIGURE 8.

Comparison of the potential energies of the various PTP1B protein models as a function of the RMS differences to the x-ray structures in complex with the inhibitors. A, B, and C are for the inhibitors 1, 2, and 3, respectively. The open circles indicate the five models, which were predicted to have the best (i.e., lowest) binding energy.

CONCLUSION

In this study we have presented and evaluated a computational docking strategy, which applies multiple conformations of the protein target. Using this approach, significantly improved results could be obtained compared to the case where only one single conformation of the target protein is used. We have shown that a single conformation of the ligand binding site is not likely to be sufficient to address the diversity of possible binding modes. Docking of the inhibitors to the PTP1B structures in which they were cocrystallized yield good results (Fig. 4). In this case, FlexX reproduced the experimental binding conformation, and the associated predicted ΔG_bind are qualitatively in agreement with experiments. However, poor results were obtained when the compounds were docked to x-ray structures of PTP1B solved in complex with the other compounds. Thus even small steric clashes may significantly penalize a correct docking mode resulting in an underestimation of ΔG_bind. Consequently, the estimated binding energies in this scenario are not predictive and the docking modes with low estimated binding energies do not correspond to the experimentally observed binding modes. Significantly improved binding conformations and ΔG_bind values were obtained when the compounds were docked against a number of protein models. The rotamer approach described here has the advantage of being computationally fast and protein models can be generated within minutes. Inasmuch as the approach is based on conformational side-chain preferences obtained from a main-chain dependent rotamer library, it is expected that this strategy is generally applicable to account for conformational changes of side chains. In a lead optimization process, where small changes in the ligand may induce structural changes in the binding cavity, our approach has the potential of revealing the correct binding mode and may reduce the number of false-negative predictions.