Abstract
The initial stages of the gating of the mechanoselective channel of large conductance from Mycobacterium tuberculosis have been studied in atomic detail using molecular dynamics simulation techniques. A truncated form of the protein complex embedded in a palmitoyloleoylphosphatidylcholine lipid bilayer and surrounded by explicit water was simulated under different pressure conditions to mimic the effects of tension and compression within the membrane on the protein. As a direct result of lateral tension being applied to the membrane, an increase in the tilt of a subset of the transmembrane helices was observed. This in turn led to the enlargement of the pore and the disruption of the hydrophobic gate consisting of residues Ile-14 and Val-21. The simulations suggest that opening occurs in a sequential staged process. Such a mechanism could explain the partial opening or staged conductance observed in patch-clamp experiments using related large conductance mechanosensitive channel complexes.
INTRODUCTION
Mechanosensitive ion channels are integral membrane proteins that play a critical role in allowing a cell to sense physical forces within its environment. They open and close in response to mechanical stresses applied to the cell membrane or to other cytoskeletal components and have evolved the ability to respond to stresses such as gravity, touch, and changes in osmolarity. Mechanosensitive channels are believed to be the primary transducing elements in such sensory cascades (Hamill and McBride, 1993; Sachs, 1991) and have been identified in more than 30 cell types (Martinac, 1993).
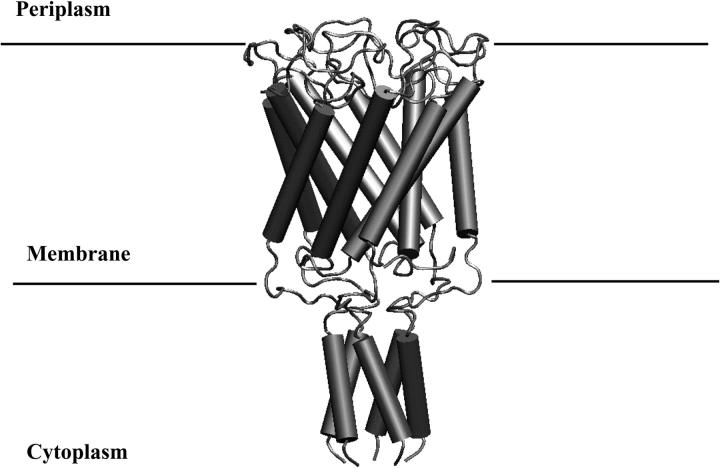
The best characterized member of this family is the prokaryotic large conductance mechanosensitive channel (MscL), which was originally isolated from Escherichia coli by Kung and co-workers (Sukharev et al., 1997). MscL is a nonselective ion channel of ∼2.5 nS conductance that is activated in vitro by the application of membrane tension (Blount et al., 1999; Sukharev et al., 1994). The channel is localized in the inner cell membrane and, at least in the case of Mycobacterium tuberculosis (Tb-MscL) for which the x-ray crystal structure has been solved, is a homopentamer (Chang et al., 1998). The protein is predominantly α-helical and can be subdivided into transmembrane and cytoplasmatic domains, as illustrated in Fig. 1. Each of the five subunits consists of two transmembrane helices, labeled TM1 (green in Fig. 2) and TM2 (blue in Fig. 2), which are tilted by 30 degrees with respect to the membrane normal (Chang et al., 1998). The TM1-helix, residues 15–43, crosses the membrane and defines the pore. A large loop (residues 44–68), which is resolved in the crystal structure, connects TM1 to TM2 (residues 69–89). TM2 again crosses the membrane and returns to the cytoplasm. Each of the TM1-helices makes contact with four other helices: two TM1-helices from the adjacent subunits and two TM2-helices, one from the same subunit and one from an adjacent subunit. Moreover, TM1 is lined with several polar and charged residues (Thr-25, Thr-28, Thr-32, Thr-35, Lys-33, and Asp-36) forming a possible pathway for solutes or even small proteins through the membrane (Fig. 2). The channel is constricted at the cytoplasmatic side by an array of hydrophobic residues (Ile-14 and Val-21), which probably act to gate passing ions and water molecules. MscL is believed to play a primary role in protecting cells exposed to osmotic downshock from lysis. Placing cells in a hypoosmotic environment leads to the influx of water into the cell. This in turn leads to an increase in turgor pressure within the cell and an increase in the tension within the membrane. MscL is believed to open in response to high levels of tension within the membrane, allowing ions and other solutes to be released from the cell and thus preventing rupture of the cell membrane.
FIGURE 1.
The MscL protein in the crystal structure (1msl.pdb).
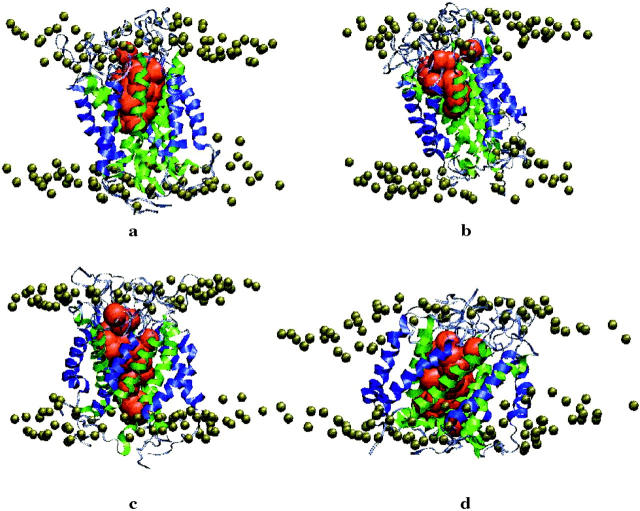
FIGURE 2.
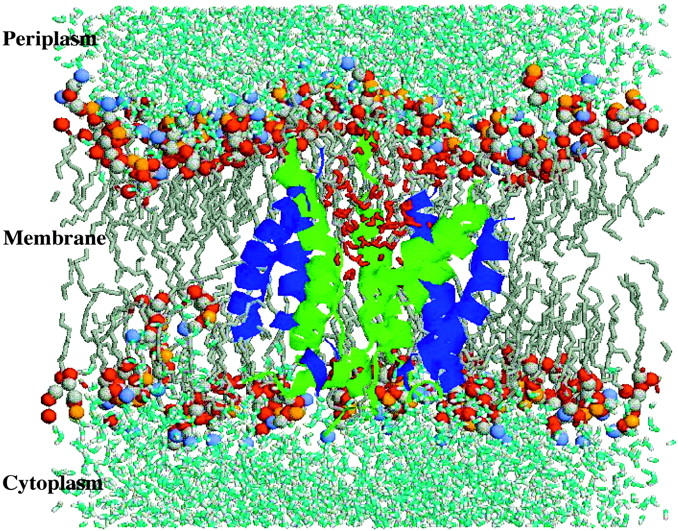
The MscL protein (TM1 helices in green, TM2 in blue) embedded in the POPC (gray) bilayer at the end of the Normal Pressure (NP) simulation. In red are depicted water molecules flowing through the pore.
Various experimental techniques have been used to study the gating mechanism of MscL. These include mutagenesis studies and the application of patch-clamp techniques (Ou et al., 1998; Yoshimura et al., 1999; Blount et al., 1997; Ajouz et al., 1998). Most experimental studies are conducted on the E. coli MscL, which gates at a pressure of around 0.1 bar, corresponding to a membrane tension of the order of 10 mN/m (Sukharev et al., 1999). The gating threshold of the tuberculosis analog Tb-MscL is approximately twice as high (Moe et al., 2000). Although such studies have revealed much in regard to the properties of the channel, there is currently no experimental technique that can be used to follow the process of pore gating in atomic detail. To obtain insight into the mechanism of gating at an atomic level, there is little choice but to turn to theoretical approaches. Sukharev and co-workers (Sukharev et al., 2001) recently postulated a possible model for the open conformation of MscL. Their approach was to simply identify parts of the protein considered to be involved in the gating process and assign the direction, angle, and distance that these units might move based on qualitative arguments. Gullingsrud and co-workers (Gullingsrud et al., 2001), taking a less subjective approach, studied MscL in a palmitoyloleoylphosphatidylcholine (POPC) membrane using molecular dynamics (MD) simulation techniques. They simulated the system for a total of 3 ns, at constant pressure and temperature. Not unexpectedly considering the limited length of the simulation, the protein remained in the closed state, close to the starting configuration. Analysis of the atomic fluctuations nevertheless showed that the protein was the least mobile in the narrowest part of the channel. Gullingsrud and co-workers also investigated the gating mechanism by simulating the isolated protein in vacuum (without solvent or membrane) while applying a constant radial force. During these simulations they observed a flattening of the helices as the pore widened. Elmore and Dougherty (Elmore and Dougherty, 2001) also simulated the wild-type and mutants of MscL in a palmitoyloleoylphosphatidylethanolamine (POPE) membrane to investigate the effects of two mutations V21A and Q15E on the stability of the protein and any variation in the intersubunit interactions. Very recently, Kong et al. (Kong et al., 2002) have tried to understand the gating of MscL from speculative simulations in which the protein is forced to go from the experimentally determined closed state to the model of the open state proposed by Sukharev and co-workers (Sukharev et al., 2001). All of these studies have either considered only the closed state, relied on a hypothetical model of the open state, or attempted to generate a model for the open state under unrealistic conditions.
In this paper we attempt to directly model the gating mechanism of MscL by applying physically appropriate forces on the protein within a realistic environment. Using essentially an all-atom representation of the protein, the membrane (POPC), and water, we follow the time evolution of the system under different stress conditions during a series of MD simulations. Our aim is to evaluate the effect of tension and compression within the membrane on the structure of the pore to shed light on the initial stages of the gating process.
MATERIALS AND METHODS
The initial model for the MscL used in the simulations was taken from the crystal structure of MscL from Tb-MscL solved by Chang and co-workers (PDB entry 1msl) (Chang et al., 1998). The five cytoplasmatic helices (Fig. 1) following Gly-101 were excised from the structure simulated. This was done for two reasons. First, they have been shown not to play an essential role in the function of MscL (Ajouz et al., 2000). Second, excising these groups significantly reduced the size of the system, making the simulations less computationally expensive. The five subunits were connected through the periplasmic loops.
The structure obtained with this procedure was refined using the WHATIF (Vriend, 1990) package to place atoms in residues which were not observed in the x-ray structure. The starting configuration for the simulations was generated as follows. In a preequilibrated POPC bilayer containing 128 lipid molecules, a cylindrical hole large enough to accommodate the protein was created in the bilayer by displacing from their starting positions all molecules whose phosphate atoms fell within 2.5 nm of the central axis of the cylinder. A short MD simulation which included an additional repulsive force that acted radially from the central axis of the cylinder was then used to drive any remaining atoms out of the region of the cylinder. The x-ray structure of the MscL protein was subsequently inserted into the cavity that had been created. The system was then solvated with simple point charge (SPC) water molecules (Berendsen et al., 1981). Fifteen chloride ions were added to neutralize the system by replacing water molecules at the positions of lowest coulomb potential. The final system consisted of 1 Tb-MscL molecule, 128 lipid molecules, 4956 water molecules, and 15 chloride ions, giving in total 24730 atoms in a rectangular box (Fig. 2). Before initiating the simulations the system was first energy minimized to relax bad contacts within the protein and between the protein and POPC molecules. The system was then simulated for 50 ps with the protein and the POPC molecules positionally restrained to allow the water molecules to relax. This was followed by two more 50-ps simulations without position restraints during which time the temperature of the system was slowly brought to 300 K and the pressure equilibrated to P0 = 1 bar.
All simulations were performed using the GROMACS software package (van der Spoel et al., 1994). The GROMOS96 forcefield (43al) (van Gunsteren et al., 1996; 1998) was used for the protein. POPC lipid parameters were taken from the work of Berger et al. (Berger et al., 1997). These lipid parameters have been used extensively with the GROMOS96 forcefield for proteins (Tieleman and Berendsen, 1998; Shrivastava et al., 2002).
The system was studied in the NPT ensemble. The temperature and pressure were maintained by weak coupling to external temperature and pressure baths with coupling times of τT = 0.1 and τP = 1.0 ps, respectively (Berendsen et al., 1984). The protein, lipids, and water were each coupled to separate temperature baths at 300 K in all simulations. A twin-range cutoff was used in which Lennard-Jones and short-range coulombic interactions within 1.0 nm were determined every step while interactions within 1.8 nm were evaluated every 10 steps together with the pair-list update. Although this is not as accurate as a full treatment of the coulomb forces using a lattice-sum method, it is much cheaper and has been tested with the forcefield and algorithms used in these simulations (Tieleman and Berendsen, 1998).
The LINCS algorithm was used to constrain all bond lengths within the protein and lipids. High-frequency motions associated with the explicit treatment of polar and aromatic hydrogens were eliminated by reconstructing the positions of the hydrogens based on the positions of the heavy atoms to which they are attached as described by Feenstra et al. (Feenstra et al., 1999). This allows a time step of 4 fs to be used without significantly affecting the thermodynamic properties of the system or the conformations sampled in extended simulations (Feenstra et al., 2002).
In total, four simulations were performed using different pressure coupling conditions. The lateral pressure Pxy and normal pressure Pz in these simulations are coupled independently (semiisotropic coupling). The difference between the lateral and normal pressure gives rise to a membrane tension γ = L(Pz − Pxy) with L denoting the membrane thickness. In the first simulation, labeled Normal Pressure (NP), a pressure of 1 bar was applied in both the lateral and normal directions, corresponding to a tensionless state of the membrane. In the second simulation labeled Press 100 (P100), a constant pressure of 1 bar was applied in the z-direction, while a pressure of 100 bar was applied in the xy-plane. Taking L = 5 nm as a typical membrane thickness, γ = −50 mN/m for the P100 simulation. This mimics hyperosmotic conditions. In the simulations Stretch 100 (S100) and Stretch 1000 (S1000), a pressure of 1 bar was again applied in the z-direction, while a negative pressure of −100 bar and −1000 bar was applied in the xy-plane of S100 and S1000, respectively. The corresponding surface tensions are γ = 50 mN/m (S100) and γ = 500 mN/m (S1000). The negative lateral pressure mimics the lateral stretching of the membrane under hypoosmotic conditions for which MscL gating is observed.
The systems labeled NP, P100, and S100 were equilibrated at their respective pressures for l00 ps with position restraints on the protein and for another 100 ps without position restraints before sampling commenced. S1000 was started from the last conformation obtained after the 30-ns-long accumulation run S100. The three systems NP, P100, and S100 were simulated for 30 ns, while S1000 (started from the last conformation obtained from S100) was terminated after 22 ns.
All simulations were performed in parallel on a Linux PC-cluster consisting of 600 MHz Pentium III dual processor machines, at a rate of 0.5 ns/24 CPU hours per machine. The analysis of the trajectories from the simulations was performed using the routines present in the GROMACS package (van der Spoel et al., 1994). The principal radii of the protein were obtained from its moments of inertia, assuming an ellipsoidal shape (Lide, 1992). Visualization of the individual structures was performed using the programs RasMol (Figs. 2 and 6) and VMD (Figs. 1 and 5) (Humphrey et al., 1996).
FIGURE 6.
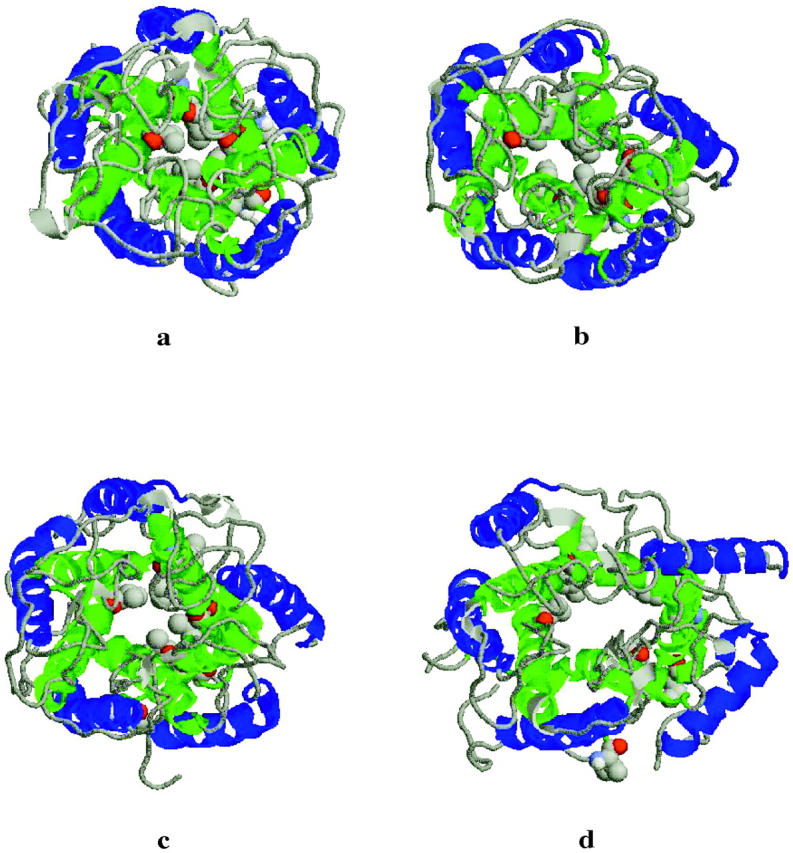
Top view of the helices and the loops in the structure at the end of the simulation: (a) Normal Pressure (NP), (b) Press 100 (P100), (c) Stretch 100 (S100), (d) Stretch 1000 (S1000). The disruption of the hydrophobic lock is evident. The residues Ile-14 and Val-21 of each subunit are presented in a cpk representation. TM1 helices in green, TM2 in blue.
FIGURE 5.
Side view of the helices, the loops, the lipid headgroups, and the water in the channel in the structure at the end of the simulation: (a) Normal Pressure (NP), (b) Press 100 (P100), (c) Stretch 100 (S100), (d) Stretch 1000 (S1000). TM1 helices in green, TM2 in blue, periplasmic loops in black, water through the pore in red.
RESULTS AND DISCUSSION
Protein fluctuations and secondary structure
In the absence of lateral tension within the membrane (NP simulation), the TM1 and TM2 helix bundles (transmembrane domains) remain close to their respective starting conformations. After 30 ns of simulation the root mean squared positional deviation (RMSD) with respect to the starting conformation after performing a least squares best fit was 0.19 nm for the TM1 bundle and 0.14 nm for the TM2 bundle. The final NP structure after 30 ns of simulation is displayed in Fig. 2. The average RMSD values in the P100 simulations are slightly higher, 0.22 nm for the TM1 bundle and 0.2 nm for the TM2 bundle. This is due to the internal helices (TM1) packing closer to one another as a consequence of the increased pressure applied in the plane of the membrane. This will be discussed further later. In the S100 simulation there is a clear increase in the average RMSD values for both the TM1 and TM2 bundles to 0.24 nm and 0.25 nm, respectively. The higher tension applied in the plane of the membrane in the S1000 simulation results in a sudden increase in the RMSD between 2.5 and 8 ns, bringing the RMSD values to 0.49 nm for the TM1 bundle and 0.59 nm for TM2 bundle. Note, the RMSD values quoted above correspond to treating all of the TM1 or TM2 helices as a bundle. Thus, the values reflect the relative motion of the TM1 or TM2 helices, not variations within a given helix (which is much smaller). The RMSD values treating the protein as a whole (including the very flexible external loops) are: 0.22 nm for NP, 0.25 nm for P100, 0.33 nm for S100, and 0.62 nm for S1000 with respect to the starting conformation. In general, the secondary structure of the individual helices is very well conserved. Even by the end of the S1000 simulation where some fraying of the helices is clearly evident there has been only a 10% drop in helical content.
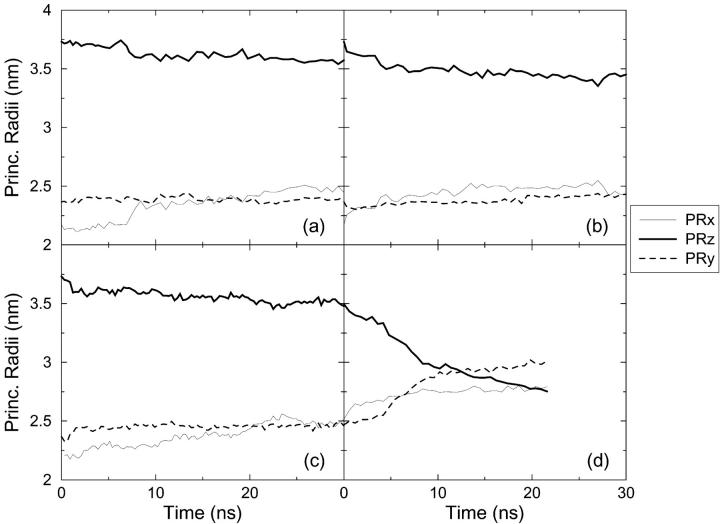
The conformational change that the system undergoes at high negative lateral pressure is also evident in changes in the principal radii of the protein. Fig. 3 shows the principal radii as a function of simulation time for each of the four pressure conditions simulated. In the S1000 simulation there is an abrupt decrease in the principal radius along the z-axis as evident in Fig. 3 d. In contrast, the two lateral dimensions expand. This redistribution around the z-axis (pore axis) is consistent with pore opening. No equivalent change in the principal radii was evident in the other simulations (Fig. 3, a–c). Except for some fraying involving residues at the cytoplasmatic end of the TM1 and TM2 helices and the region around Ile-14 and Val-21 in S1000, the loss of secondary structure during the simulations is minimal. Thus, from the simulations the gating mechanism would appear to involve primarily a spatial rearrangement of the helices in response to the applied tension in the membrane as opposed to an unfolding-refolding transition. This seems to be accompanied by a structural variation in the region around Ile-14 and Val-21, a point that will be discussed further below. Based on their mechanistic analysis, Oakley et al. had proposed that the formation of ordered secondary β-type structure involving the external (periplasmic) loop might be associated with the conformational transition leading to the open conformation of the pore (Oakley et al., 1999). In the current simulations the external loops remain unstructured under all conditions examined. In particular, no formation of regular or ordered secondary structure was apparent in the S1000 simulation associated with the conformational changes observed.
FIGURE 3.
Evolution of the Principal Radii during the four simulations: (a) Norm Press (NP), (b) Press 100 (P100), (c) Stretch 100 (S100), (d) Stretch 1000 (S1000).
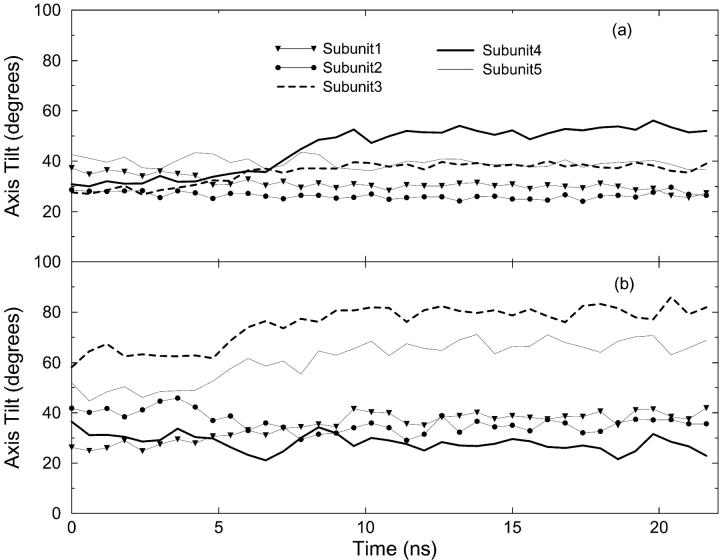
Helix tilting and conformational changes
Tilting of the helices in the TM1 and TM2 bundles has been assumed by several workers to be associated with pore opening. Figs. 4 a and 4 b show, respectively, the time evolution of the tilt of the axis of each of the five TM1 and TM2 helices in the simulation S1000 with respect to the axis of the pore. In the simulations NP and P100 no marked change in the tilt of the helices is observed. In the S100 simulation a slight increase in the tilt angle of one of the TM2 helices toward the end of the simulation is observed. The application of a more negative pressure in the xy-plane in the simulation S1000 results in a significant increase in the lateral tilt angle of the axes of TM2 in subunits 3, 5 (Fig. 4 b). A less pronounced but still significant increase in the tilt angle of the TM1 helix of 4 is also evident (Fig. 4 a). To illustrate the effect that changes in the tilt of these helices has on the structure of the protein and the enlargement of the pore, the final structure from each simulation is displayed in Figs. 5 and 6 (side and top views, respectively). In addition, in Fig. 5 the headgroups of the lipids and the water molecules inside the pore are also displayed. As can be seen, tension in the S1000 system (Figs. 5 d and 6 d) results in a pronounced change in the tilt of the helices, the enlargement of the TM2 bundle, and the movement of one TM1 helix into the space created by the motion of the TM2 helices. The pore widens noticeably.
FIGURE 4.
Variation of the axis tilt of the (a) TM1 and (b) TM2 helices in the Stretch 1000 (S1000) simulation.
Key residues
The hydrophobic residues Ile-14 and Val-21 create a constriction near the cytoplasmatic surface at the N-terminal end of TM1 (Chang et al., 1998). The small diameter of the channel in this region in the crystal, ∼0.2 nm, makes it likely that this structure represents the closed, or a nearly closed, state. In the simulations NP and P100, where the channel should remain in a closed state, the hydrophobic patch formed by residues Ile-14 and Val-21 remains stable throughout. In fact, in the P100 simulation, where a positive lateral pressure was applied, the pore becomes even more constricted (radius of the hole ∼0.18 nm). In contrast, in simulations S100 and S1000, in which a negative lateral pressure is applied mimicking the stretching of the membrane, the diameter of this region increases. Associated with this, the close packing in the hydrophobic patch is lost, potentially allowing water and ions to pass through the pore. In the S1000 simulation the radius of the pore increases to ∼1.2 nm (Fig. 6). Several mutagenesis studies have shown that hydrophilic substitutions in this region destabilize the closed state permitting the channel to gate at a lower membrane tension. The most effective “gain-of-function” mutations are substitutions of either Ile-14 or Val-21 (or both) by charged residues (Oakley et al., 1999; Yoshimura et al., 2001). The hydrophobic residues Ile-14 and Val-21 are highly conserved among MscL homologs, further suggesting that the control of the gating mechanism is based on this “hydrophobic lock” hypothesis (Moe et al., 2000).
The membrane
The application of lateral tension and the structural changes in the pore result in a reorganization of the structure of the membrane. In particular, the thickness of the membrane (calculated as the distance between the peaks in the density plot of the lipid headgroups across the simulation box) tends to decrease from a value of 4.8 nm and 4.6 nm in simulations P100 and NP, respectively, to values of 4.0 nm and 2.7 in the stretching simulations S100 and S1000, respectively. Fig. 5 d shows that in the case of the S1000 simulation the thickness of the membrane is not uniform, but decreases away from the protein as the membrane is stretched. Close to the protein the membrane maintains its thickness, matching the dimensions of the protein. Although typical cells disrupt at pressures only slightly higher than the gating pressures (Levina et al., 1999), during this set of simulations the membrane did not rupture even at the highest tension simulated. MD simulations of pure dipalmitoylphosphatidylcholine (DPPC) lipid bilayers, however, do show spontaneous rupture (on a ns time scale) for lateral pressures exceeding −200 bar (Tieleman et al., 2002). The presence of the protein therefore seems to have a stabilizing effect on the surrounding membrane.
The mechanism of opening
The mechanism by which the MscL channel opens has been debated for some time. Some have proposed a concerted mechanism, in which tension within the membrane leads to a simultaneous motion of all helices in the TM1 and TM2 bundle away from the central axis opening the pore (Spencer et al., 1999). Others have postulated that the outer TM2 helices act as a tension sensor, and can expand significantly before the internal part of the channel opens. This model considers that the periplasmic loops act as “strings” connecting the tension-sensing rim to the internal region of the complex. The channel opens when the tension-sensing rim transfers enough force via these loops to pull the internal TM1 bundle into the open state (Sukharev et al., 2001).
Our simulations suggest a third possibility. When enough tension (mimicked by the “negative” pressure in the xy-plane in the S1000 simulation) is applied, a partial reorganization of the structure is observed. There is an increase in the tilt of the helices with respect to the axis of the pore, followed by the separation of two helices within the TM2 bundle. A TM1 helix then moves into the space that has been created, expanding the central cavity. At the same time, the hydrophobic cluster consisting of residues Ile-14 and Val-21 from each of the five subunits forming the TM1 bundle is disrupted, creating a channel through the pore. The intersubunit salt-bridges between Lys-33 from one subunit and Asp-36 (this bridge is present for more than 90% of the time in simulation S1000) from the next subunit remain stable, with the possible effect of maintaining the overall stability of the global structure of the protein.
A series of new experimental papers concerning the mechanism of MscL gating appeared after this work was first submitted for review (Perozo et al., 2002a; Perozo et al., 2002b; Betanzos et al., 2002). In particular, Perozo and co-workers, using electron paramagnetic resonance (EPR) spectroscopy in combination with site directed spin labeling, obtained results which are consistent with the opening pathway being characterized by the tilting of the TM1 and TM2 helices. They find there is an increase in the tilt of the TM1 helix of 15 degrees and of the TM2 helix of 17 degrees. This is consistent with the magnitude of the changes shown in Fig. 4, which also shows a larger increase in tilt in the cases of the TM2 helices. The EPR experiments also suggest that the TM1 helix rotates around its principal axis by ∼70 degrees. We find that as the outer TM2 helix tilts, the associated TM1 helix changes its relative position and rotates away from the center of the pore. In the current set of simulations, however, only a single TM1 helix moves significantly, and more events would be required to test if such motion could explain the change observed in the EPR signal. Betanzos et al. (Betanzos et al., 2002) provide convincing evidence that the pore opens with an iris-like action. In particular, they show that disulfide bonds engineered between TM1 and TM2 helices of adjacent subunits (Cys-32–Cys-81) do not prevent gating, indicating that at least this region remains in contact during gating.
Perozo and co-workers find there is an increase in the accessibility of the hydrophobic residues lining the pore, indicated by spectral broadening for residues Ile-24 and Ala-28. Our calculations show that, during opening, the hydrophobic core obstructing the pore is disrupted and the accessibility of this area to solvent increases, as indicated in Fig. 5. The average solvent surface accessible area for Ile-24 and Ala-28 increases from 1 to 3 nm2 passing from simulation NP to simulation S1000. Perozo and co-workers attempted to model the process of opening based on their experimental observations. Treating the helices as rigid subunits, they generated a series of intermediate states that had an overall appearance and an increase in the tilt of the helices comparable to that found in our simulations. It should be noted, however, that unlike the simulations, such modeling studies inforce that the structural changes occur in a concerted manner. Thus, Perozo and co-workers generate idealized models. As they acknowledge, additional intermediate states would be needed to explain, among other things, the multiple subconducting states detected using patch-clamp methods (Perozo et al., 2002a).
What has been simulated in this study is just the first stage of the transition from a closed to a fully opened pore. Nevertheless, the mechanism implied by the simulations could explain the step-like partial or staged opening observed in patch-clamp experiments (Sukharev et al., 2001). Moreover, this picture is consistent with much of the most recent experimental data obtained by Perozo et al. (Perozo et al., 2002a). Clearly, the tension (γ = 500 mN/m) at which the gating is observed in the S1000 simulation is nonphysiological, being more than an order of magnitude larger than that required experimentally (Sukharev et al., 1999; Moe et al., 2000). However, the opening threshold defined by Moe et al. (Moe et al., 2000) for Tb-MscL is the pressure at which single channel openings were observed every 2 s. This timescale is well beyond that which can be simulated in atomic detail. Opening on a shorter timescale would correspond to a more negative threshold pressure. The large lateral pressure in the S1000 simulation was therefore needed to observe the process of opening on the timescale of MD. This will induce artifacts. In fact, simulation S1000 was terminated after 22 ns, as it was considered that the changes induced in the membrane and the partial fraying of the TM1 and TM2 helices made the simulation progressively less reliable. We note, however, that this fraying primarily occurs after the main opening event and most likely does not influence the observed mechanism. As the nature of the pore opening mechanism is mechanical, it is assumed that the basic features involved in the initial stages of the gating of MscL in the simulations will be similar to those under physiological conditions. It is also worth noting that some expansion of the structure (partial opening) is already evident at the end of simulation S100. There is some disruption of the hydrophobic lock and a noticeable increase in water within the pore (Figs. 5 c and 6 c). This is occurring at a tension of γ = 50 mN/m, much closer to the physiological gating conditions.
In contrast to the previous simulation studies of Gullingsrud et al. (Gullingsrud et al., 2001), who applied radial forces to an isolated MscL complex, in the absence of water and membrane lipids, the current simulations incorporate a detailed representation of the whole system. In particular, we have shown that water does not have a dramatic effect in terms of stability of the secondary structure elements and that the disruption of the hydrophobic core is a consequence of the mechanical reorganization of the helices, thus providing a detailed view of the mechanism by which MscL opens.
CONCLUSIONS
The simulations presented in this paper provide a detailed atomistic picture of the initial stages of the transition of the mechanosensitive Tb-MscL pore complex from a closed to an open state. As a result of the direct application of negative lateral pressure within the membrane, we observed an increase in the tilt of several of the helices in the transmembrane region of the complex as the first stage of the gating mechanism. This was followed by the enlargement of the pore and the disruption of the hydrophobic “gate” close to the cytoplasmatic side consisting of residues Ile-14 and Val-21. Once this gate is disrupted water and ions could, in principle, pass through the open pore. The simulations suggest that opening occurs in a staged process of which only the first has been illustrated. This might explain the partial opening or staged conductance observed in some patch-clamp experiments.
Acknowledgments
The authors thank R. Friesen and B. Poolman for helpful discussions.
The research was supported by a Marie Curie fellowship, contract number CT-2000-00606.
References
- Ajouz, B., C. Berrier, M. Besnard, B. Martinac, and A. Ghazi. 2000. Contribution of the different extramembranous domains of the mechanosensitive ion channel MscL to its response to membrane tension. J. Biol. Chem. 275:1015–1022. [DOI] [PubMed] [Google Scholar]
- Ajouz, B., C. Berrier, A. Garrigues, M. Besnard, and E. Ghazi. 1998. Release of thioredoxin via the mechanosensitive channel MscL during osmotic downshock of Escherichia coli cells. J. Biol. Chem. 273:26670–26674. [DOI] [PubMed] [Google Scholar]
- Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. Di Nola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, and J. Hermans. 1981. Interaction models for water in relation to protein hydration. In Intermolecular Forces. B. Pullman, editor. Reidel, Dordrecht.
- Berger, O., O. Edholm, and F. Jahnig. 1997. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 72:2002–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betanzos, M., C. S. Chiang, H. R. Guy, and S. Sukharev. 2002. A large iris-like expansion of a mechanoselective channel protein induced by membrane tension. Nat. Struct. Biol. 9:704–710. [DOI] [PubMed] [Google Scholar]
- Blount, P., S. I. Sukharev, P. Moe, and C. Kung. 1997. Mechanosensitive channels of E. coli: a genetic and molecular dissection. Biol. Bull. 192:126–127. [DOI] [PubMed] [Google Scholar]
- Blount, P., S. I. Sukharev, P. C. Moe, B. Martinac, and C. Kung. 1999. Mechanosensitive channels of bacteria. In Methods in Enzymology, Vol. 294. M. Conn, editor. Academic Press, London. 458–482. [DOI] [PubMed]
- Chang, G., R. H. Spencer, A. T. Lee, M. T. Barclay, and D. C. Rees. 1998. Structure of the MscL homolog from Mycobacterium tuberculosis: a gated mechanosensitive ion channel. Science. 282:2220–2226. [DOI] [PubMed] [Google Scholar]
- Elmore, D. E., and D. A. Dougherty. 2001. Molecular dynamics simulations of wild-type and mutant forms of the Mycobacterium tuberculosis MscL channel. Biophys. J. 81:1345–1359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feenstra, K. A., B. Hess, and H. J. C. Berendsen. 1999. Improving efficiency of large time-scale molecular dynamics simulations of hydrogen-rich systems. J. Comput. Chem. 20:786–798. [DOI] [PubMed] [Google Scholar]
- Feenstra, K. A., C. Peter, R. M. Scheek, W. F. van Gunsteren, and A. E. Mark. 2002. A comparison of methods for calculating NMR cross-relaxation rates (NOESY and ROESY intensities) in small peptides. J. Biomol. NMR. 23:181–194. [DOI] [PubMed] [Google Scholar]
- Gullingsrud, J., D. Kosztin, and K. Schulten. 2001. Structural determinants of MscL gating studied by molecular dynamics simulations. Biophys. J. 80:2074–2081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamill, O., and D. McBride. 1993. Molecular clues to mechanosensitivity. Biophys. J. 65:17–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD—Visual Molecular Dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- Kong, Y., Y. Shen, T. E. Warth, and J. Ma. 2002. Conformational pathways in the gating of Escherichia coli mechanosensitive channel. Proc. Natl. Acad. Sci. USA. 99:5999–6004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levina, N., S. Totemeyer, N. R. Stokes, P. Louis, and M. A. Jones. 1999. Protection of Escherichia coli cells against extreme turgor by activation of MscS and MscL mechanosensitive channels: identification of genes required for MscS activity. EMBO J. 18:1730–1737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lide, D. R. editor. 1992. Handbook of Chemistry and Physics, CRC Press LLC, Boca Raton, FL. 1991–1992.
- Martinac, B. 1993. Thermodynamics of Membrane Receptors and Channels. Ellis Horwood series in chemical engineering. CRC Press LLC, Boca Raton, FL.
- Moe, P. C., G. Levin, and P. Blount. 2000. Correlating a protein structure with function of a bacterial mechanosensitive channel. J. Biol. Chem. 40:31121–31127. [DOI] [PubMed] [Google Scholar]
- Oakley, A. J., B. Martinac, and M. C. J. Wilce. 1999. Structure and function of the bacterial mechanosensitive channel of large conductance. Protein. Sci. 8:1915–1921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou, X., P. Blount, R. J. Hoffman, and C. Kung. 1998. One face of a transmembrane helix is crucial in mechanosensitive channel gating. Proc. Natl. Acad. Sci. USA. 95:11471–11475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perozo, E., D. M. Cortes, P. Sompornpisut, and B. Martinac. 2002a. Open channel structure of MscL and the gating mechanism of mechanosensitive channels. Nature. 418:942–948. [DOI] [PubMed] [Google Scholar]
- Perozo, E., A. Kloda, D. M. Cortes, and B. Martinac. 2002b. Physical principles underlying the transduction of bilayer deformation forces during mechanoselective channel gating. Nat. Struct. Biol. 9:696–703. [DOI] [PubMed] [Google Scholar]
- Sachs, F. 1991. Mechanical transduction by membrane ion channels: a mini review. Mol. Cell. Biochem. 104:57–60. [DOI] [PubMed] [Google Scholar]
- Shrivastava, I. H., D. P. Tieleman, P. C. Biggin, and M. S. P. Sansom. 2002. K+ versus Na+ ions in a K channel selectivity filter: a simulation study. Biophys. J. 83:633–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer, R. H., G. Chang, and D. C. Rees. 1999. Feeling the pressure: structural insights into a gated mechanosensitive ion channel. Curr. Opin. Struct. Biol. 9:448–454. [DOI] [PubMed] [Google Scholar]
- Sukharev, S. I., P. Blount, B. Martignac, and C. Kung. 1997. Mechanosensitive channels of Escherichia coli: the MscL gene, protein, and activities. Annu. Rev. Physiol. 59:633–657. [DOI] [PubMed] [Google Scholar]
- Sukharev, S. I., P. Blount, B. Martinac, F. R. Blattner, and C. Kung. 1994. A large conductance mechanosensitive channel in E. coli encoded by MscL alone. Nature. 368:265–268. [DOI] [PubMed] [Google Scholar]
- Sukharev, S. I., S. R. Durell, and H. R. Guy. 2001. Structural models of MscL gating mechanism. Biophys. J. 81:917–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sukharev, S. I., W. J. Sigurdson, C. Kung, and F. Sachs. 1999. Energetic and spatial parameters for gating of the bacterial large conductance mechanosensitive channel, MscL. J. Gen. Physiol. 113:525–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tieleman, D. P., and H. J. C. Berendsen. 1998. A molecular dynamics study of the pores formed by Escherichia coli OmpF porin in a fully hydrated palmitoyloleoylphosphatidylcholine bilayer. Biophys. J. 74:2786–2801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tieleman, D. P., H. Leontiadou, A. E. Mark, and S. J. Marrink. 2002. Simulation of pore formation in lipid bilayers by mechanical stress and electric fields. J. Am. Chem. Soc. In press. [DOI] [PubMed]
- van der Spoel, D., R. van Drunen, and H. J. C. Berendsen. 1994. GROningen MAchine for Chemical Simulations. Department of Biophysical Chemistry, BIOSON Research Institute, Nijenborgh 4, NL-9717 AG Groningen. E-mail to gromacs@chem.rug.nl.
- van Gunsteren, W. F., S. R. Billeter, A. A. Eising, P. H. Hünenberger, P. Krüger, A. E. Mark, W. R. P. Scott, and I. G. Tironi. 1996. Biomolecular Simulation: The GROMOS96 Manual and User Guide. vdf Hochschulverlag, ETH Zurich, Switzerland.
- van Gunsteren, W. F., X. Daura, and A. E. Mark. 1998. GROMOS forcefield. In Encyclopedia of Computational Chemistry, Vol. 2. P. von Rague Scheleyer, N. L. Allinger, T. Clark, J. Gasteiger, P. A. Kollman, H. F. Schaefer, III, and P. R. Schriener, editors Wiley and Sons, Chichester, USA. 1211–1216.
- Vriend, G. 1990. WHAT IF: a molecular modeling and drug design program. J. Mol. Graph. 8:52–56. [DOI] [PubMed] [Google Scholar]
- Yoshimura, K., A. Batiza, and C. Kung. 2001. Chemically charging the pore constriction opens the mechanosensitive channel MscL. Biophys. J. 80:2198–2206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshimura, K., A. Batiza, M. Schroeder, P. Blount, and C. Kung. 1999. Hydrophilicity of a single residue within MscL correlates with increased channel mechanosensitivity. Biophys. J. 77:1960–1972. [DOI] [PMC free article] [PubMed] [Google Scholar]