Abstract
A novel bead modeling technique has been developed for the analysis of the sedimentation velocity behavior of flexible fibrils. The method involves the generation of a family of bead models representing a sample of the conformations available to the molecule and the calculation of the sedimentation coefficients of these models by established techniques. This approach has been used to investigate the size distribution of amyloid fibrils formed by human apolipoprotein C-II (apoC-II). ApoC-II fibrils have a simple and homogeneous ribbon morphology with no evidence of amorphous aggregation. Freshly prepared apoC-II forms fibrils with systematically larger sedimentation coefficients upon increasing protein concentration (modes of 100, 300, and 800 for apoC-II concentrations of 0.3, 0.7, and 1.0 mg/mL, respectively). The sedimentation coefficient distributions are not affected by rotor speed, and are not significantly changed by dilution once the fibrils are formed. The kinetics of aggregation (1 mg/mL apoC-II) as assessed using thioflavin T and preparative pelleting assays reveal that monomeric apoC-II is depleted after ∼12 h incubation at room temperature. In contrast, the sedimentation coefficient distribution of fibrils continues to grow larger over a period of 48 h to an average value of 800 S. Calculations using the bead modeling procedure suggest maximum sedimentation coefficients for individual apoC-II fibrils to be around 100 S. The larger experimentally observed sedimentation coefficients for apoC-II fibrils indicate an extensive and time-dependent tangling or association of the fibrils to form specific networks.
INTRODUCTION
Sedimentation velocity analysis has long been recognized as a powerful technique for the determination of the size, shape, and hydrodynamic behavior of soluble macromolecules. Recent methodological advances in this area have greatly expanded the range of systems amenable to this form of analysis (Schuck et al., 2002). In particular, the development of algorithms that allow sedimentation velocity data to be analyzed in terms of a continuous distribution of sedimentation coefficients has allowed its application to complex heterogeneous mixtures of macromolecules and highly self-associated systems (Perugini et al., 2000). A continuing difficulty with sedimentation velocity analysis, however, has been its application to flexible macromolecules and macromolecular complexes. This limitation arises from the complex relationship between the shape of a particle and its sedimentation coefficient. In the case of rigid particles, this relationship has been approximated in a number of ways, most notably by the bead modeling approach, in which the shape of the particle is approximated by an ensemble of spherical beads from which an expected sedimentation coefficient can be calculated (Garcia de la Torre and Bloomfield, 1981). Treatments of flexible systems have thus far been limited to relatively simple models of the hinged motions between rigid protein domains. In this approach, the flexibility of the model is treated according to the rigid body treatment in which hydrodynamic properties are averaged over an appropriately weighted average of rigid conformations. These models have been employed in the interpretation of hydrodynamic data of IgG molecules (Diaz et al., 1990) and myosin rods (Iniesta et al., 1988) in terms of their respective flexibilities. Until this point, however, such an approach has been lacking for flexible fibrils such as amyloid.
The self-association of proteins into amyloid fibrils is associated with several disease states including Alzheimer's (Selkoe, 1996; Masters et al., 1985) and Parkinson's (Pan et al., 1993). Although amyloidogenic proteins share no similarity in primary sequence or native structure, they all aggregate to form linear, unbranched assemblies with a core of cross β-structure (Sunde and Blake, 1998). This β-sheet core provides amyloid with its key diagnostic attributes: the ability to bind to and alter the spectral properties of thioflavin T and Congo red, with Congo red-bound amyloid fibrils exhibiting green birefringence under cross-polarized light (LeVine, 1993; Klunk et al., 1999). Despite this common core structure, the superstructural morphology of amyloid fibrils varies considerably between proteins and is often heterogeneous even within the same protein preparation, such as observed with amylin (Goldsbury et al., 1997) and the SH3 domain (Jimenez et al., 1999). Amyloid fibril formation may also involve morphological transitions during fibrillogenesis from small protofilaments into cable- or ropelike structures, as instanced by Aβ and SH3 domain amyloidosis (Harper et al., 1999; Goldsbury et al., 2000; Guijarro et al., 1998).
It is becoming increasingly evident that different assembly states of amyloid fibrils have distinct biological properties (Lansbury, 1999). For example, the presence of amorphous and protofilament classes of protein aggregate promote higher levels of cytotoxicity to cell cultures than older, more mature fibrils (Bucciantini et al., 2002). In addition, the cytotoxicity of unrelated and nonnaturally occurring amyloid fibrils suggests that all amyloid-related aggregates induce toxicity via a similar mechanism and that amyloid has a common structural motif (Bucciantini et al., 2002).
We chose to investigate the properties of apolipoprotein (apo) C-II amyloid fibrils as a model system for probing fibril size distributions and fibril-fibril interactions such as tangling. ApoC-II, a 79-amino acid protein normally associated with plasma lipoproteins, forms amyloid fibrils under lipid-free conditions in vitro and has been proposed as a good model for the several apolipoproteins that form amyloid fibrils in vivo and are related to disease states (Hatters et al., 2000). An important property of apoC-II fibrils is a homogenous morphology consisting of simple flexible ribbons with no amorphous aggregation (Hatters et al., 2000). However, the highly twisted and tangled nature of the fibrils when imaged by electron microscopy raises the possibility that the fibrils form specific or nonspecific fibril-fibril interactions. Evidence for this is seen when apoC-II amyloid is prepared at high concentrations (10 mg/mL), or fibrils are concentrated from dilute solutions, where translucent gels form that resist dissolution (Hatters et al., 2000; unpublished results). Similar gel formation is also commonly observed with other amyloid fibrils such as those formed by synthetic amyloid β-sheet tapes (Aggeli et al., 1997).
In this study, we exploit the newly developed ls-g*(s) method of sedimentation velocity analysis (Schuck and Rossmanith, 2000) and a unique and generalizable means of relating sedimentation coefficients to the size and shape of flexible molecules. ls-g*(s) is well suited to large species, such as amyloid, where the effect of diffusion on the sedimentation coefficient becomes negligible (Schuck and Rossmanith, 2000). This has several advantages over other techniques in that the size distribution of the total species in solution can be measured over a wide range of sedimentation coefficients (from 1 to 4000 S), and of large macromolecular complexes (Schuck and Rossmanith, 2000). As with other sedimentation velocity techniques, however, it is limited by the absence of a direct relationship between sedimentation coefficient and fibril size. To this end we use bead models of simulated wormlike chains based on the experimentally measured ribbon geometry, twist, and persistence length of apoC-II fibrils. Bead models of the wormlike chains are used to calculate sedimentation coefficients using the same methodology developed for bead models of proteins (Garcia de la Torre et al., 1994). We show that the experimentally measured sedimentation coefficient distributions of apoC-II fibrils are too large to be accounted for as simple noninteracting ribbons. This work provides evidence for an irreversible time- and concentration-dependent formation of fibrillar networks, preceding the formation of gels. We propose that such fibril tangling and network formation is a significant process in the development of protein aggregates in vivo with the potential of affecting normal cellular processes.
MATERIALS AND METHODS
Materials
ApoC-II was expressed (Wang et al., 1996) and purified (Hatters et al., 2000) as described previously. The purified protein ran as a single band on SDS-PAGE. The purified protein stock was stored at a concentration of 40 mg/mL in 6.5 M guanidine hydrochloride, 10 mM Tris, pH 8.0 at 4°C. Refolding buffer used in the experiments consists of 100 mM sodium phosphate, 0.1% sodium azide, pH 7.4.
Amyloid preparation
ApoC-II was prepared by direct dilution from the stock into refolding buffer to a final concentration of between 0.2–1 mg/mL apoC-II. Freshly prepared apoC-II consists almost entirely of monomers. Amyloid was allowed to form by incubation of freshly prepared apoC-II at room temperature.
Kinetics of amyloid aggregate formation
The time course of apoC-II aggregation was followed using thioflavin T reactivity or preparative centrifugation followed by assay of the supernatant. For thioflavin T assays, 20 μL of apoC-II (1 mg/mL in refolding buffer) was added to microtiter wells containing 230 μL of 100 mM sodium phosphate, 0.1% sodium azide, 5.4 μM thioflavin T, pH 7.4. After 5 min incubation, the fluorescence was monitored using an fmax plate reader equipped with a 444/485 nm excitation/emission filter set. For the pelleting assay, 200 μL of apoC-II solution (1 mg/mL in refolding buffer) was sedimented at 120,000 g (55,000 rpm in a TLA-100 rotor; Beckman TL-100 ultracentrifuge) for 30 min at 20°C. 50 μL of supernatant was collected and added to 175 μL refolding buffer in a microtiter plate followed by rapidly mixing with 75 μL of fluorescamine solution (0.5 mg/mL in acetonitrile). After 5 min incubation, the fluorescence was monitored using an fmax plate reader equipped with a 350/460 nm excitation/emission filter set.
Sedimentation velocity analysis
Samples were analyzed using an XL-A analytical ultracentrifuge (Beckman Coulter, Fullerton, CA) equipped with an AnTi60 rotor at 20°C. Protein samples (300–400 μL) were added to epon-filled centerpieces, with refolding buffer in the reference compartment. Radial absorbance data were acquired at wavelengths of 280 or 292 nm, radial increments of 0.002 cm in continuous scanning mode, and rotor speeds of between 4000 and 10,000 rpm. Scans were taken at 5- or 10-min intervals. The sedimenting boundaries were fitted to a model describing the sedimentation of a distribution of sedimentation coefficients with no diffusion (ls-g*(s)) using SEDFIT (Schuck and Rossmanith, 2000). Data were fitted using a Tikhonov-Phillips regularization parameter of p = 0.95, and 200 sedimentation coefficient increments in the range of 20–3000 S, depending on the sample. To correct for residual monomeric apoC-II, which sediments negligibly at the rotor speeds used, we fitted a time independent noise background contribution to the overall radial absorbance.
Electron microscopy
Copper grids (400 mesh) were coated with thin carbon film and glow discharged in nitrogen. Samples of apoC-II (1.0 mg/mL) in refolding buffer were applied to the grid and allowed to equilibrate for 30 s. The samples were washed twice with refolding buffer followed by staining with 3–4 drops of 2% potassium phosphotungstate at pH 6.0–7.0. The grids were air-dried and examined using a JEOL 2000FX transmission electron microscope (Brooksvale, NSW, Australia) operating at 120 kV. Micrographs were recorded at nominal magnifications of ×40,000.
Modeling
Persistence length estimations from two-dimensional images
The persistence length of apoC-II amyloid fibrils in solution was estimated from conformational parameters measured by electron microscopy. During deposition onto the electron microscope grid, the three-dimensional solution conformation of amyloid is inevitably altered by the transformation onto a two-dimensional surface. For this deposition process, fibrils can either conformationally equilibrate as they settle or directly adhere to the surface through grid-fibril attractive forces. Where only weak interactions exist between the two-dimensional surface and fibrils, conformational equilibrium is attained before deposition. DNA molecules reach conformational equilibrium when deposited onto nonadhesive surfaces whereas they deposit in kinetically trapped conformations on surfaces for which they have greater affinity (Rivetti et al., 1996). We make the assumption that apoC-II amyloid fibrils have minimal affinity with the EM grid and therefore equilibrate on that surface during deposition. This assumption is supported by the observation that fibrils are easily washed entirely off the grid. The mean-square end-to-end distance of a fibril of contour length L and persistence length P assuming conformational equilibrium in two dimensions is given by Rivetti et al. (1996):
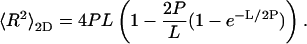 |
(1) |
Bead modeling and determination of sedimentation coefficients
ApoC-II amyloid fibrils are simulated as chains of n linear segments, each of length l and zero mass. Spherical beads of radius l/2 and mass m are positioned at the vertices of the chain. The apoC-II amyloid ribbon has a width of 13 nm, determined by electron microscopy (Hatters et al., 2000), and a thickness of 2 nm, determined by atomic force microscopy (unpublished data). Addition of waters of hydration to a level of 0.4 g water per gram of protein increases these dimensions to give a volume per unit length of 40 nm2. The value of l is selected such that the resulting model has an identical average volume per unit length, whereas m is chosen to give the model a density consistent with the apoC-II amino acid composition. Our results are relatively insensitive to the assumed level of hydration. For example, taking a value for hydration of 0.3 g per gram of protein reduces the volume per unit length of the model to 36.5 nm2, producing a corresponding increase in sedimentation coefficient of ∼3% for the longest fibrils considered.
Computationally, each chain segment is taken as a vector along the z axis of a local coordinate frame. The z axis of this frame thus represents the fiber axis, whereas the y axis is taken as normal to the plane of the fibril ribbon and the x axis parallel to the amyloid β-strands. The orientation of each segment in the coordinate frame of the previous one is defined by three angles, θ, φ, and τ, which are rotations about the x, y, and z axes, respectively. Thus θ represents bend perpendicular to the plane of the amyloid ribbon, φ represents bend in the plane of the ribbon, and τ represents twist along the fiber axis. The full trajectory of each chain is defined by expressing the coordinates of chain segments 2 through n in the frame of the first chain element.
To generate randomized chain conformations, the values of θ, φ, and τ at each joint of the chain are determined as normally distributed pseudo-random numbers with standard deviation, σ, about a mean for each angle. We have set the mean values for θ and φ to 0, reflecting the assumption that observed curvature reflects fibril flexibility and not an intrinsic bend. We have also assumed negligible bending in the plane of the amyloid ribbon, thus σφ = 0, allowing σθ to be determined from the relation (Koo et al., 1990):
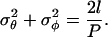 |
(2) |
The twist of the apoC-II amyloid ribbons was measured from electron micrographs, where the helical repeat was determined as the distance between the midpoints of two consecutive narrow segments of low density within an amyloid fibril. This corresponds to sections in which the amyloid ribbon lies perpendicular to the surface. The helical repeat thus represents a 180° twist in the amyloid ribbon. Observed helical repeat lengths fit well to a normal distribution with a mean of 53 nm and a standard deviation of 12 nm. From these values the mean and standard deviation of τ was determined.
Sedimentation coefficients of bead models thus produced were calculated using HYDRO (Garcia de la Torre et al., 1994). The flexibility of the amyloid fibrils is treated according to the so-called rigid body approach of Zimm (1980): it is assumed that each fibril samples the available conformational space on a faster timescale than that of the sedimentation velocity experiment, thus a monodisperse sample of fibrils of given size can be expected to sediment with a single sedimentation coefficient equal to the time average of the conformations sampled. As the fibrils are inherently straight, with bending being a Brownian process restricted by the persistence length of the fibril, a sufficiently large ensemble of bead models of given length, produced as described above, can be anticipated to reflect the conformational space sampled by fibrils of that length. Based on these considerations, we have determined the expected sedimentation coefficient for fibrils of given length as the average of the sedimentation coefficients calculated for each of an ensemble of 100 bead models of that length.
To investigate the effect of the ribbonlike morphology of apoC-II fibrils on their sedimentation behavior, we also generated bead models that reflected this structure. In this case a row of six beads was centered on the beginning of each chain segment, extending along the positive and negative x axis of the local coordinate frame. Again each bead has diameter equal to the chain segment length, selected such that the model has appropriate density and volume.
RESULTS
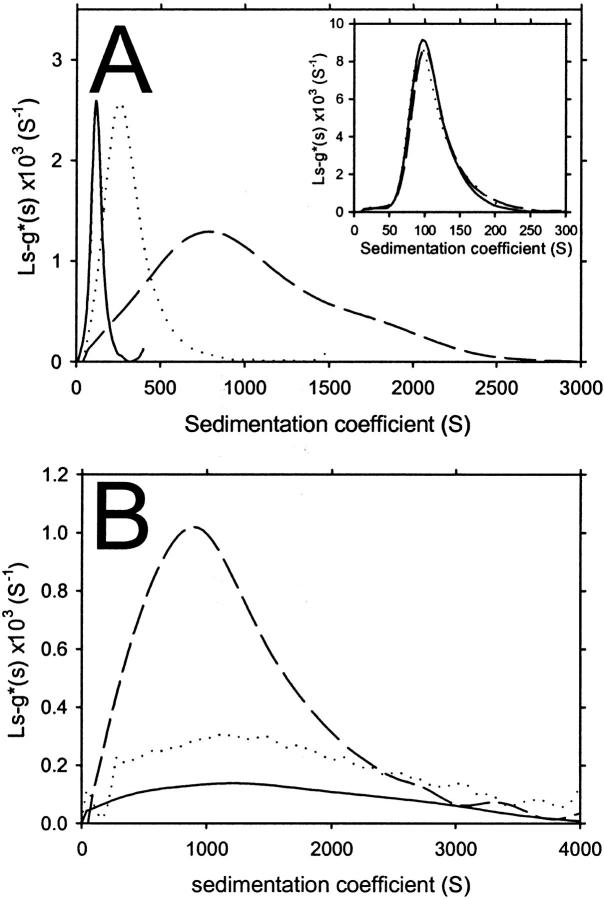
We initially investigated the sedimentation velocity behavior of apoC-II samples prepared at three different concentrations and incubated for seven days at room temperature. In Fig. 1, the sedimentation velocity data of each sample are defined by a significant proportion of fast-moving material, consistent with the presence of amyloid fibrils, and a minor population of monomeric apoC-II (1 S; Hatters et al., 2000, 2001), which does not significantly sediment at the rotor speed used in this experiment (4000 rpm). An important observation is the dramatic increase in the rate of movement of the sedimenting boundary with the initial apoC-II concentration, suggesting that the fibrils become larger with increasing apoC-II concentration. To quantitate this effect, each of the data sets in Fig. 1 were fitted to a continuous sedimentation coefficient distribution, ls-g*(s), with the fits shown as solid lines. For apoC-II at a concentration of 0.3 mg/mL, the sedimentation coefficient distribution has a mode of ∼100 S (Fig. 2 A). This is similar to previously published data for apoC-II fibrils formed at this concentration (Hatters et al., 2002). For apoC-II incubated at concentrations of 0.7 and 1.0 mg/mL, the modal values are ∼350 and 800 S, respectively with broad sedimentation coefficient ranges (Fig. 2 A).
FIGURE 1.
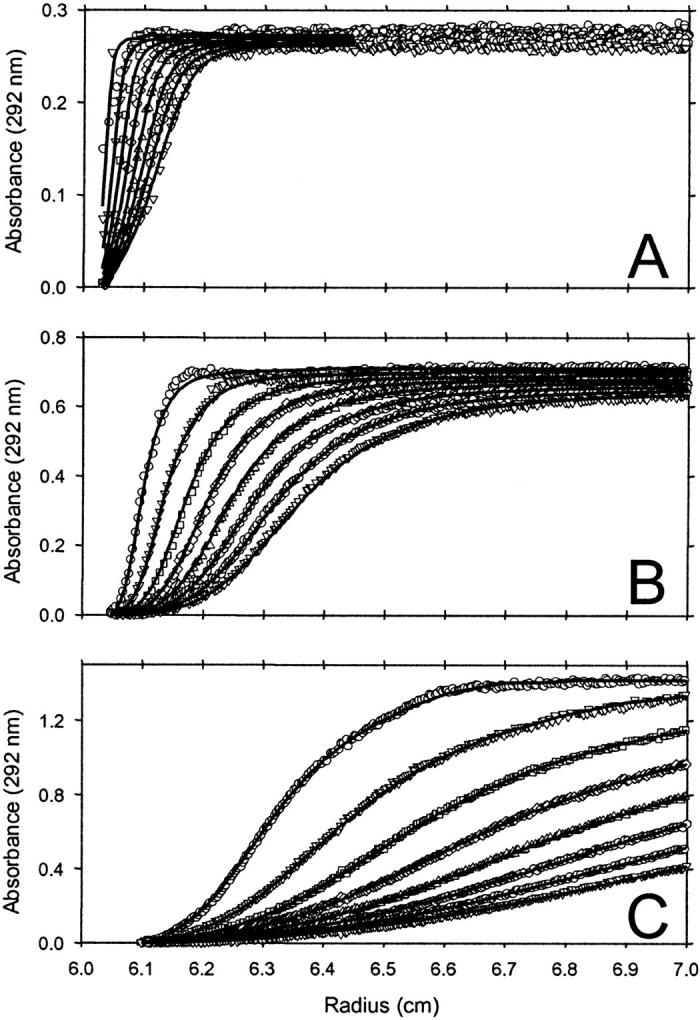
Sedimentation velocity analysis of apoC-II fibrils formed by one week incubation at (A) 0.3, (B) 0.7, and (C) 1.0 mg/mL. Centrifugation was performed at 4000 rpm, with radial scans taken at 10-min intervals. For clarity, every second scan has been omitted from the figure. Symbols indicate the order of acquisition as follows: ○,▿,□,⋄,▵, ,○,▿. Solid lines represent fits of the radial scans to ls-g*(s) distributions. Data shown have been corrected for time-independent background absorbance.
,○,▿. Solid lines represent fits of the radial scans to ls-g*(s) distributions. Data shown have been corrected for time-independent background absorbance.
FIGURE 2.
Continuous sedimentation coefficient distributions of apoC-II amyloid fibrils determined using ls-g*(s) analysis of sedimentation velocity data. (A) ApoC-II fibrils formed by one-week incubation at 0.3 (solid line), 0.7 (dotted line), and 1.0 mg/mL (dashed line), from data acquired at 4000 rpm (the raw data and fits are shown in Fig. 1). (Inset) ApoC-II fibrils formed by one-week incubation at 0.3 mg/mL, from data acquired at 4000 rpm (solid line), 8000 rpm (dotted line), and 10,000 rpm (dashed line). (B) ApoC-II fibrils formed by one-week incubation at 1 mg/mL, with centrifugation performed with samples undiluted (dashed line), diluted twofold (dotted line), or diluted fourfold (solid line).
To confirm that these sedimentation coefficient distributions reflected the behavior of individual sedimenting species and were not influenced by bulk flow through the solution column, we also performed the sedimentation analysis of the seven-day incubated, 0.3 mg/mL apoC-II sample at rotor speeds of 6000 and 10,000 rpm. ls-g*(s) analysis provided good fits to the data (not shown) with the sedimentation coefficient distributions superimposing (inset to Fig. 2 A). This provides confidence that the data in Fig. 2 A represent the size distributions of apoC-II amyloid fibrils formed at the three starting concentrations.
We also tested the effect of dilution on the sedimentation coefficient distribution of preformed fibrils by sedimentation analysis of seven-day incubated apoC-II (1 mg/mL) diluted two- and fourfold. The corresponding sedimentation coefficient distributions of these samples (Fig. 2 B) show that dilution of preformed fibrils does not significantly alter the modal sedimentation coefficient or range of values. This suggests the larger fibrils are irreversibly formed and not dissociated by dilution.
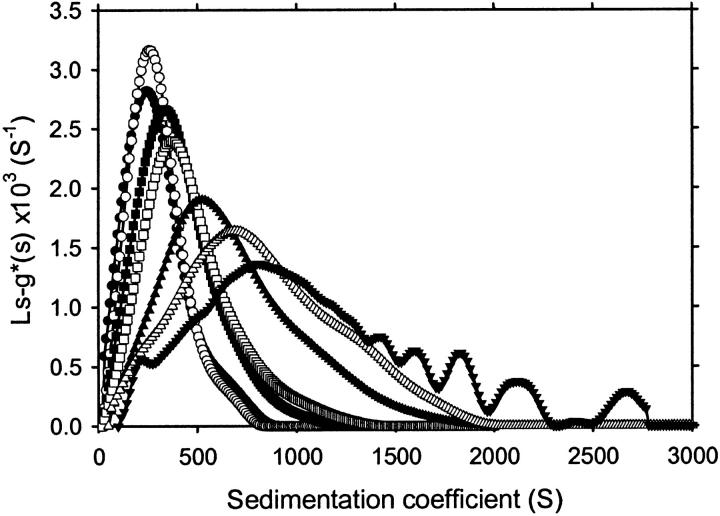
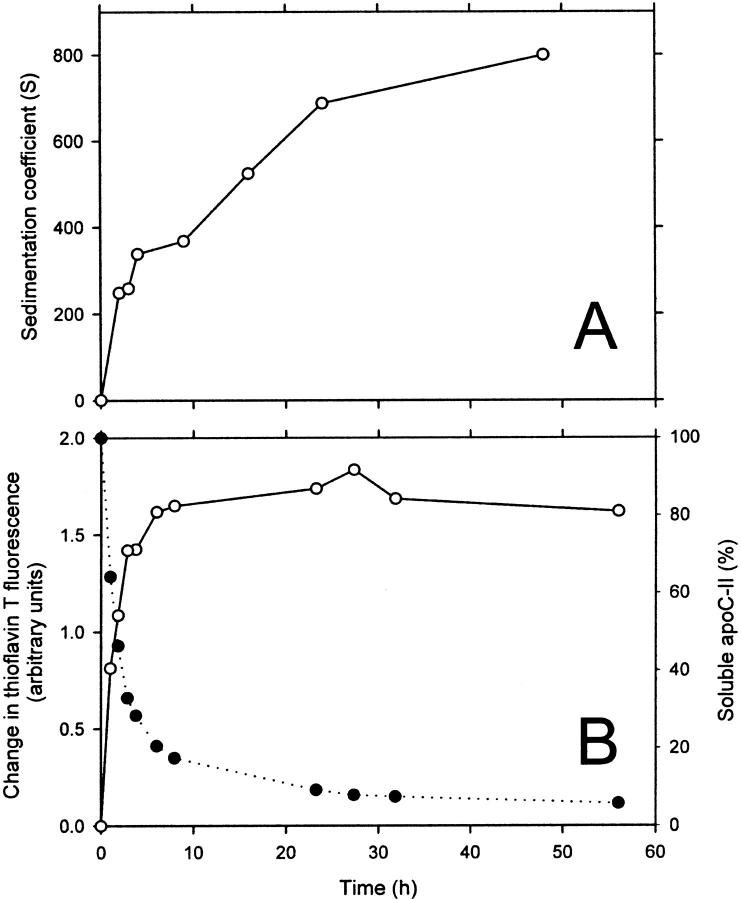
The time dependence of apoC-II fibril formation was investigated by sedimentation velocity analysis using a fixed initial protein concentration (1 mg/mL). Samples were subjected to centrifugation using a rotor speed of 4000 rpm and the radial scans were fitted to ls-g*(s) sedimentation coefficient distributions (Fig. 3). Upon incubation, the sedimentation coefficient distribution becomes progressively larger, with fibrils incubated for 48 h having a modal sedimentation coefficient value of 800 S and a range of between 50 and 3000 S (Fig. 3). The modal sedimentation coefficient is plotted in Fig. 4 A as a function of incubation time before analytical ultracentrifugation. Fig. 4 A includes an initial time point value of 1 S, determined previously for the sedimentation coefficient of freshly prepared apoC-II (Hatters et al., 2000). The modal sedimentation coefficient rises steadily to a value of 800 S after 48 h. It is noteworthy that even at early incubation times, at least 90% of the absorbance is fast-sedimenting, suggesting that fibrils continue to grow larger even when monomeric apoC-II is depleted.
FIGURE 3.
Time-dependent changes in the continuous sedimentation coefficient distribution of apoC-II amyloid fibrils formed at 1 mg/mL. Samples were incubated for 2 h (•), 3 h (○), 4 h (▪), 9 h (□), 16 h (▴), 24 h (▵), and 48 h (▾). The oscillations seen in the distribution at 48 h at sedimentations coefficients >1300 S were not stable features of the analysis and were not seen, for example, if the range of sedimentation coefficients was sampled logarithmically rather than linearly.
FIGURE 4.
(A) Modal sedimentation coefficient of 1 mg/mL apoC-II as a function of time, determined from the data in Fig. 3. (B) Time course of amyloid formation (1 mg/mL) as measured by thioflavin T reactivity (left axis, open circles) and pelleting and assay of the supernatant for fluorescamine reactivity (right axis, closed circles).
The kinetics of apoC-II amyloid formation at a concentration of 1 mg/mL was investigated in more detail using thioflavin T reactivity to measure the amount of amyloid fibrils present. Thioflavin T binds stoichiometrically to apoC-II amyloid fibrils causing large increases in its fluorescence emission at a wavelength of 480 nm when excited at 450 nm (Hatters et al., 2001). Fig. 4 B shows the thioflavin T reactivity of apoC-II samples (1 mg/mL) incubated for various times. The thioflavin T fluorescence signal reaches its maximum level after ∼12 h, indicating that the amount of apoC-II amyloid fibrils present does not increase beyond this point. We also assayed aggregate formation directly using preparative centrifugation followed by assay of the supernatant for monomer concentration, as described previously (Hatters et al., 2002). In the pelleting assay, the supernatant protein concentration decreases with a kinetic profile consistent with that of the development of thioflavin T reactivity. After 10 h, more than 80% of the apoC-II is depleted from the supernatant. The substantial increase in the modal sedimentation coefficient of apoC-II after most of the monomers are converted to amyloid fibrils (12 h) suggests extensive aggregation of the fibrils to form larger networks or assemblies.
We further investigated the time dependence of amyloid formation by apoC-II at 1 mg/mL using negative staining electron microscopy. No structures could be detected in samples of freshly prepared material (data not shown), indicating the absence of any significantly aggregated material and consistent with previous observations that indicate that freshly prepared apoC-II is exclusively monomeric (Hatters et al., 2000). After 30 s incubation, isolated short ribbons were detected (typical view shown in Fig. 5 A). Within 2 min, fibrils were observed that were mostly of indeterminate length (data not shown). By 60 min, the grids were coated in heavily overlapping fibrils (Fig. 5 B) that did not change in gross morphology, but continued to become more extensive in coverage on the EM grid by 48 h (Fig. 5 C). The extensive overlapping of the fibrils observed in these images is consistent with the sedimentation velocity data that suggest network formation and tangling. However, since the electron micrographs represent images of the fibrils as they have settled on the two-dimensional EM grid, it is not possible to infer with certainty the presence of fibril networks in solution. These data do highlight, however, the simple homogeneous morphology of apoC-II amyloid fibrils and show that the fibrils grow rapidly once nucleated.
FIGURE 5.
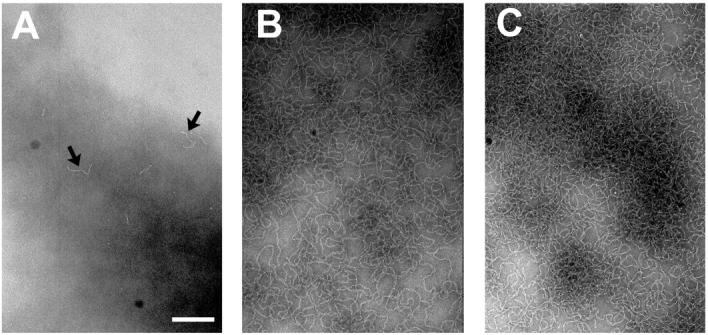
Negative staining electron microscopy of apoC-II (1 mg/mL) as a function of incubation time. (A) 30 s. (B) 60 min. (C) Two days. Scale bar = 200 nm. Arrows in panel A highlight nascent fibrils.
To provide more compelling evidence for the presence of extensive tangling and fibril association, we sought to further analyze the determined sedimentation coefficient size distributions in terms of fibril size and morphology. To this end, we defined a relationship between the sedimentation coefficient and amyloid fibril length by calculating the theoretical sedimentation coefficient of fibril bead models. Bead models of simulated wormlike chains were calculated to reflect the geometric dimensions, ribbon twist, and solution flexibility of apoC-II amyloid fibrils. The flexibility of the fibrils was determined by calculation of the persistence length of the amyloid fibrils from fibrillar contour lengths and corresponding end-to-end distances measured from electron micrographs. Fits of contour length versus the square of the end-to-end distance to Eq. 1 yield a persistence length of apoC-II amyloid fibrils of 36 nm (data not shown). These results can be compared to a persistence length of 53 nm measured for DNA imaged by AFM using the same conformational assumptions (Rivetti et al., 1996).
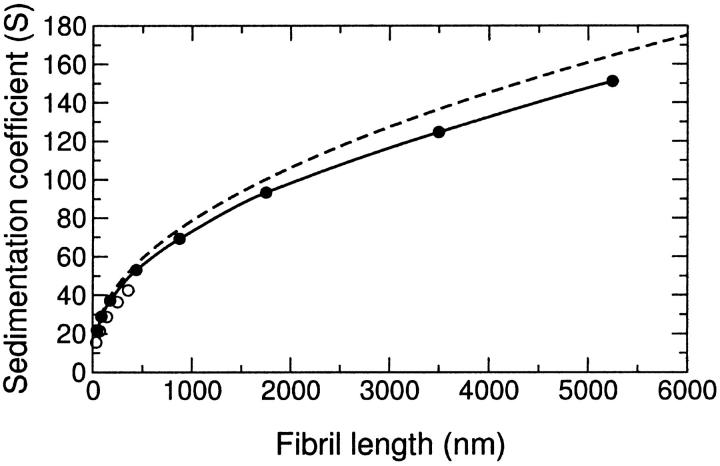
The simulated fibrils were converted into bead models composed of repeating cross-sectional segment units of either six beads or one bead (represented schematically in Fig. 6). The six-bead models more accurately reflect the ribbonlike morphology of the amyloid fibrils, whereas the simplicity of the one-bead model allows the examination of much longer fibril lengths. Fig. 7 shows histograms of the sedimentation coefficients calculated for 100 wormlike chains for each given contour length. As the wormlike chain becomes longer, the sedimentation coefficient distribution becomes broader, reflecting an increased variability in the chain conformations available to the population as the fibrils become substantially longer than the persistence length (36 nm). The sedimentation coefficient distributions derived from the six-bead models (not shown) were similar to the one-bead model, although the average sedimentation coefficient is slightly lower, particularly at shorter fibril lengths. Thus, it is evident that a one-bead model has sufficient resolution to adequately describe polymers of the lengths investigated. Fig. 8 shows the average sedimentation coefficients derived from these models and their standard deviations for the different contour lengths. This data can be compared with excellent agreement to the approximate analytical solution for the sedimentation coefficients of long wormlike chains derived by Hearst and Stockmayer (1962, Fig. 8). This agreement facilitates the extrapolation of the result beyond the fibril length limit established by the computational cost of the bead modeling approach. Such extrapolation suggests that single linear fibrils must attain a length of several centimeters to sediment at the rates observed in this study. Fibrils of this length would have mass of more than 1011 Da. By way of comparison, a smooth sphere of equivalent density and sedimentation coefficient would have a radius of ∼40 nm and mass of 2 × 108 Da. On the basis of these considerations and the kinetic discrepancy between the depletion of monomeric apoC-II and the increase in sedimentation coefficient, a considerably more plausible explanation for our experimentally observed sedimentation velocity behavior is the formation of complex fibril-fibril associations such as tangling or network formation.
FIGURE 6.
Schematic representation of two alternative bead models of wormlike chains simulating apoC-II fibrils. (A) One-bead model. (B) Six-bead model.
FIGURE 7.
Histogram of sedimentation coefficients of one-bead models of wormlike chains. Numbers above histogram subset represent contour length of wormlike chains. Sample size is 100 wormlike chains per data set.
FIGURE 8.
Sedimentation coefficients of bead models of simulated wormlike chains. The mean sedimentation coefficient from 100 chains for each contour length is shown using one-bead (•) and six-bead (○) models. The approximate analytical solution of Hearst and Stockmayer (1962) is shown as a dashed line.
DISCUSSION
We have described a novel approach to the analysis of the size distribution of amyloid fibrils based on sedimentation velocity analysis and a Monte Carlo implementation of the rigid body treatment of the hydrodynamics of flexible chains. This approach is generalizable to the analysis of any system of macromolecules with well-defined flexibility. Previous studies to elucidate fibril size include quasielastic light-scattering experiments on Aβ amyloid fibrils (Lomakin et al., 1996, Walsh et al., 1997). Although this technique provides a general assessment of the hydrodynamic radii of smaller fibrils in solution (<150 nm for Aβ fibrils), the data become difficult to interpret for heterogeneous mixtures of long and flexible fibrils (Lomakin et al., 1999). The approach developed here, on the other hand, exploits continuous sedimentation coefficient analysis enabling its application to heterogeneous mixtures over a broad range of sizes.
The extremely large sedimentation coefficients observed for amyloid fibrils formed by apoC-II are strongly suggestive of some form of fibril-fibril aggregation or tangling that is irreversible by dilution. This is supported by the observation that the observed sedimentation coefficients continue to increase even after monomeric apoC-II has been depleted from solution and the amount of thioflavin T reactive material present has ceased to increase (Fig. 4). Because fibril tangling will increase the turbidity of apoC-II solutions, it seems likely that fibril tangling may explain the previously observed discrepancy between the kinetics of turbidity development and the kinetics of amyloid fibril formation monitored by thioflavin T fluorescence or pelleting assays (Hatters et al., 2002).
The tangling of amyloid fibrils is presumably an important step in the process by which soluble fibrils are deposited into insoluble amyloid deposits in vivo, with significant relevance to amyloid-related disease states. In the case of the systemic amyloidoses, for instance, pathology appears to be solely related to the development of massive amyloid deposits and resulting impairment of organ function (Pepys, 1995). In the case of other amyloid-related diseases, however, it has been suggested that insoluble deposits play a protective role by sequestering cytotoxic protofibrillar species (Lansbury, 1999; Bucciantini et al., 2002). In either case, an understanding of the processes that may effect fibril-fibril interactions in vivo will be key to understanding amyloid-related pathogenesis. Fibril tangling is also likely to be an important consideration in attempts to engineer amyloidlike structures with functionally valuable material properties. As such, experimental techniques that enable direct inference of fibril tangling such as those described here may well prove invaluable in medical and engineering studies of fibrillar systems.
Danny M. Hatters' present address is Gladstone Institute of Cardiovascular Disease, PO Box 419100, San Francisco, CA 94141.
References
- Aggeli, A., M. Bell, N. Boden, J. N. Keen, P. F. Knowles, T. C. McLeish, M. Pitkeathly, and S. E. Radford. 1997. Responsive gels formed by the spontaneous self-assembly of peptides into polymeric beta-sheet tapes. Nature. 386:259–262. [DOI] [PubMed] [Google Scholar]
- Bucciantini, M., E. Giannoni, F. Chiti, F. Baroni, L. Formigli, J. Zurdo, N. Taddei, G. Ramponi, C. M. Dobson, and M. Stefani. 2002. Inherent toxicity of aggregates implies a common mechanism for protein misfolding diseases. Nature. 416:507–511. [DOI] [PubMed] [Google Scholar]
- Diaz, F. G., A. Iniesta, and J. Garcia de la Torre. 1990. Hydrodynamic study of flexibility in immunoglobulin IgG1 using Brownian dynamics and the Monte Carlo simulations of a simple model. Biopolymers. 30:547–554. [DOI] [PubMed] [Google Scholar]
- Garcia de la Torre, J., and V. A. Bloomfield. 1981. Hydrodynamic properties of complex, rigid, biological macromolecules: theory and applications. Q. Rev. Biophys. 14:81–139. [DOI] [PubMed] [Google Scholar]
- Garcia de la Torre, J., S. Navarro, M. C. Lopez Martinez, F. G. Diaz, and J. J. Lopez Cascales. 1994. HYDRO: a computer program for the prediction of hydrodynamic properties of macromolecules. Biophys. J. 67:530–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldsbury, C. S., G. J. Cooper, K. N. Goldie, S. A. Muller, E. L. Saafi, W. T. Gruijters, M. P. Misur, A. Engel, U. Aebi, and J. Kistler. 1997. Polymorphic fibrillar assembly of human amylin. J. Struct. Biol. 119:17–27. [DOI] [PubMed] [Google Scholar]
- Goldsbury, C. S., S. Wirtz, S. A. Muller, S. Sunderji, P. Wicki, U. Aebi, and P. Frey. 2000. Studies on the in vitro assembly of Aβ 1-40: implications for the search for Aβ fibril formation inhibitors. J. Struct. Biol. 130:217–231. [DOI] [PubMed] [Google Scholar]
- Guijarro, J. I., M. Sunde, J. A. Jones, I. D. Campbell, and C. M. Dobson. 1998. Amyloid fibril formation by an SH3 domain. Proc. Natl. Acad. Sci. USA. 95:4224–4228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper, J. D., S. S. Wong, C. M. Lieber, and P. T. Lansbury, Jr. 1999. Assembly of A beta amyloid protofibrils: an in vitro model for a possible early event in Alzheimer's disease. Biochemistry. 38:8972–8980. [DOI] [PubMed] [Google Scholar]
- Hatters, D. M., R. A. Lindner, J. A. Carver, and G. J. Howlett. 2001. The molecular chaperone, alpha-crystallin, inhibits amyloid formation by apolipoprotein C-II. J. Biol. Chem. 276:33755–33761. [DOI] [PubMed] [Google Scholar]
- Hatters, D. M., C. E. MacPhee, L. J. Lawrence, W. H. Sawyer, and G. J. Howlett. 2000. Human apolipoprotein C-II forms twisted amyloid ribbons and closed loops. Biochemistry. 39:8276–8283. [DOI] [PubMed] [Google Scholar]
- Hatters, D. M., A. P. Minton, and G. J. Howlett. 2002. Macromolecular crowding accelerates amyloid formation by human apolipoprotein. J. Biol. Chem. 277:7824–7830. [DOI] [PubMed] [Google Scholar]
- Hearst, J. E., and W. H. Stockmayer. 1962. Sedimentation constants of broken and wormlike coils. J. Chem. Phys. 37:1425–1433. [Google Scholar]
- Iniesta, A., F. G. Diaz, and J. Garcia de la Torre. 1988. Transport properties of rigid bent-rod macromolecules and of semiflexible broken rods in the rigid-body treatment. Analysis of the flexibility of myosin rods. Biophys. J. 54:269–275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jimenez, J. L., J. I. Guijarro, E. Orlova, J. Zurdo, C. M. Dobson, M. Sunde, and H. R. Saibil. 1999. Cryo-electron microscopy structure of an SH3 amyloid fibril and model of the molecular packing. EMBO J. 18:815–821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klunk, W. E., R. F. Jacob, and R. P. Mason. 1999. Quantifying amyloid by congo red spectral shift assay. Methods Enzymol. 309:285–305. [DOI] [PubMed] [Google Scholar]
- Koo, H. S., J. Drak, J. A. Rice, and D. M. Crothers. 1990. Determination of the extent of DNA bending by an adenine-thymine tract. Biochemistry. 29:4227–4234. [DOI] [PubMed] [Google Scholar]
- Lansbury, P. T., Jr. 1999. Evolution of amyloid: what normal protein folding may tell us about fibrillogenesis and disease. Proc. Natl. Acad. Sci. USA. 96:3342–3344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeVine, H., 3rd. 1993. Thioflavine T interaction with synthetic Alzheimer's disease beta-amyloid peptides: detection of amyloid aggregation in solution. Protein Sci. 2:404–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lomakin, A., G. B. Benedek, and D. B. Teplow. 1999. Monitoring protein assembly using quasielastic light scattering spectroscopy. Methods Enzymol. 309:429–459. [DOI] [PubMed] [Google Scholar]
- Lomakin, A., D. S. Chung, G. B. Benedek, D. A. Kirschner, and D. B. Teplow. 1996. On the nucleation and growth of amyloid beta-protein fibrils: detection of nuclei and quantitation of rate constants. Proc. Natl. Acad. Sci. USA. 93:1125–1129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masters, C. L., G. Simms, N. A. Weinman, G. Multhaup, B. L. McDonald, and K. Beyreuther. 1985. Amyloid plaque core protein in Alzheimer disease and Down syndrome. Proc. Natl. Acad. Sci. USA. 82:4245–4249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan, K. M., M. Baldwin, J. Nguyen, M. Gasset, A. Serban, D. Groth, I. Mehlhorn, Z. Huang, R. J. Fletterick, F. E. Cohen, and S. B. Prusiner. 1993. Conversion of alpha-helices into beta-sheets features in the formation of the scrapie prion proteins. Proc. Natl. Acad. Sci. USA. 90:10962–10966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepys, M. B. 1995. The acute phase response and C-reactive protein. In Oxford Textbook of Medicine, 3rd ed. D. J. Weatherall, J. G. Ledingham, and D. A. Warrel, editors. Oxford University Press, Oxford. 1512–1524.
- Perugini, M. A., P. Schuck, and G. J. Howlett. 2000. Self-association of human apolipoprotein E3 and E4 in the presence and absence of phospholipid. J. Biol. Chem. 275:36758–36765. [DOI] [PubMed] [Google Scholar]
- Rivetti, C., M. Guthold, and C. Bustamante. 1996. Scanning force microscopy of DNA deposited onto mica: equilibration versus kinetic trapping studied by statistical polymer chain analysis. J. Mol. Biol. 264:919–932. [DOI] [PubMed] [Google Scholar]
- Schuck, P., M. A. Perugini, N. R. Gonzales, G. J. Howlett, and D. Schubert. 2002. Size-distribution analysis of proteins by analytical ultracentrifugation: strategies and application to model systems. Biophys. J. 82:1096–1111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuck, P., and P. Rossmanith. 2000. Determination of the sedimentation coefficient distribution by least-squares boundary modeling. Biopolymers. 54:328–341. [DOI] [PubMed] [Google Scholar]
- Selkoe, D. J. 1996. Amyloidosis of Aβ 42 as the common pathogenetic mechanism of all forms of Alzheimer's disease. Neurobiol. Aging. 17:S37–S37. [Google Scholar]
- Sunde, M., and C. C. Blake. 1998. From the globular to the fibrous state: protein structure and structural conversion in amyloid formation. Q. Rev. Biophys. 31:1–39. [DOI] [PubMed] [Google Scholar]
- Walsh, D. M., A. Lomakin, G. B. Benedek, M. M. Condron, and D. B. Teplow. 1997. Amyloid beta-protein fibrillogenesis. Detection of a protofibrillar intermediate. J. Biol. Chem. 272:22364–22372. [DOI] [PubMed] [Google Scholar]
- Wang, C. S., D. Downs, A. Dashti, and K. W. Jackson. 1996. Isolation and characterization of recombinant human apolipoprotein C-II expressed in Escherichia coli. Biochim. Biophys. Acta. 1302:224–230. [DOI] [PubMed] [Google Scholar]
- Zimm, B. H. 1980. Chain molecule hydrodynamics by the Monte-Carlo method and the validity of the Kirkwood-Riseman approximation. Macromolecules. 13:592–602. [Google Scholar]