Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Apr;84(4):2619–2633. doi: 10.1016/S0006-3495(03)75067-X

A 2D-ELDOR Study of the Liquid Ordered Phase in Multilamellar Vesicle Membranes

Antonio J Costa-Filho 1, Yuhei Shimoyama 1, Jack H Freed 1
PMCID: PMC1302828  PMID: 12668470

Abstract

2D-ELDOR spectroscopy has been employed to study the dynamic structure of the liquid-ordered (Lo) phase versus that of the liquid-crystalline (Lc) phase in multibilayer phospholipid vesicles without (Lc) and with (Lo) cholesterol, using end-chain and headgroup labels and spin-labeled cholestane. The spectra are in most cases found to be dramatically different for these two phases. Thus, visual inspection of the 2D-ELDOR spectra provides a convenient way to distinguish the two phases in membranes. Detailed analysis shows these observations are due to increased ordering in the Lo phase and modified reorientation rates. In the Lo phase, acyl chains undergo a faster rotational diffusion and higher ordering than in the Lc phase, whereas spin-labeled cholestane exhibits slower rotational diffusion and higher ordering. On the other hand, the choline headgroup in the Lo phase exhibits faster motion and reduced but realigned ordering versus the Lc phase. The microscopic translational diffusion rates in the Lo phase are significantly reduced in the presence of cholesterol. These results are compared with previous studies, and a consistent model is provided for interpreting them in terms of the differences in the dynamic structure of the Lo and Lc phases.

INTRODUCTION

In biological membranes, a wide variety of lipids are contained in the bilayer structures. Although biomembranesconsist of many components in a liquid-crystalline (Lc)state,they can be approximated as a homogeneous phase only aftersome spatial-temporal averaging. When the homogeneous state is broken by some physico-chemical stimuli such asinteractions with ions, proteins, and sterols, heterogeneity frequently appears. That is, there is lateral phase separation, characterized by the formation of microdomains, which have been termed lipid rafts (Simons and Ikonen, 1997). Thus the raft model refers to the heterogeneity in biomembranes. One can alsofind domains in the model bilayer membranes of binary or ternary mixtures of lipids and cholesterol, where liquid-ordered (Lo) domains exist in equilibrium with the Lc phase (Brown and London, 1997, 1998; Feigenson and Buboltz, 2001).

Cholesterol, or its related sterol derivatives, is mainly found in plasma membranes of eukaryotic cells, where it can constitute as high as 50 mol% of the lipid composition (Bloom et al., 1991). It mainly functions as a passive modulator of the membrane (Bloch, 1995), altering membrane fluidity and enhancing order in the biomembranes (Singer and Nicholson, 1972). More recently, it has been appreciated that its presence leads to the Lo domains due to the specific interactions between cholesterol and lipids with at least one saturated acyl chain. These domains, or rafts in biological membranes, have been shown to be involved in transmembrane signal transduction (Field et al., 1995, 1997). It was found that when the concentration of cholesterol in the membrane is above 22 mol%, the membrane is transformed to the Lo phase (Ipsen et al., 1987). Membranes in the Lo phase have some special physical properties. As in the gel phase, acyl chains in the Lo phase are more ordered than in the Lc phase. However, both the translational and rotational rates of lipid molecules of the Lo phase are faster than that of the gel phase implying liquidlike fluidity. NMR measurements (Vist and Davis, 1990) have revealed that there are no shear-restoring forces in membranes in the Lo phase; thus, these membranes behave like a simple two-dimensional fluid (Bloom et al., 1991). In the absence of cholesterol, acyl chains in the Lc phase have a higher mobility, but with a lower ordering than in the gel phase. Therefore, the Lc phase is sometimes referred to as a “liquid-disordered” phase.

Early evidence for the existence of an Lo phase came from various experimental techniques. Using the TEMPO partitioning parameter evaluated from continuous-wave (cw) electron spin resonance (ESR) spectroscopy, the first phase diagram was established for a binary mixture of phospholipid and cholesterol (Shimshick and McConnell, 1973). Two coexisting phases were observed in ESR spectra from polar-headgroup spin labels incorporated in the lipid-cholesterol mixed membranes (Recktenwald and McConnell, 1981). Coexisting phases of Lc and Lo, and phase separation, were confirmed by fluorescence recovery after photobleaching (FRAP) (Rubenstein et al., 1979) and freeze-fracture TEM methods (Kleemann and McConnell, 1976).

Cw-ESR in macroscopically aligned model membranes of POPC and DMPC has shown that the rotational diffusion coefficient of the cholestane (CSL) probe decreased by a factor of 10 at 30 mol% of cholesterol concentration whereas its ordering significantly increased (Shin and Freed, 1989a; Shin et al., 1990). There was some indication that a phase separation occurred at higher cholesterol concentration in POPC (Shin and Freed, 1989b).

Using NMR and DSC methods, a phase diagram of a binary mixture consisting of perdeuterated DPPC and cholesterol was mapped out at the concentration range of 0–25 mol% of cholesterol (Vist and Davis, 1990). The diagram revealed an unknown phase, i.e., a β-phase, recognized later as the Lo phase and three distinct regions of two-phase coexistence.

Quasielastic neutron scattering experiments showed high-frequency cholesterol motion in the Lo phase in the oriented multibilayer membranes of binary mixtures of DPPC-cholesterol (Gliss et al., 1999). Highly anisotropic motions of cholesterol were detected in the frequency range of 1 GHz in the Lo phase, which is a timescale also relevant to ESR-spin labeling measurements.

The Lo phase has been reported in ternary and quaternary lipid mixtures of cholesterol-sphingomyelin-glycophospholipid membranes using ESR (Wolf and Chachaty, 2000) and wide- and small-angle x-ray scattering (Wolf et al., 2001). The ESR evidence of the Lo phase was somewhat indirect, but complementary x-ray data gave more direct proof. The ternary and quaternary mixtures of sphingomyelin-DPPC-cholesterol membranes showed two-component ESR spectra, indicating the existence of Lo phase and gel phase domains at high cholesterol concentration range (Veiga et al., 2001). This was observable by a lipid spin-labeled on the 14 position of the acyl chain. However, the peak separation of the two-component spectrum is not clear, so that spectral simulations are needed.

High-frequency ESR (Barnes and Freed, 1998; Freed, 2000) has shown considerable advantages in investigating the dynamic structure of membrane phases. 94 GHz ESR spectroscopy has revealed lateral lipid-chain ordering in the Lo phase, upon addition of cholesterol (Gaffney and Marsh, 1998; Livshits and Marsh, 2000). A multifrequency ESR approach using at least two microwave frequencies (e.g., 250 GHz and 9.5 GHz) enables the study of the dynamic structure of lipid membranes (i.e., the Lo versus Lc phase) to a greater precision (Lou et al., 2001). ESR at higher frequencies is more sensitive to the faster dynamic modes, whereas at lower frequencies ESR is more sensitive to the slower modes. This scheme revealed that upon addition of cholesterol, the acyl-chain motion is more restricted in its range of motion, but it is allowed to engage in faster motion, whereas the overall ordering and motion of the lipid molecule are only slightly affected.

We have developed a 2D-electron-electron double resonance (2D-ELDOR) methodology for measuring microscopic rotational and translational diffusion in lipid vesicle membranes, (Patyal et al., 1990, 1997; Gorcester et al., 1990; Crepeau et al., 1994; Borbat et al., 1997, 2001; Freed, 2000). This method provides enhanced spectral resolution for ordering and dynamics as compared to conventional cw-ESR. Cw-ESR spectra are inhomogeneously broadened by the macroscopic disorder characteristic of vesicles, as compared to macroscopically ordered membranes, thus enhancing the problem of ambiguity in the spectral analysis (Crepeau et al., 1994; Patyal et al., 1997). However, the 2D ELDOR lineshapes are much more informative, especially for the echolike 2D-ELDOR signal (Sc−) (Gamliel and Freed, 1990; Crepeau et al., 1994; Lee et al., 1994; Patyal et al., 1997; Freed, 2000; Borbat et al., 2001), since they enable one to better distinguish the homogeneous broadening (HB) (reporting on the dynamics) from the inhomogeneous broadening (IB) (reporting on the microscopic ordering). Furthermore, the off-diagonal peaks in 2D-ELDOR spectra, (i.e., the crosspeaks) are a measure of the magnetization transfer by spin relaxation processes during the mixing time (Tm). The growth of crosspeaks with increasing Tm provides qualitative and quantitative information on microscopic translational diffusion, via the relaxation mechanisms of spin exchange and intermolecular magnetic dipolar interactions, and on rotational diffusion via spin relaxation due to the intramolecular electron-nuclear dipolar (END) interaction of the nitroxide moiety.

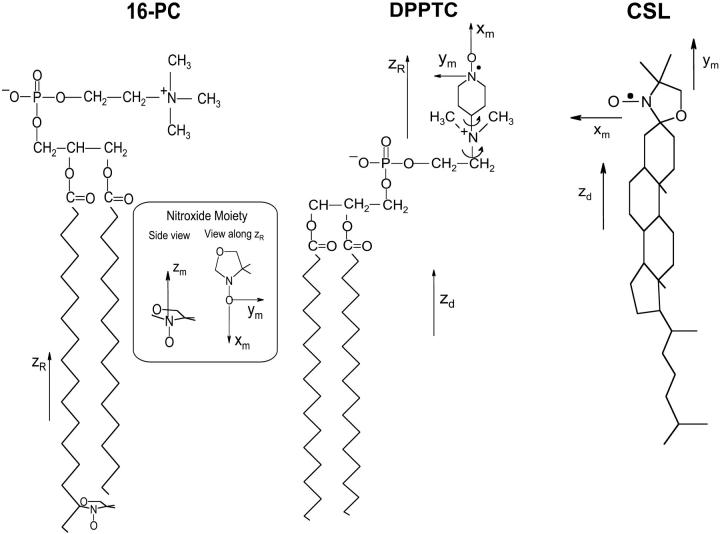
The primary objective of the present work is to characterize by means of 2D-ELDOR the Lo phase in membranes of DPPC-cholesterol and sphingomyelin-cholesterol, and to compare these results with the Lc phase in membranes of pure lipid. In the present report, we will show that just visual inspection of the 2D-ELDOR spectra is sufficient to allow one to distinguish the Lc and the Lo phases using the end-chain labeled lipid, 16-PC, and a spin-labeled cholesterol analog, CSL (cf. Fig. 1). These spin labels are in pure lipid vesicles in the Lc phase, as well as in vesicles of a lipid/Chol = 1/1 mixture, which is in the Lo phase. One observes that the crosspeaks, which exist in the 2D-ELDOR spectra from spin labels in the Lc phase, are quenched in those spectra from the Lo phase. Furthermore, there is more extensive IB clearly visible in the 2D spectral plane for those spectra from the Lo phase. This demonstrates that 2D-ELDOR is a powerful technique for identification of the phase structure of lipid membranes. In addition, we also make use of the headgroup label lipid DPPTC (cf. Fig. 1) in pure DPPC and DPPC/Chol vesicles to monitor the changes induced by the presence of cholesterol on the polar headgroup region of the bilayers.

FIGURE 1.

FIGURE 1

Open in a new tab

Chemical structures of spin labels 16-PC, CSL, and DPPTC showing the principal magnetic axes (xm, ym, zm). The reference frames given by zR used to define the rotational diffusion and ordering tensors are shown for each spin label. The zd axis is the normal to the bilayer surface.

We also present a quantitative analysis of the dynamic structure of the molecules in these phases by means of least-squares comparisons of the experimental spectra with theoretical simulations. The great spectral sensitivity provided by 2D-ELDOR to dynamic structure leads to reliable ordering and diffusional parameters to distinguish and compare the properties of the Lo and Lc phases. In addition, we compare our present results to those of previous studies of cholesterol-containing membranes (Ipsen et al., 1987; Shin and Freed, 1989a; Ge et al., 1999; Lou et al., 2001; Feigenson and Buboltz, 2001).

EXPERIMENTAL

Materials

The lipids 1,2-dipalmitoyl-sn-glycero-phosphatidylcholine (DPPC) and brain sphingomyelin (SM), and the spin labels 1-palmitoyl-2-(16-doxyl stearoyl) phosphatidylcholine (16-PC) and dipalmitoylphosphatidyl tempo (2,2,6,6,-tetramethyl-1-oxy) choline (DPPTC) were purchased from Avanti Polar Lipids (Alabaster, AL.). The spin label 3β-doxyl-5α-CSL, a cholesterol analog, and cholesterol were purchased from Sigma Chemical (St. Louis, MO.). All materials were used without further purification.

Preparation

Measured stock solutions of the lipids (DPPC or SM), cholesterol, and 16-PC in chloroform were mixed in a glass tube. The total weight of dried lipids was 2 mg, and the concentration of spin labels was 0.5 mol% of the lipids for all samples. Upon evaporation of the solvent by N2 flow, the lipids formed a thin film on the wall of the tube. Then, the samples were evacuated with a mechanical pump overnight to remove trace amounts of the solvent. After the addition of 2 mL of 50 mM Tris (pH 7.0), 160 mM sodium chloride, and 0.1 mM EDTA, the lipids were scraped off the wall, and the solution was stirred for 1 min and kept in the dark at room temperature for at least 2 h for hydration. Samples were then pelleted using a desktop centrifuge, and transferred to a 1.5-mm inner diameter capillary. The capillary was then placed into a glove bag and submitted to N2 purging for 3 h to deoxygenate the sample, thus removing additional sources of homogeneous broadening. The capillary was sealed with paraffin.

2D-ELDOR measurements

All experiments were carried out in the 2D-FT-ESR spectrometer at 17.3 GHz, as described elsewhere (Borbat et al., 1997). For 2D-ELDOR experiments, three 4-ns π/2 pulses were used. (cf. Fig. 2, inset). One collects the free induction decay signal after the third pulse as a function of time, t2. This is repeated for different settings of the time, t1, between the first two pulses, which is referred to as the preparation time. Fourier transforming (FT) with respect to t1 and t2 yields 2D-ELDOR spectra with respect to the respective frequencies f1 and f2 (cf. Fig. 2). This experiment is then repeated for several values of mixing time, Tm (i.e., the time between the second and third π/2 pulses), yielding a series of 2D-ELDOR spectra for each sample (cf. Fig. 2). This provides a third time variable for the 2D-ELDOR experiment.

FIGURE 2.

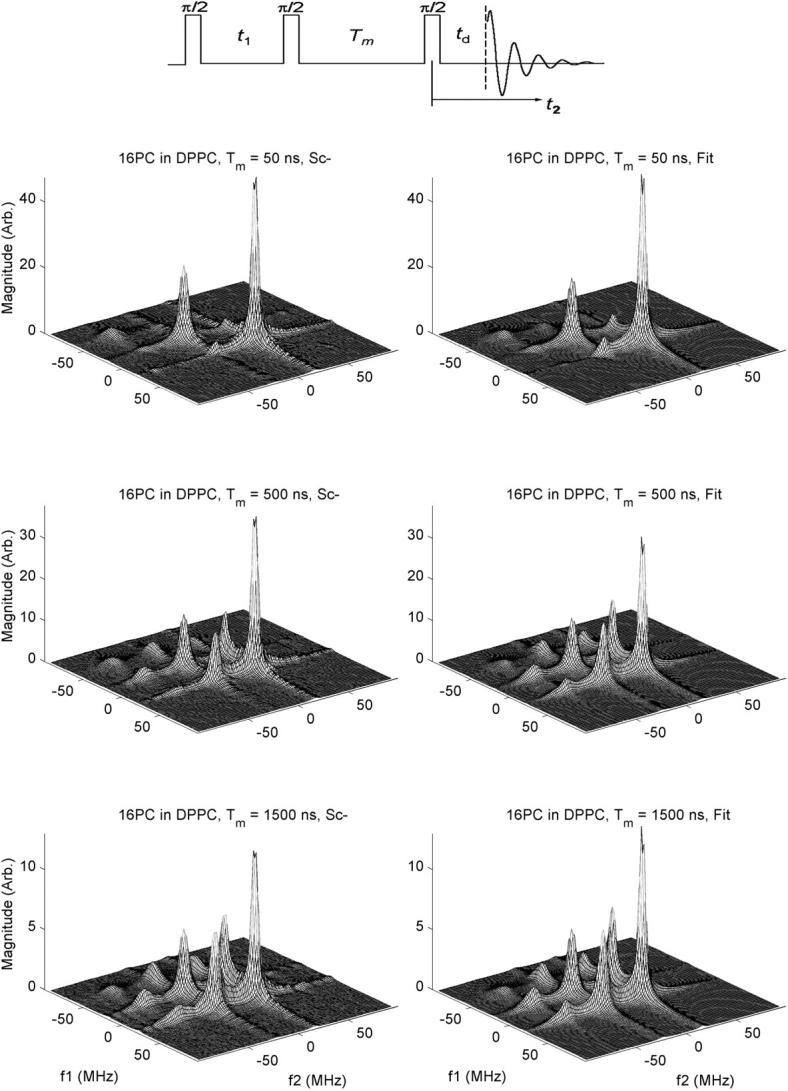
FIGURE 2

Open in a new tab

Experimental 2D-ELDOR spectra (left side) and their best-fit simulations (right side) for 16-PC in pure DPPC vesicles for values of mixing time Tm = 50, 500, and 1,500 ns. In the inset above are shown the three π/2 pulse sequence used for the 2D-ELDOR experiment as well as the relevant times: t1, t2, Tm, and td. The frequencies f1 and f2 are given relative to the applied microwave frequency.

We collected the free induction decay signal with a spectrometer dead time, td, of 35 ns for all samples. The preparation time, t1, was stepped out with 128 steps of 1 ns each, from an initial value of 35 ns. Each signal was collected as a function of t2 for a total of 256 complex data points with an effective step size in t2 of 1 ns. (This was achieved by automatically interleaving five separate collections, each sampled using 5-ns steps with appropriate ns time delays.) A 32-step phase cycling sequence (Patyal et al., 1997) was used to eliminate the unwanted signals such as the image peaks, transverse signals, and axial peaks. A full data collection for a single value oft1 consisted of 1000 averages for each of the 32-phase cycle steps. Acomplete 2D-ELDOR experiment took ∼60 min at a 10 kHz signal averaging rate. The experiment was repeated for three different values of Tm.

The full “hypercomplex” signal was collected. This refers to in-phase and out-of-phase spectral components with respect to both time variables t1 and t2 (or alternatively to their FT variables f1 and f2), which are then conveniently separated into two pairs of complex 2D spectra referred to as Sc+ and Sc− components (Gamliel and Freed, 1990; Crepeau et al., 1994). The Sc− component results from the coherence pathway that has echolike properties resulting in sharper 2D spectra and less signal decay during the dead time, so it was used in the subsequent analysis. We have used the magnitude spectra to avoid phase problems caused by the finite dead times and deviations from uniform coverage (Gorcester et al., 1990; Patyal et al., 1997).

The sample temperature was regulated using a gas flow-type cryostat with a commercial temperature controller (Bruker model ER4111VT), and it was kept close to 50°C.

Nonlinear least-squares simulations

The FT magnitude spectra were analyzed to obtain the ordering, and rotational and translational motional parameters. The simulation program consists of a nonlinear least-squares (NLLS) simultaneous fit of the Sc− spectra for the different Tm to models based on the Stochastic-Liouville theory for time domain ESR, (Schneider and Freed, 1989; Lee et al., 1994; Budil et al., 1996).

The simulation program makes use of the following coordinate systems to study the rotational dynamics and orientational ordering of the spin label. The first axis system is the laboratory frame, (xL, yL, zL), with its z axis being defined as the static magnetic field direction. The second coordinate frame is the bilayer orienting potential frame (xd, yd, zd), also called the local director frame, which has its zd axis parallel to the local bilayer normal. The third reference frame is the molecular rotational diffusion frame (xR, yR, zR) with the zR axis being the main molecular symmetry axis for the radical moiety. This is also taken as the molecular ordering frame for convenience, as well as usually by simple symmetry considerations. The fourth reference system is the magnetic tensor frame (xm, ym, zm) in which the g and A (or hyperfine) tensors are defined. The xm axis points along the N-O bond, the zm axis is parallel to the 2pz axis of the nitrogen atom, and ym is perpendicular to the others. The coordinate systems for each spin label used are shown in Fig. 1, where the spin label 16-PC is shown as a z-ordering nitroxide moiety, (i.e., its zm axis is parallel to zR), CSL as a y-ordering one, (i.e., ym ‖ zR), and DPPTC as an x-ordering one (i.e., xm ‖ zR). Thus, the order parameters obtained from the fit represent the degree of alignment of the spin-labeled lipid molecule.

The orienting potential in a lipid bilayer, U(Ω), can be expressed as an expansion in generalized spherical harmonics,

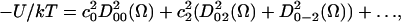graphic file with name M1.gif (1)

where Ω = (α,β,γ) are the Euler angles between the molecular frame of the rotational diffusion tensor and the local director frame. c02 and c22 are dimensionless potential energy coefficients, k is Boltzmann's constant, and T is the temperature.

The order parameter, S0, is defined as

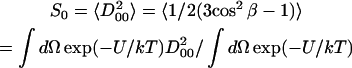graphic file with name M2.gif (2)

and measures the angular extent of the rotational diffusion of the nitroxide moiety. Thus, a large value of S0 indicates very restricted motion. Another order parameter, S2 = 〈D022 + D0−22〉, is defined in a similar way and represents the deviation from axial symmetry of the molecular alignment relative to the local director. (Here, DMKL(Ω) is a Wigner rotation matrix element). The order parameters are thus used to express the local (microscopic) ordering of lipid molecules in the macroscopically disordered membrane dispersions. The structure of the lipid dispersion, where locally the lipid molecules are aligned along a preferential axis, but globally the lipid bilayer segments are oriented randomly, gives rise to the so-called MOMD (Microscopic Order and Macroscopic Disorder) model (Meirovitch et al., 1984; Budil et al., 1996). The fitting program accounts for MOMD by treating the final simulated spectrum as a superposition of the spectra from all fragments (Patyal et al., 1997; Lee et al., 1994).

The rotational mobility of the spin-labeled lipids is characterized by rotational diffusion constants, R⊥ and R‖, which represent the principal values of an axially symmetric rotational diffusion tensor. They represent the rotational rates of the nitroxide moiety around axes perpendicular and parallel, respectively, to the main symmetry axis of the radical z′ axis. Hence, for 16-PC, R⊥ and R‖ are the rotational motion about axes perpendicular and parallel to the long hydrocarbon chain of the lipid molecule, whereas for CSL, R⊥ is the wagging motion of the long molecular axis (Fig. 1). For the headgroup labeled DPPTC, R⊥ represents the rotational motion of the nitroxide headgroup (Ge and Freed, 1998). The translational mobility is characterized by the Heisenberg exchange frequency, ωexc, which measures the rate of bimolecular encounters of the labeled molecules.

The first step in the NLLS was to choose reasonable starting values for the ordering (S0 and S2) and rotational (R⊥ and R‖) parameters (Patyal et al., 1997). During the simulations, we varied either 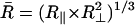Inline graphic and N = R‖/R⊥ (Patyal et al., 1997; Shin and Freed, 1989a) or equivalently R⊥ and R‖. Such transformations of the representation of the rotational diffusion tensor are necessary in the least-square fittings to avoid high correlations between the components (Budil et al., 1996). To ensure that a global minimum was reached, and to avoid local minima, we restarted the fitting procedure with several sets of seed values. The hyperfine (hf) and g tensors needed for the fits were previously determined by cw simulations of rigid limit spectra (Ge et al., 1999; Ge and Freed, 1998; Barnes and Freed, 1998). Additional fitting parameters included Gaussian IB as well as a Lorentzian homogeneous width contribution, (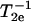Inline graphic), representing additional broadening mechanisms.

RESULTS

Features of 2D-ELDOR spectra

We show in Fig. 2 2D-ELDOR Sc− spectra for the case of 16-PC in pure DPPC vesicles for three different mixing times, Tm. On the left side we show the experimental results; on the right side are the NLLS fits. In the upper set, for Tm = 50 ns, which is quite short, only the so-called auto peaks are clearly seen. They are along the diagonal, corresponding to f1 = f2. Because of slow motional effects, these auto peaks are fairly broad, and they exhibit a substantial variation in width (hence in amplitudes, which go inversely with the widths along both the f1 and f2 axes). Thus the sharpest and most intense auto peak appears at the highest frequency of f1 = f2 ≅ 15 MHz. (This high-frequency peak is, in cw-ESR, the low-field peak). The middle auto peak at f1 = f2 ≅ −25 MHz is broader and less intense. The lowest frequency auto peak is at f1 = f2 ≅ −65 MHz, and is so weak that it is hardly visible at the magnification shown in Fig. 2. (These frequencies are given relative to the applied microwave frequency). This corresponds to the well-known feature of cw-ESR spectra of nitroxides in membranes, (e.g., Ge et al., 1999) that the high-field line is significantly broader than the others. In fact, this effect is enhanced at 17.3 GHz used in this study compared to ∼9.3 GHz used in most cw-ESR studies, due to the increased role of the g tensor in the broadening. Furthermore, in 2D-ELDOR, intensity variations of the spectral lines are increased, because the broader the line, the faster is its T2 decay. Therefore, the broadest auto peak loses relatively more intensity during the finite dead time, td (cf. Fig. 2, inset), during the pulse sequence. (In fact, in simulations of these 2D-ELDOR spectra where td has been set equal to zero, this low frequency and broad auto peak is clearly seen).

In addition, we note that these 2D auto peaks are inhomogeneously broadened by the MOMD effect discussed in the previous section, which is known to affect the low-frequency peak (i.e., the high-field line in cw-ESR) the most. In summary, the 3 hf line pattern of conventional (first derivative) ESR is seen along the f1 = f2 diagonal of the 2D-ELDOR spectrum as the (absorption) auto peaks, plus there are additional modifications compared to cw-ESR.

For the longer Tm's, of 500 and 1500 ns, new features appear for f1 ≠ f2, i.e., off the f1 = f2 diagonal. They result from transfer of the spins from one hf line to another during the mixing time, Tm, due to either 14N nuclear spin flips induced by rotational modulation of the END interaction or by Heisenberg spin exchange (HE) between colliding nitroxide radicals as they diffuse in the membranes (Gorcester et al., 1990; Patyal et al., 1997). One observes in Fig. 2 how these “crosspeaks” grow in as Tm increases, and this is a measure of these two cross-relaxation (or exchange) processes. They are, in general, distinguishable by virtue of their different “selection rules,” viz. END interactions lead to crosspeaks predominantly between adjacent auto peaks (so-called ΔMI = ±1 crosspeaks), whereas HE leads to crosspeaks between all auto peaks (i.e., ΔMI = ± 1 and ± 2) with equal probability. They are also discriminated by their well-known different contributions to the hf line widths. These crosspeaks are most prominent for the largest Tm of 1500 ns.

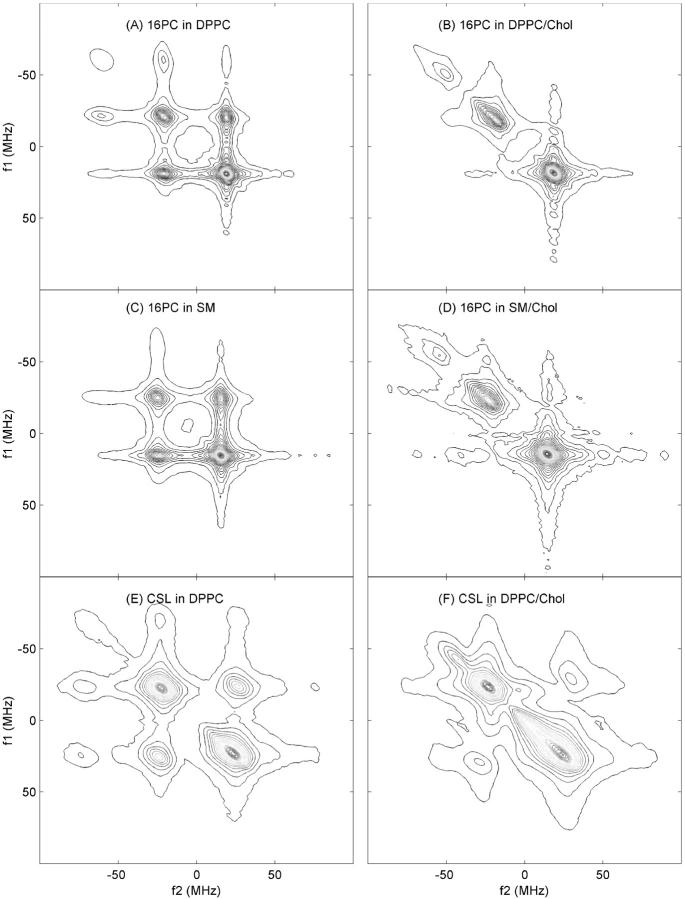
In Fig. 3, we show contours of the 2D-ELDOR Sc− spectra for 16-PC in DPPC (Fig. 3 A), 16-PC in SM (Fig. 3 C), and CSL in DPPC (Fig. 3 E), all for Tm of 500 ns. All the three auto peaks and six crosspeaks are evident in Fig. 3 A (with the ΔMI = ± 2 crosspeaks the weakest) as well as in Fig. 3 E, but in Fig. 3 C the resolution of the contours is insufficient to see all nine peaks. These contour plots on the left panels of Fig. 3 are from pure lipid dispersions (Lc phase). The right side of Fig. 3 shows the spectra from 16-PC and CSL in equimolar mixtures of lipid and cholesterol (Lo phase). One observes that the Lo phase yields 2D-ELDOR spectra that are qualitatively different from those from the Lc phase, and this enables one to characterize the phase of the sample just by visual inspection. Since the differences in the spectra from the Lc versus Lo phases are enhanced at substantial Tm, we show in Fig. 3 those for Tm = 500 ns.

FIGURE 3.

FIGURE 3

Open in a new tab

Contour plots of the 2D-ELDOR spectra at 17.3 GHz, mixing time Tm = 500 ns, T = 50°C, for the Lc phase (left) and Lo phase (right) of: (A) 16-PC in pure DPPC; (B) 16-PC in DPPC/Chol; (C) 16-PC in pure SM; (D) 16-PC in SM/Chol; (E) CSL in pure DPPC; (F) CSL in DPPC/Chol vesicles.

From a qualitative comparison of these Lc and Lo spectra, we can discern key features between them. However, let us first compare the results of Fig. 3, A, C, and E, for pure lipid. The similarity of Fig. 3, A and C, indicates that the dynamic structure of 16-PC in DPPC and in SM vesicles is quite similar, but the spectrum of CSL in DPPC in Fig. 3 E shows quite different behavior in that the 2D spectral lines are much broader. The sharp peaks observed in the 16-PC spectra in the Lc phase result from the substantial motional averaging out of the effects of the hf and g tensor terms in the spin Hamiltonian, as expected for a label at the end of the acyl chain. That is, one expects relatively rapid end-chain fluctuations that are relatively unhindered in their motion, (i.e., very low ordering). On the other hand, the rigid sterol moiety CSL should show slower motions that in addition are restricted by adjacent molecules resulting in significantly greater microscopic ordering. Both these factors will yield broader spectra. The dominant effect here (that follows from the quantitative analysis given below) is the effect of increased ordering that leads to IB by the MOMD effect, i.e., the large ordering leads to substantially different spectra for each orientation of the locally ordered lipid with respect to the magnetic field, but all orientations are present in the macroscopically disordered (or unaligned) vesicle sample.

When we now compare the Lc with Lo phase spectra (i.e., Fig. 3, A with B, C with D, and E with F), we observe much broader 2D spectra as well as the effective loss (or suppression) of crosspeaks for the Lo phase. The much broader peaks result from significantly increased ordering (plus the MOMD effect as just described) in the Lo phase. This MOMD-induced IB is observed to have the following effect, which is most prominent in Fig. 3 F. The broadening of the auto peaks along the f1 = f2 diagonal is significantly greater than that perpendicular to it. This arises because, along f1 = f2, one sees the “normal” ESR spectrum with all its inhomogeneous (and homogeneous) broadening, whereas in the orthogonal direction, the echolike properties of the Sc− 2D-ELDOR noted above leads to suppression of inhomogeneous (but not homogeneous) broadening. This interesting feature is confirmed by the detailed simulations described below, and shown in Fig. 4. The loss of crosspeaks in the Lo phase is also due, in part, to the increased ordering, as we describe in more detail in the Discussion.

FIGURE 4.

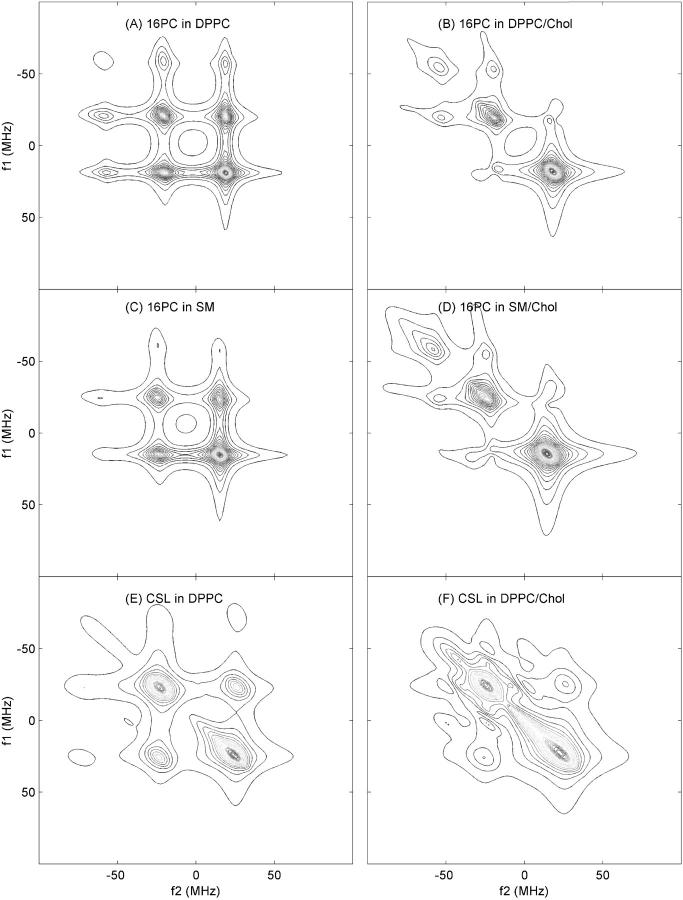
FIGURE 4

Open in a new tab

Contour plots of the best NLLS fits to the experimental 2D-ELDOR spectra shown in Fig. 3. The plots A–F correspond to the same cases as in Fig. 3.

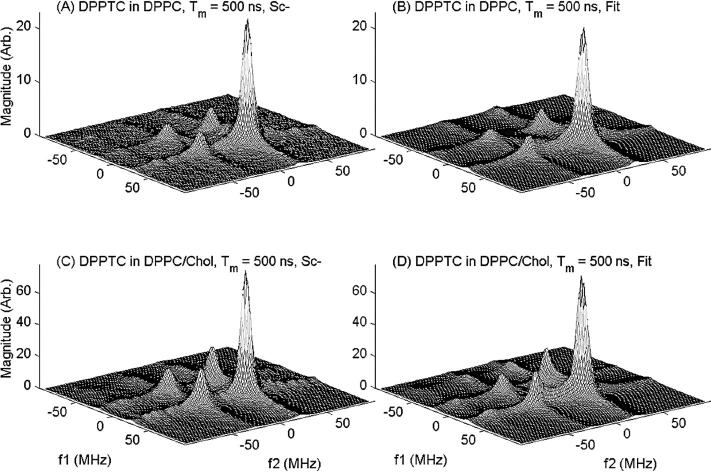
The 2D-ELDOR spectra of the headgroup spin label DPPTC is the only case that does not show significant qualitative differences between the Lc and the Lo phases, (cf. Fig. 5), but there are differences in detail. For example, one observes a more rapid growth of the crosspeaks with Tm in the spectra from the Lo phase, which is the reverse behavior to that of the other cases discussed above. The interpretation of these smaller differences between Lo and Lc cases is best left to the quantitative spectral analyses.

FIGURE 5.

FIGURE 5

Open in a new tab

Experimental 2D-ELDOR spectra (left side) and their best-fit simulations (right side) for DPPTC in pure DPPC vesicles (A and B) and in 1:1 DPPC/Chol vesicles (C and D) for a mixing time of 500 ns.

We turn now to the NLLS fitting of these 2D-ELDOR Sc− spectra, which quantifies these aspects of dynamic structure and confirms the qualitative descriptions.

2D-ELDOR simulations for Lo and Lc phases

Simulations and NLLS fitting of 2D-ELDOR Sc− spectra from the spin labels 16-PC, CSL, and DPPTC in DPPC and DPPC/Chol mixtures, as well as 16-PC in SM and SM/Chol, were performed as described above. We show in Fig. 2 a comparison of experimental and simulated spectra for 16-PC in DPPC as a function of mixing time. In Fig. 4 we show the best fit simulated contours plots for the experimental ones shown in Fig. 3. The remaining case of the DPPTC headgroup label is shown in Fig. 5.

Table 1 lists the best-fit parameters obtained from the NLLS fits to all spectra measured for the different mixing times, Tm. Indeed, we find that the results of Table 1 both confirm and quantify the qualitative observations of the previous subsection and provide further insights. Thus it is clear from Table 1 that the motions of the acyl-chain label 16-PC are faster in the Lo phase than in the Lc phase, with an increase in R⊥ by a factor of two to three. This means that lipid acyl chains are more fluid in the presence of higher concentration of cholesterol. The order parameter of 16-PC in the Lo phase is substantially greater than in the Lc phase. These are typical features of the dynamic molecular structure of bilayers in the Lo phase as reported previously (Ipsen et al., 1987; Shin and Freed, 1989a; Ge et al., 1999). The increase in the ordering leads to the increased broadening of the auto peaks resulting from the MOMD model as described above. Thus, from the acyl-chain point of view, the Lo membranes are characterized by two apparently opposite physical properties: high ordering and a very fluid lipid phase (Straume and Litman, 1987; Ge et al., 1999). Also, a greater exchange rate (ωexc = 2.6 × 106 s−1) is found in the pure DPPC/16-PC membranes, due to the greater microscopic translational diffusion motion for the Lc phase than that for Lo phase. This is another factor that slows the development of crosspeaks in the spectra obtained from the cholesterol-enriched vesicles.

TABLE 1.

Parameters obtained from the NLLS fits for 16-PC, CSL, and DPPTC spin labels in pure DPPC and DPPC/Chol vesicles at 50°C

Sample R⊥ (× 108 s−1) R‖ (× 109 s−1) S0 S2 ωexc (× 106 s−1)
DPPC/16-PC* 2.5 7.5 0.16 −0.28 2.6
DPPC/Chol/16-PC* 4.4 9.0 0.41 −0.30 —§
SM/16-PC* 2.1 1.7 0.16 −0.17 1.8
SM/Chol/16-PC* 6.8 3.1 0.43 −0.23 —§
DPPC/CSL† 0.36 0.80 0.75 0.03 4.5
DPPC/Chol/CSL† 0.14 0.21 0.90 0.01 0.2
DPPC/DPPTC‡ 0.11 0.49 0.75 —§ 4.8
DPPC/Chol/DPPTC‡ 0.76 4.7 0.53 −0.19 —§
Open in a new tab
*

Magnetic parameters for 16-PC: Axx = Ayy = 5.0 G; Azz = 33.0 G; gxx = 2.0089; gyy = 2.0058; gzz = 2.0021 (Ge et al., 1999); diffusion tilt: ϕ = 31° (Patyal et al., 1997).

†

Magnetic parameters for CSL: Axx = 4.9; Ayy = 5.5; Azz = 33.1; gxx = 2.0087; gyy = 2.0057; gzz = 2.0021 (Barnes and Freed, 1998).

‡

Magnetic parameters for DPPTC: Axx = 5.6; Ayy = 5.6; Azz = 34.6; gxx = 2.0082; gyy = 2.0053; gzz = 2.0015 (Ge and Freed, 1998).

§

Very small values, so kept fixed at 0.

Estimated errors: R⊥ (5%), R‖ (10%), S0 (1%), S2 (1%), ωexc (10%).

The simulation parameters for sphingomyelin membranes with and without cholesterol show an overall similar behavior in their rotational diffusion rates and order parameters as observed for DPPC-containing bilayers (Table 1). Thus, liquid ordered phases in both SM and DPPC membranes can be characterized in a very similar manner, as we previously suggested.

The rotational diffusion rates for CSL in the lipid vesicles are much smaller than those for 16-PC, irrespective of the presence of cholesterol, as expected (Shin and Freed, 1989a). This is readily ascribed to the internal acyl-chain motions, which are greatest at the end of the chain (Cassol et al., 1997; Lou et al., 2001). Unlike 16-PC, the presence of cholesterol slows down the rotational motion of CSL as inferred from the values of R⊥ and R‖ in Table 1. This is in good agreement with previous observations on oriented membranes (Shin et al., 1990), that CSL undergoes slower motion in cholesterol-rich membranes. In the presence of cholesterol, the order parameter of CSL increases to as high as So = 0.90.

The HE rate (ωexc) as obtained from our simulations yielded similar values for both 16-PC and CSL in the Lc phase of pure DPPC membranes. This means that the microscopic collision rates between the lipids or between cholesterol molecules are essentially the same, as a result of 2D lateral diffusion. In the Lo phase the HE was greatly suppressed for the lipid-cholesterol membranes as monitored by both labels. It seems that the tighter packing of lipid and cholesterol molecules in the Lo phase discourages collisions between the nitroxide radicals attached to the glycerolipids and the cholestanes. This is consistent with observations of macroscopic diffusion being reduced in the presence of substantial cholesterol by FRAP (Rubenstein et al., 1979) and by dynamic imaging of diffusion ESR (Shin and Freed, 1989a; Shin et al., 1990; Freed, 1994). (As ωexc decreases, due to increased microscopic viscosity, the effect of intermolecular dipolar interactions between nitroxides should increase (Lee et al., 1994). There is some indication of this in the expected increase in the residual homogeneous line broadening, represented by T2e−1, that we observe in nearly all cases in the Lo phase.)

The behavior of the polar headgroup probed by the DPPTC spin label and reflected in the 2D-ELDOR would appear to be only modestly different in the presence of cholesterol when compared to the results obtained from the acyl-chain region, since no large differences in the Lo versus Lc phase spectra were observed by visual inspection as noted above. However, NLLS fits to these data reveal that a substantial increase in the rotational diffusion rates as well as a modest decrease in the local ordering of the DPPTC spin label are induced upon addition of cholesterol. This is in agreement with results from cw-ESR (Ge et al., 1999; Tanaka et al., 1997) and dielectric relaxation studies (Henze, 1980). The spacer effect of cholesterol molecules has been suggested for the weakening of the interactions between headgroups (Yeagle al., 1975; McIntosh et al., 1989). The results of exchange rates in the headgroup region also follow the same behavior observed for 16-PC and CSL (cf. Table 1), as would be expected.

DISCUSSION

Presence and absence of crosspeaks in 2D-ELDOR spectra

A prominent feature of the 2D-ELDOR spectra that is qualitatively different for the Lc and Lo phases is the presence of substantial crosspeaks for the former and its absence for the latter, (cf. Figs. 3 and 4). This enables one to make qualitative distinctions between these two phases from just the patterns of the 2D-ELDOR spectra, as we have already pointed out.

In all cases illustrated in Figs. 3 and 4, we find from Table 1 that the ordering is increased in the Lo phase over that in the Lc phase. This increase in microscopic ordering is one reason for the suppression of the crosspeaks in the Lo phase. As a result of this increased ordering, the range of orientational motion is more restricted in the Lo phase. This reduces the effectiveness of the rotational modulation of the anisotropic hf interaction to induce 14N nuclear spin flips that transfer the spins from one hf line to another, which is a key process yielding crosspeaks as discussed earlier. In the cases of 16-PC in DPPC and in SM, the increased rotational diffusion rate in the Lo phase (cf. Table 1) is a key factor in reducing the rate of 14N nuclear spin flips arising from rotational modulation of the hf interaction. (For the case ofCSL with its much slower rotational diffusion rates, anincrease in these rates in the Lo phase (cf. Table 1) will also reduce the rate of nuclear spin flips, WN. That is, approximate theory gives WN ∝ (1 − S02) τ⊥/(1 + τ⊥2ωN2), where τ⊥ = 1/6R⊥ and ωN, the nuclear Larmor frequency is ∼2π × 40 MHz = 2.6 × 108 s−1 (Saxena and Freed, 1997b). Thus for 16-PC, τ⊥2ωN2 ≪ 1, whereas for CSL it is ≥ 1, and the maximum in WN occurs for τ⊥2ωN2 = 1.) In addition, we also see from Table 1 that the other dynamic process contributing to crosspeak development, viz. the ωexc, is also suppressed.

There is another factor that reduces the amplitudes of the crosspeaks, also attributable to the increase in microscopic ordering: i.e., the increased IB resulting from the MOMD effect that we have previously discussed. We noted that intheSc− 2D-ELDOR spectra, there is partial suppression ofIB of the auto peaks due to their echolike properties. However, since the IB due to MOMD is different for the different hf lines, and the crosspeaks result from magnetization transfer between different hf lines, then the echolike cancellation is less effective for these peaks. Thus the increase in IB resulting from the increased ordering in the Lo phase will reduce the amplitudes of these crosspeaks relative to the auto peaks. Furthermore, the reduced suppression of IB leads to their faster decay during the dead-time period. This is borne out by simulations (not shown) of the 2D-ELDOR spectra expected for zero dead time, td. In these simulations, the crosspeaks are indeed relatively more prominent than in the experimentally relevant case of finite, but small, td (= 35 ns.).

In addition, as we previously discussed, the 2D-ELDOR Sc− spectra from the Lo phase show the characteristic increased IB of the auto peaks with reduced broadening along the spectral direction orthogonal to the f1 = f2 diagonal, which enhances the qualitative differences between the spectra from the Lo and Lc phases.

The subtle interplay of relaxation processes, homogeneous and IB mechanisms, and their effects on the shapes of auto- and crosspeaks is most effectively disentangled by means of NLLS fitting of the 2D spectral data as shown above.

Dynamic structure of Lo phase

A partial phase diagram for DPPC/Chol (Vist and Davis, 1990) and theoretical modeling of the phase diagram (Ipsen etal., 1987) indicate that at cholesterol concentrations above ∼22 mol%, the membrane is in an Lo phase. This phase has been defined by a contradictory concept, i.e., “fluid yet ordered” (Feigenson and Buboltz, 2001). Therefore, we discuss the Lo phase through these ordering and fluidizing effects.

Ordering

The addition of cholesterol accelerates the acyl-chain orientational ordering. This has been observed by various physical techniques, including D-NMR, x-ray diffraction, fluorescent spectroscopy, and ESR. In the present study, the order parameters measured by 16-PC as well as CSL in the Lo phase yielded substantially greater values than in the Lc phase. The ordering effect is due to the strong van der Waals interactions between acyl chains and the planar rings of the rigid sterol backbone of cholesterol, which may reduce gauche conformers in acyl chains. The rigidity of the cholesterol clearly makes it more effective in restricting the range of acyl chain motion than would neighboring lipids with flexible acyl chains.

Fluidity: rapid acyl-chain fluctuations

In the Lo phase, acyl chains are fluidized by the presence of cholesterol. This has been observed by a variety of techniques, such as fluorescence (Straume and Litman, 1987), FRAP (Rubenstein et al., 1979), D-NMR (Vist and Davis, 1990) and ESR (Lou et al., 2001). Our 2D-ELDOR measurements show that the motions of the acyl-chain label 16-PC are faster in the Lo phase than in the Lc phase. On the other hand, the cholesterol label CSL undergoes a slower motion when packed together in the Lo phase. We interpret the first observation as due to less friction on the acyl chain from an adjacent rigid cholesterol molecule versus the “rubbing” effect of an adjacent fluctuating acyl chain. In this way, an adjacent cholesterol can restrict the range of internal motion of the acyl chains and yet allow faster motion within this restricted range. However, the second observation shows that the overall motion is affected differently. Rigid cholesterols obviously do inhibit the overall motional rates of their neighbors. This interpretation bears some similarity to the result of the recent multifrequency ESR study (Lou et al., 2001), where it was shown that the overall motional rates and ordering of 16-PC in the Lo phase are differently (i.e., less) affected by cholesterol than the acyl-chain motions. Of course, in the case of the rigid CSL, there is no internal motion, only overall motion that can reorient the nitroxide moiety.

Reorientation of the headgroup in the Lo phase

The DPPTC spin label exhibits a different behavior for the polar headgroup of DPPC versus the acyl-chain region. There are three main effects on the headgroup by the presence of cholesterol that we observed. First, a decrease was detected in the local ordering of the spin label headgroup upon addition of cholesterol. A disordering of the headgroup upon addition of cholesterol was previously observed by nuclear Overhauser experiments, suggesting that cholesterol disrupts the molecular interactions between headgroups (Yeagle et al., 1975). Second, the rotational diffusion rates increase substantially in the presence of cholesterol in agreement with previous cw-ESR (Ge et al., 1999; Tanaka et al., 1997) and dielectric relaxation studies (Henze, 1980). It is consistent with reduced interactions between headgroups yielding reduced friction to motion. Third, the headgroup of DPPC with x-ordering (cf. Fig. 1) in the Lc phase realigns somewhat. This is likely also due to the spacer effect of cholesterol that weakens the interactions between headgroups. (Yeagle et al., 1975; McIntosh et al., 1989). The nature of this realignment is clarified by transforming the traceless ordering tensor given by S0 and S2 to its Cartesian form: Sxx, Syy, and Szx (Schneider and Freed, 1989). Here by x, y, and z we mean the magnetic tensor frame (cf. Fig. 1), but we have dropped the m subscript for convenience. In this notation, we have in the Lc phase that Sxx = 0.75 and Syy = Szz = −0.38. But in the Lo phase Sxx = 0.53, Syy = −0.50, and Szz = −0.03. This corresponds to reduced alignment of the magnetic x axis along the bilayer normal (zd in Fig. 1), but the magnetic y axis is now well-aligned in the plane perpendicular to zd. (This arrangement still allows for the rapid internal rotation of the nitroxide-bearing moiety as depicted in Fig. 1 and observed in Table 1). In fluorescence spectroscopy using dipyrene-PC as a probe, the excimer/monomer ratio showed that headgroup realignment of DPPC was induced by addition of cholesterol (Feigenson and Buboltz, 2001). Our finding of headgroup realignment of DPPTC supports the so-called umbrella model suggested by Huang and Feigenson (1999) in which the PC headgroup shields the added cholesterol from the aqueous phase.

Overall view: synergism

Samsonov et al. (2001) have shown that domain formation, such as raft formation, is headgroup dependent, i.e., saturated PE or PS do not substitute for PC or SM. This most likely means that the zwitterionic character of PC and SM is more favorable for the Lo phase than charged headgroups (e.g., PE and PS). As cholesterol is inserted, it functions as a spacer (Feigenson and Buboltz, 2001). Thus, the interlipid separation increases, and the headgroup can reorient more freely. Simultaneously, cholesterol preferentially packs the saturated acyl-chain lipids and induces higher ordering. Therefore, interactions with the headgroup stabilize the associations between saturated sphingolipids or DPPC and cholesterol, thus creating Lo rafts (Simons and Ikonen, 2000). All of our 2D-ELDOR observations on the dynamic structure of the Lo phase are consistent with such a synergistic behavior involving both the headgroups and the acyl chains.

A comparison of 2D-ELDOR and cw-ESR studies

In the Results section, as well as in earlier subsections of the Discussion, we have noted comparisons between our 2D-ELDOR results and those from cw-ESR studies. In general, these comparisons have shown qualitative agreement between these two versions of ESR spectroscopy. We now present more detailed comparisons. However, we emphasize that cw-ESR spectra do not exhibit the same dramatic sensitivity to differences in dynamic structure of Lo versus Lc phases that we have found in the 2D-ELDOR spectra. This generally poorer resolution for cw-ESR spectra renders their interpretation more ambiguous than for 2D-ELDOR spectra, especially for membrane vesicles exhibiting the MOMD effect (Patyal et al., 1997).

One way to improve cw-ESR resolution is to employ macroscopically aligned membranes (Shin and Freed, 1989a,b; Shin et al., 1990; Ge et al., 1994; Freed, 1994). These can be analyzed with high reliability (Budil et al., 1996), so they are appropriate for comparison. However, the morphology of these aligned membranes is known to be somewhat different from that of vesicles (Ge and Freed, 1998), so this limits their utility. The best comparisons for our present purposes are with fully hydrated aligned membranes (∼24% water by weight). Shin et al. (1993) studied oriented samples of CSL in DMPC and in DMPC/Chol = 3/2 at ∼50°C. They obtained results that are remarkably close to the values found in the present work with DPPC vesicles. (Their values of S0 = 0.54, R⊥ = 0.32 × 108 s−1, R‖ = 0.63 × 109 s−1 in DMPC, and S0 = 0.89, R⊥ = 0.13 × 108 s−1, and R‖ = 0.13 × 109 s−1 for DMPC/Chol are very close to those in Table 1 except for the larger S0 of 0.75 for pure DPPC). This comparison suggests that the CSL probe is not very sensitive to morphological differences that might be present in the two types of sample. Results for 16-PC in fully hydrated and macroscopically aligned DMPC membranes exist (Cassol et al., 1997) but not in DMPC/Chol. These results are somewhat different (S0 = 0.10, R⊥ = 5.7 × 108 s−1, and R‖ = 1.9 × 109 s−1) than those in Table 1 for DPPC, a fact that may reflect the shorter 14 carbon acyl chains of DMPC than those of the 16-PC, i.e., the end chain of the spin label is less hindered and more mobile.

Ge et al. (1999) in their study of the Lo phase of detergent-resistant membranes from RBL-2H3 cells utilized reference studies with DPPC and SM pure vesicles and DPPC vesicles containing cholesterol. In their fitting of the cw-ESR spectra, they attempted to at least partially overcome the ambiguity of these spectra (resulting from their more limited resolution to dynamic structure) by studying some of the samples over a range of temperatures and requiring consistency in fitted parameters versus temperature. Their results for 16-PC in DPPC and DPPC/Chol = 1 at 50°C were fit with substantially lower ordering, as well as faster motion in the case of pure DPPC than the results in Table 1. Nevertheless their work did show the substantial increase in S0 in the Lo versus the Lc phase. In comparisons with results from the detergent-resistant membranes, representing a Lo phase, but at 20° or 37°C, they find CSL to be more ordered and the headgroup label SD-Tempo less ordered in the Lo phase, which is similar to our observations. Also, SD-Tempo did show a greater R⊥ in the Lo phase but the trend in R⊥ for CSL was the reverse of what we found. Thus the qualitative picture that emerges from that work is similar to that of the present study with differences in detail.

Tanaka et al. (1997) used VO2+ ions to study headgroup dynamics in DPPC and DPPC/Chol lipid dispersions. They found that the VO2+ ions bind tightly to the phosphate group. They used a simplified slow-motional analysis wherein they fit the cw-ESR spectra to a single average rotational diffusion coefficient, R, and ignored microscopic ordering. However, we have clearly seen the importance of the MOMD effect in the 2D-ELDOR spectra. Nevertheless, they find a small increase in R when cholesterol is added, and their values are close to what we obtained for R⊥ of DPPTC in DPPC/Chol vesicle membranes.

Wolf and Chachaty (2000) have studied 5- and 16-labeled doxyl stearic acids in lipid mixtures containing SM (plus glycophospholipids) with and without cholesterol. They analyzed their cw spectra in terms of the stochastic Liouville theory, (Schneider and Freed, 1989; Budil et al., 1996). For 16-SA spin label they report two components, one with S0 = 0.40 (gellike SM regions) and the other with S0 ≈ 0.1 (fluidlike glycophospholipid regions) at 37°C. Addition of cholesterol yields just a single component with S0 = 0.27 as well as an increased motional rate (they assumed an isotropic diffusion tensor). Although their results on mixed lipid systems cannot be directly compared with the present study, they do illustrate that the results from lipid mixtures can be somewhat different from those of pure lipids.

Veiga et al. (2001) also studied the effect of cholesterol on lipids and lipid mixtures using chain-labeled lipids, but they just utilized a simple feature in their analysis, (viz. the differences in outer hyperfine splitting) permitting only a qualitative discussion. With 14-PC they could discern two components at 4°C in SM/Chol and SM/PC/Chol whereas only a single component is present in the absence of cholesterol. They interpret this as due to a cholesterol-poor gel phase and a cholesterol-rich Lo phase in coexistence. A more quantitative analysis would be desirable to clarify the observations in that study. One may expect 2D-ELDOR studies could be of help in this regard.

High-frequency ESR provides considerable advantages that arise in part from its improved orientational resolution as compared to ESR at conventional frequencies, e.g., 9 GHz (Barnes and Freed, 1998; Freed, 2000). Gaffney and Marsh (1998) and Livshits and Marsh (2000), working at 94 GHz, have shown the very substantial lineshape variations obtained from placing spin labels at different positions along the acyl chain in DMPC vesicles and by adding cholesterol (at 22°C). Livshits and Marsh (2000) have employed simplified analyses to provide preliminary interpretation. Comparisons between vesicle membranes with DMPC/Chol ratios of 3:2 versus pure DMPC are not so clear in their work, since different spin labels are used in both cases. However, their general conclusion that cholesterol causes in-plane ordering of the lipid chains is consistent with our results, although their analysis did not directly yield order parameters. Their estimate of an assumed isotropic R for 16-SA spin label in DMPC is only a little larger than our result for R⊥ for 16-PC in DPPC.

Lou et al. (2001) have studied the spectra from 16-PC in DPPC and DPPC/Chol = 1 at both 250 GHz and 9 GHz. Their analysis of the 9-GHz spectra using the MOMD model led to the same results obtained previously by Ge et al. (1999) (of S0 = 0 and R⊥ = 4.1 × 108 s−1 in DPPC and S0 = 0.21 and R⊥ = 4.1 × 108 s−1 in DPPC/Chol = 1 at 50°C), which differ somewhat from the results of Table 1, as already noted above. However, their analysis of the 250-GHz spectra led to markedly different results from those at 9 GHz (viz. S0 = 0.17 and R⊥ = 12 × 108 s−1 in DPPC and S0 = 0.38, and R⊥ = 16 × 108 s−1 for DPPC/Chol = 1 at 45°C]. Although these values of S0 are quite close to those in Table 1, the R⊥ are considerably larger.

Lou et al. were able to reconcile the apparent discrepancy between the results obtained at the two frequencies. They found that the results at 250 GHz could properly be interpreted in terms of the MOMD model as relating to just theinternal ordering and dynamics of the ends of the acyl chains, with the slower overall lipid dynamics “frozen-out” on the timescale of the 250-GHz experiment, (Freed, 2000; Borbat et al., 2001). The 9-GHz spectra however, are affected by both the internal and overall motions. Thus Lou etal. reanalyzed the 9-GHz results in terms ofamodel(known as the SRLS or slowly relaxing local structure model) that explicitly includes both the slower overall and the faster internal dynamics of the lipids. The original MOMD fits to the 9-GHz spectra, which did not distinguish between internal and overall dynamics, should therefore be interpreted as simplified composites to the more complex dynamics.

The implications of the study of Lou et al. are significant for the 2D-ELDOR studies in the present work, which have been analyzed by the simpler MOMD model. The results in Table 1 should therefore be interpreted as composites of both the internal and overall motions (except perhaps for the rigid CSL). Clearly the 2D-ELDOR results at 17.3 GHz represent a somewhat different composite of these processes (perhaps closer to that provided by the 250-GHz cw-ESR), and this warrants further study. Finally, we note that the fact that 9-GHz cw ESR appeared to be successfully fit by both the simpler MOMD model and the more sophisticated one (i.e., SRLS) in the study of Lou et al. is, in fact, another example of the rather low resolution to dynamics provided by the cw-ESR. On the other hand, it has been shown that individual 2D-ELDOR spectra provide enough detail relating to the dynamics to justify the application of the more sophisticated SRLS model (Sastry et al., 1996). (The work of Sastry et al. was on macroscopically aligned Lc phases, and an equivalent analysis has yet to be extended to macroscopically disordered membrane vesicles). We do note that there are a number of small discrepancies between our best MOMD fits and the 2D-ELDOR results that can be discerned in Figs. 2–5. These are quite possibly manifestations of the more subtle details of the molecular dynamics that are not included in the MOMD analysis (cf. Crepeau et al., 1994; Patyal et al., 1997).

2D-ELDOR and lateral phase separation in membranes

In the Introduction, we have pointed out that in biomembranes, lateral phase separation may occur yielding microdomains, and that this can also be found in mixed model membranes (also noted in the previous subsection). In this study we have focused on a comparison of the pure Lc and Lo phases, and we have emphasized the dramatic differences in the 2D-ELDOR spectra from these two phases for most of the labels that we have used. We wish to make some comments on the potential applicability of 2D-ELDOR to those biological or model membranes that exhibit two (or possibly more) phases. To address this issue, we have performed some simple spectral simulations. For example, we have synthesized a two-component spectrum from 16-PC consisting of 50% Lc phase (pure DPPC) and 50% Lo phase (DPPC/Chol = 1) using the experimentally determined parameters given in Table 1. We then employed a version of the NLLS fitting program that we have recently generalized (Crepeau and Freed, unpublished) to include the simultaneous fitting of several components in the 2D-ELDOR program, along the lines previously done for cw-ESR spectra (Budil et al., 1996). We found that this NLLS program reliably distinguishes the two components and returned the correct ordering and diffusional parameters. This is encouraging for future applications of 2D-ELDOR to membranes containing two (or more) phases.

In addition, we do wish to emphasize capabilities of 2D-ELDOR that were not needed in the present study on single phases, but which are available to provide enhanced resolution in multicomponent cases. First of all, in the present study, we utilized magnitude spectra, as has commonly been done in the past (Borbat et al., 1997; Budil et al., 1996; Crepeau et al., 1994: Patyal et al., 1997), because they are most convenient to work with. However, it is possible to obtain 2D-absorptionlike spectra from the experiments after special processing to correct for phase variations along the frequency axes (Saxena and Freed, 1997a). The resulting 2D-absorption spectra display sharper lines and considerably improve the spectral resolution (Saxena and Freed, 1997a,b). The synthesized two-component spectrum discussed in the previous paragraph was also synthesized in the 2D-absorption mode. We found that indeed the resolution is improved and the two-component features become more evident in these spectra. Additionally, one can distinguish between spectral components that have different decay times (nominally T2's). One way this may be achieved is to increase the dead time simply by discarding data points for early times in t1 and t2, (cf. Fig. 2, inset). Then the component with the longer decay time will appear to be relatively enhanced. We do find that the 16-PC spectrum from the Lo phase (with the broader lines) does exhibit a somewhat faster decay rate than that from the Lc phase. (The primary source of the difference in decay rates between the 2D-ELDOR spectra from the Lo and Lc phases is found to be the greater IB of the former due mainly to the MOMD effect. The HB is generally smaller than the IB for the spectra from both phases, and there are only small differences in the HB of the spectra from these two phases.) This feature can be useful, even though the decay rates for these phases are not so different that one could make the Lo component disappear, whereas the Lc component remains strong. These (and additional, cf. Gorcester et al., 1990) approaches are likely to make 2D-ELDOR of considerable use in studies of more complex membranes.

CONCLUSIONS

  1. The crosspeaks in the 2D-ELDOR spectra from an acyl-chain labeled phospholipid, 16-PC, in DPPC and SM bilayers, and from a cholestane spin label, CSL, in DPPC bilayers that are observed in the Lc phase disappear upon incorporation of cholesterol into the bilayers. Thus, a simple visual inspection of the absence or presence of crosspeaks enables one to discriminate the Lo from the Lc phase within the lipid bilayer, whereas a quantitative analysis of the 2D-ELDOR spectra leads to a precise differentiation of the dynamic structures in the Lo versus Lc phases.

  2. In the Lo phase, lipid acyl chains exhibit increased ordering and increased rotational diffusional rates; the rigid cholesterols also experience increased ordering but decreased rotational diffusion, and the lipid headgroup regions exhibit some decrease and realignment in their ordering with substantial increase in rotational diffusion. The microscopic collision rates between these spin labels are reduced in the Lo phase.

  3. These results are readily rationalized in terms of the umbrella model of Huang and Feigenson (1999). The inserted cholesterol acts as a rigid spacer, allowing greater freedom for movement of the lipid headgroups, which themselves shield the cholesterol from the aqueous phase. The rigid cholesterol offers less friction to internal motion of acyl chains even as it restricts the range of their motions, and inhibits motion of other cholesterols.

  4. The sharp distinctions observed between Lo and Lc phases in the model systems studied should serve as a basis for characterizing the molecular dynamic structures of different domains in biological membranes.

Acknowledgments

The authors thank Drs. Richard Crepeau and Petr Borbat for their considerable help with 2D-ELDOR techniques and instrumentation, Dr. Z. Liang for his help with the spectral simulations, and Dr. M. Ge for very helpful discussions. Computations were performed at the Cornell Theory Center.

A.J.C-F. thanks the Brazilian agency CNPq for financial support. Y.S. thanks Grant-in-Aid program (11875019) from the Ministry of Education, Culture, Sports, Science and Technology of Japan. This work was supported by National Institutes of Health grants from National Institute of General Medical Sciences and National Institutes of Health/National Center for Research Resources, and National Science Foundation.

Antonio J. Costa-Filho's present address is Biophysics Group, Instituto de Física de São Carlos, Universidade de São Paulo, C.P. 369, São Carlos 13560-970, Brazil.

Yuhei Shimoyama's permanent address is Department of Physics, Hokkaido University of Education, Hakodate 040-8567, Japan.

References

  1. Barnes, J. P., and J. H. Freed. 1998. Dynamics and ordering in mixed model membranes of dimyristoylphosphatidylcholine and dimyristoylphosphatidylserine: a 250-GHz electron spin resonance study using cholestane. Biophys. J. 75:2532–2546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bloch, K. 1995. Cholesterol: evolution of the structure and function. In Biochemistry of Lipid and Membranes. D. E. Vance and J. E. Vance, editors. Benjamin/Cummings Publishing, Menlo Park, CA. 24.
  3. Bloom, M., E. Evans, and O. G. Morritsen. 1991. Physical properties of the fluid lipid-bilayer component of cell membranes: a perspective. Q. Rev. Biophys. 24:293–397. [DOI] [PubMed] [Google Scholar]
  4. Borbat, P. P., A. J. Costa-Filho, K. A. Earle, J. Moscicki, and J. H. Freed. 2001. Electron spin resonance in studies of membranes and proteins. Science. 291:266–269. [DOI] [PubMed] [Google Scholar]
  5. Borbat, P. P., R. H. Crepeau, and J. H. Freed. 1997. Multifrequency two-dimensional Fourier transform ESR: an X/Ku-band spectrometer. J. Magn. Reson. 127:155–167. [DOI] [PubMed] [Google Scholar]
  6. Brown, D. A., and E. London. 1997. Structure of detergent resistant membrane domains: does phase separation occur in biological membranes? Biochem. Biophys. Res. Commun. 240:1–7. [DOI] [PubMed] [Google Scholar]
  7. Brown, D. A., and E. London. 1998. Functions of lipid rafts in biological membranes. Annu. Rev. Cell Dev. Biol. 14:111–136. [DOI] [PubMed] [Google Scholar]
  8. Budil, D. E., S. Lee, S. Saxena, and J. H. Freed. 1996. Nonlinear-least squares analysis of slow-motion EPR spectra in one and two dimensions using a modified Levenberg-Marquardt algorithm. J. Magn. Reson. A120:155–189. [Google Scholar]
  9. Cassol, R., M. Ge, A. Ferrarini, and J. H. Freed. 1997. Chain dynamics and the simulation of ESR spectra from oriented phospholipid membranes. J. Phys. Chem. B. 101:8782–8789. [Google Scholar]
  10. Crepeau, R. H., S. Saxena, S. Lee, B. Patyal, and J. H. Freed. 1994. Studies of lipid membranes by two-dimensional Fourier transform ESR: enhancement of resolution to ordering and dynamics. Biophys. J. 66:1489–1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Feigenson, G. W., and J. T. Buboltz. 2001. Ternary phase diagram of dipalmitoyl-PC/dilauroyl-PC/cholesterol: nanoscopic domain formation driven by cholesterol. Biophys. J. 80:2775–2788. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Field, K. A., D. Holowka, and B. Baird. 1995. Fc ɛRI-mediated recruitment of p53/56lyn to detergent-resistant membrane domains accompanies cellular signaling. Proc. Natl. Acad. Sci. USA. 92:9201–9205. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Field, K. A., D. Holowka, and B. Baird. 1997. Compartmentalized activation of the high affinity immunoglobulin E receptor within membrane domains. J. Biol. Chem. 272:4276–4280. [DOI] [PubMed] [Google Scholar]
  14. Freed, J. H. 2000. New technologies in electron spin resonance. Annu. Rev. Phys. Chem. 51:655–689. [DOI] [PubMed] [Google Scholar]
  15. Freed, J. H. 1994. Field gradient ESR and molecular diffusion in model membranes. Annu. Rev. Bioph. Biom. 23:1–25. [DOI] [PubMed] [Google Scholar]
  16. Gaffney, B. J., and D. Marsh. 1998. High-frequency, spin-label EPR of nonaxial lipid ordering and motion in cholesterol-containing membranes. Proc. Natl. Acad. Sci. USA. 95:12940–12943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gamliel, D., and J. H. Freed. 1990. Theory of two-dimensional ESR with nuclear modulation. J. Magn. Reson. 89:60–93. [Google Scholar]
  18. Ge, M., D. E. Budil, and J. H. Freed. 1994. ESR Studies of spin-labeled membranes aligned by isopotential spin-dry ultracentrifugation: lipid-protein interaction. Biophys. J. 67:2326–2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Ge, M., K. A. Field, R. Aneja, D. Holowka, B. Baird, and J. H. Freed. 1999. Electron spin resonance characterization of liquid-ordered phase of detergent-resistant membranes from RBL-2H3 cells. Biophys. J. 77:925–933. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Ge, M., and J. H. Freed. 1993. An ESR study of interactions between gramicidin A′ and phosphatidylcholine bilayers. Biophys. J. 65:2106–2123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Ge, M., and J. H. Freed. 1998. Polarity profiles in oriented and dispersed phosphatidylcholine bilayers are different: an electron spin resonance study. Biophys. J. 74:910–917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Gliss, C., O. Randel, H. Casalta, E. Sackmann, R. Zorn, and T. Bayerl. 1999. Anisotropic motion of cholesterol in oriented DPPC bilayers studied by quasielastic neutron scattering: the liquid ordered phase. Biophys. J. 77:331–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Gorcester, J., G. L. Millhauser, and J. H. Freed. 1990. Two-Dimensional Electron Spin Resonance. In Modern Pulsed and Continuous Wave Electron Spin Resonance. L. Kevan and M. Bowman, editors. Wiley, New York. 119–194.
  24. Henze, R. 1980. Dielectric relaxation in lecithin/cholesterol/water mixtures. Chem. Phys. Lipids. 27:165–175. [Google Scholar]
  25. Huang, J., and G. W. Feigenson. 1999. A microscopic interaction model of maximum solubility of cholesterol in lipid bilayers. Biophys. J. 76:2142–2157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Ipsen, J. H., G. Karlstrom, O. G. Mouritsen, H. Wennerstrom, and M. J. Zuckermann. 1987. Phase-equilibria in the phosphatidylcholine-cholesterol system. Biochim. Biophys. Acta. 905:162–172. [DOI] [PubMed] [Google Scholar]
  27. Kleemann, K., and H. M. McConnell. 1976. Interactions of proteins and cholesterol with lipids in bilayer membranes. Biochim. Biophys. Acta. 419:206–222. [DOI] [PubMed] [Google Scholar]
  28. Lee, S., D. E. Budil, and J. H. Freed. 1994. Theory of two-dimensional Fourier transform ESR for ordered and viscous fluids. J. Chem. Phys. 99:7098–7107. [Google Scholar]
  29. Livshits, V. A., and D. Marsh. 2000. Simulation studies of high-field EPR spectra of spin-labeled lipids in membranes. J. Magn. Reson. 147:57–67. [DOI] [PubMed] [Google Scholar]
  30. Lou, Y., M. Ge, and J. H. Freed. 2001. A multifrequency ESR study of the complex dynamics of membranes. J. Phys. Chem. B. 105:11053–11056. [Google Scholar]
  31. McIntosh, T. J., A. D. Magid, and S. A. Simon. 1989. Cholesterol modifies the short-range repulsive interactions between phosphatidylcholine membranes. Biochemistry. 28:17–25. [DOI] [PubMed] [Google Scholar]
  32. Meirovitch, E., A. Nayeem, and J. H. Freed. 1984. An analysis of protein-lipid interactions based on model simulations of ESR spectra. J. Phys. Chem. 88:3454–3465. [Google Scholar]
  33. Patyal, B. R., R. H. Crepeau, and J. H. Freed. 1997. Lipid-gramicidin interactions using two-dimensional Fourier-transform electron spin resonance. Biophys. J. 73:2201–2220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Patyal, B. R., R. H. Crepeau, D. Gamliel, and J. H. Freed. 1990. Two-dimensional Fourier transform ESR in the slow-motional and rigid limits: 2D-ELDOR. Chem. Phys. Letts. 175:453–460. [Google Scholar]
  35. Recktenwald, D. J., and H. M. McConnell. 1981. Phase-equilibria in binary mixtures of phosphatidylcholine and cholesterol. Biochemistry. 20:4505–4510. [DOI] [PubMed] [Google Scholar]
  36. Rubenstein, J. L. R., R. A. Smith, and H. M. McConnell. 1979. Lateral diffusion in binary mixtures of cholesterol and phosphatidylcholines. Proc. Natl. Acad. Sci. USA. 76:15–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Samsonov, A. V., I. Mihalyov, and F. S. Cohen. 2001. Characterization of cholesterol-sphingomyelin domains and their dynamics in bilayer membranes. Biophys. J. 81:1486–1500. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Sastry, V. S. S., A. Polimeno, R. H. Crepeau, and J. H. Freed. 1996. Studies of spin relaxation and molecular dynamics in liquid crystals by two-dimensional Fourier transform ESR: I. Cholestane in butoxy benzylidene-octylaniline and dynamic cage effects. J. Chem. Phys. 105:5753–5772. [Google Scholar]
  39. Saxena, S., and J. H. Freed. 1997a. Absorption lineshapes in two-dimensional ESR and the effects of slow motions in complex fluids. J. Magn. Res. 124:439–454. [DOI] [PubMed] [Google Scholar]
  40. Saxena, S., and J. H. Freed. 1997b. Two-dimensional ESR and slow motions. J. Phys. Chem. A. 101:7998–8008. [Google Scholar]
  41. Schneider, D. J., and J. H. Freed. 1989. Calculating slow motional magnetic resonance spectra: a user's guide. In Biological Magnetic Resonance, Vol. 8. L. J. Berliner and J. Reuben, editors. Plenum Publishing, New York. 1–76.
  42. Shimshick, E. J., and H. M. McConnell. 1973. Lateral phase separation in binary mixtures of cholesterol and phospholipids. Biochem. Biophys. Res. Commun. 53:446–451. [DOI] [PubMed] [Google Scholar]
  43. Shin, Y. K., D. E. Budil, and J. H. Freed. 1993. Thermodynamics and dynamics of phosphatidylcholine-cholesterol mixed-model membranes in the liquid crystalline state: effects of water. Biophys. J. 65:1283–1294. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Shin, Y. K., and J. H. Freed. 1989a. Dynamic imaging of lateral diffusion by electron spin resonance and study of rotational dynamics in model membranes. Effect of cholesterol. Biophys. J. 55:537–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Shin, Y. K., and J. H. Freed. 1989b. Thermodynamics of phosphatidylcholine-cholesterol mixed model membranes in the liquid crystalline state studied by the orientational order parameter. Biophys. J. 56:1093–1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Shin, Y. K., J. K. Moscicki, and J. H. Freed. 1990. Dynamics of phosphatidylcholine-cholesterol mixed model membranes in the liquid crystalline state. Biophys. J. 57:445–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Simons, K., and E. Ikonen. 1997. Functional rafts in cell membranes. Nature. 387:569–572. [DOI] [PubMed] [Google Scholar]
  48. Simons, K., and E. Ikonen. 2000. How cells handle cholesterol. Science. 290:1721–1726. [DOI] [PubMed] [Google Scholar]
  49. Singer, S. J., and G. L. Nicholson. 1972. The fluid mosaic model of the structure of cell membranes. Science. 175:720–731. [DOI] [PubMed] [Google Scholar]
  50. Straume, M., and B. J. Litman. 1987. Influence of cholesterol on equilibrium and dynamic bilayer structure of unsaturated acyl phosphatidylcholine vesicles as determined from higher order analysis of fluorescence anisotropy decay. Biochemistry. 26:5121–5126. [DOI] [PubMed] [Google Scholar]
  51. Tanaka, H., H. Saito, and H. Kawazura. 1997. Use of VO2+ as a spin label for dynamics of polar headgroup in phosphatidylcholine bilayers. Chem. Phys. Lipids. 85:45–51. [Google Scholar]
  52. Veiga, M. P., J. L. R. Arrondo, F. M. Goni, A. Alonso, and D. Marsh. 2001. Interaction of cholesterol with sphingomyelin in mixed membranes containing phosphatidylcholine studied by spin-label ESR and IR spectroscopies. A possible stabilization of gel-phase sphingolipid domains by cholesterol. Biochemistry. 40:2614–2622. [DOI] [PubMed] [Google Scholar]
  53. Vist, M. R., and J. Davis. 1990. Phase equilibria of cholesterol/dipalmitoylphosphatidylcholine mixtures: 2H nuclear magnetic resonance and differential scanning calorimetry. Biochemistry. 29:451–464. [DOI] [PubMed] [Google Scholar]
  54. Wolf, C., and C. Chachaty. 2000. Compared effects of cholesterol and 7-dehydrocholesterol on sphingomyelin-glycerophospholipid bilayers studied by ESR. Biophys. Chem. 84:269–279. [DOI] [PubMed] [Google Scholar]
  55. Wolf, C., K. Koumanov, B. Tenchov, and P. J. Quinn. 2001. Cholesterol favors phase separation of sphingomyelin. Biophys. Chem. 89:163–172. [DOI] [PubMed] [Google Scholar]
  56. Yeagle, P. L., W. C. Hutton, and R. B. Martin. 1975. Headgroup conformation and lipid-cholesterol association in phosphatidylcholine vesicles: a 31P(1H) nuclear Overhauser effect study. Proc. Natl. Acad. Sci. USA. 72:3477–3481. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES