Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Apr;84(4):2691–2699. doi: 10.1016/S0006-3495(03)75074-7

Mapping Mechanical Strain of an Endogenous Cytoskeletal Network in Living Endothelial Cells

Brian P Helmke *, Amy B Rosen †,‡, Peter F Davies †,‡,§
PMCID: PMC1302835  PMID: 12668477

Abstract

A central aspect of cellular mechanochemical signaling is a change of cytoskeletal tension upon the imposition of exogenous forces. Here we report measurements of the spatiotemporal distribution of mechanical strain in the intermediate filament cytoskeleton of endothelial cells computed from the relative displacement of endogenous green fluorescent protein (GFP)-vimentin before and after onset of shear stress. Quantitative image analysis permitted computation of the principal values and orientations of Lagrangian strain from 3-D high-resolution fluorescence intensity distributions that described intermediate filament positions. Spatially localized peaks in intermediate filament strain were repositioned after onset of shear stress. The orientation of principal strain indicated that mechanical stretching was induced across cell boundaries. This novel approach for intracellular strain mapping using an endogenous reporter demonstrates force transfer from the lumenal surface throughout the cell.

INTRODUCTION

Hemodynamic forces acting on the endothelium play a central role in modulating vascular physiology and the pathogenesis of atherosclerosis (Davies, 1995). As part of the adaptive response of endothelial cells (ECs) to changes in the local fluid dynamic environment, the cytoskeleton and associated linking molecules are proposed to serve as force transmission pathways throughout the cytoplasm (Davies, 1995; Ingber, 1997; Tzima et al., 2001). Shear stress induces significant adaptation of all three principal cytoplasmic cytoskeletal networks (Galbraith et al., 1998) as well as reorganization of adherens junctions (Langille, 2001), communication junctions (DePaola et al., 1999), and sites of focal adhesion to the substrate (Wernick et al., 1998). For example, the timescale of focal adhesion elongation and alignment parallel to the flow direction (Wernick et al., 1998) corresponds to that of actin cytoskeleton reorganization (Galbraith et al., 1998), suggesting that mechanisms of force-induced remodeling of these two structures are not mutually independent.

Although structural adaptation of the cytoskeleton to onset of shear stress has been described (Dewey et al., 1981; Galbraith et al., 1998; Levesque and Nerem, 1985), rapid movement of cytoskeleton-associated elements in living cells has only recently been measured (Helmke et al., 2000; Helmke et al., 2001; Li et al., 2002; Wernick et al., 1998). Onset of shear stress induces rapid initiation of actin ruffles near edges of single cells that becomes directional after ∼30 min as cells begin to migrate in the downstream direction (Li et al., 2002). Using green fluorescent protein-labeled vimentin (GFP-vimentin) as an endogenous marker, we have recently shown that elements of the intermediate filament (IF) network in confluent monolayers of ECs are significantly displaced after onset of shear stress (Helmke et al., 2000). Average filament displacement magnitude was greater with increased height in the cell and was magnified in downstream regions of the cell (Helmke et al., 2001). We propose that such cytoskeletal displacement results in spatial redistribution of cytoplasmic mechanical strain at a subcellular length scale.

Current imaging and computational techniques to map cytoplasmic strain lack the resolution to permit direct prediction of localized cytoplasmic force distribution. Cytoplasmic strain has been measured in migrating leukocytes (Simon and Schmid-Schonbein, 1990) and in endothelial cells during substrate stretch (Caille et al., 1998) using internalized microspheres. These measurements allowed computation of subcellular deformation averaged over relatively large regions of the cytoplasm by assuming that the cytoplasm could be described as a viscoelastic continuum. However, the cytoskeleton and other structures confer heterogeneous mechanical properties at a subcellular length scale (Ingber, 1997). Thus, more precise mapping of local mechanical interactions within the cell is required in order to directly relate extracellular mechanical stimuli to mechanisms of biochemical signaling. Improved resolution of cytoskeletal strain mapping can be obtained using the endogenous structural marker GFP-vimentin, deconvolution microscopy, and the novel application of image analysis and computational tools. Here we present computation of intracellular strain in the IF cytoskeleton that reveals localized strain focusing consistent with a decentralized model of endothelial mechanotransduction (Davies, 1995; Helmke and Davies, 2002).

METHODS

Cell culture and transfection

Bovine aortic endothelial cells were cultured in complete growth medium as described previously (Helmke et al., 2000). Cells were transfected with pEGFP-hVIM-Myc (a kind gift from Dr. Robert D. Goldman (Yoon et al., 1998)) using a liposomal method (Helmke et al., 2000; Helmke et al., 2001) according to manufacturer's recommendations (Lipofectin, Gibco, Gaithersburg, MD). GFP-vimentin was transiently expressed and distributed to the endogenous intermediate filament cytoskeleton (Helmke et al., 2000; Yoon et al., 1998), as indicated by colocalization with an antibody against vimentin (Yoon et al., 1998) (Helmke, unpublished data). IF function was indistinguishable from that measured in cell lines that stably expressed GFP-vimentin (Helmke et al., 2000).

As described previously (Helmke et al., 2001), 0.1-μm red fluorescent microspheres (Molecular Probes, Eugene, OR) were adhered onto sterile glass coverslips (Bioptechs, Butler, PA). Cells expressing GFP-vimentin were plated over the microspheres and grown to confluence. All experiments were performed with confluent monolayers of cells. A set of coplanar microspheres served as fiducial markers for coverslip movement during time-lapse image acquisition.

Flow experiments and image acquisition

Coverslips with confluent monolayers of GFP-vimentin–expressing endothelial cells were assembled into a heated parallel plate flow chamber maintained at 37°C (Bioptechs). The chamber was assembled into a closed loop and perfused by gravity from an upstream reservoir. Shear stress during flow intervals was 12 dyn cm−2.

Dual wavelength wide field fluorescence optical sections were acquired using a DeltaVision Restoration Microscope (Applied Precision, Issaquah, WA). Spatial and temporal normalization of the illumination intensity allowed quantitative analysis of the measured fluorescence intensity of GFP and red microspheres (Helmke et al., 2001). Image stacks of cells expressing GFP-vimentin in a physiological distribution of intermediate filaments were acquired every 3 min under no flow conditions with 0.25-μm spacing between optical sections. After a step change in flow was imposed, stacks of images were acquired with the same spacing and interval. In some experiments, flow was stopped, and image acquisition continued as the protocol was repeated. A total of five cells from separate flow experiments were analyzed.

Image processing and computation of strain tensor

In each 3-D image stack, three optical sections from varying heights above the coverslip were selected for analysis. The following steps were performed using softWoRx software (Applied Precision) to enhance contrast and improve precision of the subsequent computational methods. A median filter was applied to minimize high-frequency shot noise, and two iterations of a high-pass filter were used to improve contrast between regions of high and low intensity. Finally, the images were filtered with two iterations of a low-pass filter to smooth the intensity distribution.

Using Scion Image (Scion Corp., Frederick, MD), a statistical method was designed to determine a threshold intensity value, 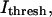Inline graphic that optimized the extraction of filament positions. At the z-position closest to the coverslip, 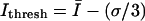Inline graphic was computed from the global intensity distribution, where 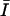Inline graphic is mean intensity and σ is the standard deviation of intensity computed over the entire image. Since optical sections higher above the coverslip had lower signal-to-noise, these optical sections were manually masked before processing to include only regions known to contain IF. For the masked images, the mean intensity from the region of interest (ROI) was selected as the threshold value; i.e., 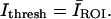Inline graphic All optical sections were then converted to binary images and were skeletonized to represent filaments by a one-pixel-thick line.

Cytoskeletal positions where three or more filaments intersect were defined as vertex points. A MATLAB (The MathWorks, Natick, MA) algorithm was written to extract the positions of these branching points from the skeletonized images. Vertices were extracted for each of the three z-sections, and coordinates were followed over the entire range of time using a particle-tracking algorithm implemented in IDL (Research Systems, Boulder, CO) that was based on a probability model for distance moved between time points (Crocker and Grier, 1996). Displacement of most vertices occurred in-plane; the few vertices that appeared or disappeared were ignored. Previous measurements demonstrated that maximum IF displacement on this timescale was of order 1 μm (Helmke et al., 2000). Since resolution parallel to the optical axis was ∼0.68 μm, movement of most vertices was detectable within the optical thickness of a single optical slice. Thus, in the following analysis, strain was assumed to occur in the plane of the optical section.

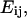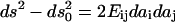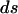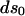The intracellular deformation field as a function of time was described by the Lagrangian strain tensor Inline graphic computed as Inline graphic where Inline graphic and Inline graphic are the final and initial distances, respectively, between adjacent vertices of interest, 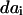Inline graphic is the projected initial distance onto the ith axis, and the Einstein summation convention is implied. Since 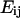Inline graphic is symmetric, three components are unknown. A system of three equations was derived using distances from three adjacent line segments drawn between vertices. The resulting tensor 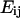Inline graphic gives the average strain field within the triangle formed by the line segments. Delaunay triangulation was employed to draw the smallest possible set of triangles connecting all vertices in the set of tracked points. Eigenvectors of 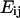Inline graphic were computed to yield the magnitudes and orientations of principal components of strain for each triangle and time interval. 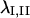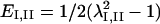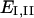Finally, principal stretch ratios Inline graphic were computed as Inline graphic where Inline graphic are the principal values of strain in the I and II directions, respectively. Note that the principal stretch ratios give the maximum and minimum stretch along axes oriented such that the deformation contains no shear components. Furthermore, the product of principal stretch ratios 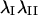Inline graphic is unity if projected area is conserved during deformation. All computations were carried out using MATLAB.

Statistical analysis

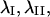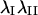Magnitude and orientation of principal stretch in each optical section were analyzed to determine whether significant differences existed as a function of height in the cell or time. Since frequency histograms of Inline graphic and Inline graphic demonstrated that these quantities were not normally distributed (data not shown), nonparametric comparisons were made among median values using the sign test. Briefly, the test statistic B+ is the number of values in the sample greater than the sample median M. For large samples (n > 25), the probability density for the quantity 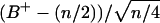Inline graphic approximates the standard normal distribution. 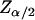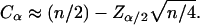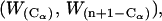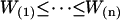In order to compute the 95% confidence interval, Inline graphic is computed from the standard normal cumulative distribution with α = 0.05, allowing estimation of the test statistic Inline graphic Finally, the confidence interval is given by Inline graphic where Inline graphic are the data values ranked in increasing order. Groups were considered statistically different if no overlap existed among confidence intervals.

Preliminary analysis of orientation angles of principal stretch 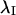Inline graphic suggested that they could not be described by a von Mises distribution (data not shown). Consequently, a nonparametric analysis was developed to compare groups (Fisher, 1993). The data were first rotated π/2, and both ends of the orientation axis were considered. The resulting modified data set had N = 2n values on the circular interval (0, 2π). The axial data was converted to vectorial data by the transformation 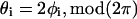Inline graphic where {φi} is the set of rotated axial data values. The summary statistics

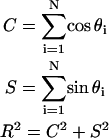graphic file with name M26.gif

were used to compute the mean resultant length 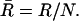Inline graphic

The mean direction of the vectorial data was computed from

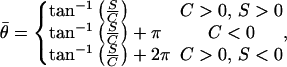graphic file with name M28.gif

and the axial rotation and transformation were inverted using 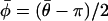Inline graphic to yield the mean orientation of 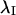Inline graphic on the interval (−π, π).

In order to compute a 95% confidence interval for orientation, the first two centered sample trigonometric moments m1 and m2, respectively, are computed as

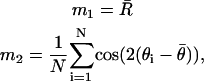graphic file with name M31.gif

where 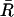Inline graphic is the mean resultant length and 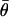Inline graphic is the mean orientation of 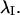Inline graphic These moments allow computation of the sample circular dispersion 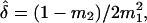Inline graphic and the circular standard error of the mean direction 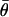Inline graphic is then given by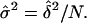 Inline graphic

Finally, if 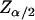Inline graphic defines a 100(α/2)% confidence interval on the standard normal distribution N(0, 1), then a 100(1 − α)% confidence interval for 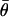Inline graphic is given by (θL, θU), where

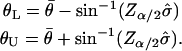graphic file with name M40.gif

The value α = 0.05 was used to compute a 95% confidence interval, and the resulting values were rotated and transformed according to

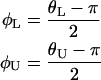graphic file with name M41.gif

to give the confidence interval around the mean orientation of 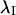Inline graphic on the interval (−π, π).

RESULTS

Analysis of intracellular structure

To measure intracellular mechanical deformation using an endogenous structural marker, the IF network in confluent ECs was visualized after transfection with GFP-vimentin as described previously (Helmke et al., 2000; Helmke et al., 2001). Fluorescence optical sections were acquired before and immediately after the onset of unidirectional laminar flow such that the cells were subjected to a step change in shear stress to 12 dyn cm−2. Deconvolution and image restoration of 3-D fluorescence images yielded a precise spatial distribution of IFs labeled with GFP-vimentin. Image segmentation produced a binary skeleton that accurately represented the locations of IFs in the fluorescence optical sections (Fig. 1). Since a single optical section only contained fluorescence intensity from IFs located within ∼0.68 μm of the focal plane, corresponding to the resolution limit along the optical axis, filament segments often appeared disconnected or free floating within the binary skeleton. Since connection points, or vertices, among filaments were the only features used to compute mechanical deformation, the presence of these disconnected filament segments did not affect the computational results.

FIGURE 1.

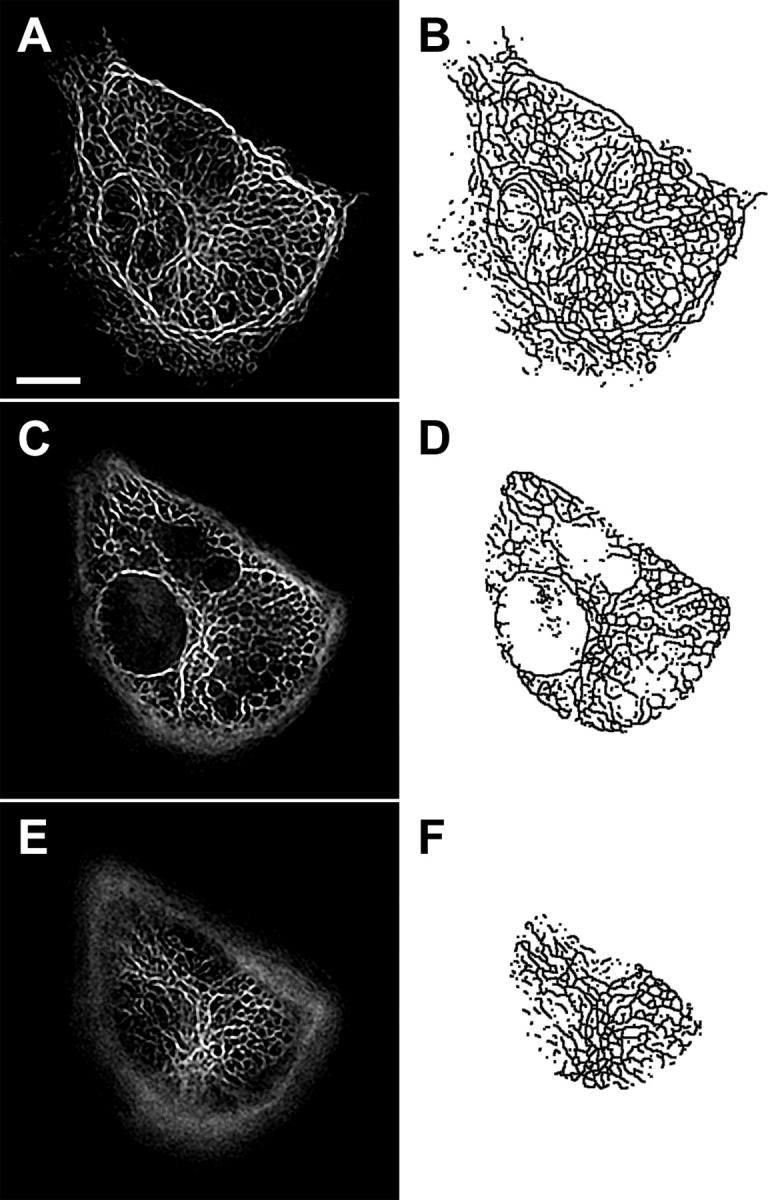
FIGURE 1

Open in a new tab

IF skeleton in one cell of a confluent monolayer of ECs. (A, C, E) Fluorescence optical sections showing IFs after image restoration and (B, D, F) corresponding binary skeletons extracted from each image. Pairs of images are located (A, B) 0.3 μm, (C, D) 2.4 μm, and (E, F) 4.6 μm above the coverslip. Adjacent ECs in the monolayer are not expressing GFP-vimentin after transient transfection. Scale bar, 10 μm.

Flow-induced cytoskeletal displacement

Onset of unidirectional laminar shear stress induced significant regional displacement of IFs within minutes (Helmke et al., 2001). Comparison of skeleton images extracted from the fluorescence data accurately represented spatial patterns of IF wiggling and stretching (Fig. 2 A). Tracking of vertices at the intersections of skeleton segments revealed the spatial distribution of filament movement as a function of time (Fig. 2 B). Although the spatial distribution of vertex displacement was heterogeneous, coordinated patterns of displacement of adjacent vertices were often observed, indicating translation of filament segments. In addition, displacement of adjacent vertices by different magnitude or direction indicated that stretching or deformation of the connecting filament segment occurred during the interval. This was confirmed by direct comparison of the corresponding fluorescence and skeleton images.

FIGURE 2.

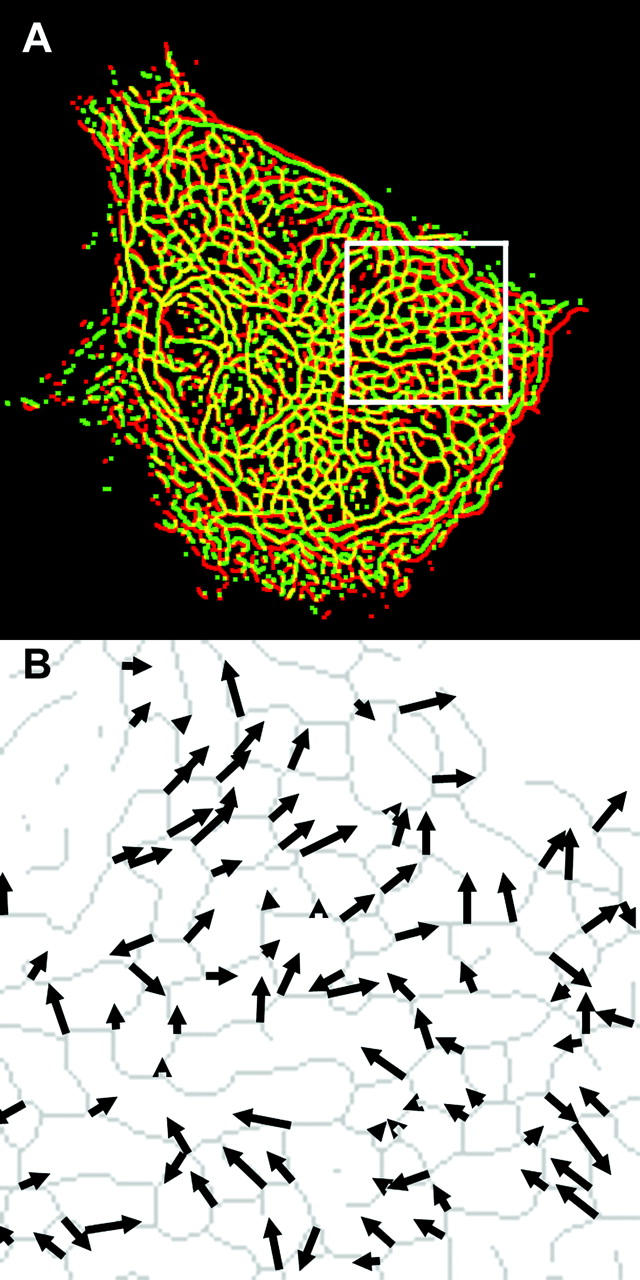
FIGURE 2

Open in a new tab

IF displacement field induced by onset of shear stress. (A) Merged color image showing extracted skeletons from an optical section just before (red) and 3 min after (green) onset of shear stress (12 dyn/cm2, left to right). Yellow indicates overlap corresponding to zero filament displacement. (B) Vertex displacement field from the inset box in (A). Arrow length and orientation indicate magnitude and direction of displacement of the corresponding vertex on the skeleton (gray), shown just before flow onset.

Strain induced by onset of shear stress

The relative displacement of adjacent vertices in the IF skeleton represents a mechanical deformation or strain. In order to maximize spatial precision, the set of vertices from each skeleton was connected by Delaunay triangulation. This computational geometry technique yielded a set of triangles for which no vertex was enclosed within another triangle (Fig. 3). Thus, relative displacements were computed for a set of smallest possible distances among adjacent vertices, and the resulting strain field contained a high degree of spatial detail. The components of the Lagrangian strain tensor averaged over the spatial region enclosed by a triangle were computed by solving a system of three equations constructed using the relative change in distances measured along the sides of the triangle.

FIGURE 3.

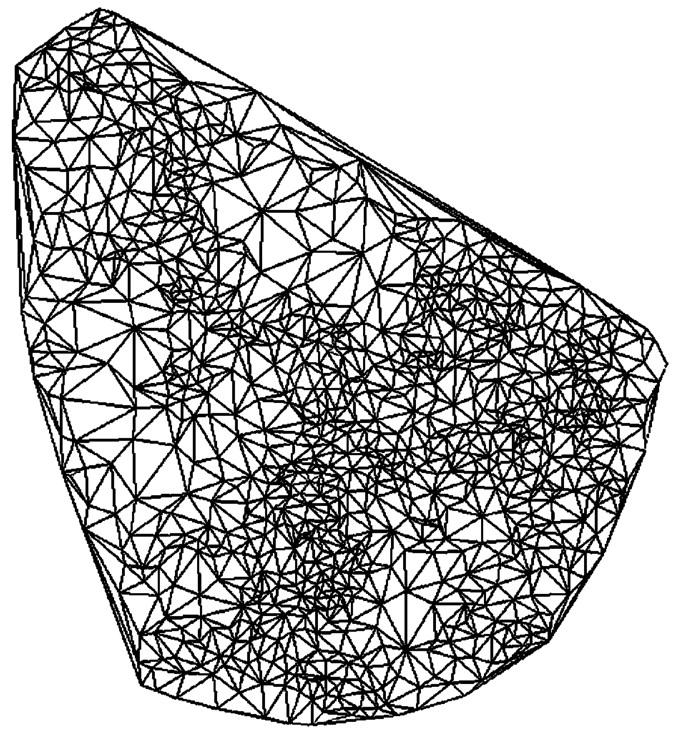
FIGURE 3

Open in a new tab

Delaunay triangulation of vertices in an optical section. Vertex points on the skeleton in Fig. 1 A were connected by triangles that did not contain another vertex, yielding a set of smallest possible spatial subregions over which the strain tensor was computed.

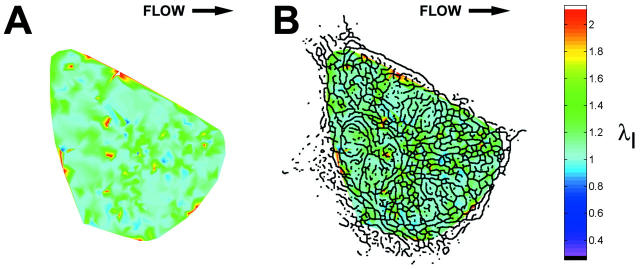
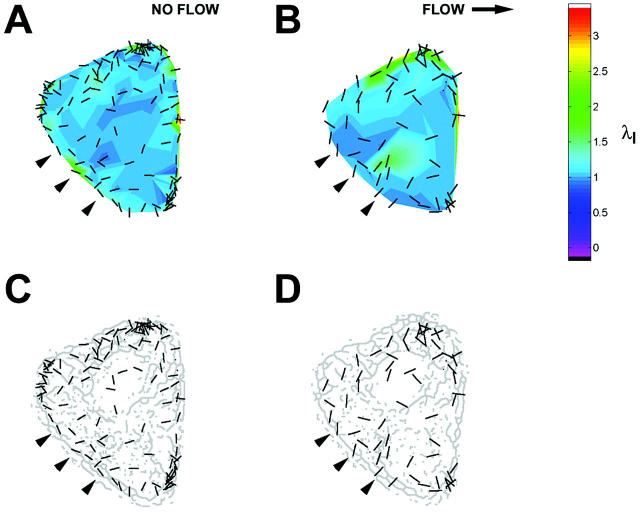
Onset of shear stress induced an increase in IF strain that was highly localized within the cell as illustrated by the principal stretch ratio (Fig. 4). This example is representative of the behavior of all five cells analyzed. Spatial concentration of principal stretch ratio λI occurred at discrete sites throughout the cytoplasm, including near the coverslip (Fig. 4 A). In each cell, these focal concentrations of maximum stretch represented by λI often corresponded to closely interconnected network elements in the IF skeleton (Fig. 4 B). The spatial distribution was significantly altered by onset of shear stress (Fig. 5). Highly localized peaks in stretch magnitude, termed strain focusing, were redistributed within 3 min after onset of shear stress. Strain focusing was most significant near the coverslip (Fig. 5, A and B). Although a less focused distribution of strain magnitude was measured in central regions of the cytoplasm (Fig. 5, C and D), strain focusing often occurred near the nuclear boundary. Interestingly, the orientation of principal stretch along the upstream edge of the cell was often rotated from parallel to perpendicular to the cell edge (Fig. 5, C and D, and Fig. 6, A and B). Although the locations where reorientation of principal stretch direction varied from cell to cell, comparison to IF morphology in these regions in all five cells analyzed demonstrated that principal stretch was oriented longitudinally along IFs near the cell edge under no-flow conditions (Fig. 6 C), and onset of shear stress induced maximum stretch perpendicular to these IFs (Fig. 6 D).

FIGURE 4.

FIGURE 4

Open in a new tab

IF strain field in an optical section. (A) Magnitude (color scale) of principal stretch ratio λI during a 3-min interval immediately after onset of shear stress (12 dyn/cm2, left to right). (B) Skeleton image superimposed on magnitude of principal stretch as a spatial reference. Note strain focusing at dense interconnections among IF segments.

FIGURE 5.

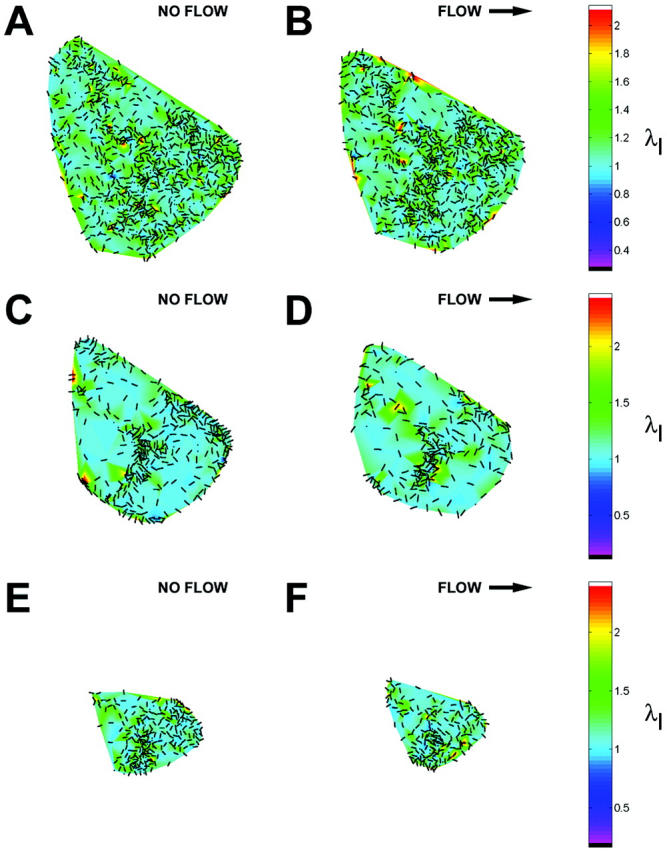
FIGURE 5

Open in a new tab

Redistribution of strain focusing during onset of shear stress. Magnitude (color scale) and orientation (bars) of principal stretch ratio λI during consecutive 3-min intervals (A, C, and E) before and (B, D, and F) after onset of shear stress (12 dyn/cm2, left to right). Values are shown for optical sections located (A and B) 0.3 μm, (C and D) 2.4 μm, and (E and F) 4.6 μm above the coverslip.

FIGURE 6.

FIGURE 6

Open in a new tab

Reorientation of principal stretch direction near the upstream cell boundary during onset of shear stress. (A and B) Magnitude (color scale) and orientation (bars) of principal stretch ratio λI in an optical section located 2.4 μm above the coverslip during consecutive 3-min intervals (A) before and (B) after onset of shear stress (12 dyn/cm2, left to right). (C and D) Comparison of orientation of principal stretch (bars) with skeleton morphology. Along the upstream edge, onset of shear stress induced a change of orientation (arrowheads) from parallel to IF along the cell edge to perpendicular.

Since the stretch ratio magnitude within an optical section was not normally distributed, a nonparametric analysis was computed to detect whether flow induced changes in strain distribution for entire optical sections within a single cell (Fig. 7). Median values of principal stretch were relatively constant in time (Fig. 7, A and C), demonstrating that strain focusing is not detectable in measurements performed at a whole-cell length scale. Although median λI in an apical optical section increased somewhat after onset of shear stress, the increase was not significant as predicted by 95% confidence intervals (Fig. 7 A). The global median value of the product λIλII did not differ significantly from unity during any time intervals (Fig. 7 D), demonstrating that flow-induced strain focusing does not result in overall change in area enclosed by the IF network within an optical section.

FIGURE 7.

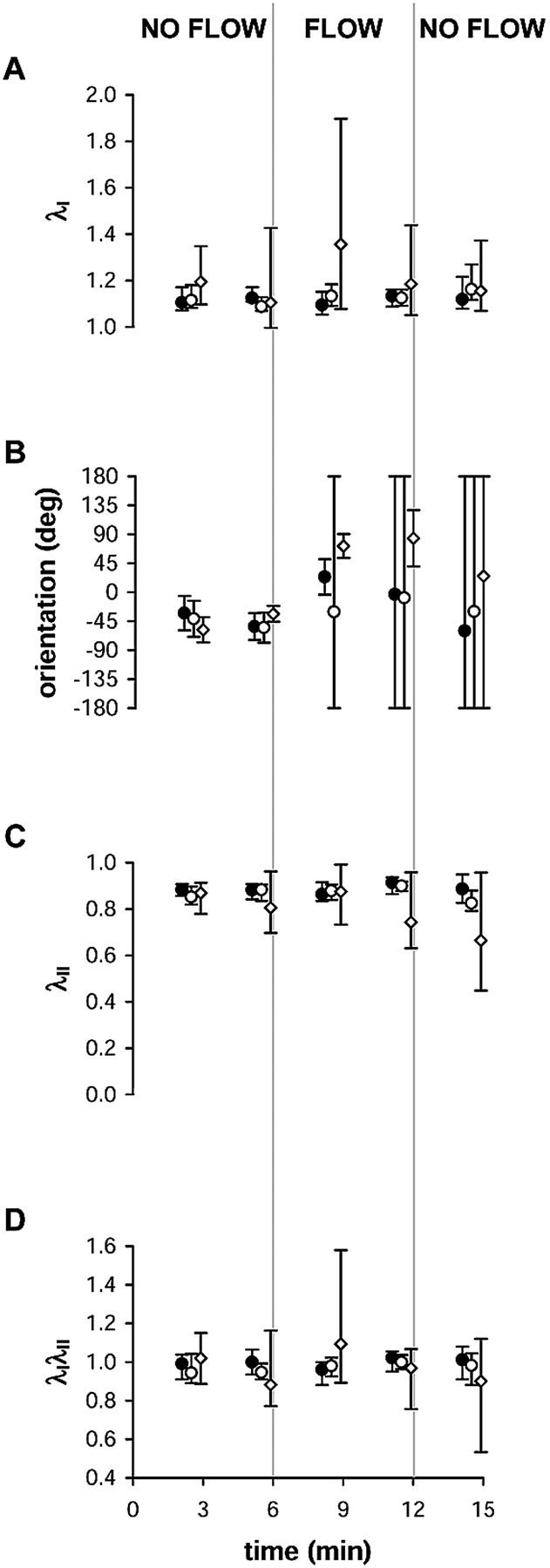
FIGURE 7

Open in a new tab

Analysis of (A) median principal stretch ratio λI, (B) mean orientation of λI, (C) median principal stretch ratio λII, and (D) median principal stretch ratio product λIλII as a function of time during changes in shear stress acting on a cell. Values are computed from all triangles in single optical sections located 0.3 μm (closed circles), 2.4 μm (open circles), or 4.5 μm (open diamonds) above the coverslip within a single cell in the monolayer. Error bars show 95% confidence intervals for each optical section.

Onset of shear stress induced significant changes in the mean orientation of λI (Fig. 7 B). Under no-flow conditions, cells exhibited a preferred orientation of λI that was constant with height. After onset of shear stress, significant rotation of λI orientation was measured in two of the five cells. In the other three cells, rotation was not significant because confidence intervals indicated that no preferred orientation existed. In the two cells for which principal stretch direction was rotated after onset of flow, variability in orientation increased in all optical sections until a preferred orientation no longer existed, as demonstrated by confidence intervals that encompassed the whole circle. This suggests that the orientation of λI was random throughout the cytoplasm or was unimodal locally at an intracellular length scale, since either of these possibilities would result in a low value for von Mises concentration parameter computed across the entire optical section (Fisher, 1993).

DISCUSSION

Multiple structural and functional adaptations of endothelial cells to the hemodynamic environment have been documented (Davies, 1995), including an increase in intracellular calcium concentration (Ando et al., 1988) and activation of G proteins (Ohno et al., 1993) within seconds after onset of steady laminar shear stress. However, rapid intracellular structural movement has only recently been reported (Helmke et al., 2001). It is likely that relative displacement or mechanical deformation of adjacent cytoskeletal elements modulates physical interactions among associated signaling proteins that may contribute to initiation of mechanochemical signaling networks. The present study reports for the first time intracellular strain distribution at high spatial resolution measured from endogenous features in living cells.

These studies clearly demonstrate novel features of intracellular mechanics at a length scale relevant to mechanisms of mechanotransduction. The high spatial resolution made possible by computing strain fields from endogenous intracellular features reveals significant local deformation of IF morphology in endothelial cells that is associated with filament bending and relative displacement of connection points among filaments in the network. In addition, strain magnitude and orientation are spatially redistributed within minutes after onset of unidirectional laminar shear stress acting at the cell surface, suggesting that significant changes in the intracellular mechanical environment modulate an integrated mechanochemical signaling response. Strain magnitude in areas of dense IF segments near the coverslip was highly localized. This strain focusing indicates that local mechanics are determined principally by mechanical interactions with specialized structures such as focal adhesion complexes or intercellular junctions. Furthermore, local alterations in mechanical properties at locations of IF strain focusing also result from interactions among cross-linking proteins and other cytoskeletal elements such as microfilaments (Shah et al., 1998) and microtubules (Svitkina et al., 1996). Although strain was more broadly distributed in central regions of the cytoplasm, peaks in strain magnitude induced by shear stress were often located at the nuclear boundary or in perinuclear regions (Fig. 6), suggesting that extracellular applied forces can act directly on the nucleus. The magnitude of principal stretch in focused peaks is larger than that measured in previous studies of endothelial cells exposed to substrate stretching (Caille et al., 1998), demonstrating significant deformation of local segments of the IF network that were not detected in measurements at lower spatial resolution.

The complex distribution of displacement and strain indicate that cells do not undergo simple shear deformation during onset of unidirectional shear stress. Instead, the intracellular mechanical response depends on cytoskeletal network structure and interactions with other structural components of the cytoplasm. However, onset of shear stress induced increased IF displacement with height in the cell (Helmke et al., 2001), and an increased number of strain focusing peaks were often computed in apical optical sections. Taken together, these observations are consistent with increased sensitivity of the cell surface to either magnitude or gradients of shear stress that may depend on cell topography (Davies et al., 1997), temporal changes in force distribution (Bao et al., 2001), membrane mechanics (Butler et al., 2001), or distribution of signaling molecules (Gudi et al., 1996).

The computation of mechanical strain at high spatial resolution has several advantages. Strain was computed using the displacement of endogenous features on the IF cytoskeleton using a GFP fusion protein. Since the expression of GFP-vimentin does not affect physiological IF polymerization dynamics (Yoon et al., 1998), measurements of displacement and deformation are more accurate than when using exogenously introduced markers such as microspheres. Furthermore, spatially averaged strain computed from displacements of internalized microspheres (Caille et al., 1998; Simon and Schmid-Schonbein, 1990) requires the assumption that the cytoplasm can be represented by a viscoelastic continuum. In contrast, measurement of intracellular strain at high resolution will lead to more precise structured material models of the cell that will more directly relate extracellular mechanical forces to mechanisms of biochemical signaling. Although it is likely that the cell deforms in 3-D, the high-resolution strain field computed from 2-D optical sections nevertheless reveals novel features of IF deformation that are only visible at a subcellular length scale. Strain focusing represents local alterations in mechanical properties or force transmission, and future studies comparing locations of strain focusing and specialized structures involved in signaling will reveal physical interactions involved in the initiation of mechanochemical signaling.

Several factors may contribute to errors in estimation of cytoplasmic strain, including vertex tracking, estimation of vertex coordinates, and dependence of strain magnitude on triangle size. Manual tracking of randomly selected vertices connecting IF segments revealed that the automated tracking method accurately reported vertex positions. Less than 5% of manually tracked points were reported incorrectly at any point in the time-lapse sequences, even though the tracking method was designed for a lower spatial density of particles (Crocker and Grier, 1996). Additional analysis was performed in order to evaluate whether the locally finite stretch ratio magnitudes computed here were related to the size of spatial elements (triangles). Values of λI computed manually from randomly selected vertices had values in the range 1.2–1.4, which agrees well with previous reports of cytoplasmic strain using internalized microspheres (Caille et al., 1998; Simon and Schmid-Schonbein, 1990). Using vertices selected near the edges of cells yielded λI values of 1.01–1.05, confirming that intracellular strains are larger than overall cell shape changes (Simon and Schmid-Schonbein, 1990). By analogy, it is not surprising that large values of strain focusing were computed at even higher spatial resolution, whereas median stretch ratio magnitude for an entire optical section was relatively constant (Fig. 7, A and C). As the length of a spatial element is reduced, the relative length change for a fixed absolute change in distance between points is increased, resulting in a larger computed strain magnitude. In order to determine whether high spatial resolution limited the detection of small stretch ratio magnitude, an analysis using the smallest resolvable equilateral triangle was performed. Vertices in this triangle were initially separated by 0.878 μm. Stretching the triangle along its height by 0.5 pixel (0.055 μm) resulted in λI = 1.07; shearing the triangle by 0.5 pixel resulted in λI = 1.04. Since λI had much larger magnitude at locations of strain focusing, this worst-case model demonstrates that triangle size did not limit the ability to detect strain at high spatial resolution.

In order to further verify the accuracy of the computed stretch ratios, areas of triangles connecting adjacent vertices were compared to the product λIλII. The relative change in individual triangle areas agreed well with trends reported by λIλII, and the mean value did not vary significantly with time. This confirms that median λIλII accurately reports that overall area of the IF network in a 2-D optical section did not vary with time or onset of shear stress (Fig. 7 D). However, computed values do not reflect movement or strain along the optical axis that represents 3-D movement of IF segments. Instead, principal strain magnitude is projected onto the plane of the optical slice. Since resolution along the optical axis is lower than that in the optical plane, very few vertices moved in or out of the plane during these relatively short intervals. Thus, small vertical displacements had negligible effect on the projected strain values. Furthermore, out-of-plane motion would likely cause the projected strain magnitude to be underestimated, resulting in even larger values for magnitude of principal strain. Confirmation of this hypothesis will require extension of the current method to 3-D in order to more accurately measure local changes in element volume. Nevertheless, projection of 3-D movement onto 2-D optical sections represents the highest resolution approximation of IF strain currently available.

In all cells studied, the variability of stretch orientation increased significantly after onset of shear stress independent of the height of the optical section (Fig. 7 B). However, an increase in the confidence interval to include the entire circle may indicate multiple preferred orientations locally near sites of strain focusing rather than randomness of stretch direction. For example, stretch orientation near the upstream boundary of the cell (verified using brightfield microscopy) was often perpendicular to the edge and its associated IFs (Fig. 6, B and D). The mean orientation in this spatial region exhibits significant variability even though the direction of stretch is not random with respect to local structure. Thus, a more careful analysis reveals the spatial relationships among strain directions and cytoskeletal structure locally near sites of strain focusing.

Several mechanisms may be proposed to explain the high stretch magnitudes computed in areas of strain focusing. Vimentin polymer gels in vitro are capable of undergoing high strains without breakage (Janmey et al., 1991). However, it is likely that intracellular mechanical properties are determined by a composite response of all three principal filament networks. Copolymers of vimentin and actin also stretch without breakage even though they exhibit higher shear modulus than polymers of pure vimentin (Janmey et al., 1991). Thus, IFs may serve to maintain mechanical integrity of the cytoplasm during cellular adaptation to shear stress that includes disassembly and reassembly microfilament and microtubule networks (Galbraith et al., 1998). Furthermore, strain focusing reflects a role for IF either directly or via interactions with microfilaments or microtubules during mechanical adaptation of other specialized structures such as focal adhesion sites (Wernick et al., 1998), gap junctions (DePaola et al., 1999), and adherens junctions (Langille, 2001).

Since strain focusing may be localized near such specialized cellular structures, these measurements of strain in the IF network have important implications for regulation of cell physiology. Localized changes in force or stiffness induced by shear stress may modulate molecular interactions or protein conformations to initiate signaling via focal adhesion proteins (Li et al., 1997), small G proteins that regulate actin dynamics (Li et al., 1999), cadherins associated with adherens junctions (Langille, 2001), or multiple signaling proteins associated with cell surface caveolae (Rizzo et al., 1998). For example, strain focusing often occurred in optical sections near the basal cell surface (Fig. 4). Comparison of strain focusing locations to IF network morphology suggests that finite deformations occur locally that serve to modulate molecular interactions among the cytoskeleton, scaffolding proteins, and structural assemblies. The total area of high stretch ratio magnitude was less than the area of close adhesions measured previously (Davies et al., 1993), suggesting that not all focal adhesion sites experience significant flow-induced deformation via the IF cytoskeleton. However, a direct comparison of cytoskeletal strain focusing locations to focal adhesion activation has not yet been performed. In addition to strain focusing putatively near focal adhesion sites, spatial organization of flow-mediated signaling may also occur at other sites in the cell. For example, activation of the small G-protein Rac is spatially localized in regions of lamellae associated with increased actin dynamics (Kraynov et al., 2000) that have also been implicated in the shear stress-induced migration of single isolated endothelial cells (Li et al., 2002). In addition, redistribution of intracellular mechanical forces by the cytoskeleton may directly or indirectly regulate gene expression (Janmey, 1998). Cytoplasmic IFs may transmit force to the nucleus directly via interactions with the nuclear lamina (Goldman et al., 1986), and shear stress mediates translocation of plakoglobin away from adherens junctions to the nucleus where it interacts with transcription factors (Noria et al., 1999). Finally, previous observations of parallel displacement of IFs near adjacent cell boundaries (Helmke et al., 2001) together with strain focusing near these regions suggest that the cell is capable of regulating barrier permeability in the presence of a complex local mechanical environment. Taken together, these observations suggest that strain focusing may play an important role in modulation of physiological and pathological functions such as endothelial barrier function, transendothelial transport, intercellular communication, and migration or wound repair.

References

  1. Ando, J., T. Komatsuda, and A. Kamiya. 1988. Cytoplasmic calcium response to fluid shear stress in cultured vascular endothelial cells. In Vitro Cell. Dev. Biol. 24:871–877. [DOI] [PubMed] [Google Scholar]
  2. Bao, X., C. Lu, and J. A. Frangos. 2001. Mechanism of temporal gradients in shear-induced ERK1/2 activation and proliferation in endothelial cells. Am. J. Physiol. 281:H22–H29. [DOI] [PubMed] [Google Scholar]
  3. Butler, P. J., G. Norwich, S. Weinbaum, and S. Chien. 2001. Shear stress induces a time- and position-dependent increase in endothelial cell membrane fluidity. Am. J. Physiol. 280:C962–C969. [DOI] [PubMed] [Google Scholar]
  4. Caille, N., Y. Tardy, and J. J. Meister. 1998. Assessment of strain field in endothelial cells subjected to uniaxial deformation of their substrate. Ann. Biomed. Eng. 26:409–416. [DOI] [PubMed] [Google Scholar]
  5. Crocker, J. C., and D. G. Grier. 1996. Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 179:298–310. [Google Scholar]
  6. Davies, P. F. 1995. Flow-mediated endothelial mechanotransduction. Physiol. Rev. 75:519–560. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Davies, P. F., K. A. Barbee, M. V. Volin, A. Robotewskyj, J. Chen, L. Joseph, M. L. Griem, M. N. Wernick, E. Jacobs, D. C. Polacek, N. DePaola, and A. I. Barakat. 1997. Spatial relationships in early signaling events of flow-mediated endothelial mechanotransduction. Annu. Rev. Physiol. 59:527–549. [DOI] [PubMed] [Google Scholar]
  8. Davies, P. F., A. Robotewskyj, and M. L. Griem. 1993. Endothelial cell adhesion in real time. Measurements in vitro by tandem scanning confocal image analysis. J. Clin. Invest. 91:2640–2652. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. DePaola, N., P. F. Davies, W. F. Pritchard, Jr., L. Florez, N. Harbeck, and D. C. Polacek. 1999. Spatial and temporal regulation of gap junction connexin43 in vascular endothelial cells exposed to controlled disturbed flows in vitro. Proc. Natl. Acad. Sci. USA. 96:3154–3159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Dewey, C. F., Jr., S. R. Bussolari, M. A. Gimbrone, Jr., and P. F. Davies. 1981. The dynamic response of vascular endothelial cells to fluid shear stress. J. Biomech. Eng. 103:177–188. [DOI] [PubMed] [Google Scholar]
  11. Fisher, N. I. 1993. Statistical Analysis of Circular Data. Cambridge: Cambridge University Press.
  12. Galbraith, C. G., R. Skalak, and S. Chien. 1998. Shear stress induces spatial reorganization of the endothelial cell cytoskeleton. Cell Motil. Cytoskeleton. 40:317–330. [DOI] [PubMed] [Google Scholar]
  13. Goldman, A. E., G. Maul, P. M. Steinert, H. Y. Yang, and R. D. Goldman. 1986. Keratin-like proteins that coisolate with intermediate filaments of BHK-21 cells are nuclear lamins. Proc. Natl. Acad. Sci. USA. 83:3839–3843. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gudi, S. R., C. B. Clark, and J. A. Frangos. 1996. Fluid flow rapidly activates G proteins in human endothelial cells. Circ. Res. 79:834–839. [DOI] [PubMed] [Google Scholar]
  15. Helmke, B. P., and P. F. Davies. 2002. The cytoskeleton under external fluid mechanical forces: hemodynamic forces acting on the endothelium. Ann. Biomed. Eng. 30:284–296. [DOI] [PubMed] [Google Scholar]
  16. Helmke, B. P., R. D. Goldman, and P. F. Davies. 2000. Rapid displacement of vimentin intermediate filaments in living endothelial cells exposed to flow. Circ. Res. 86:745–752. [DOI] [PubMed] [Google Scholar]
  17. Helmke, B. P., D. B. Thakker, R. D. Goldman, and P. F. Davies. 2001. Spatiotemporal analysis of flow-induced intermediate filament displacement in living endothelial cells. Biophys. J. 80:184–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ingber, D. 1997. Tensegrity: the architectural basis of cellular mechanotransduction. Annu. Rev. Physiol. 59:575–599. [DOI] [PubMed] [Google Scholar]
  19. Janmey, P. A. 1998. The cytoskeleton and cell signaling: component localization and mechanical coupling. Physiol. Rev. 78:763–781. [DOI] [PubMed] [Google Scholar]
  20. Janmey, P. A., U. Euteneuer, P. Traub, and M. Schliwa. 1991. Viscoelastic properties of vimentin compared with other filamentous biopolymer networks. J. Cell Biol. 113:155–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kraynov, V. S., C. Chamberlain, G. M. Bokoch, M. A. Schwartz, S. Slabaugh, and K. M. Hahn. 2000. Localized Rac activation dynamics visualized in living cells. Science. 290:333–337. [DOI] [PubMed] [Google Scholar]
  22. Langille, B. L. 2001. Morphologic responses of endothelium to shear stress: reorganization of the adherens junction. Microcirculation. 8:195–206. [DOI] [PubMed] [Google Scholar]
  23. Levesque, M. J., and R. M. Nerem. 1985. The elongation and orientation of cultured endothelial cells in response to shear stress. J. Biomech. Eng. 107:341–347. [DOI] [PubMed] [Google Scholar]
  24. Li, S., P. J. Butler, Y. Wang, Y. Hu, D. C. Han, S. Usami, J.-L. Guan, and S. Chien. 2002. The role of the dynamics of focal adhesion kinase in the mechanotaxis of endothelial cells. Proc. Natl. Acad. Sci. USA. 99:3546–3551. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Li, S., B. P. Chen, N. Azuma, Y. L. Ju, S. Z. Wu, B. E. Sumpio, J. Y.-J. Shyy, and S. Chien. 1999. Distinct roles for the small GTPases Cdc42 and Rho in endothelial responses to shear stress. J. Clin. Invest. 103:1141–1150. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Li, S., M. Kim, Y. L. Hu, S. Jalali, D. D. Schlaepfer, T. Hunter, S. Chien, and J. Y.-J. Shyy. 1997. Fluid shear stress activation of focal adhesion kinase. Linking to mitogen-activated protein kinases. J. Biol. Chem. 272:30455–30462. [DOI] [PubMed] [Google Scholar]
  27. Noria, S., D. B. Cowan, A. I. Gotlieb, and B. L. Langille. 1999. Transient and steady-state effects of shear stress on endothelial cell adherens junctions. Circ. Res. 85:504–514. [DOI] [PubMed] [Google Scholar]
  28. Ohno, M., G. H. Gibbons, V. J. Dzau, and J. P. Cooke. 1993. Shear stress elevates endothelial cGMP. Role of a potassium channel and G protein coupling. Circulation. 88:193–197. [DOI] [PubMed] [Google Scholar]
  29. Rizzo, V., A. Sung, P. Oh, and J. E. Schnitzer. 1998. Rapid mechanotransduction in situ at the luminal cell surface of vascular endothelium and its caveolae. J. Biol. Chem. 273:26323–26329. [DOI] [PubMed] [Google Scholar]
  30. Shah, J. V., L. Z. Wang, P. Traub, and P. A. Janmey. 1998. Interaction of vimentin with actin and phospholipids. Biol. Bull. 194:402–405. [DOI] [PubMed] [Google Scholar]
  31. Simon, S. I., and G. W. Schmid-Schonbein. 1990. Cytoplasmic strains and strain rates in motile polymorphonuclear leukocytes. Biophys. J. 58:319–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Svitkina, T. M., A. B. Verkhovsky, and G. G. Borisy. 1996. Plectin sidearms mediate interaction of intermediate filaments with microtubules and other components of the cytoskeleton. J. Cell Biol. 135:991–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Tzima, E., M. A. del Pozo, S. J. Shattil, S. Chien, and M. A. Schwartz. 2001. Activation of integrins in endothelial cells by fluid shear stress mediates Rho-dependent cytoskeletal alignment. EMBO J. 20:4639–4647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Wernick, M. N., M. L. Griem, A. Robotewskyj, and P. F. Davies. 1998. Image analysis of the dynamic changes of adhesion sites in endothelial cells subjected to directional flow in vitro. Journal of Vascular Investigation. 4:15–23. [Google Scholar]
  35. Yoon, M., R. D. Moir, V. Prahlad, and R. D. Goldman. 1998. Motile properties of vimentin intermediate filament networks in living cells. J. Cell Biol. 143:147–157. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES