The Effects of Intense Submicrosecond Electrical Pulses on Cells

Abstract

A simple electrical model for living cells predicts an increasing probability for electric field interactions with intracellular substructures of both prokaryotic and eukaryotic cells when the electric pulse duration is reduced into the sub-microsecond range. The validity of this hypothesis was verified experimentally by applying electrical pulses (durations 100 μs–60 ns, electric field intensities 3–150 kV/cm) to Jurkat cells suspended in physiologic buffer containing propidium iodide. Effects on Jurkat cells were assessed by means of temporally resolved fluorescence and light microscopy. For the longest applied pulses, immediate uptake of propidium iodide occurred consistent with electroporation as the cause of increased surface membrane permeability. For nanosecond pulses, more delayed propidium iodide uptake occurred with significantly later uptake of propidium iodide occurring after 60 ns pulses compared to 300 ns pulses. Cellular swelling occurred rapidly following 300 ns pulses, but was minimal following 60 ns pulses. These data indicate that submicrosecond pulses achieve temporally distinct effects on living cells compared to microsecond pulses. The longer pulses result in rapid permeability changes in the surface membrane that are relatively homogeneous across the cell population, consistent with electroporation, while shorter pulses cause surface membrane permeability changes that are temporally delayed and heterogeneous in their magnitude.

INTRODUCTION

The basic effects of an electric field on a living cell can be described by considering the cell to be a conductive body (the cytoplasm) surrounded by a dielectric layer (the surface membrane). When an electric field is applied to this cell (by placing the cell in a conductive medium between two electrodes and applying a unipolar voltage pulse to the electrodes), the resulting current causes accumulation of electrical charges at the cell membrane and consequently a voltage across the membrane. If the membrane voltage exceeds a critical value, structural changes in the surface membrane occur that cause pore formation/increased permeability, a process known as electroporation (Weaver, 1995). If the membrane voltage is not excessive and the duration of the pulse is limited, the increased membrane permeability can be reversible and the cell survives, an effect that is used for electrochemotherapy and gene delivery into cells (Dev et al., 2000).

The time required to charge the surface membrane is dependent upon the electrical parameters of both the cell and the medium in which it is suspended. For a spherical cell with a surface membrane that is an ideal dielectric layer (no leakage currents) and for low volume concentration of cells in suspension, the charging time constant is (Cole, 1937):

(1)

where C_m is the capacitance of the surface membrane per unit area, D is the cell diameter, ρ_c is the resistivity of the cytoplasm, and ρ_a is the resistivity of the medium in which the cell is suspended. For a cell with a diameter of 10 μm, resistivities of cytoplasm and medium of 100 Ω-cm, and a membrane capacitance of 1 μF/cm², τ_c is 75 ns.

The charging time constant is a measure of the time during which the cell interior is exposed to the applied pulsed electric field. This is equivalent to the statement that the outer membrane becomes increasingly transparent for oscillating electric fields when the angular frequency of the oscillation exceeds a value given by the inverse of the charging time (Schwan, 1985). A spherical cell model, which describes the coupling of electric fields to nuclear membranes, has been introduced by Foster (2000). To describe the effect of short pulses on the cell interior, it is assumed that a nonconducting membrane surrounds the target cell substructure (e.g., the cell nucleus) and the cell itself. An electrical equivalent circuit that takes the internal structure into account is shown in Fig. 1. Application of an electric field to the cell suspension results in conduction currents in the suspending medium and cytoplasm and a corresponding displacement current through both membranes, the outer one and the membrane surrounding the subcellular structure. Such a structure could be the nucleus or any other membrane-bound intracellular substructure.

FIGURE 1.

Cross section of a spherical cell with centrally located nucleus, embedded in a medium. The equivalent circuit for the cell contains the capacitors of the outer cell membrane, C_m; the nuclear membrane, C_n; the resistors, which represent the electrical conduction of the cytoplasm, R_c1–3; and the nucleoplasm, R_n. C_s and R_s represent the capacitance and resistance of the medium.

There are two main effects on membrane-bound substructures caused by very rapidly varying electric fields. The first is an increasing charging of the inner membrane, with increased rate of change in the applied electric field intensity. This effect, which is based on capacitive coupling, leads to substantial subcellular, transmembrane voltages if high electric field pulses (whose characteristic rise times are less than the charging time of the surface membrane) are applied. For mammalian cells, this time is typically on the order of a hundred nanoseconds. To reach the transmembrane voltages V that are required for intracellular electroporation, which are presumably of the same order needed for surface membrane poration (V > 1V), the pulsed electric field amplitude needs to reach values of ∼2 V/d, with d being the diameter of the substructure. For substructures of micrometer diameter, this is >10⁶ V/m. The second effect, which is coupled to this intracellular membrane charging effect, is increasing energy deposition through joule heating in the substructure. For electrical pulses with the same total energy, the energy deposition into the cellular substructure is orders of magnitude higher for nanosecond compared to multimicrosecond pulses.

Besides knowledge of the electrical parameters of surface membranes, intracellular membranes, the cytoplasm and intraorganelle environments, exact predictions of the response of surface and intracellular membranes require accurate models of the cell in response to electric fields. While data based on time domain dielectric spectroscopy of cell suspensions have yielded information on the electrical parameters of cellular substructures (Polevaya et al., 1999), cell models which take intracellular responses to external electric fields into account are still based on relatively crude assumptions (Foster, 2000; Schoenbach et al., 2001).

Because the effects of short pulses on the breakdown of membranes surrounding subcellular structures have been demonstrated previously (Schoenbach et al., 2001), in this study we sought to examine and compare the temporal development of long versus short pulsed electric field effects on surface membrane permeability and cellular morphology.

EXPERIMENTAL SET-UP AND PROCEDURES

An experimental system was designed and built which allows observation of the temporal evolution of fluorescent and light microscopy changes in living cells following electrical pulse applications (Fig. 2). A similar set-up has been used by Prausnitz et al. (1995) to perform millisecond measurements of transport during and after millisecond duration electroporation pulses. The cell chamber (Fig. 2) was examined at 400× magnification using an Olympus IX70 inverted microscope (Olympus America, Melville, NY). The chamber consisted of a 51 × 76 mm glass microscope slide with two 0.1-mm stainless steel electrodes attached to the surface with silicone adhesive. The electrodes were one rectangular and one asymmetric hexagon positioned to achieve opposing electrode surfaces 5 mm long with a gap of 0.33 mm. After placement of 45–70 μL of cell suspension in the channel between the electrode surfaces, a standard square 0.17-mm thick glass cover slip was laid over the electrode gap and the chamber was placed on the microscope stage. Solid copper contacts were laid onto the stainless steel electrodes, the field for observation was selected, and the experiment was begun.

FIGURE 2.

Experimental set-up with enlarged sketch of the treatment slide chamber. The gap between the two stainless steel electrodes is 330 μm. High voltage pulses range from 100 V to 2.5 kV, with pulse duration range from 60 ns to 100 μs.

Jurkat cells, clone E6-1 are a nonadherent, T-lymphocyte cell line (American Type Culture Collection, Manassas, VA) that was grown and passed in RPMI 1640 medium supplemented with 10% fetal bovine serum, 1% glutamine, 1% penicillin/streptomycin. Cells were routinely passed every 2–3 days when their concentrations were between 0.2–1 × 10⁶/mL. At the time of experiment, Jurkat cells were washed once in Hanks' balanced salt solution without Ca²⁺ and Mg²⁺ (HBSSw/o), adjusted to 1–1.5 × 10⁷/mL in HBSSw/o, combined 1:1 with 30 μM propidium iodide (PI) in HBSSw/o, and placed in the electrode chamber. During experiments, cell/propidium iodide suspensions were held for up to 3 h at room temperature in the dark. The size of the Jurkat cells is heterogeneous, most cells varying between 7–20 μm in diameter: occasional cells are 30–40 μm in diameter, all of which are small relative to the dimensions of the electrode gap (330 μm × 100 μm × 5000 μm).

PI is a fluorescent dye used extensively as an indicator for surface membrane integrity in living cells (Rols and Teissie, 1998). It is excluded from the cell interior by an intact surface membrane where it is nonfluorescent under the conditions used. If the surface membrane is breached, PI rapidly enters the cell and readily binds to nucleic acids in the nucleus, developing red fluorescence. The intensity of red fluorescence varies with the amount of PI bound to the nucleic acids, providing quantitative information when subsaturating amounts of PI have entered the cell.

Electrical pulses (Fig. 3) with durations of 60 ns, 300 ns, 10 μs, and 100 μs and amplitudes of 0.1–5 kV (producing corresponding electric fields between the electrodes of 3–150 kV/cm) were used in experiments. Pulse voltages, V, were chosen such that the electrical energy density, W, applied for time, τ, to the cell suspension which had an electrical resistivity, ρ,

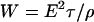(2)

covered approximately the same range for each pulse duration. For example, a 100 μs square pulse with an electric field of 3 kV/cm applied to the suspension between the electrodes provided the same energy density as a 300 ns pulse with 55 kV/cm, i.e., 9 J/cm³, for a measured resistivity of ∼100 Ω-cm in the cell suspension. The maximum energy density, obtained with 100 μs pulses with electric fields of 6 kV/cm in the cell suspension, was consequently 36 J/cm³. Assuming a homogeneous distribution of the energy, the increase in temperature under these extreme conditions was 8.7 K. For shorter pulses, e.g., with duration of 300 ns and a 60 kV/cm electric field, the calculated temperature increase was 2.5 K.

FIGURE 3.

Oscilloscope tracings of representative 100 μs, 10 μs (upper tracings), 300 ns, and 60 ns (lower tracings) pulses.

The 60 ns and 300 ns pulses were produced by a Blumlein circuit switched by a pressurized spark gap (Deng et al., 2000). The Blumlein circuit consisted of two 50 Ω coaxial cables, which gave a total impedance of 100 Ω. This value was chosen to match the impedance of the cable, Z, to the resistance of the cell suspension between the two electrodes, R. In this case, the energy stored in the cables is transferred into the load in the form of a rectangular power pulse, with the pulse duration determined by the length of the cable and the speed of electromagnetic waves in the dielectric of the cable (Mankowski and Kristiansen, 2000). For the cables used in this device, the dielectric constant is ɛ_r = 2.25, producing a wave velocity 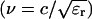of 2 × 10⁸ m/s with c being the speed of light in a vacuum. The total pulse duration, T, for the Blumlein circuit is determined by the length of the two cables, l, as T = l/ν. The rise time of the pulse (e.g., the time to reach a steady state mode with a current of I = V_o/Z) is determined by the closing switch, where V_o is the value of the applied voltage. In this device, a spark gap with a closing time of less than 10 ns was used to produce 60 ns and 300 ns pulses (Fig. 3, bottom) with amplitude jitter of less than 5%. Since the amplitude of the voltage applied is below 1 kV for pulses with duration in excess of 1 μs, a pulse generator using MOS field effect transistors (BIMOSFET; IXBH 40N160, IXYS Corporation, Santa Clara, CA) could be used. The rise time of these pulses (Fig. 3, top) is ∼50 ns, which is short compared to the pulse duration. The maximum voltage of the long pulse was 1.6 kV, limited by the maximum operating voltage of the BIMOSFET; the maximum voltage of the short pulses was 5 kV, limited by the hold-off voltage of the cable connectors.

The application of and cellular responses to electric field pulses were visualized and recorded using a low-light, computer-controlled CCD camera (Olympix FKI300, Olympus America, Melville, NY). The maximum recording speed of the camera, 100 frames/s (10 ms/frame), was long compared to the pulse duration of the applied electric fields but was sufficient for use since the biological processes of interest developed on a time scale long compared to 10 ms (in practice, the temporal acquisition of PI fluorescence evolved over times long even compared to seconds). Software (Merlin, LSR, Cambridge, England, UK) was used to control the camera, with either a 10-second (for most experiments) or 3-second (for experiments examining the orientation of PI uptake relative to the electrodes) pause between images and 1.6 seconds required to acquire and process each image. To minimize quenching of specimen fluorescence and specimen heating, ultraviolet illumination of the specimen (excitation 340 nm, emission 500 nm) was blocked with a software-controlled (Merlin Software) filter changer for the 10 s separating each image. Each experimental condition was observed over ∼30 min (155 frames) with the pulsed electric field application administered 58–70 s (frame 5–6) after the start of the experimental run. For the first 15 min of each run (frames 2–80), a white light image rather than a fluorescent image was acquired approximately every 100 s. Over the subsequent 15 min (frames 81–155), white light images were acquired approximately every 5 min through the end of the experiment. White light illumination intensity and CCD camera sensitivity were adjusted so that image gray scale sensitivity ranges for both fluorescence and white light images were in the 50–350 unit range.

At completion of each experiment, analysis of the fluorescent images was performed using Merlin software. For each series of fluorescent images making up an experimental run, areas of interest (using the default size setting) were defined manually for each cell in the field based upon their positions over time from one white light image to the next. As controls, an area of image background and a dead cell in the field were also designated as areas of interest. The average gray scale intensity of each area of interest was then automatically calculated for each image in the series. Consequently, the temporal development of PI fluorescence in individual cells across time could be graphed as gray scale intensity versus time, and referenced to background and dead cell fluorescence. In some experiments, the temporal development of fluorescence in two areas of the nucleus, the side closest to the anode and the side closest to the cathode, were recorded simultaneously.

Cell areas were estimated from the white light images by importing each white light image into drawing software (CorelDraw 9, Corel, Montreal, Canada), tracing the circumference of each cell in the field, filling the circumference to create an image object, importing sets of image objects (as .tif files) into image analysis software (SigmaScanPro 4, Jandel Scientific, San Rafael, CA), and measuring the area of each image object (cell) in units of pixels². A mean cell area for each time point in a run was calculated, and across different experiments, these values from corresponding time points were averaged to yield the mean ± SE area values reported.

Unless otherwise specified, data are expressed as mean ± SE values. Mean values are compared by Student's t-test, and probabilities <0.05 are declared statistically significant.

RESULTS

The measurements performed with pulses of various durations, ranging from 100 μs to 60 ns, showed a clear tendency: the effects of relatively long (microsecond) pulses on membrane integrity occurred rapidly, suggesting a direct effect upon the surface membrane (i.e., primary electroporation). In contrast, the effects of shorter (submicrosecond) pulses were delayed, suggesting a secondary/indirect effect on the surface membrane (Fig. 4).

FIGURE 4.

Representative gray scale recordings from individual cells in the same visual field following 100 μs, 10 μs, 300 ns, or 60 ns pulses. Dotted lines represent gray scale recording from a dead cell (PI saturated) in the same video field except for the 300 ns pulse, whose video field did not contain a dead cell. Therefore, the dead cell tracing in that panel was taken from a subsequent experimental run (same day, same experiment) which used identical gray scale range settings.

The application of long pulses (100 μs) in the first minute of an experiment resulted in PI uptake in 15–39% of cells (n = 6–7) by the end (30 min) of the experiment depending on the amplitude of the electric field (Table 1). The magnitude of dye uptake was variable (Fig. 4), 137 ± 2 (n = 11) gray scale units at the end of the experiment, and only on rare occasions did individual cell dye uptake equal that of already dead cells found in the preparation (background intensity 108.5 ± 0.05 (n = 157) gray scale units, dead cell intensity 221.3 ± 0.5 (n = 157) gray scale units). Uptake occurred rapidly, with median onset in the fifth minute of the experiment (Fig. 5). For pulse durations of 10 μs, 3–45% of cells ultimately took up PI depending on the applied electric field, the magnitude of uptake was variable (149 ± 7 (n = 11) gray scale units at the experiment end), and median onset of uptake was also in the fifth minute of the experiment (Fig. 5). As the pulse duration shortened through 60 ns, the median onset of PI uptake became progressively delayed: 300 ns pulse, 10th minute; 60 ns pulse, 16th minute (Fig. 5), and the magnitude of dye uptake remained variable: 300 ns pluse, 154 ± 6 (n = 15) gray scale units; 60 ns pulse, 161 ± 16 (n = 11) gray scale units. Despite this delay in onset of PI uptake with short pulses, the percentages of cells ultimately taking up PI following the largest pulse amplitudes used for 60 and 300 ns pulses were similar: 27 ± 15% – 54 ± 9%. In all except the 60 ns pulse conditions, increasing pulse amplitudes were associated with increasing percentages of cells taking up PI (Table 1).

TABLE 1.

Percentages of cells showing PI uptake (≥10 units increase in gray scale intensity) after pulsed electric field application

		Percentage of cells
Pulse duration	Electric field	Mean	Standard error	(n)
Control	0	2	1	(25)
100 μs	3 kV/cm	15	5	(7)
	6 kV/cm	39	10	(6)
10 μs	3 kV/cm	3	1	(8)
	6 kV/cm	45	11	(8)
300 ns	30 kV/cm	17	9	(9)
	45 kV/cm	41	13	(9)
	60 kV/cm	54	9	(9)
60 ns	30 kV/cm	8	5	(4)
	45 kV/cm	15	9	(4)
	60 kV/cm	20	10	(8)
	75 kV/cm	27	15	(6)

FIGURE 5.

Normalized distributions for time of onset of PI uptake observed with multimicrosecond and submicrosecond pulsed electric field applications. Arrows indicate median time of onset for each pulse duration.

The spatial development of dye uptake was also examined for multimicrosecond and submicrosecond pulses. For long pulses, onset of fluorescence uptake followed shortly after pulse application, and fluorescence increased more rapidly in that part of the nucleus oriented toward the anode (Fig. 6). For shorter pulses, onset of fluorescence was delayed as shown in Fig. 6, and the spatial development of the fluorescence occurred without obvious orientation to the direction of the applied electric field. Thus, for long pulses, surface membrane integrity was lost immediately with anodic preference; for short pulses, loss of surface membrane integrity was delayed and did not have a discernable electrode preference.

FIGURE 6.

Charge distribution (upper left) and corresponding voltage distribution along the cell axis (upper right), indicating that the membrane voltage depends on the polarity of the electrodes. Lower panels show mean ± SE gray scale values for anodic and cathodic regions of nuclei in cells exposed to multimicrosecond (lower left) and submicrosecond (lower right) pulsed electric field applications, illustrating more rapid anodic dye uptake with longer pulses and absence of this effect with short pulses.

The changes in cell morphology induced by long pulses were most striking: cells went from showing somewhat refractile edges with little intracellular detail visible before pulse application, to diminished refractile edges and appearance of intracellular detail (Fig. 7). Similar changes occurred with short pulses, although they became less striking as the pulse duration went from 300 ns to 60 ns. In association with these morphologic changes, cells that underwent multimicrosecond and 300-ns pulse exposures all increased their two-dimensional cell areas by 15 min, while cells exposed to 60 ns pulses had no significant increase in their cell areas (Table 2).

FIGURE 7.

Representative microscopic images of cells before (left) and 15 min after (right) the pulsed electric field applications specified.

TABLE 2.

Effects of pulse duration on cell size

Pulse Duration	Pre-pulse	Post-pulse	End
Control (n = 13)	2930 ± 200*		2943 ± 215
60 ns (n = 13)	2677 ± 66	2739 ± 77	2849 ± 79
300 ns (n = 14)	2621 ± 46	2845 ± 69†	3614 ± 79‡
10 μs (n = 10)	2712 ± 59	2940 ± 80†	3531 ± 164‡
100 μs (n = 8)	2894 ± 41	3215 ± 77†	3583 ± 81‡

Pre-pulse, white light image immediately before pulse application.

Post-pulse, first white light image after pulse application.

End, white light image at 15 min.

^*Data shown are mean ± SE values for two-dimensional cell areas in pixels².

^†p < 0.05 versus pre-pulse.

^‡p < 0.05 versus post-pulse.

DISCUSSION

Information on the cellular effects of submicrosecond pulsed electric fields is limited (Müller et al., 2001). Our data suggest that these effects are different from ordinary electroporation in at least three ways. First, instead of rapid permeabilization of the surface membrane, indicated by the rapid uptake of PI by cells, the membranes of cells exposed to short pulses become permeable to PI after a relatively long lag time following pulse application. In the case of 60 ns pulses, the median for this lag time was 15 min. Second, dye uptake is not polarized toward the anode. Third, cell swelling, which occurs after pulses ≥300 ns duration, does not occur, suggesting that shorter pulses minimize uncompensated redistribution of sodium and water through the surface membrane, as occurs with electroporation.

We interpret these results as proof that for short electrical pulses, the effects on the cell membrane cannot be described in terms of conventional electroporation. Increased permeability of the cell membrane (indicated by dye uptake) occurs progressively longer after pulse application as the pulse duration shortens, and this temporal separation from the pulse application suggests that the membrane permeability effects are more likely due to alterations of cellular function rather than direct effects on surface membrane structure. The increase in cell size seen with pulses longer than 60 ns likely represents colloid osmotic swelling of cells in physiologic buffer, and as such, would be typical of electroporation with delayed resealing of the pores (Hui and Li, 2000).

As to why the temporal delay in increased surface membrane permeability occurs as the pulse duration shortens, several potential explanations can be proposed. We currently hypothesize (Schoenbach et al., 2002) that the dramatically increased energy deposition into intracellular structures that occurs with submicrosecond, compared to multimicrosecond, pulses plays a major role in the effects observed. Depending on the intracellular target(s) of these effects, release of normally sequestered intracellular components (e.g., release of hydrolytic enzymes from ruptured lysosomes or release of free Ca²⁺ from ruptured endoplasmic reticulum) or physical damage to structures themselves (e.g., DNA strand breaks or disruption of mitochondria) may occur that eventually becomes inconsistent with cellular survival. Apoptosis induction could result from such effects (Beebe et al., 2002), as has previously been reported after long pulses (Hoffmann et al., 1999). If this were the case, then the delayed onset of PI uptake observed after short pulses might well represent increased membrane permeability due to secondary necrosis, as is seen in many cell types following in vitro apoptosis induction. At present, testing for a relationship between short pulse applications and apoptosis induction using this microscope-based pulse system is ongoing.

The fact that short (nanosecond) pulses cause quite different effects on cell membranes than long (multimicrosecond) pulses is also obvious from the changing location of dye uptake at the circumference of the cell membrane. Whereas for long pulses the uptake is preferentially from the anode-facing side of the cell, for short pulses, the location of the dye uptake is randomly distributed over the cell surface. This asymmetric permeabilization of the cell membrane has been observed by others (Gabriel and Teissie, 1997; Djuzenova et al., 1996) and is assumed to be due to the increased potential at this location due to the contribution of the resting potential to the external field-induced potential. The asymmetry indicates the direct effect of the electric field on the permeabilization of the surface membrane, i.e., electroporation. The observed distribution of dye uptake location following short pulses, on the other hand, shows that breaching the membrane at these locations is a secondary effect, possibly induced by electric field interactions with subcellular structures that lead to secondary cellular events, including apoptosis induction (Beebe et al., 2002).

The application of pulsed electric fields with duration and amplitude characteristics that avoid thermal effects affords the opportunity to affect either surface or intracellular structures, depending on pulse duration. Whereas the effects of pulses that are long compared to the charging time of the surface membrane are well known and utilized in clinical applications, short pulses present a new area for development of diagnostic methods and therapies. The potential to utilize short pulses to manipulate intracellular structure and/or function may allow development of novel approaches to neoplasia, tissue remodeling, and/or wound healing. Continued research in this area is required to better understand the interactions between intense electric field applications and cellular structure/functions.