Role of Hyperpolarization-Activated Currents for the Intrinsic Dynamics of Isolated Retinal Neurons

Abstract

The intrinsic dynamics of bipolar cells and rod photoreceptors isolated from tiger salamanders were studied by a patch-clamp technique combined with estimation of effective impulse responses across a range of mean membrane voltages. An increase in external K⁺ reduces the gain and speeds the response in bipolar cells near and below resting potential. High external K⁺ enhances the inward rectification of membrane potential, an effect mediated by a fast, hyperpolarization-activated, inwardly rectifying potassium current (K_IR). External Cs⁺ suppresses the inward-rectifying effect of external K⁺. The reversal potential of the current, estimated by a novel method from a family of impulse responses below resting potential, indicates a channel that is permeable predominantly to K⁺. Its permeability to Na⁺, estimated from Goldman-Hodgkin-Katz voltage equation, was negligible. Whereas the activation of the delayed-rectifier K⁺ current causes bandpass behavior (i.e., undershoots in the impulse responses) in bipolar cells, activation of the K_IR current does not. In contrast, a slow hyperpolarization-activated current (I_h) in rod photoreceptors leads to pronounced, slow undershoots near resting potential. Differences in the kinetics and ion selectivity of hyperpolarization-activated currents in bipolar cells (K_IR) and in rod photoreceptors (I_h) confer different dynamical behavior onto the two types of neurons.

INTRODUCTION

Isolated retinal bipolar cells from tiger salamanders act like adaptive filters: at resting potential, their response gain and time constant are maximal, and transfer functions are lowpass. With membrane depolarization, gain is reduced, response speed increases, and dynamics become bandpass, as indicated by the emergence of an undershoot in the impulse responses. The adaptive behavior involves a voltage-dependent K⁺ channel that activates during depolarization (Mao et al., 1998, 2002).

Hyperpolarization-activated currents have been observed in bipolar cells in goldfish (Kaneko and Tachibana, 1985), white bass (Lasater, 1988), zebra fish (Connaughton and Maguire, 1998), and rat (Karschin and Wässle, 1990) and in photoreceptors of salamander (Bader et al., 1982; Bader and Bertrand, 1984; Hestrin, 1987; Barnes and Hille, 1989; Wollmuth and Hille, 1992), lizard (Maricq and Korenbrot, 1990), newt (Satoh and Yamada, 2000), guinea pig (Demontis et al., 1999), and monkey (Yagi and Macleish, 1994). The hyperpolarization-activated current has been shown to influence filtering properties between rods and bipolar cells in cats, as reflected in changes of the electroretinographic (ERG) b-wave induced by blocking the conductance (Gargini et al., 1999). Extracellular factors affect properties of hyperpolarization-activated channels in bipolar cells and in photoreceptors. In particular, ions such as K⁺ and Na⁺ affect conductance and permeability of the channels (Bader and Bertrand, 1984; Kaneko and Tachibana, 1985; Hestrin, 1987; Wollmuth and Hille, 1992), as is the case for the hyperpolarization-activated currents in other parts of the nervous system (Pape, 1996; Hille, 2001).

K⁺ may also regulate visual sensitivity of the retina of skate (Dowling and Ripps, 1976; Kline et al., 1978). The ERG b-wave reflects the response of the Müller cells to a K⁺ influx (Kline et al., 1978) in skate and that of ON-bipolar cells in rabbit (Dick et al., 1985) and tiger salamander (Tian and Slaughter, 1995). This is another reason to hypothesize that bipolar cells' responses might be influenced by extracellular K⁺ via a hyperpolarization-activated current.

In this study, we examine the relation between the properties of hyperpolarization-activated channels and the intrinsic dynamics of bipolar cells and rod photoreceptors, as characterized by their effective impulse responses. Using computer simulation, we demonstrate that the differences in dynamics are associated with the differences in the kinetics of the hyperpolarization-activated channels in bipolar cells and rod photoreceptors. By comparing the hyperpolarization-activated channels in bipolar cells (K_IR) and in rod photoreceptors (I_h), we highlight the roles of the hyperpolarization-activated channels in the two types of neurons for visual signal filtering in the retina.

METHODS

Dissociation of retina and whole-cell patch-clamp recording

Retinae of tiger salamanders (Kons Scientific Co., Inc., Germantown, WI) were enzymatically dissociated (MacLeish et al., 1984) in a solution containing 10 units/ml papain (Worthington Biochemical Corp., Lakewood, NJ) and (in mM) 84 NaCl, 3 KCl, 25 NaHCO₃, 0.5 NaH₂PO₄, 1 Na pyruvate, 0.5 CaCl₂, 16 glucose, 2 d,l-cysteine HCl, and 0.02 phenol red, bubbled with a mixture of 95% O₂ and 5% CO₂. The retinae were digested for 30–45 min, rinsed, triturated, and plated onto coverslips treated with the antibody Sal-1 (MacLeish et al., 1983). The isolated cells were maintained for up to one week in 10°C in a medium containing (in mM): 108 NaCl, 3 KCl, 0.5 MgCl₂, 0.5 MgSO₄, 1 NaHCO₃, 0.5 NaH₂PO₄, 1 Na pyruvate, 0.1 choline Cl, 1.8 CaCl₂, 1 HEPES, 16 glucose, 0.02 phenol red, and 50 μg/ml bovine serum albumin. Osmolarity was adjusted to 240 mOsm and pH to 7.2–7.4.

Isolated bipolar cells were identified by their characteristic Landolt club, an enlargement of the primary dendrite from an initially narrower segment of the dendrite (Hare et al., 1986; Mao et al., 1998). Rod photoreceptors were identified by their inner segments (MacLeish et al., 1983). Whole-cell patch-clamp recordings were made typically within two days after retina dissociation using a List EPC-7 amplifier (set at 3 kHz) and PCLAMP6 software and interface (Axon Instruments, Inc., Foster City, CA). Electrodes were pulled from borosilicate micropipettes (Drummond Scientific Company, Broomall, PA) on a BB-CH-PC puller (Mecanex S.A., Nyon, Switzerland), and had a 1-μm tip opening and 5–15 MΩ resistance, filled with an internal solution containing (in mM): 113 KCl, 5 MgCl₂, 10 HEPES, 0.05 EGTA, 1 NaATP, with osmolarity adjusted to 240 mOsm and pH to 7.2. External solutions (A, B, C, and D) are listed in Table 1, all with osmolarity 240 mOsm and pH 7.4.

TABLE 1.

External solutions

Solution	NaCl	KCl	Choline Cl	CaCl2	MgCl2	Glucose	HEPES	Phenol red	CsCl
A	108	3	0	2.5	1	16	5	0.02	–
B	70	0.75	37	2.5	1	16	5	0.02	–
C	70	12	26	2.5	1	16	5	0.02	–
D	70	12	16	2.5	1	16	5	0.02	10

Concentrations in mM.

Characterization of the hyperpolarization-activated channel of bipolar cells

The hyperpolarization-activated currents of bipolar cells were obtained by standard voltage-clamp techniques and analyzed with PCLAMP6 software. To enhance the current, the recordings were obtained in external solutions that contained high K⁺ (12 mM, solution C). The currents were isolated by the application of the channel blocker Cs⁺ (10 mM, solution D) and a current subtraction protocol in which pairs of current recordings corresponding to the same set of voltage commands were subtracted to obtain the current component blocked by Cs⁺. The reversal potential of the channel was estimated from families of impulse responses by using a novel method (see Results). The permeability ratio for Na⁺ vs. K⁺ (P_Na⁺/P_K⁺) of the channel was calculated from the Goldman-Hodgkin-Katz voltage equation (Hodgkin and Katz, 1949; Hille, 2001). This channel in bipolar cells was found to have the properties of a classical anomalous inward rectifier, and thus is henceforth termed K_IR, to distinguish it from the hyperpolarization-activated I_h channel in rod photoreceptors. Ion channel properties were analyzed with PCLAMP6 software. Statistical and other analyses were performed with EXCEL.

It must be noted that because we did not compensate for the series resistance, the plotted clamping voltages do not indicate the true transmembrane voltage under voltage-clamp mode. The size of this clamping error depends on membrane current. Based on an assumed 15-MΩ resistance, a membrane current of 1,000 pA gives rise to a clamping error of 15 mV; for a more physiologic 200-pA membrane current, the clamping error is 3 mV. Series resistance does not introduce more than negligible error in voltage under current-clamp conditions: the maximum current injection of 100 pA would cause an error of at most 1.5 mV. The main conclusions of this paper are drawn from voltage measurements in current clamp mode and thus are not affected by the series resistance.

Characterization of dynamics using the m-sequence method

The dynamics of bipolar cells were characterized under current clamp by their effective impulse responses at a range of mean membrane voltages maintained by injecting currents with means ranging from −25 to 100 pA. Superimposed on each mean current were fluctuations whose temporal profile was determined by a binary m-sequence (Sutter, 1987; Victor, 1992). The set of effective impulse responses captures the cells' response to incremental changes in input current (which contain a broad spectrum of frequency components) at each depolarization level. Details of the m-sequence method can be found in Sutter (1987), Victor (1992), and Mao et al. (1998). Briefly, a binary m-sequence of order M is a cyclic binary sequence {m₁, m₂, …, m_N} of length N = 2^M − 1 whose autocorrelation for all nonzero time lags is very nearly zero. In the present study, we used M = 11 and N = 2047, and the binary sequence {m₁, m₂, …, m_N} of −1's and 1's was translated into a time-varying current S(t) by S(t) = μ + αm_i, iT_s ≤ t ≤ (i + 1)T_s, in which α (in pA) is the current amplitude scale factor and T_s (in ms) is the time interval. μ (in pA) is the mean current and determines whether the cell is depolarized (μ > 0), hyperpolarized (μ < 0), or held at resting potential (μ = 0). For each μ, the cell's effective impulse response, h(t), was estimated by a cross correlation between the m-sequence current input and the cell's membrane voltage response (in mV). The relationship among the discretized impulse response h_n = h(nT_s), the m-sequence current S_n = S(nT_s), and the membrane-voltage response R_n = R(nT_s), is determined by a cross correlation after correction for a DC offset (Mao et al., 1998):

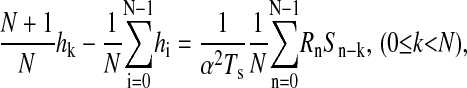in which subscripts on S are interpreted mod N.

The impulse response h(t) has units of mV/(pA·ms), or mV/f Coulomb. For each impulse response, we define DC gain as the limit of amplitude of transfer function (the Fourier transform of the impulse response) as frequency approaches zero. From this definition, DC gain can be calculated as the integral of impulse response with respect to time, or, equivalently, the area under the impulse response curve. The initial decay of each impulse response was also fitted with a single exponential function and the time constant for each impulse response was obtained directly from the fitted exponential function (Mao et al, 1998; Mao, 1997).

Since both DC gain and time constant (or speed) of a bipolar cell's impulse response depend strongly on the mean membrane voltage (Mao et al., 1998), a series of m-sequence currents with different mean levels μ (typically, −25, −3, 0, 3, 7, 15, 25, 50, 75, and 100 pA) was needed to capture the range of a bipolar cell's dynamic behavior, and the time interval T_s was adjusted according to μ, to accommodate the speed of the cell's response at each membrane voltage. Experimental details concerning these choices are given in Mao et al. (1998, 2002). With this choice of stimuli, bipolar cells indeed behave in an approximately linear manner if mean current is held constant. Specifically, at any given level of mean current μ, increasing or decreasing the current amplitude α by a factor of 10, or increasing or decreasing the time interval T_s by a factor of three, did not change the estimated impulse response. Impulse responses were plotted in an (I,V) (current-voltage) plane so that the (I,V) coordinates for the origin of each impulse response indicate the mean current (I) and the corresponding mean voltage (V) of the cell. Impulse responses were also plotted on a semilogarithmic scale for the analysis of curvature used to obtain reversal potential of the underlying voltage-gated channels (Figs. 1 E and 5 E).

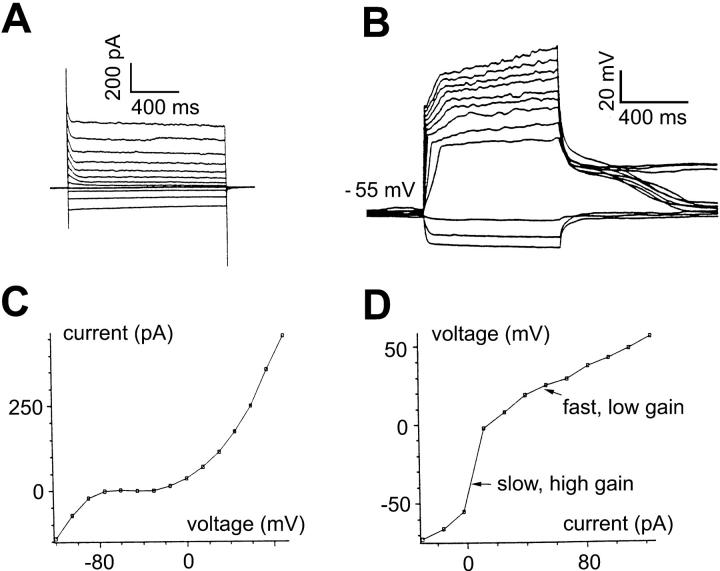
FIGURE 1.

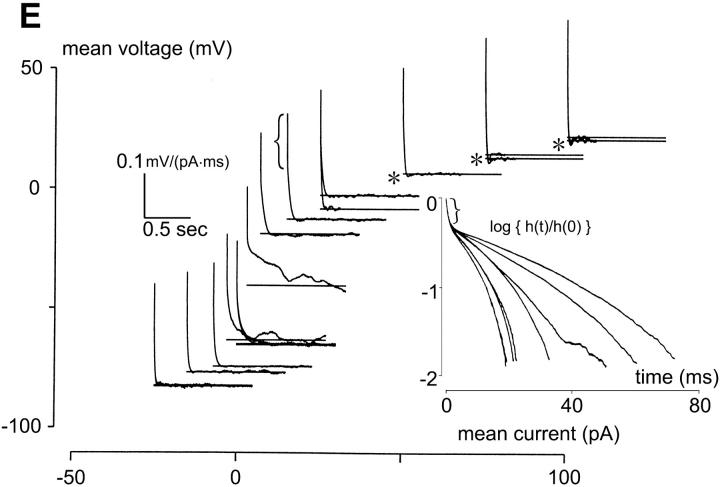
Membrane currents and intrinsic dynamics of bipolar cell. All recordings in solution A. (A) Current responses of a bipolar cell to voltage-clamp pulses ranging from −120 to 90 mV, in 15-mV increments. An outward current was activated at membrane voltages >−30 mV and a prominent hyperpolarization-activated, inwardly rectifying current at membrane voltages <−50 mV. (B) Voltage responses of the bipolar cell to current-clamp pulses ranging from −30 to 124 pA, in 14-pA increments. (C) Current-voltage relationship obtained from the current responses at the end of each of the voltage-clamp pulses shown in A. (D) Voltage-current relationship obtained from the voltage responses at the end of each of the current-clamp pulses shown in panel B. Note both outward and inward rectifications. (E) Effective impulse responses obtained by the m-sequence method and plotted in the (I,V) plane (as described in Methods). For depolarizing mean currents, the impulse response is rapidly attenuated, and also contains undershoots (asterisks). Consistent with the presence of the hyperpolarization-activated current in panel A, for hyperpolarizing mean currents (−7 pA, −15 pA, −25 pA), membrane voltage shows inward rectification as evidenced by an attentuation of the impulse response. Impulse responses are also speeded up, due to the inwardly rectifying current, but there is no undershoot. (E, inset) Semilogarithmic plots of the impulse responses for depolarizing mean currents (15 pA, 25 pA, 50 pA, 75 pA, and 100 pA). The faster impulse response curves correspond to the more depolarizing mean currents. All impulse responses are convex, indicating that their declining phase is faster than that of exponential decline (which would be a straight line). The initial segments of all impulse responses reflect the series resistance of the recording pipette (indicated by brackets).

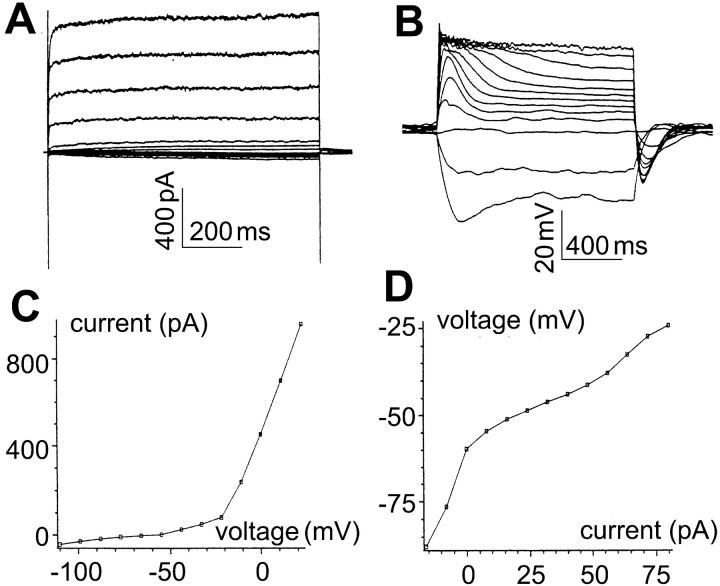
FIGURE 5.

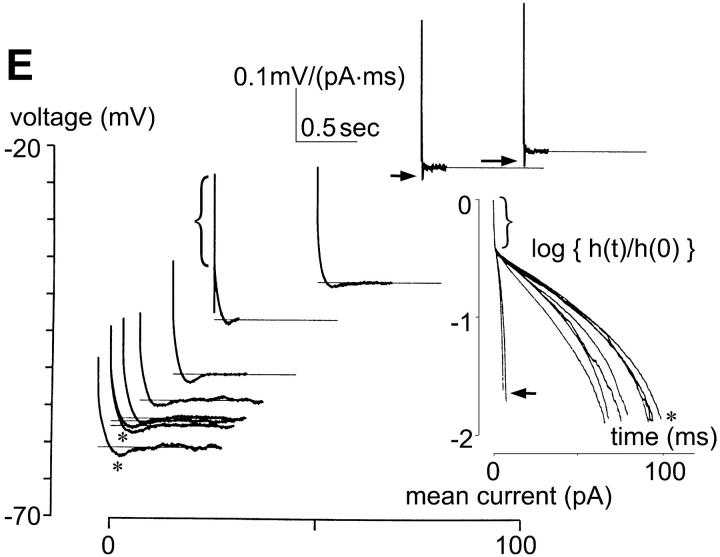
Membrane currents and intrinsic dynamics of the rod photoreceptor. All recordings in solution B (0.75 mM K⁺). (A) Current responses of a rod photoreceptor to voltage-clamp pulses ranging from −110 to 22 mV, in 11-mV increments. The large outward currents, presumably carried by K⁺, contain only a delayed-rectifierlike component. Slowly activated, small, but still distinguishable, currents are seen for voltages ranging from −30 mV to −100 mV. (B) Voltage responses of the rod photoreceptor to current-clamp pulses ranging from −16 to 80 pA, in 8-pA increments. The voltage responses show slow overshoots for a broad range of current steps. (C) Current-voltage relationship, obtained from the current responses at the end of each of the voltage-clamp pulses shown in A. (D) Voltage-current relationship, obtained from the voltage responses at the end of each of the current-clamp pulses shown in B. (E) Effective impulse responses obtained as described in Methods. The impulse responses have undershoots in two ranges of membrane voltage: slow undershoots (asterisks) over a broad range near the resting potential, probably due to the I_h channel; fast undershoots (arrows) with marked depolarization, probably due to the delayed-rectifier K⁺ channel. (E, inset) All the impulse responses in panel E are plotted on a semilogarithmic scale. All impulse responses are convex. Two impulse responses (arrows), much faster than the others, correspond to mean currents 75 and 100 pA, presumably due to the outward delayed-rectifier K⁺ conductance. The initial segments of impulse responses reflect series resistance of the recording pipette (indicated by brackets).

The same set of m-sequence currents was also used to obtain impulse responses of rod photoreceptors because their gains and time constants change with membrane voltage in qualitatively similar fashion. Data acquired from m-sequence experiments were analyzed with in-house software written in C and PostScript II.

Computer simulations

We studied the role of hyperpolarization-activated channels in shaping the impulse responses of bipolar cells and rod photoreceptors by computer simulations written in C and PostScript II using Runge-Kutta algorithms (Press et al., 1992). The geometric characteristics of isolated bipolar cells and rod photoreceptors allow a model with all elements lumped and in parallel with each other, under the assumption of space clamping and effective uniform membrane distribution of all conductances. The simulation aims at a qualitative study of the mechanism underlying different consequences of hyperpolarization-activated channels for intrinsic dynamics of bipolar cells and rod photoreceptors. Thus, generic channel parameters were used, with adjustment made with respect to the voltage range for the activation of the channels. The modeling for both bipolar cell and rod photoreceptor was simplified by restriction of the membrane voltage to the range <−50 mV, in which only the hyperpolarization-activated channel activates, so that the dynamics of the outwardly rectifying K⁺ channel need not be considered. The complete set of parameters used is listed in Table 2. Impulse responses were estimated by applying literal impulses (100-pA amplitude and 50-μs duration) superimposed on various mean currents. (This provides results that are equivalent to the m-sequence method, but is computationally more efficient (Mao et al., 2002)). Impulse responses are plotted in an (I,V) plane, as are those obtained experimentally.

TABLE 2.

Parameters for simulation of a hyperpolarization-activated channel for bipolar cells and rod photoreceptors

Element	Value	Reversal potential	Kinetics
Cm membrane capacitance	10 pF	NA	NA
gns nonspecific leakage conductance	0.15 nS	0 mV	ohmic
gKleak voltage-independent K+	0.15 nS	−90 mV	ohmic
gh hyperpolarization-activated	2 nS	−75 mV or −20 mV See*	See*

^*Kinetics for the hyperpolarization-activated channel modified from Barnes and Hille (1989).

For bipolar cells:

α = a₁/(1 + exp((V + b₁)/c₁), a₁ = 0.3 ms⁻¹, b₁ = 98 mV, c₁ = 10 mV

β = a₂/(1 + exp(−(V + b₂)/c₂), a₂ = 0.3 ms⁻¹, b₂ = 30 mV, c₂ = 20 mV

n = α/(α + β), τ = 1 /(α + β)

g = g_h (1−(1 + 3n)(1 − n)³)

Reversal potential, –75 mV

For rod photoreceptors:

α = a₁/(1 + exp((V + b₁)/c₁), a₁ = 0.03 ms⁻¹, b₁ = 98 mV, c₁ = 10 mV

β = a₂/(1 + exp(−(V + b₂)/c₂), a₂ = 0.03 ms⁻¹, b₂ = 30 mV, c₂ = 20 mV

n = α/(α + β), τ = 1/(α + β)

g = g_h (1 − (1 + 3n)(1 − n)³)

Reversal potential, −20 mV

RESULTS

Current-voltage relationship and the dynamics of bipolar cells

Under voltage-clamp conditions, 52 bipolar cells were recorded in the standard solution (solution A) and all contained an outward current activated at voltages >−30 mV. One third of bipolar cells recorded also contained an inward, fast-activating current at voltages <−50 mV (Fig. 1 A). This current was small in a solution containing 3 mM K⁺ (solution A), which may reflect a low conductance, a small driving force, or both. The voltage responses of the bipolar cell to current-clamp steps are shown in Fig. 1 B. Fig. 1 C shows the I-V relationship of the bipolar cell obtained for its steady-state current responses to voltage-clamp steps in Fig. 1 A. Fig. 1 D shows V-I relationship of the bipolar cell obtained for its voltage responses to current-clamp steps in Fig. 1 B. It has a steep slope near the resting potential and levels off with depolarizing currents, consistent with the presence of a delayed-rectifier K⁺ channel (Kaneko and Tachibana, 1985; Lasater, 1988; Karschin and Wässle, 1990; Mao et al., 1998, 2002). In the bipolar cells that show an inward-rectifying current at hyperpolarizing voltages <−50mV, including this one, inward rectification is shown by the membrane potential response to hyperpolarizing current steps (Fig. 1 D) and even more clearly by the current responses to hyperpolarizing voltages (Fig. 1 C).

The dynamics of bipolar cells were characterized by effective impulse responses using the m-sequence method (Fig. 1 E). Impulse responses are slow near resting potential (i.e., for mean current of 0 pA), but are much faster with more depolarizing mean currents. Thus, gain and time constant, estimated from the impulse responses (see Methods), are maximal at resting potential and decrease with membrane depolarization. Depolarization also induces bandpass behavior, as indicated by the undershoot in the impulse responses (asterisks). Impulse responses at hyperpolarizing voltages are also speeded up, presumably by the activation of the hyperpolarization-activated inward-rectifying conductance, but contain no undershoot.

Impulse responses that contain undershoots and bandpass behavior are closely related phenomena, as studied in Mao et al. (2002). If an impulse response contains an undershoot, then the amplitude of transfer function may not be maximal at zero frequency, whereas in the absence of an undershoot, the amplitude of the transfer function must be maximal at zero frequency because it is the integral of the impulse response. The extreme effect of an undershoot is that the integrals of the positive part and the negative part of the impulse response cancel out. In this case, the zero-frequency transfer function has amplitude of 0, whereas at higher frequencies the transfer function amplitude is nonzero.

The inset of Fig. 1 E shows impulse responses plotted on semilogarithmic coordinates for the depolarizing mean currents 15, 25, 50, 75, and 100 pA. All impulse responses are convex, indicating an accelerating decline.

External K⁺ reduces gain and time constant in bipolar cells

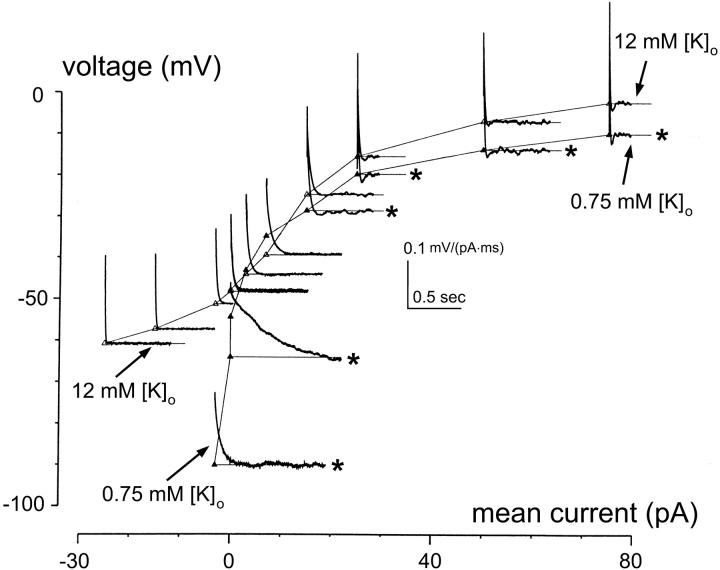
We tested the effect of [K⁺]_o on dynamics in 10 bipolar cells. Fig. 2 shows the static voltage-current relationship and impulse responses under high (12 mM) and low (0.75 mM) external K⁺. In the higher [K⁺]_o condition (open triangles), gain and time constant near and below resting potential were reduced (as reflected by the more rapid descent to zero of the impulse responses, as well as by the shallower slope of the V-I curve). (In the following, all gains and time constants are measurements at resting potentials.) On average, gains were 2.5 ± 1.0 gΩ (mean ± SD, n = 10) and time constants 42 ± 13 ms (n = 10). For reference, in standard solution (solution A, 3 mM K⁺), gains were 5.0 ± 2.1 gΩ (n = 52) and time constants were 100 ± 52 ms (n = 52) (Mao et al., 1998). On the other hand, near removal of K⁺ (solution B, 0.75 mM K⁺) increases gain and time constant substantially (solid triangles): gains were 9.6 ± 2.3 gΩ (n = 10) and time constants 187 ± 62 ms (n = 10). Since each cell was recorded in both high and low [K⁺]_o conditions, we calculated the ratios of reduction of gain and time constant by the higher [K⁺]_o: 0.27 ± 0.10 (n = 10) for gain and 0.26 ± 0.14 (n = 10) for time constant. Thus, a 15-fold increase of [K⁺]_o reduces gain and time constant by a factor of approximately four. Moreover, the effects of external K⁺ on gain and time constant are reversible, as indicated by I-V curves obtained from step responses after multiple interleaved exchanges of high and low external K⁺ (data not shown).

FIGURE 2.

Effect of external K⁺ on the intrinsic dynamics of bipolar cells. Static voltage- current relation (I-V curves) and impulse responses of a bipolar cell recorded in solution B (0.75 mM [K⁺]_o, ▴) and solution C (12 mM [K⁺]_o, ▵). Representative impulse responses for the two ionic conditions are estimated and plotted in the (I,V) plane as described in Methods. Asterisks mark those obtained at 0.75 mM [K⁺]_o. Note that at 12 mM [K⁺]_o, a 15-fold increase from 0.75 mM, I-V curves show inward rectification near and below resting potential and impulse responses are greatly speeded up in that voltage range.

The effect of high K⁺ on dynamics is mediated by a Cs⁺-sensitive inwardly rectifying conductance

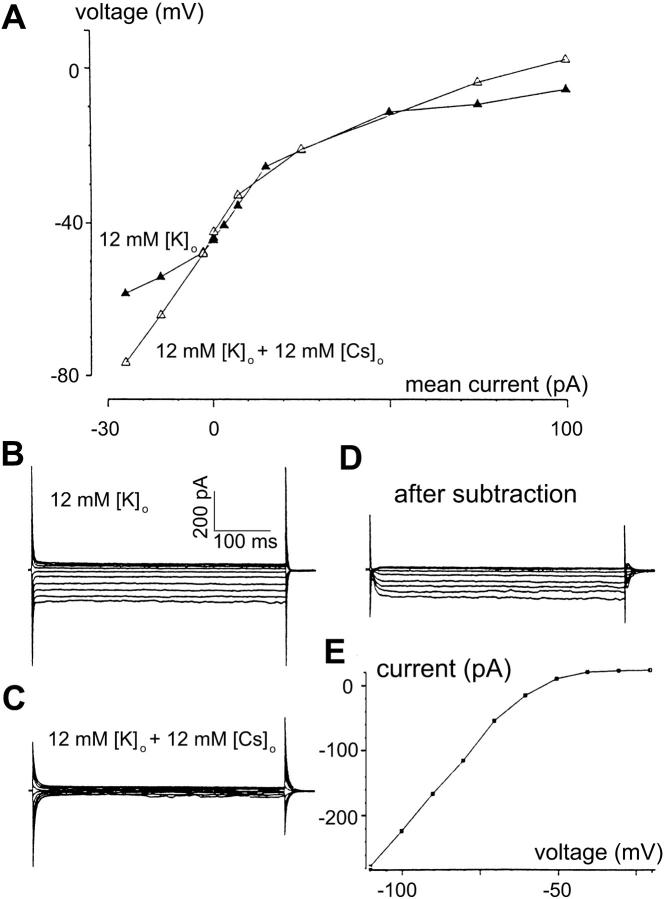
After establishing that higher external K⁺ indeed reduces gain and time constant, we next asked whether such an effect could be at least partially blocked. Since the effect occurred near and below resting potential, the voltage range in which the hyperpolarization-activated channel activates, we reasoned that the effect of higher external K⁺ may be mediated by this channel. If so, then agents that block the channel should increase the gain and time constant of a cell whose gain and time constant had been reduced by a high external K⁺. We used external Cs⁺ (Hagiwara et. al, 1976; Pape, 1996) to test this possibility. Fig. 3 A (solid triangles) shows (in another bipolar cell) that, in higher [K⁺]_o (12 mM, solution C), the slope of the V-I curve near and below resting potential was shallow, compatible with the decreased gain and time constant seen in Fig. 2. In solution D (10 mM Cs⁺, 12 mM K⁺), the slope of the V-I curve near and below the resting potential became steeper (indicating larger gains and/or time constants in that region). The hyperpolarization-activated conductance was studied with standard voltage-clamp methods in 12 mM [K⁺]_o, without (solution C) and with (solution D) 10 mM Cs⁺. As seen in Fig. 3, B–E, external Cs⁺ blocks an inward current that activates at membrane voltage <−50 mV. These results suggest that the reduction of gain and time constant by high [K⁺]_o concentration near and below resting potential is mediated by the Cs⁺-sensitive hyperpolarization-activated conductance (Hagiwara et al., 1976; Pape, 1996).

FIGURE 3.

Higher K⁺ effect on bipolar cell dynamics is mediated via a Cs⁺-sensitive hyperpolarization-activated inwardly rectifying conductance. (A) Voltage-current relation derived from recordings on a bipolar cell in high [K⁺]_o (12 mM) without Cs⁺ (solution C, ▴) and with Cs⁺ (solution D, ▵). Cs⁺ suppresses inward rectification induced by high [K⁺]_o. (B) Current responses to voltage-clamp steps in solution C (without Cs⁺). Note that the activation of the inward current is almost instantaneous. (C) Currents responses to the same set of voltage-clamp steps as in panel C, but recorded in solution D (with 10 mM Cs⁺), show suppression by Cs⁺ of the inwardly rectifying current. (D) The inward-rectifying current isolated by subtraction of currents in panel C from the corresponding currents in panel B. (E) I-V curve of the isolated current shows activation at <−50 mV.

A method for estimating the reversal potential of the inwardly rectifying channel

The reversal potential of a hyperpolarization-activated channel, E_h, was estimated from impulse responses of bipolar cells by a novel method. This method is based on the assumption that at the membrane voltage under consideration, the channel of interest is the only voltage-dependent channel that operates. In graphical form (Fig. 4 A), the approach and rationale is as follows. Initial segments of impulse responses (down to 1% of the initial peak) were plotted on semilogarithmic coordinates. The declining phase was examined, and classified as convex, concave, or straight. An impulse response with a purely exponential time course (no voltage-dependent conductances) generates a straight line on the semilogarithmic plot. At V < E_h (here, E_h = −75 mV), the declining phase of the impulse responses is accelerated by the voltage-activated current. Consequently, the impulse response declines faster than a pure exponential, and generates a convex curve on the semilogarithmic plot. (Note that here we use the subscript “h” generically to indicate a channel activated by hyperpolarization, and not specifically to denote the I_h-channel.) At V > E_h, the hyperpolarization-activated channel acts to slow down the declining phase of the impulse response. Its slope turns less negative as the channel opens, and thus the impulse response is concave on the semilogarithmic plot. At the transition point from V > E_h to V < E_h, where the membrane potential equals the reversal potential of the conductance, the opening of the channel is irrelevant to the impulse response dynamics. The impulse response is a simple exponential, because (as we assumed) all other relevant channels are not voltage dependent, and appears as a straight line on the semilogarithmic plot. That is, even though the channel is opened, there is no current through it (for lack of driving force), and thereby its effect is nulled. This transition voltage is exactly at the reversal potential of the hyperpolarization-activated channel, E_h.

FIGURE 4.

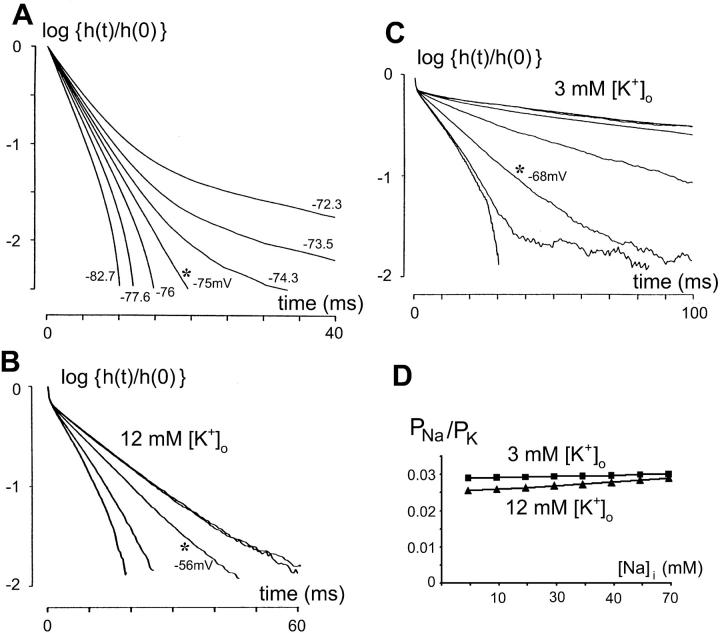
Estimating the reversal potential of a hyperpolarization-activated channel from a family of impulse responses. (A) Computer simulation demonstrating the validity of the method for estimating the reversal potential of hyperpolarization-activated channel. Parameters of the model bipolar neuron for the simulation are listed in Table 2. The hyperpolarization-activated channel has a reversal potential of E_h = −75 mV. The impulse responses above and below the known reversal potential (−75 mV) are calculated as described in Methods and are plotted on the semilogarithmic scale. All the curves emanate from a common point and, in clockwise direction, these curves correspond to progressively more negative membrane voltage (in mV, −72.3, −73.5, −74.3, −75.0, −75.9, −77.6, and −82.7). At membrane voltages >−75 mV, the impulse response is concave; at voltages <−75 mV, impulse response is convex. Note that a transition between the two behaviors occurs precisely at the membrane potential equal to the reversal potential E_h −75 mV, at which the slope of the impulse response becomes a straight line (asterisk). (B) The method in panel A applied to the impulse responses for mean currents of 0 pA, 0 pA (repeated, two nearly overlapping curves), −3 pA, −15 pA, −25 pA, recorded from a bipolar cell in solution C (12 mM [K⁺]_o). The impulse response is concave (capacitive) for 0 pA and turns convex (inductive) between −3 pA and −15 pA. The membrane potential at the transition (asterisk), ∼−56 mV, is read from the V-I curve (not shown) at the point corresponding to −3 pA, and taken as an estimate of the reversal potential of the hyperpolarization-activated channel. (C) The method in panel A applied to the impulse responses for mean currents of 0 pA, 0 pA (repeated, two nearly overlapping curves), −3 pA, −7 pA, −15 pA, −25 pA, −25 pA (repeated), recorded from another bipolar cell in solution A (3 mM [K⁺]_o). The impulse response is concave (capacitive) for 0 pA, −3 pA, −7 pA, and turns convex (inductive) between −15 pA and −25 pA. The membrane potential at the transition (asterisk), ∼−68 mV, is read from the V-I curve (not shown) at −15 pA and taken as an estimate for the reversal potential of the hyperpolarization-activated channel. Note the convexity of the two traces for −25 pA is judged from the smooth portion of the curves at time <30 ms. The trace to the right contains much noise and has an amplitude that has decreased by more than one order of magnitude at times >40 ms. The portion corrupted by noise was ignored in the analysis of curvature. (D) The permeability ratio for Na⁺ vs. K⁺ (P_Na⁺/P_K⁺) for a range of [Na]_i (3–70 mM) is calculated as described in text. The average of the 14 reversal potentials of the hyperpolarization-activated channel under 3 mM [K⁺]_o was used for estimating P_Na⁺/P_K⁺ at that ionic condition. Similarly, average of 16 reversal potentials was used for P_Na⁺/P_K⁺ estimation for 12 mM [K⁺]_o condition.

We demonstrated (Fig. 4 A) the validity of the above method by computer simulations in which the slopes of impulse responses around the reversal potential of the model hyperpolarization-activated channel (E_h = −75 mV) were examined in a model bipolar neuron with parameters listed in Table 2. At a membrane potential >−75 mV, the slope of the impulse response is concave; at <−75 mV, the slope is convex. A transition occurs precisely at the membrane potential equal to E_h: the slope becomes a straight line. Varying the conductance G_h (in the range 1–10 nS) did not affect the estimated reversal potential: the straight slope persistently occurs at −75 mV (data not shown).

For practical reasons, we took the membrane voltage at which the impulse response curve was the closest to a straight line to be the (estimated) reversal potential of the hyperpolarization-activated channel. Also, in some recordings in solutions with 3 mM [K⁺]_o, no such transition occurred at all. In such cases, the most negative membrane potential, where the impulse response was closest to a simple exponential, was used for the estimate. Finally (see for example the −25 pA curves in Fig. 4 C), we note that the determination of convexity versus concavity must be restricted to portions of the impulse response in which noise contamination is not significant.

Reversal potential of the hyperpolarization-activated channel indicates permeability mainly to K⁺ in bipolar cells

Examples of applying the above method for estimating the hyperpolarization-activated channel reversal potential are shown in Fig. 4 B (for 12 mM [K⁺]_o) and Fig. 4 C (for 3 mM [K⁺]_o). The application of the method, as noted above, depends on the assumption that at the membrane voltages under consideration, the channel of interest (the hyperpolarization-activated channel) is the only voltage-dependent channel that operates. One indication that this assumption is valid for the hyperpolarization-activated channel in bipolar cells is that, if there were two or more voltage-dependent channels present at the hyperpolarizing potentials, the impulse responses would not be pure exponential at any holding potential, but, instead, would have shown sigmoidal or even more complicated curves on a semilogarithmic plot, indicating mixtures of both convex and concave characteristics. The mean reversal potential estimated was −53 ± 7 mV (n = 16) from impulse responses obtained in solution C (12 mM [K⁺]_o) and −73 ±12 mV (n = 14) from impulse responses obtained in solution A (3 mM [K⁺]_o). For both conditions, the pipette solution is the same (113 mM [K⁺]_i).

From the above average reversal potentials estimated for the two solutions (A and C), we estimated the ratio of permeability for Na⁺ to that for K⁺ (P_Na⁺/P_K⁺) using Goldman-Hodgkin-Katz voltage equation (Hodgkin and Katz, 1949; Hille, 2001). We assumed that the hyperpolarization-activated channel was permeable only to K⁺ and Na⁺ in both solution A ([K⁺]_o = 3 mM, [K⁺]_i = 113 mM, Nernst potential −91 mV) and solution C ([K⁺]_o = 12 mM, [K⁺]_i = 113 mM, Nernst potential −57 mV). Because [Na⁺]_i, is unknown, we calculated P_Na⁺/P_K⁺ over a wide range of assumed values for [Na⁺]_i (3–70 mM) and examined the sensitivity of the estimates of the P_Na⁺/P_K⁺ ratio to [Na⁺]_i. As shown in Fig. 4 D, P_Na⁺/P_K⁺ is confined to the range 0.025–0.03, across a wide range of assumed values of [Na⁺]_i. Thus, the hyperpolarization-activated current in bipolar cells is overwhelmingly a K⁺-permeable channel. Additional evidence for a K⁺ current as the cause of the inward rectification under hyperpolarizing conditions has been gained from experiments using agents that block K⁺ current, e.g., tetraethylammonium (TEA), Cs⁺, Ba²⁺. Impulse responses obtained in the presence of these blockers show behavior of a passive RC circuit, with identical, simple exponential for impulse responses at all membrane voltages and frequency responses whose amplitude at higher frequencies has slope −1 at hyperpolarizing as well as depolarizing membrane voltages (Mao, 1997; Mao et al., 1998). Thus, we use the term K_IR to refer to this hyperpolarization-activated, inwardly rectifying K⁺ current in bipolar cells.

Activation of an I_h channel in rod photoreceptors leads to bandpass behavior

The hyperpolarization-activated channel in rod photoreceptors (n = 8) leads to filtering behavior that differs from that of bipolar cells, and also appears to have a different ionic permeability. Fig. 5 shows current responses to voltage-clamp pulses (A), voltage responses to current-clamp pulses (B), and the I-V relationships obtained from the steady-state current (C) and voltage (D) responses typical of rods. The hyperpolarization-activated current is indicated by the slowly activated responses (negative deflections, Fig. 5 A) at voltages <−40 mV. The current increases with increasing hyperpolarization (with a slope corresponding to a conductance of ∼1.2 nS). The amplitude of the I_h current was much smaller than the large K⁺ current activated at voltages >−30 mV, which may reflect a relatively low conductance caused by the low external K⁺ and/or a relatively low driving force. The data were recorded in solution B containing low K⁺ (0.75 mM), which probably accounts for the relatively small size of hyperpolarization-activation current (Fig. 5, A and B). This current is likely of the I_h type (Hestrin, 1987; Bader et al., 1982; Bader and Bertrand, 1984; Fain et al., 1978; Barnes and Hille, 1989; Wollmuth and Hille, 1992; Yagi and MacLeish, 1994; Gargini et al., 1999; Satoh and Yamada, 2000). Fig. 5, E and inset, show impulse responses estimated by the m-sequence method. Despite the relatively small current, we observed pronounced and slow undershoots near the resting potential (∼−60 mV) (asterisks in Fig. 5 E). According to the I-V curves in Fig. 5 C, the I_h channel is activated at the resting potential. On the other hand, the activation of depolarization-activated K⁺ channel is unlikely to extend to the range of resting potential (−60 mV), because the outward current has a sharp increase in conductance only for voltages >−20 mV. The slope of this rise corresponds to a conductance of ∼12 nS.

For reasons detailed above, the bandpass behavior associated with the slow undershoots in response to hyperpolarizing currents is likely due to the slow I_h currents that are active in this voltage range. This is distinct from the fast undershoots seen in rods with markedly depolarizing voltages (arrows in Fig. 5 E), associated with the activation of the outwardly rectifying K⁺ channels. The two types of undershoots seem to be well separated in voltage range, because none of the impulse responses show indication of a mixture of the two types of undershoot. Indeed, between voltage −25 and −35 mV, the slower undershoots in impulse responses become attenuated. This indicates that the channel associated with undershoots near resting potential and the channel associated with undershoots >−30 mV are unlikely to have overlapping activation voltage ranges. Notably, all the impulse responses are convex on the semilogarithmic scale, which indicates that all these channels behave as an inductive element (Fig. 5 E, inset).

The convexity of the impulse responses at voltages >−25 mV indicates inductive behavior of the delayed-rectifier type K⁺ currents similar to those in our previous studies (Mao et al., 1998, 2002). The convexity of the impulse responses near resting potential, on the other hand, indicates that the channel associated with the slow undershoots also behaves as an inductive element. Since this channel appears to be an I_h channel, the reversal potential of the channel must be more positive than resting potential, using the criteria of Mauro et al. (1970) and Detwiler et al. (1980) for inductive behavior. This in turn suggests that the rod photoreceptor I_h channel is more permeable to Na⁺ than the K_IR channel of bipolar cells, as the following analysis shows. Because at voltage −40 mV, the impulse responses still show significant undershoots and inductive behavior (Fig. 5 E), the reversal potential of the I_h channel must be >−40 mV, which implies P_Na⁺/P_K⁺ > 0.32 via the Goldman-Hodgkin-Katz voltage equation ([K⁺]_i = 113 mM, [K⁺]_o = 0.75 mM, [Na⁺]_i = 3 mM, [Na⁺]_o = 70 mM). Therefore, the relative permeability to Na⁺ of the I_h channel in the rod photoreceptor shown in Fig. 5 must be at least one order of magnitude higher than that of K_IR in bipolar cells. As noted above, data shown in Fig. 5 are recorded in very low K⁺ (0.75 mM, solution B), indicating that the I_h conductance in rod photoreceptors is also less affected by low external K⁺ than the K_IR conductance in bipolar cells.

Hyperpolarization-activated channels affect the impulse responses of bipolar cells and rod photoreceptors differently, as studied by computer simulation

The role of hyperpolarization-activated channels in shaping the impulse responses of bipolar cells and rod photoreceptors near and below resting potential was explored by single-compartment computer modeling. Table 2 lists parameters for both types of neurons. The hyperpolarization-activated channel for rod photoreceptor has slower kinetics and a more positive reversal potential (a₁ = 0.03 ms⁻¹, a₂ = 0.03 ms⁻¹, E_h = −20 mV) than that for bipolar cell. Note that our simulations and Table 2 do not include a depolarization-activated K⁺ channel (such as the delayed rectifier or A-channel) because such a conductance is immaterial for simulation of behavior at and below resting potential. Fig. 6 A shows simulations for bipolar cells and Fig. 6 B for rod photoreceptors. Both results qualitatively mimic the behavior of the two types of neurons observed in experiments. These simulations demonstrate that whether a voltage-dependent channel cause undershoots depends on the reversal potential of the conductance V_rev and the nature of the voltage-dependence ∂g/∂V. For an ion channel to cause inductive behavior, it must be true that (V−V_rev)∂g/∂V > 0 (Mauro et al., 1970; Detwiler et al., 1980). Thus, the hyperpolarization-activated channel can cause undershoots only at voltage more negative than its reversal potential. This likely accounts for the absence of undershoots in the bipolar cells' impulse responses under standard ionic conditions (3 mM [K⁺]_o and 113 mM [K⁺]_i), but the presence of undershoots in rods under the same ionic conditions. Together, the recordings and simulations suggest that the hyperpolarization-activated channels in rod photoreceptors and in bipolar cells have different kinetics (fast versus slow gating) and permeabilities to K⁺ and Na⁺ (different reversal potentials). Finally, as Fig. 4, A–C reveals, the hyperpolarization-activated channel may cause both inductive and capacitative behavior in bipolar cells, depending on the operating voltage range relative to the reversal potential (V−V_rev).

FIGURE 6.

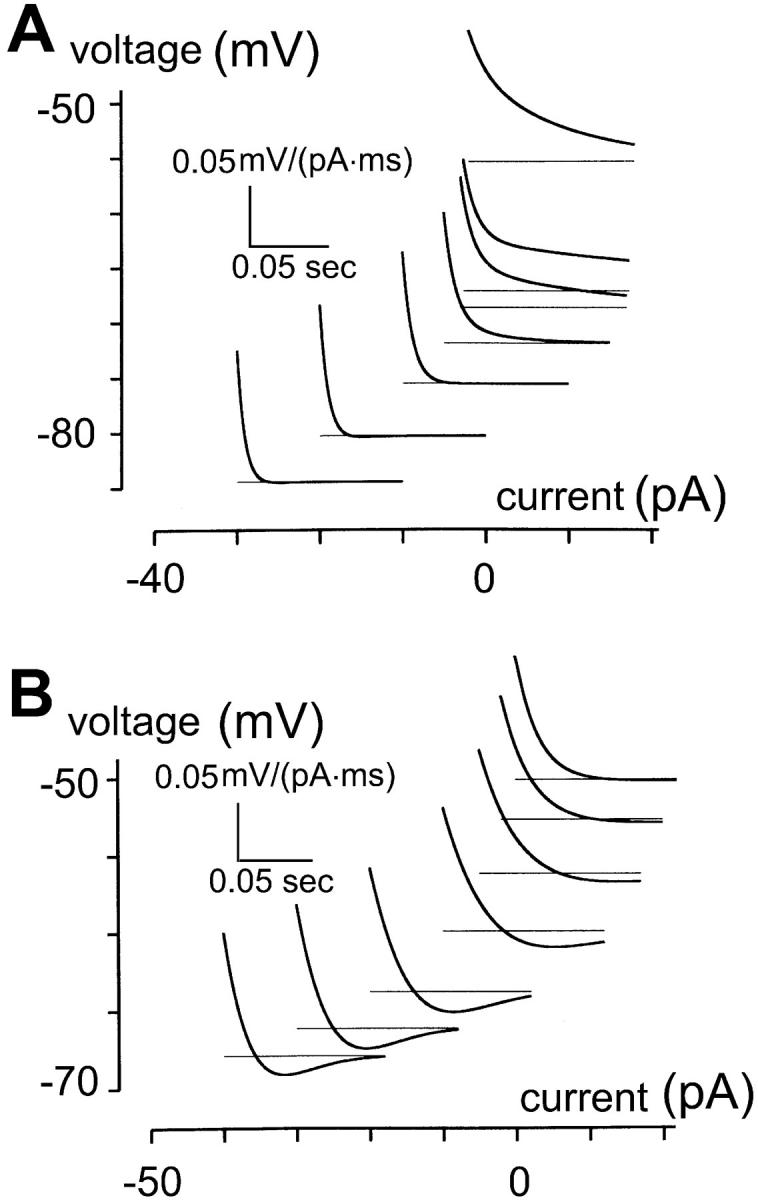
Simulations of impulse responses of bipolar cells and rod photoreceptors. (A) Simulation of bipolar cells with parameters listed in Table 2. The reversal potential of the hyperpolarization-activated channel, E_h, is −75 mV. Since the simulation is restricted to voltage ranges <−50 mV, depolarization-activated K⁺ channels are not included in the model. Impulse responses for bipolar cells, estimated as described in Methods, contain no undershoot, even though the impulse responses are speeded by the activation of the hyperpolarization-activated channel. (B) Simulation of rod photoreceptors. The same set of parameters in Table 2 was used, except that time constant of the hyperpolarization-activated channel conductance is 10 times slower than that for bipolar cells and its reversal potential E_h is −20 mV. Impulse responses for rod photoreceptors contain pronounced undershoots near and below resting potential.

DISCUSSION

Types of hyperpolarization-activated currents in bipolar cells and in rod photoreceptors

Bipolar cells of many species contain a hyperpolarization-activated current that is designated as an I_h current on the basis of its permeability, rather than a more classical anomalous inward rectifier, as supported by findings in Kaneko and Tachibana (1985), Karschin and Wässle (1990), Lasater (1988), and Connaughton and Maguire (1998). However, a fast hyperpolarization-activated current with the properties of a classical inward rectifier coexists in bipolar cells of some animals (Lasater, 1988; Connaughton and Maguire, 1998). For instance, the inward rectifiers in white bass (Lasater, 1988) fall into two types: one, found in small bipolar cells, has slow kinetics and is Cs⁺-sensitive; the other, found in large bipolar cells, has very fast kinetics and is Cs⁺-insensitive. Bipolar cells of zebra fish express a hyperpolarization-activated inward current that is not affected by barium or cesium, nor by external solution containing 0 mM Na⁺, in addition to a current that apparently is of I_h type (Connaughton and Maguire, 1998). In our recordings, the estimated relative permeability to Na⁺ vs. K⁺, though nonzero, is small (<0.05). Recognizing that no term captures all aspects of the hyperpolarization-activated currents in bipolar cells, we term this inwardly rectifying K⁺ current K_IR, as distinct from the I_h current of rod photoreceptors, to emphasize the low relative permeability of this channel to Na⁺. The effort to correlate physiologically distinguished bipolar cell types with intrinsic membrane currents has been difficult and tentative at best, in dissociated preparations (Lasater, 1988; Kaneko and Tachibana, 1985) and in retinal slices (Connaughton and Maguire, 1998). Further complicating the categorization of bipolar cell types in salamander is the fact that both ON- and OFF-bipolar cells receive rod and cone inputs (Hare et al., 1986). Moreover, protein kinase C (PKC) labeling for rod bipolar cells has been unsuccessful in salamander (Hirano, personal communication) despite the success of the method for mammals such as rats, in which all the dissociated bipolar cells are of rod bipolar type, as found in Karschin and Wässle (1990). We surmise that the subset of bipolar cells that contain K_IR channel (one-third of all bipolar cells recorded) are of the OFF-bipolar type, given the range of voltage in which the channel operates.

In contrast, the hyperpolarization-activated current in rod photoreceptors is slow, has a reversal potential indicating substantial permeability to Na⁺, and causes pronounced bandpass behavior. It is thus of the I_h type; the existence of such currents in rod photoreceptors is well established in the literature (Hestrin, 1987; Bader et al., 1982; Bader and Bertrand, 1984; Fain et al., 1978; Barnes and Hille, 1989; Wollmuth and Hille, 1992; Yagi and MacLeish, 1994; Gargini et al., 1999; Satoh and Yamada, 2000).

Physiological significance of the hyperpolarization-activated channel for bipolar cells, rods, and for transmission of signals between the two

Bipolar cells are known to operate in a fairly narrow voltage range (Werblin and Dowling, 1969; Attwell et al., 1987; Belgum and Copenhagen, 1988). Since the activation voltage of the current is more positive than the reversal potential of the current, K_IR may enhance light response in OFF-bipolar cells, by increasing the speed, and possibly the size, of the response to small inputs. The increase in the speed of the responses at hyperpolarized membrane potentials can be inferred by the accelerated speed of the impulse responses. This acceleration of a response by an inwardly rectifying K⁺ current has been proposed for horizontal cells in catfish (Dong and Werblin, 1995). Secondly, activation of the K_IR current may also reduce the amplitude of the light response in OFF-bipolar cells under circumstances in which conductances with reversal potentials significantly different from that of K⁺ remain (e.g., residual Na⁺ conductances during submaximal light responses.) Especially if changes in ionic conditions (e.g., an increase in extracellular K⁺) lead to a relatively less hyperpolarized reversal potential of the K_IR channel, the channel would reduce the size of the light response.

In rods, the activation of the I_h channel in the inner segment will accelerate and bandpass filter the light response (Fain et al., 1978; Attwell and Wilson, 1980). Given the generally slow process of phototransduction, such acceleration enhances temporal resolution of the retina at the very first stage of visual processing. The acceleration of the rod response necessarily affects responses of both ON- and OFF-bipolar cells as well, because both types of bipolar cells receive rod as well as cone input (Hare et al., 1986). Thus, the I_h channel in the inner segment of rods indirectly accelerates the light responses of both ON- and OFF-bipolar cells by speeding up the output signals to the bipolar cells.

Intrinsic dynamics of retinal neurons differ due to differences in hyperpolarization-activated cation channels

The intrinsic dynamics of rod photoreceptors associated with the I_h channel stands in contrast with that associated with the K_IR channel in bipolar cells. The I_h current in rod photoreceptors is much slower than the K_IR current in bipolar cells, and its reversal potential is more positive than the resting potential. Consistently, near resting potential, impulse responses of rods are convex (asterisk in Fig. 5 E, inset), and contain a slow and prominent undershoot. Signals in rod photoreceptors are known to undergo highpass filtering that involves voltage-activated conductances (Fain et al., 1978; Detwiler et al., 1980; Owen and Torre, 1983; Demontis et al., 1999). It is likely that the I_h conductance contributes to this and does not merely serve to limit the operating voltage range. In contrast, the K_IR conductance in bipolar cells never causes undershoots, most likely because its reversal potential is near or below resting potential, due to its selective permeability to K⁺. The fast kinetics of the K_IR channel in bipolar cells may also prevent it from causing an undershoot: for a voltage-activated channel to cause undershoots, a delay in the activation of the channel is required (Mao et al., 2002).

While the I_h current in photoreceptors likely contributes to its highpass dynamics (Owen and Torre, 1983; Demontis et al., 1999), a full account of the highpass behavior of rod photoreceptors may involve more than one current. In addition to the I_h channel, an I_KX channel, permeable to K⁺ but deactivated by hyperpolarization, may also contribute to the highpass behavior in rods (Beech and Barnes, 1989). Nevertheless, the general criterion for an ion channel to cause inductive or capacitative filtering remains the same, namely, whether the incremental conductance change ∂g/∂V and displacement of voltage from reversal potential V−V_rev is of the same sign (inductive) or opposite (capacitative).

General significance of ion channel kinetics and ion selectivity for signal processing in neurons

Finally, the analysis of the curvature of the impulse responses reveals whether and at what voltage range a voltage-dependent channel will act as an inductive or capacitative element. As described above, this can be used to determine the reversal potential of a voltage-dependent channel. The approach as presented here has room for improvement, both experimentally and analytically. By decreasing the current increments for the current injection, the voltage increments within the activation range of the hyperpolarization-activated current can be narrowed. For instance, voltage precision can be improved by limiting the voltage range to 30 mV (e.g., from −50 mV to −80 mV) and increasing the number of injected currents to 11. Were the I-V relationship linear around the voltage of interest, such a protocol would yield a precision of 3 mV (corresponding to equally spaced voltage increments). Because the relationship is nonlinear, this full improvement is not likely to be realized; a realistic estimate of the precision is probably closer to 5 mV. Analytically, interpolation of a quantitative measurement of curvature (such as one based on the second derivative) can be used to determine a more precise voltage for the curvature transition.

The analysis of impulse response curvature can be used to predict certain physiological behaviors, such as filtering properties (see above) and oscillation. For example, a hyperpolarization-activated conductance with a reversal potential above resting potential (which supports inductive behavior at and below the resting potential) matched with a second conductance that supports inductive behavior above resting potential (such as a delayed-rectifier K⁺ conductance) can sustain membrane oscillation. Oscillatory behavior in rods suggests the involvement of a hyperpolarization-activated I_h channel (Miyachi et al., 1984). An I_h channel with a reversal potential above resting potential underlies oscillations of nonspiking neurons as well as subthreshold resonance of spiking neurons in many systems (McCormick and Pape, 1990; Pape, 1996; Sugihara and Furukawa, 1996; Hutcheon et al., 1996; Cadetti and Belluzzi, 2001). We suggest that this is because the I_h channel is distinguished in providing inductive behavior for neurons at hyperpolarized membrane voltages.