Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Apr;84(4):2768–2780. doi: 10.1016/S0006-3495(03)75081-4

The Effect of Asymmetric Surface Potentials on the Intramembrane Electric Field Measured with Voltage-Sensitive Dyes

Chang Xu 1, Leslie M Loew 1
PMCID: PMC1302842  PMID: 12668484

Abstract

Ratiometric imaging of styryl potentiometric dyes can be used to measure the potential gradient inside the membrane (intramembrane potential), which is the sum of contributions from transmembrane potential, dipole potential, and the difference in the surface potentials at both sides of the membrane. Here changes in intramembrane potential of the bilayer membranes in two different preparations, lipid vesicles and individual N1E-115 neuroblastoma cells, are calculated from the fluorescence ratios of di-4-ANEPPS and di-8-ANEPPS as a function of divalent cation concentration. In lipid vesicles formed from the zwitterionic lipid phosphatidylcholine (PC) or from a mixture of the negatively charged lipid phosphatidylserine (PS) and PC, di-4-ANEPPS produces similar spectral changes in response to both divalent cation-induced changes in intramembrane potential and transmembrane potential. The changes in potential on addition of divalent cations measured by the fluorescence ratios of di-4-ANEPPS are consistent with a change in surface potential that can be modeled with the Gouy-Chapman-Stern theory. The derived intrinsic 1:1 association constants of Ba and Mg with PC are 1.0 and 0.4 M−1; the intrinsic 1:1 association constants of Ba and Mg with PS are 1.9 and 1.8 M−1. Ratiometric measurements of voltage sensitive dyes also allow monitoring of intramembrane potentials in living cells. In neuroblastoma cells, a tenfold increase of concentration of Ba, Mg, and Ca gives a decrease in intramembrane potential of 22 to 24 mV. The observed changes in potential could also be described by Gouy-Chapman theory. A surface charge density of 1 e−/115 Å2 provides the best fit and the intrinsic 1:1 association constants of Ba, Mg, and Ca with acidic group in the surface are 1.7, 6.1, and 25.3 M−1.

INTRODUCTION

Most biological membranes contain zwitterionic lipids, acidic lipids, and acidic groups on membrane-bound proteins and hence bear a layer of net negative charge on both inner and outer surfaces. The negative surface charge sets up a negative surface potential and ionic double layer in the aqueous solution adjacent to the membrane. The simplest description of the surface potential is the Gouy-Chapman-Stern theory (Grahame, 1947; Davies and Rideal, 1963; Barlow, 1970), which assumes the charge is uniformly smeared over a perfect impenetrable plane surface. This theory gives the relationship between surface potential, the surface charge density and the ionic concentration in the aqueous phase (Eqs. 1, 4, and 5). The surface potential plays a critical role in cell adhesion, cell spreading, chemotaxis, endo-exocytosis, and binding of biological active cationic species, such as anesthetics, ion channel antagonists, enzymes, and their substrates (Wojtczak et al., 1982; Volwerk et al., 1986; McLaughlin and Aderem, 1995; Edwards and Newton, 1997). In addition, the negative surface potential plays a significant role in ion transport. The negative surface potentials can affect the steady-state conductance of the ion channels in the membrane, inasmuch as 1), they determine the local ion concentration at the channel orifice; and 2), the difference in surface potentials between both sides of a membrane produces an electric potential drop across the membrane (intramembrane potential), thereby changing the electric driving forces within the membrane (Frankenhaeuser, 1960).

There are two common experimental methods to study surface potential on cell membranes. One is the cell electrophoresis method, which can directly measure membrane surface potential in the aqueous phase adjacent to the membrane. This method has been extensively used to study the electrokinetic properties of monodispersed suspensions of erythrocytes (Nakano et al., 1994) and other blood cells (Vassar et al., 1976; Makino et al., 1993). One disadvantage of this method is that most cell types are not free and monodispersed and have to be treated by enzymatic, chemical, or mechanical means to produce a monodispersed suspension. Such treatment will probably change the surface potential. Another complication in these electrophoresis measurements is that they determine the ζ-potential at an idealized plane of shear at some distance from the membrane surface. Only when this distance is known can it be used to estimate the true surface potential. Monitoring dynamic changes in cell membrane physiology would also be difficult with ζ-potential measurements.

Changes in the surface potential can also be determined by measuring current-voltage (I-V) characteristics of membrane ion channels under varying ionic conditions or pH, under the assumption that all the shifts reflect a modulation of the intramembrane electric field arising from changes in surface potential (Frankenhaeuser and Hodgkin, 1957; Chandler et al., 1965; Gilbert and Ehrenstein, 1969; Mozhayeva and Naumov, 1970; Begenisich, 1975; Hille et al., 1975). But shifts in channel kinetics are not always reliable measurements of the change in intramembrane potential produced by asymmetric surface potentials. First, it has been found that different channels on the same cell are not always affected equally (Frankenhaeuser and Hodgkin, 1957; Hille, 1968), possibly because the gating machinery of channel proteins may experience different local electric fields. Secondly, the binding of divalent cation or charged molecules to the channel protein may not only change a local electric field but also directly disrupt the gating apparatus of the channel protein. For example, in squid axon, Zn2+ changes Na channel activation and deactivation unequally (Gilly and Armstrong, 1982).

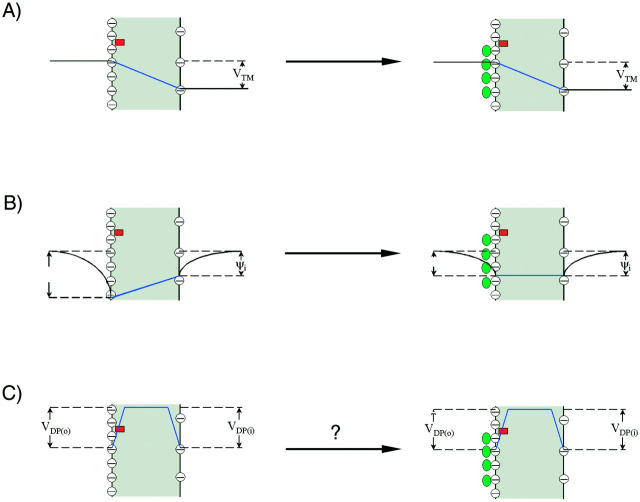
It is generally accepted that asymmetric surface potentials in lipid bilayer or cell membranes generate an electric field within the membrane (intramembrane electric field; Chandler et al., 1965; for review, also see Hille, 2001). The schematic relationship between surface potential and intramembrane electric field is depicted in Fig. 1. It is assumed, first, that the charges are smeared out over both the outer and inner surface of the membrane, and secondly, that the intramembrane electric field set up by the surface charge asymmetry is constant (i.e., the potential drops linearly across the membrane; see Goldman, 1943; Hodgkin and Katz, 1949; Chandler et al., 1965). It has been shown that calculation of the change in intramembrane potential from the difference between asymmetric surface potentials based on the above two assumptions can adequately describe the experimental measurements of the change in intramembrane potential, either by nonactin-induced conductance (Alvarez et al., 1983) and capacitance measurements (Schoch et al., 1979; Alvarez et al., 1983) in lipid bilayers, or by voltage-shifts of ion channels in cell membranes (Frankenhaeuser and Hodgkin, 1957; Chandler et al., 1965; Gilbert and Ehrenstein, 1969; Mozhayeva and Naumov, 1970; Begenisich, 1975; Hille et al., 1975; Zhou and Jones, 1995).

FIGURE 1.

FIGURE 1

Open in a new tab

Effect of extracellular cations on the potential profile across a cell plasma membrane. The dye chromophores (red rectangle) is sensing the electric field (blue line) generated by transmembrane potential (VTM) (A), the difference between the external surface potential (ψo) and internal surface potential (ψi) (B), and the dipole potential at the outer surface (VDP(o)) (C). We define all potential differences as potential inside minus potential outside. When the negative charges on the outer surface are neutralized and bound by cations (green oval), the equilibrium values of VTM is unchanged. However, the ψo is reduced, leading to an increase in intramembrane potential across the membrane, although ψi is unchanged. The effect of divalent cation binding on dipole potential is relatively small, especially at the concentrations used in this study. Therefore, the change in intramembrane potential, 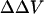Inline graphic, which is calculated from Eq. 7 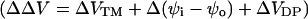Inline graphic, is approximately equal to −Δψo.

In this study, we used voltage-sensitive dyes to measure changes in intramembrane potential caused by asymmetric surface potentials in both lipid vesicles and cell membranes. Voltage-sensitive dyes have been widely used for measuring transmembrane potentials of cells, organelles, and membrane vesicles (Cohen and Salzberg, 1978; London et al., 1987; Waggoner, 1979; Loew, 1988; Gross and Loew, 1989). It has been found that some voltage-sensitive dyes are sensitive to surface potential in the aqueous phase adjacent to the membrane. For example, the fluorescence intensities of both negatively charged dyes such as Merocyanine 540 (Aiuchi and Kobatake, 1979), 1-anilinonaphthalene-8-sulfonate (ANS; see Aiuchi et al., 1977), and the oxonols (Krasne, 1980), and the positively charged cyanines (Krasne, 1980) in lipid bilayers could be changed by surface potential, inasmuch as the amount of the dyes bound to the membrane correlates closely to the membrane surface potential. However, no attempts have been made to quantitatively measure the surface potentials using these voltage-sensitive dyes, partially due to the difficult calibration of these dyes. Also, the charged dyes can redistribute either from one aqueous phase to the other or between the membrane and the aqueous phase in a voltage-dependent manner, thus confounding the surface potential measurement (Krasne, 1980). Bearing these considerations in mind, in this article we use styryl potentiometric dyes, di-4-ANEPPS or di-8-ANEPPS, to probe the surface potential. These dyes have the following advantages: (a) they respond linearly to membrane potential, that is, the relationship between the spectral shift (or the change in fluorescence ratio) and membrane potential is linear with a sensitivity of 9% to 13% per 100 mV, (b) instead of a potential dependent change in the degree or site of binding, an electrochromic mechanism underlies the response (Loew et al., 1979; Loew and Simpson, 1981; Fluhler et al., 1985), (c) they have no net charge at neutral pH, and (d) they produce a spectral shift in response to voltage and therefore can be used for dual wavelength ratio imaging, obviating problems of dye bleaching and uneven staining.

Previous studies from this lab show that the dual wavelength fluorescence ratio of these chromophores can be used to measure a local intramembrane electric field associated with transmembrane potentials (Montana et al., 1989; Bedlack, et al., 1992; Zhang et al., 1998) and dipole potentials (Gross et al., 1994; Bedlack et al., 1994). In this article, we decreased the surface charge density on the external face of the membrane surface by adding divalent cations barium, magnesium, and calcium to the solution bathing the outer membrane surface. The dyes would then sense a change in the electric field arising from the asymmetric surface potentials, which is equivalent to a membrane hyperpolarization (or a decrease in intramembrane potential) (Fig. 1). This article shows that dual wavelength ratiometric measurements of the fluorescence of styryl voltage-sensitive dyes can be used to measure changes of the intramembrane potential as a function of divalent cation concentration in both well-defined liposomes and single N1E-115 neuroblastoma cells.

The effect of divalent cations on surface potential in lipid bilayers has been extensively studied using the electrophoresis method. It has been found that an appropriate form of the Gouy-Chapman-Stern theory for surface potentials at surfaces with smeared charges bathed by electrolyte solutions (Grahame, 1947; Davies and Rideal, 1963; Barlow, 1970; McLaughlin et al., 1981) can describe the measured surface potential very well (Cevc, 1990; McLaughlin et al., 1981; McLaughlin, 1989) by accounting for both divalent cations screening of fixed surface charge and direct binding interactions with phospholipids. To assess whether the dye ratio was primarily detecting the change in surface potential, we fit the measured change in intramembrane potential to the same form of the Gouy-Chapman-Stern theory, and compared the derived association constants with data from electrophoresis measurements.

THEORY AND CALCULATIONS

Lipid vesicles

The relation between the surface potential and a uniformly distributed surface charge density is given by the Grahame (1947) equation:

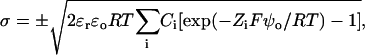graphic file with name M1.gif (1)

where σ is the surface charge density in electronic charges per Å2, Ci is the concentration of the ith ionic species in the bulk solution in mol/l, Zi is its valence, and ψo is the surface potential at the membrane interface (in mV). The concentrations of free monovalent (C+(o)) and divalent cations (C2+(o)) at the membrane surface are related to bulk concentrations (C+ or C2+) by Boltzmann factors:

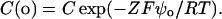graphic file with name M2.gif (2)

At 21°C, RT/F = 25 mV, (2ɛrɛoRT)1/2=(272 Å2e−1M1/2)−1 and Eq. 1 can be rewritten as:

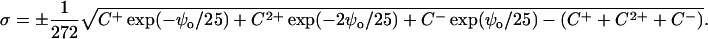graphic file with name M3.gif (3)

We also assume that a monovalent cation binds to one PS molecule in the membrane, with an association constant K1 (in 1/mol); a divalent cation may bind one PS molecule in the membrane, with an association constant K2 (in 1/mol); a divalent cation may also bind one PC in the membrane, with an association constant K3 (in 1/mol) and the Langmuir adsorption isotherm is valid (Eisenberg et al., 1979). Then, the free surface charge density, σ, is related to the total surface concentration (no-ion binding) of PS ({PS}tot) and PC ({PC}tot) by the following formula (McLaughlin et al., 1981):

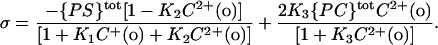graphic file with name M4.gif (4)

It is assumed that each PS and PC molecule occupies an area of 70 Å2 (McLaughlin et al., 1981). The combination of Eqs. 3 and 4 is referred to as a Stern equation. A least-squares analysis was performed to fit the measured surface potentials to the combination of Eqs. 3 and 4, and to obtain the estimates of K2 and K3.

N1E-115 neuroblastoma cell

Assuming the cell surface is a ion-impenetrable plane and the surface charge density has a uniform distribution, again, the relation between the surface potential and the surface charge density is given by the Eq. 1.

However, in the case of a cell membrane we do not know the profile of charged and neutral lipids that comprise the outer surface. Therefore, we adopt a simpler model consisting of a single association constant for each of the cations with the charged species on the surface. The total negative surface charge density in the absence of cations is taken as σtot (per Å2). Divalent cations still form 1:1 complexes with the negative molecules with intrinsic association constants K2. Monovalent cations form 1:1 complexes with the negative molecules with intrinsic association constants K1. The association constant is estimated with the following equation for free surface charge at the boundary between the surface charge layer and the bulk solution:

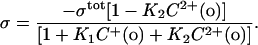graphic file with name M5.gif (5)

In contrast to the formula (Eq. 4) we used for lipid vesicles, this equation does not explicitly deal with the neutral lipids and therefore the surface charge density of neutral lipid ({PC}tot in Eq. 4) and the association constant of divalent cations to neutral lipids (K3) are omitted. Similarly, a least squares analysis was performed to fit the measured data to the combination of Eqs. 3 and 5, and to obtain the estimates of the values of σtot, K1, and K2.

Calculation of changes in intramembrane potentials

The measured fluorescence ratios of di-4-ANEPPS and di-8-ANEPPS in the presence of various concentrations of divalent cations are normalized to the fluorescence ratios before the addition of divalent cations. Because the relative percent change in fluorescence ratio is lineally proportional to the changes in intramembrane potential (Montana et al., 1989; Zhang et al., 1998), the changes in intramembrane potential, 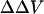Inline graphic, can be calculated as:

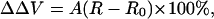graphic file with name M7.gif (6)

where A is the proportionality constant that corresponds to the voltage sensitivity of the dye, R is the fluorescence ratio (440 nm/505 nm excitation ratio for both di-4-ANEPPS and di-8-ANEPPS) in the presence of divalent cations, and R0 is the fluorescence ratio in the absence of divalent cations. In principle, 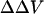Inline graphic contains contributions from several sources:

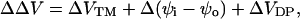graphic file with name M9.gif (7)

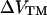where Inline graphic is the change in transmembrane potential, ψi is the surface potential at the inner surface, ψo is the surface potential at the outer surface, and 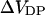Inline graphic is the change in dipole potential.

METHOD

Lipid vesicles

Solutions were buffered with 20 mM HEPES/Tris, pH 7.0 (21°C), and contained 140 mM NaCl in the absence of any divalent salts. Small unilamellar liposomes were made as described by Deamer and Uster (1983). Briefly, lipid vesicles were prepared by drying a chloroform solution of 10 mg of egg phosphatidylcholine (Sigma Chemical Co., St Louis, MO; type XI-E) or a mixture of 70% egg phosphatidylcholine and 30% bovine brain phosphatidylserine (Avanti Polar-Lipids Inc., Birmingham, Al) under a stream of argon for a minimum of 3 h, resuspending the lipids in 1 mL of the buffer and sonicating to clarity with a Laboratory Supplies Company G1128P1T sonifier (Hicksville, NY) under an argon atmosphere. For fluorescence measurements, 60 μL of the vesicle suspension was diluted into 3 mL of buffer containing 0.2 μM di-4-ANEPPS. The background scattered light intensity was found to increase with both PC and PC:PS vesicles upon addition of divalent cations and therefore was subtracted from the corrected excitation spectra. The corrected excitation spectra of the vesicle suspension were measured with a Spex CM dual-wavelength fluorescence spectrometer (Spex Industries, Edison, NJ). All experiments were performed at 21°C.

Cell preparation

N1E-115 mouse neuroblastoma cells were grown and maintained in Dulbecco's modified Eagle's medium containing 10% fetal bovine serum. Cells were grown until 50% confluent before seeding on uncoated glass coverslip. Differentiation was initiated by replacing the media with one containing 0.5% fetal bovine serum and 1% dimethylsulfoxide. Cells were cultured for a further 2–4 days to complete differentiation and achieve neuronal morphology.

Dye loading

To stain cells with voltage-sensitive dye, each coverslip was washed in buffered Hank's salt solution that contains no calcium, and then incubated for 20 min at 4°C in the same buffer supplemented with 1-(3-sulfonatopropyl)-4-[β[2-(di-n-octylamino)-6-naphthyl]vinyl]pyridinium betaine (di-8-ANEPPS; 0.5 μM) and Pluronic F-127 (BASF, Wyandotte, MI) (PF-127; 0.05%). Coverslips were then rinsed 3 times with fresh buffer.

Dual wavelength imaging

Stained cells were mounted on an inverted Zeiss microscope (Axiovert 135 TV) and viewed with an oil immersion objective (Plan-apochromat 63 × 1.40). Dual wavelength images pairs of di-8-ANEPPS (excitation at 440 and 530 nm, emission >570 nm) were acquired using a cooled CCD camera (Photometrics, Model CE200A, Tucson, AZ) on the microscope, controlled by Cellscan Acquisition Control unit. An additional magnification of ×2.5 was used when fluorescent images were taken. Exposure time was 0.7 s for 440 nm and 1.4 s for 530 nm. A 2 × 2 binning of CCD pixels was used to increase the signal and minimize exposure time. Autofluorescence signals were negligible at both excitation wavelengths compared with di-8-ANEPPS fluorescence. All microscopy experiments were performed at room temperature (21°C).

Patch clamp

Micropipettes were pulled from glass capillaries (Drumond Scientific 100) using a Brown-Flaming micropipette puller (Sutter Instrument, Model P-80, San Francisco, CA) with a tip diameter of 1–2 μm. The resistance of the pipettes varied from 3 to 7 MΩ. During calibration of the dye, the membrane was clamped in a whole cell configuration to various levels from −80 to 60 mV with a voltage step of 20 mV. A pair of images was taken at each potential.

RESULTS

Lipid vesicles

We first studied the effect of divalent ions Magnesium (Mg) and Barium (Ba) on the fluorescence intensity of di-4-ANEPPS bound to the lipid vesicles. Calcium was not used in this experiment since we found that it caused severe aggregation of the lipid vesicles and therefore increased the background scattered light intensity dramatically even before the addition of di-4-ANEPPS. The reasons we chose di-4-ANEPPS are that the voltage sensitivity of di-4-ANEPPS has been well characterized (Montana et al., 1989) and that we found the adsorption of this dye to the lipid vesicles could quickly reach equilibrium and remain unchanged during our measurements, which usually last 40 min. The calibrated fluorescence excitation spectra of di-4-ANEPPS bound to PC and PC:PS vesicles at different divalent ion (Ba, Mg) concentration are pictured in Fig. 2. The lipid-bound dye has an excitation maximum at 467 nm. Clearly, the effect of increasing divalent cations is not simply a spectral shift, but also an increase in emission intensity. This is partly because of an intramembrane potential-dependent shift in the emission spectrum (data not shown), which manifests itself as a change in intensity at the 610-nm emission wavelength used for the excitation scan. To remove the effect of the change in emission intensity, the excitation spectra obtained in the presence of various concentration of divalent were normalized to the integrated intensity obtained without divalent cations, determined from the area under each excitation spectra. This way we found that the wavelengths with the maximum positive and negative changes in the normalized difference spectra were around 440 and 505 nm (Fig. 2, B and D), which is consistent with our previous finding that the maximum positive and negative shift in excitation spectrum induced by changes in transmembrane potential occurs at 440 and 505 nm (Montana et al., 1989). Montana et al. (1989) also found that the ratio of di-4-ANEPPS fluorescence excited at 440 and 505 nm has a linear relationship to transmembrane potential with a slope of 9%/100 mV. To measure the intramembrane potential change induced by various concentrations of divalent ions, the ratio of fluorescence excited by these two wavelengths was recorded for a series of vesicle suspensions in the presence of varying concentrations of divalent cations, and the change in intramembrane potential (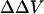Inline graphic) is calculated by Eq. 6, with the proportionality constant, A, equal to 9% per 100 mV.

FIGURE 2.

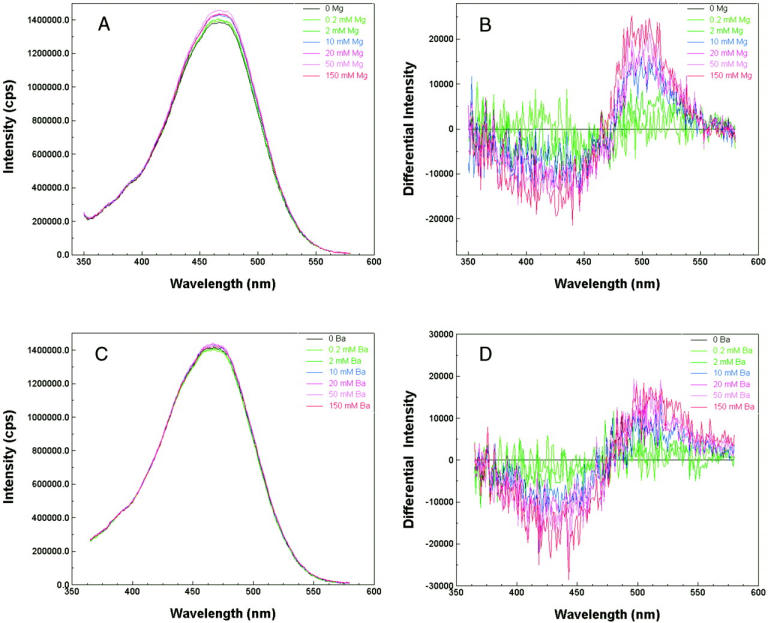
FIGURE 2

Open in a new tab

Effect of divalent cations on the fluorescence excitation spectra of PC:PS lipid vesicles containing 0.2 μM di-4-ANEPPS. A 10 mg/mL stock solution of lipid vesicles was diluted 50-fold into a cuvette containing 0.2 μM di-4-ANEPPS, 140 mM NaCl (pH 7.0). The emission wavelength is 610 nm. (A and C) Excitation spectra for a series of PC:PS vesicle suspensions containing various concentration of Mg and Ba, respectively. The spectra were normalized by the area under each curve to the same integrated intensity. (B and D) Normalized difference excitation spectra for the same PC:PS vesicle suspensions as in A and C, respectively. The difference between the spectra obtained without Mg (or Ba) and with various concentration of Mg (or Ba) is displayed.

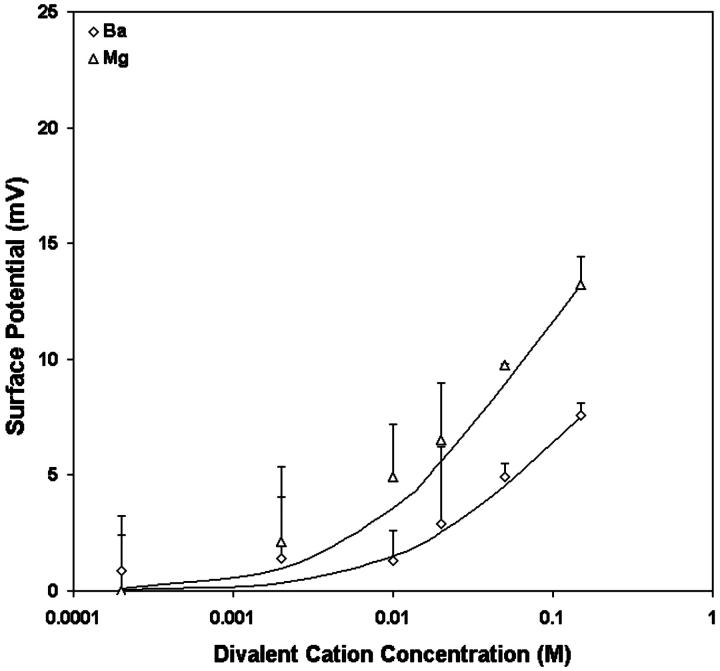
Table 1 shows the effects of different divalent cations (Ba, Mg) on Inline graphic of vesicles formed from fresh egg yolk PC in the presence of 0.14M NaCl. The observed potential change for Ba and Mg can be well described by the Stern equation, with intrinsic association constants, K3, of 1.0 and 0.4 M−1 for Mg and Ba, respectively (Fig. 3).

TABLE 1.

Average intramembrane potential changes (Inline graphicV) induced by various concentrations of divalent ions in lipid vesicles formed from egg PC

Inline graphic (mV)
C2+ (M) C+ (M) C− (M) Ba (n = 6) Mg (n = 6)
0 0.14 0.14 0 0
0.0002 0.14 0.1404 0.9 ± 2.4 0.01 ± 2.4
0.002 0.14 0.144 1.4 ± 2.7 2.1 ± 3.3
0.01 0.14 0.164 1.3 ± 1.3 4.9 ± 2.3
0.02 0.14 0.184 2.9 ± 3.3 6.5 ± 2.5
0.05 0.14 0.244 4.9 ± 0.6 9.8 ± 0.1
0.15 0.14 0.444 7.6 ± 0.6 13.3 ± 1.2
Open in a new tab

FIGURE 3.

FIGURE 3

Open in a new tab

The effects of Ba (open diamonds), Mg (open triangles) on the surface potentials of PC vesicles. Each point represents the mean of the surface potential measurements of six vesicle preparations. The curves are the theoretical results for surface potential for the best-fit K3 values where K3 is the 1:1 association constant of the divalent cation with PC: K3 = 0.4 M−1 for Ba; 1 M−1 for Mg.

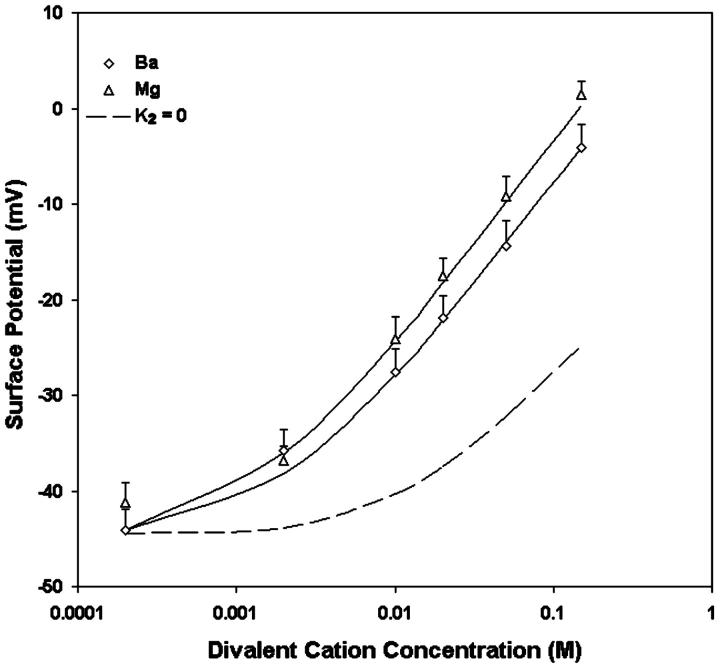
We also measured the 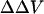Inline graphic upon adsorption of divalent ions to a membrane composed of 30% negative lipid PS and 70% zwitterionic lipid PC. The addition of divalent cations Ba and Mg to the bathing solution causes a decrease in intramembrane potential (Table 2). The experimental data shown in Table 2 were analyzed in terms of the association constant of Na+ (K1) and divalent ions (K2) to PS according to the Stern equation proposed by McLaughlin et al. (1981). We assumed that Na+ forms 1:1 complex with PS with the intrinsic association constant, K1, of 0.6 M−1 (Eisenberg et al., 1979; McLaughlin et al., 1981), and all divalent cations forms only 1:1 complexes with PS. When the concentration of divalent cations is 0, the Stern Equation is solved by least-squares analysis and gives the initial surface potential without the addition of divalent cations a value of −45 mV. We used the same value of K3 that had been derived from the adsorption of divalent ions to pure PC. Fig. 4 shows that the theoretical curves with the values of K1 = 0.6 for Na, 1.9 for Mg, and 1.8 M−1 for Ba, fit the experimental data very well. The theoretical curve assuming no-divalent ion binding with the PS and PC (K1 = 0.6; K2 = 0; K3 = 0) is shown by a dashed line. All divalent cations cause a larger effect on surface potential than calculated by this theoretical “screening” curve. For an equimolar replacement, the sequence of effectiveness of various divalent ions for changing surface potential in both PC and PC:PS lipid vesicles is Mg > Ba.

TABLE 2.

Average intramembrane potential changes (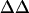Inline graphicV) induced by various concentrations of divalent ions in lipid vesicles formed from mixtures of 70% egg PC and 30% brain PS

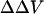Inline graphic (mV)
C2+ (M) C+ (M) C− (M) Ba (n = 5) Mg (n = 7)
0 0.14 0.14 0 0
0.0002 0.14 0.1404 0.4 ± 2.2 4.0 ± 2.0
0.002 0.14 0.144 8.7 ± 2.2 7.6 ± 1.6
0.01 0.14 0.164 17.0 ± 2.3 20.4 ± 2.2
0.02 0.14 0.184 22.6 ± 2.3 27.0 ± 1.9
0.05 0.14 0.244 30.1 ± 2.6 35.3 ± 2.1
0.15 0.14 0.444 40.5 ± 2.4 44.9 ± 1.5
Open in a new tab

FIGURE 4.

FIGURE 4

Open in a new tab

The effects of Ba (open diamonds) and Mg (open triangles) on the surface potentials of vesicles formed from mixtures of 70% egg PC and 30% brain PS. Each point represents the mean of the surface potential measurements from five to seven vesicle preparations. The curves are the theoretical predictions of the Stern equation with K1 = 0.6 M−1, the same corresponding K3 values derived from Fig. 3, and optimized fits for K2, the 1:1 association constant of the divalent cation with PS: K2 = 1.8 M−1 for Ba; 1.9 M−1 for Mg. As a reference, the dashed line is the theoretical prediction for surface potential assuming K2 = 0.

N1E-115 Neuroblastoma cells

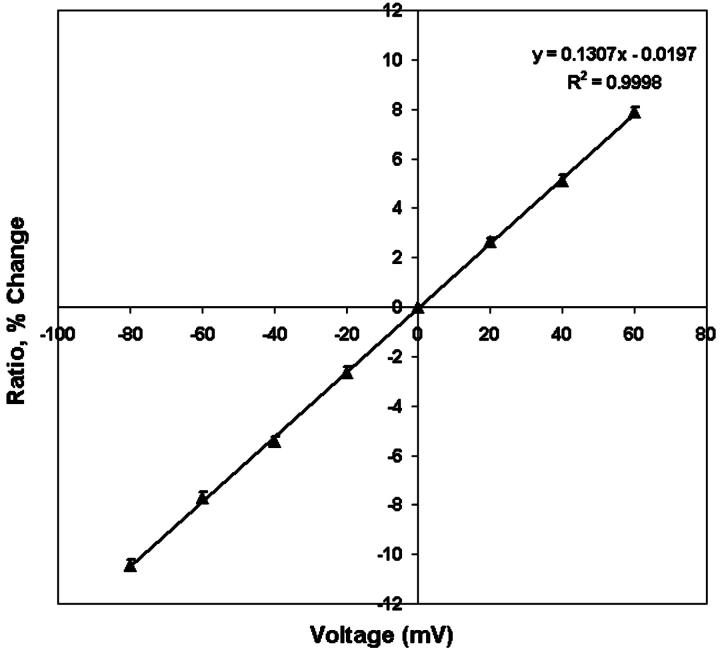
Using combined patch clamp recording and dual wave-length imaging as described by Zhang et al. (1998), we were able to measure the 440-nm/530-nm fluorescence ratios along the plasma membrane of a single cell as a function of the applied transmembrane potential (Fig. 5). The average resting potential of these differentiated neuroblastoma cells measured by current clamp is −41.6 ± 1.7 mV (n = 10). This value is comparable to the resting potential value Zhang et al. (1998) measured in the same type of cells (−40.7 ± 2.2 mV). To avoid variance from cell to cell, we normalized the ratio observed at different transmembrane potential (Vm) to the ratio observed when Vm is equal to 0 mV. Consistent with Zhang's result, Di-8-ANEPPS showed linear dependence of fluorescence ratio on potential with a slope of +13% per 100 mV. Because ratio imaging of di-8-ANEPPS can only measure the changes in intramembrane potential, in the following experiment, various concentrations of divalent cations are added to the bathing medium that contains zero divalent cations and changes in intramembrane potential are calculated by Eq. 6, with the proportionality constant, A, equal to 13% per 100 mV.

FIGURE 5.

FIGURE 5

Open in a new tab

Calibration of the membrane-stained dye di-8-ANEPPS in N1E-115 neuroblastoma cell. Cells were voltage-clamped at different voltage levels and pairs of dual wavelength (440 nm and 530 nm) images were taken at each holding potential. Each 440-nm/530-nm ratio was normalized to the ratio observed when Vm was equal to 0 mV and expressed as its relative change and plotted versus the holding potential. The calibration line was derived from linear regression of the scattered data, indicating a + 13% change of fluorescence ratio per 100 mV with a correlation coefficient R2 of 0.9998.

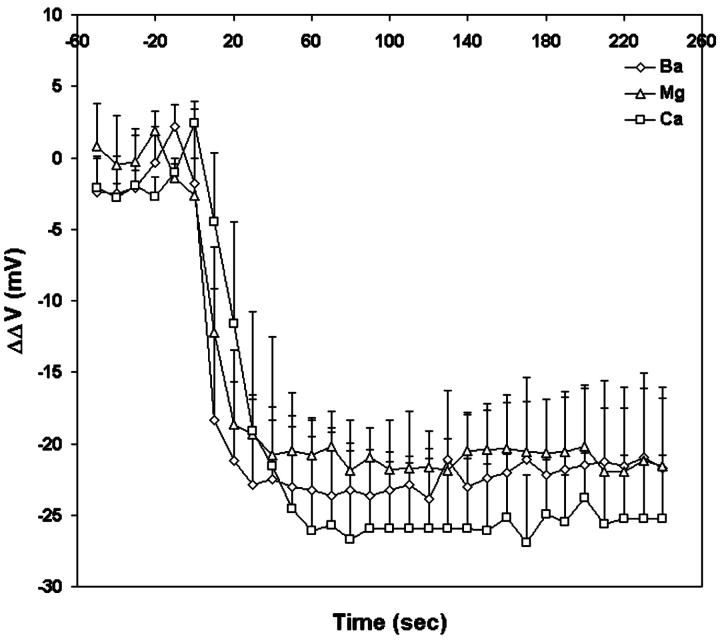
Dual wavelength ratiometric imaging of di-8-ANEPPS in the membrane of differentiating N1E-115 cells reveals that a tenfold increase in the concentration of external divalent cations from 0.2 mM induces a substantial decrease in the fluorescence ratio, which plateaus at ∼50 s for Ca, 40 s for Mg, and 30 s for Ba, respectively (Fig. 6). The changes in the average steady-state intramembrane potential are −22.4 mV for Ba, −21.1 mV for Mg, and −25.6 mV for Ca. Fig. 7 shows the time courses of the changes in fluorescence ratio in a typical single cell after increasing extracellular Ca from 0 to 2 mM. As shown in Fig. 7, a decrease in the apparent cell size occurred. There are two possible contributions to the change in cell diameter in these images. First, an increased extracellular osmolarity after adding 2 mM calcium chloride to the bath solution from 294 mM to 300 mM may cause the cell to shrink. Secondly, even a slight shrinkage of the cell may cause its central plane to move out of focus and appear smaller under the microscope. We therefore repeated these experiments under nonkinetic conditions in which the osmolarity was maintained with appropriate levels of sucrose by exchanging the bathing medium. No cell shrinkage was observed under these conditions, but the decrease in the steady-state intramembrane potential induced by 2 mM Ca was the same (−60.5 ± 1.5 mV, n = 4) as the kinetic runs where 2 mM Ca was added directly to the bath and cell shrinkage was observed. (−57.4 ± 6.4 mV, n = 10). Furthermore, the decrease in intramembrane potential reached maximum after 60 s and remained the same for the following 150 s, whereas the diameter of the cell decreased 3.49% by 60 s and continued to decrease by 2.91% for the following 150 s; the absence of synchrony between the two phenomena therefore also suggest that cell shrinkage is not reflected in the fluorescence ratio measurement. Finally, it should be noted that because our image analysis uses wide-field detection and the dual excitation wavelength ratio of total integrated emission from the cell periphery, cell shape changes and focal drift cannot confound the measurement.

FIGURE 6.

FIGURE 6

Open in a new tab

Kinetics of the change in intramembrane potential on neuroblastoma cells induced by a tenfold increase in divalent cation concentration in the external medium. At time = 0, 2 mM Ba (open diamonds), Mg (open triangles), and Ca (open circles) are externally applied to the bathing medium containing 0.2 mM of the corresponding divalent cation. Each point represent the mean of the surface potential measurements of six cells.

FIGURE 7.

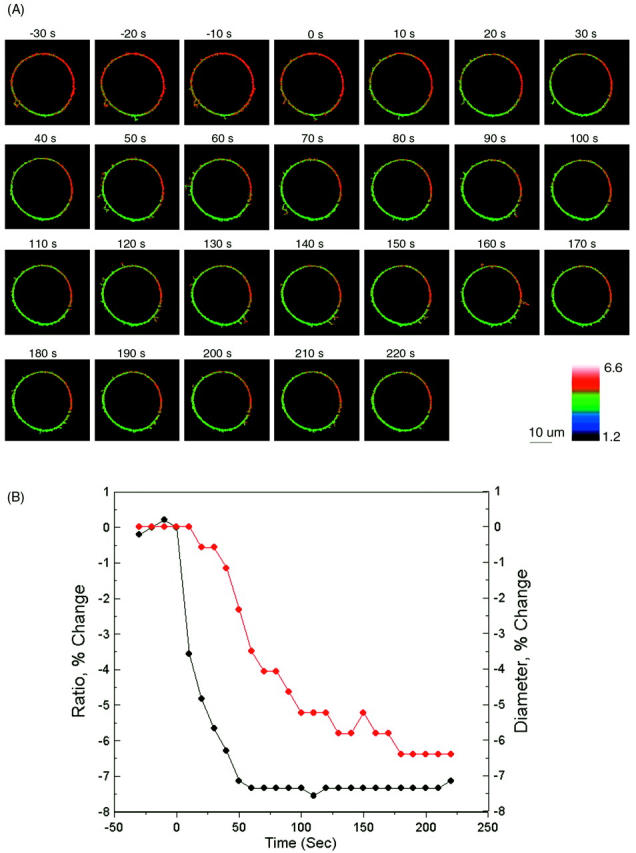
FIGURE 7

Open in a new tab

Visualizing the effect of calcium on intramembrane potential with di-8-ANEPPS in N1E-115 neuroblastoma cells. (A) At time = 0, 2 mM Ca was externally applied to the bathing medium (initially containing 0 mM Ca) of a cell stained with di-8-ANEPPS. The 440-nm/530-nm fluorescence ratios are displayed in pseudocolor. (B) The time-dependent change in surface potential does not parallel the change in cell diameter. The changes in 440-nm/530-nm ratio (black) and cell diameter (red) are both calculated relative to values before the addition of Ca. The relative changes in intramembrane potential were calculated from the calibration Equation: 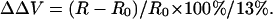Inline graphic

We also noticed that the fluorescence ratio was not uniformly distributed along the cell surface. For example, the cell in Fig. 7 shows a higher than average fluorescence ratio at the membrane arc centered at 3 o'clock. The non-uniformity is not due to an uneven background, since all the images are carefully corrected for background and flat-field variations. The non-uniformity is persistent when the transmembrane potential of the whole cell is clamped at different levels (data not shown) and when the surface charges are screened and neutralized overall after elevation of extracellular calcium. Therefore, the non-uniformity is not likely to be caused by unequal transmembrane potential or unequal surface charge distribution. Instead, it is possibly a result of variations in dipole potential along the cell surface as demonstrated in our earlier studies (Zhang et al., 1998; Bedlack et al., 1994).

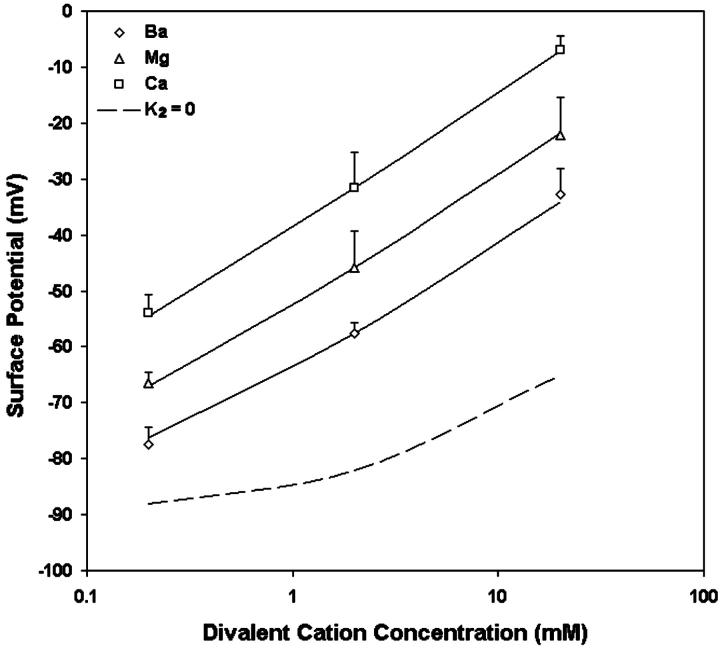
The average changes in intramembrane potential induced by various divalent cations are shown in Table 3. As shown in Fig. 8, it is found that when the concentration of the divalent cations (in logarithmic scale) is between 0.2 and 20 mM, the observed changes in surface potentials almost fall on a straight line. A tenfold increase of concentration of divalent cations causes an average increase in surface potential of 22.3 mV for Ba, 22.1 mV for Mg, and 23.5 mV for Ca. This result agrees very well with the surface potential changes we measured by increasing the concentration of divalent cations from 0.2 to 2 mM (Fig. 6). A least-squares analysis was carried out to fit the measured potential changes to the combination of Eqs. 3 and 5, and to find the values for the association constants of the divalent cations, the association constant of Na and the net charge densities (Table 4). The values for these parameters were used for the theoretical curves in Fig. 8. The theoretical curve with the condition in which the divalent ions do not bind the acidic group (i.e., K2 = 0) is illustrated in dashed line. The observed changes in surface potential induced by increasing concentration of divalent cations are much larger than predicted by the “screening” curve, indicating the significance of binding. The intrinsic dissociation constants of Ba, Mg, and Ca with the acidic group in the surface of neuroblastoma cells are 1.7, 6.1, and 25.3 M−1, respectively. The density of acidic groups at the outer surface of the neuroblastoma cells are estimated as 8.7 × 1017e−/m2, which is equivalent to a surface charge density of 1 e−/115 Å2.

TABLE 3.

Average intramembrane potential changes (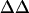Inline graphicV) induced by various concentrations of divalent ions in the surface region of N1E-115 neuroblastoma cells

Inline graphic (mV)
C2+ (M) C+ (M) C− (M) Ba Mg Ca
0 0.14 0.14 0 0 0
0.0002 0.14 0.1404 11.6 ± 3.0 (n = 9) 22.5 ± 2.0 (n = 6) 35.0 ± 3.4 (n = 7)
0.002 0.14 0.144 31.5 ± 1.8 (n = 8) 43.2 ± 6.4 (n = 8) 57.4 ± 6.4 (n = 10)
0.02 0.14 0.184 56.2 ± 4.7 (n = 8) 66.8 ± 6.8 (n = 8) 82.0 ± 2.6 (n = 9)
Open in a new tab

FIGURE 8.

FIGURE 8

Open in a new tab

The effect of Ba (open diamonds), Mg (open triangles), and Ca (open circles) on the intramembrane potential of N1E-115 neuroblastoma cells. Each point represents the mean of the surface potential measurements of six to nine cells. The curves are the theoretical predictions of the Stern equation using the values of all parameters in Table 4. For reference, the dashed line is the theoretical prediction for surface potential with K2 = 0.

TABLE 4.

Characterization of ionizable groups at the outer membrane surface of N1E-115 neuroblastoma cells, with the average surface charge densities (σnet) and intrinsic association constants for different divalent cations

K1 (M−1) K2 (M−1)
σnet (e−/Å2) ψ0 (mV) Na Ba Mg Ca
−0.0087 −89 0.02 1.7 6.1 25.3
Open in a new tab

For an equimolar replacement, the sequence of effectiveness of various divalent ions for changing surface potential in neuroblastoma cells is also Ca > Mg > Ba.

DISCUSSION

This study shows that the dual-wavelength voltage-sensitive dyes di-4-ANEPPS and di-8-ANEPPS can be used to measure the effect of divalent cations on intramembrane potential in both compositionally defined liposomes and in cells. The measured changes in intramembrane potential in both liposomes and cells can be described by the Gouy-Chapman-Stern theory, consistent with a change in surface potential at the external face of the membrane. In liposomes, the association constants for Ba and Mg, derived from a least-squares fitting of the measured data to Gouy-Chapman-Stern theory, agree quite well with the association constants derived from electrophoresis measurements. These results support the idea that the change in intramembrane potential induced by divalent cations is a result of asymmetric surface potentials. This analysis permits estimation of the charge density on the outer surface of cell membranes and demonstrates that the dual wavelength ratio can be used to monitor physiologically important changes in surface potential in living cells.

It is important to emphasize that these zwitterionic styryl dyes, fundamentally, measure the intramembrane electric field at the location of the chromophores within the bilayer. An implicit assumption in our analysis of the fluorescence ratios is that the internal dielectric of the membrane is uniform so that the difference in surface potential produces a linear gradient in potential (Fig. 1). We have expressed the changes in this electric field as a change in intramembrane potential, 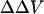Inline graphic, which is defined as the equivalent transmembrane potential change that would produce the observed change in dye ratio. The measured 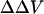Inline graphic induced by a change in surface potential at the outer membrane-aqueous interface represents, therefore, a change in the potential profile within the membrane, rather than a direct assay of the outer surface potential. Indeed, Gross et al. (1994) found that the fluorescence ratio of di-8-ANEPPS was almost completely insensitive to changes in surface potential, as long as such changes were symmetrically applied to both the inner and outer membrane surfaces. Our work shows that in PC/PS and PC unilamellar lipid vesicles, di-4-ANEPPS displays spectral shifts in response to induced changes in surface potential at the outer membrane-aqueous interface similar to those determined in response to transmembrane potential (Fig. 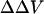2), supporting the idea that changes in surface potential shift the spectral responses of di-4-ANEPPS by affecting Inline graphic.

As a way to determine whether the measured 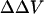Inline graphic arises from asymmetrical surface potential alone, which makes it equal to the change in surface potential in the aqueous phase at the interface, we compared the observed changes in potential with predictions of an appropriate form of the Gouy-Chapman-Stern (GCS) theory (Grahame, 1947; McLaughlin et al., 1981). The GCS theory assumes the charge is uniformly smeared over a perfect impenetrable plane surface. The ions in the electrolyte solution interact with the charged surface not only by electrostatic forces but also bind to the charged groups on the surface where the Langmuir adsorption isotherm is valid. Although the approximations underlying GCS theory are clearly not valid on a molecular scale (i.e., the surface charge is composed of stochastically distributed bound ionic groups that may be penetrated to varying depths by both solvent and solute molecules), it has been found to be able to describe the surface potential of both artificial and biological membranes very well (Cevc, 1990; McLaughlin et al., 1981; McLaughlin, 1989). In our Stern equation (Eqs. 3 and 4), we assume divalent cations bind to zwitterionic lipid PC in a 1:1 manner, inasmuch as 31P-NMR studies suggested that Ca2+ binds to PC headgroups with a stoichiometry of 1:1 (Petersheim et al., 1989). We also assume each divalent cation binds to one PS molecule (McLaughlin et al., 1981), although there is evidence that PS molecules can be involved in 2:1 PS-Ca2+ association (Lopez-Garcia et al., 1993).

The measured change in potential induced by divalent Mg and Ba in both PC and PC:PS vesicles can be described quite well by the GCS theory (Figs. 3 and 4). Our results with PC vesicles suggest that the intrinsic association constants of Mg and Ba with PC are 1.0 and 0.4 M−1, respectively (Fig. 3). These numbers agree quite well with values of 1 ∼ 2 and 0.3 M−1 deduced from the ζ-potential measurements (McLaughlin et al., 1978; McLaughlin et al., 1981). Our results with PC:PS vesicles suggest that the intrinsic association constants of Mg and Ba with PS are 1.9 and 1.8 M−1, respectively (Fig. 4). McLaughlin et al. (1981) refitted the data derived from measurement of the cation-induced change in intramembrane potential in PS (Ohki and Sauve, 1978) or within a PS bilayer using conductance probes (McLaughlin et al., 1971) to GCS theory, by assuming that a), the dipole potential does not change on addition of divalent cations; b), Na binds to PS with an association constant of 0.6 M−1 (Eisenberg et al., 1979); and c), divalent cation forms a 1:1 complex with a PS molecule. They found those data can be fitted very well to the curves calculated from the Stern equation with the association constant of Mg with PS K2 = 3 M−1. This value agrees very well with our result (1.9 M−1). They did not calculate the association constants for Ba from the data obtained by McLaughlin et al. (1971), which showed that the relative effectiveness of divalent cations to change surface potential in PS bilayers is Ca > Mg > Ba. Therefore, the intrinsic association constant calculated for Ba from the data obtained by McLaughlin et al. (1971) should be less than 3 M−1, again consistent with our finding (1.8 M−1). The association constants for Mg, 8 M−1, and Ba, 20 M−1, derived from ζ-potential measurement (McLaughlin et al., 1981), are both somewhat higher than the values, 1.9 M−1 and 1.8 M−1, respectively, derived from the fluorescence ratio method described here.

There remains a concern as to whether binding of divalent cations to the membrane can change dipole potential, since it has been reported that divalent cations could cause reorientation (Scherer and Seelig, 1989; Bechinger and Seelig, 1991) and dehydration of the phospholipid headgroup (Hauser and Shipley, 1985; Dluhy et al., 1983). It is believed that divalent cations generally can change only the membrane surface potential and have no measurable effect on dipole potential (Matsumura and Furusawa, 1998), except for very large (like hexamethonium; see Alvarez et al., 1983), or small (like Be2+; see Ermakov et al., 2001) ions. In particular, Ca2+ has been found not to change dipole potential in lipid bilayers composed of phosphatidylserine (PS; see also Alvarez et al., 1983), phosphatidylcholine (PC; see also McLaughlin et al., 1978), and phosphatidylethanolamine (PE; see also Matsumura and Furusawa, 1989). Magnesium (Mg) has no effect on dipole potential in PS bilayers (Ermakov et al., 2001). It appears that Barium (Ba) also has no significant effect on dipole potential in PS bilayers, since the effect of Ba on intramembrane potential in PS bilayer measured with conductance probe agrees very well with the Gouy-Chapman surface potential theory (McLaughlin et al., 1971). However, Clarke and Lüpfert (1999), using d-8-ANEPPS, found that applying high concentrations (0.5 M) of Ba and Mg symmetrically to both the inner and outer membrane surfaces of PC vesicles could cause decreases in dipole potential from a value of 320 to 300 and 294 mV, respectively. Indeed, the styryl dyes are quite sensitive to dipole potential (Gross et al., 1994; Clarke, 1997, 2001; Clarke and Kane, 1997). Therefore, there is a possibility that the measured 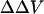Inline graphic in our experiments could have a contribution from a change in the dipole potential induced by the cations. Arguing against this, however, we find that the measured 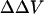Inline graphic induced by the lower levels of Ba and Mg used in our study can be accommodated very well by the GCS theory with almost the same association constants as those derived from ζ-potential measurements.

We also measured the divalent cation-induced intramembrane potential change in N1E-115 neuroblastoma cells. Changes in intramembrane potential induced by asymmetric surface potentials in neurons are often determined from a shift of the current-voltage relationship of ion channels present on the cell surface. Hille et al. (1975) measured voltage shifts in sodium activation in frog myelinated nerve fibers. They found that a tenfold increase in external divalent cation concentration led to a shift of +20 to +25 mV. In squid giant axon, Frankenhaeuser and Hodgkin (1957) found a tenfold change in external Ca concentration produced shifts in sodium conductance of 21.4 mV. Zhou and Jones (1995) measured the activation curve of calcium channel in frog sympathetic neurons and found a tenfold increase of external Ba produces a shift of about +20 mV. These values agree quite well with our observations, which show that a tenfold increase of concentration of divalent cations causes an average increase in surface potential of 22.3 mV for Ba, 22.1 mV for Mg, and 23.5 mV for Ca, respectively (Fig. 8). Our result provides evidence that the shift of the voltage dependence of these ion channels is due to the overall decrease (in absolute value) in the intramembrane potential.

Traditional methods for the study of surface potential are usually single-point measurements and would be difficult to adapt to kinetic studies of cell physiology. Our method allowed us to follow the kinetics of 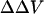Inline graphic induced by a tenfold increase in divalent cation concentration. We found that the reaction reaches steady state at 50 s for Ca, 40 s for Mg, and 30s for Ba, respectively (Fig. 6). Because of the slow time course, we conclude that the adsorption of divalent cations to biological membranes is not simply limited by diffusion, but must involve complex interactions between the divalent cations and the membrane components. The steady-state bimolecular rate constant for this reaction estimated from our observation is ∼0.3 M−1 s−1 for Ca, 0.1 M−1 s−1 for Mg, and 0.2 M−1 s−1. These slow rates could suggest that significant lipid bilayer reorganization accompanies binding of the divalent cations.

The divalent cation-induced change in intramembrane potential in N1E-115 cells can be fitted to an appropriate form of GCS theory (Eqs. 3 and 5). The obtained association constant of divalent cations with the negatively charged group is 25.3 M−1 for Ca, 6.1 M−1 for Mg, and 1.7 M−1 for Ba; the obtained surface charge density is 1 e−/115 Å2. These values agree well with the values derived from measurement of the shift in calcium channel activation, assuming divalent cation bind to membrane (1 e−/200 Å2, assuming the association constant is 13.5 M−1 for Ca, 5.5 M−1 for Mg and Ba, see Ganitkevich et al., 1988; 1 e−/185 Å2, assuming the association constant for Ba is 2.3 M−1, see Smith et al., 1993). The agreement between the 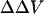Inline graphic estimated by the dyes and the theoretical surface potential in cell membranes is consistent with the idea that the divalent cation-induced 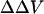Inline graphic arises from asymmetric surface potentials. However, as pointed out by Hille (2001), “if one is free to postulate a variety of charge distributions with arbitrary ion binding and pKa values, a good fit to a specific model is no proof of its correctness.” As opposed to the well-defined liposomes, where we know the surface charge density, a possible change in dipole potential associated with divalent cation binding to the cell surface cannot be excluded.

In conclusion, we have described ratiometric imaging techniques for measuring divalent cation-induced intramembrane potential, presumably arising from asymmetric surface potentials. This method opens the exploration of surface potential changes induced by biochemical signaling events, such as phosphorylation, dephosphorylation, or lipid metabolism. One can imagine there would be circumstances under which asymmetric surface potentials might modulate the function of not only ion channels, but also other membrane signaling events. Using dual wavelength voltage-sensitive dyes, we can monitor the intramembrane potential changes associated with modulation of surface potentials at either the external or cytosolic interfaces under various physiological conditions in real time.

Acknowledgments

We are pleased to acknowledge Dr. Boris Slepchenko, Jim Schaff, and Dr. Mei-de Wei for providing advice and help in various aspects of this research.

We are also grateful for the support of the National Institute of General Medical Science through grant GM35063.

References

  1. Aiuchi, A., N. Kamo, K. Kurihara, and Y. Kobatake. 1977. Significance of surface potential in interaction of 8-anilino-1-naphthalenesulfonate with mitochondria: fluorescence intensity and ζ-potential. Biochemistry. 16:1626–1630. [DOI] [PubMed] [Google Scholar]
  2. Aiuchi, T., and Y. Kobatake. 1979. Electrostatic interaction between merocyanine 540 and liposomal and mitochondrial membranes. J. Membr. Biol. 45:233–244. [DOI] [PubMed] [Google Scholar]
  3. Alvarez, O., M. Brodwick, R. Latorre, A. McLaughlin, S. McLaughlin, and G. Szabo. 1983. Large divalent cations and electrostatic potentials adjacent to membranes. Experimental results with hexamethonium. Biophys. J. 44:333–342. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Barlow, C. A. 1970. The electrical double layer. In Physical Chemistry, An Advanced Treatise. H. Eyring, editor. Academic Press, Inc., New York. pp. 167–246.
  5. Bechinger, B., and J. Seelig. 1991. Interaction of electric dipoles with phospholipid head groups. A 2H and 31P NMR study of phloretin and phloretin analogues in phosphatidylcholine membranes. Biochemistry. 30:3923–3929. [DOI] [PubMed] [Google Scholar]
  6. Bedlack, R. S., M. Wei, and L. M. Loew. 1992. Localized membrane depolarizations and localized calcium influx during electric field-guided neurite growth. Neuron. 9:393–403. [DOI] [PubMed] [Google Scholar]
  7. Bedlack, R. S., M. Wei, S. H. Fox, E. Gross, and L. M. Loew. 1994. Distinct electric potentials in soma and neurite membranes. Neuron. 13:1187–1193. [DOI] [PubMed] [Google Scholar]
  8. Begenisich, T. 1975. Magnitude and location of surface charges on Myxicola giant axons. J. Gen. Physiol. 66:47–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cevc, G. 1990. Membrane electrostatics. Biochim. Biophys. Acta. 1031:311–382. [DOI] [PubMed] [Google Scholar]
  10. Chandler, W. K., A. L. Hodgkin, and H. Meves. 1965. The effect of changing the internal solution on sodium inactivation and related phenomena in giant axons. J. Physiol. 180:821–836. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Clarke, R. J. 1997. Effect of lipid structure on the dipole potential of phosphatidylcholine bilayers. Biochim. Biophys. Acta. 1327:269–278. [DOI] [PubMed] [Google Scholar]
  12. Clarke, R. J. 2001. The dipole potential of phospholipid membranes and methods for its detection. Adv. Colloid. Interface Sci. 89–90:263–281. [DOI] [PubMed] [Google Scholar]
  13. Clarke, R. J., and C. Lüpfert. 1999. Influence of anions and cations on the dipole potential of phosphatidylcholine vesicles: a basis for the Hofmeister effect. Biophys. J. 76:2614–2624. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Clarke, R. J., and D. J. Kane. 1997. Optical detection of membrane dipole potential: avoidance of fluidity and dye-induced effects. Biochim. Biophys. Acta. 1323:223–239. [DOI] [PubMed] [Google Scholar]
  15. Cohen, L. B., and B. M. Salzberg. 1978. Optical measurement of membrane potential. Rev. Physiol. Biochem. Pharmacol. 83:35–88. [DOI] [PubMed] [Google Scholar]
  16. Davies, J. T., and E. K. Rideal. 1963. Interfacial Phenomena. Academic Press, Inc., New York.
  17. Deamer, D. W., and P. S. Uster. 1983. Liposome preparation: methods and mechanisms. In Liposomes. M. J. Ostro, editor. Marcel Dekker, Inc. New York. pp. 27–51.
  18. Dluhy, R. A., D. G. Cameron, H. H. Mantsch, and R. Mendelsohn. 1983. Fourier transform infrared spectroscopic studies of the effect of calcium ions on phosphatidylserine. Biochemistry. 22:6318–6325. [Google Scholar]
  19. Edwards, A. S., and A. C. Newton. 1997. Regulation of protein kinase C βII by its C2 domain. Biochemistry. 36:15615–15623. [DOI] [PubMed] [Google Scholar]
  20. Eisenberg, M., T. Gresalfi, T. Riccio, and S. McLaughlin. 1979. Adsorption of monovalent cations to bilayer membranes containing negative phospholipids. Biochemistry. 18:5213–5223. [DOI] [PubMed] [Google Scholar]
  21. Ermakov, Y. A., A. Z. Averbakh, A. I. Yusipovich, and S. Sukharev. 2001. Dipole potentials indicate restructuring of the membrane interface induced by gadolinium and beryllium ions. Biophys. J. 80:1851–1862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Fluhler, E., V. G. Burnham, and L. M. Loew. 1985. Spectra, membrane binding, and potentiometric responses of new charge shift probes. Biochemistry. 24:5749–5755. [DOI] [PubMed] [Google Scholar]
  23. Frankenhaeuser, B. 1960. Sodium permeability in toad nerve and in squid nerve. J. Physiol. (Lond.). 152:159–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Frankenhaeuser, B., and A. L. Hodgkin. 1957. The action of calcium on the electrical properties of squid axons. J. Physiol. (Lond.). 137:218–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Ganitkevich, V. Ya., M. F. Shuba, and S. V. Smirnov. 1988. Saturation of calcium channels in single isolated smooth muscle cells of guinea-pig taenia caeci. J. Physiol. 399:419–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Gilbert, D. L., and G. Ehrenstein. 1969. Effect of divalent cations on potassium conductance of squid axons: determination of surface charge. Biophys. J. 9:447–463. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Gilly, W. F., and C. M. Armstrong. 1982. Slowing of sodium channel opening kinetics in squid axon by extracellular zinc. J. Gen. Physiol. 79:935–964. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Goldman, D. E. 1943. Potential, impedance, and rectification in membranes. J. Gen. Physiol. 27:37–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Grahame, D. C. 1947. The electrical double layer and the theory of electrocapillarity. Chem. Rev. 41:441–501. [DOI] [PubMed] [Google Scholar]
  30. Gross, D., and L. M. Loew. 1989. Fluorescent indicators of membrane potential: microspectrofluorometry and imaging. Methods Cell Biol. 30:193–218. [DOI] [PubMed] [Google Scholar]
  31. Gross, E., R. S. Bedlack, Jr., and L. M. Loew. 1994. Dual-wavelength ratiometric fluorescence measurement of the membrane dipole potential. Biophys. J. 67:208–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Hauser, H., and G. G. Shipley. 1985. Comparative structural aspects of cation binding to phosphatidylserine bilayers. Biochim. Biophys. Acta. 813:343–346. [DOI] [PubMed] [Google Scholar]
  33. Hille, B. 1968. Charges and potentials at the nerve surface. Divalent ions and pH. J. Gen. Physiol. 51:221–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hille, B. 2001. Modification of gating in voltage-sensitive channels. In Ion channels of excitable membranes. B. Hille, Editor. Sinauer Associates, Inc. Sunderland. p 635–662.
  35. Hille, B., A. M. Woodhull, and B. I. Shapiro. 1975. Negative surface charge near sodium channels of nerve: divalent ions, monovalent ions, and pH. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 270:301–318. [DOI] [PubMed] [Google Scholar]
  36. Hodgkin, A. L., and B. Katz. 1949. The effect of sodium ions on the electrical activity of the giant axon of the squid. J. Physiol. (Lond.). 108:37–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Krasne, S. 1980. Interactions of voltage-sensing dyes with membranes. II. Spectrophotometric and electrical correlates of cyanine-dye adsorption to membranes. Biophys. J. 30:441–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Loew, L. M. 1988. How to choose a potentiometric membrane probe. In Spectroscopic Membrane Probes. L. M. Loew, editor. CRC Press, Boca Raton. pp. 139–152.
  39. Loew, L. M., and L. L. Simpson. 1981. Charge-shift probes of membrane potential: a probable electrochromic mechanism for p-aminostyrylpyridinium probes on a hemispherical lipid bilayer. Biophys. J. 34:353–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Loew, L. M., S. Scully, L. Simpson, and A. S. Waggoner. 1979. Evidence for a charge-shift electrochromic mechanism in a probe of membrane potential. Nature. 281: 497–499. [DOI] [PubMed] [Google Scholar]
  41. London, J. A., D. Zecevic, and L. B. Cohen. 1987. Simultaneous optical recording of activity from many neurons during feeding in Navanax. J. Neurosci. 7:649–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Lopez-Garcia, F., V. Micol, J. Villalain, and J. C. Gomez-Fernandez. 1993. Infrared spectroscopic study of the interaction of diacylglycerol with phosphatidylserine in the presence of calcium. Biochim. Biophys. Acta. 1169:264–272. [DOI] [PubMed] [Google Scholar]
  43. Makino, K., T. Taki, M. Ogura, S. Handa. M. Nakajima, T. Kondo, and H. Ohshima. 1993. Measurements and analyses of electrophoretic mobilities of RAW117 lymphosarcoma cells and their variant cells. Biophys. Chem. 47:261–265. [DOI] [PubMed] [Google Scholar]
  44. Matsumura, H., and K. Furusawa. 1989. Electrical phenomena at the surface of phospholipid membranes relevant to the sorption of ionic compounds. Adv. Colloid Interface Sci. 30:71–109. [DOI] [PubMed] [Google Scholar]
  45. Matsumura, H., and K. Furusawa. 1998. Phospholipid membranes. Surf. Sci. Series. 76:519–533. [Google Scholar]
  46. McLaughlin, A., C. Grathwohl, and S. McLaughlin. 1978. The adsorption of divalent cations to phosphatidylcholine bilayer membranes. Biochim. Biophys. Acta. 513:338–357. [DOI] [PubMed] [Google Scholar]
  47. McLaughlin, S. 1989. The electrostatic properties of membranes. Annu. Rev. Biophys. Biophys. Chem. 18:113–136. [DOI] [PubMed] [Google Scholar]
  48. McLaughlin, S. G. A., G. Szabo, and G. Eisenman. 1971. Divalent ions and the surface potential of charged phospholipid membranes. J. Gen. Physiol. 58:667–687. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. McLaughlin, S., and A. Aderem. 1995. The myristoyl-electrostatic switch: a modulator of reversible protein-membrane interactions. TIBS. 20:272–276. [DOI] [PubMed] [Google Scholar]
  50. McLaughlin, S., N. Mulrine, T. Gresalfi, G. Vaio, and A. McLaughlin. 1981. Adsorption of divalent cations to bilayer membranes containing phosphatidylserine. J. Gen. Physiol. 77:445–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Montana, V., D. L. Farkas and L. M. Loew. 1989. Dual-wavelength ratiometric fluorescence measurements of membrane potential. Biochemistry. 28:4536–4539. [DOI] [PubMed] [Google Scholar]
  52. Mozhayeva, G. N., and A. P. Naumov. 1970. Effect of surface charge on the steady-state potassium conductance of nodal membrane. Nature. 228:164–165. [DOI] [PubMed] [Google Scholar]
  53. Nakano, Y., K. Makino, H. Ohshima, and T. Kondo. 1994. Analysis of electrophoretic mobility data for human erythrocytes according to sublayer models. Biophys. Chem. 50:249–254. [DOI] [PubMed] [Google Scholar]
  54. Ohki, S., and R. Sauve. 1978. Surface potential of phosphatidylserine monolayers. I. Divalent ion binding effect. Biochim. Biophys. Acta. 511:377–387. [DOI] [PubMed] [Google Scholar]
  55. Petersheim, M., H. N. Halladay, and J. Blodnieks. 1989. Tb3+ and Ca2+ binding to phosphatidylcholine. A study comparing data from optical, NMR, and infrared spectroscopies. Biophys. J. 56:551–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Scherer, P. G., and J. Seelig. 1989. Electric charge effects on phospholipid headgroups. Phosphatidylcholine in mixtures with cationic and anionic amphiphiles. Biochemistry. 28:7720–7728. [DOI] [PubMed] [Google Scholar]
  57. Schoch, P., D. F. Sargent, and R. Schwyzer. 1979. Capacitance and conductance as tools for the measurement of asymmetric surface potentials and energy barriers of lipid bilayer membranes. J. Membr. Biol. 46:71–89. [DOI] [PubMed] [Google Scholar]
  58. Smith, P. A., F. M. Aschcroft, and C. M. S. Fewtrell. 1993. Permeation and gating properties of the L-type calcium channel in mouse pancreatic cells. J. Gen. Physiol. 101:767–797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Vassar, P. S., E. M. Levy, and D. E. Brooks. 1976. Studies on the electrophoretic separability of B and T human lymphocytes. Cell. Immunol. 21:257–271. [DOI] [PubMed] [Google Scholar]
  60. Volwerk, J. J., P. C. Jost, G. H. de Haas, and O. H. Griffith. 1986. Activation of porcine pancreatic phospholipase A2 by the presence of negative charges at the lipid-water interface. Biochemistry. 25:1726–1733. [DOI] [PubMed] [Google Scholar]
  61. Waggoner, A. S. 1979. The use of cyanine dyes for the determination of membrane potentials in cells, organelles, and vesicles. Methods Enzymol. 55:689–695. [DOI] [PubMed] [Google Scholar]
  62. Wojtczak, L., K. S. Famulski, M. J. Nalecz, and J. Zborowski. 1982. Influence of the surface potential on the Michaelis constant of membrane-bound enzymes: effect of membrane solubilization. FEBS Lett. 139:221–224. [DOI] [PubMed] [Google Scholar]
  63. Zhang, J., M. D. Robert, M. Wei, and L. M. Loew. 1998. Membrane electric properties by combined patch clamp and fluorescence ratio imaging in single neurons. Biophys. J. 74:48–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Zhou, W., and S. W. Jones. 1995. Surface charge and calcium channel saturation in bullfrog sympathetic neurons. J. Gen. Physiol. 105:441–162. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES