Abstract
A mathematical model for the regulation of induction in the lac operon in Escherichia coli is presented. This model takes into account the dynamics of the permease facilitating the internalization of external lactose; internal lactose; β-galactosidase, which is involved in the conversion of lactose to allolactose, glucose and galactose; the allolactose interactions with the lac repressor; and mRNA. The final model consists of five nonlinear differential delay equations with delays due to the transcription and translation process. We have paid particular attention to the estimation of the parameters in the model. We have tested our model against two sets of β-galactosidase activity versus time data, as well as a set of data on β-galactosidase activity during periodic phosphate feeding. In all three cases we find excellent agreement between the data and the model predictions. Analytical and numerical studies also indicate that for physiologically realistic values of the external lactose and the bacterial growth rate, a regime exists where there may be bistable steady-state behavior, and that this corresponds to a cusp bifurcation in the model dynamics.
INTRODUCTION
The operon concept (Beckwith, 1987b), introduced by Jacob et al. (1960), has had a profound and lasting effect on the biological sciences. Not long after the operon concept was developed, Goodwin (1965) gave the first mathematical analysis of operon dynamics. Griffith then put forward a more complete analysis of simple repressible (negative feedback, Griffith (1968a)) and inducible (positive feedback, Griffith (1968b)) gene control networks, and Tyson and Othmer (1978) have summarized these results. Extensions considering the stability of inducible operons were published by Selgrade (1979, 1982) and Ji-Fa (1994), but none of these treatments considered the role of the DNA transcription and mRNA translation delays, though Tyson and Othmer pointed out that both should be considered.
Bliss et al. (1982) were some of the first to explicitly consider transcriptional and translational delays in their modeling of the tryptophan operon. Many subsequent workers studying tryptophan dynamics (Sinha, 1988; Sen and Liu, 1989; Xiu et al., 1997) ignored these delays although including other biological details, but the tryptophan delays were considered by Santillán and Mackey, (2001a,b). Maffahy and Savev (1999) modeled lac operon dynamics and included transcriptional and translational delays, but Wong et al. (1997) failed to treat these elements of the lac operon despite their inclusion of much of the relevant biological detail. Recent work on gene network regulation can be found in Tyson and Mackey (2001).
In this paper we offer a model of the induction process in the lac operon, including much of the relevant biological detail considered by Wong et al. (1997) (but neglecting catabolite repression) as well as the transcriptional and translational delays considered by Maffahy and Savev (1999). A more complete mathematical analysis of a reduced version of the model presented here is possible, and was considered by N. Yildirim, D. Horike, and M. C. Mackey (unpublished results). Section 2, “The Model”, develops the model and gives a set of realistic parameters estimated from the biological literature (presented in detail in Appendix B). It also examines the nature of the steady states (as deduced in Appendix C) and briefly considers their stability (Appendix D). Section 3, “Comparison with Experimental Data”, compares the numerical predictions of the model temporal behavior with three sets of data taken from the literature, and the paper ends with a discussion in Section 4, “Conclusions”.
THE MODEL
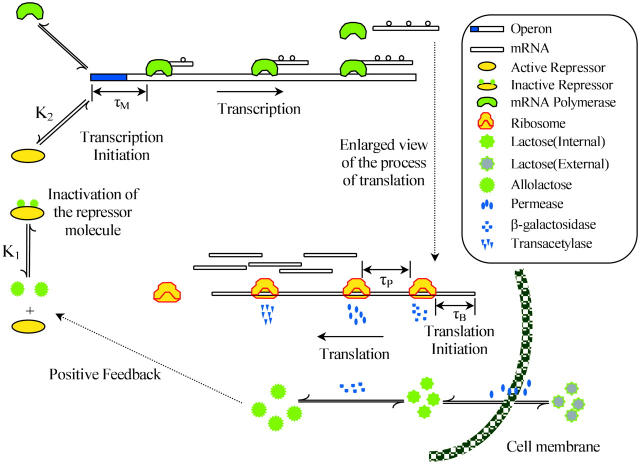
To develop our model for regulation of the lac operon, it will be helpful to refer to Fig. 1. This control system functions in the following manner. In the absence of glucose available for cellular metabolism, but in the presence of external lactose (Le), lactose is transported into the cell by a permease (P). Intracellular lactose (L) is then broken down into glucose, galactose, and allolactose (A) by the enzyme β-galactosidase (B). The allolactose feeds back to bind with the lactose repressor and enables the transcription process to proceed.
FIGURE 1.
Schematic representation of the lactose operon regulatory system.
In more detail, the lac operon consists of a promoter/operator region and three larger structural genes, lacZ, lacY, and lacA. Preceding the lac operon is a regulatory operon responsible for producing a repressor (R) protein. In the absence of allolactose (A), the repressor R binds to the operator region and prevents the RNA polymerase (which binds to the promoter region) from transcribing the structural genes. However, if allolactose is present, a complex is formed between allolactose and the repressor that makes binding of the repressor to the operator region impossible. In that case, the RNA polymerase bound to the promoter is able to initiate transcription of the structural genes to produce mRNA.
Once the mRNA has been produced, the process of translation is initiated. The lacZ gene encodes for the mRNA responsible for the production of β-galactosidase (B) and translation of the lacY gene produces mRNA ultimately responsible for the production of a membrane permease (P). The mRNA produced by transcription of the lacA gene encodes for the production of thiogalactoside transacetylase, which is thought to not play a role in the regulation of the lac operon (Beckwith, 1987a) and will not be further considered here.
As shown in Appendix A, following Yagil and Yagil (1971), if the amount of repressor R bound to the operator O is small, then in a large population of cells the fraction of operators not bound by repressor (and therefore free to synthesize mRNA) is given by
 |
(1) |
where n was interpreted as the number of molecules of allolactose required to inactivate the repressor, K1 is the equilibrium constant for the repressor-allolactose reaction, and K2 is the equilibrium constant for the operator-repressor reaction, K = 1 + K2 Rtot, and Rtot is the total amount of repressor. Notice that there will be maximal repression when A = 0, but even at maximal repression there will still be a basal level of mRNA production (“leakage”) proportional to K−1. We are now in a position to develop our model for the lac operon regulation.
The dynamics of mRNA production are given by Eq. 2,
 |
(2) |
which is derived as follows. First, note that the production of mRNA from DNA via transcription is not an instantaneous process but requires a period of time, τM, for RNA polymerase to traverse the three structural genes. The rate of change of M is a balance between a production term αM f and a loss term 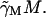 The argument of f in the production term is
The argument of f in the production term is  where
where  to account for the time, τM, required to produce the mRNA. The factor
to account for the time, τM, required to produce the mRNA. The factor  accounts for the growth dependent allolactose dilution during the transcriptional period. In the total absence of allolactose, on occasion repressor will transiently not be bound to the operator and RNA polymerase will initiate transcription. Γ0 denotes this spontaneous rate of mRNA production. The loss term in Eq. 2,
accounts for the growth dependent allolactose dilution during the transcriptional period. In the total absence of allolactose, on occasion repressor will transiently not be bound to the operator and RNA polymerase will initiate transcription. Γ0 denotes this spontaneous rate of mRNA production. The loss term in Eq. 2, 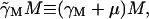 is made up of an mRNA degradation term (γMM) and an effective loss due to dilution (μM).
is made up of an mRNA degradation term (γMM) and an effective loss due to dilution (μM).
The dynamics of β-galactosidase are described by Eq. 3,
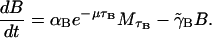 |
(3) |
Again realize that β-galactosidase production through mRNA translation is not instantaneous but requires a time, τB. We assume that the rate of production of B is proportional to the concentration of M a time τB ago 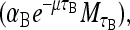 where again the exponential factor takes into account the dilution of mRNA due to cell growth. The loss rate of B is given by
where again the exponential factor takes into account the dilution of mRNA due to cell growth. The loss rate of B is given by 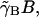 where as before
where as before 
For the allolactose dynamics,
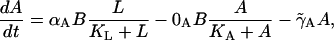 |
(4) |
the first term in Eq. 4 gives the β-galactosidase mediated gain in allolactose from the conversion of lactose following the studies of Huber et al. (1976). The second term accounts for allolactose loss via conversion to glucose and galactose, again mediated by β-galactosidase (Martínez-Bilbao et al., 1991; Huber et al., 1994). The last term takes into account the degradation and dilution of allolactose.
The lactose dynamics are more complicated and given by Eq. 5:
 |
(5) |
The first term in Eq. 5 accounts for the augmentation of intracellular lactose L through the permease facilitated transport of Le. The proportionality constant αL is a decreasing function of extracellular glucose (Saier, 1976). The second term deals with intracellular lactose loss to the extracellular fluid because of the reversible nature of the permease-mediated transport (Saier, 1976; Osumi and Saier, 1982; Postma et al., 1996; Saier et al., 1996). The coefficient βL is not dependent on the external glucose levels. The third term accounts for the conversion of lactose to allolactose as well as the hydrolysis of lactose to glucose and galactose via β-galactosidase (B). The fourth term accounts for the decrease in internal lactose concentration due to degradation and dilution.
To describe the permease dynamics
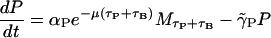 |
(6) |
we have Eq. 6. There, the first term reflects the assumption that permease production is directly proportional (proportionality constant αP) to the mRNA concentration a time (τP + τB) in the past, where τP is the translation time between mRNA and permease. The delay is taken to be the sum of the β-galactosidase and permease translation times under the assumption that permease production cannot start until β-galactosidase production is complete. The exponential factor  accounts for dilution of mRNA concentration due to cell growth. The second term accounts for the degradation and dilution of permease.
accounts for dilution of mRNA concentration due to cell growth. The second term accounts for the degradation and dilution of permease.
We have carried out an extensive search of the existing literature for data that would allow us to estimate the model parameters in Eqs. 2–6. The results of our determinations are summarized in Table 1, and the details of how we arrived at these parameter values are contained in Appendix B.
TABLE 1.
The estimated parameters for the model as determined in Appendix B
| n | 2 | μmax | 3.47 × 10−2 min−1 |
|---|---|---|---|
| γM | 0.411 min−1 | γB | 8.33 × 10−4 min−1 |
| γA | 0.52 min−1 | Γ0 | 7.25 × 10−7 mM/min |
| K | 7,200 | αM | 9.97 × 10−4 mM/min |
| τB | 2.0 min | αA | 1.76 × 104 min−1 |
| KL1 | 1.81 mM | αB | 1.66 × 10−2 min−1 |
| KA | 1.95 mM | βA | 2.15 × 104 min−1 |
| τM | 0.1 min | KL | 9.7 × 10−4 M |
| γL | 0.0 min−1 | γP | 0.65 min−1 |
| αL | 2880 min−1 | αP | 10.0 min−1 |
| τP | 0.83 min | βL1 | 2.65 × 103 min−1 |
| KLe | 0.26 mM | K1 | 2.52 × 10−2 (μM)−2 |
The full model as formulated in Eqs. 2–6 can have one, two, or three steady states depending on the values of the parameters (μ, Le). The details of how these steady states are determined are contained in Appendix C. The results of these considerations are presented in Fig. 2. There we show in  space the region where a nonnegative steady state can exist. Note in particular that for a range of Le values, there may be three coexisting steady-state values of the intracellular allolactose levels,
space the region where a nonnegative steady state can exist. Note in particular that for a range of Le values, there may be three coexisting steady-state values of the intracellular allolactose levels, 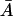 and, consequently, of
and, consequently, of 
FIGURE 2.
The region in the  space where a nonnegative steady state can exist as a function of external lactose levels Le for the model when all parameters are held at the estimated values in Table 1 and when
space where a nonnegative steady state can exist as a function of external lactose levels Le for the model when all parameters are held at the estimated values in Table 1 and when 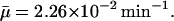 The shaded area shows the region where a steady state is not defined, whereas the solid line is the locus of
The shaded area shows the region where a steady state is not defined, whereas the solid line is the locus of 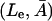 values satisfying the steady state. The inset box shows that at large values of Le, there is still a separation of the line for the steady state from the region where steady states are not defined. Notice that for these values of the parameters, there is a range of Le values for which there are three coexisting steady-state values of allolactose A. The asterisk located at the right-most kink locates the minimal concentration of extracellular lactose required for induction, and our calculations indicate that it should be on the order of 62.0 μM.
values satisfying the steady state. The inset box shows that at large values of Le, there is still a separation of the line for the steady state from the region where steady states are not defined. Notice that for these values of the parameters, there is a range of Le values for which there are three coexisting steady-state values of allolactose A. The asterisk located at the right-most kink locates the minimal concentration of extracellular lactose required for induction, and our calculations indicate that it should be on the order of 62.0 μM.
Whether or not there can be coexisting steady states depends on the growth rate μ, and an examination of the dependence of the criteria for the existence of steady states  on (μ, Le) reveals that in
on (μ, Le) reveals that in 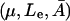 space there is a cusp bifurcation occurring that is dependent on the growth rate μ and extracellular lactose levels Le.
space there is a cusp bifurcation occurring that is dependent on the growth rate μ and extracellular lactose levels Le.
This cusp bifurcation in the model in 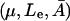 space is of the following nature. There is a minimal growth rate
space is of the following nature. There is a minimal growth rate  such that for values of the growth rate μ ∈ [0, μmin], there is a unique steady-state level of allolactose
such that for values of the growth rate μ ∈ [0, μmin], there is a unique steady-state level of allolactose 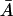 for any given value of external lactose levels Le. At μ = μmin, the concentration of external lactose required for induction is
for any given value of external lactose levels Le. At μ = μmin, the concentration of external lactose required for induction is 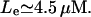 However, as μ becomes larger, μ ∈ [μmin, μmax, the system may have three steady-state values of
However, as μ becomes larger, μ ∈ [μmin, μmax, the system may have three steady-state values of 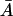 at a given external lactose level Le. This is the situation depicted in Fig. 2, where we used
at a given external lactose level Le. This is the situation depicted in Fig. 2, where we used 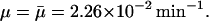 For this value of μ, the lactose concentration required for induction (and marked with an asterisk in Fig. 2) is
For this value of μ, the lactose concentration required for induction (and marked with an asterisk in Fig. 2) is  which compares well with the results of a study using an artificial inducer of the lac operon, isopropylthiogalactoside (IPTG) (Baneyx, 1999). There it was found that 50–100 μM IPTG is sufficient as a lower bound to achieve full induction.
which compares well with the results of a study using an artificial inducer of the lac operon, isopropylthiogalactoside (IPTG) (Baneyx, 1999). There it was found that 50–100 μM IPTG is sufficient as a lower bound to achieve full induction.
A full stability analysis of the steady states of this model is impossible, since the eigenvalue equation determining local stability is a fifth order quasipolynomial containing three delays. Consequently, we have contented ourselves with a numerical examination of the stability properties of the steady states. Briefly, the results of our numerical stimulations presented in Appendix D are as follows. When a single steady state exists, we have found that the numerical behavior is such that the model solutions always converge to that steady state at large times. When there are three coexisting steady states, the numerical solutions to the model either converged to the lower or upper branch of the S-shaped curve for various initial conditions. These results, as well as numerous others that are not shown, lead us to conclude that the middle branch of the S-shaped steady-state curve (see Fig. 2) corresponds to a steady state that is globally unstable. The nature of the boundary between initial conditions leading to the convergence to the upper or lower branch solution appears to be complicated, and it may well be a fractal basin boundary (Losson and Mackey, 1993).
COMPARISON WITH EXPERIMENTAL DATA
Given the parameter values determined in Table 1, we numerically solved the model equations to compare the predicted behavior with three distinct experimental data sets.
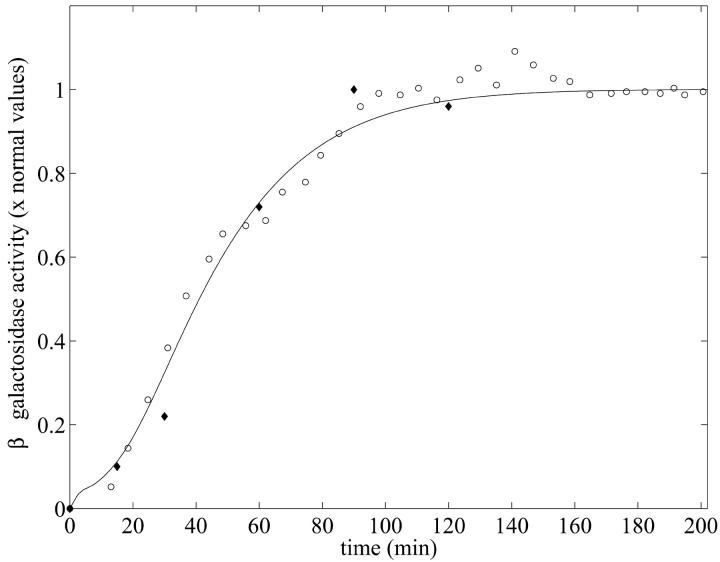
The first data set is from Knorre (1968), in which changes of the specific β-galactosidase concentration after a step change from glucose to lactose growth for Escherichia coli ML30 were measured. The second data set is from Pestka et al. (1984). In this paper, Pestka et al. studied specific inhibition of translation of single mRNA molecules and gave data for the specific activity of β-galactosidase versus time for E. coli 294 in the presence of IPTG. These two data sets and the model simulation determined using MATLAB's dde23 (Shampine and Thompson, 2000) routine are shown in Fig. 3.
FIGURE 3.
β-galactosidase activity versus time when Le = 8.0 × 10−2 mM. The experimental data sets were taken from Knorre (1968) for E. coli ML30 (○) and from Pestka et al. (1984) for E. coli 294 (♦). The model simulation (solid line) was obtained using the parameters of Table 1 with a growth rate  The selection of initial conditions is described in the text.
The selection of initial conditions is described in the text.
For this simulation, initial values for the variable were chosen as A0 = 3.80 × 10−2, M0 = 6.26 × 10−4, L0 = 3.72 × 10−1, P0 = 1.49 × 10−2, and B0 = 0.0 mM, all of which are close to the steady-state values given in Table 2 when Le = 8.0 × 10−2 mM. (With this value of Le, there is a single unique steady state). To compare these two sets of experimental data with the model simulation predictions, the data were scaled so the steady-state values of measured β-galactosidase activities and those produced by the simulation were equal. As seen in Fig. 3, there is relatively good agreement between both sets of experimental data and the model-predicted temporal approach of β-galactosidase activity to its steady-state value.
TABLE 2.
Steady-state values when Le = 8.0 × 10−2 mM
 |
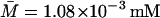 |
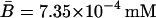 |
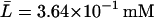 |
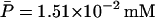 |
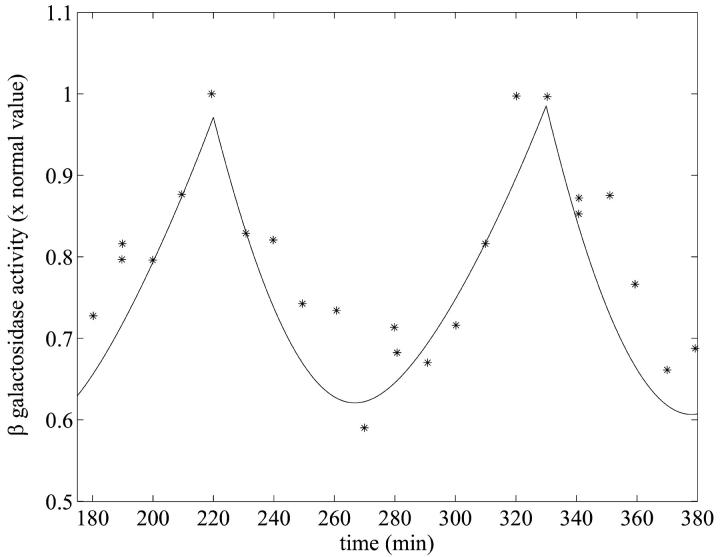
As a third test of the model, a data set from Goodwin (1969) was used. In this paper, the dynamic behavior of β-galactosidase was studied in chemostat cultures of E. coli synchronized with respect to cell division by periodic phosphate feeding at a period equal to the bacterial doubling time. Experimentally, oscillations in β-galactosidase concentration were observed with a period equal to the feeding period.
To mimic the periodic phosphate feeding in our simulation, we assumed that the bacterial growth rate varies as a function of time in manner given by
 |
(7) |
Here,  is the maximal growth rate for the bacteria, T is the period of the feeding and α is a positive parameter with dimension min−2. mod(t, T) is a function that gives the remainder on division of t by T. Selection of this type of function is motivated by the observation that growth rates decrease as nutrient levels fall and sharply increase after the addition of nutrient.
is the maximal growth rate for the bacteria, T is the period of the feeding and α is a positive parameter with dimension min−2. mod(t, T) is a function that gives the remainder on division of t by T. Selection of this type of function is motivated by the observation that growth rates decrease as nutrient levels fall and sharply increase after the addition of nutrient.
μ(t) takes its maximal value of 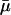 when t = T × k, (k = 1, 2, 3, …), which corresponds to the times that phosphate was added. The minimal value of this function,
when t = T × k, (k = 1, 2, 3, …), which corresponds to the times that phosphate was added. The minimal value of this function,  at
at 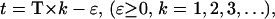 represents the minimal amount of nutrient left in the vessel. Assuming no nutrient is left ɛ minutes before the addition of phosphate and letting
represents the minimal amount of nutrient left in the vessel. Assuming no nutrient is left ɛ minutes before the addition of phosphate and letting  α can be estimated if the doubling time (T) is known:
α can be estimated if the doubling time (T) is known: 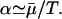
With a feeding period of T = 100 min, we have 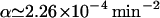 for
for  , which is the value we have estimated for our model (cf. Appendix B). In Fig. 4, we compare the data on β-galactosidase activity from the forced culture as a function of time with the model predictions.
, which is the value we have estimated for our model (cf. Appendix B). In Fig. 4, we compare the data on β-galactosidase activity from the forced culture as a function of time with the model predictions.
FIGURE 4.
Oscillation in β-galactosidase activity in response to periodic phosphate feeding with period T = 100 min, which is the culture doubling time. The experimental data (*) together with the model simulation (solid line) using the parameters of Table 1 and  are presented. The experimental data are taken from Goodwin (1969). In the numerical simulation, periodic phosphate feeding was imitated by choosing a periodic function given by Eq. 7. The simulation was calculated by numerically solving the system of delay differential equations given by Eqs. 2–6. The initial conditions are the same as those values given in Table 2 for Le = 8.0 × 10−2 mM.
are presented. The experimental data are taken from Goodwin (1969). In the numerical simulation, periodic phosphate feeding was imitated by choosing a periodic function given by Eq. 7. The simulation was calculated by numerically solving the system of delay differential equations given by Eqs. 2–6. The initial conditions are the same as those values given in Table 2 for Le = 8.0 × 10−2 mM.
With respect to the predicted bistability at sufficiently large growth rates, illustrated in Fig. 2, evidence presented by Novick and Wiener (1957) and Cohn and Horibata (1959) qualitatively substantiate the existence of this behavior for values of the growth rate exceeding μmin. However, we are unable to determine if the quantitative ranges of Le for which we have predicted bistability correspond to the conditions under which it was seen in Novick and Wiener (1957) and Cohn and Horibata (1959).
CONCLUSIONS
Here we have developed, and analytically and numerically analyzed, a mathematical model for the regulation of the lac operon in E. coli. The final model consists of five nonlinear differential delay equations with delays due to the DNA transcription and mRNA translation processes. The model equations describe the dynamics of the permease (P) facilitating the internalization of external lactose (Le); internal lactose (L); β-galactosidase (B), which is involved in the conversion of lactose to allolactose, glucose, and galactose; the allolactose (A) interactions with the lac repressor, and mRNA (M). We have gone to considerable effort to make valid and reasonable estimates of the 24 parameters in the model. We were successful in identifying 22 of these parameters from published data, but were forced to determine the growth rate μ and γA by fitting the model to the data of Knorre (1968).
We have tested our model against two sets of β-galactosidase activity versus time data. These data came from the experimental work presented in Knorre (1968), in which changes of the specific β-galactosidase concentration after a step change from glucose to lactose growth for E. coli ML30 were measured, and the work of Pestka et al. (1984). In this latter paper, data were presented for the specific activity of β-galactosidase versus time for E. coli 294 in the presence of IPTG. These two data sets and the model simulation are shown in Fig. 3, and there is a remarkable degree of concordance between the data and the model predictions.
As a third test of the model, data from Goodwin (1969) giving the dynamic behavior of β-galactosidase was studied in chemostat cultures of E. coli synchronized with respect to cell division by periodic phosphate feeding at a period equal to the bacterial doubling time. Experimentally, oscillations in β-galactosidase concentration were observed with a period equal to the feeding period. Fig. 4 shows the β-galactosidase activity data as well as the model predictions. Again, there is a satisfying degree of agreement.
Analytical and numerical studies of the model also predict that for physiologically realistic values of external lactose and the bacterial growth rate, a regime exists where there may be bistable steady-state behavior, and that this corresponds to a cusp bifurcation in the model dynamics. This prediction is qualitatively confirmed by the observations of Novick and Wiener (1957) and Cohn and Horibata (1959). Although a full analysis of the stability properties of the model is not possible due to its complexity, we have found that the basic properties contained in a reduced version of this model N. Yildirim, D. Horike, and M. C. Mackey (unpublished results) (2002) (which considered only the dynamics of M, B, and A) are apparently retained in this much more complicated model as far as we are able to ascertain analytically and numerically.
This agreement between the model predictions for the lactose operon and existing data, and similar agreement between a mathematical model for the tryptophan operon (Santillán and Mackey, 2001a,b), highlight the desirability and necessity of closer cooperation between experimentalists and modelers to further validate and refine mathematical models of simple and more complicated gene regulatory networks.
To close, we wish to touch on the nature of the mathematical model presented here. The model considered in this paper is formulated with the explicit assumption that one is dealing with large numbers cells (and hence of large numbers of molecules) so that the law of large numbers is operative. However, the situation is quite different if one is interested in the dynamics of small numbers (or single) prokaryotic or eukaryotic cells, for then the numbers of molecules are small. Adequate means to analytically treat such problems do not exist in a satisfactory form as of now (Gillespie, 1992; Kepler and Elston, 2001; Swain et al., 2002), and one is often reduced to mostly numerical studies (Gillespie, 1977; McAdams and Shapiro, 1995; Arkin et al., 1998). The situation is analogous to examining the interactions between small numbers of interacting particles (where the laws of mechanics or electrodynamics hold), and then deriving from these formulations the behavior of large numbers of identical units as is done (not completely successfully even at this point) in statistical mechanics. We view this connection between the “micro” and “macro” levels as one of the major mathematical challenges facing those interested in the understanding of gene control networks.
Acknowledgments
We thank Dr. Photini Pitsikas for her initial suggestion of this problem, Profs. Claire Cupples and Moisés Santillán for their advice on parameter estimation and general comments, and Mr. Daisuke Horike for many helpful discussions.
This work was supported by the Scientific and Technical Research Council of Turkey, the North Atlantic Treaty Organization, the Mathematics of Information Technology and Complex Systems (Canada), the Natural Sciences and Engineering Research Council (grant OGP-0036920, Canada), Le Fonds pour la Formation de Chercheurs et l'Aide à la Recherche (grant 98ER1057, Québec), and the Leverhulme Trust (UK).
APPENDIX A: REPRESSOR DYNAMICS
Let R be the repressor, E the effector (allolactose in our case), and O the operator. The effector is known to bind with the active form R of the repressor. We assume, as do Yagil and Yagil (1971), that this reaction is of the form
 |
(8) |
where they took n to be the effective number of molecules of effector required to inactivate the repressor R. Furthermore, the operator O and repressor R are assumed Yagil and Yagil (1971) to interact according to
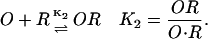 |
(9) |
Let the total operator be Otot:
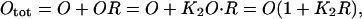 |
(10) |
and the total level of repressor be Rtot:
 |
(11) |
The fraction of operators not bound by repressor (and therefore free to synthesize mRNA) is given by
 |
(12) |
If the amount of repressor R bound to the operator O is small
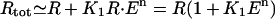 |
(13) |
so
 |
(14) |
and consequently
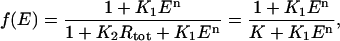 |
(15) |
where K = 1 + K2Rtot. Notice that there will be maximal repression when E = 0 but even at maximal repression there will still be a basal level of mRNA production proportional to K−1.
APPENDIX B: PARAMETER ESTIMATION
In the model given by Eqs. 2–6, there are 24 parameters in total that must be estimated to characterize the system completely. In this section, we give the estimation of each of these parameters.
μ: The maximal value of the dilution rate μ can be estimated from the shortest interdivision time of E. coli, which is ∼20 min (Watson, 1977). Given this, μmax = ln 2/20 min−1 = 3.47 × 10−2 min−1. We have also estimated a value of μ, denoted by
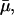 together with the value of γA by least-square fitting of the experimental β-galactosidase concentration data given in Knorre (1968) using the fminsearch and dde23 (Shampine and Thompson, 2000) routines in MATLAB. We found
together with the value of γA by least-square fitting of the experimental β-galactosidase concentration data given in Knorre (1968) using the fminsearch and dde23 (Shampine and Thompson, 2000) routines in MATLAB. We found  , indicating that these cultures were growing with a doubling time of 30 min. The results of this estimation were tested for several initial starting points for μ and γA, and the estimation procedure always converged to the same values of
, indicating that these cultures were growing with a doubling time of 30 min. The results of this estimation were tested for several initial starting points for μ and γA, and the estimation procedure always converged to the same values of  and γA.
and γA.γA: The value of γA was estimated as 5.2 × 10−1 min−1 together with the value of μ by using least-square fitting of the experimental β-galactosidase activity data given in Knorre (1968) as above.
γM: Leive and Kollin (1967) found that the
 of β-galactosidase mRNA was 2 min to give a value of
of β-galactosidase mRNA was 2 min to give a value of 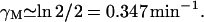 In a comparable experiment, Blundell and Kennell (1974) found
In a comparable experiment, Blundell and Kennell (1974) found  to give
to give  We have taken the average of these two figures to give
We have taken the average of these two figures to give 
γB: The rate of breakdown of β-galactosidase was measured by Mandelstam (1957) and found to be 0.05 per h corresponding to 8.33 × 10−4 min−1. Rotman and Spiegelman (1954) also reported that the maximal rate of breakdown of β-galactoside is 0.005 min−1, and noted that it is possibly much smaller than this value. We have taken the Mandelstam value.
K: Yagil and Yagil (1971) analyzed a number of published data sets, and from their calculations we find the average value is

n: Again from Yagil and Yagil (1971), we have an average Hill coefficient of 2.09. We have taken n = 2.
K1: The average dissociation constant of effector-repressor complex was
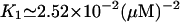 from the results of Yagil and Yagil (1971).
from the results of Yagil and Yagil (1971).- αM: The steady-state value of lac mRNA in the absence of induction is thought to be one molecule per cell. This corresponds to a “concentration” of 2.08 × 10−6 mM if we take the E. coli volume to be 8 × 10−16 liter. When the cells are maximally induced, the lac mRNA level is raised a thousand times compared to this uninduced steady-state value (Savageau, 1999). From Eq. 2 at a steady state,
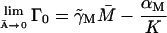
(16)
From Eqs. 16 and 17, αM is 9.97 × 10−4 mM–min−1.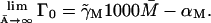
(17) -
Γ0: The term Γ0 was included in our model for the following reason. Assume that the term in question is not there, which is equivalent to taking Γ0 ≡ 0. An examination of Eq. 2 in a steady state yields
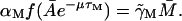 Let the level of lac mRNA in the maximally induced state be given by
Let the level of lac mRNA in the maximally induced state be given by 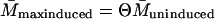 . The maximally induced state corresponds to
. The maximally induced state corresponds to 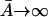 and
and  The uninduced state corresponds to
The uninduced state corresponds to 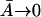 and
and  Thus we have two relations,
Thus we have two relations,
and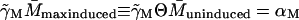
Taking the ratio of these two relations gives Θ ≡ K and from above, K = 7200, which would imply a value for Θ which is 7.2 times larger than what is experimentally observed (Θ = 1000). Thus the inclusion of the term Γ0.
- αB: At a steady state, from Eq. 3 we have
Kennell and Reizman (1977) reported that steady-state value of β-galactosidase is ∼20 molecules per cell, which means that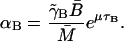
(18) 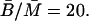 Using the value of γB reported by Mandelstam (1957) for nongrowing bacteria,
Using the value of γB reported by Mandelstam (1957) for nongrowing bacteria, 
- αA: Huber et al. (1975) studied the kinetics of β-galactosidase and found Vmax = 32.6 U/mg of β-galactosidase and KM = 0.00253 M when lactose was the substrate. whereas Vmax = 49.6 U/mg of β-galactosidase and KM = 0.00120 M when allolactose is the substrate. (U is defined as μM of glucose or galactose produced per minute.) Given that the molecular mass of β-galactosidase is 540,000 Da, and 1 Da = 1.66 × 10−21 mg, 1 mol of β-galactosidase is equivalent to 6.02 × 1023 × 5.4 × 105 × 1.66 × 10−21 = 5.39 × 108 mg of β-galactosidase, so 1 mg of β-galactosidase is equivalent to 1.85 × 10−3 μmol. Therefore,

βA: From the data of Huber et al. (1975), we have
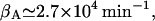 whereas Martínez-Bilbao et al. (1991) gives
whereas Martínez-Bilbao et al. (1991) gives 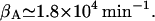 We have taken the average of
We have taken the average of 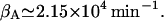
- KL: The volume of one E. coli is ∼8.0 × 10−16 liter and its mass is ∼1.7 × 10−12 g to yield a density of 2.1 × 103 g/liter. The parameter KL in our model corresponds to the parameter Km,Lac/ρ in Wong et al. (1997) model and the values and the units of these two parameters reported in this paper are ρ = 3.0 × 102 g of dry cell weight per liter and Km,Lac = 1.4 × 10−4 M, which gives
To obtain an estimate for KL in M, we can multiply this value by the density of the cell, which gives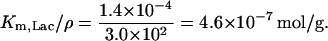
 in agreement with the value of 1.4 ± 0.3 × 10−3 M estimated by Martínez-Bilbao et al. (1991). We have taken the latter value.
in agreement with the value of 1.4 ± 0.3 × 10−3 M estimated by Martínez-Bilbao et al. (1991). We have taken the latter value. KA: This parameter in our model corresponds to Km,Allo/ρ in the Wong et al. (1997) model, and they took Km,Allo ≃2.8 × 10−4 M. Hence,
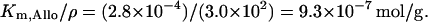 Using the procedure followed in the estimation of KL, the value of KA is calculated to be 1.95 mM.
Using the procedure followed in the estimation of KL, the value of KA is calculated to be 1.95 mM.- τM: In this model, we are considering the transcription and translation of two genes, lacZ and lacY. Translation of lacZ starts shortly after transcription initiation. For the translation of lacY to begin, lacZ must be completely transcribed. Knowing that lacZ has 1022 amino acids and DNA chain elongation rate is at least 490 nucleotides per second, which is equivalent to 9800 amino acids per minute, according to Bremmer and Dennis (1996), the time for lacZ to be completely transcribed is at most
This is an upper bound on τM.
- τB: lacZ is 1022 amino acids long and the mRNA elongation rate varies between 12 and 33 amino acids per second (Monar et al., 1969; Kennell and Reizman, 1977). Talkad et al. (1976) also reported the translation rate is between 8 and 15 amino acids per second. If we take the mRNA elongation rate as 8 amino acids per second to estimate an upper bound value for τB, we obtain
If the elongation rate is 33 amino acids per second, then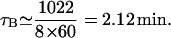
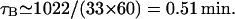 Sorensen et al. (1989) estimated an average value for τB of 82 s experimentally, which is 1.37 min. We have taken the upper bound as
Sorensen et al. (1989) estimated an average value for τB of 82 s experimentally, which is 1.37 min. We have taken the upper bound as 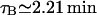 but used
but used 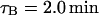 .
. γL: We assumed
 implying that the degradation rate for intracellular lactose is negligible when compared with the bacterial growth rate, as did Wong et al. (1997).
implying that the degradation rate for intracellular lactose is negligible when compared with the bacterial growth rate, as did Wong et al. (1997).γP: West and Stein (1973) studied the kinetics of induction of β-galactosidase permease in E. coli and estimated the mean half life of permease ranges from 1.3 min to 1.9 min, which yields a range for 0.53–0.78 min−1 for the degradation rate of permease γP. We have taken an average of these two estimates to give
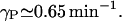
αL: Wright et al. (1981) studied on lactose carrier protein of E. coli and measured the active transport turnover number as 48 × 60 = 2880 min−1 in EDTA-treated cells of the strain ML308-225. We have taken the same value αL = 2880 min−1.
-
αP: Eq. 6 gives
at a steady state. From Kennell and Reizman (1977), we know that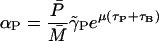
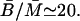 The steady-state molar ratio of β-galactosidase to permease was given as
The steady-state molar ratio of β-galactosidase to permease was given as 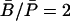 by in Maloney and Rotman (1973). From this we estimate
by in Maloney and Rotman (1973). From this we estimate 
Lee and Bailey (1984) studied the growth rate effects on productivity of recombinant E. coli populations and obtained an empirical relation for the transcription rate as a function of the bacterial growth rate. From this relation, we have αP = 17.37 min−1 when μ = 2.21 × 10−2 min−1, which is the value we have estimated. We have taken an intermediate value between these two estimates:

βL1: From Wong et al. (1997), we have βL1 = 2148 min−1. Lolkema et al. (1991) gave a range for βL1 as 840–3000 min−1. We have chosen as βL1 = 2650 min−1.
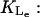 From Wong et al. (1997), we have
From Wong et al. (1997), we have
based on the data of Lolkema et al. (1991), Huber et al. (1980), Page and West (1984), and Wright et al. (1981).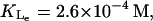
 From Wong et al. (1997), we have
From Wong et al. (1997), we have
wherein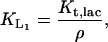
from Lolkema et al. (1991), Huber et al. (1980), Page and West (1984), and Wright et al. (1981), and ρ is as given before. Thus
Multiplying by the density of the cell (2.1 × 103 gm/L) gives us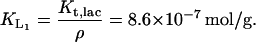

- τP: lacY is 399 amino acids long and the mRNA elongation rate varies between 8 and 33 amino acids per second (Monar et al., 1969; Kennell and Reizman, 1977; and Talkad et al., (1976). If we take the mRNA elongation rate to be 8 amino acids per second to estimate an upper bound value for τP, we obtain
If the elongation rate is 33 amino acids per second, then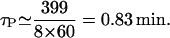
 We have taken the maximal value to be
We have taken the maximal value to be 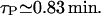
APPENDIX C: STEADY-STATE ANALYSIS OF THE MODEL
In this section, the steady-state analysis of the system is investigated and a necessary condition derived for existence of positive steady state(s). Let 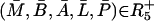 be the steady state of the system given by Eqs. 2–6. At a steady state, by definition, there are no temporal changes and thus the steady state(s) are defined implicitly by
be the steady state of the system given by Eqs. 2–6. At a steady state, by definition, there are no temporal changes and thus the steady state(s) are defined implicitly by
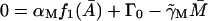 |
(19) |
 |
(20) |
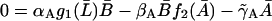 |
(21) |
 |
(22) |
 |
(23) |
where 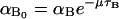 and
and 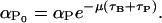 Moreover, f1, f2, g1, and g2 are all monotone increasing functions given by
Moreover, f1, f2, g1, and g2 are all monotone increasing functions given by
 |
(24) |
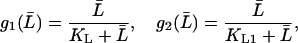 |
(25) |
where 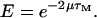
For a steady state to make sense in a biological context, it is necessary that it be nonnegative. Now from Eqs. 20 and 23, we easily have
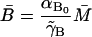 |
(26) |
 |
(27) |
Furthermore, from Eq. 19, 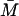 can be written in terms of
can be written in terms of  as,
as,
 |
(28) |
Note that 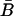 and
and 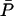 are nonnegative whenever
are nonnegative whenever  is nonnegative, and from Eq. 28 we always have
is nonnegative, and from Eq. 28 we always have  Further, from Eq. 21 we can write
Further, from Eq. 21 we can write 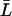 in terms of
in terms of 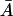 :
:
 |
(29) |
where
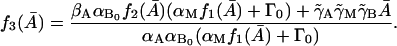 |
(30) |
Condition I for a nonnegative steady state
From Eq. 29, to have a nonnegative steady-state value of 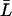 ,
,
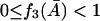 |
(31) |
must be satisfied.
Now consider Eq. 22, and substitute Eqs. 26 and 27. After rearrangement, we obtain
 |
(32) |
where
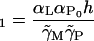 |
(33) |
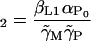 |
(34) |
 |
(35) |
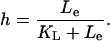 |
(36) |
The left side of Eq. 32 is always positive for all nonnegative values of  , which leads to the following second condition for a biologically sensible steady state:
, which leads to the following second condition for a biologically sensible steady state:
Condition II for a nonnegative steady state
Since the left side of Eq. 32 is always nonnegative, the condition
 |
(37) |
must be satisfied.
Theorem 1
(Necessary condition for existence of a positive steady state.) For the existence of a positive steady state for the model given by Eqs. 2–6,
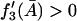 |
(38) |
is a necessary condition for 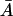 in an interval defined by the intersection of the intervals for which Eqs. 31 and 37 are satisfied.
in an interval defined by the intersection of the intervals for which Eqs. 31 and 37 are satisfied.
Proof
The left side of Eq. 32 is a monotone increasing function of  when K1 > 0, and has a minimal value of (αM/K0) + Γ0 when
when K1 > 0, and has a minimal value of (αM/K0) + Γ0 when 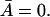 Further, it reaches its maximal value of αM + Γ0 as
Further, it reaches its maximal value of αM + Γ0 as 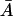 becomes large. Furthermore, the right side of Eq. 32 is zero when
becomes large. Furthermore, the right side of Eq. 32 is zero when  Therefore, for the existence of a positive root, it is trivial that the right of Eq. 32 must be an increasing function of
Therefore, for the existence of a positive root, it is trivial that the right of Eq. 32 must be an increasing function of 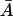 for values of
for values of 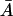 and
and  satisfying Eqs. 31 and 37.
satisfying Eqs. 31 and 37.
To prove that the condition 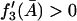 is a necessary condition for the right side of Eq. 32 to be an increasing function of
is a necessary condition for the right side of Eq. 32 to be an increasing function of  let
let
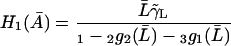 |
(39) |
so that
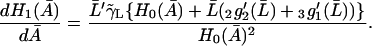 |
(40) |
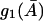 and
and  are Michaelis-Menten type functions and
are Michaelis-Menten type functions and  and
and  are positive. Since
are positive. Since 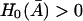 the condition
the condition
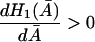 |
is satisfied whenever
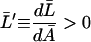 |
holds.
Further, from Eq. 29 we have
 |
(41) |
and from Condition I, 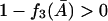 must be satisfied for nonnegative steady states. Thus the right side of Eq. 41 is always positive when
must be satisfied for nonnegative steady states. Thus the right side of Eq. 41 is always positive when 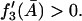 Therefore,
Therefore, 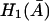 is an increasing function when
is an increasing function when  in an interval defined by the intersection of the intervals for which Eqs. 31 and 37 are satisfied. This completes the proof.
in an interval defined by the intersection of the intervals for which Eqs. 31 and 37 are satisfied. This completes the proof.
APPENDIX D: NUMERICAL STABILITY OF THE MODEL
A full stability analysis of the steady states of this model is impossible, since the eigenvalue equation determining local stability is a fifth order quasipolynomial containing three delays. Consequently, we have contented ourselves with a numerical examination of the stability properties of the steady states.
Briefly, the results of our numerical stimulations are as follows. When a single steady state exists, we have found that the numerical behavior is such that the model solutions always converge to that steady state at large times.
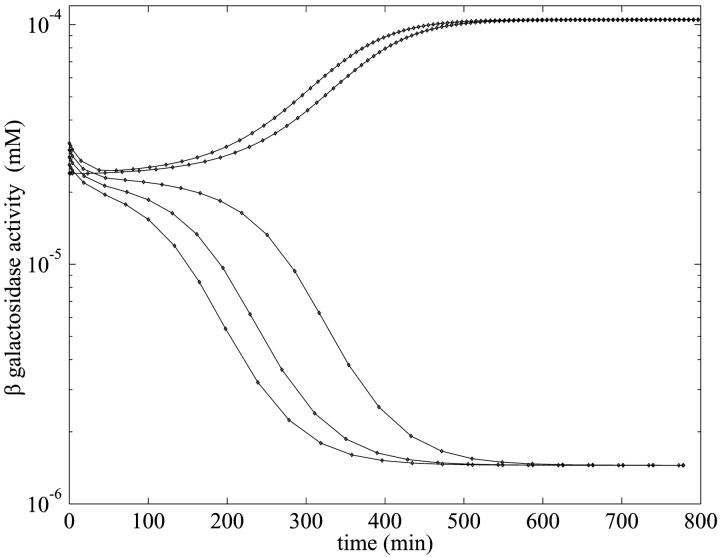
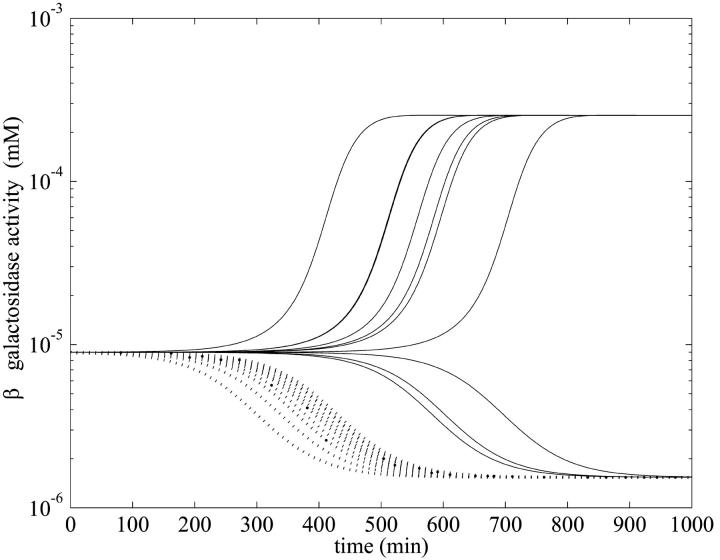
When there are three coexisting steady states as illustrated in Fig. 2, the behavior is slightly more complicated and is illustrated in Fig. 5 when Le = 3.0 × 10−2. At this value, the system has the three steady states given in Table 3. As seen from the results in Fig. 5, the numerical model solutions either converged to the lower or upper branch of the S-shaped curve (see Fig. 2) for various initial conditions. These results, as well as numerous others that are not shown, lead us to conclude that the middle branch of the S-shaped steady-state curve corresponds to a steady state that is globally unstable.
FIGURE 5.
Semilog plot of β-galactosidase activity versus time (min) showing bifurcation in the numerical simulation with the parameters of Table 1 for five initial conditions and 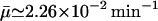 when Le = 3.0 × 10−2 mM, which is in the range of lactose concentration for the existence of three steady states. The selection of the five initial conditions is described in the text.
when Le = 3.0 × 10−2 mM, which is in the range of lactose concentration for the existence of three steady states. The selection of the five initial conditions is described in the text.
TABLE 3.
Multiple steady states and their numerical values when Le = 3.0 × 10−2 mM
| Steady states |  |
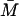 |
 |
 |
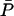 |
|---|---|---|---|---|---|
| I | 4.31 × 10−3 | 2.14 × 10−6 | 1.44 × 10−6 | 1.01 × 10−1 | 2.98 × 10−5 |
| II | 6.43 × 10−2 | 3.46 × 10−5 | 2.34 × 10−5 | 1.36 × 10−1 | 4.83 × 10−4 |
| III | 1.42 × 10−1 | 1.54 × 10−4 | 1.04 × 10−4 | 1.39 × 10−1 | 2.16 × 10−3 |
For this simulation, we choose five equally distributed initial β-galactosidase levels between 0.24 × 10−4 and 0.32 × 10−4 mM and kept all other variables at their steady-state values corresponding to the values on the middle branch of the S-shaped curve in Fig. 2 when Le = 3.0 × 10−2 mM, and computed the temporal evolution of the model variables. For initial β-galactosidase values equal to or greater than 3.0 × 10−5, the simulated curves converged to 1.04 × 10−4, which is the value on the upper branch of the steady-state curve, whereas for the other initial values, the β-galactosidase values converged to 1.44 × 10−6, which is the steady-state value on the lower branch.
However, the relatively simple behavior shown in Fig. 5 is deceptive, as shown in Fig. 6. There we present numerical evidence that the attractor boundary in initial function space separating behaviors where one approaches the lower or upper locally stable steady state of Fig. 2 is not totally straightforward. The potentially rich nature of the boundary is revealed by taking initial functions that oscillate about the unstable branch of the steady-state curve. The ensuing dynamical behavior is highly reminiscent of the existence of a fractal basin boundary that has been noted in other, simpler, differential delay systems (Losson and Mackey, 1993).
FIGURE 6.
Semilog plot of β-galactosidase activity versus time showing effects of selection of the initial condition for t ∈[−τ, 0] in the numerical simulation with the parameters of Table 1 and various initial values of mRNA and allolactose oscillating around the unstable steady-state values corresponding to the middle branch of Fig. 2 when 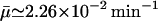 and Le = 4.0 × 10−2 mM (which is in the range of lactose concentration for coexistence of three steady states). The solid lines show the β-galactosidase activity when the initial allolactose functions are
and Le = 4.0 × 10−2 mM (which is in the range of lactose concentration for coexistence of three steady states). The solid lines show the β-galactosidase activity when the initial allolactose functions are 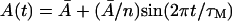 (n = 1, 2, …10), t ∈[−τM, 0], and the other variables are at the steady-state values on the middle branch. (Here
(n = 1, 2, …10), t ∈[−τM, 0], and the other variables are at the steady-state values on the middle branch. (Here 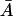 is the unstable steady-state value of A on the middle branch). The dotted lines depict the temporal changes in β-galactosidase activity when
is the unstable steady-state value of A on the middle branch). The dotted lines depict the temporal changes in β-galactosidase activity when 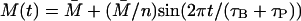 (n = 1, 2, …10) for t ∈[−(τB + τP),0]. Again all the other variables are at the steady-state values when Le = 4.0 × 10−2 mM and
(n = 1, 2, …10) for t ∈[−(τB + τP),0]. Again all the other variables are at the steady-state values when Le = 4.0 × 10−2 mM and 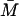 is also the steady-state value of A on the middle branch. The steady-state values are
is also the steady-state value of A on the middle branch. The steady-state values are 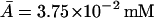 ,
, 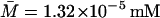 ,
, 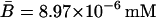 ,
, 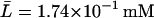 , and
, and 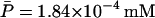 , when Le = 4.0 × 10−2 mM.
, when Le = 4.0 × 10−2 mM.
Necmettin Yildirim's permanent address is Atatürk Üniversitesi, Bilgisayar Bilimleri Uygulama ve Araştırma Merkezi, 25240 Erzurum, Turkey.
References
- Arkin, A., J. Ross, and H. H. McAdams. 1998. Stochastic kinetic analysis of developmental pathway bifurcation in phage λ-infected Escherichia coli cells. Genetics. 149:1633–1648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baneyx, F. 1999. Recombinant protein expression in Escherichia coli. Curr. Opin. Biotechnol. 10:411–421. [DOI] [PubMed] [Google Scholar]
- Beckwith, J. 1987a. The lactose operon. In Escherichia coli and Salmonella: Cellular and Molecular Biology, Vol. 2. F. C. Neidhardt, J. L. Ingraham, K. B. Low, B. Magasanik, and H. E. Umbarger, editors. American Society for Microbiology, Washington, DC. 1444–1452.
- Beckwith, J. 1987b. The operon: An historical account. In Escherichia coli and Salmonella: Cellular and Molecular Biology, Vol. 2. F. C. Neidhardt, J. L. Ingraham, K. B. Low, B. Magasanik, and H. E. Umbarger, editors. American Society for Microbiology, Washington, DC. 1439–1443.
- Bliss, R. D., R. P. Painter, and A. G. Marr. 1982. Role of feedback inhibition in stabilizing the classical operon. J. Theor. Biol. 97:177–193. [DOI] [PubMed] [Google Scholar]
- Blundell, M., and D. Kennell. 1974. Evidence for endonucleolytic attack in decay of lac messenger RNA in Escherichia coli. J. Mol. Biol. 83:143–161. [DOI] [PubMed] [Google Scholar]
- Bremmer, H., and P. P. Dennis. 1996. Modulation of chemical composition and other parameters of the cell by growth rate. In Escherichia coli and Salmonella: Cellular and Molecular Biology, Vol. 2. F. C. Neidhardt, R. Curtiss, J. L. Ingraham, E. C. C. Lin, K. B. Low, B. Magasanik, W. S. Reznikoff, M. Riley, M. Schaechter, and H. E. Umbarger, editors. American Society for Microbiology, Washington, DC. 1553–1569.
- Cohn, M., and K. Horibata. 1959. Inhibition by glucose of the induced synthesis of the β-galactosidase-enzyme system of Escherichia coli: analysis of maintenance. J. Bacteriol. 78:613–623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie, D. T. 1977. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81:2340–2361. [Google Scholar]
- Gillespie, D. T. 1992. A rigorous derivation of the chemical master equation. Physica A. 188:404–425. [Google Scholar]
- Goodwin, B. 1965. Oscillatory behaviour in enzymatic control process. Adv. Enz. Regul. 3:425–438. [DOI] [PubMed] [Google Scholar]
- Goodwin, B. C. 1969. Control dynamics of β-galactosidase in relation to the bacterial cell cycle. Eur. J. Biochem. 10:515–522. [DOI] [PubMed] [Google Scholar]
- Griffith, J. S. 1968a. Mathematics of cellular control processes. I. Negative feedback to one gene. J. Theor. Biol. 20:202–208. [DOI] [PubMed] [Google Scholar]
- Griffith, J. S. 1968b. Mathematics of cellular control processes. II. Positive feedback to one gene. J. Theor. Biol. 20:209–216. [DOI] [PubMed] [Google Scholar]
- Huber, R. E., M. Gupta, and S. Khare. 1994. The active site and mechanism of the β-galactosidase from Escherichia coli. Int. J. Biochem. 26:309–318. [DOI] [PubMed] [Google Scholar]
- Huber, R. E., G. Kurz, and K. Wallenfels. 1976. A quantitation of the factors which affect the hydrolase and transgalactosylase activities of β-galactosidase (E. coli) on lactose. Biochemistry. 15:1994–2001. [DOI] [PubMed] [Google Scholar]
- Huber, R., R. Pisko-Dubienski, and K. Hurlburt. 1980. Immediate stoichiometric appearance of β-galactosidase products in the medium of Escherichia coli cells incubated with lactose. Biochem. Biophys. Res. Commun. 96:656–661. [DOI] [PubMed] [Google Scholar]
- Huber, R. E., W. Wallenfels, and G. Kurz. 1975. The action of β-galactosidase Escherichia coli on allolactose. Can. J. Biochem. 53:1035–1039. [DOI] [PubMed] [Google Scholar]
- Jacob, F., D. Perrin, C. Sanchez, and J. Monod. 1960. L'operon: groupe de gène à expression par un operatour. C. R. Acad. Sci. 250:1727–1729. [PubMed] [Google Scholar]
- Ji-Fa, J. 1994. A Liapunov function for four dimensional positive feedback systems. Quar. Appl. Math. 52:601–614. [Google Scholar]
- Kennell, D., and H. Reizman. 1977. Transcription and translation initiation frequencies of the Escherichia coli lac operon. J. Mol. Biol. 114:1–21. [DOI] [PubMed] [Google Scholar]
- Kepler, T. B., and T. C. Elston. 2001. Stochasticity in transcriptional regulation: origins, consequences, and mathematical representations. Biophys. J. 81:3116–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knorre, W. A. 1968. Oscillation of the rate of synthesis of β-galactosidase in Escherichia coli ML 30 and ML 308. Biochem. Biophys. Res. Commun. 31:812–817. [DOI] [PubMed] [Google Scholar]
- Lee, S. B., and J. E. Bailey. 1984. Analysis of growth rate effects on productivity of recombinant Escherichia coli populations using molecular mechanism models. Biotechnol. Bioeng. 67:805–812. [DOI] [PubMed] [Google Scholar]
- Leive, L., and V. Kollin. 1967. Synthesis, utilization and degradation of lactose operon mRNA in Escherichia coli. J. Mol. Biol. 24:247–259. [DOI] [PubMed] [Google Scholar]
- Lolkema, J., N. Carrasco, and H. Kaback. 1991. Kinetic analysis of lactose exchange in proteoliposomes reconstituted with purified lac permease. Biochemistry. 30:1284–1290. [DOI] [PubMed] [Google Scholar]
- Losson, L., and M. C. Mackey. 1993. Solution multistability in first order nonlinear differential delay equations. Chaos. 3:167–176. [DOI] [PubMed] [Google Scholar]
- Maffahy, J. M., and E. Savev. 1999. Stability analysis for a mathematical model of the lac operon. Quar. Appl. Math. 57:37–53. [Google Scholar]
- Maloney, P. C., and S. M. Rotman. 1973. Distribution of suboptimally induced β-D-galactosidase in Escherichia coli. J. Mol. Biol. 73:77–91. [DOI] [PubMed] [Google Scholar]
- Mandelstam, J. 1957. Turnover of protein in starved bacteria and its relationship to the induced synthesis of enzyme. Nature. 179:1179–1181. [DOI] [PubMed] [Google Scholar]
- Martínez-Bilbao, M., R. E. Holdswards, L. A. Edwards, and R. E. Huber. 1991. A highly reactive β-galactosidase Escherichia coli resulting from a substitution of an aspartic acid for Gly-794. J. Biol. Chem. 266:4979–4986. [PubMed] [Google Scholar]
- McAdams, H. H., and L. Shapiro. 1995. Circuit simulation of genetic networks. Science. 269:650–656. [DOI] [PubMed] [Google Scholar]
- Monar, H., D. Goodman, and G. S. Stnet. 1969. RNA chain growth rates in Escherichia coli. J. Mol. Biol. 39:1–29. [DOI] [PubMed] [Google Scholar]
- Novick, A., and M. Wiener. 1957. Enzyme induction as an all-or-none phenomenon. Proc. Natl. Acad. Sci. USA. 43:553–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osumi, T., and M. H. Saier. 1982. Regulation of lactose permease activity by the phosphoenolpyruvate: sugar phosphotransferase system: Evidence for direct binding of the glucose specific enzyme III to the lactose permease. Proc. Natl. Acad. Sci. USA. 79:1457–1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Page, M. G. P., and I. C. West. 1984. The transient kinetics of uptake of galactosides into Escherichia coli. Biochem. J. 223:723–731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pestka, S., B. L. Daugherty, V. Jung, K. Hotta, and R. K. Pestka. 1984. Anti-mRNA: specific inhibition of translation of single mRNA molecules. Proc. Natl. Acad. Sci. USA. 81:7525–7528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Postma, P. W., J. W. Lengeler, and G. R. Jacobson. 1996. Phosphoenolpyruvate-carbohydrate phosphotransferase systems. In Escherichia coli and Salmonella: Cellular and Molecular Biology, Vol. 1. F. C. Neidhart, R. Curtiss, J. L. Ingraham, E. C. C. Lin, K. B. Low, B. Magasanik, W. S. Reznikoff, M. Riley, M. Schaechter, and H. E. Umbarger, editors. American Society for Microbiology, Washington, DC. 1149–1174.
- Rotman, R., and S. Spiegelman. 1954. On the origin of the carbon in induced synthesis of β-galactosidase. J. Bacteriol. 68:419–429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saier Jr., M. H. 1976. Inducer exclusion and regulation of the melibose, maltose, glycerol, and lactose transport systems by the phosphoenolpyruvate: sugar phosphotransferase system. J. Biol. Chem. 251:6606–6615. [PubMed] [Google Scholar]
- Saier, M. H., T. M. Ramseier, and J. Reizer. 1996. Regulation of carbon utilization. In Escherichia coli and Salmonella: Cellular and Molecular Biology, Vol. 1. F. C. Neidhardt, R. Curtiss, J. L. Ingraham, E. C. C. Lin, K. B. Low, B. Magasanik, W. S. Reznikoff, M. Riley, M. Schaechter, and H. E. Umbarger, editors. American Society for Microbiology, Washington, DC. 1325–1343.
- Santillán, M., and M. C. Mackey. 2001a. Dynamic behaviour in mathematical models of the tryptophan operon. Chaos. 11:261–268. [DOI] [PubMed] [Google Scholar]
- Santillán, M., and M. C. Mackey. 2001b. Dynamic regulation of the tryptophan operon: a modeling study and comparison with experimental data. Proc. Natl. Acad. Sci. USA. 98:1364–1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savageau, M. A. 1999. Design of gene circuitry by natural selection: analysis of the lactose catabolic system in Escherichia coli. Biochem. Soc. Trans. 27:264–270. [DOI] [PubMed] [Google Scholar]
- Selgrade, J. F. 1979. Mathematical analysis of a cellular control process with positive feedback. SIAM J. Appl. Math. 36:219–229. [Google Scholar]
- Selgrade, J. F. 1982. A Hopf bifurcation in single loop positive feedback systems. Quar. Appl. Math. 40:347–351. [Google Scholar]
- Sen, A. K., and W. Liu. 1989. Dynamic analysis of genetic control and regulation of amino acid synthesis: the tryptophan operon in Escherichia coli. Biotechnol. Bioeng. 35:185–194. [DOI] [PubMed] [Google Scholar]
- Shampine, L. F., and S. Thompson. 2000. Solving DDEs with MATLAB. www.radford.edu/∼thompson/webddes/.
- Sinha, S. 1988. Theoretical study of tryptophan operon: application in microbial technology. Biotechnol. Bioeng. 31:117–124. [DOI] [PubMed] [Google Scholar]
- Sorensen, M. A., C. G. Kurland, and S. Pedersen. 1989. Codon usage determines translation rate in Escherichia coli. J. Mol. Biol. 207:365–377. [DOI] [PubMed] [Google Scholar]
- Swain, P. S., M. Elowitz, and E. Siggia. 2002. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl. Acad. Sci. USA. 99:12795–12800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talkad, V., E. Schneider, and D. Kennell. 1976. Evidence for variable rates of ribosome movement in Escherichia coli. J. Mol. Biol. 104:299–303. [DOI] [PubMed] [Google Scholar]
- Tyson, J. J., and M. C. Mackey. 2001. Molecular, metabolic and genetic control: An introduction. Chaos. 11:81–83. [DOI] [PubMed] [Google Scholar]
- Tyson, J. J., and H. G. Othmer. 1978. The dynamics of feedback control circuits in biochemical pathways. In Progress in Biophysics, Vol. 5. R. Rosen, editor. Academic Press, New York. 1–62.
- Watson, J. D. 1977. Molecular Biology of the Gene, 3rd ed. W. A. Benjamin, New York.
- West, I. C., and W. D. Stein. 1973. The kinetics of induction of β-galactoside permease. Biochim. Biophys. Acta. 308:161–167. [DOI] [PubMed] [Google Scholar]
- Wong, P., S. Gladney, and J. D. Keasling. 1997. Mathematical model of the lac operon: inducer exclusion, catabolite repression, and diauxic growth on glucose and lactose. Biotechnol. Prog. 13:132–143. [DOI] [PubMed] [Google Scholar]
- Wright, J. K., I. Riede, and P. Overath. 1981. Lactose carrier protein of Escherichia coli: interaction with galactosides and protons. Biochemistry. 20:6404–6415. [DOI] [PubMed] [Google Scholar]
- Xiu, Z. L., A. P. Zeng, and W. D. Deckwer. 1997. Model analysis concerning the effects of growth rate and intracellular tryptophan level on the stability and dynamics of tryptophan biosynthesis in bacteria. J. Biotech. 58:125–140. [Google Scholar]
- Yagil, G., and E. Yagil. 1971. On the relation between effector concentration and the rate of induced enzyme synthesis. Biophys. J. 11:11–27. [DOI] [PMC free article] [PubMed] [Google Scholar]