Role of the Dielectric Constants of Membrane Proteins and Channel Water in Ion Permeation

Abstract

Using both analytical solutions obtained from simplified systems and numerical results from more realistic cases, we investigate the role played by the dielectric constant of membrane proteins ɛ_p and pore water ɛ_w in permeation of ions across channels. We show that the boundary and its curvature are the crucial factors in determining how an ion's potential energy depends on the dielectric constants near an interface. The potential energy of an ion outside a globular protein has a dominant 1/ɛ_w dependence, but this becomes 1/ɛ_p for an ion inside a cavity. For channels, where the boundaries are in between these two extremes, the situation is more complex. In general, we find that variations in ɛ_w have a much larger impact on the potential energy of an ion compared to those in ɛ_p. Therefore a better understanding of the effective ɛ_w values employed in channel models is desirable. Although the precise value of ɛ_p is not a crucial determinant of ion permeation properties, it still needs to be chosen carefully when quantitative comparisons with data are made.

INTRODUCTION

Continuum electrostatics, that is, solving the Poisson equation for a charge distribution embedded in dielectric media, has been playing a prominent role in modeling of ion permeation across membrane channels (for recent reviews, see Partenskii and Jordan, 1992; Roux et al., 2000; Kuyucak et al., 2001; Tieleman et al., 2001). Early calculations of the potential energy profiles of ions along the central axis of model channels provided useful insights about their permeation properties (Parsegian, 1969; Levitt, 1978; Jordan, 1982). The effect of the ionic atmosphere on the channel potentials was later explored by combining the Poisson and Boltzmann equations (Jordan et al., 1989). The Poisson-Boltzmann formalism is, however, an equilibrium theory, and to study the permeation process itself requires a nonequilibrium theory. At the continuum level, this is provided by the Nernst-Planck equation (Levitt, 1986). Self-consistent solution of the Poisson and Nernst-Planck equations leads to the Poisson-Nernst-Planck formalism, which has been used in numerous studies of ion channels (for reviews, see Eisenberg, 1996, 1999). An alternative nonequilibrium method is to follow the motion of individual ions using Brownian dynamics simulations. Here too, one needs to solve the Poisson equation to calculate the electric forces acting on ions (Kuyucak et al., 2001).

The only method that dispenses with continuum electrostatics is molecular dynamics (MD) simulations, where all the atoms in a system are treated explicitly. Recently several attempts have been made to calculate the conductance of a channel from MD simulations (Suenaga et al., 1998, Crozier et al., 2001). However, to obtain statistically meaningful results, very high applied potentials (∼1 V) and concentrations (∼1 M) had to be used in these simulations. Considering the nonlinear nature of the current-voltage and current-concentration relations at high voltages and concentrations, extrapolation of such results to the physiological range (∼0.1 V and ∼0.1 M) remains problematic. Despite the dramatic increases in computational power, a direct study of ion conduction across membrane channels under physiological conditions is still not feasible within the MD framework. Thus for the foreseeable future, continuum electrostatics will continue to play an important role in investigation of structure-function relations in ion channels.

According to the conventional picture of permeation, ions execute a Brownian motion in solution and drift across a channel under the influence of the electrochemical forces acting on them. In models that rely on continuum electrostatics, one requires two sets of parameters to calculate the permeation properties of ions: their diffusion coefficients in the channel and the dielectric constants of the membrane protein (ɛ_p) and channel water (ɛ_w). The diffusion coefficients can be estimated in a straightforward manner from MD simulations of ions in model channels (Smith and Sansom, 1999; Allen et al., 2000). Since their influence on permeation is manifestly obvious (conductance of ions increases with their diffusion coefficient), we do not dwell on them further here. The effect of the dielectric constants on ion permeation, on the other hand, is much more complicated. To start with, dielectric constants are well defined only for isotropic homogeneous media. For anisotropic inhomogeneous media such as in ion channels, one should ideally introduce dielectric tensors that are both space dependent and nonlocal (Partenskii and Jordan, 1992). Thus use of dielectric constants in channels is a functional approximation that can only be justified a posteriori. Another complicating factor is that ions interact with fixed charges in the protein and induced charges on the boundary, and each interaction may have a different dependence on the dielectric constants and the channel geometry. Finally, compared to the globular proteins, much less is known about the values of the dielectric constants of membrane proteins and channel waters, either experimentally or from theoretical considerations based on microscopic MD simulations. As a result, in most channel models, the canonical values of ɛ_p = 2 and ɛ_w = 80 are employed without worrying too much about how variations from these values may change the results.

There is evidence from MD studies of water in pores that confinement significantly reduces orientational polarizability of water molecules, leading to a much smaller ɛ_w value compared to the bulk value of 80 (Sansom et al., 1997; Green and Lu, 1997, Tieleman and Berendsen, 1998; Allen et al., 1999). However, such studies of pure water in pores are of limited relevance for the effective ɛ_w values used in ion permeation. This is because the electric field of an ion in its first hydration shell is orders of magnitude larger than the average (or external) field in pure water. Thus as long as an ion's hydration shell remains intact in a pore, its charge is screened effectively and the use of a bulklike ɛ_w may be justified. The recent high-resolution structure of the KcsA potassium channel (Zhou et al., 2001) provides a direct evidence for this: the potassium ions are observed to be eightfold coordinated by either water or protein oxygens even in the narrow selectivity filter. Brownian dynamics simulations of the KcsA channel are also very suggestive in this regard: the conductance of the channel steadily decreases when ɛ_w is reduced from 80 and vanishes at ɛ_w ∼ 40 (Chung et al., 1999). Here we aim to provide a better understanding of this behavior within the framework of continuum electrostatics. Provided that microscopic foundations of continuum electrostatics can be justified, a longer term goal would be to determine the effective ɛ_w values in channels directly from MD simulations.

The situation with regard to ɛ_p is also ambiguous. The commonly used value of ɛ_p = 2 takes into account only the electronic polarizability of the protein and ignores potential contributions from other sources such as reorientation of polar and charged residues. Moreover, unlike water, proteins are quite inhomogeneous and it is harder to justify their representation by a uniform dielectric constant. Microscopic estimates from MD simulations indicate that, when the charged residues on the surface of globular proteins are explicitly modeled, ɛ_p in the interior remains in the range of 2–6 (Smith et al., 1993; Simonson and Brooks, 1996; Simonson, 1998; Pitera et al., 2001). Phenomenological studies of globular proteins with semimacroscopic models suggest a similar range for ɛ_p (Nakamura, 1996; Schutz and Warshel, 2001). Although there are no such microscopic estimates for membrane proteins, use of a similar range appears reasonable and has been adapted in some recent studies of the KcsA channel (Roux and MacKinnon, 1999; Chung et al., 2002; Burykin et al., 2002). The value of ɛ_p is claimed to have a large impact on the conductance of the channel in the latter work whereas the former two suggest otherwise. Here we present a careful analysis of the electrostatic potential energy of ions in channels that clarifies the influence of ɛ_p variations on ion permeation.

We remark that a great deal of work has been done on the microscopic foundations of continuum electrostatics in the gramicidin channel (Partenskii and Jordan, 1992; Jordan et al., 1997), and the results were mainly negative for a continuum dielectric description of this channel. This is not surprising, given that an ion and water molecules are in a single-file configuration in this narrow channel (radius 2 Å), and unlike most biological channels, the first hydration shell of an ion in the gramicidin channel remains incomplete (Tian and Cross, 1999). Indeed a recent detailed test of continuum electrostatics in the gramicidin channel has shown that it fails to reproduce most of the observed properties of gramicidin (Edwards et al., 2002). In contrast, application of continuum electrostatics to biological channels have so far led to reasonable descriptions of their properties, for example, nicotinic acetylcholine receptor (Chung et al., 1998), KcsA potassium (Chung et al., 1999, 2002; Mashl et al., 2001), calcium (Corry et al., 2001), porin (Schirmer and Phale, 1999; Im and Roux, 2002). Although agreement with data does not necessarily validate application of continuum electrostatics to these channels, it gives further incentive for microscopic studies to justify such applications.

ANALYTICAL RESULTS

Analytical solutions of the Poisson equation can be obtained only for some special boundaries, which do not provide very realistic representations for globular or membrane proteins. Nevertheless, insights gathered from the study of these simplified systems will be very useful in understanding the results obtained for more realistic boundaries using numerical techniques, which are necessarily less transparent. For this purpose, we represent the globular proteins with spheres and the membrane proteins with cylinders or torus with a water-filled hole through their center. We also consider an infinite plane as a simple intermediate between the two cases, where the physics is most transparent. In each case, we study how changes in the dielectric constants influence the Coulomb interaction energy U_c of an ion in the solution with a fixed charge in the protein, as well as the ion's dielectric self energy U_s due to the charges it induces on the boundary. The latter is always repulsive, so the former has to be attractive to facilitate permeation of ions. In the following, we call “dielectric self energy” simply “self energy”. Because we treat charges as discrete quantities, there is no possibility of confusing this quantity with the self energy associated with a continuous charge distribution. A particularly simple representation of the results is obtained by using ɛ_p/ɛ_w as a small expansion parameter. For the canonical values of ɛ_p = 2 and ɛ_w = 80, ɛ_p/ɛ_w = 1/40. Here we consider variations in the dielectric constants such that the condition 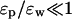is still satisfied.

Plane boundary

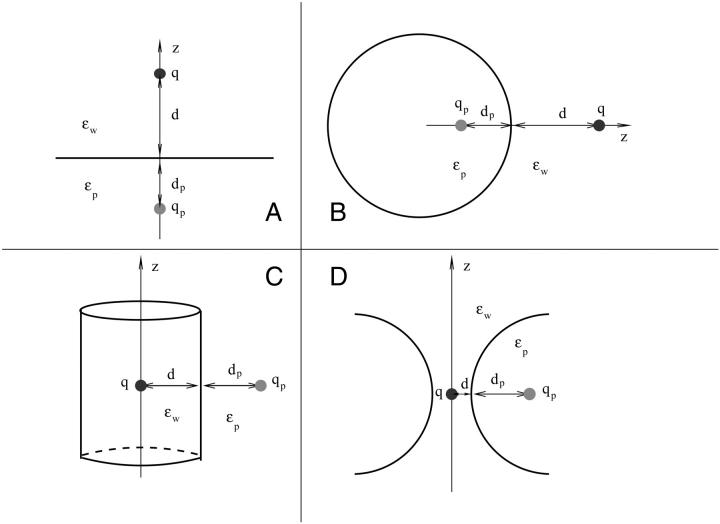
We first consider the simplest and most transparent case of an ion with charge q at a distance d from a planar water-protein (or lipid) interface (Fig. 1 A). For clarity, we consider the self and Coulomb potential energies separately. From the superposition principle, the total potential energy of the ion is given by the sum of these two contributions. For the planar boundary, the Poisson equation can be easily solved using the image charge method and gives for the self (reaction) potential acting on the ion (Jackson, 1975)

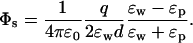(1)

Substituting this result in the self energy, and expanding in ɛ_p/ɛ_w, we obtain

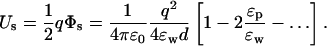(2)

It is seen that, of the two dielectric constants, ɛ_w has by far the largest effect on the self energy of the ion. Reducing ɛ_w by half from 80 to 40 increases U_s by 90% (almost double), whereas doubling ɛ_p from 2 to 4 reduces U_s by only 5%. Thus the physical picture based on the dielectric screening of the ionic charge by ɛ_w remains more or less intact for the self energy of an ion near a planar boundary.

FIGURE 1.

The simplified systems used in analytical solutions of the Poisson equation: (A) plane, (B) sphere, (C) cylinder, and (D) torus.

The potential on the same test ion due to a charge q_p in the protein at a distance d_p from the interface (see Fig. 1 A) can be similarly calculated using the image charge method

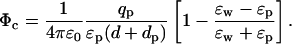(3)

Here we have deliberately written the direct (first term) and the induced charge (second term) contributions to the potential separately to point out its difference from the self potential in Eq. 1. Both terms are inversely proportional to ɛ_p, which gives the impression that charges in the protein are shielded by its dielectric constant in much the same way as ions in water. This is basically the intuitive argument used in stressing the importance of ɛ_p in ion permeation. However, it ignores the fact that the potential due to the induced charges is nearly of the same magnitude but of opposite sign as the direct term, and almost cancels it. Using Eq. 3 in the potential energy of the ion and expanding in ɛ_p/ɛ_w, we obtain

(4)

The dependence of the potential energy in Eq. 4 on the dielectric constants is seen to be very similar to that in Eq. 2. For example, halving ɛ_w still leads to near doubling of U_c (95% increase) whereas doubling ɛ_p reduces it by merely 2.5%, far from the 50% drop one would expect from the shielding of q_p by ɛ_p. Thus contrary to the intuitive arguments based on the dielectric screening of the protein charges by ɛ_p, variations in the value of ɛ_p has a relatively minor effect on the total potential energy of an ion near a plane boundary. We also observe that for d ≈ d_p, a residual charge of q_p = −q/4 in the protein is sufficient to cancel the repulsive self energy. Finally, for future reference we note that the magnitude of the self energy for a unit charge e is U_s = 1.6/d kT when d is in Angstrom and ɛ_p = 2 and ɛ_w = 80 are employed.

Spherical boundary

The above results provide useful insights about the dependence of the potential energy of an ion on the dielectric constants in a very simple case. The approximation of the protein surface by a plane, however, is rather drastic, and we need to check whether these results still stand when a more realistic geometry is employed. To this end, we consider a spherical boundary, for which the Poisson equation can be solved by expanding the potential in spherical coordinates (Jackson, 1975). The self potential acting on an ion at a distance d from a sphere of radius a is given by (see Fig. 1 B)

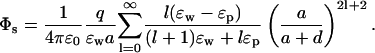(5)

This potential is too complicated for a direct interpretation because, unlike the plane boundary, the ɛ and space dependence are mixed through the sum. Nevertheless, these two parts can be separated by noticing that because 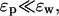the coefficient of ɛ_p in the denominator can be changed from l → l + 1 with negligible error. This is indicated in Fig. 2 A, where the self energy calculated with the approximate expression is seen to be indistinguishable from the exact one. With this approximation, the dielectric constants can be taken out of the summation in Eq. 5 and the remaining power series can be summed as described in the Appendix. Using Eq. 19 and expanding in ɛ_p/ɛ_w, the self energy of the ion outside the sphere can be expressed as

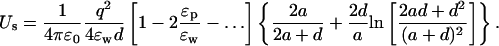(6)

This expression differs from the plane result in Eq. 2 by the extra terms in the curly brackets, which are entirely geometrical in nature. Otherwise the dependence of the self energy on the dielectric constants is the same as in the plane case. In an exact calculation, the coefficient of ɛ_p/ɛ_w in Eq. 6 comes out slightly smaller than 2, hence ɛ_p dependence of U_s in a sphere is actually suppressed relative to that of the plane (see Fig. 3 A).

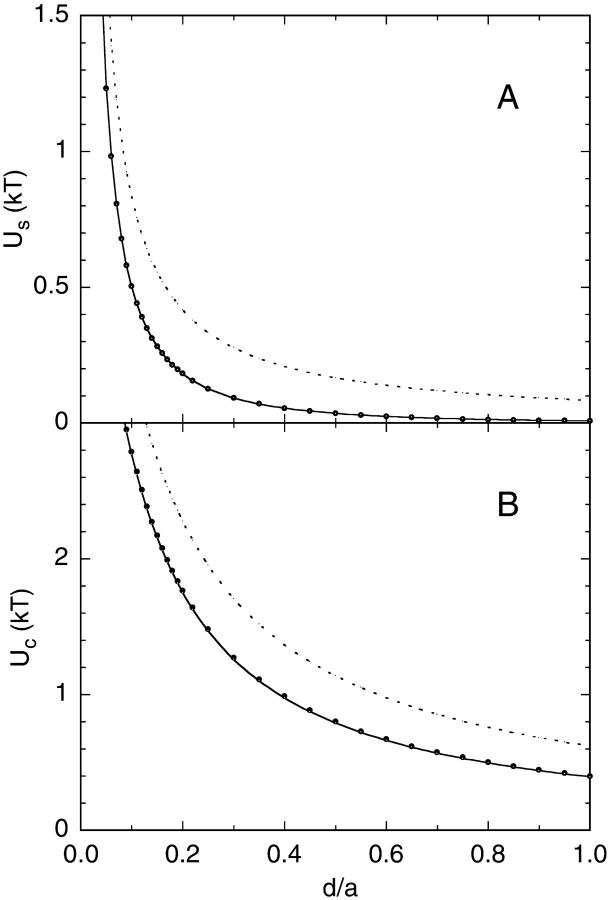
FIGURE 2.

(A) The self energy of an ion as a function of the distance d from a spherical protein. The ion has a unit charge e and the radius of the sphere is a = 20 Å. The filled circles show the exact results obtained using Eq. 5 and the solid curve shows the approximate result obtained by substituting l → l + 1 in the denominator of Eq. 5. The dotted line is the self energy of an ion at a distance d from a plane boundary. (B) The interaction energy of the same ion with a unit charge fixed at a distance d_p = 2 Å from the protein surface. The meaning of the curves are the same as in A. In both figures, dielectric constants of ɛ_p = 2 and ɛ_w = 80 are employed.

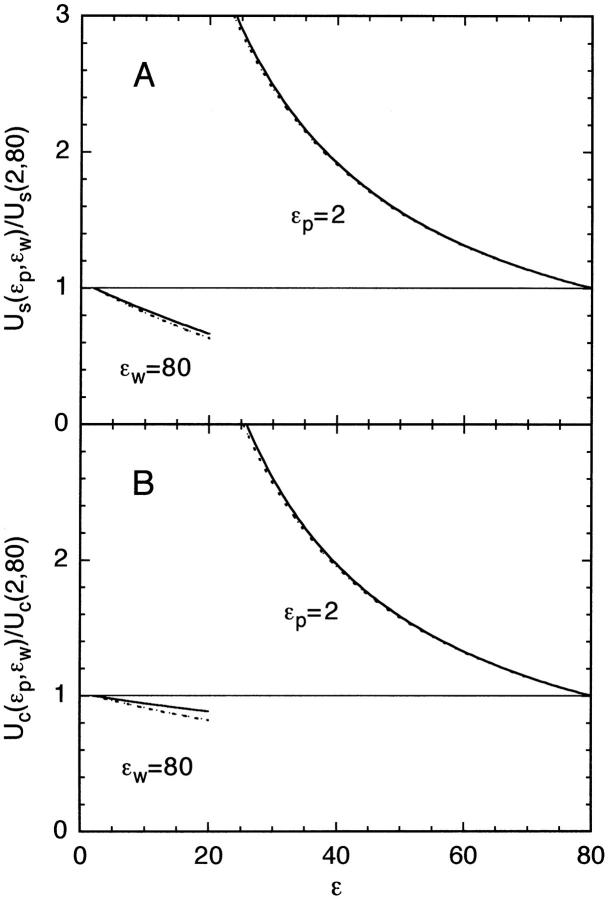
FIGURE 3.

Dependence of the self (A) and Coulomb (B) energies on the dielectric constants ɛ_p and ɛ_w. Both energies are normalized with the value at ɛ_p = 2 and ɛ_w = 80. The left side shows the effect of varying ɛ_p from 2 to 20 while ɛ_w is fixed at 80, and the right side shows the variation with ɛ_w while ɛ_p = 2. The radius of the sphere is a = 20 Å, the ion is at d = 4 Å from the protein surface, and the fixed charge is at d_p = 2 Å. The solid lines show the cases when the ion is outside the sphere, which nearly overlaps with the plane results (dotted lines).

In Fig. 2 A, we compare the distance dependence of the self energy of an ion for the plane and sphere boundaries. Notice that as the ion approaches the sphere (i.e., d → 0), the extra terms in the curly brackets in Eq. 6 go to 1, and the two results merge. These extra terms correspond to the curvature and finite size effects and lead to a reduction in the self energy of the ion outside a sphere relative to a plane. Recently, applications of continuum theories to ion channels have been criticized because they neglect the self energy of ions (Moy et al., 2000; Corry et al., 2000). It is clear from Fig. 2 A that this is not a problem for ions near a globular protein—unless the ions are touching the protein, their self energy would be negligible compared to their kinetic energy.

The potential on the test ion due to a charge q_p in the protein at a distance d_p from the surface can be similarly calculated (see Fig. 1 B)

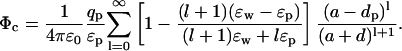(7)

As in Eq. 3, we have written the direct and the induced charge contributions to the potential separately to point out the near cancellation between the two terms. To make progress, we combine the two terms and change the coefficient of ɛ_p in the denominator from l → l + 1. As shown in Fig. 2 B, this approximation causes negligible error in the potential energy of the ion while enabling the summation of the series. Using Eq. 22 for the sum and expanding in ɛ_p/ɛ_w, the interaction energy of the ion with the protein charge becomes

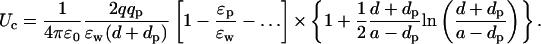(8)

Again, this expression differs from the plane result by the geometrical terms in the curly brackets, which go to 1 as the charges approach the boundary. A comparison of the Coulomb energy for the sphere and plane geometries is presented in Fig. 2 B. Note that the drop in the Coulomb energy of the ion with distance is not as severe as in the case of the self energy because the former has a monopole dependence (1/r) whereas the leading term in the latter has a dipole nature (1/r²).

The conclusions to be drawn from the above comparison of the potential energy of an ion near planar and spherical boundaries are that the differences arise mainly from the geometrical factors but, as far as dependence on the dielectric constants is concerned, the two boundaries lead to very similar results. This is highlighted in Fig. 3, which shows the variation of the self (A) and Coulomb (B) energies with ɛ_p and ɛ_w for the planar (dashed line) and spherical (solid line) boundaries. The small differences between the potential energies for the two boundaries arise from the fact that the exact expressions are employed in the calculations. Thus the insights gathered about the dependence of the potential energy of an ion on the dielectric constants in a plane boundary equally applies to that of a sphere. Similar results are obtained for more general spheroidal shapes such as ellipsoid (Hoyles et al., 1996). Generalizing these observations to ions outside globular proteins, we infer that an ion's potential energy has a dominant (1/ɛ_w) dependence on ɛ_w and a much weaker residual dependence on ɛ_p.

In the above example, ions are external to the protein, whereas in channels they are mostly surrounded by the protein. Although a water-filled sphere is not a very good approximation to ion channels, it will be interesting to see the effect of confinement on an ion's potential energy. Besides, this problem has applications to water-filled cavities in proteins, e.g., iron depositing protein ferritin. For this purpose, we switch the dielectric constants around and reflect the positions of the charges about the boundary in Fig. 1 B. The self potential of an ion inside a water-filled sphere of radius a and at a distance d from the protein surface is given by

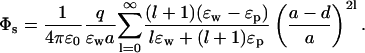(9)

Similarly, the potential acting on this ion due to a charge q_p in the protein at a distance d_p from the surface is given by

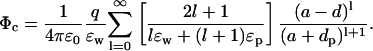(10)

These potentials look very similar to those in Eqs. 5 and 7. However, there is an important difference in the monopole (l = 0) terms that completely changes their dependence on the dielectric constants. This is most easily seen when the ion is at the center of the sphere (d = a), in which case all the terms vanish except the dominant monopole term. The self and Coulomb energies of the ion are then given by

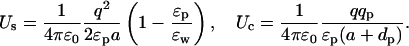(11)

Contrasting these energy expressions with those in Eqs. 6 and 8, we see a complete reversal of the roles played by ɛ_p and ɛ_w: the dominant dependence on the dielectric constants has changed from 1/ɛ_w when the ion is outside to 1/ɛ_p when the ion is inside. Thus despite the fact that in both cases ion is in water and its charge is screened by ɛ_w, the final dependence of its potential energy on the dielectric constants is determined by the boundary, and more importantly, whether the ion is external or internal to it. Dependence of the potential energy on ɛ_w in Eq. 11 is particularly interesting in this regard: contrary to the shielding arguments, U_s actually decreases with decreasing ɛ_w whereas U_c remains constant. For other positions of the ion, as long as d is not much smaller than a, the monopole term dominates the series and the above observations remain largely valid.

Another consequence of this reversal of the ɛ dependence is that the self energy of an ion confined in a sphere is more than one order of magnitude larger compared to that of an external ion (e.g., for the canonical values of ɛ_p and ɛ_w, U_s = 137/a kT when a is an Å, which is 85 times larger than the corresponding plane result). This enhancement in the self energy basically follows from the fact that the ratio ɛ_w/ɛ_p is large. But perhaps a physically more enlightening reason is that the total charge induced on the sphere by an external ion vanishes, whereas it is given by q(1/ɛ_p − 1/ɛ_w) for an internal ion regardless of its position. Thus, although the self energy may be neglected in continuum theories for external ions, this is not so easy to justify for internal ones—even for a relatively large cavity with radius 20 Å, 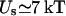for a central ion, which is five times its kinetic energy.

Cylindrical boundary

The simplest analytically solvable boundary mimicking an ion channel is that of an infinite cylinder. Because it confines an ion, we expect some similarities with the sphere problem discussed above. The self potential acting on an ion on the central axis of a cylinder of radius a (see Fig. 1 C) is given by (Smythe, 1968)

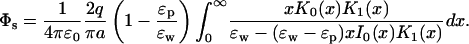(12)

Here I_n(x) and K_n(x) are the modified Bessel functions. Just as in the case of a central ion in a sphere, the space and ɛ dependence are decoupled in Eq. 12. Unfortunately, the integral in Eq. 12 diverges for ɛ_p = 0, and an expansion in ɛ_p/ɛ_w that would identify the leading ɛ dependence of the potential is not possible. The Coulomb potential acting on this ion due to a charge q_p in the protein at a distance d_p from the surface (see Fig. 1 C) is given by

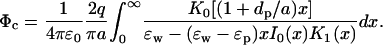(13)

Apart from a residual dependence on the ratio d_p/a, this integral is similar to the one in Eq. 12 and suffers from the same divergence problem for ɛ_p = 0. Therefore, we evaluate the integrals in Eqs. 12 and 13 numerically, and plot the ɛ_p and ɛ_w dependence of the resulting self and Coulomb energies of the ion in Fig. 4, A and B (dashed lines). For comparison, the corresponding potential energies of a central ion in a sphere (Eq. 11) are also plotted (solid lines). Because of its symmetry, the effect of confinement on the potential energy of an ion is maximal in a sphere. In a cylinder, the induced charges are spread further away from the ion, and the effect of confinement is somewhat reduced. For example, for the canonical values of ɛ_p and ɛ_w, U_s = 47/a kT, which is three times smaller than the corresponding sphere result. This explains the movement of the cylinder results in Fig. 4 from those of the sphere toward the plane results (Fig. 3). Nevertheless, the potential energies of an internal ion in Fig. 4 display a broadly similar dependence on the dielectric constants even for very diverse boundaries as sphere and infinite cylinder. It may appear that the ɛ_w dependence of the results exhibit a larger deviation compared to the ɛ_p dependence. But this is because the same scale is used in the plot. Otherwise the relative deviations in the two cases are quite similar. Accordingly, we expect the potential energy of an ion confined by a protein boundary to exhibit a strong (1/ɛ_p) dependence on ɛ_p and a weaker residual dependence on ɛ_w.

FIGURE 4.

Similar to Fig. 3 but for an ion at the center of a water-filled sphere (solid line) or on the central axis of an infinite cylinder (dashed line). The results are independent of the geometrical parameters for U_s and U_c in the sphere and for U_s in the cylinder. For U_c in the cylinder, d_p/a = 0.1 is employed. For larger ratios of d_p/a (corresponding to smaller cylinder radii), the dashed lines in B move slightly toward the solid lines. Note that U_c in the sphere overlaps with the unit line.

Toroidal boundary

In an infinite cylinder, ions are absolutely confined by the boundary, which is not true in the case of ion channels. Rather they present mixed boundaries that are partly open (along the channel axis) and partly closed. Thus for a finite length cylinder, we expect the infinite cylinder results in Fig. 4 to move further toward the plane results. The crucial question is by how much. This requires numerical solution of the Poisson equation and will be discussed in the next section. Here we address this issue using a torus-shaped boundary, which can still be solved analytically (Kuyucak et al., 1998). In fact, as comparisons of potential energy profiles demonstrate, the toroidal boundary gives a reasonable approximation to vestibular channels such as nicotinic acetylcholine receptor (Kuyucak et al., 1998). Hence the results presented for the torus will have general relevance for vestibular channels.

The radius of the toroidal ring is taken as 40 Å and the radius of the channel at the neck (z = 0) is 4 Å. The Coulomb interaction is calculated by placing four charges with magnitude e/4 at 90° intervals around a ring of radius 6 Å on the z = 0 plane. This choice stems from the fact that charges that control the selectivity of vestibular channels are usually located at the narrow neck region.

The analytical solutions of the Poisson equation in toroidal coordinates are, unfortunately, very complicated and it is not possible to extract the ɛ dependence of the potential energy of an ion from them. Therefore, we directly plot the dependence of the self and Coulomb energies on the dielectric constants ɛ_p and ɛ_w in Fig. 5. For reference we note that both energies have bell-shaped profiles that peak at the center of the torus with U_s = 3.7 kT and U_c = 6.8 kT at the center, dropping to U_s = 0.2 kT and U_c = 0.5 kT at the mouth (z = 40 Å), when the canonical values of ɛ are employed. Their variation with ɛ_p and ɛ_w at these locations are shown in Fig. 5 with solid lines—the lower of the two curves depicting the z = 0 and the upper one z = 40 Å results. The infinite cylinder (dashed line) and plane (dotted line) results are included in the figure for reference purposes. As one would expect, the ɛ dependence in both energies move from the cylinder toward the plane results as the ion is moved from the center to the mouth of the torus. The ɛ_p dependence remains roughly in the middle of those of the cylinder and plane. For example, doubling ɛ_p from 2 to 4 reduces U_s by 15% in the torus (at z = 0), whereas the corresponding drops in the plane and cylinder are 5% and 39%, respectively. Similarly, U_c drops by 12% when ɛ_p is doubled, to be compared with 2.5% drop in the plane and 36% in the cylinder. The ɛ_w dependence of the energies in Fig. 5 are seen to remain much closer to those of the plane. To give an example, halving ɛ_w from 80 to 40 increases U_s by 70% and U_c by 75%; the corresponding increases are 90% and 95% in the plane, and 22% and 27% in the cylinder. Thus the effects of confinement are greatly reduced in a semiopen toroidal boundary. Consequently the ɛ dependence of the potential energies in a vestibular channel are closer to those of an open boundary rather than an infinite cylinder. This means that the potential energy of an ion will be very sensitive to the chosen value of ɛ_w, as noted earlier (Kuyucak et al., 1998, Fig. 8), but not so much to ɛ_p.

FIGURE 5.

Similar to Fig. 3 but for an ion at the center (z = 0) and mouth (z = 40 Å) of a torus-shaped channel (solid lines). On each side, the lower solid line depicts the z = 0 result. The dotted and dashed lines show the results for the plane and cylinder boundaries from Figs. 3 and 4.

FIGURE 8.

The Coulomb energy of a test ion along the z axis due to a fixed ion on the z axis at −12.5 Å. The self energy of the test ion is not included in U_c. The dashed line is obtained using the canonical values of ɛ_p = 2 and ɛ_w = 80. The solid lines show how U_c changes from this reference result when ɛ_p is increased to 5 while keeping ɛ_w = 80 (lower curve), and when ɛ_w is reduced to 40 while keeping ɛ_p = 2 (upper curve). The dotted line at the bottom shows U_c in bulk water.

A common feature of all the results presented in Figs. 3, 4, and 5 is that the self and Coulomb energies have very similar functional dependences on ɛ_p and ɛ_w. This implies that variations from the canonical values of ɛ_w and ɛ_p will simply scale the total potential energy profile of the ion up or down without changing its overall shape. That is, an energy well or a barrier will remain so even when very different ɛ values are employed, only their magnitude will change. In the case of ɛ_w dependence in a torus, this symmetry between U_s and U_c is maintained because we have not distinguished between the ɛ values of bulk and channel water. Use of a uniform ɛ_w value is, of course, necessary to obtain analytical solutions in the toroidal coordinates. To address such issues as well as to discuss the effect of more general boundaries on an ion's potential energy, one has to resort to numerical solutions of the Poisson equation.

NUMERICAL RESULTS

Numerical solutions of the Poisson equation can be obtained most efficiently using the boundary element method (Levitt, 1978). Accuracy of this method, without compromising its efficiency, has been greatly enhanced by incorporating corrections due to the curvature of the boundary in the solutions (Hoyles et al., 1998). We have slightly modified this code to allow different dielectric constants for channel and bulk waters. This is achieved by placing imaginary planes at the mouths of a channel that separates the pore region from the bulk water. Outside the pore region, ɛ = 80 is fixed, whereas inside ɛ_w is treated as a variable. When ɛ_w < 80, charges are induced on these imaginary planes, which are calculated according to the boundary element algorithm. Born energy difference due to the change in the dielectric constant is taken into account by adding

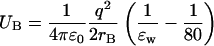(14)

to the potential energy of the ion in the pore region. Here r_B is the Born radius of the test ion, which we take as 2 Å. With this method, potential energy can be calculated up to a distance of r_B of the ion from the planes. The remaining part is obtained by interpolating between the potential energy values on either side of the planes. Besides the potential energy of a single ion, here we also study how the ion-ion interactions are influenced by variations in the dielectric constants. This is an important consideration for multi-ion channels such as potassium and calcium channels.

Single ion potential energy

For the numerical calculations, we use a cylindrical channel with length 35 Å and radius 4 Å (see the inset in Fig. 6). These choices are motivated by typical lipid thickness and the effective radius of a hydrated ion. The mouth region of the channel is rounded with a radius of curvature of 5 Å to avoid difficulties with sharp corners in solving the Poisson equation. Because the position of the charges in the protein makes a difference in a finite-length channel, the Coulomb energy is calculated using two different sets of charges. The first is just like in the torus study above: four charges with magnitude e/4 are placed around a ring of radius 6 Å on the z = 0 plane. In the second case, two of these rings, each with a total charge of e, are placed near the entrance of the channel at z = ±12.5 Å. This charge configuration mimics the mouth charges seen in many channels with relatively narrow pore openings. When different ɛ values are used for channel and bulk water, the imaginary planes are placed at z = ±16 Å. First the Poisson equation is solved without the protein charges, which gives the self energy of the ion. This calculation is then repeated with the protein charges to obtain the total potential energy of the ion. The Coulomb energy is determined by subtracting the self energy from the total.

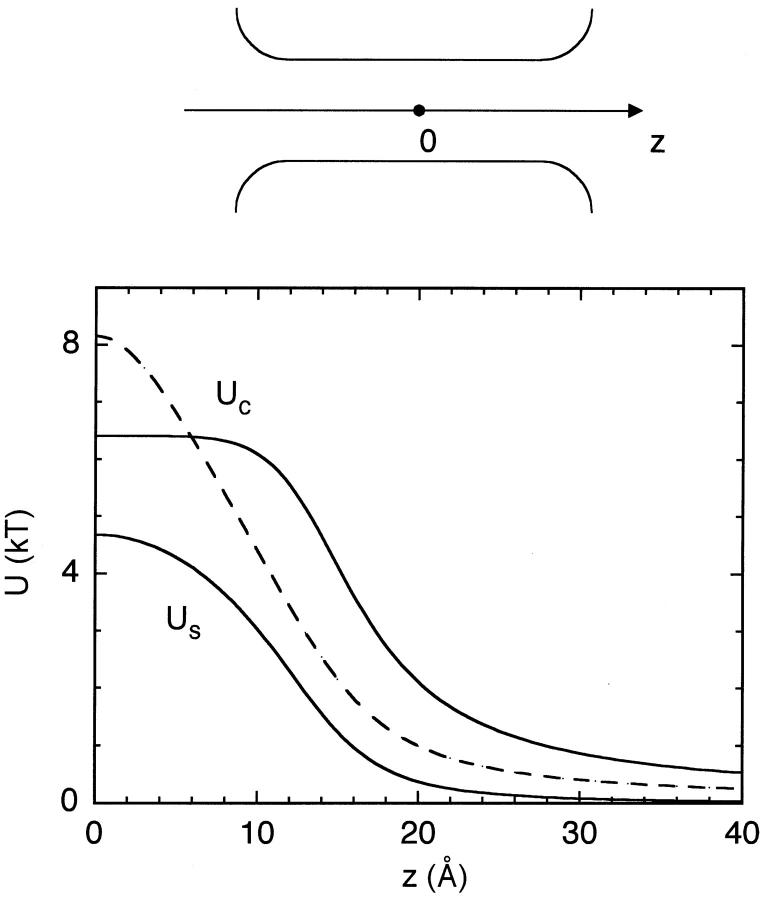
FIGURE 6.

Self and Coulomb energy profiles of an ion with charge e along the central axis of a cylindrical channel. A cross section of the channel along its central axis is shown in the inset. The two Coulomb energy profiles correspond to the charge configurations at the mouth (solid line) and at the center of the channel (dashed line).

In Fig. 6, we show the self and Coulomb components of the potential energy of the test ion along the central axis of the channel. The canonical values of the dielectric constants are employed in these calculations. Note that because we use positive charges in the protein and for the test ion for ease of comparison, Coulomb interactions are repulsive. In reality, protein charges would be opposite to that of the ion's, leading to an attractive U_c. The main purpose of this figure is to point out the effect of the location of the protein charges on the potential energy of the ion. If the height of U_c is adjusted so as to cancel U_s at the center, mouth charges would lead to a 2 kT deep well at the entrance whereas central charges would result in a barrier of half a kT there. This suggests that for single-ion channels, charges placed at the mouth could provide a more efficient conduction pathway for ions compared to centrally located charges. We also note that the focusing effect of the dielectric boundary results in an almost constant U_c inside the pore for the mouth charges.

The ɛ dependence of the potential energy components shown in Fig. 6 is investigated in Fig. 7. As in the torus study, the finite cylinder results in the figures (solid lines) are bracketed between the infinite cylinder (dashed line) and plane (dotted line) results. For simplicity, we consider only their variations at z = 0, where the energy profiles peak. As the test ion is moved away from the center, the results move slowly toward those of the plane. This behavior is similar to that observed in a torus (Fig. 5) but it is much less accentuated in a cylinder. We first consider the ɛ_p dependence of the potential energy. The results for mouth and central charges almost overlap in Fig. 7 B, indicating that the ɛ_p dependence of U_c is not affected much by the location of the protein charges. Dependence of U_s on ɛ_p in A is also seen to be very similar to those of U_c. In fact, the only visible difference of the cylinder results from those of the torus (Fig. 5) is that the rate of drop in the potential energy with ɛ_p is slightly faster: both U_s and U_c are reduced by 19% when ɛ_p is doubled from 2 to 4. This is about half the reduction found for the infinite cylinder, which shows how the loss of absolute confinement of the ion has further eroded impact of ɛ_p on its potential energy.

FIGURE 7.

Similar to Fig. 3 but for an ion at the center (z = 0) of a finite cylindrical channel. In B, the lower solid line on each side shows U_c due to the protein charges at the mouth of the channel, whereas the upper one is due to the centrally placed charges. The dotted and dashed lines show the results for the plane and infinite cylinder boundaries from Figs. 3 and 4 as before.

The above observations indicate that increasing ɛ_p will simply lead to a scaling down of the potential energy of the ion. This scaling factor is ∼0.81 for doubling ɛ_p from 2 to 4, or 0.74 for going from 2 to 5. To see whether such simple estimates determined from a cylindrical channel have any relevance for more realistic channel models, we compare them with those obtained from the KcsA structure (Doyle et al., 1998; Morais-Cabral et al., 2001). In a study of potential energy profiles in the KcsA channel, Chung et al. (2002, Fig. 12) have found that increasing ɛ_p from 2 to 5 led to a scaling down of the potential energy of an ion near the interior binding site by a factor of 0.72. Considering that the KcsA channel has a rather irregular shape, the cylinder estimate of 0.74 appears to be quite good. The channel current, on the other hand, is found to decrease slightly when ɛ_p is increased, which is opposite to that one would expect from a uniform scaling down of the potential energy. This anomaly is explained by the fact that the scaling factor found in this study is not uniform but gets smaller as the test ion approaches the selectivity filter, which has two resident K⁺ ions. The nonuniformity results in a slightly increased residual barrier (by ∼0.6 kT) near the cavity region, leading to a small reduction (∼20%) in the channel current. Because Coulomb repulsion among ions may play a role in this behavior, we will return to this issue after discussing the ɛ dependence of ion-ion interactions in the next section.

The most important observation about the ɛ_w dependence of the potential energies in Fig. 7 is that the symmetry between U_s and U_c is broken, that is, they exhibit rather different dependence on ɛ_w. This clearly arises from using different ɛ values for bulk and channel waters because when ɛ_w is varied simultaneously (not shown in the figure to avoid cluttering), very similar results are obtained for U_s and U_c. As one would expect, the Born energy leads to a steeper increase in U_s, which is very close to the plane result. In contrast, the ɛ_w dependence of U_c is much less steep and also depends on the position of the protein charges. For example, for the mouth charges U_c almost overlaps with the infinite cylinder result whereas for the central charges it remains between those of cylinder and plane. This suppression in the ɛ_w dependence of U_c (relative to the uniform ɛ_w case) is due to the negative charges induced by the protein charges on the imaginary planes. Because the mouth charges are very close to the planes, the contribution of the induced charges on these planes to the total potential are much larger compared to the central charges, resulting in a smaller U_c.

The asymmetric behavior of U_s and U_c, and the dependence of U_c on the position of protein charges, make it more difficult to predict how the total potential energy of an ion would change with ɛ_w. Nevertheless, it is possible to make inferences about the impact of ɛ_w variations on barriers and wells in the energy profile of an ion. A barrier is dominated by U_s, and therefore should steeply increase with decreasing ɛ_w. A binding site near the entrance of a channel, on the other hand, gets relatively little help from a slowly increasing U_c, and as a result the energy well will get shallower with decreasing ɛ_w (for very deep wells, this may occur at smaller ɛ_w). We thus expect the energy profile of an ion to shift upward for ɛ_w < 80, the amount of shift being more accentuated at the barriers compared to the wells. Such an ɛ_w dependence has indeed been observed in model studies of the KcsA channel (Chung et al., 1999, Fig. 6)—the residual barrier faced by a permeating ion near the cavity region is found to rise steeply with decreasing ɛ_w, becoming roughly doubled at ɛ_w ∼ 40 consistent with the results in Fig. 7. For ɛ_w ≤ 40, the channel ceases to conduct, thus the influence of variations in ɛ_w on ion permeation is far greater compared to those in ɛ_p. Similar observations can be made for centrally located binding sites. However, such binding sites are usually associated with vestibular channels, and therefore not considered further here.

Ion-ion interactions

Many biological ion channels contain multiple ions, and it has been conjectured that the Coulomb repulsion plays an important role in facilitating the permeation process. For completeness, we investigate how variations in ɛ values influence the Coulomb interaction between a pair of ions in a finite cylindrical channel as considered above. Both ions have a unit charge, and one of them is fixed on the z axis near the mouth of the channel (z = −12.5 Å) whereas the other is moved along the z axis. This choice is motivated by the observation that binding sites are usually located near the entrance in cylindrical channels. Because the self energy of the mobile ion is already discussed above, here we consider only the Coulomb part due to the fixed ion, that is, we calculate the potential due to the fixed ion along the z axis and multiply this with e. This quantity excludes the self energy of the mobile ion from the total ion-ion interaction.

The Coulomb energy profile of the test ion is shown in Fig. 8. Here the dashed curve is obtained using ɛ_p = 2 and ɛ_w = 80. The upper and lower solid lines indicate how this result is modified when ɛ_w = 40 and ɛ_p = 5 are employed, respectively. For reference, the Coulomb interaction in bulk water at the same distance is shown with dotted lines at the bottom. It is seen that the presence of the channel leads to a remarkable enhancement in the Coulomb repulsion compared to the bulk values. Further, whereas U_c drops with distance, the rate is much slower than 1/r within the channel due to the focusing effect of the dielectric boundary. Finally, the energy scale in the figure is similar to that in Fig. 6, indicating that the Coulomb repulsion makes a matching contribution to the ion's potential energy as the other components. These features help to explain why the ion-ion repulsion plays a significant role in the permeation process in multi-ion channels.

The ɛ dependence of U_c at z = 0 gives a virtually identical result as the mouth charges in Fig. 7 B, and therefore is not duplicated. However, there is substantial difference between ion-ion repulsion and the other components when it comes to position dependence—the latter results, as noted above, exhibit negligible variation with the position of the test ion in the channel. Comparison of the solid lines in Fig. 8 with the dashed line, on the other hand, indicates a clear position dependence in ɛ_p and ɛ_w variations. This nonuniform scaling of U_c with ɛ is most visible when the ions are a few Å apart, and becomes negligible when the test ion is near the center.

Returning back to the comparison with the KcsA results, we observe that the nonuniform scaling of U_c with ɛ_p in Fig. 8 may have contributed to the small increase in the residual barrier when ɛ_p is increased from 2 to 5 (Chung et al., 2002). This, however, is not sufficient to explain the whole effect, and geometrical factors, such as presence of a cavity, must also have contributed to the final result. With regard to the ɛ_w dependence and the doubling of the residual barrier when ɛ_w is halved from 80 to 40, the contribution from the ion-ion repulsion (∼1 kT) remains rather marginal compared to that from the self energy (∼7 kT). Thus Coulomb interactions due to other ions have a reduced sensitivity to ɛ_w variations similar to those due to fixed charges in protein (Fig. 7 B).

CONCLUSIONS

Potential of a charge q immersed in a bulk dielectric medium with constant ɛ is screened by q/ɛ. This dielectric screening is often employed to get a quick estimate of how the potential of a charge would change with ɛ in more complex situations. The primary aim of this study has been to point out that such estimates are only reliable away from boundaries. Presence of a boundary and its curvature could have a drastic effect on the potential of an ion, and completely change its ɛ dependence. This is illustrated with an ion outside and inside a spherical boundary, where the dominant ɛ dependence of its potential energy changes from 1/ɛ_w in the former case to 1/ɛ_p in the latter.

Because ion channels have mixed boundaries and their shapes could vary from vestibules to cylinders, it is difficult to give general rules about the influence of ɛ variations on the potential energy of ions. Nevertheless we find that when ɛ for the channel and bulk water are distinguished and the Born energy is included, the self energy of an ion exhibits a dominant 1/ɛ_w behavior remarkably similar to that seen in open boundaries such as plane and sphere. Because the Coulomb component of the potential energy displays a much milder dependence on ɛ_w, we expect the residual barriers in the energy profile of an ion to rise rapidly with decreasing ɛ_w, leading to an exponential suppression of the current. Thus as a phenomenological parameter, ɛ_w exercises a large influence on channel conductance, and therefore, it is desirable to have a better understanding of the effective ɛ_w values currently used in channel models from microscopic studies. Moderating the value of ɛ_w using organic solvents and measuring the changes in the ensuing conductance levels (as suggested by a reviewer) could provide a more direct test for the predictions made in this study.

The ɛ_p dependence of the potential energy of an ion in a channel remains in between those of open and closed boundaries. Also there is conformity among the behavior of its various components. Thus an increase in ɛ_p is expected to lead to a uniform scaling down of the energy profile of an ion with a concomitant increase in its permeation rate. Because this is a comparatively small effect, other geometrical factors can easily modify this behavior as indeed observed in the KcsA channel. Although variations in ɛ_p cause relatively small changes in the energy profile of an ion, because of the exponential dependence of channel current on residual barriers, its value still has to be chosen carefully when the aim is quantitative comparisons with physiological data.

APPENDIX

The approximation to the self potential in Eq. 5 involves the power series

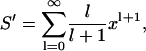(15)

where x = a²/(a + d)². This is related to the standard series

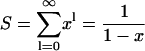(16)

by the expression

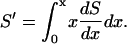(17)

Using Eq. 16 in Eq. 17 and evaluating the algebra gives

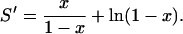(18)

Substituting the value of x, we obtain

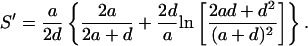(19)

The approximate form of the Coulomb potential in Eq. 7 involves the power series

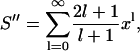(20)

where x = (a − d_p)/(a + d). Writing 2l + 1 = (l + 1) + l, this series can be expressed in terms of the series S and S′ introduced above as S″ = S + S′/x. Using the results from Eqs. 16 and 18, we get

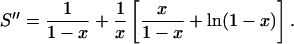(21)

Simplifying and substituting back x yields

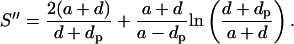(22)