Profiling Charge Complementarity and Selectivity for Binding at the Protein Surface

Abstract

A novel analysis and representation of the protein surface in terms of electrostatic binding complementarity and selectivity is presented. The charge optimization methodology is applied in a probe-based approach that simulates the binding process to the target protein. The molecular surface is color coded according to calculated optimal charge or according to charge selectivity, i.e., the binding cost of deviating from the optimal charge. The optimal charge profile depends on both the protein shape and charge distribution whereas the charge selectivity profile depends only on protein shape. High selectivity is concentrated in well-shaped concave pockets, whereas solvent-exposed convex regions are not charge selective. This suggests the synergy of charge and shape selectivity hot spots toward molecular selection and recognition, as well as the asymmetry of charge selectivity at the binding interface of biomolecular systems. The charge complementarity and selectivity profiles map relevant electrostatic properties in a readily interpretable way and encode information that is quite different from that visualized in the standard electrostatic potential map of unbound proteins.

INTRODUCTION

Charge complementarity has been a familiar concept that we have learned since our elementary science days. Plus and minus charges attract. However, in the context of the energetics of receptor-ligand binding in aqueous environment, the picture is not as simple or intuitive. In general, desolvation produces a free energy change opposite in sign to the Coulomb electrostatic interaction energy. Hence, the net change in the electrostatic component of binding free energy is the result of a delicate balance between the receptor-ligand electrostatic interaction and desolvation effects. The result is that for a defined receptor-ligand binding mode, there exists a unique optimal charge distribution of the ligand that balances the competing electrostatic contributions to binding affinity (Chong et al., 1998). This means for example that a binding site of highly negative electrostatic potential does not necessarily bind a highly positively charged ligand better than a less positively charged one. We have recently developed a rapid method for calculating the charge distribution for optimal electrostatic complementarity in a complex (Sulea and Purisima, 2001). This method allows us to obtain the optimal charge distribution as well as the stringency of charge preference (charge selectivity) near the optimum. We have previously tested the charge optimization of binding electrostatics on three systems: Binding of monovalent cations to the 18-crown-6 ether, binding of calcium ions to calcium-binding sites of parvalbumin, and binding of ligand fragments in the primed subsites of cathepsin B (Sulea and Purisima, 2001). The optimal ligand charges that we obtained matched closely the theoretical ligand charges. Using their implementation of the charge optimization method, Tidor and co-workers also analyzed recently two systems: binding of a transition-state analog to chorismate mutase (Kangas and Tidor, 2001) and barstar binding to barnase (Lee and Tidor, 2001a,b). Again, the optimal charge distribution of the ligand was found to be similar to the theoretical one, and a few suboptimal regions were identified. These applications of the charge optimization methodology illustrate how the notion of charge complementarity means not only pairing of oppositely charged groups but also having the correct charge magnitude.

The depiction of molecular surfaces that are color coded by electrostatic potential (ESP), e.g., produced by the program GRASP (Nicholls et al., 1991) has been extensively used to provide a global understanding of the electrostatic profile of a molecule. Of tremendous popularity, GRASP-generated solvent-screened ESP maps are routinely used as a qualitative tool to highlight the electrostatic complementarity as a necessary ingredient for good binding interactions. However, these electrostatic potentials characterize the unbound state of the molecule under investigation and hence, their interpretation in terms of binding complementarity seems somewhat inappropriate, even if used at a very qualitative level. Energetically, the fundamental limitation of these solvent-screened electrostatic potentials of the unbound molecule is that they ignore the important desolvation effects incurred upon binding. Electrostatically, not taking into account desolvation effects eliminates the existence of the optimal complementary charge.

In this article, we propose a novel technique for analysis of the protein surface in terms of electrostatic binding complementarity and selectivity. The charge optimization methodology is applied in a probe-based approach that simulates the binding process to the target protein. A singly charged, low-dielectric, virtual probe-ligand is positioned at various locations in molecular contact around the protein. The shape of the probe-ligand is constructed to be locally complementary to the shape of the protein. At each position of the probe-ligand around the protein we calculate the probe charge that optimizes the electrostatic free energy of binding. We also calculate the binding cost of deviating from the optimal charge value (charge selectivity). The calculated optimal charge and charge selectivity values are then projected back onto the molecular surface of the target protein for a more informative display. Illustrative applications of the method are presented for bovine trypsin and for the third PDZ domain of the brain synaptic protein PSD-95. The resulting charge complementarity and selectivity profiles of these proteins are first analyzed and then interpreted in terms of implications toward the understanding of molecular selection and recognition in biomolecular systems. Comparative analyses of the profiles relative to experimental data available in the literature, to charge optimization calculations performed on actual ligands, and to the commonly used solvent-screened ESP maps of the unbound proteins will be discussed, and an assessment of the robustness of the profiles to calculation parameters is provided in Appendix 1.

MATERIALS AND METHODS

Structure preparation

Preparation of protein structures for electrostatic calculations was done in SYBYL 6.6 (Tripos, Inc., St. Louis, MO). AMBER molecular mechanics force field (Cornell et al., 1995) partial atomic charges were assigned to the protein and water molecules. The ionization state at physiological pH was adopted, i.e., ionized forms for side chains of Arg, Lys, Asp, and Glu residues, and neutral forms for the His side chains.

The 1.5 Å-resolution crystal structure of the bovine trypsin complexed with benzamidine (Katz et al., 1995) was retrieved from the Protein Data Bank (PDB entry 4bty). A single calcium ion bound to the trypsin molecule and located ∼25 Å from the amidinium group of benzamidine was retained. The benzamidine ligand and most of the crystallographic water oxygen atoms were removed. However, 20 solvent molecules were treated explicitly. Of these, one mediates the trypsin-benzamidine interaction, 17 are buried within trypsin, and two complete the coordination sphere of the bound Ca²⁺ ion. Hydrogen atoms were added to the protein and to the retained water molecules. To satisfy a correct hydrogen-bonding pattern, the catalytic His was protonated at the Nδ nitrogen atom whereas the other two were protonated at the Nɛ nitrogen atom. N- and C-termini of the protein chain were treated in the ionized forms. The position of the hydrogen atoms of the protein and water molecules were refined through an energy minimization with all nonhydrogen atoms fixed at their crystallographic position. This was done with the AMBER force field (Cornell et al., 1995), a distance-dependent dielectric constant (4r_ij) and an 8 Å nonbonded cutoff, up to a root-mean-square gradient of 0.01 kcal/(mol·Å).

The 1.8 Å-resolution crystal structure of the third PDZ domain (PDZ-3) from the brain synaptic protein PSD-95 in complex with the CRIPT peptide (Doyle et al., 1996) was retrieved from the Protein Data Bank (PDB entry 1be9). The peptidic ligand and all but three buried crystallographic water molecules were removed. Hydrogen atoms were added to the protein and to the retained water molecules. His-17 and His-72 were protonated at the Nɛ and Nδ atoms, respectively. Because there was no electron density for the side-chain atoms of residues Phe-1 and Asp-32 of the domain, these were first built in a sterically accessible conformation. The N- and C-termini of the protein chain were capped with the neutral acetyl and methylamino blocking groups, respectively. The position of the hydrogen atoms of the protein and water molecules, as well as of all atoms of the constructed Phe-1 and Asp-32 side chains and blocking groups were refined through an energy minimization with all the other atoms fixed at their crystallographic position. This was done in the same way as for the trypsin molecule (see above).

Theoretical charge distributions of actual ligands were used for a comparative purpose only. The theoretical charge distribution of benzamidine was calculated by a two-stage restrained fitting procedure (Bayly et al., 1993; Cornell et al., 1993) to the single-point Hartree-Fock 6-31G^* electrostatic potential calculated in GAMESS (Schmidt et al., 1993) on the AM1 (Dewar et al., 1985; Stewart, 1990) optimized geometry obtained in MOPAC 6.0 (QCPE, Indiana University, Bloomington, IN). The theoretical charge distribution of the free-carboxylate C-terminal valine residue of the CRIPT peptide was taken from the AMBER parameter set of atomic partial charges (Cornell et al., 1995), and it is also a RESP ab initio charge distribution.

Probe-ligand

The construction and positioning of the probe-ligand around the protein molecule is depicted schematically in Fig. 1 a, and includes several steps. First, the molecular surface (MS) of the protein was constructed with the program GRASP (Nicholls et al., 1991) using a solvent radius of 1.4 Å, and adapted AMBER van der Waals radii, R^* (Cornell et al., 1995) for the protein atoms. The polar hydrogen radius was set to 1.0 Å, the carboxylate oxygen radius was reduced to 1.5 Å, and the radii of all polar nonhydrogen atom types were scaled by a factor of 0.89 (thus effectively reducing R^* values to σ for these atom types). Scaling down the radii of polar heavy atoms will position the probe-ligand closer to the polar atoms of the protein in an attempt to simulate hydrogen-bonding contacts. From each vertex of the triangulated molecular surface, probe positions were defined by projecting the normal out to a distance of 1.4 Å, thus effectively defining points on the solvent accessible surface (SAS) of the protein. The construction of SAS locations as outward extensions from the MS will facilitate mapping the calculated properties back onto the MS for a more informative display. At each probe position in turn, a virtual probe-ligand was constructed as the union of all 1.4 Å-radius spheres centered on probe positions within a certain distance, R-cutoff, around the current probe position declared as the “center” of the probe-ligand. This procedure generates a probe-ligand having a shape locally complementary to the protein. The low-dielectric probe-ligand carries a single charge located at its center. Each protein-bound virtual probe-ligand was then individually subjected to a charge optimization calculation at its center (see below).

FIGURE 1.

Molecular surface profiles of charge complementarity and selectivity are obtained by charge optimization of ligand-binding electrostatics in a probe-based approach. (a) Schematic diagram illustrating the positioning and construction of probe-ligands with local shape complementarity around the protein (see also Materials and Methods section). (b) Examples of shape-adapting probe-ligands positioned around trypsin and used in charge optimization calculations.

A virtual probe-ligand generated in this way simulates binding of a single charge embedded in a low-dielectric cavity of optimal local shape complementarity around the target protein. The shape-adaptable probe-ligands model more realistically the molecular geometry of an actual complementary functional group, as opposed to a simple spherical probe. We note that these probe-ligands model the outer atomic layer of an actual ligand contacting the protein. The molecular “thickness” of a probe-ligand is 2.8 Å, but effectively thicker probe-ligands can be formed in relatively narrow pockets of the protein. The density of probe positions on SAS is variable, lower around convex MS areas and higher around concave MS regions. However, even around convex protein regions, the density of defined SAS locations is high enough to create a smooth molecular surface of the probe-ligand. Note the even density of the corresponding MS patches where the calculated properties are profiled.

A total of 12,506 probe positions were generated around trypsin, and 13,018 around the PDZ domain. Results in this article are presented for an R-cutoff of 4.0 Å, but profiles around both proteins were also generated with sets of probe-ligands constructed with R-cutoff of 2.0 Å, 3.0 Å, and 5.0 Å at the same locations (Supplementary material). Examples of constructed ligands around trypsin are shown in Fig. 1 b.

Electrostatic binding calculations

The electrostatic component of the protein-ligand binding free energy, 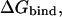was calculated as (Sulea and Purisima, 2001):

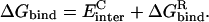(1)

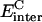is the intermolecular Coulomb interaction energy in the bound state. 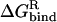is the change in the reaction field energy between the bound and free states and represents the electrostatic contribution of the solvation free energy to the intermolecular binding process. The protein-ligand complex represents the bound state, whereas the free, unbound state is obtained by rigid infinite separation of the ligand from the complex. The Coulomb term was calculated with infinite cutoff and a dielectric constant of 2. The electrostatic contribution to solvation was calculated within the continuum dielectric model with a solute interior dielectric constant of 2 and a solvent dielectric constant of 78.5. Reaction field energies were computed by solving the Poisson equation with the boundary element method (BEM) implemented in the BRI BEM program (Purisima, 1998; Purisima and Nilar, 1995) and using the SIMS molecular surface program (Vorobjev and Hermans, 1997). Protein atoms were assigned AMBER van der Waals radii, R^*, and partial charges (Cornell et al., 1995). AMBER radii were used with two modifications: The polar hydrogen radii were set to 1.0 Å and the carboxylate oxygen radius was reduced to 1.5 Å. These radii performed well in previous charge optimization calculations (Sulea and Purisima, 2001).

Charge optimization of binding electrostatics

It has been shown previously that the dependence of the protein-ligand electrostatic binding free energy, 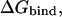has a quadratic form on the partial charges at the atomic centers of the ligand (Lee and Tidor, 2001a,b; Sulea and Purisima, 2001). The first step in charge optimization calculations consists in determining the coefficients in this quadratic dependence:

(2)

where q is the vector of the n variable partial atomic charges, q_i, at the atomic centers i of the ligand. The desolvation matrix, A, the interaction vector, b, and the scalar term, c, are independent of q, but depend on the molecular geometry, the charges on the protein, and the fixed charges on the ligand. The matrix element A_ij is the difference in the reaction field potential at the position of q_i in the bound and unbound states when q_j is set to a unit charge and all other charges are set to zero. Because the ligand desolvation matrix, A, is positive definite, the quadratic form in Eq. 2 implies that the electrostatic binding free energy has a well-defined unique minimum with respect to ligand charges (Fig. 2 a). The vector component b_i is the change upon binding of the Coulomb and reaction field potentials at the position of q_i due to the nonvarying charges only. The free term, c, is the change upon binding of the Coulomb and reaction field energies with all the varying charges zeroed. The coefficients in Eq. 2 (i.e., the matrix elements A_ij, the vector components b_i, and the scalar c) are obtained as described previously (Sulea and Purisima, 2001).

FIGURE 2.

Charge optimization of binding affinity. (a) The net binding free energy, which is the sum of the desolvation effects and Coulomb interaction, has a quadratic dependence on the ligand charge with a unique minimum corresponding to the optimal charge. (b) Charge selectivity, Sq, is defined as the energy increase upon an absolute deviation of 1e from the optimal charge. The ligand charge is constrained within a chemically meaningful range of [−1; +1] e (unshaded) during optimization of binding affinity. For optimal charges capped at ±1e, Sq represents the energy increase upon the charge deviation from the capped value to zero.

Given the coefficients in Eq. 2, the second step in charge optimization calculations consists of finding the unique minimum of the 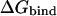function with respect to the ligand charges. This is done by solving the system of linear equations obtained by setting the gradient of the quadratic form to zero, and leads to a unique optimal charge distribution of the ligand that affords maximal binding affinity in the given protein-ligand binding mode.

In the probing approach, these calculations were repeated for the center of the probe-ligand at each of its locations around the protein. Because the probe-ligand is singly charged, the quadratic charge dependence of protein-probe electrostatic binding free energy can be written as:

(3)

where q is the varying charge at the center of the probe-ligand.

In the case of multiatomic actual ligands, the dependence of 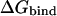on the charge distribution over the atomic centers of the ligand was determined as the functional form in Eq. 2. Varying charges at all the 18 atomic centers of benzamidine were included in the charge dependence of electrostatic free energy of binding to trypsin. In the case of the CRIPT peptide (Acetyl-Gln-Thr-Ser-Val-COO⁻) bound to the PDZ domain, only the charges at the 17 atomic centers of the free-carboxylate C-terminal valine residue were included in the charge dependence of the remainder of the peptide being assigned AMBER partial atomic charges. Calculations were based on the crystallographic coordinates of the complexed ligands to which hydrogen atoms were added.

Partial atomic charges were constrained within the [−1; +1] e interval during optimization to reflect chemically meaningful charge magnitudes. However, this constraint was rarely needed. At the vast majority of the locations of the probe-ligand, the unconstrained optimal charge at its center was within the [−1; +1] e interval. Also, most of the atom-centered charges of the unconstrained optimal charge distribution of actual ligands were within the [−1; +1] e interval.

Selectivity for the optimal charge

For a singly charged ligand like the probe-ligand, the sensitivity of to deviations from the optimal charge is reflected by the steepness, or the breadth, of the parabola describing the charge dependence of electrostatic binding free energy. This is embodied in the coefficient of the quadratic term, A/2 in Eq. 3, which can be interpreted as a measure of charge selectivity, Sq, of the binding free energy for the optimal charge value. Specifically, A/2 accounts for the binding free energy increase incurred upon an absolute deviation of 1e from the optimal charge value (Fig. 2 b). The higher the value of the quadratic term coefficient, the steeper the parabola of charge dependence of binding affinity, and the higher the charge selectivity at a given location around a target molecule is. A slightly different definition of charge selectivity is applied if the optimal charge falls outside the [−1; +1] e range of chemically meaningful charges, in which case the optimal charge is capped at ±1e (Fig. 2 b). In this case, Sq is given by the energy increase due to the charge displacement from the capping value to zero. Sq has energy units (kcal/mol) per 1e deviation toward within the [−1; +1] e interval from the constrained optimal charge, 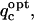and is expressed as:

(4)

For a multiatomic ligand whose charge distribution is optimized for binding using Eq. 2, the A_ii matrix element corresponding to the atomic center i is also a measure of selectivity for the optimal charge at the given atomic center, but only if all the other (n − 1) varying charges are set to their optimal value.

RESULTS AND DISCUSSION

Probe-based charge complementarity and selectivity profiles were generated for two proteins: the bovine trypsin and the third PDZ domain of the brain synaptic protein PSD-95. Their ligands provide examples of various types of electrostatic complementarity at geometrically diverse locations at the protein surface. Benzamidine bound to trypsin has a buried positively charged amidinium group and a more solvent-accessible nonpolar phenyl ring. Conversely, the CRIPT peptide bound to the PDZ domain provides an example of electrostatic recognition of a buried neutral side chain and a more solvent-exposed negatively charged carboxylate.

In this section of the paper we will first present, analyze and interpret each type of profile for the two target proteins, with special emphasis on the implications of charge selectivity in molecular recognition. The profiles will then be compared with: i), relevant structural and biochemical experimental data available in the literature, ii), theoretical data obtained from charge optimization calculations for binding of actual ligands to the target proteins, and iii), the commonly used solvent-screened ESP maps of the unbound proteins. A discussion about the robustness of the results to the calculation parameters is given in Appendix 1.

Charge complementarity profile

The charge complementarity profiles of trypsin and PDZ domain are shown in Fig. 3 (left). About 13,000 probe locations were used for each protein. The electrostatic complementarity profile, which is expressed in charge units, indicates a spectrum of optimal complementary charges preferred by the target protein along its molecular surface. It is apparent that the spectrum of interacting optimal charges generally covers the [−1; +1] e range of chemically meaningful partial atomic charges. This is seen more quantitatively in Fig. 4 a (top) showing the histograms for the distribution of optimal charge values for the two investigated proteins.

FIGURE 3.

Global views of molecular surface profiles of charge complementarity (left) and charge selectivity (right) for trypsin (top) and PDZ domain (bottom).

FIGURE 4.

Distribution of optimal charge and charge selectivity for trypsin (left) and PDZ domain (right). (a) Histograms showing the percent distribution of optimal charge (top) and charge selectivity (bottom). (b) Distribution of charge selectivity with respect to the optimal charge.

The optimal charge at the majority (∼93%) of the tested locations span a chemically plausible range of ±0.7e. This range is common to the theoretical partial atomic charges that can be calculated for most of organic and biological molecules. It is interesting to note that these optimal charges display a Gaussian-type distribution that peaks very close to neutral charge, with ∼88% of the locations having 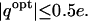Only for a small fraction of the tested locations (∼4%) was the optimal complementary charge outside the [−1; +1] e range of chemically meaningful partial atomic charges. Thus, constraining optimal charges within [−1; +1] e interval was rarely needed.

The charge complementarity profile by itself provides an incomplete electrostatic characterization of the binding surface. The stringency of the requirement for these optimal charges varies significantly across the binding surface (see “Charge selectivity profile”).

Charge selectivity profile

The charge complementarity profile has to be accompanied by the corresponding charge selectivity profile (Fig. 3, right). This would allow one to assess not only the sign and the magnitude of the charge that is complementary at a given location around the target molecule, but also the strictness of selection for this optimal charge, i.e., distinct sites may prefer the same charge (sign and magnitude) but can select for that charge with very different stringency. Highly selective sites would have a relatively steep curvature in the charge dependence of the binding free energy profile around the optimal charge value whereas low-selectivity sites would have a shallow curvature.

The charge selectivity profiles of trypsin and PDZ domain shown in Fig. 3 (right) indicate a significant variation in charge selectivity along their molecular surfaces. By cross comparison of the charge complementarity and selectivity profiles of the same protein, it is easy to find numerous occurrences where the same value of (constrained) optimal charge is selected with significantly different stringencies. Thus, both the complementarity and selectivity profiles are needed for the characterization of binding electrostatics with respect to the charge of the interacting solute.

As in the optimal charges case, the histograms showing the distribution of charge selectivity values are similar for the two investigated proteins (Fig. 4 a, bottom). The Sq values range from 0 to 45 kcal/mol per 1e deviation from the optimal charge value, based on the current settings for the parameters used in continuum electrostatic calculations (see Materials and Methods section). We can use a cutoff for the Sq values to filter out probe locations. For example, with a cutoff of Sq > 30 for high charge-selectivity regions, we obtain a relatively small subset of the sampled surface. As seen in Fig. 4 b, a few locations around trypsin prefer (are complementary to) positive charges (of ∼0.5e) with very high selectivity (>40 kcal/mol per 1e deviation from the optimal charge value). However, we see that in general the charge selectivity hot spots are not restricted to those with corresponding sizable complementary charges. In fact, for both studied proteins, many high-selectivity sites select for near-zero complementary charges. It is interesting to see that the protein molecule can generate a very tight electrostatic control on the binding of complementary neutral ligands.

Synergy of shape and charge selectivity hot spots

Examination of charge selectivity profiles at the protein molecular surface (Fig. 3) indicates another interesting pattern. The regions of high selectivity for the optimal complementary charge (the charge selectivity hot spots) map onto concave pockets at the molecular surface. As shown earlier, the majority of the locations around the protein are much more tolerant to charge deviations from the optimal value. The regions of lowest selectivity for the preferred charge correspond to convex areas of the molecular surface, whereas those with intermediate Sq values are associated with flat areas. The low selectivity of convex regions for their corresponding optimal complementary charge is quite interesting, because charged and polar side chains are often highly located in such regions. Charge selectivity, unlike charge complementarity, is related to molecular shape rather than to the protein charge distribution. This is a consequence of the fact that at a given atomic center of the ligand, the corresponding quadratic term coefficient represents the ligand desolvation potential due to the change upon binding in the solvent exposure at that atomic center when all the other charges are zeroed (Sulea and Purisima, 2001). The binding of small ligands (such as our probes) to concave surfaces results in a greater desolvation change than binding to a convex surface. Hence, the steepness of the parabola defining the optimal complementary charge is higher for concave surfaces. The charge selectivity profiles shown in Fig. 3 follow this behavior. (See Appendix 2 for a discussion of charge selectivity and ligands with multiple varying charges.)

The relationship between charge selectivity and local shape at the binding surface of the protein is further illustrated in Fig. 5. We see a reasonable correlation (r² ≅ 0.8) between Sq and the local curvature of the molecular surface calculated with the program GRASP (Nicholls et al., 1991). However, the local geometry of the solute cavity alone cannot quantitatively account for the charge selectivity, due to the less-local shape dependence of the reaction field energy. Although it may appear as intuitive that the concave regions at the protein surface impose the largest desolvation penalties upon binding, the role of shape characteristics in controlling the stringency of charge complementarity requirements has not been explicitly demonstrated or recognized so far. Our results obtained in this study can have significant implications to the global understanding of protein-ligand binding in biomolecular systems. Well-shaped concave pockets are often associated with ligand-binding sites. These locations afford significant binding affinity in the form of van der Waals interactions for those ligands that meet the very stringent shape complementarity requirements. Our theoretical profiling data show that these pockets, which can be regarded as shape selectivity hot spots, also impose charge selectivity. Although the relative stiffness of the shape and charge complementarity requirements is difficult to assess, our finding suggests that the synergistic combination of the charge and shape selectivities at the hot spots contribute significantly toward molecular selection and recognition.

FIGURE 5.

Correlation between charge selectivity, Sq, and local curvature of the protein molecular surface calculated with the program GRASP (Nicholls et al., 1991).

Asymmetry of charge selectivity at the binding interface

Previous studies have pointed out that the charge complementarity is not symmetric for the interacting molecules in a complex (Lee and Tidor, 2001a). Greater binding enhancements relative to the theoretical charge distribution could be obtained by optimizing the charge distribution of barnase for binding to barstar, than by optimizing the charge distribution of barstar for binding to barnase. This effectively shows that barstar (the inhibitor) is closer to being optimized electrostatically for binding to barnase (the enzyme) than the other way around (i.e., the enzyme is further from the optimum than is the ligand). Molecular evolution has been invoked as a plausible explanation for this behavior (Lee and Tidor, 2001a).

Our charge selectivity profiles clearly indicate that for the binding partners the selectivity to the optimal charge need not be symmetric either. Consider the situation of interlocking concave-convex binding interfaces common to many protein-ligand complexes and protein-protein complexes. A small ligand typically has a convex shape complementary to a concave binding site of the protein. In protein-protein complexes exposed side chains of one protein bind to concave pockets in the other. Around the binding interface, an atomic center inside the convex solute facing a concave pocket would occupy a high charge-selectivity site. In contrast, the corresponding atomic center in the concave binding partner would occupy a low charge-selectivity site in the context of binding to its convex partner. In other words, the high charge selectivity outside concave binding surfaces implies high charge selectivity inside the complementary convex ligand. This suggests a physical basis for the importance of optimizing the partial charges embedded in the convex solute (the ligand). In the barnase-barstar interface mentioned earlier, the convex part belongs to barstar and the concave part to barnase. Hence, not only is barstar more optimized electrostatically than barnase is, it also has a stricter requirement for its partial charges.

We see that, although the charge selectivity profiles indicate low selectivity around the convex regions of a protein, their own partial charge must conform to strict requirements for optimal charge complementarity dictated by the charge distributions and concave shapes of potential binding partners.

Comparison with experimental data

The optimal charge complementarity profile can be compared with the chemical nature (or more quantitatively, with the theoretical charge distribution) of ligands whose structure in complex with the target protein has been determined experimentally. Here, the charge complementarity profile of trypsin is compared with the trypsin-bound benzamidine inhibitor, and the charge complementarity profile of the PDZ domain is compared with the PDZ domain-bound CRIPT peptide. Benzamidine, a molecule with relative molecular weight of only 121, inhibits bovine trypsin with a K_i of 16.6 μM (Mares-Guia et al., 1977) by binding to the S1 subsite of the enzyme. The C-terminal five amino acid residues of the CRIPT peptide, Lys-Gln-Thr-Ser-Val-COO⁻, interact with the PDZ domain, with the free carboxylate C-terminal valine residue considered as a key structural determinant of binding (Doyle et al., 1996). Dissociation constants from this PDZ-3 domain of PSD-95 in the range of 1–4 μM were determined for peptides comprising the C-terminal 6–11 residues of CRIPT (Lim et al., 2002; Niethammer et al., 1998). In addition, the crystallographic structures of trypsin-benzamidine (Katz et al., 1995) and PDZ domain-CRIPT peptide (Doyle et al., 1996) complexes were those used to generate the charge complementarity and selectivity profiles of the two proteins after removal of the ligands (see Materials and Methods section).

In Fig. 6 we overlay the experimental bound structure of the ligands together with the optimal charge complementarity profile of the proteins. In both cases, the profile at the ligand-binding site agrees with the chemical nature of the complexed ligands. The positively charged guanidinium group of benzamidine binds in a region of positive optimal charges. The less-charged benzene ring of benzamidine corresponds to a region with slightly positive optimal charges. In the case of the PDZ domain-CRIPT peptide complex, the agreement is particularly pronounced at the critical free-carboxylate C-terminal valine residue. The negatively charged free-carboxylate group overlays with a patch of negative optimal charge in the PDZ domain. The neutral aliphatic side chain of the valine residue corresponds to optimal charges very close to neutral. Other equivalences between the bound residues of the CRIPT peptide and the charge complementarity profile of the PDZ domain are apparent.

FIGURE 6.

Comparison of charge complementarity profiles (left) and charge selectivity profiles (right) of trypsin (top) and PDZ domain (bottom) with the nature of specific ligands complexed with their respective target protein at experimentally determined binding sites. Benzamidine is bound to trypsin, and the free-carboxylate C-terminal valine-containing CRIPT peptide is bound to the PDZ domain.

A more quantitative analysis can be made by comparing ESP-fit partial charges of the ligands (see Materials and Methods section) with the charge complementarity displayed in a different way in Fig. 7. The locations of the charged center of probe-ligands situated within 2 Å from the actual ligand are displayed as spheres color coded by optimal charge. We see that the polar hydrogen atoms of the guanidinium group of benzamidine have theoretical partial charges of 0.413e, and the hydrogen atoms of the benzene ring of benzamidine have theoretical partial charges in the range of 0.143–0.170e. These partial atomic charges are in good agreement with the profiled optimal charges of ∼0.5e in the region accommodating the guanidinium group, and of ∼0.2e in the region binding the benzene ring of benzamidine. For the C-terminal valine residue of the CRIPT peptide, the free-carboxylate oxygen atoms have theoretical partial charges of −0.682e, and the side-chain methyl groups each has a group charge of −0.054e and hydrogen partial atomic charges of 0.084e. These theoretical atomic charges match closely the calculated optimal charges of ∼−0.5e in the region corresponding to the free-carboxylate group, and of ∼0.0e in the region associated with the side-chain methyl groups.

FIGURE 7.

Comparison of charge optimization results obtained in the probing approach with those obtained by optimization of charge distribution for actual ligands. (a) Benzamidine binding site of trypsin. (b) Free-carboxylate C-terminal valine binding site of the PDZ domain. Left panels show the calculated optimal charge distribution over the atomic charges of the actual ligand for binding to its respective target. The theoretical charge distribution of the actual ligand is shown in parenthesis and italicized. Also shown are the A_ii coefficients of the charge dependence of binding free energy corresponding to the atomic centers of the actual ligands (i.e., the diagonal elements of the ligand desolvation matrix A in Eq. 2, which indicate the charge selectivity at a given atomic center with the charges of the other atomic centers fixed at their optimal value). Stereo views on the right show the charge complementarity profile (top) and charge selectivity profile (bottom). These profiles are represented by the charged “center” of the probe-ligand at various positions within 2 Å from the actual ligand. Centers are displayed as spheres color coded by optimal charge and charge selectivity (see legends).

It should be pointed out that our calculations of optimal charges on actual ligands assume a rigid extraction of the ligand, i.e., no conformational change upon binding. Conformational flexibility is an important issue but is beyond the scope of this work. It is encouraging, however, that even for the flexible CRIPT peptide chemically reasonable optimal charges are obtained.

Charge selectivity versus ligand SAR

We can also compare the charge selectivity profiles of trypsin and PDZ domain with the bound structure of their respective ligands. We see in Figs. 6 and 7 that the guanidinum group of benzamidine corresponds to an area with the highest charge selectivity, which is over 40 kcal/mol per 1e deviation from the optimal charge value of ∼0.5e. In contrast, the charge selectivity profile of trypsin indicates that the region corresponding to the benzene ring of benzamidine is much more tolerant to charge deviation from the optimal value. In the region of the para position of the benzene ring, the selectivity is ∼20 kcal/mol per 1e deviation from the approximately neutral optimal charge. In the case of the C-terminal valine residue of the CRIPT peptide, the charge selectivity profile shows that the region accommodating the aliphatic side chain is highly specific to the neutral optimal charge, even more specific than the region of the carboxylate oxygen atoms to the corresponding negative optimal charge. It is quite interesting to see that the protein molecule produces such a tight electrostatic control on the binding of an interacting solute ligand carrying neutral charge. Other regions of the charge selectivity profile of the PDZ domain in the peptide-binding site region are less specific to their optimal charges.

A more quantitative validation of the charge selectivity profile is more difficult to provide because it represents a relative electrostatic binding free energy. The difficulty arises from the paucity of suitable experimental biochemical data that provide changes in the binding free energy resulting solely from the change in partial atomic charges across the series of ligand congeners, with changes in other nonelectrostatic contributions to binding being minimal (e.g., minimal change of shape and flexibility).

With these requirements in mind, we examine (see Figs. 6 and 7) the change in binding affinity within a series of para-substituted benzamidine analogs (Mares-Guia et al., 1977), and within a series of P1 variants of the bovine pancreatic trypsin inhibitor, BPTI (Krowarsch et al., 1999). Ligand analogs are selected from each series such that they display different electrostatic properties while generally preserving the molecular geometry and degree of flexibility within the series. The change in binding affinity between p-amino-benzamidine and p-carboxy-benzamidine is 1.83 kcal/mol, favoring p-amino-benzamidine. This indicates that trypsin will accept the negatively charged carboxylate group (CO₂⁻) over the neutral amino group (NH₂) at the para position of benzamidine with little loss in binding affinity, in agreement with the trypsin profiles in this region showing relatively low charge selectivity for an almost neutral, slightly positive optimal charge. In contrast, the relative binding affinity between the nearly isosteric P1-Lys BPTI and P1-Met BPTI is 7.39 kcal/mol, in the favor of P1-Lys BPTI consistent with the strong calculated selectivity for a positive optimal charge in the S1 subsite of trypsin. The crystal structures of P1-Lys-BPTI/trypsin complex show that the NH₃⁺ group of P1-lysine of BPTI interacts at the bottom of the S1 subsite of trypsin, where the amidinium group of benzamidine binds (Helland et al., 1999). In fact, the S1 subsite of trypsin is known to have a narrow charge selectivity, because binding affinities to trypsin of BPTI with positively charged cognate P1 residues (Arg and Lys) are 10⁵-fold higher than noncognate P1 residues (Krowarsch et al., 1999). It is a measure of success that our approach could unambiguously demonstrate the presence of the charge selectivity hot spot of trypsin at the bottom of the S1 pocket.

The data for PDZ domains (Songyang et al., 1997; Vaccaro et al., 2001) are not as clear cut and are more qualitative (Lim et al., 2002). Nevertheless, the charge selectivity profile of the PDZ domain agrees with the preferred binding motif, X-(Ser/Thr)-X-(Val/Ile/Leu)-COO⁻. In particular, this motif is consistent with the very stringent requirements for neutral optimal charge in the region accommodating the side chain of the C-terminal valine, and somewhat lower, moderate selectivity for the negative optimal charge in the region corresponding to the C-terminal free-carboxylate group. Also, the less-defined preference at the X-positions of the motif is consistent with the lower charge selectivity in these regions of the protein. One disagreement is the relatively low selectivity for optimal charge seen in the region of a preferred Ser or Thr residue in the second position of the peptide ligand. We note, however, that the charge complementarity profile correctly predicted the preference for a positive partial charge in this region (Fig. 6), in agreement with the positive partial charge of the hydroxyl hydrogen atom of Thr or Ser, which establishes a hydrogen bond with a conserved His residue of the PDZ domain (Doyle et al., 1996).

Probe- versus whole-ligand charge optimization

The charge selectivity and complementarity profiles generated with probe-ligands positioned around the protein surface are clearly an approximation of the charge optimization calculations that can be performed on actual protein-bound ligands (Kangas and Tidor, 2001; Lee and Tidor, 2001a,b; Sulea and Purisima, 2001). The approximate nature of the probing approach is primarily due to two distinct features of the probe-ligand: i), it is singly charged, and ii), its charged “center” has a constant radius and uniformly contacts the protein regardless of the local protein environment. These two characteristics also result in the probe-ligand simulating a single, outer layer of ligand atoms that is in immediate contact with the protein (i.e., positioned on the solvent-accessible surface of the protein). In addition, in the case of an actual, multiatomic ligand, all atom-centered charges “see” each other and are embedded by the same low-dielectric solute cavity of the ligand molecule, whereas a number of singly charged probe-ligands with protein-complementary but different shapes are required to sample the region of the actual ligand contacting the protein. Nevertheless, the use of the probe-ligand facilitates profiling the binding characteristics of a protein surface toward a generic ligand. However, given the differences between the probe-ligand and an actual ligand, it is important to assess the degree of similarity between the results of charge optimization calculations based on the two types of ligands.

In Fig. 7 we compare the binding-optimized charge distribution and associated charge selectivites (expressed as A_ii coefficients; see Materials and Methods section) at the atomic centers of actual ligands with the charge complementarity and selectivity profiles obtained in the probe-based approach. For actual ligands, the charge distribution of benzamidine (18 atomic centers) was optimized for binding to trypsin. Similarly, the charge distribution over the 17 atomic centers of the free-carboxylate C-terminal valine residue of the CRIPT peptide was optimized for binding to the PDZ domain. Calculations are based on the crystallographic coordinates of the actual ligands bound to their targets. We note the good agreement between the binding-optimized and theoretical charge distributions of the actual ligands, suggesting that these ligands are well optimized electrostatically for binding to their respective targets. It may seem odd that these ligands with near-optimal charge complementarity are only micromolar binders. The reason is that although poor charge complementarity generally leads to poor binding affinity, good charge complementarity often yields no significant net binding affinity due to the interplay of Coulomb interactions and desolvation cost. As has been pointed out (Kangas and Tidor, 1998), electrostatic interactions may contribute to binding specificity rather than affinity.

The positions of the virtual probes approximate the locations of the ligand atoms in direct contact with the protein surface. The optimal charges and charge specificities obtained in the probe-based profiling agree well with those of the first layer of actual ligand atoms (see Fig. 7). In some cases, such as with the polar hydrogens of the amidinium group of benzamidine, the ligand atoms approach the molecular surface much more closely than the virtual probe can. It is encouraging if somewhat surprising that, even in those cases, the single charge-center probe captures the behavior of the first-layer ligand atoms. In contrast, the optimal charges profile for the second layer of ligand atoms is not well reproduced by the virtual probes. For example, the nitrogen atoms of the amidinium group have negative optimal partial charges calculated for binding to trypsin, and also negative theoretical partial charges, but virtual probes near the nitrogens have positive optimal charges required by the first-layer atoms. Similarly, the carbon atom of the C-terminal free-carboxylate group has a positive optimal partial charge calculated for binding to the PDZ domain, and also positive theoretical partial charge, but corresponds to negative optimal charges for the virtual probe. One could think of the virtual probes in those positions as trying to mimic a united atom combining the first- and second-layer atoms. In the case of the NH₂ atoms of amidinium, a net positive charge results consistent with the probe calculations. For the carboxylate group, we have a net negative charge consistent with the probe charge. It should be noted that the inability to independently mimic first- and second-layer atoms using the single charge virtual probe is not a serious handicap for profiling intermolecular binding interactions because of primary importance is the exposed first layer of protein-contacting atoms of the ligand.

This comparative analysis leads to the conclusion that the charge complementarity and selectivity profiles based on probe-ligands represent an approximate method that captures the essential patterns that can be obtained by the more quantitative calculations performed on actual ligands. A number of improvements in the definition and construction of probe-ligands are being considered to reduce the approximate nature inherent to the probing approach, while maintaining its practical aspect. Because in real-life practice, the chemical nature and/or the bound location of actual ligands are often unknown, the implementation of the charge optimization of binding electrostatics methodology in a probe-based approach provides one of the only tools in mapping the charge complementarity and selectivity profiles of unbound proteins.

Comparison with the standard ESP map of unbound proteins

In Fig. 8 we present the usual solvent-screened ESP maps at the molecular surface of trypsin and PDZ domain, calculated with the program GRASP (Nicholls et al., 1991). These maps can be compared with the charge complementarity and selectivity profiles of these proteins shown in Figs. 3 and 6. The information and insights that we obtain from the charge complementarity and selectivity profiles are quite different from those visualized in the standard ESP map of the uncomplexed protein. This latter representation provides information about the polarity along the molecular surface and can qualitatively suggest what the complementary polarity of a ligand should be. Although there is a reasonable general, qualitative agreement between the ESP map and the charge complementarity profile, it is not possible to assess how selective the binding site is to the complementary charge with the ESP map alone.

FIGURE 8.

Solvent-screened ESP maps calculated with the program GRASP (Nicholls et al., 1991) at the molecular surface of unbound trypsin (top) and unbound PDZ domain (bottom). Panels on the right zoom-in to binding sites of actual ligands. For comparative purpose, the orientation is kept the same as in Fig. 3 for the global views (left), and as in Fig. 6 for the close-up views (right).

In addition, we are able to express the electrostatic binding complementarity in charge units (e) in the charge complementarity profile, as opposed to the ESP maps, which are expressed in potential units (kcal/mol/e). Expressing electrostatic binding complementarity in charge units is easier to interpret chemically, because the charge similarity can be directly and quantitatively assessed between the optimal complementary charges around the target protein and the theoretical partial atomic charges of candidate ligands. Such a quantitative assessment of electrostatic similarity is much more difficult in potential units.

But most of the discrepancy between the charge complementarity and selectivity profiles on one hand, and the standard ESP maps on the other hand, is seen around the solvent-exposed charged and polar groups in convex regions of the molecular surface. These locations are often characterized by high values of negative or positive electrostatic potential and commonly interpreted in terms of charge complementarity. Although the charge complementarity profile indeed suggests a significant magnitude of the complementary polarity in these regions, we showed that in general such locations are energetically nonselective to both the sign and magnitude of the interacting complementary charge. Also related to the charge selectivity issue, it is not clear how to interpret the regions of low electrostatic potential in the ESP map, as being selective for neutral charge or as being charge nonselective. Thus, the interpretation of the solvent-screened electrostatic potential map of the free protein in terms of electrostatic binding selectivity to optimal complementarity is not straightforward. The conceptually very different probe-based charge optimization of binding electrostatics described in this article allows us to profile relevant electrostatic binding quantities in a readily interpretable way.

CONCLUSIONS

In this article, we applied the charge optimization of binding electrostatics concept and methodology in a probe-based approach to delineate the optimal charge complementarity and selectivity around a target protein molecule. Interacting optimal charges that we found generally span a chemically meaningful range of values characteristic to most organic and biological molecules. The protein molecule can produce a very tight electrostatic control on the binding of complementary neutral charges. Selectivity to the optimal charge of the interacting probe-ligand does not depend on the electrostatic properties of the target molecule, but rather on its shape characteristics. High selectivity is concentrated in well-shaped concave pockets at the protein surface, whereas solvent-exposed convex regions are nonselective to their corresponding optimal charge. This suggests the synergy of charge and shape selectivity hot spots toward molecular selection and recognition in biomolecular systems, as well as the asymmetry of charge selectivity at the binding interface for shape-complementary interacting solutes. The charge complementarity profile agrees well with the theoretical charge distribution of known ligands at their experimentally determined binding sites on the protein. The charge selectivity profile is in qualitative agreement with experimental biochemical data reflecting electrostatic selectivity. Published applications have suggested that charge optimization methodology can be used as a molecular design tool in the case when the structure of the protein with a bound ligand is known. Our probe-ligand-based profiles represent an approximate method that captures the essential patterns that can be obtained by the more quantitative calculations performed on actual ligands. Because in actual practice the chemical nature and/or the target-bound location of actual ligands are often unknown, the implementation of the charge optimization of binding electrostatics methodology in a probe-based approach provides one of the only tools in mapping the charge complementarity and selectivity profiles of unbound proteins. In addition, the dependence of the results to adjustable parameters involved in the definition of the probe-ligand and in the charge optimization of binding electrostatics calculations appears reasonably weak (see Appendix 1) and will not compromise the general application of the method. The information and insights that we obtain from such charge complementarity and selectivity profiles are also quite different from those visualized in the standard electrostatic potential map of the uncomplexed protein, by profiling relevant electrostatic binding quantities in a readily interpretable way.

Supplementary material

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org/. Correlation plots on the effect of R-cutoff value (4.0 Å versus 2.0 Å, 3.0 Å, and 5.0 Å) on the optimal charge and its selectivity profiled around trypsin and PDZ domain.

APPENDIX 1

Robustness of the results to calculation parameters

It is important to evaluate the robustness of the profiles presented here to the adjustable parameters employed in their calculation. We delineate two classes of parameters that might affect the charge complementarity and selectivity profiles: i), parameters used in the positioning and construction of the probe-ligands, and ii), parameters characteristic to general electrostatic calculations and charge optimization of binding electrostatics calculations.

A number of decisions had to be made in the positioning and construction of probe-ligands, some of which resulted in the approximate nature of the profiles as discussed earlier. The greatest impact on the geometry of the solute cavity is due to the R-cutoff parameter (see Materials and Methods section, and Fig. 1 a) that controls the extent of the probe-ligand from its charged “center” on the solvent-accessible surface of the protein. The results presented throughout this work were obtained with an R-cutoff of 4.0 Å. We also carried out additional calculations using the same set of locations of the charged “center” on the solvent-accessible surface of the protein, but with the R-cutoff value set to 2.0 Å, 3.0 Å, and 5.0 Å. The results, given in Fig. S1 as Supplementary material, indicate that the charge complementarity and selectivity profiles generated with an R-cutoff of 4.0 Å correlate well with the profiles obtained with the other R-cutoff values tested for both proteins, with r² > 0.83 for the optimal charge values, and r² > 0.96 for charge selectivity values. This demonstrates that the profiles are very robust to the extent of the low-dielectric cavity of the probe-ligand around its center where the charge optimization calculation is performed. We recommend R-cutoff values higher than 2.0 Å for our implementation of charge optimization based on the BEM method for solving the Poisson equation, due to some numerical instabilities in reaction field calculations at lower R-cutoff values (e.g., at the R-cutoff of 0.0 Å corresponding to spherical water-sized probe-ligands, due to formation of narrow collars in the bound state around the very convex regions of the protein). There is also the question of how the number and positioning of the virtual atoms on the solvent-accessible surface of the protein affect the profiles. Although there is some intrinsic randomness in probe positioning on SAS from the vertices on the triangulated molecular surface, we believe that the profiles will not be significantly different if generated with a slightly perturbed set of locations. This is fully supported by previous charge optimizations calculations that showed similar optimal charge distributions obtained on slightly perturbed ligand-protein binding modes (Kangas and Tidor, 2001).

It is widely known that in the electrostatic calculations with continuum models, solute parameters such as interior dielectric constant, D_in, atomic radii, and partial atomic charges greatly affect the results. The optimal charges resulting from optimization of binding electrostatics, however, are very robust to the variation of these parameters. This is because the optimal charge is taken as a ratio of two electrostatic binding potentials, i.e., the A and b coefficients in Eq. 3. Thus, the pronounced dependencies of calculated reaction field and Coulomb energies on D_in and on the parameter set of atomic radii and partial charges, are much attenuated in the calculation of the optimal charge for binding. In applications on chemical systems, we have shown in a previous publication (Sulea and Purisima, 2001) that the magnitude of the optimal charge remains almost unchanged upon variation of interior dielectric constant from 1 to 10. In fact, it can be demonstrated that the dominant term in the expression of optimal charge depends on D_out/(D_out − D_in), where the exterior medium dielectric constant, D_out, is 78.5. Our more recent calculations indicate little dependence of the optimal charge on a particular set of parameters used for atomic radii and nonvarying charges (data not shown). In fact, Tidor and co-workers obtained plausible optimal charge distributions for strong-binding specific ligands (Lee and Tidor, 2001a,b; Kangas and Tidor, 2001) using CHARMM PARAM19 parameter set (Brooks et al., 1983) or PARSE parameter set (Sitkoff et al., 1994) of atomic charges and radii, and a D_in of 4, which are quite different from our settings (see Material and Methods section). In respect to charge selectivity, it can be demonstrated analytically that the quadratic term coefficient does not depend on partial atomic charges (see Sulea and Purisima, 2001, and also the earlier discussion on synergy of shape and charge selectivities). The dependence of charge selectivity on D_in is very pronounced, but to a good approximation proportional with (D_out − D_in)/(D_outD_in), such that the A/2 coefficient becomes smaller at higher D_in. Thus, the magnitude of the absolute values in the charge selectivity profile has to be treated with caution. It is the pattern of charge selectivity that can be examined and interpreted at any (reasonable) value of D_in, due to the proportional dependence of the quadratic term coefficient on D_in. Our recent calculations on charge optimization of multiatomic ligands also indicate that the diagonal terms A_ii in the ligand desolvation matrix in Eq. 2 are not overly sensitive to the various sets of atomic radii tested (data not shown).

APPENDIX 2

Charge selectivity and multiatomic ligands

The relationship between shape and charge selectivity is not as straightforward for multiatomic ligands as it is for single varying-charge ligands. If multiple charge centers in the ligand are allowed to vary, the off-diagonal coefficients A_ij of the A matrix define the interdependence between the simultaneously varying charges at atoms i and j. This allows concerted changes in charges that incur a lower energetic cost than that reflected by the diagonal term, A_ii, our measure of charge selectivity for single-charge-center ligands. Hence, unlike the single charge case, the energetic cost of a charge deviating from its optimal value will depend not only on molecular geometry but on the other varying ligand charges as well. However, even for a multiatomic ligand, A_ii (which depends only on molecular geometry) remains a useful measure of charge selectivity. A small A_ii, as obtained for atom i binding to a convex protein surface, clearly indicates a low charge selectivity. On the other hand, a large A_ii, as obtained by binding to a concave protein surface, signals high charge selectivity in the following sense. A large A_ii imposes a strong constraint on the collective behavior of the charge i and the one or more coupled j charges with large A_ijs. In such cases, a large A_ii reflects the difficulty of changing charge i independently of the other charges to which it is strongly coupled (significant A_ij). Hence, binding site shape continues to have a strong influence on charge selectivity even for multiatomic ligands.