Tonic and Phasic Guanidinium Toxin-Block of Skeletal Muscle Na Channels Expressed in Mammalian Cells

Abstract

The blockage of skeletal muscle sodium channels by tetrodotoxin (TTX) and saxitoxin (STX) have been studied in CHO cells permanently expressing rat Nav1.4 channels. Tonic and use-dependent blockage were analyzed in the framework of the ion-trapped model. The tonic affinity (26.6 nM) and the maximum affinity (7.7 nM) of TTX, as well as the “on” and “off” rate constants measured in this preparation, are in remarkably good agreement with those measured for Nav1.2 expressed in frog oocytes, indicating that the structure of the toxin receptor of Nav1.4 and Nav1.2 channels are very similar and that the expression method does not have any influence on the pore properties of the sodium channel. The higher affinity of STX for the sodium channels (tonic and maximum affinity of 1.8 nM and 0.74 nM respectively) is explained as an increase on the “on” rate constant (≈0.03 s⁻¹ nM⁻¹), compared to that of TTX (≈0.003 s⁻¹ nM⁻¹), while the “off” rate constant is the same for both toxins (≈0.02 s⁻¹). Estimations of the free-energy differences of the toxin-channel interaction indicate that STX is bound in a more external position than TTX. Similarly, the comparison of the toxins free energy of binding to a ion-free, Na⁺- and Ca²⁺-occupied channel, is consistent with a binding site in the selectivity filter for Ca²⁺ more external than for Na⁺. This data may be useful in further attempts at sodium-channel pore modeling.

INTRODUCTION

Tetrodotoxin (TTX) and saxitoxin (STX) are naturally occurring, competitive, high-affinity blocking ligands for the voltage-dependent sodium channel (for reviews, see Narahashi, 1974; Kao, 1986; Hille, 2001). Although the two toxins differ in their chemical structure, and one is a monovalent cation while the other is a divalent cation, a certain similarity between the two toxins does exist. Both contain a diol group, TTX contains one guanidinium group, and STX contains two. Guanidinium is an organic cation that is known to be able to pass through the sodium channel (Hille, 1971). Guanidinium and diol groups are thought to be essential for binding either toxin. Comparing the permeability of different organic cations that permeate the sodium channel, it has been proposed that the part of the channel where the toxins finally stick is near a narrow ionic selectivity filter, whose opening is approached through a larger antechamber (Hille, 1971, 1975). According to this scheme, the guanidinium group found in both toxin molecules enters the sodium channel, where it becomes stuck because the rest of the molecule is too bulky to pass. The channel structures that interact with the toxins have been located in the SS1-SS2 (or P) regions of the four repeats of the sodium channel polypeptide. In particular, single point mutations mapping these regions have demonstrated that most mutations that produce effects in permeability also affect toxin sensibility (Terlau et al., 1991; Pusch et al., 1991; Noda et al., 1989; Heinemann et al., 1992b; Satin et al., 1992; Kontis and Goldin, 1993).

Use-dependence (UD) of block by guanidinium toxins is a common feature of STX and TTX block of all voltage-gated sodium channels (Carmeliet 1987; Eickhorn et al., 1990; Makielski et al., 1993; Salgado et al., 1986; Lönnendonker, 1989; Patton and Goldin, 1991; Satin et al., 1994; Conti et al., 1996; Boccaccio et al., 1999). The phenomenon consists of an increase of toxin block upon activation of the channel by depolarizing pulses. Based on the trapped-ion model proposed by Salgado and collaborators (1986), we have elaborated a detailed kinetic scheme to account for the UD of guanidinium toxins (Conti et al., 1996; Boccaccio et al., 1999). In this model, the lower resting affinity for toxin binding arises because the toxin molecules often bind to channels that are already hosting a Na⁺ or a Ca²⁺ in a deeper site. The ion remains trapped in the pore because the intracellular gate is closed, and it destabilizes the binding by exerting repulsion on the toxin. As the channel opens upon a depolarization, the trapped ion can escape to the intracellular medium increasing the stability of the bound toxin. We have shown that this model quantitatively accounts for all the measurable properties of the tonic and phasic TTX block of brain Nav1.2 sodium channels expressed in oocytes (Conti et al., 1996; Boccaccio et al., 1999). The model predicts that the size of the effect depends on the repulsion energy between a bound TTX and a trapped cation, whereas the kinetics is mainly governed by the rate constants of second-order association and first-order dissociation constants of the TTX-receptor complex.

We report here studies of the use-dependent block by TTX and STX of skeletal muscle sodium channels, Nav1.4, permanently expressed in mammalian cells. We have verified that the ion-trapped model is fully applicable for TTX-UD in this preparation, and that the binding characteristics of the toxin to Nav1.2 and Nav1.4 are roughly identical. From the comparison of the UD of TTX and STX in this preparation we have concluded that the higher affinity of STX is due to a faster second-order association constant, and the more pronounced UD of STX can be only partially be accounted for by the higher electric charge of the molecule.

METHODS

Experiments were done with Chinese hamster ovary cells (CHO) permanently transfected with the expression vector pcDNA3 (Invitrogen, Carlsbad, CA) containing the full-length cDNA coding for the rat Nav1.4 sodium channel α-subunit (Trimmer et al., 1989). The current density and the electrophysiological properties of this cell line were fully reproducible (Moran et al., 2000; Tammaro et al., 2002).

Sodium currents were measured using the patch-clamp technique in the whole-cell configuration (Hamill et al., 1981) using an Axopatch-200 amplifier (Axon Instruments, Union City, CA). Borosilicate glass micropipettes (Hilgemberg, Mansfield, Germany) were fire-polished to a tip diameter yielding a resistance of 2.2–2.8 MΩ in the working solutions. The pipette was filled with (in mM): NaCl 25,CsF 110, EGTA 10, TEA 2, HEPES-KOH 10; pH = 7.3. The external solution had the following composition (in mM): NaCl 100, KCl 5, CaCl₂ 2, TEA 20, HEPES-KOH 10; pH 7.4. Osmolarity in both solutions was adjusted to 300 mOsm/Kg with manitol. The use of intracellular Cs⁺ and intra- and extracellular TEA⁺ abolished most of the endogenous potassium currents.

For experiments at different extracellular Ca²⁺ concentrations, CaCl₂ was varied from 0.2 mM to 5 mM. Aliquots of freshly thawed small volumes of stock solutions (100 μM) of STX (Calbiochem, San Diego, CA) or TTX (Sigma, St. Louis, MO) were mixed with the extracellular working solution before each experiment to obtain the desired concentration. Measurements were taken under continuous perfusion, controlled by a Rapid Solution Changer RSC-160 (Bio-Logic, Claix, France).

The output of the patch-clamp amplifier was filtered by the built-in low-pass, four-pole Bessel filter with a cutoff frequency of 5 kHz and sampled at 20 kHz. The membrane patch was kept at a holding potential of −120 mV. Pulse stimulation and data acquisition used 16 bit D-A and A-D converters (ITC-16, Instrutech, Port Washington, NY) controlled with the Pulse software (Heka Electronik, Lambrecht, Germany). Linear responses were estimated from subthreshold stimulation, partially compensated analogically, and digitally subtracted with a standard P/4 protocol. The access resistance was always less than 7 MΩ and the cell capacitance was between 5 and 40 pF, as measured by the compensating circuit of the amplifier. The series resistance was usually compensated between 80% and 85%. All measurements were done at a controlled temperature of 19 ± 0.5°C. Records were taken at least 6 min after establishing the whole-cell and voltage-clamp configuration, a time estimated to be long enough in this preparation to allow the removal of the ultra slow inactivation, and the stabilization of the voltage-dependent properties of the channels (Wend et al., 1992; Cummins and Sigworth, 1996; Tammaro et al., 2002).

Data were analyzed using custom software developed in the Igor environment (Wavemetrics). Data is expressed as mean values ± SE (number of experiments). Statistical comparisons were done with a Student's t-test, and statistical significance was defined by p < 0.05. A simplex method was used for curve fitting.

The model

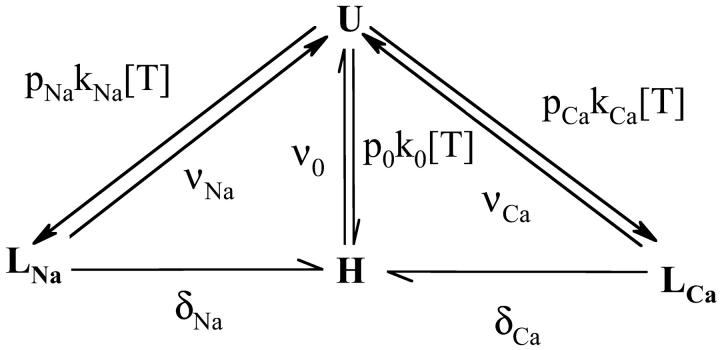
The analysis of the interaction between TTX or STX and the sodium channel was done in the framework of the UD model that we have previously described (Conti et al., 1996; Boccaccio et al., 1999). The model is based on the trapped-ion hypothesis (Salgado et al., 1986), that we have represented as a four-state system, using Scheme 1, where U represents the toxin-free channel, L_Na and L_Ca represents the low-affinity blocked states, the channel contains a Na⁺ or a Ca²⁺ respectively, and H is the high-affinity blocked state with the toxin bound to an ion free channel. The rate constants for toxin association (k₀, k_Na, and k_Ca) and dissociation (ν₀, ν_Na, and ν_Ca) are assumed to be independent to the voltage (Conti et al., 1996). We assume that δ_Na = δ_Ca = 0 for large hyperpolarizing potentials that keep the channels tightly closed. Conversely, at any potential where the channels open, δ_Na and δ_Ca are extremely high, so that the trapped cation will escape from the channel with a probability close to unity, and all channels in state L_Na and L_Ca will switch to state H. The conditional probabilities of cation occupancy of the toxin-free channel are given by

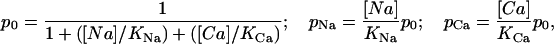(1)

where K_Na and K_Ca are the dissociation constants for Na⁺ and Ca²⁺ for the closed channel respectively. The fraction of unblocked currents, 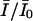, representing the probability of the unblocked state U for large negative potentials at rest, such as there are no transitions between the low affinity states L_Na and L_Ca and the state H, is

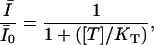(2)

where tonic dissociation constant K_T is given by

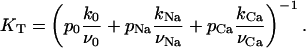(3)

SCHEME 1.

The use-dependence can be defined as the decay of the probability of the toxin-free state U during a train of depolarizing pulses. The fraction of unblocked channels, estimated by the ratio of peak currents relative to the resting (tonic) condition, 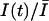, is described by:

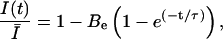(4)

where the extra-block probability B_e is defined as 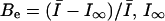being the asymptotic value of the peak current for repetitive stimulation, and τ is the time constant of the process. We have previously demonstrated that B_e and τ are functions of the stimulation pulse interval, and for a high-frequency stimulation (≥1 Hz) they tend to a limiting value (Conti et al., 1996).

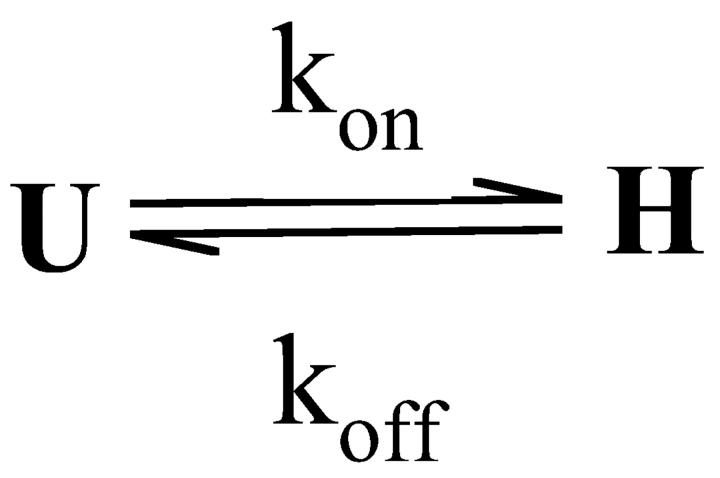
The saturated extra block develops during a train of stimulation, where δ_Na → ∞ and δ_Ca → ∞, depleting the pool of channels in the low affinity states L_Na and L_Ca at a much higher rate than transitions between state U and these states. This results in a reduction of Scheme 1 to Scheme 2, with k_on = p₀k₀ + p_Nak_Na + p_Cak_Ca. Consequently, the steady-state fraction of unblocked channels, 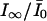, is given by

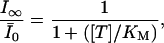(5)

where the maximum affinity for the toxins, described by the dissociation constant K_M, is defined by

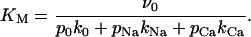(6)

SCHEME 2.

In this condition of repetitive stimulation, as states L_Na and L_Ca are no longer occupied in reducing the scheme in a simple two-state system, the time constant τ of the relaxation of the unblocked currents from I₀ to I_∞ given by

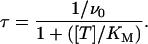(7)

From Eqs. 2 and 5, we can express the saturated extra-block parameter as

(8)

where B_i is the fraction of saturable binding affinity inhibited at resting conditions, that define the maximum UD effect, and is defined as

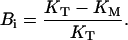(9)

Therefore, according to Eqs. 3 and 6, the maximum UD effect is given by

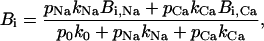(10)

where B_i,Na and B_i,Ca are the maximum specific inhibition for each cation, defined by

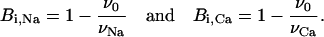(11)

We assume that the binding process is insensitive to the ion occupancy of the pore, hence k₀ = k_Na = k_Ca = k_on. Therefore, as K_M is independent to the ion concentration, Eq. 6 becomes

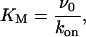(12)

and Eq. 10 becomes

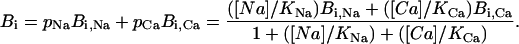(13)

RESULTS

Tonic block

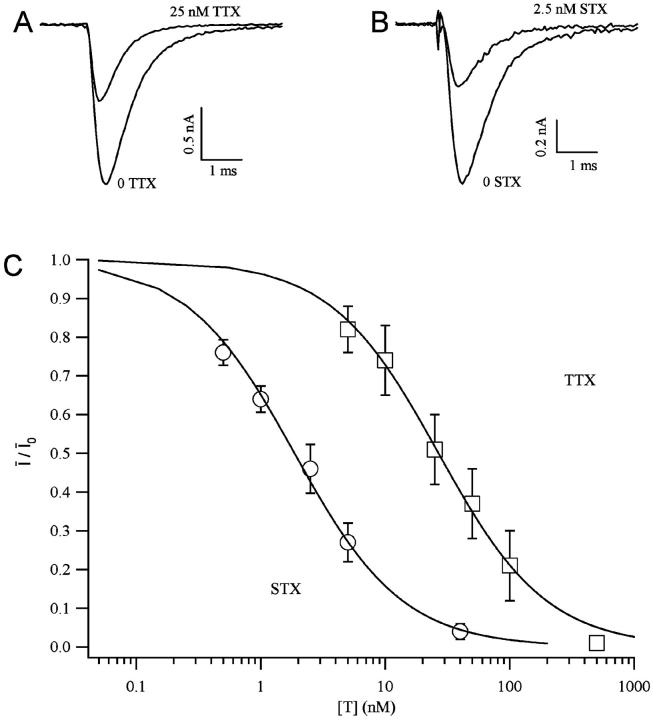
The sodium currents expressed in transfected cells were reversibly reduced by extracellular perfusion with guanidinium toxins, TTX and STX, without significantly modifying the kinetics of the currents (Fig. 1, A and B). To measure the tonic block, we first measured the peak current evoked by a short depolarizing pulse in the absence of toxin, Ī₀, then we perfused the cell with a given toxin concentration [T] for at least 3 min, keeping the cell at a holding potential of −120 mV. The current Ī, evoked by the same pulse after the resting period, was used to estimate the fraction of unblocked channels, Ī/Ī₀. Estimates of Ī/Ī₀ for various toxin concentrations are plotted against the toxin concentration [T] in Fig. 1 C, summarizing the results obtained from three to seven different experiments for each toxin. The dose-response curves were fitted with Eq. 2, yielding the estimates of K_T shown in Table 1. We find that the tonic affinity of the sodium channel for STX (K_T ≈ 1.8 nM) is roughly 15-fold higher than for TTX (K_T ≈ 27 nM), in agreement with results reported for other preparations (Terlau et al., 1991; Stephan et al., 1994; Penzotti et al., 1998; Ritchie and Rogart, 1977).

FIGURE 1.

Tonic blockage of Nav1.4 channels by guanidinium toxins. Sodium currents from Nav1.4-transfected CHO cells were elicited by a depolarizing pulse from a holding potential of −120 mV to a test potential of −10 mV. The records were obtained in normal solution with 2 mM Ca²⁺. Control records were obtained in absence of toxins. A similar reduction of the current occurs after perfusion with 25 nM TTX (A) or 2.5 mM STX (B). (C) Dose-response curves for TTX (squares) and STX (circles). The toxin-free probability under resting conditions is defined as the fraction of sodium current remaining after the addition of the toxin at a concentration given in the abscissa in logarithmic units. Symbols represent mean values (±SE) from at least three measurements at any given toxin concentration. Continuous lines are the least-squares fitting with Eq. 2, yielding the estimates given in Table 1.

TABLE 1.

UD parameters for the interaction of TTX and STX with the Nav1.4 sodium channel expressed in mammalian cells

	TTX
	CHO cells	Oocytes	STX
KT (nM)	26.6 ± 5.6	26 ± 4	1.8 ± 0.2
KM (nM)	7.7	8.6	0.74
Bi	0.63	0.62	0.76
kon (s−1 nM−1)	0.0029	0.0021	0.029
ν0 (s−1)	0.020	0.019	0.022

Data were obtained with an extracellular solution containing 100 mM Na⁺ and 2 mM Ca²⁺. Data obtained on Nav1.2 expressed in frog oocytes (Conti et al., 1996; Boccaccio et al., 1999) are presented for comparison.

Use-dependence

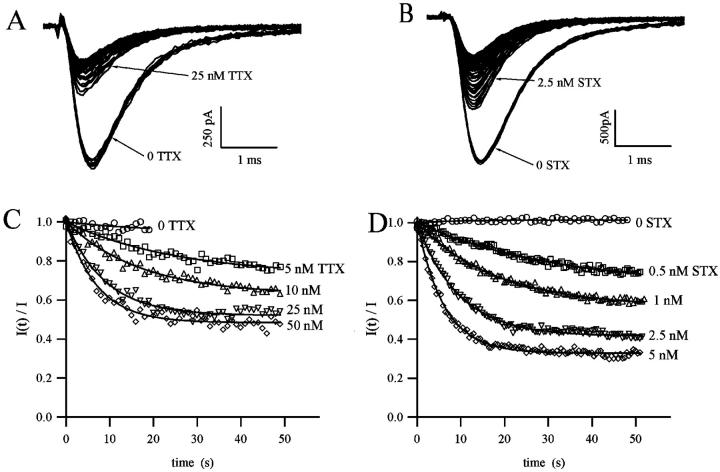
The blockage of sodium channels by guanidinium toxins is use-dependent, that is, when tested repetitively with a train of stimuli, the fraction of blocked channels increases monotonically with the number of stimuli. To test that the peak current reduction during a train of pulses is not due to rundown, or to an accumulation of the inactivation produced by each pulse, currents were evoked with a train of short depolarizing pulses at 1–2 Hz in the absence of toxin in the extracellular solution. As shown in Fig. 2, A and B, control currents did not change in amplitude or shape by repetitive stimulation. After perfusion with solutions containing STX or TTX, the first stimulus evoked a reduced current indicating that a fraction of channels were blocked in tonic conditions. Further reduction of the current was observed for successive pulses, until the peak amplitude reached a new stationary value, as shown in Fig. 2, A and B.

FIGURE 2.

Use-dependence of blockage of sodium currents by TTX and STX. (A and B) Sodium current from Nav1.4-transfected CHO cells were elicited by 2-Hz trains of depolarizing pulse from a holding potential of −120 mV to a test potential of 0 mV. Records were obtained in normal solution with 2 mM Ca²⁺. Ten control records obtained in absence of toxins are superimposed, indicating that no changes in the current amplitude or shape are produced by the repetitive stimulation. A reduction of current occurs after perfusion with 25 nM TTX (A) or 2.5 nM STX (B), and further reduction of the amplitude is observed as the channel is continuously activated. The time course of the fraction of unblocked channels, I(t)/Ī, was measured at different TTX (C) and STX (D) concentration, as indicated. Continuous lines are the least-squares fitting with a single exponential decay described in Eq. 4.

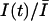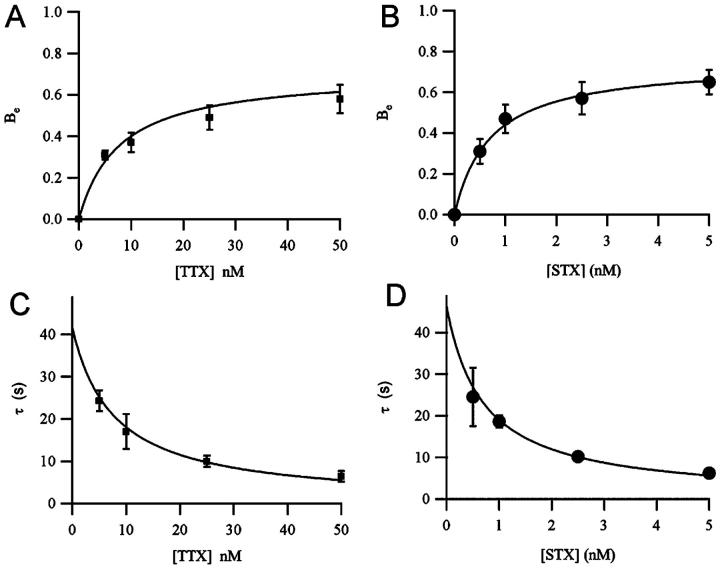
The fraction of unblocked channels during a pulse train was estimated by the ratio of peak currents relative to the resting (tonic) condition, . In Fig. 2, C and D, we present the time course of 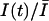as measured by different concentrations of STX and TTX. Data were well fitted by the single exponential decay described by Eq. (4), yielding the extra-block probability, B_e, that indicates the amplitude of the maximum UD effect, and the time constant of the process, τ. In Fig. 2, B and C, it is observed that B_e increased and τ becomes faster as the toxin concentration is increased.

As shown before, using the ion-trapped model to analyze the UD it is possible to obtain the first-order dissociation rate constant of the toxin from the ion-free pore, ν₀, and the dissociation constant of toxin binding in the ion-free pore, K_M. Pooled data, obtained from different experiments, are presented in Fig. 3. The plots of B_e and τ data against the toxin concentration were simultaneously fitted with Eqs. 7 and 8. These fits provided estimates of K_M, which was found ∼10 times lower for STX than TTX (≈0.7 nM and ≈7 nM respectively), and of ν₀, which had very similar values for the two toxins (0.022 s⁻¹ and 0.020 s⁻¹ for STX and TTX, respectively). These data allow identifying which of the two processes, binding and unbinding, is the cause of the difference in affinity between STX and TTX. The second-order association rate constant, k_on, for each toxin can be evaluated by the Eq. 12, yielding ∼0.03 s⁻¹ nM⁻¹ for STX and ∼0.003 s⁻¹ nM⁻¹ for TTX. Hence, the higher affinity of STX for the sodium channel (in ion-free pore conditions) is due to a larger rate of “on” binding, k_on, while the “off” rate is the same.

FIGURE 3.

Dependence of the maximum extra-block (A and B) and the time constant of cumulative UD (C and D) on the toxin concentration. Data were obtained from sodium currents elicited by 1- or 2-Hz trains of depolarizing pulses in normal solution with 2 mM Ca²⁺. Symbols represent mean values (±SE) from at least three measurements at a given toxin concentration. Continuous lines are the simultaneous fitting with Eqs. 7 and 8 for TTX (A and C) and for STX (B and D). The fitting parameters, providing estimates of ν₀, K_M, and B_i, are presented in Table 1.

The maximum UD effect, defined in Eq. 8 as B_i, is higher for STX (0.76) than for TTX (0.63), revealing that in these conditions, the difference between the tonic block and the maximum block is more pronounced for STX that for TTX. Since the conditional probability of ion-occupancy of a toxin-free channel is obviously not influenced by the toxin, this difference in the maximum UD effect would indicate that, according to Eq. 10, the contribution of the maximum specific inhibition for each cation, B_i,Na and B_i,Ca, is larger for STX than for TTX. Therefore, according to Eq. 11, the dissociation rates when the channel is occupied by Na⁺ and Ca²⁺, ν_Na and ν_Ca, are larger for STX than for TTX. A summary of the UD data evaluated for STX and TTX is presented in Table 1.

It is noteworthy to observe that the results of K's, B_i, and ν₀ for TTX obtained here with Nav1.4-transfected mammalian cells are very similar to those obtained previously, applying similar experimental protocols, Nav1.2 channels expressed in frog oocytes (Boccaccio et al., 1999; Conti et al., 1996). This indicates that the outer pore of sodium channels isoforms expressed in brain (Nav1.2) and adult skeletal muscle (Nav1.4), with respect to binding properties of guanidinium toxins and probability of occupancy of a resting (closed) channel by a cation, are substantially similar (see Table 1).

Ca²⁺ dependence of STX blockage

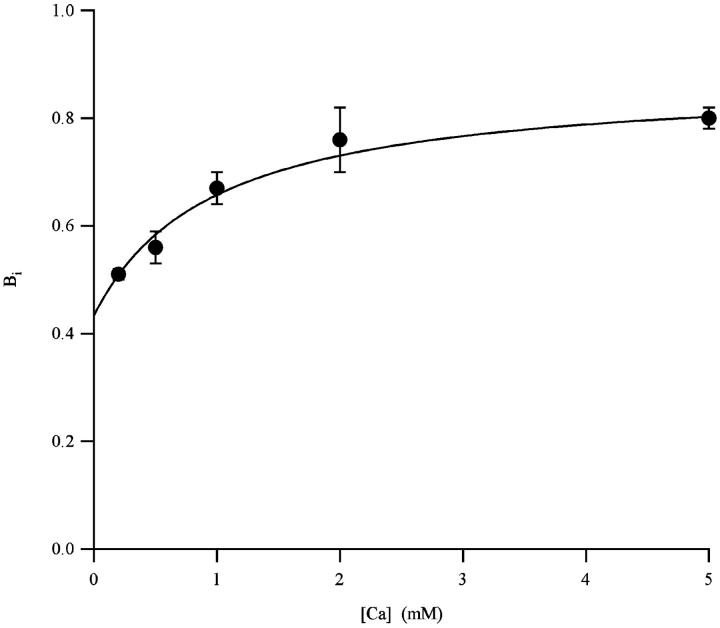
The formulation of the four-states ion-trapped model outlined in Scheme 1 predicts that the maximum UD-effect, B_i, depends on the contribution of the interaction of the two possible trapped cations, Na⁺ and Ca²⁺. The relative contribution of Na⁺ and Ca²⁺ in the magnitude of the UD can be discriminated by evaluating the maximum UD effect and different ion concentration (Conti et al., 1996). We have evaluated B_i for STX varying the Ca²⁺ concentration (0.2, 0.5, 1, 2, and 5 mM). We did not succeed in carrying out experiments at concentrations lower than 0.2 mM, as the patch instability in these conditions prevents long-lasting measurements necessary for B_i evaluation.

Measurements of B_i at different Ca²⁺ concentrations are shown in Fig. 4. B_i data at a given Ca²⁺ concentration was obtained measuring the asymptotic UD extra-block, B_e, and the UD time constant, τ, at different STX concentrations, as shown in Fig. 3. To fit data with Eq. 13, K_Na was kept at 34 mM, as estimated by measuring the competition of cations on STX binding (Weigele and Barchi, 1978). Results of the fit are summarized in Table 2, where they are also compared with those obtained for the UD of TTX on Nav1.2 expressed in frog oocytes. These results indicates that the magnitude of both UD contributions, B_i,Na and B_i,Ca, are larger for STX than for TTX.

FIGURE 4.

Maximum STX UD effect as a function of Ca²⁺. Each symbol represents the results (mean ± SE) of the fit of B_e and τ with Eqs. 7 and 8 at a given Ca²⁺ concentration. The least-squares fit of data with Eq. 13 is represented as a continuous line.

TABLE 2.

Na⁺- and Ca²⁺-specific maximum UD effect, B_i,Na and B_i,Ca, for TTX and STX

	ν0	KNa (mM)	Bi,Na	νNa	KCa (mM)	Bi,Ca	νCa
STX	0.022	34	0.56 ± 0.08	0.05	0.24 ± 0.01	0.88 ± 0.04	0.183
TTX	0.020	34	0.45 ± 0.06*	0.036	0.16 ± 0.08*	0.78 ± 0.04*	0.091

For STX, parameters were obtained from the fit of Fig. 4 with Eq. 13. Sodium and calcium dissociation constants, K_Na and K_Ca, are also shown. K_Na was fixed 34 mM (Weigele and Barchi, 1978). The dissociation rate of the toxin from an ion-free channel, ν₀, and from channels occupied by Na⁺ or Ca²⁺, ν_Na and ν_Ca, were calculated from Eq. 11.

^*Data obtained on Nav1.2 expressed in frog oocytes (Conti et al., 1996; Boccaccio et al., 1999).

DISCUSSION

Our measurements of tonic and phasic block of Nav1.4 channels expressed by transfected CHO cells are in remarkable agreement with those obtained on Nav1.2 channels expressed by cRNA-injected Xenopus laevis oocytes. The region of the channel putatively facing the pore walls (Penzotti et al., 1998, 2001; Choudhary et al., 2002; Lipkind and Fozzard, 2000) is noteworthily well-conserved, with only one residue, in the first repeat, which is different between the two studied phenotypes (F385 in Nav1.2 and Y401 in Nav1.4). Moreover, this difference seems not to be relevant for the toxin affinity, as the conservative mutation Y401F in Nav1.4 does not change the STX binding properties significantly (Favre et al., 1995), while other mutations, to nonaromatic residues, reduce the TTX and STX affinity (Penzotti et al., 2001; Favre et al., 1995; Backx et al., 1992; Heinemann et al., 1992a). Hence, our results confirm the substantial equivalence of the two different models of heterologous expression and the essential identity of the receptor site (same structure of Na1.2 and Na1.4).

Both TTX data and our new data concerning the tonic and phasic block of Nav1.4 channels by STX are very well described in terms of the ion-trapped model that did explain the UD of TTX on oocytes (Conti et al., 1996), and was demonstrated to provide a good analysis framework to study single point mutations of the Nav1.2 pore (Boccaccio et al., 1999). The analysis with this model provides a set of kinetic parameters that describe the toxin-channel interactions and their modification due to the presence of a specific trapped ion. The set of parameters that we can obtain from the analysis of UD for a given extracellular ionic concentration consists of two different dissociation constants for toxin binding under tonic and saturating stimulations respectively, K_T and K_M, the maximum UD-effect, B_i, and the association and free-channel dissociation rate constants, k_on and ν₀. We carried out the analysis of the TTX interactions with Nav1.4 in ionic conditions equivalent to those that we had previously applied on Nav1.2 (Boccaccio et al., 1999; Conti et al., 1996). Considering the highly conserved amino acid sequence of the pore vestibule of these two channels, we expect very similar properties for the interactions of TTX with Nav1.2 and Nav1.4. Indeed, as presented in Table 1, tonic block and UD data obtained with the two systems studied are in remarkably good agreement. Hence, we can conclude that, as expected, the interaction of Nav1.2 and Nav1.4 channels with TTX is practically the same, as revealed by the invariance of the maximum affinity which is expressed in terms of K's of the second-order association rate constants, k_on, and the dissociation rate constant, ν₀. Moreover, the expression system, transfection of cDNA on mammalian cell lines or microinjection cRNA on Xenopus oocytes, apparently does not have any influence on the pore properties of the sodium channel.

Compared to the TTX binding properties, the lower tonic and phasic dissociation constants of STX confirm the well-known fact that STX is more potent than TTX (Terlau et al., 1991; Stephan et al., 1994; Penzotti et al., 1998; Ritchie and Rogart, 1977). A current hypothesis to explain this difference among the two guanidinic toxins is based on the higher electric charge of STX (Penzotti et al., 1998; Ritchie and Rogart, 1977). In fact, if one assumes that a large part of the interaction of a toxin with the outer pore of the sodium channel occurs between the guanidinium groups and the acidic side chains of the channel protein, then STX, with two guanidinium, would bind more tightly than TTX which has only one guanidinium group. Intuitively, this charge difference would result in a more stabilized binding of STX, with a longer permanency in the mouth of the channel. However, our data show that this intuitive simple explanation is incorrect. Both the kinetics of the UD phenomenon and the workout data show that the first-order dissociation rate constant of the toxin from the ion-free pore, ν₀, evaluated for TTX and STX, are nearly identical (0.020 s⁻¹ and 0.022 s⁻¹ respectively). This indicates that when the two toxins are bound to the channel and the pore is free from ions, they have the same probability to remain in its binding site independently to their electric charge. Such charge independence argues in favor of the idea that the guanidinium toxin-sodium channel polypeptide interaction is mainly nonelectrostatic. However, that interpretation is in contrast with the observation that charge modifications in the residues that are putatively involved in the toxin binding result in a strong change of toxin affinity (Terlau et al., 1991; Pusch et al., 1991; Noda et al., 1989; Heinemann et al., 1992b; Satin et al., 1992; Kontis and Goldin, 1993), and that ν₀ is heavily modified by such mutations (Boccaccio et al., 1999). In fact, the molecular model of the sodium-channel pore proposed by Lipkind and Fozzard (1994), and successively refined based on point mutation experiments (Penzotti et al., 1998) and on Kcsa homology (Lipkind and Fozzard, 2000), suggest that the 1,2,3 guanidinium group of TTX and the 7,8,9 guanidinium group of STX are near to the DEKA ring, the selectivity filter motif of the channel, while the second charged group of STX, the 1,2,3 guanidinium group, would interact with an aspartate residue in the IV repeat. A possible explanation for this paradox is that the charged residues on the putative toxin receptor are involved in the maintenance of its relative orientation, without a direct involvement of their side chains on the binding of STX or TTX to the sodium channel.

Differently, the second-order dissociation time constant k_on for STX, 0.029 s⁻¹ nM⁻¹ is ∼10 times larger than 0.0029 s⁻¹ nM⁻¹ measured for TTX. Therefore, the higher potency of STX is due to its higher rate of “on,” while the probability of its dissociation from the channel is the same as that of TTX.

We have found that STX has a larger maximum UD effect (B_i = 0.76) than TTX (B_i = 0.63) According to our ion-trapped model, B_i is independent to the second-order association rate constant, k_on, but depends only on the dissociation rate constants, ν₀, ν_Na, and ν_Ca, as shown in Eq. 13. As stated above, both guanidinic toxins have a similar ν₀, and probability of occupancy of the channel by a cation—which occurs before the toxin binding—is invariant. Therefore, a bigger maximum UD effect is due to an increase of the ion-specific maximum UD effect, B_i,Na and B_i,Ca, as a consequence to the increase of the dissociation rate constants ν_Na and ν_Ca in the presence of a trapped ion. A comparison of the values of B_i,Na and B_i,Ca estimated here for STX with those that we have previously estimated for TTX (Conti et al., 1996) shown in Table 2 confirm this hypothesis.

Energetic considerations of the differences on the interactions of STX and TTX and the sodium channel can lead to some interesting conclusions. We can state that the free energy of the channel-toxin complex undergoes changes, depending on the simultaneous presence of the trapped cation. Hence, the difference of ΔG_ion between an ion-free and an ion-occupied channel is

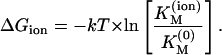(14)

In the simplest model, one can tentatively assume that the most important contributions to ΔG_ion arrives from the electrostatic interaction between the trapped cation and the guanidinium part toxin. Considering the charges of Na⁺ and Ca²⁺, and assuming a single point charge for the toxin, even for the divalent STX, we can write that,

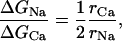(15)

where r_Ca and r_Na are the toxin-to-trapped-ion distance. In the hypothesis that the toxin-to-ion distance is independent of the species of the trapped ion, we would expect that ΔG_Na/ΔG_Ca = 0.5. This theoretical value is different than 0.40 and 0.39, which are estimated for TTX and for STX, respectively. As a consequence, we have estimated that the ratio r_Ca/r_Na for both toxins is ∼0.8, meaning that in either case the trapped Ca²⁺ is located nearer than the trapped Na⁺ to the guanidinium groups of the toxin (see Table 3). Similarly, to evaluate the ratio of the toxin to trapped ion distances, r_TTX and r_STX, we can write:

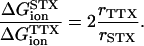(16)

TABLE 3.

ΔG_ion of interaction of TTX and STX and the trapped ions Na⁺ and Ca²⁺

	ΔGion
	Na+	Ca2+	rCa/rNa
TTX	0.598 kT	1.514 kT	0.790
STX	0.821 kT	2.120 kT	0.775
rTTX/rSTX	0.686	0.700

ΔG_ion was calculated according to Eq. 15, and is expressed in kT. The resulting distance ratios for the toxin-trapped ion distances are also presented.

In this case, for either trapped ion the ratio r_TTX/r_STX is ∼0.7, indicating that TTX is located nearer to the trapped ion, probably bound more deeply than STX. A more externally bound configuration for STX could be consistent with the greater bulkiness of STX with respect to TTX.

An absolute estimate of the relative positions of the toxin and the trapped ion is difficult to obtain at this stage. A very rough estimate of the distance between TTX and a trapped Na⁺, assuming the dielectric constant of water, yields r_Na ≅ 11.5 Å. Assuming that a guanidinium group of either toxin is close to the selectivity filter motif DEKA (Penzotti et al., 1998) and that the residue ring that forms the binding site for the toxin is in the entrance of the narrow selective filter, in a hypothetical pore structure predicted by homology with the Kcsa structure (Lipkind and Fozzard, 2000), the trapped ion would be located in the inner entrance of the filter. Another possibility is that the trapped ion is actually located at a shorter distance from the toxin, and most of the electrostatic forces produced by the presence of the cation are counterbalanced by polarization and/or neutralization of charged residues of the channel, attenuating the electrostatic energy between the ion and the toxin, contrary to what we have assumed in these calculations.

A complete image of the structure of the sodium-channel pore and the toxin-channel interactions is difficult to obtain from the available data. However, these data provide more constraints to be used in the modeling of the sodium channel before the crystallographic structure becomes available, and perhaps will represent an aid for design of sodium-channel targeted drugs.