Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 May;84(5):3111–3122. doi: 10.1016/S0006-3495(03)70036-8

Mechanism of the Lamellar/Inverse Hexagonal Phase Transition Examined by High Resolution X-Ray Diffraction

Michael Rappolt *, Andrea Hickel †, Frank Bringezu †, Karl Lohner †
PMCID: PMC1302872  PMID: 12719241

Abstract

For the first time the electron density of the lamellar liquid crystalline as well as of the inverted hexagonal phase could be retrieved at the transition temperature. A reliable decomposition of the d-spacings into hydrophobic and hydrophilic structure elements could be performed owing to the presence of a sufficient number of reflections. While the hydrocarbon chain length, dC, in the lamellar phase with a value of 14.5 Å lies within the extreme limits of the estimated chain length of the inverse hexagonal phase 10 Å < dC < 16 Å, the changes in the hydrophilic region vary strongly. During the lamellar-to-inverse hexagonal phase transition the area per lipid molecule reduces by ∼25%, and the number of water molecules per lipid increases from 14 to 18. On the basis of the analysis of the structural components of each phase, the interface between the coexisting mesophases between 66 and 84°C has been examined in detail, and a model for the formation of the first rods in the matrix of the lamellar phospholipid stack is discussed. Judging from the structural relations between the inverse hexagonal and the lamellar phase, we suggest a cooperative chain reaction of rod formation at the transition midpoint, which is mainly driven by minimizing the interstitial region.

INTRODUCTION

In the framework of our research, liposomes serve as membrane systems mimicking either the cytoplasmic membrane of bacteria or erythrocyte membranes, which differ markedly in their membrane architecture and lipid composition (Lohner et al., 1997; Lohner and Prenner, 1999). A wealth of information exists concerning the phospholipid composition of individual Gram-negative and Gram-positive bacteria. Besides anionic phospholipids, they contain phosphatidylethanolamine (PE), e.g., 82% of the inner membrane of Escherichia coli. Antimicrobial peptides are primarily thought to kill bacteria by permeation of their cytoplasmic membrane (Lohner, 2001). One remarkable feature is that antimicrobial peptides induce the formation of cubic phases in lipid extracts of E. coli (Staudegger et al., 2000) and in PE model membranes (Hickel and Lohner, 2001), which seems to be most pronounced near the liquid crystalline lamellar/inverse hexagonal phase transition (Lα–HII). In pure PE lipid systems, such as dioleoyl-PE (DOPE), cubic phases do not form instantaneously, but instead, it can take days of equilibration until the evolution of a bicontinuous cubic lattice is accomplished (So et al., 1993). Alternatively, cubic phases can be induced by temperature cycling of several hundred or thousand times through the lamellar/inverse hexagonal phase transition (Shyamsunder et al., 1988; Erbes et al., 1994). Further, it has been shown that several sodium salts and the disaccharides sucrose and trehalose strongly accelerate the formation of the cubic phase in PE dispersions upon cycling through the Lα ↔ HII phase transition (Tenchov et al., 1998). Hence, there is evidence that the formation of cubic phases in PE is strongly connected to the lamellar/inverse hexagonal phase region. However, even though the inverse hexagonal phase possesses the simplest topology of all nonlamellar lipid structures, little agreement could be achieved about the molecular details of the formation of this phase (for reviews see Seddon, 1990; Siegel, 1999). Thus, in this work we revisit the topic of the inverse hexagonal phase formation, with the aim to serve on-going investigations on the role of antimicrobial peptides to strongly destabilize the lamellar phase of PEs in the lamellar/inverse hexagonal coexistence region.

Furthermore, over the past 20 years, many scientists have concentrated their attention on the lamellar/inverse hexagonal phase transition, because of its importance for understanding membrane fusion (Jahn and Grubmüller, 2002). Fusion of biological membranes is governed by physical principles, and in recent years many model calculations on low-energy intermediates have been published (Siegel, 1993; Kuzmin et al., 2001). However, it still remains a great puzzle whether the transition states are primarily determined by lipid physics or by protein-lipid interactions (Chernomordik, 1996; Bradshaw et al., 2000; Epand, 2000). Inverted hexagonal lipid phases have also regained some special attraction in the scientific community, because they can form complexes with DNA, which mimic natural viruses in their ability to act as synthetic carriers of extracellular DNA across the outer cell membranes for gene delivery (Koltover, et al., 1998).

The liquid crystalline Lα–HII phase transition is mainly apparent for lipids with small, weakly hydrated headgroups. Increasing temperature expands the interfacial area. This leads to energetically unfavorable contact between the aqueous and hydrophobic regions, resulting in the formation of an inverse hexagonal phase, where such lipids can adopt inverse curvature at the interface, allowing the chains to splay and at the same time reduce the headgroup area at the interface (Seddon et al., 2000). Since the topologies of the involved phases are quite different, there exist some energetic barriers for the Lα–HII phase transition. First, there is a high cost of exposing the acyl chain region of the lipid to water as the interface geometry changes. Second, the initial radial growth of the HII rods is accompanied by the uptake of water (the lamellar and inverse hexagonal phase have different fractional hydration volumes) and third, the hydrocarbon chains are forced to assume a variety of lengths to fill out the hexagon in the HII phase (Tate et al., 1992; Turner and Gruner, 1992). So far, several models have been proposed for structures mediating this transition. But it seems still valid today that “many more experiments are necessary to sort out the important factors of the transition,” as stated 10 years ago by Tate and colleagues (Tate et al., 1992).

Using mainly freeze-fracture electron microscopy, “lipidic particles” (LIPs) have been discovered in various lipid mixtures. Since on some replicas the strings of LIPs could be seen to be co-linear with the adjacent HII phase, these particles have been assigned to play an important role to mediate the formation of the inverse hexagonal phase as intrabilayer inverted micelles (Verkleij et al., 1978, 1979; Verkleij, 1984). This view has been contradicted by other groups (Miller, 1980; Hui and Stewart, 1981), who suggested that LIPs represent intermembrane attachment sites of two opposing bilayers rather then intrabilayer micelles. First-sketches published by Hui et al. (1982) to explain the molecular rearrangement and the involved topological elements during the membrane fusion and also pore formation are still widespread concepts. Only today, the technical terms have changed a bit: after adhesion of two opposing bilayers an intermembrane attachments site can form (stalklike topology), which can either directly induce a pore (interlamellar attachment) or convert into an extended area of intermembrane contact (transmonolayer contact, or hemifusion). The latter intermediate may also convert into a pore. On the basis of either conical intermembrane connection sites (stalklike topology) or spherical intermembrane connection sites—likely containing inverted micelles—a detailed model for the Lα–HII phase transition has been published (Hui et al., 1983). In any case, the starting point for the formation of the inverse hexagonal phase are believed to be line defects, due to string formation of conical or spherical LIPs, which convert either into walls or tubes, respectively. In 1986, Siegel pointed out that inverted micellar intermediates may seed line defects as an alternative to their coalescing into tubes directly. In another model it was proposed (Caffrey, 1985), that rod formation begins at a region of the bilayer, which has folded back on itself. This topology causes high internal stress, and local dimpling inward to the planar region of the membrane eventually pinching off an isolated cylinder of water. Note that each of the pictures given above involves structures forming between bilayers, and it has been very common to believe that HII tubes can only form being commensurate with the Lα lattice, i.e., that the lamellar d-spacing matches the repeat distance in the [1,0] direction of the inverse hexagonal phase. However, direct experimental evidence is poor that in an early step of transition the lamellar and inverse hexagonal lattice could match in a co-planar fashion (Tate et al., 1992). Even under fastest heating conditions with a laser-induced temperature jump, the coexisting lamellar and inverse hexagonal lattices are never commensurate (Laggner et al., 1991). These authors describe the transition plane in such a way, that no loss of long-range order occurs, but without fixing the inclination angle between the lamellar and inverse hexagonal lattice to the commensurate value of 60°. We like to stress that all-above models are based on line defects for the formation of the first rods, but recently, a completely different mechanism has been presented (Siegel and Epand, 1997; Siegel, 1999). Here, in a quite complex manner the aggregation of transmonolayer contacts (hemifusion contacts) into a body-centered cubic or primitive tetragonal phase is described. This phase is believed to serve as a precursor for the formation of the HII phase.

Apart from diverging ideas of how to explain the cooperative and relatively fast Lα–HII phase transition in PEs, several of the proposed models suffer from incorrect geometrical dimensions, e.g., too thick water layers are shown. The most common reason for this lies in the lack of detailed structural information. This was one impetus, to carry out x-ray diffraction experiments in the lamellar/inverse hexagonal phase region of PEs using a high brilliance Synchrotron source. For the first time we could retrieve the electron density of the lamellar liquid crystalline as well as of the inverse hexagonal phase at the transition midpoint, and this with a reliable decomposition of the lattice spacings into hydrophobic and hydrophilic structure elements. Not only is the interface region between the two phases now presented in a realistic manner, but also a hypothesis for the mechanism of this phase transition will be discussed that hopefully will stimulate new discussions on the molecular mechanism of the formation of the inverse hexagonal phase.

MATERIALS AND METHODS

Sample preparation

1-Palmitoyl-2-oleoyl-sn-phosphatidylethanolamine (POPE) was purchased from Avanti Polar Lipids, Alabaster, AL (purity >99% with not more than 5% acyl migration in the chain; information by Avanti Polar Lipids), and used without further purification. For x-ray diffraction measurements multilamellar liposomes were prepared by dispersing 20 wt% of lipid in quartz bi-distilled and deionized water. To ensure complete hydration, the lipid dispersions were shock-frozen in liquid nitrogen, thereafter thawed for 15 min, reaching a final temperature of 50°C (∼26°C above the main transition), and finally vigorously vortexed for 2 min. For further annealing of the liposomes the above procedure was repeated six times. This method of liposome preparation was also used for DSC experiments, which resulted in fully reproducible excess heat capacity curves upon rescans displaying a narrow, cooperative chain-melting transition.

Before and after all experiments the purity of the phospholipid was checked by thin layer chromatography using CHCl3/CH3OH/NH3,conc. (75:25:6 v/v) as solvent. Aluminum sheets, silica gel 60, purchased from Merck (Darmstadt, Germany) were used as stationary phase. All phospholipid samples showed only a single spot before and after the measurements.

Small angle x-ray diffraction

Diffraction patterns were recorded on the Austrian SAXS beamline at ELETTRA, Trieste (Amenitsch et al., 1998; Bernstorff et al., 1998) using a one-dimensional position sensitive detector (Petrascu et al., 1998) covering the corresponding s-range (s = 2π sin(θ)/λ) of interest from ∼1/450 Å−1 to 1/12 Å−1. The angular calibration of the detector was performed with silver-behenate (CH3(CH2)20−COOAg): d-spacing 58.38 Å (Huang et al., 1993). The lipid dispersions were measured in a thin-walled, 1-mm diameter quartz capillary in a steel cuvette (Anton Paar, Graz, Austria), which was inserted into a brass block. This sample holder block was in thermal contact with a water circuit, i.e., it was connected to a water bath with a freely programmable control unit (Unistat CC, Huber, Offenburg, Germany). To avoid air convection at the capillary, the entrance and exit windows of the block have been covered with a thin polymer film. The temperature was measured in the vicinity of the capillary in the sample holder block with a Pt-element (100 Ω). Before exposure, the sample was equilibrated for a period of 10 min for a given temperature. To prevent radiation damage, the capillaries were translated horizontally by 1 mm to an unexposed portion of the sample after every second measurement. Exposure times were typically 300 s.

Differential scanning calorimetry (DSC)

Calorimetric experiments were performed with the Microcal VP-DSC high-sensitivity differential scanning calorimeter (Microcal, Northampton, MA). A scan rate of 0.5°C/min was used, and scans were performed between 10 and 90°C. Experiments were repeated at least twice to ensure reproducibility. The total lipid concentration used for the DSC scans was 2.0 mg ml−1. Data acquisition and analysis was done using Microcal's Origin software (Microcal). The enthalpy change of the phase transition, ΔH, was obtained from the area under the peak and the mass of phospholipid. To calculate the area under the peak, the baseline was formed by connecting the linear segments of the heat capacity curve between the start and endpoint of the transition. Using a cubic polynomial connection—that also takes into account the slope of the linear segments—gave identical results. The phase transition temperature was defined as the temperature at the peak maximum.

X-ray diffraction data analysis

The electron density maps of the phospholipid samples in the Lα and HII phases, respectively, were derived from the small-angle x-ray diffractograms by standard procedures (for example see Harper et al., 2001). After the raw data had been corrected for detector efficiency, and the background scattering both from water and the sample cell had been subtracted, all Bragg peaks were fitted by Lorentzian distributions. The fittings were carried out with the software package Origin 5.0 (Microcal Software, Northampton, MA). For the inverse hexagonal phase the intensities were also calibrated for the multiplicity, i.e., by dividing the intensity of the (2,1) peak by 2 (Turner and Gruner, 1992). Thereafter, a Lorentz correction was applied by multiplying each peak intensity (peak area) by its corresponding wave vector s2 (for discussion, see Warren, 1969). The square root of the corrected peak intensity was finally used to determine the form factor F of each respective reflection. The electron density profile relative to the constant electron density profile of the water was calculated by the Fourier synthesis

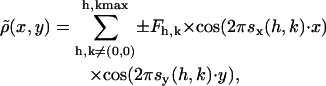graphic file with name M1.gif (1)

where Fh,k is the amplitude of the peak at the position s(h,k) and h,k are the indices of each reflection. The phase information for each diffraction order is either positive or negative for a centrosymmetric electron density profile such as occurs for both lipid phases. In the temperature region between 30°C and 85°C, a maximum of four orders could be resolved for the Lα phase, and in the inverse hexagonal phase, the (1,0), (1,1), (2,0), (2,1), and (3,0) reflections were recorded. The best phasing choice for the lamellar liquid crystalline (− − + −) as well as for the inverted hexagonal phase (+ − − + +) were taken from Harper et al. (2001), who have studied seven different diacyl phosphatidylethanolamines. We also checked all other phase combination for the lamellar phase, but only the presented phasing resulted in electron density profiles (see Fig. 4 A) that show: 1) a good similarity in the hydrocarbon chains region to, for example, the very well-studied Lα phase of dipalmitoylphosphatidylethanolamine (DPPE) (Pabst et al., 2000a); and 2) display the proper headgroup size, dH (Fig. 4 A), of ∼8 Å (Katsaras et al., 1993). All other phase combinations lead to improper structural features such as a too big hydrocarbon core, missing methyl trough, and a too small headgroup size, just to mention some of the most important failures. For the inverse hexagonal phasing, we checked only the phase of the (2,1) reflection, inasmuch as it had been reported by Turner and Gruner (1992) that it changes its sign at very high temperature. Nevertheless, choosing the phase of the (2,1) reflection negative resulted in a nonuniform electron density for the water region and too strong a radial fluctuation of the water core radius. Thus, it is not surprising that our system (POPE) has the same phasing as, for example, DOPE at 20°C.

FIGURE 4.

FIGURE 4

Open in a new tab

(A) Electron density profile of the Lα phase of POPE at 30°C (refers to Fig. 2 A). The decomposition of the bilayer is defined in the upper scheme. The steric bilayer thickness, dL, and water layer thickness, dW, are given according to the Eqs. 2 and 3. The distance between the two electron density maxima defines the phosphate-to-phosphate group distance, dPP. The headgroup size, dH, is fixed to a value of 8 Å (for details, see the Data Analysis section). (B) The steric bilayer thickness, dL (▪), and water layer thickness, dW (○), as function temperature in the range of 30–74°C are shown.

The decomposition of the lamellar d-spacing, d, into structural components such as bilayer, dL, and water layer thickness, dW, is not trivial, and their errors lie typically in the range of 1–2 Å (Pabst et al., 2000a). Applying gravimetric methods, the errors might be even higher (Nagle and Tristram-Nagle, 2000). Therefore, we favor keeping the decomposition as simple as possible. Space-filling molecular models show that the PE headgroup size, dH (Fig. 4 A), should be ∼8 Å in the Lα phase (headgroup volume = 252 Å3; McIntosh and Simon, 1986a)). Thus, we can define the steric lipid bilayer thickness simply as

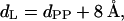graphic file with name M2.gif (2)

in which dpp is defined as the phosphate-to-phosphate group distance. This approach is taken from McIntosh and Simon, 1986b) (see also Fig. 4 A). Consequently, the water layer thickness, dw, is then given by

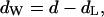graphic file with name M3.gif (3)

where d is the repeat distance of the lamellar lattice.

Corresponding structural parameters are given for the inverse hexagonal lattice,

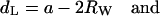graphic file with name M4.gif (4)
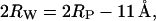graphic file with name M5.gif (5)

where a is the unit cell parameter of the inverse hexagonal cell, and Rp is the mean water core radius, defined as the mean distance from the center of the rod to the phosphate groups (see Fig. 5 A). Also, for the inverse hexagonal phase, the lipid headgroup extension is fixed. The value of 11 Å is taken from cylindrical model fittings to highly resolved electron density maps of DOPE at 50 and 80°C, respectively (Turner and Gruner, 1992).

FIGURE 5.

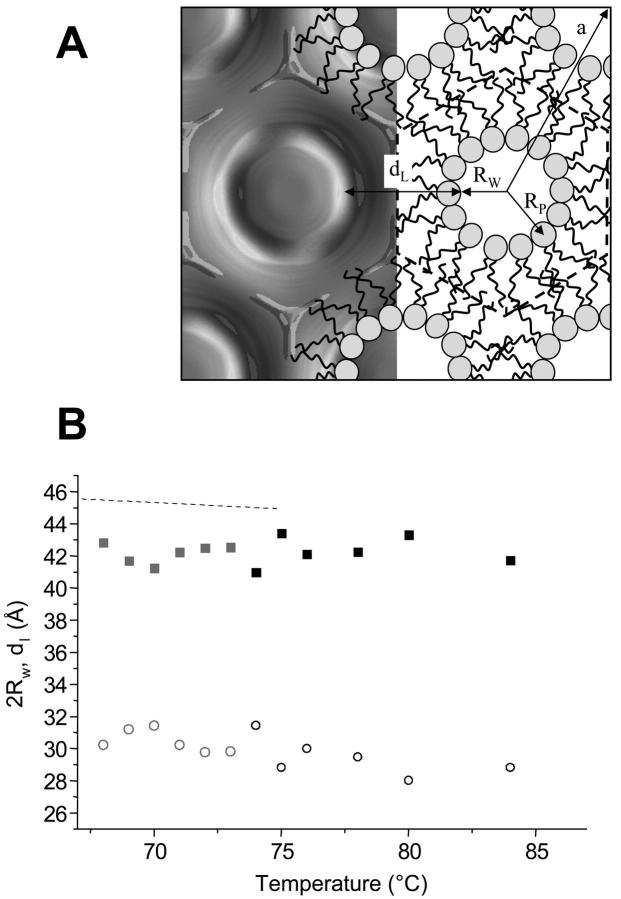
FIGURE 5

Open in a new tab

(A) Electron density map of POPE at 84°C (left, refers to Fig. 2 B). The organization of the lipid molecules is schematically demonstrated on the right-hand side: RP is the phosphate to the center of the water core distance, and RW is the radius of the water core (see also Eq. 5). The Wigner-Seitz cell is defined by the dashed line, i.e., the origin is set to the center of the water core, and dL is defined as the lipid layer thickness along the direction of the unit cell vector (compare Eq. 4). (B) The minimum bilayer thickness, dL (▪), and the water core diameter, 2 RW (○), as a function temperature in the range of 68–84°C, are shown. Data points, which have been determined from three-peak reconstructions, are kept in gray (for details, see Data Analysis). The dashed line displays the corresponding steric bilayer thickness of the lamellar phase.

While the steric distances are of special importance for the investigation of interbilayer interactions (Rand and Parsegian, 1989; Petrache et al., 1998), the Luzzati method dividing the lipid/water aggregate into two compartments only (see Luzzati, 1968; and for a review, see Nagle and Tristram-Nagle, 2000), is useful to derive the lateral area per lipid. The interface between hydrophobic and hydrophilic regions, respectively, is roughly determined by the position of the headgroup center (see dPP and RP in Figs. 4 A and 5 A, respectively). The area, A, per lipid at the lipid/water interface is calculated as

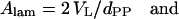graphic file with name M6.gif (6)
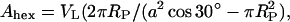graphic file with name M7.gif (7)

where VL is the lipid volume. The estimation of the volume of the POPE lipid was carried out according to a method described elsewhere (Harper et al., 2001) and relies on experimental data of DOPE from Tate and Gruner (1989).

Finally, some remarks on the reliability of the decomposition have to be discussed briefly. The most useful quantitative information from the electron density profiles of the lamellar phase is the phosphate-to-phosphate distance, dPP (Fig. 4 A), in the bilayer, which can be generally obtained within a few Å provided that at least four diffraction orders are resolved (Nagle and Tristram-Nagle; 2000; Pabst et al., 2000a). Therefore, we do not give any value for dPP above 74°C, where we could only record three or less orders (see Table 1). Recalling the precision of gravimetric and x-ray diffraction methods, it is generally accepted to set the headgroup-to-headgroup distance equal to the Luzzati bilayer thickness (see Eq. 6; see also Fig. 4 A).

TABLE 1.

Basic parameters given for the lamellar phase of POPE between 30 and 80°C: amplitudes of the first four-order reflections, d-spacing, phosphate-to-phosphate group distance dpp, and volume of the lipid molecule, VL

T (°C) Amplitudes 1, 2, 3, 4 d (Å) dpp (Å) VL (Å3)
30 1.0 0.13 0.24 0.34 53.6 40.0 1175
35 1.0 0.14 0.22 0.32 52.9 39.5 1180
40 1.0 0.17 0.23 0.29 52.5 39.0 1185
45 1.0 0.16 0.25 0.31 52.0 38.6 1190
50 1.0 0.15 0.23 0.30 51.5 38.4 1190
54 1.0 0.17 0.25 0.31 51.2 38.0 1195
58 1.0 0.16 0.24 0.28 50.9 37.8 1200
60 1.0 0.15 0.23 0.31 50.8 37.9 1200
62 1.0 0.15 0.22 0.27 50.7 37.8 1200
64 1.0 0.16 0.21 0.31 50.5 37.7 1205
66 1.0 0.14 0.23 0.25 50.4 37.5 1205
67 1.0 0.14 0.25 0.25 50.3 37.4 1205
68 1.0 0.15 0.23 0.32 50.3 37.4 1205
69 1.0 0.16 0.26 0.26 50.2 37.3 1205
70 1.0 0.14 0.23 0.26 50.1 37.3 1210
71 1.0 0.16 0.24 0.31 50.0 37.2 1210
72 1.0 0.15 0.25 0.30 50.0 37.0 1210
73 1.0 0.16 0.23 0.25 49.9 37.1 1210
74 1.0 0.13 0.22 0.35 49.9 37.4 1210
75 1.0 0.12 0.26 – 49.8 – 1210
76 1.0 0.25 – – 49.9 – 1215
78 1.0 – – – 49.7 – 1215
80 1.0 – – – 49.6 – 1215
Open in a new tab

In the inverse hexagonal lattice for DOPE it was found that the water core radius is circular within 5% (Turner and Gruner, 1992), and the mean value of the water core radius, RP, compares well to the measured averaged water core radius with gravimetric methods (Tate and Gruner, 1989). Thus, again, the position of the phosphorus group can be interpreted as the location of the Luzzati interface. But how reliable is it to define the position of the phosphorus group through the maximum of the electron density map? Highly resolved diffraction data on 1-stearoyl-2-oleoyl-phosphatidylethanolamine, SOPE (data not shown) and on DOPE (Turner and Gruner, 1992) have demonstrated, that the five-, seven-, and 10-peak reconstruction of the electron density map results in mean values of Rp, which agree with the Luzzati radius within 1 Å. However, the maximum peak position of the electron density shifts significantly, if only the first three or four reflections are taken into account to reconstruct the electron density map. Thus, if at least the first five peaks of the inverse hexagonal phase are recorded, the decomposition of the lipid/water aggregate into hydrophobic and hydrophilic compartments can be obtained within a few Å of precision. Very low resolution data may also be used to estimate RP, if only (1,0), (1,1), and (2,0) reflections are detected. In the temperature range from 74 to 84°C, we compared the results obtained for RP by three- and five-peak density reconstruction, respectively. We found that the RP value is systematically underestimated in the three-peak analysis, showing an astonishingly stable scaling factor of 1.12 ± 0.02. Therefore, we also included in this work the values from three-peak analysis in the temperature range between 68 and 73°C, taking into account the above-mentioned scaling factor (see Table 2; see also Fig. 5 B and Fig. 6). All basic parameters (d, a, dPP, RP, and VL) which have been used for the decomposition (Eqs. 2–5) are summarized in Tables 1 and 2.

TABLE 2.

Basic parameters given for the inverse hexagonal phase of POPE between 66 and 84°C: amplitudes of the reflections (1,0), (1,1), (2,0), (2,1), and (3,0); the unit cell spacing a; the distance from the center of the rod to the phosphate group RP; and volume of the lipid molecule, VL

T (°C) Amplitudes 1,0; 1,1; 2,0; 2,1; 3,0 a (Å) RP (Å) VL (Å3)
66 1.0 0.68 – – – 73.6 – 1205
67 1.0 1.11 – – – 73.4 – 1205
68 1.0 0.82 0.99 – – 73.1 20.6* 1205
69 1.0 1.09 0.97 – – 72.9 21.1* 1205
70 1.0 1.23 0.84 – – 72.7 21.2* 1210
71 1.0 1.00 0.68 – – 72.5 20.6* 1210
72 1.0 0.96 0.83 – – 72.3 20.4* 1210
73 1.0 0.95 0.74 – – 72.4 20.4* 1210
74 1.0 0.98 0.76 0.29 0.30 72.4 21.2 1210
75 1.0 0.97 0.76 0.14 0.20 72.3 19.9 1210
76 1.0 0.98 0.76 0.18 0.27 72.1 20.5 1215
78 1.0 0.97 0.75 0.14 0.32 71.8 20.2 1215
80 1.0 0.96 0.74 0.13 0.18 71.4 19.5 1215
84 1.0 0.98 0.75 0.19 0.26 70.6 19.9 1220
Open in a new tab
*

Values have been scaled up as described in the data analysis section.

FIGURE 6.

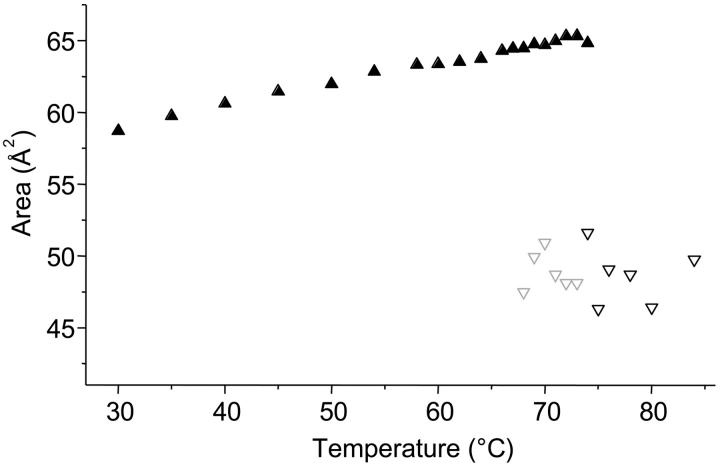
FIGURE 6

Open in a new tab

Area per lipid molecule in the Lα-phase (▴) and in the HII-phase (∇) at the Luzzati interface. Data points, which have been determined from three-peak reconstructions, are kept in gray (for details, see Data Analysis).

RESULTS

The Lα–HII phase transition is expected to be first-order due to symmetry considerations, and therefore, should occur at ambient pressure at a well-defined temperature TH (Toombes et al., 2002). Fig. 1 A shows the excess heat capacity curve of aqueous dispersions of POPE in the Lα–HII phase transition region, while SAX diffraction patterns obtained from POPE in the pure phases and at the phase transition temperature are given in Fig. 2. At a scan rate of 0.5°C/min the transition temperature has been recorded at 74.8°C with a width at half-height of 2.5°C and a transition enthalpy, ΔHH, of 2.0 kJ/mol. This compares to a value of 21.7 kJ/mol for the main transition enthalpy (data not shown). The measured transition enthalpies are in excellent agreement with values in literature, which, for example, rank for ΔHH from 1.7 to 2.0 kJ/mol (see database LIPIDAT; Caffrey, 1993).

FIGURE 1.

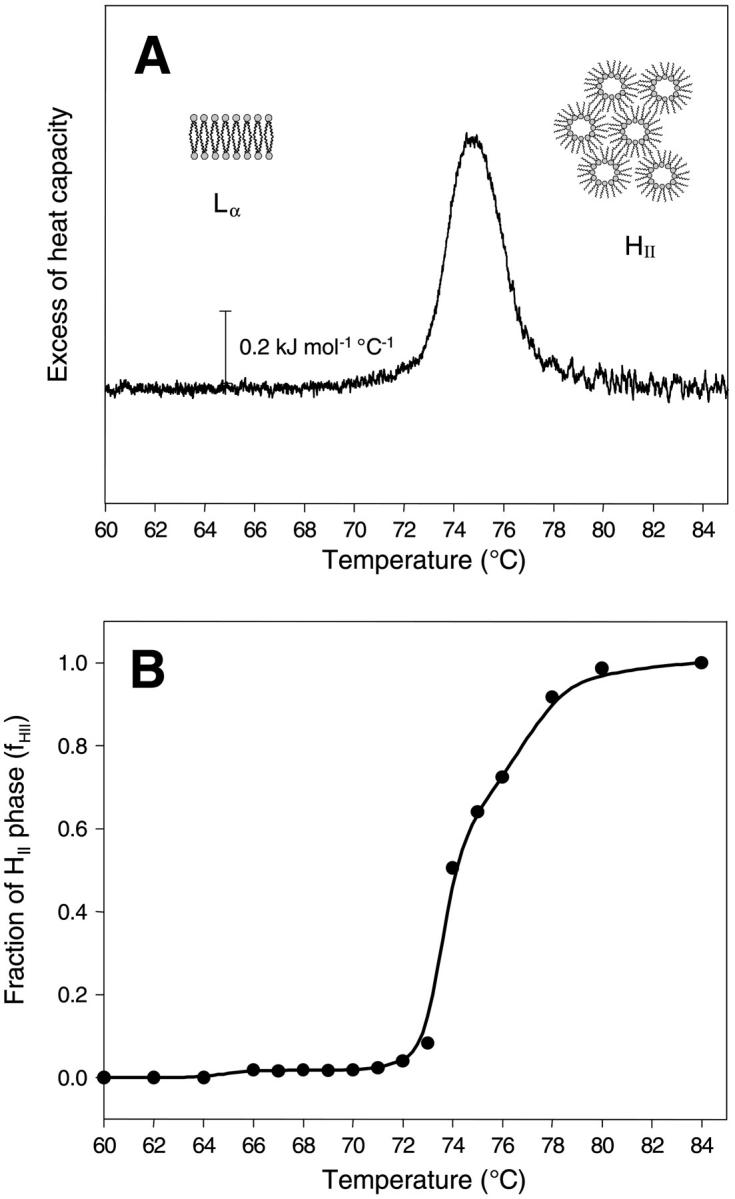
FIGURE 1

Open in a new tab

(A) Excess heat capacity curve of the Lα–HII phase transition region of POPE. The scan rate was 0.5°C/min. (B) Fraction of the HII phase as derived from the x-ray data. For details, see text.

FIGURE 2.

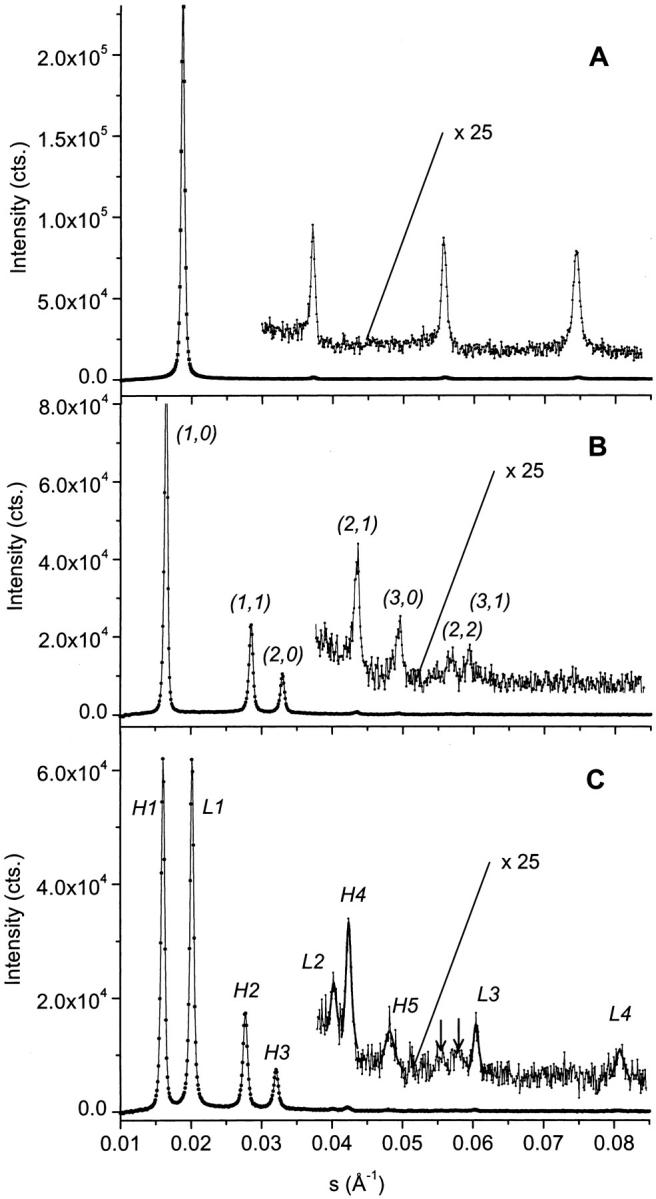
FIGURE 2

Open in a new tab

Small-angle x-ray diffractograms of aqueous dispersions of POPE in the Lα phase at 30°C (A), in the HII phase at 84°C (B), and at the transition midpoint of both phases at 74°C (C). All diffraction patterns show nonsmoothed data. Additionally, best fits to the weakest reflections are given at the transition midpoint. Two arrows mark the positions of the (2,2) and (3,1) reflections of the hexagonal phase.

The fractional conversion of the inverse hexagonal phase, fHII, was obtained by expressing the peak area of the (1,0) reflection of the inverse hexagonal phase as a function of temperature (Fig. 1 B). The intensity is normalized relative to the signal, when 100% of the sample is in the inverse hexagonal phase, i.e., the intensity at 84°C is set to unity. This parameter is proportional to the volume fraction giving rise to the diffraction pattern. However, it is only an approximate measure of the relative fraction, since the unit cell changes, and hence the structure factor may also alter (Rappolt and Rapp, 1996). The transition temperature, TH, derived from the x-ray data, lies at ∼74°C in reasonable agreement with our DSC data. Already at 66°C, traces of the inverse hexagonal phase are visible (fHII ∼2%), which is close to the onset of the phase transition as seen in the excess heat capacity curve. The lamellar phase is resistant up to ∼80°C, in agreement with the microcalorimetric measurements.

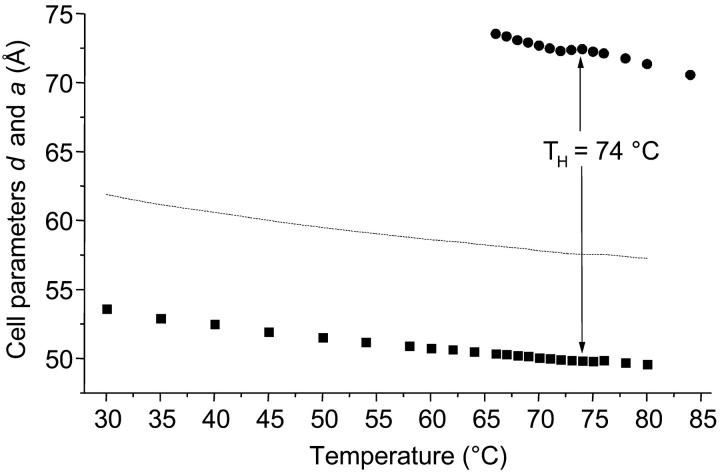
A closer look to the coexistence range is given in Fig. 3, in which the cell parameters of both phases (d and a) are shown. The coexistence range spans over a range of at least 14°C, i.e., from 66 to 80°C. Over the complete coexistence range the lattices of the two phases are clearly not commensurate. The condition for commensurate lattices (Tate et al., 1992),

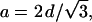graphic file with name M8.gif (8)

is never fulfilled. The HII cell parameter, a, would have to be as small as ∼60 Å to be commensurate with the initial Lα phase.

FIGURE 3.

FIGURE 3

Open in a new tab

Cell parameters of POPE. The lamellar d-spacing (▪) decreases almost linearly in the temperature range from 30 to 80°C. The dotted line demonstrates which value the unit cell parameter of the inverse hexagonal phase, a, (•) should possess, so that its lattice is commensurate with the lamellar lattice.

To get better insight into the structural details in the coexistence range, it is necessary to be able to decompose the lipid/water aggregates into their hydrophobic and hydrophilic components. As described in detail in the Data Analysis section, this can be achieved for the lamellar phase with realistic proportions, if at least the first four orders are resolved. The same accounts for the decomposition of the electron density map in the inverse hexagonal phase, if at least the first five reflections could be recorded.

In Fig. 4 A the relative electron density profile of the Lα phase of POPE at 30°C is shown. Four different regions can easily be distinguished, viewing from left to right: a thin water layer with a medium electron density (0.334 e/Å3), the headgroup region around the density maximum (0.54 e/Å3), again a medium density for the hydrocarbon chain region (0.30 e/Å3) and the lowest for the methyl trough (0.16 e/Å3). The above-given absolute values for the electron densities have been taken from Harper et al., 2001. In Fig. 4 B the steric bilayer thickness, dL, and the water layer thickness, dW, are given as a function of temperature. In contrast to the Luzzati definition of the water layer thickness (dW Luzzatti = d − dPP, see also the Data Analysis section), the steric definition of the water layer thickness describes only the free liquid space between adjacent bilayers. As can be judged from Fig. 4 B, both the lipid bilayer thickness and the free water spacing decline monotonously with temperature. This means that adjacent bilayers continuously approach each other. This is just the opposite effect as seen in the behavior of phosphatidylcholines, e.g., 1-palmitoyl-2-oleoyl-sn-phosphatidylcholine. While upon increase of temperature the bilayer thickness monotonously decreases and the area per lipid increases, the free fluid space between the lipid bilayers swells from 17 to 22 Å, most probably due to increasing undulations of the membranes (Pabst et al., 2000b).

For the inverse hexagonal phase corresponding structural parameters have been defined in Fig. 5 A (right-hand side). The decomposition of the water/lipid organization along the unit cell axis (origin set to the midpoint of the water core) shall be compared to the proportions of the structural elements of the lamellar phase. Only in the direction, where the phosphate to phosphate distance, dPP, is minimal, the lipid arrangement is similar to the lamellar bilayer motif shown in Fig. 4 A. Thus, the inverse hexagonal bilayer thickness, dL, is defined according to Eq. 4, and is displayed in Fig. 5 B together with the corresponding bilayer thickness of the lamellar phase (dashed line) between 66 and 84°C.

Whereas the free water core diameter, 2 RW, is much larger than the bilayer separation in the Lα phase (30 Å ≫ 5 Å), the difference in the bilayer thicknesses is only ∼3 Å (Fig. 5 B). Comparing the chain lengths, dC, of the phospholipids at the transition midpoint shows that the hydrophobic regions of both phases match quite well. At 74°C the hydrocarbon chain length in the lamellar phase is 14.5 Å (dC = d/2 − dW/2 − dH, Fig. 4 A) and lies within the extreme limits of the estimated chain length in the inverse hexagonal phase: 10 Å < dC < 16 Å. The minimum chain length of the lipid in the inverse hexagonal phase is given by

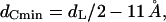graphic file with name M9.gif (9)

where the minimum bilayer distance, dL, is defined in Fig. 5 A and 11 Å is the estimated dimension of the radial headgroup extension (see Data Analysis). The lipid chains are most extended in the interstitial regions. These regions of minimum electron density are nicely seen at the corners of the Wigner-Seitz cell in Fig. 5 A (left-hand side), or by imagining a superimposed clock face; then the interstitial regions lie at 12, 2, 4, 6, 8, and 10 o'clock, respectively. Considering the geometry of the inverse hexagonal lattice (e.g., see Tate and Gruner, 1989), we estimate the maximum acyl chain length in the inverse hexagonal phase,

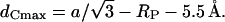graphic file with name M10.gif (10)

To calculate the values of dCmin and dCmax of the inverse hexagonal phase the values in Table 2 were used.

In Fig. 6 we compare the area per lipid molecule at the Luzzati interface (Eqs. 6 and 7). Since the Luzzati interface roughly intersects the center of the headgroups, the molecular area per lipid may be considered as the headgroup area. The headgroup area at this water/lipid interface shows that the molecular areas are considerably larger (∼25%) in the Lα phase and increase more rapidly with an increase in temperature than in the HII phase (see also Harper et al., 2001). However, so far analyzable (from 66 up to 74°C), the variation of Alam in the coexistence region is, with values between 63.3 and 64.3 Å2 , relatively small (Fig. 6), and may practically be considered as constant.

Finally, we estimated the number of waters per lipid from the area per lipid. Recalling the short argument in the Data Analysis section, the volume fraction of water, ΦW, need not necessarily be measured with the gravimetric method, but can be determined geometrically (Luzzati, 1968):

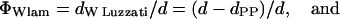graphic file with name M11.gif (11)
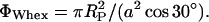graphic file with name M12.gif (12)

Note that Eq. 12 simply expresses the effective water area per unit cell area. Combining Eqs. 6 and 7 with Eqs. 11 and 12 lead to the useful expressions

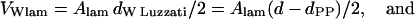graphic file with name M13.gif (13)
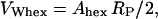graphic file with name M14.gif (14)

where VW is the effective water volume per single molecule in the respective phases. Assuming the water volume of a single water molecule to be 30 Å3, we find, at the transition midpoint, 14 waters per lipid in the Lα phase and 18 waters per lipid in the HII phase.

These values compare well to the hydration properties of DOPE at 10°C, which is ∼6°C above TH. From gravimetric measurements Tate and Gruner (1989) determined ΦWhex to have a value of 0.31, which is identical to the hydration limit of the inverse hexagonal phase in POPE estimated from our values at 74°C. In a recent study, extrapolated structural data derived from x-ray diffraction experiments were given for DOPE at 10°C (Harper et al., 2001). Applying the formulas from Eqs. 13 and 14 to their data result in 13 waters per lipid in the Lα phase and 18 waters per lipid in the inverse hexagonal phase, which is in excellent agreement with our data. All parameters, which characterize the hydration state of the lamellar and inverse hexagonal phase in POPE, are summarized in Table 3.

TABLE 3.

Comparison of the headgroup area, A; the water volume per lipid VW; and the number of waters per lipid nW given for the lamellar and inverse hexagonal phase in POPE

T (°C) Alam (Å2) Ahex (Å2) VWlam (Å3) VWhex (Å3) nWlam nWhex
30 59 – 400 – 13.5 –
35 60 – 400 – 13.5 –
40 61 – 410 – 13.5 –
45 62 – 410 – 13.5 –
50 62 – 405 – 13.5 –
54 63 – 415 – 14.0 –
58 63 – 415 – 14.0 –
60 63 – 410 – 13.5 –
62 64 – 410 – 13.5 –
64 64 – 410 – 13.5 –
66 64 – 415 – 14.0 –
67 65 – 415 – 14.0 –
68 65 48 415 490 14.0 17
69 65 50 420 530 14.0 18
70 65 51 415 540 13.5 18
71 65 49 415 510 14.0 17
72 65 49 420 490 14.0 17
73 65 48 420 490 14.0 17
74 65 52 405 550 13.5 18
75 – 47 – 460 – 16
76 – 49 – 500 – 17
78 – 49 – 490 – 17
80 – 47 – 450 – 15
84 – 50 – 500 – 17
Open in a new tab

DISCUSSION

As mentioned already in the Introduction, the Lα–HII phase transition may be accompanied by the formation of the bicontinuous cubic phase, QII (Erbes at al., 1994). However, the formation of QII phases in diacyl-PEs is slow, and our chosen temperature protocol avoided any formation of the latter (see Materials and Methods). The first traces of the HII phase are detected between 66 and 72°C (Fig. 1 B). The estimated volume fraction is only ∼2%, and does not change in this temperature interval. From the natural sequence of lyotropic liquid crystalline phases, which is governed by the average mean interfacial curvature (Seddon et al., 2000), the series of Lα–QII–HII phases can be expected with increasing temperature. Therefore, this temperature region is destined for the formation of cubic phases.

From a topological point of view, the HII phase is the most simple nonlamellar lipid phase. However, the relation between the lamellar and inverse hexagonal cell parameters measured near equilibrium (Fig. 3) is not commensurate, i.e., dlam does not equal d(1,0)hex (epitaxial relationship). Thus, there is significant evidence for nonequilibrium states between the lamellar and hexagonal phases as the transition proceeds. Therefore, extensive investigations have been carried out on the kinetics of the Lα–HII transition (for a review, see Laggner and Kriechbaum, 1995). Caffrey and co-workers have used several heating techniques (Caffrey, 1985; Caffrey et al., 1990), but with heating rates in the order of 30°C/s the initial HII lattice spacing was always well above a commensurate spacing for the lamellar phase. Transition times for dihexadecyl-PE were found to be <3 s. Somewhat faster heating rates were achieved by Tate and co-workers (Tate et al., 1992) with electrical heating pulses of 50 ms length, whereby the initial lattice dimension in the HII phase of DOPE samples were clearly smaller than equilibrium values. Thus the authors believed the inverse hexagonal lattice to be commensurate with the Lα spacing (Eq. 8). However, all data points were measured slightly above the commensurate value of 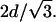Inline graphic Even under extreme heating conditions, using an infrared laser allowing heating rates of 5000°C/s (Rapp and Goody, 1991), the coexisting lamellar and inverse hexagonal lattices of SOPE never fulfilled an epitaxial relationship (Kriechbaum et al., 1989; Laggner and Kriechbaum, 1991; Laggner et al., 1991).

For SOPE the T-jump initially induced a rapid thinning of the lamellar phase from 54 to 51 Å. Here our measurements for POPE suggest, that the “thin Lα phase” reflects a nonequilibrium state. The thinning of the d-spacing of ∼3 Å/10°C, is about three times the rate one would expect from equilibrium data (compare Fig. 3 and Table 1). The constant number of waters per lipid, nWlam, (Table 3) observed over the whole temperature range suggests that the formation of the thin Lα phase is not water-diffusion limited. This is in contrast to the findings for the liquid lamellar crystalline phase of PCs, where the rapid formation of an anomalous, thin Lα phase is mainly caused by a water deficit directly after the temperature perturbation (Rappolt et al., 2000; Pabst et al., 2000b). Moreover, this excited thin Lα phase in PEs is not only seen in the Lα–HII phase transition, but in temperature jumps carried out in the pure Lα phase region (Laggner et al., 1998). Therefore, it must be assumed that the thin Lα phase forms due to a rearrangement of the interbilayer water. Although the fraction of the thin Lα phase immediately starts to decrease strongly, the first, weak sign of the hexagonal phase formation becomes detectable only after a lag time period of ∼20–30 ms, i.e., in this time window a cooperative formation of the HII phase with long-range order is suppressed. At the beginning the lattice spacings amount to 68 Å and increase with time to 73 Å. The swelling of the lattice is completed within a few seconds (half-time 0.1 s), and it is instructive to estimate the water fraction ΦWhex of the initial hexagonal phase. If we assume the hydrocarbon chain region unaltered (the temperature after the laser pulse is nearly constant for the first second), then the change in the unit cell parameter can be assigned completely to changes in the water core, i.e.,

graphic file with name M16.gif (15)

Further, one can expect ΦWhex equilibrium for SOPE to be nearly equal to the measured value of POPE (Harper et al., 2001). Inserting the given values in Eq. 15, ΦWhex inital results in 0.27, which is very close to the value one would expect for the lamellar phase (Eq. 11, Table 1). Thus, we can conclude that the first formation of the inverse hexagonal phase with long-range order appears at constant ΦW, while the last step is water-diffusion limited, since the timescale of water diffusion in the inverse hexagonal phase compares well to water-diffusion rates in multilamellar vesicles studied in the pure Lα phase region (Pabst et al., 2000b).

In Fig. 7 A we have illustrated a realistic view of the interface region between the lamellar and inverse hexagonal phase at the transition midpoint. Please note that, for clarity, the interface region has been displayed over four repeat distances only, and that adjacent monolayers, as well as further membrane stacks, have been omitted. The calculated electron density maps of both phases as determined from our experimental data (parameters given in Tables 1 and 2) have been inclined in such a manner that the lattices fulfill the condition

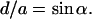graphic file with name M17.gif (16)

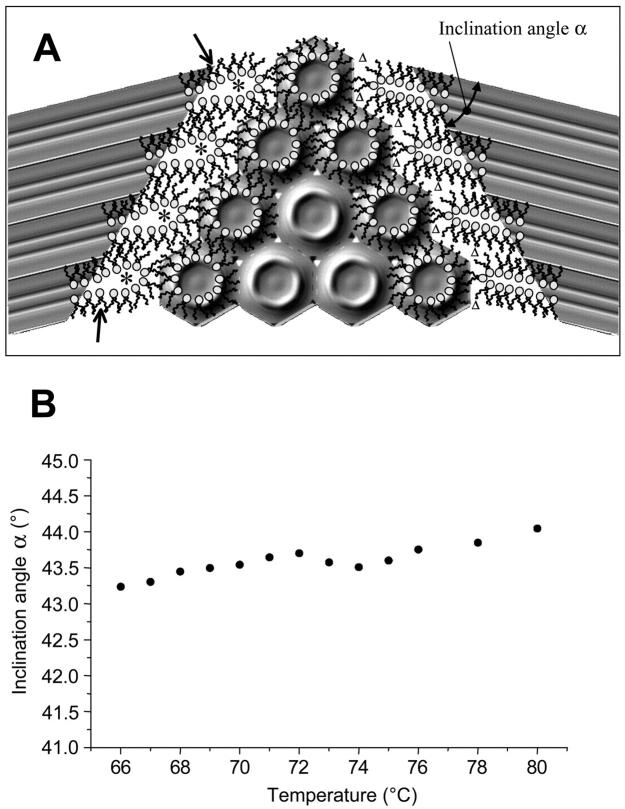
In this way, the path lengths of lipid molecules to rearrange in the interface region is minimized (Laggner and Kriechbaum, 1991). Moreover, in the coexistence range the inclination angle is nearly constant (Fig. 7 B). This means that the geometrical relationship between the two phases remains the same between 66 and 80°C, and thus the constraints for the formation of the inverse hexagonal phase do not alter much.

FIGURE 7.

FIGURE 7

Open in a new tab

(A) Sketch of the interface between the Lα and HII phases at the transition midpoint (TH = 74°C). For both phases, the electron density maps have been calculated using the amplitudes given in Tables 1 and 2, respectively (refer to Fig. 2 C). Since the two lattices are not commensurate, the inclination, α, between them differs clearly from 60°. On the left-hand side, the interface region has been filled with lipid molecules in such a way that the interstitial regions are minimized. Creation of water cores is indicated by asterisks. On the right-hand side, the lipid molecules are restricted to permit only negative curvature at the polar interface, but automatically the interstitial regions enlarge (Δ). (B) Inclination angle (•) plotted as a function of temperature.

As shown schematically in Fig. 7 A, the interface region between the two phases is occupied ideally by the lipid molecules, if each two monolayers of adjacent membranes fuse and create a water core (*) at the interface (Fig. 7 A, left-hand side). It is important to assert that this kind of backfolded monolayer might be energetically unfavorable because of inherent positive curvature regions (see arrows in Fig. 7 A). On the other hand, extreme negative curvature, avoiding the formation of a water core, and thus suppressing energetically unfavorable positive curvature regions, would lead to large interstitial regions (Δ) (see Fig. 7 A, right-hand side). Since formation of voids in the hydrophobic core is also energetically unfavorable (Lohner, 1996, and references therein), it is obvious that the interface region has to balance a delicate interplay between minimizing the volume of the interstitial region and keeping free bending energies low. Indeed, Kozlov et al. (1994) have shown with model calculations that the differences in free energy per lipid molecule can be separated in four different contributions. For conditions of excess water, they ascertain that the bending energy and the interstitial energy compete, whereas the roles of hydration and van der Waals interactions are relatively small. Finally, pinching off an isolated cylinder of water from the lamellar stack at the interface would lower the free bending energy of the lipids. In this case, all of them could accommodate their natural tendency to fill a wedge-shaped volume. However, some lipids would have to expose their chains to interbilayer water of the Lα phase during this step, which is—as discussed above—a critical barrier for the formation of the inverse hexagonal phase.

As already mentioned in the Introduction, there are several pathways possible for the formation of a line defect such as tight junction between two bilayers, including a pair of intramembrane cylinders (Kachar and Reese, 1982), fusion of interbilayer contact points into wall defects (Hui et al., 1983), or line defects seeded by inverted micellar intermediates (Siegel, 1986). In Fig. 8 A, for instance, we have depicted a water core as a possible line defect for the creation of the first rods within the lamellar lipid bilayer stack. So far, we have not considered point defects to be the leitmotif for the lamellar/inverse hexagonal phase transition. Siegel and Epand (1997) proposed a modified stalk mechanism for this transition, and suggested the existence of three-dimensional transmonolayer contact aggregates (Siegel, 1999). Such structures were not detected in our samples. However, in contrast to our experiments on multilamellar vesicles, they used large unilamellar vesicle systems, which might explain the absence of the three-dimensional precursor phase in our samples.

FIGURE 8.

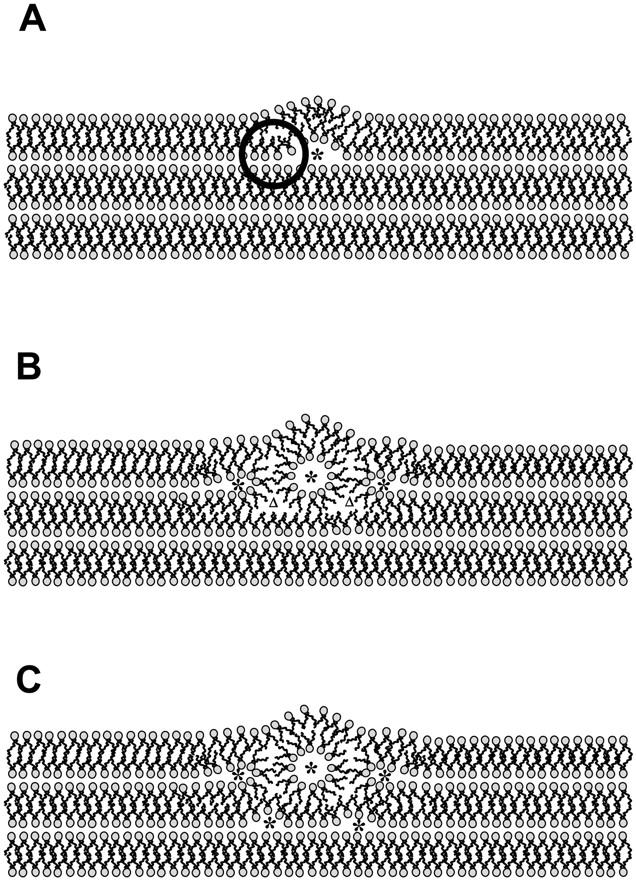
FIGURE 8

Open in a new tab

Hypothesis of the growth mechanism of the first few rods. Note that the molecular dimensions of the lamellar phase and the lipid rod are realistic, because they are deduced from the electron density maps at the transition temperature TH = 74°C. (A) Creation of a line defect, e.g., a water core (*) may form spontaneously. The circle marks an unfavorable positive curvature region. (B) Formation of the first rod; the minimization of the volume of the interstitial region induces the formation of new water cores (*, left and right of the rod). Two not-yet-filled void regions are marked with an upper triangle (Δ). (C) The interstitial regions (Δ) of B are now filled, but consequently inducing two more water cores (*) below the first rod.

In Fig. 8 B the formation of a first rod is shown. Its relative dimension is deduced from the electron density map of the inverse hexagonal phase at 74°C (see Tables 1 and 2, Fig. 7). Since it is very likely that the first formation of isolated cylinders of water appear at constant ΦW (see above discussion of the laser-induced transition), we reduced the water core diameter slightly according to Eq. 15. But the diameter of the first tube is still relatively large, and a rather stress-free formation in the lamellar matrix is, therefore, more likely to appear in the outer leaflets of the liposome. Once a tube has formed, the minimization of the volume of the interstitial region induces new sites for the creation of water cores (*, left and right of the rod). Two not-yet-filled void regions, marked with an upper triangle (Δ) in Fig. 8 B, demonstrate the consecutive induction of two more water cores below the first rod (Fig. 8 C). Thus, only filling up interstitial regions of the first rod given creates new line defects for the formation of further rods, triggering the formation of adjacent cylinders, and so on throughout the bulk of the lipid matrix (compare also Caffrey, 1985).

The Lα–HII phase transition is accompanied by the high cost of exposing the hydrocarbon chains to water. However, a cooperative transition mechanism can overcome this limitation (Fig. 8). Also, there is evidence that the water fraction difference between the initial lamellar and the final inverse hexagonal phase is not the first rate-limiting step. We have presented a realistic model for the interface region between the two phases allowing a cooperative turnover (Fig. 7). Although the lattices do not fulfill an epitaxial relation, a transition mechanism without loss of long-range order is possible, if the lattices are inclined to each other by ∼44° (see also Laggner and Kriechbaum, 1991). Additionally, the geometrical details of the rod formation are discussed above, which are mainly governed by the contribution of voids in the bending and interstitial interactions (Kozlov et al., 1994). In any case, it seems indispensable for the cooperative formation of the inverse hexagonal phase, that the domain growth takes place in the multilamellar matrix of liposomes with a rather reduced hydration. Only in a water-poor system (in the Lα phase the free water volume per lipid is only ∼150 Å3), the unavoidable cost of exposing hydrocarbon chains to water regions can be kept as small as possible. This has also been demonstrated for POPE bilayer stacks at a relative humidity just below 100%, where in the Lβ gel phase they can undergo a lamellar-to-inverse hexagonal transition only after one-third of free water has been removed (Katsaras et al., 1993).

Acknowledgments

The financial support of the Fonds zur Förderung der Wissenschaftlichen Forschung in Österreich (project P15657 to K.L.), and the Deutsche Forschungsgemeinschaft (project BR1826/2-1 to F.B.), is gratefully acknowledged.

Frank Bringezu's present address is Inst. F. Med. Physik u. Biophysik, Liebigstrasse 27, D-04103 Leipzig, Germany.

References

  1. Amenitsch, H., M. Rappolt, M. Kriechbaum, H. Mio, P. Laggner, and S. Bernstoff. 1998. First performance assessment of the SAXS beamline at ELETTRA. J. Synch. Rad. 5:506–508. [DOI] [PubMed] [Google Scholar]
  2. Bernstorff, S., H. Amenitsch, and P. Laggner. 1998. High-throughput asymmetric double-crystal monochromator for the SAXS beamline at ELETTRA. J. Synch. Rad. 5:1215–1221. [DOI] [PubMed] [Google Scholar]
  3. Bradshaw, J. P., M. J. M. Darkes, T. A. Harroun, J. Katsaras, and R. M. Epand. 2000. Oblique membrane insertion of viral fusion peptide probed by neutron diffraction. Biochemistry. 39:6581–6585. [DOI] [PubMed] [Google Scholar]
  4. Caffrey, M. 1985. Kinetics and mechanism of the lamellar gel/lamellar liquid crystal and lamellar/inverted hexagonal phase transition in phosphatidylethanolamine: a real-time x-ray diffraction study using synchrotron radiation. Biochemistry. 24:4826–4844. [DOI] [PubMed] [Google Scholar]
  5. Caffrey, M. 1993. LIPIDAT: A Database of Thermodynamic Data and Associated Information on Lipid Mesomorphic and Polymorphic Transitions. CRC Press, Boca Raton.
  6. Caffrey, M., R. L. Magin, B. Hummel, and J. Zhang. 1990. Kinetics of the lamellar and hexagonal phase transitions in phosphatidylethanolamine. Time-resolved x-ray diffraction study using a microwave-induced temperature jump. Biophys. J. 58:21–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chernomordik, I. 1996. Non-bilayer lipids and biological fusion intermediates. Chem. Phys. Lipids. 81:203–213. [DOI] [PubMed] [Google Scholar]
  8. Epand, R. M. 2000. Membrane fusion. Biosci. Rep. 29:435–441. [DOI] [PubMed] [Google Scholar]
  9. Erbes, J., C. Czeslik, W. Hahn, R. Winter, M. Rappolt, and G. Rapp. 1994. On the existence of bicontinuous cubic phases in dioleoylphosphatidylethanolamine. Ber. Bunsenges. Phys. Chem. 98:8776–8779. [Google Scholar]
  10. Hickel, A., and K. Lohner. 2001. The influence of antimicrobial peptides on membrane curvature strain. Biophys. J. 80:713. [Google Scholar]
  11. Harper, P. E., D. A. Mannock, R. N. A. H. Lewis, R. N. McElhaney, and S. Gruner. 2001. X-ray diffraction of some phosphatidylethanolamine lamellar and inverted hexagonal phases. Biophys. J. 81:2693–2706. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Huang, T. C., H. Toraya, T. N. Blanton, and Y. J. Wu. 1993. X-ray powder diffraction of silver behenate, a possible low-angle diffraction standard. J. Appl. Crystallogr. 26:180–184. [Google Scholar]
  13. Hui, S. W., and T. P. Stewart. 1981. “Lipidic particles” are intermembrane attachment sites. Nature. 290:427–428. [DOI] [PubMed] [Google Scholar]
  14. Hui, S. W., T. P. Stewart, and L. T. Boni. 1983. The nature of lipidic particles and their roles in polymorphic transitions. Chem. Phys. Lipids. 33:113–116. [DOI] [PubMed] [Google Scholar]
  15. Hui, S. W., T. P. Stewart, L. T. Boni, and P. L. Yeagle. 1982. Membrane fusion through point defects in bilayers. Science. 212:921–923. [DOI] [PubMed] [Google Scholar]
  16. Jahn, R., and H. Grubmüller. 2002. Membrane fusion. Curr. Opin. Cell Biol. 14:488–495. [DOI] [PubMed] [Google Scholar]
  17. Kachar, B., and T. S. Reese. 1982. Evidence of lipidic nature of tight junction strands. Nature. 296:464–466. [DOI] [PubMed] [Google Scholar]
  18. Katsaras, J., K. R. Jeffrey, D. S.-C. Yang, and R. M. Epand. 1993. Direct evidence fir the partial dehydration of the phosphatidylethanolamine bilayers on approaching the hexagonal phase. Biochemistry. 32:10700–10707. [DOI] [PubMed] [Google Scholar]
  19. Koltover, I., T. Salditt, J. O. Rädler, and C. R. Safinya. 1998. An inverted hexagonal phase of cationic liposome-DNA complexes related to DNA release and delivery. Science. 281:78–81. [DOI] [PubMed] [Google Scholar]
  20. Kozlov, M. M., S. Leikin, and R. P. Rand. 1994. Bending, hydration and interstitial energies quantitatively account for the hexagonal-lamellar-hexagonal reentrant phase transition in dioleoylphosphatidylethanolamine. Biophys. J. 67:1603–1611. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kriechbaum, M., G. Rapp, J. Hendrix, and P. Laggner. 1989. Millisecond time-resolved x-ray diffraction on liquid-crystalline phase transitions using infrared laser T-jump technique and synchrotron radiation. Rev. Sci. Instrum. 60:2541–2544. [Google Scholar]
  22. Kuzmin, P. I., J. Zimmerberg, Y. A. Chizmadzhev, and F. S. Cohen. 2001. A quantitative model for membrane fusion based on low-energy intermediates. Proc. Natl. Acad. Sci. USA. 98:7235–7240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Laggner, P., H. Amenitsch, M. Kriechbaum, G. Pabst, and M. Rappolt. 1998. Trapping of short-lived intermediates in phospholipid phase transitions: the Lα*-Phase. Faraday Discuss. 111:31–40. [DOI] [PubMed] [Google Scholar]
  24. Laggner, P., and M. Kriechbaum. 1991. Phospholipid phase transitions: kinetics and structural mechanisms. Chem. Phys. Lipids. 57:121–145. [DOI] [PubMed] [Google Scholar]
  25. Laggner, P., and M. Kriechbaum. 1995. Time-resolved x-ray small-angle diffraction with synchrotron radiation on phospholipid phase transitions. pathways, intermediates and kinetics. In Modern Aspects of Small-Angle Scattering. H. Brumberger, editor. Kluwer Academic Publishers, Dordrecht. pp. 387–407.
  26. Laggner, P., M. Kriechbaum, and G. Rapp. 1991. Structural intermediates in phospholipid phase transitions. J. Appl. Crystallogr. 24:836–842. [Google Scholar]
  27. Lohner, K. 1996. Is the high propensity of ethanolamine plasmalogens to form non-lamellar lipid structures manifested in the properties of biomembranes? Chem. Phys. Lipids. 81:167–184. [DOI] [PubMed] [Google Scholar]
  28. Lohner, K. 2001. The role of membrane lipid composition in cell targeting of antimicrobial peptides. In Development of Novel Antimicrobial Agents: Emerging Strategies. K. Lohner, editor. Horizon Scientific Press, Wymondham. pp. 149–165.
  29. Lohner, K., A. Latal, R. I. Lehrer, and T. Ganz. 1997. Differential scanning microcalorimetry indicates that human defensin, HNP-2, interacts specifically with biomembrane mimetic systems. Biochemistry. 36:1525–1531. [DOI] [PubMed] [Google Scholar]
  30. Lohner, K., and E. J. Prenner. 1999. Differential scanning calorimetry and x-ray diffraction studies of the specificity of the interaction of antimicrobial peptides with membrane-mimetic systems. Biochim. Biophys. Acta. 1462:141–156. [DOI] [PubMed] [Google Scholar]
  31. Luzzati, V. 1968. X-ray diffraction studies of water lipid systems. In Biological Membranes, Vol. 1. D. Chapman, editor. Academic Press, London. pp. 71–123.
  32. McIntosh, T. J., and S. A. Simon. 1986a. Area per molecule and distribution of water in fully hydrated dilauroylphosphatidylethanolamine bilayers. Biochemistry. 25:4948–4952. [DOI] [PubMed] [Google Scholar]
  33. McIntosh, T. J., and S. A. Simon. 1986b. Hydration force and bilayer deformation: a reevaluation. Biochemistry. 25:4058–4966. [DOI] [PubMed] [Google Scholar]
  34. Miller, R. 1980. Do “lipidic particles” represent intermembrane attachment sites? Nature. 287:166–167. [DOI] [PubMed] [Google Scholar]
  35. Nagle, J. F., and S. Tristram-Nagle. 2000. Structure of lipid bilayers. Biochim. Biophys. Acta. 1469:159–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Pabst, G., M. Rappolt, H. Amenitsch, and P. Laggner. 2000a. Structural information from liposomes at full hydration: Full q-range fitting with high quality x-ray data. Phys. Rev. E. 62:4000–4009. [DOI] [PubMed] [Google Scholar]
  37. Pabst, G., M. Rappolt, H. Amenitsch, S. Bernstorff, and P. Laggner. 2000b. X-ray cinematography of temperature-jump relaxation probes the elastic properties of fluid bilayers. Langmuir. 16:8994–9001. [Google Scholar]
  38. Petrache, H. I., S. Tristram-Nagle, R. Zhang, R. M. Suter, and J. F. Nagle. 1998. Interbilayer interactions from high-resolution x-ray scattering. Phys. Rev. E. 57:7014–7024. [Google Scholar]
  39. Petrascu, A.-M., M. H. J. Koch, and A. Gabriel. 1998. A beginners' guide to gas-filled proportional detectors with delay line readout. J. Makromol. Sci. Phys. B37:463–483. [Google Scholar]
  40. Rand, R. P., and V. A. Parsegian. 1989. Hydration forces between phospholipid bilayers. Biochim. Biophys. Acta. 988:351–376. [Google Scholar]
  41. Rapp, G., and R. S. Goody. 1991. Light as a trigger for time-resolved structural experiments on muscle, lipids, p21 and bacteriorhodopsin. J. Appl. Crystallogr. 24:857–865. [Google Scholar]
  42. Rappolt, M., G. Pabst, G. Rapp, M. Kriechbaum, H. Amenitsch, C. Krenn, S. Bernstorff, and P. Laggner. 2000. New evidence for gel-liquid crystalline phase coexistence in the ripple phase of phosphatidylcholines. Eur. Biophys. J. 29:125–133. [DOI] [PubMed] [Google Scholar]
  43. Rappolt, M., and G. Rapp. 1996. Simultaneous small- and wide-angle x-ray diffraction during the main transition of dimyristoylphosphatidylethanolamine. Ber. Bunsenges. Phys. Chem. 100:1153–1162. [Google Scholar]
  44. Seddon, J. M. 1990. Structure of the inverted hexagonal (HII) phase, and non-lamellar phase transitions in lipids. Biochim. Biophys. Acta. 1031:1–69. [DOI] [PubMed] [Google Scholar]
  45. Seddon, J. M., J. Robins, T. Gulik-Krzywicki, and H. Delacroix. 2000. Inverse micellar phases of phospholipids and glycolipids. Phys. Chem. Chem. Phys. 2:4485–4493. [Google Scholar]
  46. Shyamsunder, E., S. M. Gruner, M. W. Tate, D. C. Turner, P. T. C. So, and C. P. S. Tilcock. 1988. Observation of inverted cubic phase in hydrated dioleoylphosphatidylethanolamine membranes. Biochemistry. 27:2332–2336. [DOI] [PubMed] [Google Scholar]
  47. Siegel, D. P. 1986. Inverted micellar intermediates and the transitions between lamellar, inverted hexagonal, and cubic lipid phases. I. Mechanism of the Lα-to-HII phase transition. Biophys. J. 49:1155–1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Siegel, D. P. 1993. Energetics of intermediates in membrane fusion: comparison of stalk and inverted micellar intermediate structures. Biophys. J. 65:2124–2140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Siegel, D. P. 1999. The modified stalk mechanism of the lamellar/inverted phase transitions and its implication for membrane fusion. Biophys. J. 76:291–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Siegel, D. P., and R. M. Epand. 1997. The mechanism of lamellar-to-inverted hexagonal phase transitions in phosphatidylethanolamine: implications for membrane fusion mechanisms. Biophys. J. 73:3089–3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. So, P. T. C., S. M. Gruner, and S. Erramilli. 1993. Pressure-induced topological phase transition in membranes. Phys. Rev. Lett. 70:3455–3458. [DOI] [PubMed] [Google Scholar]
  52. Staudegger, E., E. J. Prenner, M. Kriechbaum, G. Degovics, R. N. A. H. Lewis, R. N. McElhaney, and K. Lohner. 2000. X-ray studies on the interaction of the antimicrobial gramicidin-s with microbial lipid extracts: evidence for cubic phase formation. Biochim. Biophys. Acta. 1468:213–230. [DOI] [PubMed] [Google Scholar]
  53. Tate, M. W., and S. M. Gruner. 1989. Temperature dependence of the structural dimensions of the inverted hexagonal (HII) phase of phosphatidylethanolamine-containing membranes. Biochemistry. 28:4245–4253. [DOI] [PubMed] [Google Scholar]
  54. Tate, M. W., E. Shyamsunder, S. M. Gruner, and K. L. D'Amico. 1992. Kinetics of the lamellar-inverse hexagonal phase transition determined by time-resolved x-ray diffraction. Biochemistry. 31:1081–1092. [DOI] [PubMed] [Google Scholar]
  55. Tenchov, B., R. Koynova, and G. Rapp. 1998. Accelerated formation of the cubic phases in phosphatidylethanolamine dispersions. Biophys. J. 75:853–866. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Toombes, G. S., A. C. Finnefrock, M. W. Tate, and S. M. Gruner. 2002. Determination of Lα-HII phase transition temperature for 1,2,-dioleoyl-sn-glycero-3-phosphatidyl-ethanolamine. Biophys. J. 82:2504–2510. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Turner, D. C., and S. M. Gruner. 1992. X-ray diffraction reconstruction of the inverted hexagonal ( HII) phase in lipid-water systems. Biochemistry. 31:1340–1355. [DOI] [PubMed] [Google Scholar]
  58. Verkleij, A. J. 1984. Lipidic intramembranous particles. Biochim. Biophys. Acta. 779:43–63. [DOI] [PubMed] [Google Scholar]
  59. Verkleij, A. J., C. Mombers, W. J. Gerritsen, L. Leunissen-Bijvelt, and P. R. Cullis. 1978. Fusion of phospholipid vesicles in association with the appearance of lipidic particles as visualized by freeze-fracturing. Biochim. Biophys. Acta. 555:358–361. [DOI] [PubMed] [Google Scholar]
  60. Verkleij, A. J., C. Mombers, J. Lenissen-Bijvelt, and P. H. J. Th. Ververgaert. 1979. Lipidic intramembranous particles. Nature. 279:162–163. [DOI] [PubMed] [Google Scholar]
  61. Warren, B. E. 1969. X-Ray Diffraction. Dover reprint (1990) of the edition published by the Addison Wesley Publishing Company, Reading.

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES