Interaction between Artificial Membranes and Enflurane, a General Volatile Anesthetic: DPPC-Enflurane Interaction

Abstract

The structural modifications of the dipalmitoylphosphatidylcholine (DPPC) organization induced by increasing concentration of the volatile anesthetic enflurane have been studied by differential scanning calorimetry, small-angle, and wide-angle x-ray scattering. The interaction of enflurane with DPPC depends on at least two factors: the enflurane-to-lipid concentration ratio and the initial organization of the lipids. At 25°C (gel state), the penetration of enflurane within the lipids induces the apparition of two different mixed lipid phases. At low anesthetic-to-lipid molar ratio, the smectic distance increases whereas the direction of the chain tilt changes from a tilt toward next-neighbors to a tilt between next-neighbors creating a new gel phase called L_β′^2NNN. At high ratio, the smectic distance is much smaller than for the pure L_β′ DPPC phase, i.e., 50 Å compared to 65 Å, the aliphatic chains are perpendicular to the membrane and the fusion temperature of the phase is 33°C. The electron profile of this phase that has been called L_βⁱ, indicates that the lipids are fully interdigitated. At 45°C (fluid state), a new melted phase, called L_α², was found, in which the smectic distance decreased compared to the initial pure L_α¹ DPPC phase. The thermotropic behavior of the mixed phases has also been characterized by simultaneous x-ray scattering and differential scanning calorimetry measurements using the Microcalix calorimeter of our own. Finally, titration curves of enflurane effect in the mixed lipidic phase has been obtained by using the fluorescent lipid probe Laurdan. Measurements as a function of temperature or at constant temperature, i.e., 25°C and 45°C give, for the maximal effect, an enflurane-to-lipid ratio (M/M), within the membrane, of 1 and 2 for the L_α² and the L_βⁱ lamellar phase respectively. All the results taken together allowed to draw a pseudo-binary phase diagram of enflurane-dipalmitoylphosphatidylcholine in excess water.

INTRODUCTION

General anesthetics are nonspecific in the sense that they have diverse shapes and sizes and possess a wide variety of chemical groups (alcohols, alkanes, ethers, halogenated derivatives, barbiturics, etc.). This structural and chemical diversity is often taken to imply an underlying nonselectivity in the action of these agents toward their targets. Indeed, in addition to the traditional view that general anesthetics act by disrupting the structure and/or the dynamic of the lipid portion of the nerve cells, it is found that most of them act at multiple molecular sites in the central nervous system: GABAA- and NMDA-receptors/ion channels and many Na⁺ and K⁺ channels. Thus, general anesthesia is a multidimensional phenomenon, and anesthetics are unique drugs in pharmacology in that they affect all macromolecules.

By the early 1980s (Franks and Lieb, 1979, 1981, 1984, 1998), the hypothesis that the anesthetic site of action could be directly on the membrane protein instead of the lipidic phase has been documented. It was shown that, at clinical concentration, the principal effect of general anesthetics is on ligand-gated rather than voltage-gated ion channels. Moreover, stereo selectivity of some anesthetics has been demonstrated (see Jones and Harrison, 1993, and Franks and Lieb, 1994, for a review). However, despite an overwhelming body of experiments, the controversy as to whether the anesthetics' primary site of action are the membrane lipids, the membrane proteins, or the lipid-protein interface remains unresolved. Among others, the physicochemical properties of the site of action of these molecules is still an open question whose difficulty arises mostly from the absence of a specific fingerprintlike site inferred by the diversity of the effective molecules (Eckenhoff and Johansson, 1997).

Most recently, Cantor (1997, 2001) proposed a thermodynamic model to explain how the presence of anesthetics within the membrane may induce changes in the membrane structure that would, in fine, indirectly affect the function of the membrane protein. The model assumes that an anesthetic would always interact either with the interface or with the hydrophobic core of the bilayer. Such inhomogeneous distribution within the membrane would induce an inhomogeneous increase of the lateral pressure which, in turn, would specifically affect the activity of a membrane protein.

A number of recent studies on simple lipidic models focus on the location of anesthetic within the membrane where the water-lipid interface, the lipid headgroup, or the aliphatic chain appear as likely sites. The controversy also exists in this domain. On the one hand, studies performed by Raman (Craig et al., 1987), infrared (Tsai et al., 1990), and NMR spectroscopies (Koehler et al., 1978; Gaillard et al., 1991; Xu and Tang, 1997; Tang et al., 1997) indicate that the anesthetic molecules are preferentially located at the membrane-water interface. Namely, enflurane and halothane were shown to induce a dehydration of both the P=O group and the C=O group of the glycerol backbone of DMPC bilayers by breaking the hydrogen bonding (Tsai et al., 1990). On the other hand, ²H-NMR (Baber et al., 1995) or ¹³C solid-state NMR (Mavromoustakos et al., 1997) experiments suggest that anesthetics are more deeply inserted in the aliphatic chain region. In 1979, Franks and Lieb studied the interaction of nitrous oxide, halothane, and cyclopropane with lecithin/cholesterol bilayers by x-ray and neutron scattering, and showed that their only effect, at very high concentration, was to increase the disorder of the acyl chain whereas the thickness of the membrane remains unchanged.

Molecular dynamics simulation (Tu et al., 1998; Koubi et al., 2000) showed that halothane distribution into dipalmitoylphosphatidylcholine (DPPC) fluid bilayers is not homogeneous in the membrane. According to their modelization, halothane molecules are found preferentially segregated in the upper part of the acyl chain, near the C₅ of the acyl chain, inducing lateral expansion and a concomitant contraction in the membrane thickness. These simulation experiments seem to reconcile apparent controversial conclusions deduced from other studies performed on diverse lipid systems. However, they were performed on small systems (limited number of lipid and water molecules), and the inhomogeneous distribution of halothane within the membrane was only seen for high anesthetic-to-lipid ratios.

All these studies were performed on different lipids (DPPC, DMPC, DPPC/cholesterol), in different phases (L_β′ or L_α phases), and with different anesthetic and lipid concentrations, making the comparison difficult between the different studies.

In this work, we have studied the interaction of enflurane, a halogenated volatile anesthetic, with DPPC, the aim being to characterize the structural modifications of the lipid organization in different initial states (gel or fluid), at different enflurane-to-lipid ratios and from low to high anesthetic concentrations. An attempt has been done to draw the phase diagram of enflurane-DPPC mixtures in excess water, i.e., a pseudo-binary phase diagram. The techniques used to characterize the organization of the amphiphiles in the mixtures were essentially differential calorimetry (DSC) and small- and wide-angle x-ray scattering (SAXS and WAXS). Fluorescence spectroscopy using the lipidic probe Laurdan was also used to estimate the amount of enflurane in interaction with the lipids in the different mixtures.

MATERIALS AND METHODS

Materials

DPPC was purchased from Avanti Polar Lipids and Laurdan from Molecular Probes. Enflurane (trademark Ethrane; 2-chloro-1,1,2- trifluoroethyl difluoromethyl ether) was from Anaquest.

Lamellar phases and liposomes preparation

Either DPPC lamellar phases or liposomes were prepared. When needed, DPPC, solubilized in chloroform, was added with Laurdan (final Laurdan-to-lipids ratio: 0.1 mol%). The lipids were dried under nitrogen and lyophilized overnight. The dry lipids were hydrated in buffer (10 mM Tris, 150 mM KCl, pH 8) at 50°C and vortexed to form a suspension of lamellar phases. Lamellar suspensions were used for the SAXS, WAXS, and DSC measurements. When required, i.e., for the fluorescence measurements, the lamellar suspension was sequentially extruded at 45°C through Nucleopore filters (pore diameters of 0.8, 0.4, 0.2, 0.1, and 0.05 μm) to finally get large homogeneous unilamellar vesicles, ∼150 nm in diameter, as estimated from light-scattering measurement. The lamellar suspensions and the liposomes were then kept at room temperature.

Fluorescence spectroscopy

The phase transition of DPPC-Laurdan liposomes was followed by fluorescence measurements. The liposome suspension was placed in a quartz cuvette in a computer-controlled Fluoromax fluorimeter (Spex Instruments, Jobin Yvon, Longjumeau, France) equipped with four photomultipliers (Paternostre et al., 1995). The cell holder was thermostated using a cryostat (RC6, Lauda, Germany) and a homemade system was used to raise the temperature of the cell holder from 20 to 50°C at a constant rate of 0.5°C/min. To assess any temperature difference between the sample and the cryostat, blank calibration runs were performed with a thermocouple immersed in a 2-ml liposome sample, before and after each series of measurements. The emission spectrum of Laurdan between 380 and 650 nm (λ_ex = 360 nm) was continuously recorded during the temperature rise.

It is important to notice that enflurane is volatile. Its partition coefficient between air and water is not negligible; thus, some precautions need to be taken to control the enflurane concentration in the sample. To validate comparison between different experiments, a rigorous procedure has been followed. Identical quartz cuvettes have been used. A cap and a Teflon disk tightly closed these cuvettes. Moreover, the experiments have been done on precisely the same volume of samples, i.e., 2 ml of liposome suspensions at the desired concentration, so as to maintain a constant air volume in the cuvette. Each enflurane addition was done at the lowest temperature by injection through a small hole in the Teflon disk, closed by a metal cap. No significant amount of enflurane was lost upon opening of this metal cap. This has been carefully checked by repeated experiments. The absence of leak was also assessed by some measurements repeated after standing for 24 h; the variation of the transition temperature between experiments never exceeded 5%.

Differential scanning calorimetry (DSC)

DSC measurements were performed on an Arion high sensitivity flux type microcalorimeter. Highly purified lauric acid was used to standardize the temperature and quantitative heat determinations. The transition temperature was determined at the onset of the transition, i.e., the intercept of the baseline with the tangent to the low temperature side of the thermal peak. Samples consisted typically in 300 μl of DPPC multilayers at a lipid concentration of 14.9 mg/ml (20.3 mM). A very low heating rate of 0.08°C/min (20–25 to 50°C range) was selected to ensure peak resolution and temperature homogeneity. Samples were normally recovered after each heating cycle so that that enflurane concentration could be increased step by step on the same DPPC sample by accurate weighing of the sample after each scan and each anesthetic addition.

X-ray scattering

For the x-ray scattering experiments, samples consisted of lamellar phases which had not been extruded. They were contained in calibrated diameter glass capillaries (1.4 < φ < 1.5 mm, Glas, Muller, Berlin) and their volume did not exceed 20 μl. To avoid any anesthetic evaporation, two capillaries where used: the sample was placed in one of the capillary and the other one, smaller, was embedded into the previous one to decrease as much as possible the air volume available. The two capillaries were then sealed with paraffin. Before and after each x-ray scattering measurement, DSC experiments were performed directly on the capillary using the homemade Microcalix, and the thermograms were compared. Using this sample conditioning method, no loss of enflurane was detected. The diffraction spacings were calibrated using the lamellar peaks of silver behenate (d = 53.380 Å) and the triclinic chain packing of tristearine (4.59 Å, 3.85 Å, 3.70 Å) as standards. Small- (SAXS) and wide- (WAXS) angle x-ray scattering measurements were done at the DCI Synchrotron Facility of LURE (Orsay, France) on the D22 station for varying temperature experiments and on the D43 station for high-precision statistic experiments.

On the D22 station, measurements were carried out using a monochromatic (1.55 Å) x-ray beam, 300 × 2000 μm² selected by two parallel Ge(111) crystals. The sample and reference cavities for capillaries are horizontal and two linear Position Sensitive Detectors, which allow simultaneous SAXS and WAXS measurements, collect scattering in the vertical direction. Samples were heated in a home made calorimeter, Microcalix, enabling simultaneous differential scanning calorimetry on the very same sample (Keller et al., 1998; Andrieux et al., 1998). A temperature controller (900 HP, Eurotherm, Dardilly, France) enabled accurate (±0.01°C) temperature recording in the −30°C to +130°C range. The heating rate was fixed at 1°C/min, and the time sequence for the acquisition of the SAXS and WAXS data was 50 s for the accumulation and 10 s for the recording, giving one x-ray pattern every minute (i.e., for each 1°C temperature rise).

For the experiments performed at station D43, measurements we carried out using a monochromatic (1.45 Å) focused x-ray beam selected by a parabolic Ge(111) crystal. The beam was defined by a 500-μm collimator. The x-ray diffraction patterns were recorded, at exposure time of 30–50 min, using an image plate (15 × 20 cm²) which was further digitized for analysis. The sample holder could accommodate up to seven samples simultaneously and it was thermostated by a computer-controlled oven. Two sample-to-detector distances (268 and 140 mm) were used to determine of the repetitive distances of the lipid bilayers and the distance between the aliphatic chains of the lipids.

All samples exhibited powder diffraction Debye-Sherrer rings. Hence, the scattering intensities as a function of the radial wave vector, q = 4π/λ × sin(θ), was determined by circular integration using a homemade procedure under IGOR-PRO (Zantl, 2001). The diffraction peaks were fitted by a Gaussian superimposed over a linear background, yielding the peak position q_n = 2πn/d_lam and its area A_n, together with d_lam, the repeat distance of the lamellar structure.

Electron density reconstruction

The electron density variations are related to the Bragg peak intensities by

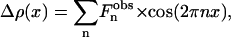(1)

with, after Lorentz polarization corrections at small angles,

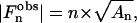(2)

where n is the Bragg reflection order and A_n is the area of the Bragg reflection. Due to the centrosymmetry of the lamellar structure, the phase of 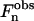is restricted to be either 0 or π, and consequently 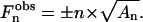Therefore, to determine the electronic density profile, the sign of each 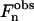has to be determined. It is important to notice that the x = x + d_lam/2 translated solution only changes the sign of the 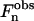with and even n because:

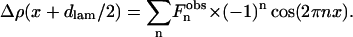(3)

Therefore, the observation of n Bragg reflections gives 2ⁿ available electronic density variations. As there is an identical translated solution in the case of each electronic density, there are only 2ⁿ⁻¹ non-equivalent solutions.

To solve the phase problem (the sign problem in our case), the true phase can be deduced from simple molecular assumptions on the electronic density profiles in the layers (Harper et al., 2001; Artzner et al., 2000). If these reasonable molecular criteria are well defined, they could allow elimination of most of the improbable electron profiles among the 2ⁿ⁻¹ solutions that we have at the end of the calculation. We know that in a lipid lamellar system, we have at least three different electron density optima: 1), the lipid headgroup, having the highest electron density due to the phosphate group; 2), the aliphatic chains having the lowest electron density; and 3), the water layer having an electron density lower than that of the polar headgroup and slightly higher that that of the aliphatic chain.

Therefore, we can assume that, 1), the phosphate electron density will create two maxima; 2), the aliphatic and the water layers will define two minima; and 3), the water layer will have a higher electron density than the aliphatic one. Moreover, according to crystallographic criteria, the origin, x = 0, corresponds to one of the two symmetry planes of the lamellar structure, thus, 4), the center of either the aliphatic region or the liquid layer is at the origin. These four criteria are valid for all kinds of phospholipidic lamellar systems. Moreover, we have additional criteria for pure DPPC L_β′ phase: 5), the minimum of the electron density is in the part of the terminal methyl group of the aliphatic chain and this minimum is located in the symmetrical position x = 0 or x = 1/2; and 6), according to the literature, the phosphate-to-phosphate distance across the DDPC bilayer in the L_β′ phase is ∼42–45 Å.

RESULTS

Thermal behavior of DPPC in the presence of enflurane

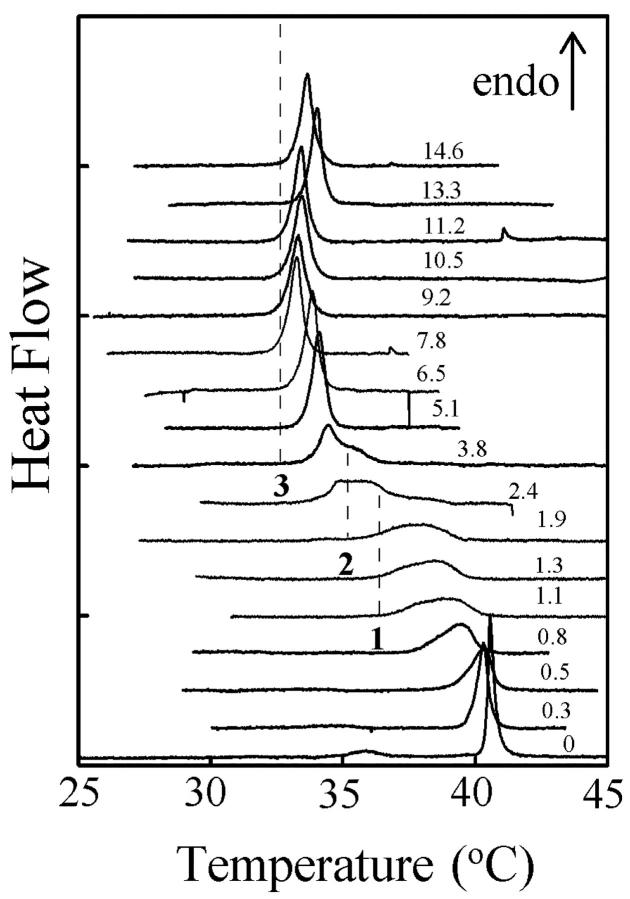
The calorimetric curves of DPPC/enflurane mixtures at different anesthetic/lipid total ratios (R_tot = [enf]_tot / [lip]_tot) have been recorded and compared to that of pure DPPC multilamellar liposomes (Fig. 1). In this set of experiments the same initial lipid sample at 20 mM was used and aliquots of enflurane were added step by step after each recording (see Material and Methods). As previously shown in the literature for the interaction of halothane with DPPC lamellar phase (Gaillard et al., 1991), enflurane decreases the main transition temperature of DPPC (T_t) in a concentration-dependent manner. The events which occur upon increasing R_tot can be grouped as follows:

FIGURE 1.

Calorimetric curves of pure DPPC multilayers (lower trace) and of different enflurane/DPPC mixtures ([Lip]_tot = 20.3 mM). The R_tot are indicated on each curve. The dashed lines 1, 2, and 3 indicate the isothermal event detected on the calorimetric curves.

−0 < R_tot < 0.8

The pretransition between L_β′ and P_β′ disappears. The T_on of the main transition slightly decreases from 40.3 to 39.4°C and the width of its endothermic peak (T_off − T_on) increases from 0.5 to 1.5°C, indicating a decrease of the cooperativity of the transition.

−1.1 < R_tot < 1.9

The endothermic peak is still broader (width = 3.5°C) and a shoulder is visible on the low temperature side of the transition at 36°C, suggesting the existence of an invariant transition (dashed line 1 on Fig. 1).

−2.4 < R_tot < 3.8

A new sharp endothermic peak located at ∼34°C is followed by an isothermal peak at 35°C (dashed line 2 on Fig. 1). At R_tot = 2.4, some trace of the broad transition observed for lower R_tot (1.1 < R_tot < 1.9) is still visible.

−3.8 < R_tot < 14.6

Only one sharp well-defined peak with a constant area is recorded (T_on = 33.0 ± 0.5°C, dashed line 3 on Fig. 1). This thermal event already takes place for the two lower R_tot. The width of this sharp endothermic peak is 1.1°C ± 0.1°C, indicating a highly cooperative transition.

These calorimetric curves indicate a progressive evolution of the structures toward that observed at R_tot = 3.8 and over. In particular, the successive invariants indicate that intermediate and precise structures are formed before the appearance of a final one, the melting of which is at 33°C. The existence of this last invariant transition indicates that the parameter of this new structure does not change in a large range of enflurane concentrations. As a consequence, this new phase should coexist with pure enflurane and its x-ray pattern should remain the same all along the R_tot > 3.8 enflurane concentration range.

Structural characterization of enflurane-DPPC mixtures at 25°C

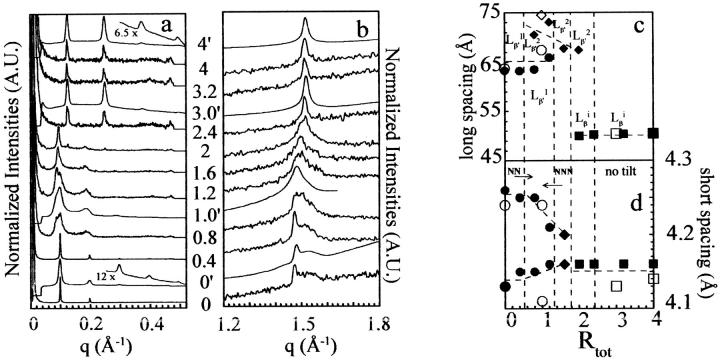
Results from SAXS and WAXS experiments are shown in Fig. 2 for enflurane-DPPC mixtures of R_tot = 0–4 at 25°C, a temperature well below that of the new transition observed for high R_tot at 33°C.

FIGURE 2.

SAXS (a) and WAXS (b) patterns at 25°C for different DPPC-enflurane mixtures. The R_tot are indicated at the level of each trace: the superscript prime identifies traces measured on D43 line ([lip] = 61 mM). The others are those measured on D22 line ([lip] = 100 mM). Traces 0′ and 4′ are scale-expanded to make visible the higher order of Bragg peaks. (c and d) Long and short spacings as a function of R_tot. Unfilled and solid symbols correspond to measurements on D43 and D22 lines, respectively. (Circles, diamonds, and squares stand for L_β′^1NN, L_β′^2NNN, and L_βⁱ phases, respectively.)

At low R_tot (0.4), both SAXS and WAXS patterns are similar to those of the pure DPPC lamellar phase (Fig. 2, a and b), indicating that this low anesthetic concentration does not modify the initial DPPC organization. The lamellar spacing deduced from the SAXS patterns is 63–64 Å, in full agreement with the literature (see also Table 1 and Fig. 2 c). Deconvolution of the WAXS patterns gives the two parameters of the pseudo-hexagonal lattice of the chain packing, i.e., 4.14 ± 0.01 Å and 4.25 ± 0.01 Å, which are also in good agreement with the literature.

TABLE 1.

Long and short spacings determined from SAXS and WAXS patterns respectively, recorded at 25°C on either D43 or D22 line (LURE); the data are presented as a function of R_tot of the samples

		Long spacings, 25°C						Short spacings, 25°C
Rtot	Lamellar phase	1st order d (Å)	2nd order d (Å)	3rd order d (Å)	4th order d (Å)	5th order d (Å)	Average d (Å)	Peak 1 d (Å)	Peak 2 d (Å)
		D43 ([lip] = 61 mM)
0	Lβ′	64	64	63	63	64	64	4.24	4.13
1	Lβ′1NN	66	69				67.5	4.24	4.11
	Lβ′2NNN	73	76				74.5
3	Lβi	49	51	51	50		50.5	4.13
4	Lβi	51	51	50	51		51	4.14
		D22 ([lip] = 100 mM)
0	Lβ′	63	63	63	63		63	4.26	4.13
0.4	Lβ′1NN	63	63				63	4.25	4.15
0.8	Lβ′1NN	64	63				63.5	4.25	4.15
	Lβ′2NNN	74	68				71
1.2	Lβ′1NN	65	67				66	4.21	4.16
	Lβ′2NNN	73	73				73
1.6	Lβ′2NNN	67	68				67.5	4.20	4.16
2	Lβ′2NNN	66	68				67	4.16
	Lβi	50	50				50
2.4	Lβi	50	51				50.5	4.16
3.2	Lβi	50	51				50.5	4.16
4	Lβi	50	51				50.5	4.16

For the SAXS data, the spacings are calculated from the angle of each reflection order detected on the patterns, and the average value is calculated from the values obtained for all the peaks. When the SAXS patterns show the coexistence of two lamellar phases, the long spacings obtained for each series of peaks are calculated.

For 0.8 < R_tot < 1.2, the SAXS measurements exhibit equidistant broad peaks. First-order diffraction clearly indicates the presence of two different lamellar spacings: that of the original pure DPPC and a new one at lower angle. Increasing enflurane concentrations favor this low angle peak, clearly indicating the appearance of a greater lamellar spacing and the coexistence, within this concentration range, of two distinct lamellar structures. The different lamellar spacings obtained after deconvolution of the patterns (summarized in Table 1 and plotted on Fig. 2 c) are ∼71–75 and 64–68 Å for the new and the L_β′ DPPC-like phases, respectively.

The WAXS patterns of these samples are also changed by comparison with those of lower R_tot = 0.4. The shapes of the peaks are broader and less asymmetric (Fig. 2 b). This change must likely be due to the superposition of two powder patterns coming from two coexisting lamellae, i.e., a mixture of the initial pure DPPC chain packing and a new chain packing coming from the new lamellar structure. Indeed, according to the literature (Tardieu and Luzzati, 1973; Zantl et al., 1999) this particular shape may be attributed to a change of the direction of the tilt of the chain from toward-next-neighbor to between-next-neighbors. These two lamellar structures formed at these R_tot have been called L_β′^1NN for the L_β′ DPPC-like lamellar structure and L_β′^2NNN for the new lamellar structure characterized by the new spacing and the new tilt. The rationale for such notation is the chain tilt (β′←β) and its direction toward the next ^1NN or between the next ^2NNN neighbor(s).

At R_tot = 1.6, the SAXS pattern exhibits one preponderant lamellar spacing at the low q position (lamellar spacing = 67.5 Å, Table 1). Deconvolution did not allow determination of the shoulder position, indicating that its relative intensity is very low and that at this R_tot, almost only the L_β′^2NNN phase is present. The WAXS pattern of this sample is similar to the ones obtained for lower R_tot and confirms the presence of the L_β′^2NNN lamellar structure.

For R_tot = 2, SAXS exhibits two distinct series of equidistant peaks. Clearly, two structures with very different lamellar spacings coexist: one with a spacing of 67 Å comparable to that observed at R_tot = 1.6, i.e., the L_β′^2NNN phase, and another with a much smaller spacing of 50 Å. The WAXS pattern shows a superposition of two chain packings, the one obtained at lower R_tot and a new one giving rise to a sharp peak at ∼1.55 Å⁻¹.

At R_tot values from 2.4 to 4, SAXS and WAXS patterns are constant. SAXS exhibits equidistant and sharp peaks with an associated lamellar spacing of 50 Å while WAXS patterns are sharp, symmetric, and centered at 4.13–4.14 Å. Such a sharp reflection is expected when the chain director is perpendicular to the membrane (Tardieu and Luzzati, 1973; Tang et al., 2000; Zantl et al., 1999). Interestingly, similar WAXS patterns, centered at 4.1 Å, have been recorded by Adachi et al. (1995) for an interdigitated mixed ethanol-DPPC phase.

This new lamellar phase, which appears alone within the high R_tot range, most likely corresponds to the new organization evidenced by the DSC experiments. This drastic decrease of the interlamellar distance can be due to either a decrease of the water layer or a decrease of the bilayer thickness. The melting of the new structure occurs at 33°C. However, in the calorimetry experiments, which were performed at a lipid concentration of 20 mM, this new phase appeared for a R_tot range between 3.8 and 14.6 whereas in the x-ray scattering measurements, it appears at an R_tot of 2. This discrepancy is likely due to the difference in lipid concentration used for the different experiments, i.e., 20 mM for calorimetry and 100 or 61 mM for x-ray scattering (depending on the experimental setup used). Enflurane is highly volatile and its partition among air, water, and lipids is difficult to control. Nevertheless, the higher volumic fraction of water in DSC measurements can explain the relatively higher R_tot required for the appearance of the new phase, in that particular case.

From the WAXS patterns, it is possible to calculate the cross-sectional area of a single aliphatic chain. In the L_β′ of the pure DPPC system, the unit cell is known to be orthorhombic and this unit cell contains two aliphatic chains. From the x-ray pattern, the two distances, d₂₀ and d₁₁, are determined from the q-vector using the well-known relation:

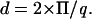(4)

The two parameters a and b of the orthorhombic cell are then calculated using Eqs. 5 and 6:

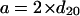(5)

(6)

in which d₁₁ and d₂₀ are the two distances determined by the q-vector on the x-ray pattern. The sharp peak is attributed to d₂₀ and the large one to d₁₁. From this calculation, a cross-sectional area of 20.1 Ų/aliphatic chain is determined for the DPPC in L_β′ phase, in good agreement with the 20.4-Å value of the literature (Tardieu and Luzzati, 1973). In the samples with high enflurane content, the symmetrical shape of the diffraction peak indicates that the chains are packed in an hexagonal lattice and from the q-vector determined at the maximum of the peak, the unit cell parameter a can be calculated using Eq. 7:

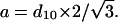(7)

In the case of a hexagonal unit cell, the surface of the cell (a × d₁₀) is directly the cross-section area of one aliphatic chain and this determination gives a value of 19.7–19.8 Ų / chain. This surface is significantly lower than that occupied by one aliphatic chain in the L_β′ pure DPPC phase. It thus rules out the possibility of penetration of enflurane within the aliphatic core of the membrane.

The more accurate SAXS pattern obtained at R_tot = 4 presents four reflection orders (Fig. 2 a, curve 4′, and Table 2), allowing the calculation of the electron profile shown in Fig. 3. This electron profile has been compared to that of pure L_β′ DPPC phase calculated from the five Bragg reflections of its SAXS pattern (Fig. 2 a, curve 0′). Calculations gave 16 (2⁵/2) and 8 (2⁴/2) solutions for electron profiles, respectively. Using the criteria defined above (see Material and Methods) among the 16 different electron profiles obtained for the pure DPPC L_β′ phase, we could eliminate 15 electron profiles which were incompatible with the defined molecular and crystallographic criteria (Table 2). This methodology has already been used to solve the low-resolution structures of fully hydrated dispersion of phosphatidylethanolamine lamellar and inverted hexagonal phase (Harper et al., 2001). The remaining electron profile for pure L_β′ DPPC phase is shown on Fig. 3 (Table 2) and it is in full agreement with the literature (Wiener et al., 1989). The liquid layer is estimated at 23 Å and the membrane thickness at 42 Å. In the case of enflurane-DPPC mixture (R_tot = 4), the first four molecular and crystallographic criteria eliminate seven among a total of eight possible solutions. The remaining possible one is sketched in Fig. 3. Interestingly, the water layer does not decrease, whereas the membrane thickness is greatly reduced, from 42 Å in the absence of anesthetic to 26 Å in its presence. Since the WAXS data clearly indicate that the chains are perpendicular to the membrane for this value of R_tot, the results can only be interpreted in terms of interdigitation of the lipids. Moreover, these results also imply that the anesthetic remains close to the polar headgroups, causing the righting and the interdigitation of the chains as suggested by the electron profiles. This new interdigitated phase is referred to as L_βⁱ, following the rationale given above.

TABLE 2.

Data used to calculate the electron density variation of pure DPPC L_β′ phase and of Enf-DPPC (R_tot = 4) samples; the x-ray data are from the patterns obtained on D43 line (LURE)

	Pure Lβ′ DPPC phase (25°C)			Enf-DPPC, Rtot = 4 (25°C)
Order (n)	Position (Å−1)	lFobsl	Chosen phase	Position (Å−1)	lFobsl	Chosen phase
1	0.098	14.25	−	0.124	4.87	−
2	0.197	12	+	0.248	10.62	+
3	0.297	7.44	+	0.374	4.29	+
4	0.397	6.04	+	0.496	4.34	−
5	0.494	4.45	−

FIGURE 3.

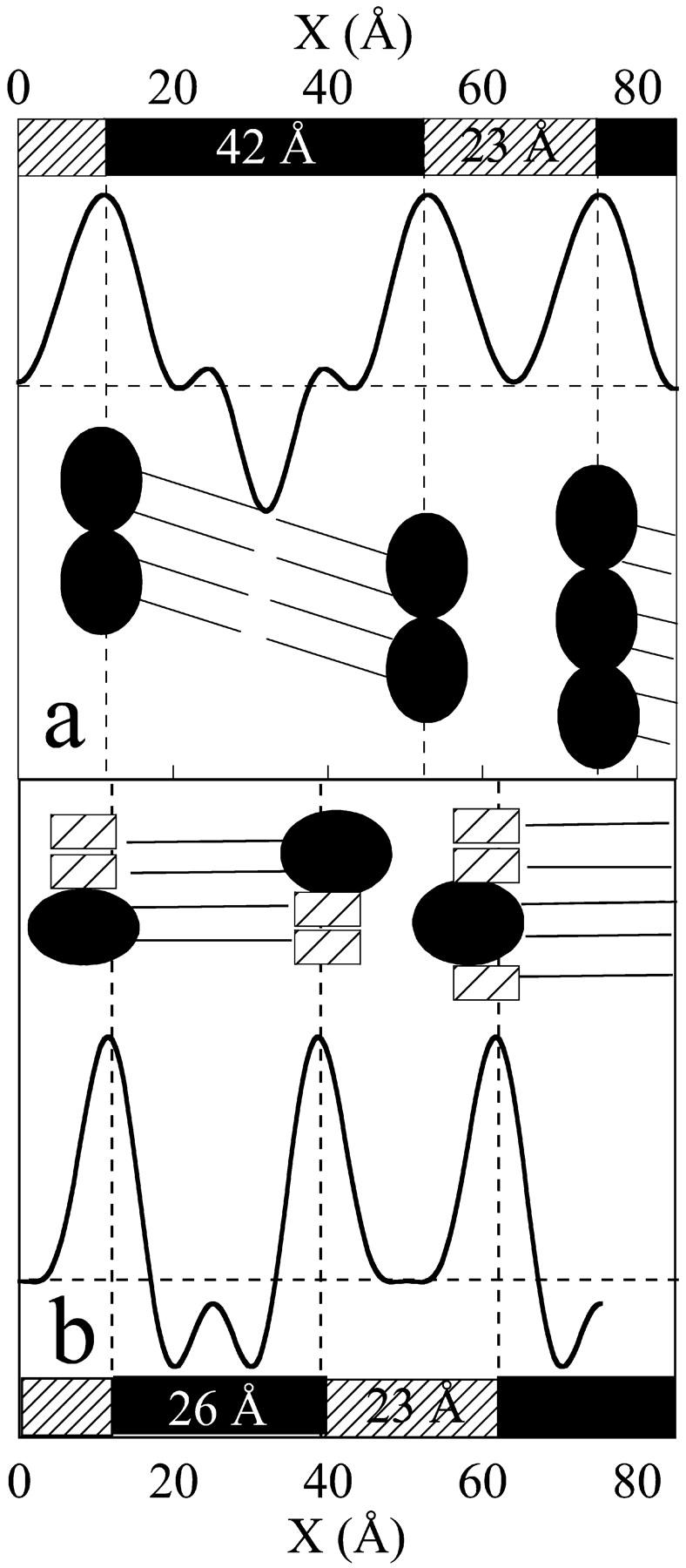
Electron profiles calculated from the SAXS patterns of DPPC and Enf-DPPC (0′ and 4′ traces of Fig. 2). Electron profile of pure L_β′ DPPC lamellar phase (a) and of Enf-DPPC lamellar phase (b). A schematic representation of the lipid organization is also drawn on each panel. These schemes take into account the tilt orientation deduced from the WAXS patterns. The enflurane molecules are represented by a hatched box.

Structural characterization of DPPC-enflurane mixtures at 45°C

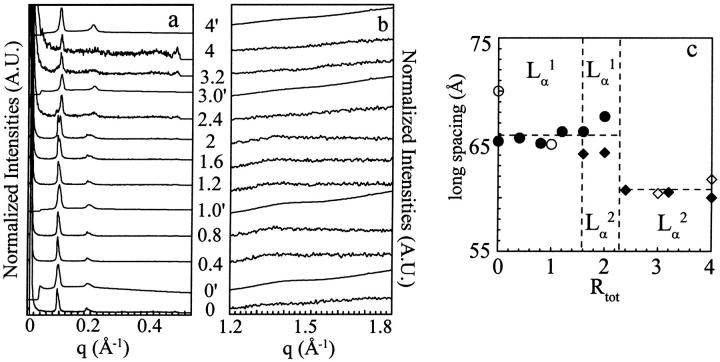
The experiment just described here above was repeated at 45°C, a temperature well over that of the new 33°C transition. The WAXS patterns (Fig. 4 b) recorded for the 10 different enflurane-DPPC mixtures indicate that the chains are melted at this temperature.

FIGURE 4.

SAXS (a) and WAXS (b) patterns at 45°C on different DPPC-enflurane mixtures. The R_tot are indicated at the level of each trace. The superscript prime identifies traces measured on D43 line ([lip] = 61 mM). The others are those measured on D22 line ([lip] = 100 mM). (c) Long spacing as a function of R_tot. Unfilled and solid symbols correspond to measurements on D43 and D22 lines, respectively. (Circles and diamonds stand for L_α¹ and L_α² phases, respectively.)

The SAXS patterns obtained for the samples of R_tot ranging from 0 to 1.2, are identical and are similar to the one obtained for the L_α DPPC phase (Fig. 4 a). Therefore, the lamellar phase observed for these ratios has been called L_α¹ (Fig. 4 c and Table 3).

TABLE 3.

Long spacings determined from SAXS patterns recorded at 45°C on either D43 or D22 line (LURE); the data are presented as a function of R_tot of the samples

		SAXS, 45°C
Rtot	Lamellar phase	1st order d (Å)	2nd order d (Å)	Average d (Å)
		D43 ([Lip] = 61 mM)
0	Lα1	70	70	70
1	Lα1 + Lα2	65	65	65
3	Lα2	60	61	60.5
4	Lα2	62	62	62
		D22 ([Lip] = 100 mM)
0	Lα1	65	66	65.5
0.4	Lα1	65	66	65.5
0.8	Lα1	65	66	65.5
1.2	Lα1	66	67	66.5
1.6	Lα1	66	67	66.5
	Lα2	64	65	64.5
2	Lα1	67	68	67.5
	Lα2	63	66	64.5
2.4	Lα2	61	61	61
3.2	Lα2	61	60	60.5
4	Lα2	60.0	–	60.0

The spacings are calculated from the angle of each reflection order detected on the patterns, and the average value is calculated from the values obtained for all the peaks. When the SAXS patterns show the coexistence of two lamellar phases, the long spacings obtained for each series of peaks are calculated.

For 1.6 < R_tot < 2, coexistence of two lamellar structures is visible: two long spacings are detected, one remaining at about the same value than that of pure DPPC L_α phase (66 Å) and another with a smaller spacing of 64 Å (Table 3). As R_tot increases, the peak at low q, corresponding to the initial L_α phase, decreases in favor of the peak at high q, corresponding to a new fluid lamellar phase. This new phase is indicated as L_α² in Fig. 4 c.

For 2.4 < R_tot < 4, the SAXS patterns exhibit equidistant Bragg peaks that are indicative of only one lamellar spacing of 61–60 Å, corresponding to the new L_α² phase which was already appearing at lower R_tot (Table 3).

The 45°C measurements show that little, if any, structural change does occur until R_tot reaches ∼1.5; over this value, the lamellar spacing is reduced from 66 to 61 Å (Fig. 4 c).

Thermotropism of DPPC-enflurane binary mixtures and construction of the pseudo-binary phase diagram of DPPC-enflurane in excess water

In this set of measurements, the homemade Microcalix calorimeter has been used at the D22 station, allowing the simultaneous record of the endotherms and of the SAXS and WAXS patterns. The heating rate was fixed at 1°C/min, 12 times faster than that used in the DSC experiments described before. The consequence of this high heating rate is that some smaller thermal events were unresolved on the calorimetric curves.

Fig. 5 shows a typical set of data obtained, in this case, at R_tot = 2.4 ([lip]_tot = 100 mM). The calorimetric curve exhibits only one energetic transition centered at 33°C while SAXS and WAXS patterns show the evolution of the long spacing (SAXS, Fig. 5 a) and of the chain packing (WAXS, Fig. 5 b), between 13 and 50°C. At low temperature, from 13 to 33°C, equidistant Bragg peaks corresponding to a unique and constant interlamellar distance of 50 Å are recorded. At 34°C the x-ray pattern indicates that the sample is a mixture of the lamellar phases obtained at low and at high temperature. For temperature higher than 34°C, the x-ray patterns indicate that one type of lamellar phase is responsible for the equidistant Bragg peaks. A shift toward the high q accompanies the temperature rise, indicating a temperature-dependent decrease of the interlamellar distance.

FIGURE 5.

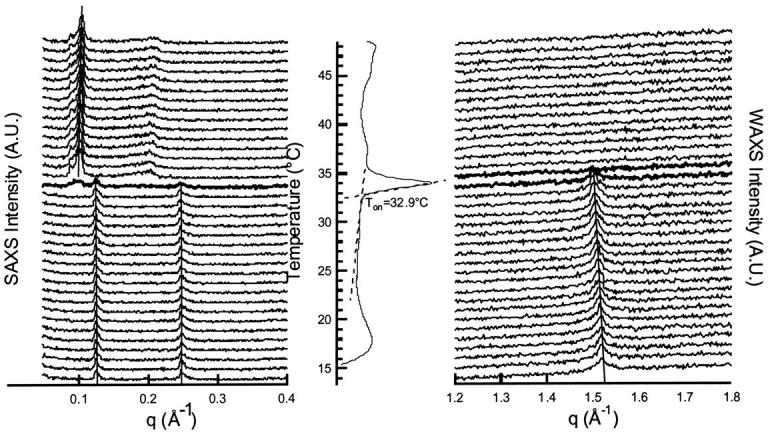
SAXS, WAXS, and DSC of an enflurane-DPPC mixture at R_tot = 2.4 ([lip] = 100 mM).

In the WAXS patterns, the melting temperature of the chain observed for this sample is between 34°C and 35°C, whereas the T_on determined on the endotherm is lower at 32.9°C. As already seen at 25°C for the same R_tot, the wide-angle pattern is symmetric below the melting temperature. Moreover a progressive shift of the peak toward the small angle, i.e., an expansion of the chain packing with increasing temperature, is visible. Within the same temperature range, no change of interlamellar distance is detectable.

This type of experiment has been performed for nine enflurane-DPPC mixtures with R_tot of 0, 0.4, 0.8, 1.2, 1.6, 2, 2.4, 3.2, and 4. From the calorimetric curves, because of the limitations due to the high heating rate, we only have measured the T_on of the thermal event (Fig. 5 b). To illustrate true broadening of the transition in the coexistence regions, the solidus and the liquidus lines, reported on Fig. 7, were corrected by the width of the pure DPPC main transition as suggested by Mabrey and Sturtevant (1976).

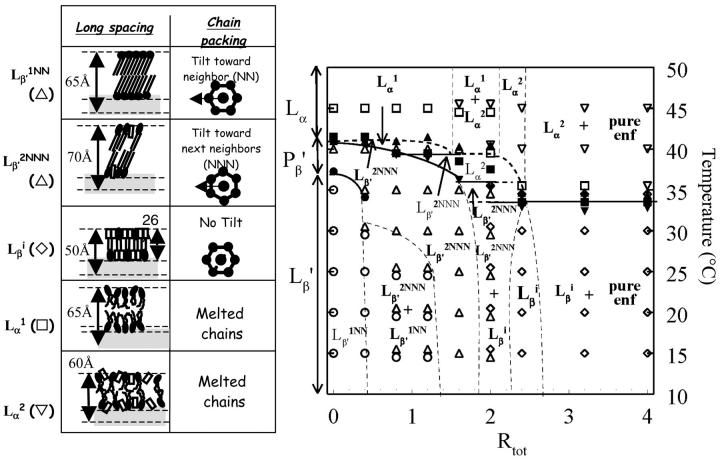
FIGURE 7.

Pseudobinary phase diagram built from x-ray and DSC data. The thermal events are represented by closed symbols whereas open symbols represent specific phases. The abscise of the phase diagram is the R_tot of the samples. ▾, T_on of the main transition; ▴, T_off of the main transition; ▪, chain melting temperature measured on WAXS patterns; and •, T_on of the L_β′–P_β′ transition. The structural information and symbolic representation of the different specific phases are given on the left of the diagram.

The WAXS patterns recorded during the heating cycles were also used to determine the chain-melting temperature. DSC and WAXS gave identical melting temperatures at low and high R_tot, i.e., between 0 and 0.8 and between 2.4 and 4. But, for 1.2 < R_tot < 2, WAXS always gave a higher melting temperature than the T_on determined from the endotherms.

On the Fig. 6, we have reported the SAXS and WAXS patterns obtained for eight of the nine R_tot used in this part of the study (the x-ray patterns of the R_tot = 4 sample, omitted in this figure, are similar to those recorded for the R_tot = 3.2 sample). For each sample we have presented the patterns obtained at six different temperatures (15, 20, 25, 30, 35, 40, and 45°C). From these data it is possible to determine the temperatures at which the different structures, already characterized at low (25°C) and high (45°C) temperatures, appear or disappear. We focused on the temperature range within which the different phases exist, namely L_β′^1NN (which is structurally very close to the pure DPPC L_β′ phase), L_β′^2NNN (which is structurally very close to the pure DPPC P_β′ phase), and L_βⁱ (which is the interdigitated phase).

FIGURE 6.

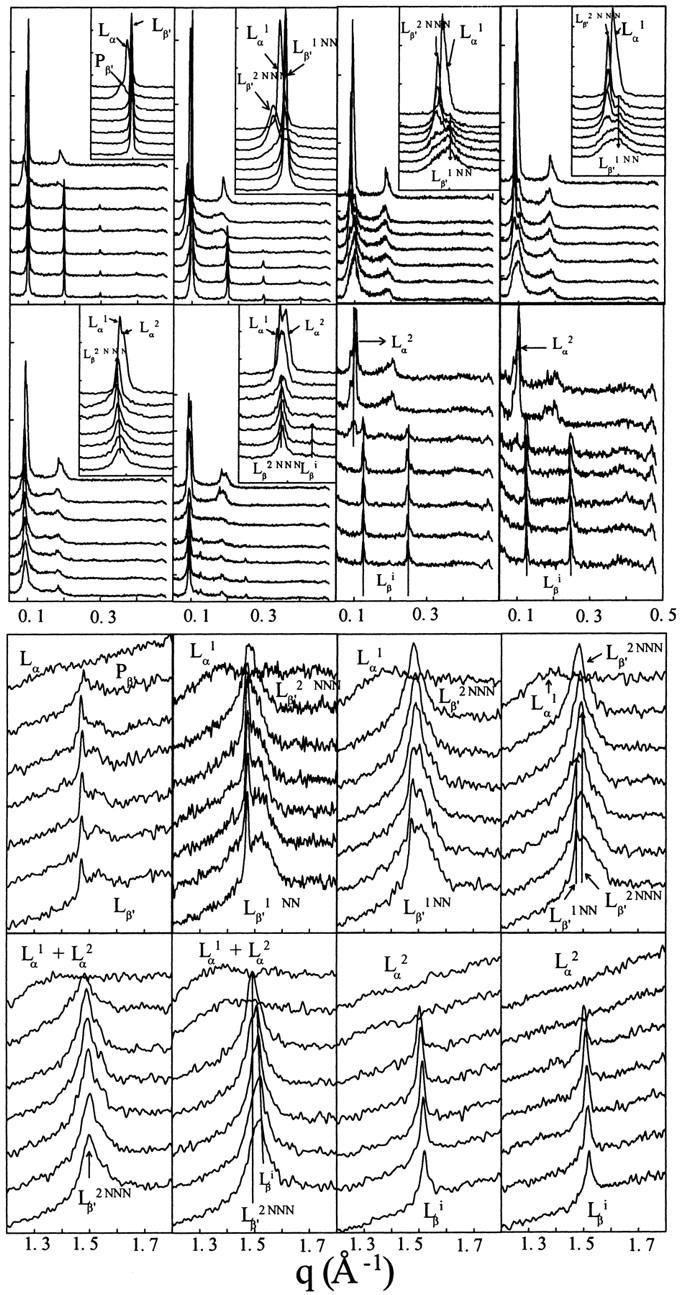
SAXS (upper panels) and WAXS (lower panels) patterns of different enflurane/DPPC mixtures at different R_tot and temperatures. In both groups of panels, from left to right and top to bottom, the R_tot of the samples are 0, 0.4, 0.8, 1.2, 1.6, 2, 2.4, and 3.2. In each set of traces, the curves, from bottom to top, correspond to measurements at 15, 20, 25, 30, 35, 40, and 45°C. In some cases, inserts present a zoom on the first order of the Bragg peak to evidence coexistence of different lamellar structures.

The concentration and temperature ranges of each of these phases are reported on Fig. 7 as a function of the R_tot of the sample. The result is a pseudo-binary phase diagram. It is interesting to note that the temperature range of existence of the L_β′^2NNN phase increases with the enflurane/lipid ratio, and that this phase is even present alone at 15°C for a R_tot of 1.6 and melts at ∼36.5°C. The temperature domain of the L_βⁱ phase is almost constant whatever the R_tot (from 2 to 3.2); this phase is already present at 15°C and always melts between 30 and 35°C giving rise to the energetic endothermic transition recorded by DSC for these mixtures.

Above the liquidus and depending on the R_tot, two fluid phases have been observed alone or in coexistence: L_α¹ and L_α². The first one is structurally very close to the L_α of pure DPPC and the other has a smaller interlamellar distance than the L_α¹ phase. On this phase diagram, domains of coexistence of L_βⁱ or of L_α² phases with pure enflurane is required. However, as pure enflurane has neither thermal nor x-ray signature, the positions of the domain limits are uncertain.

On the phase diagram of Fig. 7, the dashed lines represent the limits that we have estimated; their positions are not very accurate. However the limits represented by solid lines have been precisely determined, either by DSC or by x-ray scattering. It is also important to note that the three isothermal straight solid lines have been deduced from both the calorimetry curves obtained on the Arion microcalorimeter and WAXS and SAXS data.

Evaluation of enflurane molecules in interaction with DPPC

This part of the study is devoted to the determination of the evolution of the enflurane partitioning among lipids, air, and water, as a function of temperature. For this purpose, we have used the lipidic probe Laurdan, which is known for its sensitivity to the gel-to-fluid phase transition. However, the high level of light scattering by lamellar phases only allowed measurements on diluted small unilamellar liposomes of DPPC ([lip] from 1 to 12.5 mM by comparison to 20 mM for DSC, and 60 or 100 mM for x-ray scattering).

We have first checked for any effect of the probe itself (inserted in the liposomes at 0.1% (M/M)) on the phase transition of DPPC in multilamellar and unilamellar liposomes. DSC of Laurdan containing liposomes showed that the phase-transition temperature of DPPC is almost unchanged by the presence of the lipid probe. The endotherms obtained for multilamellar or for unilamellar liposomes (results not shown) are obviously different: in the last case, the main peak is preceded by a broad shoulder, attributed, according to the literature (Biltonen and Lichtenberg, 1993), to some inhomogeneity in the liposome sizes. However, the T_on determined by the tangent method is similar in the two systems. Interestingly, we also observed that the L_β–P_β′ transition is absent in unilamellar liposomes.

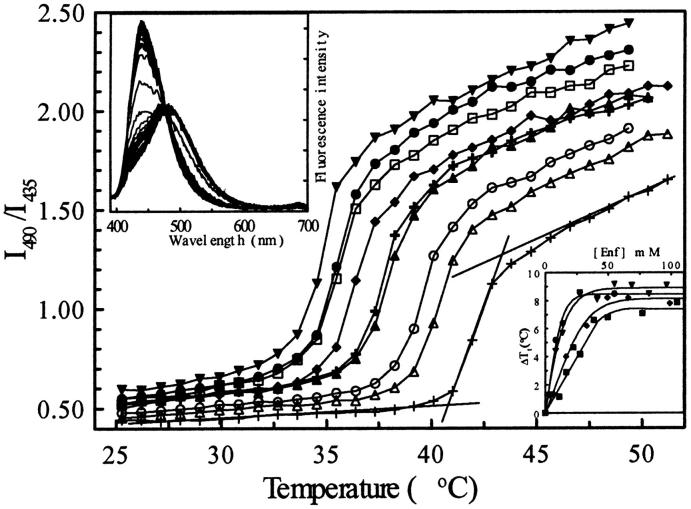
Fig. 8 shows the temperature-dependence change of Laurdan fluorescence measured at constant lipid concentration and increasing enflurane concentrations. In the gel phase, the emission spectrum of Laurdan is centered near 435 nm, whereas in the fluid liquid crystalline phase, it locates at ∼490 nm. During the transition a progressive change of the spectrum is observed, allowing to follow the phase transition by plotting the fluorescence intensity ratio I₄₉₀/I₄₃₅ as a function of temperature. The transition temperature is determined by the tangent method, as indicated on Fig. 8 and it is in good agreement with the calorimetric data (average value on six measurements 41.5 ± 0.7°C).

FIGURE 8.

Evolution of the fluorescence intensity ratio I₄₉₀/I₄₃₅ of Laurdan. The different curves were obtained at constant [DPPC] = 0.85 mM and enflurane concentrations of 0 (+); 8.2 (▵); 13.7 (○); 27.5 (▴); 41.2 (+); 54.9 (♦); 68.7 (□); 82.4 (•); and 96.1 (▾) mM. The transition temperature is determined by the graphic tangent method as indicated on the figure for the curve obtained for pure DPPC liposomes. (Upper inset), Emission spectra of Laurdan (λ_ex = 370 nm) during an increase of temperature from 25 to 48°C at 0.22°C/min ([DPPC] = 0.85 mM and [Enf] = 13.7 mM). (Lower inset) Enflurane concentration-dependent shift of the T_on obtained from the fluorescence experiment at lipid concentrations of 1 mM (•), 2 mM (▾), and 7 mM (♦), and from DSC (▪, [Lip] = 20.3 mM).

The different curves presented on Fig. 8 indicate, as expected from the DSC experiments, that enflurane induces a concentration-dependent decrease of the temperature of the main transition (T_t) of DPPC. The shifts of the main transition temperature measured either by fluorescence at low lipid concentration or by DSC at much higher lipid concentration are also compared in Fig. 8 (lower inset). There is some difference between the maximal temperature shifts measured by fluorescence and by DSC (≤2°C). However, the overall phenomenon seems to be similar.

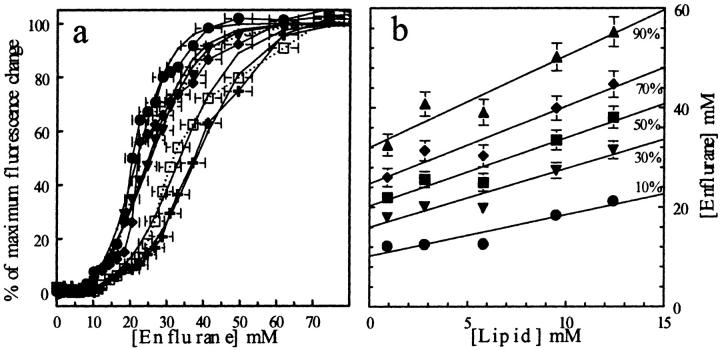
The curves of Fig. 8 also show that enflurane induces a concentration-dependent change in the fluorescence intensity ratio (I₄₉₀/I₄₃₅) at a constant temperature. Therefore, we have examined the effect of increasing concentration of enflurane on the emission spectra of Laurdan incorporated into the liposomes at 25 and 45°C. In these experiments, DPPC-Laurdan liposomes were continuously stirred and the enflurane concentration was increased by stepwise addition of small amounts of enflurane directly into the cuvette. The fluorescence spectrum of Laurdan was recorded after each addition. Measurements were repeated for a series of initial lipid concentrations ranging from 0.9 to 12.5 mM. The results are presented in Figs. 9 a and 10 a where the fluorescence changes are expressed in terms of percentage of maximal change of I₄₉₀/I₄₃₅ as a function of enflurane concentration.

FIGURE 9.

(a) Fluorescence changes of Laurdan (expressed in percent of maximal change) as a function of [enflurane] at 25°C. The curves correspond to DPPC concentrations of 0.9 (•), 2.8 (▾), 5.8 (♦), 9.5 (□), and 12.5 (+) mM. (b) Relation between the enflurane concentrations required to reach 10, 20, 50, 70, and 90% of the maximum fluorescence change as a function of lipid concentration (see Table 4 and text for details).

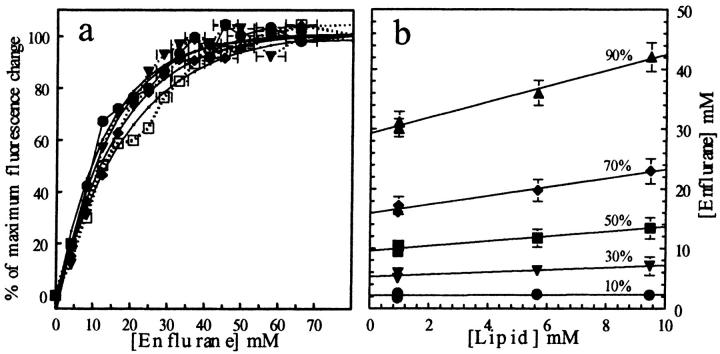
FIGURE 10.

(a) Fluorescence changes of Laurdan (expressed in percent of maximal change) as a function of [enflurane] at 45°C. The curves correspond to DPPC concentrations of 0.9 (•), 1 (▾), 5.7 (♦), and 9.7 (□) mM. (b) Relation between the enflurane concentrations required to reach 10, 20, 50, 70, and 90% of the fluorescence changes as a function of lipid concentration (see Table 4 and text for details).

The shape of the curves obtained at 45°C are different from those obtained at 25°C especially with respect to the concentration threshold for insertion of enflurane only observed at 25°C. A similar set of experiments has also been performed at 25°C on Dimyristoyl-phosphatidylcholine (DMPC) which has a T_m of 21°C, to get rid of the supplementary evaporation problem enhanced at 45°C and to compare the partitioning behavior of enflurane in L_β′ and L_α phases at the same temperature (data not shown). Similar results were obtained indicating that the measurements done at 45°C on the DPPC system was accurate enough to give a good estimation of the enflurane partitioning.

These dose-response curves allow the determination of the evolution of the enflurane partitioning between lipids and “water and air.” Indeed, enflurane is a volatile anesthetic, and it equilibrates not only between water and lipids but also between water and air. As the method used here is only able to detect the anesthetic molecule in contact with the lipids (Laurdan is essentially a probe of the lipid environment), it is not possible to distinguish between the molecules in air or in water.

On Figs. 9 b and 10 b, the enflurane concentration needed to reach 10, 30, 50, 70, and 90% of the maximal effect recorded at 25°C and 45°C has been plotted versus the lipid concentration. Even if the error bars are important, it has been possible to fit the points with straight lines, the intercepts of which give the concentration of enflurane which is not in interaction with the lipids ([Enf]_w+air), and the slopes of which give the enflurane-to-lipid ratio within the aggregates ([Enf]/[Lip]). The data are summarized in Table 4. At 45°C, 90% of the maximal effect of enflurane was obtained at [Enf]/[Lip]. = 1.3. At 25°C, the same effect is obtained at [Enf]/[Lip]. = 1.9, whereas the [Enf]_w+air were comparable (30 and 34 mM, respectively) at both temperatures.

TABLE 4.

Partition coefficient data obtained from fluorescence experiments performed either at 25°C or at 45°C

	DPPC 25°C			DPPC 45°C
% of changes (Laurdan)	[Enf]H2O+air* (mM)	[Enf]H2O† mM	[Enf]/[Lip]ag‡	[Enf]H2O+air* (mM)	[Enf]H2O† mM	[Enf]/[Lip]ag‡
10	10	0.9§	0.8	2.2	0.1§	0.02
20	13	1.2	1.1	3.6	0.3§	0.1
30	16	1.45	1.2	5.3	0.5§	0.2
40	18	1.6	1.3	7.3	0.7	0.3
50	20	1.8	1.4	9.6	0.9	0.4
60	22	2.0	1.5	12.3	1.1	0.6
70	25	2.3	1.6	15.9	1.4	0.7
80	28	2.5	1.7	20.9	1.9	1.0
90	32	2.9	1.9	29.3	2.7	1.3

^*[Enf]_H2O+air is the concentration of enflurane that is not in interaction with the lipids in the lamellar phases.

^†[Enf]_H2O was estimated from the [Enf](_air+H2O) assuming that the partition coefficient of enflurane between air and water is ∼10 and that the air and the water volumes in the cuvette were similar.

^‡[Enf]/[Lip]_ag is the enflurane-to-lipid concentration ratio within the lamellar phases. These values are determined from the origin and the slope of the linear relationships plotted on Figs. 9 (25°C) and 10 (45°C), respectively.

^§The [Enf]_H2O in bold are those that fall within the clinical concentration range.

From the data of Table 4, we have estimated the total enflurane to lipid molar ratio R_tot, required to form the L_βⁱ (25°C) and the L_α² (45°C) phases at high lipid concentration, i.e., 61 and 100 mM, the concentrations used for SAXS and WAXS experiments. Wd found 2.4 (61 mM) and 2.2 (100 mM) for the L_βⁱ plase and 1.8 (61 mM) and 1.6 (100 mM) for the L_α² phase. These R_tot are in good agreement with the experimental R_tot (see Figs. 2 c and 4 c). Thus, our estimation of the partition of enflurane among air and water and lipids, as determined by fluorescence measurements, must be in the correct range.

DISCUSSION

The effect of increasing concentration of enflurane on the organization of the lipid bilayer formed by DPPC has been examined as a function of temperature by fluorescence, DSC, SAXS, and WAXS measurements. The interpretation of the different results enabled the construction of a pseudo-binary phase diagram mostly characterized by the formation of new phases with different spacings and ending by an interdigitated phase, at 25°C. As a function of R_tot, the different lamellar phases are L_β′^1NN, L_β′^2NNN, and L_βⁱ.

The first one, L_β′^1NN, has a long spacing of ∼65 Å, a chain-packing (pseudo-hexagonal lattice), and a tilt (toward the next-neighbor) comparable to those found for the L_β′ phase of pure DPPC system. Moreover, the fluorescence data, indicating that enflurane at low concentration does not interact with the membrane, support the idea that the L_β′^1NN phase corresponds, in fact, to the unchanged L_β′ lamellar phase of pure DPPC.

L_β′^2NNN is detected in coexistence with L_β′^1NN lamellar phase. It has a long spacing (∼70 Å), a chain-packing (pseudo-hexagonal lattice), and a tilt (between next-neighbors) similar to those found for pure DPPC P_β′ (Smith et al., 1988; Zantl et al., 1999). The increase of the interlamellar distance compared to L_β′^1NN lamellar phase, considering that the chains remain tilted, suggests that enflurane interacts with the polar headgroups of the lipids. Indeed, this interaction would induce a righting of the polar headgroups, causing in return the increase of the long spacing. Moreover, this interpretation is in agreement with the fact that this lamellar phase looks like the P_β′ lamellar phase of DPPC. Grabielle-Madelmont et al. (1999) have shown that such interaction occurs in the mixed lasalocid-DPPC system at low R_tot. They observed that the mixed lamellar phase has the same interlamellar distance, chain-packing, and tilt than the P_β′ phase, but they also show that the interaction of the antibiotic with the polar headgroup of the DPPC forbids the formation of the surface ripples. We had no access to the q-range where the periodic ripple of the P_β′ phase creates a weak peak near 0.045 Å⁻¹ (characteristic wave periodicity of 140 Å) and we could not see if, as in the case of the interaction of lasalocid with DPPC, the ripple of the P_β′ phase had disappeared or not.

Finally, the L_βⁱ phase is detected either in coexistence with the L_β′^2NNN lamellar phase or in excess of enflurane for all the R_tot above 2. It has a much smaller lamellar periodicity, no tilt, and the surface occupied by one aliphatic chain (19.7–19.8 Ų) is comparable to the surface occupied by alkanes in R_II phases (a rotator phase in which the chains are untilted and packed in an hexagonal lattice; Sirota, 1997). This is a strong indication in favor of a preferential interaction of enflurane with the polar headgroups of the lipids. The interdigitation of the chain would be a response of the membrane to the important increase of the surface pressure induced by the penetration of enflurane in the interfacial region. Moreover, an estimation of two molecules of enflurane per molecule of lipid within the aggregates has been obtained from fluorescence experiments. From the x-ray data and this estimation, a model for the interdigitated phase was proposed, where the two molecules of enflurane are located in the lipid polar headgroup region in front of the two methyl groups of the opposed phospholipid (Fig. 3). However, by calculating the molar volume of enflurane, we found 124 cm³. The same type of calculation gives for the simple butane molecule (representing an hydrogenated aliphatic small chain) a molar volume of 94.5 cm³ and for the 1-chloro-2-methoxyethane, which is, compared to enflurane, the totally hydrogenated molecule, a molar volume of 96 cm³. It is obvious that the presence of five fluor atoms in the enflurane molecule is responsible for this high molar volume. On the other hand, the high molar volume of enflurane compared to the molar volume of simple hydrogenated chains suggests that the estimation of two molecules of enflurane per molecule of lipid for the composition of the interdigitated phase might be overestimated.

It is noteworthy that comparable interdigitated phases have been observed for mixtures of DPPC with few other water soluble amphiphiles such as ethanol, acetonitrile, acetone, propionaldehyde, and tetrahydrofurane (McIntosh et al., 1983; Simon and McIntosh, 1984; Nambi et al., 1988). It is also the case with the water-soluble form of the local anesthetic tetracaine (Auger et al., 1988). It has been shown that such interdigitated lamellar phases are formed with soluble surface-active molecules that interact with the polar headgroups of the lipids. In our case, enflurane is a poorly soluble molecule, but its short fluorinated aliphatic chain reduces its solubility in hydrogenated chains maintaining the molecule at the level of the polar headgroups of the lipids. Interestingly, it has also been shown that the 20-mol % of cholesterol in phosphatidylcholine bilayer prevents the formation of the interdigitated phase induced by the penetration of ethanol (Komatsu and Rowe, 1991).

At 45°C, enflurane induced two distinct fluid lamellar phases: L_α¹ and L_α². L_α¹ is detected either alone or in coexistence with L_α² for 1.6 < R_tot < 2. For this lamellar phase, the interlamellar spacing is fully comparable to the one found for L_α phase of pure DPPC system. The L_α² phase is detected either in coexistence or alone for R_tot higher than 2. The L_α² is characterized by a smaller spacing of ∼60–64 Å. Again, this decrease in the interlamellar distance may be explained, by a preferential interaction of enflurane with the polar headgroup region, in response to the increase of the interfacial surface. Moreover, a decrease of the smectic distance is theoretically predicted for such interfacial interaction of a xenobiotic with a bilayer structure (Koubi et al., 2000).

The estimation of the partitioning of enflurane between DPPC liposomal membranes and the two other phases constituted by water and air was an experimentally difficult part of the work. The fluorescent probe Laurdan was chosen for its sensitivity to the gel-to-fluid DPPC transition (Parasassi et al., 1991) and for its ability to detect the incorporation of surface active molecules within the membrane (Paternostre et al., 1995). Moreover, the ability of Laurdan to detect interdigitated lipidic phase induced by alcohol has also been shown (Zeng and Chong, 1995). However, to reduce light scattering, we had to work on unilamellar liposomes, in a lower lipid concentration range than that used for the other experiments. An additional difficulty also comes from the volatility of the anesthetic. Nevertheless, it has been possible to quantitate the effect of increasing concentration of enflurane on the main transition temperature of DPPC on different concentrations of unilamellar liposomes, and to estimate the quantity of enflurane in interaction with DPPC at both low and high temperatures, i.e., 25 and 45°C.

From fluorescence experiments performed at either 25°C or 45°C, the estimation of the enflurane-to-lipid ratio within the aggregates ([Enf]/[lip])_ag gives, for the maximal effects, a value of 2 and 1, respectively, indicating that less anesthetic was required to reach the maximal effect visualized by Laurdan in fluid than in gel phase. The dose response curves also show that, at 25°C, the anesthetic has little if any effect at low concentration, whereas at 45°C this concentration threshold is not observed, indicating that the incorporation of enflurane in the membrane is easier in the fluid than in the gel state. On another hand, the quantities of enflurane estimated for the maximal effects shows that more enflurane can penetrate in the gel than in the fluid state. These observations are somewhat in contradiction and may result from two possibilities: 1) the lack of sensitivity of Laurdan for the incorporation of high amount of enflurane when lipids form L_α phase, or 2) an overestimation of the enflurane-to-lipid ratio required for the formation of the interdigitated phase, as it is underlined above.

From the fluorescence data it was also possible to get an estimation of the anesthetic concentration in water (Table 4). Maximal enflurane effect occurs at 3 mM, which is 5 times higher than the concentration estimated by Franks and Lieb, (1998) for clinically relevant concentration. Our values of [Enf]_water may well be overestimated too, particularly if we think of the evaporation problem but, nevertheless, the same set of data shows that a sensitive fluorescence change is visible from concentrations as low as 0.1 mM.

A very interesting and perhaps most important conclusion of the study is that, in all cases, there is no need to invoke enflurane interactions other than with the polar headgroups of the lipids. Enflurane is, as few other volatile anesthetic molecules (halothane or isoflurane, for example), a partly fluorinated amphiphile (five fluors and two hydrogens for enflurane). The mixing of fluorinated and hydrogenated molecules, even if their amphiphilic or hydrophobic natures are similar, is often difficult and leads to phase separation (Mukerjee and Yang, 1976; Mukerjee, 1994). This property supports the hypothesis that enflurane cannot deeply penetrate within the aliphatic core of the bilayer, as predicted theoretically (Cantor, 1997, 2001). However, only small changes of the organization of the lipids were recorded for clinically relevant anesthetic concentrations. Therefore, the theory of Cantor may be necessary but not sufficient to explain anesthesia. Indeed, it cannot explain why a small aliphatic detergent such as octylglucoside, for example, which possesses a large polar headgroup compared to alcohols and interacts with membranes exactly in the way that Cantor predicts for anesthetics, does not produce anesthesia.

Even if the pure lipidic system studied in this work is far from the reality, its different phases remains a good model for the different phases and domains which exist in natural membranes. Our results strongly suggest that enflurane preferentially interacts with the lipids at the water-lipid interface. Such a behavior is in agreement with experimental, simulation, and theoretical works, indicating that the anesthetic mechanism is partly related to the inhomogeneous distribution of anesthetics within the membrane and to its consequences on the functionality of the proteins contained therein. Indeed, a membrane protein, due to its conformation and amino acid sequence, also presents hydrophilic-hydrophobic interfaces that can be potential sites for anesthetics. The question would be then to determine if the affinity of enflurane for the protein sites is equal or not to the affinity of enflurane for lipidic sites, and if the initial or local state of the lipids can modulate this affinity.