Nucleosome Repositioning via Loop Formation

Abstract

Active (catalyzed) and passive (intrinsic) nucleosome repositioning is known to be a crucial event during the transcriptional activation of certain eukaryotic genes. Here we consider theoretically the intrinsic mechanism and study in detail the energetics and dynamics of DNA-loop-mediated nucleosome repositioning, as previously proposed by earlier works. The surprising outcome of the present study is the inherent nonlocality of nucleosome motion within this model–being a direct physical consequence of the loop mechanism. On long enough DNA templates the longer jumps dominate over the previously predicted local motion, a fact that contrasts simple diffusive mechanisms considered before. The possible experimental outcome resulting from the considered mechanism is predicted, discussed, and compared to existing experimental findings.

INTRODUCTION

The nucleosome, the most abundant DNA-protein complex in nature, is the basic unit of eukaryotic chromatin organization. It is roughly a cylinder of 6-nm height and 10-nm diameter, consisting of a protein octamer core and 147 basepairs (bp) of DNA tightly wrapped around it in 1 and 3/4 left-handed superhelical turns. The genes of all higher organisms, ranging from simple ones such as yeast, to the most elaborate, such as those of humans, are all organized in long arrays of nucleosomes with short DNA segments (linkers) of 50–100 bp interpolating between them, comparable to a beads-on-a-string chain (Widom, 1998; Kornberg and Lorch, 1999; Wolffe, 1999). The higher order organization of these units, being most probably a solenoid or zig-zag, crossed-linkerlike fiber with a 30-nm diameter, is still under great dispute, although it received increasing theoretical and experimental support in recent years. Above that scale of organization, the higher order structures which link the 30 nm to the final big-X-like structure, the packed chromosome, are still unknown. Although there are several biologically motivated speculations about the chromosome, its definite structure remained a puzzle for the last 20 years, defying all biophysical, biochemical, and molecular genetics efforts to resolve it because of its intrinsic softness and fuzziness.

An additional obstacle for understanding the chromatin structure is the fact that it is highly dynamic on all organization scales. Starting at the macroscopic chromosome level we see that its structure can strongly vary throughout the cell cycle on timescales of hours or days. Below that on timescales of seconds and minutes, the structure of the 30-nm fiber itself is subjected to great variations due to transcription, replication, biochemical modification, and other dynamic processes. Finally, at the lowest organization level, the nucleosome itself has been shown to be a dynamical structure being moved along the DNA by chromatin remodeling complexes on expense of ATP (Vignali et al., 2000; Peterson, 2000).

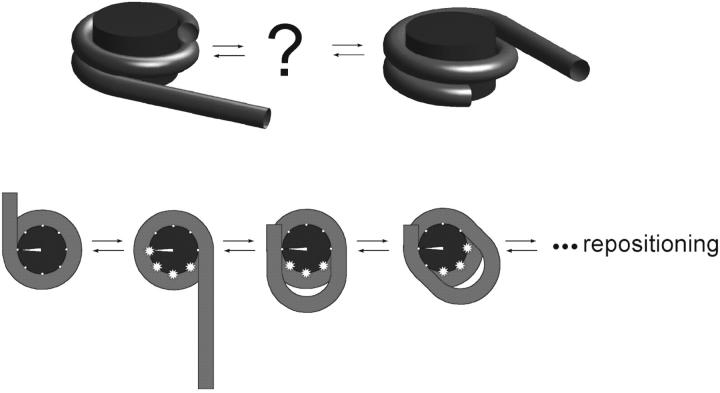
Interestingly, it was experimentally observed (Beard, 1978; Spadafora et al., 1979; Pennings et al., 1991; Meersseman et al., 1992) that nucleosomes can even move autonomously on short DNA segments. This intrinsic repositioning behavior was shown to be strongly temperature-dependent. At room temperature it occurs roughly on timescales of ∼1 h, indicating the existence of significant energetic barriers. Besides the fact that the repositioning does indeed occur and is of intramolecular nature (the nucleosome stays on the same DNA segment), the underlying scenario could not be figured out. It was speculated by Pennings and co-workers (Pennings et al., 1991; Meersseman et al., 1992) that the mechanism was some type of nucleosome sliding or corkscrew motion. An alternative explanation which appears to be more consistent with the discrete jumps and large barriers observed by Pennings and co-workers has been recently proposed by Schiessel et al. (2001). In this model, the basic step in the repositioning process is a partial unwrapping of DNA from the very ends of the nucleosome (Polach and Widom, 1995; Anderson and Widom, 2000), followed by a backfolding of DNA with a small 10-bp mismatch (compare to Fig. 1). The result of this process is the formation of a small DNA bulge or loop on the octamer surface. Once trapped on the nucleosome surface, this small defect carrying some discrete quantum of DNA extra length (a multiple of 10 bp, the DNA repeat length) can propagate by diffusion in both directions. If the loop happens to surround the nucleosome and comes out at the opposite side (with respect to where it was created), the nucleosome is eventually repositioned by a distance given by the pulled-in extra length. The energetic barrier and rates of repositioning were computed and were shown to be consistent with the experiment by Pennings and co-workers (Pennings et al., 1991; Meersseman et al., 1992). Moreover, the 10-bp discrete step repositioning observed in the experiment (discrete bands, no 1-bp spaced intermediates) came out as a natural consequence of the loop length quantization. The latter is enforced by the strongly preferred DNA minor groove-octamer interaction and the discrete binding sites at the nucleosome surface as deduced from the crystallographic structures (Luger et al., 1997).

FIGURE 1.

The basic problem setting: how does the histone octamer move along the DNA template? (Bottom) The DNA loop mechanism as proposed in Schiessel et al. (2001).

In Schiessel et al. (2001), small loops with short excess length of typically ∼1 − 2 × 10 bp were considered, and it was shown that the looping energies involved increase rapidly with the excess length, implying that only the shortest (10-bp) loop contributes significantly to the repositioning mechanism. Consequently, the model predicts a classical discrete random walk with a jump size of 10 bp,—instead of a 1-bp motion that would be implied by a sliding/corkscrewing mechanism. Apart from this discrepancy in the elementary step size, both models predict very similar behavior: a local one-dimensional diffusive motion along the DNA chain.

In this article we will carefully reanalyze the idea of loop-mediated repositioning by applying the classical tool of the Kirchhoff kinetic analogy, which provides us with analytic solutions of the loop problem and enables us to look at loops of any given excess length. The main outcome of our study will be a different picture of the repositioning that physically results from the looping mechanism: on short up to moderately long segments of up to 2 − 3 × l_P (l_P: DNA persistence length), the repositioning occurs via jumps, with the largest possible loops being the most dominant ones in contrast to short 10-bp steps as conjectured before. For longer and very long (infinite) DNA segments there is an optimal jump size of order ∼O(l_p) and the behavior is superdiffusive in contrast to the previously predicted diffusive mechanism. As we will see below, these predictions allow us to clearly distinguish between different repositioning mechanisms in experiments expected to be performed in near future (S. Mangenot, private communication).

ENERGETICS OF LOOPS

Let us now consider the energetics of an intranucleosomal DNA loop. We will describe it within the framework of the Euler-Kirchhoff theory for the static equilibrium of rods (Fig. 2). For simplicity, we can in first approximation assume the nucleosome and the loop-forming DNA to be in one plane and the DNA to be free of any twisting deformation. (The first assumption is justified by the fact that the loop touches the octamer surface at roughly the same height on both sides, i.e. the tangents of the loop at its boundaries are close to being in the nucleosome plane. Because we will be interested in energy-minimizing states only, we neglect the twist containing shapes that always show a higher elastic energy.) In this case the energy cost for the loop formation is simply divided into two components—the planar elastic DNA-bending and a histone octamer-DNA interaction:

(1)

The bending energy (within the linear elasticity approximation) can be written in terms of the local DNA curvature κ:

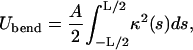(2)

with A ≈ 50 nm × k_BT being the bending rigidity of DNA at room temperature and physiological salt concentrations (Hagerman, 1988). The rod is assumed to be parameterized by its contour length parameter s ranging from −L/2 to L/2, with L being the total length of the loop. The latter can be expressed in terms of two independent quantities: the excess length ΔL and the nucleosome opening angle α (Fig. 2):

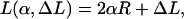(3)

where R ≈ 4 nm is the effective nucleosome radius, or more precisely, the distance from the center of the nucleosome to the central DNA axis. Because the DNA can enter the nucleosome only in quantized orientations (with its minor groove phosphates) and bind only to discrete positions on the protein surface (Luger et al., 1997), the excess length ΔL = n × h_DNA is a good approximation to an integer multiple of the DNA repeat length h_DNA = 3.4 nm.

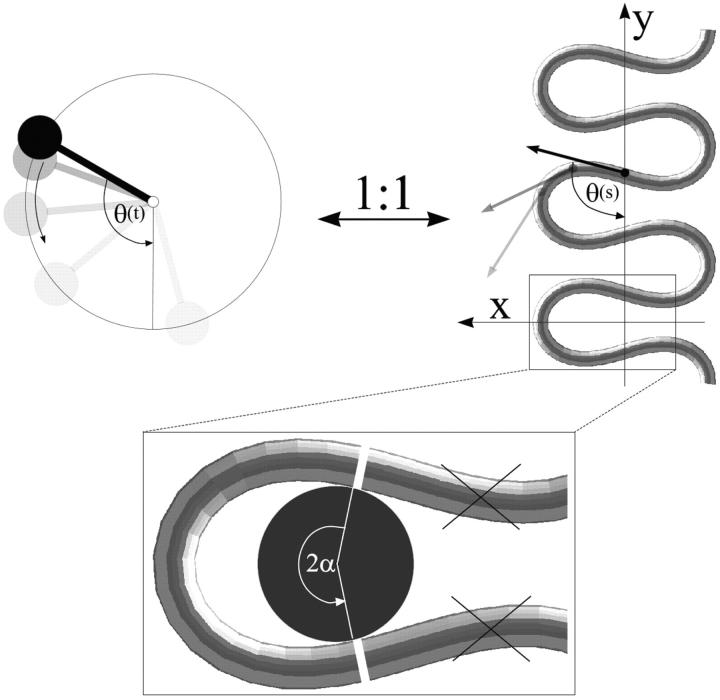
FIGURE 2.

The Kirchhoff kinetic analogy between the spinning top and the bent/twisted rod depicted for a special case: the plane pendulum–planar rod equivalence. The inset shows how an intranucleosomal loop can be constructed by inscribing the octamer (gray disk) into the bent rod. The nucleosome opening angle 2α accounts for the adsorption energy cost (see text for details).

The second part U_ads in the total energy Eq. 1 comes from the predominantly electrostatic interaction between the positively charged protein surface and the negatively charged DNA. It can be roughly measured from experiments probing the competitive protein binding to nucleosomal DNA (Polach and Widom, 1995; Anderson and Widom, 2000). Neglecting the discreteness of charges (binding sites) on the histone octamer surface, it can, in first approximation, be assumed to be proportional to the opening angle α and the adsorption energy density ɛ_ads:

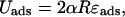(4)

with ɛ_ads ≈ 0.5 − 1.0 k_BT/nm as roughly extracted from Polach and Widom (1995). (In Eq. 4 we assume that the interaction is only short-ranged (contact interaction), which is justified by the very short Debye screening length of ≈1 nm under physiological salt conditions. We note here also that ɛ_ads is the net adsorption energy per length, i.e., the difference between the pure adsorption energy and the bending energy density A/2R².) Here and in the following, we assume an intermediate value of ɛ_ads = 0.7 k_BT/nm.

Ground states of trapped loops

To compute the ground state for a trapped intranucleosomal loop, we have to consider shapes that minimize the total energy 1 under two constraints.

The excess length ΔL is prescribed. Therefore, we have the relation Eq. 3 between the opening angle and the total loop length L:

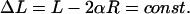(5)

At the two ends s = ±L/2, the rod has to be tangential on an inscribed circle of given radius, representing the nucleosome (because of the symmetry, we have to impose the conditions only on one side):

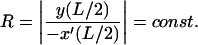(6)

Here, 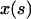and 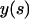are the Cartesian coordinates of the rod axis as a function of the arc-length parameter s (Fig. 2). The absolute value in the second constraint needs to be introduced formally for dealing with crossed rod solutions (which we consider later on), and can be omitted for simple uncrossed loops.

For an analytical description it is convenient to use the angle 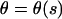between the DNA tangent and the y-axis (compare to Fig. 2) as a variable describing the DNA centerline. In this case the integrated sine (cosine) of θ over the arc-length parameter s gives the x(y) Cartesian coordinate of any point along the rod, and the squared derivative 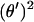gives the rod curvature κ. Furthermore, the nucleosome opening angle α is simply related to θ at the boundary:

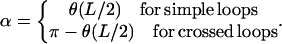The two constraints Eq. 5 and Eq. 6 can be rewritten in terms of θ and then be introduced into the minimization by two Lagrange multipliers μ_1/2. We then arrive at the following functional

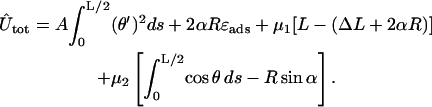(7)

Here, the first line is the bending plus adsorption energy contribution, and the second and third lines are the imposed length and tangency constraints. Eq. 7 can be rearranged in a more familiar form:

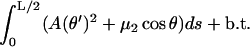(8)

Here, b.t. denotes the boundary terms (depending on 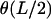only) that obviously do not contribute to the first variation inside the relevant s interval. The integral in Eq. 8 is evidently analogous to the action integral of the plane pendulum, with 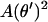corresponding to the kinetic and −μ₂ cos θ to the potential energy of the pendulum. The latter analogy is indeed nothing but the Kirchhoff's kinetic mapping between deformed rods and the spinning top, which contains our present problem as a simple special case. The Kirchhoff's analogy states that the equilibrium conformations of weakly deformed thin rods can be mapped on the time dynamics of a symmetric spinning top subjected to a gravitational force. It has been repeatedly applied (with or without direct reference to Kirchhoff) to DNA-related problems during the last 20 years (e.g., see Benham, 1977, 1979; Le Bret, 1979, 1984; Coleman et al., 1995; Swigon et al., 1998; Tobias et al., 2000; Shi and Hearst, 1994; Fain and Rudnick, 1997, 1999; Schiessel et al., 2000). For a nice visual review on the spinning-top-elastic-rod analogy, the reader is referred to Nizette and Goriely (1999), where the general solutions together with a ‘kinetic dictionary (time t ↔ length parameter s; gravitational force ↔ rod tension μ₂; axis of revolution ↔ tangent vector; etc.), are also provided.

The nice thing about Kirchhoff's analogy, apart from its esthetic content, is that it provides us with explicit expressions for DNA shapes subjected to twist, bending, and various geometric/topological constraints. In our simple planar and twistless case, the spinning top simply reduces to the simple plane pendulum. The conformations of the corresponding planar and twistless rods, also called the Euler elastica, are most generally given by

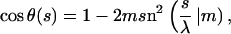(9)

which can be integrated to obtain the general planar rod shape in Cartesian coordinates:

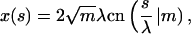(10)

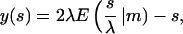(11)

with sn, dn, cn(.|m) being the Jacobi elliptic functions with the parameter m and

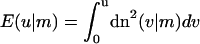(12)

denoting the incomplete elliptic integral of the second kind in its practical form. (Some useful formulas and relations for the elliptic functions and integrals are briefly sketched in Nizette and Goriely, 1999, and found in Abramowitz and Stegun, 1972, in full depth.) The two parameters m > 0 and λ > 0 in Eqs. 10 and 11 characterize the shape and the scale of the solution, respectively. These solutions are up to trivial plane rotations, translations, reflections, and shifting of the contour parameter 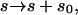the most general planar Euler elastica corresponding to the plane pendulum. For different parameters m, one obtains different rod shapes corresponding to different solutions of the spinning top (plane pendulum) motion (Nizette and Goriely, 1999). The case m = 0 describes a pendulum at rest corresponding to a straight rod; for 0 < m < 1 one has strictly oscillating pendulums corresponding to point symmetric rod shapes, where the turning points of pendulum have their counterparts in points of inflections of the rod. For m < 0.72, the rod is free of self-intersections like the one depicted in Fig. 2, and for m larger than 0.72, the rods show varying complexity with a multitude of self-intersections. For m = 1, one has the so-called homoclinic pendulum orbit corresponding to a rod solution having only one self-intersection and becoming asymptotically straight for 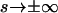(for details, see Nizette and Goriely, 1999). For even higher values of m, i.e., for m ≥ 1, we have revolving pendulum orbits corresponding to rods with self-intersections lacking point symmetry and points of inflection. (Usually the parameter m is artificially assumed to be confined to 0 ≤ m ≤ 1, but by the Jacobi's real transform for elliptic functions—see Abramowitz and Stegun, 1972—they stay well defined even for m > 1). Finally, the limiting case corresponds to the circular rod shape.

To describe a trapped loop, we need to use Eqs. 10 and 11, imposing the constraints of Eqs. 5 and 6. It turns out to be more convenient to replace the parameter set (λ,m,L) with the new (but equivalent) set 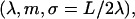where we introduced the new dimensionless parameter σ, which we call the contact parameter. (A more intuitive parameter set, α,m,λ, using the opening angle α = α(σ,m), produces technical problems with non-uniqueness of loop representation.) From Eq. 6 together with 10 and 11, we can immediately extract the scaling parameter λ and the opening angle, in terms of the contact parameter σ and the shape parameter m:

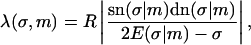(13)

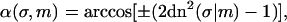(14)

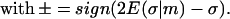(15)

Plugging this back into Eq. 5, we obtain the final form of the implicit constraint

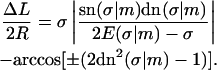(16)

The curvature 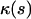and the bending energy Eq. 2 follow from the explicit solution Eq. 9 to be

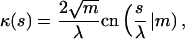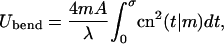(17)

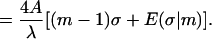(18)

The latter expression, together with Eqs. 1, 4–15, gives the final expression for the total energy with the sign chosen ± as in Eq. 15.

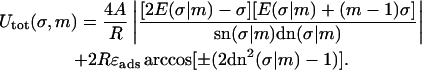(19)

Now our problem of finding the ground-state loop for a given excess length ΔL reduces to a two-variable (σ,m) minimization of Eq. 18 under the constraint Eq. 16. This final step has to be performed numerically; we present the results of this minimization in the next chapter.

LOOP ZOOLOGY: SIMPLE AND CROSSED LOOPS

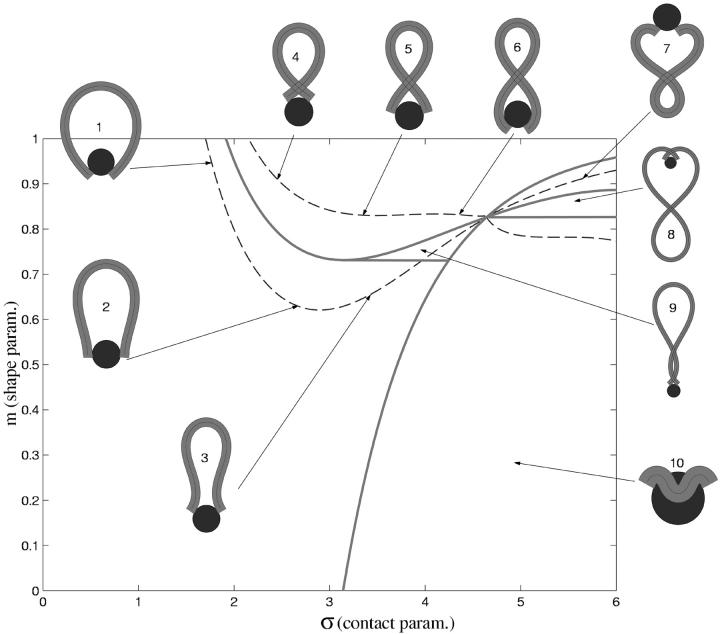
We can scan now through the σ − m parameter plane and look at the shapes of the solutions and their energies. In Fig. 3, we see a small (but most important) part of the whole parameter space and the corresponding different loop geometries. The dashed lines indicate parameter values which lead to constant excess length ΔL = 10 × 3.4 nm (corresponding to 100 bps) in accordance with the constraint Eq. 16. The shapes 1–7 are examples of such 100-bp loops with different geometries. The whole parameter plane is subdivided by separation lines (solid) into regions of structurally different solutions. The large region starting at σ = 0 contains exclusively simple loops (like 1, 2, and 3) without self-intersections and nucleosome penetration. Above that simple-loop region we find loops with a single self-intersection (4, 5, and 6), and to the right the loops penetrate the nucleosome, like loop 10. There are also three other regions with single and double crossing points (7, 8, and 9) where the loop can also be on the “wrong” side of the nucleosome, as in Eqs. 7 and 8.

FIGURE 3.

The set of possible ground-state solutions is characterized by two parameters—the contact point parameter σ and the loop shape parameter m. Solutions with constant excess length ΔL (here 10 × 3.4 nm) are located along the dashed lines (e.g., loops 1–7). The solid lines separate loops with different geometric characteristics: simple (1, 2, and 3), crossed (4, 5, and 6), and “exotic” (7, 8, 9, and 10) loop shapes.

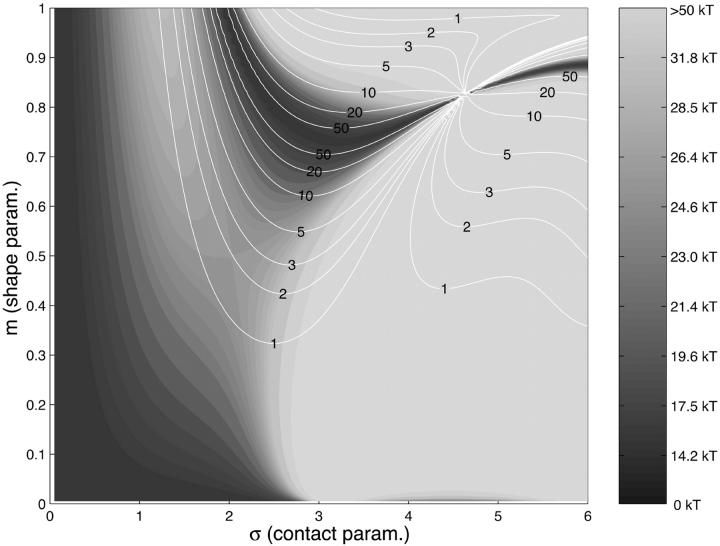
We are interested in the energy-minimizing loops and the underlying minimal energies as functions of the excess length ΔL. A density plot of these energies as function of the parameters σ and m together with the corresponding lines of constant ΔL (with ΔL = 1,2, …, 50 × 3.4 nm) is given in Fig. 4. As can be seen from Fig. 3 there are, for a given ΔL, different branches of (σ,m) values corresponding to uncrossed, simply crossed, and other exotic structures. Of all these structures for the short excess length ΔL 20 × 3.4 nm, the energetically dominant ones are the simple (uncrossed) loops, which we study first. Loops with larger and excess length form crossed structures, and are studied in Crossed and Entropic Loops, found further below.

FIGURE 4.

Density plot of the total loop energy Eq. 18 (grayscale level sets) as a function of σ and m (same parameter range as in Fig. 3). The white contours denote lines of constant excess length ΔL = 1, 2, 3, 5, 10, 20, 50 × 3.4 nm. For given excess length, the ground state is the point on the corresponding white line with the darkest background (note the different branches for given ΔL). The parameters are ɛ_ads = 0.7 k_BT/nm, A = 50 nm × k_BT, and R = 4 nm.

Simple loops

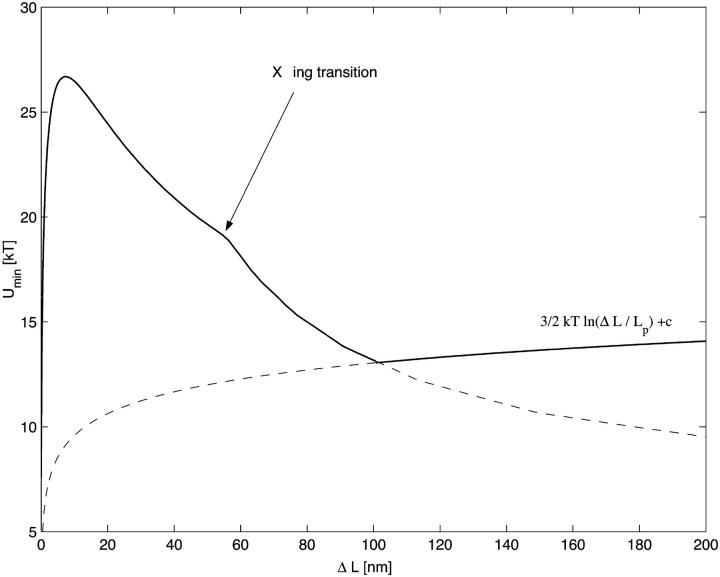
For simple uncrossed loops, it is a straightforward numerical task to minimize Eq. 18 under the constraint of constant excess length, Eq. 16. For ɛ_ads = 0.7 k_BT/nm and all the other parameters as above (A = 50 nm × k_BT, R = 4 nm), the ground-state energy U_min as a function of the excess length ΔL is shown in Fig. 5 (for ΔL ≤ 60 nm; for longer ΔL-values, crossed loops are more favorable, as discussed in the next section). Remarkably, we find that the loop energy is nonmonotonous: for small ΔL U_min increases with ΔL as 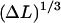(in accordance with Schiessel et al., 2001, where only small loops were studied). At some critical excess length ΔL = ΔL_crit (which is approximately ΔL_crit ≈ 2.2 × 3.4 nm for ɛ_ads = 0.7 k_BT/nm), the loop energy reaches a maximum (here U_min(ΔL_crit) ≈ 26 k_BT). Beyond that, the energy decreases with increasing ΔL.

FIGURE 5.

The ground state loop energy plotted versus the excess length ΔL. Note the energy maximum occurring for shorter loops. For much longer loops (∼ΔL = 60 nm) a transition from simple uncrossed to crossed loop shapes occurs leading to a kink in U_min(ΔL). In the regime of low 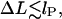the elastic energy prevails strongly over entropy, whereas for large loops, the entropy starts to dominate the behavior, producing a shallow energy minimum in the crossover regime which roughly defines the predominant loop size.

In the following we show how this behavior can be explained on the basis of the loop geometry. Naively, one might argue as follows; for excess lengths shorter than the persistence length of DNA, it is increasingly difficult to store additional length into the loop because it requires increasing DNA deformation. On the other hand, for loops longer than l_P, the bending energy contribution becomes very small, and hence one expects such ground-state loops relaxing with increasing ΔL. However, the reason for occurrence of a maximum of U_min around ≈2 excess DNA lengths, a value which is considerably smaller than the persistence length, is not obvious. To understand this finding, one has to go beyond the simple handwaving heuristics and take a close look at the details of the loop geometry.

To this end, we introduce here a simple approximation technique that leads to explicit expressions which can be more easily handled than the exact, yet complicated expressions given above. We call this method the circle-line approximation, and give a detailed exposition in the Appendix. As we will see, this method is quite accurate and, at the same time, very intuitive.

Looking at the geometrical shapes of the loops in Fig. 3, we notice that each of them is subdivided into several sections of very high and very low curvature (see also Eq. 17). In first approximation, we replace the high curvature regions by sections of circles, and the low curvature regions by straight lines (compare to Fig. 6). Furthermore, to keep the smoothness we assume that the lines are tangents to the circles. Generally, to have reasonable approximations of all possible loop shapes, we would need to consider compositions of several circles and lines (see loops 3, 6, and 7). However, if the adsorption energies are not too high, i.e., if the opening angle α is ‘soft enough’ and does not impose such a severe bending as in loop 3, such multiply-bent loops will not be relevant as ground-state solutions. As it turns out for our problem we already obtain a quite-good approximation by assuming that the loop consists of a single circular arc and two lines only. It is characterized by two quantities : 1), the arc radius r, and 2), the nucleosome opening angle α (compare to Fig. 6 and Appendix). With these assumptions and after some elementary geometry, the constraint Eq. 5 becomes simply:

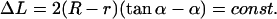(20)

Note that the (more complex) second constraint Eq. 6 is eliminated through the ansatz per se. The total loop energy is given in terms of the loop radius r and the opening angle α,

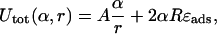and by applying the constraint Eq. 20 (which this time can be solved explicitly), we obtain U_tot in terms of α and given ΔL,

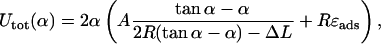(21)

which is explicit in α. We note that this approximation for U_tot is only reasonable for 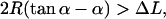i.e., for not too small an α (versus ΔL), otherwise the bending contribution diverges or even becomes negative (the latter is obviously absurd). The reason for this is that for very small angles α, compared to ΔL, uncrossed circle-line loops cannot exist for geometrical reasons. There, this most basic approximation breaks down, and we would have to approximate the loop by more than one circular segment. But as mentioned above, such loops (α small compared to ΔL) are not candidates for the ground state for moderate 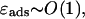and we therefore dispense with giving a discussion of this case.

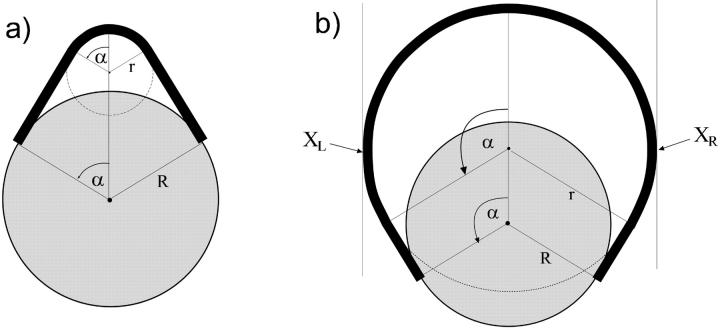
FIGURE 6.

Two generic types of simple loop geometries (in the circle-line approximation): (a) the subcritical loop with opening angle α < π / 2, and (b) the supercritical loop with α > π / 2. In the former case, the introduction of further excess length leads to an energy increase, but in the latter case, to a relaxation of stress; the introduction of additional length at points X_L and X_R followed by a relaxation of the structure obviously decreases the total energy.

The nice thing about Eq. 21 is that despite its simplicity and approximate nature it reproduces the position of the maximum in Fig. 5 quite well. We find the condition for the critical excess length ΔL_crit from a simple geometric distinction between two loop shapes: the subcritical loop (Fig. 6 a) with its tangents not being parallel to the x-axis (α = π/2), and the supercritical loop (Fig. 6 b) having two or more tangents parallel to the line α = π/2 . Suppose now that we add excess length to a subcritical loop by keeping the angle α = const. Obviously the loop energy increases because the loop radius r becomes smaller. On the other hand, in the supercritical case, we have the opposite situation: the loop energy decreases with increasing ΔL. This is simply because we could cut the loop at two points (X_L and X_R in Fig. 6), introduce there the additional length (without changing the energy), and then relax the shape by letting it evolve to the new equilibrium while keeping α = const. Thus, we can obtain the condition for the critical excess length ΔL_crit by assuming that the corresponding minimum α-min of U_tot just crosses the critical line π/2 line, i.e., 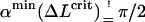for the searched ΔL_crit:

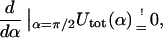(22)

which can be solved for ΔL^crit:

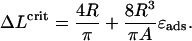(23)

The latter can now be inserted in Eq. 21, leading to

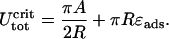(24)

For the given values of R, A, and ɛ_ads (R = 4 nm, A = 50 nm k_BT, and ɛ_ads = 0.7 k_BT/nm), we obtain ΔL^crit = 7.37 nm and 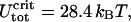which is in satisfactory agreement with the exact numeric results (ΔL^crit = 7.19 nm and 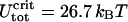). More generally, for not-too-high adsorption energies (ɛ_ads = 0.5 − 2.0 k_BT/nm), the circle-line approximation works well, and Eqs. 23 and 24 reproduce the exact positions of the critical point with, typically, a 5–15% accuracy.

For an explicit parametric representation of the minimal energy curve within the circle-line approximation, which in particular implies the upper results, the reader is referred to the Appendix, where the usefulness of this approach is also demonstrated for some other examples.

Crossed and entropic loops

A closer inspection of Fig. 4 shows that the ground state of loops switches from simple uncrossed loops to crossed loops when one reaches an excess length ∼50 nm (note that this switching behavior was previously observed by Coleman et al., 1995 for DNA held at the ends at different orientations; the mechanical (T = 0) stability of crossed/uncrossed structures was considered by Tobias et al., 2000). However, as can be seen for the crossed structures 4–6 in Fig. 3, these loops have a self-penetration at the crossing point. Therefore, a planar theory is, in principle, not sufficient to describe such structures. One possible formal cure for this problem would be to leave the plane geometry and to consider the rod's self-contacts with the corresponding point forces, etc., in three dimensions, as done by Coleman et al. (2000) in a general theory of rod self-contacts. However, such a procedure leads to a significant loss of transparency, not only because of the third dimension entering the scene but also due to the necessity to subdivide the rod into different regions with different forces acting in each of them. Instead of following Coleman et al. (2000), we decided to treat the self-interaction in a perturbative manner as follows. If the self-contact point is not too close to the nucleosome, the rod is not severely deflected out of the plane by its self-interaction. Thus, the loop is nearly planar, with some out-of-plane bending in Z-direction of the rod sections between the nucleosome and the crossing point. This costs some additional bending energy, U_def, that is approximately given by (see Appendix):

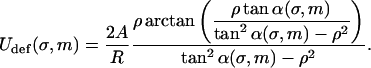(25)

Here, ρ = d/R with d ≈ 1 nm denoting the DNA radius. We neglect the slight twisting of the rod induced by the non planarity of the DNA and consider the bending only. The deflection energy Eq. 24 can be phenomenologically incorporated into the model by simply adding it to Eq. 18 as a correction term to obtain the final form of the total energy :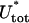

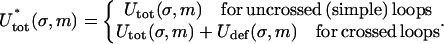With this additional modification of U_tot we numerically computed the minimal energy (ground-state) solution for any given excess length ΔL. The graph of the ground-state energy versus ΔL is shown in Fig. 5. We find that, even with the inclusion of the out-of-plane deflection, there is still a critical length ΔL_cross (here ≈ 60 nm) where the crossed loops become energetically more favorable than the simple uncrossed. This behavior that we call the crossing transition can be rationalized by noting that, for long-enough loops, the adsorption energy (proportional to α) starts to dominate over the bending energy so that loops with smaller α become increasingly favorable. From the critical length ΔL_cross on, the gain in adsorption energy (by diminishing α) is more than sufficient to outweigh the (slight) increase in bending energy, together with the additional self-interaction term, Eq. 24.

Increasing the length even further, we leave the elastic energy dominated regime in which the entropic effects can be neglected due to short loop length (persistence length). For larger lengths, entropic effects become more and more important, and we ultimately enter the entropic loop regime. The crossover between these two regimes is hard to handle analytically (Yamakawa, 1997); for the case of closed loops, a perturbative description has been given by Yamakawa and Stockmayer (1972). For our purpose, it is sufficient to consider the asymptotic behavior only. In the large loop limit where the loop is longer than several l_P, the chain loses its orientational memory exponentially, and behaves roughly as a random walk which starts from and returns to the same point. The entropic cost for gluing the ends of a random walk (long loop) together is then given by

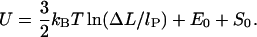(26)

The first constant, E₀ ≈ 6.5 k_BT, is the bending + adsorption energy contribution of the overcrossing DNA segments leaving/entering the nucleosome, which can be determined by minimizing the crossed-loop energy (see Appendix; see also Eq. 30) for 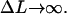The second additive constant, S₀ ∼ O(k_BT), accounts for the entropic contribution of DNA-histone octamer interaction volume (the proximity necessary for the histone octamer and DNA to see each other). Although the latter constant is not easy to estimate, the following prediction is not sensitive to any additive constant. The free energy minimum occurs at the overlap between the elastic 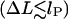and entropic 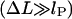regions, where the decreasing elastic energy is overtaken by the increasing entropic contribution.

The free energy, Eq. 25, leads to an algebraically decaying probability w(ΔL) for the jump-lengths scaling as 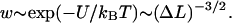In general, power law distributions of the form 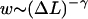with γ > 1 lead to superdiffusive behavior of the random walker (here, the nucleosome). According to Levy's limit theorem, the probability distribution of the random walker (more precisely, the distribution of the sums of independent random variable drawn out from the same probability distribution, 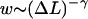) converges to a stable Levy distribution of index γ − 1 (Bouchaud and Georges, 1990; Klafter et al., 1993; Sokolov et al., 1997). This so-called Levy flight differs in many respects from the usual diffusion process, as for short time intervals big jumps are still available with significant probability. Moreover, all moments (possibly besides the first few ones) diverge. For our case γ = 3/2, even the first moment does not exist. We note that the value 3/2 is based on the assumption of an ideal chain (no excluded volume); in general, the excluded volume leads to self-avoiding-walk statistics with a slightly larger value of γ ∼ 2.2 (Sokolov et al., 1997; see also de Cloizeaux and Jannick, 1990). In that case, one has a finite value of the first moment, i.e., of the average jump length.

THE DYNAMICS OF NUCLEOSOME REPOSITIONING

In the preceding sections we have computed the typical energies involved in the formation of arbitrary-sized loops. We start now considering the repositioning dynamics by assuming that a slow creation followed by a fast thermal migration of loops around the nucleosome is the governing mechanism for nucleosome repositioning. To describe the time-dependent evolution of the nucleosome position, we consider its probability distribution along a DNA segment with free length (i.e., total DNA length minus the nucleosome-covered 147 bp) of N × 10 bp, and write the master equation governing the jump process,

(27)

where p_i is the probability for the nucleosome being at the admissible position i (spaced by a multiple of 10 bp from the initial position) on the DNA segment. The transition rate matrix, 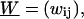is given by

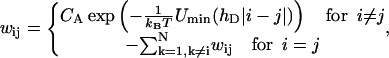(28)

where h_D = 3.4 nm (DNA helical pitch). C_A denotes the Arrhenius constant involved in the loop formation process that has, in principle, to be determined experimentally. The rough estimate of is provided in Schiessel et al. (2001), where it was shown that C_A is essentially given by the inverse lifetime of the loop (denoted by A in that article). This means that typical repositioning times range from seconds to hours.

The (formal) explicit solution of Eqs. 27 and 28, together with the previously obtained minimal energy U_min, is given by

The latter solution can now be considered for different cases—for short or long DNA chains, and for the nucleosome placed in the middle or at the end of the chain.

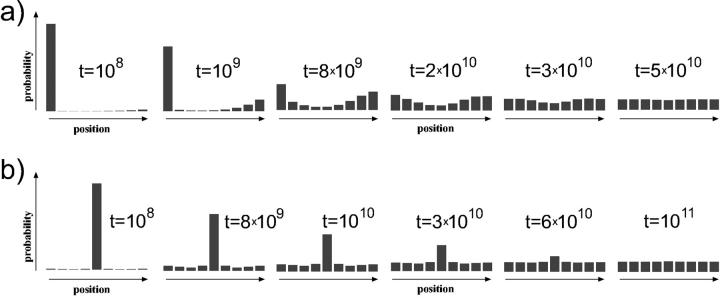
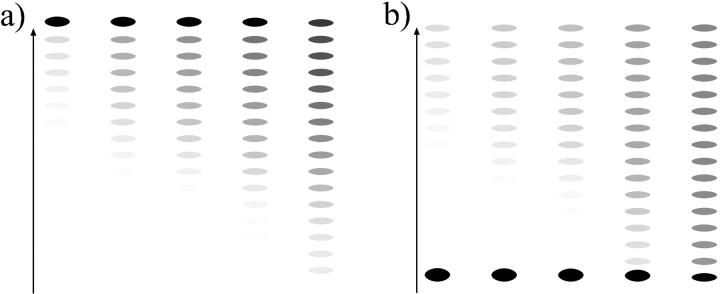
For short DNA segments, we expect a slow repositioning rate due to high energies involved in small loop formation. In Fig. 7 we depict the repositioning of a nucleosome on a DNA piece of a length 147 + 90 bp. Starting from an end-positioned nucleosome (Fig. 7 a), we observe a behavior that is completely different from a local diffusion mechanism: the jumps bigger than ≈2 × 3.4 nm start to dominate over the smaller local ones, which follows from the loop formation energy; see Fig. 5. Consequently, in the initial phase of repositioning of such an end-positioned population, the nucleosomes will predominantly jump between the two end positions. Later, on a much larger timescale, they gradually start to explore the positions toward the middle of the DNA segment.

FIGURE 7.

Relaxation dynamics of two initial states of nucleosome positions on a short DNA segment (147 + 90 bp): (a) the nucleosome starting from an end, and (b) the nucleosome starting from the middle position. The time unit is the inverse Arrhenius activation factor 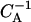(compare text).

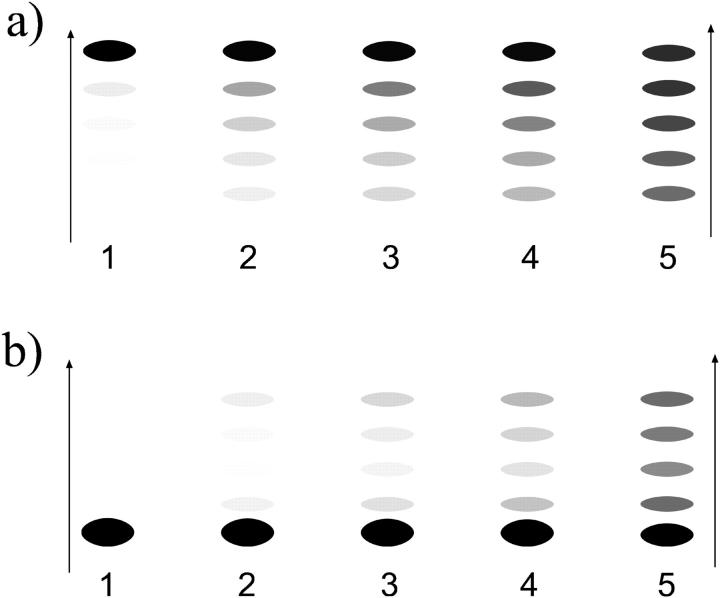
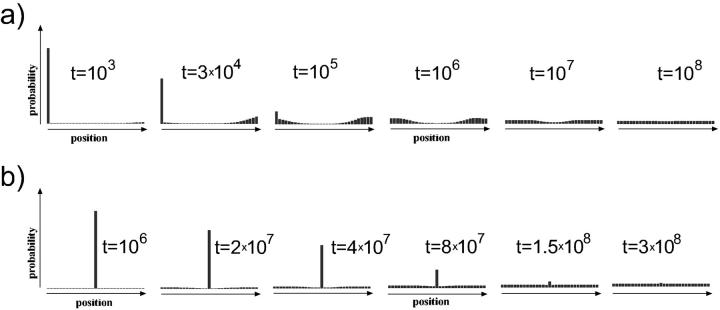
Could such a behavior be extracted from an experiment using gel-electrophoretic separation (as in Pennings et al., 1991, and Meersseman et al., 1992)? The basis of such separations is the fact that the gel-electrophoretic mobility of nucleosomes on DNA pieces (longer than 147 bp) increases roughly linearly with its distance from the middle position; i.e., DNA pieces with the nucleosome sitting close to the end run much faster in gels than do equivalent middle-positioned nucleosomes. We can exploit this (empirical) fact to mimic the outcome of a gel-electrophoresis experiment (see Figs. 8 and 10). In Fig. 8 a, we depict such a simulated gel pattern for the middle-positioned nucleosome. Since symmetric species are not distinguished by this experimental method and are projected onto the same bands (symmetric left/right positions lead to the same mobility), the expected nonlocality of motion cannot be extracted from the structure of the bands.

FIGURE 8.

Typical (one-dimensional) gel electrophoresis signatures expected for the relaxation dynamics of the two species from Fig. 7: (a) nucleosome starts from an end, and (b) from the middle position. Lanes 1–5 correspond to incubation times (1, 5, 10, 20, 100) × 10⁸ 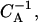respectively. Note that the population of distant bands in b, lanes 2–4 occurs first, in sharp contrast to what we expect from a simple (local) diffusive behavior.

FIGURE 10.

The (one-dimensional) gel-electrophoresis signatures simulated for the relaxation dynamics of the two initial species from Fig. 9. (a) End-positioned lanes 1–5, corresponding to incubation times (1, 2, 3, 10, 50) × 10⁴ 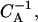and (b) centrally-positioned lanes, corresponding to incubation times (1, 2, 3, 10, 50) × 10⁶ .

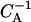For the same short DNA segment, but with the nucleosome starting from the middle position (Fig. 7 b), the situation is slightly different: the neighboring positions are populated more homogeneously, although there is a small initial underpopulation of the 2 × 3.4 nm distant position as expected from the energy maximum occurring there. In this case, a slight initial population gap can be observed in gel electrophoresis (Fig. 8 b), which in this case would be sufficient to distinguish between a large jump and a diffusive behavior, inasmuch as the latter would obviously lack the population gap.

In the case of longer DNA (but still not entropic segments) like the 147 + 300 bp segment in Figs. 9 and 10, similar effects as for the short segments are expected but with significantly faster relaxation times by typically 2–3 orders of magnitude as compared to the corresponding short segment populations. The corresponding (simulated) electrophoretic gels are shown in Fig. 10, where, for the centrally-positioned case (Fig 10 b), the population-gap effect is even more pronounced than in the short-segment case.

FIGURE 9.

Relaxation dynamics of two initial states of nucleosome positions on a longer DNA segment (147 + 300 bp): (a) end-positioned and (b) centrally-positioned initial species. Note the initial difference in relaxation timescales for a and b (which are due to different loop energies involved).

For even longer DNA segments, we expect the gap effect to persist and the optimal jump size to be ∼2 − 3 × l_P, corresponding to the free-energy minimum in Fig. 5. For very long DNA segments, the nucleosome repositioning behavior implied by the big-loop mechanism becomes strongly nonlocal, which contrasts a local diffusive motion as expected, from a corkscrew motion (Beard, 1978; Spadafora et al., 1979; Pennings et al., 1991; Meersseman et al., 1992), or a small-loop repositioning, as considered by Schiessel and co-workers (Schiessel et al., 2001). As mentioned above, this superdiffusive behavior has diverging moments which strongly imply enhanced nucleosome transport along very long DNA pieces. However, such an ideal superdiffusion of nucleosomes could hardly occur in vivo, because free DNA segments between subsequent nucleosomes (DNA linkers) are never longer than ∼O(l_P). Furthermore, the neighboring nucleosomes might be significant barriers for loop migration (if not for loop formation) around the nucleosome, which is an indispensable event for loop-mediated repositioning.

CONCLUSIONS AND DISCUSSION

In this study, we examined a possible mechanism for the repositioning of nucleosomes along DNA, which is based on the formation and diffusion of intranucleosomal loops. The most important outcome of this study is the prediction of two classes of loops that might occur: 1), small 10-bp loops; and 2), large loops with a wide distribution of stored lengths with a weak peak at roughly two times the DNA persistence length.

The small loops were already discussed by Schiessel et al. (2001) and led to the prediction of repositioning steps of 10 bps. Furthermore, the repositioning time should be of the order of an hour, a consequence of the large activation energy required to form a loop. This might explain the strong temperature dependence of the typical repositioning time (Meersseman et al., 1992). In fact, by lowering the temperature from 37° to 4°C, no redistribution within 1 h was detected in that experiments. Assuming a loop-formation energy of 23 k_BT, one finds, indeed, a slowing down of this process by a factor of 13.

On the other hand, the large loop repositioning considered here turns out to be energetically much more favorable. Loops with an extra length of 2 l_P have an energy that is roughly 12–13 k_BT smaller than that of a 10-bp loop. To a certain extent this is because such loops can have a very small nucleosome opening angle by forming crossed loops, but the main contribution stems from the significantly decreased DNA bending energy. One therefore expects that repositioning via large loops should be the dominant process on sufficiently large DNA pieces, and that the typical times are much shorter than the one for small loop repositioning (say, of the order of minutes).

So far, however, the experiments did not report such events. Meersseman and co-workers (Pennings et al., 1991; Meersseman et al., 1992), for instance, found, on short DNA pieces of 207-bps length, results that are consistent with 10-bp repositioning—as we would expect for such short DNA fragments. However, when they redid the experiment with a 414-bp-long piece, a tandem repeat of the 207-bp DNA, their analysis of the complicated band patterns observed in two-dimensional gel electrophoresis did not show any indication that the nucleosome was able to move from one half to the other.

Hence, the question arises if the repositioning observed in these experiments was facilitated via the loop mechanism or if it occurred via a different process. An analysis of the results is made especially difficult by two complications: 1), the nucleosomes seem to prefer to sit on the ends of the DNA fragments, and 2), most of the experiments use strong positioning sequences (like the 5S rDNA sequence). This means that, independent of what the repositioning process might be, the nucleosomes have certain preferred positions, and these might obscure the underlying repositioning process.

With regard to this fact, let us consider two other repositioning mechanisms that one could imagine. The first one is that the nucleosome detaches completely from the DNA and attaches at some other position (or even a different DNA molecule). This process, however, seems to be excluded by two facts (among others). First, that no repositioning from one half to the other of the 414-bp DNA or to competitor DNA fragments was observed (Pennings et al., 1991; Meersseman et al., 1992); and secondly, once completely detached from the DNA template, the histone octamer becomes unstable and disintegrates into one tetrameric and two dimeric subunits, which makes an effective nucleosome reconstitution difficult.

The other mechanism could be a local corkscrew motion, as already suggested by Pennings and co-workers (Pennings et al., 1991). This process would lead to a repositioning with one bp per step. The preponderance of 10-bp steps observed for the 5S rDNA experiments could then be explained as being due to the fact that the positioning sequence prefers the nucleosome rotationally positioned on one side of the DNA, where it can be easily bent around the octamer. Also, 10-bps (and even a few multiples of 10 bps) apart, this effect can still be seen and hence the nucleosome would prefer positions in multiples of 10-bps apart. To our best knowledge, the experiments to date do not allow us to distinguish whether the 10-bp repositioning works via small loops or via corkscrew motion.

It would therefore be important to perform experiments on DNA pieces that do not provide the nucleosome with a preferred rotational setting. In that case, the 10-bp footprint should disappear if nucleosomes reposition themselves via corkscrew motion. It would also be important to perform experiments with rather long DNA fragments, since we expect that large-loop repositioning can be detected in such systems.

Finally, we note that nucleosome repositioning in vivo is facilitated via so-called chromatin remodeling complexes—huge multiprotein complexes that harness energy by burning ATP (Vignali et al., 2000; Peterson, 2000; Kornberg and Lorch, 1999). There are basically two major classes: ISWI and SWI/SNF. The first one seems to induce small-scale repositioning which might work via twisting DNA that leads to a corkscrew movement as discussed above. It might, however, also be possible that this complex induces small loops on the nucleosome as recent experiments on nicked DNA suggest (Längst and Becker, 2001). The other class of remodeling complexes seems to induce large loop structures, as they have been observed recently via electron spectroscopy (Bazett-Jones et al., 1999). Independently of what the detailed functions of these remodeling complexes might be, it is tempting to speculate that they catalyze and direct processes which might even take place when they are not present—like small-loop and large-loop formation as well as corkscrew motion. In this case, the computed looping energy (Fig. 5) and repositioning rates might give a first hint about ATP requirements and the dynamics of enzymatic repositioning.

Another interesting and very prominent system known to mediate nucleosome repositioning via loop formation is, unexpectedly, the ubiquitous RNA-Polymerase (RNA-P). It is found to be able to transcribe DNA through nucleosomes without disrupting their structure, yet moving them upstream of the DNA template, i.e., in the opposite direction of transcription (Felsenfeld et al., 2000). To rationalize this seemingly paradoxical finding, Felsenfeld and co-workers introduced a DNA looping model which assumes that the RNA-P crosses the nucleosome in a loop. This would indeed explain the backwards directionality of repositioning. An interesting question in this context is how our intranucleosomal loops considered above relate to those formed by the RNA-P. Can we say something about the repositioning distance distribution, and does the looping energy (Fig. 5) apply here? The geometry of RNA-P–DNA complex on a nucleosome is certainly different from the simple loop case, as ingoing and outgoing DNA from RNA-P enclose a rather soft, yet preferential angle of ≈100° (dependent on RNA-P type; see Rees et al., 1993; Rivetti et al., 1999; Schulz et al., 1998). The latter facilitates the loop formation as the free DNA has to bend less to fold back onto the octamer surface. Besides the apparent differences from the naked intranucleosomal loops problem, a slight generalization of our present model which incorporates the preferential RNA-P opening angle can be performed within the same mathematical framework developed here. It would be interesting to compute the resulting nucleosome transfer distance on short and long DNA templates in an analogous manner as performed above. An outcome of such a study could be, for instance, an answer to a question such as: what is the highest linear nucleosomal density in polynucleosomal arrays, up to which nucleosomes are not to be removed from the DNA template (due to loop formation and nucleosome transfer prohibited by the neighboring nucleosome) during transcription?

Such fundamental biological questions make a further elaboration of intranucleosomal loop theory, its generalization to different loop geometries and, finally, its application to different loop-creating proteins (SWI/SNF, RNA-P), an intriguing task for future work.

APPENDIX: THE CIRCLE-LINE APPROXIMATION

Although Kirchhoff's analogy provides us with essentially analytic solutions for the rod deformed in plane, the occurrence of boundary conditions (like Eqs. 5 and 6) prevents us, in most cases, from obtaining analytical expressions of all the parameters characterizing the solution (like σ and m above). To overcome this problem, we suggest here a simple geometric approximation scheme which will prove to be useful in obtaining analytic results for loops within a reasonable accuracy (usually with a deviation of 5–15% from the exact numeric results).

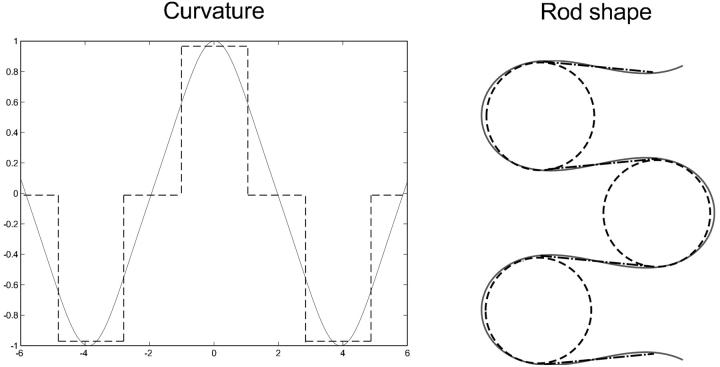
The main idea is the following. The curvature and the energy (Eqs. 17 and 18) of the loop contains the cn(σ|m) function, which for 0 < m < 1 has the typical oscillatory behavior depicted in Fig. 11 (left). This suggests us to approximate the curvature function simply by a step function consisting of an alternating sequence of negative, zero, and positive piecewise constant curvatures. Consequently the corresponding rod shape (Fig. 11, right) is approximated by a sequence of circles (positive/negative constant curvature) and lines (zero curvature). An analogous approximation procedure can also be performed in the case m > 1 where the cn function has a natural analytical continuation into a dn function with a modified second argument (see Abramowitz and Stegun, 1972).

FIGURE 11.

The circle-line approximation for planar rods. The curvature of an equilibrium rod shape (cn function), Eq. 17, is approximated by a periodic sequence of step functions. The latter corresponds to an approximation of the rod shape by a sequence of straight lines (κ = 0) and circles (κ = const.) glued together in a smooth manner (continuous tangents).

Using this approximation ansatz, several problems concerning planar rods reduce to elementary geometry, as seen from the following simple but illustrative examples.

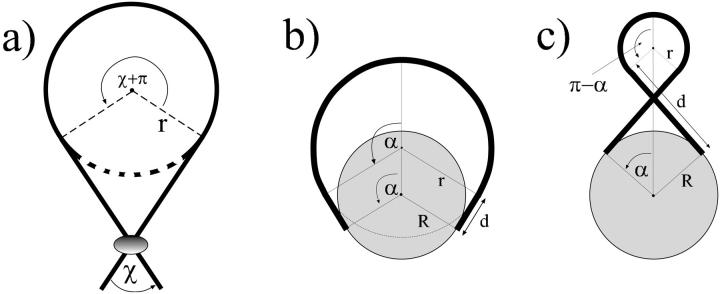
The Yamakawa-Stockmayer angle

Yamakawa and Stockmayer (1972): Two points on the rod are glued together without restricting the orientation of the tangents, e.g., a protein connects two distant points on DNA (Fig. 12 a). What is the preferred angle χ between the tangents in the ground state of the rod? By imposing a fixed total rod length L we have the simple constraint from which we can eliminate r and write the elastic energy of the configuration as 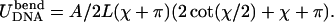Its minimization leads to the transcendent condition χ_min + π = tanχ_min with the only relevant solution, χ_min ≈ 77.5°. The latter angle differs by 5% from the exact result χ_min ≈ 81.6° by Yamakawa and Stockmayer (1972), which is satisfactory regarding the simplicity of the computation.

FIGURE 12.

Three applications of the circle-line approximation. Problems with complex constraints reduce to simple geometries leading to good approximations: (a) the Yamakawa-Stockmayer angle, (b) simple loops, and (c) crossed loops (see the Appendix text for details).

Simple and crossed loops (Fig. 12, b and c)

We can easily derive an approximate energy expression for simple/crossed loops as a function of the excess length ΔL and the opening angle α. By applying simple geometry the excess length constraint can be easily eliminated (the tangency constraint is trivially fulfilled by the ansatz) and we arrive at

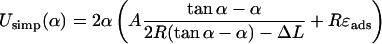(29)

for simple loops, and

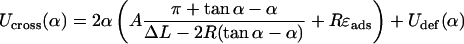(30)

for crossed loops, where A, R, and ɛ_ads are defined as above and U_def is the excluded volume interaction at the crossing point, which is considered below (and applied in the main text as Eq. 24). We remark that the above expressions for U_simp and U_cross are valid within certain α intervals, which are given by the restriction 0 < α < π and by the condition that the first terms in the brackets of Eqs. 29 and 30 are positive (these are the necessarily positive bending-energy contributions in the two cases).

These fairly simple expressions can now be used in the two cases to obtain explicitly the ground-state energies by minimizing Eq. 29 and Eq. 30 with respect to α. For instance, setting we obtain a transcendental equation for α. We can now use the fact that this condition is algebraic in ΔL so that we can solve it for 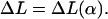Thus, instead of finding α = α(L) (which cannot be given in an explicit form), we obtain explicitly its inverse:

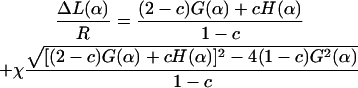(31)

with the abbreviations

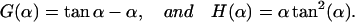In Eq. 31 the introduced dimensionless constant is 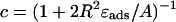(0 < c < 1, and c = 0.69 here) and χ is the sign accounting for different branches of the α-parameterized solution

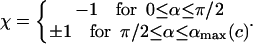(32)

Note that for α ≤ π / 2 there is only one branch, but for α > π / 2 we have two branches (±1) for ΔL(α). (The latter means that for π/2 ≤ α ≤ α_max there are two different excess loop lengths leading to the same (equilibrium) angle α, i.e., with increasing ΔL the nucleosome angle α opens but after passing some critical point on the ΔL axis, it starts closing again). The maximal opening angle 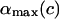is obtained by setting the discriminant (expression below the square root) in Eq. 31 equal to 0.

From Eq. 31 together with Eq. 29 we obtain an explicit parametric representation of the minimal-energy curve for simple loops. A comparison of the approximate minimal energies (Eq. 31 and Eq. 29) with the exact minimal energy (Fig. 5 for ΔL ≤ 60 nm), is shown in Fig. 13. We find that the quantitative agreement is quite satisfactory, taking the simplicity of our ansatz into account. We note here that analogous computations, as we have shown for simple loops, can be performed for crossed loops as well.

FIGURE 13.

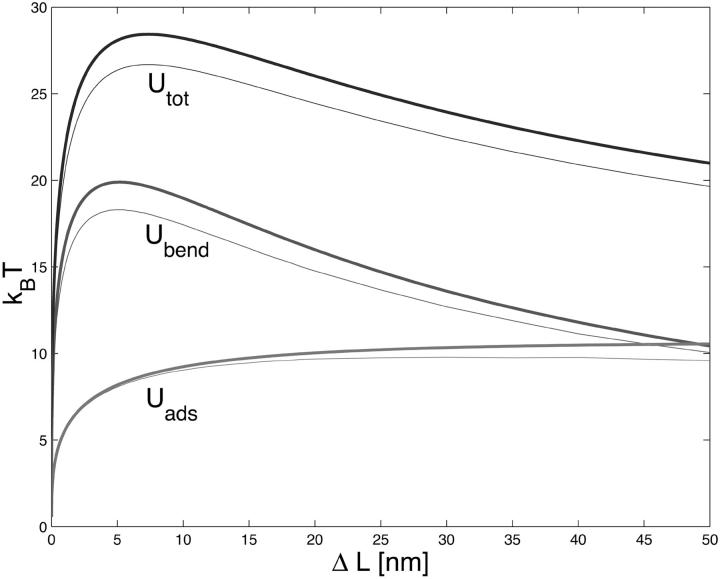
Comparison of the adsorption and bending energy contributions (U_ads and U_bend) as well as the total ground-state energy U_tot of the simple loop. The fat lines represent the circle-line approximation (see Eq. 29), whereas the thin lines show the corresponding exact expressions, Eqs. 1 and 18 (thin line). The parameters are ɛ_ads = 0.7 k_BT/nm, A = 50 nm × k_BT, and R = 4 nm.

For ΔL → 0, we find, after an appropriate expansion of U_simp ∼ α = 0, that the ground-state energy scales as 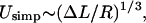in agreement with Schiessel et al. (2001). Further, we obtain the excess length at which the loop ground-state energy is maximal by setting 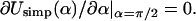From this follows the critical length ΔL_crit as discussed in the main text (see Eq. 23). This simple approximate expression for ΔL_crit agrees within 2–15% with the exact numerical result for a wide range of adsorption energies, with deviations becoming larger for adsorption energies above ɛ_ads = 2.0 k_BT/nm (data not shown).

The overcrossing potential for crossed loops (Fig. 14)

The outgoing DNA path is perturbed out of the plane due to the interaction with the ingoing DNA (and vice versa in a symmetrical manner). Because of that, our simple planar phantom model (no self-interaction) needs modifications. Instead of solving this (nonplanar) problem within the general theory of self-interacting deformed rods as in Coleman et al., 2000 (which is a feasible but rather technical numerical task), we can treat the out-of-plane deformation perturbationally. The first assumption we make here is that the overall shape of the crossed loop does not deviate much from a planar configuration, although the orientation of its (effective) plane might be slightly deflected from the nucleosomal plane. Consequently, the small perturbation out of the plane and the deformation in plane essentially decouple into a sum of two energy contributions as in Eq. 30. Again by simple geometry (Fig. 13), the second (out of the plane) term in Eq. 30 can, in first approximation, be written as

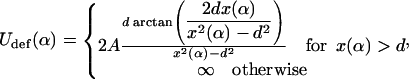(33)

where d ≈ 1 nm is the thickness of DNA and 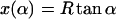the length of the crossed segment. In our simple approximation. the self-interaction energy diverges for x → d + 0 as 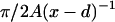(extreme deformation) and approaches zero for x → ∞ as 4Ad²x⁻³ (weak deformation). (Here, we neglected the electrostatic contribution to the self-energy of the crossing point that is minimized for perpendicular crossing (α = π/4); using the classical result of Brenner and Parsegian (1974), this energy can be estimated to be of order 1 k_BT/sin(π − 2α), which is much smaller than the bending energy contribution, Eq. 33),

FIGURE 14.

The out-of-plane deflection of the incoming/outgoing DNA due to excluded volume in the top projection (left) and seen from the side (right). In the latter case (for the sake of visual clarity), the two rods are depicted in a single plane, i.e., rotated around their contact point (gray dot).

We finally note that, besides the above-given examples, it is possible to apply the circle-line approximation to several other standard problems of rod theory like the first, and especially the higher order Euler buckling instabilities, to qualitatively obtain the known results from buckling theory with very little effort. Thus, the circle-line approximation, when applied appropriately, turns out to be very useful, and generally allows computationally inexpensive qualitative and quantitative insights into the behavior of (planary) deformed rods.