Abstract
Two novel water-soluble fluorescein myo-inositol phosphate (FLIP) substrates, butyl-FLIP and methyl-FLIP, were used to examine the kinetics and subsite interactions of Bacillus cereus phosphatidylinositol-specific phospholipase C. Butyl-FLIP exhibited sigmoidal kinetics when initial rates are plotted versus substrate concentration. The data fit a Hill coefficient of 1.2–1.5, suggesting an allosteric interaction between two sites. Two substrate molecules bind to this enzyme, one at the active site and one at a subsite, causing an increase in activity. The kinetic behavior is mathematically similar to that of well-known cooperative multimeric enzymes even though this phosphatidylinositol-specific phospholipase C is a small, monomeric enzyme. The less hydrophobic substrate, methyl-FLIP, binds only to the active site and not the activator site, and thus exhibits standard hyperbolic kinetics. An analytical expression is presented that accounts for the kinetics of both substrates in the absence and presence of a nonsubstrate short-chain phospholipid, dihexanoylphosphatidylcholine. The fluorogenic substrates detect activation at much lower concentrations of dihexanoylphosphatidylcholine than previously reported.
INTRODUCTION
Enzymes that act on substrates such as polypeptides, nucleic acids, oligosaccharides, or lipid membranes often interact with more than one substrate molecule. Bovine pancreatic ribonuclease A (RNase A), for example, interacts with several nucleotides of RNA, permitting it to undergo diffusion along the RNA chain, hence increasing its catalytic efficiency (Kelemen and Raines, 1999). The term subsites has been used to describe this multiple interaction phenomenon seen for RNase A. RNase A has only one active site, and cooperative effects in the kinetics due to interactions with other nucleotides within or near that site have been reported (Moussaoui et al., 1998). Phospholipases are another example where an enzyme having one active site interacts with many substrate molecules under physiological conditions. The degree of association varies greatly with the phospholipase. At one extreme is the small (13–16 kDa) secreted phospholipase A2 that has been extensively studied in a specially designed scooting mode system (Berg et al., 2001). In this system, the enzyme undergoes two-dimensional diffusion without hopping off the membrane surface. Near the other limit is Bacillus cereus phosphatidylinositol-specific phospholipase C (PI-PLC, EC 3.1.4.10) with low interfacial processivity/weak binding to membranes. This relatively small monomeric enzyme (35 kDa) consists of 298 amino acid residues in a single polypeptide chain and one active site. B. cereus PI-PLC, and closely related bacterial isozymes, are becoming an important model system for the ubiquitous PI-PLCs found in most living organisms, and are of interest in their own right as possible virulence factors (for a review see Griffith and Ryan (1999)). The bacterial enzymes cleave phosphatidylinositol (PI) in a rapid intramolecular transphosphorylation reaction, to form diacylglycerol and D-myo-inositol 1,2-cyclic phosphate, I(1,2)cP. In a second reaction, the cyclic phosphorylase activity of PI-PLC catalyzes the slow hydrolysis of I(1,2)cP to D-myo-inositol 1-phosphate, I(1)P. Bacterial PI-PLCs, but not eukaryotic PI-PLCs, also catalyze the release of proteins tethered to membranes by glycosylphosphatidylinositol anchors (Low, 1989). Eukaryotic PI-PLCs are important in signal transduction pathways, cleaving phosphatidylinositol 4,5-bisphosphate to generate two second messengers, diacylglycerol and D-myo-inositol 1,4,5-trisphosphate (Rhee, 2001).
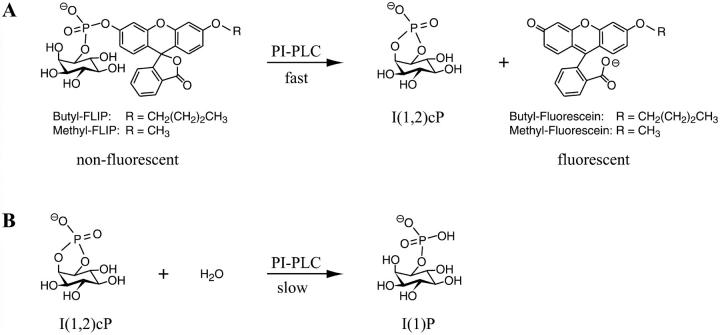
The enzymatic activity of a PI-PLC increases in the presence of organized lipid substrates containing certain phospholipids. This interfacial activation of bacterial PI-PLCs, activation by specific nonsubstrate lipids, e.g., phosphatidylcholines, along with evidence for allostery, have been noted in studies of both the first reaction (Hendrickson et al., 1992; Lewis et al., 1993; Rebecchi et al., 1993; Volwerk et al., 1994), and in more detailed studies of the second reaction catalyzed by PI-PLC (Zhou et al., 1997a,b, 1999; Zhou and Roberts, 1998). The kinetics of the physiologically important cleavage of PI, or phosphorylated derivatives in the case of eukaryotic PI-PLCs, are often complex and difficult to interpret owing to the fact that the lipids self-associate into bilayer or multilayer structures and the enzyme undergoes a combination of scooting and hopping between these aggregates. To aid in clarifying the kinetics, fluorogenic substrates have been synthesized recently and provide a novel approach to the study of the first reaction (Zaikova et al., 2001). The hydrophobicity of fluorescein myo-inositol phosphate (FLIP) can be changed by altering the length of the alkyl group attached to fluorescein (Fig. 1 A). As occurs with the natural PI substrate, PI-PLC catalyzes the turnover in a rapid transphosphorylation reaction, yielding two products, as shown in Fig. 1 A. One is a highly fluorescent compound that can be monitored continuously at very low concentrations. The other is I(1,2)cP, the same product as obtained from the natural substrate PI. The subsequent slow hydrolysis of I(1,2)cP is shown in Fig. 1 B. We report here the first detailed kinetic analysis with these new fluorogenic substrates. Two members of the series were employed, butyl-FLIP and methyl-FLIP. The kinetics appear different because butyl-FLIP not only binds to the active site but also to a subsite, activating the reaction, whereas methyl-FLIP does not bind to the subsite. Addition of a known activator, dihexanoylphosphatidylcholine (diC6PC), displaces butyl-FLIP from the activator site, changing the sigmoidal kinetics to hyperbolic kinetics. All of these effects are fitted quantitatively to a general two-site model based on one active site and one subsite. Together, the results provide a clear example of allosteric interactions between two subsites during the first reaction of B. cereus PI-PLC, and fit in nicely with the useful but more qualitative two-site treatment reported for the second reaction of PI-PLC (Zhou and Roberts, 1998). The fluorogenic substrates also provide new information about activation at very low diC6PC concentrations.
FIGURE 1.
Reactions catalyzed by bacterial PI-PLC. (A) Cleavage of two fluorogenic substrates derived from fluorescein, butyl-FLIP, and methyl-FLIP. In this intramolecular phosphotransferase reaction, the nonfluorescent substrate is cleaved to produce I(1,2)cP and a highly fluorescent product. (B) In a second reaction catalyzed by PI-PLC, I(1,2)cP is slowly hydrolyzed, opening the ring to form I(1)P.
MATERIALS AND METHODS
Materials
The fluorogenic substrates butyl-FLIP and methyl-FLIP were prepared as previously described (Zaikova et al., 2001). PI-PLC from B. cereus was prepared by the method of Ryan et al. (1996) and is available from Molecular Probes (Eugene, OR). DiC6PC was obtained from Avanti Polar Lipids (Alabaster, AL). Polyethylene glycol (PEG 8000) was from Sigma (St. Louis, MO), and HEPES was from Calbiochem (San Diego, CA).
Enzyme assay procedure
The following buffer solutions were prepared: 2× assay buffer (200 mM HEPES, 2 mM EDTA, 0.016% PEG 8000, pH 7.0) and enzyme dilution buffer (6 mM HEPES, 0.06 mM EDTA, 0.1% PEG 8000, pH 7.0). Stocks of butyl-FLIP (2 mg/mL) and methyl-FLIP (12 mg/mL) were made up in deionized water and kept at room temperature. For the experiments involving the effects of an inert short-chain lipid, stock solutions of either 10 mM or 200 mM diC6PC were prepared in 1× assay buffer and stored on ice.
Accurate concentrations of the solutions of the fluorogenic substrate and short-chain phospholipid were determined by phosphate analysis (Cogan et al., 1999). Working dilutions of PI-PLC were prepared from a 0.1 U/μL (2800 U/mg) stock stored at −20°C in 50% glycerol. One unit is the amount of enzyme that converts 1 μmol of PI substrate to product per minute under the conditions specified. The enzyme was first diluted 100-fold in an Eppendorf tube with enzyme dilution buffer, followed by a second 10-fold dilution to give a concentration of 1.0 nM.
Assays were carried out in a total volume of 0.8 mL in 4.5 mL polymethacrylate fluorescence cuvettes (Fisher Scientific, Pittsburgh, PA) in a Hitachi F-4500 fluorescence spectrometer with temperature maintained at 25°C using a Fisher Model 9105 circulating water bath. A 3-min time scan was first taken with all components except the enzyme present in the cuvette. Then 10 μL of 1.0 nM PI-PLC was added, the solution was mixed by pulling it up and down in a pipetter several times, and a second 3-min time scan was recorded. To correct for traces of product present in the substrate preparation and a slight increase in fluorescence occurring in assay buffer at pH 7.0, which results from the decomposition of a very small amount of substrate, the initial time scan was subtracted from the second scan before processing of the data. The resulting change in fluorescence was converted to units of nM fluorescent product produced per second by making use of a calibration curve prepared by converting a solution of substrate completely to product by extended treatment with very dilute sodium hydroxide. Curve fitting of the kinetics data was carried out using GraFit (Erithacus Software Limited, Horley, UK) and Mathcad (MathSoft, Cambridge, MA).
Controls
Since some of the plots of initial rates versus substrate concentration were sigmoidal, a number of control experiments was carried out to rule out the possibility that artifacts might be responsible. Three tests were carried out to determine whether the product might be adhering to the plastic cuvettes used in the kinetics experiments, thus affecting the measured fluorescence values: 1), Varying amounts of fluorogenic substrate were added to plastic cuvettes in assay buffer, and the fluorescence from the small amount of product present in the substrate was measured and plotted as a function of the amount of substrate added. These plots were always linear regardless of whether a different cuvette was used for each concentration of substrate or multiple additions of substrate were made to the same cuvette. 2), Varying amounts of the fluorescent product were added to cuvettes in assay buffer to prepare a calibration curve relating the amount of fluorescence to concentration of product. The calibration curve was linear over a wide range of concentrations including those where the sigmoidal behavior was observed, deviating from linearity only at high concentrations due to the inner filter effect. 3), The amount of product fluorescence in plastic cuvettes in assay buffer was found to be comparable to that in quartz cuvettes. In addition, no differences were observed in enzyme assays carried out in plastic versus quartz cuvettes. These tests all suggest that binding of the fluorescent product to the walls of the plastic cuvettes does not contribute significantly to the kinetic data obtained here. The possibility that preferential binding of fluorogenic substrate to the cuvettes occurred was also examined. Since only the product is fluorescent, possible substrate-cuvette binding was examined indirectly after conversion of substrate to product. Two cuvettes were prepared containing assay buffer and substrate. One of the cuvettes also contained 1 mM diC6PC. After incubation for 15 min at room temperature, the liquid in each cuvette was drawn off, and the cuvettes gently rinsed once with water, which was then removed and replaced with dilute sodium hydroxide. The fluorescence in each cuvette was then measured with no significant differences being observed. Since sodium hydroxide rapidly converts any substrate present to fluorescent product, any substrate remaining on the walls of the cuvette should be detectable as increased fluorescence. Since the level of fluorescence was similar regardless of whether or not diC6PC was present, it is highly unlikely that differences in the kinetic data can be attributed to substrate binding to the cuvettes. Another possible cause of the sigmoidal shape is that the small amount of product always present in the substrate causes activation. However, this possibility has been ruled out by a control experiment deliberately adding product and checking for activation. The possibility of some self-association of the nonfluorescent substrate was examined by studying the optical absorption spectra as a function of concentration in the same buffer used for the kinetic experiments. No evidence of self-association was observed for either substrate. Instead of pursuing additional studies on one substrate, the strategy followed here was to study two substrates of different hydrophobicities, which are shown to fit the same general two-site model. However, the question of self-association of product was examined because the water solubility of the product is expected to be much lower than that of the substrate, and it is the product fluorescence that is being monitored. We addressed this question by synthetically preparing pure product of the butyl-FLIP reaction and measuring the fluorescence versus concentration in the same buffer as was used for the kinetics. The fluorescence intensity was linear over the range measured, 0–5 μM product, and the initial rates were always measured before the concentration of product reached this limit. The linearity of the fluorescence with concentration is an indication that aggregation did not occur to any significant extent under these experimental conditions. Finally, a decrease in the enzyme activity during a set of experiments could cause a deviation from hyperbolic behavior. This possibility was checked by assaying the activity at the beginning and end of an experimental set.
Kinetic models
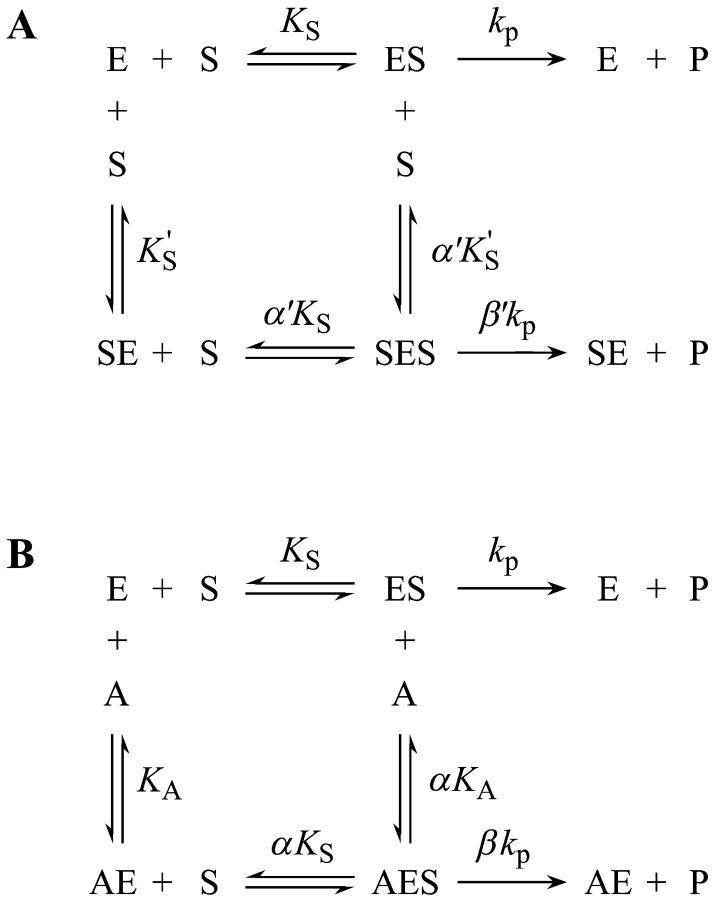
A two-site model was used to fit the data. In the first case (Fig. 2 A), the substrate binds to two sites cooperatively: the active site and an activator/effector site. The quasiequilibrium approximation is made, rather than the steady-state approximation, because the turnover number is moderate (kp or kcat is on the order of 150 s−1). Allowance has been made for different dissociation constants for S from the active site, KS, and the activator site, 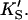 The symmetry in the equilibrium constants, i.e., KS,
The symmetry in the equilibrium constants, i.e., KS, 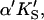 and
and 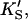 α′KS in this model is a result of the thermodynamic requirement that the Gibbs energy ΔG° for the reactions forming the ternary complex SES must be independent of path. Referring to Fig. 2 A, the equilibria are KS = [E][S]/[ES], α′KS = [SE][S]/[SES],
α′KS in this model is a result of the thermodynamic requirement that the Gibbs energy ΔG° for the reactions forming the ternary complex SES must be independent of path. Referring to Fig. 2 A, the equilibria are KS = [E][S]/[ES], α′KS = [SE][S]/[SES], 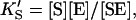 and
and 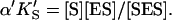 Equilibria are written as dissociations with the notation of Segel (1975), except for the primes, which are necessary to distinguish between the two models discussed here. The rate of the reaction is the sum of the rates of formation of product: v = kp[ES] + β′kp[SES]. The unknown concentrations [ES] and [SES] can be eliminated by substituting the above equilibrium expressions to give
Equilibria are written as dissociations with the notation of Segel (1975), except for the primes, which are necessary to distinguish between the two models discussed here. The rate of the reaction is the sum of the rates of formation of product: v = kp[ES] + β′kp[SES]. The unknown concentrations [ES] and [SES] can be eliminated by substituting the above equilibrium expressions to give
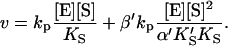 |
The conservation equation for enzyme is [E]T = [E] + [ES] + [SE] + [SES] where [E]T is the concentration of total enzyme present, [E] is the concentration of free enzyme, and the remaining terms are concentrations of the three complexes of enzyme with substrate. Eliminating the unknown concentrations [SE], [ES], and [SES] using the equilibrium expressions, and taking the ratio of the initial velocity to the total enzyme, v/[E]T, gives
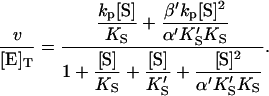 |
(1) |
Or, equivalently, this equation can be expressed in the familiar form v/Vmax, where Vmax = kp[E]T, the maximum rate when S is not bound to the activator site. Eq. 1 resembles that for a classical cooperative dimer (Segel, 1975). The difference is that one of the singly occupied complexes (SE) does not yield product, and the affinities of the two S binding sites (KS and 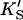 ) need not be identical. When S does not bind to the activator site, the reaction proceeds entirely through the upper branch of Fig. 2 A, and the rate equation reduces to the simple Michaelis-Menten model
) need not be identical. When S does not bind to the activator site, the reaction proceeds entirely through the upper branch of Fig. 2 A, and the rate equation reduces to the simple Michaelis-Menten model
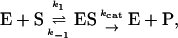 |
with kcat = kp; and KM becomes KS when quasiequilibrium conditions are assumed.
FIGURE 2.
The two-site scheme used in analyzing the present enzyme kinetic data. (A) In the absence of an activator, the substrate binds at two sites, the active site and an activator/effector site. (B) In the presence of an activator, the short-chain phospholipid diC6PC, the activator binds only to the activator site and is able to displace the substrate from this site. These two schemes, separately and in combination, were fitted to the data. E, enzyme; S, substrate; A, activator; and P, reaction product.
In the second variation of the model, shown in Fig. 2 B, an activator, A, binds to the activator/effector site and S binds to the active site. From Fig. 2 B, the equilibria are KS = [E][S]/[ES], αKS = [AE][S]/[AES], KA = [A][E]/[AE], and αKA = [A][ES]/[AES]. The rate of cleavage is the sum of the two terms: v = kp[ES] + βkp[AES]. Following the same steps as in the derivation of Eq. 1, the equation for the initial rate is (Segel, 1975)
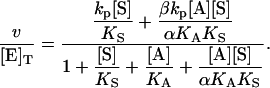 |
(2) |
The most useful case of Eq. 2 involves holding [A] fixed at an arbitrary value, whereas [S] is varied. Rearranging Eq. 2 gives the Michaelis-Menten equation in the form
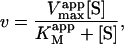 |
(3) |
where
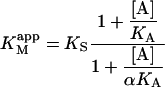 |
(4a) |
and
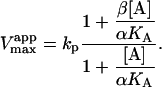 |
(4b) |
The apparent Vmax is normalized by dividing by the enzyme concentration. Otherwise Eq. 4 b would have the term Vmax in place of kp since Vmax is defined to be the maximum rate in the absence of any activator, Vmax = kp[E]T. The apparent Vmax and apparent KM are constants only when [A] is held constant.
Similarly, the two models of Fig. 2 can be combined into one kinetic scheme. The rate becomes the sum of three terms: v = kp[ES] + β′kp[SES] + βkp[AES]. The conservation equation for enzyme is [E]T = [E] + [ES] + [SE] + [AE] + [AES] + [SES]. The corresponding expression for the initial rate is
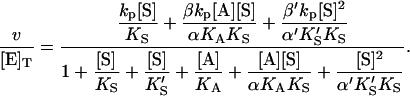 |
(5) |
In the absence of activator, i.e., [A] = 0, or poor activator binding, 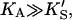 Eq. 5 reduces to Eq. 1. In the other limit, as the activator concentration increases and if
Eq. 5 reduces to Eq. 1. In the other limit, as the activator concentration increases and if 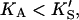 the activator completely displaces S from the activator site, and Eq. 5 approaches Eq. 2. Thus, Eq. 5 is the general equation that describes the system both with and without added activator.
the activator completely displaces S from the activator site, and Eq. 5 approaches Eq. 2. Thus, Eq. 5 is the general equation that describes the system both with and without added activator.
RESULTS
Reaction products
When analyzed by a thin layer chromatography method (Hedberg et al., 2001), the inositol phosphate product formed by the cleavage of the fluorogenic substrate is predominately I(1,2)cP as examined using methyl-FLIP (K. Hedberg, private communication). The other product is the derivative of fluorescein shown in Fig. 1 A. This reaction can be compared to cleavage of the natural substrate PI to form I(1,2)cP and diacylglycerol. Thus, the mode of action of the phospholipase on the synthetic substrate methyl-FLIP is the same as on its natural substrate. The I(1,2)cP produced by either the natural or fluorogenic substrate can be hydrolyzed in a much slower reaction catalyzed by PI-PLC to form I(1)P (Fig. 1 B).
Progress curves
The initial rates of cleavage of fluorogenic substrates at pH 7 and 25°C were determined by monitoring the fluorescence of the products as a function of time. Fig. 3 A shows the typical time course of the increase in fluorescence observed as a function of the enzyme concentration. The substrate was butyl-FLIP, and similar behavior was obtained for methyl-FLIP. Initial rates were calculated from the slopes of the lines and were reproducible to within 5%. Fig. 3 B is a plot of the initial rates versus the amount of PI-PLC added. The syntheses yield a racemic mixture of fluorogenic substrates. Here and throughout this report the substrate concentration [S] refers to that of the active D-enantiomer, i.e., one half of the concentration of racemic substrate. It has been shown in a previous study of chromogenic synthetic substrate, myo-inositol 1-(4-nitrophenyl phosphate), abbreviated NPIP, that only the D-enantiomer is cleaved by PI-PLC. The L-enantiomer was neither a substrate nor an inhibitor (Leigh et al., 1992). Dividing the racemic concentration by a factor of two gave identical kinetics with the pure D-enantiomer of NPIP. Similar substrate stereospecificity was observed with a short-chain PI, where the D-enantiomer was active and the L-enantiomer was neither a substrate nor an inhibitor of Bacillus thuringiensis PI-PLC, an enzyme nearly identical to B. cereus PI-PLC (Lewis et al., 1993). Although some binding of the L-enantiomer of the fluorogenic substrates to the activator site can not be ruled out, such binding would not change any of the major conclusions of this paper. In the present study, the observed linearity of the reaction rate with time and with enzyme concentration establishes that the fluorogenic substrates are behaving as expected for a water-soluble monomeric substrate interacting with a monomeric enzyme.
FIGURE 3.
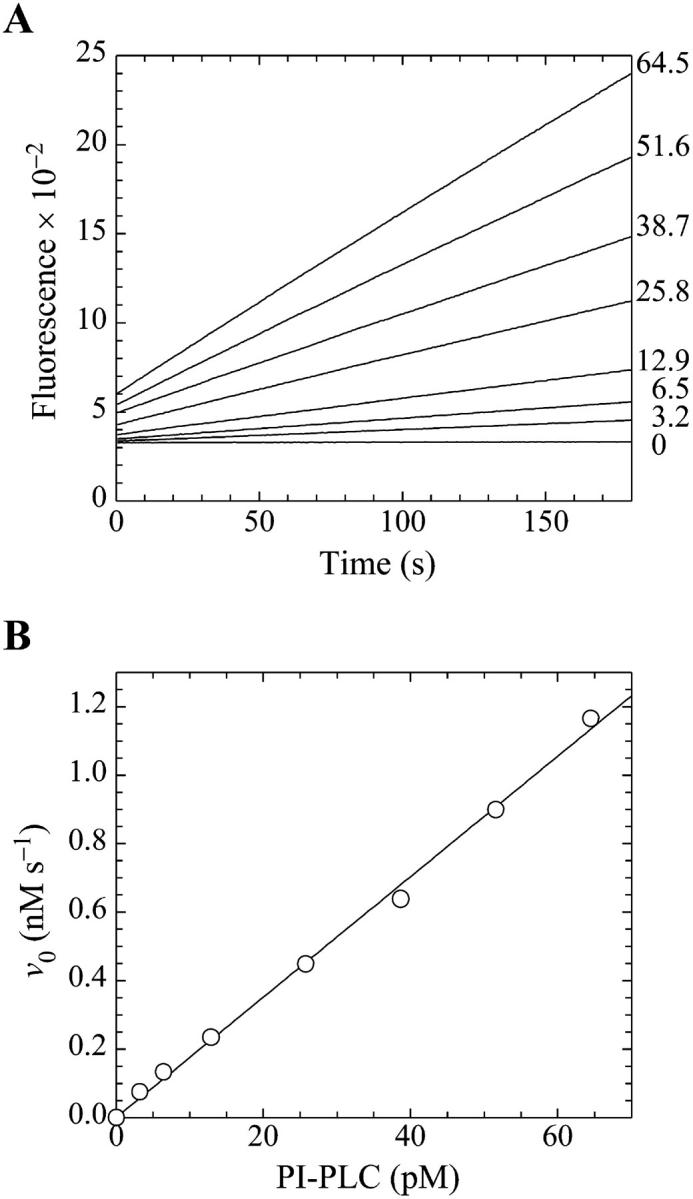
Demonstration of the linearity of the assay. (A) Fluorescence emission intensity in arbitrary units at 520 nm (excitation at 465 nm) for the cleavage of butyl-FLIP by PI-PLC measured as a function of time. The lines are continuous sets of data points. The substrate concentration in each case was 20.6 μM active D-enantiomer (i.e., one half of the concentration of the racemic mixture), and the numbers at the right indicate the concentrations of enzyme (pM) used in the assays. (B) The initial rates from panel A versus the concentration of PI-PLC. The solid line is a linear regression fit to the data points.
Initial rates as a function of butyl-FLIP substrate concentration
The initial rates of butyl-FLIP cleavage as a function of substrate concentration are plotted in Fig. 4 A. Surprisingly, the experimental curve was sigmoidal, rather than a rectangular hyperbola as would be expected for simple Michaelis-Menten kinetics. The data cannot be fitted using the Michaelis-Menten equation. Instead, as a first step, the data were fitted to the empirical Hill equation, which in enzyme kinetics takes the form (Cornish-Bowden, 1999; Segel, 1975)
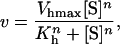 |
(6) |
where Vhmax, Kh, and n are empirical parameters derived from the data, and [S] is the concentration of substrate. The values of these parameters obtained from a nonlinear regression fit of the data of Fig. 4 A were Vhmax = 315 ± 11 s−1, Kh = 0.15 ± 0.01 mM, and n = 1.5 ± 0.05. The fit to the Hill equation is excellent (dotted line in Fig. 4 A). All data were plotted normalized for enzyme concentration, i.e., initial rates in the form of (nanomolar product formed)/s divided by the nanomolar enzyme concentration, so that the parameter Vhmax is also normalized. The experiment was repeated five times. The mean value of the Hill coefficient was 1.33 with a sample standard deviation of 0.10. The mean value of Kh was 0.21 mM with a sample standard deviation of 0.05. There was considerable variation in Vhmax (the five values were 430 s−1, 316 s−1, 166 s−1, 315 s−1, and 103 s−1). Lower activities corresponded to older enzyme preparations (i.e., vials of stock from which more aliquots had been removed), so this was not a random error and it would be inappropriate to average the results. Phospholipases are surface-active enzymes and are more likely to bind to surfaces or impurities than are typical water-soluble enzymes, contributing to variations in effective enzyme activities and resulting in vertical shifting of the entire initial rates versus [S] curves. However, the shapes of the butyl-FLIP curves were always sigmoidal and the variation of activities within a specific set of experiments was small, as is evident in Fig. 4 A.
FIGURE 4.
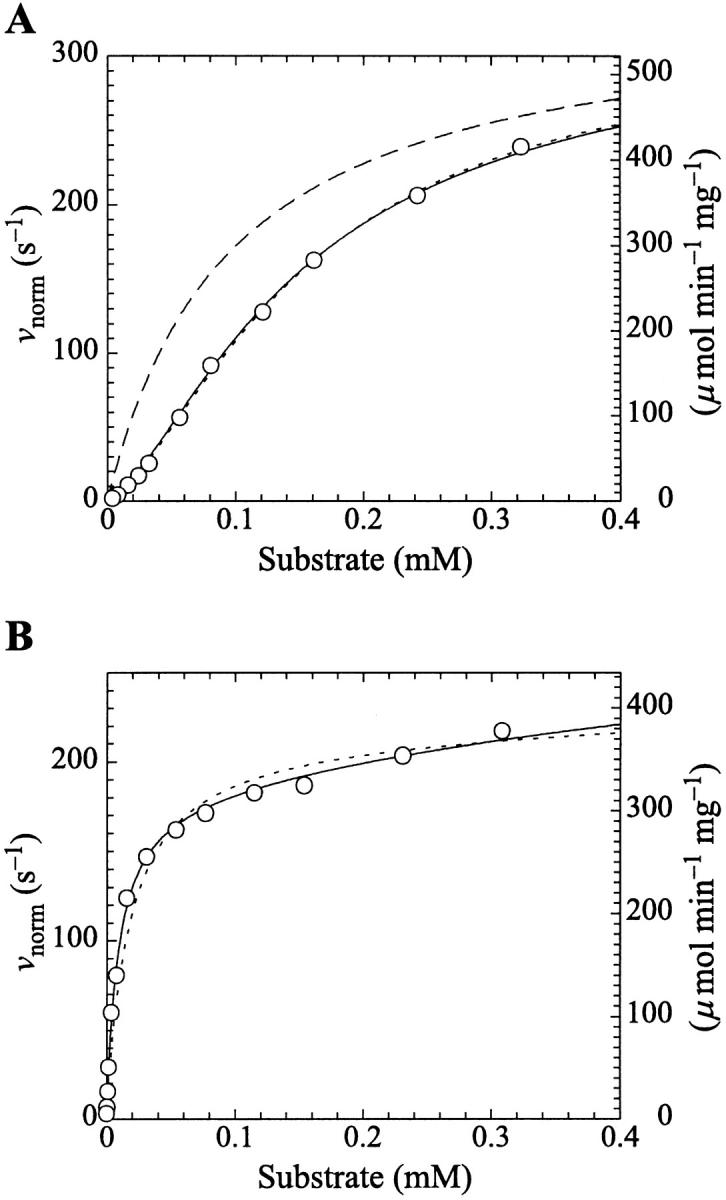
PI-PLC kinetics with butyl-FLIP substrate. (A) Cleavage of butyl-FLIP without activator gives sigmoidal kinetics. The dotted line is a plot of the Hill equation, with n = 1.5. The solid line was calculated for the two-site model using Eq. 2. The reference curve (dashed line) represents the hypothetical case where the only productive complex is SES. (B) Cleavage of butyl-FLIP in the presence of a fixed concentration of activator lipid, 1.07 mM diC6PC, yields approximately hyperbolic kinetics. The dotted line was calculated using Eq. 5 for the general two-site model under the stringent requirement that the input parameters KS, α′, 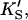 and β′ be identical to those in panel A where no activator is present, and only the two parameters—α and β describing the activator-enzyme complex, and kp—were allowed to vary. The solid line was also calculated using Eq. 5, but relaxing the restriction on the variation of other parameters. Parameter values are given in Table 1. The initial rates are plotted using two common conventions in enzymology: μmol of product per second per μmol enzyme (abbreviated s−1) and μmol of product per minute per mg enzyme (abbreviated μmol min−1 mg−1). The same conventions are used in the following figures. To convert between these two scales, multiply initial rates in μmol min−1 mg−1 by 34.53/60 to obtain rates in s−1. The factor of 34.53 is the molecular weight of B. cereus PI-PLC in kDa, and the divisor is the conversion from minutes to seconds. The PI-PLC concentration was 12.9 pM in both experiments.
and β′ be identical to those in panel A where no activator is present, and only the two parameters—α and β describing the activator-enzyme complex, and kp—were allowed to vary. The solid line was also calculated using Eq. 5, but relaxing the restriction on the variation of other parameters. Parameter values are given in Table 1. The initial rates are plotted using two common conventions in enzymology: μmol of product per second per μmol enzyme (abbreviated s−1) and μmol of product per minute per mg enzyme (abbreviated μmol min−1 mg−1). The same conventions are used in the following figures. To convert between these two scales, multiply initial rates in μmol min−1 mg−1 by 34.53/60 to obtain rates in s−1. The factor of 34.53 is the molecular weight of B. cereus PI-PLC in kDa, and the divisor is the conversion from minutes to seconds. The PI-PLC concentration was 12.9 pM in both experiments.
The two-site model of Fig. 2 A also provides an excellent fit to the butyl-FLIP data. Fitting the data to Eq. 1 by standard nonlinear regression methods such as the gradient-search method or the Marquart method was not practical because of the number of parameters involved and the well-known local minima problem (Bevington and Robinson, 1992; Draper and Smith, 1998). Instead, the curve was fitted visually. This process does not lead to a unique set of specific parameters. The solid line of Fig. 4 A was calculated using a set of parameters that give good curve fitting with Eq. 1. The parameters are given in Table 1. The calculated solid line superimposes almost exactly on the fit to the Hill equation. As can be seen from Eq. 1, at high substrate concentrations the terms in [S]2 dominate and the shape of the curve depends on the product β′kp. Only this product and not the individual values of β′ and kp can be determined from the high substrate limit. At low [S] the linear terms in Eq. 1 dominate, so the term in kp, rather than the product β′kp, becomes significant. The experimental region of very low [S] in Fig. 4 A was examined with the aim of estimating kp, given KS and 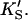 Comparing the results with the product β′kp, obtained from the high [S] region, suggests β′ > 1, i.e., 1.1–1.4. It is clear that β′ is not much greater than 1.
Comparing the results with the product β′kp, obtained from the high [S] region, suggests β′ > 1, i.e., 1.1–1.4. It is clear that β′ is not much greater than 1.
TABLE 1.
Kinetic parameters for the butyl-FLIP activity of B. cereus PI-PLC obtained by fitting to the two-site model
| Data set | Curve shape | No. of fitted parameters | diC6PC (mM) | KS (mM) | α′ |
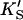 (mM) (mM) |
kp (s−1) | β′ | KA (mM) | α | β |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fig. 4 A Solid line | Sigmoidal | 5 | 0 | 0.5 | 0.2 | 0.15 | 240 | 1.4 | — | — | — |
| Fig. 4 B Dotted line | Hyperbolic (approx.) | 3 | 1.07 | 0.5 | 0.2 | 0.15 | 218 | 1.4 | 0.2 | 0.03 | 1.0 |
| Fig. 4 B Solid line | Hyperbolic (approx.) | 7 | 1.07 | 0.5 | 0.1 | 0.04 | 220 | 1.5 | 0.2 | 0.02 | 0.9 |
| Fig. 5 | Hyperbolic | 7 | 0–1 | 0.5 | 0.2 | 0.15 | 100 | 1.4 | 0.2 | 0.02 | 1.0 |
The data of Fig. 4 were simulated with a five-parameter (KS, α′, 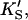 β′, kp) fit using Eq. 1, or equivalently using Eq. 5 with [A] = [diC6PC] = 0. KA was held constant at 0.2 mM. Fig. 4 B was simulated with Eq. 5 by two methods. In the first method, the four parameters (KS, α′,
β′, kp) fit using Eq. 1, or equivalently using Eq. 5 with [A] = [diC6PC] = 0. KA was held constant at 0.2 mM. Fig. 4 B was simulated with Eq. 5 by two methods. In the first method, the four parameters (KS, α′, 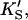 β′) were fixed at values arrived at for Fig. 4 A, and only three parameters (kp, α, β) were allowed to vary. In the second method, all seven parameters (KS, α′,
β′) were fixed at values arrived at for Fig. 4 A, and only three parameters (kp, α, β) were allowed to vary. In the second method, all seven parameters (KS, α′, 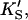 β′, kp, α, β) were allowed to vary. The fit to the data of Fig. 5 was carried out with Eq. 5, varying the same seven parameters, and [S] = 8.6 μM butyl-FLIP. Values were arrived at by visual curve fitting and are thus semiquantitative. Estimated errors are 10% for KS and 20% for α′,
β′, kp, α, β) were allowed to vary. The fit to the data of Fig. 5 was carried out with Eq. 5, varying the same seven parameters, and [S] = 8.6 μM butyl-FLIP. Values were arrived at by visual curve fitting and are thus semiquantitative. Estimated errors are 10% for KS and 20% for α′, 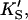 β′, α, β. The variation in kp was larger due to differences in enzyme activity from different preparations (see text).
β′, α, β. The variation in kp was larger due to differences in enzyme activity from different preparations (see text).
Initial rates of butyl-FLIP cleavage in the presence of diC6PC
Introducing monomeric concentrations of the inert, nonsubstrate activator lipid diC6PC dramatically affected the appearance of the kinetic curves. The plot of the initial rates versus substrate concentration was approximately hyperbolic up to [S] = 0.2 mM (Fig. 4 B). The diC6PC concentration was held constant at 1.07 mM. As noted previously, the activities varied with the enzyme stock solution. This variability was dealt with by running controls with no activator present with every experiment, so that activities could be matched. The reason the initial rates of Fig. 4 B are approximately hyperbolic at low [S] is that the activator concentration is constant, and the reaction can be described by the kinetics scheme of Fig. 2 B. At higher [S], some substrate also binds at the activator site, mixing the kinetic scheme given in the lower branch of Fig. 2 A with that of Fig. 2 B. The more general Eq. 5 takes into account both kinetic schemes and therefore should fit the data. The dotted line in Fig. 4 B was calculated from Eq. 5 with the restriction that the input parameters KS, α′, 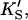 and β′ be identical to those in Fig. 4 A where no activator is present. The parameter kp is slightly lower, corresponding to a lower enzyme activity for this preparation, consistent with controls. The solid line in Fig. 4 B provides an even better fit to the data by allowing other parameters to vary. The values of the parameters are given in Table 1. The activator concentration [A] is known, and parameters KA, α, and β describe the interaction of the activator with the enzyme. NMR data on equilibrium binding of diC6PC to B. thuringiensis PI-PLC indicates a single binding site with KA (i.e., Kd) = 0.5 ± 0.2 mM (Zhou et al., 1997a). This value should be a good approximation for KA of B. cereus PI-PLC since it is nearly identical to B. thuringiensis PI-PLC, differing in only seven amino acid residues. We used a slightly smaller value, KA = 0.2 mM, because it appeared to provide a better fit to the data.
and β′ be identical to those in Fig. 4 A where no activator is present. The parameter kp is slightly lower, corresponding to a lower enzyme activity for this preparation, consistent with controls. The solid line in Fig. 4 B provides an even better fit to the data by allowing other parameters to vary. The values of the parameters are given in Table 1. The activator concentration [A] is known, and parameters KA, α, and β describe the interaction of the activator with the enzyme. NMR data on equilibrium binding of diC6PC to B. thuringiensis PI-PLC indicates a single binding site with KA (i.e., Kd) = 0.5 ± 0.2 mM (Zhou et al., 1997a). This value should be a good approximation for KA of B. cereus PI-PLC since it is nearly identical to B. thuringiensis PI-PLC, differing in only seven amino acid residues. We used a slightly smaller value, KA = 0.2 mM, because it appeared to provide a better fit to the data.
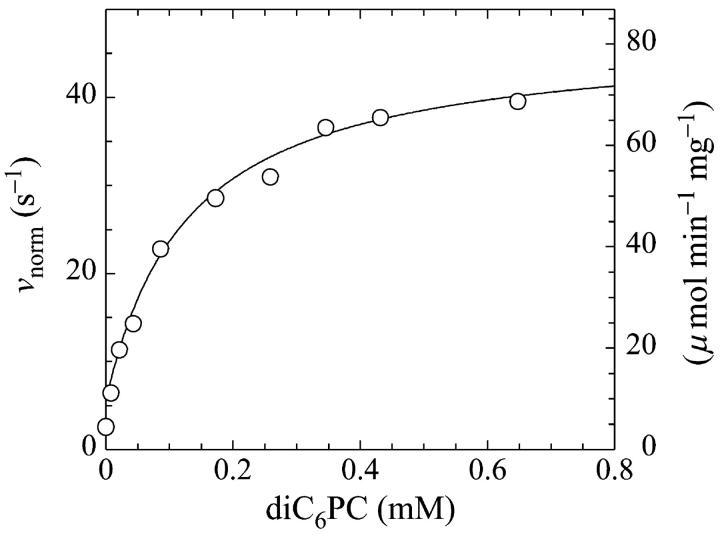
The activation as a function of the concentration of diC6PC at a fixed value of the substrate is shown in Fig. 5. The activity rises sharply at very low concentrations of nonsubstrate activator lipid diC6PC, then reaches a maximum around 0.7–1.0 mM diC6PC. The experiment was repeated with similar results. The solid line was calculated using Eq. 5 with [S] = 8.6 μM and the set of parameters given in Table 1. The kp is lower (100 s−1) due to lower enzyme activity.
FIGURE 5.
The rate of cleavage of butyl-FLIP increases as a function of the diC6PC activator concentration. The onset of activation is far below the CMC (15 mM), suggesting that monomers of diC6PC activate. The concentration of butyl-FLIP was held constant at 8.6 μM (D-enantiomer). The PI-PLC concentration was 12.9 pM. The solid line was calculated from the general Eq. 5 with a set of parameters similar to those used in fitting the data in Fig. 4 B. Parameters are given in Table 1.
Methyl-FLIP kinetics
Kinetics with methyl-FLIP were simpler to analyze than with butyl-FLIP. Plots of the initial rates versus substrate concentration can be approximated by a hyperbolic curve (Fig. 6 A), indicating that methyl-FLIP is binding only to the active site and not to the activator site. Fitting of the data by nonlinear regression using the Michaelis-Menten equation returns the values KM = 0.81 ± 0.10 mM and normalized Vmax = 101 ± 5 s−1. The errors refer to the fit of a single set of data. The experiment was repeated, yielding a similar value of KM (0.85 ± 0.1 mM) but a larger value of Vmax (209 ± 15 s−1). The higher value represents a more active enzyme, but the experimental set giving the lower value was selected for Fig. 6 A because it more closely matched the activity of the preparation corresponding to Fig. 6 B. Addition of a fixed concentration of diC6PC increases the rate of cleavage of methyl-FLIP (Fig. 6 B). A fit of the Michaelis-Menten equation to the initial rate data of Fig. 6 B yielded the parameters 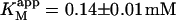 and
and 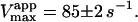
FIGURE 6.
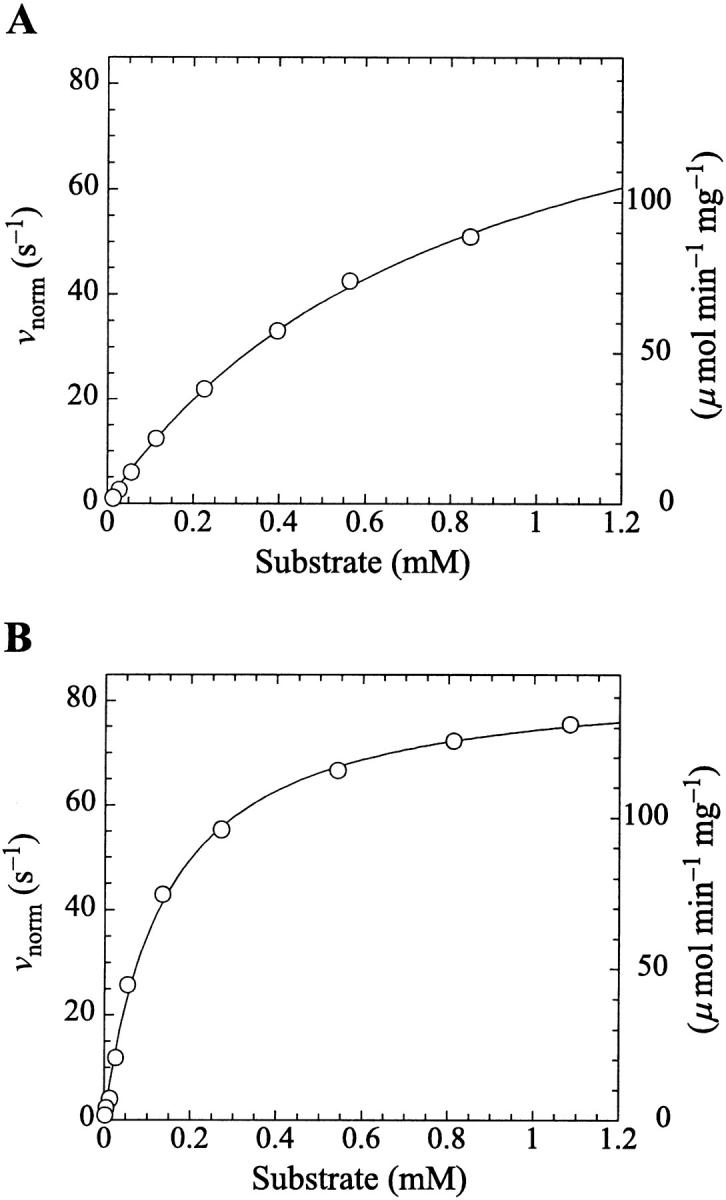
Michaelis-Menten kinetics is observed with the substrate methyl-FLIP. (A) Initial rates versus substrate concentration (D-enantiomer). (B) The initial rates are enhanced by the presence of the nonsubstrate lipid, diC6PC (0.69 mM). The solid lines are fits to the Michaelis-Menten equation. Parameters are given in Table 2. The PI-PLC concentration was 12.9 pM.
DISCUSSION
The fluorogenic substrates are cleaved rapidly by B. cereus PI-PLC. Using two substrates, butyl-FLIP and methyl-FLIP, differing only in the length of the hydrocarbon chain bonded to fluorescein, it was possible to provide greater insight regarding B. cereus PI-PLC than using either substrate alone. The minor structural difference produces striking differences in the enzyme kinetics. One substrate, butyl-FLIP, binds to both the active site and to an activator site whereas methyl-FLIP binds only to the active site. Although the kinetic analysis is different, the results are consistent with the same model. Both substrates detect activation by concentrations of diC6PC much lower than observed previously.
Butyl-FLIP and sigmoidal kinetics
The plot of initial rates versus [S] yields sigmoidal kinetics (Fig. 4 A). The Hill equation provides an excellent fit to the experimental data. Repeat experiments produced Hill coefficients n in the range of 1.3–1.5, which implies cooperativity with a probable value of n = 2. In principle, this could correspond to two substrate molecules binding to one monomeric enzyme, i.e., one active site and one effector site, or it could reflect the binding of substrate molecules to two active sites of a dimeric protein. The latter possibility was discarded because there is no evidence for dimeric associations in any of the crystallographic studies and because these experiments are being carried out at very low (picomolar) enzyme concentrations. Also, there are no sigmoidal effects observed in prior studies of the chromogenic substrate NPIP at similar B. cereus PI-PLC concentrations (Leigh et al., 1992; Shashidhar et al., 1991). Sigmoidal curves and other deviations from the normal hyperbolic kinetics can be the result of experimental artifacts. For this reason, additional control experiments were performed, the results of which make this trivial explanation unlikely. Sigmoidal curves can arise in monomeric enzymes without ligand-induced conformational changes under special circumstances when there are two different substrates, or a substrate plus effector, and two kinetic pathways (Segel, 1975), but there is no reason to believe that this more complex explanation applies to the present system. Cooperativitylike effects in monomeric enzymes can also occur by a hysteretic mechanism (Cornish-Bowden and Cardenas, 1987; Neet, 1995), i.e., ligand binding to an enzyme with different conformations having long lifetimes, rather than by subsite interactions. However, the crystal structure of B. cereus PI-PLC shows this enzyme to be a single domain protein, a compact distorted (βα)8 barrel closely related to that first observed for triose phosphate isomerase (TIM) (Heinz et al., 1995, 1999). The TIM barrel is a common folding motif that occurs in a large number of enzyme structures and, to our knowledge, there is no evidence for slowly changing conformers in this type of structure under physiological conditions.
The advantage of the Hill equation is that it provides a simple three-parameter fit to the data. The limitation is that it is an empirical equation. The simplest reaction mechanism that accounts for the data is a two-site model (Fig. 2). This model was originally solved analytically for the steady state by Botts and Morales in their classic 1953 paper of an enzyme influenced by a modifier (Botts and Morales, 1953; Di Cera et al., 1996). In this model there are two reactions running in parallel. The top reaction of Fig. 2 A is the familiar reaction of a substrate S with enzyme E to form an enzyme-substrate complex ES, which then breaks down to form enzyme and product P or dissociates to form free enzyme and substrate. If this were the only reaction path the plot of initial rates versus [S] would yield a rectangular hyperbola, as described by the Michaelis-Menten equation. However, if S binds in random order to an activator/effector and the catalytic site, then there are two additional complexes present, SE and SES, where the activator site is shown on the left and the active site on the right of the enzyme for clarity. In actuality these are probably subsites in close proximity within the active site region. The relationship between the Hill equation and the two-site model can be seen by taking the strong interaction limit of the two-site model. This limit corresponds to all substrate being cleaved from the doubly occupied enzyme SES, and occurs at high [S]. In this limit, 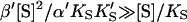 and
and 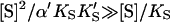 or
or 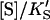 and Eq. 1 reduces to
and Eq. 1 reduces to
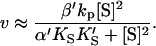 |
(7) |
Comparing the limiting two-site case in Eq. 7 with the Hill Eq. 6, and substituting in the parameters to the two-site model gives the limiting values Vhmax ≈ β′kp = 1.4 × 240 s−1 = 336 s−1, 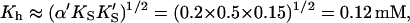 and n = 2. These values are not far from the empirical Hill parameters Vhmax = 315 s−1, Kh = 0.15 mM, and n = 1.5. This implies that there is a significant interaction between sites.
and n = 2. These values are not far from the empirical Hill parameters Vhmax = 315 s−1, Kh = 0.15 mM, and n = 1.5. This implies that there is a significant interaction between sites.
DiC6PC activates the cleavage of butyl-FLIP over the entire range of concentrations measured. There is some decrease in net activation at higher concentrations (data not shown), suggesting binding of diC6PC at an additional site, either the active site or a second subsite. The critical micelle concentration (CMC) for diC6PC is 15 mM (Tausk et al., 1974; Zhou et al., 1997b). The maximum activation of butyl-FLIP cleavage was an order of magnitude below 15 mM, so the effects are likely caused by diC6PC monomers binding to one or more subsites on the enzyme surface, rather than interfacial activation by a phospholipid-water interface. The two-site model leads to an interesting prediction. If an activator is introduced that successfully competes with S for the effector site, then the initial rate versus [S] sigmoidal kinetic curve will become hyperbolic providing the activator concentration is held constant. The experimental results of Fig. 4 B show that this is indeed the case for diC6PC, as is readily seen by comparing Fig. 4 A and Fig. 4 B. Eq. 5 provides a quantitative way to analyze the kinetics with or without diC6PC. It is gratifying that the curve fitting was successful using the same input parameters as for Fig. 4 A. That is, the values determined in the absence of activator were fixed in fitting the experimental data in the presence of activator with Eq. 5. Furthermore, since the concentration of butyl-FLIP was held constant and the fractional occupancy of the activator site by diC6PC was much greater than the fractional occupancy of the activator site by butyl-FLIP under the experimental conditions chosen, it is possible to apply Eq. 4, a and b, to estimate the apparent kinetic constants. This is equivalent to treating the system with the kinetic scheme in Fig. 2 B. According to Eq. 4 a, 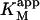 depends only on KS, α, KA, and the activator concentration [A]. Taking the parameters of Table 1 obtained by curve fitting of Fig. 4 B (solid line) and substituting into Eq. 4 a gives
depends only on KS, α, KA, and the activator concentration [A]. Taking the parameters of Table 1 obtained by curve fitting of Fig. 4 B (solid line) and substituting into Eq. 4 a gives 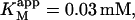 in reasonable agreement with the value 0.01 mM obtained by fitting the low [S] region to the Michaelis-Menten equation. Similarly, Eq. 4 b predicts
in reasonable agreement with the value 0.01 mM obtained by fitting the low [S] region to the Michaelis-Menten equation. Similarly, Eq. 4 b predicts 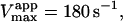 incorporating the same scaling factor of 0.9 as used in fitting with Eq. 5. This is in agreement with the value of 195 s−1 obtained by fitting the low [S] region to the Michaelis-Menten equation. The approximate agreement obtained using Eqs. 4 and 5 supports the conclusion that under the experimental conditions chosen, the activator diC6PC outcompetes butyl-FLIP for the activator site. Since β is close to 1, the main effect is due to the large decrease in α, indicating that occupation of the activator site increases substrate binding at the catalytic site. The increase in catalytic efficiency (kcat/KM) upon binding of diC6PC can be obtained by comparing the ratios before and after addition of activator. With the activator site vacant, kcat/KM = kp/KS and in the presence of diC6PC the ratio is βkp/(αKS). The ratio of these two values reduces to β/α ∼ 40–50, so binding of diC6PC causes an order of magnitude increase in the catalytic efficiency. The ratio of the catalytic efficiency of butyl-FLIP activation to that without butyl-FLIP binding to the activator site reduces to the ratio β′/α′. The uncertainty in this ratio is larger but it is clear that butyl-FLIP bound to the activator site also causes an order of magnitude increase in the catalytic efficiency.
incorporating the same scaling factor of 0.9 as used in fitting with Eq. 5. This is in agreement with the value of 195 s−1 obtained by fitting the low [S] region to the Michaelis-Menten equation. The approximate agreement obtained using Eqs. 4 and 5 supports the conclusion that under the experimental conditions chosen, the activator diC6PC outcompetes butyl-FLIP for the activator site. Since β is close to 1, the main effect is due to the large decrease in α, indicating that occupation of the activator site increases substrate binding at the catalytic site. The increase in catalytic efficiency (kcat/KM) upon binding of diC6PC can be obtained by comparing the ratios before and after addition of activator. With the activator site vacant, kcat/KM = kp/KS and in the presence of diC6PC the ratio is βkp/(αKS). The ratio of these two values reduces to β/α ∼ 40–50, so binding of diC6PC causes an order of magnitude increase in the catalytic efficiency. The ratio of the catalytic efficiency of butyl-FLIP activation to that without butyl-FLIP binding to the activator site reduces to the ratio β′/α′. The uncertainty in this ratio is larger but it is clear that butyl-FLIP bound to the activator site also causes an order of magnitude increase in the catalytic efficiency.
Methyl-FLIP kinetics
The analysis of the methyl-FLIP kinetic data was much simpler because the plots of initial rates versus substrate concentration were approximately hyperbolic (Fig. 6 A). The methyl-FLIP substrate binds only to the active site, and not to the activator site. This is reasonable considering the lower hydrophobicity of methyl-FLIP. Methyl-FLIP also exhibits slightly lower binding to the active site compared to butyl-FLIP, as judged by the KM (KS) values. The effect of addition of a fixed concentration of diC6PC is easily seen in comparing Fig. 6 A and Fig. 6 B. The kinetic curves remain hyperbolic and the activity increases. The most important observation is that the activation occurs at very low diC6PC concentrations, in agreement with the butyl-FLIP data, suggesting that the effect is caused by monomers of the short-chain lipid binding to the enzyme. The possibility that more than one diC6PC is involved cannot be ruled out, but monomer binding is the most attractive model in this low concentration region. Cobra venom phospholipase A2 (PLA2), has been shown to act as a nucleation site for premicellar aggregates of diC6PC and diheptanoylphosphatidylcholine (diC7PC) (Bukowski and Teller, 1986), and inhibition studies of pancreatic PLA2 suggest aggregates of enzyme with short-chain anionic lipids can form below the CMC (Rogers et al., 1996). However, the interaction of phospholipids with PLA2 is much stronger than with PI-PLC, judging from the tendency of PLA2 to exhibit scooting mode kinetics (Berg et al., 2001), and the Ca2+ ions required in the PLA2 reaction solution can facilitate microaggregation. As mentioned above, NMR studies on PI-PLC indicate that only one diC6PC molecule binds to B. thuringiensis PI-PLC with a KA (i.e., Kd) of 0.5 ± 0.2 mM (Zhou et al., 1997a). Thus, it is reasonable to conclude that at very low diC6PC, only one molecule of this lipid binds to PI-PLC. As the concentration is increased, additional diC6PC molecules bind until near the CMC where premicellar aggregation is likely to occur. Above the CMC the entire interfacial region of the enzyme is in contact with diC6PC molecules. The two-site model used here is entirely compatible with current theories of interfacial activation. The binding of the first phospholipid represents an initial step in the process that eventually leads to interfacial activation, accompanied by scooting-and hopping-mode kinetics.
The value of 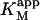 decreases in the presence of diC6PC, indicating that the activator increases the binding of substrate to enzyme. The data fit the two-site model of Fig. 2 B with α = 0.14 ± 0.01, as derived from Eq. 4 a. The value of β is more difficult to determine accurately because of day-to-day variations in enzyme activity. The two values of
decreases in the presence of diC6PC, indicating that the activator increases the binding of substrate to enzyme. The data fit the two-site model of Fig. 2 B with α = 0.14 ± 0.01, as derived from Eq. 4 a. The value of β is more difficult to determine accurately because of day-to-day variations in enzyme activity. The two values of 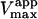 in Table 2 would suggest that there is a decrease upon addition of diC6PC. However, controls indicate that lower enzyme activity in the set of experiments involving addition of diC6PC was a contributing factor. Adjusting for the difference in activity, and using Eq. 4 b, it is estimated that β = 1.0 ± 0.15. This means there is very little effect on Vmax (i.e., kcat). Occupation of the activator site by the first molecule of diC6PC causes a five- to 10-fold increase in catalytic efficiency, β/α.
in Table 2 would suggest that there is a decrease upon addition of diC6PC. However, controls indicate that lower enzyme activity in the set of experiments involving addition of diC6PC was a contributing factor. Adjusting for the difference in activity, and using Eq. 4 b, it is estimated that β = 1.0 ± 0.15. This means there is very little effect on Vmax (i.e., kcat). Occupation of the activator site by the first molecule of diC6PC causes a five- to 10-fold increase in catalytic efficiency, β/α.
TABLE 2.
Kinetic parameters for the methyl-FLIP activity of B. cereus PI-PLC obtained by fitting to the Michaelis-Menten equation
| Data set | Curve shape | diC6PC (mM) |
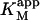 (mM) (mM) |
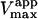 (s−1) (s−1) |
|---|---|---|---|---|
| Fig. 6 A | Hyperbolic | 0 | 0.81 ± 0.01 | 101 ± 5 |
| Fig. 6 B | Hyperbolic | 0.69 | 0.14 ± 0.01 | 85 ± 2 |
Data fit by standard nonlinear regression methods. The uncertainties listed refer to one data set. The variation of 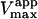 between data sets was much greater due to differences in enzyme activity of preparations used on different days (see text). The kinetic constants are apparent values only in the presence of the activator, diC6PC.
between data sets was much greater due to differences in enzyme activity of preparations used on different days (see text). The kinetic constants are apparent values only in the presence of the activator, diC6PC.
Comparison with literature data on PI-PLC kinetics
Utilizing single-chain thiophosphate analogs of PI (Cn-thio-PI) of various chain lengths (n = 8, 12, and 16), Hendrickson and co-workers reported that B. cereus PI-PLC exhibited an interfacial effect (Hendrickson et al., 1992). The specific activities of these PI analogs were relatively low, but increased above the CMC. The specific activity also increased significantly upon introduction of hexadecylphosphatidylcholine, which forms mixed micelles with Cn-thio-PI. In studies using short-chain PIs, it has been shown that B. thuringiensis PI-PLC (Lewis et al., 1993) and mammalian PI-PLC-δ1 (Rebecchi et al., 1993) exhibit a three- to fivefold interfacial activation upon micelle formation, respectively, compared to activity toward monomeric substrates. The characteristics of PI-PLC binding to the phospholipid-water interface was examined using a combination of techniques: intrinsic protein fluorescence, UV absorbance, fluorescence quenching, as well as enzyme activity on PI in vesicles, and on the water-soluble substrate analog NPIP (Volwerk et al., 1994). These data were interpreted in terms of interfacial enzymology, an approach that separates binding to the interface from the catalytic events on the interface. It is estimated that the average processivity is ∼40–50 catalytic cycles per binding event, i.e., before the enzyme hops off the surface. The selectivity at the active site is much greater than binding of the enzyme to the interface. The zwitterionic dioleoylphosphatidylcholine does not bind at the active site, whereas ditetradecylphosphatidylmethanol, an anionic phospholipid, does bind at the active site and is a competitive inhibitor. The catalysis by PI-PLC of the water-soluble substrate NPIP was activated by the presence of dioleoylphosphatidylcholine vesicles. The threefold activation was largely due to an increase in Vmax with little change in KM and is consistent with a model in which the phospholipid interface acts as an allosteric effector. This experiment was the impetus for the present study. The results agree in that activation is observed. However, the detailed kinetics are different, since in the present system, monomers of activator are studied. Also, sigmoidal kinetics were not observed in NPIP kinetics, arguing for weak binding of NPIP to the effector site (Leigh et al., 1992). The main effect of activation on butyl-FLIP and methyl-FLIP cleavage is the very large increase in substrate binding to the active site. There are only minor effects on kcat. In a study of B. thuringiensis PI-PLC in the presence of mixed micelles of long-chain PI and short-chain lipids, it was reported that higher activities were observed at higher short-chain PC concentrations (Zhou et al., 1997b).
This literature involves the intramolecular phosphotransferase reaction catalyzed by PI-PLC, i.e., the cleavage of the natural substrate PI or substrate analogs, directly related to the reaction studied here (Fig. 1 A). The second reaction of PI-PLC, the slower cyclic phosphodiesterase activity that hydrolyzes I(1,2)cP (Fig. 1 B), has also been the subject of a number of studies. Roberts and co-workers (Zhou et al., 1997b) have examined this reaction using several different detergent micelles and phospholipid vesicles, and the largest interfacial activation was seen with species having the PC headgroup. The KM decreased in the presence of detergents and the Vmax increased substantially. In a related study combining NMR, fluorescence, and activity measurements, it was concluded that PI-PLC binds one molecule of PC with a dissociation constant under 1 mM, as measured for diC6PC and diC7PC (Zhou et al., 1997a). In a follow-up study by the same group, the effect of short-chain lipids on the hydrolysis of I(1,2)cP was examined using a model similar to Fig. 2 B, but adapted for inhibition studies, as in Segel (1975). There is a significant phosphodiesterase activity increase around the CMC of diC6PC. Anionic short-chain phospholipids with smaller headgroups, such as phosphatidylmethanol and phosphatidic acid, can bind to both the activator site and to the active site with different affinities, producing a combination of activation and competitive inhibition, depending on the conditions (Zhou and Roberts, 1998).
The present study provides an additional important observation: There is significant activation at very low concentrations of diC6PC, suggesting activation upon binding of one molecule of phospholipid to a subsite. The activation is seen clearly in both the butyl-FLIP and methyl-FLIP kinetic data. This activation was not seen previously in studies of either the first or second reaction of PI-PLC. Most of the published studies of the first reaction did not examine this low concentration region where the activation peak occurs, and the effect may not be significant in the second reaction because the substrate, I(1,2)cP, lacks hydrophobic groups. The crystal structure has revealed several hydrophobic amino acid residues that are exposed to solvent in the area around the active site, where subsites could exist close to the active site in the C-terminal loop region of the TIM barrel. A short hydrophobic α-helix and a loop are poorly defined in the electron density map, and may be involved in a flexible lid, which undergoes a conformational change upon contact of the hydrophobic substrate PI or the fluorogenic analogs (Griffith and Ryan, 1999; Heinz et al., 1995, 1999). Another contribution of the present study is the presentation and analysis of a clear example of subsite interaction and allostery in the physiologically important phosphotransferase reaction of PI-PLC, i.e., the first reaction in Fig. 1. Technically, PI-PLC is not classified as an enzyme exhibiting cooperativity because this term is used to describe hemoglobin and multimeric enzymes that bind ligands or substrates at identical sites and are involved in the control of biological processes. The subsites of PI-PLC are not identical to the active site. However, the mathematics and modeling are similar. The kinetics of cleavage of butyl-FLIP by PI-PLC is an example of nonessential activation that coincidentally becomes a cooperative model because the substrate binds to the activator site. The activations by low concentrations of diC6PC observed with butyl-FLIP and methyl-FLIP are events that precede the interfacial activation process.
A similar phenomenon occurs in the well-known monomeric enzyme RNase A. PI-PLC shares remarkable similarity to RNase A in the two reactions that are catalyzed and the mechanisms of these reactions (Griffith and Ryan, 1999; Kravchuk et al., 2001; Ryan et al., 2001). Both enzymes utilize two catalytic histidines (His-12 and His-119 in RNase A, His-32 and His-82 in B. cereus PI-PLC) in a general acid catalysis mechanism. Analysis of the crystal structures shows that the imidazole rings of His-12 and His-119 of RNase A can be superimposed on the cognate imidazoles of His-32 and His-82 of PI-PLC, although the rest of the structures are very different (Heinz et al., 1995). Like PI-PLC, RNase A catalyzes two reactions. The first is a rapid cleavage of RNA by transphosphorylation from the 5′-hydroxyl group of one nucleotide to the 2′ position of the adjacent nucleotide, forming a 2′,3′-cyclic phosphodiester. In a second and slower hydrolysis reaction, the 2′,3′-cyclic phosphodiester ring is opened to form the corresponding 3′-nucleodide. In both RNase A and B. cereus PI-PLC, the monomeric cyclic phosphodiesters are released into the medium as products, and the subsequent hydrolysis reaction does not proceed significantly until most of the original substrate (RNA or PI) has been cleaved. RNase A binds RNA at only one active site cleft. This active site cleft is lined with cationic residues that interact with the bound nucleic acid. Both reactions of RNase A exhibit cooperativity under appropriate conditions (Irie et al., 1984; Walker et al., 1975, 1976). For example, uridine or cytidine 2′,3′-cyclic phosphate at low concentrations binds at the primary catalytic site and exhibits Michaelis-Menten kinetics. At high concentrations, these substrates bind at other subsites within the cleft, yielding complex multiphasic kinetics for which no detailed mathematical model is yet available. The cleavage rate is modulated by cooperative interactions between several of the substrate binding subsites (Moussaoui et al., 1998). PI-PLC kinetics are simpler to analyze since only one subsite and one active site account for the main effects. This makes it possible to derive analytical expressions to account quantitatively for the kinetics both in the absence and presence of activator, as discussed above.
SUMMARY
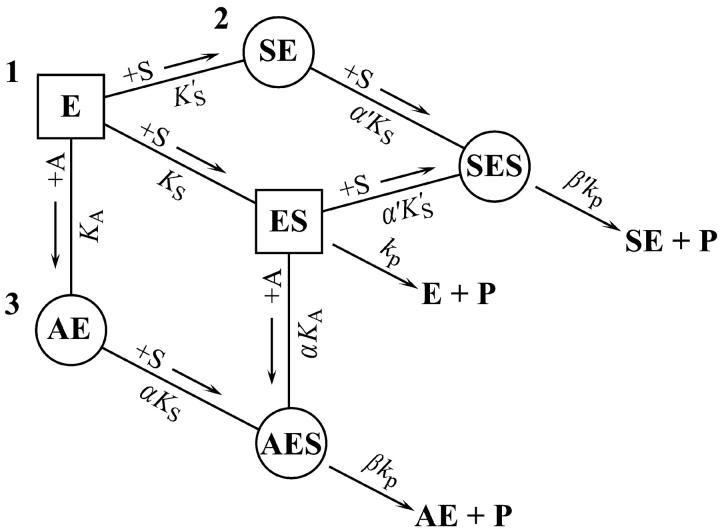
The new fluorogenic substrates have two important characteristics: 1), high sensitivity due to a high fluorescence yield combined with a comparatively low KM, and 2), monomeric solubility in water. As a result, new phenomena can be detected, and analyzed using standard kinetic methods. B. cereus PI-PLC cleaves the fluorogenic substrate butyl-FLIP, yielding sigmoidal kinetics in plots of initial rate versus substrate concentration. In the presence of the monomeric short-chain phospholipid diC6PC, the activity is increased and the curve becomes a rectangular hyperbola. A two-site model is presented, which describes the kinetics both in the absence and presence of activator (Fig. 7). The mathematical model is similar to that of textbook examples of positive cooperativity in multimeric enzymes, but the physical significance is different. Instead of arising from global allosteric transitions propagated from one site to another as is the case in regulatory enzymes of metabolic pathways, or oxygen binding to hemoglobin, local subsites are involved in phospholipases, which collectively enhance the binding and catalytic efficiency of the enzymes on membrane surfaces. The methyl-FLIP substrate does not bind to the activator site, and therefore exhibits standard Michaelis-Menten kinetics. Both butyl-FLIP and methyl-FLIP detect activation by very low concentrations of diC6PC.
FIGURE 7.
Summary of the two-site model. This model is a combination of the two schemes of Fig. 2. Three branches lead to product, P. The activator site can be occupied by diC6PC (branch 3) or by butyl-FLIP (branch 2), but not by methyl-FLIP, which does not bind significantly to the activator site under the experimental conditions. Any one branch by itself would yield a hyperbolic curve representative of simple Michaelis-Menten kinetics. Sigmoidal kinetics are observed for butyl-FLIP because the binding of S at the subsite to form SE increases the affinity of the active site for S, and the enzyme switches from ES (branch 1) to SES (branch 2) with increasing [S]. The squares and circles indicate two different conformations of residues in the active site/interfacial binding region. Abbreviations are the same as in Fig. 2.
Acknowledgments
We are indebted to Drs. Irwin H. Segel and Mahendra K. Jain for stimulating discussions. We express appreciation to our colleagues, Dr. Karen K. Hedberg and Ms. Margret Ryan, for their help and useful comments.
This work was supported by grants GM 25698 to O.H.G. and GM 27137 to J F.W.K. from the National Institute of General Medical Sciences.
References
- Berg, O. G., M. H. Gelb, M.-D. Tsai, and M. K. Jain. 2001. Interfacial enzymology: the secreted phospholipase A2-paradigm. Chem. Rev. 101:2613–2654. [DOI] [PubMed] [Google Scholar]
- Bevington, P. R., and D. K. Robinson. 1992. Data Reduction and Error Analysis for the Physical Sciences. WCB/McGraw-Hill, Boston.
- Botts, J., and M. Morales. 1953. Analytical description of the effects of modifiers and of enzyme multivalency upon the steady-state catalyzed reaction rate. Trans. Faraday Soc. 49:696–707. [Google Scholar]
- Bukowski, T., and D. C. Teller. 1986. Self-association and active enzyme forms of Naja naja naja and Crotalus atrox phospholipase A2 studied by analytical ultracentrifugation. Biochemistry. 25:8024–8033. [DOI] [PubMed] [Google Scholar]
- Cogan, E. B., G. B. Birrell, and O. H. Griffith. 1999. A robotics-based automated assay for inorganic and organic phosphates. Anal. Biochem. 271:29–35. [DOI] [PubMed] [Google Scholar]
- Cornish-Bowden, A. 1999. Fundamentals of Enzyme Kinetics. Portland Press, London.
- Cornish-Bowden, A., and M. L. Cardenas. 1987. Co-operativity in monomeric enzymes. J. Theor. Biol. 124:1–23. [DOI] [PubMed] [Google Scholar]
- Di Cera, E., K. P. Hopfner, and Q. D. Dang. 1996. Theory of allosteric effects in serine proteases. Biophys. J. 70:174–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Draper, N. R., and H. Smith. 1998. Applied Regression Analysis. Wiley-Interscience, New York.
- Griffith, O. H., and M. Ryan. 1999. Bacterial phosphatidylinositol-specific phospholipase C: structure, function, and interaction with lipids. Biochim. Biophys. Acta. 1441:237–254. [DOI] [PubMed] [Google Scholar]
- Hedberg, K. K., E. B. Cogan, G. B. Birrell, and O. H. Griffith. 2001. Sensitive fluorescent quantitation of myo-inositol 1,2-cyclic phosphate and myo-inositol 1-phosphate by high-performance thin-layer chromatography. J. Chromatogr. B Biomed. Sci. Appl. 757:317–324. [DOI] [PubMed] [Google Scholar]
- Heinz, D. W., M. Ryan, T. L. Bullock, and O. H. Griffith. 1995. Crystal structure of the phosphatidylinositol-specific phospholipase C from Bacillus cereus in complex with myo-inositol. EMBO J. 14:3855–3863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinz, D. W., J. Wehland, and O. H. Griffith. 1999. Structure and mechanism of Ca2+-independent phosphatidylinositol-specific phospholipases C. ACS Symp. Ser. 718:80–90. [Google Scholar]
- Hendrickson, H. S., E. K. Hendrickson, J. L. Johnson, T. H. Khan, and H. J. Chial. 1992. Kinetics of Bacillus cereus phosphatidylinositol-specific phospholipase C with thiophosphate and fluorescent analogs of phosphatidylinositol. Biochemistry. 31:12169–12172. [DOI] [PubMed] [Google Scholar]
- Irie, M., F. Mikami, K. Monma, K. Ohgi, H. Watanabe, R. Yamaguchi, and H. Nagase. 1984. Kinetic studies on the cleavage of oligouridylic acids and poly U by bovine pancreatic ribonuclease A. J. Biochem. (Tokyo). 96:89–96. [DOI] [PubMed] [Google Scholar]
- Kelemen, B. R., and R. T. Raines. 1999. Extending the limits to enzymatic catalysis: diffusion of ribonuclease A in one dimension. Biochemistry. 38:5302–5307. [DOI] [PubMed] [Google Scholar]
- Kravchuk, A. V., L. Zhao, R. J. Kubiak, K. S. Bruzik, and M.-D. Tsai. 2001. Mechanism of phosphatidylinositol-specific phospholipase C: origin of unusually high nonbridging thio effects. Biochemistry. 40:5433–5439. [DOI] [PubMed] [Google Scholar]
- Leigh, A. J., J. J. Volwerk, O. H. Griffith, and J. F. Keana. 1992. Substrate stereospecificity of phosphatidylinositol-specific phospholipase C from Bacillus cereus examined using the resolved enantiomers of synthetic myo-inositol 1-(4-nitrophenyl phosphate). Biochemistry. 31:8978–8983. [DOI] [PubMed] [Google Scholar]
- Lewis, K. A., V. R. Garigapati, C. Zhou, and M. F. Roberts. 1993. Substrate requirements of bacterial phosphatidylinositol-specific phospholipase C. Biochemistry. 32:8836–8841. [DOI] [PubMed] [Google Scholar]
- Low, M. G. 1989. The glycosyl-phosphatidylinositol anchor of membrane proteins. Biochim. Biophys. Acta. 988:427–454. [DOI] [PubMed] [Google Scholar]
- Moussaoui, M., M. V. Nogués, A. Guasch, T. Barman, F. Travers, and C. M. Cuchillo. 1998. The subsites structure of bovine pancreatic ribonuclease A accounts for the abnormal kinetic behavior with cytidine 2′,3′-cyclic phosphate. J. Biol. Chem. 273:25565–25572. [DOI] [PubMed] [Google Scholar]
- Neet, K. E. 1995. Cooperativity in enzyme function: equilibrium and kinetic aspects. Methods Enzymol. 249:519–567. [DOI] [PubMed] [Google Scholar]
- Rebecchi, M. J., R. Eberhardt, T. Delaney, S. Ali, and R. Bittman. 1993. Hydrolysis of short acyl chain inositol lipids by phospholipase C-δ1. J. Biol. Chem. 268:1735–1741. [PubMed] [Google Scholar]
- Rhee, S. G. 2001. Regulation of phosphoinositide-specific phospholipase C. Annu. Rev. Biochem. 70:281–312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers, J., B. Z. Yu, S. V. Serves, G. M. Tsivgoulis, D. N. Sotiropoulos, P. V. Ioannou, and M. K. Jain. 1996. Kinetic basis for the substrate specificity during hydrolysis of phospholipids by secreted phospholipase A2. Biochemistry. 35:9375–9384. [DOI] [PubMed] [Google Scholar]
- Ryan, M., T. Liu, F. W. Dahlquist, and O. H. Griffith. 2001. A catalytic diad involved in substrate-assisted catalysis: NMR study of hydrogen bonding and dynamics at the active site of phosphatidylinositol-specific phospholipase C. Biochemistry. 40:9743–9750. [DOI] [PubMed] [Google Scholar]
- Ryan, M., M. P. Smith, T. K. Vinod, W. L. Lau, J. F. W. Keana, and O. H. Griffith. 1996. Synthesis, structure activity relationships, and the effect of polyethylene glycol on inhibitors of phosphatidylinositol-specific phospholipase C from Bacillus cereus. J. Med. Chem. 39:4366–4376. [DOI] [PubMed] [Google Scholar]
- Segel, I. H. 1975. Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems. John Wiley & Sons, New York.
- Shashidhar, M. S., J. J. Volwerk, O. H. Griffith, and J. F. Keana. 1991. A chromogenic substrate for phosphatidylinositol-specific phospholipase C: 4-nitrophenyl myo-inositol-1-phosphate. Chem. Phys. Lipids. 60:101–110. [DOI] [PubMed] [Google Scholar]
- Tausk, R. J. M., J. Karmiggelt, C. Oudshoorn, and J. T. G. Overbeek. 1974. Physical chemical studies of short-chain lecithin homologues. I. Influence of the chain length of the fatty acid ester and of electrolytes on the critical micelle concentration. Biophys. Chem. 1:175–183. [DOI] [PubMed] [Google Scholar]
- Volwerk, J. J., E. Filthuth, O. H. Griffith, and M. K. Jain. 1994. Phosphatidylinositol-specific phospholipase C from Bacillus cereus at the lipid-water interface: interfacial binding, catalysis, and activation. Biochemistry. 33:3464–3474. [DOI] [PubMed] [Google Scholar]
- Walker, E. J., G. B. Ralston, and I. G. Darvey. 1975. An allosteric model for ribonuclease. Biochem. J. 147:425–433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker, E. J., G. B. Ralston, and I. G. Darvey. 1976. Further evidence for an allosteric model for ribonuclease. Biochem. J. 153:329–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaikova, T. O., A. V. Rukavishnikov, G. B. Birrell, O. H. Griffith, and J. F. Keana. 2001. Synthesis of fluorogenic substrates for continuous assay of phosphatidylinositol-specific phospholipase C. Bioconjug. Chem. 12:307–313. [DOI] [PubMed] [Google Scholar]
- Zhou, C., D. Horstman, G. Carpenter, and M. F. Roberts. 1999. Action of phosphatidylinositol-specific phospholipase Cγ1 on soluble and micellar substrates. Separating effects on catalysis from modulation of the surface. J. Biol. Chem. 274:2786–2793. [DOI] [PubMed] [Google Scholar]
- Zhou, C., X. Qian, and M. F. Roberts. 1997a. Allosteric activation of phosphatidylinositol-specific phospholipase C: specific phospholipid binding anchors the enzyme to the interface. Biochemistry. 36:10089–10097. [DOI] [PubMed] [Google Scholar]
- Zhou, C., Y. Wu, and M. F. Roberts. 1997b. Activation of phosphatidylinositol-specific phospholipase C toward inositol 1,2-(cyclic)-phosphate. Biochemistry. 36:347–355. [DOI] [PubMed] [Google Scholar]
- Zhou, C., and M. F. Roberts. 1998. Nonessential activation and competitive inhibition of bacterial phosphatidylinositol-specific phospholipase C by short-chain phospholipids and analogues. Biochemistry. 37:16430–16439. [DOI] [PubMed] [Google Scholar]