Heterogeneity of ADP Diffusion and Regulation of Respiration in Cardiac Cells

Abstract

Heterogeneity of ADP diffusion and regulation of respiration were studied in permeabilized cardiomyocytes and cardiac fibers in situ and in silico. Regular arrangement of mitochondria in cells was altered by short-time treatment with trypsin and visualized by confocal microscopy. Manipulation of matrix volumes by changing K⁺ and sucrose concentrations did not affect the affinity for ADP either in isolated heart mitochondria or in skinned fibers. Pyruvate kinase (PK)-phosphoenolpyruvate (PEP) were used to trap ADP generated in Ca,MgATPase reactions. Inhibition of respiration by PK-PEP increased 2–3 times after disorganization of regular mitochondrial arrangement in cells. ADP produced locally in the mitochondrial creatine kinase reaction was not accessible to PK-PEP in intact permeabilized fibers, but some part of it was released from mitochondria after short proteolysis due to increased permeability of outer mitochondrial membrane. In in silico studies we show by mathematical modeling that these results can be explained by heterogeneity of ADP diffusion due to its restrictions at the outer mitochondrial membrane and in close areas, which is changed after proteolysis. Localized restrictions and heterogeneity of ADP diffusion demonstrate the importance of mitochondrial functional complexes with sarcoplasmic reticulum and myofibrillar structures and creatine kinase in regulation of oxidative phosphorylation.

INTRODUCTION

While the mechanisms and regulation of respiration and ATP production in mitochondrial oxidative phosphorylation in isolated mitochondria in vitro are elucidated to high degree of perfection (Nicholls and Ferguson, 2002), cellular mechanisms of regulation of these processes in vivo are still matters of discussion. In the oxidative muscle cells, in particular in the heart, two theories are usually considered: 1), parallel activation of contraction and mitochondrial dehydrogenases and ATP synthase by calcium ions (McCormack et al., 1990; Korzeniewski, 1998; Territo et al., 2000; Balaban, 2002); and 2), feedback regulation by channeling of metabolites, in particular ADP, AMP, and creatine via organized phosphotransfer networks (Bessman and Geiger, 1981; Walliman et al., 1992; Saks et al., 1998a; Dzeja et al., 1998; Garlid, 2001). However, the delivery of phosphate acceptors ADP and creatine from myofibrils and subcellular membranes into mitochondria is also necessary in case of “parallel activation” (Garlid, 2001; Saks et al., 1998a), due to the respiratory control phenomenon (Chance and Williams, 1956). The parallel-activation hypothesis apparently assumes a priori that this phosphate acceptor diffusion is very rapid and does not participate in the control of respiration. This assumption is still not verified.

On the other hand, several groups have very recently described close functional and structural interconnections among mitochondria, myofibrils, and sarcoplasmic reticulum (Seppet et al., 2001; Saks et al., 2001; Kaasik et al., 2001; Nozaki et al., 2001). Structural organization of mitochondria into functional complexes with myofibrils and sarcoplasmic reticulum (intracellular energetic units; ICEUs) may be a basic pattern of organization of energy metabolism in the oxidative muscle cells (Saks et al., 2001) and may lead to heterogeneity of ADP diffusion in the cells.

The purpose of this work was to study further the metabolic consequences of organization of mitochondria into these functional complexes and their role in regulation of respiration in the cells in vivo. Confocal microscopy was used to visualize the alterations of regular arrangement of mitochondria in the cells by rather selective short-time proteolysis with trypsin. Channeling of endogenous ADP to mitochondria within these complexes was studied by use of the competitive enzyme system—pyruvate kinase-phosphoenolpyruvate (Gellerich and Saks, 1982). This method allowed also to investigate the channeling and movement of ADP produced in the mitochondrial intermembrane space, to study the importance of mitochondrial creatine kinase and outer membrane permeability for regulation of respiration. These data were used as a basis for in silico studies of heterogeneity of ADP diffusion by the reaction-diffusion mathematical modeling of compartmentalized energy transfer (Aliev and Saks, 1997; Vendelin et al., 2000). Also, the role of mitochondrial matrix volume changes in regulation of the mitochondrial affinity for exogenous ADP was studied by changing the osmolarity and composition of solutions. The results showed that the experimental data obtained in this and earlier studies can be explained by heterogeneity of diffusion of phosphorus metabolites discovered by Kinsey and de Graaf (Kinsey et al., 1999; de Graaf et al., 2000). In heart cells this heterogeneity may be the result of local restrictions of ADP permeability through the outer mitochondrial membrane and close areas inside the functional complexes. The fitting of the results of calculations with experimental data showed that apparent diffusion coefficient for ADP may be locally decreased by more than order of magnitude.

MATERIALS AND METHODS

Animals

Male Wistar rats (300–350 g) were used in all experiments. The investigation conforms with the Guide for the Care and Use of Laboratory Animals published by the National Institutes of Health (NIH Publication No. 85-23, revised 1985).

Isolation of mitochondria from cardiac muscle

Mitochondria were isolated from rat heart as described previously (Saks et al., 1975).

Isolation and culturing of adult cardiac myocytes

Calcium-tolerant myocytes were isolated by perfusion of rat hearts with a collagenase-containing medium as described earlier by Kay and co-workers (Kay et al., 1997).

Preparation of skinned muscle fibers

Skinned (permeabilized) fibers were prepared from rat cardiac muscle according to the method described (Saks et al., 1998b).

Determination of the rate of mitochondrial respiration in skinned fibers and cardiomyocytes

The rates of oxygen uptake were recorded by using two-channel high resolution respirometer (Oroboros Oxygraph, Paar KG, Graz, Austria) or a Yellow Spring Instruments Oxygraph (Yellow Spring, OH, USA) in solution B (measurement of ADP kinetics of respiration) or using KCl solution for cytochrome-c test (for composition see below), additionally containing respiratory substrates and 2–5 mg/ml of bovine serum albumin. Some experiments with isolated mitochondria were performed in the sucrose medium. Determinations were carried out at 25°C, and solubility of oxygen was taken as 215 nmol per ml (Kuznetsov et al., 1996).

Fluorimetric determination of membrane potential in isolated heart mitochondria and swelling of mitochondrial matrix

Rhodamine (Rh) 123 fluorescence was recorded at 503 nm (excitation) to 530 nm (emission) in Photon Technology International Fluorescence Imaging System (South Brunswick, NJ, USA). The fluorescence intensity of Rh 123 (0.25 μM) in 2 ml of gently stirred solution B at 25°C was recorded, then isolated rat heart mitochondria were added to a final concentration of 0.1 mg/ml. The Rh 123 uptake in response to addition of mitochondria in the presence of substrates (glutamate/malate) shows the generation of a transmembrane gradient of potential (Δψ). The addition of an uncoupling agent, FCCP (0.1 μM), completely depolarized the membrane due to collapse of Δψ and resulted in the release of the Rh 123 out of the mitochondria and return to initial level of fluorescence. To test the stability of the system, the fluorescence of the Rh 123 in presence of energized mitochondria was recorded for more than 1 h.

The same system was used to record the changes in the intensity of scattered light to observe the alterations in the intramitochondrial volumes (matrix volume and the volume of intermembrane space). For this, both the excitation and emission wavelength were set at 520 nm. Addition of mitochondrial suspension (isolated in sucrose solution) into solution B containing respiratory substrates (glutamate/malate) resulted in rapid increase of the recorded signal, followed by rather slow decrease of signal due to the mitochondrial matrix swelling caused by the entry of K⁺ (Kowaltowski et al., 2001).

Confocal microscopy

Two independent methods were used to visualize the mitochondrial position in the permeabilized cells and skinned muscle fibers.

Imaging of mitochondria by MitoTraker Green FM

MitoTraker Green FM (Molecular Probes, Leiden, The Netherlands) is a frequently used a fluorescent probe in mitochondrial imaging (Bowser et al., 1998; Lemasters et al., 1998). Permeabilized cardiomyocytes or skinned fibers were incubated with 100 nM of MitoTraker Green FM in solution B with 2% of bovine serum albumin for 45 min at 4°C without exogenous substrates. Then, fibers or cells were washed with solution B, fixed with 4% paraformaldehyde for 10 min at room temperature and washed in a phosphate saline containing in mM: NaCl 56, KH₂PO₄ 1.5, KCl 2.7, and Na₂HPO₄ 8, and three times with water. The loaded preparations were placed on the glass coverslips and mounted in a mixture of mowiol and glycerol to which 1,4-diazabicyclo-[2,2,2]-octane (ACROS Organics, Pittsburgh, PA, USA) was added to stabilize samples against photobleaching. Samples were observed (excitation at 490 nm, emission at 516 nm) by confocal microscopy performed with a LSM510 NLO Zeiss. The confocal system was equipped with a 40× oil immersion objective lens (NA 1.4).

Imaging of autofluorescence of mitochondrial flavoproteins

Flavoproteins were imaged using a confocal microscope (LSM510 NLO, Zeiss, Jena, Germany) with a 40× water immersion lens (NA 1.2). The use of such a water immersion prevented from geometrical aberrations. The autofluorescence of flavoproteins was excited with the 488 nm line of an Argon laser, the laser output power was set to an average of 8 mW. The fluorescence was collected through a 510-nm dichroic beamsplitter and a 505–550 nm bandpass filter. The pinhole aperture was set to one Airy disk unit.

Determination of the pyruvate kinase activity

The activity of pyruvate kinase (PK) in stock solutions was assessed by a coupled lactate dehydrogenase system. The decrease in the NADH level was determined spectrophotometrically in Uvikon 941 Plus (Kontron Instruments, Herts, UK) in solution B supplemented with 0.3 mM NADH, 1 mM phosphoenolpyruvate (PEP), 2 mM ADP and 4-5 IU/ml of lactate dehydrogenase in response to addition of different amounts of PK at 25°C.

Determination of protein concentration

Protein concentration in mitochondrial preparations was determined by the ELISA method using the EL ×800 Universal Microplate Reader (Bio-Tek Instruments, Winooski, VT, USA) with a BCA kit (Protein Assay Reagent, Pierce, Rockford, IL, USA).

Solutions

Composition of the solutions used for preparation of skinned fibers and in respirometry was based on the information of the ionic composition of muscle cell cytoplasm (Godt and Maughan, 1988).

Solution A

Contained, in mM: CaK₂EGTA 1.9, K₂EGTA 8.1 (free calcium concentration 0.1 μM), MgCl₂ 9.5, dithiothreitol (DTT) 0.5, potassium 2-(N-morpholino)-ethanesulfonate (K-MES) 50, imidazole 20, taurine 20, Na₂ATP 2.5, and phosphocreatine 15, pH 7.1 adjusted at 25°C.

Solution B

Contained, in mM: CaK₂EGTA 1.9, K₂EGTA 8.1, MgCl₂ 4.0, DTT 0.5, K-MES 100, imidazole 20, taurine 20, and K₂HPO₄ 3, pH 7.1 adjusted at 25°C. For respiration rate determinations, pyruvate 5 (or glutamate 5) and malate 2 were added as substrates.

Sucrose solution for respirometry

Contained, in mM: sucrose 240, EGTA 1, HEPES 50, and KH₂PO₄ 3, pH 7.2; bovine serum albumin 2 mg/ml, glutamate 5 mM, and malate 2 mM.

KCl solution for cytochrome-c test

Contained, in mM: KCl 125, HEPES 20, glutamate 4, malate 2, Mg-acetate 3, KH₂PO₄ 5, EGTA 0.4, and DTT 0.3, pH 7.1 adjusted at 25°C and 2 mg/ml of bovine serum albumin was added.

Reagents

All reagents were purchased from Sigma (St. Louis, MO, USA) except ATP and ADP, which were obtained from Boehringer (Mannheim, Germany).

Analysis of the experimental results

The values in figures are expressed as mean ± SD. The apparent K_m for ADP was estimated from a linear regression of double-reciprocal plots. Statistical comparisons were made using the ANOVA test (variance analysis and Fisher test), and P < 0.05 was taken as the level of significance.

MATHEMATICAL MODELING OF COMPARTMENTALIZED ENERGY CROSSTALK

Model description

In this article, we used a modified version of our original mathematical model of compartmentalized energy transfer (Aliev and Saks, 1997; Vendelin et al., 2000). The spatially inhomogenous reaction-diffusion model of energy transfer considers the reactions in three main compartments of cardiac cells (Fig. 1): the myofibril together with the myoplasm, the mitochondrial intermembrane (IM) space, and the mitochondrial inner membrane-matrix space. This corresponds to the main components of the ICEUs (Saks et al., 2001). The metabolites described by the model in the myofibrils and IM space are ATP, ADP, AMP, phosphocreatine (PCr), creatine (Cr), and Pi. All these metabolites diffuse between the cytosolic and IM compartments, where the metabolites are involved in the creatine kinase (CK) and adenylate kinase (AK) reactions. In addition, the ATP is hydrolyzed in the myofibrils. In the IM space, the mitochondrial CK reaction is coupled to the adenine nucleotide translocase (ANT); the coupling is moderated by a diffusional leak of the intermediates. The metabolites described by the model in the matrix compartment and in the inner membrane are NADH, coenzyme-Q, cytochrome-c, protons, ATP, ADP, and Pi. Three coupled reactions representing the production of proton-motive force by complexes I, III, and IV are included in the model, as originally described (Korzeniewski, 1998). Proton-motive force is consumed by ATP synthase and membrane leak. The ANT rate is considered to depend on membrane potential. Pi is transported by a phosphate carrier. The description of respiratory chain processes was adapted from a model by Korzeniewski (Korzeniewski, 1998; Vendelin et al., 2000). Modified version of this model is described in details in Appendix.

FIGURE 1.

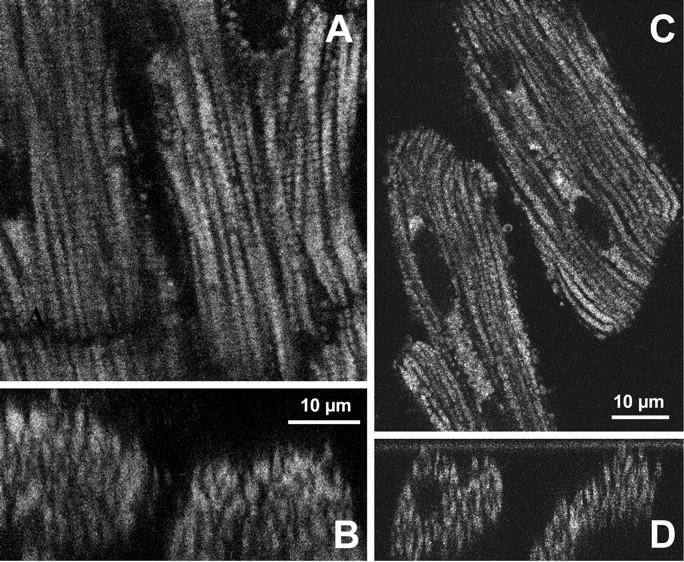
(A) Confocal image of mitochondrial flavoproteins autofluorescence in skinned cardiac fibers. Note the very regular intracellular arrangement of mitochondria between myofibrils. The diffusion distance from medium to core of cells is ∼10 μm, and apparent K_m for exogenous ADP is 250–350 μM (see the text). (B) Corresponding cross section showing the distribution of mitochondria in Z-plan of the permeabilized fibers from control rat heart. A decline in signal intensity visible as a function of fiber depth is a consequence of the laser light absorption and scattering by the tissue, and is not due to the heterogeneity of oxidized state. Notice good separation of the fibers from each other. (C) Confocal image of mitochondrial flavoproteins autofluorescence in permeabilized isolated cardiac cells. Note very regular intracellular arrangement of mitochondria between myofibrils. The diffusion distance from medium to core of cells is 5–10 μm, and apparent K_m for exogenous ADP is 200–300 μM (Kummel, 1988; Kay et al., 1997). (D) Corresponding cross section showing the distribution of mitochondria in Z-plan of the permeabilized cardiac cells from control rat heart.

In the model, the apparent diffusion coefficient of a metabolite in the myofibrillar and cytoplasmic compartments, D^app = DF × D₀ (where DF is a diffusion coefficient factor and D₀ is a diffusion coefficient in the bulk water phase in cytoplasm; see Appendix), was varied by giving different values to DF. DF smaller than 1 is due to restrictions of the diffusion on the way from solution into the vicinity of mitochondria (into the functional complexes of mitochondria with sarcoplasmic reticulum and myofibrillar MgATPase). For each DF we calculated permeability factor PF of the outer mitochondrial membrane for the metabolite—a fraction of permeability coefficient for passive diffusion across the outer mitochondrial membrane. Thus, changes of apparent diffusion coefficients and apparent permeability of the outer mitochondrial membrane for all metabolites are described by two parameters—DF and PF. In the case of the trypsin-treated fiber, the only parameter that was changed in the model was PF, since DF was taken to be equal to two making the diffusion coefficients of the metabolites equal to the diffusion coefficients in the water (exceeding that in cell bulk water by a factor of 2; de Graaf et al., 2000) due to almost complete disorganization of cell structure (see below).

The detailed description of the version of the model used is given in the Appendix.

Protocol of the simulations

We simulated the two series of experiments: 1), rate of oxygen consumption by skinned cardiac fibers as a function of ATP and ADP concentrations in solutions; and 2), inhibition of mitochondrial respiration rate by the competitive ADP-consuming PK-PEP system in skinned fibers before and after trypsin treatment.

The following parameters in the model were unknown or presented with the range of values: 1), apparent diffusion coefficient in the myofibrillar and cytoplasmic compartment; 2), permeability of mitochondrial outer membrane to ATP and ADP; and 3), apparent K_m for ATP of ATPases (the nature of the ATPases as a source of endogenous ADP was not precisely identified).

The following procedure was used to determine the influence of the parameters on the solution and to estimate the range of parameter values corresponding to the measured data. 1), apparent K_m(ATP) for MgATPase were given fixed values of 100 and 300 μM, and DF was varied from 0.007 to 1. 2), for each DF value, PF was determined by fitting model solution with the measured respiration rate-ATP and ADP relationship. 3), Degree of inhibition of respiration rate by PK-PEP system at different PK activities was computed for the entire scale of DF and PF values found from the previous step. The range of DF values was determined from the comparison of computed and measured inhibition of respiration by PK.

The fitting of the respiration rate ATP and ADP relationship was performed by minimizing the following sum of squared normalized errors,

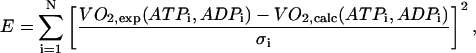(1)

where summation was performed over all combinations of the metabolite concentrations ATP_i and ADP_i used in the measurements; VO_2,exp and VO_2,calc is the measured and computed respiration rate; and σ_i is the SD of the measured respiration rate. The average error ɛ was computed from E, using

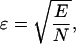(2)

where N is the number of experimental points used during the fitting.

Numerical methods

The model equations were numerically solved by a finite-element method in conjunction with Galerkin's method. The resulting system of ordinary differential equations was solved by the backward differentiation formula that is able to treat stiff equations. The accuracy of the solution was tested by comparing different spatial discretizations and varying the tolerance of the ordinary differential equation solver. The finite-element discretization was performed using the software package Diffpack (Bruaset and Langtagen, 1997) and the system was integrated using the DVODE package (Brown et al., 1989). The finite-element mesh was generated using software package GEOMPACK (Joe, 1991). The required optimization was performed using the Levenberg-Marquardt algorithm (Moré et al., 1984).

RESULTS

On the possible role of matrix volume changes in regulation of apparent affinity of mitochondria in situ for exogenous ADP

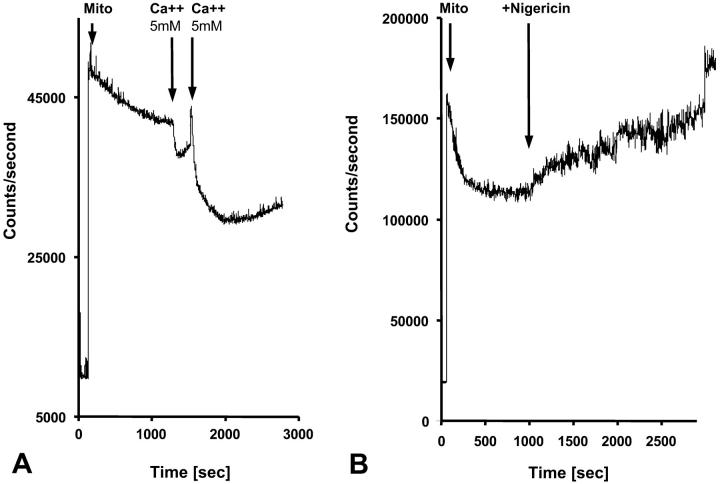
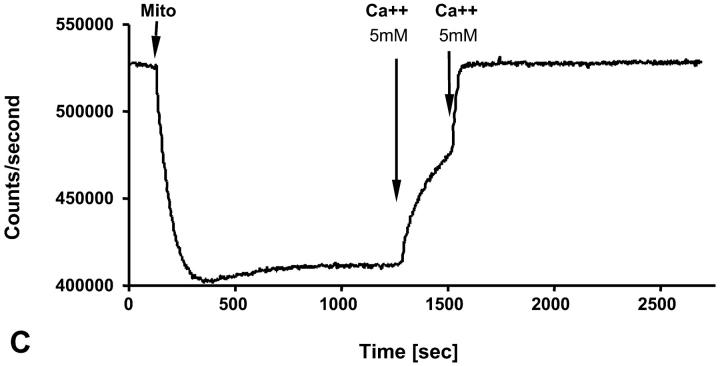
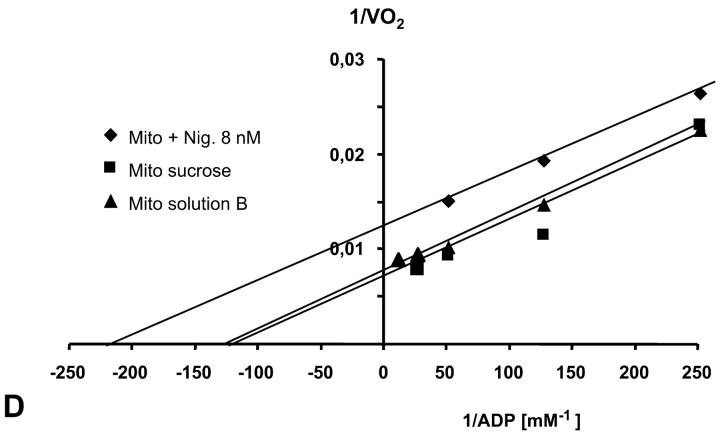
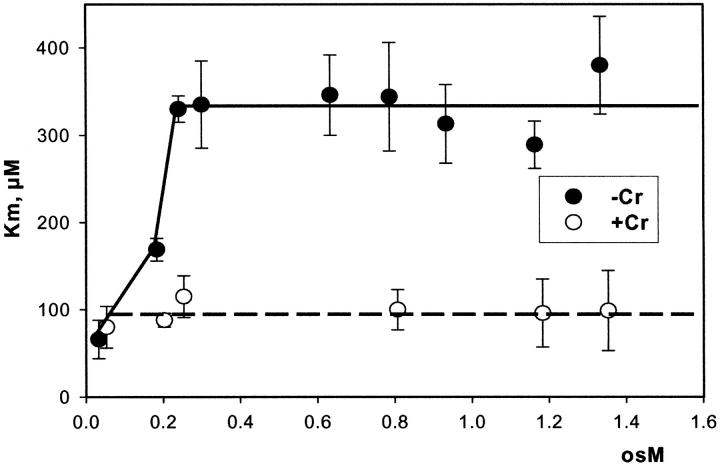
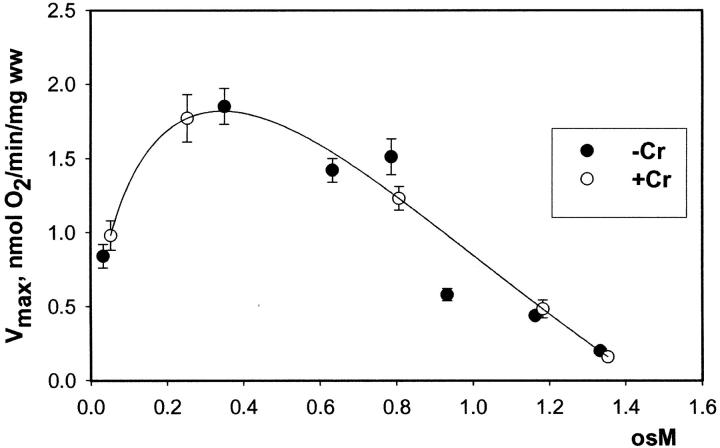
It has recently been proposed that mitochondrial functional characteristics, in particular their apparent affinity for exogenous ADP might be influenced by changes in the volumes of mitochondrial matrix and intermembrane space (Dos Santos et al., 2002). According to this hypothesis, the increase of the matrix volume, and correspondingly the decrease of the intermembrane space volume, may create the diffusion restrictions for ADP because of its complex architecture (Dos Santos et al., 2002), and in this way increase the apparent K_m for ADP. To check the possible contribution of these volume changes in an elevated apparent K_m for ADP in the cells, we studied the regulation of respiration by ADP in both isolated mitochondria and skinned fibers, in solutions with different osmolarity and K⁺ concentration. Isolated heart mitochondria were incubated in the sucrose medium without K⁺, and in solution B with 126 mM K⁺. Fig. 2 A shows changes of the light scattering by isolated mitochondrial suspension during transition from a sucrose solution into high K⁺ solution. The decrease of the intensity of scattered light shows that the matrix volume increases significantly because of K⁺ entry via potassium channel, which becomes open in the absence of ATP (Kowaltowski et al., 2001). Reversal of K⁺ uptake by nigericine (Nicholls and Ferguson, 2002) diminished the swelling of mitochondrial matrix (Fig. 2 B). Fig. 2 shows the changes of intensity of Rh 123 fluorescence in solution into which isolated mitochondria were added. Oxidative substrates generated normal membrane potential in solution B (Fig. 2 C). To find out the extreme possible swelling of the mitochondrial matrix, Ca²⁺ was added in high concentration for opening of the permeability transition pore (Fig. 2 A) which resulted also in collapse of membrane potential (Fig. 2 C). However, the matrix volume changes during transition from sucrose to solution B (swelling of the matrix without rupture of the membranes) had no influence on the value of the apparent K_m (ADP), which remained always very low, in the range of 5–10 μM (Fig. 2 D). Fig. 3, left, shows that the high apparent K_m for exogenous ADP in permeabilized cardiac fibers was not changed by increasing osmolarity of the solution from isoosmotic (0.24 osM) up to highly hyperosmotic conditions (1.3 osM) by addition of sucrose, which induces significant contraction of sucrose impermeable matrix space and an increase in intermembrane space volume (Devin et al., 1998; Saad-Nehme et al., 2001). The only result is a decrease of V_max of respiration, but there are no changes in the apparent K_m for ADP (Fig. 3, left and right). Dos Santos and co-workers demonstrated also that in the presence of polyethylene glycol, a slight decrease in the osmolarity of medium increased the apparent K_m for exogenous ADP, but that further significant decrease of osmolarity resulted in the rupture of outer mitochondrial membrane and strong decrease in apparent K_m value for exogenous ADP in isolated mitochondria in vitro (Dos Santos et al., 2002). These findings agree with our earlier data that the high experimental values of apparent K_m for ADP are related to the controlled permeability of the outer mitochondrial membrane for adenine nucleotides (Saks et al., 1995). This conclusion is also in accord with the results shown in Fig. 3, left: in hypoosmotic solutions (<0.24 osM) the apparent K_m for exogenous ADP in permeabilized fibers decreases rapidly.

FIGURE 2.

Recording of changes in matrix volumes by light scattering of isolated rat heart mitochondria during transitions to solution with respiratory substrates. Effects of nigericin and calcium. Isolated mitochondria were added into the fluorimetric chamber in the presence of substrates. (A) Mitochondria isolated in a sucrose medium (250 mM) without respiratory substrates (see Materials and Methods) were added into solution B with glutamate and malate as respiratory substrates and with K⁺, whose entry by K⁺-channel (open in absence of ATP) induces swelling, which is observed as a decrease of the intensity of reflected light. Addition of Ca²⁺ (5 mM, 2 times) induced maximal mitochondrial swelling due to opening of the permeability transition pore, which is seen as a decrease of optical density at 520–520 nm. (B) The same as A, in solution B addition of nigericin (in absence of bovine serum albumin to avoid binding of nigericin) resulted in some contraction of matrix of mitochondria due to K⁺–H⁺ exchange (Nicholls and Ferguson, 2002). (C) Isolated mitochondria were introduced into the spectrofluorimeter chamber with solution B with glutamate and malate as substrates, and the Rh 123 fluorescence was recorded as described in Materials and Methods. Normal membrane potential was seen in solution B. Two successive additions of 5 mM Ca²⁺ led to a complete depolarization of the mitochondrial membrane, accompanied with the complete collapse of membrane potential and release of Rh 123 from mitochondrial matrix into the medium. (D) The dependence of respiration rate upon the ADP concentration in Lineweaver-Burk plots in sucrose solution and solution B without and with nigericin. Both in sucrose solution and solution B the apparent K_m for ADP was equal to 8 μM. Nigericin induced the parallel shift of a straight line, giving both lower K_m and V_m.

FIGURE 3.

The effects of changes in osmolarity on the kinetic parameters of regulation of mitochondrial respiration in permeabilized cardiac fibers by exogenous ADP. The measurements were made in solution B into which sucrose was added to achieve the osmolarity indicated. Creatine, if present, was used in 20 mM concentration. (Left) Changes in apparent K_m for exogenous ADP. (Right) Changes in V_max.

Thus, in some experimental conditions, permeability of the outer mitochondrial membrane for adenine nucleotides may be influenced by changes in intramitochondrial volumes (Dos Santos et al., 2002). However, the affinity of in situ mitochondria (permeabilized cells) for exogenous ADP in isoosmotic or slightly hyperosmotic solution B is low (apparent K_m is high) due to interaction of mitochondria with other cellular structures, but clearly, this is not due to increased mitochondrial matrix volume.

Changes of the control of respiration rate by creatine and endogenous ADP during disorganization of the ICEU structure

The complex structural organization of the cardiac cells, the regular mitochondrial arrangement in the oxidative muscle cells into ICEUs and the control of mitochondrial outer membrane permeability for ADP by some cytoskeletal proteins (Saks et al., 2001; Seppet et al., 2001) may cause local, region-specific restrictions for ADP diffusion, and prevent exogenous ADP from diffusing into and endogenous ADP from diffusing out of the space inside of ICEU. To quantitatively evaluate these restrictions as well as the role of both mitochondrial outer membrane and creatine kinase (MiCK) in regulation of respiration in this highly organized system, we applied a competitive enzyme method, using pyruvate kinase with PEP to trap the endogenously regenerated ADP (Gellerich and Saks, 1982). This method allows also to follow the route of ADP, produced in the mitochondrial intermembrane space by mitochondrial creatine kinase, MiCK—whether all this locally produced ADP is transported by ANT into matrix for rephosphorylation, or if some part of it may leak out into medium via the VDAC channel through the outer mitochondrial membrane where it will be consumed by the PK-PEP system. In the latter case, the ADP-dependent respiration rate should decrease. In this way, we can evaluate the state of the mitochondrial outer membrane and changes in its permeability for ADP.

These experiments were carried out before and after disorganization of the ICEU structure by selective proteolysis and the experimental results were analyzed with use of the quantitative mathematical model of the compartmentalized energy transfer.

Fig. 4, A and B show that practically complete disorganization of regular mitochondrial arrangement in the cells can be achieved by 5 min treatment of fibers with 1 μM trypsin. This figure shows confocal images of mitochondria visualized by MitoTraker Green and progressive changes in their position within myocardial fibers after short-time proteolytic treatment. In the control fibers, the mitochondrial arrangement was very regular, with a characteristic striated pattern (Fig. 4 A) due to their localization at the center of sarcomeres, in good agreement with numerous earlier data (Kay et al., 1997; Bowser et al., 1998; Duchen, 1999; Saks et al., 2001; Boudina et al., 2002). Already after 5 min of treatment with trypsin in a low concentration of 1 μM, one can clearly see the destruction of these regular structures (Fig. 4 B). This confirms our earlier observations made by using the electron microscopy (Saks et al., 2001). Oxygraphic measurements have shown that neither the intactness of the mitochondrial outer membrane as measured by cytochrome-c test nor the maximal capacities of respiration per wet weight were changed by trypsin treatment, and this treatment did not change the respiratory properties of the isolated heart mitochondria (Kuznetsov et al. 1996).

FIGURE 4.

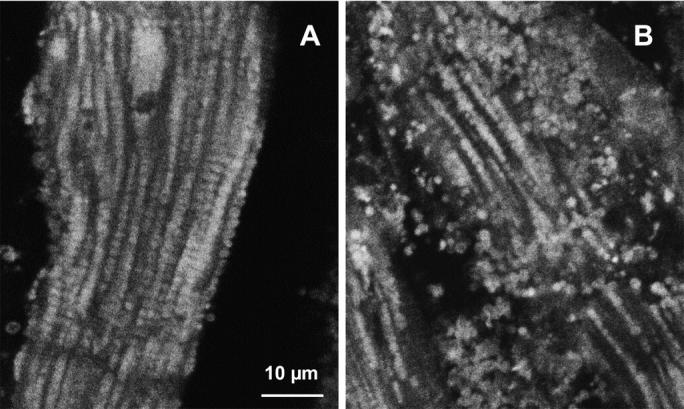
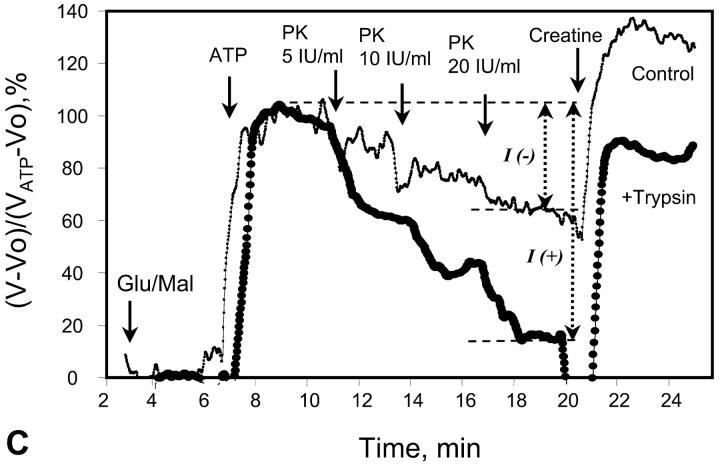
Alterations of regular arrangement of mitochondria and of regulation of respiration in permeabilized cardiac fibers by trypsin treatment. (A and B) Confocal imaging of mitochondria using MitoTraker Green FM fluorescence. Permeabilized cells were preloaded with MitoTraker Green FM and fixed as described in Methods section. (A) Control fibers; and (B) after incubation with 1 μM of trypsin for 5 min at 4°C. (C) Representative oxygen consumption traces showing changes of metabolic channeling of endogenous ADP from Ca,MgATPases to mitochondria. For visualization of metabolic channeling, PK-PEP competitive enzyme method was used before and after treatment of permeabilized cardiac fibers with trypsin, leading to the disorganization of regular arrangement of mitochondria: the t-test. (The first derivative of oxygraph recordings of oxygen consumption are shown, directly showing the values of respiration rate.) ATP was added to the final concentration of 2 mM. (Thin line, control fibers. Thick line, fibers treated with 5 μM of trypsin for 15 min at 4°C.) I(−) and I(+) indicate inhibition of mitochondrial respiration by the competing PK-PEP system without (−) and with (+) trypsin treatment. At the end of each experiment, creatine (20 mM) was added.

The effects of PK + PEP on mitochondrial respiration in permeabilized fibers activated by endogenous ADP in the presence of 2 mM MgATP were studied before and after treatment with 1 μM trypsin described above. The degree of inhibition of mitochondrial respiration indicates the ADP flux taken away from mitochondria by the competing, ADP-consuming pyruvate kinase system. In the case of direct channeling of endogenous ADP from ATPases to mitochondria, this inhibition is expected to be rather small due to the effect of microcompartmentation and limited accessibility of endogenous ADP to the PK-PEP system. Fig. 4 C shows the results of one representative experiment. In intact fibers, the increase of pyruvate kinase activity to 20 IU/ml decreased the rate of oxygen consumption to not more than 30–40% (Fig. 4 C). Activation of creatine kinase reaction by creatine (20 mM) in the presence of MgATP significantly increased the respiration rate up to 120–130% of the initial value, which is close to the maximal State 3 respiration rate (Fig. 4 C). Remarkably, this effect was seen despite the presence of the high activity of the exogenous ADP-consuming system, PK + PEP. This result is explained by local production of ADP in the intermembrane space by the mitochondrial creatine kinase (MiCK) reaction functionally coupled to the adenine nucleotide translocase (Saks et al., 1995; Walliman et al., 1992; Kay et al., 2000). Clearly, this compartmentalized ADP is almost totally inaccessible for the exogenous PK.

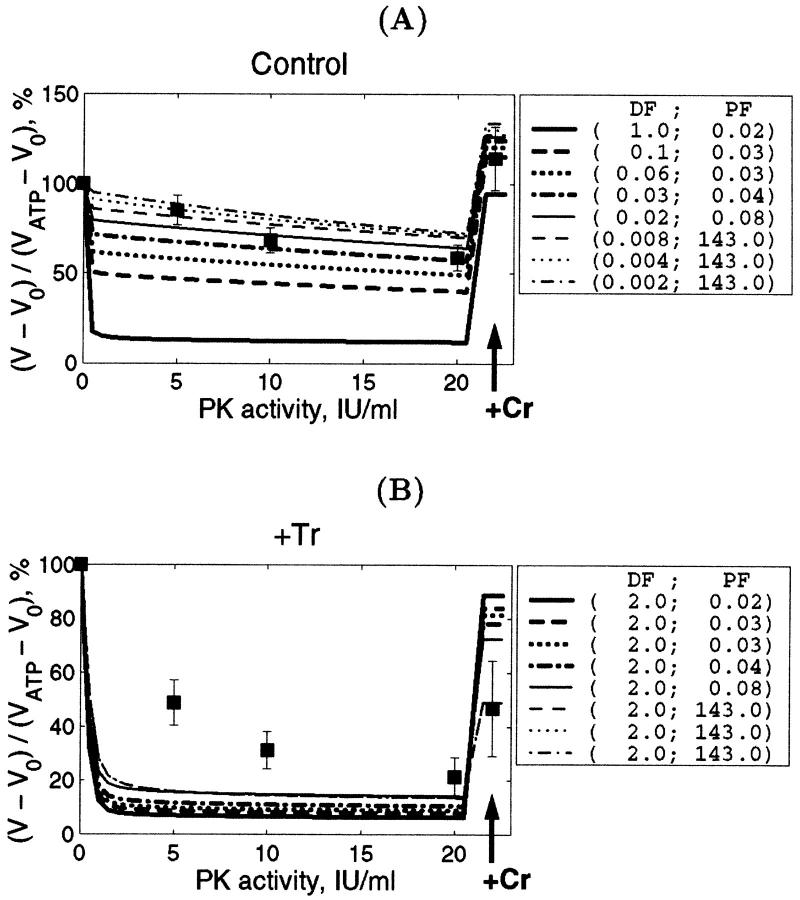
The degree of inhibition of respiration by PK-PEP system in absence of creatine was drastically increased by trypsin treatment (Fig. 4 C). In this case the respiration rate decreased rapidly by increasing the added pyruvate kinase activity, reaching 80% inhibition at 20 IU/ml. This demonstrates, therefore, that most of the endogenous ADP became available for the pyruvate kinase, before being used by mitochondria. The ratio of the degree of inhibition of MgATP (source for endogenous ADP)-dependent respiration by pyruvate kinase after trypsin treatment to that before trypsin treatment T = I(+)/I(−), shown in Fig. 4 C, may be taken as an index (the t-test) of disorganization extent of mitochondrial functional complexes with the extramitochondrial MgATPases.

Creatine still activated the respiration, but to a remarkably lesser extent than in the control, most probably because of the increased permeability of the outer mitochondrial membrane for ADP after trypsin treatment (Kuznetsov et al., 1996, see the next section). Indeed, in the presence of PK + PEP the concentration of ATP was constant and equal to 2 mM. Under these conditions, it is known that 20 mM creatine activates the MiCK maximally, and the functional coupling of MiCK with adenine nucleotide translocase is intact in mitochondria isolated with the use of trypsin (Saks et al., 1975; Jacobus and Saks, 1982). Therefore, decrease of the activation of respiration by creatine from 120 to 130% (with respect to rate with ATP alone) to ∼60% (Fig. 4 C) after disorganization of regular arrangement of mitochondria by trypsin treatment shows increased leak of ADP from the intermembrane space through outer membrane, and thus the increased permeability of the latter. The significant part of ADP generated by MiCK is still, however, rapidly carried by ANT into mitochondrial matrix due to its functional coupling with MiCK (see the Appendix). Remarkably, after disorganization of ICEUs by trypsin, creatine activated the respiration rate in the presence of the PK-PEP system exactly to the same extent as in experiments with isolated rat heart mitochondria under similar conditions—up to the 50% of the State 3 rate of respiration (Gellerich and Saks, 1982; see also Appendix). Thus, in trypsinized fibers, mitochondrial outer membrane becomes as permeable for ADP as in isolated mitochondria in vitro.

Mathematical modeling: apparent diffusion coefficient of ADP may be decreased locally by order of magnitude in comparison with its diffusion in water

The modified mathematical model of compartmentalized energy transfer was adapted in this work to study the diffusion of exogenous and endogenous ADP in skinned cardiac fibers before and after the disorganization of the ICEUs' structure. For this, the model was used to calculate the mitochondrial respiration rates as function of: 1), the concentration of exogenous ADP; 2), the concentration of exogenous ATP as a source of endogenous ADP; and 3), to analyze the different effects of the PK-PEP system on the respiration before and after treatment of the fibers by trypsin. In the model, two parameters describing the ADP diffusion were varied to fit the experimental data: DF, called the diffusion fraction, and permeability fraction, PF, describing the permeability of the mitochondrial outer membrane for ADP (see the model description and Appendix).

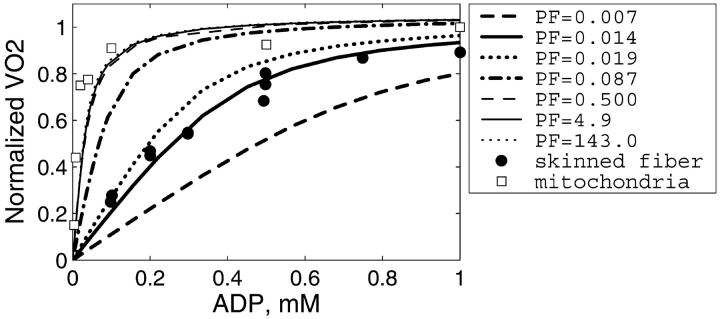
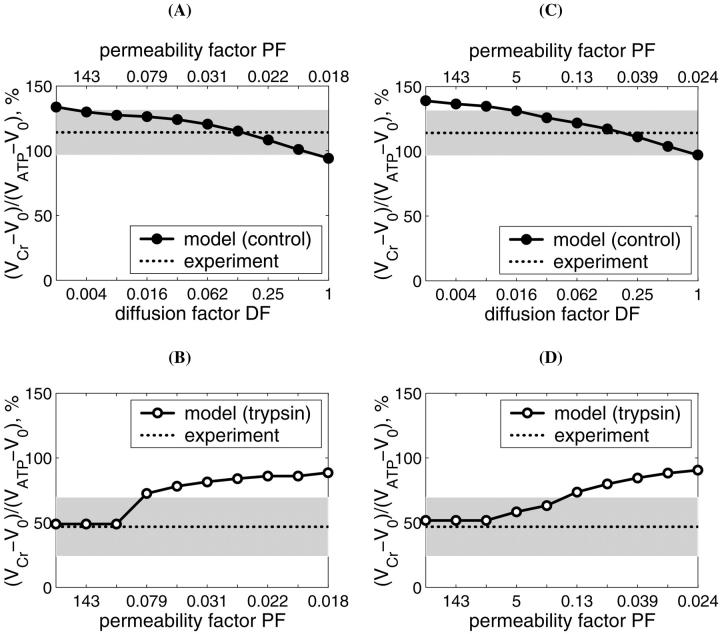
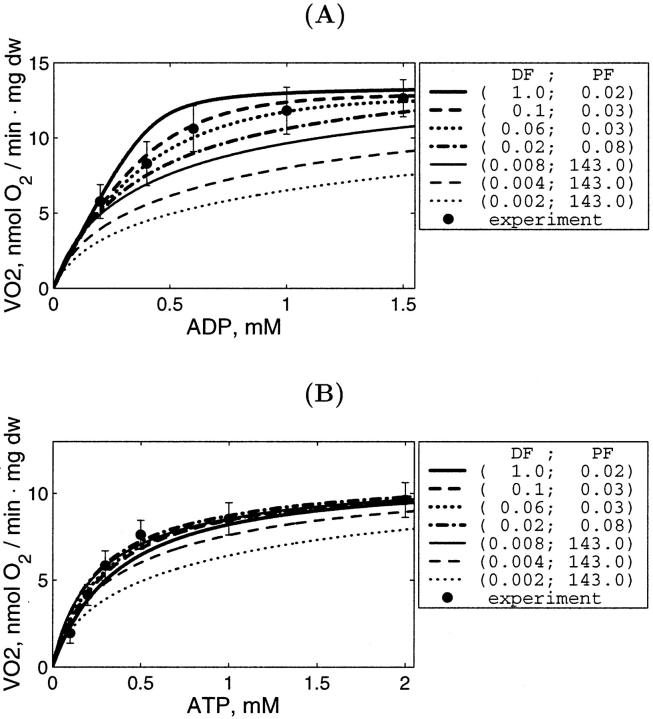
It is clear that restriction of diffusion in some regions inside the cells (heterogeneity of diffusion) influences the dependence of the respiration rate on exogenous ADP and ATP concentrations. To analyze these problems, first the diffusion coefficient for metabolites inside the control fibers (D^app) was taken to be equal to its value in the bulk water phase of cells (D₀, DF = 1), but the permeability of the mitochondrial outer membrane for ADP (expressed as PF) was varied, in accordance with our initial hypothesis (Saks et al., 1995). The results of these simulations are shown in Fig. 5. The comparison of these results with experimental data on the dependence of the rate of respiration on the exogenous ADP concentration (Fig. 5) showed that under these conditions, the increase of the outer membrane permeability for ADP increases the affinity of the system for ADP, as expected, approaching the experimental data for isolated mitochondria in vitro. According to our simulations (Fig. 5), calculated respiration rate is almost maximal when PF > 0.5, i.e., diffusion through mitochondrial outer membrane is not limiting the rate of respiration at the values of PF exceeding 0.5. Quantitatively, the experimental points (Fig. 5) for skinned fibers fit the theoretical curve for intact permeabilized fibers only for very low value of PF (0.014 vs. >0.5 that approached the isolated mitochondria). This result is in excellent accord with the calculations by Aliev and Saks, who also found a value of 0.014 for a parameter resm in the first version of the model (Aliev and Saks, 1997), where the parameter resm was an equivalent of PF used in this work, describing the changes in permeability of outer mitochondrial membrane for ATP and ADP in skinned cardiac fibers in situ. Thus, in principle, high K_m for exogenous ADP can be explained by very low permeability of the outer mitochondrial membrane for this substrate, due to the low conductance state of VDAC (Colombini, 1994; Rostovtseva and Colombini, 1997), in accordance with our previous hypothesis (Saks et al., 1994; 1995).

FIGURE 5.

Dependence of the calculated mitochondrial respiration rate in permeabilized cardiac fibers on the concentration of exogenous ADP computed with different mitochondrial outer membrane permeability factors (PF). The diffusion coefficients of the metabolites within the fiber are taken to be equal to the coefficient values measured in bulk water phase of cells (Aliev and Saks, 1997). Simulations are compared with the measurements of the respiration in isolated mitochondria (open squares) and in skinned fibers (solid circles). Note that reduction of the outer membrane permeability increases the apparent K_m(ADP) of the mitochondrial respiration. Good fit with the experimental data for permeabilized fibers is obtained for PF = 0.014. For isolated mitochondria, good fit is obtained for PF = 0.5 and higher.

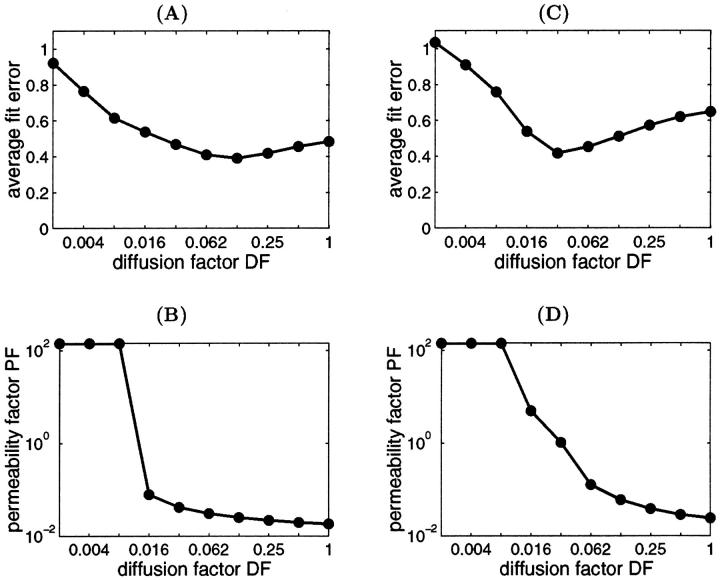
However, in addition to the experiments with determination of the K_m for exogenous ADP, we simulated also the results of experiments on competition between mitochondria and the exogenous PK-PEP system for endogenous ADP, generated by intracellular ATPases. We found that in this case the value DF = 1 does not explain the effect of trypsin on the competitive inhibition of endogenous-ADP dependent respiration by the PK-PEP system (see below). Therefore, it was assumed that there must be some additional restrictions for ADP diffusion outside the outer mitochondrial membrane; for example, between different functional units. Further modeling was made by decreasing the average diffusion coefficient by decreasing DF for ADP outside of the mitochondrial outer membrane, and by optimization procedure finding the corresponding PF value for the best fit with experiments on the dependencies of VO₂ on exogenous ADP or ATP concentrations. The procedure to find optimal DF is shown in Fig. 6, A and C, and PF simultaneously for best fitting in Fig. 6, B and D. Low fit errors were found for DF > 0.008, and PF between 0.018 and 5, but decrease of DF < 0.008 resulted in elevated value of the PF to optimize the average fit error; nevertheless, the fitting with experimental data was increasingly lost.

FIGURE 6.

The average difference (average fit error, ɛ in Eq. 2) between computed and measured VO₂–[ATP] or [ADP] relationships (A and C) and the found optimal permeability factor (B and D) at different diffusion factor DF values. The simulations were performed with K_m of ATPase for ATP and apparent K_m for ADP = 100 μM (A and B) and 300 μM (C and D). Note that the difference between computed and measured respiration rate is increasing at DF < 0.008. At the small diffusion factor values (DF < 0.008), the permeability factor is very high and the further increase of the permeability factor will not reduce the difference between simulated and measured data.

As mentioned above, the additional experiments carried out in this study gave us another possibility to estimate DF values independently by simulation of the competition between mitochondria and PK system for endogenous ADP before and after treatment of the fibers with trypsin. The efficiency of the PK-PEP system in competition with mitochondria for endogenous ADP depends on the rates of diffusion of endogenous ADP inside the fibers between Ca,MgATPases and mitochondria, and between Ca,MgATPases and solution. These results are described in Fig. 8. Fig. 8, A and C show the statistically analyzed data of the changes of the respiration rate with the increase of the PK activity in the medium for the nontreated skinned cardiac fibers with the normal structure; and in Fig. 8, B and D, the same for fibers treated with 5 μM trypsin for 15 min. For nontreated fibers the good fit between calculated and experimental data is found for the values of DF smaller than 0.06, the best fit for DF = 0.02. When the diffusion coefficient for ADP was that for the cellular bulk water phase (DF = 1), the calculated effect of the PK system was very strong and the theoretical curves in Fig. 8, A and C are far below the experimental points for intact fibers. On the contrary, after treatment with trypsin, when the structure of muscle cell was disorganized (see Fig. 4), in the presence of 20 IU/ml of PK the good fit was achieved for DF = 2 (Fig. 8, B and D): theoretical curve was within the range of experimental errors. Some restriction of diffusion may still be present, however, since the mean experimental values are slightly higher for lower PK activity than the theoretical curve (Fig. 8). In this situation the PF has little influence, as it could be intuitively expected: when the ADP diffusion between ATPases and surrounding solution is not restricted and thus very rapid, all endogenous ADP becomes available for the PK system. Since the PK system has very high total activity if compared with the total activity of ATP synthase in mitochondria in our experiments, there is no ADP left for the transmembrane transport if ADP diffusion to the solution is fast. As a consequence, the permeability of the outer mitochondrial membrane has only minor effect on model simulation results in this case (ADP is mostly rephosphorylated by the PK system).

FIGURE 8.

Reduction of endogenous ADP-dependent respiration rate in the presence of 2 mM MgATP by increasing PK activity in the solution in control experiment (A and C) and after trypsin treatment (B and D). Arrows indicate addition of 20 mM Cr into the solution to stimulate respiration. Note the good correlation between simulations and the measurements in control conditions for DF values <0.06. Simulations with different K_m for ATP and ADP of ATPase are compared: A and B correspond to K_m value of 100 μM; and C and D correspond to K_m value of 300 μM. D^app (see Methods and Appendix) in A and C was as in cellular bulk water phase (Aliev and Saks, 1997) reduced by factor DF; and in B and D, as in water solution.

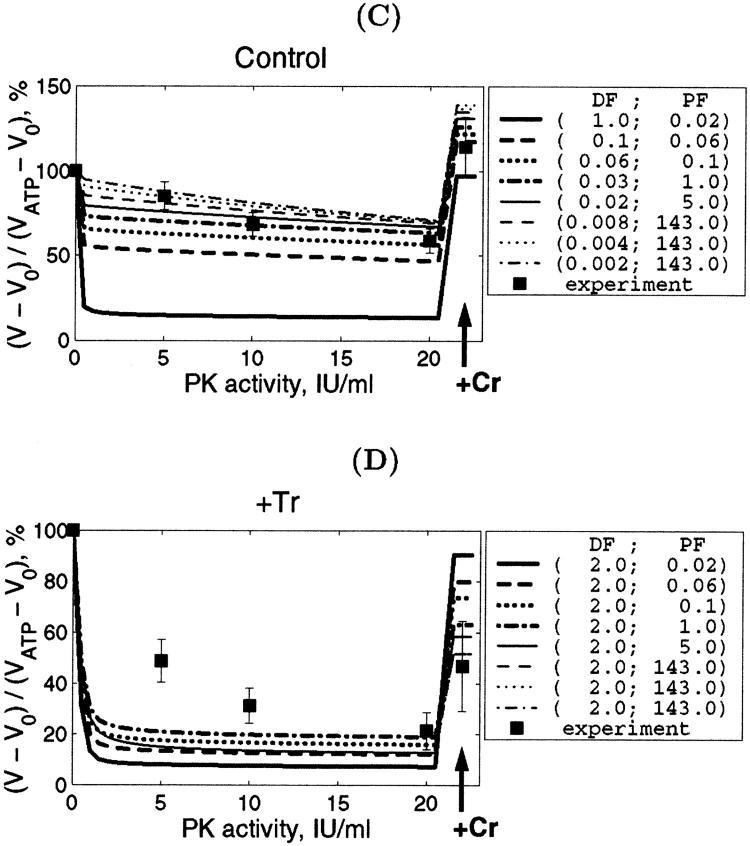
Important information on the distribution of diffusion restrictions in the permeabilized cardiac cells can be obtained from the stimulation of respiration by addition of 20 mM Cr in the presence of the PK-PEP system (Figs. 8 and 9). Fig. 8 shows the simulated effect of creatine addition on the respiration rate in the presence of PEP and 20 IU/ml of PK, in comparison with the experimental data. In all cases the stimulatory effect of creatine on the respiration in the presence of the powerful ADP-consuming PK + PEP system is well reproduced by the model, and the degree of stimulation remarkably depends upon the values of the PF for mitochondrial outer membrane. For nontreated fibers, the computed respiration rate in the presence of creatine was always within the experimental error range, with slight decrease of VO₂ with increase of DF (Fig. 8, A and C and Fig. 9), and the respiration rate always exceeded that before addition of creatine and even that before addition of PEP-PK, reaching the level of 115 ± 13% of initial value observed in the presence of ATP (Fig. 8, A and C). This is explained by effective production of ADP by coupled mitochondrial creatine kinase reaction in the intermembrane space of mitochondria. However, when the trypsin treatment was simulated by setting DF = 2, the influence of PF on the respiration stimulation by Cr became remarkable (Fig. 9, C and D, and Fig. 10): the maximal level of activation by creatine decreased with increase of PF (Fig. 8, B and D). Since the measured respiration rate after the trypsin treatment is increased by creatine to 50 ± 23% of initial rate in skinned fibers, these simulations showed that PF should be at least 1.0 after trypsin treatment (Fig. 8 D).

FIGURE 9.

Mitochondrial respiration rate activated by 20 mM creatine in the presence of 2 mM MgATP and 20 IU/ml PK + PEP. The respiration rates are expressed in percents of initial values obtained with 2mM MgATP in solution and without creatine and any PK activity (compare with Fig. 8). Computed rate (solid lines with dots) is presented as a function of DF and PF (control, A and C) or PF only with DF = 2 (trypsin-treated, B and D). To simplify comparison between computed and measured data, we presented the measured respiration rate by its average value (indicated by dotted line on the plots) and the SD (the shaded area corresponds to the region within the SD from the mean measured value). Note that the perfect fit is obtained when the computed line crosses the line corresponding to the measured rate. After treatment of permeabilized fibers with trypsin, this crossing point is shifted to the direction of increased PF.

FIGURE 10.

Computer analysis of the affinity of mitochondrial respiration for exogenous ADP in the permeabilized cells in situ. (A) Calculated dependency of mitochondrial respiration rate on the concentration of exogenous ADP after trypsin treatment. Insert shows the values of PF for DF = 2. (B) The dependence of apparent K_m for exogenous ADP before trypsin treatment upon DF and corresponding PF values. The apparent K_m was computed using diffusion factor and mitochondrial outer-membrane-permeability factor values shown in the x-axis (top and bottom). (C). The same as in Fig. 10 B; after trypsin treatment, diffusion coefficient D₀ in the skinned fiber is assumed to be as in water. The only variable is PF.

The influence of DF and PF on the rate of respiration stimulated by creatine is analyzed quantitatively in Fig. 9. Fig. 9, A and C show the simulated effects of 20 mM of creatine on respiration in the presence of 20 IU/ml PK and PEP for intact, nontreated permeabilized fibers in dependence of DF with optimized values of PF. Simulated rates of respiration always exceed the initial one, and decrease of DF resulted in increase of PF and vice versa (Fig. 9, A and C). The experimental values (dotted lines) of creatine-stimulated respiration fit the calculated dependencies if DF is between 0.06 and 0.25 (see the crossing points of dotted and solid lines) and corresponding PF between 0.02 and 0.13 (Fig. 9, A and C). After treatment with trypsin, when DF was taken to be equal to 2, the only parameter of importance was PF, and the experimental values were explained by PF exceeding the value of at least 1 (Fig. 9 D), and good fit of mean experimental value with simulation results was observed for PF exceeding 5 (Fig. 9, B and D). That means that treatment with trypsin results in significant increase of permeability of the mitochondrial outer membrane, and the decreased effect of creatine on respiration in the presence of PK and PEP in this case is explained by a leak of ADP from intermembrane space across this membrane.

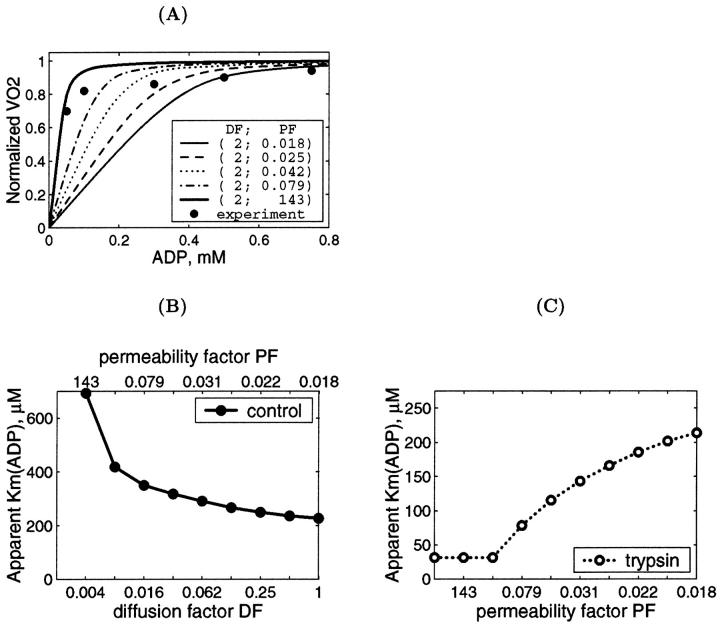
Finally, we simulated directly the dependence of VO₂ on the exogenous ADP concentration after the treatment of fibers with trypsin (Fig. 10 A). This treatment decreases the apparent K_m for exogenous ADP from 250–350 to 40–70 μM (Kuznetsov et al., 1996; Saks et al., 2001), close to that of isolated mitochondria (∼20 μM) (Chance and Williams, 1956; Saks et al., 1991; Liobikas et al., 2001). On the basis of the results shown in Figs. 8 and 9, DF value was taken to be equal to 2. Fig. 10 A shows that the maximal value of permeability factor of the outer mitochondrial membrane, PF, close to 143 allows to satisfactorily simulate the experimental data. More precisely, the influence of both factors DF and PF on the value of the apparent K_m for exogenous ADP is shown in Fig. 10 for the control fibers (Fig. 10 B) and after trypsin treatment (Fig. 10 C). In the control fibers without trypsin treatment, a decrease of DF (values shown at lower x-axis) elevates the K_m value, and the upper x-axis show the PF values which give the best fit for each DF. The usually observed apparent K_m values equal to ∼300–350 μM correspond to DF values ∼0.06 and corresponding PF values ∼0.03 (Fig. 10 B). When the cell structure is disorganized by trypsin and DF = 2, increase in PF results in rapid decrease of the apparent K_m for exogenous ADP, in good accord with all experimental data (Kuznetsov et al., 1996; Saks et al., 2001). In this case the experimental values of the apparent Km for exogenous ADP between 40 and 70 μM correspond to the range of PF values >0.5–1 (Fig. 10 C). This is in agreement with conclusions made above.

Thus, the values of PF may be decreased in the permeabilized cells in situ up to two orders of magnitude, and that of DF by one order of magnitude, in comparison with the isolated mitochondria in vitro.

DISCUSSION

The results of this work show that the regulation of mitochondrial respiration in the cardiac cells is closely related to the structural organization of the mitochondria into functional complexes with myofibrils and sarcoplasmic reticulum. These complexes (the ICEUs) may represent a basic pattern of organization of intracellular energy metabolism (Seppet et al., 2001; Saks et al., 2001; Kaasik et al., 2001). The regular arrangement of mitochondria and their structural organization is usually seen in unfixed preparations by confocal imaging (Bowser et al., 1998; Duchen, 1999; Saks et al., 2001). Quantitative analysis of the experimental data by the mathematical modeling of compartmentalized energy transfer showed that ADP diffusion inside the cells is heterogenous and the diffusion coefficient may be decreased locally by more than an order of magnitude. This occurs in addition to restriction of permeability of the mitochondrial outer membrane for ADP in the cell in vivo. In these structurally and functionally organized systems, the central role of regulation of respiration belongs to the CK and AK networks (Dzeja et al. 1998; Saks et al., 1998b).

The unusually high values of the apparent K_m for exogenous ADP in permeabilized cardiac cells have been found in many laboratories since 1988 (Kummel, 1988; Saks et al., 1991, 1993, 2001; Veksler et al., 1995; Kuznetsov et al., 1996; Milner et al., 2000; Liobikas et al., 2001; Anflous et al., 2001; Boudina et al., 2002; Toleikis et al., 2001). Similarly, high values of this parameter were found in several other oxidative muscles (Kay et al., 1997; Burelle and Hochachka, 2002) and in hepatocytes (Fontaine et al., 1995), but not in fast skeletal muscle (Kuznetsov et al., 1996; Veksler et al., 1995; Burelle and Hochachka, 2002). Thus, this phenomenon is clearly tissue-specific, it certainly does not depend on cell size and thus cannot be explained trivially by the existence of long diffusion distances in the fibers (Kay et al., 1997). There are many data showing the possible role of the outer mitochondrial membrane in this phenomenon. Rupture of the outer mitochondrial membrane by controlled (moderate) hypoosmotic shock (Saks et al., 1993; Fontaine et al., 1995) or its perforation by the proapoptotic protein Bax (Appaix et al. 2002) reduces the apparent K_m for exogenous ADP to the level close to that for isolated mitochondria in vitro. This is also in accord with the data showing that the affinity of isolated mitochondria for ADP can be decreased by some polymers such as Koenig's polyanions, probably because of their influence on the structure of VDAC channels in the outer mitochondrial membrane (Gellerich et al., 1994). On the other hand, manipulations with the mitochondrial matrix and intermembrane space volumes in isolated mitochondria in vitro and in skinned fiber in situ by variations of osmolarity and K⁺ concentrations showed that these volume changes cannot explain the high value of apparent K_m for ADP in permeabilized cells in isoosmotic solutions (see Figs. 2 and 3). This conclusion is in accord with the recent data by Liobikas and co-workers who also did not see any effect of osmolarity (under hyperosmotic conditions) on the apparent K_m for ADP (Liobikas et al., 2001).

Another attempt to explain high values of apparent K_m for ADP in permeabilized cardiac cells was made recently by Kongas and co-workers (Kongas et al., 2002). These authors proposed that the muscle fiber bundle should be considered as an homogenous system, with uniform distribution of both mitochondrial enzymes and cellular ATPases, and without any limitations for the diffusion of ADP, as in bulk water phase. The cell structure and sizes were ignored. Such a homogenous system theory predicted that the high K_m could be expected only for large bundles with a diameter >70–100 μm as a result of simple ADP concentration gradient formation between medium and the cell, with these gradients depending upon the overall MgATPase activity. However, this is evidently in contrast with experimental observation, which show equally high apparent K_m values in permeabilized cardiac cells (Kummel, 1988; Saks et al., 1991; Kay et al., 1997) and permeabilized myocardial fibers (Saks et al., 1993; Anflous et al., 2001; Boudina et al., 2002; Liobikas et al., 2001) with maximal diffusion distance ∼8–10 μm (diameter 15–20 μm, see Fig. 1, A–D), where no ADP concentration gradients in water phase between medium and core of the cells are formed (Saks et al., 2001). Moreover, experimental results show the same high apparent K_m value for ghost cardiomyocytes where the MgATPase activity is decreased by factor of 5 by the selective extraction of myosin (Saks et al., 1993; Kay et al., 1997), and on the other hand, apparent K_m for exogenous ADP is very low (8–15 μM) in fibers from fast-twitch skeletal muscle with large diameter (50–80 μm) at pCa = 7 (Kuznetsov et al., 1996; Burelle and Hochachka, 2002). These results show clearly that the apparent K_m for exogenous ADP is independent of the MgATPase activity and diffusion distance of ADP in water phase, and is related to the intracellular structures and processes. The Amsterdam group tried to explain the equally high values of apparent K_m for ADP in permeabilized and ghost fibers as a result of an increase of D₀, the ADP diffusion coefficient in homogenous bulk water phase (only this coefficient was taken into consideration by these authors), to compensate the decrease of ATPase activity. This explanation means, however, that the velocity of the Brownian movement of ADP molecules in homogenous medium and the kinetic energy of ADP should be increased by extraction of myosin, in conflict with the first law of thermodynamics. Thus, the homogenous system theory of Amsterdam group is in conflict with existing data and not able to describe the features of energy metabolism regulation in situ.

The results of our present study show that the high values of apparent K_m for exogenous ADP in permeabilized cardiac cells and direct channeling of ADP from endogenous ATPases to mitochondria are explained by the heterogeneity of ADP diffusion inside the cells (Saks et al., 2001), caused by strong interaction of mitochondria with cytoskeleton and other cellular systems, and thus, by the complex intracellular organization.

Application of confocal imaging of mitochondria has shown two important aspects. First, very high degree of order in the mitochondrial distribution and arrangement in the cardiac cells has been demonstrated. Mitochondria in unfixed muscle fibers are localized in parallel rows between myofibrils and positioned in the middle of sarcomeres at the level of A-band, giving rise to the striated pattern of their intracellular arrangement in muscle cells visible from confocal images (Fig. 1). The second observation is that this type of organization, these structural and functional complexes of mitochondria can be extremely easily destroyed by short proteolytic treatment, this resulting in loss of the heterogeneity of ADP diffusion.

The phenomenon of heterogeneity of the intracellular diffusion of phosphorus metabolites in muscle cells was discovered in red and white skeletal muscles from fish by Kinsey and co-workers (Kinsey et al., 1999) and in rat skeletal muscle by de Graaf and co-workers (de Graaf et al., 2000) as an anisotropy of the diffusion of PCr and ATP, using in vivo ³¹P-NMR diffusion spectroscopy. Pulsed-field gradient nuclear magnetic resonance was applied to measure the apparent diffusion coefficients in different directions as functions of diffusion time (Kinsey et al., 1999; de Graaf et al., 2000). The method measures, in fact, the displacement, λ, of the molecule for the diffusion time, t_dif, and the apparent diffusion coefficient, D^app, is given by the Einstein-Smoluchowski's equation, λ² = 2D^app t_dif (de Graaf et al., 2000). The apparent diffusion coefficient changed with time, showing diffusion restrictions and heterogeneity in dependence of direction (de Graaf et al., 2000; Kinsey et al., 1999). The radial diffusion coefficient was smaller than the axial one (in direction of fiber orientation), showing the anisotropy of the diffusion (Kinsey et al., 1999). The timescale over which the changes in the D^app occurred showed that the sarcoplasmic reticulum and mitochondria appear to be the principal intracellular structures that inhibit mobility of metabolites in an orientation-dependent manner (Kinsey et al., 1999; de Graaf et al., 2000).

In this work, we arrived at similar conclusions with respect to the diffusion of ADP in cardiac cells. It is concluded that this is a heterogenous process and restricted at the outer mitochondrial membrane and in closely related areas. The features of experimental dependencies of the VO₂ on the exogenous ADP (and ATP) concentrations, including the high apparent K_m for this substrate, the alterations of the apparent affinity for exogenous ADP by trypsin as well as changes of metabolic channeling of ADP by this proteolytic treatment—all could be explained by variations in the apparent diffusion constants, D^app, and outer mitochondrial membrane permeability, and thus by the alterations of the heterogeneity of the intracellular diffusion of ADP (and ATP). The apparent diffusion coefficient for ADP described in this work was found to be decreased at least by an order of magnitude, and thus much more significantly than described before for PCr and ATP (only several times, Kinsey et al., 1999; de Graaf et al., 2000). This may reflect the differences in the experimental protocols used; whereas by NMR methods, only average effects for the whole tissue can be determined, use of permeabilized cells in combination with mathematical simulations allows to analyze the diffusion pathway in more detail, and for some small distance of diffusion the restrictions may be much more significant than for an average value of D^app.

Modeling the effects of creatine on the mitochondrial endogenous ADP-dependent respiration in the presence of the ADP-trapping system of PK + PEP supported both the conclusion of the central role of the mitochondrial creatine kinase in regulation of respiration, and the importance of changes in outer mitochondrial membrane permeability for adenine nucleotides after treatment of fibers with trypsin. In the model, the functional coupling of mitochondrial creatine kinase (MiCK) with ANT was described by a phenomenological kinetic equation, reflecting metabolic channeling of ATP and ADP between these two proteins. In addition, controlled permeability of the outer mitochondrial membrane was assumed (see the Appendix). In good agreement with the experimental data, activation of the MiCK reaction by 20 mM creatine resulted in maximal activation of the respiration up to the real State 3 level despite the presence of the PK-PEP system. That means that the local pools of ADP generated by the MiCK reaction near the ANT were completely protected from the competitive PK-PEP system, despite some leaks of ADP into the intermembrane space (see Appendix), and the MiCK reaction exerted its central role in the almost full control of respiration. The effect of creatine was seen also after the treatment by trypsin, but in this case the relative degree of activation was much lower than before trypsin treatment and very close to that seen in isolated mitochondria (Gellerich and Saks, 1982). The quantitative analysis of these data by the model of compartmentalized energy transfer (Figs. 9 and 10) confirmed that the permeability of the outer mitochondrial membrane is restricted in the cells in situ and increased after proteolytic treatment. Restrictions for the ADP diffusion and decreased permeability of the outer mitochondrial membrane for this substrate in intact cells apparently increase the importance of the phosphocreatine-creatine kinase and adenylate kinase pathways of energy transfer and metabolic signaling (Bessman and Geiger, 1981; Walliman et al., 1992; Saks et al., 1994, 1998b, 2001; Dzeja et al., 1998, 1999; Kay et al., 2000; reviewed recently by Wyss and Kaddurah-Daouk, 2000, and Ellington, 2001).

These conclusions were recently experimentally confirmed by Jacqueline Hoerter's group in excellent series of in vivo studies of cardiac cell energetics by using NMR inversion transfer methods in combination with mathematical analysis (Joubert et al., 2001; 2002a,b). The results of NMR inversion experiments were analyzed by a model of steady-state kinetic exchange between different compartments inside the cell, and the best fit was obtained for the three compartment system of both ATP and creatine kinase compartmentation (Joubert et al., 2001). These are the mitochondrial, cytoplasmic, and myofibrillar compartments, where the creatine kinase isoenzymes operate in the distinct steady states, and directions and their substrate concentrations are different (Joubert et al., 2002a). Remarkably, mitochondrial creatine kinase was shifted in the working heart in the steady-state direction of aerobic phosphocreatine (and ADP) production, out of equilibrium, and in myofibrils—in reverse direction of ATP production (Joubert et al., 2001, 2002a). This is consistent with all biochemical data and with the studies on permeabilized fibers, and with the results of our mathematical modeling, which are based on reaction-diffusion kinetics inside the cells (Aliev and Saks, 1997; Vendelin et al., 2000; Kay et al., 2000). Moreover, their recent conclusion of heterogenous distribution of ADP in the perfused rat heart cells (Joubert et al., 2002b) is in complete accord with our results reported in this study showing the heterogeneity of the intracellular diffusion of ADP.

All these results show the importance of the feedback metabolic regulation of mitochondrial respiration by the structurally and functionally organized energy transfer networks, in particular of MiCK, in cardiac and oxidative muscle cells in vivo. The alternative mechanism of parallel activation of contraction and mitochondrial enzymes by calcium proposed by Balaban and others (Korzeniewski, 1998; Balaban et al., 2002) may have only minor importance in regulation of mitochondrial respiration in the heart under physiological conditions, when the cardiac work and mitochondrial respiration are regulated by the Frank-Starling mechanism, based on the sarcomere length-force relationship. Starling and Visscher showed that increase in the diastolic volume of left ventricle resulted in linear increase of cardiac work and oxygen consumption (Starling and Visscher, 1926). These results were reproduced on the isolated working rat hearts by Neely and co-workers (Neely et al., 1967) and Williamson and co-workers (Williamson et al., 1976). It was shown on this model that increasing the rate of left ventricle filling may increase the rate of oxygen consumption by an order of magnitude without significant changes in ATP and phosphocreatine levels (Williamson et al., 1976). Use of microinjected calcium probes showed no changes in cytoplasmic calcium transients under these conditions (Kentish and Wrzosek, 1998; Shimizu et al., 2002). Inhibition of calcium release from sarcoplasmic reticulum decreased both calcium transients and contractile force, but did not change the force-length relationship (Kentish and Wrzosek, 1998). Thus, the regulation of mitochondrial respiration in cardiac cells under physiological conditions may be observed without any changes in the calcium transients, making any role of the proposed mechanism of parallel activation (Balaban et al., 2002) in this process very uncertain and possibly only of minor importance, if any. Indeed, adrenergic activation of calcium cycle discussed by Balaban (2002) only shifts the Starling curve upward (positive inotropy), but does not change the phenomenon. This was clear already in 1926 when Starling and Visscher wrote, “There is evidence that adrenaline increases oxygen consumption at a given fiber length, without, however, altering the general correspondence between changes in diastolic volume and in oxygen consumption” (Starling and Visscher, 1926). The increase in left ventricle volume increases the consumption of ATP and production first of ADP and then creatine (Ventura-Clapier et al., 1994) in myofibrils due to increased number of activated crossbridges (Lakatta, 1991), and thus simply increases the metabolic feedback signaling.

The general nature of the mathematical terms DF = D^app/D₀ and PF in the inhomogenous reaction diffusion model (see Appendix) does not permit to localize precisely the restrictions of the diffusion within ICEU or between them. The model analysis performed in our previous article (Vendelin et al., 2000) also showed low sensitivity of modeled ADP concentration profiles to the DF values: increasing the DF value above 1 had no effect on the results of calculations, and significant changes in the ADP profile was observed only when DF was decreased by order of magnitude. Similarly, good fitting with the experimental data was seen in the present study only for the DF values in the range of 0.002–0.06 (see the previous section). Identification of the nature of these restrictions is an interesting task of model developing and experimental research. From the experiments with ghost fibers from which a main part of myosin has been removed but which still have very high apparent K_m for exogenous ADP (that can still be decreased by trypsin, Saks et al., 1993; Kuznetsov et al., 1996), we may conclude that this effect is not exclusively due to diffusion barriers localized in the sarcomeric space. In these ghost fibers only the mitochondria, sarcoplasmic reticulum and cytoskeleton are left intact and the regular structures are surprisingly well preserved (Kay et al., 1997). In case of such preparation, the restrictions should be rather close to the mitochondrial membrane due to interactions of mitochondria with cytoskeletal systems and probably other cellular structures (Smirnova et al., 1998; Yaffe, 1999), or to the membranes of both mitochondria and sarcoplasmic reticulum that have been shown to have direct structural and functional contacts for calcium channeling (Rizzuto et al., 1998) and participate in cluster formation in many cells (Manella et al., 1998). Taken together, the data reported here agree, in general, with the macromolecular organization of the cell described by Srere (1985, 2000), Clegg (1986), and Ovadi (1995).

FIGURE 7.

Calculated dependencies of mitochondrial respiration rate on the concentration of exogenous ADP (A) or ATP (B) computed by the model at different apparent diffusion fraction values. For each selected diffusion fraction value, an optimal mitochondrial outer membrane permeability was found to fit the measured data. The values of diffusion fraction DF and the corresponding values of permeability fraction (PF) are shown in right inserts. Note that the computed VO₂ is considerably smaller than the measured one for very small diffusion fraction values (DF < 0.02).

APPENDIX

The complete description of the model has been published in Vendelin et al., 2000. Here, we describe the modified features of the mathematical model first introduced in this study. First, the general description of model modifications is given. Second, we present the equations describing the diffusion within the fiber and the applied boundary conditions. Third, we describe the phenomenological modeling of the functional coupling between mitochondrial creatine kinase and adenine nucleotide translocase.

The model of heterogenous intracellular diffusion of ATP and ADP

In this model, the reaction rates of all enzymes were reduced four times in comparison with the data of earlier publication (Vendelin et al., 2000) to take into account the difference in the temperature (25°C was used in this study with skinned cardiac fibers instead of 37°C, used previously). The ATPase activity, V_ATP in skinned fibers is taken to be nonperiodic (noncontracting fibers), but stationary and dependent on the concentrations of MgATP and MgADP, MgATP and MgADP, according to the equation:

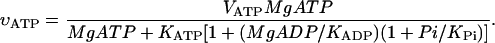(A1)

Since inorganic phosphate (Pi) concentration was not changed in this work but kept constant at 3 mM, in calculations we used an apparent dissociation constant for ADP, K′_ADP = K_ADP/(1+Pi/K_Pi). We assumed here that K_ATP and K′_ADP were the same and are in the range from 100–300 μM (Yamashita et al. 1994). The ATPase activity was assumed to be distributed homogenously in the myofibrillar compartment and cytoplasm.

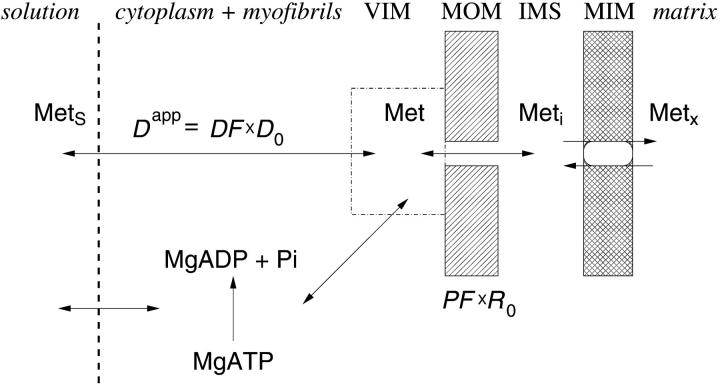
To apply the model for investigation of intracellular diffusion of ADP, we took into account the geometry of permeabilized isolated cardiac cells and skinned cardiac fibers directly measured in nonfixed preparations by confocal microscopy (Fig. 1, A–D) and the boundary conditions imposed in experiments. The permeabilized cardiac cell was considered as cylinder with 20 μm in diameter (Fig. A1). Because of careful separation of fibers before permeabilization, the diameter of skinned cardiac muscle fibers was close to that of cardiomyocytes (Fig. 1, A and C). This is in accord with an observation that the apparent K_m for exogenous ADP is equally very high both for isolated cardiomyocytes and skinned cardiac fibers (Kummel 1988; Saks et al., 1991, 1993; Kay et al. 1997). We assumed that the concentrations of the metabolites within the solution were uniform due to the stirring during the experiments. Using this assumption and taking into account small ratio of diameter to the length of the fiber, we simulated the diffusion between the fiber and solution only in one cross section. The cross section was populated with mitochondria (diameter 1 μm), which were distributed randomly in the cross section to fill one-quarter of the fiber volume (Fig. A1) in accordance with confocal imaging of mitochondrial flavoproteins (Fig. 1, B and D). The concentrations of the metabolites in the solution and the fiber were approximated in the following way. The content of metabolites in the solution was not fixed but changed in accordance with the uptake of the metabolites by the fiber in compliance with the conservation law. The relative volumes of fibers (cells) and surrounding solution were taken into account (their ratio was assumed to be 1/1000). Within the fiber (cell), the concentration of the metabolites in myoplasm and myofibrils was approximated using the finite elements (triangles at the gray area, Fig. A1). The diffusion path of a metabolite was divided into the following three parts (Fig. A2): 1), restricted diffusion from solution through the cytoplasmic and myofibrillar space into the vicinity of each mitochondria, with an apparent diffusion coefficient, D^app; 2), passive diffusion through the outer mitochondrial membrane with permeability coefficient PF × R; and 3), carrier-mediated exchanges from intermembrane space into mitochondrial matrix. In our simulations, the concentrations of the metabolites were computed at the nodal points of the elements giving the spatial distribution of the metabolites within the fiber. The finite element discretization was used for the myofibrillar and myoplasmic compartments only. Inside one given mitochondrion (white holes, Fig. A1), the concentrations were assumed to be independent from the spatial coordinate. The concentrations of metabolites within distinct mitochondria are different because of variations of concentrations of metabolites surrounding every mitochondria in myofibrillar and myoplasmic compartments. The flux of the metabolites between mitochondrion and the myoplasmic/myofibrillar compartment is determined by permeability of the outer membrane and by the gradients of the concentrations of the metabolites in the intermembrane space and on the finite element nodes lying on the boundary between mitochondrion and myoplasmic/myofibrillar compartment. The concentrations of the metabolites (ATP, ADP, creatine, phosphocreatine, and Pi) in mitochondrial matrix were calculated from their concentrations in the intermembrane space and by the kinetics of adenine nucleotide and phosphate transport kinetics (Vendelin et al., 2000). Respiration rates were calculated as the functions of the metabolite concentrations in mitochondrial matrix (Vendelin et al., 2000). Since the concentrations within each mitochondrion were different, the respiration rates were different too. When comparing with the experimental measurements, an average respiration rate was used.

FIGURE A1.

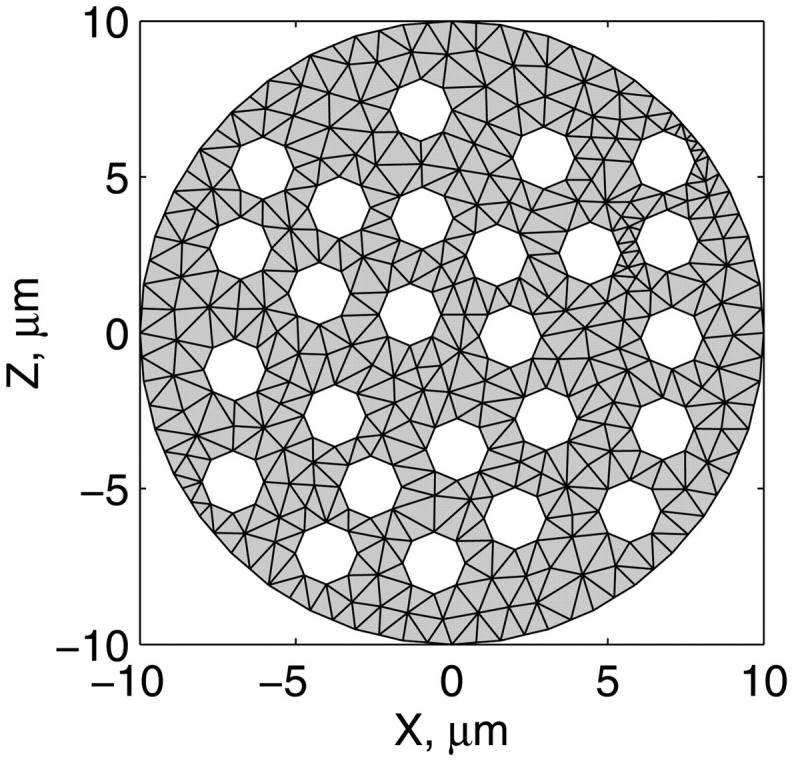
The scheme for mitochondrial distribution in the cross section of cells used in mathematical model. The scheme is based on the data of Fig. 1, A–D. The randomly distributed white holes in the cross section correspond to the mitochondria. The discretization of the cross section by the finite elements is presented.

FIGURE A2.

Schematic presentation of ADP (and ATP) diffusion pathways from solution into mitochondrial matrix. Met_s, Met, Met_i, and Met_x = metabolite concentrations in the solution, in the vicinity of the mitochondria (VIM, inside ICEU), in the mitochondrial intermembrane space, and in mitochondrial matrix, correspondingly. MOM, IMS, and MIM = mitochondrial outer membrane, intermembrane space, and inner membrane, respectively. D^app, D₀, and DF = apparent diffusion coefficient, diffusion coefficient of metabolite in bulk water phase, and diffusion factor (see the text), correspondingly. R₀ is the permeability coefficient for passive diffusion of metabolite across the outer mitochondrial membrane, and PF is the permeability factor for this metabolite (see Appendix).

In some calculations we added PK reaction rate υ_PK description (Saks et al., 1984). Homogenous distribution of PK was assumed in solution and myofibrillar and cytoplasmatic compartments of permeabilized cell or fiber.

Diffusion within the fiber and applied boundary conditions

The dynamics of the metabolites in the myofibril and myoplasm are described by the following system of reaction-diffusion equations:

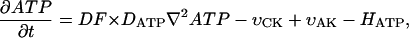(A2)

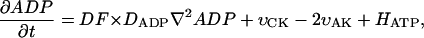(A3)

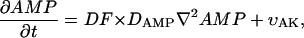(A4)

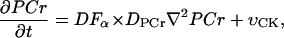(A5)

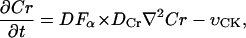(A6)

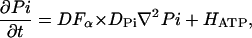(A7)

where ATP, ADP, AMP, PCr, Cr, and Pi are the total concentrations of the metabolites in the myofibril and myoplasm, D_Met is the diffusion coefficient of the metabolite Met (ATP, ADP, AMP, PCr, Cr, or Pi) in myoplasm (Meyer et al., 1984), υ_CK is creatine kinase (CK) rate, υ_AK is adenylate kinase (AK) reaction rate, and H_ATP is the rate of the ATP hydrolysis in the myofibril. The values of the diffusion coefficients were as follows: D_ATP = D_ADP = D_AMP = 145 μm²/s, D_PCr = D_Cr = 260 μm²/s, and D_Pi = 327 μm²/s (Aliev and Saks, 1997). The factor DF describes the changes in the diffusion coefficients and is referred to as a diffusion factor in this study for ATP, ADP, and AMP. Factor DF_α is used to change the diffusion coefficient for PCr, Cr, and Pi, DF_α was taken to be equal to DF in simulations unless stated otherwise. The symbol ∇² denotes the Laplace operator.

The metabolites in the myofibril and myoplasm are subjected to the two different types of boundary conditions. The flux between the myoplasm and mitochondrion is described by

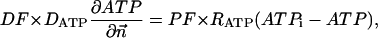(A8)

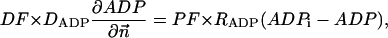(A9)

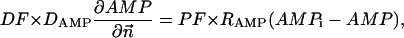(A10)

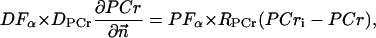(A11)

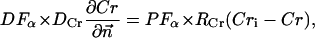(A12)

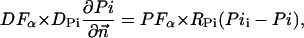(A13)

where Met_i is the concentration of the metabolite Met in the mitochondrial intermembrane space of the corresponding mitochondrion, R_Met is the passive permeability coefficient of the mitochondrial outer membrane, and PF is the permeability factor changed in this study. Factor PF_α is used to change the permeability of the mitochondrial outer membrane for PCr, Cr, and Pi; PF_α was taken to be equal to PF in simulations if it was not stated otherwise. The values of R_Met were as follows: R_ATP, R_ADP, and R_AMP were taken to be 145 μm/s; R_PCr, and R_Cr were taken to be 260 μm/s; R_Pi was equal to 327 μm/s. The difference among R_ATP, R_ADP, and R_AMP values used in this study and our earlier model (Vendelin et al, 2000) is due to the different presentation of the flux equation (Eqs. A8–A13). Namely, in this study we reduce the permeability of the outer mitochondrial membrane by changing PF. Earlier (Vendelin et al., 2000), this factor was already incorporated into the values of R_ATP, R_ADP, and R_AMP. It is important to note that the maximal PF > unity due to the reference values R_Met used by us. The maximal possible value of PF, corresponding to the diffusion through the membrane without any restriction, can be estimated from the diffusion coefficient and the thickness of the outer membrane Δl: PF^max = D_Met/(Δl × R_Met). Assuming that outer membrane thickness is ∼7 nm, and taking into account the values of D_Met and R_Met in this study, PF^max = 143. Thus, the value of PF is between zero and 143.

The flux between the fiber and solution is described by

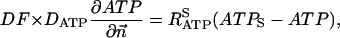(A14)

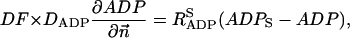(A15)

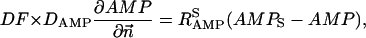(A16)

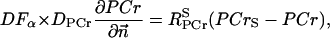(A17)

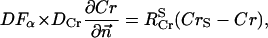(A18)

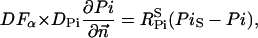(A19)

where Met_S is the concentration of the metabolite Met in solution and R_Met^S is the permeability of surface of the fiber. It was assumed that the boundary of the fiber does not restrict diffusion of the metabolites. This assumption was realized in the model by using R_Met^S 100 times larger than the corresponding R_Met factor. The large R_Met^S values used ensured that the concentrations of the metabolites were the same as in solution at the boundary of the fiber.

The equations presented above were used to find the distribution of the metabolites in the fiber. The spatial discretization was performed using the finite element model; elements are shown on Fig. A1. The metabolite concentrations within the mitochondria (in the intermembrane space and matrix) were computed using Eqs. 25–72 (published in Vendelin et al., 2000).

Functional coupling between mitochondrial creatine kinase and adenine nucleotide translocase

Functional coupling of mitochondrial creatine kinase (MiCK) and adenine nucleotide translocase (ANT) has been well established as an experimental phenomenon (Saks et al., 1994, 1995; Kay et al., 2000). A phenomenological description of this coupling was proposed by Vendelin and co-workers (Vendelin et al., 2000), but an important type of experiment was not addressed in that article. Namely, the experiments with the pyruvate kinase (PK) system as a competitor of oxidative phosphorylation for ATP regeneration from ADP were not considered (Gellerich and Saks, 1982). Later testing of the model in that respect showed the in silico coupling to be too strong, making it almost impossible for the added pyruvate kinase to decrease the rate of oxidative phosphorylation, even when present in large excess. This is in contradiction with experimental measurements, in which maximum drop of about one-half of the initial value in the respiration rate has been detected in the experiments with isolated heart mitochondria (Gellerich and Saks, 1982). Therefore, an improved version of the model of MiCK/ANT coupling was required to account for the experiments with compartmentalized creatine kinase coupled to oxidative phosphorylation and inhibition of the latter by the PK system.

In this new model, similarly to Aliev and Saks (1997) and Vendelin and co-workers (Vendelin et al., 2000), functional coupling of MiCK and ANT was assumed to occur by means of high local ATP and ADP concentrations in a narrow space microcompartment (a “gap”) between coupled enzymes. Basic principles underlying the model composition were as in Vendelin's study (Vendelin et al., 2000): 1), ANT was assumed to translocate adenine nucleotides between matrix space and microcompartment and, partly, intermembrane space; 2), MiCK was linked to ATP and ADP both in the intermembrane space and microcompartment; 3), diffusion between the microcompartment and intermembrane space was considered to be restricted; and 4), due to the infinitely small capacity of the microcompartment, for each adenine nucleotide, the influx was taken to be equal to its efflux.

To reconcile simulations with the experimental data under inspection in this study, a phenomenological approach combining adherence to experimentally determined parameter values with parameter optimization was used.

Model description

The new model of MiCK/ANT coupling is a simplified version of the approach presented earlier (Vendelin et al., 2000), involving isolated mitochondria with ANT and MiCK bound to the inner membrane. The description of oxidative phosphorylation was adapted from Korzeniewski (1998) as in Vendelin's study (Vendelin et al., 2000). ANT and MiCK kinetics will be described in more detail later. When modeling the experiments which were performed on isolated mitochondria (which was done to test the model of functional coupling between ANT and MiCK), the diffusion between intermembrane space and the solution was taken to be infinitely fast, rendering the concentrations of metabolites equal in those two compartments. Consequently, the amounts of adenine nucleotides were tracked in two distinct compartments: in the solution or intermembrane space (marked by the index i following the abbreviation of the metabolites: ADP_i and ATP_i) and in the microcompartment or “gap” (index g: ADP_g and ATP_g). PCr and Cr were present only in the solution.

The creatine kinase reaction rate υ_CK was divided into υ_CK,G, which involves nucleotides in the microcompartment, and υ_CK,I, which involves nucleotides in the solution:

(A20)

In the phenomenological description of the creatine kinase reaction, the form of rate equations was taken from Jacobus and Saks (1982) and Vendelin (Vendelin, et al., 2000):

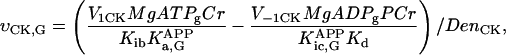(A21)

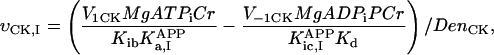(A22)

where

(A23)

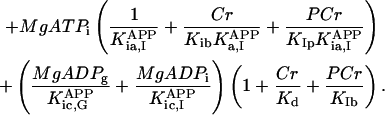The constants V_1CK, V_−1CK, K_ia,G^APP, K_ia,I^APP, K_a,G^APP, K_a,I^APP, K_ib, K_ic,G^APP, K_ic,I^APP, K_id, K_d, K_Ip, and K_Ib in the equations are considered as model parameters. Constants marked with the superscript APP were optimized, and the others were obtained from literature. Note that the optimized constants do not necessarily relate to any specific kinetic property of creatine kinase. The kinetic constants taken from literature were real kinetic parameters of the enzyme measured experimentally. However, when the creatine kinase is coupled to the oxidative phosphorylation via ANT, the measured constants for adenine nucleotides then become apparent, inasmuch as these substrates participate now in two functionally coupled processes (Jacobus and Saks, 1982). In this work, the optimization of these selected constants was made to fit the phenomenological equation of the same form as the real kinetic equation for the creatine kinase, with the experimental data. This optimization procedure was used already in our earlier publication (Vendelin et al., 2000).

Description of ANT kinetics was based on the phenomenological model by Korzeniewski (1998) as in Vendelin's study (Vendelin et al., 2000). The net rate of ATP export by ANT from the matrix to the microcompartment and the intermembrane space is

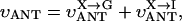(A24)

where 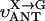is the rate of ATP export by ANT from the matrix to the microcompartment and 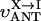is the rate of ATP export by ANT from the matrix directly to the intermembrane space. These rates are described by the following kinetic equations:

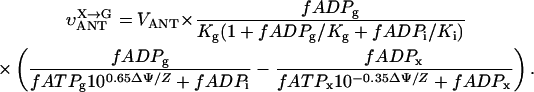(A25)

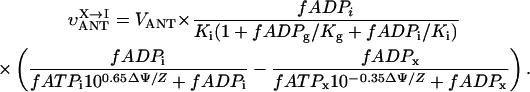(A26)

In the two equations above, fATP_g, fADP_g, fATP_i, fADP_i, fATP_x, and fADP_x are the concentrations of Mg²⁺ free nucleotides in the microcompartment, intermembrane space, and matrix, respectively. K_g and K_i are ANT reaction dissociation constants, ΔΨ is membrane potential, and V_ANT is the maximal relative nucleotide transportation rate. Parameter Z is equal to

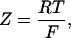(A27)

where R is the gas constant, T is the absolute temperature, and F is the Faraday's number.

The capacity of the microcompartment is considered to be infinitesimal. Therefore, for ATP and ADP, the influx of the metabolite is balanced by its efflux:

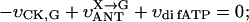(A28)

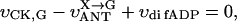(A29)

where the leak of nucleotides was governed by

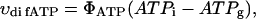(A30)

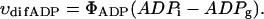(A31)

The changes of ATP and ADP concentrations in the solution were calculated as follows:

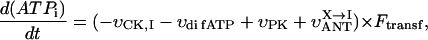(A32)

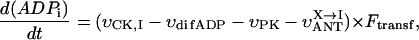(A33)

with F_transf as the units transformation factor, and υ_PK as the rate of pyruvate kinase reaction. The formula for the latter was obtained from Saks and co-workers (Saks et al., 1984).

The concentrations of Cr, PCr, Mg²⁺, and Pi and phosphoenolpyruvate (if present) were fixed at the onset of the simulations and were assumed to be essentially constant during the experiment. If PK was not in solution, then the concentration of ATP_i was also taken to be constant. The differential equations governing the system were solved until stationary values of the variables were obtained. When the concentration of ADP_i had stabilized, the right sides of Eqs. A33 and A32, if used, were equal to zero, and hence the results of simulations did not depend on the factor F_transf. All values of the model parameters pertinent to the description of MiCK/ANT coupling are given in Table A2.

Experimental data

The adequacy of the model was tested in regard to the following experimental data obtained from measurements with isolated mitochondria. 1), Dependence of the rate of phosphocreatine production on ATP concentration was measured at different creatine and phosphocreatine concentrations in the presence of oxidative phosphorylation (Jacobus and Saks, 1982). 2), After adding pyruvate kinase into the solution containing respiring mitochondria and phosphoenolpyruvate, the decrease in the rate of oxidative phosphorylation as a function of PK activity was detected (Gellerich and Saks, 1982). The relative activities of MiCK and PK required in our simulations were estimated from the measured rate of oxidative phosphorylation assuming that the MiCK reaction rate is equal to the rate of ATP production in mitochondrial oxidative phosphorylation (Jacobus and Saks, 1982). And 3), In isolated mitochondria, the creatine kinase reaction coupled to oxidative phosphorylation results in the reversal of the creatine kinase reaction as opposed to the noncompartmentalized creatine kinase in case of nonrespiring mitochondria in certain conditions (Saks et al., 1975).

Parameter optimization

The kinetic parameters of the creatine kinase reaction (Eqs. A21–A23) were initially taken to be equal to kinetic parameters of isolated creatine kinase. To obtain a satisfying fit with selected experimental data, some of those parameters (marked with the superscript APP) as well as nucleotide exchange constants (Φ_ATP and Φ_ADP) were subjected to optimization. Note that the exchange constants Φ are different from the diffusion coefficients D.

At each step of the procedure, the values of the parameters were changed and residual function calculated. The latter consisted of the following terms: 1), differences between calculated and measured phosphocreatine production rates as a function of the amount of ATP in the solution (12 different initial concentrations, ranging from 50 μM up to 2000 μM) in the presence of oxidative phosphorylation, at creatine concentrations 3, 5, 10, 15, and 25 mM and phosphocreatine concentrations 0, 2.5, 5, 7.5, 10, and 15 mM; the amount of ADP in the solution at the onset of experiments was taken to be equal to zero (Jacobus and Saks, 1982); and 2), the decrease in the rate of oxidative phosphorylation after adding pyruvate kinase into the solution; the pyruvate kinase activities of 0.5, 0.8, 9.7, and 37.2 IU/ml were used, which corresponded to decreases of 47%, 49%, 58%, and 60% (Gellerich and Saks, 1982). With the minimum number of eight variables subjected to optimization (Φ_ATP, Φ_ATP, K_ia,I^APP, K_ia,G^APP, K_a,I^APP, K_a,G^APP, K_ic,I^APP, and K_ic,G^APP), the simulations yielded a satisfying accordance with the selected experimental data.

Numerical methods

The system of ordinary differential equations was solved by using the Adams backward differentiation formula that is able to treat stiff equations. The optimization was performed using the Levenberg-Marquardt algorithm. The accuracies of the solutions were tested by varying the tolerance of the ordinary differential equation solver or the nonlinear equation solver.

Simulation results

The values of model parameters, both optimized and experimental, yielding a good fit with the data are listed in Table A2. Some solutions of the model replicating phosphocreatine production rate are depicted in Fig. A3. The simulations at different concentrations of creatine and phosphocreatine rendered results in similar accordance with experimental data (results not shown). Table A1 displays both experimental and theoretical decrease in phosphocreatine production rate as a function of added pyruvate kinase activity into the solution.

FIGURE A3.

Computed and experimental rate of phosphocreatine production as a function of ATP concentration in the solution at 15 mM of creatine and different phosphocreatine concentrations (0, 5, and 15 mM). The concentration of ADP at the onset of simulations was taken to be equal to zero. Experimental values were obtained from Jacobus and Saks (1982), using the rate equation of the mitochondrial creatine kinase reaction with experimentally determined dissociation constants.

TABLE A1.

Decrease in respiration rate after adding pyruvate kinase into the solution containing respiring isolated mitochondria (measured data is obtained from Gellerich and Saks, 1982)

	Decrease in the respiration rate (%)
PK activity (IU/ml)	measured	computed
0	0	0
0.50	47	49
0.80	49	50
10	58	54
37	60	61

TABLE A2.

CK/ANT coupling parameters

Constant	Dimension	Value	Reference (optimized parameters are marked by *)
ΦATP, ATP exchange constant	(relative)	1.0 × 10−10	*
ΦADP, ADP exchange constant	(relative)	2.0 × 10−7	*
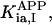MiCK rate equation parameter	μM	111,056	*
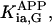MiCK rate equation parameter	μM	283	*
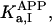MiCK rate equation parameter	μM	14,797	*
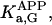MiCK rate equation parameter	μM	13	*
Kib, MiCK rate equation parameter	μM	28,800	Jacobus and Saks, 1982
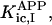MiCK rate equation parameter	μM	77,491	*
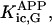MiCK rate equation parameter	μM	64,334	*
Kid, MiCK rate equation parameter	μM	1400	Aliev and Saks, 1997
Kd, MiCK rate equation parameter	μM	500	Aliev and Saks, 1997
KIb, MiCK rate equation parameter	μM	28,800	Aliev and Saks, 1997
KIp, MiCK rate equation parameter	μM	35,000	Jacobus and Saks, 1982
V1ck, MiCK maximal forward reaction rate	(relative)	0.234	Jacobus and Saks, 1982
V−1CK, MiCK maximal backward reaction rate	(relative)	1.0	Jacobus and Saks, 1982
Kg, ANT reaction dissociation constant	μM	4.25	Vendelin et al., 2000
Ki, ANT reaction dissociation constant	μM	4.25	Vendelin et al., 2000
Vant, ANT maximal reaction rate	(relative)	20
ΔΨ, Membrane potential	mV	−180
F, Faraday's number	J × mol−1 × mV−1	8.3
R, Gas constant	J × mol−1 × K−1	96.5
T, Temperature	K	298.0

Additionally, the model was checked for an important property of the creatine kinase system not stated in the residual function at optimization. The creatine kinase reaction rates at fixed concentrations of metabolites in the solution (the concentrations of ATP, ADP, PCr, Cr, and Pi were 0.12, 0.05, 2, 40, and 5 mM, respectively), were estimated both with the presented model of MiCK/ANT coupling and with noncompartmentalized MiCK in case of inhibited mitochondrial respiration. The calculations were in accord with the experimental finding (Saks et al., 1975), that in these instances the MiCK reaction rates have opposite directions.