Revealing the Properties of Dendritic Voltage-Gated Channels: A New Approach to the Space Clamp Problem

Dendrites remain one of the last unexplored frontiers of the central nervous system. Their small caliber and complex structure have rendered them resistant to investigation since their discovery more than a century ago. Nevertheless, in recent years a few intrepid experimentalists have voyaged to the distal dendrites, and have been richly rewarded for their efforts. Dendrites appear to contain different sets of channels to the soma, indicating that channel distributions and properties must be tightly regulated to create neuronal subcompartments with distinct electrophysiological signatures (Häusser et al., 2000; Migliore and Shepherd, 2002). These findings have been made using a combination of techniques. First, patch-clamp recordings from dendrites (Usowicz et al., 1992; Stuart et al., 1993) have allowed dendritic voltage-gated channels to be mapped using both cell-attached and outside-out patch techniques. Second, two-photon imaging techniques, together with statistical analysis of signal fluctuations, have been used to estimate channel properties on dendritic spines and shafts (Sabatini and Svoboda, 2000). Third, quantitative immunogold techniques (Lörincz et al., 2002) have been used to examine the anatomical distribution of channels down to the submicron level. In this issue of Biophysical Journal, Schaefer et al. (2003) present a fresh approach for extracting the densities and functional properties of dendritic channels using a combination of modeling and experiments.

Why is yet another technique necessary? Both cell-attached and excised-patch methods suffer from uncertainty about the area of the membrane patch, which is also likely to be variable from patch to patch, even with consistent pipette geometry. The number of ion channels per patch is an additional large source of variability, in particular for channels that are present at low density. Thus, conductance density estimates obtained from patches are not very reliable. Furthermore, there are some indications that patch formation and excision may alter channel properties. Quantitative high-resolution imaging methods show great promise, but present formidable challenges to the experimentalist, and probably cannot be used to extract kinetic data. Immunogold methods can only provide relative densities of specific channel subunits; determining the absolute densities of the channels, and their functional properties require complementary, independent methods. As a consequence of these limitations, we still lack the quantitative description of dendritic voltage-gated channels that is required for a deep understanding of excitability in dendrites, as achieved for the squid axon more than 50 years ago by Hodgkin and Huxley (1952).

The method developed by Schaefer et al. is based on whole-cell dendritic recordings, which yield much larger currents and thus better signal-to-noise ratios than excised or cell-attached patch techniques. However, as any seasoned electrophysiologist knows, such recordings are subject to the problem of inadequate “space clamp,” which has bedeviled the field of ion channel research from the beginning. It is a simple consequence of the fact that dendrites are not isopotential, and therefore accurate control of dendritic voltage from a point voltage clamp is not possible, regardless of whether it is located at the soma or in the dendrites (Fig. 1). As a consequence, key biophysical parameters of voltage-gated channels, such as kinetics, voltage-dependence, and conductance density, can be seriously distorted (Fig. 1 C), as are synaptic currents originating from dendritic synapses. The solution used by Hodgkin and Huxley for this problem—to insert a wire down the length of the squid axon to render the entire axon isopotential—is obviously not practical for dendrites. Instead, Schaefer et al. have devised a clever numerical algorithm that estimates and corrects for the errors introduced by inadequate space clamp. The method requires a detailed compartmental model of the neuron incorporating the channel type under study to simulate clamp currents obtained during the experiment. Using an iterative approach, conductance densities are varied systematically until the simulated currents match the experimentally measured clamp currents. This allows the densities and properties of the dendritic voltage-gated channels to be estimated with high precision, and with relatively few assumptions regarding the distribution and properties of the channels. While such a “correction” approach has been used before for neurons that can be represented by simplified models, the solution proposed by Schaefer et al. goes beyond previous methods in that it can be applied to any morphology. The authors have also carefully assessed the sensitivity of the algorithm to the quality of the compartmental model, uncertainty about the channel models and their distribution, and experimental noise.

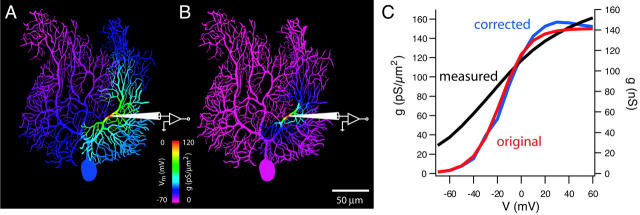
FIGURE 1.

(A) Steady-state distribution of voltage (coded by color) in a Purkinje cell compartmental model during a voltage step to 0 mV applied via a dendritic patch pipette. (B) Activation of a Purkinje cell delayed rectifier K channel with a uniform dendritic distribution (150 pS/μm²) during the voltage step shown in A. (C) Correction of the K⁺ channel activation curve using the algorithm of Schaefer et al. (2003). Red, original conductance density; black, measured conductance; blue, corrected conductance density.

In a sense, the approach taken by Schaefer et al. transforms the problem of space clamp into an advantage. The activation of nonregenerative voltage-gated currents by a voltage clamp applied via a dendritic pipette remains highly local (Fig. 1 B), since it results from the product of the voltage distribution (Fig. 1 A) and the activation curve of the channel (Fig. 1 C). Thus, the less isopotential the neuron, the better the method works, and the higher the spatial resolution that can be achieved. Given the relatively large currents obtainable with the whole-cell approach, the authors show that only a few dendritic recordings are necessary to establish quantitatively a channel gradient along the dendrite (rather than the dozens required using excised or cell-attached patch methods). The algorithm can also be used to correct conventional voltage-clamp measurements made at the soma, and thus is complementary to the nucleated patch technique for recording somatic channel properties.

The method is not a panacea: it does not actually solve the problem of inadequate space clamp, but only corrects for it, and thus measuring channel properties in regions remote from the recording electrode (especially in the thinnest, most inaccessible distal dendrites) remains a challenge. In its current form the method only works for nonregenerative voltage-gated currents such as K⁺ channels and I_h, since it cannot easily account for voltage escape during regenerative events (although these problems may be overcome with future refinements of the algorithm). Finally, this approach demands experimental finesse as well as patience: although it can work with only one dendritic electrode, two-electrode voltage clamp is preferred to eliminate series resistance errors; and a detailed compartmental model must be laboriously and carefully constructed from the same cell as recordings were made from.

Despite these caveats, the method developed by Schaefer et al. provides an important new strategy for measuring the properties of dendritic voltage-gated channels that complements and extends existing methods. Together with the voltage-jump technique for extracting the time course and amplitude of synaptic conductances (Häusser and Roth, 1997), the two main challenges posed by inadequate space clamp, namely the inability to accurately record synaptic and voltage-gated currents, are now both addressed by analytical approaches to circumvent the limitations of the experimental techniques. With experimentalists now equipped with this new set of tools, we can be confident that dendrites may soon be yielding many more of their secrets.