Molecular Dynamics Simulations of Peptides and Proteins with Amplified Collective Motions

Abstract

We present a novel method that uses the collective modes obtained with a coarse-grained model/anisotropic network model to guide the atomic-level simulations. Based on this model, local collective modes can be calculated according to a single configuration in the conformational space of the protein. In the molecular dynamics simulations, the motions along the slowest few modes are coupled to a higher temperature by the weak coupling method to amplify the collective motions. This amplified-collective-motion (ACM) method is applied to two test systems. One is an S-peptide analog. We realized the refolding of the denatured peptide in eight simulations out of 10 using the method. The other system is bacteriophage T4 lysozyme. Much more extensive domain motions between the N-terminal and C-terminal domain of T4 lysozyme are observed in the ACM simulation compared to a conventional simulation. The ACM method allows for extensive sampling in conformational space while still restricting the sampled configurations within low energy areas. The method can be applied in both explicit and implicit solvent simulations, and may be further applied to important biological problems, such as long timescale functional motions, protein folding/unfolding, and structure prediction.

INTRODUCTION

In recent years there has been an increasing use of theoretical methods, especially molecular dynamics (MD) simulations, to gain insights into structure-function relationships in proteins (Doniach and Eastman, 1999). One of the main questions to be answered when assessing the usefulness of MD simulations of proteins in understanding biological functions is the degree to which the simulations adequately sample the conformational space of the protein. If a given property is poorly sampled over the MD simulations, the results obtained have a limited usefulness.

A straightforward way to solve this problem is to increase the simulation time. With the improvements in computer power and algorithms, we have progressed to tens of nanoseconds now (Daggett, 2000). This timescale is still too short to observe many important protein processes, such as slow conformational changes and protein folding/unfolding. The inefficiency in sampling is a result of the frustrated nature of the energy landscape. While the exploration of different conformational states and the mechanism of transitions between different conformational states are of more interest than examining local fluctuations during a simulation, the system will spend most of the time in locally stable states—interesting escaping events being rarely observed in a conventional simulation (Eastman et al., 1999).

To extend the capability of atomic simulations, new techniques need to be developed to improve the sampling efficiency considerably. Various methods have been proposed, such as the multicanonical ensemble algorithm (Hansmann and Okamoto, 1993; Nakajima et al., 1997), adaptive umbrella sampling (Bartels and Karplus, 1998), conformational flooding (Grubmuller, 1995), chemical flooding (Muller et al., 2002), and essential dynamics simulation (Amadei et al., 1996). Among them, the last three are based on collective coordinates.

The use of collective coordinates has become an important technique to extract functionally relevant motions from simulation results (Kitao and Go, 1999; Berendsen and Hayward, 2000). Computational techniques to determine collective motions are varying. Principal component analysis (PCA) or essential dynamics analysis (EDA) (Amadei et al., 1993) can be carried out on a large number of configurations in MD or Monte Carlo (MC) trajectories, or a large set of experimental structures. The CONCOORD method (de Groot et al., 1997) uses a very crude approximation of atomic interactions to generate a large number of configurations that satisfy a set of atomic distance constraints and then PCA or EDA can be applied. Normal mode analysis (NMA) uses a harmonic approximation of the full atomic force field and a single experimental structure suffices. The most time-consuming aspects of NMA are energy minimization and diagonalization of the Hessian matrix using an atomic force field. Coarse-grained models, such as the Gaussian network model (GNM) (Haliloglu et al., 1997) and the anisotropic network model (ANM) (Atilgan et al., 2001), have been designed to reproduce a few collective modes using simplified pairwise Hookean potential and have been successful in predicting atomic fluctuations. By the above methods, an “essential subspace” spanned by a small number of collective modes can be obtained. Collective coordinates are widely employed to investigate protein dynamics. Recent studies have shown that functionally relevant motions occur along the direction of a few collective coordinates, which dominantly contribute to atomic fluctuation. Kitao et al. (1998) have used PCA and a jumping-among-minimum model to elucidate the energy landscapes of proteins. The analyses applied to a 1-ns MD trajectory of the human lysozyme in water indicate that, 1), the energy surfaces of individual conformational substates are nearly harmonic and mutually similar; and 2), protein motions consist of three types of collective modes, namely, multiply hierarchical modes (the number of which accounts for only 0.5% of all modes, yet dominate contributions to total mean-square atomic fluctuation), singly hierarchical modes, and harmonic modes. Intersubstate motions are observed only in a small-dimensional subspace spanned by the axes of multiply and singly hierarchical modes.

Collective coordinates can be used as a basis set for efficient sampling. In MC simulations, normal modes are used as variables and the sampling step size is scaled by normal mode amplitudes (Noguti and Go, 1985). In the conformational flooding (Grubmuller, 1995) and chemical flooding methods (Muller et al., 2002), according to the collective modes obtained from short MD simulations, a coarse-grained description of conformational substate is derived from which bias potential can be constructed. The bias potential destabilizes the initial conformation and lowers free energy barriers of structural transitions, thus complex conformational transitions and chemical reactions may be observed and followed in a simulation. The Berendsen group developed an “essential dynamics” simulation method. In this method, protein motions are constrained to move along the essential collective modes, while the motions along the other degrees of freedom obey the usual equations of motions (Amadei et al., 1996). de Groot et al. (1996a,b) have applied this technique in the study of a 13-residue peptide hormone, guanylin, and a 85-residue protein, HPr. The region of conformational space obtained from the essential dynamics sampling includes the area sampled by the normal MD and extends beyond. Abseher and Nilges (2000) applied restraints in essential subspace on an ensemble of MD trajectories that proceed otherwise independently in parallel. The results show that weak restraints on the ensemble variance suffice for an increase in sampling efficiency along collective modes by two orders of magnitude.

One disadvantage of the essential dynamics method is that the collective modes need to be obtained from a predetermined set of protein conformations, usually from a relatively short period of simulation. Such a set usually represents only local fluctuations. As collective modes are treated as linear combinations of Cartesian coordinates, they are, in principle, conformation-dependent. That is, the essential subspace may vary when the protein conformation belongs to different local states. The method we introduced here uses the collective modes obtained by the coarse-grained model ANM (Atilgan et al., 2001) to guide the atomic-level MD simulation. Using the ANM, the collective modes are estimated using a single protein conformation without carrying out a long simulation. These modes can be updated frequently during the simulation since computation of the collective modes using ANM is rapid, which allows us to give up the severe assumption that the essential subspace is invariant in the conformational space. Another key strategy in our method is that the motions along the collective modes are amplified by coupling them to a thermal bath at higher temperature than the remaining motions, which is achieved by taking advantage of the weak-coupling algorithm (Berendsen et al., 1984). The idea comes from the molecular dynamics docking method (Di Nola et al., 1994; Mangoni et al., 1999). The original method consists of a separation of the center-of-mass motion of the substrate from its internal motions, and a separate coupling to different thermal baths for both types of the motions of the substrate and for the motions of the receptor. Using higher center-of-mass temperature and room temperature for the internal degrees of freedom of the substrate, an efficient search in the translational and rotational subspace is achieved without disturbance of the internal structure. The separate temperature bath approach has also been employed in a novel MD simulation, in which the protein and solvent have been simulated at different temperatures to demonstrate the key roles of solvent in controlling functionally important fluctuations (Vitkup et al., 2000).

Algorithmatically, our amplified-collective-motions (ACM) approach comprises the following steps: 1), estimate the collective modes according to a single protein configuration in the MD simulation using ANM, and the collective modes updated frequently during the simulation; 2), project the velocities of the atoms into two subspaces: the subspace spanned by the limited number of slow collective modes (essential subspace) and the rest; and 3), couple the velocities in different subspaces with different thermal baths, the essential subspace coupled to higher temperature and the remaining coupled to normal temperature bath. We expect the essential subspace can be sampled adequately and large amplitude motions of the protein can be observed during the ACM simulation. In the meanwhile, local interactions and higher frequency motions are kept at normal temperature, allowing local structures to relax to accommodate the large amplitude motions in the collective coordinates.

Here, we briefly describe the construction of the following sections. We firstly describe the theory and methods of ACM, and then computational details for two test systems, an S-peptide analog and bacteriophage T4 lysozyme (T4L). Subsequently, we provide some results and discussion, which demonstrate the efficiency of the ACM method. Finally, we provide concluding remarks.

THEORY AND METHODS

Gaussian network model and the anisotropic network model

The Gaussian network model (GNM) assumes that the protein in the folded state is equivalent to a three-dimensional elastic network (Kloczkowski et al., 1989; Erman et al., 1989). The junctions are identified with the C^α atoms in the protein, and the interactions between residues in close proximity are replaced by harmonic springs (Miyazawa and Jernigan, 1985; Tirion, 1996; Bahar et al., 1997). Applications to several proteins demonstrated that the predicted equilibrium fluctuations of C^α from GNM show excellent agreement with experiments. It should be noted that GNM is a scalar model and all fluctuations are implicitly assumed to be isotropic. In fact, the fluctuations of the proteins are in general anisotropic, and it is important to assess the directions of collective motions, as these can be directly relevant to biological functions and mechanisms. So, an extension of GNM, called the anisotropic network model (ANM), has been developed (Atilgan et al., 2001). Recently, Ming et al. (2002a,b) have developed a quantized elastic deformational model that combines and enhances the above elastic network models and the vector quantization method for computing intrinsic deformation motions of protein structures by using low-resolution electron density maps.

In our method, we adapted ANM. For a folded protein, the junctions are identified with the center-of-mass of each residue. According to ANM, harmonic potential can be written as

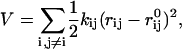(1)

where k_ij, r_ij, and 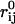are the force constant, distance, and equilibrium distance between center-of-mass of residues i and j, respectively. In this work, k_ij are given by

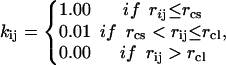(2)

where r_cs is the cutoff distance of the first interaction shell, and r_cl is the longer cutoff distance, which is set to avoid more than six ‘0’ eigenvalues, as Atilgan et al. (2001) suggested.

In the case of N_r residues, the Cartesian coordinates are r_i = (x_i, y_i, z_i), and the second derivatives of the overall potential can be organized in the 3N_r × 3N_r Hessian matrix H. H is composed of N_r × N_r super-elements, each of size 3 × 3:

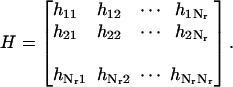(3)

The ij_th super-element h_ij (i ≠ j) is

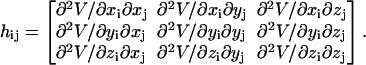(4)

The elements of h_ij are given by

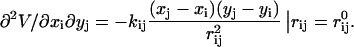(5)

The diagonal super-elements are

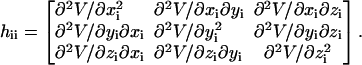(6)

The elements of h_ii are given by

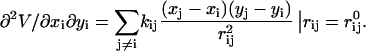(7)

The symmetric matrix H can be diagonalized by a unitary coordinate transformation U,

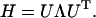(8)

Here Λ is the diagonal matrix consisted of the eigenvalues (λ_i) of H, organized in ascending order. The i_th column of U is the eigenvector associated with λ_i. There are 3N_r eigenvalues, of which the initial six associated with overall translations and rotations are zero. The remaining 3N_r-6 nonzero eigenvalues and corresponding eigenvectors reflect the respective frequencies and Cartesian components of the individual modes. The first few slow, long wavelength collective modes may represent functionally relevant motions of the protein.

The amplified collective motion method

Before going into the technical details of the ACM method, we first introduce the weak-coupling method briefly (Berendsen et al., 1984). The weak-coupling method is usually used to couple MD simulations to external baths in, for example, constant temperature (T₀) simulations. In a constant temperature simulation, the kinetic energy of the protein at time t (E_k(t)) can be given as

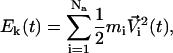(9)

where m_i and V_i(t) are atomic mass and velocity of atom i, respectively. N_a is the number of atoms in the protein. The instantaneous temperature T(t) is

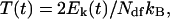(10)

in which N_df is the number of degrees of freedom of the protein and k_B the Boltzmann constant. According to the weak coupling scheme, a temperature-scaling factor can be calculated

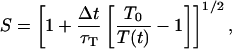(11)

where Δt is the MD time step, and τ_T is the temperature relaxation time (a larger τ_T indicates a weaker coupling). The factor S is used to uniformly scale the velocities of the next time step, making the actual temperature relax toward T₀.

Our technique is based on the weak-coupling method. From V(t), we can obtain the velocity of the center-of-mass of each residue,

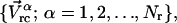where N_r is the number of residues in the protein. The dimension of the V_rc vector is 3N_r, and the dimension of each mode calculated by ANM is also 3N_r. If we select the first n_l collective modes to form an essential subspace, the projection of V_rc along these n_l modes is given as

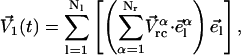(12)

where e_l is the l_th collective mode and e_l^α the component of the Cartesian coordinates of residue α in e_l. V₁(t) is the projection of the velocities into the essential subspace. The projection of V(t) in the rest subspace can be simply calculated as

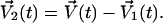(13)

We apply the weak-coupling method to these two parts of the velocities, separately. For V₁, the reference temperature is higher (T_h) and the corresponding temperature-scaling factor is S_h. V₂ is coupled to the normal temperature (T_l), the scaling factor being S_l, and

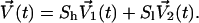(14)

By this method, we try to enhance sampling efficiency along the collective modes by coupling them to the higher temperature thermostat. We expect to observe large-magnitude collective motions in the protein within a relatively short simulation.

COMPUTATIONAL DETAILS

S-peptide analog

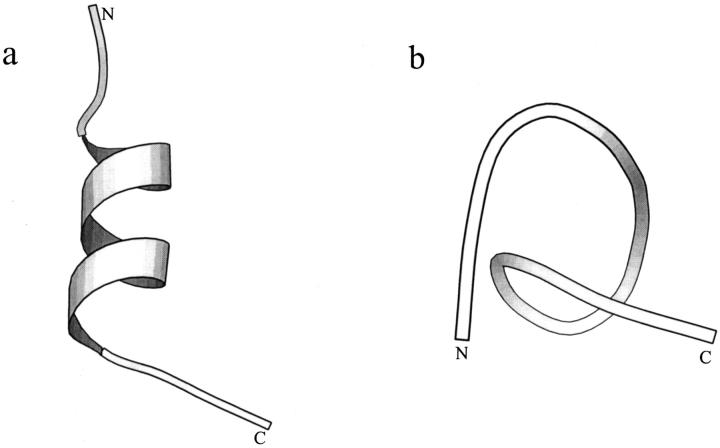
The first set of test simulations were undertaken to study the folding/unfolding of a 15-residue α-helical analog of Ribonuclease A S-peptide (Tirado-Rives and Jorgensen, 1991). The peptide consists of α-helix (residues 4–12), N-terminal (1–3), and C-terminal (13–15) random coils (Fig. 1 a).

FIGURE 1.

Structures of the S-peptide analog. (a) Native structure. (b) Denatured structure after 20-ns MD simulation at 358 K (Zhang et al., 2001). The figures are created by MOLSCRIPT (Kraulis, 1991).

We had performed several MD simulations for this peptide with an explicit water model (Zhang et al., 2001). Our results indicated that, at low temperature (278 K) the helix is stable, whereas at high temperature (358 K), after 20-ns simulation, the native α-helix is denatured completely (Fig. 1 b). Here, we selected two structures as the starting structures: the initial native structure and the final unfolded structure for further simulations (Fig. 1). Instead of an explicit water model, we used an implicit solvent model—the generalized Born/surface area (GBSA) water model (Still et al., 1990)—for the peptide simulations. Multiple simulations were performed, which are divided into four groups based on the starting conformation and simulation procedure. These groups are: conventional simulations starting from the native structure at 274 K (noted as NA); ACM simulations starting from the native conformation (noted as NA_ACM); conventional simulations starting from the unfolded conformation (noted as UN); and ACM simulations starting from the unfolded conformations (noted as UN_ACM).

Stochastic dynamics simulations (van Gunsteren et al., 1981) have been used for the implicit solvent simulations, and the GBSA model has been used in conjunction with the GROMOS96 43A1 force field (Zhu et al., 2002). After energy minimization with the steepest descent method, the system was equilibrated by 50-ps GBSA simulations, during which the positions of nonhydrogen atoms were restrained. All atoms were given an initial velocity obtained from a Maxwellian distribution at 274 K. Since the system only contains the peptide (151 atoms), we believe the above procedures were enough to generate equilibrated structures for the successive sampling simulations. The simulations within each of the four groups were started using different sets of initial velocities.

During the normal GBSA simulations (NA and UN), the peptide was coupled to a temperature bath of reference temperature 274 K with a relaxation time of 0.1 ps. Bonds were kept rigid using the SHAKE method (relative geometric tolerance = 10⁻⁴) (Ryckaert et al., 1977). The nonbonded interactions were calculated without cutoff. A time step of 2 fs was used. The ACM simulations (NA_ACM and UN_ACM) were otherwise the same as the control simulations, except that a few of the slowest collective modes and the rest have been coupled to separate temperature baths, respectively. The short (r_cs) and long-range cutoff distances (r_cl) in the ANM analysis were set as 0.7 nm and 1.4 nm, respectively. Either the first three or the first five modes were coupled to the higher temperature (T_h = 358 K), with a relaxation time of 0.01 ps, and the other modes were coupled to the lower temperature (T_l = 274 K and τ_Tl = 0.1 ps). The collective modes were recalculated either every 10 or every 25 time steps, according to the new current configuration of the peptide. The computational cost of recalculating the ANM modes with such frequencies can be nearly ignored relative to the simulation steps. Average temperatures of the selected lowest collective modes and the rest during one UN_ACM simulation were listed in Table 1. Since only a few modes (five slowest modes) were coupled to the higher temperature (T_h = 358 K), the actual temperatures of them have large fluctuations. The average value is 345 K, lower than the reference temperature. This may be caused by the weak coupling between motions along the slowest modes and the remaining motions, and the mixing of different modes as they evolve with the conformation. The other degrees of freedom have much smaller fluctuations in temperature and the average temperature is nearly the same as the reference temperature. Although a few modes were coupled to the higher temperature, the average temperatures of the entire system in the ACM simulations are only ∼1 K higher than that in the conventional simulations.

TABLE 1.

Temperatures (in K) of the ACM simulations on the S-peptide analog and T4 lysozyme

	S-peptide analog*		T4 Lysozyme
	Five higher-temperature collective modes	Other modes	Three higher-temperature collective modes	Other modes
Tref†	358	274	800	300
Tav‡	345(105)	274(19)	751(112)	299(5)

^*Results of one of the ACM simulations starting from the unfolded S-peptide analog.

^†The reference temperatures in the weak-coupling scheme.

^‡The average temperatures of the corresponding degrees of freedom in the simulations (30 ns of the S-peptide analog and 3 ns of T4 lysozyme). Numbers in parentheses are standard deviations of the averaging.

The software used was based on the simulation package GROMOS96 (van Gunsteren et al., 1996) with modifications to introduce ACM. Some analyses were performed using GROMACS tools (van der Spoel et al., 1999), and DSSP was used for calculations of secondary structures (Kabsch and Sander, 1983).

Bacteriophage T4 lysozyme

Bacteriophage T4 lysozyme (T4L) is composed of two domains connected by a long α-helix. There is a deep opening between the N-terminal and C-terminal domains, which is the active site cleft for oligosaccharide binding (Anderson et al., 1981). Many crystal structures of T4L and its mutants have been found that indicate the hinge-bending-type domain motion opening or closing up the cleft (Faber and Matthews, 1990; Zhang et al., 1995).

The crystal structure of T4L (entry 2LZM of the PDB) determined at 1.7 Å resolution was used as the starting structure (Weaver and Matthews, 1987). Rectangular periodic boundary conditions were used with box length of 5.263 nm × 5.687 nm × 7.827 nm (the minimum distance between the solute and the box boundary is 1.0 nm). SPC water molecules were added from an equilibrated cubic box containing 216 water molecules (Berendsen et al., 1981). Some of the added water molecules were removed so that no water oxygen atom is closer than 0.23 nm to a nonhydrogen atom of the protein or another water oxygen atom. The system, protein and water, was initially energy-minimized for 500 cycles using the steepest descent method. Eight Cl⁻ ions were added to compensate the net positive charge on the protein. These ions were introduced by replacing water molecules with the highest electrostatic potential. The energy was again minimized using steepest descent method. The final system contains 1703 protein atoms, eight Cl⁻ ions and 7018 water molecules, leading to a total size of 22,765 atoms. 200-ps equilibration MD runs were performed, in which the temperature was gradually increased from 50 K (20 ps), 100 K (20 ps), 150 K (20 ps), 200 K (20 ps), 250 K (20 ps), and 300 K (100 ps), together with an increase of the temperature coupling constant (from 0.01 to 0.1 ps) and a decrease of the position restraints force constant (from 50,000 to 10,000 kJ mol⁻¹ nm⁻²). Then two 3-ns productive runs were performed, respectively.

One conventional MD at 300 K (S₃₀₀) was performed using an isothermal-isobaric simulation algorithm (Berendsen et al., 1984). Protein and solvent was coupled separately to temperature baths of reference temperature with a coupling time of 0.1 ps. The pressure was also kept constant by weak coupling to a bath of reference pressure (P₀ = 1 atm; coupling time τ_p = 0.5 ps). Bonds were kept rigid using the SHAKE method with a relative geometric tolerance of 10⁻⁴ (Ryckaert et al., 1977). Long-range forces were treated using twin-range cutoff radii of R_cp = 0.8 nm for the charge group pair list, and R_cl = 1.4 nm for the longer-range nonbonded interactions. The pair list was updated every 20 fs. Reaction-field forces were included (Tironi et al., 1995), originated from a dielectric permitivity of 54 for SPC water (Smith and van Gunsteren, 1994). A time step of 2 fs was used. The other is ACM simulation (S_ACM), which was otherwise the same as the control simulation, except for modifications to temperature coupling. Short- and long-range cutoff distances of 0.7 nm and 1.0 nm, respectively, were used in ANM. We selected the three slowest collective modes (n_l = 3). These three degrees of freedom were coupled to the higher temperature T_h = 800 K, with a relaxation time of 0.01 ps, and the other modes were coupled to the temperature T_l = 300 K (τ_Tl = 0.1 ps). The average temperatures were 751 K and 299 K for the collective modes and the rest, respectively (Table 1). The total number of degrees of freedom of T4L is over 5000 and only three collective modes were coupled to 800 K. The temperature averaged over all degrees of freedom of the system in S_ACM is almost the same as in S₃₀₀. The collective modes were recalculated every 100 time steps according to the new current configuration of the protein. The most time-consuming part of the ACM algorithm compared to usual MD is the diagonalization of the 3N_r × 3N_r Hessian matrix (Dhillon, 1997). However, N_r is only the number of residues and the updating of ANM modes is not done for every step. For the S-peptide analog the additional cost of ACM over usual MD is ignorable. For T4L, ACM increases the computational cost by only ∼10% over usual MD with the above setup.

The same software has been used as in the simulations of the S-peptide analog. EDA (Amadei et al., 1993) was performed with WHAT IF (Vriend, 1990).

RESULTS AND DISCUSSION

Folding/unfolding of S-peptide analog

Although we performed multiple simulations of the peptide, considering the similar results among simulations within one group, we only report the results of one simulation from each group, respectively.

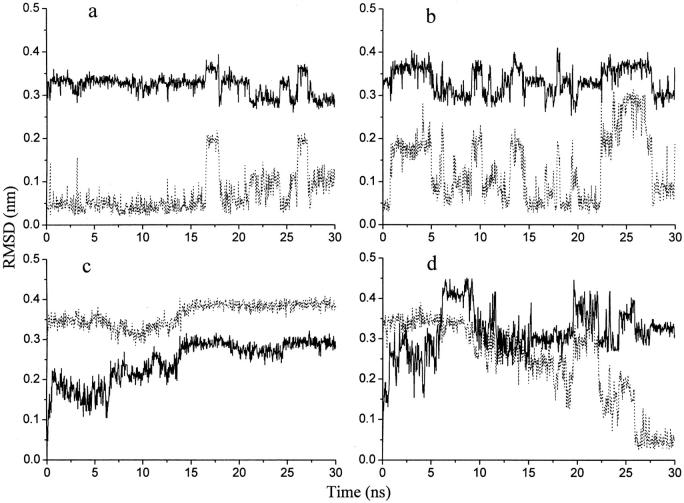
Root-mean-square deviations (RMSD) from the starting structure for the backbone atoms from residues 4–12 were calculated (Fig. 2). The helix is stable during the NA simulations (Fig. 2 a), which show agreement with our previous results (Zhang et al., 2001). Compared with Fig. 2 a, during the NA_ACM simulations, the native α-helix is also kept very well, only with significantly larger structural fluctuations (Fig. 2 b). In the UN simulations, RMSD are stable and show little change after a period of time, which indicate the peptide has been “trapped” in a single non-native substate (Fig. 2 c). We have carried out 10 UN_ACM simulations. In eight of them, the unfolding peptide refolds into the native helix (Fig. 2 d). The refolding time (the first time when the RMSD from the native structure is <0.1 nm) ranged from 20 to 90 ns. After refolding, the behaviors of the peptide in the UN_ACM simulations are similar to its behaviors in the NA_ACM simulations (Fig. 2 b). In only two UN_ACM simulations, refolding has not been observed within 100 ns.

FIGURE 2.

Root-mean-square deviations (RMSD) of backbone atoms between residues 4–12 in the S-peptide analog during some simulations. RMSD from the native structure (dotted lines); RMSD from the denatured structure (solid lines). (a) Conventional simulation beginning with the native structure (NA). (b) ACM simulation beginning with the native structure (NA_ACM). (c) Conventional simulation initiated with the denatured structure (UN). (d) ACM simulation initiated with the denatured structure (UN_ACM).

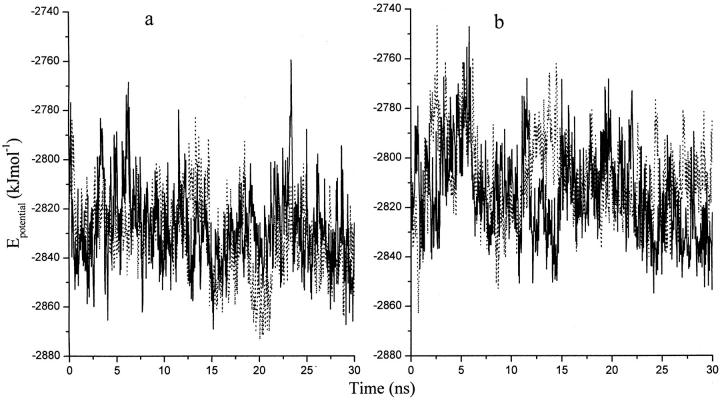
The potential energies (the GBSA free energy of solvation included) of each group of simulations were calculated (Fig. 3). Several conclusions can be drawn according to the results. First, the average potential energy of the denatured structures (−2808.2 ± 30.6 kJ mol⁻¹) is higher than that of the native structures (−2831.3 ± 29.8 kJ mol⁻¹). Second, the energies during the ACM simulations (−2828.2 ± 31.1 kJ mol⁻¹ and −2814.9 ± 32.1 kJ mol⁻¹ for simulations starting from the native and unfolded states, respectively) have only slightly larger fluctuations than that in the conventional simulations. This is because a few collective modes have been coupled to a higher temperature. However, the average energy values in the ACM simulations are still in a reasonable range. Third, the potential energy decreases with simulation time in the UN_ACM simulation (Fig. 3 b, solid line), in agreement with the RMSD figure indicating the refolding process (Fig. 2 d).

FIGURE 3.

Potential energies in the simulations of the S-peptide analog. (a) NA (dotted line); NA_ACM (solid line). (b) UN (dotted line); UN_ACM (solid line). The energy values are averaged every 30 ps.

The results of the UN_ACM simulations indicate that the ACM method can drive the system to escape the unfolded local minima and expand the sampling region selectively, without extending the accessible conformational space to irrelevant high-energy regions. That is, the efficiency of the ACM method comes from that the technique can both expand the accessible conformational space while still restricting the sampling within lower-energy region of the conformational space. The ACM method is quite different from conventional simulations at elevated temperatures. In the latter the system may also escape from local minima, but only at the cost of destabilizing local interactions, extending the accessible conformational space to irrelevant high-energy unfolded states (Zhang et al., 2001). As the overall density of states increases rapidly with elevated temperature, conventional high temperature simulations generally decrease the overall efficiency of the sampling. In the ACM simulations of the peptide, only a few collective modes are coupled to a higher temperature. The motions along these modes are expected to dominate the conformational transitions during the refolding. The higher temperature increases the chance of escaping local traps both off and along the refolding pathway, whereas the accessible conformational space does not expand to the same intractable extent as in usual high temperature simulations.

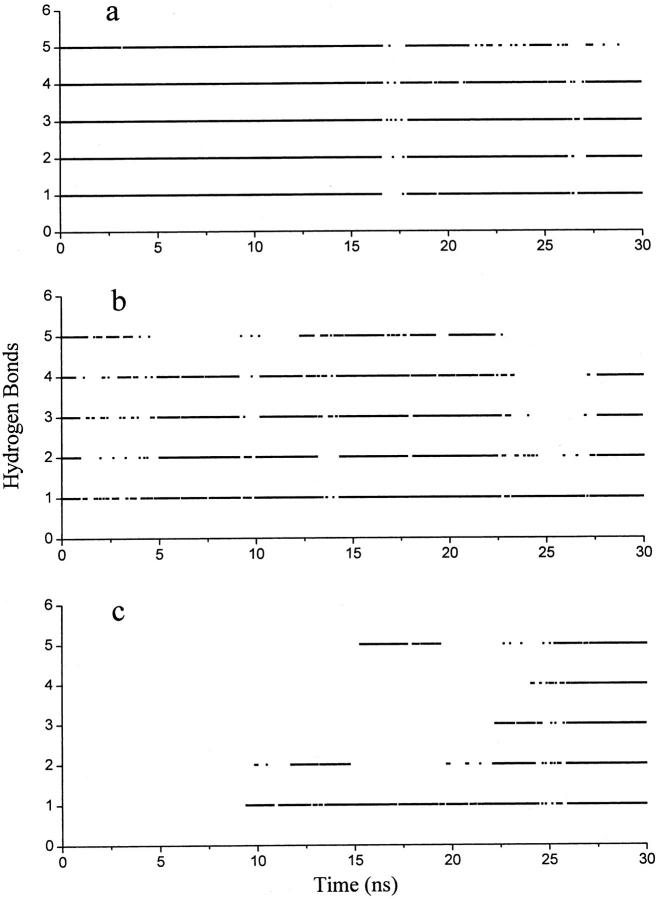
Among the 10 UN_ACM simulations, peptide refolding was observed in eight simulations. It is interesting to study the folding/unfolding pathways based on these multiple trajectories. The forming and breaking of five native i + 4 → i hydrogen bonds, i.e., Phe8:NH-Ala4:CO (HB₁), Leu9:NH-Ala5:CO (HB₂), Arg10:NH-Ala6:CO (HB₃), Glu11:NH-Lys7:CO (HB₄), and His12:NH-Phe8:CO (HB₅), were monitored (Fig. 4), which shows correspondence with the folding/unfolding of the peptide (Fig. 2). The five hydrogen bonds are stable in the NA simulations (Fig. 4 a) and less stable in NA_ACM simulations (Fig. 4 b). No native hydrogen bonds formed during the UN simulations. In the refolding process of UN_ACM simulations, the hydrogen bonds near the N-terminal of the peptide formed first, and then the hydrogen bonds near the C-terminal (Fig. 4 c). Instead, the breaking of the hydrogen bonds took place first near the C-terminal in the unfolding process (Zhang et al., 2001). The results indicate that the α-helical hydrogen bonds near the N-terminal may be intrinsically more stable than those near the C-terminal, forming earlier in the folding process and being disrupted later in the unfolding process.

FIGURE 4.

Forming and breaking of the five native hydrogen bonds (HB₁-HB₅) of the S-peptide analog during some simulations. (a) NA. (b) NA_ACM. (c) UN_ACM. A maximal distance of 0.25 nm between hydrogen and acceptor and a maximal angle of 60° between donor-hydrogen-acceptor were used. The numbering of hydrogen bonds: Phe8:NH-Ala4:CO (HB₁); Leu9:NH-Ala5:CO (HB₂); Arg10:NH-Ala6:CO (HB₃); Glu11:NH-Lys7:CO (HB₄); and His12:NH-Phe8:CO (HB₅).

Domain motions in bacteriophage T4 lysozyme

Besides the experimental structures, theoretical studies also reveal that the first two largest amplitude essential modes determined from the MD trajectories of T4L, which describe the domain motion, are identified as being the closure and twist modes (de Groot et al., 1998).

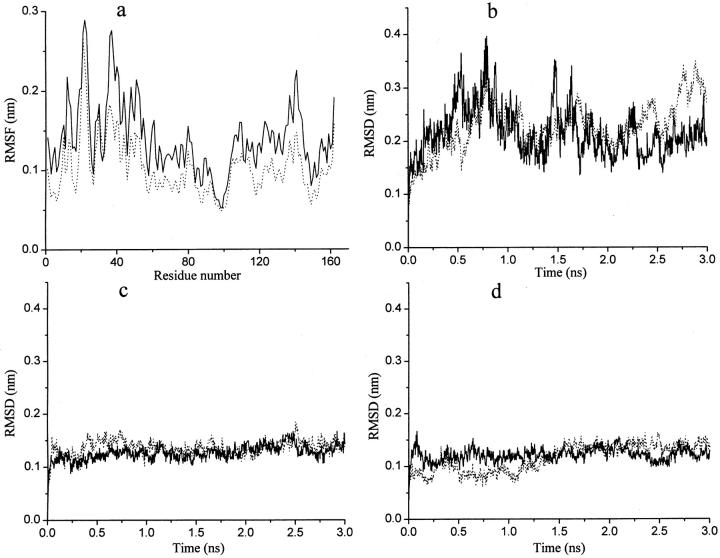
Root-mean-square fluctuations (RMSF) of the C^α atoms from residues 1–162 were calculated for the two simulations (Fig. 5 a). S_ACM shows significantly larger fluctuations than S₃₀₀. As expected, the increased motions in the ACM simulation mainly come from the interdomain motion in T4L. Root-mean-square deviations (RMSD) from the starting structure of the C^α atoms from residues 1–162 (Fig. 5 b), N-terminal domain (residues 13–65, Fig. 5 c), and C-terminal domain (residues 75–162, Fig. 5 d) indicate that the larger amplitude motions in S_ACM do not come from the intradomain motions of the N- and C-terminal domains. The secondary structures as well as the structures of each domain have been well-maintained in the ACM simulation.

FIGURE 5.

Some properties during the T4 lysozyme simulations. The control simulation S₃₀₀ (dotted lines) and the ACM simulation S_ACM (solid lines). (a) Root-mean-square fluctuations (RMSF) of C^α atoms from residues 1–162. (b) RMSD from the starting structure of the C^α atoms from residues 1–162. (c) RMSD of the C^α atoms of the N-terminal domain (residues 13–65). (d) RMSD of the C^α atoms of the C-terminal domain (residues 75–162).

The essential dynamics analysis (EDA), which is based on the diagonalization of the covariance matrix, can distinguish large, concerted internal motion from small, random internal motion (Amadei et al., 1993). First, EDA was performed on a cluster of 38 x-ray crystallographic structures, which may be representatives of accessible conformations of T4L under physiological conditions (Zhang et al., 1995). The EDA results are nearly the same as published data (de Groot et al., 1998), although only C^α atoms of residues 1–162 are used to construct the covariance matrix. The results indicate that the first two eigenvectors contribute ∼90% to the total positional variations among the experimental structures.

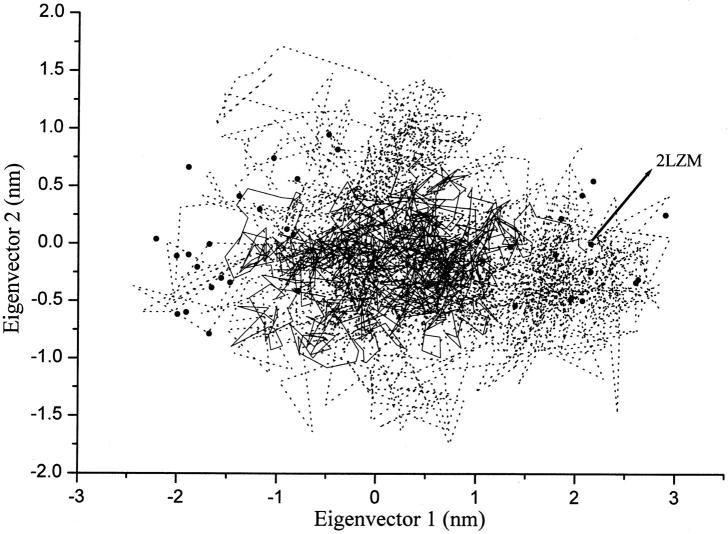
As indicated by de Groot et al. (1998), the first mode obtained by EDA on the x-ray cluster corresponds to a closure motion (defined by an effective hinge axis perpendicular to the line connecting the centers of mass of the two domains) and the second mode consists of a twist of the two domains, with the effective hinge axis being more parallel to the line connecting the two centers of mass. We projected the x-ray structures and the trajectories of the two simulations onto the plane defined by the above two modes to compare the extent of variations in the x-ray structures and the two simulations (Fig. 6). Along the first mode, there seem to be two distinct clusters of the x-ray structures. Structures to the left region are open structures, and structures to the right are closed. The MD simulation (S₃₀₀), which started with a closed structure (indicated by an arrow in Fig. 6), spend most of the time at the intermediate region between the two clouds of the x-ray structures, but does not reach positions corresponding to either the most open or the most closed configurations in the x-ray cluster. The ACM simulation (S_ACM), started with the same structure as S₃₀₀, fluctuates much more significantly toward all directions in the plane than the usual MD and x-ray clusters. These results suggest that the expanded sampling in S_ACM is mainly the interdomain motion in T4L. Among the set of 38 x-ray structures, we selected the structure with the maximum and the minimum projections on the closure and twist modes, respectively. In Fig. 7 a, each pair of structures was superimposed. Between the extreme structures along the closure mode, the RMSD of C^α atom positions is 0.40 nm (Fig. 7 a, left). Along the twist mode the corresponding RMSD is 0.14 nm (Fig. 7 a, right). The same were performed on the sets of conformations sampled in the usual (Fig. 7 b) and ACM simulations (Fig. 7 c), respectively. In S_ACM, both the closure and the twist motions have larger amplitudes than in S₃₀₀ and in the x-ray structure set, in agreement with Figs. 5 and 6.

FIGURE 6.

Two-dimensional projections of the T4 lysozyme structures from x-ray and the two simulations onto the plane defined by the closure and the twist mode. 38 x-ray structures (solid circles). The initial structure of MD, 2LZM (arrow); trajectory of the S₃₀₀ simulation (solid line); and trajectory of the S_ACM simulation (dotted line).

FIGURE 7.

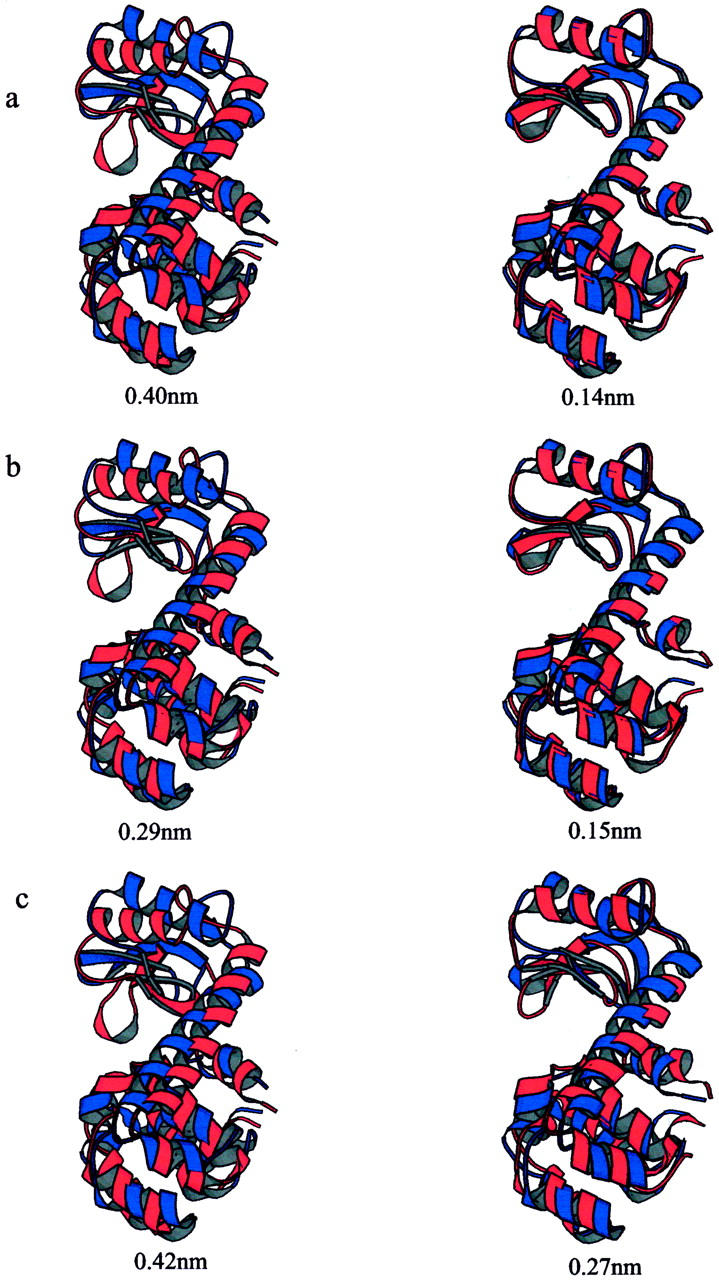
Superimposed structures indicating the observed domain motions of T4 lysozyme. From three set of structures: (a) x-ray structures, (b) conformations sampled in the usual MD simulation, and (c) conformations sampled in the ACM simulation; the structures with the maximum (red) and the minimum (blue) projections along the closure mode are superimposed on the left, and the structures with the maximum (red) and the minimum (blue) projections along the twist mode are superimposed on the right. RMS deviations of C^α atom positions between the superimposed structures are indicated under each set of the structures. The graphs have been created with MOLSCRIPT (Kraulis, 1991).

In S_ACM, we only coupled the three slowest collective modes to the higher temperature. We used the initial structure in the ACM simulation to calculate the ANM modes and estimated the overlaps between the slow collective modes and the first two essential modes calculated using the set of x-ray structures. These overlaps are computed as the projections of the x-ray essential modes on the subspace formed by the slow ANM modes. We found that the first three ANM modes significantly cover the x-ray modes. The overlap coefficients are 0.87 for closure mode and 0.76 for twist mode, respectively, with a coefficient of 1.0 for complete coverage. This explains why the interdomain motion of T4L in S_ACM is much more obvious than in S₃₀₀. The intradomain motion in S_ACM is nearly the same as in S₃₀₀, because all the other modes except the first three were coupled to the normal temperature (300 K), the same as in S₃₀₀.

In our conventional MD simulation of T4L, a large part of the region of x-ray structures could not be sampled within 3 ns, but the ACM simulation seemed to cover the x-ray structures within the same simulation time (Fig. 6). Dynamical transitions among the x-ray structures are much more obvious in S_ACM. We expect further such simulations with ACM may grasp the essential motions at much longer timescales, which can have more extensive relations with functions.

Comparisons with other sampling methods

Collective coordinates have been used in the study of protein motions for quite some time. In the ACM method presented here, the collective modes are obtained using the coarse-grained model ANM (Atilgan et al., 2001). The ANM approximation seems sufficient to reproduce the slow dynamics as well as the harmonic modes obtained by NMA, using all-atom empirical potentials. In the case of T4L, the first few slowest ANM modes are able to significantly cover the first two essential modes obtained on a set of crystal structures. ANM is computationally more efficient than NMA and EDA. More importantly, by using ANM we can update the collective modes ‘on the fly’. We also do not need a known set of conformers to determine the essential modes or to assume the essential modes to be invariant. This is not the case in the essential dynamics simulation method (Amadei et al., 1996). For large systems, the updating of the ANM modes can be computationally expensive if it is done every MD step. This is, however, unnecessary. An “ideal” updating frequency is that it can catch up with the changes in the essential subspace with minimum additional computational cost. This should not be an issue in practice, because while larger systems require more efforts to obtain the ANM modes, the physical processes of interest generally take place at longer timescales. For T4 lysozyme in explicit water, updating the ANM modes every 100 steps (0.2 ps) only increases the computational cost by 10%. One does not need to risk violating the physical requirement by reducing the frequency further to gain little in additional computational efficiency. For both systems we studied, we expect the conformational changes, that may lead to significantly different slow conformational subspaces, to take place for significantly longer than the respective time intervals for ANM updating.

One key strategy in the ACM approach is to couple only the first few low-frequency collective modes to a higher temperature. Compared with other previously described sampling methods employing higher temperatures, such as the multicanonical ensemble algorithm (Hansmann and Okamoto, 1993; Nakajima et al., 1997), the temperatures of the entire system are elevated in the latter approaches. As a result, the higher energy regions are nondiscriminatively sampled. This significantly expands the accessible conformational space, introducing additional burden on sampling. The other methods, such as adaptive umbrella sampling (Bartels and Karplus, 1998), conformational flooding (Grubmuller, 1995), and chemical flooding (Muller et al., 2002), achieve higher sampling efficiency by flattening the potential energy surface. In the ACM method, the potential energy function is the same as in the conventional simulation. The expansion of sampling is along the slow modes, i.e., low potential energy valleys on the potential energy surface.

There are still some disadvantages to our method. In the ACM simulations, a number of collective modes are coupled to a higher temperature at all times; that is, the system is always in a nonequilibrium state. There remains the question of how to extract the thermodynamics properties of the system from such simulations. Another disadvantage has to do with our selection of the slowest modes for higher temperature coupling. In some cases, the functional motions of the proteins we are interested in may not occur along these slowest collective modes. Future work is needed on how to pick up the collective modes of functional importance in such cases and selectively excite them in simulations.

CONCLUSIONS

Teeter and Case (1990) showed that the collective modes are sensitive to the force field; however, the frequency distributions and fluctuations were remarkably similar. In addition, the subspace spanned by a small number of collective coordinates is invariant in many cases and is almost independent of the details of actual approximations to the physical interactions between atoms and residues (Kitao and Go, 1991; Kitao et al., 1994). Based on the coarse-grained model ANM, we can calculate the collective modes of the protein at little cost. We have shown that by coupling these modes to higher temperatures, the most important collective motions can be amplified significantly and the essential subspace of protein dynamics can be sampled more adequately.

In our first application to demonstrate the method, multiple GBSA simulations of the S-peptide analog were performed. For the ACM simulations starting from the native structure, the native structure is stable, but larger fluctuations than the conventional simulations are observed. Among the total 10 ACM simulations started from the denatured structure, peptide refolding was observed in eight simulations; the peptide was not trapped in local, non-native minima as is the case in conventional simulations. It seems that the ACM method can expand the conformational space of the peptide extensively while restricting the sampling within the low-energy regions. The peptide results are interesting also in the sense that, to our knowledge, ANM has only been used to investigate the collective motions of folded structures before our work.

In the T4 lysozyme case, compared with the conventional simulation which sampled a restricted area in the conformational space, the interdomain motions observed in the ACM simulation (S_ACM) are much more obviously and in good agreement with the observed variances of different x-ray structures. As in the peptide case, the amplified motions are restricted to the long wavelength collective modes, with the secondary structures and individual domains almost undisrupted, compared with the conventional simulation.

Applications of the ACM method may be abundant, such as large-magnitude functional motions of protein, folding/unfolding pathways of peptides and proteins, and structure predictions. Our results indicated that the method could be used in both explicit and implicit solvent simulations and may be generally applicable to many different MD and MC formalisms. Of course, the method needs further improvements to investigate these important biological problems efficiently.