Dielectric Self-Energy in Poisson-Boltzmann and Poisson-Nernst-Planck Models of Ion Channels

Abstract

We demonstrated previously that the two continuum theories widely used in modeling biological ion channels give unreliable results when the radius of the conduit is less than two Debye lengths. The reason for this failure is the neglect of surface charges on the protein wall induced by permeating ions. Here we attempt to improve the accuracy of the Poisson-Boltzmann and Poisson-Nernst-Planck theories, when applied to channel-like environments, by including a specific dielectric self-energy term to overcome spurious shielding effects inherent in these theories. By comparing results with Brownian dynamics simulations, we show that the inclusion of an additional term in the equations yields significant qualitative improvements. The modified theories perform well in very wide and very narrow channels, but are less successful at intermediate sizes. The situation is worse in multi-ion channels because of the inability of the continuum theories to handle the ion-to-ion interactions correctly. Thus, further work is required if these continuum theories are to be reliably salvaged for quantitative studies of biological ion channels in all situations.

INTRODUCTION

Continuum theories of electrolytes, such as the Poisson-Boltzmann (PB) and Poisson-Nernst-Planck (PNP) equations, have been widely used in studies of ion channels during the last two decades. For example, the PB equation has been employed in calculation of the forces and energy profiles seen by ions in channels (e.g., Levitt, 1985; Jordan et al., 1989; Weetman et al., 1997; Adcock et al., 1998; Cheng et al., 1998), and to determine the ionization states of side chains (Roux et al., 2000; Ranatunga et al., 2001) under equilibrium conditions. Similarly, the PNP equations have been used to investigate the permeation properties of many channels (for review see Eisenberg, 1999; and for recent applications see Kurnikova et al., 1999; Cardenas et al., 2000; Nonner et al., 2000; Hollerbach et al., 2000; Hollerbach and Eisenberg, 2002). Recently the application of continuum theories to narrow ion channels (i.e., radius smaller than the Debye length of the electrolyte) was called into question, as they were found to overestimate electrolytic shielding effects (Moy et al., 2000, Corry et al., 2000, Graf et al., 2000). The PB equation predicts that high concentrations of counterions accumulate around a fixed test ion in a narrow channel, which act to eliminate the repulsive image forces due to the polarization charges induced at the channel walls. Such high concentrations of counterions around a test ion are not seen when the mobile ions are treated explicitly as in Brownian dynamics (BD) simulations. In BD, the image forces felt by individual counterions prevent them from easily entering the channel and thereby suppress the large degree of shielding seen in the PB theory. Similarly, in PNP calculations the currents passing through narrow channels are found to be much larger than in corresponding BD simulations, again as a direct consequence of higher ionic concentrations found in the former method.

Extensive comparisons with BD simulations indicate that the problems in both continuum theories arise from the fact that the dielectric self-energy contribution to the ions' potential energy is not properly taken into account (Moy et al., 2000, Corry et al., 2000). Because the self-energy is proportional to the square of the charge, it is positive for all ions, and it would repel them from the dielectric channel boundaries leading to a suppression of their concentrations. In numerical solutions of the PB and PNP equations, however, the charge of mobile ions is distributed throughout the channel and only a fraction of an ionic charge is found in a given region. This leads to a reduced amount of induced charges on the channel boundary, and the quadratic dependence of the self-energy on charge means that its effect is significantly underestimated. In reality, an ion carrying a unit charge of e induces charges on the channel boundary in an all-or-nothing way—either a large image force is induced (repelling the ion away from the boundary) or there is no ion and thus no force. The lack of dielectric self-energy was accentuated in many of the PNP calculations carried out previously, in particular those with no fixed charges in the channel walls (Corry et al., 2000). In these PNP results equal amounts of positive and negative electrolyte were found in the channel, and so there was no net charge at any given point. Thus, no charge was induced along the dielectric boundaries. This was in contrast to the BD simulations in which the positive and negative ions entered the channel at different times, and so each induced a large amount of surface charges and felt a large repulsive force from the channel boundaries. As shown by Corry et al., 2000, the failure to treat induced charges correctly in standard PNP models leads to currents much larger than those observed in BD.

Mean field theories of electrolytes have been commonly used to determine charge transport in semiconductors (Haensch, 1991; Assad et al., 1998) as well as to describe the electric field around globular proteins (Davis and McCammon, 1990; Sharp and Honig, 1990). Thus it may be surprising that the lack of dielectric self-energy has only been noted as a problem relatively recently. However, generally the dimensions of these systems are much greater than the Debye length. In such cases the effects of image forces can be shielded out by the surrounding electrolyte. Image forces are also more significant inside channels where the ion is surrounded by dielectric boundaries rather than facing them on just one side (Kuyucak et al., 2001). Thus, there has been little need to deal with the interaction with dielectric boundaries more carefully in semiconductors or around globular proteins as is required in ion channels.

Given the computational simplicity of the continuum theories compared to simulation approaches and their widespread use, it would be desirable to find a solution to the problem of dielectric self-energy highlighted above. A possible approach is to include an explicit self-energy term in the formalism that would mimic the effect of the induced surface charges on ions entering the channel. Such a term would prevent the buildup of large counterion concentrations around a test ion and may eradicate the spurious shielding effects seen in the continuum models. This approach to correct the continuum theories is being pursued elsewhere (Schuss et al., 2001; Mamonov et al., 2002; Coalson et al., 2002), but no explicit tests of its performance have been published. Here we examine the consequences of including a dielectric self-energy term in the PB and PNP formalisms. The forces calculated using the modified Poisson-Boltzmann and the currents found from the modified Poisson-Nernst-Planck equations are again compared with Brownian dynamics simulations to assess whether the suggested modification improves the performance of the continuum approaches in ion channels.

Another potential problem in applications of the continuum theories to ion channels is the spurious self-energy that arises from continuous distribution of an ion's charge. Distributing an ionic charge across a region leads to interactions of the charge with itself that are not present when the charge is localized at a single point. In single-ion channels, this is a relatively minor problem compared to that of dielectric self-energy, and perhaps because of this, it has not been considered in earlier literature. The significance of this effect, however, grows rapidly with the number of ions resident in a channel. Therefore, to understand and interpret the results obtained in multi-ion channels we will also discuss this spurious self-energy contribution in continuum theories in some detail.

METHODS

Modified PB equation

In Poisson-Boltzmann theory, the mobile ions are treated as a continuous charge density distributed according to the Boltzmann factor

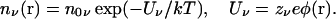(1)

Here n_0ν is a background (or reference) density of ions of species ν, U_ν is the electrostatic potential energy of an ion with charge z_νe, and φ(r) is the average potential at the position r determined from the solution of Poisson's equation

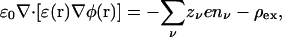(2)

where ρ_ex represents all the other external charge sources in the system such as fixed charges in the protein. The PB equation follows upon substituting the density from Eq. 1 into Eq. 2.

A crucial assumption of PB theory is that at a given point, the same average potential acts on all ions regardless of their valence, and hence the potential energy of anions and cations have opposite signs. This is a reasonable assumption to make in a homogeneous system but it cannot be justified in an inhomogeneous one with dielectric boundaries. Near a water-protein interface, a mobile ion with charge z_νe induces polarization charges of the same sign on the boundary. These charges, in turn, generate a reaction potential φ_R that acts to repel the ion from the boundary. The potential energy due to this reaction field, called the dielectric self-energy, is given by

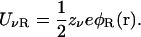(3)

Since φ_R is itself proportional to z_νe, U_νR depends on the square of the ionic charge, and hence it is always positive regardless of the valence of ions. Thus the dielectric self-energy contribution to the total potential energy of an ion is the same for cations and anions, which is incompatible with the assumption in Eq. 1. The upshot is that the PB equation cannot lead to a suppression of ionic densities near a dielectric boundary because it fails to take into account the dielectric self-energy contribution. A similar problem occurs in the Gouy-Chapman solutions of the PB equation where counterions build up at a charged electrode. In that case, this unphysical behavior is avoided by introducing a Stern or Helmholtz layer that excludes ions from the immediate neighborhood of the boundary. While the presence of this layer is motivated by the finite size of ions or the effect of the solvent layer, in practice its thickness is used as a free parameter to fit the experimental data. In any case, the physics of repulsive self-energy is very different and cannot be modeled by such a simple exclusion zone for ions.

The above discussion about the lack of dielectric self-energy in the PB equation also suggests an apparently simple remedy: modify the Boltzmann factor in Eq. 1 by adding a dielectric self-energy term to the potential energy

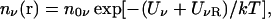(4)

so that the modified PB equation in a 1:1 electrolyte becomes

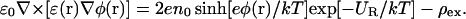(5)

As an ion approaches a dielectric boundary, U_R grows rapidly, and the exponential factor in Eq. 5 provides a natural mechanism to suppress the ion densities. The difficulty in this scheme, of course, lies in the calculation of U_R in a many-body system in a self-consistent manner. For a single ion, the self-energy is well-defined—one just needs to solve Poisson's equation for the single ion and substitute the computed reaction potential in Eq. 3. In a dilute electrolyte solution, where the effect of the reaction field created on one ion by another can be neglected, this simple recipe should be quite adequate for the self-energy correction. However, at higher concentrations, the approximation of the reaction potential with that of a single ion becomes problematic. Ion-to-ion correlations can be included into continuum electrolyte theories, such as has been done to describe the formation and behavior of highly charged ‘macro-ions’ and DNA molecules (e.g., Grosberg et al., 2002; Gelbart et al., 2000). In most cases these studies do not include the effect one ion has on another due to the reaction potential created at a dielectric interface as the calculations are carried out in a region of uniform dielectric constant, although some include dielectric boundaries with simple geometries (Nguyen et al., 2000). In continuum theories, incorporating the effect that the reaction field that is created by one ion has on another with more complicated geometries is a difficult problem. Thus, it is of interest to see whether the inclusion of the self-energy correction at the single-ion level (i.e., only the influence the reaction field created by an ion has on itself) improves the accuracy of the PB solutions sufficiently so that they can be used in ion channels with some confidence. For this purpose, we compare the results of the modified PB equation with those obtained from BD simulations.

The modified PB equation is solved using a finite difference method as described previously for the standard PB equation (Moy et al., 2000). The values of dielectric self-energy are calculated by solving Poisson's equation using the same technique, but with all the electrolyte concentrations set to zero. A unit charge is placed at each of the grid points used in the finite difference computation and the calculated values of U_R are stored on the computer in a table. Entries from this table are utilized during the solution of the modified PB equation (Eq. 5).

Modified PNP equations

The conduction of ions in an electrolyte solution is described by the Nernst-Planck equation

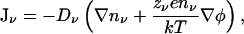(6)

where D_ν is the diffusion coefficient of the ions of species ν. When Eq. 6 is combined with Poisson's equation (Eq. 2), one obtains the PNP equations, which provide a consistent framework for the description of ion transport in homogenous systems. As in the case of the PB theory, the presence of dielectric boundaries creates problems for the application of PNP to narrow channels because the dielectric self-energy of ions is not properly taken into account.

The PNP equations can be modified in a similar manner to the PB equation by including a specific dielectric self-energy term in the potential energy of an ion:

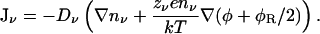(7)

The analogy between Eq. 7 and the modified PB equation can be seen most clearly when the current vanishes. Then Eq. 7 can be easily integrated yielding the modified Boltzmann factor given in Eq. 4. Here we solve Eq. 7 simultaneously with Eq. 2 using a finite difference procedure as described previously for the PNP equations (Corry et al., 2000). The values of dielectric self-energy are implemented in this process using a table as in the solution of the modified PB equation.

Self-energy in continuum theories

In continuum electrostatics, self-energy refers to the intrinsic potential energy of a charge (or charge distribution) with itself. This is different from the dielectric self-energy discussed above, which arises from the interaction of a charge with a dielectric boundary. Because an ion's self-energy is constant and has no effect on the results, it is routinely ignored in electrostatic calculations involving discrete charges, and only the Coulomb interactions among the charges are considered. In continuum theories, however, charges are distributed continuously and it is not possible to isolate the self-energy from the Coulomb interaction. Thus when Poisson's equation is solved in the PB and PNP theories, the calculated potential energy of ions necessarily contains a spurious self-energy contribution. This is not a concern in typical applications of continuum theories, which involve a large number of ions (N ≫ 1) in a nearly neutral electrolyte solution. First, the self-energy is proportional to N whereas Coulomb interaction scales as N², so its relative contribution would be negligible for large N. Secondly, near electroneutrality in a large system means that the self-energy due to any excess charge has to be small. To give an example, when a charge q is uniformly spread in a water-filled sphere of radius R, the self-energy associated with this distribution is given by

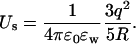(8)

For a unit charge with a dielectric constant of ɛ_w = 80, this yields U_s = 4.2 / R kT where R is in Å. Thus, in a large system (e.g., R > 100 Å), self-energy due to an excess ionic charge is completely negligible.

Ion channels do not satisfy either condition. They contain a rather small volume of electrolyte which is far from being electroneutral—at least for the majority of channels that are either cation- or anion-selective. Because the PB and PNP equations strive to maintain electroneutrality, this was not an apparent problem in earlier applications of the continuum theories to ion channels. The introduction of a dielectric self-energy term, however, leads to a suppression of the counterions in the channel and thereby exposes the problem of self-energy more conspicuously. To appreciate the magnitude of this effect, we show in Fig. 1 its influence in the simple case of electrolyte contained within a sphere. In Fig. 1 A, a single ionic charge is confined inside a 4 Å radius sphere with ɛ = 80 everywhere so that there are no dielectric boundaries. A single ion should, thus, move freely within the sphere occupying all space evenly. In contrast, the average concentration found using the (standard) PB equation (Fig. 1 A) exhibits a central depression, which is simply caused by the Coulomb repulsion among the charges distributed at all grid points. The potential energy of this charge distribution is ∼1 kT. This self-energy is, of course, entirely spurious because the potential energy of an isolated ion is zero.

FIGURE 1.

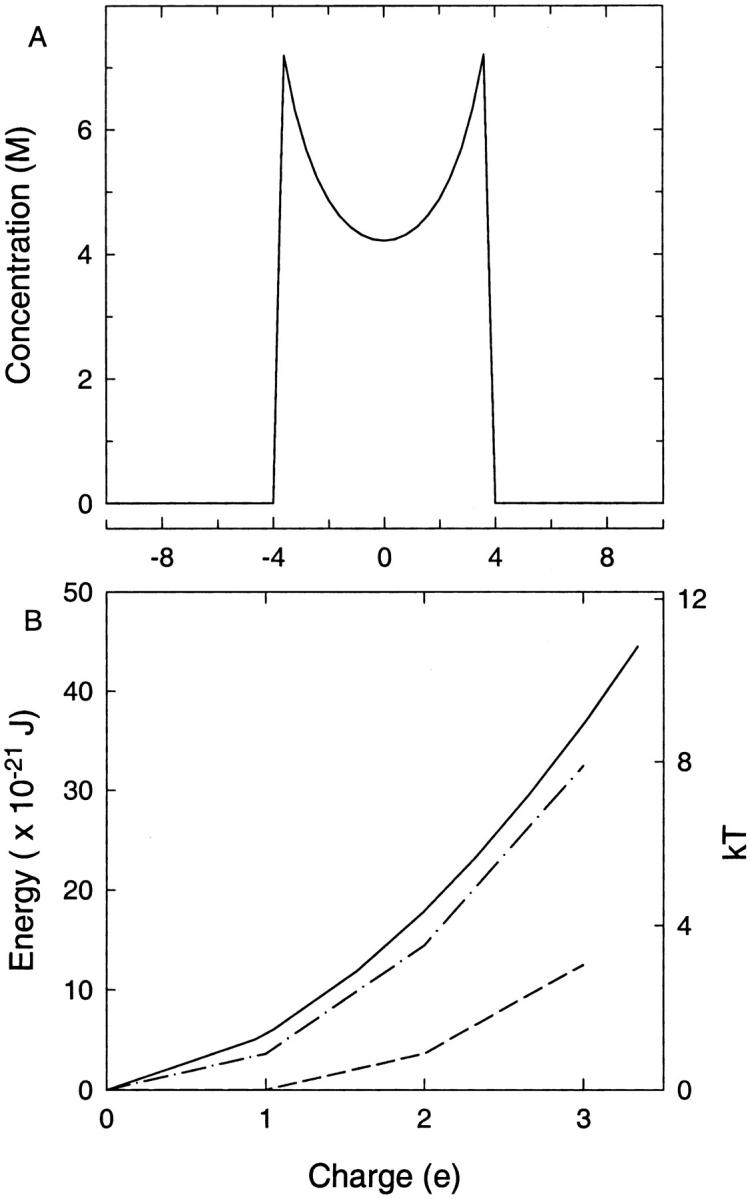
Spurious self-energy contribution to the total potential energy when the ionic charges are distributed continuously. In both cases the charge is contained inside a 4-Å radius sphere and ɛ = 80 is used everywhere. (A) The concentration found using the standard PB equation is plotted against the radial position when there is a net charge of e in the sphere. (B) The energy of the system as the charge in the sphere is increased. Results are shown as found from the PB equation at 298 K (solid line), 0 K (dash-dot line), and as calculated with discrete ions at 0 K (dashed line).

When the number of ions in the system is increased, the magnitude of the error increases before it starts to decrease at the large N limit. This is illustrated in Fig. 1 B, where the potential energy of the system is plotted as a function of the number of monovalent ions in the sphere. The solid line shows the potential energy obtained from the solution of the PB equation at room temperature (T = 298 K). As the charge in the sphere is increased, the potential energy is seen to increase roughly proportional to the charge squared. Thus, for two ions it is ∼4 kT, and for three ions, 9 kT. The dash-dot line in the figure shows the minimum electrostatic energy of the system that would be obtained at T = 0 K when all the charges collapse to the boundary. Because the two curves are quite similar, we simply present the minimum electrostatic potential energy for the corresponding discrete charge configurations (dashed line in Fig. 1 B). The discrepancy between the continuum and discrete representations of the potential energy is seen to grow with increasing number of ions. For two ions, the contribution of the spurious self-energy to the total potential energy is ∼3 kT which we expect to have a sizable impact on the results of the continuum theories. The error introduced by spurious self-energy would obviously be much greater when dealing with divalent ions.

While channels are cylindrical and do not absolutely confine ions, we expect the order-of-magnitude estimates presented above will have a bearing on the results of the modified PB and PNP equations, particularly in ion channels occupied by more than one ion. Whenever there is a net charge buildup inside the channel, the repulsion arising from the spurious self-energy will tend to push the electrolyte out of the channel, leading to a lowering of the concentration inside. This additional repulsion mechanism is required to understand some of the results presented below, especially in the case of multi-ion channels.

Brownian dynamics

Brownian dynamics simulations are carried out to compare results for the force on ions in the channel and the current across the channel with those found in the modified PB and PNP equations. BD provides a useful comparison as the mobile ions in the electrolyte are treated explicitly, whereas the dielectric boundaries are handled using continuum electrostatics in a similar manner to the continuum approach. Thus differences between BD and continuum theory results arise directly from using discrete ions rather than a continuous charge distribution.

The use of Brownian dynamics in ion channel simulations has been described previously in our previous articles (Chung et al., 1999; Moy et al., 2000; Corry et al., 2000, 2002; Kuyucak et al., 2001), and indeed some of the same data are utilized here as in those earlier studies. Very briefly, in BD the motions of individual ions are simulated using the Langevin equation in which the effects of surrounding water molecules are represented by frictional and random forces. The electric forces acting on the ion at each time step, including Coulomb interactions, interactions with the dielectric channel boundary, and any applied membrane potential are calculated by solving Poisson's equation using an iterative boundary element method (Hoyles et al., 1998). Additional forces that represent the short range interaction of ions, hydration effects, and interactions with the channel boundary are also employed (Corry et al., 2001). Ions are initially given random positions in reservoirs attached to each end of the channel, and the Langevin equation is solved at discrete time steps of 100 fs following a third-order algorithm (van Gunsteren and Berendsen, 1982). In the multi-ion channels, a shorter time step of 2 fs is utilized for ions inside the channel.

When comparing forces on an ion in the channel with the solutions of the modified PB equations, an ion is held at a fixed position in the channel while the other ions are free to move throughout the system. The force acting on the ion is averaged over the simulation period. When comparing with the modified PNP equations, all ions are free to move.

RESULTS

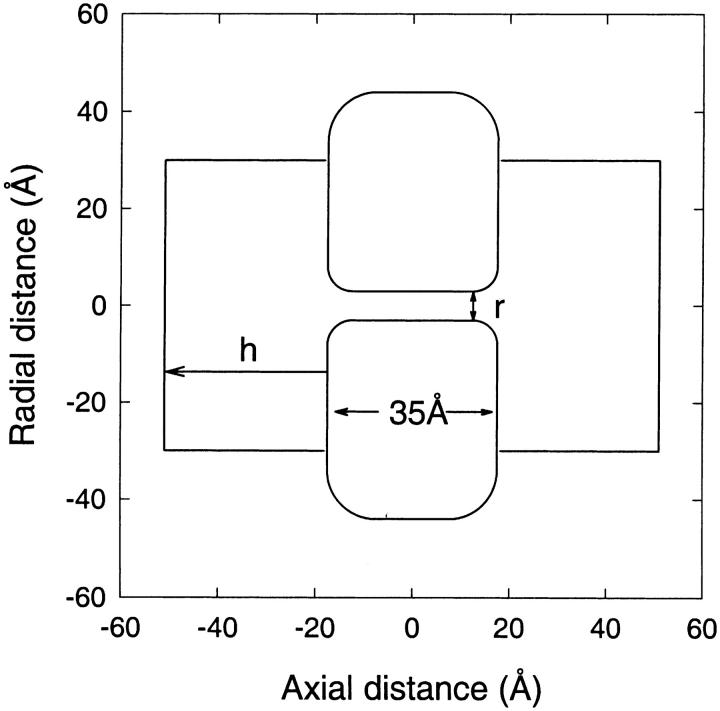
Because our aim is to see how much the inclusion of the dielectric self-energy term improves the continuum theories, we will compare the results of the modified PB and PNP equations with those obtained from BD simulations as well as from the standard PB and PNP equations. As the latter two theories have been compared extensively previously (Moy et al., 2000; Corry et al., 2000), we will rely on some of those results here. Therefore, the same schematic cylindrical channel with rounded corners is adapted in most of the comparisons (Fig. 2). The channel has a fixed length of 35 Å and its radius is varied from r = 3 to 13 Å. Two reservoirs with a radius of 30 Å and a variable height are attached to the channel. The height of the reservoir varies with the radius of the channel. For example, the height is h = 25 Å when the pore radius is 3 Å. For larger channel radii, h is adjusted to keep the entire volume of the system constant. The dielectric constants are set to 2 in the protein and 80 for the water. An average concentration of 300 mM is used in all cases, corresponding to 24 Na⁺ and 24 Cl⁻ ions in the BD simulations. The Debye length for this concentration is 5.6 Å.

FIGURE 2.

Cylindrical channel models used in comparisons of PB and PNP theory with BD simulations. A three-dimensional channel model is generated by rotating the cross section about the central axis by 180°. The cylindrical section is 25 Å in length, and the rounded corners have a radius of curvature of 5 Å, bringing the total length of the channel to 35 Å. The radius of the cylinder r is varied from 3 to 13 Å. The reservoir height h is adjusted so as to keep the total (reservoir and channel) volume constant when the radius is changed.

Modified PB equation

The modified PB equation is tested by calculating the force on a fixed test ion as well as potential and concentration profiles within model channels. Rather than repeating all the tests made in Moy et al. (2000), we present a selected few that convey the main results in a compact way. Because the cylindrical channel with no fixed charges exposes the problem of dielectric self-energy most clearly, we consider this case first. The test ion is held fixed at z = 12.5 Å, where the force on the ion is greatest, and the average force on the ion and the net screening charge within the channel are calculated using the modified PB equation. The results are compared to those obtained from the BD simulations and standard PB equation in Fig. 3 as a function of the channel radius. Fig. 3 A shows that the inclusion of the dielectric self-energy term dramatically reduces the concentration of counterions in the channel, well below that of the standard PB equation and the BD simulations. Only in the narrowest channel studied (r = 3 Å), where there is no screening charge in the channel, does the modified PB results agree with those of BD. Thus the unwanted shielding effects found in the standard PB equation are removed in channels with radius r ≤ 3 Å as desired. But, at larger channel radii, the amount of countercharge in the channel stays below that found in the BD simulations, indicating that the electrolyte screening is suppressed too much. Suppression of the countercharges in modified PB persists even after an agreement between the standard PB and BD results is obtained at r > 12 Å. However, this is due to the exclusion of ions from the immediate vicinity of the channel boundary by the dielectric self-energy term in Eq. 5, and does not affect the dynamics of an ion on the central axis. This is demonstrated in Fig. 3 B, where the axial component of the forces on the ion in modified PB and BD are seen to agree for r > 10 Å. Otherwise, the forces on the test ion mirror the behavior seen in Fig. 3 A. That is, in the r = 3 Å channel, both the BD and modified PB results agree with the single-ion result as there are no screening charges in the channel. But in intermediate radii channels, the modified PB predicts larger forces than BD because the screening charges are suppressed.

FIGURE 3.

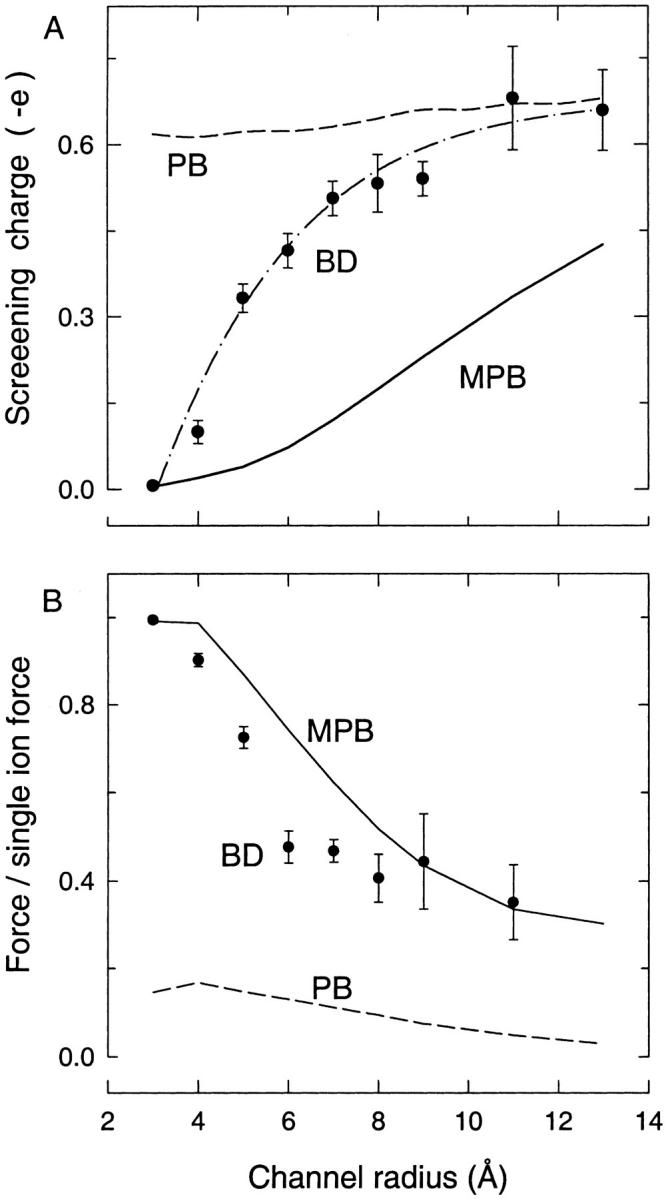
Pore size dependence of the screening charge and force on a cation held at z = 12.5 Å. (A) The net screening charge in the channel (from z = −15 to 15 Å) is plotted as a function of the channel radius. The modified PB (MPB) results are shown by the solid line, standard PB by the dashed line, and the BD values by the solid circles fitted with the dash-dot line. (B) The axial component of the force on the test ion normalized by the force on a single ion (calculated by solving Poisson's equation) is plotted as the channel radius is increased. Symbols are as in A.

The overall conclusion from Fig. 3 is that the inclusion of the dielectric self-energy term leads to a dramatic improvement in the PB results, especially for the narrow channels. However, in the intermediate radii channels, the discrepancy in the force when compared to BD is still large (∼50%), and is likely to be important in quantitative studies of ion channels. In a nutshell, the modified PB equation overcompensates for the dielectric self-energy in the standard PB equation, and now underestimates shielding rather than overestimating it.

Biological ion channels contain fixed charges in the protein walls that create valence selectivity. For completeness, we examine the more realistic case of a r = 4 Å channel with negative charges at the entrances. These negative charges cancel the energy barriers encountered by cations, while roughly doubling their height for anions, thus making the channel cation-selective. Here, we place a ring of eight negative monopoles each with charge −0.09 e spread evenly near the channel mouths at z = ±12.5 Å and set 1 Å inside the boundary. In Fig. 4 A we plot the potential profile through the channel as found from the PB equation (upper dashed line), modified PB equation (MPB, solid line), BD simulations (dash-dot line) and Poisson's equation with no electrolyte (lower dashed line). Here there is no test ion in the channel as this has already been considered above. The potential found from the modified PB equation shows a significant improvement compared to the standard PB results. Interestingly, although the modified PB potential displays a considerable drop, it does not overshoot the BD result as in Fig. 3.

FIGURE 4.

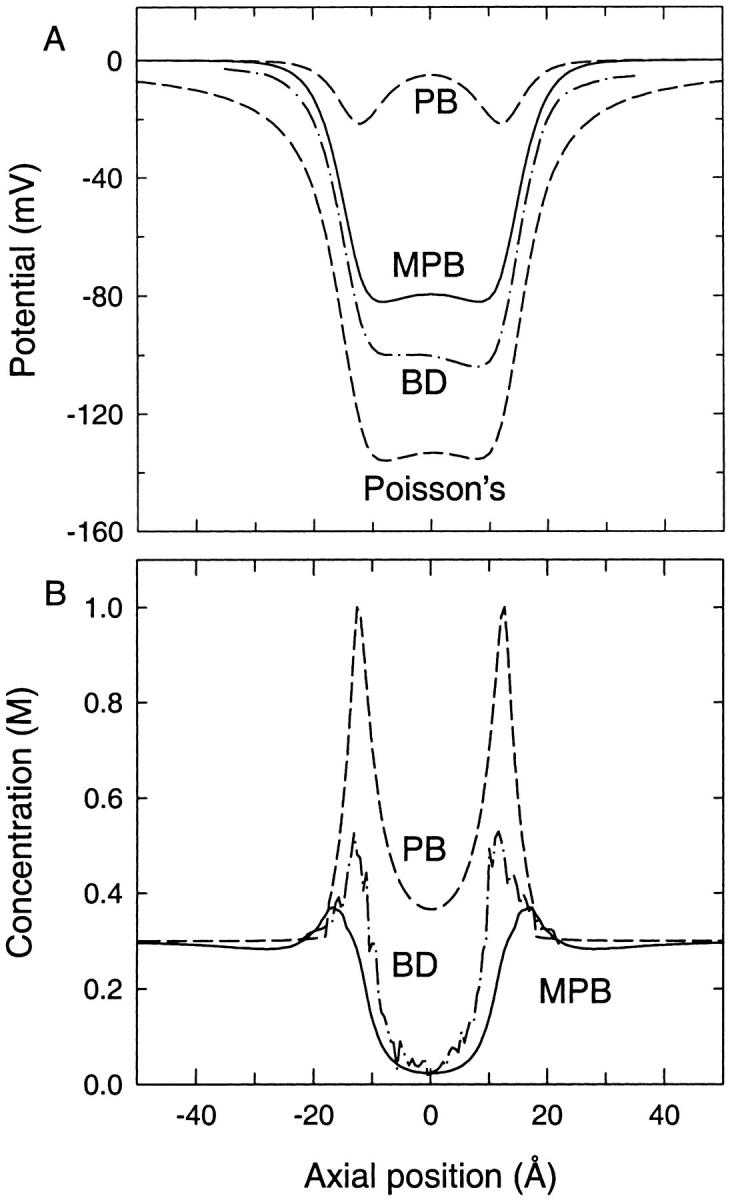
(A) Potential profiles found in a 4-Å radius cylindrical channel with charges in the protein and no fixed test ion found using the standard PB equation (upper dashed line), modified PB equation (solid line), and BD (dash-dot line) with 300 mM NaCl solution in the baths. The potential found from Poisson's equation with no electrolyte is shown by the lower dashed line. (B) Concentration profiles corresponding to the results in A.

A similar improvement is observed in the cation concentration profiles in Fig. 4 B. In this case, the modified PB concentrations slightly overshoot those of BD. Again this is caused by the suppression of ionic concentrations near the boundary by the dielectric self-energy term. We stress that unlike the PB equation, the modified PB equation is not self-consistent because the additional term representing dielectric self-energy is included in Eq. 5 in an ad hoc manner. In the potential plot, the modified PB results lie closer to the standard PB results than those found from BD. However, in the concentration plot the reverse is true. The reason for this is that the potential plotted in Fig. 4 A is φ found from Eq. 5, whereas the concentration in Fig. 4 B is determined from φ + φ_R/2 as indicated in Eq. 4.

We next consider the gramicidin A channel, which offers a more realistic case study. A model of the channel is constructed from the recent NMR data (Ketchem et al., 1997), including the partial charges of all the protein atoms as described previously (Edwards et al., 2002). In Fig. 5, A and B, we show the potential profile and concentration of cations found in this channel in a similar manner to Fig. 4. In the absence of an electrolyte, the potential has a deep well created by the partial charges in the protein, which act to attract cations into the channel. Using the standard PB equation, the potential is flattened out because, as seen in Fig. 5 B, a large concentration of cations enters the channel and almost cancels the Coulomb potential of the partial charges. When the modified PB equation is used, however, we find that this potential profile remains largely unchanged from the solution of Poisson's equation because the dielectric self-energy term leads to a large suppression of the cation concentration in the channel. The potential found from the modified PB equation is remarkably similar to that found from the BD simulations, the two agreeing within a few percent. Comparing the concentration profiles in Fig. 5 B, we find that in both cases the concentration of ions in the channel is quite low. Thus in the gramicidin A channel, the inclusion of the dielectric self-energy term in the PB equation yields a dramatic improvement. This may not be surprising as the channel is very narrow and is found to be occupied only 10% of the time by a single cation. This means that the dielectric repulsion from the channel boundary is a dominant effect, and it can be approximated quite well by the repulsion felt by a single ion.

FIGURE 5.

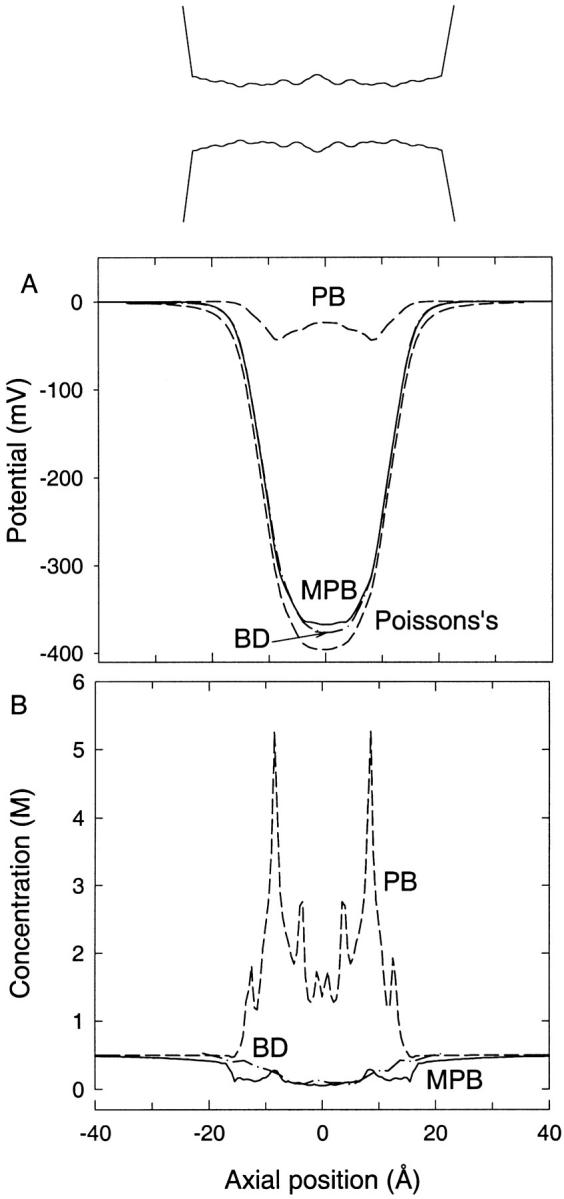
(A) Potential and (B) concentration profiles as in Fig. 4 except in the gramicidin A channel. A concentration of 500 mM KCl is used in both cases. The shape of the channel is shown in the inset.

As a final test of the modified PB equation, we consider the KcsA potassium channel. Not only does this channel have a more complicated geometry, it is also always occupied by multiple ions. The contribution of dielectric self-energy calculated by using a single ion is likely to be a poor approximation. Also, ion-to-ion interactions that are difficult to describe in a continuum approach may become important, and errors due to the spurious self-energy are more likely to be significant. An open-state shape of the channel is constructed from the KcsA crystal structure (Doyle et al., 1998) as described previously (Chung et al., 2002). The profile of this channel shape is shown at the top of Fig. 6. The narrow selectivity filter of the channel is surrounded by carbonyl oxygen atoms whose partial negative charges create a deep potential well as seen from the solution of Poisson's equation (lower dashed line in Fig. 6 A). These negative charges attract potassium ions into the channel, whose presence decreases the size of this well. When the standard PB equation is used, enough cations enter the channel so as to cancel out the potential well. In BD simulations, two ions are found in the selectivity filter on average. Because the volume of this section of the channel is very small, this leads to a very large concentration there as seen in Fig. 6 B. The two peaks in the concentration plot show the likely positions of the ions. These ions again act to cancel the potential well in the channel. The discrepancy between the potential profiles obtained with the BD and the modified PB is greater than that obtained with the BD and the standard PB (Fig. 6 A). Less cation concentration builds up in the channel, which results in a very deep potential well (∼700 mV) in the modified PB equation.

FIGURE 6.

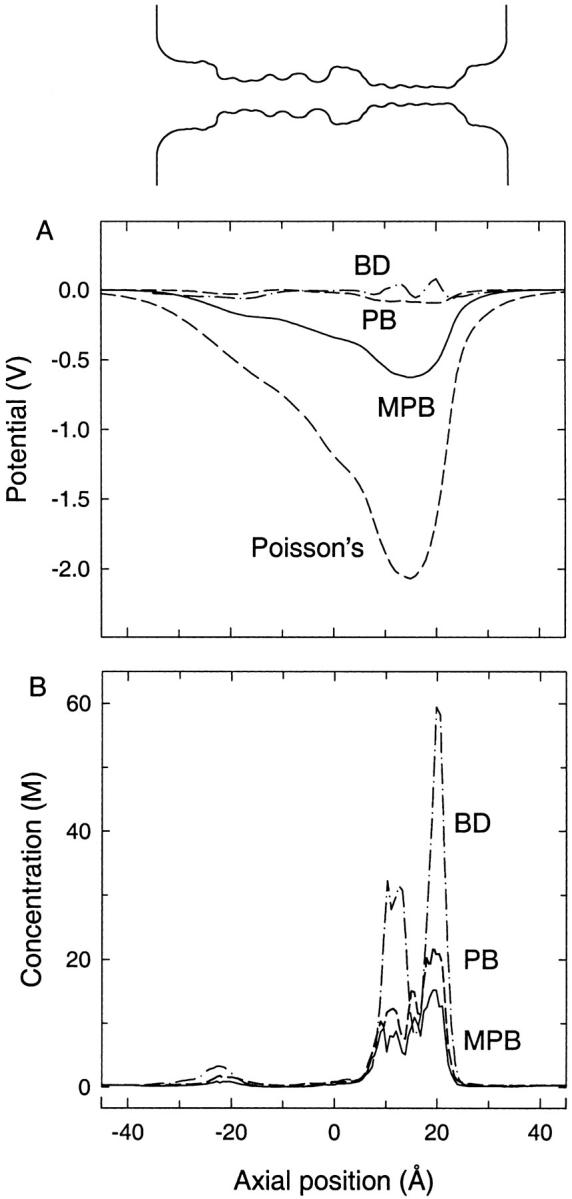
(A) Potential and (B) concentration profiles as in Fig. 4 except in the KcsA potassium channel. A concentration of 300 mM KCl is used in both cases. The shape of the channel is indicated in the inset.

Examining the concentration profiles in Fig. 6 B, we note that even the standard PB equation predicts a much lower concentration than is found using BD. Indeed, whereas BD predicts a total of four ions in the channel, the PB equation predicts 2.5 and the modified PB only 1.5 ions. (Note that the channel is wider at the left-hand side, and so even though the peak in concentration there looks small, it represents at least one ion.) The most likely reason for this suppression in the concentration is the spurious self-energy in the PB solutions. In the KcsA channel, multiple ions are present in the narrow selectivity filter, and the spurious self-energy of this charge distribution acts to reduce the concentration there in the PB solutions. A second observation is that the inclusion of the dielectric self-energy term has a relatively small impact on the concentration compared to the dramatic suppression seen in single-ion channels. This happens because the dielectric self-energy is taken into account at the single-ion level and when there are multiple ions in the channel, its effect is underestimated. The overall conclusion is that, unlike the single-ion channels, the modified PB equation leads to inferior results in this multi-ion channel compared to the standard PB equation. It appears that the spurious self-energy in a multi-ion channel more than compensates for the lack of dielectric self-energy in the PB equation, and hence its explicit inclusion results in an overestimate of the magnitude of the repulsive forces acting on ions.

Modified PNP equations

As a first test case, we again consider the schematic cylindrical channel shown in Fig. 2 without any charges in the protein. Following the tests carried out in a previous article (Corry et al., 2000), we calculate the current passing through this channel using the modified PNP equations and compare them to currents derived from BD simulations. All calculations are carried out using a symmetrical 300 mM NaCl solution and an applied potential of 105 mV between the reservoir ends. In Fig. 7, we plot the channel conductance for cylindrical channels as a function of the channel radius. Here the conductance is normalized by the cross-sectional area of the channel to factor out the trivial increase in current with increasing area. The old PNP results of Corry et al. (2000) are indicated by the dashed lines and show the slight downward trend created by access resistance effects. The currents in narrow channels found from BD (data points fitted by dash-dot lines) are well below the PNP values due to the repulsive self-energy barrier retarding the permeation of ions through the channel. A similar suppression occurs in modified PNP, when the dielectric self-energy term is included explicitly in the PNP equations. Indeed, the currents carried by both cations and anions are essentially zero in the 3-Å radius channel in agreement with the BD results. The normalized conductance climbs as the channel radius is increased in a similar manner to that seen in BD. There are some differences in intermediate radii channels, but the differences are remarkably small (∼35%). It appears that the inclusion of an explicit dielectric self-energy term in the PNP equations can reproduce the BD results reasonably well in these bare channels.

FIGURE 7.

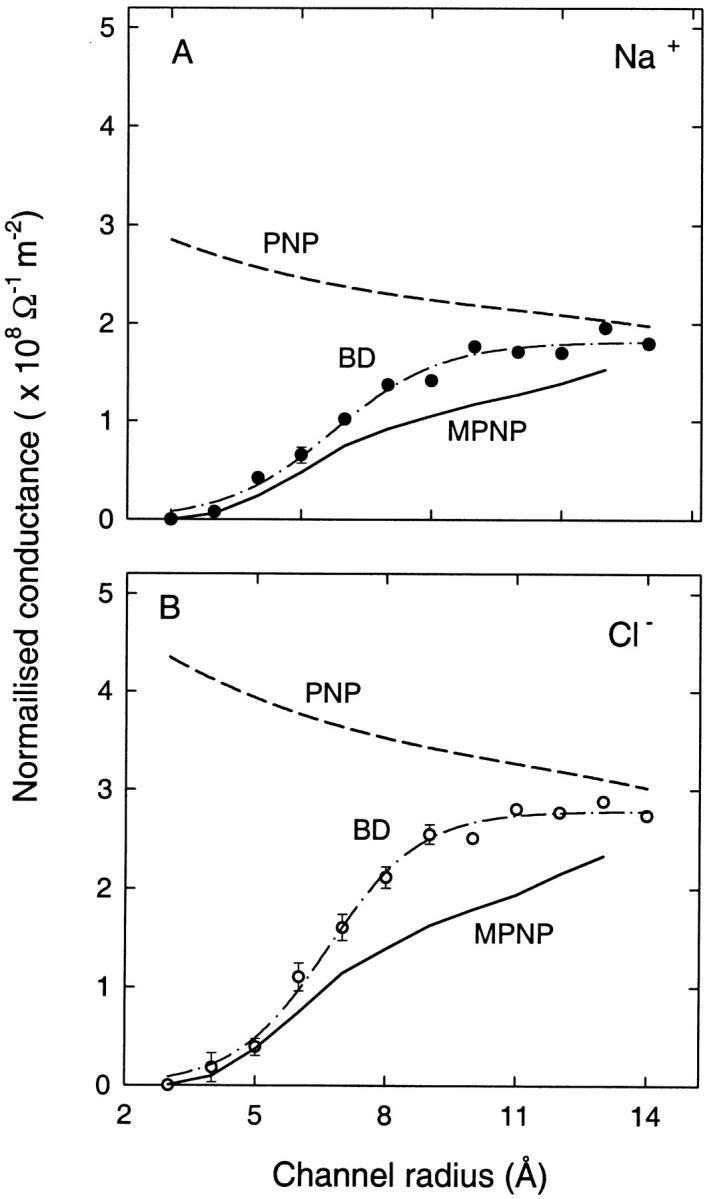
Conductance of Na⁺ (A) and Cl⁻ (B) ions for bare (no fixed charge) channels of varying radii normalized by the cross-sectional area. The results of the modified PNP equations (solid lines), standard PNP (dashed lines), and BD simulations (data points fitted by dash-dot lines) are shown. The ions are driven across the channel with an applied field of 105 mV between the reservoir ends and a 300 mM NaCl solution is maintained in the reservoirs.

Next we consider the simple cation-selective channel studied in Fig. 4. The presence of the negative charges has been shown to spoil the coexistence of anions and cations and reduce the perfect shielding seen in PNP studies of bare channels (Corry et al., 2000). As a result, discrepancy between PNP and BD results gets smaller in charged channels, especially for cation currents (Fig. 8 A). The results obtained with the modified PNP (Fig. 8, solid lines) lie below those obtained with BD, and the previous agreement between PNP and BD for cation currents at intermediate radii channels is spoiled. In the intermediate radii channels, there remains roughly a factor-of-2 discrepancy between the cation currents found from modified PNP and BD. The results from both techniques converge again at larger radii.

FIGURE 8.

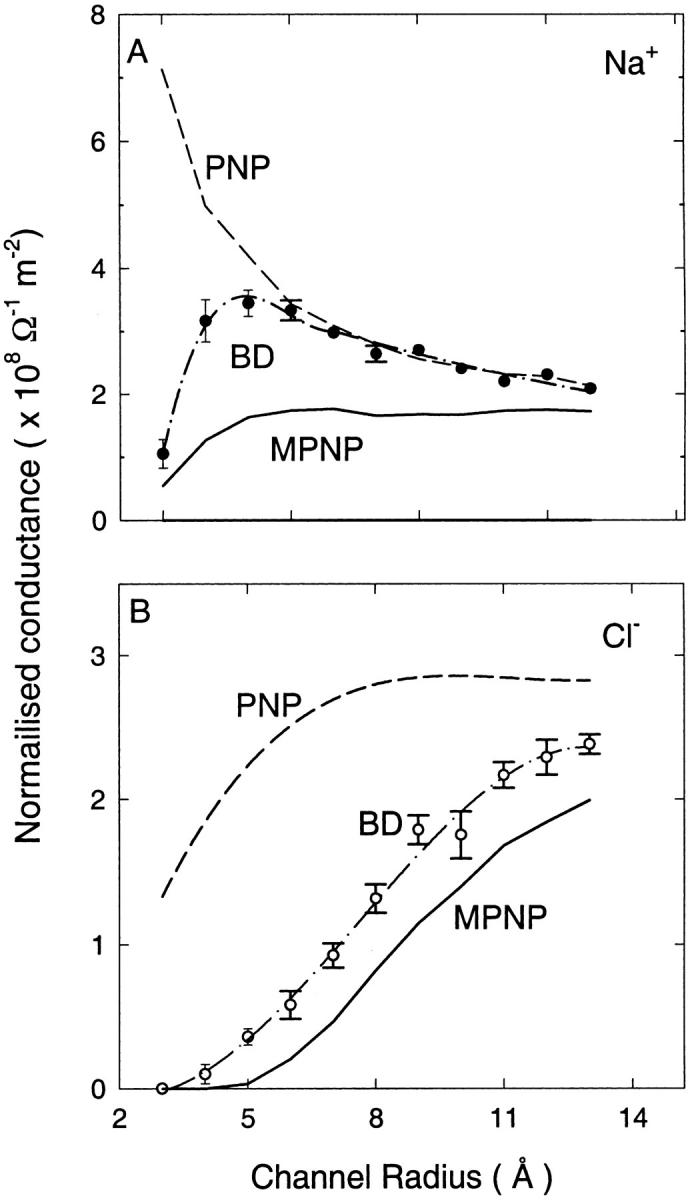
Normalized conductance in cylindrical channels with fixed charges in the channel walls; otherwise, as in Fig. 7.

The reason for the discrepancy between the modified PNP and BD results is explained in Fig. 9, where we plot the cation (Fig. 9 A) and anion (Fig. 9 B) concentrations in the 4-Å radius channel with fixed charges. In Fig. 9 B, inclusion of the dielectric self-energy term is seen to stop anions from entering the channel, preventing the large concentration found using the standard PNP equations and yielding a much better agreement with BD. But Fig. 9 A shows that the cation concentration is reduced too much at the channel entrances in the modified PNP compared to BD. Obviously, the lower cation concentration results in a smaller current in the modified PNP theory. The inclusion of the dielectric self-energy term has led to a dramatic improvement in bare channels, but the improvement is not as good in charged channels because the modification appears to overcompensate for the electrolyte shielding. Although the conductance results are more realistic and demonstrate a more accurate qualitative behavior, quantitatively there are still significant deviations from the BD predictions.

FIGURE 9.

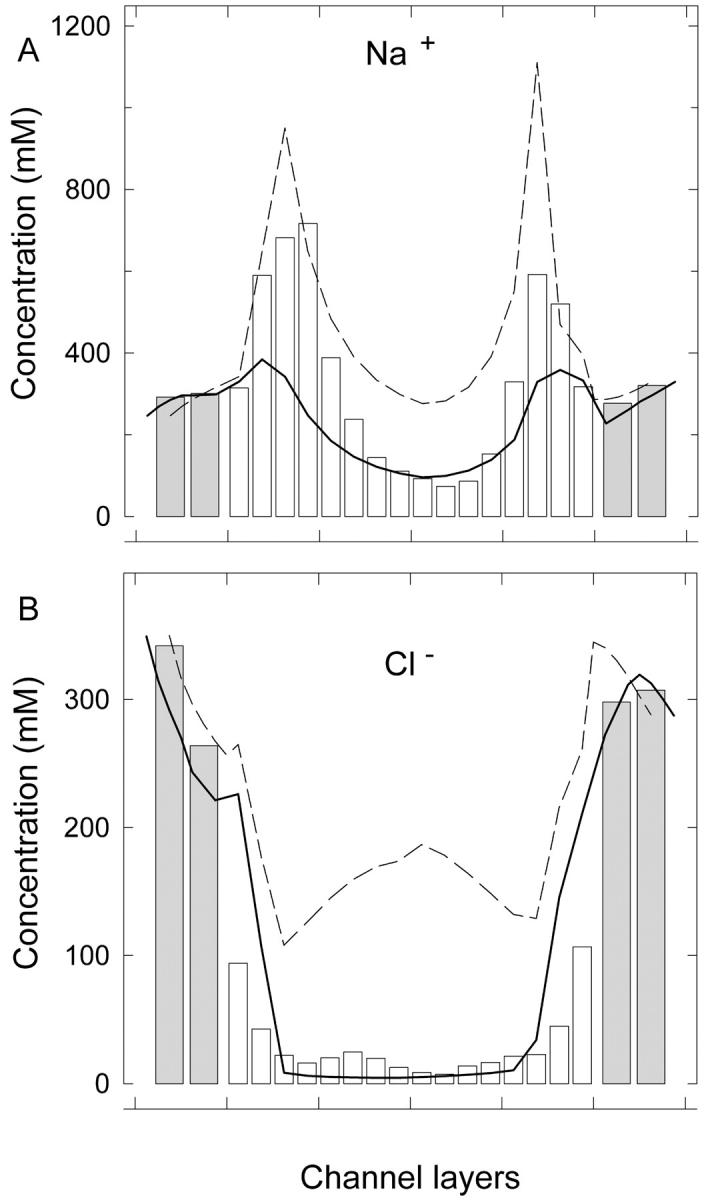
Concentration profiles for (A) Na⁺ and (B) Cl⁻ ion in a 4-Å radius cylindrical channel with fixed charges as found from the modified PNP equations (solid line), standard PNP (dashed line), and BD simulations (bars). The pore is divided into 16 equal segments along the channel axis, and the average concentration in each segment is plotted.

So far we have considered single-ion cylindrical channels in testing the modified PNP equations. We next discuss multi-ion channels, where our attempt to remedy the defect in the continuum approximation may not be as successful as in channels occupied by a single ion. First we examine the currents flowing through a model L-type calcium channel discussed previously (Corry et al., 2001). The shape of the channel is shown in the inset at the top of Fig. 10, and includes a narrow selectivity filter surrounded by four negatively charged glutamate residues. These residues strongly attract cations, holding one calcium ion, or two sodium ions permanently in the channel. Conduction requires the entry of another ion making it a two-calcium or a three-sodium ion process (Corry et al., 2001).

FIGURE 10.

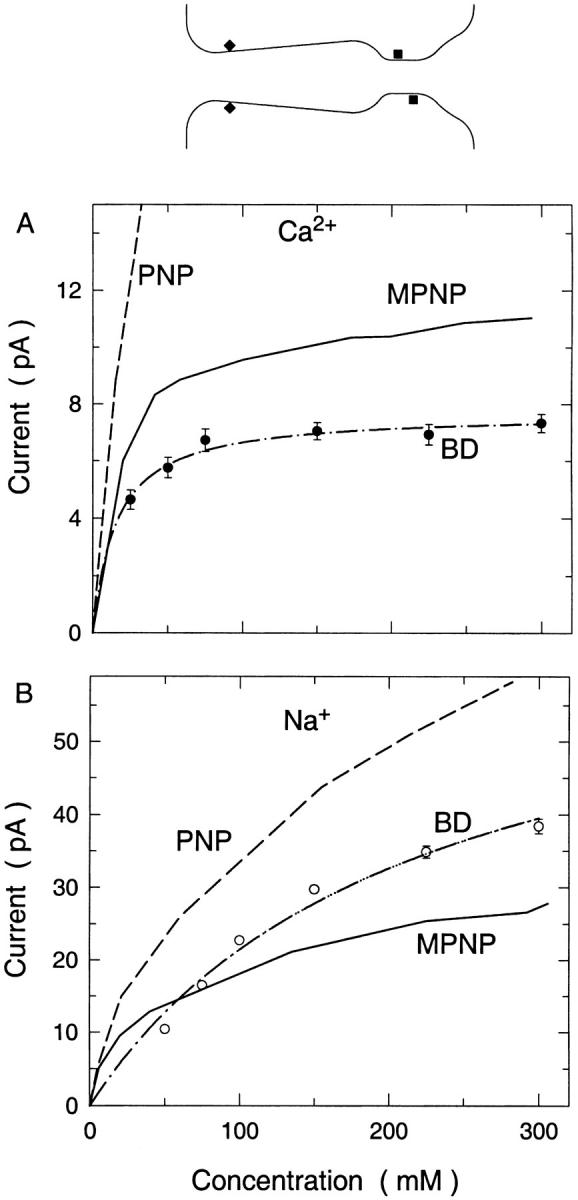
Current-concentration relationships for (A) CaCl₂ and (B) NaCl in the L-type calcium channel. Results found from BD simulations (data points fitted by dash-dot line), the standard PNP equations (dashed line), and the modified PNP equations (solid line) are shown. The shape of the channel and the locations of two of the four glutamate residues (squares), and the negative ends of the intracellular helix dipoles (diamonds) are shown in the inset. Diffusion coefficients used are 1.33 and 0.79 × 10⁻⁹ m² s⁻¹ for sodium and calcium.

The standard PNP equations give very poor results in this channel. The magnitude of the calcium currents predicted are too large by an order of magnitude. Indeed the calcium currents are slightly greater than the sodium currents, the reverse of what is found using BD and in experiment. The results found using the modified PNP equation are more sensible. Notably, the calcium current is reduced to a more appropriate value, only ∼35% greater than expected. The current shows an initial nonlinearity at low concentrations, suggesting that saturation has been obtained. But after this it appears to increase fairly linearly. The sodium current is only reduced a small amount when the dielectric self-energy term is added. The calcium current is reduced much more due to the larger dielectric self-energy experienced by divalent ions.

Another difference between the modified PNP and BD results worth noting is the different number of ions that are found in the channel. The average number of cations and anions in the channel with either 150 mM CaCl₂ or 150 mM NaCl that were found using the different theories are shown in Table 1. In BD simulations the conduction of calcium ions is essentially a two-ion process. One calcium ion resides in the selectivity filter, and a second must enter for conduction to take place. Indeed, the most common situation is for two ions to reside in the selectivity filter, and the rate-limiting step in conduction is for one of these ions to exit the selectivity filter. Thus, it is found that there are, on average, almost two ions in the channel. The modified PNP equations, however, predict just over one ion in the channel. It also predicts a more realistic number of sodium ions in the channel, but overall the inclusion of the dielectric self-energy term does not improve the results of the theory when considering the number of ions in the channel.

TABLE 1.

Number of ions in L-type calcium channel with either 150 mM CaCl₂ or 150 mM NaCl, estimated from PNP, modified PNP, and BD

	Number of ions in channel, 150 mM CaCl2		Number of ions in channel, 150 mM NaCl
	Ca2+	Cl−	Na+	Cl−
PNP	1.98	0.48	3.31	0.22
MPNP	1.12	0.01	2.61	0.01
BD	1.91	0.08	3.03	0.07

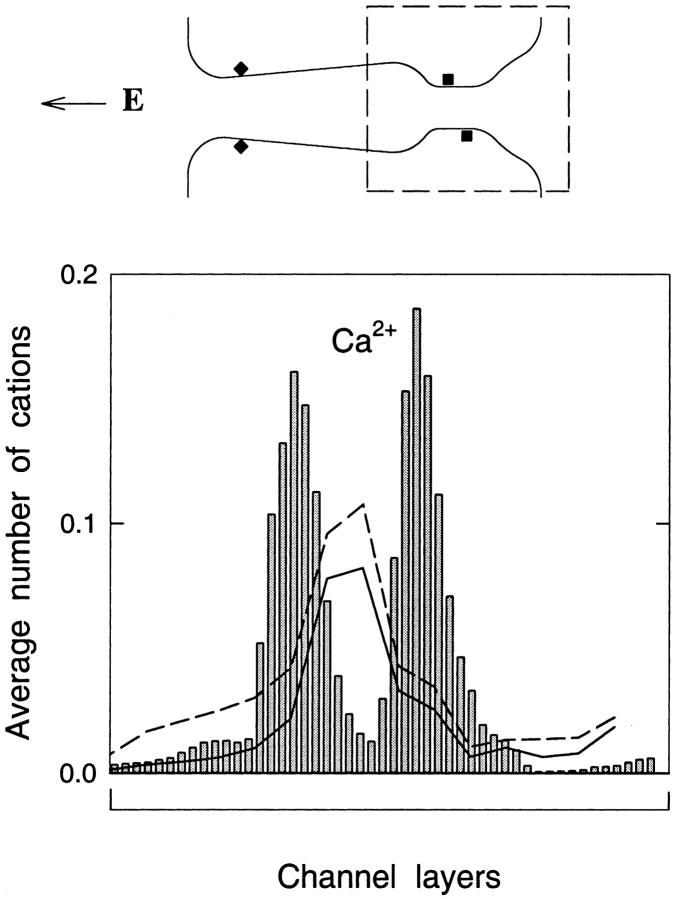
The differences in ion numbers in the channel is highlighted in Fig. 11, in which the channel is divided into layers, and the average number of ions in each determined. Here we show the number of ions in the right-hand half of the channel (selectivity filter and external vestibule) using 150 mM CaCl₂. In the BD simulations, two ions are usually present in this region, and this is clearly seen in the two large concentration peaks which indicate the most likely positions of the ions. The standard or modified PNP theory, however, shows a broader peak in the selectivity filter which only represents approximately one ion.

FIGURE 11.

Average number of ions in layers comprising the right-half of the calcium channel as found from BD simulations (bars) as well as the standard (dashed line) and modified (solid line) PNP equations using 150 mM CaCl₂. The section of the channel for which the concentration is plotted is indicated by the dashed box in the inset.

As the continuum approach cannot capture the dynamics of permeation, it is more limited in the types of questions it can be used to answer. For example, in our BD studies of the calcium channel, we have been able to simulate mixtures of calcium and sodium ions to better understand channel selectivity. The divalent calcium ions are more strongly bound to the glutamate charges than a sodium ion. A shortcoming of the present continuum approach is that this feature cannot be reproduced as it requires the localization of divalent and monovalent charges in discrete positions and a representation of their movement in time.

Finally we examine currents in a potassium channel. Rather than using the full-atom model described earlier when using the Poisson-Boltzmann equation, we have employed a simplified channel that gives similar currents as described elsewhere (Chung et al., 2002). The reason for using this model is that it is simpler to include in the PNP routines and we can also adjust the dimensions of the model more easily, such as, for example, widening the intracellular pore diameter to examine how such alterations vary the results of the PNP theory. The shape of the channel is shown at the top of Fig. 12.

FIGURE 12.

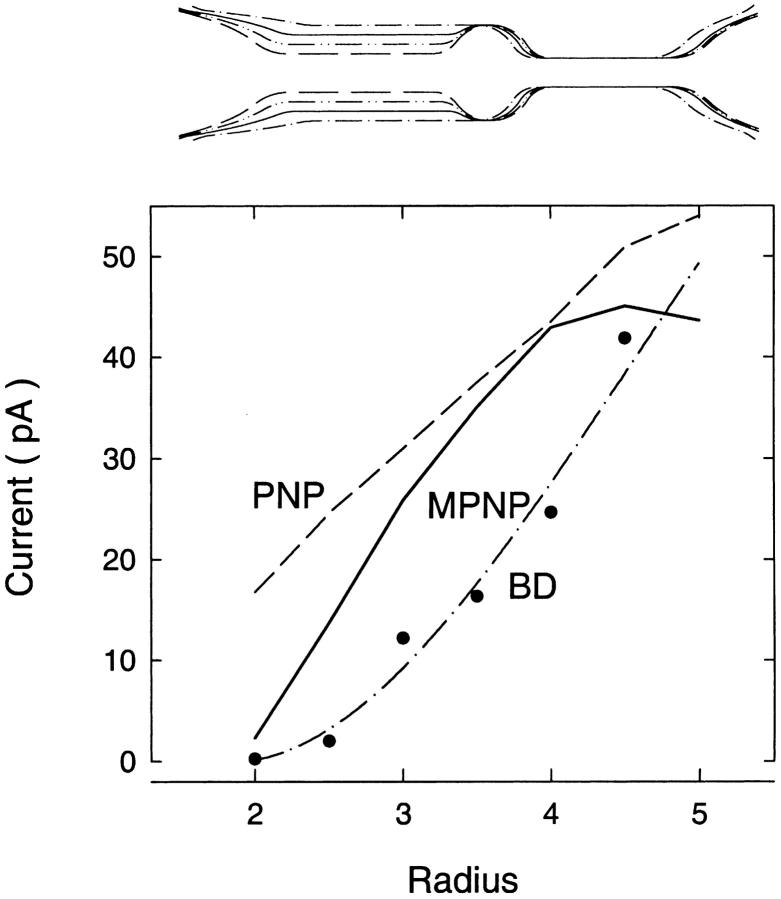
Current passing through the simplified potassium channel model plotted against the intracellular pore radius of the channel as found from BD simulations (data points fitted by dash-dot line), the standard (dashed line), and modified (solid line) PNP equations. The shape of the channel is shown in the inset.

In Fig. 12 we show how the current in the channel varies as we widen the intracellular pore diameter as done elsewhere (Chung et al., 2002) using the PNP and modified PNP equations or BD simulations. When we consider the magnitude of the currents shown in Fig. 12 A, the results look remarkably similar to those in the cylindrical channels. The standard PNP equations predict too great a current in all cases, but the modified PNP equations appear to give more reasonable results at narrow and wide radii. The discrepancies in the magnitude of the modified PNP and BD currents are largest in the intermediate radii channels, where the modified PNP yields currents that are ∼2× larger than the corresponding BD results. It is worth noting that the modified PNP theory overestimates the current by a factor of >100 in the 2-Å channel. The agreement is much better in wider channels, where the difference between the BD and modified PNP results are 74% and 8% in the 4- and 5-Å channels.

When we consider the average number of ions in the channel, we find that the modified PNP equations again predict too few ions as shown in Table 2, particularly in the narrower channels. Whereas the BD simulations find 3.5 ions in the narrow 2-Å radius channel, the modified PNP equations find one less: only 2.5 ions. Although this may not seem important if the currents are reasonably accurate, knowing the number of ions involved in the permeation process is essential if we are to understand the process properly. Thus the inclusion of the dielectric self-energy term certainly improves the PNP results, but substantial errors are still encountered in the predicted currents and ion concentrations.

TABLE 2.

Number of ions in differing radii potassium channels found from various models

	Number of ions in channel, 2-Å radius		Number of ions in channel, 5-Å radius
	K+	Cl−	K+	Cl−
PNP	3.38	0.24	3.98	0.47
MPNP	2.51	0.06	2.92	0.04
BD	3.51	0.09	3.00	0.03

DISCUSSION AND CONCLUSIONS

Compared to simulation methods such as Brownian and molecular dynamics, the continuum theories offer a considerably simpler and less time-consuming alternative for studying ion channels. Thus it is desirable to find a solution to the recently raised dielectric self-energy problem that limits the application of continuum theories to very large channels with radius r > 10 Å. The simplest method to achieve this is to modify the PB and PNP theories by including an explicit dielectric self-energy term when calculating electrolyte concentrations, as the lack of such a self-energy is at the root of the problem. The tests presented here show that inclusion of the dielectric self-energy term at a single-ion level leads to a significant improvement in the performance of the PB and PNP equations in ion channels.

When using the modified PB equation, the greatest improvement is obtained in the narrowest single-ion channels studied. This is because the dielectric self-energy term has the largest effect in such channels, and its inclusion in the PB equation almost eradicates ion concentrations in the channel in accordance with the BD simulations. Agreement between the modified PB theory and BD simulations is also retained in wide channels with r > 2 Debye lengths. However, at intermediate channel radii the agreement is not as good, and errors of up to 50% are common. The validity of the modified PNP theory in single-ion channels mimics that of the modified PB equation. Accurate results are obtained in very narrow and very wide channels, but errors are present at intermediate radii. Inclusion of the dielectric self-energy term yields a general qualitative improvement, but where the standard continuum equations overestimate electrolyte shielding, the modified continuum equations underestimate it in many cases.

The overall performance of the modified continuum equations is worse in the multi-ion potassium and calcium channels considered here. In the KcsA potassium channel, the concentration obtained from the modified PB equation is found to be too low in the selectivity filter. The qualitative shape and magnitude of the potential also exhibit significant discrepancies when compared to the BD results. The modified PNP equations do better when applied to a highly charged calcium channel model. The predicted calcium currents are a little too high and the sodium currents too low, but, overall the inclusion of dielectric self-energy yields more realistic current values. In both the KcsA and calcium channel models, the channel is highly charged and there are multiple ions resident in the channel. The interactions between the discrete ions are expected to play an important role in ion dynamics, which is difficult to describe in the continuum picture. For example, the magnitude of the dielectric repulsion acting on an ion will be modified in the presence of a second ion. Because the dielectric self-energy correction is introduced at the single-ion level, this effect is likely to be underestimated in a multi-ion channel. In addition, the spurious self-energy associated with a continuous charge distribution becomes more important in a multi-ion channel, although this may somewhat counteract the lack of dielectric self-energy. The incorrect numbers of ions inhabiting the multi-ion channels predicted by the continuum theories may be a manifestation of the inaccuracies involved in describing interactions between ions in the channel. The problems highlighted in these and earlier studies also indicate that the validity of using the PB equation for calculating pK_A values in ion channels needs to be assessed.

More sophisticated statistical mechanical descriptions of electrolytes are being developed, but as far as we are aware, none of these theories attempt to take into account the dielectric self-energy term in ion channels. The primary applications of density functional theory in inhomogeneous systems are concerned with electrolytes near a highly charged plane (Henderson et al., 2000) or hard-sphere fluids in a cavity (Gonzalez et al., 1997), neither of which is directly relevant to ion channels. In the former, the image forces are simply ignored (considering the high charge on the planes, this is presumably a good approximation), whereas in the latter there are no image forces.

Recently, there have been a number of attempts to build finite ion size effects into continuum models of ion channels using the mean spherical approximation or density functional theory (Nonner et al., 2000; Goulding et al., 2000; Boda et al., 2002). It is worth considering whether the discrepancies between the modified continuum theories and BD simulations could be improved by doing this. The BD simulations differ from the continuum models by allowing finite sizes for ions, as well as by including them as discrete charges which induce surface charges. Thus, it is possible that this is creating discrepancies between the results of the models, as well as the lack of dielectric surface charge. However, the inclusion of ion sizes would only worsen the level of agreement seen between the modified PB theory and BD simulations seen here. This is clear if we look at the cases where the theories disagree. As stated above, the modified PB theory tends to overestimate the size of the repulsive forces acting on ions in the channel. This means that the concentrations of ions are below that found from BD. Taking into account the finite size of ions in the continuum theory would act to limit how densely charge can be packed into the channel. This, of course, would tend to decrease the concentration in the channel further and worsen the agreement with BD simulations. Thus, it is important that the effects of dielectric self-energy are considered in future mean field studies of ion channels.

The continuum theories are designed for use in systems containing a large number of ions, which is obviously not satisfied in ion channels. Therefore, their application to ion channels needs to be continuously monitored to check against spurious and nonphysical effects. Here we have shown that attempts to improve the PNP and PB equations by including a specific dielectric self-energy term work reasonably well in some cases, but not all. This appears to be a promising direction for improvement, but further work is required to remove all the shortcomings highlighted in this work. Until a more sophisticated continuum description can be developed that overcomes the problems raised here, simulation methods remain as more reliable tools for investigation of ion channels. Brownian and molecular dynamics are now well-developed for this purpose. They can be used to predict basic permeation properties of channels such as conductance that used to be the forte of the continuum theories. In addition, they allow exploration of phenomena such as ionic mixtures and ion selectivity that cannot be studied using continuum approaches.