Azimuthal Frustration and Bundling in Columnar DNA Aggregates

Abstract

The interaction between two stiff parallel DNA molecules is discussed using linear Debye-Hückel screening theory with and without inclusion of the dielectric discontinuity at the DNA surface, taking into account the helical symmetry of DNA. The pair potential furthermore includes the amount and distribution of counterions adsorbed on the DNA surface. The interaction does not only depend on the interaxial separation of two DNA molecules, but also on their azimuthal orientation. The optimal mutual azimuthal angle is a function of the DNA-DNA interaxial separation, which leads to azimuthal frustrations in an aggregate. On the basis of the pair potential, the positional and orientational order in columnar B-DNA assemblies in solution is investigated. Phase diagrams are calculated using lattice sums supplemented with the entropic contributions of the counterions in solution. A variety of positionally and azimuthally ordered phases and bundling transitions is predicted, which strongly depend on the counterion adsorption patterns.

INTRODUCTION

Many biological systems contain densely packed DNA assemblies, as, for example viral phage heads and sperm. For the proper functioning of these biological systems, including humans, it is of extreme importance that the mechanisms carrying out the packaging of DNA in the cell work in a robust manner, since, for example, it is believed that DNA packing in chromatin plays an important role in gene regulation (Wolffe, 1992). In light of the rapidly growing field of gene therapy it is of great interest to understand the mechanisms actually responsible in living organisms for condensing DNA into densely packaged assemblies. The first step to this end is a model of DNA which is able to capture its most significant characteristics, with the second step consisting of devising a theory for DNA assemblies. In the last few years, many efforts have been made on the theoretical side to understand the interaction of two DNA molecules and DNA condensation with a variety of methods, including molecular dynamics and Brownian dynamics simulations (Grønbech Jensen et al., 1997; Kornyshev and Leikin, 1997; Ha and Liu, 1997; Podgornik and Parsegian, 1998; Shklovskii, 1999; Kornyshev and Leikin, 1999; Sottas et al., 1999; Nguyen et al., 2000; Allahyarov and Löwen, 2000; Ha and Liu, 2001). The matter is complicated by the fact that due to its chemical structure DNA is a helical molecule, rendering solutions for the DNA-DNA interaction considerably complicated. Moreover, the overall electroneutrality condition dictates that counterions be present in the solution, and the latter screen the electrostatic repulsion between the DNA rods. Only far from their axes can DNA molecules be apprehended as uniformly charged cylinders: this is the simplest approximation possible in an investigation of the DNA-DNA interaction and one that neglects the helical symmetry completely (see, for example, Grønbech Jensen et al., 1997; Levin et al., 1999; Hansen and Löwen, 2000; Levin, 2002; Strey et al., 1999, 1997; Oosawa, 1971; Stigter, 1977; Manning, 1978; Frank-Kamenetskii et al., 1987; and references therein). It has to be expected that such an approximation works well for distances much larger than the scale of the helical symmetry of the DNA molecule, R ≫ H, where H ≈ 3.4 nm is the DNA pitch length. This approach amounts to calculating the interaction of two homogeneously charged cylinders, whereby the continuously smeared charges along the cylinders create an electrostatic repulsion of two DNA molecules (exponentially screened by the electrolyte). Indeed, predictions for force-distance curves on the grounds of a traditional Derjaguin-Landau-Verwey-Overbeek theory for homogeneously charged cylinders turned out to be accurate for separations larger than several nanometers, whereas significant deviations in the biologically more relevant range of smaller separations (Kornyshev and Leikin, 1997) emerged. It can be concluded that apart from investigations where only the far-field behavior is of importance, it is crucial to consider the helical symmetry of DNA molecules, since the interaction potential in the relevant regime of intermediate distances is dramatically changed by the presence of a highly inhomogeneous charge distribution. An additional effect is provided by the fact that DNA is a polyelectrolyte molecule; in an aqueous solution, its cations dissolve into the solution, leaving behind a negatively charged DNA phosphate backbone. A major fraction of the cations condenses in the Bjerrum layer (Manning, 1978) around the molecular surface. With cations specifically adsorbing onto the DNA surface present in the solution, however, the scenario changes; the DNA molecules can be fully neutralized (Wilson and Bloomfield, 1979; Widom and Baldwin, 1980; Heath and Schurr, 1992) or even overcharged (Pelta et al., 1996). The interaction potential is thus additionally influenced by the amount and type of counterions present in the solution.

To condense DNA in an aggregate, either osmotic stress (Rau et al., 1984) or counterions specifically adsorbing on DNA have to be applied as condensing agents (Bloomfield, 1996). The latter can be, e.g., salts with Mn²⁺, Cd²⁺, spermidin, protamine, or cobalt hexammine (Bloomfield, 1996) cations, which are known to preferentially adsorb in the DNA grooves (Tajmir-Riahi et al., 1993; Fita et al., 1983; Hud et al., 1994; Shui et al., 1998). The sensitivity to the type of counterion for DNA aggregation (Bloomfield, 1996) is manifest in the fact that other counterions, such as, e.g., Ca²⁺ or Mg²⁺, which are known to exhibit a high affinity to phosphates and thus predominantly adsorb on the strands, do not induce DNA aggregation. A model should thus incorporate/reproduce these subtle effects and be able to explain the mesomorphism (Podgornik et al., 1998) of DNA aggregates stemming from the presence of different types of counterions.

Once the interaction of DNA molecules is derived by means of some theory, one can turn to the next step and calculate the properties of DNA assemblies. The structural organization and properties of such condensates in vivo are largely unknown but have been, in the last several years, under investigation in in vitro experiments (Robinson, 1961; Wilson and Bloomfield, 1979; Livolant and Bouligand, 1986; Livolant, 1991; Rau and Parsegian, 1992a,b; Rill et al., 1991; Ma and Bloomfield, 1994). Simple model systems able to predict the spatial as well as the orientational structure of these condensates are highly desirable for a better elucidation of the mechanisms occurring in vivo. Previous work has shown (Kornyshev and Leikin, 1998a) that it is a reasonable approximation/simplification to focus on columnar assemblies, neglecting possible tilting effects, as we will explain later. Most of the work relied on approximating DNA as homogeneously charged rods (Grønbech Jensen et al., 1997; Ha and Liu, 1997; Podgornik and Parsegian, 1998; Shklovskii, 1999; Nguyen et al., 2000). Only when taking into account, however, the helicity of DNA molecules, a relevant feature for the properties of such a columnar DNA assembly emerges: a nontrivial interplay between the torsional and translational degrees of freedom.

A mean-field calculation of this problem was presented in Lorman et al. (2001), whereas the full statistical mechanical problem of columnar DNA assemblies was recently solved in Harreis et al. (2002) using a pair potential for the DNA-DNA interaction devised in Kornyshev and Leikin (1997). The motivation for the present article is twofold: first, we give more details and background for the calculations already published in Harreis et al. (2002). In this work, it was found that the dependence of the optimal azimuthal orientation angle of two DNA molecules on their interaxial separation gives rise to azimuthal frustrations in an aggregate, thereby inducing phase transitions between different ordered orientational structures. Furthermore, depending on the type and amount of counterions condensed on the DNA surface, strong attractions were found, resulting in DNA bundling transitions. More importantly, the second motivation for the present work is to discuss the effect of discretized charges along the DNA strands and the effect of the dielectric jump at the DNA surface on the phase behavior. We find that although the phase boundaries shift quantitatively, especially at high densities, the global topology of the phase diagrams remains unaffected. This gives evidence for the fact that the topology of the phase diagram itself is generic, i.e., will be stable also with respect to further changes in the interaction, including, for example, hydration forces that are sometimes modeled through a distance-dependent dielectric constant (Lee et al., 2002).

THE MODEL

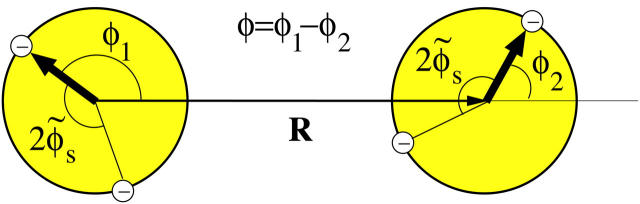
DNA is a helical biomolecule with two charged phosphate strands helically winding around a core region consisting of nucleotide basepairs. The two strands are not symmetrically distributed around the molecule's core region, but rather are separated by an azimuthal angle of 2φ̃_s ≈ 0.8 π, see Fig. 1 for an illustration. Under physiological conditions, DNA is present in the B-DNA conformation, a right-handed helical molecule (Saenger, 1984). In B-DNA, there are N = 10 nucleotides per helical turn with a helical pitch length of H ≈ 34 Å. Each nucleotide contains a negatively charged phosphate group, giving rise to a total charge of q = −10 e per helical pitch, which translates into a surface charge density of σ = 16.8 μC/cm². To model the interaction, we envision the molecules as long, rigid cylinders with a hard-core radius of a = 9 Å. Strictly speaking, this approximation is only appropriate for DNA fragments of contour lengths up to the persistence length L_p, which is typically found to be 500 Å–1000 Å (depending on the ionic strength; see Kornyshev and Leikin, 2000). Samples of parallel packed arrays have, however, been prepared for contour lengths of up to 100 L_p (Rau et al., 1984; Podgornik et al., 1996). In our model the phosphate backbone is accounted for by continuous helical line charges located on the surface of the DNA hard-core cylinder. We also calculated pair interactions for discrete charge patterns on the DNA surface, as we will discuss in detail later. Each DNA duplex furthermore carries a compensating positive charge stemming from the adsorbed counterions, which are modeled in the same way as the phosphate backbone as continuous line charges. The degree of charge compensation will be referred to as 0 < θ < 1, whereas the fractions of condensed counterions in the minor and major grooves, and on the two strands, are accounted for by f₁, f₂, and f₃, respectively, where f₁ + f₂ + f₃ = 1 holds. The nonadsorbed, mobile counterions in solution screen the Coulomb interactions between the helices, causing at large separations an exponential decay of the latter with the Debye screening length κ⁻¹.

FIGURE 1.

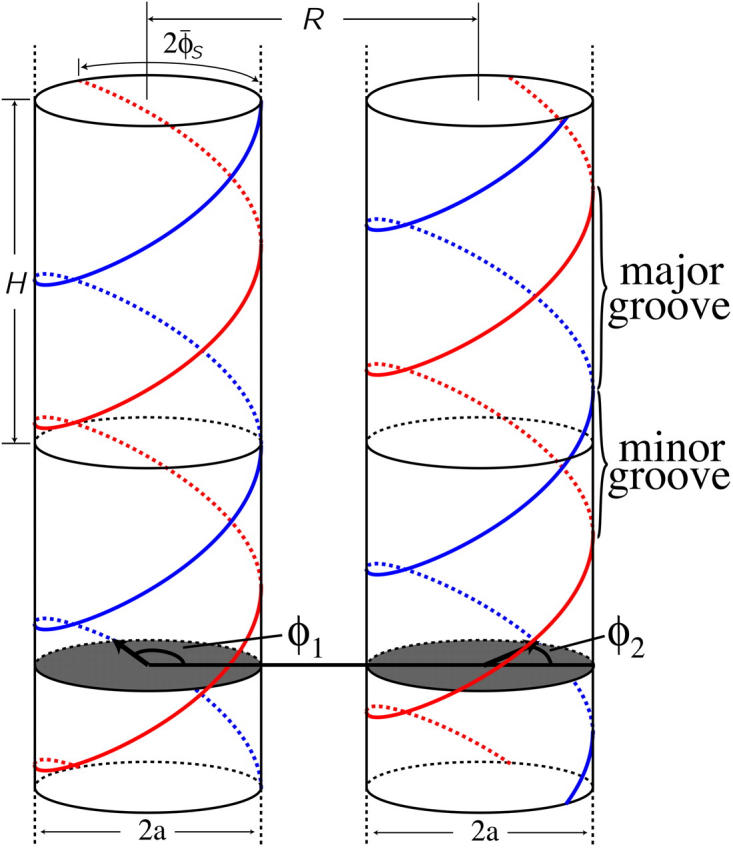
Illustration of two model DNA molecules at an interaxial separation R. The molecules are assumed to be rigid, long cylinders of radius a with a helical pitch length of H ≈ 34 Å. In between the two DNA helices a major and a minor groove are formed, due to the asymmetry in the azimuthal angle between the two helices, 2φ_s ≈ 0.8. See text and Fig. 2 for an explanation of the angles φ₁ and φ₂.

We wish, at this point, to discuss advantages and drawbacks of the present model that is characterized by a Debye-Hückel approach combined with the ion condensation model. Quite generally speaking, the two great advantages of the resulting Yukawa-type interaction are its great simplicity and its remarkable flexibility. Although not all situations, especially those of small separations might be accurately described quantitatively, possible deviations can be compensated by introducing the concept of effective, renormalized charges, as has been shown, for example, in Löwen (1994a). In the specific case of DNA-DNA interactions, previous work (Allahyarov and Löwen, 2000) has investigated the question of DNA-DNA interaction in the framework of the primitive model of electrolytes. The authors thereby relied on microscopically resolved molecular dynamics simulations. The DNA molecules were modeled, as in the present study, as rigid cylinders having all structural parameters of B-DNA. More specifically, in the reference cited, the double helical charge pattern was incorporated via discrete charges exhibiting an effective diameter, placed on the cylindrical surfaces of the DNA molecules. The solvent was accounted for by its dielectric constant (ε) as in the present work, but counter- and salt ions were explicitly included. It has been found in this reference that Yukawa-like effective interactions, resulting from a canonical tracing out of the microions, are capable of describing the potentials for DNA interaxial separations R > 25 Å. The authors furthermore showed that the behavior for interaxial separations R < 25 Å could be equally well described by a Yukawa potential; nevertheless, a different, separation-dependent effective charge has to be introduced for this range. To quantitatively reproduce the DNA-DNA pair potential, one is thus dealing with a Yukawa potential with a distant-dependent effective charge which saturates for R > 25 Å. It will, in general, be different from the input value of the Yukawa segment model as employed in the present work. It has thus to be expected that the R-dependent part of the pair interaction as shown in the present work will be affected by this charge renormalization. The angular part of the interaction will not be influenced, however, except for a scaling by an overall trivial factor, since the interaction is short-ranged and, as will be shown in what follows, the phase behavior is dominated by the nearest-neighbor interactions. The most important predictions of this study will not be affected: it is the location of the minimal azimuthal orientational angle between two DNA molecules that governs the frustrations and thus the equilibrium structure in the DNA aggregate. Furthermore, the phase diagrams in the case of repulsive interactions exhibit very small density jumps at the phase transitions, implying that the same effective charge, thus the same pair potential, can be employed in both phases. Although the absolute values of the free energies of the various phases will be affected by charge renormalization, the comparisons between those, and hence the location of the phase boundaries, will not. In the case of attractive interactions between two DNA molecules, the attractions occur only at a specific mutual azimuthal orientation. Since, as we have argued above, the latter remains unmodified by charge renormalization, it can be concluded that the same statement holds for the phase diagrams caused by these attractions. We could, as we will discuss in the following sections, furthermore illustrate that the predicted phase diagrams are, in their essential features, qualitatively robust against variations of the underlying pair potential, such as inclusion/exclusion of the dielectric jump at the DNA surface. We thus have good grounds to believe that although corrections to the pair potential are necessary, the predictions regarding macroscopic behavior are robust. Thus, the current approach captures the essential physics governing the biological phenomena at hand.

In our model, we study formally the two extreme cases of dielectric constants ε₁and ε in the DNA core and in the solvent, respectively. The first case is that we assume no dielectric jump at all, ε/ε₁ = 1, whereas the other limit is ε/ε₁ = ∞. In the first case, it is more convenient to formulate the interaction in terms of a Yukawa-segment model, whereas the second case has been elaborated in a practical form by Kornyshev and Leikin (1999). The motivation to study different ε/ε₁ is to check effects of the discontinuity formally. In reality one would expect ε/ε₁ ≈ ∞ since the dielectric constant of bulk water is very high. Close to the DNA surfaces, however, it is not at all clear whether the effect of a dielectric discontinuity as described by macroscopic electrostatics is justified. More realistic dielectric effects were taken into account by a space-dependent dielectric constant (Lado et al., 1998). One could surmise that if the resulting interaction and phase behavior is similar for the two limiting cases ε/ε₁ = 1 and ε/ε₁= ∞, dielectric effects on this molecular scale are not actually very important at all. This in turn gives evidence for at least qualitative stability of our results under application of more realistic interactions stemming from more refined molecular calculations.

The main characteristics of the model DNA molecules are illustrated in Fig. 1. For clarity, possible condensed counterion strands have been omitted in the illustration. The azimuthal orientation of molecule i is referred to by its azimuthal angle φ_i, which is defined in the following way. A plane (shaded gray in Fig. 1) perpendicular to the parallel axes of the two DNA molecules hits the dark colored 5′–3′ strand (Sinden, 1994) of each molecule at the point indicated by the vector originating from molecule's i axis, which we may formally call spin. The angle φ_i formed by this vector and some arbitrary reference direction on the plane, taken, for clarity, to be the vector connecting the two molecules' axes, is the azimuthal orientation angle of molecule i. We assume that the DNA molecules are parallel, as depicted in Fig. 1, which is justified by reasons given in A Theory for DNA Assemblies. If we furthermore assume the molecules to be infinitely long and their charge distributions to be described by helical line charges as illustrated in Fig. 1, their mutual state can be described by two parameters: their interaxial separation R as well as their mutual azimuthal orientation, φ = φ₁ − φ₂. The problem thus reduces to an effective two-dimensional problem of x-y spins interacting via a potential U(R,φ). We further illustrate this point in Fig. 2, which depicts the gray-shaded plane included in Fig. 1 in more detail. It has to be noted that the problem may only be viewed as effectively spatially two-dimensional under the assumption of continuous line charges. For discrete charge patterns, the orientations φ₁ and φ₂ both enter the pair potential. Let us assume discrete charges to illustrate the validity of this statement. The two molecules shall be separated by a vector R, as shown in Fig. 2, with molecule 1 at an angle φ₁ and molecule 2 at an angle φ₂ relative to R in a given plane P that perpendicularly cuts the molecular axes. The points where the 5′–3′ strands of molecules 1 and 2 hit the plane P shall be denoted by p₁ and p₂, respectively. Both in p₁ and p₂ discrete charges are located as is the case in Fig. 2. Were the interaction only to depend on the mutual azimuthal orientation, φ = φ₁ − φ₂, a configuration with both molecules turned by Δφ should yield the same interaction. Obviously, after turning both molecules the 5′–3′ strands will hit P in new locations 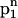and 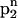. This means altered charge distances in the contribution of plane P to the total DNA-DNA interaction. Since the total interaction is the sum of the contributions of all charges (planes), the interaction might still be conserved if another plane along the molecule contributed the same value after the rotation as P did before the rotation and vice versa. The only plane capable to switch configuration with P through a rotation by Δφ is a plane P′ shifted by Δz = H Δφ/2π relative to P along the molecular axes. The 5′–3′ strands will then cut through P′ in p₁′ = p₁ and p₂′ = p₂. With a discrete charge pattern, however, charges will only be located in p₁′ and p₂′ if Δz is commensurate with the rise of the charge pattern along the molecular axes, or in other words, if Δφ = n 2π/N holds, with nεN and N the number of DNA charges per helical pitch and strand. If on the other hand, continuous line charges are used, the original plane P and P′ are equivalent without any further condition and contribute the same amount to the interaction. The only requirement to be met is that the molecules be at least one helical pitch long, so that the existence of P′ is guaranteed. The mutual azimuthal angle φ can, for continuous line charges under the additional condition of infinitely long molecules, equivalently be thought of as a relative vertical shift z = Hφ/2π of the two molecules. We will come back to a more detailed discussion on discrete charge patterns versus continuous line charges at a later point in the next section.

FIGURE 2.

A plane perpendicular to the parallel axes of two DNA molecules separated by vector R hits the DNA strands denoted by the white circles with a minus inside; 2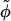_s is the azimuthal width of the minor groove. The vectors joining the axes with the points where the 5′–3′ strand (Sinden, 1994) hits the plane may be formally called spins. The angle φ between the two spins characterizes the mutual azimuthal orientation of the molecules.

THE PAIR POTENTIAL

As already sketched in the Introduction, the pair potential will be considered under different assumptions concerning dielectric jump and charge distributions. The approach is, on a general level, based on the linear screening theory picture, yielding a Yukawa-like, screened Coulomb interaction for any pair of charges on the two molecules (Schneider et al., 1985, 1986, 1987). We will first resort to considering the case of no dielectric jump and refer to this situation as the Yukawa-segment-model potential. The Yukawa-segment idea has been tested against microion resolved simulations in Löwen (1994a,b) and has been used for calculating dynamical correlations in Tobacco-Mosaic Virus suspensions and phase diagram calculations of the latter in Kirchhoff et al. (1996) and Graf and Löwen (1999), respectively. Here, the Yukawa-segment approach furthermore allows for testing the influence of a discrete charge pattern as opposed to continuous line charges. The second case includes the dielectric jump at the DNA surface, yet necessitates continuous line charges. We will refer to it in the following as Kornyshev-Leikin potential.

Yukawa-segment-model potential

The canonical starting point for the Yukawa-segment-model is to exactly mimic the discrete number of charges present in real DNA molecules. The second generic case, opposed to the former, is to assume the charge distributions to be continuous line charges. Although the first approach might, at first sight, seem superior to the latter, it has to be kept in mind that the ‘real’ charge distribution will definitely be not pointlike, but rather smeared on the whole phosphate group, two charges of which are closely neighbored, so that a modulated continuous line charge distribution should be the most realistic way of modeling the DNA charge distribution. Such an approach, however, requires an input from quantum chemical calculations and is therefore beyond the scope of the present study. We will now first illustrate the general approach to the calculation of the pair potential and then come back to a discussion of the differences between the discrete and the continuous charge distribution version.

We assume linear screening to act between any two charge elements q_i and q_j on the continuous helical line charges of the DNA molecules, yielding a Yukawa interaction (Schneider et al., 1985, 1986, 1987),

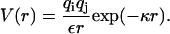(1)

Here, κ = 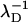is the inverse Debye screening length and ε = 81 is the dielectric constant of the solvent (water). To access the total pair interaction of two DNA molecules, we have to integrate along each pair of interacting helical line charges (strands) (or sum in the case of discrete charge patterns).

Let molecule 1 be at the origin of the coordinate system and molecule 2 at R = Rx, see Fig. 2. In its most general form, a helix, parameterized by its helical angle ϕ, furthermore depends on a set 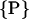of additional parameters. This set of parameters 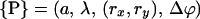consists of the helix radius a, the helical rise λ = H/2π, the position (r_x,r_y) of the helix axis in the x-y plane and the angular offset Δϕ of the helix, indicating where the helix starts to rise from the x-y plane. Making use of the special conditions present in our case, namely that we only consider molecules residing on the x-axis and that all helices exhibit the same radius as well as the same helical rise, 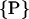can be reduced to only consist of r_x and Δϕ, 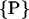= (r_x,Δϕ). The corresponding helix parameterization for one single helix reads as

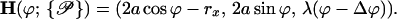(2)

The angular offset Δϕ is set to φ₁ for the first strand on the first molecule. Thereby the angular offsets of all other strands involved are uniquely determined by the DNA geometry, for example, the second DNA phosphate strand on molecule 1 has Δϕ = 2φ̃_s+φ₁, the counterion strand in the minor groove is characterized by Δϕ = φ̃_s+φ₁ and the counterion strand in the major groove has Δϕ = π − 2φ̃_s+φ₁ as angular offset. The charge strands on molecule 2 follow the same logic, except that their respective offsets have a term of φ₂ instead of φ₁, since the rotation of molecule 2 has to be accounted for; see again Fig. 2 for an illustration. The interaction between one strand on molecule 1 and another strand on molecule 2 is given by

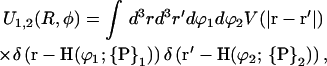(3)

which is a diverging quantity, since the integral in Eq. 3 includes the two infinitely long strands. What we are interested in for our purpose is the interaction that segments of a given length L experience. As the Yukawa-type interaction between all charge segments decays exponentially and since, due to the periodicity, all helical pitches are the same, we may to this end, proceed in the following way. On molecule 1 one pitch length H serves as integration interval, whereas on molecule 2 we integrate from −∞ to ∞. Practically, due to the exponential decay in the potential, convergence of the integral is obtained after a maximum of 10 pitch lengths H has been integrated. The result is the interaction energy of one pitch on strand 1 with the total length of molecule 2. Multiplication of this quantity with the number of pitches L/H to be taken into account for a length L yields the interaction of a segment of length L on strand 1 with a segment of length L on strand 2, whereby endpoint effects are ignored via the integration from −∞ to ∞.

The total interaction of a segment of length L on molecule 1 with one on molecule 2, then, is the sum over the interactions of all strands on molecule 1 with all strands on molecule 2, including the DNA phosphate strands as well as the condensed counterion strands:

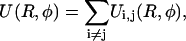(4)

where the symbolic notation above implicitly assumes i to be taken from the set of all strands on molecule 1 and j correspondingly from molecule 2. Inserting the Yukawa-segment interaction, Eq. 1 in Eq. 4 and carrying out the r and r′ integrations in Eq. 3, together with the above consideration on the integration intervals, yields the expression

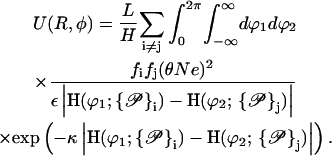(5)

Here and in Eq. 4, the index i is taken from the set i ∈ {s₁⁽¹⁾, s₂⁽¹⁾, c₁⁽¹⁾, c₂⁽¹⁾} and j covers j ∈ {s₁⁽²⁾, s₂⁽²⁾, c₁⁽²⁾, c₂⁽²⁾}, whereas 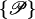_i shows the dependence of the given strand on the specific geometrical parameters determining its parameterization. By s_k^(l) the k^th phosphate strand on the l^th molecule is denoted, whereas c_k^(l) describes the corresponding counterion strand. In s_k^(l) the counterion strands which are condensed on the phosphate strands are included, since they only trivially renormalize the charge carried by the phosphate strands. This enters into the charge fraction parameters f_i and f_j in the following way:

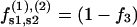(6)

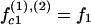(7)

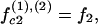(8)

where f₁, f₂, and f₃ are the fractions of counterions condensed in the minor and major grooves, and on the two strands, respectively, satisfying f₁ + f₂ + f₃ = 1.

The differences of a discrete charge potential to a continuous line charge potential can be estimated by tuning the number of charges per pitch length, N. As we discussed in The Model, for discrete charges the interaction does depend on both molecules' orientations φ₁ and φ₂ and not only on the difference φ = φ₁ − φ₂ as it is the case for continuous line charge distributions. For discrete charge patterns, this opens up two different routes: The first and simpler is to set φ₁ = 0 and look at U(R,φ₁ = 0,φ₂), whereas the second and more refined one is to vary φ₁ and φ₂ to then consider U(R,φ) at φ=φ′₁ − φ′₂, where φ′₁ and φ′₂ have been obtained as energetically optimal combination for a given mutual azimuthal orientation φ of the two DNA molecules.

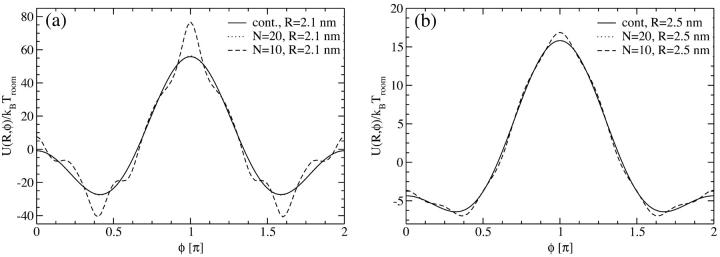
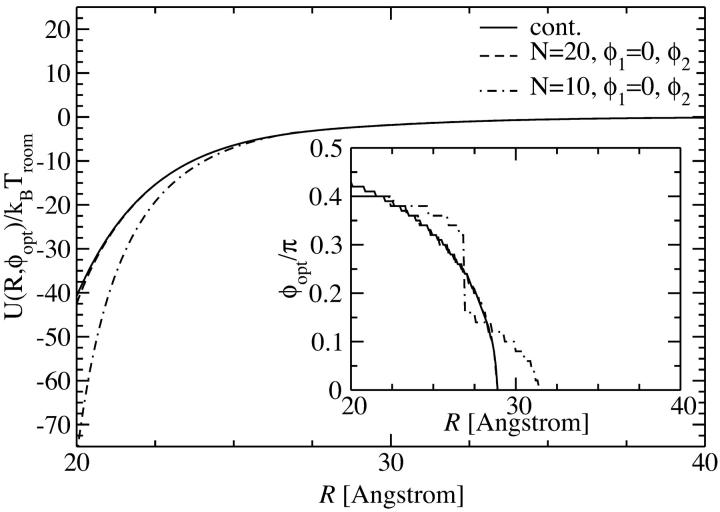
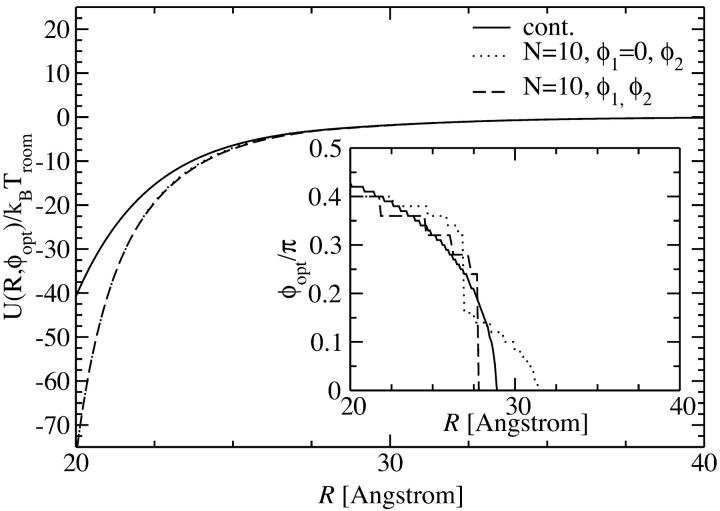
The first approach is taken in Fig. 3, where the pair interaction per persistence length L_p, U(R,φ₁ = 0,φ₂), is displayed as a function of the azimuthal orientation angle φ₂ with φ₁ = 0 fixed, at two fixed interaxial separations, R = 2.1 nm and R = 2.5 nm, for N = 10 and N = 20 charges, as well as for a continuous line charge. The counterion condensation parameters are f₁=0.3, f₂=0.7, and f₃ = 0. It can be seen that already for N = 20 the obtained potential curve is indistinguishable from that for the continuous line charge potential at both interaxial separations. For N = 10 charges, on the other hand, deviations exist predominantly for R = 2.1 nm, but have decreased to a minuscule level for R = 2.5 nm. A more detailed structure of the pair potential as a function of the azimuthal orientation is apparent for the smaller separation. The differences mainly pertain to the region around the maximum and the two minima. The position of the global minimum, however, the most important parameter for the behavior in an assembly, is practically unchanged. This assertion is only based on the observation of the potential at two fixed interaxial separations. Its main point, however, is sustained by the data shown in the inset of Fig. 4, where we show the optimal azimuthal orientation angle φ_2,opt, again at f₁ = 0 fixed, as a function of the DNA-DNA interaxial separation R. The corresponding potential is shown in the main graph of Fig. 4. The detailed behavior of the optimal azimuthal alignment angle is different for N = 10 charges from that for N = 20 charges and continuous line charges, whereas the latter are indistinguishable from one another. The key points for the behavior in an aggregate, however, remain unchanged for all cases: first, the optimal angle is nonzero for all interaxial separations smaller than R^* ≈ 30 Å and second, for very small intersurface separations the optimal angle is ∼0.42 π.

FIGURE 3.

Yukawa-segment pair potential per length L_p as a function of the azimuthal orientation angle φ₂ with φ₁ = 0 fixed, at interaxial separations (a) R = 2.1 nm and (b) R = 2.5 nm, for θ = 0.9 and f₁ = 0.3, f₂ = 0.7, and f₃ = 0. At both interaxial separations the potential is displayed for N = 10, N = 20 charges as well as for continuous line charges.

FIGURE 4.

Yukawa-segment pair potential per length L_p as a function of the interaxial separation R of two DNA molecules, at the optimal angle φ_2,opt(R), depicted for N = 10, N = 20 charges as well as for continuous line charges. The dependence of the optimal angle on the interaxial separation R is shown in the inset.

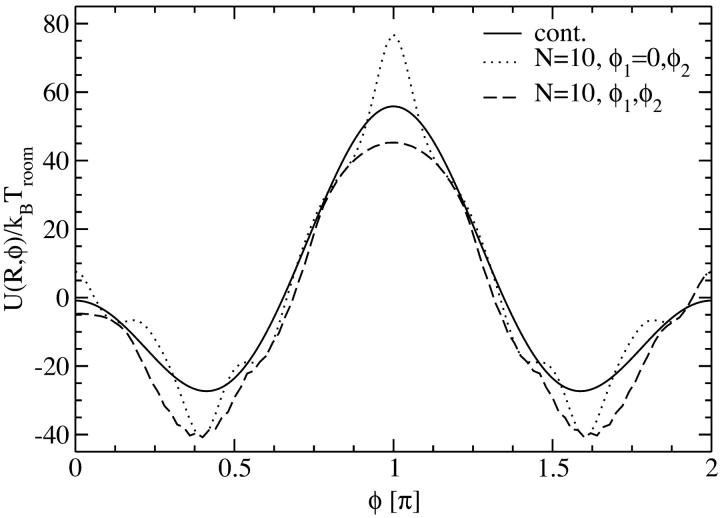
The second approach to discrete charge patterns is to calculate the interaction for all combinations of φ₁ and φ₂ and then to minimize the obtained potential energy on curves of constant φ = φ₁ − φ₂. This is the more realistic version of the approach shown above, yet it is still an approximation for an aggregate since the optimized combinations of φ₁ and φ₂ for a given φ will not be possible with respect to all neighbors of a given DNA molecule. In Fig. 5 we compare this approach for N = 10 discrete charges at an interaxial separation R = 2.1 nm with the one presented above and with the continuous line charge version. We again have θ = 0.9, f₁ = 0.3, f₂ = 0.7, and f₃ = 0 for the counterion condensation parameters. The resulting potential curve is the lowest in energy, as one should expect from the procedure applied. The structure is close to the one induced by continuous line charge distributions and the minima are found at exactly the same loci as when keeping φ₁ fixed at φ₁ = 0; they are thus practically at the same positions as for the continuous line charge version. Again, from the analysis of one single interaxial separation we thus conjecture that the overall behavior of the pair potential will not present significant deviations from the reference continuous charge case. This statement is confirmed by analyzing the inset of Fig. 6, where we show the optimal azimuthal angles as a function of the interaxial separation R for the three different approaches to the charge distributions. Again, the dependence of the optimal azimuthal angle on the interaxial distance is very similar for the three cases studied, which will induce similar angular frustration behavior in an assembly. In detail, the optimal angle curve is closer to the one for a continuous charge distribution in the case where both angles φ₁ and φ₂ are free to rotate and the energetically optimal combination yielding the desired mutual azimuthal orientation φ = φ₁ − φ₂ is chosen, as compared to the case where φ₁ is set to zero. As far as the behavior of the pair interaction at optimal azimuthal angle, shown in the main graph of Fig. 6, is concerned, both discrete charge versions fall on the same line, which shows a deviating course from the continuous version's behavior in the close-interaxial separation regime, whereas it approaches the continuous case's curve fast for larger R and both lines agree for R > 25 Å. We repeated the analysis of Figs. 5 and 6 for N = 20 charges. Here, no difference to the continuous charge distribution results could be discerned.

FIGURE 5.

Yukawa-segment pair potential per length L_p as a function of the azimuthal orientation angle φ (solid line, continuous line charge distribution), as a function of φ = φ₁ − φ₂ with the optimal combination of φ₁ and φ₂ as described in the text (dashed line, N = 10 discrete charges) and as function of φ₂ with φ₁ = 0 fixed (dotted line, N = 10 discrete charges). All interactions are at an interaxial separation R = 2.1 nm, for θ = 0.9 and f₁ = 0.3, f₂ = 0.7, and f₃ = 0.

FIGURE 6.

Yukawa-segment pair potential per length L_p as a function of the interaxial separation R of two DNA molecules, at the optimal azimuthal orientation angle φ_opt (solid line, continuous line charge distribution), at the optimal angle φ_opt = (φ₁ − φ₂)_opt with the optimal combination of φ₁ and φ₂, as described in the text (dashed line, N = 10 discrete charges) and as function of φ₂ with φ₁ = 0 fixed (dotted line, N = 10 discrete charges). All interactions are for counterion condensation parameters θ = 0.9 and f₁ = 0.3, f₂ = 0.7, and f₃ = 0. The dependence of the optimal angle on the interaxial separation R is shown in the inset.

We can thus conclude that, first, the behavior of a DNA assembly will most probably not qualitatively differ for a discrete charge model with the real DNA charge number N = 10 and a continuous line charge model. The results will, however, in a quantitative manner depend on the underlying pair potential, especially for high concentrations, since, in Figs. 4 and 6 we found that for very close intersurface separations the pair interactions differed for a discrete and a continuous charge pattern on the DNA surface. Second, since already for N = 20 the results are indistinguishable from the ones for continuous line charges, we can furthermore surmise that a modulated continuous line charge distribution, as briefly discussed above to be the most realistic model, would not significantly differ even on the level of the pair potential. According to this reasoning, we will henceforth focus on continuous line charges, thereby avoiding the problem that for discrete charge patterns the potential depends on both molecules' azimuthal orientations φ₁ and φ₂, which significantly complicates matter for the strict analysis of an assembly.

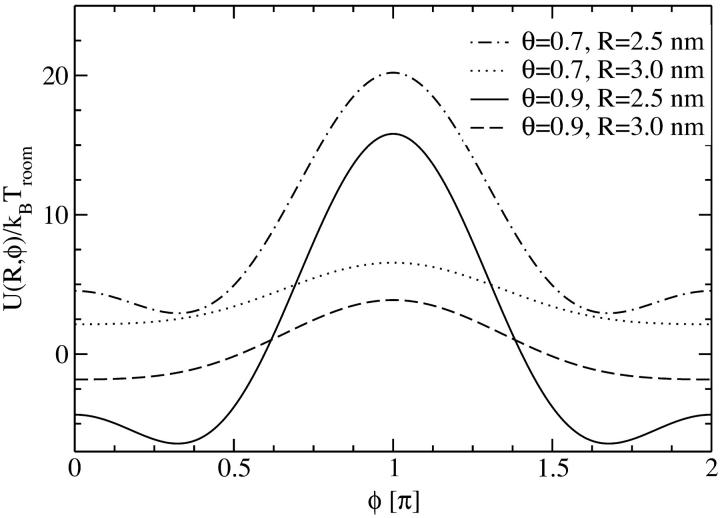
Let us now investigate the effect of different amounts and types of counterions adsorbed on the DNA molecular surface. The type of counterion is herein modeled by the ratio of adsorbed charges in the minor and major grooves, as well as on the strands to the DNA phosphate backbone charge. We restrict our analysis to the most relevant cases: we will investigate θ = 0.9 (meaning that 90% of the DNA charge is compensated by adsorbed counterions) with counterions adsorbing predominantly in the major groove, represented by charge fractions f₁ = 0.3, f₂ = 0.7, and f₃ = 0, as well as with counterions exhibiting a high affinity to phosphates and thus condensing on the strands: f₁ = 0, f₂ = 0, and f₃ = 1. A charge compensation value of θ = 0.9 is known to be typical for DNA condensation (Kornyshev and Leikin, 1999; Bloomfield, 1996). Furthermore we calculate the potential for θ = 0.7, which is a lower bound still occurring in DNA aggregation phenomena. Here, we also assume f₁ = 0.3, f₂ = 0.7, and f₃ = 0. In Fig. 7 the potential is displayed as a function of the azimuthal angle φ for two fixed interaxial separations, R = 2.5 nm and R = 3.0 nm, for f₁ = 0.3, f₂ = 0.7, f₃ = 0, and θ = 0.9 and θ = 0.7. For both amounts of adsorbed counterions, the potential curves qualitatively agree. Due to the higher degree of charge compensation, however, the θ = 0.9 potential values are smaller. In a subsequent step we minimize the potential with respect to the azimuthal alignment angle φ, obtaining U(R,φ_opt). The result is displayed in Fig. 8. Both potentials being induced by situations where the majority of counterions condenses in the major groove are strongly attractive, with the one for θ = 0.9 exceeding the one for θ = 0.7. The potential stemming from a situation with all counterions condensed on strands, on the other hand, is purely repulsive.

FIGURE 7.

Yukawa-segment pair potential for two segments of length L_p as a function of the mutual azimuthal orientation angle φ of two DNA molecules, at fixed interaxial separations as indicated in the legend, for θ = 0.9 and θ = 0.7. f₁=0.3, f₂ = 0.7, and f₃ = 0 were used for the fractions of condensed counterions in the minor and major groove and on the strands, at different interaxial separations, as indicated in the legend.

FIGURE 8.

Yukawa-segment pair potential for two segments of length L_p as a function of the interaxial separation R of two DNA molecules, at the optimal angle φ_opt(R), depicted for different values of the counterion condensation parameter and for different counterion adsorption patterns. The dependence of the optimal angle on the interaxial separation R is shown in the inset.

What is the origin of this qualitative difference? The mechanism can be thought of as a zipper (Kornyshev and Leikin, 1999). Having a high charge compensation in the major groove creates a big charge separation: a negative helical line charge is located at the phosphate backbone position; a positive helical line charge rests in the adjacent major groove. With two opposing DNA molecules appropriately oriented, this allows for positive and negative charges to directly face each other as complementary parts in a zipper, creating a strong attraction between the two molecules. If counterion condensation solely occurs on strands, this mechanism is absent, creating a purely repulsive potential, as seen in Fig. 8 in the case of θ = 0.9, f₁ = 0, f₂ = 0, and f₃ = 1. In any case, the potential quickly decays toward zero for increasing interaxial separations so that in an assembly the dominant contributions to the total potential energy will stem from the nearest neighbors. The optimal angle, as a function of the interaxial separation, plotted in the inset of Fig. 8, is practically unaffected by this mechanism: in all three cases displayed, the optimal angle is nonzero for interaxial separations smaller than R_* ≈ 28.25 Å, and zero else. Furthermore, a very similar increase from zero at R_* to φ_opt(R = 20 Å) ≈ 0.47 π is observed in all cases.

Let us finally remark that the Yukawa-segment model has the advantage of being very general and flexible. Any linearized field theory necessarily ends up with an effective Yukawa-type interaction. If hydration effects are included within a field theoretical description, the leading term for the effective interaction has again a Yukawa form. The electrostatic effects are well-described even at strong coupling provided the charges and screening lengths are suitably renormalized, as recently demonstrated in microion-resolved computer simulations of two parallel DNA strands (Allahyarov and Löwen, 2000).

Kornyshev-Leikin potential

The Kornyshev-Leikin approach rewrites the result of linear screening theory in terms of a helical Fourier expansion (ε₁ ≪ ε) (Kornyshev and Leikin, 1997, 1998a,b). The pair interaction potential per unit length features a hard-core repulsion for interaxial separations R ≤ 2a, and for R > 2a reads as:

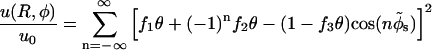(9)

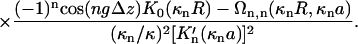The total interaction U(R,φ) per segment of length L is simply U(R,φ) = Lu(R,φ). In Eq. 8 Δz denotes a vertical displacement, equivalent to the azimuthal alignment angle φ = (2π/H)Δz. Furthermore, u₀ = 8πσ²/εκ² (≈ 2.9 k_BT/Å at physiological ionic strength), and 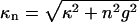. The function Ω_n,m(x,y) is given by

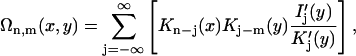(10)

with the modified Bessel functions K_n(x) and I_j(y). The primes denote derivatives. As can be seen, the dependence of the pair potential on the mutual orientation angle φ is affected by the distributions f_i, i = 1,2,3 of the condensed counterions (Kornyshev and Leikin, 1999). The dependence on the interaxial separation R is exponential. Keeping only the n = 0 term in the sum of Eq. 8 yields a pair potential of homogeneously charged cylinders, depending on R only. Summing up to |n| = 2 results in the approximation u(R,φ) ≅ C(R) − A(R)cos φ + B(R)cos 2φ. Already at this level does the interaction potential u(R,φ) show a peculiar dependence on the mutual azimuthal orientation angle, being a remarkable effect of DNA double-strandedness, as discussed above in the previous subsection. Here, A(R), B(R), and C(R) > 0 depend on the parameters of DNA structure as well as on the distribution of adsorbed ions, and A(R) > B(R) at large interaxial separations R. This potential has two symmetric azimuthal minima at 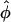_± ≠ 0 for distances smaller than a critical one at which A(R) = 2B(R), and one minimum at 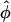= 0 for larger R. It thus already captures, to quite a good degree, the essential features of the full interaction potential as observed in the previous section in the framework of the Yukawa-segment model.

Let us now investigate the full potential. Due to rapid convergence of the sum in Eq. 8, truncation after the |n| = 5 terms suffices for the evaluation of the fully converged pair interaction potential. In Fig. 9 we show the KL potential U(R,φ_opt) at optimized azimuthal alignment angle, φ_opt, as plotted for the YS case in Fig. 8. It can be seen that the results are very similar to the ones discussed above for the YS potential. Counterion condensation on strands (f₁ = 0, f₂ = 0, and f₃ = 1) gives rise to an exclusively repulsive potential, whereas condensation of a majority of the counterions in the major groove (f₁ = 0.3, f₂ = 0.7, and f₃ = 0) results, at both charge compensations θ = 0.7 and θ = 0.9, in an attractive pair interaction. Differences in the KL approach to the YS approach can, however, also be inferred from a comparison of Fig. 8 and Fig. 9. These refer to the behavior at small intersurface separations. In the case of the YS model, the interaction decays monotonically to the contact value at R = 20 Å. Here, for the KL potential, however, the potential drops to its minimum value close to surface contact, but then rises again upon further approach. Furthermore a quantitative difference can be seen for θ = 0.7 and f₁ = 0.3, f₂ = 0.7, f₃ = 0, since in the KL case the attraction for this combination of parameters is much weaker than it was found to be for the YS model. Both observations can be attributed to the fact that in the KL case the dielectric jump is taken into account with ε/ε₁ = ∞, where ε is the dielectric constant of the solvent (water) and ε₁ is the dielectric constant of the DNA core. This allows for image charges at the DNA surface, bringing about a short-ranged repulsive part in the interaction, as evidenced in the potential curves in Fig. 9. Nonetheless, this short-range repulsion does not affect the behavior of the optimal angle as a function of the interaxial separation as compared to the one found in the YS case. We show the corresponding data in the inset of Fig. 9. The same functional form as for the YS potential is obtained, except for the fact that R_*^KL ≈ 29.5 Å is found to be slightly larger than R_*^YS ≈ 28.25 Å in the YS case.

FIGURE 9.

Kornyshev-Leikin pair potential as a function of the interaxial separation R of two DNA molecules, at the optimal angle φ_opt(R), depicted for different values of the counterion condensation parameter and for different counterion adsorption patterns. The dependence of the optimal angle on the interaxial separation R is shown in the inset.

We now have two realizations of the linear Debye-Hückel potential for the DNA interaction at hand stemming from different levels of modeling realized in the Debye-Hückel framework, which show differences with respect to the short-range behavior. In the following section we will present a theory to investigate the statistical properties of a columnar DNA assembly. We will thereby rely on the two YS and KL potentials as discussed above. The interesting question to be pursued apart from the main objective, being the general properties of such assemblies, is if and how the differences in the pair potentials affect the behavior of the assembly.

A THEORY FOR DNA ASSEMBLIES

In the previous sections we showed that under the assumption of continuous line charges and infinitely long, rigid, parallel DNA molecules, the pair interaction potential U(R,φ) of two DNA molecules only depends on the interaxial separation R and the mutual azimuthal orientation angle, φ. The problem of statistical properties of columnar aggregates of long rigid DNA molecules may thus be mapped on a two-dimensional problem of particles that we may formally refer to as x-y spins, interacting via this unusual potential U(R,φ) (see Fig. 2; see also Kornyshev and Leikin, 1997). We repeat from previous subsections that the dominant contributions to the potential U(R,φ) arise from the nearest neighbor interactions, as the R-dependent parts of the potential exponentially decrease with R. Before going into more detail on the theory for DNA assemblies we can, on the basis of the knowledge of the pair potential, already surmise a general trend in the behavior: we know that the potential has two symmetric azimuthal minima at 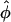_± ≠ 0 for distances smaller than a critical one and one minimum at 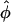= 0 for larger R. Although the 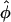= 0 case is compatible with any lattice, 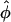≠ 0 results in frustrations of positional and orientational order (Strey et al., 2000). Due to the R-φ coupling in the interaction potential, one may expect peculiar positional and orientational structures in the aggregate, a feature known as the mesomorphism of DNA assemblies (Podgornik et al., 1998). Carrying the formal analogy to spin systems further, we may refer to the orientational structure in the assembly also as spin or magnetic structures.

Lattice sums

For all cases studied in this article, the pair interaction U(R,φ) is greater than k_BT, so that the energy needed to destroy the translational or orientational order in an assembly must be more than several k_BT at room temperature. Hence focusing on the ground state analysis of the basic structures of the assembly provides the representative thermodynamic states. This reasoning is further sustained by evidence from polymer crystallization, stating that upon compression the effective persistence length (this persistence length has to be distinguished from a smaller correlation scale which is decreasing due to deflections of the polymer within the tube; see Vroege and Lekkerkerker, 1992) of polymers increases, bringing them into columnar alignment at high packing fractions. Since, as we already argued above, the problem is effectively two-dimensional, we consider the five two-dimensional Bravais lattices, i.e., the hexagonal (HEX), square (SQ), rectangular (REC), rhombic (RHO), and oblique (OBL) lattices to assess the representative thermodynamic states. As for the exploration of the ordered spin structures, we are, in principle, facing infinitely many degrees of freedom: every DNA molecule in the lattice has a continuous spectrum of possible orientations. We can, however, make use of a pair potential property that we noted in The Pair Potential, namely, that the pair interaction drops exponentially as a function of the interaxial separation R. Assuming that its range would solely encompass interactions contained in a fundamental unit cell (elementary plaquette), the approach could be much simplified in the following way. We restrict our analysis to finding the minimal energy state of this fundamental unit cell alone. This is achieved by minimizing the energy of the plaquette with respect to all spin angles residing on the elementary plaquette. Since no interactions beyond unit cells are assumed to be present, periodical repetition of this minimized unit cell along the lattice directions guarantees to give the ground state of the whole lattice. Due to the exponential decay of the R-dependent factors in the pair interaction potential this already presents an amazingly good approximation for our purposes. Since strictly speaking the range of the potential may extend beyond nearest neighbor interactions in some cases, we adopt a perturbation approach in the following way: the whole lattice is generated by periodical repetition of the elementary plaquette structure, involving two or three degrees of freedom depending on the lattice type under exploration, but interactions of higher order neighbors are nonetheless included in the calculation of the lattice sums.

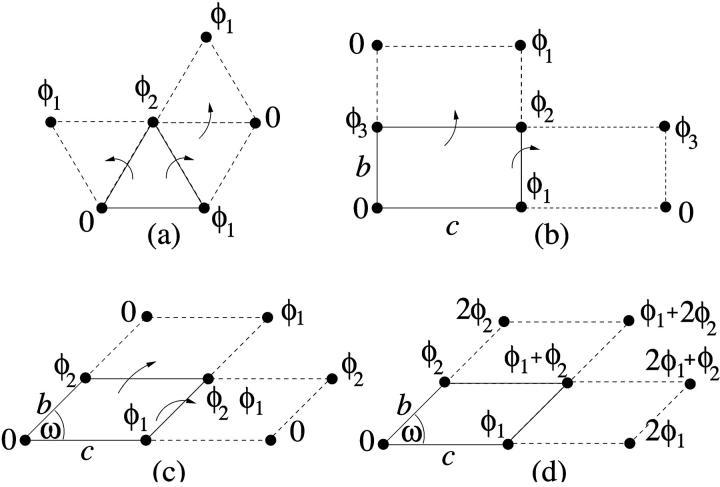
The algorithms employed for generating the ordered spin structures on the whole lattice building on the fundamental unit cell differ depending on the lattice type. They are schematically illustrated in Fig. 10. One of the spins in the elementary plaquette is chosen as reference (φ = 0). This leaves two degrees of freedom (φ₁, φ₂) in the case of the HEX lattice, and three degrees of freedom (φ₁, φ₂, and φ₃) for the REC and SQ lattices. The HEX lattice can be build up by periodically reflecting the unit cell across its edges, as is shown in Fig. 10 a. The same holds for the REC lattice with three free orientations per plaquette; see Fig. 10 b. In the case of the RHO and OBL lattices, however, employing the same procedure as for the REC lattice with three free spin angles per plaquette does not produce identical plaquettes: due to the fact that the geometrical symmetry of the unit cell is broken (a short and a long diagonal exist), mirror reflections across the edges generate different plaquettes on the whole lattice. The lattice may nonetheless be filled with identical plaquettes by employing two algorithms which are depicted in Fig. 10, c and d. In the first, spins of orientation φ₁ and φ₂ are placed along the edges, whereas the third free orientation angle is chosen to be φ₃ = φ₂ – φ₁. The whole lattice is then populated by successive mirror reflections ensuring that pairs of spins across all diagonals have the same relative angle of φ₂ – φ₁.

FIGURE 10.

A schematic view of generating candidate ordered spin phases of the system. (a) for the HEX lattice; (b) for the REC and SQ lattices; and (c) and (d) for the RHO and OBL lattices.

The second algorithm is illustrated in Fig. 10 d. Again, spin angles of values φ₁ and φ₂ are chosen along the edges, whereas φ₃ is assigned a value of φ₁ + φ₂. The lattice is then built up by increasing the angular value by φ₂ along the oblique direction and by φ₁ along the horizontal lattice direction. The resulting lattice exhibits unit cells in which all pairs of spins across short diagonals have an angle difference of φ₁ – φ₂, whereas pairs of spins across long diagonals are separated by an angular difference of φ₁ + φ₂.

Lattice sums are then calculated and a minimization of the lattice energy with respect to the orientational degrees of freedom {φ_i}, the geometrical degrees of freedom (being the size ratios b/c for the REC lattice and/or the geometrical angle ω for RHO and OBL lattices; see Fig. 10), is carried out. The result of the minimization procedure is the optimized lattice-sum energy, U_X(Φ,ρ), where X stands for the lattice type, and Φ = (φ₁,φ₂,…,φ_N), denotes the configuration of the N spins in the system.

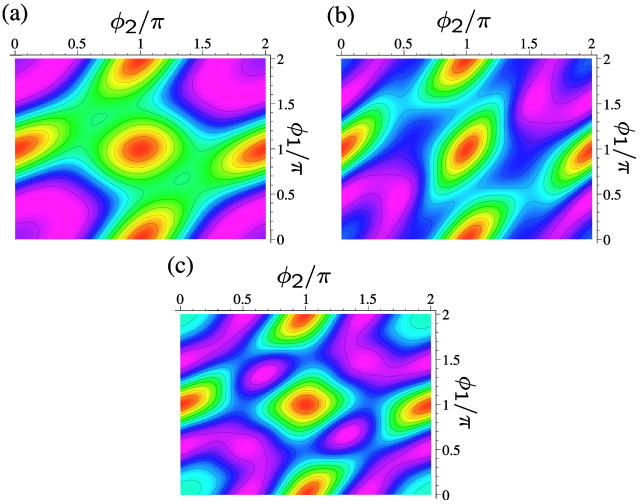
Three examples of lattice sums for fixed DNA density πρa² and fixed salt concentration n_s at a charge compensation θ = 0.9 and f₁ = 0, f₂ = 0, and f₃ = 1 are displayed in Fig. 11, a–c. They depict the total energy stemming from the lattice sum as contour plots as a function of φ₁ and φ₂. They are representative of three different phases emerging for these parameters. The meaning of the three phases will be explained in detail in the next section. It can be clearly discerned from the contour plots that a certain symmetry prevails in the aggregate with respect to φ₁ and φ₂ whereby the symmetry axis is the line φ₁ = φ₂. The location of the minima evolves from φ₁ = 0.21 π, φ₂ = 0.42 π (Fig. 11 a) via φ₁ = 0.46 π, φ₂ = 0.46 π (Fig. 11 b) to φ₁ = π/3, φ₂ = 2π/3 (Fig. 11 c), whereby lattice sums at correspondingly symmetric angles are found to have equally low values.

FIGURE 11.

Lines of constant energy as stemming from lattice sum calculations of DNA-salt mixtures for the KL model as a function of the azimuthal angles φ₁ and φ₂, with θ = 0.9 and f₁ = f₂ = 0, f₃ = 1. Magenta indicates low energies whereas red encodes high energy values. The lattice here is HEX. (a) πρa² = 0.44, n_s = 0.2 mol/l; (b) πρa² = 0.60, n_s = 0.2 mol/l; and (c) πρa² = 0.75, n_s = 1.7 mol/l.

The two-dimensional DNA-concentration ρ is varied within 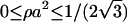, the upper limit being the close-packed configuration in a HEX lattice. We vary the salt concentration n_s in the assembly within 0.0001 mol/l ≤ n_s ≤ 3mol/l, including strongly deionized situations and physiological salt concentrations. For the lower limit of the two-dimensional DNA concentration the following remark is in order. The molecules remain parallel down to density ρa² ≈ 0.1, corresponding to interaxial separations R ≈ 34 Å, at which the cholesteric phase (CP) appears (Livolant and Bouligand, 1986; Livolant, 1991; Durand et al., 1992; Podgornik et al., 1996). A theory of the CP is beyond the scope of this work, thus we draw our phase diagrams down to ρa² = 0, with the reminder that for large interaxial separations the CP is stable. Although the CP is not included in the present theory, we have, for low two-dimensional DNA concentration, to take into consideration the low-density two-dimensional fluid. We achieve this by the following scheme: for every screening parameter κ which is associated with a given phase point (ρ,n_s), we map the interaction potential for φ = 0, given by Eq. 5 or Eq. 8, respectively, onto an effective hard-disk interaction potential, making use of the Barker-Henderson rule (Hansen and McDonald, 1986), providing us with the effective hardcore diameter d(κ). Using the known result (π/4)ρ_md(κ)² = 0.691 for the melting density ρ_m of hard disk systems (Mitus et al., 1997), the melting line can be estimated.

Volume and kinetic energy terms

To access the full thermodynamics of the DNA solution-salt mixture, we have to add the contributions to the free energy stemming from the counter- and co-ions, with numbers N_± and concentrations c_±, respectively. In a simplified picture, they can be thought of as the entropic, ideal-gas-like contributions of the free, noncondensed counterions (kinetic energy terms) and the interaction of the DNA macroions with their associated double-layer of salt microions. These degrees of freedom contribute an extensive term, independent of particle coordinates and momenta, to the free energy of the system, with terminology footing on the volume terms' extensivity. Although the volume terms lack the dependence on the current phase point of the system, they still represent an important contribution to the total free energy of the system, as they constitute a nontrivial, nonvanishing density-dependent term in the Hamiltonian. They are of importance in a wide number of multicomponent systems: Ashcroft and Stroud (1978) noted their influence on mixtures with quantum and classical components, Rowlinson (1984) pointed out their relevance in general terms, Grimson and coworkers (Canessa et al., 1988; Grimson and Silbert, 1991) analyzed their influence on charged colloids, and they were calculated by Graf and Löwen (1998) for charge-stabilized colloidal suspensions; see also van Roij (van Roij et al., 1999) and Denton (1999). For charged cylindrical molecules Graf and Löwen (1999) calculated the contributions from volume and kinetic energy terms to be

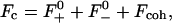(11)

where 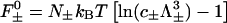are the ideal gas contributions (with Λ± being the thermal de Broglie wavelengths of the counter- and co-ions) and

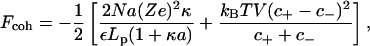(12)

is a cohesive term. In Eq. 11, e is the electron charge, Z|e| = 2πaL_pσ(1 − θ) is the uncompensated DNA charge, c₊ = Zρ/L_p + n_s and c₋ = n_s. Finally, V is the volume of the system and 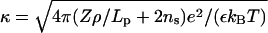for monovalent salt ions.

The total Helmholtz free energy for a given lattice type X is then given as the sum of the lattice sum of the DNA assembly, U_X, and the volume and kinetic energy terms of the salt solution, F_c: F = U_X + F_c.

THE PHASE DIAGRAM

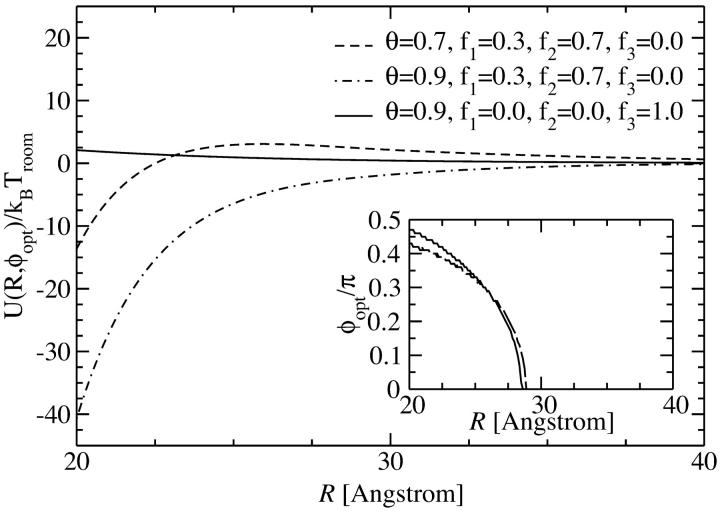
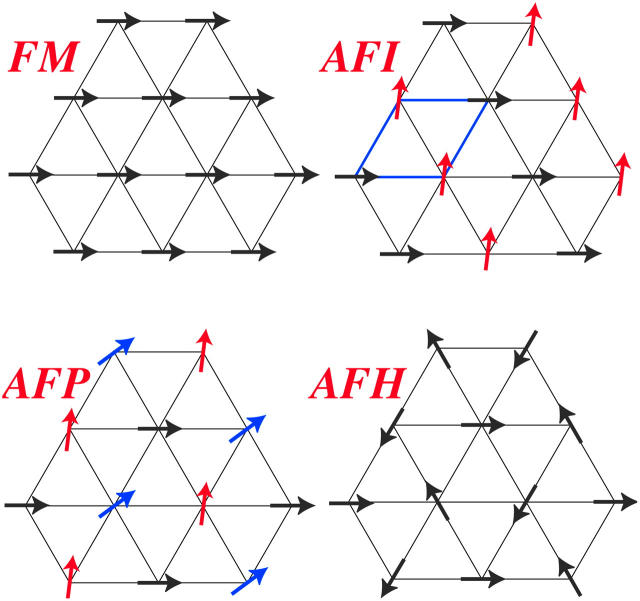
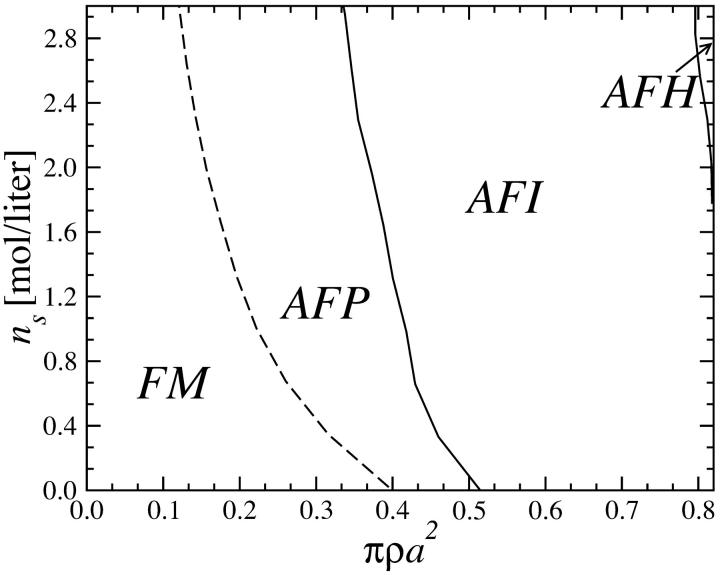
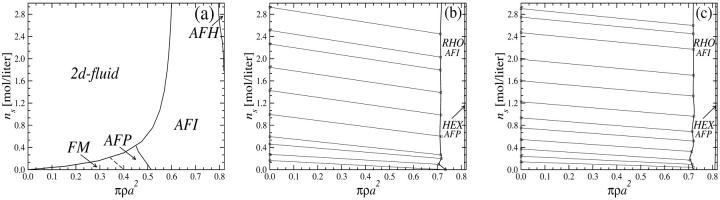
We now apply the considerations of the previous section to the calculation of the phase diagrams of columnar DNA assemblies. Let us focus on the YS model for the moment and then turn our attention to the KL model. The first choice of parameters we investigate corresponds to the adsorbed counterions being exclusively condensed on strands, i.e, f₁ = f₂ = 0 and f₃ = 1. In this case the DNA-DNA interaction is purely repulsive; see, for example, Figs. 8 and 9. Correspondingly, we find the system to crystallize into the HEX lattice at all DNA densities. Hexagonal lattice structures are evidenced in sperm nuclei and a number of bacteriophages (Livolant, 1991) and were also observed in vitro (Giannoni et al., 1969; Lerman et al., 1976; Livolant et al., 1989). Adding to the repulsive R-dependent interaction, the effect of the nontrivial R-φ coupling is present, giving rise to a large variety of orientational (spin, magnetic) structures to occur due to the azimuthal frustration of the system. The orientational structures are schematically shown in Fig. 12 and the phase diagram of the DNA-salt mixture is plotted in Fig. 13. Four different orientational phases can be discerned. The FM phase is stable at low DNA concentrations. It is ferromagnetic: all DNA molecules have the same azimuthal orientation. The AFP phase has a three-state antiferromagnetic Potts (Yeomans, 1992) type of ordering, with one-third of the spins pointing in a reference direction φ = 0, one-third in the angle φ₀ and one-third in the angle 2φ₀, where φ₀ grows with DNA concentration. The phase denoted AFI displays antiferromagnetic-Ising ordering, with half of the DNA molecules having one azimuthal orientation on one of the sublattices and a different orientation on the other. Finally, the AFH phase has the orientational ordering of the two-dimensional antiferromagnetic Heisenberg model, with spins residing in the three sublattices of the hexagonal lattice having mutual orientational angles of 120° to one another. The AFH phase is thus a special case of the AFP phase. The transition between the FM and AFP phases is second-order but the AFP → AFI and AFI → AFH transitions are first-order with very narrow density gaps (Graf and Löwen, 1998). As can be seen, for the average intermolecular separations occurring in the FM phase, the optimal azimuthal angle between the molecules is zero. The nontrivial phases arise at higher densities of the aggregates, as a result of the frustrated character of the φ-dependence of the pair potential. Similar mesophases were found recently within the framework of a phenomenological Landau theory (Lorman et al., 2001). Representative lattice sums for the AFP, AFI, and AFH phases are shown in Fig. 11. Including the two-dimensional fluid estimate into the calculation, parts of the phase diagram at lower two-dimensional DNA densities get preempted by the two-dimensional fluid, as is shown in Fig. 14 a.

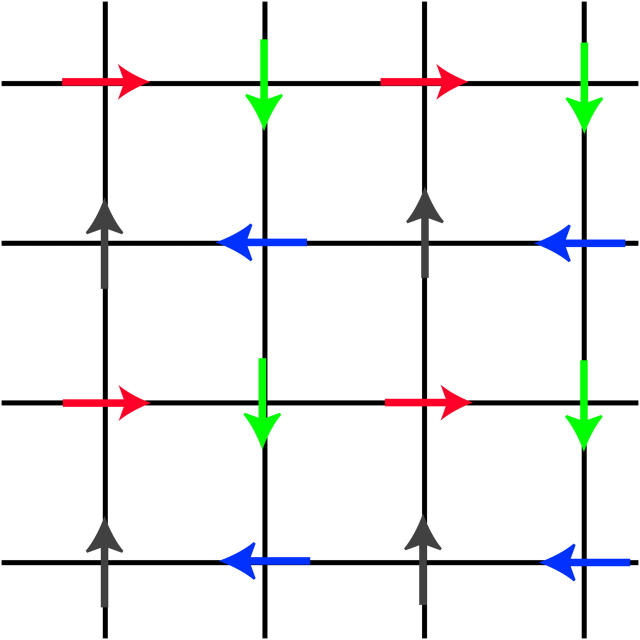
FIGURE 12.

The four stable magnetic phases. The arrows indicate the azimuthal orientations of DNA molecules. The acronyms, using magnetic terminology, stand for ferromagnetic (FM), antiferromagnetic Ising (AFI), antiferromagnetic Potts (AFP), and antiferromagnetic Heisenberg (AFH).

FIGURE 13.

Phase diagram of DNA-salt mixtures for the YS model as a function of the DNA packing fraction πρa² and salt concentration n_s in the aggregate: θ = 0.9, f₁ = f₂ = 0, and f₃ = 1; the lattice here is HEX. Dashed lines denote second-order magnetic transitions, solid lines first-order ones.

FIGURE 14.

Phase diagrams of DNA-salt mixtures for the YS model as a function of the DNA packing fraction πρa² and salt concentration n_s in the aggregate: (a) θ = 0.9, f₃ = 1; the lattice here is HEX. (b) θ = 0.7, f₁ = 0.3, and f₂ = 0.7; (c) θ = 0.9, f₁ = 0.3, and f₂ = 0.7. Dashed lines denote second-order magnetic transitions, solid lines first-order ones. The geometrical transitions between different lattices in b and c are second order; the straight lines are tielines between coexisting phases.

Changing the type of counterions present in the solution to counterions with a preference to adsorb into the major groove, i.e., choosing f₁ = 0.3, f₂ = 0.7, and f₃ = 0, drastically changes the picture. As we showed in The Pair Potential, the counterion condensation in grooves provides a “zipper” mechanism, leading to an attraction between the DNA molecules, since the positively charged sections of one molecule can approach the negatively charged sections of the other through an appropriate mutual orientation. This attraction leads to nonconvex parts in the Helmholtz free energy F(ρ,n_s), causing an instability in this regime, as nonconvexity means, via P = −∂F/∂V, regions of negative pressure in the system. Performing a double tangent construction removes the nonconvex parts in the free-energy curve and thereby yields broad phase coexistence tielines between dense DNA aggregates and DNA free solutions, connecting coexisting (ρ,n_s) state points. See Appendix A for a more detailed discussion. The occurrence of a broad phase-coexistence regime can be seen in Fig. 14 b for the case f₁ = 0.3, f₂ = 0.7, and f₃ = 0 for θ = 0.7. The oblique tielines result from the requirement that the electrolyte chemical potentials be equal at both coexisting phases, as is explained in more detail in Appendix A. In the one-phase region, a rhombic phase with an AFI-orientational structure shows up for the density regime directly adjacent to the phase coexistence line and a HEX crystal with AFP magnetic ordering appears at very high DNA concentrations. One might have, a priori, conjectured that an SQ phase with orthogonal magnetic order would win the game at high concentrations in the solely attractive YS case, since the angular part of the interaction favors ≈π/2 angular ordering for small separations and would thus be nonfrustrated on a SQ lattice; see Fig. 15. It has to be kept in mind, however, that although one has, for a given packing fraction, four neighbors closer in an SQ lattice than in a RHO or HEX lattice at the same packing fraction, which is favorable without repulsions, in a HEX lattice there are six neighbors at a slightly larger distance. The same effect is present in a RHO lattice, although there, the symmetry is broken with four nearest and four next-nearest neighbors as in the SQ lattice but with another nearest neighbor distance to next-nearest neighbor distance ratio, which turns out to favor the RHO lattice with the potential curve that we have in the YS case. Increasing θ to 0.9 does not qualitatively affect the phase diagram. The DNA-aggregate coexistence with DNA-free solutions turns out to be slightly broader, due to stronger attractions prevailing in the pair potential. The results are depicted in Fig. 14 c. We thus observe a significant qualitative difference in the macroscopic behavior of DNA columnar assemblies depending on the type of adsorbed counterions. If they solely adsorb on strands, i.e., f₁ = f₂ = 0 and f₃ = 1, all phase transitions occur in the azimuthal variables. With counterions condensed in grooves, a DNA bundling transition into a high DNA density rhombic phase takes place. The crossover from one topology (no DNA bundling) to the other (DNA bundling) can be estimated by holding f₁ = 0.3 fixed and increasing f₂ at the cost of f₃. For a charge compensation parameter θ of, for example, θ = 0.7 it is found to occur at (f₂,f₃) = (0.63,0.07). Here, all phase diagrams are plotted as a function of the electrolyte concentration in the aggregate. Taking into account the Donnan equilibrium (Rice et al., 1961), the phase diagrams, recalculated as a function of the salt in the reservoir, are qualitatively the same as the ones shown.

FIGURE 15.

A possible SQ phase with orthogonal magnetic ordering.

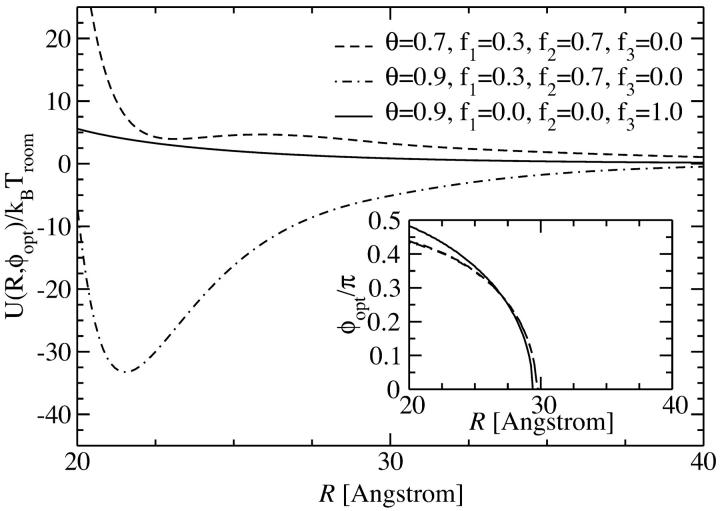
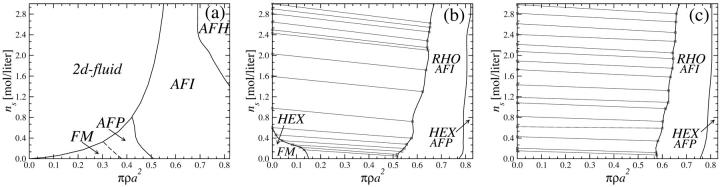
The same procedure is now applied to the KL pair potential. Again, we first investigate θ = 0.9 and f₁ = f₂ = 0 and f₃ = 1. The phase diagram is shown in Fig. 16 a. It is apparently very similar to the corresponding phase diagram of the YS model. The orientational structures found are the same as in the latter case and even the loci of the phase transitions are practically unchanged, except for the AFI → AFH transition, which occurs for lower ρ and n_s values. The two-dimensional fluid regime is smaller, being sign of the fact that the KL pair potential is steeper, i.e., stronger repulsive than the YS pair potential due to the image charge effect included in the KL model. Switching to counterion condensation in grooves, i.e., f₁ = 0.3, f₂ = 0.7, and f₃ = 0, again broad phase coexistence regions of a high-density DNA aggregate with a DNA free salt solution are observed; see Fig. 16, b and c. For the case of the lower of the two charge compensation parameters investigated, θ = 0.7, the high-density DNA assembly does not coexist with a DNA-free salt solution at all salt concentrations n_s, but rather coexists with a low-density HEX crystal with an imprinted FM orientational structure in the low salt concentration regime. This is, in this respect, qualitatively different from the corresponding phase diagram found in the case of the YS interaction. It is due to the much less attractive KL pair potential, as can be seen from a comparison of the curves for θ = 0.7 in Figs. 8 and 9. Due to the same reason the phase coexistence region turns out to be narrower for θ = 0.7 than it is for θ = 0.9, see again Fig. 16, b and c. The same statement holds for a comparison of the KL phase diagrams with the YS phase diagrams. Although in both cases the high-density DNA assembly exhibits a RHO lattice with an AFI-orientational order and then a transition to a HEX crystal complemented by an AFP magnetic structure, the phase coexistence region is significantly broader in the latter case. This behavior can be traced back to the pair potential in the same manner as above, as the YS interaction has a stronger attractive part and lacks the repulsive branch for close intersurface separations. (See Figs. 8 and 9.) The bundling transition induced by the strong zipper attractions will thus favor smaller interaxial separations between the bundled DNA molecules. We finally note that both the physical situation and the mechanism of DNA condensation put forward in this work are complementary to those studied by Sottas et al. (1999). In the latter work, attention was focused on very long, supercoiled DNA molecules in which the helical charge pattern has not been explicitly considered. Thereby, dispersionlike attractions have been introduced to explain DNA condensation. Here, we deal with short, straight DNA segments in which electrostatic attractions stemming from appropriate azimuthal orientations provide the dominant physical mechanism leading to attractions.

FIGURE 16.

Phase diagrams of DNA-salt mixtures for the KL model as a function of the DNA packing fraction πρa² and salt concentration n_s in the aggregate: (a) θ = 0.9, f₃ = 1; the lattice here is HEX. (b) θ = 0.7, f₁ = 0.3, and f₂ = 0.7; (c) θ = 0.9, f₁ = 0.3, and f₂ = 0.7. Dashed lines denote second-order magnetic transitions, solid lines first-order ones. The geometrical transitions between different lattices in b and c are second order; the straight lines are tielines between coexisting phases.

SUMMARY AND CONCLUDING REMARKS

Summarizing, we calculated the phase diagrams for columnar DNA assemblies, building on different levels of approximation in the pair interaction potential. We found that details of the interaction as manifest by the two potentials used for calculating the phase diagrams are not destroying the topology of the phase diagrams. The resulting phase diagrams showed significant agreement for the case of repulsive interactions, induced by counterion condensation on strands. For counterion condensation in the grooves, yielding strongly attractive interactions, the phase diagrams qualitatively agreed for the high charge compensation value, θ = 0.9, whereas for a lower charge compensation of θ = 0.7, an additional low-density HEX DNA phase was present in the KL model phase diagram which was absent in the YS case.

In conclusion we could put forward qualitatively robust predictions for the features and phase diagrams of columnar DNA assemblies. An experimental verification of the predictions of the theory would be highly desirable. Such a task, however, poses severe problems since the reliable experimental data available, to date, pertain to highly concentrated phases (Grimm and Ruprecht, 1991; Langridge et al., 1960; Dover, 1977), corresponding to small interaxial separations of the DNA molecules. In this regime the number of the basic assumptions inherent to the form of the pair potential may be questioned. The Debye-Bjerrum approximation becomes inadequate; as well, the independence of solvent dielectric constant on the aggregate density is questionable at high aggregate densities. Furthermore effects of nonlocal polarizability, and, more important, hydration effects come into play. The increase of experimental resolution in x-ray diffraction could open the way for the study of less dense aggregates. Particularly challenging is the predicted specific effect of cation adsorption on the phase diagram. Since the adsorption isotherms and the distributions of the adsorbed ions are poorly known, one should concentrate here on qualitative effects, that is, the (dis)appearance of mesophases triggered by different DNA condensing counterions.

Although in this work we focused on DNA as representative for helical (bio)molecules, the approach presented is, in general, not at all restricted to DNA alone, but rather can all types of molecules bearing helical charge patterns, such as RNA, collagen, guanosine, viral particles (e.g., tobacco mosaic virus), polysaccharide helices, and α-helical domains of many proteins as well as microtubules be treated within the same framework. Furthermore, the formalism used here is not restricted to columnar assemblies, but rather can be applied to other systems, such as bundles of α-helices, which form domains in many proteins, interactions between transmembrane α-helices and DNA-DNA interaction in nucleosomes, where only locally a parallel alignment of helical charge patterns may be assumed.

APPENDIX A: ON DETERMINING PHASE COEXISTENCE REGIONS

The problem to be solved is the phase behavior of a two-component system, with, in our case, one component being DNA, the other being salt with numbers N₁ and N₂ respectively. The number of counterions is directly coupled to N₂ (as the salt co- and counterions are to each other) via the condition of global charge neutrality. Assume the Helmholtz free energy F(N₁, N₂, V, T) to be known. Statistical mechanics and thermodynamics state that the free energy shall be convex for the system to be stable. The route to achieve this in simple one-component systems is the so-called double tangent construction whereby the nonconvex parts are “bridged” by a tangent onto the two points N^A and N^B where the concave parts of the free-energy curve start. These two points are the delimiting loci of phase coexistence between phase A at N^A and phase B present at N^B. The conditions to be fulfilled for stability and which are, by construction properly incorporated in the double tangent construction: equality of pressure, P^A = P^B and equality of chemical potentials, μ^A = μ^B in the two phases. Generalizing this for a two-component system, a corresponding two-component double tangent construction has to satisfy the following conditions: μ₁^A = μ₁^B, μ₂^A = μ₂^B, and P^A = P^B. The second of these three conditions can automatically be fulfilled by operating on μ₂ = const curves only.

It is thereby convenient to carry out a Legendre transformation to the semigrand potential Y(N₁, μ₂, V, T) = F(N₁, N₂, V, T) − μ₂N₂ (Dijkstra et al., 1999). It is understood that by keeping μ₂ fixed, N₂ becomes a function of N₁. We will henceforth omit the arguments V and T for simplicity. Consider now

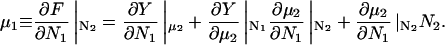(A1)

Since 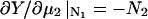according to the definition of Y as Legendre transform of F above, the last two terms cancel and we obtain:

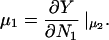(A2)

In an analogous way we obtain

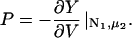(A3)

Introducing now the semigrand potential density y(n₁,μ₂) = V⁻¹Y(N₁,μ₂,V) with n₁ = V⁻¹N₁, it is straightforward to show that

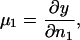(A4)

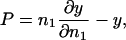(A5)

demonstrating that μ₁^A = μ₁^B and P^A = P^B is guaranteed by performing a common tangent construction on the y–versus −n₁ curves. In applying the above considerations to the present case, we have the salt chemical potential μ_s ≡ μ₂ and the DNA density ρ ≡ n₁. In Fig. 17 the semigrand potential surface y(ρ,μ_s) for the KL model is shown as a function of DNA density ρ and salt chemical potential μ_s, for a charge compensation of θ = 0.9. The counterion parameters are f₁ = 0.3, f₂ = 0.7, and f₃ = 0. One can clearly discern the nonconvex parts which lead to phase coexistence. The double tangent construction is performed on the curve displayed in Fig. 18 as indicated by the dashed line. It shows the semigrand potential y(ρ,μ_s = const) as a function of DNA density ρ at constant salt chemical potential, μ_s = const. Due to the broad nonconvex part, the broad phase coexistence region emerges in the phase diagrams. The oblique tielines are obtained by calculating the salt concentrations 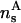and 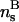at the coexisting DNA densities ρ^A and ρ^B.

FIGURE 17.

Semigrand potential per unit volume y(ρ,μ_s) as a function of reduced DNA density and salt chemical potential, for the KL model and parameters θ = 0.9, f₁ = 0.3, f₂ = 0.7, and f₃ = 0.

FIGURE 18.

Semigrand potential per unit volume y(ρ,μ_s) on a line of constant DNA chemical potential for the KL model as a function of the reduced DNA density and for parameters θ = 0.9, f₁ = 0.3, f₂ = 0.7, and f₃ = 0. Also shown (dashed line) is the common tangent connecting the coexisting phase points.