Discrete Models of Autocrine Cell Communication in Epithelial Layers

Abstract

Pattern formation in epithelial layers heavily relies on cell communication by secreted ligands. Whereas the experimentally observed signaling patterns can be visualized at single-cell resolution, a biophysical framework for their interpretation is currently lacking. To this end, we develop a family of discrete models of cell communication in epithelial layers. The models are based on the introduction of cell-to-cell coupling coefficients that characterize the spatial range of intercellular signaling by diffusing ligands. We derive the coupling coefficients as functions of geometric, cellular, and molecular parameters of the ligand transport problem. Using these coupling coefficients, we analyze a nonlinear model of positive feedback between ligand release and binding. In particular, we study criteria of existence of the patterns consisting of clusters of a few signaling cells, as well as the onset of signal propagation. We use our model to interpret recent experimental studies of the EGFR/Rhomboid/Spitz module in Drosophila development.

INTRODUCTION

Epithelial layers provide a common substrate for pattern formation in development (Hogan, 1999). In general, cell-to-cell communication produces spatially nonuniform patterns in the expression of genes that guide the development of tissues and organs. The design principles of epithelial patterning are being formulated only now (Freeman and Gurdon, 2002). An important family of epithelial patterning mechanisms relies on secreted chemical signals. Typically, a ligand released by a group of cells interacts with the extracellular matrix and cell surface receptors as it spreads through the tissue. Ligand transport can be integrated with positive and negative intracellular feedback loops (Freeman, 2000). For example, ligand-receptor binding can stimulate ligand synthesis and secretion (Freeman and Gurdon, 2002). Ligand release can be regulated by the occupancy of cell surface receptors. Receptor occupancy, in turn, may be determined by the balance between ligand transport, binding, and degradation; see Fig. 1 D.

FIGURE 1.

(A) The geometry of the problem is motivated by cell communication in Drosophila oogenesis. Epithelial cells cover the large oocyte. EGF receptors are uniformly distributed across the epithelial layer and are absent on the surface of the oocyte. (B) Ligands diffuse in a thin gap between the epithelial layer and a reflective surface. (C) The two model layers considered in this article—periodic arrays of squares and hexagons. (D) Main processes in ligand binding and transport. (E) Ligand binding stimulates ligand release. Receptor activation leads to the degradation of a factor inhibiting the transcription of the ligand-releasing protease. In the absence of inhibition, the protease is synthesized and generates the secreted ligand.

Here, we consider a general problem of interaction between cells arranged in an epithelial layer and communicating by secreted ligands. The original motivation for the problem comes from Drosophila egg development (Spradling, 1993), where pattern formation proceeds in the follicular epithelium—a layer of columnar epithelial cells that envelop the oocyte. Follicle cells are much smaller (5–7 μm) than the oocyte (100–300 μm); see Fig. 1 A. Reciprocal oocyte/follicle cell interactions pattern the eggshell and establish the embryonic axes (Van Buskirk and Schupbach, 1999). These events rely on the epidermal growth factor receptor (EGFR), a well-studied receptor tyrosine kinase (Nilson and Schupbach, 1999; Wells, 1999). EGFRs are uniformly distributed across the follicular epithelium and are absent on the oocyte surface (Sapir et al., 1998). EGFR is activated by ligands secreted from the oocyte and from the follicle cells themselves. Secreted ligands diffuse in the thin (<1 μm) gap between the follicle cells and the oocyte; see Fig. 1 B. Release of EGFR ligands is regulated by the intracellular proteases (Urban et al., 2002). Interestingly, the expression of these proteases (Rhomboids), is positively regulated by EGFR signaling (Hsu et al., 2001; Peri et al., 1999; Sapir et al., 1998; Wasserman and Freeman, 1998); see Fig. 1 E. To summarize, ligands diffuse in a thin gap between receptor-covered epithelium and a reflective surface; receptor activation stimulates further ligand release by activating the expression of the intracellular protease.

Similar signaling/transport arrangements are encountered later in fruit fly development and in other species, both for the EGFR and other signaling systems (Doraiswamy et al., 2000; Freeman and Gurdon, 2002).

The gene expression patterns in developing epithelial layers can be very fine-grained. In many cases, the width of the signaling patterns is only a couple of cells (Carmena et al., 2002; Hatini and DiNardo, 2001; Peri et al., 1999; Ruohola-Baker et al., 1993; Sapir et al., 1998). What is the appropriate biophysical description for such systems? There have been several attempts to use continuum models for the analysis of such patterns, e.g., those of Lander and co-workers (Lander et al., 2002), and Shvartsman and co-workers (Shvartsman et al., 2002). These models assume that the relevant length scale of the pattern is greater than the size of a single cell. The validity of such an assumption may be difficult to reconcile with the fine-grained nature of experimentally observed signaling patterns. Starting from the work of Othmer and Scriven, a number of discrete models for cellular layers has been proposed (Collier et al., 1996; Meir et al., 2002; Monk, 1998; Othmer and Scriven, 1971; Owen et al., 1999, 2000; von Dassow et al., 2000). However, in these models the form of cell-to-cell couplings has been chosen on purely phenomenological grounds.

Here, we systematically derive discrete models of cell-to-cell communication from a mechanistic description of autocrine and paracrine signaling in epithelial layers. These models are discrete because they treat each cell individually. The models are also long-ranged: they use the state of the entire layer in describing the dynamics of each cell and thus take into account non-nearest neighbor cell-to-cell interactions. Our derivation is based on the introduction of coupling coefficients that characterize the communication of cells by secreted ligands. These coupling coefficients are directly linked to the biophysical parameters of the transport problem. Central to our approach is the use of the separation of timescales between diffusing and intracellular species. We argue that binding and transport are fast and are therefore dynamically slaved to the slow intracellular variables when the intracellular processes involve transcription and protein synthesis. With the coupling coefficients at hand, we are then able to formulate discrete models that account for particular intracellular processes, such as receptor-mediated activation of ligand release, and study their properties associated with discreteness.

DESCRIPTION OF THE MATHEMATICAL MODEL

Our model accounts for the coupled dynamics of extracellular ligand, ligand-receptor complexes, and ligand-releasing proteases in each cell within the epithelial layer. In formulating the model, we assume that the system operates in the ligand-limited regime and that the free receptors are in excess. This is supported by experiments in several model organisms (Freeman and Gurdon, 2002). Following the standard receptor binding analysis, this approximation requires that the concentration of ligand is less than the equilibrium binding constant, k_D = k_off/k_on. With this in mind, a mechanistic model of transport and signaling in an idealized epithelium consisting of a two-dimensional periodic array of identical cells in a single flat layer geometry takes the following form (Fig. 1, B and D):

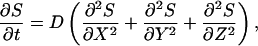(1)

(2)

(3)

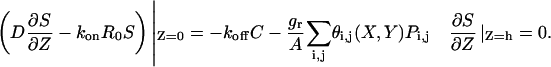(4)

Here, is the concentration of ligand in the extracellular space, is the number of ligand-receptor complexes per unit area on the cell surfaces, P_i,j(t) is the amount of ligand-releasing protease in the cell with index i,j (one index for each dimension of the two-dimensional cell lattice; for concrete indexing schemes in particular cell geometries, see Appendix), X and Y are the coordinates in the plane of the epithelial layer, Z is the transverse coordinate, and t is time. 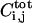is the total number of ligand-receptor complexes on the surface of cell i,j. D is the diffusion coefficient of the ligand in the extracellular space, k_onR₀ is the product of the rate of ligand-receptor forward binding and the number of receptors per unit area, k_off is the ligand-receptor complex dissociation constant, and k_e is the rate of ligand-induced receptor internalization.

Thus, Eq. 1 models the three-dimensional extracellular ligand diffusion in the gap of width h between the layer of cells and an impermeable barrier, whereas Eq. 2 describes the reversible ligand-receptor binding and the first-order receptor-mediated endocytosis (Lauffenburger and Linderman, 1993), Fig. 1 D. In the dynamic balance for ligand-receptor complexes, 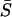is the ligand concentration at the receptor-covered cell surfaces.

Similarly, Eq. 3 models the ligand-releasing protease dynamics in each cell within the epithelial layer. These dynamics consist of the combination of the first-order degradation characterized by rate constant k_p and a sigmoidal generation function 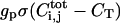characterized by the production rate g_p and the threshold C_T. Such parameterization lumps a number of processes together and is common in modeling of regulatory networks (Bolouri and Davidson, 2002; Ferrell, 1997; Smolen et al., 2000). In the following we choose σ(x) to be the Heaviside function, thus assuming a sharp threshold; our results do not significantly depend on the precise form of σ(x). Furthermore, our first-order degradation combines the degradation at the mRNA and protein level. Let us emphasize that this thresholdlike generation term is a function of the total number of ligand-receptor complexes on the i,j^th cell. Therefore, it is related to the distribution of complexes by the integral over the area of the i,j^th cell surface (Eq. 3). This is supported by at least one direct measurement (Dyson and Gurdon, 1998).

The boundary condition for Eq. 1 on the surface of the epithelial layer (Z = 0), which couples the diffusion of the ligand with its secretion (as a result of intracellular processes), is given by Eq. 4. It accounts for the reversible binding and protease-mediated ligand release. The source term in this boundary condition is spatially nonuniform and varies from cell to cell across the layer. There are two contributions to this term: dissociation of ligand-receptor complexes and protease-mediated ligand release. The latter is assumed to be uniform over each cell's surface, which is expressed by the characteristic function θ_i,j(X,Y), which is equal to ‘1’ on the surface of the i,j^th cell and ‘0’ elsewhere, and is regulated by the availability of the ligand-releasing protease. Ligand release is modeled as first-order with respect to the protease, with the release rate per cell given by g_rP_i,j (A is the area of the cell surface). Ligand-precursor, on which the ligand-releasing protease is acting, is assumed to be in excess. There is also a no-flux boundary condition at the impermeable barrier (Z = h) in Eq. 4.

Goals of the article and plan of the analysis

The model describes the coupled dynamics of cells in an idealized epithelial layer. To characterize these dynamics, we need to track both the extracellular and intracellular variables in the system of integrodifferential Eqs. 1–4. We would like to quantify the spatial extent of cell-to-cell communication and to analyze the effect of this coupling on the dynamics of individual cells. As an application, we consider the consequences of activating ligand release in a small group of cells within the layer. Such perturbations are implemented using techniques for tissue-specific gene expression and are routinely employed in developmental biology (Brand and Perrimon, 1993; Duffy et al., 1998). Analysis of such perturbations requires models that can resolve individual cells. It is our goal to formulate such models.

RESULTS

Main approximations

We consider the case when the height of the medium for ligand diffusion is small relative to the appropriately chosen dynamic length scale in the problem. In terms of the original model parameters, this translates into the inequality h ≪ D/k_s, where characterizes the steady-state rate of ligand degradation. In this case, the spatial variation of the ligand field in the z-direction is negligible: 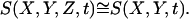This approximation is expected to be very accurate for the chosen set of geometric and dynamic parameters.

In addition to reducing the number of spatial dimensions, we reduce the number of dependent variables. Our argument is based on the timescale separation between the ligand dynamics and those of the intracellular protease. In our description, ligand binding stimulates the transcription of the ligand-releasing protease. Since this process happens on a timescale that is longer in comparison to those of binding, transport, and endocytosis, we can set the time derivatives in the dynamic balances for extracellular and receptor-bound ligand to ‘0’. This approximation imposes the following constraints on the timescales: and (see Appendix).

Together with the assumption of the ligand-limited regime, these approximations lead to the following model:

(5)

(6)

where

Hence, the problem in Eqs. 1–4 is reduced to the equation for protease dynamics in individual cells coupled to the steady linear reaction-diffusion equation for extracellular ligand. The linear problem for the ligand field can be easily solved for any particular pattern of protease activity. The resulting instantaneous field, can then be integrated over the area of each cell to provide arguments for the protease generation function. This leads to a fully discrete model for cell communication. In the following, this programme is implemented for square and hexagonal cells. Before that, we rescale the problem and describe the dimensionless groups.

Nondimensionalization

Eqs. 5–6 are rendered dimensionless by the following transformations,

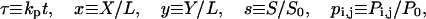(7)

where

(8)

For estimates of the relevant quantities, see Table 1.

TABLE 1.

Model parameters

Parameter	Description	Typical value
A	Cell surface area	2.5 × 10−7 cm2
Lx	Cell width (squares)	5 × 10−4 cm
2Lv	Cell width (hexagons)	5 × 10−4 cm
D	Ligand diffusivity	1 × 10−7 cm2 s−1
h	Height of the extracellular medium	5 × 10−5 cm
ke	Ligand-induced internalization rate constant	0.1 min−1
kon	Receptor-ligand association constant	0.1 nM−1 min−1
koff	Receptor-ligand complex dissociation constant	0.1 min−1
kp	Protease degradation rate constant	0.03 min−1
ks = kekonR0/(ke + koff)	Ligand degradation constant	5 × 10−5 cm s−1
Qs = grgp/kp	Rate of ligand release per cell	500 molecules/cell/min
R0	Number of receptors per cell	1 × 104 receptors/cell
CT	Threshold for activating the positive feedback	500 complexes/cell

Notice that P₀ and S₀ determine the maximum levels of protease and ligand concentrations. In fact, these values are attained when ligand release is at its maximal “on” level uniformly throughout the layer (p_i,j = 1 for all cells). Associated with these maximum values is the maximum level of ligand-receptor complexes 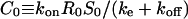and the maximum total number of ligand-receptor complexes per cell, (Tables 2 and 4).

TABLE 2.

Model variables

Variable	Description
S	Ligand concentration
C	Ligand-receptor complex surface concentration
	Total number of complex molecules over the cell
Pi,j	Number of active protease molecules per cell
t	Time
X,Y	Coordinates in the plane of the epithelium
Z	Transverse coordinate
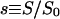	Dimensionless ligand concentration
	Dimensionless ligand-receptor complex surface concentration
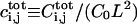	Dimensionless total number of complex molecules over the cell ij
	Dimensionless number of active protease molecules per cell
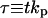	Dimensionless time
	Dimensionless spatial variable

TABLE 4.

Scaling factors

Variable	Description
	Ligand concentration
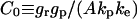	Ligand-receptor complex surface concentration
	Total number of complex molecules over a cell
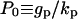	Number of active protease molecules per cell
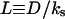	The dynamic length scale

After rescaling, the problem takes the following form:

(9)

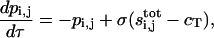(10)

where 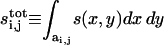and the integration is now over the rescaled cell area 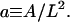Recall that we chose

There are only two dimensionless groups in the resulting dimensionless system

(11)

The first group characterizes the balance between ligand degradation and transport. The second group is the rescaled threshold in the protease generation function.

To complete the derivation of the discrete model we solve the transport problem for the extracellular ligand. Since the problem is linear, the solution can be evaluated as a superposition of fields due to secretion from individual cells.

Ligand field for a single-cell source

Consider a single ligand-releasing cell placed at the origin of the epithelial layer 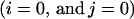, secreting the ligands with the dimensionless rate p_0,0 = 1. Then, the resulting ligand field q(x,y) satisfies:

(12)

where 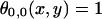everywhere on the surface of the cell placed at the origin, and ‘0’ everywhere else. The ligand fields computed for a particular set of parameters for square and hexagonal cells are shown in Fig. 2.

FIGURE 2.

The steady-state ligand field due to a single ligand-releasing cell. (A) Square cells, L_x = 5 × 10⁻⁴ cm. (B) Hexagonal cells, 2L_v = 5 × 10⁻⁴ cm. Other parameters: h = 5 × 10⁻⁵ cm, k_e = 0.1 min⁻¹, k_off = 0.1 min⁻¹, R₀ = 1 × 10⁴ molecules/cell surface, D = 1 × 10⁻⁷ cm² s⁻¹, k_on = 0.1 nM⁻¹ min⁻¹, and Q_s = 100 molecules/cell/min. The fields were computed by solving Eq. 12 using an adaptive mesh finite element package (FEMLAB).

Using the two-dimensional cosine transform, the ligand field can be found as

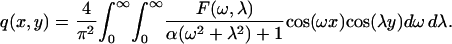(13)

Here, F(ω,λ) is the cosine transform of θ_0,0 (x,y). See Fig. 6, A and B, and the discussion in the Appendix. The function F(ω,λ) depends both on the shape and the size of the cell. The expressions for F(ω,λ) for the square and hexagonal cells are given in the Appendix.

The formula for the ligand field in Eq. 13 can be used to evaluate the integrals in the argument of the function specifying the protease production. Specifically, to evaluate the rate of protease production by the ij-th cell, we compute the total amount of ligand over its surface (see Eq. 10). For a single source of strength p_0,0, we have:

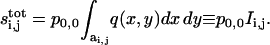(14)

The last expression is a crucial result of this article, as it defines the coupling coefficients for cell communication by secreted ligands. Clearly, s_i,j depend only on the relative position between the i,j^th cell and the source. Thus, the same formula can be used to compute the ligand generated by an arbitrary cell.

Cell-to-cell coupling coefficients

The coefficients lead to a number of useful expressions. The number of ligand-receptor complexes on the surface of the i,j^th cell due to the ligand-releasing cell at the origin can be found as:

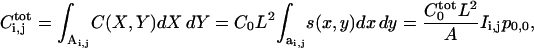(15)

where is the total number of ligand-receptor complexes on the cell surface when the entire layer is producing ligand at the maximum rate. Hence, to compute the number of complexes due to a single cell, one has to multiply this maximal value by the interaction coefficient and divide the result by the dimensionless cell area :

Using linear superposition, we express the total number of ligand receptor complexes for an arbitrary pattern of protease activity:

(16)

where we used translational symmetry. The analogous equation holds for the extracellular ligand: 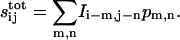For arrays of square and hexagonal cells these coefficients are explicitly computed in the Appendix.

Discrete model for cell communication

We now use the coupling coefficients to formulate a discrete model of cell communication. Substituting the expression for 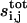into the protease balance, we obtain:

(17)

Hence, the original system of integrodifferential equations has been reduced to a system of ordinary differential equations (with explicitly available coupling coefficients). As a result, we have a dynamical system that describes the protease dynamics in each cell within the epithelial layer. The model is long-ranged, inasmuch as the dynamics in each cell depend on the pattern of protease activity in the entire layer. The model is fully discrete, since we resolve individual cells and have “removed” the continuum part of the problem.

Parametric analysis of coupling coefficients

Given the expressions for the interaction coefficients (see Appendix), we can examine their dependence on the biophysical parameters of the original problem. In the case of EGFR signaling in Drosophila egg development, the cell area (A) and the height of the gap between the oocyte and follicle cells (h) have been estimated from microscopic images: (h ∼ 0.5 μm, A ∼ 25 μm²; see Spradling, 1993). The extracellular diffusivity of the ligand (Spitz) and the binding/internalization rate constants can be estimated from the corresponding values in the mammalian EGFR systems. Using these parameters, we present the dependence of the coupling coefficients on the ligand diffusivity and the forward-binding rate constant in Fig. 3. Note that we plot the coupling coefficients as functions of the distance between cells. This is done only for convenience in representing discrete data points; of course in the fully discrete context, the coupling coefficients are anisotropic (although the degree of anisotropy proves to be rather small both for square and hexagonal cells). Similarly, the lines connecting the points in Fig. 3 are used only to guide the eye.

FIGURE 3.

Normalized coupling coefficients (, see text for details) plotted as a function of cell-to-cell distance, k, defined as the ratio of the Euclidian distance divided by the cell size. (A) Effect of ligand-receptor affinity k_on (square cells, L_x = 5 × 10⁻⁴ cm, D = 1 × 10⁻⁷ cm² s⁻¹). (B) Effect of ligand diffusivity D (hexagonal cells, 2L_v = 5 × 10⁻⁴ cm; k_on = 0.1 nM⁻¹ min⁻¹). All other parameters are as in Fig. 2.

The computation in Fig. 3 probes the spatial operation of an autocrine system, a mode of cell-to-cell signaling where cells can both release and recapture the ligand. The spatial decay of coupling coefficients is controlled by kinetics and transport. The rate of the decay increases with the forward-binding rate constant and decreases with the ligand diffusivity. We find that for the biophysically relevant set of parameters—the geometry of the egg chamber and the transport/kinetic rate constants—the interaction coefficients decay rapidly as a function of the cell-to-cell distance. In fact, the interaction between the cells separated by more than 3–4 cell diameters is negligible. This is in line with the conclusions of genetic experiments that can indirectly estimate the spatial range of ligand action in vivo (Bergmann et al., 2002; Freeman, 1997; Peri et al., 2002).

The rapid decay of the coupling coefficients can be exploited in the computational analysis of the discrete problem, Eq. 17. In simulating the arrays of cells, one has to evaluate the coupling only between the finite (and small) number of cells. This greatly simplifies the evaluation of the right-hand side of Eq. 17.

Analysis of the positive feedback circuit

We now illustrate the use of our model in a number of computational experiments with the positive feedback circuit, Fig. 1. Our computations are directly related to the recent results in Drosophila egg development, reviewed in Amiri and Stein (2002). In one of the experiments, Peri and co-workers used genetics to permanently activate the protease and hence, the ligand release, in a small (2–4) group of cells within the follicular epithelium (Peri et al., 2002). The ligand (Spitz) acts on the cognate receptors (EGFR) on the surfaces of epithelial cells. The authors then followed the level of expression of the gene controlled by the receptor (pipe; see Amiri and Stein, 2002). It was found that pipe was repressed both in the Spitz-releasing cells and in their neighbors. It is well known that ligand-receptor (EGFR/Spitz) binding in this system stimulates the expression of the ligand-releasing protease (Rhomboid) and that the released ligand (Spitz) can activate the protease in the neighboring cells; see Fig. 1, B and E. So what prevents the perturbation from spreading across the cellular layer? What controls the effect—the strength of ligand release, the extracellular transport, or the size of the perturbation (the number of cells constitutively expressing the protease)? Our computations illustrate how these questions might be addressed within the presented biophysical framework.

First, we construct stable stationary solutions of the discrete problem of cell-to-cell communication, Eq. 17. Let us emphasize that these solutions have no counterparts or analogs in the continuous reaction-diffusion models with bistable nonlinearity. For illustrative purposes, we consider simple three-cell perturbations in the square and hexagonal lattices, Fig. 4. In experiments, cells within these clusters expressed the protease independently of ligand-receptor binding. In terms of our model, this means that the protease level in these cells is constant. For the Heaviside nonlinearity, the stable level of the protease can have only two values: the “on” state, for which p_i,j = 1, and the “off” state, where p_i,j = 0.

FIGURE 4.

Stable localized patterns generated by the positive feedback. Existence of the localized three-cell patterns for squares (A) and hexagons (B) as a function of ligand release rate and ligand-receptor affinity. The shaded area corresponds to the stable localized pattern. Crossing the upper boundary ignites the neighboring cells. Crossing the lower boundary leads to the extinction of the pattern. (C) A one-dimensional cut (Q_s = 300 molecules/cell/min) through the diagram in A showing the disconnected region of existence of the localized pattern. Localized patterns are realized both for low and high ligand-receptor affinities. (D) Critical rate of ligand release necessary to destabilize the localized pattern as a function of the number of cells in it, k_on = 0.1 nM⁻¹ min⁻¹. A–D: C_T = 500 molecules/cell. Other parameters are as in Fig. 2.

The transition between the two states is induced when the argument of the protease generation function exceeds the critical value given by C_T (Eq. 11). The argument, in turn, depends on the pattern of protease activity in the entire cellular layer (see Eq. 17). For the cases shown in Fig. 4, the condition for the “off → on” transition (ignition) of one of the cells next to the original perturbation can be written as:

These conditions are written for the three-cell perturbation placed at the origin of the cell lattice. For each case, the cell most susceptible to this transition is marked on the insets of Fig. 4, A and B. See Appendix for the definition of the indexing schemes.

In writing the “ignition” condition, we keep the dependence of coupling coefficients on α, the dimensionless group combining the kinetic and transport properties (refer to the definition in Table 3). Using this condition, the value of the critical threshold in the right-hand side can be computed for every value of α. This defines an upper boundary of the localized three-cell patterns in Fig. 4, A and B. Thus, the construction of the stability boundary amounts to evaluating only a small number of coefficients.

TABLE 3.

Dimensionless parameters

Variable	Description	Typical value
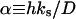	Damköhler number	2.768 × 10−2
	Dimensionless threshold in the sigmoidal nonlinearity
	Relative timescale of binding and trafficking	0.15
	Relative timescale of the ligand transport	1.632 × 10−2
	Dimensionless cell surface area

Using the definitions of α and C_T (Eq. 11), we translate these dimensionless groups into the dimensional parameters of the reaction transport problem in Eqs. 1–4. In Fig. 4 we plot these boundaries as functions of ligand-release rate and the ligand-receptor affinity, the two parameters that have been shown to regulate the operation of autocrine loops in a number of cell culture EGFR systems. In our computations, the range of ligand affinity was dictated by the large amount of binding data available for the EGFR system (Lauffenburger and Linderman, 1993; Wiley et al., 2003). The rate of ligand release suggested by our computations spans the range attainable in the experiments with cultured autocrine EGFR-expressing cells (DeWitt et al., 2001; Dong et al., 1999). At this time, there are no quantitative data on ligand-release rates in vivo.

In addition to static perturbations, such as those used by Peri and co-workers (Peri et al., 2002), we can consider the perturbations that transiently activate ligand release in a group of cells. What is the outcome of a transient perturbation? Will it decay to zero or persist when the stimulus is turned off? The condition under which a pattern is extinguished (i.e., at least one of the cells within the cluster undergoes the transition to the “off” state) can also be easily formulated as a simple equation for a small group of coupling coefficients. For example,

This equation defines the lower boundaries in the two-parameter diagrams in Fig. 4, A and B.

FIGURE 5.

Response of a cellular layer to a localized perturbation in protease release. (A) The structure of the perturbation. B–D, The ligand fields induced by the perturbation computed for different ligand-release rates. (B) Q_s = 100 molecules/cell/min. Ligand field 40 min after the perturbation. The perturbation decays. (C) Q_s = 200 molecules/cell/min. The perturbation generates a stable pattern of the same structure. (D) Q_s = 300 molecules/cell/min. The perturbation generates an “ignition” wave (see text for details). All parameters are as in Fig. 4 A.

To study the evolution of a transient localized perturbation, we simulated the dynamical problem with an initial condition specified by a given pattern of the protease activity. For example, Fig. 5 presents three qualitatively different outcomes resulting from activating ligand release in a three-cell cluster, Fig. 5 A. The ligand fields presented in this figure were generated by first solving the discrete model for the protease pattern, and then using this pattern as the source term in a linear ligand transport problem. For ligand affinities and release rates within the domain of existence of a localized pattern, this perturbation evolves into a stable signaling pattern that is confined to three cells, Fig. 5 C. This is in marked difference with the analogous continuous system, in which a localized perturbation either decays or results in the onset of signal propagation. Increasing the rate of ligand release leads to overstepping of the upper stability boundary, Fig. 5 D. In this case, the localized perturbation acts as a “seed” for an ignition front that travels outwards, leaving the cells in the “on” state. This is similar to the continuous case (Přibyl et al., 2003). For low rate of ligand release, the transient activation of protease activity induces only a transient response, Fig. 5 B.

An interesting feature of the two-parameter diagrams in Fig. 4, A and B, is the presence of a clear minimum in the dependence of the critical rate of ligand release on the ligand-receptor binding affinity. In terms of the model, it means that the domain of parameters for which the particular localized pattern exists is disconnected. This is illustrated by a one-dimensional cut through the two-parameter diagram, Fig. 4 C. We verified that overstepping both the left and the right boundaries in this plot generates an ignition front (see the discussion above). The nature of these transitions can be described as follows. For low ligand affinities, binding and transport cannot generate the number of ligand-receptor complexes that are necessary for activating the positive feedback. On the other hand, very high binding affinities prevent an efficient transport of ligand. This regime corresponds to the case, when ligand is degraded before it is passed on to the neighbors.

Finally, Fig. 4 D demonstrates that the effect of the localized perturbation is critically affected by the size of the perturbation. For the examples presented in Fig. 4 D, the upper stability boundary that was correlated with the initiation of “ignition” fronts is negatively correlated with the size of the perturbation. The fact that the stability boundary strongly depends on the size of the perturbation is an immediate consequence of the fact that coupling beyond nearest neighbors is important. Experiments with constitutively active ligand release are frequently limited by the ability to control the size of the perturbation (Peri et al., 2002). We suggest that the corresponding results should be interpreted with care. In particular, for the same values of binding, signaling, and transport parameters, changing the size of the perturbation can move the system between the regimes of localized and long-range signaling.

CONCLUSIONS

We have developed discrete models of cell-to-cell communication in epithelial layers. In analyzing autocrine and paracrine signals, we consider the molecules, the feedback loops, and the geometry of cell-to-cell communication that are conserved across species (Casci and Freeman, 1999). EGFR system serves as a paradigm for autocrine/paracrine tissue regulation, and in multiple developmental and pathological contexts EGFR is controlled by the positive feedback loop discussed in this article (Wells, 1999). Indeed, the EGFR/Ras/MAPK-mediated feedback from ligand binding to ligand release operates in many mammalian systems (Dent et al., 1999; Doraiswamy et al., 2000; Gechtman et al., 1999; Montero et al., 2002). At this time all models of EGFR system are formulated at the level of a single cell (Wiley et al., 2003). Our work is aimed at the development of mechanistic models at the tissue level.

One of our main results is the derivation of cell-to-cell coupling coefficients as a function of geometric, cellular, and molecular parameters of the ligand transport problem. These coefficients provide a quantitative framework for the analysis of cell-to-cell interactions by diffusing ligands in epithelial layers. Our explicit expressions for the coupling coefficients obtained for particular geometries can be used to estimate the range of cell communication in epithelial layers. Note, however, that our approach—“removing” the continuum part of the problem by slaving it to intracellular variables through the introduction of cell-to-cell coupling coefficients—is not limited to periodic arrays of cells of simple shapes and can be applied to arbitrary cell arrangements.

In addition to the general analysis of autocrine signals in epithelial layers, we have analyzed a discrete and nonlinear model of the positive feedback between ligand release and binding. In particular, we found a class of stable stationary solutions in the form of clusters of a few signaling cells. The existence of these solutions is due to the essential discreteness of the considered system. These results can be applied to the EGFR signaling in Drosophila oogenesis. This is possible due to the well-characterized “geometry” of cell communication in this problem, and to the availability of molecular and cellular data for the EGFR system. The results on localized patterns can be used to analyze the patterned states generated by the localized activation of ligand release in the follicular epithelium (Pai et al., 2000; Peri et al., 2002).

While this work has been primarily motivated by the EGFR-mediated cell communication, recent advances in cell biology of developmental signaling pathways enable the formulation of mechanistic models for other systems. Recent data on ligand-receptor affinity in the Wingless pathway can be combined with the spatially resolved measurements of Wingless transport (Dubois et al., 2001; Lloyd et al., 2002; Pfeiffer et al., 2002). This provides a good incentive for the development of transport models that could account for the processes of intracellular ligand trafficking (Entchev et al., 2001; Seto et al., 2002).

The rapid decay of coupling coefficients suggested by our computations is in line with the conclusions of experimental studies of the EGFR system, both in vitro and vivo. We suggest that, in epithelial layers, many autocrine and paracrine networks may be operating in the regime of “almost” next-nearest neighbor coupling. If, as a result of future quantitative experiments, this turns out to be the case, then modeling of epithelial layers might draw from a large body of mathematical results available for lattice dynamical systems; see Cahn et al., 1998; Chow et al., 1998 for example.

Our approach has a number of limitations. While the ligand-limited regime and the “thin-fin” approximation are likely to hold for a large number of developmental contexts, special care has to be paid to assessing the validity of the assumption about the separation of the timescales corresponding to binding and transport and the intracellular variables. New methods have to be developed for the regime when this condition is not satisfied. In addition, we assumed that the generation of the ligand-releasing protease is a thresholdlike function of the current level of ligand-receptor complexes. More complex parameterizations of this dependence can be considered. We verified numerically that similar results are obtained if one uses a sufficiently sharp Hill function for the sigmoidal nonlinearity.

Another important issue that needs to be addressed is the effect of the noise on the signaling patterns due to the low number of molecules involved. In fact, a simple calculation shows that for realistic parameters (see Table 1) the number of ligand molecules over a single cell must be of order unity for the ligand-limiting regime to be realized. This must be reconciled with the use of the continuous approximation for ligand diffusion (Eq. 1). Let us point out, however, that the relevant quantity for the signaling patterns here is the number of ligand-receptor complexes per cell which acts as an input to the protease production. In contrast to the number of ligands, the number of complexes turns out to be large; for realistic parameters, ∼ 10³. This is essentially due to the fact that the average lifetime of the ligand-receptor complexes ∼(k_e + k_off)⁻¹ is much longer than the timescale of ligand-receptor binding ∼h/k_s (see Table 1). Therefore, for these values of the effect of the fluctuations in the number of extracellular ligands will be averaged over times ∼(k_e + k_off)⁻¹ and to the leading order can be neglected. In this sense, Eq. 1 should be viewed as the equation for the probability density of finding a ligand molecule in a given infinitesimal volume element. We have performed preliminary Monte Carlo simulations that confirm these statements.

The combination of kinetic models with the detailed information about the subcellular structures has been very successful in the analysis of intracellular events (Slepchenko et al., 2002). We argue that a similar approach is critical for the analysis at the tissue level. A rapidly growing number of well characterized developmental systems makes this approach both necessary and feasible (Freeman and Gurdon, 2002).

APPENDIX

Dimensionless model

Upon rescaling Eqs. 1–4 according to Eqs. 7 and 8, we obtain:

(A1)

where According to this equation, for 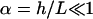, the variation of s in the z-direction is negligible. Hence, Using this fact and averaging Eq. A1 over the vertical coordinate, we get, approximately,

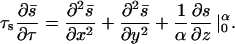Combining this with the rescaled versions of Eqs. 2 and 3 and using the boundary conditions in Eq. A1, we get

(A2)

(A3)

(A4)

where Eqs. A2–A4 contain four dimensionless parameters: 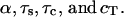For the thin-fin approximation in Eq. A1, α (i.e., ratio of the geometrical and the dynamical length) has to be small. This condition is satisfied for the typical parameter set used in the model analysis (see Table 3). Furthermore, the relative timescales of extracellular ligand and ligand-receptor complexes are small: and ; see Table 3. The steady-state approximation for these variables leads to Eqs. 9 and 10 (in the original scaling).

Coupling coefficients for square cells

Now we compute the coupling coefficients for square cells of size L_x. Let F(ω,λ), be the cosine transform of θ_0,0(x,y):

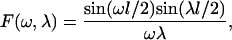(A5)

where l = L_x/L is the dimensionless cell width (see Fig. 6 A). The coupling coefficients can then be found via integration of Eqs. 13 and 15. After tedious but straightforward algebra, we obtain:

(A6)

where m and n are the position indices that determine the locations of the m,n^th cells in the lattice (see Fig. 6 C).

FIGURE 6.

(A) Solution of Eq. 12 for the square cells was derived on the two-dimensional semi-infinite domain with the origin in the center of the square. The dimensionless area of the square is 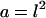. (B) Solution of Eq. 12 for the hexagons was derived on the two-dimensional, semi-infinite domain with origin in the center of the hexagon. The dimensionless area of the hexagon is a = 3 × r × v. (C) Indexing used for the computation of coupling coefficients for square cells. (D) Indexing used for the computation of coupling coefficients for hexagonal cells.

Coupling coefficients for hexagonal cells

For the hexagonal cells with dimensionless width 2v = 2L_v/L, the cosine transform F(ω,λ) of θ_0,0 is given by

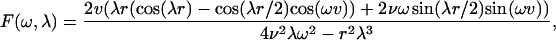(A7)

where is the side of the hexagon (see Fig. 6 B).

From Eq. 14, the interaction coefficient is 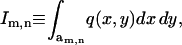where the function q(x,y) is defined by Eq. 13. To compute the coupling coefficients, we integrate this expression over the m,n^th cell. This requires evaluating the integral With the indexing scheme (see Fig. 6 D), the position of cell centers on the hexagonal lattice is given by

(A8)

Then, after a straightforward calculation the integral for the m,n^th cell, can be written as:

(A9)

This expression can be substituted into Eqs. 13 and 14. After a long calculation, the coupling coefficients become:

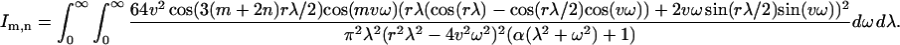(A10)

General comments

The integrals given by Eqs. A6 and A10 can be easily computed numerically. We have used adaptive integration routines in Mathematica and MATLAB for this purpose. The computation of a single coefficient takes several seconds on a very modest PC. Given the fact that coupling coefficients decay rather quickly as a function of the lattice indices, the vector field for the discrete problem is constructed very efficiently. In the current form, the coupling coefficients depend on the dimensionless cell size (l, or v and r) and a dimensionless parameter inherited from the original three-dimensional problem. By rescaling the variables of integration in the final expressions (Eqs. A6 and A10), that 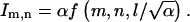Thus, up to a constant, the integrals in A6 and A10 depend on a single dimensionless parameter 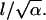Returning to the dimensional parameters, we find that is equal to the cell size, l (or v and r), normalized by the length scale for ligand variations along the surface 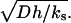The original cell communication system operates in a discrete regime when the ratio of these length scales is >1. The cells are essentially uncoupled for very large values of . Small values of correspond to the continuum regime.