Two Components of Voltage-Dependent Inactivation in Ca_v1.2 Channels Revealed by Its Gating Currents

Abstract

Voltage-dependent inactivation (VDI) was studied through its effects on the voltage sensor in Ca_v1.2 channels expressed in tsA 201 cells. Two kinetically distinct phases of VDI in onset and recovery suggest the presence of dual VDI processes. Upon increasing duration of conditioning depolarizations, the half-distribution potential (V_1/2) of intramembranous mobile charge was negatively shifted as a sum of two exponential terms, with time constants 0.5 s and 4 s, and relative amplitudes near 50% each. This kinetics behavior was consistent with that of increment of maximal charge related to inactivation (Qn). Recovery from inactivation was also accompanied by a reduction of Qn that varied with recovery time as a sum of two exponentials. The amplitudes of corresponding exponential terms were strongly correlated in onset and recovery, indicating that channels recover rapidly from fast VDI and slowly from slow VDI. Similar to charge “immobilization,” the charge moved in the repolarization (OFF) transient became slower during onset of fast VDI. Slow VDI had, instead, hallmarks of interconversion of charge. Confirming the mechanistic duality, fast VDI virtually disappeared when Li⁺ carried the current. A nine-state model with parallel fast and slow inactivation pathways from the open state reproduces most of the observations.

INTRODUCTION

Inactivation, a process that puts channels in closed unresponsive states, and usually occurs after activation, is a widespread and prominent characteristic of ion channels. It has major physiological importance, as it controls the duration of phenomena such as action potentials (by affecting voltage-operated channels) and excitation-contraction coupling (affecting, in this case, intracellular Ca²⁺ release channels).

In cardiac L-type Ca²⁺ channels, inactivation can be driven, in addition to voltage, by the passage of current (current-dependent inactivation, or CDI). CDI is characterized by a U-shaped dependence on conditioning voltage and by additional dependence on the permeant ion species. Its structural underpinnings comprise the action of constitutively bound calmodulin to the channel, which either inactivates or potentiates the channel upon Ca²⁺ binding (Peterson et al., 1999, 2000; Qin et al., 1999; Zuhlke et al., 1999; Erickson et al., 2001, Mouton et al., 2001). Voltage-dependent inactivation (VDI) of L-type Ca²⁺ channels has been studied comparatively less than their CDI. Based on the kinetics of decay of Ba²⁺ currents, fast and slow VDI mechanisms have been proposed (Kass and Sanguinetti, 1984; Hering et al., 2000; Stotz and Zamponi, 2001a). Additionally, from the changes in the kinetics of decay of Ba²⁺ currents in mutants of intracellular regions of Ca²⁺ channels, a hinged-lid mechanism has been suggested (Bernatchez et al., 1998; Cens et al., 1999; Stotz et al., 2000; Stotz and Zamponi, 2001a). Because of the direct effects of Ba²⁺ on inactivation, however, a description of VDI in isolation can only be drawn from studies of gating currents (Ferreira et al., 1997b). Though part of these studies have been made in native cells, they face the problem of heterogeneity of gating currents as cardiac L-type Ca²⁺ channels coexist with other voltage-dependent channels, which contribute their own gating current. Because of these problems, we took advantage of characterizing VDI in expressed cardiac L-type Ca²⁺ channels in tsA 201 cells, which are virtually devoid of intrinsic voltage-dependent channels that could interfere in the measurements of gating currents.

A variety of inactivation phenomena have been described for voltage-dependent channels, on a wide range of timescales, from milliseconds to seconds. Different mechanisms have been characterized initially by the presence of fast (milliseconds) and slow (seconds) time constants in their onset and recovery. For some mechanisms, the structural underpinnings are clearly identified, while in others molecular identification has just begun. One aim of the present work is to probe the existence of multiple kinetic components of VDI in cardiac L-type Ca²⁺ channels, through the study of changes in gating currents during inactivation.

At the level of the voltage sensor, inactivation in voltage-dependent channels is associated with charge “immobilization” and/or charge interconversion. Charge immobilization has been described in fast inactivation of voltage-dependent Na⁺ and Shaker K⁺ channels (N-type) (Armstrong and Bezanilla, 1977; Bezanilla et al., 1991; Bezanilla, 2000). The main hallmark of charge immobilization is the slowing of the voltage sensor movement upon repolarization, which leads to the reduction of the charge measured at the trailing edge of the depolarization that caused inactivation (Q_OFF) (Armstrong and Bezanilla, 1977; Yellen, 1998; Bezanilla, 2000). Charge thus immobilized recovers (remobilizes) with a steep voltage-dependence, becoming available to move in a new depolarization. This remobilization manifests itself as a slow component of Q_OFF. Because the kinetics behavior of this slow component becomes similar to that of the regular, not-immobilized charge at large hyperpolarizations, the effect differs from the shift of the Q-V curve that follows charge interconversion (discussed below). In other words, when recovery from inactivation is fast and limited by the movement of the voltage sensor itself, the result is charge immobilization. Schematically, charge immobilization has been pictured as the result of a ball-and-chain or a hinged-lid mechanism in which the internal mouth of the pore is occluded by a cytoplasmic moiety of the channel (Armstrong and Bezanilla, 1977; Hoshi et al., 1990; Bezanilla et al., 1991; Eaholtz et al., 1994; Yellen, 1998; Bezanilla, 2000). The binding of the particle to the channel retards the return of the voltage sensor, leading to immobilization of charge. A second aim of the present work is to look for a phenomenologically similar mechanism in Ca_v1.2 channels, by studying their gating currents in tsA 201 cells.

Charge interconversion, implied in a model by Bezanilla et al. (1982) to explain long-term inactivation of Na⁺ channel gating currents, has been described in the DHP receptor of skeletal muscle and L-type Ca²⁺ channels in native cardiac muscle (Brum and Rios, 1987; Shirokov et al., 1992; Josephson, 1996; Ferreira et al., 1997a; Shirokov et al., 1998). During activation the charge moves between its cis (inner) and trans (outer) positions, with half-distribution potential (V_1/2) near 0 mV in expressed Ca_v1.2 (Shirokov et al., 1998). This mode of charge movement, associated with activation and deactivation of the skeletal and cardiac L-type Ca²⁺ channels, has been termed Charge 1. The signature of charge interconversion is the possibility of return of the mobile charge to a cis position before recovery from inactivation. The intramembranous charge remains mobile between its cis and trans positions, but it is voltage-shifted, with V_1/2 near −90 mV (Shirokov et al., 1998). This second mode of charge movement, which takes place within inactivated channels, has been termed Charge 2. Otherwise stated, this form of inactivation, which is slow in onset and recovery, seems to have its recovery limited intrinsically, by a step that is not associated with measurable intramembranous charge movement. Consequently, charge can be moved back and forth among inactivated states and one can speak of charge interconversion between a mode that moves ineffectually among inactivated states, i.e., Charge 2, and a normal or reprimed mode, Charge 1. Charge interconversion shares properties with changes in gating currents associated with slow inactivation of voltage-dependent Na⁺ and K⁺ channels (Bezanilla et al., 1982; Starkus and Rayner, 1991; Olcese et al., 1997). The structural basis of slow inactivation in these channels is not elucidated, though it may be related to changes in the whole channel, particularly in the pore and outer vestibule (Yellen et al., 1994; Baukrowitz and Yellen, 1995; Loots and Isacoff, 1998; Bezanilla, 2000; Vilin et al., 1999; Ong et al., 2000). We have previously reported some of the characteristics of charge interconversion in expressed Ca_v1.2 (Shirokov et al., 1998). In this article, we explore its kinetic aspects in further detail.

Extracellular ions alter inactivation in different ways. Usually, higher occupancy of the ion binding site/s related to inactivation delays its onset (though the converse case has also been described; see De Biasi et al., 1993; Yellen, 1998). In Shaker and other voltage-dependent K⁺ channels, slow inactivation includes a variety of mechanisms (termed C, P, and U-type inactivation), which are all modulated by the nature and concentration of the ions present in the extracellular solutions (Hoshi et al., 1991; Lopez-Barneo et al., 1993; De Biasi et al., 1993; Olcese et al., 1997; Klemic et al., 2001). Taking into account these reports, we also tested whether extracellular cations modulate gating current changes associated with inactivation in expressed Ca_v1.2 channels.

In this article, we biophysically characterize VDI by studying gating currents in L-type cardiac Ca²⁺ channels (Ca_v1.2) expressed in tsA201 cells. The results are consistent with the presence of two distinct processes: one is fast, and involves charge immobilization; the other is slow, and results in charge interconversion. Interestingly, the presence of divalent (or trivalent) cations in the extracellular solution appears to be required for the development of the fast inactivation process.

METHODS

Experiments were done with the tsA201 cell line (large T-antigen-transformed human embryonic kidney). Cells were grown in DME medium supplemented with 10% FBS, 100 U/ml penicillin, and 0.1 mg/ml streptomycin (Sigma Chemical, St. Louis, MO) in 5% CO₂. Cardiac rabbit α_1C, rat brain β_2a, and rabbit skeletal muscle α₂δ cDNAs, were cloned in pCR3, pCMV, and pMT2 plasmid vectors, respectively. High purity (A₂₆₀/A₂₈₀ ≥ 1.95) large-scale plasmid preparations were obtained using standard protocols (Qiagen, Chadworth, CA). Transfections were done with 6 μg of each expression plasmid in 60-mm dishes using a modified calcium phosphate precipitation method. Electrophysiological recordings were made within 24–48 h posttransfection on round nonclustered cells. No sizable ionic or gating currents were observed in tsA201 cells in the absence of transfection. After transfection, the fraction of cells selected and patched that had Ca²⁺ currents was 40–60%.

Cells were placed in a small chamber and perfused by continuous flow of external solutions. Records were obtained by a standard whole-cell patch-clamp procedure using an Axopatch 200B amplifier (Axon Instruments, Foster City, CA) and a 16-bit A/D–D/A converter card (HSDAS 16, Analogic, Peabody, MA) on a PC computer. Ionic currents were sampled at 1–3 kHz and gating currents (detailed below) at 10–40 kHz, depending on pulse duration.

The internal solution contained (in mM): 150 CsOH (or NMG), 110 Glutamate, 20 HCl, 10 HEPES, 5 MgATP, and 10 EGTA (pH adjusted to 7.6 by addition of CsOH). Osmolality of the internal solution was routinely measured and adjusted to 300–320 mosmole/Kg. External recording solutions contained (in mM): 140 TEA-Cl, 10 Tris, and either 10 CaCl₂ or 10 BaCl₂. Lithium external solution contained (in mM): 150 LiCl, 10 HEPES. In some experiments, 0.5 μM CaCl₂ was added to this solution to stabilize the patch seal. In gating current experiments, 10–20 μM GdCl₃ was added to the external solution with 10 mM Ca²⁺. All external solutions were adjusted to pH 7.2 and 300–320 mosmole/Kg. All experiments were carried out at room temperature (∼20°C).

Patch electrodes were pulled from Corning 7052 glass (Warner Instruments, Hamden, CT) and had resistances of 1–3 MΩ. Whole-cell capacitance, calculated as the area under a linear capacitive transient elicited by a −10 mV pulse, was 6–25 pF. Series resistance, calculated from the capacitive transient, was between 5 and 13 MΩ. The charging time constant was typically 100 μs. The linear capacitance was analogically subtracted as described in Shirokov et al. (1998), unless stated otherwise. Parameters of the compensation circuitry were set with a 20 mV pulse from −90 mV to reduce residual linear transients. The capacitive transients thus recorded are gating currents. Occasionally, as a reference, asymmetric currents were obtained after subtraction of scaled control currents and compared with those obtained with the analogic subtraction procedure. In these cases, control currents were elicited by pulses from −90 to −110 mV, before each depolarization and after holding the cell at −90 mV for 30 s.

Charge transfer was calculated as the time integral of the current transient after subtraction of a steady current, determined as the average over 10 ms at the end of the pulse. Data are presented as averages ± SE. Exponential time courses were fitted by the function Y₁ = b + a exp(−t/τ) or the function Y₂ = b + a_slow exp(−t/τ_slow) + a_fast exp(−t/τ_fast). In all cases in which both fits converged, the statistical significance of the fit improvement provided by the two-exponential function Y₂ was evaluated. The test was based on the likelihood ratio statistic LRS = (ssr₁ − ssr₂)/σ² (Bickel and Doksum, 1977), in which ssr₁ and ssr₂ are the sums of squares of the residuals for the two fits, and σ² is the variance of the record. LRS has a χ² distribution with 2 degrees of freedom (the difference between the number of free parameters of Y₂ and Y₁). If the statistic exceeds 6.0, the improvement in fit provided by the two-exponential function is significant, to >5%. σ² was estimated by ssr₂/(N − 5), which, being probably in excess, gave an underestimate of LRS.

RESULTS

Gating currents inactivate in two kinetic stages

Current methods for the study of VDI of cardiac L-type Ca²⁺ channels use I_Ba (Kass and Sanguinetti, 1984; McDonald et al., 1994; Hering et al., 2000). Because there is Ba²⁺-dependent inactivation (Markwardt and Nilius, 1988; Mazzanti et al., 1991; Ferreira et al., 1997b), VDI is defined here as that which affects the voltage sensor, and is evaluated through the effects on intramembranous charge movements.

As with the dihydropyridine (DHP) receptor of skeletal muscle and voltage-dependent Na⁺ and K⁺ channels, there is a shift of the Q-V curve to more negative voltages upon inactivation of cardiac L-type Ca²⁺ channels, native or heterologously expressed (Bezanilla et al., 1982; Starkus and Rayner, 1991; Bezanilla, 2000; Shirokov et al., 1992; 1998; Josephson, 1996). The time course of such shift upon conditioning depolarizations of different durations was studied as a measure of the onset of VDI. Fig. 1 shows the result of such an experiment in a typical cell expressing the Ca_v1.2 channel. To obtain the Q-V curve, test pulses in the range of −170 to 90 mV were applied from a brief 50-ms interpulse at −60 mV, where charge movement activation starts (Fig. 1 A). As detailed in Methods, the transient portion of the capacitance-compensated record is largely constituted by gating current. To inactivate the channel, conditioning depolarizations to +40 mV of increasing durations (listed as T_C in Fig. 1) were applied before the test pulses (Fig. 1 A). In the absence of inactivation (T_C = 0 s), most of the charge moves at potentials positive to −60 mV (Fig.1 B). Upon a 1-s conditioning depolarization there is a reduction in the amount of charge that moves positive to −60 mV and an increase in the amount of charge that moves negative to −60 mV. Qp, the charge moved by a large positive pulse from −60 mV, measures approximately the amount of charge available for channel activation (Charge 1), while Qn, transferred during a large negative pulse from the same starting voltage, measures the charge available to move in inactivated channels (Charge 2; see Shirokov et al., 1992, 1998). Unless stated otherwise, Qn and Qp are measured at the leading edge of the test pulse. According to the Q-V plots in Fig. 1 B, the reduction in Qp caused by inactivating pulses equals the increment in Qn. The magnitude of such complementary changes increased with T_C, reaching asymptotically a maximum at ∼15 s. For each conditioning duration, the dependence of the charge transfer on the membrane potential (V_m) was well-fitted by the Boltzmann expression

(1)

where Q(V_m) is the charge moved upon depolarization from −60 mV to V_m; V_1/2 is the potential of equi-distribution; K a steepness parameter; and Q_T the expression's maximum. Thus, upon inactivation, the total charge (Q_T) is conserved and the slope factor (K) is increased (value range 27–37 mV).

FIGURE 1.

Voltage-shift of the gating charge upon inactivation. (A) Gating currents elicited by a test pulse (protocol at top) between an interpulse level of −60 mV and a variable test voltage, after an inactivating conditioning depolarization of duration T_C to +40 mV. The three groups of currents correspond to different T_C, as indicated. (B) Charge transfer versus test voltage, obtained from the records shown in A. (•), T_C = 0 s (reference); (○), T_C = 1 s; and (▴), T_C = 15 s. Curves are fits of the function Q = Q_T/(1 + exp−(V_m − V_1/2)/K) − Qn. Values for this cell were: Q_T = 1000 f_C for all conditioning durations, V_1/2 = 4.95 mV (T_C = 0 s), −47 mV (for T_C = 1 s), and −70 mV (15 s). K = 27 mV (0 s), 35 mV (1 s), and 37 mV (15 s).

Q-V curves, averaged after normalization by Q_T, are shown in Fig. 2 A for conditioning depolarizations of increasing duration. The solid lines represent the best fits by Eq. 1 (without Qn). Inactivating conditioning pulses of longer duration caused a greater voltage shift. V_1/2 is plotted versus T_c in Fig. 2 B. The inset shows that V_1/2 evolves as the sum of two exponentials, of time constants 0.5 s and 4 s, with the fast component comprising 60% of the total. The best fit of a single exponential plus a constant (equation for Y₁ as described in Methods; see also Fig. 2, dashed line), does not well-describe the data. Therefore, viewed through the resulting shift in the voltage distribution of the mobile charge, onset of VDI proceeds with two distinct kinetic components.

FIGURE 2.

The shift in V_1/2 evolves with two kinetic components. (A) Average Q versus V in 12 experiments with the protocol illustrated in Fig. 1. Before averaging, charge transfer was shifted to a value of ‘0’ at large negative voltages, and normalized to its maximum, Q_T, in the same experiment. (•), T_C = 0; (○), T_C = 1 s; and (▴), T_C = 15 s. Curves represent the best fit of the function 1/(1 + exp−(V_m − V_1/2)/K) to each set. (B) V_1/2 versus T_C. The curve represents the best fit with the function V_m = V_{1/2 fast} exp(−t/τ_fast) + V_{1/2 slow} exp(−t/τ_slow) + V_{1/2 inf}. Best fit parameters of the double exponential fit were: V_{1/2 fast} = 48 ± 8 mV; τ_fast = 0.52 ± 0.07 s V_{1/2 slow} = 36 ± 8 mV; τ_slow = 4.15 ± 2.05 s; and V_{1/2 inf} = −79.05 mV. For the semilog plot, V_{1/2 fast} and V_{1/2 slow} were normalized to the total change in V_1/2 (ΔV_1/2, _T = V_1/2, (_{TC, 0}) − V_{1/2 inf}). The dashed line represents the best fit of a single exponential plus a constant.

The same conclusion is reached studying the time courses of Qp or Qn moved at extreme test voltages during the onset of inactivation. In Fig. 3 A the values of charge transfer are plotted against test potential for a reference situation (“0 s conditioning”) and after two conditioning pulses of different duration (1 s and 15 s). The symbols corresponding to the extreme values of V_m, representing charges Qp or Qn, are enclosed within boxes in thick line, while boxes in thin line enclose charges elicited by intermediate test pulses, positive or negative. In Fig. 3 B are the boxed values, plus other values not shown in Fig. 3 A, plotted as a function of T_C. The evolution of Qn and Qp (large symbols) was similar, essentially parallel to the evolution of V_1/2 shown in Fig. 2 B. In contrast, the charge transfer at membrane potentials that did not elicit maximal charge movement (small symbols) was not very dependent on T_C. Hence, it was of little use as a monitor of onset of VDI.

FIGURE 3.

Charge transferred by large pulses varies with conditioning duration. (A) Q versus V. The boxes mark test voltages for which the charge displacement will be represented versus T_C in other panels. Boxes in thick dashed lines correspond to extreme voltages, eliciting Qp or Qn.(B) Charge transferred at test voltages boxed, versus conditioning duration. For Qp or Qn the dependences with T_C were close to a sum of two exponentials, and had a similar time course. At intermediate test voltages the changes in charge transfer were minor (small black squares). (C) Average change of Qn or Qp versus T_C (n = 14), normalized and shifted as indicated to facilitate comparison. The best fit of a sum of two exponentials (continuous line), is superimposed. Addition of Qp and Qn is constant and is also shown in the same graph (dotted line). Log scales are used. (D) Semilog plots of data and fits of double and single exponential plus a constant (continuous and dashed lines, respectively). Coexponential promotion of Qn was transformed in a exponential decay (1 − ΔQn/ΔQn_max). Best fit parameters: Qn_fast = 0.51 ± 0.03, τ_fast = 0.47 s ± 0.042, Qn_slow = 0.49 ± 0.03, and τ_slow = 4.61 s ± 0.834. Qp_fast = 0.48 ± 0.07, τ_fast = 0.42 ± 0.06 s, Qp_slow = 0.51 ± 0.07, and τ_slow = 3.8 ± 0.8 s.

The increase in Qn and the reduction in Qp were normalized to the corresponding maximum values in every cell. Average normalized values are jointly plotted versus T_C in Fig. 3 C. To better illustrate both components simultaneously, values were plotted on log scales. The solid lines represent the best fit by sums of two exponential functions. The kinetics of reduction of Qp mirror that of increase in Qn, as confirmed by the constancy of their sum (dotted line in Fig. 3 C), indicating the conservation of total mobile charge. To show at a glance the biexponential onset of VDI, the evolution of both types of charge versus conditioning duration was plotted in Fig. 3 D in a semilog scale. The dashed line represents the best fit of a single exponential plus a constant to the increase in Qn. The two-exponential fit (solid line) is clearly better. In agreement, the LRS was also high (∼135), indicating significant improvement over the single exponential fit. For the evolution of Qp, the two-exponential fit was also justified compared with the single exponential (LRS ∼ 27).

Measuring the onset of VDI through the increase in Qn has some advantages that will be used later in this article: 1), it provides information about the shift of the Q-V curve, from charge transfer data obtained at just one potential; and 2), it does not require blocking ions or drugs, as no ion channels are gated open at the required negative potentials, as argued before by Shirokov et al. (1993). The later advantage was used to measure onset of VDI in Li⁺.

In sum, inactivating depolarization determines a shift in the voltage distribution of mobile charge measured from an interpulse potential of −60 mV. The shift follows a biexponential time course, suggesting the existence of two processes. The time constants and relative amplitudes of the fast and slow components were the same when estimated with three different protocols (change in Qn, change in Qp, and evolution of V_1/2), reflecting the essential equivalence of all methods.

The kinetic components remain separate during recovery

Recovery from VDI was evaluated measuring Qn after a large inactivating depolarization and an interval of recovery of variable duration (Tip), as illustrated in Fig. 4 A. Fig. 4, B and C, shows plot currents, and Fig. 4 D shows charge transfers, in the leading edge of the large negative pulse that mobilizes Qn. After 1-s depolarizations, which mainly cause fast VDI, recovery of Qn at −60 mV was almost complete in 4 s. Fig. 4 E shows that recovery from VDI is also well-described by the sum of two exponential functions, with time constants 0.17 s and 3.7 s. For this conditioning pulse, the relative amplitudes (a_fast/(a_fast + a_slow) and a_slow/(a_fast + a_slow)) of the fast and slow recovery terms were 74% and 22%, respectively. Upon 20-s conditioning depolarizations (Fig. 4 C, and large black symbols in Fig. 4, D and E), recovery was also well-described by two exponentials of similar time constants, but the relative amplitudes of the components were 55% and 40%, respectively. Clearly, when a greater development of the inactivation of slow onset was allowed, the component of slow recovery increased as well.

FIGURE 4.

Recovery from VDI is described by two kinetically distinct components. Pulse protocol (A) and gating currents after 1 s (B, left) and 20 s (C, right) conditioning pulses and different recovery times (Tip, listed next to gating currents) at −60 mV. Qn diminishes as recovery time increases. (D) Average Qn (normalized to Qn after 50 ms of recovery) versus recovery time at −60 mV after T_C = 1 s (n = 13) or 20 s (n = 8). The slow component of recovery is increased upon a longer conditioning pulse. These results suggest that VDI that occurs slowly recovers slowly. (E) The semilog plot is shown. Best fit parameters for recovery of Qn after either conditioning pulse: τ_fast = 0.17 s and τ_slow = 3.7 s. Relative amplitudes: for T_C = 1 s, a_fast/a_T = 0.74, a_slow/a_T = 0.22; and for T_C = 20 s, a_fast/a_T = 0.55, a_slow/a_T = 0.40 (a_T = a_fast + a_slow).

To further examine this point, the amplitudes of each component of onset were compared with those of recovery in several cells. The amplitudes were normalized to Q_T in each cell, to reduce variations in amplitude resulting from different expression levels, then plotted as onset versus recovery (Fig. 5). For both components, there was a strong correlation between amplitudes of onset and recovery. This finding suggests that inactivation proceeds along two alternative pathways of different kinetics—a dual view of inactivation, pursued further in the Discussion.

FIGURE 5.

The amplitudes of kinetically distinct components of onset and recovery are highly correlated. (Left) Amplitude of fast recovery (a_fast) versus that of fast onset VDI (Qn_fast), normalized to Q_T (r² ∼ 0.88). (Right) Normalized amplitudes of slow recovery (a_slow) versus that of slow onset VDI (Qn_slow) (r² ∼ 0.81). Amplitudes of both components were taken from each cell under experiments like those reported in Fig. 3 (onset) and Fig. 4 (recovery).

Gating currents evolve with two known signatures

The kinetic separation of two components, which remains patent throughout onset and recovery, may correspond to two different inactivation mechanisms that, viewed through gating currents, might have signatures of charge immobilization or charge interconversion. Though both types of inactivation promote a reduction of charge related to activation, kinetics and voltage-dependence of recovery from inactivation are different. One of the signal features of charge immobilization is that the process of recovery is essentially cotemporal with the restoration of gating charge. Because such recovery becomes faster at more negative potentials, it is possible to monitor the return of gating charge from its immobilized state as a visible inward transient upon large hyperpolarizations. After returning to the cis position, this restored charge has all the usual properties, including its characteristic voltage-dependence activating in a range positive to −60 mV.

In contrast, the signature of charge interconversion is the appearance of a different mode of charge, which can move in either direction while the channel remains inactivated (Bezanilla et al., 1982; Brum and Rios, 1987; Starkus and Rayner, 1991). In this case, the charge is never immobilized but just voltage-shifted, mobile between its cis and trans positions with a V_1/2 near −90 mV (Shirokov et al., 1998). Because of these differences, it is possible to distinguish charge immobilization from charge interconversion by evaluating the ratio between transfers of charge at the ON (or leading) and OFF (or trailing) edges of a large negative-going pulse. For pulse durations shorter than the characteristic recovery times, an ON/OFF ratio much greater than ‘1’ is expected for charge immobilization, while for charge interconversion the ratio should be near ‘1’. A more detailed justification of this prediction is given in the Discussion.

Test pulses to −150 mV were applied from an interpulse level of −60 mV (sustained for 50 ms), after different intervals T_C of conditioning depolarization. Gating current traces are shown in Fig. 6 A. For every conditioning duration, the charge transfer was greater during the ON transient. The plot of the ratio (termed Qn_ON/Qn_OFF) versus T_C is in Fig. 6 B. The ratio first increased with T_C, decreasing later to a steady level.

FIGURE 6.

Qn induced upon fast and slow VDI has different signatures. (A) Records elicited by hyperpolarizing pulses, to obtain Qn. Longer-lasting conditioning depolarizations increased charge transfer in ON and OFF transients. Qn_ON increases more and more rapidly than Qn_OFF. (B) Qn_ON/Qn_OFF ratio for conditioning pulses of increasing durations (n = 14).

For conditioning of short durations, the proportion of fast VDI is greater, then decays at longer durations of conditioning, while that of slow inactivation increases. Hence the evolution of Qn_ON/Qn_OFF when conditioning time increases is parallel to the relative weight of fast inactivation. In other words, when fast inactivation predominates, the ON and OFF transfers of Qn are very different. As argued before, this corresponds to the signature of charge immobilization (charge recovers rapidly to the resting state at −150 mV, producing the measurable ON transient, but this charge has normal voltage distribution; hence, it does not move in the OFF step to −60 mV.)

With the conditioning pulse of long duration, instead, the fraction of slow inactivation increases, and Qn_ON/Qn_OFF was found to increase in parallel. This is consistent with conversion to Charge 2, which is distributed with a V_1/2 near −90 mV. Hence, it moves back and forth when V_m is changed between −60 and −150 mV.

In conclusion, the changes in gating currents brought about by VDI were first found to take place in two kinetic stages, separate for both onset and recovery. They also present, separately in each kinetic component, the respective hallmarks of charge immobilization and charge interconversion, which in turn resemble features described for fast and slow inactivation in other voltage-dependent channels. Additional correspondences were found studying the voltage-dependence of recovery from inactivation.

Recovery from fast VDI is more steeply voltage-dependent than recovery from slow VDI

Voltage-dependence of recovery from fast VDI was studied determining the kinetics of reduction of Qn at a variable recovery or interpulse voltage, Vip, in a cell conditioned by a brief pulse at +40 mV (Fig. 7 A). Fig. 7 B shows traces of gating currents elicited by pulses from −60 to −150 mV, after different recovery times (Tip = 0.05 s or 0.1 s) and voltages (Vip = −60 or −120 mV). In Fig. 7 C are plots of average Qn (normalized to Q_T) versus recovery time at three values of Vip. It can be seen that recovery from fast inactivation was much faster at −120 mV than at −60 mV. The results additionally show that a 0.4-s sojourn at −120 mV is sufficient to recover from fast VDI. This observation suggests a method to evaluate the properties of slow VDI in isolation.

FIGURE 7.

Voltage-dependence of recovery from fast VDI. (A) Pulse protocol: a 0.4-s conditioning pulse promotes fast VDI with negligible slow VDI. (B) Representative gating currents for recovery times (Tip) and voltages (Vip) indicated. Qn was recorded between −60 and −150 mV. (C) Average values of recovery of Qn normalized to Q_T, at different recovery voltages (n = 6). The time constants corresponding to Vip −60, −90, and −120 mV, were 0.2, 0.12, and 0.037 s, respectively.

To study the voltage-dependence of recovery from slow inactivation, the duration of the conditioning pulse was increased to 12 s (Fig. 8 A) and the kinetics of recovery were determined at different voltages, as done previously. Additionally, slow VDI was isolated by preceding the variable interpulse by a fixed 0.4-s interval at −120 mV, which recovers the channels from fast VDI. Fig. 8 B shows gating currents, with Tip and Vip indicated next to the traces. The values of Qn thus obtained are plotted versus Tip and Vip in Fig. 8 C. There is little voltage-dependence of recovery. Recovery time constants, from single-exponential fits to data in Figs. 7 C and 8 C, are plotted versus Vip in Fig. 8 D. The voltage-dependence of recovery from fast VDI (open symbols) is steeper than that of slow VDI.

FIGURE 8.

Voltage-dependence of recovery from slow VDI. (A). Protocol: a 12-s conditioning pulse (of duration sufficient to induce slow VDI), followed by a 400-ms interpulse to −120 mV (to allow recovery from fast VDI). (B) Representative gating currents for recovery times (Tip) and voltages (Vip) indicated. (C) Average values of recovery of Qn normalized to Q_T, at different recovery voltages (n = 5). (D) Semilog plot of time constants of recovery (τ_n) versus recovery voltages. For better comparison, the maximum changes in scales for the right and left axis are of the same order of magnitude. Time constants were obtained from the best single exponential fits to plots shown in Figs. 7 C and 8 C. Values for Vip −60, −90, and −120 mV, were 4.2, 3.8, and 2.7 s, respectively. Voltage-dependence of recovery from fast VDI is steeper than that of slow VDI.

A slow phase of charge movement increases during fast VDI

A characteristic feature in the onset of charge immobilization is the appearance of a relatively slow phase of gating current decay during the OFF of a depolarizing pulse. This slow component has the time course of recovery from inactivation and part of it is lost in the baseline noise at repolarizing potentials (−70 mV). The charge movement underlying that phase, increases its relative weight in Q_OFF with the onset of inactivation (Armstrong and Bezanilla, 1977). As inactivation develops, charge movement in the OFF fast phase diminishes whereas that in the OFF slow phase increases. Seeking such features, the OFF kinetics of the gating currents were studied with the pulse protocol in Fig. 9 A: pulses of different durations to +40 mV, followed by repolarization to −60 mV. OFF gating current was adequately fitted by the sum of two exponentials, of which the slow one is represented in Fig. 9 B. With longer lasting depolarizations, the gating charge transferred in the OFF was reduced, while the relative weight of gating charge associated with the slow phase was increased. The amount of charge transferred by each phase is plotted versus pulse duration in Fig. 9 C. The complementary changes in magnitude are associated with fast VDI, as both develop in a similar time range of less than 1 s.

FIGURE 9.

A slow phase of charge movement increases during the onset of fast VDI. (A). Pulse protocol: gating currents were recorded at the trailing edge of test pulses of different durations (Tp). Sampling rate was changed immediately before the end of the test pulse. (B) OFF gating currents after depolarizations of different durations (listed) in the time range of fast VDI. (Thick trace) Slow term of the two-exponential fit. (C). Average values of charge transferred by fast (Q_fast) and slow (Q_slow) terms of the fit (n = 12).

Together, these properties of fast VDI resemble charge immobilization in voltage-dependent Na⁺ and K⁺ channels (Armstrong and Bezanilla, 1977; Roux et al., 1998). The sole difference is in the timescales of onset, which in the Ca²⁺ channel are at least tenfold slower.

Fast VDI is modulated by extracellular cations

When divalent ions are removed from the extracellular solutions, Ca²⁺ channels become permeant to monovalent cations (Hess et al., 1986). Two prior observations—that the kinetics of inactivation of L-type Ca²⁺ channel currents carried by monovalent ions is slow in native and expressed channels (Hadley and Hume, 1987; Ferreira et al., 1997b), and that mutations in the IS6 region (presumably a part of the channel pore) alter VDI substantially (Zhang et al., 1994)—suggest that divalent ions may play a role in fast VDI. This possibility was tested in measurements with Li⁺ as the main extracellular cation.

Inactivation of Li⁺ current through the expressed Ca²⁺ channels is very slow (Fig. 10 A). We determined the onset of VDI in these conditions (Li⁺ substituted for Ca²⁺) measuring Qn after conditioning depolarizations of increasing durations (Fig. 10 B), at conditioning voltages shifted by approximately −40 mV to offset the electrostatic changes in the absence of divalent ions. Gating currents, in Fig. 10 C, show that Qn did not increase rapidly with conditioning duration, and that Qn_ON and Qn_OFF were nearly equal. Linear capacitive transients were not greatly affected by extracellular substitution of Li⁺ for Ca²⁺. However, the time course of the gating currents corresponding to Qn was slower than that obtained in solutions with di- or trivalent cations. This finding suggests that remotion of di- or trivalents from the extracellular solution unmasks (or leads to) slow voltage-dependent steps. The plots of charge transfer versus T_C (log scales in Fig. 10 D, and semilogarithmically in Fig. 10 E) are well-fitted by a single exponential (LRS = −0.91). This is in clear contrast with the onset of Qn in the presence of Ca²⁺ and Gd³⁺, whose fit, reproduced from Fig. 3 C, is represented by the thin dashed line. Onset of inactivation also followed a double exponential in extracellular solutions containing 10 mM Ca²⁺ or Ba²⁺ without Gd³⁺, or Gd³⁺ alone (data not shown). These results imply that fast VDI is virtually absent in Li⁺ extracellular solution. What remains is a slow inactivation, with similar kinetics to slow VDI. In conclusion, fast VDI requires the presence of divalent (or trivalent) ions in the extracellular solution, while the slow inactivation does not.

FIGURE 10.

Onset of Qn in Li⁺ has a single kinetic phase. (A) Typical course of Li⁺ and Ba²⁺currents through expressed cardiac L-type Ca²⁺ channels. Fast VDI is greatly diminished in Li⁺. (B) Two-pulse protocol used to obtain Qn in Li⁺ solution. Voltages accounted for the 30 ∼ 40 mV screening. (C) Gating currents in Li⁺ solution, elicited by pulses to −170 mV (D) Onset of Qn in Li⁺ solution. Averages of ΔQn/ΔQn_max versus conditioning duration (n = 6) on log scales. (Solid line) Single exponential fit. (Dashed line) Two-exponential fit to data in Ca²⁺-containing “charge” solution (from Fig. 3). The onset of Qn in Li⁺ solution is very similar to the slow component in Ca²⁺-containing solution. (E) Semilog plot. Parameter values: τ = 3.6 s, a = 0.86, and b = 0.14.

DISCUSSION

Inactivation of cardiac L-type Ca²⁺ currents may be caused by the permeant ions, the applied change in transmembrane potential, or both. In previous work, we and others have shown that these influences are separate, with voltage effects occurring regardless of, and independent from, the ionic current (Shirokov et al., 1993; see also Hadley and Lederer, 1991). This separation has given rise to a popular paradigm for isolation of VDI, the substitution of Ba²⁺ for Ca²⁺. However, Ba²⁺ going through the channel is capable of inducing a degree of (ion or current-dependent) inactivation (Markwardt and Nilius, 1988; Mazzanti et al., 1991; Ferreira et al. 1997b). Additionally, Shirokov (1999) demonstrated further entanglement of voltage- and ion-dependent inactivation in N-type Ca²⁺ channels. Hence, there is no completely satisfactory method to isolate VDI of ionic currents without some kind of ionic manipulation that will affect inactivation.

To solve the conundrum, in the present work VDI was examined largely through its effects on the voltage sensor, as monitored by intramembranous charge movement. The consequences of VDI at the level of charge movements consist of a number of changes with two main outcomes: First, an inactivation of gating charge which progressively disappears, i.e., ceases to be mobile in the voltage range where it is normally activated; second, charge movements become increasingly prominent in a voltage range negative to the resting potential (more specifically, negative to a “watershed” potential near −60 mV). Thus, two reciprocal changes in charge movement accompany VDI, a decrease in charge transferred at potentials positive to −60 mV (termed Qp) and an increase in Qn, mobile upon hyperpolarization from −60 mV. The overall result can also be described as a negative shift of the Q-V distribution upon inactivation.

We examined these changes in L-type cardiac Ca²⁺ channels expressed in tsA201 cells, which are virtually devoid of other voltage-dependent channels. The time course of the shift of the Q-V curve during the onset of inactivation was found to have two components. Although the kinetics of shift of the Q-V curve have not been studied in Ca²⁺ channels before, some groups have proposed the existence of multiple VDI mechanisms based on the kinetics of inactivation of Ba²⁺ currents in native cells (Kass and Sanguinetti, 1984; Kay, 1991; Boyett et al., 1994; Nilius et al., 1994; Cox and Dunlap, 1994) and more recently in expressed Ca²⁺ channels (Hering et al., 2000; Stotz and Zamponi, 2001a). These studies had problems, due to the presence of multiple types of Ca²⁺ channels in native cells and the existence of a Ba²⁺-dependent inactivation (Markwardt and Nilius, 1988; Mazzanti et al., 1991; Ferreira et al., 1997b), which obscures VDI processes. In contrast, monitoring VDI at the level of the voltage sensor does not have these problems, revealing unequivocally two distinct kinetic components in VDI. Several features of these components indicate that the duality is fundamental. One is that the kinetic separation remains patent upon recovery, indicating that the channels that inactivated slowly also recover slowly; these components correlated well with kinetic components in the recovery from inactivation, suggesting alternative pathways of inactivation. Second, there were clear differences in the voltage-dependence of recovery. Third, the fast component of inactivation appeared to have a strict requirement for the presence of divalent cations in the extracellular medium. A more detailed analysis of the changes in gating currents associated with both components confirmed the duality, while highlighting a rough similarity between the two components of inactivation seen here and the fast and slow inactivation processes of other voltage-operated channels.

Fast VDI entails charge immobilization and slow VDI charge interconversion

Charge immobilization and charge interconversion are caused by distinct effects of inactivation at the level of the voltage sensor, which in turn correspond to different structural underpinnings in the voltage-dependent channels in which they have been described.

“Immobilization” of the gating charge during fast inactivation in voltage-dependent Na⁺ and K⁺ channels has several characteristics (Bezanilla, 2000): 1), reduction in the charge transferred in the OFF transient upon repolarization; 2), increase in a slow component of OFF charge movement; 3), steep increase in rate of recovery at large negative voltages; and 4), perhaps most crucially, recovery of the standard, noninactivated properties of the gating charge immediately upon return to the cis position. Charge immobilization is usually related to open channel block by a cytoplasmic tethered particle. This process is fast and slows the return of the voltage sensor to its resting position, resulting in the “immobilization” of charge (Yellen, 1998; Bezanilla, 2000). Recovery of this interference is quite voltage-dependent, leading to the loss or reduction of the shift of the Q-V curve for recovery times that outlast charge movement. This is especially well-seen at hyperpolarizing potentials. In other words, the movement of charge at hyperpolarizing potentials coincides with its repriming. As we show in this report, fast VDI in Ca_v1.2 features these biophysical characteristics, suggesting that it is caused by charge immobilization.

Meanwhile, charge interconversion (as described, for instance, in the inactivation of skeletal muscle Ca²⁺ channels, and in the slow inactivation of Na⁺ channels of the squid axon and Shaker K⁺ channels) features mostly the first of the properties listed above. Particularly telling is the difference in the fourth property. The gating charge of a slow-inactivated channel may return to the cis position upon hyperpolarization, without recovery of its resting properties, including the ability to gate the channel (Bezanilla et al., 1982, Starkus and Rayner, 1991; Olcese et al., 1997). Such inactivated charge is termed Charge 2 in skeletal and cardiac L-type Ca²⁺ channels (Brum and Rios, 1987; Shirokov et al., 1992, 1998). Thus, charge interconversion is consistent with a more stable change in the channel function upon inactivation. The process sets up slowly and is basically modal regarding the effects at the level of charge movement. It is seen mainly as a shift of the Q-V curve, maintained for recovery times that outlast charge movement, even upon hyperpolarization. In this case, the repriming of charge at hyperpolarizing potentials outlasts its own movement. The molecular mechanisms underlying the effects of slow inactivation in the gating charge are unknown and might be different among distinct voltage-dependent channels. So far, in voltage-dependent Na⁺ and K⁺ channels, it has been related to comprehensive changes in the channel molecule, involving the outer mouth and selectivity filter (Baukrowitz and Yellen, 1995; Loots and Isacoff, 1998; Yellen, 1998). The present findings regarding slow VDI are consistent with previous results in expressed Ca_v1.2 channels (Shirokov et al., 1998), which mainly regarded the steady-state properties of inactivation. They are also consistent with evidences of charge interconversion described also at the level of the cardiac L-type Ca²⁺ native channel (Shirokov et al., 1992; Ferreira et al., 1997a; Josephson, 1996).

A ring of four states accounts for either charge immobilization or charge interconversion

The properties of charge immobilization are roughly featured by a state model, represented in Diagram 1, in which the channel evolves among a resting (C), an open (O), and an inactivated state (I). Transitions C ↔ O and C ↔ I have voltage-dependence, which is not required for O ↔ I. However, models of this type do not reproduce fully several kinetic aspects of gating currents, which are better described by allosteric models of inactivation (Roux et al., 1998).

Figure 13.

A minimum allosteric model that can reproduce both features of charge immobilization and charge interconversion has four states, and is represented in Diagram 2. As argued before by Shirokov et al. (1998), this minimal model can describe qualitatively different inactivation processes, according to the voltage-dependence and ratios between rate constants. The four-state model has the additional state I^* compared to Diagram 1. This state is inactivated closed, with the mobile charge in its cis position. In this minimal model inactivation is allosterically coupled to the movement of the activation gate. Extensions of this minimal model have been usefully applied to describe a variety of inactivation processes in several voltage-dependent channels (Marks and Jones, 1992; Kuo and Bean, 1994; Roux et al., 1998; Olcese et al., 1997).

In the ring of four states model, only the horizontal transitions are voltage-dependent. These transitions are fast and account for measurable charge movement. Vertical transitions are voltage-independent. Assuming that the intrinsic microscopic rates of voltage-dependent steps are symmetric and have the same slope factor, the half-distribution potential among inactivated states (V_1/2j) is related to that of activation (V_1/2i) by the following equation,

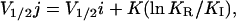(2)

where K is the slope factor, and K_I and K_R are the equilibrium constants of the O ↔ I and C ↔ I^* transitions, respectively (Brum and Rios, 1987). If K_R ≪ K_I, then V_1/2j is more negative than V_1/2i and, as a result, during inactivation, the OFF charge from an inactivating depolarizing pulse will be reduced.

If vertical transitions are slow compared to the voltage-dependent ones, the model describes charge interconversion. In this case, the speed of recovery is mostly limited by the transition I^* → C, which is slow and voltage-independent. In a channel with these characteristics, the charge will return upon hyperpolarization; but recovery (of resting properties of gating charge and channel availability to open) requires the additional I^* → C step. As a result, recovery of charge does not show a steep voltage-dependence, and it outlasts its own movement—explaining experimental findings of charge interconversion (Shirokov et al., 1998). Hence, in charge interconversion, different modes of charge movement can be defined and determined experimentally. In inactivated channels, charge moves with a different V_1/2 and in the case of charge interconversion, this shift of the Q-V curve toward more negative voltages is clearly observed regardless of the interpulse voltage. In skeletal and cardiac muscle L-type Ca²⁺ channels, these modes of charge have been termed Charge 1 (moving between the states C and O) and Charge 2 (moving between the inactivated states; see also Brum and Rios, 1987; Shirokov et al., 1992, 1998).

If vertical transitions are fast and have similar rates in the range of those exhibited by the horizontal voltage-dependent steps, then the model no longer shows a modal behavior of charge movement. As the I^* → C transition is fast, charge recovers mostly while it moves back to its cis position, and with hyperpolarizing voltages in the interpulse, a shift in the Q-V curve is less well-defined. Under these circumstances, the rate of recovery is limited mostly by charge movement among inactivated states and the four-state model behaves similarly to the model depicted in Diagram 1. This leads to a steeper and faster voltage-dependence of recovery in comparison with charge interconversion. Taking this into account, charge immobilization may accordingly be viewed as a “charge interconversion of fast recovery.” These characteristics also feature the appearance of a slow component of charge movement in the OFF gating currents, as it is classically described in charge immobilization.

In sum, an allosteric four-state model with different sets of parameters (particularly the microscopic rates of the I^* ↔ C transition) can give distinct qualitative behaviors describing either charge immobilization or charge interconversion.

The model is also useful to explain the differences, documented in Fig. 6, in the Qn_ON/Qn_OFF ratio after fast or slow inactivation. In the case of slow inactivation, Qn, the charge that moves between −60 and −150 mV, is simply Charge 2. This is a well-behaved charge, moving rapidly between two stable states that do not recover significantly to C. Hence, equality between ON and OFF transfers is featured. After fast inactivation, the charge that moves in the ON transient of a hyperpolarizing pulse corresponds to the transition I ↔ I^*, but in this case it recovers rapidly to C because the rate of I^* → C is fast. Therefore, the trailing edge of the hyperpolarizing pulse finds the charge in its resting (“remobilized”) state. As V_1/2j is negative (∼50 mV for fast VDI) and V_1/2i is ∼0 mV, K_R should be low compared to K_I. As K_R is equal to the ratio of the microscopic rates of transitions C → I^* and I^* → C, the microscopic rate of C → I^* should be low. Because of these features, charge will not transition to O at potentials below −60 mV explaining, in this way, the large asymmetry of Qn_ON/Qn_OFF ratio during fast inactivation.

A nine-state model of VDI

A nine-state model with two alternative pathways of inactivation accounts for most of the observations reported in this article (Fig. 11 A). The model does not seek to describe CDI. It is an extension of the minimal four-state model discussed before and depicted in Diagram 2. The channel activates in two steps to take into account closed states in the activation pathway as well as inactivation from closed states. Fast and slow parallel inactivation pathways diverge from the open state. Voltage-dependent transitions are represented horizontally. Vertical transitions leading to and from inactivated states are voltage-independent. The transition that represents fast VDI from the open state requires the presence of extracellular divalent cations.

FIGURE 11.

Simulations with a nine-state model. (A) Nine-state model with parallel inactivation pathways from the open state. Inactivation to state I_ja is fast, and to state I_jb is slow. Fast inactivation needs binding of di- or trivalent ions. Thick arrows indicate the preferred flow. Horizontal transitions are voltage-dependent. Vertical transitions are voltage-independent. V_1/2 were: for channel activation; V_1–2 = 0 mV, V_2–O = 20 mV; for “fast inactivated” states, Va_1–2 = −50mV, Va_2–3 = −33 mV; for “slow inactivated” states, Vb_1–2 = −82 mV, Vb_2–3 = −67 mV. Values of V_1/2 for inactivated states in each ring were determined according to Eq. 2, once V_1/2 for related activation steps and vertical transitions constants were fixed. The slope factor, K, was set at 25 mV. Equilibrium constants to fast inactivation (upper pathway) are, from left to right (see model): 0.09, 0.7, and 6; to slow inactivation (bottom pathway) are, from left to right: 0.009, 0.247, and 8. Unidirectional kinetic constants to fast inactivation are (in s⁻¹), 8.9, 6.9, and 4; to slow inactivation, 0.015, 0.22, and 2.2. Intrinsic rate constants for voltage-dependent steps were assumed to be symmetric for forward and backward transitions. Values were, from top to bottom and left to right (in s⁻¹), 50, 30, 100, 170, 50, and 30. Microscopic reversibility was tested in each ring for each simulation. (B) Gating currents obtained with the model in a nonconditioning situation and after conditioning pulses to +40 mV of 0.2 s and 4 s. The holding potential was −90 mV. Traces shown were elicited by test pulses to −150 and +90 mV from a 50-ms interpulse to −60 mV. (C) Simulated Q-V curves. Despite the particular values of the conditioning pulses used for the simulation, the model reproduces well the observed reduction in Qp and increment in Qn with longer conditioning as reported in Fig. 1. (D) As in Fig. 3, onset of Qn_ON follows a double-exponential time course. As in previous figures, log scales are used. The pulse protocol was similar to those in Figs. 3 C and 11 B, with a wider range of conditioning durations. Parameters obtained for the best fit of a sum of two exponentials were τ_fast = 0.13 and τ_slow = 2.1 s. Relative amplitudes were a_fast/a_T = 0.60 and a_slow/a_T = 0.40 (a_T = a_fast + a_slow). (Inset) Semilog plot.

With the parameter values given in Fig. 11, Qn is accounted for as the charge moved between inactivated states, while the simulated Qp moves in the activation pathway. After a conditioning depolarization, available Qp is reduced by charge immobilization in the fast inactivation pathway and by charge interconversion in the slow inactivation pathway. As voltage-independent transitions of recovery from fast VDI are rapid, the upper left state in the fast inactivation pathway is negligibly populated, reducing the effective population of states related to fast VDI to I2a and I3a. This leads to rapid transition to the closed states upon hyperpolarization. These recovery transitions are rate-limited by the horizontal step, and in consequence, voltage-dependent. Hence, in this case, voltage-dependence of recovery is steep at hyperpolarizing recovery voltages. The existence of I1a (upper left state in the fast inactivation pathway), is suggested by a shallow voltage-dependence of recovery at intermediate voltages (ranged from −90 to −50 mV). The absence of such a state would lead to a ring of three states like that shown in Diagram 1 (C1, C2, and I2a in the nine-state model). In such rings, a steep voltage-dependence of recovery is expected for all voltages below −50, provided that the V_1/2 of the I → C transition is similar to that found experimentally (−45 mV). By contrast, the intrinsically voltage-independent step of recovery from slow VDI is also the slowest. Hence, recovery from slow VDI will not feature a steep voltage-dependence. Slow VDI resembles inactivation of the DHP receptor of skeletal muscle, where two types of charge (Charge 1 and Charge 2) can be clearly distinguished, because of the slow rate-limiting steps of onset and recovery from inactivation.

The model describes several experimental findings. Simulated gating currents for extreme positive- and negative-going test pulses, are shown in Fig.11 B. Inactivation was induced by conditioning pulses to +40 mV, lasting 0.2 s (to elicit fast VDI) or 4 s (for slow VDI). These conditioning durations are approximately equal to the time constants of fast and slow VDI predicted with this set of parameters. Fig. 11 C plots charge transfer Q versus voltage, whereas the time-dependence of Q is represented in Fig. 11 D on log scales and semilogarithmically, to illustrate its evolution as sum of exponentials.

Simulations of recovery of gating currents after inactivation are illustrated in Fig. 12. Fig. 12 A represent recovery from fast inactivation, and Fig. 12 B the corresponding events after slow inactivation. The traces are gating currents elicited by a pulse to −150 mV from an interpulse at −60 mV with variable duration (Tip). Charge transfer (Qn) is plotted as a function of Tip. The time constants of onset and recovery from fast VDI are shorter in the model than in the data.

FIGURE 12.

Simulated recovery from fast or slow VDI. (A) Recovery from fast VDI. (Left) Protocol (top) and simulated traces (bottom) obtained with the nine-state model with the same parameters used for Fig. 11. To induce fast VDI, T_C was 0.2 s, a value similar to τ_f. (Right) Qn_ON/initial Qn_ON versus Tip. At either Vip (−60 or −150 mV), the time course of recovery was well-described as the sum of two exponentials (see semilog plot in inset). The fast component of recovery was hastened at the more negative Vip (τ_fast went from 32 to 5 ms). (B) Recovery from slow VDI. (Left) Protocol (top) and simulated traces (bottom). Same parameter values as in Fig. 11. A 0.4-s sojourn at −120 mV was intercalated to recover from fast VDI. T_C was 4 s (similar to Fig. 8, ∼2–3 τ_s). (Right) Qn_ON normalized to initial Qn_ON (taken after the 0.4-s pulse to recover from fast VDI). At either Vip, the time course of recovery was well-described by a single exponential (see inset). τ_s went from 1.3 at Vip = −60 mV to 0.6 s at −150 mV.

In sum, the model emulates well, qualitatively, most features of VDI: a negative shift of the Q-V distribution, onset and recovery after a sum of two exponentials, and different voltage-dependencies of recovery from fast and slow VDI.

Structural implications for Ca_v1.2 channels

Several observations indicate that two different voltage-dependent inactivation mechanisms are at work in the cardiac L-type channel. For example, fast VDI depends on the nature of extracellular cations. When divalent cations were removed from the extracellular solution, to record the Li⁺ currents through the channel, the fast component of VDI was greatly reduced (see Fig. 10). This finding suggests that fast VDI is modulated by a binding site possibly located in the extracellular mouth or the pore of the channel. Upon binding of divalent (or trivalent) cations, conformational changes in the structures responsible for fast VDI can take place. Intracellular accessibility of the pore and docking by an intracellular inactivating particle might be enhanced. A possible relationship between occupancy of regions related to the Ca²⁺ channel pore by blocking drugs and inactivation has been suggested (Hering et al., 1998). Ion requirements of fast VDI reported here agree with those considerations, suggesting that the outer vestibule or external pore has critical regions related to fast VDI (Hering et al., 1998; Berjukow et al., 2000; Berjukow and Hering, 2001; Sokolov et al., 2001). A possible docking site for the inactivating particle of fast VDI could be IS6, as this region is part of the pore structure and has been implicated in voltage-dependent inactivation of Ca²⁺ channels (Zhang et al., 1994). This mechanism works in an opposite way to other examples where extracellular cations modulate inactivation (“priming site” in the DHP receptor in skeletal muscle, see Brum et al., 1988; C-type inactivation, see Baukrowitz and Yellen, 1995). Whereas site occupancy opposes C-type inactivation in Shaker K⁺ channels or in the DHP receptor of skeletal muscle, fast VDI of the cardiac Ca²⁺ channel is promoted by occupancy of the site. Recently, Sun et al. (2000) proposed that divalent cations antagonize VDI in L-type Ca²⁺ channels of rat ventricular myocytes. The comparison of the onset of Qn in Li⁺ and in Gd³⁺ plus Ca²⁺ (or Ca²⁺ alone, data not shown), is in contrast with this view (see Fig. 10 B). In summary, the specific ionic requirements of fast VDI reported in this article can be the starting point for future structure-function studies regarding fast VDI in Ca_v1.2 channels.

The fast inactivation component resembles fast VDI in voltage-dependent Na⁺ and K⁺ channels. A possible speculative interpretation of this analogy, in agreement with other suggestions reported before (Bernatchez et al., 1998; Ferreira et al., 1999; Stotz and Zamponi, 2001a), is that there could be a hinged-lid mechanism in L-type Ca²⁺ channels. That intracellular trypsin removes inactivation of L-type channels (Hescheler and Trautwein, 1988; Obejero-Paz et al., 1991; Klockner et al., 1995; Schmid et al., 1995), also agrees with this idea. Putative locations for a hinged lid are intracellular regions of the α1 subunit (I–II linker or C-terminal region; see Hering et al., 2000; Stotz and Zamponi, 2001a,b). It has been suggested that the β2a subunit might interfere with a hinged lid (Restituito et al., 2000; Stotz and Zamponi, 2001b). Against this possibility, the present results show that fast VDI still takes place with β2a.

Relationship with other inactivation mechanisms described in Ca_v1.2

Fast and slow VDI could be considered analogous to a modal gating, where internal horizontal transitions are far more frequent than those between the horizontal pathways. Fast VDI could arise from mode I, whereas slow VDI from mode II (Pietrobon and Hess, 1990). In this view, agents that modulate interconversion of modes should change the relative weight of the kinetic components of VDI. Experiments at the level of single channel in the time range of the kinetic components will contribute to elucidate the relationship between modes of gating and the kinetic components of inactivation.

The “classical” view regarding the relationship between CDI and VDI, is that CDI does not influence VDI (Hadley and Lederer, 1991; Shirokov et al., 1993). However, recent reports suggest that VDI might be affected by high intracellular Ca²⁺ (Ferreira et al., 1998; Shirokov, 1999; Isaev et al., 2002). VDI does not require CDI or the ions that determine it, because fast VDI is seen when the channel is blocked. However, the rate of fast VDI might be modulated by CDI. The putative gates affecting fast VDI or CDI would work once the channel is open. The modulation could arise by interaction of the respective conformational changes of CDI and VDI. Alternatively, fast VDI might be directly modulated by the same ions that cause CDI. If this was the case, the differences between these mechanisms should be related to the degree of ion sensitivity of the sites (much lower for fast VDI than for CDI). Future experiments will clarify the basis and extent of the interaction between fast VDI and CDI.

Implications for charge immobilization in other channels

Charge immobilization in voltage-dependent channels is usually associated with fast voltage-dependent inactivation mechanisms. Immobilization of gating charge results from block or occlusion of the intracellular mouth of the channel by a cytoplasmic moiety, envisioned as a tethered particle. Though generally accepted, this type of interpretation applies better to the inactivating Shaker K⁺ channel than to the Na⁺ channel for which it was originally proposed (Bezanilla, 2000). The results regarding fast VDI reported in this article also lead to several questions regarding a possible generalization of such a mechanism in voltage-dependent channels. If fast VDI in Ca_v1.2 is due to charge immobilization as we propose in this article, then the comparison with known mechanisms of such type in Na⁺ and K⁺ voltage-dependent channels becomes especially interesting. The differences in kinetics and modulation by extracellular ions among them are particularly striking. Based on these analogies and differences, one plausible speculation is that the general scheme of immobilization of gating charge by an intracellular particle may be widespread among voltage-dependent channels, although the particular environment of each channel is what determines the final outcome of the interactions between tethered particle and pore. There have been several reports regarding the influence of extracellular ions in recovery from fast inactivation (Armstrong and Bezanilla, 1977; Demo and Yellen, 1991; Roux et al., 1998; Yellen, 1998; Bezanilla, 2000). The results presented here suggest that extracellular ions may also modulate charge immobilization in voltage-dependent Na⁺ and K⁺ channels.