Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Jun;84(6):3751–3758. doi: 10.1016/S0006-3495(03)75103-0

Evidence for Membrane Thinning Effect as the Mechanism for Peptide-Induced Pore Formation

Fang-Yu Chen *, Ming-Tao Lee *, Huey W Huang †
PMCID: PMC1302957  PMID: 12770881

Abstract

Antimicrobial peptides have two binding states in a lipid bilayer, a surface state S and a pore-forming state I. The transition from the S state to the I state has a sigmoidal peptide-concentration dependence indicating cooperativity in the peptide-membrane interactions. In a previous paper, we reported the transition of alamethicin measured in three bilayer conditions. The data were explained by a free energy that took into account the membrane thinning effect induced by the peptides. In this paper, the full implications of the free energy were tested by including another type of peptide, melittin, that forms toroidal pores, instead of barrel-stave pores as in the case of alamethicin. The S-to-I transitions were measured by oriented circular dichroism. The membrane thinning effect was measured by x-ray diffraction. All data were in good agreement with the theory, indicating that the membrane thinning effect is a plausible mechanism for the peptide-induced pore formations.

INTRODUCTION

Antimicrobial peptides are evolutionally ancient weapons used by animals and plants in their innate immune systems to fend off invading microbes (Boman et al., 1994; Martin et al., 1995; Ganz, 1999; Zasloff, 2002). These amphiphilic peptides are known to target the lipid matrix of cellular membranes rather than protein receptors. On the surface, their molecular properties are similar to detergents, which are known to solubilize membranes indiscriminately (Helenius and Simons, 1975). However, we do not believe that the functions of antimicrobial peptides are detergent-like. On the contrary, we expect the functions of such well-developed defense systems to be based on well-defined, controllable mechanisms. At least for a class of antimicrobial peptides that we have studied extensively, including magainins, protegrins, alamethicin, and melittin, we found that the peptides behave in a systematic manner in their interactions with lipid bilayers (Huang, 2000). Once a peptide molecule binds to a membrane, the molecule embeds itself in the headgroup region of the lipid bilayer (the S state) due to the hydrophobic interaction. Depending on the peptide concentration and the lipid composition of the bilayer, the peptide molecules may remain in the S state or subsequently change into another state (the I state) wherein the peptide molecules form transmembrane pores, apparently a mechanism to kill a cell. In a previous paper (Chen et al., 2002), we have studied the transition of alamethicin from the S state to the I state and found that the transition was well described by a mechanism based on membrane elasticity. In this paper, we present new experimental evidence that supports the full implications of this membrane elasticity theory. We will show that 1), the theory describes equally well the transition processes of forming barrel-stave pores and toroidal pores, but with a sign change between the two in a key parameter of the theory; and 2), the prediction that the membrane thickness is held constant during the transition is confirmed by x-ray diffraction measurement for both alamethicin and melittin.

We have developed several methods of detecting the state of a peptide bound to a lipid bilayer. The simplest method is oriented circular dichroism (OCD), which measures not only the secondary configuration but also the orientation of a peptide in membrane (Olah and Huang, 1988; Wu et al., 1990). To date, every antimicrobial peptide we have studied exhibited two distinct OCD spectra indicating that a peptide can bind to a membrane in two different orientations, named S and I state, respectively. The list includes α-helical peptides magainins (Ludtke et al., 1994), melittin (Yang et al., 2001), and alamethicin (Huang and Wu, 1991); β-sheet peptides protegrins (Heller et al., 1998); and cyclic peptides θ-defensins (Weiss et al., 2002). X-ray diffraction showed that the peptide in the S state caused membrane thinning in direct proportion to the peptide concentration. This was equivalent to an expansion of the membrane area by adding the peptide molecules in the headgroup region (Wu et al., 1995; Ludtke et al., 1996; Heller et al., 2000). This description was in agreement with the results of solid-state NMR (Bechinger et al., 1991; Hirsh et al., 1996), Raman spectroscopy (Williams et al., 1990), fluorescence (Matsuzaki et al., 1994), and DSC (Matsuzaki et al., 1991) measurements. In the I state, neutron diffraction detected transmembrane pores in the bilayers, but the diffraction pattern for pores would disappear if the peptides changed to the S state, for example, by temperature or hydration manipulation (He et al., 1995, 1996; Ludtke et al., 1996; Yang et al., 2001). In general, a peptide was in the S state at low peptide concentrations but changed to the I state as the concentration increased. However, the range of concentration (henceforth expressed as the peptide-to-lipid molar ratio P/L) over which a peptide changes from S to I varied greatly with the lipid composition of the bilayer and also with the peptide itself (Huang and Wu, 1991; Ludtke et al., 1994; Heller et al., 1997, 1998; Yang et al., 2001; Weiss et al., 2002). For the ease of measurement, we chose the lipid compositions in which the peptides exhibited the S-to-I transitions between P/L ∼1/150 and P/L ∼1/10 for in-depth studies.

The alamethicin transition was studied in diphytanoyl phosphatidylcholine (DPhPC) bilayers in Chen et al. (2002). The fraction of alamethicin molecules changed from the S to the I state, φ, was measured as P/L increased. The sigmoidal dependence of φ on P/L could not be explained by a micellar model of aggregation. Instead we proposed that the free energy for the state of peptide should include an elastic energy term representing the membrane thinning effect. The inclusion of this elastic energy of membrane provided a driving force for the S-to-I transition that explained the strong cooperativity exhibited in the peptide's activities. In particular, the theoretical prediction that φ is inversely proportional to P/L was borne out by the measurements of φ versus P/L in several different conditions of the bilayer.

Although alamethicin is similar to other antimicrobial peptides in its S-to-I transition behavior (Heller et al., 1998), it is unique in forming transmembrane pores described as a barrel-stave model (Baumann and Mueller, 1974). As far as we know, all other antimicrobial peptides, including melittin, form another type of transmembrane pore called the toroidal model (Ludtke et al., 1996; Matsuzaki et al., 1996; Yang et al., 2001). In this paper, we will use melittin as an example to see if the proposed theory also describes peptides that form toroidal pores. The difference between these two types of peptides is interesting. A sign change in one key parameter of the theory seems to reflect two different types of interactions. The theory also predicted that the membrane thinning should stop at the onset of S-to-I transition and membrane thickness should remain constant in the transition region. X-ray diffraction experiments were performed on both alamethicin and melittin to test this prediction.

EXPERIMENTAL MATERIALS AND METHODS

Materials

1,2-diphytanoyl-sn-glycero-3-phosphatidylcholine (DPhPC), 1,2-dimyristoyl-sn-glycero-3-phosphatidylcholine (DMPC) and 1,2-dioleoyl-sn-glycero-3-phosphatidylcholine (DOPC) were purchased from Avanti Polar Lipids (Alabaster, AL). Alamethicin and melittin were purchased from Sigma-Aldrich Chemical Co. (St. Louis, MO). Two grades of melittin were used, the sequencing grade (product no. M-1407) and the grade of purity 93% HPLC (product no. M-2272). Both gave the same results in this study. Yang et al. (2001) also found no difference between Sigma melittin and pure synthetic melittin in this type of study as long as there was no added Ca2+ in the sample. Polyethylene glycol (PEG20000) was purchased from Merck KGaA Co. (Darmstadt, Germany). All materials were used as delivered.

Sample preparation

In this study, two experimental methods were used. One was OCD (Olah and Huang, 1988; Wu et al., 1990) for the measurement of peptide orientation in lipid bilayers. Another was lamellar x-ray diffraction (LXD) for the measurement of membrane thickness. The samples used in both methods were in the form of oriented multilayers, a stack of parallel lipid bilayers on a solid substrate. The preparation of such oriented samples followed the method described in the previous study (Chen et al., 2002). Briefly, lipid and peptide of chosen P/L were codissolved in a solvent of 1:1 (v/v) methanol and chloroform. The lipid concentration was ∼1 mg per 20 μl solvent. An appropriate amount of the solution was spread onto a cleaned quartz surface—10 μl or less solution (depending on the P/L) onto a 14-mm-diameter area for OCD, or 100 μl solution onto a 20-mm-square area for LXD. When the solvent dried, the sample was vacuumed to remove the remaining solvent residues, and then slowly hydrated with water vapor until it appeared transparent. A good sample was visually smooth and showed at least five orders of Bragg diffraction by LXD. Two peptide/lipid systems were studied systematically; these were alamethicin in DPhPC and melittin in DOPC. As stated above, these peptide-lipid combinations were chosen for their ranges of P/L in their S-to-I transitions.

OCD measurement

The sample chamber for OCD was the same as used in Chen et al. (2002). The temperature was controlled at 30°C with stability of ±0.1°C. The water solution of PEG20000 was inside the sealed chamber to control the hydration of the sample via its vapor. The concentration of PEG solution used in this study was 4.75 g of PEG20000 in 10.00 g of water, which gave a vapor pressure equivalent to 98% relative humidity (RH) at 30°C, (differing by only 0.1% from 25°C) as was calibrated in Chen et al. (2002). The hydration equilibrium of the sample was ensured by an agreement of at least three OCD spectra measured over a period of 6 h. OCD was measured with a Jasco J-810 spectropolarimeter, with light incident normal to the sample surface (Wu et al., 1990). The sample was allowed to rotate around the incident light at eight angles equally spaced in one complete rotation. The averaged spectrum of the measurements at eight rotational angles was used for analysis. The rotational average ensured the elimination of possible artifacts due to linear dichroism (Wu et al., 1990). The background OCD spectra of pure lipid bilayers (i.e., without peptides) were measured separately and were removed from the spectra of the corresponding samples containing peptide.

The reason we chose 98% RH (rather than 100% RH) for this experiment was that for both OCD and LXD measurements, the sample substrate was oriented vertically. At the levels of humidity higher than 98% RH, the membranes on an open sample (i.e., on one substrate) would flow. This is not to say it is impossible to make measurements at 100% RH. An oriented membrane sample could be covered with another substrate to prevent the sample flow, as we have done previously for OCD (Chen et al., 2002; Wu et al., 1990) and for LXD (Olah et al., 1991; Wu et al., 1995). However, it would take a long equilibrating time to change the hydration of a covered (i.e., two-substrate) sample, and hydration changes are necessary in x-ray experiments for the purpose of phase determination. As we will make clear in the discussion section, the dependence of the peptide transition on hydration is gradual. There is no qualitative difference between the transitions measured at 98% RH and at 100% RH (Chen et al., 2002).

The OCD spectra for the S state and the I state of alamethicin were measured in Chen et al. (2002). The OCD spectra for the S state and the I state of melittin were measured previously by Yang et al. (2001) in DMPC bilayers in another laboratory. These spectra were remeasured and reproduced here using the instrument described here.

LXD measurement

The sample chamber for LXD was the same as used in our previous studies (Chen et al, 1997; Hung et al., 2000), except that the relative humidity was controlled by a series of PEG solutions enclosed inside the chamber. This was to ensure that the hydration levels of the sample were the same in the OCD and LXD measurements. The temperature was set at 30°C, the same temperature for the OCD measurement. In addition to the measurement at 98% RH, a series of measurements were made at lower levels of humidity for the purpose of phase determination. Precise reading for these lower levels of humidity was not necessary, because the swelling method for phase determination depended on the precise reading of lamellar repeat spacings only.

LXD was measured with Cu Kα radiation generated at 30 kV/30 mA by θ-2θ scan from θ = 0.5° to 7.5° with a step size Δθ = 0.01° at 1 s per step. The equilibrium of the sample at each humidity setting was ensured by an agreement of at least three consecutive diffraction patterns whose average was subsequently analyzed. Only samples that produced at least five discernible diffraction peaks were accepted. For P/L > 1/25, diffraction patterns showed only four discernible peaks—these results were not included in the discussion. Each peptide-lipid combination was measured with at least two separately prepared samples. Each sample was measured twice separately at least 10 h apart to check the reproducibility.

The procedure for data reduction was described in many of our papers (Chen et al, 1997; Hung et al., 2000; Ludtke et al., 1995; Wu et al., 1995; Olah et al., 1991). Briefly, the procedure started with background removal, and absorption and diffraction volume corrections. Then the integrated peak intensities were corrected for the polarization and the Lorentz factors. The magnitude of the diffraction amplitude was the square root of the integrated intensity. The phases were determined by the swelling method (Blaurock, 1971). With their phases determined, the diffraction amplitudes were Fourier transformed to obtain the trans-bilayer electron density profiles. The profiles were not normalized to the absolute scale, but they gave the correct peak-to-peak distances, since the latter are independent of normalization (Wu et al., 1995).

RESULTS AND ANALYSIS

Fraction of peptide molecules in the I state, φ versus P/L

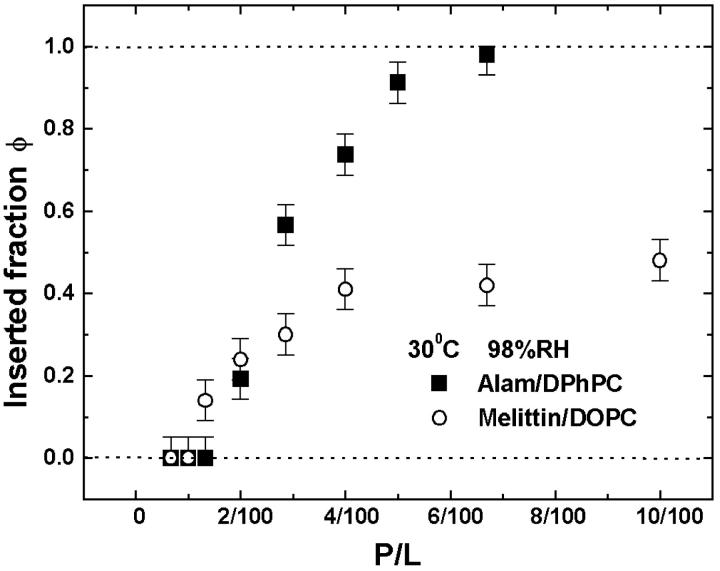
For helical peptides, including both alamethicin and melittin, the I spectrum is that of helices normal to the plane of the bilayers and the S spectrum of helices parallel to the plane (Olah and Huang, 1988; Wu et al., 1990). These spectra are somewhat different in their details from one helical peptide to another, most likely because none of such peptides is a perfect α-helix for the entire length (Okada et al., 1994). The S and I spectra of alamethicin (Wu et al., 1990) were reproduced here at P/L = 1/150 and P/L = 1/15, respectively (Fig. 1 top). Every other spectrum of alamethicin can be fit by a linear combination of these S and I spectra. From the fit, we obtained the fraction of the peptide molecules in the I state, φ (Fig. 2). The error bars, about ±0.05, represent the standard deviations of the numerical fits. We note that we have practically reproduced the previous result measured at 25°C (Chen et al., 2002), with only slight differences.

FIGURE 1.

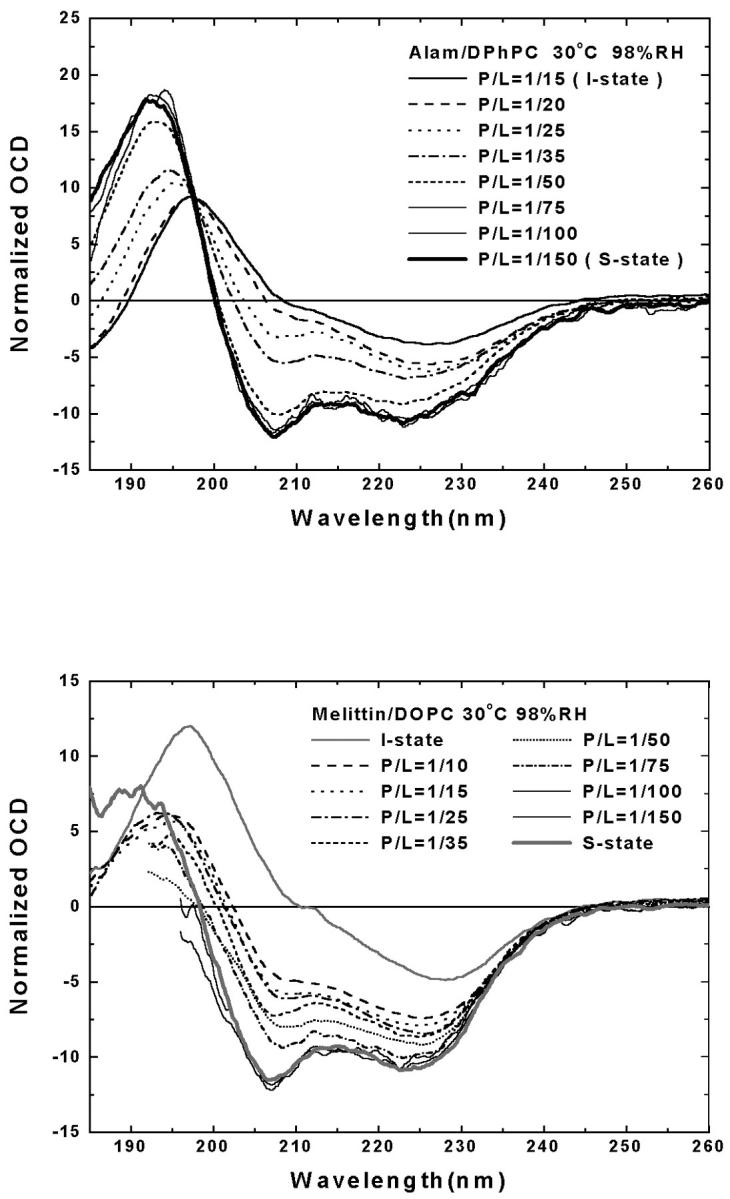
FIGURE 1

Open in a new tab

(top) OCD spectra of alamethicin in DPhPC bilayers at 30°C and 98% RH with P/L varied from 1/150 to 1/15 (lipid background removed). The spectra of P/L = 1/150 and 1/15 were the spectra for the S state and the I state of alamethicin, as established in Chen et al. (2002). All other spectra were normalized such that each was fit by a linear combination of S and I: 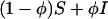Inline graphic with φ as a fitting parameter (see Chen et al., 2002). (bottom) OCD of melittin in DOPC bilayers at 30°C and 98% RH with P/L varied from 1/150 to 1/10 (lipid background removed). The high UV absorptance by DOPC made the spectra below ∼200 nm unacceptably noisy. The spectra I and S of melittin were established in Yang et al. (2001) and were remeasured here in DMPC bilayers. The spectra from DOPC bilayers were normalized as above.

FIGURE 2.

FIGURE 2

Open in a new tab

Fraction of peptide molecules occupying the I state, φ, obtained from Fig. 1 is plotted as a function of peptide concentration P/L: (solid square) alamethicin in DPhPC and (open circle) melittin in DOPC, both at 30°C and 98% RH. The error bars are the standard deviations of the numerical fits described in Fig. 1.

Fig. 1 bottom shows the OCD spectra of melittin in DOPC bilayers at 30°C and 98% RH in a series of P/Ls. The spectra here are noisier than the ones in Fig. 1 top. This is because DOPC has a much higher UV absorptance than DPhPC. Particularly at low values of P/L, the noise levels were high at wavelengths below 200 nm, because larger amounts of sample were needed to obtain sufficient peptide signals. The S and I spectra were obtained from melittin in DMPC bilayers as described in Yang et al. (2001) and were reproduced by our instrument in this study. All measured spectra of melittin could be fit with a linear combination of these S and I spectra for wavelength above 200 nm. The fraction of melittin molecules in the I state is plotted against P/L in Fig. 2.

Membrane thickness versus P/L

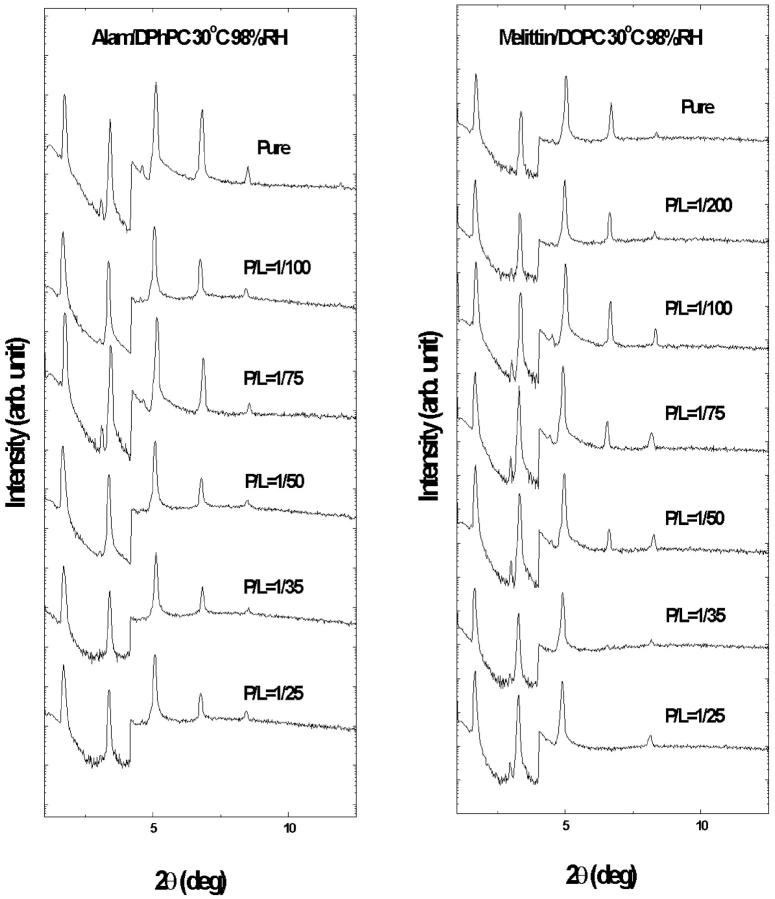
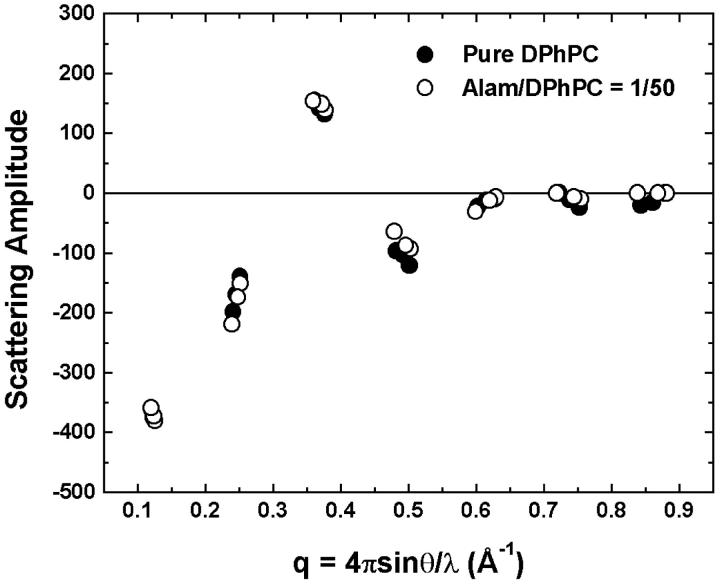
The diffraction patterns of all the samples measured at 30°C and 98% RH are shown in Fig. 3. At least five Bragg orders were recorded in each pattern. No peak broadening with Bragg order was observed, indicating that undulation fluctuations were negligible at hydration levels below 98% RH (Guinier, 1994). For peptide concentrations above P/L = 1/25, the patterns had at most four orders. Since we were measuring small changes in membrane thickness, we decided not to compare them with those with higher numbers of peaks. To determine the diffraction phases, each sample was measured in a series of relative humidities below 98% RH to produce patterns at different values of repeating spacing D. They were normalized relatively to each other by the Blaurock method (Blaurock, 1971) and plotted as a function of scattering vector q (=4πsin θ/λ, 2θ is the scattering angle and λ the x-ray wavelength) to determine the phases according to the swelling principle (Perutz, 1954; Torbet and Wilkins, 1976). Two representative examples are shown in Fig. 4.

FIGURE 3.

FIGURE 3

Open in a new tab

X-ray diffraction patterns of pure DPhPC and alamethicin in DPhPC at various P/L (left), and pure DOPC and melittin in DOPC at various P/L (right). The patterns are displaced for clarity. The steps at 2θ ∼4° were due to the use of an x-ray attenuator to reduce the count rates for the first two diffraction orders in order not to saturate the detector.

FIGURE 4.

FIGURE 4

Open in a new tab

Phasing diagrams for the x-ray diffraction of pure DPhPC and DPhPC containing alamethicin at P/L = 1/50 as examples of the swelling method (Blaurock, 1971). The repeat spacing D for pure DPhPC (DPhPC-alamethicin P/L = 1/50) was 50.1 (49.9), 51.1 (50.7), 52.1 (52.5) Å at 95.3%, 96.8%, and 98.0% RH, respectively. All other samples had similar phasing diagrams.

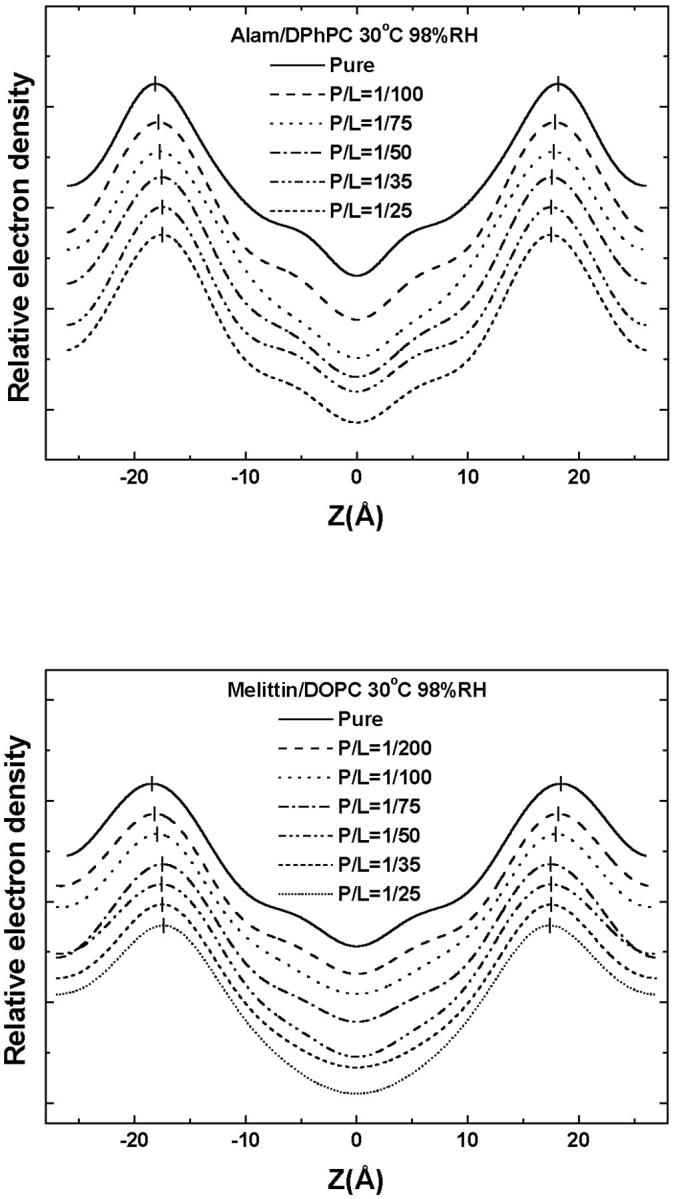
The trans-bilayer electron density profiles constructed from the diffraction data are shown in Fig. 5. We were interested in the peak-to-peak distance (PtP) as a measure of the membrane thickness. Fig. 6 shows the PtP versus P/L determined from the profiles shown in Fig. 5. The measurements were repeated with independently prepared samples, at least two for each peptide-lipid combination. We found that for alamethicin in DPhPC, the PtPs were reproducible within ±0.1 Å in the range of P/L shown. For melittin in DOPC, the PtPs were reproducible within ±0.1 Å for P/L ≤ 1/100 and within ±0.2 Å for P/L ≥ 1/75. These uncertainties are shown as error bars in Fig. 6.

FIGURE 5.

FIGURE 5

Open in a new tab

Electron density profiles of pure DPhPC and alamethicin in DPhPC at various P/L (top), and pure DOPC and melittin in DOPC at various P/L (bottom). The profiles were not normalized and were displaced for clarity. The short vertical bars indicate the positions of the peaks.

FIGURE 6.

FIGURE 6

Open in a new tab

Peak-to-peak distance (PtP) versus P/L for alamethicin in DPhPC (top) and melittin in DOPC (bottom). In each panel, the arrow indicates (P/L)*, the onset of S-to-I transition measured by OCD (see Fig. 7). The error bars represent the ranges of reproducibility (see text, Membrane thickness versus P/L). PtP decreases linearly with P/L below (P/L)*. Above (P/L)*, the PtP is constant within experimental error.

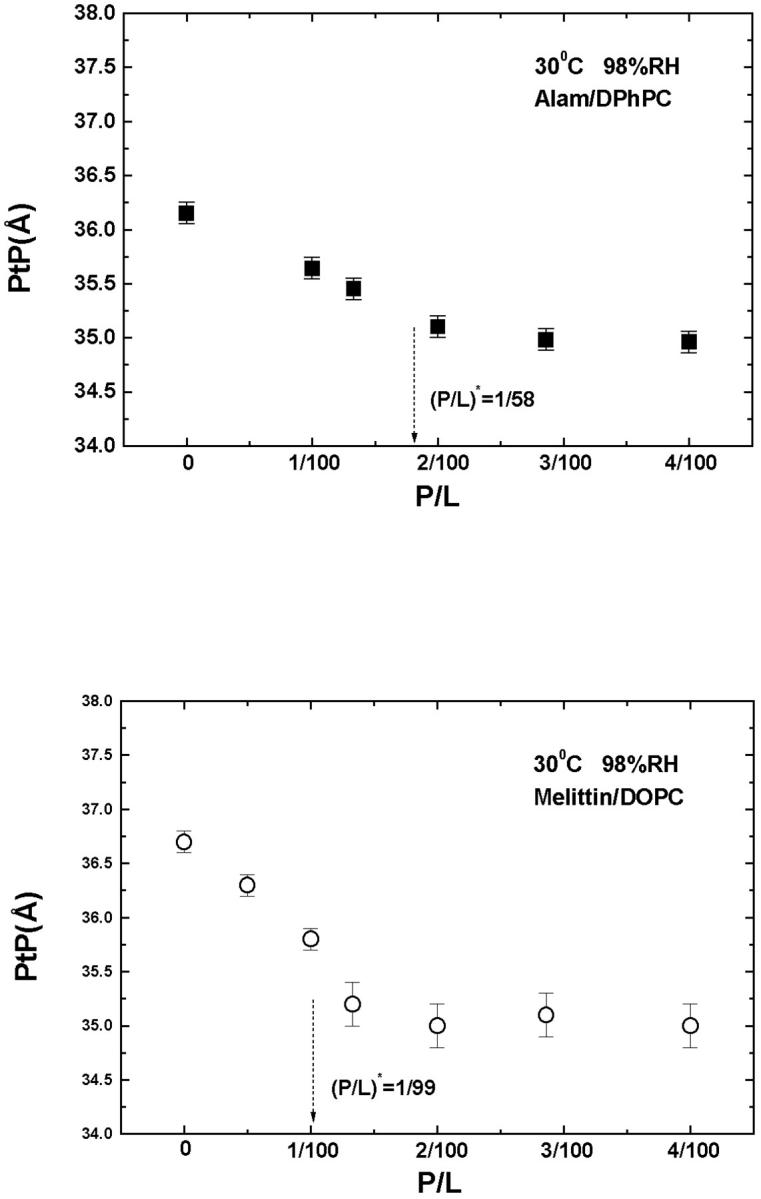
The bilayer thinning in proportion to P/L is consistent with the peptide molecules being embedded in the headgroup region. It is also consistent with the peptide being distributed in the plane of bilayer without aggregation in the S state. More direct evidence of no peptide aggregation has been provided by EPR (Barranger-Mathys and Cafiso, 1993), NMR (Hirsh et al., 1996), and fluorescence energy transfer (Gazit et al., 1994; 1995; Schümann et al., 1996) studies. As was done previously for alamethicin (Wu et al., 1995; Heller et al., 1997), magainin (Ludtke et al., 1995) and protegrin (Heller et al., 2000), we can estimate the cross section of melittin from its thinning effect shown in Fig. 6. We assume that the volume of hydrocarbon chains is constant during thinning. Then the fractional area expansion of the bilayer 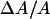Inline graphic equals 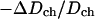Inline graphic where Dch is the thickness of the hydrocarbon region. Dch is estimated by subtracting twice the length of the glycerol region (from the phosphate to first methylene of the hydrocarbon chain), i.e., ∼10 Å, from PtP (McIntosh and Simon, 1986; Nagle and Tristram-Nagle, 2000; Harroun et al., 1999a,b). Assuming that the area expansion is due to the embedding of the peptide in the headgroup region, then 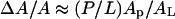Inline graphic where Ap and AL stand for the cross-sectional area of peptide and lipid, respectively. Using AL∼75 Å2 for DOPC (Nagle and Tristram-Nagle, 2000) and the PtP versus P/L in the S state (Fig. 6), one obtains Ap∼300 Å2. The lengthwise cross section of the melittin helix has been estimated by crystallographic analyses (Terwilliger et al., 1982) and monolayer studies (DeGrado et al., 1981) to be ∼400 Å2. The smaller value estimated from the thinning effect could be explained if some water molecules were displaced from the headgroup region when the peptide was embedded.

Comparison with the theory of membrane thinning

First, we briefly recapitulate our theory for peptide transition (Chen et al., 2002). An individual peptide in the S state causes a local expansion of membrane area. Because of the volume conservation of the hydrocarbon chains, an expansion in the area is equivalent to a thinning in the thickness. This local deformation of lipid bilayer extends over a range of diameter ∼40 Å or more, depending on the values of the bilayer's elastic constants (Huang, 1986, 1995). When the peptide concentration is sufficiently high such that the local deformations by neighboring peptide molecules overlap, the membrane thinning becomes approximately uniform and the amount of overall thinning is proportional to P/L. The proportionality of membrane thinning to P/L is shown in Fig. 6 where PtP decreases linearly with P/L in the region before the onset of S-I transition. This has also been confirmed by many previous measurements with other peptides (Wu et al., 1995; Ludtke et al., 1995; Heller et al., 2000; Weiss et al., 2002). The membrane elasticity theory showed that under such conditions the elastic energy of membrane thinning is proportional to (P/L)2 (Huang, 1995). This can be seen as follows. The measured membrane thinning is proportional to the area expansion of the bilayer. An expansion ΔA in the membrane area A causes a tension σ = ka(ΔA/A), where ka is the stretch coefficient (Rawicz et al., 2000). The change of free energy (normalized to per lipid) due to the occupation of peptide molecules in the S state can be written as

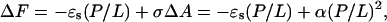graphic file with name M4.gif (1)

where −ɛs is the binding energy for a peptide molecule taken from the solution to an S state, but not including the energy of membrane thinning. The energy of membrane thinning is σΔA. The second equality in Eq. 1 made use of the proportionality of thinning to P/L, hence 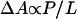Inline graphic. The parameter α is a constant times ka. In the transition region, a fraction of the peptide molecules, φ(P/L), are in the I state and the rest (1−φ)(P/L) remain in the S state. Parallel to Eq. 1, we proposed that membrane thinning in the transition region is proportional to 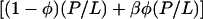Inline graphic. The factor β was introduced to distinguish the effect of membrane thinning by a peptide molecule in the I state from that of a peptide molecule in the S state. The free energy was then written as

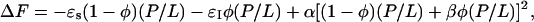graphic file with name M7.gif (2)

where −ɛI is the counterpart of −ɛs for the I state. It is essentially the energy of pore formation divided by the number of participating peptides. Depending on the structure of the pore, −ɛI may include the energy of monolayer bending as well as interaction energies between the peptides in the pore.

Although the free energy (Eq. 2) contains several free parameters, it has at least two definitive predictions. Minimization of the free energy with respect to φ, 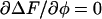Inline graphic, gives the equilibrium condition

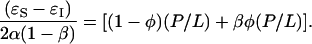graphic file with name M9.gif (3)

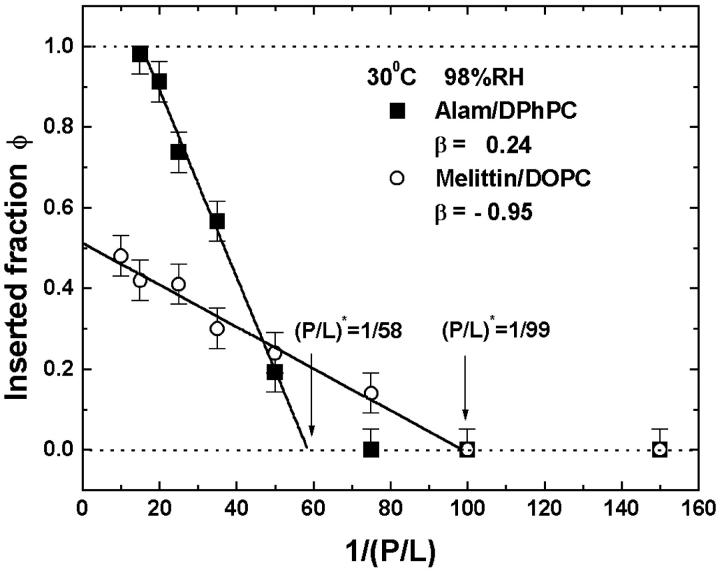
The first prediction from Eq. 3 is that φ is a linear function of 1/(P/L) in the transition region:

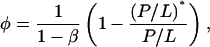graphic file with name M10.gif (4)

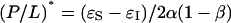where Inline graphic is a constant representing the threshold concentration for the onset of S-to-I transition. In Fig. 7, the data φ of Fig. 2 were replotted against 1/(P/L). Clearly the prediction was borne out by both alamethicin and melittin. The second prediction of the theory is that the right-hand side of Eq. 3 is constant, in fact equals to (P/L)*. The quantity in the square brackets represents the thinning effect. Therefore its constancy implies that the membrane thickness remains unchanged in the entire transition region, even though before the transition the thickness decreased linearly as P/L increased toward the onset of transition. The expression Eq. 3 includes the point φ = 0, the onset point of transition. Thus the theory predicts that the membrane thickness remains the same as at the onset point for the entire transition region. As shown in Fig. 6, the second prediction was also in good agreement with the data.

FIGURE 7.

FIGURE 7

Open in a new tab

Fraction of peptide molecules occupying the I state, φ, from Fig. 2 was replotted as a function of the inverse of peptide concentration 1/(P/L): (solid square) alamethicin in DPhPC and (open circle) melittin in DOPC, both at 30°C and 98% RH. The data fell on a straight line for P/L > (P/L)* in each case. The intercept of the straight line with the line of 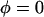Inline graphic defined the threshold concentration (P/L)*. The parameter β was obtained from a fit with Eq. 4.

DISCUSSION

In Chen et al. (2002) alamethicin was measured in three different bilayer conditions, including one at 100% RH and another at 98% RH (25°C). Both the measurements at 100% RH and 98% RH fit the theory well with slightly different parameters. Indeed the phase diagrams of S-to-I transitions have been mapped out for a number of different peptide/lipid systems in the plane of temperature and humidity (Huang and Wu, 1991; Heller et al., 1997). In all cases, hydration changes merely shifted the transition range of P/L. Thus the mechanism of transition should be the same at all levels of hydration.

It was shown in Chen et al. (2002) that the value of the parameter β must be less than one, but otherwise there is no restriction on the value of β. It is interesting to note that β is positive for alamethicin but is negative for melittin (see Fig. 7). From its definition in Eq. 2, a positive β means that a pore state has a membrane thinning effect similar to the S state but with a reduced strength. On the other hand, a negative β implies that the formation of a pore counteracts the membrane thinning effect of the S state. We do not know if this is related to the observation that alamethicin forms barrel-stave pores, whereas melittin forms toroidal pores (Yang et al., 2001). Whether all toroidal pores have a negative β remains to be seen. It is clear, however, that alamethicin and melittin interact with lipid bilayers differently in the I state, although they seem to interact with the bilayers similarly in the S state. One consequence of the sign of β is that if it is positive, the peptide can achieve 100% insertion, i.e., having a pure I state, as seen in the case of alamethicin (Fig. 7). On the other hand, a negative β prevents φ from reaching the value of one (see Eq. 4) as seen in the case of melittin (Fig. 7).

In Chen et al. (2002), we considered an alternative theory assuming that the pore formation is an aggregation effect of peptide. Although aggregation provides cooperativity, the theory does not agree with the measured φ versus P/L. In comparison, the present theory assumes that the elastic energy of membrane thinning modulates the energy difference between the surface adsorbed state and the pore state. This theory has the advantage of incorporating two independent sets of measurements, i.e., the change in the membrane thickness and the fraction of peptide in each state, both as functions of P/L. Overall the theory gives a good description for all the data, including the constancy of membrane thickness in the transition region. It also provides useful parameters for the description of peptide-bilayer interactions.

We are hopeful that the behavior of peptides in lipid bilayers can be inferred to understand the peptides' activities in cell membranes. In this regard, it should be pointed out that although in nature the peptide reaches the cell membrane by partitioning from the extracellular phase, once partitioned in the membrane the peptide would quickly translocate across the membrane and distribute on both sides of the membrane. This was observed by Matsuzaki et al. (1995) in their lipid vesicle experiment using fluorescence techniques. Even at low peptide concentrations, transient pores were formed by peptides initially bound to the outer leaflet. When the transient pores dissolved, the peptides were distributed to both sides of the bilayer. Also, the peptide-lipid ratios used in our experiment are comparable to those used in bacterial killing assays, as measured by radioactivity binding experiments (Steiner et al., 1988; Merrifield et al., 1994). As for the nonphysiological hydration conditions used in our experiment, we have shown that the behavior of peptides is basically the same in all hydration levels. Only the ranges of concentration (P/L) for the I and S states vary (continuously) with hydration. In the limit of full hydration, the property of individual bilayers in multilayers is the same as a single isolated bilayer. Both undergo significant undulation fluctuations and have the same gel-to-fluid transition temperature (Evans and Needham, 1987; Smith et al., 1990).

Acknowledgments

F.Y.C. was supported by National Science Council (Taiwan) through Contract NSC90-2112-M-008-36; H.W.H. was supported by National Institutes of Health grants GM55203 and RR14812 and by the Robert A. Welch Foundation.

References

  1. Barranger-Mathys, M., and D. S. Cafiso. 1993. Collisions between helical peptides in membranes monitored using electron paramagnetic resonance: evidence that alamethicin is monomeric in the absence of a membrane potential. Biophys. J. 67:172–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Baumann, G., and P. Mueller. 1974. A molecular model of membrane excitability. J. Supramol. Struct. 2:538–557. [DOI] [PubMed] [Google Scholar]
  3. Bechinger, B., Y. Kim, L. E. Chirlian, J. Gesell, J.-M. Neumann, M. Motal, J. Tomich, M. Zasloff, and S. J. Opella. 1991. Orientations of amphipathic helical peptides in membrane bilayers determined by solid-state NMR spectroscopy. J. Biomol. NMR. 1:167–173. [DOI] [PubMed] [Google Scholar]
  4. Blaurock, A. E. 1971. Structure of the nerve myelin membrane: proof of the low resolution profile. J. Mol. Biol. 56:35–52. [DOI] [PubMed] [Google Scholar]
  5. Boman, H. G., J. Marsh, and J. A. Goode, editors. 1994. Antimicrobial peptides. Ciba Foundation Symposium 186. John Wiley & Sons, Chichester. 1–272.
  6. Chen, F. Y., W. C. Hung, and H. W. Huang. 1997. Critical swelling of phospholipid bilayers. Phys. Rev. Lett. 79:4026–4029. [Google Scholar]
  7. Chen, F. Y., M.-T. Lee, and H. W. Huang. 2002. Sigmoidal concentration dependence of antimicrobial peptide activities: a case study on alamethicin. Biophys. J. 82:908–914. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. DeGrado, W. F., F. J. Kezdy, and E. T. Kaiser. 1981. Design, synthesis, and characterization of a cytotoxic peptide with melittin-like activity. J. Am. Chem. Soc. 103:679–681. [Google Scholar]
  9. Evans, E., and D. Needham. 1987. Physical properties of surfactant bilayer membranes: thermal transitions, elasticity, rigidity, cohesion, and colloidal interactions. J. Phys. Chem. 91:4219–4228. [Google Scholar]
  10. Ganz, T. 1999. Defensins and host defense. Science. 286:420–421. [DOI] [PubMed] [Google Scholar]
  11. Gazit, E., W. J. Lee, P. T. Brey, and Y. Shai. 1994. Mode of action of the antibacterial cecropin B2: a spectrofluorometric study. Biochemistry. 33:10681–10692. [DOI] [PubMed] [Google Scholar]
  12. Gazit, E., A. Boman, H. Boman, and Y. Shai. 1995. Interaction of the mammalian antibacterial peptide cecropin P1 with phospholipid vesicles. Biochemistry. 34:11479–11488. [DOI] [PubMed] [Google Scholar]
  13. Guinier, A. 1994. X-ray diffraction in crystals, imperfect crystals, and amorphous bodies. Dover Publications, New York.
  14. Harroun, T. A., W. T. Heller, T. M. Weiss, L. Yang, and H. W. Huang. 1999a. Experimental evidence for hydrophobic matching and membrane-mediated interactions in lipid bilayers containing gramicidin. Biophys. J. 76:937–945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Harroun, T. A., W. T. Heller, T. M. Weiss, L. Yang, and H. W. Huang. 1999b. Theoretical analysis of hydrophobic matching and membrane-mediated interactions in lipid bilayers containing gramicidin. Biophys. J. 76:3176–3185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. He, K., S. J. Ludtke, D. L. Worcester, and H. W. Huang. 1995. Antimicrobial peptide pores in membranes detected by neutron in-plane scattering. Biochemistry. 34:16764–16769. [DOI] [PubMed] [Google Scholar]
  17. He, K., S. J. Ludtke, D. L. Worcester, and H. W. Huang. 1996. Neutron scattering in the plane of membranes: structure of alamethicin pores. Biophys. J. 70:2659–2666. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Helenius, A., and K. Simons. 1975. Solubilization of membranes by detergents. Biochim. Biophys. Acta. 415:29–79. [DOI] [PubMed] [Google Scholar]
  19. Heller, W. T., K. He, S. J. Ludtke, T. A. Harroun, and H. W. Huang. 1997. Effect of changing the size of lipid headgroup on peptide insertion into membranes. Biophys. J. 73:239–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Heller, W. T., A. J. Waring, R. I. Lehrer, and H. W. Huang. 1998. Multiple states of β-sheet peptide protegrin in lipid bilayers. Biochemistry. 37:17331–17338. [DOI] [PubMed] [Google Scholar]
  21. Heller, W. T., A. J. Waring, R. I. Lehrer, T. A. Harroun, T. M. Weiss, L. Yang, and H. W. Huang. 2000. Membrane thinning effect of the β-sheet antimicrobial protegrin. Biochemistry. 39:139–145. [DOI] [PubMed] [Google Scholar]
  22. Hirsh, D. J., J. Hammer, W. L. Maloy, J. Blazyk, and J. Schaefer. 1996. Secondary structure and location of a magainin analogue in synthetic phospholipid bilayers. Biochemistry. 35:12733–12741. [DOI] [PubMed] [Google Scholar]
  23. Huang, H. W. 1986. Deformation free energy of bilayer membrane and its effect on gramicidin channel lifetime. Biophys. J. 50:1061–1070. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Huang, H. W. 1995. Elasticity of lipid bilayer interaction with amphiphilic helical peptides. J. Phys. II France. 5:1427–1431. [Google Scholar]
  25. Huang, H. W. 2000. Action of antimicrobial peptides: two-state model. Biochemistry. 39:8347–8352. [DOI] [PubMed] [Google Scholar]
  26. Huang, H. W., and Y. Wu. 1991. Lipid-alamethicin interactions influence alamethicin orientation. Biophys. J. 60:1079–1087. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hung, W. C., F. Y. Chen, and H. W. Huang. 2000. Order-disorder transition in bilayers of diphytanoyl phosphatidylcholine. Biochim. Biophys. Acta. 1467:198–206. [DOI] [PubMed] [Google Scholar]
  28. Ludtke, S. J., K. He, Y. Wu, and H. W. Huang. 1994. Cooperative membrane insertion of magainin correlated with its cytolytic activity. Biochim. Biophys. Acta. 1190:181–184. [DOI] [PubMed] [Google Scholar]
  29. Ludtke, S., K. He, and H. W. Huang. 1995. Membrane thinning caused by magainin 2. Biochemistry. 34:16764–16769. [DOI] [PubMed] [Google Scholar]
  30. Ludtke, S. J., K. He, W. T. Heller, T. A. Harroun, L. Yang, and H. W. Huang. 1996. Membrane pores induced by magainin. Biochemistry. 35:13723–13728. [DOI] [PubMed] [Google Scholar]
  31. McIntosh, T. J., and S. A. Simon. 1986. Area per molecule and distribution of water in fully hydrated dilauroylphosphatidylethanolamine bilayers. Biochemistry. 25:4948–4952. [DOI] [PubMed] [Google Scholar]
  32. Martin, E., T. Ganz, and R. I. Lehrer. 1995. Defensins and other endogenous peptide antibiotics of vertebrates. J. Leukoc. Biol. 58:128–136. [DOI] [PubMed] [Google Scholar]
  33. Matsuzaki, K., M. Harada, S. Fumakoshi, N. Fujii, and K. Miyajima. 1991. Physicochemical determinants for the interactions of magainins 1 and 2 with acidic lipid blayers. Biochim. Biophys. Acta. 1063:162–170. [DOI] [PubMed] [Google Scholar]
  34. Matsuzaki, K., O. Murase, H. Tokuda, S. Fumakoshi, N. Fujii, and K. Miyajima. 1994. Orientational and aggregational states of magainin 2 in phospholipid bilayers. Biochemistry. 33:3342–3349. [DOI] [PubMed] [Google Scholar]
  35. Matsuzaki, K., O. Murase, N. Fujii, and K. Miyajima. 1995. Translocation of a channel-forming antimicrobial peptide, magainin 2, across lipid bilayers by forming a pore. Biochemistry. 34:6521–6526. [DOI] [PubMed] [Google Scholar]
  36. Matsuzaki, K., O. Murase, H. Tokuda, N. Fujii, and K. Miyajima. 1996. An antimicrobial peptide, magainin 2, induced rapid flip-flop of phospholipids coupled with pore formation and peptide translocation. Biochemistry. 35:11361–11368. [DOI] [PubMed] [Google Scholar]
  37. Merrifield, R. B., E. L. Merrifield, P. Juvvadi, D. Andreu, and H. G. Boman. 1994. Design and synthesis of antimicrobial peptides. In Antimicrobial peptides. H. G. Boman, J. Marsh, and J. A. Goode, editors. Ciba Foundation Symposium 186. John Wiley & Sons, Chichester. 5–26. [PubMed]
  38. Nagle, J. F., and S. Tristram-Nagle. 2000. Structure of lipid bilayers. Biochim. Biophys. Acta. 1469:159–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Okada, A., K. Wakamatsu, T. Miyazawa, and T. Higashijima. 1994. Vesicle-bound conformation of melittin: transferred nuclear Overhauser enhancement analysis in the presence of perdeuterated phosphatidylcholine vesicles. Biochemistry. 33:9438–9446. [DOI] [PubMed] [Google Scholar]
  40. Olah, G. A., and H. W. Huang. 1988. Circular dichroism of oriented α-helices. I. Proof of the exciton theory. J. Chem. Phys. 89:2531–2538. [Google Scholar]
  41. Olah, G. A., H. W. Huang, W. Liu, and Y. Wu. 1991. Location of ion binding sites in the gramicidin channel by x-ray diffraction. J. Mol. Biol. 218:847–858. [DOI] [PubMed] [Google Scholar]
  42. Perutz, M. F. 1954. The structure of haemoglobin. III. Direct determination of the molecular transform. Proc. R. Soc. A. 225:264–286. [Google Scholar]
  43. Rawicz, W., K. C. Olbrich, T. McIntosh, D. Needham, and E. Evans. 2000. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 79:328–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Schümann, M., D. Margitta, T. Wieprecht, M. Beyermann, and M. Bienert. 1996. The tendency of magainin to associate upon binding to phospholipid bilayers. Biochemistry. 36:4345–4351. [DOI] [PubMed] [Google Scholar]
  45. Smith, G. S., E. B. Sirota, C. R. Safinya, R. J. Plano, and N. A. Clark. 1990. X-ray structural studies of freely suspended ordered hydrated DMPC mutimembrane films. J. Chem. Phys. 92:4519–4529. [Google Scholar]
  46. Steiner, H., D. Andreu, and R. B. Merrifield. 1988. Binding and action of cecropin and cecropin analogues: antibacterial peptides from insects. Biochim. Biophys. Acta. 939:260–266. [DOI] [PubMed] [Google Scholar]
  47. Terwilliger, T. C., L. Weissman, and D. Eisenberg. 1982. The structure of melittin in the form I crystals and its implication for melittin's lytic and surface activities. Biophys. J. 37:353–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Torbet, J., and M. H. F. Wilkins. 1976. X-ray diffraction studies of lecithin bilayers. J. Theor. Biol. 62:447–458. [DOI] [PubMed] [Google Scholar]
  49. Weiss, T. M., L. Yang, L. Ding, A. J. Waring, R. I. Lehrer, and H. W. Huang. 2002. Two states of cyclic antimicrobial peptide RTD-1 in lipid bilayers. Biochemistry. 41:10070–10076. [DOI] [PubMed] [Google Scholar]
  50. Williams, R. W., R. Starman, K. M. P. Taylor, K. Cable, T. Beeler, M. Zasloff, and D. Covell. 1990. Raman spectroscopy of synthetic antimicrobial frog peptides magainin 2a and PGLa. Biochemistry. 29:4490–4496. [DOI] [PubMed] [Google Scholar]
  51. Wu, Y., H. W. Huang, and G. A. Olah. 1990. Method of oriented circular dichroism. Biophys. J. 57:797–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Wu, Y., K. He, S. J. Ludtke, and H. W. Huang. 1995. X-ray diffraction study of lipid bilayer membrane interacting with amphiphilic helical peptides: diphytanoyl phosphatidylcholine with alamethicin at low concentrations. Biophys. J. 68:2361–2369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Yang, L., T. A. Harroun, T. M. Weiss, L. Ding, and H. W. Huang. 2001. Barrel-stave model or toroidal model? A case study on melittin pores. Biophys. J. 81:1475–1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Zasloff, M. 2002. Antimicrobial peptides of multicellular organisms. Nature. 415:389–395. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES