Time-Resolved Fluorescence and Fourier Transform Infrared Spectroscopic Investigations of Lateral Packing Defects and Superlattice Domains in Compositionally Uniform Cholesterol/Phosphatidylcholine Bilayers

Abstract

Time-resolved fluorescence and Fourier transform infrared spectroscopies were used to investigate the lateral organization of lipids in compositionally uniform and fully equilibrated 1-palmitoyl-2-oleoyl-phosphatidylcholine/cholesterol (POPC/CHOL) liposomes prepared by a recently devised low-temperature trapping method. Independent fluorescence decay lifetime and rotational dynamics parameters of diphenylhexatriene (DPH) chain-labeled phosphatidylcholine (DPH-PC) in these liposomes were recovered from the time-resolved fluorescence measurements as a function of cholesterol molar fraction (X_CHOL) at 23°C. The results indicate significantly greater lifetime heterogeneity, shorter average lifetime, rotational correlation time, and lower order parameter of the DPH moiety at X_CHOL ≈ 0.40 and 0.50 as compared to the adjacent cholesterol concentrations. Less prominent changes were also detected at, for example, X_CHOL ≈ 0.20 and 0.33. These X_CHOL's coincide with the “critical” X_CHOL's predicted by the previously proposed superlattice (SL) model, thus indicating that POPC and cholesterol molecules tend to form SL domains where the components tend to be regularly distributed. The data also support another prediction of the SL model, namely that lateral packing defects coexist with the ordered SL domains. It appears that unfavorable interaction of the DPH-moiety of DPH-PC with cholesterol results in a preferential partition of DPH-PC to the defect regions. Fourier transform infrared analysis of the native lipid O=P=O, C=O, and C-H vibrational bands of POPC/CHOL liposomes in the absence of DPH-PC revealed an increase in the conformational order of the acyl chains and a decrease in the conformational order (or increased hydration) of the interfacial and headgroup regions at or close to the predicted critical X_CHOL's. This provides additional but probe-independent evidence for SL domain formations in the POPC/CHOL bilayers. We propose that the defect regions surrounding the putative SL domains could play an important role in modulating the activity of various membrane-associated enzymes, e.g., those regulating the lipid compositions of cell membranes.

INTRODUCTION

Lateral organization of lipid molecules in membrane, particularly the formation of domains with distinct composition, has been under intensive studies during recent years. This is because of the profound functional implications of such domains in the structures and functions of cellular membranes (Simons and Ikonen, 1997; Mukherjee et al., 1998; Liu and Chong, 1999; Feigenson and Buboltz, 2001; Leidy et al., 2001; Anderson and Jacobson, 2002; Brown and London, 2002). Cholesterol appears to be a key player in the organization and functioning of mammalian cell membranes and has thus received particular attention. Several previous studies have found that bilayer properties do not change smoothly with changing cholesterol content, but significant deviations occur at certain cholesterol concentrations, e.g., 30–33 mol % (Parasassi et al., 1994) and 50 mol % (Lentz et al., 1980; Mabrey et al., 1978). Since these concentrations often corresponded to cholesterol/phospholipid (C/PL) ratios of 1:2 or 1:1, the existence of the respective C/PL “complexes” was proposed (Lundberg, 1977; Rubenstein et al., 1980; Presti et al., 1982). Recent experimental and theoretical studies by McConnell and co-workers were also interpreted to indicate the formation of such C/PL complexes (Radhakrishnan et al., 2000; Anderson and McConnell, 2001; 2002).

Another model for cholesterol lateral distribution, namely the superlattice (SL) model (or regular distribution model), has been proposed recently (reviewed in Somerharju et al., 1999; Chong and Sugar, 2002). The main distinction between the “complex” model and the SL model is that whereas the former usually proposes the existence of a single critical C/PL stoichiometry, the latter proposes a series of critical compositions, each corresponding to either a hexagonal or a centered rectangular cholesterol superlattice.

The key predictions of the SL model are that 1), membrane lateral order attains a local maximum at each superlattice (critical) composition and the factional bilayer area covered by randomly organized lipids increases when the composition moves away from a critical (SL) one; and 2), coexisting lateral packing defects surrounding the SL domain boundaries are expected to form at or near the SL compositions (Somerharju et al., 1999; Chong and Sugar, 2002). Although there is now abundant information supporting the former prediction, there is little direct experimental evidence for the latter. Accordingly, we set out to test it by studying the time-resolved fluorescence (TRF) properties of DPH-PC, i.e., a fluorescent phosphatidylcholine (PC) labeled with diphenylhexatriene (DPH) to the sn-2 acyl, as a function of cholesterol content in 1-palmitoyl-2-oleoyl-PC (POPC) bilayers. The fluorescence decay and rotational dynamics of DPH-PC are known to be sensitive to the polarity, lateral distribution heterogeneity, and rotational order properties of the host phospholipid acyl chains (Zannoni et al., 1983; Parente and Lentz, 1985; Cheng, 1989; Chen et al., 1990; Van der Meer et al., 1990; Chen and Cheng, 1996). In addition, complementary Fourier transform infrared (FTIR) measurements were carried out on the same POPC/CHOL liposomes but in the absence of any external probe to investigate the properties of the acyl-chain, interfacial, and headgroup regions of the bilayer. A recently devised low-temperature trapping (LTT) method (Huang et al., 1999), known to produce compositionally uniform and fully equilibrated PC/CHOL liposomal bilayers, was used to minimize compositional inhomogeneity and cholesterol demixing due to sample preparation.

We found major deviations in all the measured fluorescence lifetime and rotational dynamics parameters of DPH-PC at X_CHOL ≈ 0.40 and 0.50. Significant deviations were also detected at X_CHOL ≈ 0.20, 0.33 for some parameters. The FTIR measurements showed that the O=P=O, C=O, and C-H vibrational peak frequencies change abruptly at or near most of these X_CHOL's. These findings provide new spectroscopic evidence by showing that the membrane lateral order changes abruptly and the appearance of lateral packing defect regions close to the critical cholesterol concentrations as predicted by the SL model.

MATERIALS AND METHODS

Materials

POPC was purchased from Avanti Polar Lipids (Alabaster, AL) and cholesterol from Nu Chek Prep (Elysian, MN). Lipid purity (>99%) was confirmed by thin layer chromatography (TLC) on washed, activated silica gel plates (Alltech Associates, Deerfield, IL) and developed with chloroform/methanol/water = 65:25:4 for phospholipid analysis or with petroleum ether/ethyl ether/chloroform = 7:3:3 for cholesterol analysis. All solvents were of HPLC grade. Fluorescent lipid, 1-palmitoyl-2-((2-(4-(6-phenyl-trans-1,3,5-hexatrienyl)phenyl)ethyl)carbonyl)-3-sn-PC (DPH-PC), was obtained from Molecular Probes (Eugene, OR). DPH-PC consists of a 16-carbon saturated fatty acyl chain attached to the sn-1 position of the glycerol backbone and a diphenylhexatriene (DPH) fluorophore attached to the sn-2 position of the glycerol backbone via a short propanoyl chain. Concentrations of phospholipid stock solutions were determined by a phosphate assay (Kingsley and Feigenson, 1979). Aqueous buffer (pH 7.0, 5 mM PIPES, 200 mM KCl, and 1 mM NaN₃) was prepared from deionized water (∼18 MΩ) and filtered through a 0.1 μm filter before use.

Preparation of POPC/CHOL liposomes using LTT

Compositionally uniform POPC/CHOL liposomes containing 0.1 mol % of DPH-PC were prepared using a low temperature trapping (LTT) technique (Huang et al., 1999). Briefly, DPH-PC, POPC, and CHOL were dissolved and mixed in chloroform. The concentration of total lipid in each sample was fixed at 100 μM. Chloroform was first removed under a vacuum of 30 mTorr for 12 h. The dry lipid films were redissolved in dry chloroform containing 2% of methanol. These mixtures were then frozen in liquid nitrogen and subsequently lyophilized at a controlled temperature (−20 to −70°C) in such a way that the chloroform in the mixtures remained solid. After the bulk solvent had been removed, the lipid powder was kept at −20°C under a vacuum of 30 mTorr for another 12 h or more to remove any residual solvent. Just before hydration, the samples were warmed to 40°C in a stirring water bath for 1 min. Aqueous buffer (pH 7.0, 5 mM PIPES, 200 mM KCL, and 1 mM NaN₃) was added to the dry lipid films followed by vortexing for 1 min. The samples were prepared and sealed under argon under dim red light.

To ensure phase equilibrium and stability of the ternary DPH-PC/POPC/CHOL mixtures, the liposomes were stored at 23°C in the dark on a mechanical shaker for at least 10 days before the fluorescence measurements. The samples were vortexed vigorously once a day during the equilibration period. Previous x-ray diffraction measurements (Huang et al., 1999) on POPC/CHOL liposomes prepared by this LTT method showed no cholesterol precipitation within the range of X_CHOL used here. TLC measurements revealed no degradation of the bulk lipids during the equilibration.

Steady-state fluorescence and TRF measurements

Steady-state fluorescence anisotropy r measurements of DPH-PC in POPC/CHOL mixtures were performed on a GREG-PC (ISS, Champaign, IL) fluorometer using a T-mode configuration (Gratton et al., 1984). Briefly, a Liconix 4240 NB cw He-Cd UV laser (Santa Clara, CA) emitted at 325 nm was used for excitation. Two low-wavelength cutoff filters at 350 nm were used to collect the fluorescence emission. Three PMT's, two on the polarized emission sides and one on the excitation side, were used simultaneously to perform single photon counting fluorescence measurements at 23°C. Here, r is defined as (R_‖ − gR_⊥)/(R_‖ + 2gR_⊥), where R_‖ or R_⊥ are the ratios of photon counts from the parallel or perpendicular polarization emission, respectively, to the photon counts from the excitation, and g is the g-factor related with the relative sensitivity of the two emission channels and can be obtained when the excitation polarization is set to perpendicular (Gratton et al., 1984). The integration time of the detectors was 0.5 s and a total of 20 repeating measurements were accumulated and averaged to obtain r, the steady-state anisotropy. The sample was under constant stirring with a magnetic bar during the measurements.

Two independent TRF measurements, fluorescence total intensity decay I(t) and anisotropy decay r(t), were performed in the frequency domain (Lakowicz and Maliwal, 1985; Gratton et al., 1984) on an ISS GREG 200 (ISS, Champaign, IL) fluorometer equipped with digital multifrequency cross-correlation phase and modulation acquisition electronics using an L-format. Here, r(t) is defined as (I_‖(t) − I_⊥(t))/(I_‖(t) + 2I_⊥(t)), where I_‖(t) and I_⊥(t) are the fluorescence decays of the parallel and perpendicular polarized emissions, respectively, of DPH-PC upon excitation by a parallel polarized δ-pulse of light (Zannoni et al., 1983; Gratton et al., 1984). The same He-Cd laser was used for excitation. For the fluorescence intensity decay measurements, phase delay and demodulation values of the DPH-PC fluorescence signal were compared with that of a solution of (1,4-bis[2-(5-phenyloxzaolyl)]benzene standard in ethanol (assumed fluorescence lifetime, 1.35 ns) and measured at modulation frequencies ranging from 2 to 60 MHz. For the fluorescence anisotropy decay measurements, differential polarized phase shift and polarized demodulation ratio were collected at different modulation frequencies (2–76 MHz). Detailed descriptions of nanosecond-resolved fluorescence intensity and anisotropy decay measurements in the frequency domain have been described in detail elsewhere (Gratton et al., 1984; Lakowicz and Maliwal, 1985; Chen and Cheng, 1996). The sample was also under constant stirring with a magnetic bar during the time-resolved measurements. It is important to mention that the noise of the raw frequency-domain data and emission spectra of DPH-PC after more than 10 days of equilibration at 23°C were similar to those immediately or a few days after the sample preparation (results not shown). These observations suggested that no significant degradation of the fluorescent probe was evident in all our samples as a result of long-term, or more than 10 days, of equilibration.

TRF data analysis

The fluorescence intensity decay I(t) of DPH-PC was described by either a single- or double-exponential decay function using Eq. 1 as shown below:

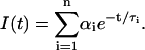(1)

In the double (n = 2) exponential fits, the long and short fluorescence decay lifetime components are indicated by τ₁ and τ₂, respectively. The molar fractions of the long and short components are defined as α₁ and α₂, respectively. The intensity-weighted averaged fluorescence lifetime 〈τ〉 can be calculated from f₁τ₁ + f₂τ₂, where f_i is the intensity fraction of the i^th component and can be expressed as α_iτ_i/(α₁τ₁ + α₂τ₂) (Gratton et al., 1984). Fluorescence intensity decay parameters, τ₁, τ₂, f₂, and 〈τ〉, were recovered from the double-exponential fits to the frequency-domain intensity decay data. These four lifetime parameters provide information about the lifetime heterogeneity and average polarity of the DPH microenvironments in lipid bilayer.

A wobbling diffusion model (van der Meer et al., 1990) was used to fit the frequency-domain anisotropy decay r(t) data. The initial anisotropy r₀, order parameter S, and rotational diffusion rate D of DPH-PC in lipid bilayers were obtained using Eq. 2:

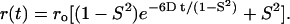(2)

In general, the initial anisotropy r_o, i.e., the anisotropy of the fluorophore at time ‘0’ after excitation, is a constant which depends on the relative orientation of the absorption and emission dipoles of the probe (Zannoni et al., 1983; Pastor et al., 1988). However, for complex rotational motions of any cylindrically symmetric probe in lipid bilayers, the recovered value of r_o may not always be a constant. Instead, the recovered value from experiment may be affected by other unresolved subnanosecond rotations, e.g., the rapid rotation around the molecular long axis of the fluorescent probe, in the lipid bilayers (Zannoni et al., 1983; Pastor et al., 1988; Cheng, 1989). Therefore, r_o may also be treated as a rotational dynamics, rather than a static parameter (Cheng, 1989). The order parameter S, which may vary from 0 to 1, describes the orientational order of the probe relative to the normal of the lipid membranes. The localized rotational diffusion constant D describes the rate of wobbling diffusion of the probe among the acyl chains of the matrix lipid. Here, we also used a rotational correlation time τ_r, defined as 1/D, as a measure of rotational mobility. With this notation, a diminished value of S or τ_r may be interpreted as an increased disorder (e.g., due to bilayer packing defect) of the local environment of DPH-PC in the host lipid bilayer.

It is important to mention that the steady-state anisotropy r is related with I(t) and r(t) according to Eq. 3 (Van der Meer et al., 1990), as given below:

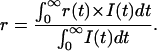(3)

Therefore, r contains both fluorescence decay and rotational dynamics information of the probe.

FTIR measurements

POPC/CHOL liposomes were prepared as for fluorescence measurements, except that the total amount of lipid was 0.8 μmol and no DPH-PC was included. After preparation and >10 days of equilibration at 23°C, the liposomes were pelleted by centrifugation at 20,000 × g for 20 min at 23°C and then applied on a single reflection horizontal attenuated total reflection sample cell (Pike Technologies, Madison, WI) at 23°C. The infrared spectra were recorded with a Magna-IR 560 FTIR spectrometer (Nicolet, Madison, WI) equipped with a deuterated triglycine sulfate detector operated at room temperature. Typically, 50 interferograms with 1 cm⁻¹ resolution were collected, averaged, Fourier-transformed, and subtracted from the background using standard procedures (Cheng, 1991) with the Omnic Software provided by Nicolet. Water and cholesterol contributions were also subtracted based on the published procedures of Kodati and Lafleur (1993). To eliminate noise, each subtracted spectrum was smoothed by a 5th degree polynomial filtering mask using the Savitzky-Golay algorithm (Savitzky and Golay, 1964). The peak positions of the smoothed spectra were subsequently determined using the peak picking routine using the same sensitivity and threshold for all lipid vibrational bands, antisymmetric O=P=O, C=O, and symmetric C-H. Fourier self-deconvolution (Parè and Lafleur, 1998) was also performed on the C=O band. The Fourier self-deconvolution, Savitzky-Golay filtering, and peak picking software were provided by Omnic (Nicolet).

Data smoothing

Several parallel sample sets, each independently prepared by LTT method, were employed both in the fluorescence (steady-state and TRF) and FTIR studies. For each such set (i), several spectroscopic raw data sets y_ij, (i.e., r, recovered fluorescence decay parameter or recovered rotational dynamics parameter), were collected, where j (=1–51) corresponds to X_CHOL varying from 0.1 to 0.6 with an increment of 0.01. The primary data set consisted of 51 data points representing averages of data from parallel sample sets. Additional smoothed data sets, one-pass and two-pass (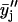) 3-point running averages, were subsequently generated. Mathematically, these one-pass and two-pass 3-point running averages are equivalent to applying data filtering masks of (1/3, 1/3, and 1/3) and (1/9, 2/9, 3/9, 2/9, and 1/9) to three and five consecutive raw data points, respectively. Overall, this multiple-pass data smoothing protocol (Whittaker and Robinson, 1967) suppresses data scatter due to random errors of spectroscopic measurements and sample preparation. A drawback of such a procedure is that it tends to suppress small, perhaps true, deviations determined by one or two data points only. Analogous data processing was also applied on the FTIR data sets. The smoothed data sets 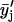and 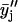were used to reduce noise and help locate any dips, peaks, or other deviations in the primary data plots, i.e., 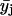versus X_CHOL. Since the relative accuracy of X_CHOL is ∼±0.003, only those deviations that were defined by two or more primary data points were usually considered. The following equations summarize the data average and smoothing protocol described above.

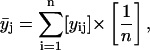(4)

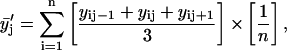(5)

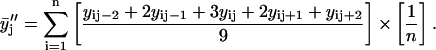(6)

Here n is the total number of parallel samples.

Statistical significance of peaks and dips

The statistical significance of the peaks and dips in the DPH-PC and FTIR parameter versus X_CHOL plots was analyzed using an un-directional t-test of unequal variances (Ferguson, 1971). The t-test allows one to assess whether the means of two different groups of measurements are statistically different from each other. In this study, the two means represented the mean of the peak or dip (y_c) at the critical X_CHOL and the mean of the adjacent or baseline value (y_b) at the nearby cholesterol content obtained from independently prepared parallel samples. The standard deviations, σ_c and σ_b, and sample sizes, n_c and n_b, for the critical and baseline values, were also obtained. From the above statistical parameters, a t-value (Ferguson, 1971), was calculated as shown in Eq. 7 below.

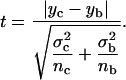(7)

The probability, or p-value, of accepting the null hypothesis of the two means being identical, i.e., y_c = y_b, was obtained from the t-distribution with degree of freedom given by n_c + n_b − 2 (Ferguson, 1971). The probability P of rejecting the null hypothesis, or probability of significance of the difference of the two means, is then defined as (1 – p) × 100%. In our case, the statistical significance of the peak or dip value as compared with two baseline values is represented by two numbers, P_L and P_R. Here P_L or P_R represents the probability that the value of a dip (or peak) is different from the adjacent starting (left) and ending (right) sides of the dip (or peak), respectively, along the composition axis based on the t-test. Raw, instead of averaged or smoothed, data sets, i.e., y_ij, from parallel samples were used in the statistical analysis. Peaks or dips with P_L or P_R < 70% were ignored. Although the 70% cutoff is arbitrary, this cutoff and the values of P_L and P_R provide a standard gauge to examine and cross-compare the critical changes of the direct and recovered parameters from the fluorescence and FTIR measurements.

RESULTS

Steady-state fluorescence anisotropy measurements

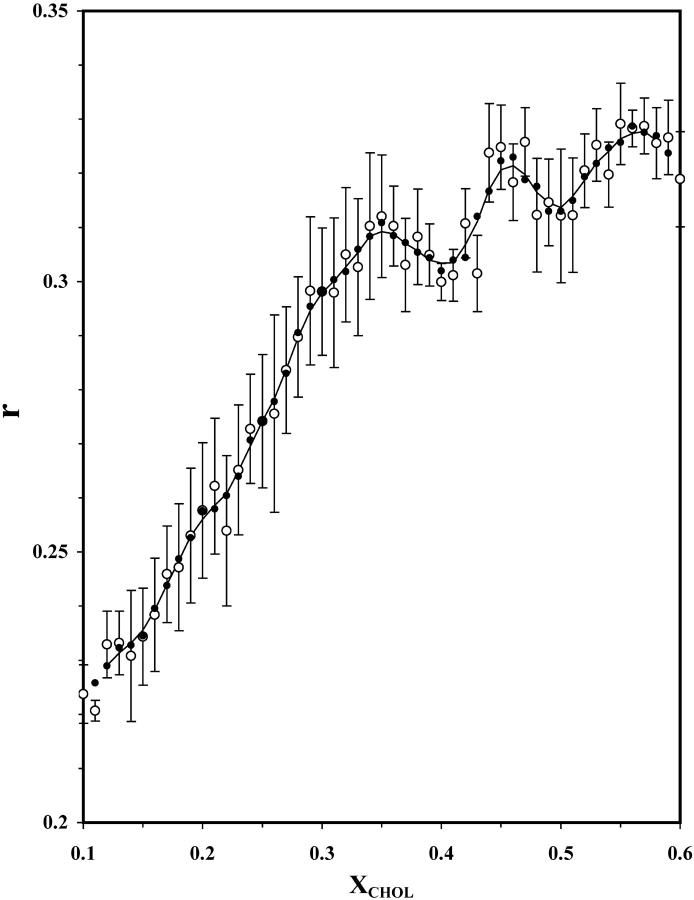
Fig. 1 shows the steady-state fluorescence anisotropy (r) of DPH-PC as a function X_CHOL. The primary data points, which are averages of four parallel samples, one-pass and two-pass running averages calculated from Eqs. 5–6 (see Materials and Methods), are shown. The value of r increased steadily with X_CHOL from 0.1 to 0.35 and then leveled off. Two major dips are clearly evident at X_CHOL ≈ 0.40 and 0.50. Both of these dips were defined by more than two primary data points and were significant as judged by their (P_L, P_R) values of (73%, 96%) and (75%, 80%), respectively (compare to Fig. 7 A). These dips were consistently observed at, and beyond, 10 days after LTT sample preparation (data not shown). Therefore, all fluorescence measurements were performed at least 10 days after preparation.

FIGURE 1.

Steady-state anisotropy of DHP-PC in POPC/CHOL bilayers versus X_CHOL. Steady-state fluorescence anisotropy of DPH-PC at 23°C as averages of four parallel samples (○). Smoothed data, one-pass (•) and two-pass (line) 3-point running averages (Eqs. 4–5 of Materials and Methods), are also shown. Each sample set was equilibrated at 23°C for at least 10 days after the preparation. Error bars represent standard errors (Ferguson, 1971) of the averages.

FIGURE 7.

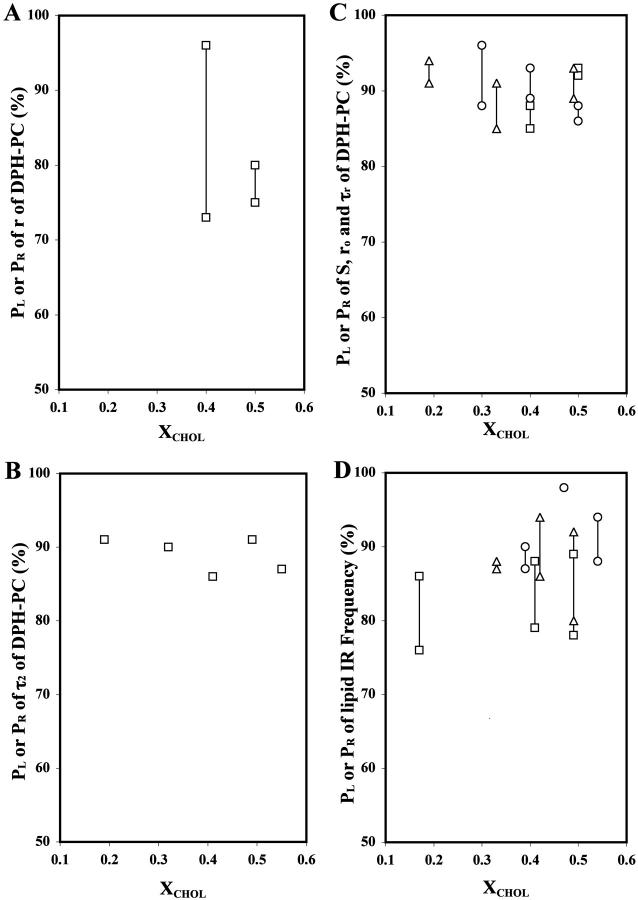
Statistical significance of the observed dips or peaks. Summary plots of probabilities of significance (P_L, P_R) of the r dips of DPH-PC (A); the τ₂ peak of DPH-PC (B); the r_o (▵), S (□), and τ_r (○) dips of DPH-PC (C); and the O=P=O (▵), C=O (□) and C-H (○) peak frequency dips of the FTIR vibrational bands (D), as a function of X_CHOL.

Time-resolved fluorescence (TRF) intensity decay measurements

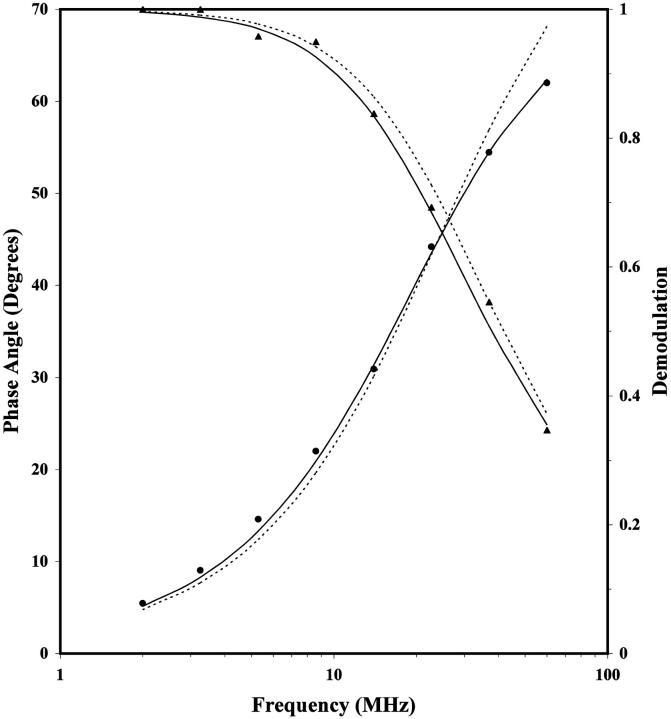
TRF intensity decay measurements of DPH-PC were performed next. Fig. 2 shows the frequency-domain data for a representative sample with X_CHOL = 0.36. Curves representing fits for a mono- and biexponential decay (Eq. 1) are also shown. A lifetime of 6.62 ns was given by the monoexponential decay model whereas the biexponential one gave the lifetimes of 7.68 and 1.23 ns. The intensity fraction φ₁ of the longer lifetime component was 0.92 and thus this lifetime represented the major fluorescence decay component of DPH-PC in the POPC/CHOL bilayers. It is clear from Fig. 2 that the biexponential model fits the data points better than the monoexponential one. This is also shown in that the reduced chi-square for the biexponential fit was almost fivefold lower than that for the 1-exponential one with this representative sample. Indeed, the biexponential model gave a better fit for all samples with X_CHOL = 0.10–0.60 (results not shown) and was thus used to analyze all the fluorescence decay data of DPH-PC in this study. A biexponential decay has previously been found for DPH-PC in other lipid bilayers (Parente and Lentz, 1985; Parasassi et al., 1991; Cheng, 1989; Sommer et al., 1992).

FIGURE 2.

Representative frequency-domain data for fluorescence intensity decay of DPH-PC in POPC/CHOL bilayers for X_CHOL = 0.36 at 23°C. The relative phase angle (•) and demodulation (▴) of the fluorescence signal of DPH-PC with respect to the excitation laser, as a function of the intensity modulation frequency of the excitation laser, are shown. This sample was equilibrated at 23°C for more than 10 days before the fluorescence measurements. The dotted and solid lines represent fits obtained from the 1-exponential and 2-exponential decay models, respectively (Eq. 1). The recovered parameters are τ = 6.624 ± 0.021 for the 1-exponential fit, and τ₂ = 1.23 ± 0.41, τ₁ = 7.68 ± 0.25 and f₁ = 0.920 ± 0.01 for the 2-exponential fit. The reduced chi-square values are 109 and 20, respectively.

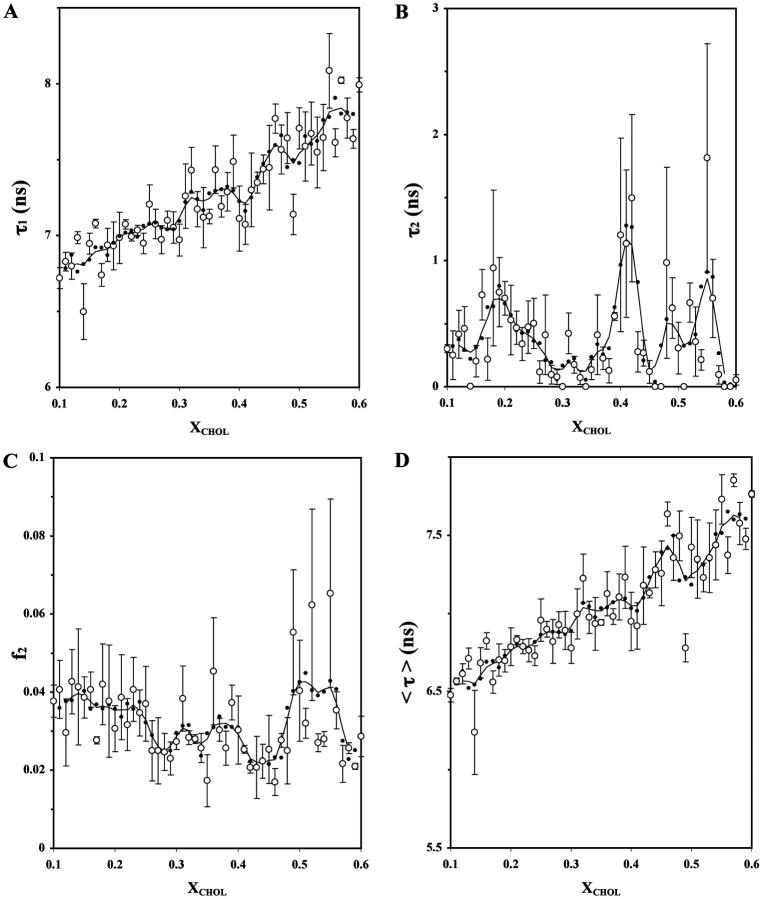
Fig. 3 shows the TRF intensity decay parameters (τ₁, τ₂, f₂, and 〈τ〉) for DPH-PC derived from biexponential fits to the frequency-domain data. Again, averaged and smoothed data are shown. The dips of τ₁, peaks of τ₂ and/or f₂ in the composition plots, usually signify changes in the extent of lifetime heterogeneity of DPH in membranes (Parente and Lentz, 1985; Cheng and Lepock, 1985; Cheng et al., 1999). As shown in Fig. 3 A, the longer lifetime component τ₁ increased with X_CHOL from ∼7 to 8 ns with two dips at X_CHOL ≈ 0.40 and 0.50, albeit the dip at X_CHOL ≈ 0.50 seems to be defined only by a single primary data point.

FIGURE 3.

Effect of X_CHOL on the fluorescence lifetime of DPH-PC in POPC/CHOL bilayers. Plots of the averages (○) of fluorescence decay parameters of DPH-PC, resolved long fluorescence lifetime τ₁ (A), resolved short fluorescence lifetime τ₂ (B), intensity fraction of the short lifetime component f₂ (C), and average fluorescence lifetime 〈τ〉 (D), in POPC/CHOL liposomes as a function of X_CHOL at 23°C from three parallel samples. See the legend of Fig. 1 for other details.

Abrupt changes may also occur at X_CHOL ≈ 0.30–0.37. The shorter lifetime τ₂ was much more strongly dependent on X_CHOL, i.e., varied from 0 to 2 ns. Prominent peaks occurred at X_CHOL ≈ 0.20, 0.33, 0.41, 0.50, and 0.55. Except the small peak at X_CHOL ≈ 0.33, all τ₂ peaks were defined by three or more primary data points. For f₂, a small peak at X_CHOL ≈ 0.30 and two broad peaks at X_CHOL ≈ 0.37 and 0.51 were found (Fig. 3 C). The intensity-weighted average fluorescence lifetime 〈τ〉 exhibited similar dips at X_CHOL ≈ 0.30–0.37, 0.41, and 0.49 as found in τ₁ (Fig. 3 D). However, the dip at X_CHOL ≈ 0.49 was defined by more than one primary data points. The peaks of τ₂ at X_CHOL ≈ 0.19, 0.32, 0.41, 0.49, and 0.55 were significant, since the values of (P_L, P_R) were determined to be (91%, 91%), (90%, 90%), (86%, 86%), (91%, 91%), and (87%, 87%), respectively, as shown in Fig. 7 B.

TRF anisotropy decay measurements

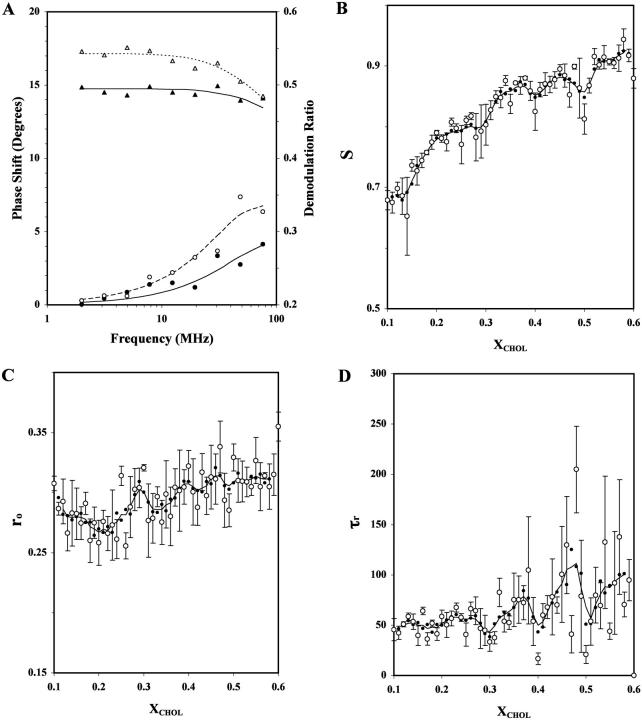
Based on the wobbling diffusion model (Eq. 2), three independent rotational dynamics parameters, i.e., the order parameter S, the initial anisotropy r_o, and the rotational correlation time τ_r (equivalent to the inverse of D, the wobbling diffusion constant; see Materials and Methods) of DPH-PC were recovered from the frequency-domain anisotropy decay data. Fig. 4 A shows the representative frequency domain data and the model fitting for X_CHOL = 0.18 and 0.36. The recovered parameters and chi-squares of the representative fits are also shown in the legend of Fig. 4 A.

FIGURE 4.

Fluorescence anisotropy decay parameters for DPH-PC versus X_CHOL in POPC/CHOL bilayers. (A) The representative frequency-domain data of fluorescence anisotropy decay of DPH-PC for X_CHOL = 0.18 (open symbols) and 0.36 (solid symbols). Plots of the relative phase shift (○,•) and demodulation ratio (▵,▴) of the fluorescence signal from the parallel and perpendicular emission channels as a function of intensity modulation frequency of the excitation laser are shown. Using the wobbling diffusion model (Eq. 2), the recovered rotational dynamics parameters (r_o, S, and D) are (0.307 ± 0.003, 0.761 ± 0.013, and 2.3 ± 0.12 × 10⁷ s⁻¹) and (0.308 ± 0.011, 0.876 ± 0.027, and 1.9 ± 0.48 × 10⁷ s⁻¹) for X_CHOL = 0.18 and 0.36, respectively. The reduced chi-square values are 29 and 32, respectively. (B–D): Plots of the average recovered rotational dynamics parameters (○), order parameter S (B), initial anisotropy r_o (C), and rotational correlation time τ_r (D), of DPH-PC in POPC/CHOL as a function of X_CHOL at 23°C from three parallel samples. These parameters were recovered from the wobbling diffusion model fits (Eq. 2) of the frequency domain anisotropy decay data. See the legend of Fig. 1 for other details.

For S, obvious dips at X_CHOL ≈ 0.4 and 0.5 and a small dip or kink at X_CHOL ≈ 0.3 are identified (Fig. 4 B). The values of (P_L, P_R) of the dips at X_CHOL ≈ 0.30, 0.4, and 0.5 were (65%, 87%), (85%, 88%), and (92%, 93%). The dip at X_CHOL ≈ 0.30 may not be significant since the P_L is <70% (see Materials and Methods). For r_o, broad dips at X_CHOL ≈ 0.20 and 0.33 and a small dip at X_CHOL ≈ 0.49 were observed (Fig. 4 C). The values of (P_L, P_R) of the above three dips were (91%, 94%), (91%, 85%), and (89%, 93%), respectively. For τ_r, prominent dips were observed at X_CHOL ≈ 0.30, 0.40, and 0.50 (Fig. 4 D). These dips at X_CHOL ≈ 0.30, 0.40, and 0.50 were found to be significant, inasmuch as the values of (P_L, P_R) were determined to be (96%, 88%), (93%, 89%), and (88%, 86%), respectively. All the above S, r_o, and τ_r dips were defined by two or more primary data points. For comparison, the values of (P_L, P_R) for S, r_o, and τ_r are co-plotted in Fig. 7 C.

FTIR measurements

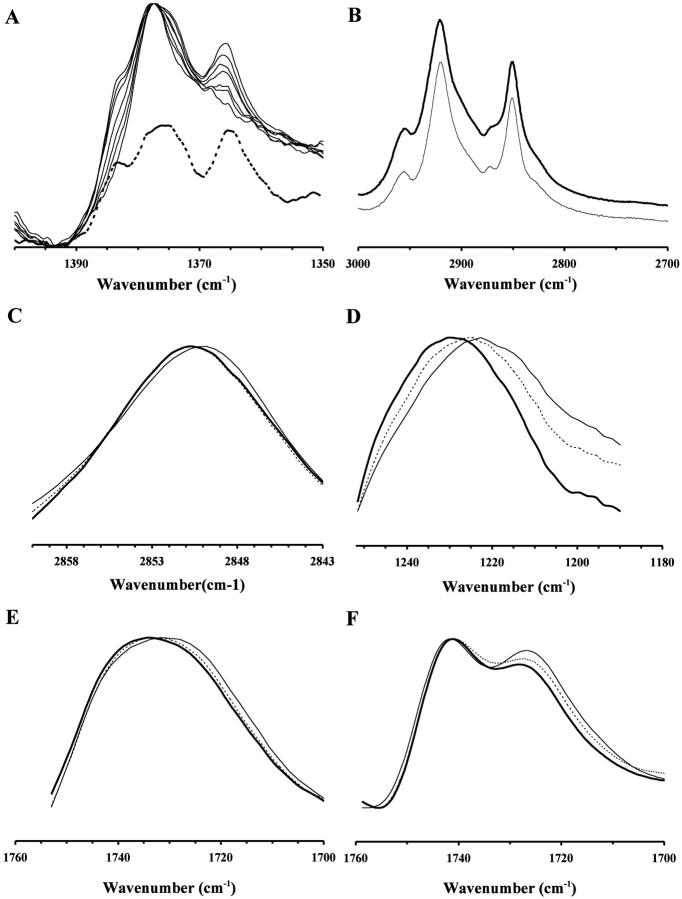
Complementary FTIR measurements on POPC/CHOL liposomes (without DPH-PC) were also preformed. Although cholesterol does not absorb in the spectral regions where the C=O and antisymmetric O=P=O vibrational bands of POPC appear, the C-H bands of cholesterol overlap with the lipid acyl-chain symmetric and antisymmetric C-H bands at ≈ 2850 and 2925 cm⁻¹ (Kodati and Lafleur, 1993). However, the presence of a cholesterol-specific absorption peak at ∼1365 cm⁻¹ allows one to correct for the contribution cholesterol to the C-H bands of POPC (Kodati and Lafleur, 1993). As shown in Fig. 5 A, a progressive increase in the relative intensity of this 1365 cm⁻¹ peak with cholesterol content (X_CHOL = 0 – 0.60) is clearly demonstrated. Fig. 5 B shows a representative raw (upper curve) and cholesterol-subtracted (lower curve) spectra for X_CHOL = 0. Fig. 5, C–E, demonstrate the effect of cholesterol on the peak positions of C-H, O=P=O, and C=O bands, respectively, for X_CHOL = 0.35, 0.40, and 0.45. The peak position for X_CHOL = 0.40 was significantly lower than that for X_CHOL = 0.35 or 0.45 for all three vibrational bands. For the C=O vibration band, Fourier self-deconvolution resolved two peaks at 1742 and 1726 cm¹, thus indicating the presence of two populations of carbonyl groups (Paré and Lafleur, 1998). Fig. 5 F shows representative deconvoluted spectra for X_CHOL = 0.35, 0.40, and 0.45. The peak positions of the resolved peaks appeared to be independent of the cholesterol content.

FIGURE 5.

FTIR spectra for POPC/CHOL bilayers at selected X_CHOL. (A) Normalized plots of the CH₂ wagging region of POPC/CHOL with X_CHOL = 0, 0.1, 0.2, 0.3, 0.4, 0.5, and 0.6 matched at the common peak at 1377 cm⁻¹. The absorption peak at 1366 cm⁻¹ peak and the shoulder at 1383 cm⁻¹ increase progressively with cholesterol concentration. The absorption of pure cholesterol in benzene in the same region is shown as the dotted line below the stacked plots of POPC/CHOL mixtures. By direct comparison, the above peak and shoulder at 1377 and 1366 cm⁻¹ are attributed to the cholesterol absorption only. The measurements were carried out at 23°C. (B) Representative C-H stretching region of POPC/CHOL with X_CHOL = 0.40 is shown as the dark line. The corresponding cholesterol-subtracted spectrum is shown as the thin line (see Materials and Methods). (C–E) Representative C-H, O=P=O, and C=O spectra of POPC/CHOL with X_CHOL = 0.35 (dotted line), 0.40 (thin line), and 0.45 (dark line). (F) Representative deconvoluted C=O vibrational spectra of POPC/CHOL with X_CHOL = 0.35 (dotted line), 0.40 (thin line), and 0.45 (dark line). The peaks of the resolved peaks are located at 1741 and 1726 cm⁻¹. The bandwidth and enhancement factors were set at 20 cm⁻¹ and 2.0, respectively, for all the samples.

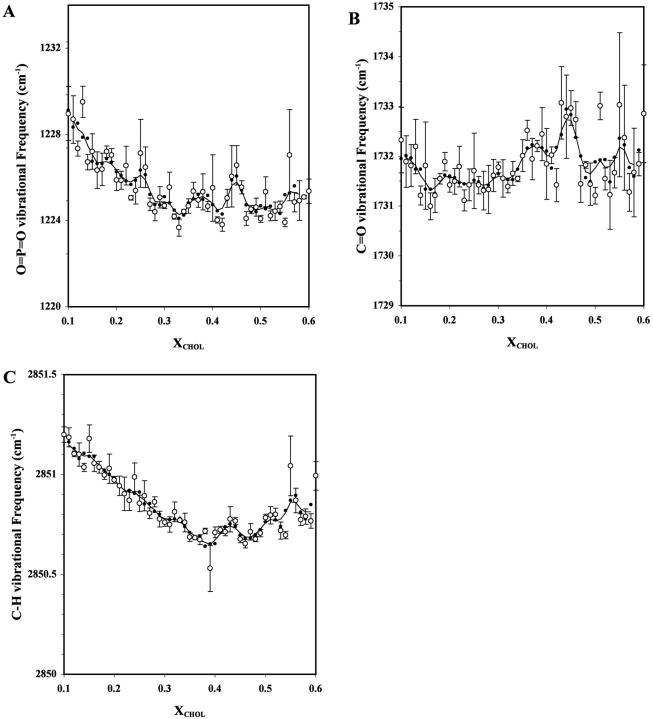
Fig. 6 shows the peak positions of the antisymmetric O=P=O (Fig. 6 A), C=O (Fig. 6 B), and symmetric C-H (Fig. 6 C) vibrational bands of POPC as a function of X_CHOL. Major dips, i.e., those defined by two or more data points, can be seen at X_CHOL ≈ 0.33, 0.42, and 0.49 for O=P=O; 0.17, 0.41, and 0.49 for C=O; and 0.39, 0.47, and 0.54 for C-H. The values of (P_L, P_R) were (88%, 87%), (86%, 94%), and (92%, 80%), respectively, for the dips of O=P=O; (76%, 86%), (88%, 79%), and (89%, 78%), respectively, for the dips of C=O; and (90%, 87%), (98%, 98%), and (94%, 88%) for the dips of C-H, respectively.

FIGURE 6.

Peak of vibrational frequency band of O=P=O (A), C=O (B), and C-H (C) of POPC in POPC/CHOL bilayers as a function of X_CHOL. The measurements were carried out at 23°C and the primary data points are averages of three parallel samples. See the legend of Fig. 1 for other details.

DISCUSSION

Previous fluorescence investigations of cholesterol SL were primarily focused on steady-state fluorescence properties of dipyrenyl lipid, free DPH, dehydroergosterol (DHE; a cholesterol analog), and other probes mainly in saturated PC/CHOL mixtures (see reviews by Somerharju et al., 1999 and Chong and Sugar, 2002). No TRF measurements covering an extensive range of X_CHOL had been reported on a PC-like probe, such as DPH-PC, in unsaturated PC/CHOL bilayers. Abrupt and statistically significant changes in the recovered physical properties (lifetime, lifetime heterogeneity, and rotational dynamics) of DPH-PC were found to occur at most critical compositions predicted by the SL-model (Virtanen et al., 1998; Chong and Sugar, 2002). Complementary FTIR measurements provide additional and probe-free information about the ordering of the acyl chain and conformation/hydration of the interfacial and headgroup regions of PC in the same liposomal membranes. Table 1 provides a direct comparison of the critical X_CHOL's from TRF and FTIR measurements with the theoretical X_CHOL's predicted by the SL-model (Virtanen et al., 1998; Chong and Sugar, 2002).

TABLE 1.

Comparison of critical mole fractions X_CHOL's from TRF and FTIR spectroscopic measurements with X_HX or X_R values predicted by superlattice model

XHX or XR	r	τ2	S	ro	τr	O=P=O	C=O	C-H
0.10H,R
0.118H,R
0.125R
0.143H
0.154H,R							0.17
0.20H,R		0.19		0.20
0.22R
0.25H
0.333R		0.32		0.33	0.30	0.33
0.40H,R	0.40	0.41	0.40		0.40	0.42	0.41	0.39
0.50H,R	0.50	0.49	0.50	0.49	0.50	0.49	0.49	0.47
		0.55*						0.54*

The critical cholesterol mole fractions X_HX and X_R correspond to superlattice arrangements with hexagonal and centered rectangular symmetries, respectively, from the superlattice model (Virtanen et al., 1995; Chong and Sugar, 2002). They are also denoted by superscripts H and R, accordingly, in the first column.

^*Critical mole fractions that do not agree (±0.03) with X_HX or X_R values.

Another unique feature of this study is that compositionally homogeneous and fully equilibrated liposomes prepared by LTT were employed for the first time in studies on the putative cholesterol superlattices. The LTT method produces compositionally homogenous PC/cholesterol bilayers, whereas the use of the traditional dry film method can lead to lipid demixing, especially at high cholesterol contents (Huang et al., 1999; Huang and Feigenson, 1999). A comparison of TRF data obtained for liposomes prepared by the dry film method revealed that the data scatter was significantly higher than when the LTT method was used (results not shown). Nevertheless, the critical X_CHOL's observed in the present study agree favorably with those observed previously using the dry film method (Chong and Sugar, 2002, Wang et al., 2002), perhaps because an extensive temperature recycling-incubation protocol was employed in the latter case (Chong and Sugar, 2002).

Abrupt changes in physical properties of DPH-PC occur at many critical cholesterol concentrations predicted by the SL model

The recovered physical parameters of DPH-PC, extra short-component fluorescence lifetime τ₂, and rotational dynamics (S, r_o, τ_r), revealed significant peaks and dips, respectively, at X_CHOL ≈ 0.20, 0.30–0.33, 0.40, and 0.50. Only τ₂ exhibited a significant peak at X_CHOL ≈ 0.55. These peaks and dips, which were defined by two or more primary data points, are statistically significant based on the t-test analysis (Materials and Methods) and are summarized in Fig. 7, B and C, respectively. All of the above critical cholesterol contents, except the one at ≈ 0.55, agree favorably (within ±0.03) with the SL compositions of 0.20, 0.33, 0.40, and 0.50 predicted by the SL model (Virtanen et al., 1995; Somerharju et al., 1999; Chong and Sugar, 2002). In agreement with previous fluorescence studies on cholesterol SL using different probes (Tang et al., 1995; Chong et al., 1996; Chong and Sugar, 2002; Wang et al., 2002), these TRF results provide strong support for the proposition that cholesterol may adopt regular, superlattice-like distributions in fluid lipid bilayers. Since POPC, rather than a fully saturated PC was used here, the present data might be relevant for natural membranes as well.

Response of DPH fluorescence to the critical compositions

As shown in Fig. 3, the intensity decay of DPH-PC has two components, i.e., τ₁ (6–8 ns) and τ₂ (0–2 ns). The physical origin of these two components is not clear but could relate to 1), the presence of DPH-PC in two different environments in the bilayer or 2), to the presence of different excited state species in a single environment. A biexponential decay has been frequently found for DPH in solvents and in homogenous or binary lipid bilayers (Parente and Lentz, 1985, 1986; Cheng, 1989; Parasassi et al., 1991; Sommer et al, 1992). A detailed study on the photophysics of free DPH revealed that a minor short-component is mainly attributable to interconversion between two different excited states (Parasassi et al., 1991). Degradation of the probe can also lead to lifetime heterogeneity, but is unlikely to explain the presence of two decay components in this study, since it is difficult to see how such putative degradation could vary so strongly with X_CHOL as shown in Fig. 3.

We think that changes in membrane domain organization are mainly responsible for the strong variation of τ₂ and f₂ with X_CHOL. This proposition is supported by that these parameters change abruptly at or close to the critical X_CHOL predicted by the SL model and that the fact that the fluorescence properties of DPH are sensitive to the physical state of a lipid bilayer (Parasassi et al., 1991). The superlattices domains are thought to be more ordered/tightly packed than the randomly organized domains and thus, X_CHOL-driven variation in the relative abundance of these two types of domains is likely to cause variation in τ and f₂. DPH lifetime parameters have been shown to be sensitive to the environmental polarity (Sommer et al., 1992; Mathai et al., 2001) as well as the local concentration of the probe (Parente and Lentz, 1986). Dips in the major long-lifetime component τ₁ and peaks in the minor short-lifetime component τ₂ could be due to probe's enrichment to defect regions and a higher environmental polarity due to the enhanced water permeation in such defect regions (Parasassi et al., 1991; Sommer et al., 1992). This explanation is supported by a previous fluorescence lifetime study (Parente and Lentz, 1986) that demonstrated a sharp decline in fluorescence lifetime of DPH when the probe-to-lipid ratio was >1/200 in PC bilayers (in the present study the probe-to-lipid ratio was 1/1000). The smaller fractional area of the defect regions as compared to the SL domains would effectively increase the local concentration of the probe. Notably, recent Monte Carlo simulations support the existence of defect regions when the composition is near an SL composition (Huang, 2002).

The recent work of Wang et al. (2002) suggests that van der Waals contacts between the steroid ring and the C2–C8 segment of the PC acyl chains is important for cholesterol SL formation. The DPH moiety of DPH-PC has two planar phenyl rings connected by a rigid hexatriene chain and extends from carbon 4 to carbon 16 of phospholipid acyl chains (Cranney et al., 1983). Thus the molecular shape and size of the DPH moiety are quite different from that of cholesterol or the phospholipid acyl chains. Accordingly, it is likely that DPH-PC cannot readily substitute either for cholesterol or PC in the superlattice, and would thus partition preferentially to the defect regions co-existing with the SL domains.

Our TRF study also provides information on the rotational dynamics of the acyl chains in POPC/CHOL lipid bilayers. Note that S and τ_r are independent rotational dynamics parameters associated with the orientational order of the cylindrical DPH probe with respect to the normal of the bilayer and the inverse of the wobbling rotational rate of DPH, respectively (Van de Meer et al., 1990). The significant decrease in both the order parameter S and the rotational correlation time τ_r at X_CHOL ≈ 0.40 and 0.50 was clearly found (Fig. 4). This observation strongly suggests that the DPH moiety of DPH-PC senses a relatively disordered and rotationally mobile region at those critical X_CHOL's. The partitioning of DPH-PC to the co-existing defect regions would explain this finding.

Steady-state anisotropy r of a cylindrical fluorophore, like DPH-PC, in lipid bilayer is inversely related with the fluorescence lifetime but directly related with S and τ_r (Zannoni et al., 1983; Gratton et al., 1984). In this study, the general increase of r with X_CHOL and the dips at X_CHOL ≈ 0.4 and 0.5 (Fig. 1) agree favorably with the same trend of 〈τ〉 (Fig. 3 D) and S (Fig. 4 B) as a function X_CHOL. Therefore, the r parameter of DPH-PC reflects mainly the orientational order, but not the lifetime of DPH-PC in the POPC/CHOL liposomes.

FTIR measurements

Since FTIR monitors the native vibrational behavior of the intrinsic bilayer components, the data are free of possible probe-induced perturbations. The present FTIR measurements on the POPC/CHOL bilayers revealed deviations at X_CHOL ≈ 0.17, 0.33, 0.40, and 0.50, i.e., at concentrations that are identical or close to those given by the TRF data. Our previous FTIR measurements on POPE/POPC mixtures (Cheng et al., 1997) also revealed dips of locations of C=O and O=P=O vibrational frequency peaks at several critical PE mole fractions predicted by the lipid headgroup SL model (Virtanen et al., 1998). The dips in C-H vibrational peak frequency plot suggest a significant reduction in the gauche rotamers, i.e., straightening of the POPC acyl chains at X_CHOL ≈ 0.40 and 0.50. The dips in the O=P=O and C=O peak frequency plots at similar cholesterol compositions suggest subtle changes in the hydration and/or conformation of the lipid phosphate headgroup and interfacial carbonyl regions of the POPC at the critical X_CHOL's. Additional dips were indicated at X_CHOL ≈ 0.33 and 0.17 for O=P=O and C=O vibration, respectively, in line with the fluorescence data indicating subtle SL-related structural changes of the PL headgroup and interfacial regions also at lower cholesterol concentration.

Deconvolution of the asymmetric C=O vibrational band revealed two peaks at 1742 and 1726 cm⁻¹ (Fig. 5) indicating two populations of carbonyl groups (Paré and Lafleur, 1998). The relative peak height of the low frequency carbonyl at X_CHOL = 0.40 is higher than that at 0.35 or 0.45. Probably, the high frequency peak derives from a population of free carbonyl groups, whereas the low frequency peak derives from a population of carbonyl groups hydrogen-bonded to water (Kodati and Lafleur, 1993). In this respect, a dip in the un-deconvoluted C=O peak frequency versus X_CHOL plot (Fig. 6 B) indicates that the hydration of the carbonyl groups of POPC increases at the critical X_CHOL's. This is because, at the predicted critical X_CHOL, the un-deconvoluted C=O band is weighted more by the low frequency deconvoluted peak. This would shift the peak of the C=O band to a lower frequency or give rise to a dip in the spectrum. Since dips in the locations of the vibrational peaks of O=P=O band were also observed, increased hydration of the lipid phosphate group at the SL compositions is indicated. However, an increase in the conformational disorder of the carbonyl and phosphate groups could also give rise to the dips in the C=O and O=P=O frequency versus X_CHOL plots independent of changes in hydration. It is not possible to separate the conformational and hydration effects based on the present data alone. Earlier studies have suggested that both the hydration of PC headgroup and the PC headgroup-headgroup distance increase in the presence of cholesterol (Kusumi et al., 1986; Ho et al., 1995; Pasenkiewicz-Gierula et al., 2000).

Why are deviations not observed at all predicted SL compositions?

In this study, obvious deviations were not observed at all the predicted SL compositions as shown in Table 1. Several things could explain this. First, significant changes in bilayer properties may not occur at each and every composition predicted by the superlattice model; for instance, because all SL distributions may not be stable enough to occur to a degree to be observed. Second, even if significant changes occur, these may not influence the fluorescence lifetime and/or the rotational dynamics behavior of DPH-PC, as well as FTIR vibrational frequency, adequately. Third, the TRF and FTIR data are relatively noisy, which could hide modest changes of lateral organizations in lipid bilayers. Fourth, the smoothing procedures used could sometimes shift the actual local minima or maxima along the composition axis, especially for those asymmetric peaks or dips. Another issue is that, in some plots, a peak is observed at some predicted critical X_CHOL whereas a dip or kink is observed at another critical X_CHOL (e.g., Figs. 3 B and 4 B). One possible explanation for this could be that when the critical compositions are closely spaced (which is the case below X_CHOL = 0.33), the composition driven order-disorder transitions start to overlap along the X_CHOL axis to an increasing degree. This could certainly abolish dips or peaks where they are predicted to occur. The fact that the predicted SL domains vary in terms of lattice symmetry, hexagonal, or centered rectangular (Virtanen et al., 1995; Chong and Sugar, 2002), could further complicate the picture.

The critical change at X_CHOL ≈ 0.55 was observed only by fluorescence lifetime parameter of DPH-PC (Fig. 3 B) and C-H vibration peak (Fig. 6 C). This critical X_CHOL does not fit in any of the predicted critical cholesterol compositions as predicted by the current SL model (Somerharju et al., 1999; Chong and Sugar, 2002). However, recent computer simulations (Huang and Feigenson, 1999) and other independent fluorescence measurements (Huang et al., unpublished results) using different fluorescent probes appear to support the existence of a change in lipid packing or domain formation at X_CHOL ≈ 0.57. More work is required to explore this critical X_CHOL.

Forces driving SL distribution of cholesterol in PC bilayers

The forces driving cholesterol toward the superlattice distribution in PC bilayers have not been determined experimentally, but it is likely the following factors play crucial important role. First, the surface area occupied by the strongly hydrated phosphocholine headgroup of PC is larger than the cross-sectional area of the acyl chains (compare to Somerharju et al., 1999). This imbalance leads both to crowding of the headgroup level and looser packing of the acyl chains as compared to lipids with similar headgroup and acyl chains cross-sectional areas (e.g., monounsaturated PEs). However, when adequate amounts of a lipid with a relatively small headgroup (e.g., cholesterol, diglyceride, or PE) is mixed with PC, the crowding is diminished or abolished and the packing (order) of the acyl chains increases (compare to Somerharju et al., 1999). In case of cholesterol, the rigid ring system of this lipids probably also contributes to this increased ordering of the acyl chains. Second, it is very likely that cholesterol also seeks to interact with PC since its headgroup (a single hydroxyl) is far too small to fully shield its hydrocarbon part from unfavorable contacts with water. This “umbrella” model is supported both by physical measurements as well as Monte Carlo simulations (Huang and Feigenson, 1999; Huang, 2002). The spacer and umbrella effects are obviously maximal when the components are evenly (rather than randomly) distributed, which would make regular lateral distributions of cholesterol energetically more favorable than random ones (Somerharju et al., 1999).

Previous work on cholesterol SLs was mainly focused on saturated PC-cholesterol bilayers (see reviews by Somerharju et al., 1999 and Chong and Sugar, 2002). POPC used here has an unsaturated hydrocarbon chain (oleoyl, 18:1c9) at its sn-2 position. As shown in Table 1, the critical compositions observed in this study seem to agree with the theoretical compositions predicted by the cholesterol superlattice model (Virtanen et al., 1995; Chong and Sugar, 2002), thus indicating that SLs can form also in lipid bilayers consisting of unsaturated PC species abundant in mammalian cell membranes. The recent work of Wang et al. (2002) demonstrated that cholesterol SLs cannot be detected if the cis double bond in an acyl chain of PC is located at the same level of the cholesterol steroid ring, i.e., between C8 and the carboxyl carbon, suggesting the importance of van der Waals interactions between the steroid ring and the C2–C8 segment of the acyl chains. This appears to agree with our observation of SL formation in POPC/CHOL system in which the oleoyl chain of POPC is at the c9 position. The molecular details of interactions of cholesterol between saturated or unsaturated acyl chains in bilayers, especially their role in SL formation, remain unclear. A preferential association of cholesterol with the saturated chains rather than unsaturated chains in mixed-chain lipid bilayers was demonstrated recently (Mitchell and Litman, 1998; Niu and Litman, 2002). Apparently, more work is needed to fully understand the effects of chain unsaturation on cholesterol SL formation.

The defect regions surrounding the putative SL domains could play an important role in modulating the activity of various membrane-associated enzymes, e.g., those regulating the lipid compositions of cell membranes. A model for superlattice-dependent regulation of enzymes responsible for synthesis of membrane lipids has been proposed (Somerharju et al., 1999). It is speculated that below a critical SL composition a major fraction of the bilayer is covered by more or less randomly organized lipids, allowing the enzymes to remain dispersed in the disordered domains and to be fully active. When a SL composition is approached, as a result of synthesis of one or more compositions, the presence of SL domains leads to segregation of those lipid synthesis enzymes to the co-existing defect regions and consequent aggregation and reversible inhibition or inactivation. The superlattice-dependent modulation of other lipid composition-regulating enzyme, e.g., phospholipase A2, has also been proposed (Liu and Chong, 1999). The details of the intriguing modulating mechanism of those lipid composition-regulating enzymes by the defect regions remain to be explored.