Abstract
Residual dipolar couplings (RDCs) and pseudocontact shifts are experimentally accessible properties in nuclear magnetic resonance that are related to structural parameters and to the magnetic susceptibility anisotropy. We have determined RDCs due to field-induced orientation of oxidized-K79A and reduced cytochrome c at pH 7.0 and oxidized-K79A cytochrome c at pH 11.1 through measurements of amide 15N-1H 1J couplings at 800 and 500 MHz. The pH 7.0 RDCs for Fe(III)- and Fe(II)-cytochrome c together with available nuclear Overhauser effects were used to recalculate solution structures that were consistent with both sets of constraints. Molecular magnetic susceptibility anisotropy values were calculated for both redox states of the protein. By subtracting the residual dipolar couplings (RDCs) of the reduced form from those of the oxidized form measured at the same magnetic field (800 MHz), we found the RDC contribution of the paramagnetic metal ion in the oxidized protein. The magnetic susceptibility anisotropy, which was calculated from the structure, was found to be the same as that of the paramagnetic metal ion obtained independently from pseudocontact shifts, thereby indicating that the elements of secondary structure either are rigid or display the same mobility in both oxidation states. The residual dipolar coupling values of the alkaline-K79A form are small with respect to those of oxidized native cytochrome, whereas the pseudocontact shifts are essentially of the same magnitude, indicating local mobility. Importantly, this is the first time that mobility has been found through comparison of RDCs with pseudocontact shifts.
INTRODUCTION
Molecules with molecular magnetic anisotropy (χmol) tend to adopt preferred orientations in an external magnetic field (Lohman and Maclean, 1978; Domaille, 1980; Bothner-By et al., 1981, 1984, 1985). Partial alignments give rise to effects that are detectable through nuclear magnetic resonance (NMR) spectroscopy (Van Zijl et al., 1984; Bothner-By, 1996). Among these, the noncompletely averaged dipolar couplings or RDCs (Tolman et al., 1995; Tjandra and Bax, 1997) represent a source of structural information (Tjandra et al., 1997; Clore et al., 1998; Meiler et al., 2000; Sass et al., 2000). More recently, RDCs in different orienting media have provided information on dynamical properties (Meiler et al., 2001; Bax and Tjandra, 1997; Tolman et al., 1997).
Heme proteins possess molecular magnetic anisotropy (Tolman et al., 1997; Banci et al., 1998; Arnesano et al., 2000). In the iron(II) diamagnetic form, magnetic anisotropy arises from the heme, aromatic moieties, and elements of secondary structure (Banci et al., 1998; Arnesano et al., 2000). In an iron(III) S = ½ heme, the molecular magnetic anisotropy arises from the diamagnetic contributions (χdia) and the dominant paramagnetic contribution of the iron(III) ion (χpara) (Banci et al., 1998; Arnesano et al., 2000). The latter contribution can be evaluated independently through analysis of the 1H pseudocontact shifts (PCs) (Williams et al., 1985; Emerson and La Mar, 1990; Banci et al., 1995, 1996; 1997a,b; Arnesano et al., 1998, 1999; Bentrop et al., 1997). In diamagnetic heme proteins, the magnetic anisotropy is small and RDCs are barely large enough to be used as structural constraints. In paramagnetic low-spin heme proteins, the RDCs are in the range −1.5 to 1.5 Hz (Tolman et al., 1997; Banci et al., 1998; Arnesano et al., 2000; Bertini et al., 2001a,b).
Mitochondrial cytochrome c is a heme protein containing diamagnetic iron(II) in its reduced form, and a paramagnetic S = ½ iron(III) in its oxidized form. In both redox states the iron ion is axially coordinated by His and Met side chains (Berghuis and Brayer, 1992; Dickerson et al., 1971; Moore and Pettigrew, 1990; Baistrocchi et al., 1996; Banci et al., 1997a,b; Scott and Mauk, 1996). The Fe-Met bond is relatively labile in oxidized cytochrome c, and at high pH the native methionine ligand is replaced either by Lys73 or Lys79, giving the so-called alkaline form of the protein (Wilson and Greenwood, 1996; Assfalg et al., 2003). We report here RDCs for both the oxidized and reduced states of cytochrome c (cyt c) at pH 7.0. These RDCs have been included in solution structure calculations together with other available constraints (Baistrocchi et al., 1996; Banci et al., 1997a,b). For the non-native form of the oxidized protein at pH 11.1, both RDCs and PCs have been estimated. From this analysis, an extensive mobility is revealed at high pH.
MATERIALS AND METHODS
Sample preparation
NMR measurements on reduced cytochrome c were made on the yeast protein expressed in Escherichia coli (Barker et al., 2001); the protein contains, at the N-terminus, a tag of three residues—A, D, and L. K79A cyt c from Saccharomyces cerevisiae was expressed and purified as previously reported (Assfalg et al., 2003). This sample was used to measure the RDCs for ferricytochrome c at pH 7.0 and for the alkaline form. The use of different mutants for measurements on the reduced and oxidized proteins at pH 7.0 is justified by the essential identity of the NMR spectra of these cyt c variants, as demonstrated previously (Assfalg et al., 2003; Barker et al., 2001). The NMR samples were prepared by dissolving the protein in 50 mM phosphate buffer at pH 7.0 to give solutions ∼2 mM in protein. For the alkaline form, the pH was increased by addition of NaOH to give pH 11.1.
NMR spectroscopy
All NMR experiments were acquired at 298 K on Avance500 and Avance800 spectrometers (Bruker, Karlsruhe, Germany).
Twenty 1JNH-modulated 2D 1H-15N heteronuclear single quantum coherence (HSQC) spectra were recorded at 500 and 800 MHz for Fe(II)-, Fe(III)-, and alkaline Fe(III)-cyt c. Dephasing delays, 2Δ, were 43.6, 45.0, 46.4, 47.8, 49.2, 50.6, 52.0, 52.6, 53.4, 54.8, 55.4, 56.2, 56.8, 57.6, 59.0, 60.4, 61.8, 63.2, and 64.6 ms. These delays included the durations of the pulsed field gradients, G4, but not the duration of the 15N 180° pulse. The intensities of cross peaks are given by Eq. 1 (Tjandra et al., 1996):
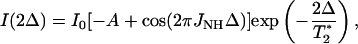 |
(1) |
where I0 is the intensity of the cross peak when Δ is null, A is a term which accounts for the unmodulated fraction of magnetization due to pulse imperfection, and 1/T2* is the effective decay rate of the transverse 15N magnetization. As previously suggested (Tjandra et al., 1996), 2Δ values should be chosen as two sets of symmetric values ∼(2n+1)/2J, where n is an integer, to take into account effects of 180° 15N pulse imperfections and to optimize the accuracy of the measurement of J. The best value of n, which depends on the value of T2*, was chosen after measuring T2* of some cross peaks from the 1JNH-modulated HSQC spectra acquired with Δ delays of 5.4, 10.8, and 21.6 ms. These delays correspond to 1/2J, 1/J, and 2/J, and yield almost completely refocused intensity for all NH moieties. Therefore, for these Δ delays the HSQC cross-peak intensities are only dependent on the transverse relaxation of 15N spins. An average T2* value of ∼40 ms was found; n was thus set as 4 and 5. Each experiment was performed with 16 scans.
{1H}-15N nuclear Overhauser effect (NOE) experiments were performed both at 400 MHz and 700 MHz. The pulse sequence is the one previously described (Grzesiek and Bax, 1993; Palmer III et al., 1992; Barbato et al., 1992; Kay et al., 1992; Grzesiek and Bax, 1993; Peng and Wagner, 1992), which includes sensitivity enhancement and water suppression with the flip-back method. {1H}-15N NOE saturated and unsaturated spectra were acquired in an interleaved fashion, with 40 scans for the 700 MHz measurements and 128 scans for the 400 MHz experiments. Phase sensitivity was achieved using Echo/Antiecho-TPPI gradient selection. A recycle delay of 3.1 s was used. 2048 complex data points with 512 complex increments were collected.
Data processing and integration of cross peaks was performed on a Silicon Graphics workstation using standard Bruker (Karlsruhe, Germany) software. Rectangular boxes at the noise level were used to define the integration region, except for overlapping cross peaks, for which smaller boxes were chosen to minimize the contribution from the unwanted peak. The obtained values were fitted to Eq. 1 with a Levenburg-Marquardt algorithm to obtain 1JHN values. Experimental errors were estimated by Monte Carlo methods.
Solution structure calculations with RDC constraints
The solution structure calculations were performed with the PARAMAGNETIC-DYANA program (Barbieri et al., 2002; information on program available at www.postgenomicnmr.net). Initial values for the molecular magnetic tensor parameters were obtained with the program FantaOrient (Banci et al., 1998; information on program available at www.postgenomicnmr.net). For each protein, 500 random structures were annealed in 10,000 steps by introducing the available NOE and PCs (Fe(III)-cyt c) constraints, together with the RDC constraints. The relative weights of all constraints were set equal to 1 and the tolerance values Ti for RDC were taken equal to the estimated measurement errors. The 20 best structures (i.e., the ones with the lowest total target function value) of the new family of conformers were used to re-estimate the tensor parameters for a new refinement step. The calculations were repeated until convergence of the tensor parameters was reached.
Determination of the magnetic susceptibility anisotropy
The molecular magnetic susceptibility tensor can be obtained from the difference in RDC values, ΔRDC, measured at two different fields. The ΔRDC values are given by the difference between the 1JHN values measured at the two different fields, corrected for the contribution due to the diamagnetic dynamic frequency shift (δDFS), which constitutes a non-negligible magnetic field-dependent contribution to apparent 1H-15N 1J (Tjandra, Grzesiek, and Bax, 1996).
ΔRDC values are given by Eq. 2 (Van Zijl et al., 1984):
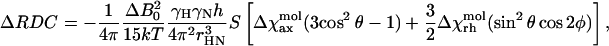 |
(2) |
where Δχaxmol and Δχrhmol are, respectively, the axial and rhombic components of the molecular tensor, χmol, θ, and φ are polar coordinates describing the orientation of the N-H bond vector in the (axis) frame of the χmol tensor, and S is the generalized order parameter. This form of the equation allows ΔRDC to be expressed as a function of the molecular χmol tensor, taking into account the relationship between it and the orientation tensor (Bertini et al., 2002). The tensor parameters were obtained with the program FantaOrient (Banci et al., 1998), which optimizes the fit of experimental ΔRDC values over the given structure. The adjustable parameters are Δχaxmol and Δχrhmol, as well as the three independent direction cosines needed to define the orientation of the χmol tensor within the laboratory frame.
An important contribution to the molecular magnetic susceptibility in paramagnetic proteins is the paramagnetic susceptibility, which is traditionally evaluated from pseudocontact shifts (Emerson and La Mar, 1990; Banci et al., 1992, 1996), according to Eq. 3, which holds within the metal-centered point-dipole/point-dipole approximation:
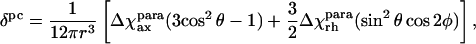 |
(3) |
where Δχaxpara and Δχrhpara are axial and rhombic anisotropies of the magnetic susceptibility tensor, θ and φ are cylindrical coordinates of the position vector of a proton, and r is the distance between the paramagnetic center and the proton in question.
Fits of the pseudocontact shifts over the structure employed the program Fantasian (available from http://www.postgenomicnmr.net), following a procedure analogous to that used with ΔRDC data.
Determination of residual dipolar splittings is an alternative to the use of dipolar chemical shifts for the study of the metal-center magnetism in paramagnetic proteins (Déméné et al., 2000; Tolman et al., 1995; Banci et al., 1998). The magnetic susceptibility tensor can be derived from the difference between the corresponding 1JHN values for the paramagnetic and diamagnetic species, measured at the same field, according to Eq. 4:
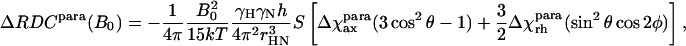 |
(4) |
with symbols defined as in Eqs. 2 and 3.
The following quantities were obtained (Eq. 5):
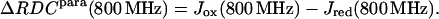 |
(5) |
The magnetic anisotropy tensor was evaluated by obtaining best fits of experimental ΔRDCpara values over a refined family of structures with the FantaOrient program.
Monte Carlo methods were used to make error estimates for all tensor parameters: 200 different calculations were performed on data sets, where 30% of experimental values were randomly eliminated from input data.
RESULTS AND DISCUSSION
The case of oxidized-K79A and reduced cytochrome c and solution structure refinements
The backbone 15N-1H 1J values were measured at 500 and 800 MHz for Fe(III)-cyt c and Fe(II)-cyt c at pH 7.0. ΔRDC800−500 values for 54 and 73 15N-1H pairs were obtained for the two species (Fig. 1, A–B). The values range between 0.78 and −0.62 for Fe(II)-cyt c, and 1.46 and −1.41 for Fe(III)-cyt c.
FIGURE 1.
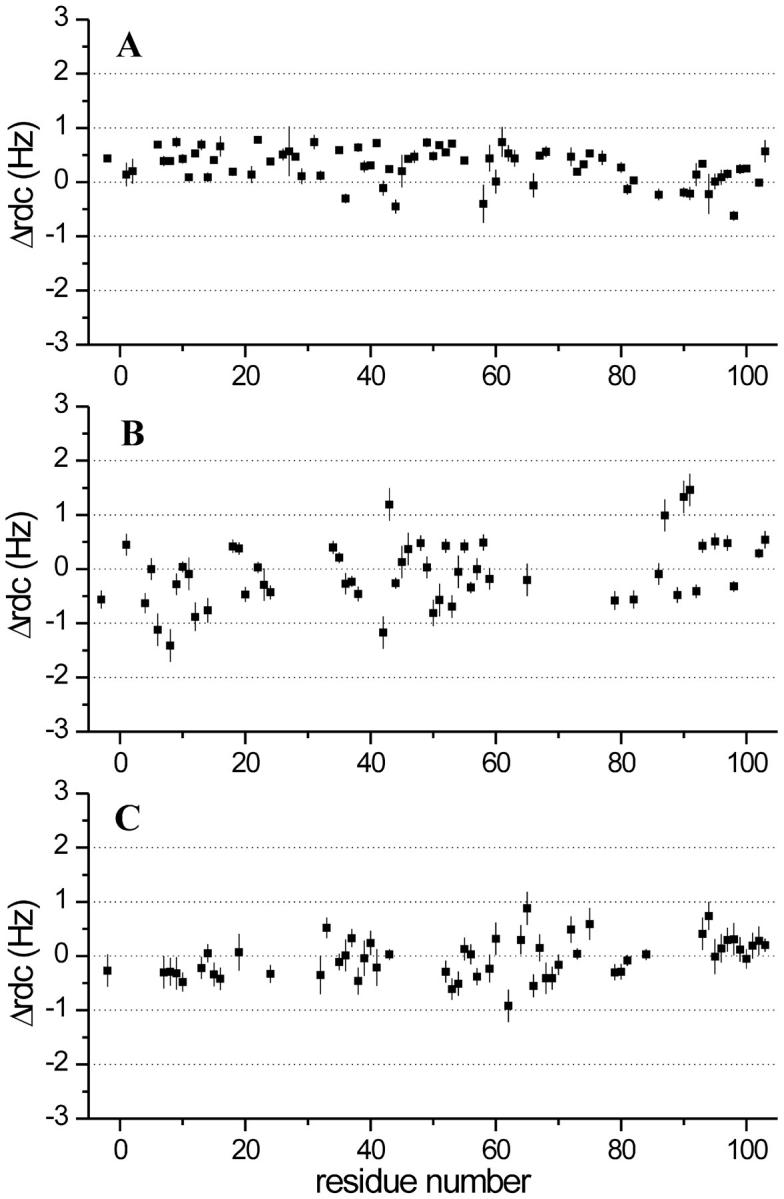
ΔRDC800–500 values measured for (A) Fe(II)-cyt c, (B) Fe(III)-cyt c, and (C) alkaline K79A Fe(III)-cyt c. The residue numbering starts at −5, as is common in the cytochrome-c literature; tuna cyt c is the reference, allowing conserved residues to have the same numbers in all mitochondrial cytochromes c.
The ΔRDC800–500 values for the oxidized protein were used to refine the solution structure simultaneously with NOEs and pseudocontact shifts. It has been reported that internal motions affect the RDC values when there is mobility in the sub-nanosecond timescale as revealed from model-free analysis or when there is conformational exchange. In the former case, a model-free S parameter <0.85 determines an observable effect (Meiler et al., 2001; Barbieri et al., 2002). In Fe(III)-cyt c, S2 values ≤ 0.7 (S ≤ 0.83) were found for the loop regions (Fetrow and Baxter, 1999). Moreover, many residues in the oxidized protein were found to experience conformational equilibria on the ms-μs timescale, with several of them on the loops and on the 60s helix (Barker et al., 2001). On this basis, the RDCs of residues 16–17, 27, 29, 31, 61, 66–69, and 99 were not included in tensor parameter and structural calculations. The 20 best structures out of the 500 calculated were retained, yielding a family of structures with root mean square deviation (RMSD) values of 0.92 ± 0.14 Å for the backbone atoms and 1.54 ± 0.12 Å for the heavy atoms. These results are virtually identical with those of the family of structures determined previously (Banci et al., 1997a). Nevertheless, although not contributing to a refinement in the structure, the availability of new constraints consistent with the NOEs gives us more confidence in the resulting solution structure. The total target function is in the range 3.33–3.92 Å2, with an average value of 3.67 ± 0.20 Å2 (the target function relative to the published solution structure, calculated with NOEs and PCs constraints, was reported to be ≤7 Å2). The contribution from the NOEs to the total target function is 1.80 ± 0.17 Å2, that from the pseudocontact shifts is 1.16 ± 0.19 Å2, and that from ΔRDC values is 0.71 ± 0.24 Å2, indicating good agreement among the different sets of constraints. Very similar results for the family of structures were obtained when ΔRDCpara values were used instead of ΔRDC800–500. The resulting family of 20 best structures has RMSD values of 0.89 ± 0.13 Å for the backbone atoms and 1.53 ± 0.14 Å for the heavy atoms. The total target function is in the range 2.96–3.45 Å2, with an average value of 3.28 ± 0.14 Å2. The contribution from the NOEs to the total target function is 1.35 ± 1.81 Å2, that from the pseudocontact shifts is 1.17 ± 0.11 Å2, and that from the ΔRDC values is 0.40 ± 0.15 Å2. Therefore, the structures refined by the two methods are virtually identical in terms of quality and fold. In Fig. 2 A, the experimental ΔRDCpara values are plotted against the values calculated for the structure with the lowest total target function. A correlation factor R = 0.94 was found for the linear fit, which corresponds to an agreement value from Meiler et al. (2001) of 0.70. It is worth mentioning that when the values corresponding to NHs of loop regions were included, a correlation factor of 0.83 was found between the calculated and observed ΔRDCs, thus confirming that those RDCs cannot be used as structural constraints.
FIGURE 2.
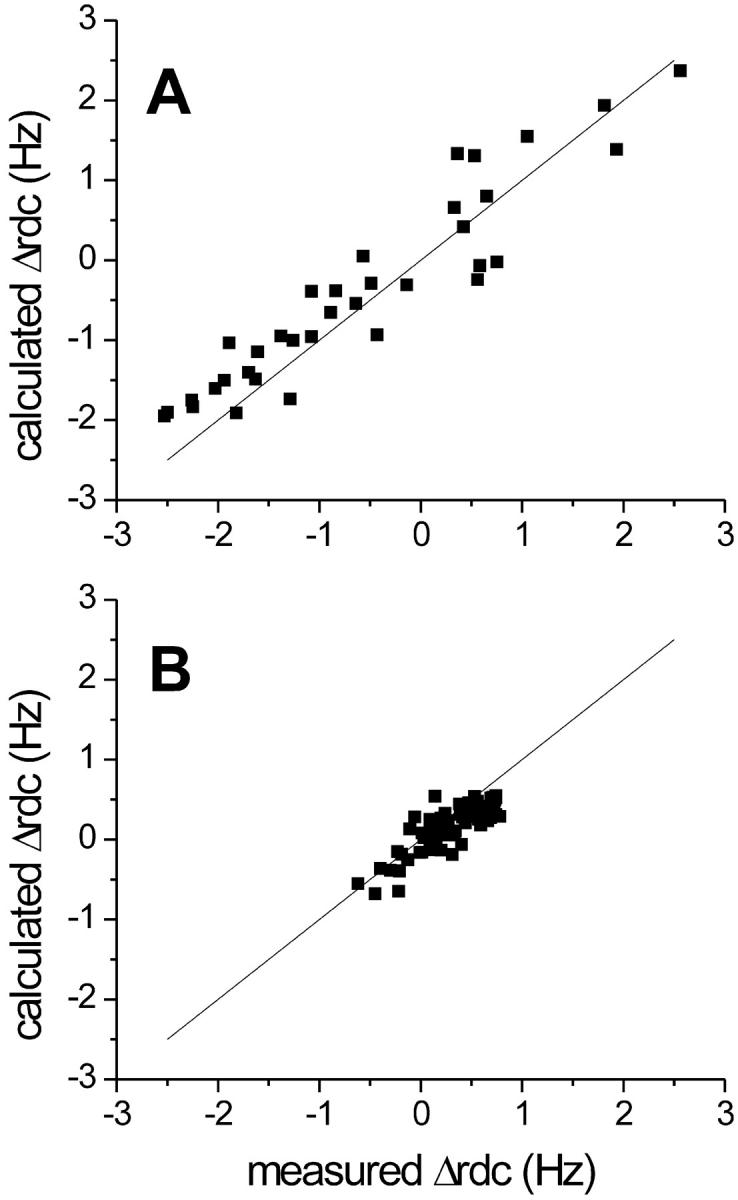
(A) Observed vs. calculated ΔRDCpara values for the refined best structure of Fe(III)-cyt c. (B) Observed vs. calculated ΔRDC800–500 values for the refined best structure of Fe(II)-cyt c.
The magnetic anisotropy tensor 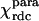 for Fe(III)-cyt c was evaluated by fitting the experimental ΔRDCpara values over the refined family of structures. It reproduces the tensor based on pseudocontact shifts
for Fe(III)-cyt c was evaluated by fitting the experimental ΔRDCpara values over the refined family of structures. It reproduces the tensor based on pseudocontact shifts 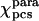 , as shown in the first and second columns of Table 1. The refined structure was also used to evaluate the molecular tensor χmol, whose principal components are reported in the third column of Table 1.
, as shown in the first and second columns of Table 1. The refined structure was also used to evaluate the molecular tensor χmol, whose principal components are reported in the third column of Table 1.
TABLE 1.
Parameters characterizing the χpara, χmol, and χdia tensors as obtained from the PCs and the ΔRDC of Fe(III)-cyt c and the ΔRDC of Fe(II)-cyt c
| Parameters |
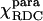 * *
|
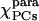 |
χmol | χdia |
|---|---|---|---|---|
| Δχax(/10−32 m3) | 2.24 ± 0.26 | 2.36 ± 0.09 | 1.12 ± 0.22 | −1.35 ± 0.09 |
| Δχrh(/10−32 m3) | −1.00 ± 0.22 | −1.20 ± 0.13 | −0.46 ± 0.19 | 0.19 ± 0.08 |
| Deviation of the z-axis from the normal to the heme plane (deg) | 25 ± 23 | 14 ± 2 | 22 ± 10 | 20 ± 3 |
| Deviation of the x-axis from α-γ meso axis (deg) | 45 ± 27 | 52 ± 10 | 56 ± 29 | 30 ± 21 |
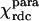 is evaluated from
is evaluated from 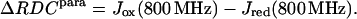
The ΔRDC800–500 values also were used to refine the Fe(II)-cyt c structure that had been obtained only through NOEs. The 20 structures with the lowest target function value were retained and provided a family of structures with RMSD values of 1.01 ± 0.14 Å for the backbone and 1.59 ± 0.15 Å for all heavy atoms. The RMSD values thus obtained are the same within experimental error as those of the family of structures determined previously. The two sets of constraints show good agreement, the total target function being in the range 1.57–2.12 Å2, with an average value of 1.99 ± 0.14 Å2. The contribution of the NOEs to the total target function is 0.90 ± 0.06 Å2 and that from the ΔRDC is 1.09 ± 0.20 Å2. The refined structure was used to evaluate the molecular tensor χdia, whose parameters are reported in the fourth column of Table 1. The molecular magnetic anisotropy for a diamagnetic protein can also be theoretically calculated as the sum of all the individual diamagnetic susceptibilities of the π-electron bonds belonging to the porphyrin group, the backbone carbonyl bonds, and the side chains of aromatic residues. The contribution from the heme group, for which a χax in the range −1.0 × 10−32 to −1.3 × 10−32 m3 has been estimated (Bothner-By et al., 1985), has been shown to be the dominant effect in globular diamagnetic iron(II) heme proteins (Tolman et al., 1997). The present results are in agreement, within 3% from the above lower limit, with this finding. The experimental ΔRDC800–500 values are plotted against the values calculated for the structure with the lowest total target function in Fig. 2 B. The agreement between experimental and calculated values, which corresponds to a correlation factor R = 0.84 for the linear fit and to an agreement factor of 0.16, confirms the consistency of RDC and structural data. Interestingly, the NHs of loop residues in Fe(II)-cyt c have experimental RDC values in good agreement with calculated ones, consistent with the finding that the reduced protein is rigid both on the ms-μs and ns-ps timescales (Barker et al., 2001; Fetrow and Baxter, 1999).
The case of alkaline-K79A-Fe(III)-cyt c and characterization of mobility
The ΔRDC800–500 values measured for Fe(III)-cyt c at pH 11.1 span a range smaller than that of oxidized protein at pH 7.0; i.e., their values are in the range +0.88 to –0.92 (Fig. 1 C). This is particularly true for residues −5 to 42 and 79 to 103. This is quite surprising if one applies the same analysis reported above for oxidized Fe(III)-cyt c at pH 7. Indeed, the χpara values estimated from PCs indicate that the alkaline form of Fe(III)-cyt c is characterized by a Δχaxpara even larger than that of Fe(III)-cyt c at pH 7.0 (Table 2). The PCs-derived magnetic tensor parameters of χpara determined for the alkaline form are in excellent agreement with those already reported by us for cyt c-CN− and cyt c-NH3, i.e., derivatives where the sixth ligand of the low-spin iron(III) has cylindrical symmetry and does not contribute to the rhombic component of χpara. On the other hand, the observed difference in ΔRDC800–500 values between the native and alkaline forms cannot be accounted for by any difference in χdia that could be induced by differences in backbone conformation. Indeed, in globular proteins the protein backbone contribution is essentially negligible (see above). Moreover, we have determined a solution structure for the alkaline Fe(III) protein based on NOE and PCs constraints (Assfalg et al., 2003), and the observed differences do not justify significantly different χdia values. We therefore propose that the reduction in ΔRDCs arises from increased mobility of the pH 11.1 conformer relative to the native structure, an explanation that is consistent with the reduced number of NOE cross peaks detectable in the NOE spectroscopy (NOESY) spectra of the alkaline form with respect to the corresponding spectra of native Fe(II) and Fe(III) cyt c (∼500 fewer NOEs were used in alkaline-cyt c structure calculations). Indeed, the presence of internal motions faster than the overall molecular tumbling reduces the NOE intensity. To have direct information on protein mobility, heteronuclear relaxation measurements and {1H}-15N NOE experiments were performed. The unavoidable local overheating of the sample during R2 measurements causes protein precipitation under the extreme pH conditions, making this experiment meaningless. Information on the effective correlation time was therefore obtained through analysis of the field-dependence of the {1H}-15N NOE intensity. Reliable values of {1H}-15N NOE, measured at 700 MHz, were obtained for 67 backbone HN resonances and were found to range from 0.56 to 0.97. The calculated average NOE value was 0.80 ± 0.09. From the measurements performed at 400 MHz, the NOEs of 62 resonances were found to range from 0.30 to 0.92, with an average value of 0.66 ± 0.17. An analysis of NOE intensities at two fields provides an estimate of the effective correlation time for nuclear reorientations. From the above values, an average effective correlation time of ∼4.0 ns is obtained, which drops to ∼3.0 ns for loop residues. In this range of correlation times, the measurements at 400 MHz become particularly useful, because small changes in effective τc values produce significant variations in NOEs, as compared with the small variations observed at 700 MHz. The effective correlation time is clearly shorter than the 5.2 ns measured for the native protein under neutral conditions (Fetrow and Baxter, 1999), indicating the presence of substantial mobility at high pH.
TABLE 2.
Parameters characterizing the χpara and χmol tensors as obtained from the PCs and the ΔRDCs of alkaline K79A Fe(III)-cyt c
| Parameters | 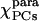 |
χmol |
|---|---|---|
| Δχax(/10−32 m3) | 2.69 ± 0.08 | 0.33 ± 0.08 |
| Δχrh(/10−32 m3) | −0.50 ± 0.17 | −0.29 ± 0.13 |
| Deviation of the z-axis from the normal to the heme plane (deg) | 12 ± 2 | 10 ± 7 |
| Deviation of the x-axis from α-γ meso axis (deg) | 85 ± 11 | 54 ± 19 |
Mobility on a timescale shorter than ms affects RDC values by reducing them. Attempts are available in the literature to reveal mobility through RDC values (Meiler et al., 2001). This is the first time that a comparison of PCs and ΔRDCpara has been used to reveal mobility.
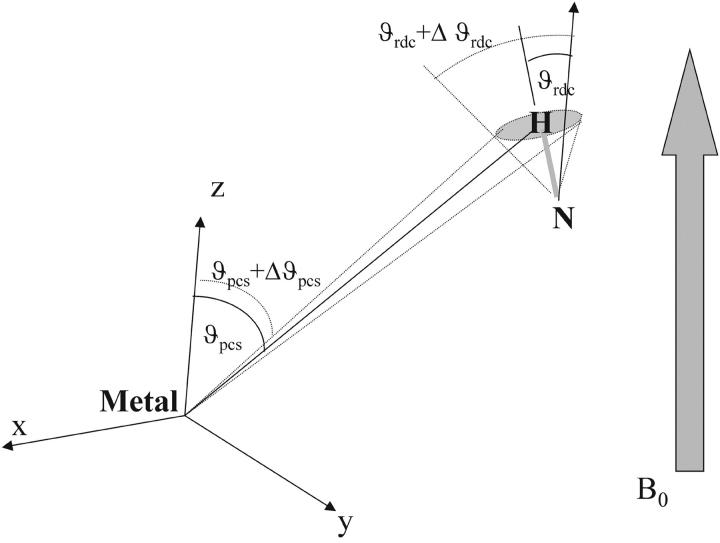
Paramagnetic systems are ideal because 1), they do not need external orienting devices that may be problematic under extreme pH conditions, and 2), they provide a reliable estimate of χpara, showing that partial orientation indeed occurs. The fact that pseudocontact shifts are not quenched by mobility that quenches RDCs indicates that the motions maintain, on average, the same metal-to-proton distances. Indeed, the orientational average of an NH vector may reduce RDCs, whereas the average polar coordinates of an amide proton, which determine the pseudocontact shift, may vary only a little. The situation is summarized in Fig. 3; a change in the orientation of an NH bond determines a sensible variation in the angle between the NH vector and the magnetic axis, whereas the angle between the same axis and the metal-H vector is only slightly affected, as in the case of the alkaline form of K79A cytochrome c.
FIGURE 3.
Mobility of amide protons affects the ΔRDCpara and PCs values to a different extent. A change in the position of the proton determines a larger change in the angle θRDC than in the angle θPCs because the metal-proton distance is larger than the nitrogen-proton distance.
CONCLUSIONS
We have analyzed PCs and RDC values for K79A Fe(III)-cyt c at pH 7.0 and 11.1. Both parameters are potentially useful as structural constraints. However, fast internal protein motions can strongly affect RDC values, thereby rendering them useless for solution structure determinations (Meiler et al., 2001; Barbieri et al., 2002). In proteins under native conditions, the extent of this effect is often negligible, but it can become very important in partially folded states, as we have found for cyt c at pH 11.1. Our analysis shows that the native and alkaline forms of Fe(III)-cyt c display pseudocontact shifts of the same order of magnitude, and therefore the resulting magnetic anisotropy tensor parameters are comparable as well as the extent of field-induced orientation. But, at variance with expectation, the ΔRDCs for alkaline cyt c are much smaller than those of the native protein at pH 7.0. Such differences in ΔRDCs are attributable to the greater mobility of the alkaline form of the protein, which has been proved by {1H}-15N NOE experiments. In principle, information on protein mobility, expressed as an order parameter SRDC, can be obtained from ΔRDC values, provided at least five independent measurements of RDC values are available (e.g., in five different orienting systems). Alkaline Fe(III)-cyt c represents the first example where the analysis of two sets of paramagnetic constraints (PCs and ΔRDCpara) reveals discrepancies that can be attributed to mobility.
For both Fe(III)-cyt c and Fe(II)-cyt c at neutral pH, RDC values were used together with available NOEs (and PCs shift for the oxidized protein) to recalculate solution structures. Although the structures are essentially the same as before, they are more reliable, as they are consistent with two or three (NOEs, PCs, and RDCs in the case of Fe(III)-cyt c) sets of constraints. From the structures, the molecular magnetic anisotropies and directions are consistent with the values of the metal ion magnetic susceptibility anisotropy obtained from pseudocontact shifts.
Acknowledgments
We thank Federico Rosell for providing samples of K79A cytochrome c.
We acknowledge support from the Ministero dell'Istruzione, dell'Università e della Ricerca, Cofinanziamento 2001 MIUR COFIN2001) and European Community Network (grant FMRX-CT98-0218 to I.B.); Italian Consiglio Nazionale delle Richerche (Progetto Finalizzato Biotecnologie grant 01.00359.PF49 to P.T.); operating grant MT-14021 from the Canadian Institutes of Health Research and a Canada Research Chair (to A.G.M.); United States National Institutes of Health grant DK19038 (to H.B.G.); and Department of Energy grant DE-FG03-02ER15359 (to J.R.W.).
References
- Arnesano, F., L. Banci, I. Bertini, J. Faraone-Mennella, A. Rosato, P. D. Barker, and A. R. Fersht. 1999. The solution structure of oxidized Escherichia coli cytochrome b562. Biochemistry. 38:8657–8670. [DOI] [PubMed] [Google Scholar]
- Arnesano, F., L. Banci, I. Bertini, and I. C. Felli. 1998. The solution structure of oxidized rat microsomal cytochrome b5. Biochemistry. 37:173–184. [DOI] [PubMed] [Google Scholar]
- Arnesano, F., L. Banci, I. Bertini, K. van der Wetering, M. Czisch, and R. Kaptein. 2000. The auto-orientation in high magnetic field of oxidized cytochrome b562 as source of constraints for solution structure determination. J. Biomol. NMR. 17:295–304. [DOI] [PubMed] [Google Scholar]
- Assfalg, M., I. Bertini, A. Dolfi, P. Turano, A. G. Mauk, F. I. Rosell, and H. B. Gray. 2003. Structural model for an alkaline form of ferricytochrome c. J. Am. Chem. Soc. 125:2913–2922. [DOI] [PubMed] [Google Scholar]
- Baistrocchi, P., L. Banci, I. Bertini, P. Turano, K. L. Bren, and H. B. Gray. 1996. Three-dimensional solution structure of Saccharomyces cerevisiae reduced iso-1-cytochrome c. Biochemistry. 35:13788–13796. [DOI] [PubMed] [Google Scholar]
- Banci, L., I. Bertini, K. L. Bren, M. A. Cremonini, H. B. Gray, C. Luchinat, and P. Turano. 1996. The use of pseudocontact shifts to refine solution structures of paramagnetic metalloproteins: Met80Ala cyano-cytochrome c as an example. J. Biol. Inorg. Chem. 1:117–126. [Google Scholar]
- Banci, L., I. Bertini, K. L. Bren, H. B. Gray, P. Sompornpisut, and P. Turano. 1997a. Solution structure of oxidized Saccharomyces cerevisiae Iso-1-cytochrome c. Biochemistry. 36:8992–9001. [DOI] [PubMed] [Google Scholar]
- Banci, L., I. Bertini, H. B. Gray, C. Luchinat, T. Reddig, A. Rosato, and P. Turano. 1997b. Solution structure of oxidized horse heart cytochrome c. Biochemistry. 36:9867–9877. [DOI] [PubMed] [Google Scholar]
- Banci, L., I. Bertini, J. G. Huber, C. Luchinat, and A. Rosato. 1998. Partial orientation of oxidized and reduced cytochrome b5 at high magnetic fields: magnetic susceptibility anisotropy contributions and consequences for protein solution structure determination. J. Am. Chem. Soc. 120:12903–12909. [Google Scholar]
- Banci, L., I. Bertini, R. Pierattelli, M. Tien, and A. J. Vila. 1995. Factoring of the hyperfine shifts in the cyanide adduct of lignin peroxidase from P. chrysosporium. J. Am. Chem. Soc. 117:8659–8667. [Google Scholar]
- Banci, L., L. B. Dugad, G. N. La Mar, K. A. Keating, C. Luchinat, and R. Pierattelli. 1992. 1H Nuclear Magnetic Resonance investigation of cobalt(II) substituted carbonic anhydrase. Biophys. J. 63:530–543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbato, G., M. Ikura, L. E. Kay, R. W. Pastor, and A. Bax. 1992. Backbone dynamics of calmodulin studied by 15N relaxation using inverse detected two-dimensional NMR spectroscopy; the central helix is flexible. Biochemistry. 31:5269–5278. [DOI] [PubMed] [Google Scholar]
- Barbieri, R., I. Bertini, G. Cavallaro, Y. M. Lee, C. Luchinat, and A. Rosato. 2002. Paramagnetically induced residual dipolar couplings for solution structure determination of lanthanide-binding proteins. J. Am. Chem. Soc. 124:5581–5587. [DOI] [PubMed] [Google Scholar]
- Barker, P. B., I. Bertini, R. Del Conte, S. J. Ferguson, P. Hajieva, E. J. Tomlinson, P. Turano, and M. S. Viezzoli. 2001. A further clue to understanding the mobility of mitochondrial yeast cytochrome c: a 15N T1p investigation of the oxidized and reduced species. Eur. J. Biochem. 268:4468–4476. [DOI] [PubMed] [Google Scholar]
- Bax, A., and N. Tjandra. 1997. Are proteins even floppier than we thought? Nat. Struct. Biol. 4:254–256. [DOI] [PubMed] [Google Scholar]
- Bentrop, D., I. Bertini, M. A. Cremonini, S. Forsén, C. Luchinat, and A. Malmendal. 1997. The solution structure of the paramagnetic complex of the N-terminal domain of calmodulin with two Ce3+ ions by 1H NMR. Biochemistry. 36:11605–11618. [DOI] [PubMed] [Google Scholar]
- Berghuis, A. M., and G. D. Brayer. 1992. Oxidation state-dependent conformational changes in cytochrome c. J. Mol. Biol. 223:959–976. [DOI] [PubMed] [Google Scholar]
- Bertini, I., M. B. L. Janik, Y.-M. Lee, C. Luchinat, and A. Rosato. 2001a. Magnetic susceptibility tensor anisotropies for a lanthanide ion series in a fixed protein matrix. J. Am. Chem. Soc. 123:4181–4188. [DOI] [PubMed] [Google Scholar]
- Bertini, I., M. B. L. Janik, G. Liu, C. Luchinat, and A. Rosato. 2001b. Solution structure calculations through self-orientation in a magnetic field of cerium (III) substituted calcium-binding protein. J. Magn. Reson. 148:23–30. [DOI] [PubMed] [Google Scholar]
- Bertini, I., C. Luchinat, and G. Parigi. 2002. Magnetic susceptibility in paramagnetic NMR. Progr. NMR Spectr. 40:249–273. [Google Scholar]
- Bothner-By, A. A. 1996. Magnetic field induced alignment of molecules. In Encyclopedia of Nuclear Magnetic Resonance. D. M. Grant, and R. K. Harris, editors. John Wiley and Sons, Chichester, UK. pp. 2932–2938.
- Bothner-By, A. A., J. P. Domaille, and C. Gayathri. 1981. Ultra high-field NMR spectroscopy: observation of proton-proton dipolar coupling in paramagnetic bis[tolyltris(pyrazolyl)borato]cobalt(II). J. Am. Chem. Soc. 103:5602–5603. [Google Scholar]
- Bothner-By, A. A., C. Gayathri, P. C. M. Van Zijl, and C. Maclean. 1984. Anisotropy of the diamagnetic susceptibility of benzene. Determination by high-field deuterium NMR. J. Magn. Reson. 56:456–462. [Google Scholar]
- Bothner-By, A. A., C. Gayathri, P. C. M. Van Zijl, C. Maclean, J.-J. Lai, and K. M. Smith. 1985. High-field orientation effects in the high-resolution proton NMR spectra of diverse porphyrins. Magn. Reson. Chem. 23:935–938. [Google Scholar]
- Clore, G. M., A. M. Gronenborn, and N. Tjandra. 1998. Direct structure refinement against residual dipolar couplings in the presence of rhombicity of unknown magnitude. J. Magn. Reson. 131:159–162. [DOI] [PubMed] [Google Scholar]
- Déméné, H., P. Tsan, P. Gans, and D. Marion. 2000. NMR determination of the magnetic susceptibility anisotropy of cytochrome c′ of Rhodobacter capsulatus by 1JHN dipolar coupling constants measurement: characterization of its monomeric state in solution. J. Phys. Chem. B. 104:2559–2569. [Google Scholar]
- Dickerson, R. E., T. Takano, D. Eisenberg, O. B. Kallai, L. Samson, A. Cooper, and E. Margoliash. 1971. Ferricytochrome c. I. General features of the horse and bonito proteins at 2.8 Å resolution. J. Biol. Chem. 246:1511–1535. [PubMed] [Google Scholar]
- Domaille, J. P. 1980. Direct measurement of the electron susceptibility anisotropy in paramagnetic complexes using high-field deuterium NMR. J. Am. Chem. Soc. 102:5392–5393. [Google Scholar]
- Emerson, S. D., and G. N. La Mar. 1990. NMR determination of the orientation of the magnetic susceptibility tensor in cyanometmyoglobin: a new probe of steric tilt of bound ligand. Biochemistry. 29:1556–1566. [DOI] [PubMed] [Google Scholar]
- Fetrow, J. S., and S. M. Baxter. 1999. Assignment of 15N chemical shifts and 15N relaxation measurements for oxidized and reduced iso-1-cytochrome c. Biochemistry. 38:4480–4492. [DOI] [PubMed] [Google Scholar]
- Grzesiek, S., and A. Bax. 1993. The importance of not saturating H2O in protein NMR. Application to sensitivity enhancement and NOE measurements. J. Am. Chem. Soc. 115:12593–12594. [Google Scholar]
- Kay, L. E., L. K. Nicholson, F. Delaglio, A. Bax, and D. A. Torchia. 1992. Pulse sequences for removal of the effects of cross correlation between dipolar and chemical-shift anisotropy relaxation mechanisms on the measurement of heteronuclear T1 and T2 values in proteins. J. Magn. Reson. 97:359–375. [Google Scholar]
- Lohman, J. A. B., and C. Maclean. 1978. Magnetic field induced alignment effects in 2H NMR spectra. Chem. Phys. Lett. 58:483–486. [Google Scholar]
- Meiler, J., N. Blomberg, M. Nilges, and C. Griesinger. 2000. A new approach for applying residual dipolar couplings as restraints in structure elucidation. J. Biomol. NMR. 16:245–252. [DOI] [PubMed] [Google Scholar]
- Meiler, J., J. J. Prompers, W. Peti, C. Griesinger, and R. Bruschweiler. 2001. Model-free approach to the dynamic interpretation of residual dipolar couplings in globular proteins. J. Am. Chem. Soc. 123:6098–6107. [DOI] [PubMed] [Google Scholar]
- Moore, G. R., and G. W. Pettigrew. 1990. Cytochromes c; Evolutionary, Structural and Physicochemical Aspects. Springer-Verlag, Berlin.
- Palmer III, A. G., N. J. Skelton, W. J. Chazin, P. E. Wright, and M. Rance.1992. Suppression of the effects of cross-correlation between dipolar and anisotropic chemical shift relaxation mechanisms in the measurements of spin-spin relaxation rates. Mol. Phys. 75:699–711. [Google Scholar]
- Peng, J. W., and G. Wagner. 1992. Mapping of spectral density function using heteronuclear NMR relaxation measurements. J. Magn. Reson. 98:308–332. [Google Scholar]
- Sass, H. J., G. Musco, S. J. Stahl, P. T. Wingfield, and S. Grzesiek. 2000. Solution NMR of proteins within polyacrylamide gels: diffusional properties and residual alignment by mechanical stress or embedding of oriented purple membranes. J. Biomol. NMR. 18:303–309. [DOI] [PubMed] [Google Scholar]
- Scott, R. A., and A. G. Mauk. 1996. Cytochrome c. A Multidisciplinary Approach. University Science Books, Sausalito, California.
- Tjandra, N., and A. Bax. 1997. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science. 278:1111–1114. [DOI] [PubMed] [Google Scholar]
- Tjandra, N., S. Grzesiek, and A. Bax. 1996. Magnetic field dependence of nitrogen-proton J splittings in 15N-enriched human Ubiquitin resulting from relaxation interference and residual dipolar coupling. J. Am. Chem. Soc. 118:6264–6272. [Google Scholar]
- Tjandra, N., J. G. Omichinski, A. M. Gronenborn, G. M. Clore, and A. Bax. 1997. Use of dipolar 1H-15N and 1H-13C couplings in the structure determination of magnetically oriented macromolecules in solution. Nat. Struct. Biol. 4:732–738. [DOI] [PubMed] [Google Scholar]
- Tolman, J. R., J. M. Flanagan, M. A. Kennedy, and J. H. Prestegard. 1995. Nuclear magnetic dipole interactions in field-oriented proteins: information for structure determination in solution. Proc. Natl. Acad. Sci. USA. 92:9279–9283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolman, J. R., J. M. Flanagan, M. A. Kennedy, and J. H. Prestegard. 1997. NMR evidence for slow collective motions in cyanometmyoglobin. Nat. Struct. Biol. 4:292–297. [DOI] [PubMed] [Google Scholar]
- Van Zijl, P. C. M., B. H. Ruessink, J. Bulthuis, and C. Maclean. 1984. NMR of partially aligned liquids: magnetic susceptibility anisotropies and dielectric properties. Acct. Chem. Res. 17:172–180. [Google Scholar]
- Williams, G., N. J. Clayden, G. R. Moore, and R. J. P. Williams. 1985. Comparison of the solution and crystal structures of mitochondrial cytochrome c. Analysis of paramagnetic shifts in the nuclear magnetic resonance spectrum of ferricytochrome c. J. Mol. Biol. 183:447–460. [DOI] [PubMed] [Google Scholar]
- Wilson, M. T., and C. Greenwood. 1996. The alkaline transition in ferricytochrome c. In Cytochrome c. A Multidisciplinary Approach. R. A. Scott, and A. G. Mauk, editors. University Science Books, Sausalito, California. pp. 611–634.