Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Jun;84(6):3924–3930. doi: 10.1016/S0006-3495(03)75120-0

A Measure of Conformational Entropy Change during Thermal Protein Unfolding Using Neutron Spectroscopy

Jörg Fitter 1
PMCID: PMC1302974  PMID: 12770898

Abstract

Thermal unfolding of proteins at high temperatures is caused by a strong increase of the entropy change which lowers Gibbs free energy change of the unfolding transition (ΔGunf = ΔH − TΔS). The main contributions to entropy are the conformational entropy of the polypeptide chain itself and ordering of water molecules around hydrophobic side chains of the protein. To elucidate the role of conformational entropy upon thermal unfolding in more detail, conformational dynamics in the time regime of picoseconds was investigated with neutron spectroscopy. Confined internal structural fluctuations were analyzed for α-amylase in the folded and the unfolded state as a function of temperature. A strong difference in structural fluctuations between the folded and the unfolded state was observed at 30°C, which increased even more with rising temperatures. A simple analytical model was used to quantify the differences of the conformational space explored by the observed protein dynamics for the folded and unfolded state. Conformational entropy changes, calculated on the basis of the applied model, show a significant increase upon heating. In contrast to indirect estimates, which proposed a temperature independent conformational entropy change, the measurements presented here, demonstrated that the conformational entropy change increases with rising temperature and therefore contributes to thermal unfolding.

INTRODUCTION

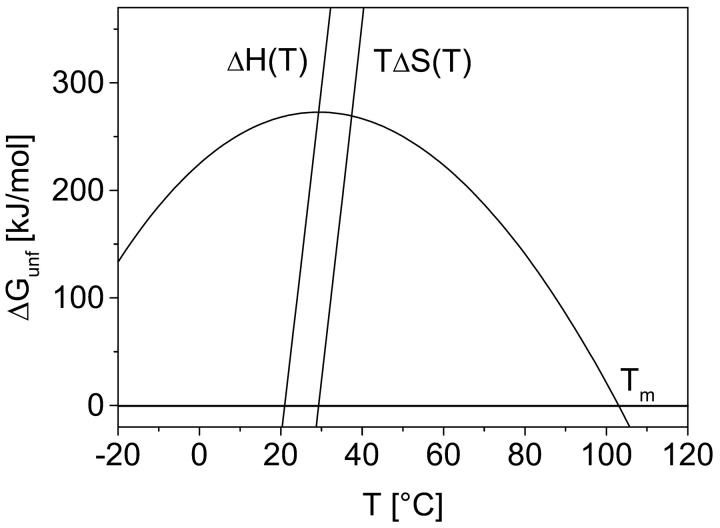
The stability of the folded state of a protein, which is the native and functional state under physiological conditions, is operated by a subtle balance of enthalpic and entropic contributions. Both contributions consist of opposing fractions which either stabilize or destabilize the folded state. The conformational entropy of the polypeptide chain is larger for unfolded state compared to the more compact folded state characterized by much more restricted conformational space. Therefore, this contribution stabilizes the unfolded state (ΔSconf > 0). The interaction of solvent water with nonpolar side chains of the protein stabilizes the folded state, because solvation of these side groups induces ordering of water which is unfavorable. Since nonpolar groups are exposed to the solvent mainly in the unfolded state and not in the folded state, this contribution stabilizes the folded state (ΔShyd < 0). With the assumption of a reversible “two-state” unfolding process (i.e., only the folded or the unfolded state occurs), the temperature dependence of the free energy ΔGunf as a function of temperature describes a parabolic-shaped curve (Fig. 1) (Becktel and Schellmann, 1987). The slope of this curve is given by the total entropy change ΔStot, which is zero at the temperature of maximal stability (compensation: ΔSconf + ΔShyd = ΔStot) and is characterized by increasing positive values with increasing temperature. At the melting temperature Tm, Gibbs energy ΔGunf becomes zero and thermal unfolding occurs. The parameters determining this curve are measured with techniques (e.g., calorimetry) that cannot distinguish between contributions related to protein-solvent interactions or related to sole protein properties, such as the conformational entropy. Nevertheless, experimental and calculated Gibbs energies of hydration of amino acid side chains were used to determine the hydration contribution and the residual conformational contribution to the entropy change (Privalov and Makhatadze, 1993; Sturtevant, 1977). According to these studies, the temperature dependence of conformational entropy change differs significantly with respect to calorimetric total entropy change. ΔSconf was either constant with temperature (Sturtevant, 1977; Baldwin, 1986) or even decreased with rising temperature (Privalov and Makhatadze, 1993; Privalov, 1997). Therefore, hydration effects were assumed to play the major role for thermal unfolding. The generally accepted view is that thermal unfolding mainly occurs because with increasing temperature fewer water molecules are tied down in regions of ordered water around nonpolar side chains (Fersht, 1999).

FIGURE 1.

FIGURE 1

Open in a new tab

The stability curve of α-amylase from B. licheniformis (BLA) with ΔGunf as function of temperature. Here the Gibbs free energy for the unfolding transition is given by ΔGunf(T) = GU − GF = ΔH(T) − T × ΔS(T) = ΔHm (1 − T/Tm) + Δcp [T − Tm − T × ln(T/Tm)] with the melting temperature Tm = 103°C, the enthalpy change ΔHm = 2686 kJ mol−1, and the change in heat capacity Δcp = 32.74 kJ mol−1 K−1 (Fitter, unpublished results; Feller et al., 1999).

As an approach to elucidate more details about the role of the conformational entropy during thermal unfolding, neutron spectroscopy was applied to measure structural fluctuations of a well characterized protein, the α-amylase from B. licheniformis (BLA, 58,550 Da). This amylolytic enzyme is rather heat stable and well characterized with respect to thermal and thermodynamic stability (Feller et al., 1999, Fitter et al., 2001a) (Fig. 1). BLA has a monomeric structure and consists of 483 residues. In the time window of neutron spectroscopy, the observed picosecond motions are dominated by side-chain reorientations and segmental movements of flexible polypeptide backbone regions (Kneller and Smith, 1994; Tarek and Tobias, 2002). To obtain a measure of the conformational entropy change contribution, conformational fluctuations for the folded and the unfolded state of α-amylase were measured as a function of temperature. Although folded proteins exhibit a certain rigidity, conformational fluctuations are, nevertheless, present in the native state. Besides their importance for protein activity (Frauenfelder et al., 1991; Rasmussen et al., 1992; Fitter et al., 1998; Kay, 1998; Zaccai, 2000) these fluctuations can contribute significantly to the conformational entropy of proteins (Karplus et al., 1987; Doig and Sternberg, 1995; Yang and Kay, 1996).

MATERIALS AND METHODS

Sample preparation and characterization

α-Amylase from B. licheniformis (purchased from Sigma-Aldrich) was dissolved in D2O buffer (30 mM Mops, 50 mM NaCl, 3 mM CaCl2, pH 7.8) and purified by the use of a desalting column (Econo-Pac 10 DG, Bio-Rad). To replace all exchangeable hydrogens of the protein by deuterium, the sample was kept for 5 h at 50°C in a buffer with 30 mM Mops, 50 mM NaCl, 3 mM CaCl2, 20 mM EDTA, pH 7.8. The H/D exchange of amide protons in the protein was monitored by measuring the amide II band (1550 cm−1) using FTIR spectroscopy (see Fitter and Heberle, 2000). The number of not exchanged hydrogens for each BLA molecule is ∼3400. Due to the procedure of keeping the protein at “prefolding” conditions (i.e., 50°C and 20 mM EDTA) for several hours, the H/D exchange of exchangeable hydrogen can be assumed as completed, in a good approximation. Therefore, we do not expect any further H/D exchange upon protein unfolding (see below). Exchanged hydrogens in the solution were removed by four subsequent washing procedures with standard D2O buffer. Finally the protein solution was separated into two aliquots, one adjusted to pH 13 (condition for the unfolded state), and the other one was left at pH 7.8 (folded state) (see Fitter et al., 2001a). CD spectroscopy revealed no significant difference between thermal unfolded and pH unfolded BLA structures. In both cases the secondary structure elements were strongly reduced with respect to the folded state (Fitter, unpublished results). Both protein solutions (30 mg enzyme/ml solution) did not show aggregation at this concentration between 30°C and 70°C.

Conformational dynamics measured with neutron spectroscopy

Quasielastic incoherent neutron scattering (QENS), which is a commonly used technique in neutron spectroscopy, makes use of the large incoherent cross section of hydrogen nuclei (∼40 times larger than incoherent cross sections of other elements in biological samples), and is well suited to study internal molecular motions in a time range from 10−9 to 10−14 s (Bee, 1988). Using samples with the protein dissolved in D2O, all nonexchangeable hydrogens (which are distributed quasihomogeneously in the molecule) serve as probes to monitor local fluctuations occurring in the structure. In a neutron scattering experiment with predominantly incoherent scattering the double differential cross section

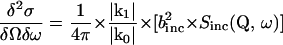graphic file with name M1.gif (1)

determines the number of neutrons scattered into a solid angle element δΩ and an energy transfer element δω. Here binc denotes the incoherent scattering length, and k0 and k1 are the wave vectors for the incident and scattered neutrons, respectively (with momentum transfer Q = k1 − k0). The information on dynamics of all individual hydrogen atoms can be obtained from the incoherent scattering function Sinc(Q, ω) using the formalisms of self-correlation functions developed by Van Hove (1954). According to the diffusive and liquidlike character of the predominant part of the motions, the quasielastic scattering (within the energy transfer range of about ±2 meV) is in the focus of the most neutron scattering studies on proteins. Because the observed hydrogens are part of the protein structure their individual diffusive motions are confined in space. Considering the diffusive character of equilibrium fluctuations occurring in proteins, the quasielastic broadening observed in the spectra can be fitted reasonably by Lorentzians.

Neutron-scattering experiments and data analysis

Three different samples (folded protein in D2O buffer, unfolded protein in D2O buffer, and D2O buffer only) were measured in a slab-shaped aluminum container (inner sample volume: 40 × 50 × 1 mm), which was sealed with a cap using a Teflon ring seal. The neutron-scattering measurements were performed with all three types of samples at 30°C, 50°C, and 70°C using the time-of-flight spectrometer IN6 (Institute Laue-Langevin, Grenoble). Time-of-flight spectra were measured using an incident wavelength of 5.1 Å with an elastic energy resolution Γres between 90 and 120 μeV (fwhm). A concentration of 30 mg BLA/ml D2O was used, which corresponds to ∼100,000 D2O molecules/BLA molecule. Assuming a scattering power of 1/11 of a deuterium with respect a hydrogen (considering coherent and incoherent contributions) one obtains ∼20% scattering from the protein. To avoid problems with strong coherent scattering from D2O, we considered only spectra with Q values <1.6 Å−1 in our data treatment. We subtracted the spectra measured with pure D2O buffer (Ssol) from those obtained with protein solutions (SPS), To isolate the incoherent scattering solely from not exchanged protein hydrogens. In this subtraction procedure we applied an “excluded volume fraction” factor of fex = 0.023 which considers the volume of 30 mg BLA/ml D2O. The excluded volume fraction factor of the protein is calculated on the basis of a specific volume for the dry protein being 0.76 ml/g.

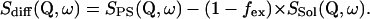graphic file with name M2.gif (2)

The obtained difference spectra were grouped from originally 120 spectra into 16 spectra. These spectra were fitted by a scattering function Smeas(Q, ω), where Q is the momentum transfer and ℏω is the energy transfer. Smeas(Q, ω) is given by

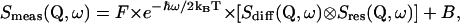graphic file with name M3.gif (3)

applying a convolution (⊗, energy convolution operator) with the resolution function Sres(Q, ω) (obtained from vanadium measurements). F denotes a normalization factor and exp(−ℏω/2kBT) gives the detailed balance factor. B is a linear and constant background. Beside internal structural fluctuations, whole molecule motions of proteins, such as translational and rotational diffusion, may occur for proteins in solution. They are much slower as compared to internal structural fluctuations. For small globular proteins the apparent diffusion coefficient (including translational and rotational diffusion of the whole protein) is on the order of 10−6–10−7 cm2 s−1. However, it was reported recently that even these slow motions can have an impact on spectra measured with neutron scattering (Perez et al., 1999). The translational diffusion is proportional to 1/R (R, hydrodynamic radius of the protein), and the rotational diffusion scales with 1/R3, whereas for both types of diffusion, the diffusion is proportional to the viscosity of the protein solution. In the case of α-amylase (with R on the order of 25–30 Å and in mM concentration) additional line broadening due to whole molecules motions can be assumed to be small with respect to the given energy resolution (Γres ≈ 100 μeV), as used in our measurements. Due to the fact that in a comparative study, contributions from whole molecule motions would cancel out to a large extent, in the applied data analysis whole molecule motions were not treated explicitly or separated from internal dynamics. Nevertheless, there will be a certain contribution from whole molecule motions, which is supposed to be more pronounced for the folded state as compared to the unfolded state (Pan et al. 1997). One can assume that slightly faster whole molecule motions of the folded and more compact structure would contribute more strongly in the time window of our neutron scattering measurements as compared to those of the unfolded state. As a consequence, this may lead to a slight underestimation of internal dynamics of the unfolded state as compared to the folded state.

Basically, the theoretical incoherent scattering for confined internal motions is given by:

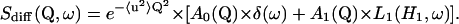graphic file with name M4.gif (4)

The scattered intensity is separated into an elastic δ(ω)-shaped component (experimentally observed with the resolution width Γres) and the quasielastic Lorentzian-shaped contribution L1(H1, ω), parameterized by the width H1 and by the quasielastic incoherent structure factor A1. The intensity of the elastic component is given by the elastic incoherent structure factor A0. Faster motions are taken into account by the Debye-Waller factor, exp(−〈u2〉 × Q2), where 〈u2〉 gives the global average mean square displacements of vibrational motions of the hydrogens. Whereas the line width of the Lorentzian H1 = (τ1)−1 is related to the corresponding correlation time τ1 of all moving hydrogens, the Q dependence of the elastic incoherent structure factor A0 gives information about the geometry and the amplitudes of the motions.

For a more detailed analysis we applied the “diffusion inside a sphere” model introduced by Volino and Dianoux (1980). Here A0 is given by

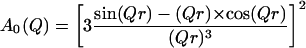graphic file with name M5.gif (5)

and is parameterized by the radius of the sphere r. It is noteworthy, that in the case of biological macromolecules the obtained correlation times τ1 and the radius value r must be understood as averaged parameters, because the dynamic behavior of the ∼3400 hydrogens in the protein is much more complex and can only be approximated by the model used here.

In this simple model the radius roughly describes the conformational space explored by the hydrogens as parts of the protein structure. Because the number of parameters which can be gained from the measurements is limited (only the Q dependence of A0), it is reasonable to use a simple model characterized by only one parameter (radius r).

Further, we have to consider the fact that a certain part of the solvent water molecules is strongly interacting with the protein (hydration water, which is often dynamically more restricted as compared to bulk water). Therefore the obtained difference spectra may show an underestimated quasielastic scattering. Here we shortly approximate the possible influence of this contribution on the analysis of internal dynamics in the protein. Assuming that a protein is more or less fully hydrated at h = 0.3–0.5 g solvent/g protein (Rupley and Careri, 1991) and that mainly this water shows a pronounced difference in the dynamical behavior with respect to bulk water we obtain in our case a contribution of hydration water to the total amount of D2O which is ∼1.4%. Scattering from the hydration water is on the order of 5% compared to the scattering of the protein.

RESULTS AND DISCUSSION

Conformational dynamics of the folded and unfolded state

To investigate scattering occurring mainly from nonexchangeable hydrogens of the protein, we analyze difference spectra with subtracted solvent scattering (see Materials and Methods). A comparison of difference spectra obtained from BLA in the folded state and in the unfolded state is shown in Fig. 2. Both spectra show a distinctive quasielastic scattering (Fig. 2, a and b, shaded area), which is much more pronounced in the case of the unfolded state as compared to the folded state. Within an energy transfer range from −1 to 2 meV, three spectral contributions, an elastic component, a single Lorentzian, and a constant background provide sufficient fit quality for the measured data. The obtained line widths of the Lorentzians H1 = 150 ± 10 μeV are the same for both states within the limit of error, and remain constant over the Q range used here. The resulting elastic incoherent structure factors (A0) are shown as a function of Q in Fig. 2 c. Here we observe clearly smaller A0 values and a steeper decrease of these values with Q for the unfolded state as compared to the folded state. This feature was analyzed in more detail by fitting the data with a simple model describing confined structural fluctuations (see Materials and Methods). In this model, localized diffusive motions, observed within our accessible Q-ω space, are spatially restricted to the volume inside a sphere with the radius r. In terms of the applied “diffusion inside a sphere” model (Volino and Dianoux, 1980) we obtain a larger radius value for the unfolded protein (r = 1.81 Å) as compared to the folded state (r = 1.17 Å). Most of the nonexchangeable hydrogens of BLA are localized in side groups (∼80%), and therefore the observed dynamics represents mainly diffusive side group reorientations with an average correlation time of ∼4.4 ps confined in the volume given by the radii. Faster vibrational motions, considered by the Debye-Waller factor, were obtained for both states with rather similar values of 〈u2〉 = 0.15 ± 0.03 Å2. Results of the vibrational motions are much less trustworthy in our data analysis, because they are much stronger influenced by the solvent subtraction procedure and by the applied background term in the fit (see Eq. 3 in Materials and Methods). Therefore, in this study we focused only on the quasielastic contribution of scattering and its impact on the conformational entropy.

FIGURE 2.

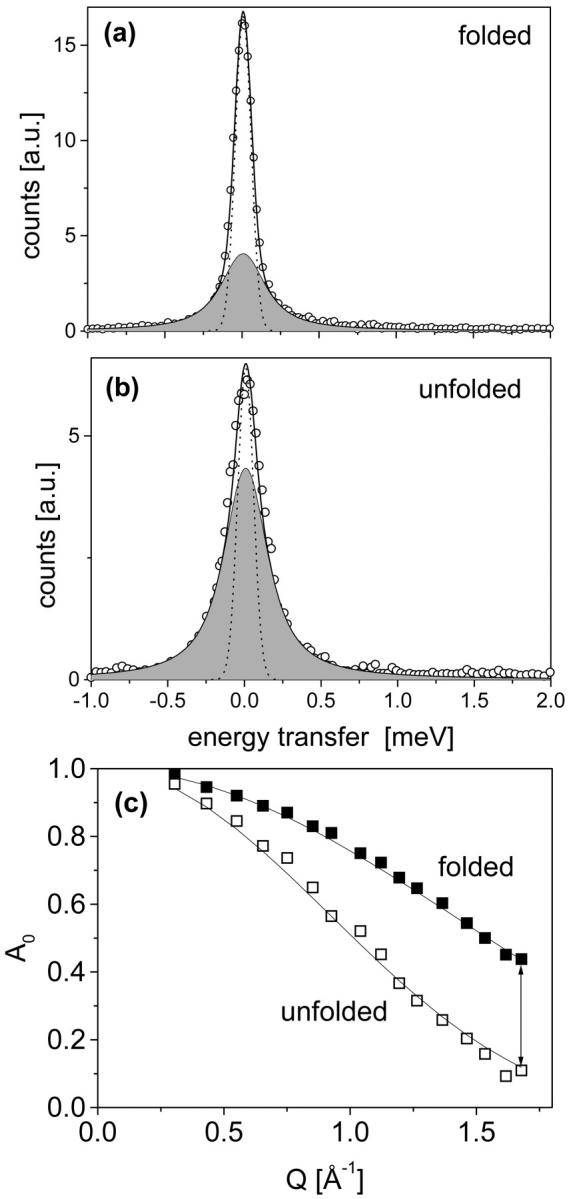
FIGURE 2

Open in a new tab

Difference spectra of BLA in the folded (a) and the unfolded (b) state. The number of scattered neutrons is given as a function of energy transfer (here for sample at T = 30°C and Q = 1.6 Å−1). The experimental data (symbols) were fitted by a total scattering function (thick solid line) which includes elastic scattering having (small) energy transfer values which cannot be resolved by the resolution function (Γres = 120 μeV (fwhm); dashed line), quasielastic scattering (shaded area) which is described by a Lorentzian (width = 150 ± 10 μev (hwhm)), and a constant background (not shown here). The lower part (c) of this figure shows the Q dependence of A0 (symbols) and the fitted Q dependence according to the diffusion inside a sphere model (solid lines).

In accordance with a vast body of experimental evidence and with principles of the famous “protein folding funnel” (Onuchic et al., 1997), the unfolded state is characterized by a larger degree of freedom for structural relaxations. Therefore, proteins in this state are more flexible (Receveur et al., 1997; Dyson and Wright, 1998; Bu et al., 2000; Fitter et al., 2001b), with less defined and heterogeneous structures, leading to a higher conformational entropy as compared to the folded state.

The temperature dependence of dynamics in both states

For a meaningful statement on the role of protein dynamics for entropy changes during thermal unfolding, data of protein dynamics as a function of temperature are required. The evolution of internal dynamics for both states as a function of temperature is already apparent in the raw data. A comparison of spectra measured with proteins in the folded and in the unfolded state is shown for three different temperatures (Fig. 3). In all spectra the strong contribution of solvent scattering (dashed line) is visible. As already shown in the previous section, we find a smaller intensity in the elastic region and more pronounced quasielastic scattering for the unfolded stated as compared to the folded state at T = 30°C (Fig. 3 a). Qualitatively, this behavior is also recognizable for the other temperatures. Interestingly, the increase of quasielastic scattering with rising temperatures is much more pronounced for the unfolded state as compared to the folded state. This important feature is analyzed in more detail by fits applied to the corresponding difference spectra. For all temperatures we obtained reasonable fits with a Lorentzian width of H1 = 150 ± 10 μeV. Within the limit of experimental errors, in the applied fits only the structure factors are affected significantly by protein unfolding or increasing the temperature. In Fig. 4 the elastic incoherent structure factors (A0) are shown for the folded (a) and the unfolded state (b). The Q dependence of the structure factors, as measured for both states at different temperatures, yields the following features: i), With increasing temperature A0 decreases more strongly with Q (i.e., more quasielastic intensity at high Q values). ii), The decrease of A0 with Q is more distinctive for the unfolded state as compared to the folded state. This result was quantified by fitting the data with the diffusion inside a sphere model. The resulting radius parameters are given in Table 1. In terms of this model we obtain larger radii, and therefore a larger part of the conformational space explored by confined motions, with increasing temperature. The important result with respect to thermodynamics is given by the fact, that the difference in conformational dynamics between the folded state and the unfolded state increases with rising temperature. Due to lower energy barriers between adjacent conformational substates in the unfolded state, a certain increase in temperature results in more pronounced thermal fluctuations as compared to the folded state.

FIGURE 3.

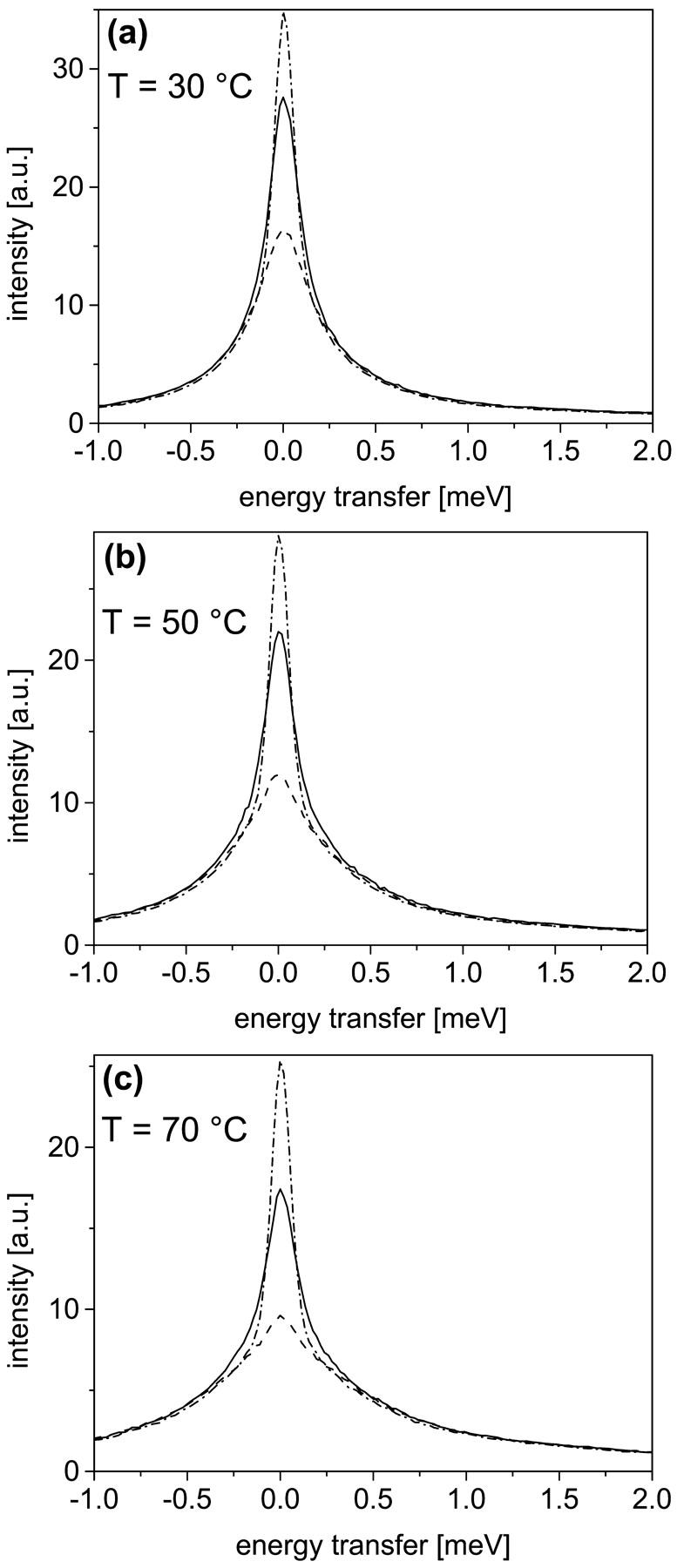
FIGURE 3

Open in a new tab

A comparison of spectra from BLA in D2O buffer solution (folded state, dashed-dotted line; unfolded state, solid line) and from D2O buffer solely (dashed line). All spectra were measured at scattering angles between 60° and 65°, which corresponds to an average Q value of 1.27 Å−1. Panels a–c show the increase of quasielastic scattering with rising temperature, which is more pronounced for the unfolded state as compared to the folded state.

FIGURE 4.

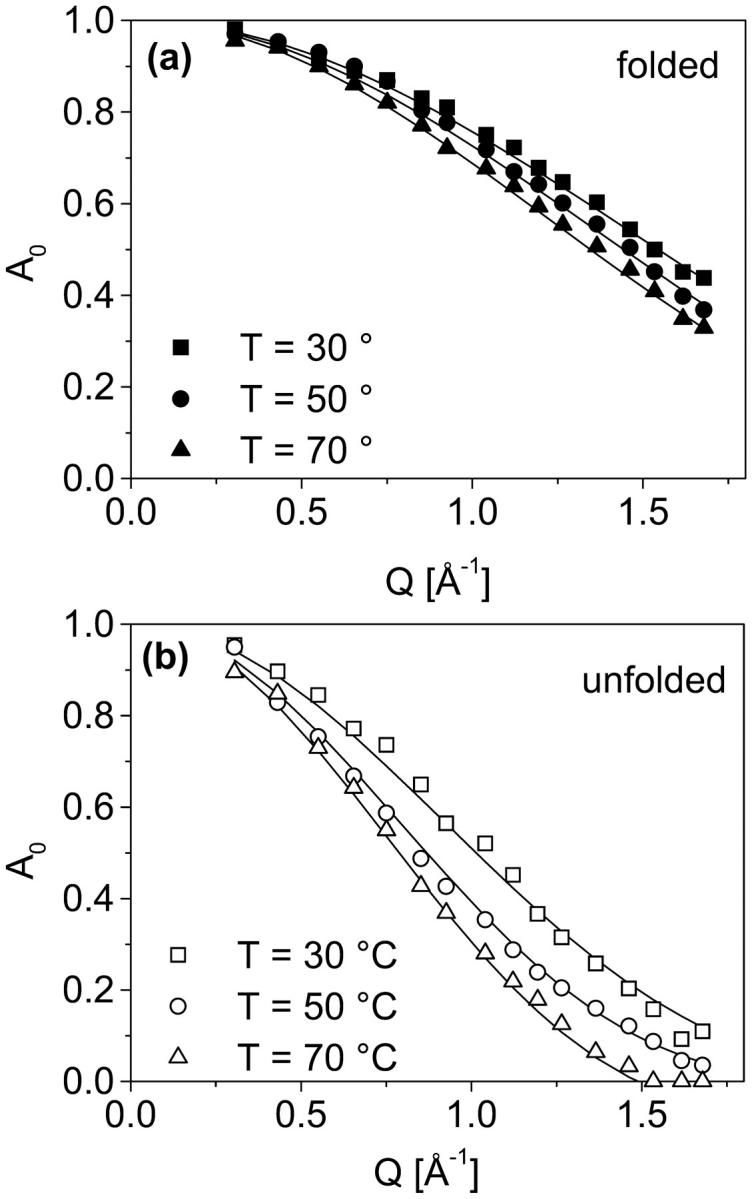
FIGURE 4

Open in a new tab

Elastic incoherent structure factors (A0) determined from difference spectra (see Fig. 2) given for the folded state (a) and the unfolded state (b) at three different temperatures. The statistical error of the obtained A0 (symbols, see also Fig. 2 c) is about ±4%. The solid lines represent structure factors calculated on the basis of the diffusion inside a sphere model. The corresponding model parameters (radius of the sphere) are given in Table 1.

TABLE 1.

Resulting radius parameter as obtained from model fits (diffusion inside a sphere)

T (°C) Folded rf (Å) Unfolded ru (Å) ΔSConf (J K−1 mol−1)/residue
30 1.17 1.81 10.85
50 1.25 2.10 12.94
70 1.35 2.41 14.45
Open in a new tab

The statistical errors of the radius parameter are about ±4% for the folded state and about ±5% for the unfolded state. On the basis of the radius values, conformational entropy changes were calculated (see next section).

Conformational entropy calculation from protein dynamics and the impact on protein stability

Proper entropy calculations are difficult, because these calculations require knowledge of the complete conformational space and are strongly influenced by correlations between the motions (Karplus et al., 1987; Schlitter, 1993). However, on the basis of the applied analytical model an estimation of a contribution to the conformational entropy related to the observed picosecond dynamics is given here. Due to the fact that mainly hydrogens located in the protein side groups (more than 80%) contribute to the observed scattering, we assume these side groups behave as single individual moving particles (average mass ∼110 Da), which explore a certain part of the conformational space during their confined diffusive motions (Receveur et al., 1997). For these groups we can calculate the conformational entropy by SConf = RlnZ. Here R is the gas constant (8.3144 J K−1 mol−1) and Z is the partition function with Z = V/λD3 determined by the de Broglie wavelength λD and the by V, the accessible volume of the conformational space occupied by the corresponding state (see e.g., Becker, 1985). With respect to our problem V can be calculated using a definition introduced with the diffusion inside a sphere model: V = 4 πr3/3. For amino acid residues moving at the given temperatures (30°C–70°C), the thermal de Broglie wavelength is Inline graphic Therefore, λD3 ≪ V and Boltzmann statistics is valid in the classical approximation (Becker, 1985). The conformational entropy change during unfolding with a radius of confinement for motions in the folded state rf and in the unfolded state ru is given by

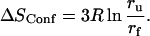graphic file with name M7.gif (6)

Using radius values as determined at 30°C we obtain for ΔSConf a value of 10.85 J K−1 mol−1 per residue (or 2.6 cal K−1 mol−1 per residue). Compared to estimated and measured ΔSConf values given in the literature (Privalov, 1997; Karplus et al., 1987; Doig and Sternberg, 1995; Creamer, 2000; Xie and Freire, 1994) our value is on average smaller by 30%–60%. Due to fact that our analysis covers mainly the picosecond time regime and contributions to the conformational entropy are also effected by fluctuations in other time regimes, this deviation is pretty reasonable. Compared to NMR studies on conformational entropy changes between different conformational states (not only between the folded and unfolded state, but also between different functionally important conformational states of the folded protein), rather similar values of ΔSconf (2–6 cal K−1 mol−1) were obtained for a calcium binding protein upon calcium binding (Spyracopoulos et al. 2001).

Further ΔSConf values of α-amylase obtained at higher temperatures are 12.94 J K−1 mol−1 per residue (at T = 50°C) and 14.45 J K−1 mol−1 per residue (at T = 70°C; see Table 1). This temperature dependence clearly demonstrates that the conformational entropy change of the unfolding transition increases upon heating and therefore contributes to thermal unfolding.

CONCLUSION

With respect to experimental techniques, mainly NMR spectroscopy is used to calculate conformational entropies (Yang and Kay, 1996) from bond vector fluctuations in the backbone (Stone, 2001) and in side chains (Lee et al., 2002). So far, temperature-dependent studies have been performed only with proteins in the folded state (Stone, 2001). As shown here and within the above given limitations, neutron spectroscopy allows a direct measure of contributions to the conformational entropy change arising from conformational picosecond fluctuations, mainly related to diffusive side group reorientations. The presented results of the dynamical behavior of α-amylase as a function of temperature are indicative for the fact that the conformational entropy change during unfolding was underestimated in the past (Privalov and Makhatadze, 1993; Sturtevant, 1977; Baldwin, 1986; Privalov, 1997) and seems to play a more important role in thermal protein unfolding.

Further studies with other proteins are required to state, whether the increasing conformational entropy change during thermal unfolding is a general phenomenon in proteins. Beyond this, further studies with other proteins give valuable information about strategies how in different proteins thermostability is determined. In particular, these findings are elucidative to understand mechanisms of thermal adaptation of thermophiles (Beadle et al., 1999; Colombo and Merz, 1999; Fitter and Heberle, 2000), and for developing thermostable enzymes for biotechnological applications (Stone, 2001; Arnold et al., 2001).

Acknowledgments

The Institute Laue-Langevin (Grenoble) and J. Ollivier are acknowledged for providing neutron beam facilities and for help during neutron scattering experiments. The author thanks G. Büldt for valuable discussions and for long standing and continuous support in his Institute.

References

  1. Arnold, F. H., P. L. Wintrode, K. Miyazaki, and A. Gershenson. 2001. How enzymes adapt: lessons from directed evolution. Trends Biochem. Sci. 26:100–106. [DOI] [PubMed] [Google Scholar]
  2. Baldwin, R. L. 1986. Temperature dependence of the hydrophobic interaction in protein folding. Proc. Natl. Acad. Sci. USA. 83:8069–8072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Beadle, B. M., W. A. Baase, D. B. Wilson, N. R. Gilkes, and B. K. Shoichet. 1999. Comparing the thermodynamic stabilities of a related thermophilic and mesophilic enzyme. Biochemistry. 38:2570–2576. [DOI] [PubMed] [Google Scholar]
  4. Becker, R. 1985. Theorie der Wärme. Springer-Verlag, Berlin.
  5. Becktel, W. J., and J. A. Schellmann. 1987. Protein stability curves. Biopolymers. 26:1859–1877. [DOI] [PubMed] [Google Scholar]
  6. Bee, M. 1988. Quasielastic Neutron Scattering. Hilger, Bristol, UK.
  7. Bu, Z., D. A. Neumann, S.-H. Lee, C. M. Brown, D. M. Engelmann, and C. C. Han. 2000. A view of dynamics changes in the molten globule-native folding step by quasielastic neutron scattering. J. Mol. Biol. 301:525–536. [DOI] [PubMed] [Google Scholar]
  8. Colombo, G., and K. M. Merz. 1999. Stability and activity of mesophilic subtilisin E and its thermophilic homolog: insights from molecular dynamics simulations. J. Am. Chem. Soc. 121:6895–6903. [Google Scholar]
  9. Creamer, T. P. 2000. Side chain conformational entropy in protein unfolded states. Proteins. 40:443–450. [DOI] [PubMed] [Google Scholar]
  10. Doig, A. J., and J. E. Sternberg. 1995. Side-chain conformational entropy in protein folding. Protein Sci. 4:2247–2251. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Dyson, H. J., and P. E. Wright. 1998. Equilibrium NMR studies of unfolded and partially folded proteins. Nat. Struct. Biol. 5 (Suppl):499–503. [DOI] [PubMed] [Google Scholar]
  12. Feller, G., D. d'Amico, and C. Gerday. 1999. Thermodynamic stability of a cold-active α-amylase from antarctic bacterium Alteromonas haloplanctis. Biochemistry. 38:4613–4619. [DOI] [PubMed] [Google Scholar]
  13. Fersht, A. 1999. Structure and Mechanism in Protein Science. W.H. Freeman and Company, New York.
  14. Fitter, J., S. A. W. Verclas, R. E. Lechner, H. Seelert, and N. A. Dencher. 1998. Function and picosecond dynamics of bacteriorhodopsin in purple membrane at different lipidation and hydration. FEBS Lett. 433:321–325. [DOI] [PubMed] [Google Scholar]
  15. Fitter, J., and J. Heberle. 2000. Structural equilibrium fluctuations in mesophilic and thermophilic α-amylase. Biophys. J. 79:1629–1636. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fitter, J., R. Herrmann, N. A. Dencher, A. Blume, and T. Hauß. 2001a. Activity and stability of a thermostable α-amylase compared to its mesophilic homologue: mechanisms of thermal adaptation. Biochemsitry. 40:10723–10731. [DOI] [PubMed] [Google Scholar]
  17. Fitter, J., R. Herrmann, T. Hauß, R. E. Lechner, and N. A. Dencher. 2001b. Dynamical properties of α-amylase in the folded and unfolded state: the role of thermal equilibrium fluctuations for conformational entropy and protein stabilisation. Physica B. 301:1–7. [Google Scholar]
  18. Frauenfelder, H., S. G. Silgar, and P. G. Wolynes. 1991. The energy landscapes and motions of proteins. Science. 254:1598–1603. [DOI] [PubMed] [Google Scholar]
  19. Karplus, M., T. Ichiye, and B. M. Pettitt. 1987. Configurational entropy of native proteins. Biophys. J. 52:1083–1085. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kay, L. E. 1998. Protein dynamics from NMR. Nat. Struct. Biol. 5:513–515. [DOI] [PubMed] [Google Scholar]
  21. Kneller, G. R., and J. C. Smith. 1994. Liquid-like side-chain dynamics in myoglobin. J. Mol. Biol. 242:181–185. [DOI] [PubMed] [Google Scholar]
  22. Lee, A. L., S. A. Kinnear, and A. J. Wand. 2002. Redistribution and loss of side chain entropy upon formation of a calmodulin-peptide complex. Nat. Struct. Biol. 7:72–77. [DOI] [PubMed] [Google Scholar]
  23. Onuchic, J. N., Z. Luthey-Schulten, and P. G. Wolynes. 1997. Theory of protein folding: the energy landscape perspective. Annu. Rev. Phys. Chem. 48:545–600. [DOI] [PubMed] [Google Scholar]
  24. Pan, H., G. Barany, and C. Woodward. 1997. Reduced BPTI is collapsed. A pulsed field gradient NMR study of unfolded and partially folded bovine pancreatic trypsin inhibitor, Protein Science 6:1985–1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Perez, J., J. M. Zanotti, and D. Durand. 1999. Evolution of the internal dynamics of two globular proteins from dry powder to solution. Biophys. J. 77:454–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Privalov, P. L., and G. I. Makhatadze. 1993. Contribution of hydration to protein folding thermodynamics. J. Mol. Biol. 232:660–679. [DOI] [PubMed] [Google Scholar]
  27. Privalov, P. L. 1997. Thermodynamics of protein folding. J. Chem. Thermodyn. 29:447–474. [Google Scholar]
  28. Rasmussen, B. F., A. M. Stoc, D. Ringe, and G. A. Petsko. 1992. Crystalline ribonuclease A losses function below the dynamical transition. Nature. 357:423–424. [DOI] [PubMed] [Google Scholar]
  29. Receveur, V., P. Calmettes, J. C. Smith, M. Desmadril, G. Coddens, and D. Durand. 1997. Picosecond dynamical changes on denaturation of yeast phosphoglycerate kinase revealed by quasielastic neutron scattering. Proteins. 28:380–387. [PubMed] [Google Scholar]
  30. Rupley, J. A., and G. Careri. 1991. Protein hydration and function. Adv. Protein Chem. 41:37–172. [DOI] [PubMed] [Google Scholar]
  31. Schlitter, J. 1993. Estimation of absolute and relative entropies of macromolecules using the covariance matrix. Chem Phys. Lett. 215:617–621. [Google Scholar]
  32. Spyracopoulos, L., P. Lavigne, M. P. Crump, S. M. Gagne, C. M. Kay, and B. D. Sykes. 2001. Temperature dependence of dynamics and thermodynamics of the regulatory protein domain of human cardiac tropin C. Biochemistry. 40:12541–12551. [DOI] [PubMed] [Google Scholar]
  33. Stone, M. J. 2001. NMR relaxation studies of the role of conformational entropy in protein stability and ligand binding. Acc. Chem. Res. 34:379–388. [DOI] [PubMed] [Google Scholar]
  34. Sturtevant, J. M. 1977. Heat capacity and entropy changes in processes involving proteins. Proc. Natl. Acad. Sci. USA. 74:2236–2240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Tarek, M., and D. J. Tobias. 2002. Role of protein-water hydrogen bond dynamics in the protein dynamical transition. Phys. Rev. Lett. 88:138101–138104. [DOI] [PubMed] [Google Scholar]
  36. Van Hove, L. 1954. Correlations in space and time and Born approximation scattering in systems of interacting particles. Phys. Rev. Lett. 95:249–262. [Google Scholar]
  37. Volino, F., and A. J. Dianoux. 1980. Neutron incoherent scattering law for diffusion in a potential of spherical symmetry: general formalism and application to diffusion inside a sphere. Mol. Phys. 41:271–279. [Google Scholar]
  38. Xie, D., and E. Freire. 1994. Molecular basis of cooperativity in protein folding. Proteins. 19:291–301. [DOI] [PubMed] [Google Scholar]
  39. Yang, D., and L. E. Kay. 1996. Contributions to conformational entropy arising from bond vector fluctuations measured from NMR-derived order parameters: application to protein folding. J. Mol. Biol. 263:369–382. [DOI] [PubMed] [Google Scholar]
  40. Zaccai, G. 2000. How soft is a protein? A protein dynamics force constant measured by neutron scattering. Science. 288:1604–1607. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES