Protein Self-Association in Solution: The Bovine Pancreatic Trypsin Inhibitor Decamer

Abstract

We have used magnetic relaxation dispersion to study bovine pancreatic trypsin inhibitor (BPTI) self-association as a function of pH, salt type and concentration, and temperature. The magnetic relaxation dispersion method sensitively detects stable oligomers without being affected by other interactions. We find that BPTI decamers form cooperatively under a wide range of solution conditions with no sign of dimers or other small oligomers. Decamer formation is opposed by electrostatic repulsion among numerous cationic residues confined within a narrow channel. Accordingly, the decamer population increases with increasing pH, as cationic residues are deprotonated, and with increasing salt concentration. The salt effect cannot be described in terms of Debye screening, but involves the ion-specific sequestering of anions within the narrow channel. The lifetime of the BPTI decamer is 101 ± 4 min at 27°C. We propose that the BPTI decamer, with a heparin chain threading the decamer channel, plays a functional role in the mast cell. We also detect a higher oligomer that appears to be a subcritical nucleation cluster of 3–5 decamers. We argue that monomeric crystals form at high pH despite a high decamer population in solution, because the ion pairs that provide the critical decamer-decamer contacts are disrupted at high pH.

INTRODUCTION

Self-interactions govern the assembly of oligomeric proteins (Jaenicke and Lilie, 2000), the pathological aggregation of misfolded proteins (Kelly, 1998), and the nucleation, growth, and polymorphism of protein crystals (Rosenberger et al., 1996; Riès-Kautt and Ducruix, 1997; Kierzek and Zielenkiewicz, 2001). Fundamental progress in these diverse fields must ultimately be based on a quantitative understanding of how proteins interact with themselves in solution. The colloidal approach, epitomized by the Derjaguin-Landau-Verwey-Overbeek theory (De Young et al., 1993; Leckband and Israelachvili, 2001), has not proven to be a fruitful avenue toward this goal (Piazza, 1999; Elcock et al., 2001). A molecular approach is evidently needed, which recognizes the structural details of the heterogeneous protein surface and takes into account a variety of short-range interactions, direct and solvent-mediated.

Whereas theoretical studies of protein self-association are still at an early stage, a vast amount of experimental work, primarily with scattering techniques, has been carried out on the phase behavior and oligomerization of globular proteins in solution. Bovine pancreatic trypsin inhibitor (BPTI) is among the proteins that have been studied most extensively in this regard. This 58-residue (6.5 kDa) basic (pI = 10.5) protein has long been thought to undergo self-association. Early sedimentation, calorimetry, and dynamic light scattering (DLS) work, reviewed by Gallagher and Woodward (1989), lead to conflicting results as to whether BPTI forms a dimer. A more recent NMR pulsed-gradient, spin-echo (PGSE) self-diffusion study concluded that BPTI is predominantly dimeric at mM concentrations, with little or no effect of pH or added salt (Ilyina et al., 1997). Several DLS and small-angle x-ray scattering (SAXS) studies (Lafont et al., 1994; Veesler et al., 1996; Lafont et al., 1997) at higher concentrations of NaCl, KSCN, or (NH₄)₂SO₄ indicated that BPTI solutions are polydisperse in the absence of added salt, but monodisperse and tetrameric at high salt concentrations (near the BPTI solubility limit). Although it has been argued that BPTI possesses a self-complementary surface that might stabilize a dimer (Zielenkiewicz et al., 1991), none of the experimental studies mentioned so far could provide unambiguous information about oligomer structure. Such information has come, not from solution studies, but from crystallography.

Until recently, all crystallographic studies of wild-type BPTI used one of three orthorhombic crystal forms, denoted I, II, and III, all with one BPTI molecule per asymmetric unit (Deisenhofer and Steigemann, 1975; Wlodawer et al., 1984, 1987b). These crystals are grown at pH 9–10, close to the isoelectric point of BPTI, with phosphate as the salting-out agent. Within the past few years, three new crystal forms, denoted A, B, and C, have been prepared by salting out BPTI with NaCl, KSCN, or (NH₄)₂SO₄ at pH 4.5 or 7.0, where BPTI has a net charge ∼+6 (Hamiaux et al., 1999, 2000; Lubkowski and Wlodawer, 1999). These new hexagonal or monoclinic crystals have five or 10 BPTI molecules in the asymmetric unit and represent different stackings of a common decamer structure.

Subsequent studies of BPTI self-association in solution have been interpreted in terms of BPTI decamers rather than dimers. In the most comprehensive of these studies, SAXS data from BPTI solutions at pH 4.5 and high concentrations of the salts used to grow crystal forms A, B, and C were shown to be consistent with a mixture of monomers and decamers (Hamiaux et al., 2000). It was thus concluded, in contrast to earlier claims (Lafont et al., 1997), that decameric BPTI crystals grow from a polydisperse solution. Similar findings have been reported in later x-ray and neutron small-angle scattering (SAS) studies (Budayova-Spano et al., 2000, 2002). Most recently, it was deduced from DLS data that BPTI in 1 M NaCl is decameric at pH 5 but monomeric at pH 7 (Tanaka et al., 2002). Furthermore, it was concluded that BPTI is monomeric under the conditions used to grow crystal forms I–III (Tanaka et al., 2002).

After a long and troubled history, it may appear that a consensus view of BPTI self-association in solution is finally emerging. However, this view is largely based on studies by SAS and DLS, techniques that do not readily distinguish oligomerization from longer-range interactions. Moreover, because these low-resolution techniques cannot unambiguously identify the oligomer structure, the interpretation of SAS and DLS data has relied heavily on recent evidence of self-association in crystals that may or may not be relevant under diverse solution conditions.

The present work is motivated by the belief that our understanding of BPTI self-association would benefit from studies by a different experimental technique: magnetic relaxation dispersion (MRD). Within the biomolecular field, MRD has previously been used mostly to study protein hydration and, in particular, internal water molecules in proteins and nucleic acids (Halle et al., 1999; Halle and Denisov, 2001). Here, we use ¹H MRD to determine the rotational correlation times (or rotational diffusion coefficients) of the oligomeric species present in solution. Whereas MRD has been used in a few earlier studies of protein self-association (Lindstrom et al., 1976; Raeymaekers et al., 1989; Koenig et al., 1990), our data extend to higher frequencies (necessary for a small protein like BPTI) and are analyzed in a more rigorous way (Halle et al., 1998).

Although the MRD method has its own limitations, it presents three decisive advantages in studies of protein self-association. First, it is insensitive to long-range interactions and therefore provides clear-cut information about oligomerization. Second, if the correlation times are sufficiently different, oligomers of different size can be resolved irrespective of the oligomer dissociation kinetics. Third, because rotational friction scales with volume whereas translational friction scales with linear dimension, rotational diffusion is a more sensitive probe of oligomerization than is translational diffusion. For example, the rotational correlation time of the BPTI decamer is a factor 8 longer than for the monomer, whereas the translational diffusion coefficients of the two species only differ by a factor 2.

The present MRD study of BPTI complements and extends previous solution studies (by SAS, DLS, and PGSE) in important ways. We identify a dominant oligomeric species with the rotational correlation time expected for the decamer present in crystal forms A, B, and C, as previously found by SAS under the low-pH and high-salt conditions used to grow decameric crystals (Hamiaux et al., 2000). In addition, we observe a larger oligomeric species that may be a subcritical crystallization nucleus. Unexpectedly, we find decamers also far from the solubility limit and even in the absence of salt. Moreover, and in contrast to a recent DLS study (Tanaka et al., 2002), we find a substantial decamer population under the high-pH conditions used to grow monomeric crystal forms. Using a salt-jump relaxation experiment, we also determine the lifetime of the BPTI decamer. These new results might seem to shatter the emerging consensus on BPTI self-association. However, in cases where our results disagree with previous conclusions, we indicate how the differences might be resolved. In addition, we are able to rationalize our results in terms of specific structural features of the BPTI decamer. We thus arrive at a consistent view of BPTI self-association in solution and in crystals. Finally, we propose a functional role for the BPTI decamer in the secretory granules of mast cells.

MATERIALS AND METHODS

Preparation of protein solutions

Bovine pancreatic trypsin inhibitor was supplied by Novo Nordisk A/S, Gentofte, Denmark (Aprotinin, batch # 84059-17-II). To remove residual salt, the protein preparation was exhaustively dialyzed (twice against deionized water and twice against millipore water). Agarose gel electrophoresis at pH 8.6, where the net charge of BPTI is +4.9, revealed only one, very weak, subsidiary band, consistent with a minor fraction (1–2%) truncated BPTI with Arg-1 and Pro-2 removed from the N-terminal by heat treatment (L. C. Petersen, Novo Nordisk A/S, personal communication). For the MRD samples, the dialyzed and lyophilized BPTI was dissolved in millipore water, giving a pH of 8.3–8.4. The pH was adjusted to within ±0.05 of the target value by μL additions of HCl or NaOH. No buffers were used. After addition of desiccator dried salt, the solution was centrifuged at 14,000 g for 3 min to remove a small fraction (<1%) of aggregated material. (In the case of K₂HPO₄, solution pH was adjusted after adding the salt.) All salts used (NaCl, CsCl, NaI, KSCN, and K₂HPO₄) were of >99% purity (purchased from Merck or BDH).

For the salt-jump kinetic relaxation experiment, we used BPTI supplied by Bayer Healthcare AG, Wuppertal, Germany (Trasylol, lot # 9104, 97% purity by HPLC). The protein was dialyzed as described above and dissolved in water with <0.001% O₂ (Fluka BioChemika).

The K₂HPO₄ solution was studied at pH 9.5, where the HPO₄²⁻ ion accounts for >99% of the phosphate. Because the proton in HPO₄²⁻ exchanges rapidly with water protons, it contributes to the observed ¹H magnetization. To contribute to the dispersion, however, protein-bound HPO₄²⁻ ions must have residence times longer than the rotational correlation time of the protein (26 ns for the BPTI decamer) but shorter than the intrinsic spin relaxation time (on the order of 1 ms). Judging from the measured dispersion amplitude factor B (see below), the HPO₄²⁻ ions that presumably are located within the decamer channel do not exchange on this timescale. This potential complication can therefore be ignored.

BPTI concentrations were determined spectrophotometrically (GBC UV-VIS 920) at 280 nm, using an extinction coefficient of 0.837 mL mg⁻¹ cm⁻¹, determined from quantitative amino-acid analysis on one sample. The solutions were then transferred to 10 mm NMR tubes. To minimize leaching of paramagnetic ions from the Pyrex glass, the NMR tubes were soaked with 3 M HCl for 24 h and then rinsed with millipore water and EDTA solution. To remove paramagnetic oxygen from the solution, the samples were gently bubbled with argon gas for 4 h and then sealed with a septum. With this procedure, the ¹H relaxation rate in a pure water sample was found to be 0.267 ± 0.008 s⁻¹, in agreement with the standard literature value of 0.266 s⁻¹ (Hindman et al., 1973), and remained within 1% of this value for at least 10 days.

Relaxation dispersion measurements

The longitudinal relaxation rate of the water ¹H resonance was measured over more than four frequency decades, from 10 kHz to 200 MHz. To cover this frequency range, we used three types of NMR spectrometers: 1), a Stelar Spinmaster fast field-cycling (FC) spectrometer (10 kHz–12 MHz); 2), a field-variable iron-core magnet (Drusch) equipped with a modified Bruker MSL 100 console or a Tecmag Discovery console (2.5 – 77.9 MHz); and 3), Bruker Avance DMX 100 and 200 spectrometers with conventional cryomagnets (100.1 and 200.1 MHz). The temperature was maintained at either 4.0 ± 0.1 or 27.0 ± 0.1°C using a Stelar variable temperature control unit (<100 MHz) or a Bruker Eurotherm regulator (at 100 and 200 MHz). Temperatures were checked using a thermocouple referenced to an ice-water bath.

In the fixed-field (non-FC) experiments, the longitudinal relaxation rate R₁ was measured with the 180° − τ − 90° inversion recovery sequence, an 8-step phase cycle, and 20 randomly ordered delay times. The total ¹H magnetization recovers bi-exponentially because it includes not only water and rapidly exchanging BPTI protons, but also a small contribution (typically, 5%) from nonexchanging BPTI protons. The latter contribution, which can increase the apparent R₁ by a few percent, was largely eliminated by integrating the water peak over a range where the spectral overlap was negligible (for non-FC experiments), or by using an acquisition delay sufficiently long that the protein magnetization had decayed before the signal was recorded (FC experiments). In this way, single-exponential recovery curves were obtained, from which R₁ was determined by a three-parameter fit. The accuracy of R₁ is estimated to ±1% (one standard deviation).

The FC technique overcomes the sensitivity problem of conventional fixed-field experiments in weak magnetic fields (Noack, 1986). The polarization and detection fields were set to 10 and 8 MHz (in ¹H frequency units), respectively. A field switching rate of 4 MHz ms⁻¹ and a switching delay of 10 ms were used. Relaxation measurements were performed with two different field cycles (Anoardo et al., 2001): the prepolarized cycle below 4 MHz and the nonpolarized cycle above 4 MHz. In either case, 15 different relaxation delays (evolution times) were used. The magnitude of the quadrature-detected signal after a 90° pulse was recorded and averaged over 32 transients with a 4-step phase cycle. The relaxation curves were invariably single-exponential. Heating of the air-core magnet during the polarization period causes a small field drift and a consequent systematic error in R₁. This heating effect was largely compensated by a feedback current proportional to the temperature of the magnet and by inserting a cooling delay to reduce the duty cycle (Anoardo et al., 2001). For R₁ values below 2 s⁻¹, a residual correction (typically, a few percent) for magnet heating effects was applied on the basis of an empirical relationship established by measuring a range of R₁ values with both field cycles at 4 MHz. The accuracy of R₁ determined by the FC technique is estimated to ±1.5–2% (one standard deviation).

Analysis of relaxation dispersion data

The measured ¹H relaxation rate is due to thermal fluctuations of intramolecular and intermolecular magnetic dipole-dipole couplings experienced by water protons and labile BPTI protons in fast or intermediate exchange (residence time <10 ms, typically) with the water protons (Abragam, 1961; Halle et al., 1999; Halle and Denisov, 2001). The relaxation dispersion, i.e., the frequency dependence of R₁, is produced by long-lived (residence time 10⁻⁹–10⁻² s) water molecules in intimate association with the protein and by labile protons with residence times in the same range.

If all residence times are long compared to the rotational correlation time τ_R of the protein, as is the case for BPTI (Denisov et al., 1995, 1996; Venu et al., 1997), the dispersion profile, R₁(ω₀), from a solution containing BPTI in N different oligomeric states, is described by the following relations (Abragam, 1961; Venu et al., 1997):

(1)

(2)

(3)

(4)

Here, b_n is the mean-square fluctuation amplitude and τ_R,n the rank-2 rotational correlation time associated with the n^th BPTI oligomer species. Furthermore, ξ_n = b_n,inter/b_n is the relative contribution from intermolecular dipole-dipole couplings to the overall fluctuation amplitude, b_n = b_n,intra + b_n,inter . The functions L_n (ω₀) will be referred to as Lorentzians, even though they are, in fact, linear combinations of two Lorentzian (reduced) spectral density functions differing by a factor 2 in frequency. Apart from an overall scaling by a factor 0.9, the functions and differ very little (Venu et al., 1997). The value of ξ_n therefore has no significant effect on the oligomer fractions that we deduce from the data. We set ξ_n = 0.33, as previously found for the four internal water molecules in BPTI (Venu et al., 1997).

The quantity α in Eq. 1 represents all frequency-independent contributions to the measured relaxation rate, including the secular (zero-frequency) intermolecular contribution (Venu et al., 1997). Because of the sparse sampling of the high-frequency regime in most of our dispersions, α could not be determined with useful accuracy. In the following, dispersion profiles will be displayed with the small frequency-independent contribution subtracted and with the frequency-dependent part normalized to the same BPTI concentration:

(5)

where N_T is the number of water molecules per BPTI molecule in the solution. This scaling is possible because the quantity b_n in Eq. 1 is inversely proportional to N_T (Halle et al., 1999; Halle and Denisov, 2001). (The relative contribution to N_T from labile BPTI protons is negligible.) As reference concentration, we use N_T = 3595, corresponding to 14.5 mM BPTI. In the presence of self-association, the scaling in Eq. 5 does not completely remove the concentration dependence, because the equilibrium concentrations of different oligomer species depend on the overall protein concentration (and, therefore, on N_T). Nevertheless, scaling is useful for displaying the effect of other variables, such as pH and salt concentration, when the variation in the BPTI concentration among the samples is small.

The experimental relaxation dispersion data were subjected to nonlinear Marquardt-Levenberg χ² minimization (Press et al., 1992) with the model function given by Eqs. 1–4. This nonlinear fit involves the 2N + 1 parameters α, b_n, and τ_R,n , with the products b_n τ_R,n constrained to be nonnegative. The number N of Lorentzians to be included in the fit was determined objectively by the F-test with a cutoff probability of 0.9 (Press et al., 1992; Halle et al., 1998). The 20 reported dispersions were thus found to be adequately modeled by two or three Lorentzians. In the final joint fits, we therefore used N = 3 throughout. On the basis of the associated rotational correlation times τ_R,n (see below), we assign these Lorentzian dispersion steps to BPTI monomers (n = 1), decamers (n = 2), and higher oligomers, hereafter referred to as polymers (n = 3). The former two steps are visually distinct with the major part of the dispersions occurring in the 10–100 MHz range for monomers and in the 1–10 MHz range for decamers.

Whereas the overlapping decamer and polymer dispersions are adequately sampled by FC measurements (extending up to 12 MHz), characterization of the monomer dispersion requires more time-consuming fixed-field measurements at higher frequencies. To reduce the experiment time, most dispersion profiles only include two measurements (100 and 200 MHz) >12 MHz. Because such “incomplete” dispersions could not be robustly fitted to three Lorentzians, they were analyzed by means of simultaneous fits to a set of dispersions, including one or more “complete” dispersions. In these joint fits, we imposed the constraint that each of the three rotational correlation times has the same value for all samples in the set. For example, in a set of samples differing only in salt concentration, we assumed that all samples contain the same three oligomer species (with the same three correlation times τ_R,n ) but at different concentrations. Although the correlation times τ_R1 and τ_R2 obtained from such joint fits are close to the values expected for the BPTI monomer and decamer, our data do not allow the dispersions to be accurately decomposed into three Lorentzian components in a unique way. In particular, a certain amount of compensating variation in correlation times and oligomer fractions can be accommodated with little effect on the quality of the fit (as measured by χ²). To obtain the most reliable estimates of the oligomer fractions, we therefore performed the joint fits with the monomer and decamer correlation times fixed at independently determined values (see below). The free parameters were thus the common polymer correlation time τ_R3 and, for each dispersion in the jointly fitted set, an α-value, and N amplitude factors b_n. Quoted uncertainties in the fitted parameter values correspond to one standard deviation and were obtained by the Monte Carlo method (Press et al., 1992) using 1000 synthetic data sets.

Rotational correlation times

Unconstrained joint fits to our MRD data yield values in the range 2.5–3.5 ns for the monomer rotational correlation time τ_R1. Because the high-frequency range is not densely sampled in our data, we have chosen to fix τ_R1 at the best available estimate of the rotational correlation time of monomeric BPTI, obtained from ¹⁵N relaxation of 3 mM BPTI in a 90:10 H₂O:D₂O mixture (no added salt) at pH 4.7 and 25°C (Beeser et al., 1997). Scaling the reported correlation time, 3.5 ns, from the water viscosity of the ¹⁵N study (0.911 cP) to the viscosity of H₂O at 27°C (0.851 cP), as in the present study, we obtain τ_R1 = 3.27 ns.

To obtain the rotational correlation time of the BPTI decamer, we carried out hydrodynamic calculations with the program HYDROPRO (Garcia de la Torre et al., 2000). In these calculations, each nonhydrogen atom in a crystallographic model of the protein (or decamer) is replaced by a spherical bead of radius a_H. The shell of beads remaining after all internal beads have been deleted is then filled with smaller spheres of radius σ that act as point sources of hydrodynamic friction. The rotational diffusion tensor D_R is computed as a function of σ and extrapolated to σ = 0 (Garcia de la Torre and Bloomfield, 1981). The rank-2 isotropic rotational correlation time is defined as τ_R = (2 Tr D_R)⁻¹. Because macroscopic continuum hydrodynamics is not strictly valid on the atomic scale, this calculation does not necessarily yield results in quantitative agreement with experiment. The approach usually adopted is to regard the bead radius a_H as an empirical parameter (rather than using the van der Waals radii of the actual atoms), the value of which is determined by requiring that the calculation agrees with the experimental value of a particular hydrodynamic quantity, such as τ_R (Garcia de la Torre et al., 2000).

Using the crystal structure 5PTI (Wlodawer et al., 1984) for monomeric BPTI (with the two disordered side chains in the major conformation), we calculated τ_R1 at 27°C for a_H values in the range 1.0–4.0 Å. Interpolation with the experimental value τ_R1 = 3.27 ns yields a_H = 2.88 Å. We then used this bead radius to calculate the rotational correlation time of the BPTI decamer from the crystal structure 1BHC (Hamiaux et al., 1999). The result is τ_R2 = 26.3 ns at 27°C. In all fits to MRD data at 27°C reported here, τ_R1 and τ_R2 were constrained to these values.

Rotational diffusion of both BPTI monomer and decamer is actually slightly anisotropic. For the 5PTI monomer, HYDROPRO calculations yield 1.28 for the ratio of the largest and smallest of the five rotational correlation times (derived from the three eigenvalues of D_R) that characterize the rank-2 spectral density function for asymmetric-top rotational diffusion (Woessner, 1962). For the more nearly spherical 1BHC decamer, the corresponding ratio is 1.08. Neither of these ratios is sufficiently large to cause a detectable deviation in the dispersion profile from spherical-top behavior. We therefore use the isotropic average of the rotational correlation times. If both monomer and decamer were spherical and of the same density, τ_R would be proportional to protein volume so that τ_R2/τ_R1 = 10. The slightly smaller value, τ_R2/τ_R1 = 26.3/3.27 = 8.05, obtained from the hydrodynamic calculations, is consistent with the more nearly spherical shape of the decamer.

Salt-jump relaxation experiment

The mean lifetime of the BPTI decamer was determined from a real-time salt-jump kinetic relaxation experiment. ¹H relaxation dispersion profiles were recorded at 27°C from solution A (13.3 mM BPTI, no salt) and solution B (14.7 mM, 0.9 M NaCl), both at pH 4.5. (These dispersion profiles, obtained with BPTI from Bayer, were consistent with the profiles obtained with BPTI from Novo Nordisk.) Equal volumes (1 mL) of solutions A and B were mixed, whereupon the approach to the new oligomerization equilibrium (corresponding to 0.45 M NaCl) was monitored by measuring the relaxation rate R₁ at a ¹H frequency of 100 kHz at intervals of 40 min during 13.4 h. The approach to equilibrium was characterized by a relaxation time constant τ_relax, determined from a nonlinear least-squares fit of the three parameters in the expression

(6)

RESULTS

From dispersion profile to oligomer fractions

Eighteen ¹H relaxation dispersion profiles were measured on BPTI solutions under different conditions of temperature, pH, and added salt (type and concentration). The relevant sample characteristics are compiled in Table 1. Fig. 1 shows the ¹H relaxation dispersion profile at 27°C from an aqueous solution containing 14.5 mM BPTI and 0.90 M NaCl at pH 4.5. The correlation times obtained from fits of Eqs. 1–4 to these data are given in Table 2 for N = 1, 2, or 3 Lorentzians. Unconstrained fits with one or two Lorentzians fail to describe the data within the experimental accuracy. An unconstrained 3-Lorentzian fit yields correlation times τ_R1 and τ_R2 close to those expected for the BPTI monomer and decamer (see Materials and Methods). Fixing these two correlation times to independently derived values (see Materials and Methods) yields a fit of similar quality as with three unconstrained correlation times.

TABLE 1.

Sample characteristics and results of fits to ¹H relaxation dispersion profiles

							Oligomer fraction†
Salt	CS (M)	pH	T (°C)	CP* (mM)	B† (108 s−2)	τR3†‡ (ns)	x1	x2	x3
none	–	4.5	27.0	14.4	1.13(1)	–	0.944(1)	0.056(1)	0
none	–	4.5	4.0	14.4	1.10(1)	–	0.956(1)	0.044(1)	0
NaCl	0.50	4.5	27.0	12.9	1.19(5)	130(6)	0.874(16)	0.125(16)	0.001(2)
NaCl	0.60	4.5	27.0	14.5	1.27(6)	80(3)	0.838(17)	0.146(17)	0.016(3)
NaCl	0.66	4.5	4.0	14.7	1.23(1)	182(12)	0.815(4)	0.166(4)	0.019(2)
NaCl	0.70	4.5	27.0	14.5	1.25(4)	80(3)	0.745(16)	0.211(15)	0.044(4)
NaCl	0.90	4.5	27.0	14.5	1.21(3)	80(3)	0.640(13)	0.255(13)	0.105(7)
CsCl	0.70	4.5	27.0	14.7	1.30(3)	80(3)	0.867(13)	0.067(14)	0.066(5)
CsCl	0.90	4.5	27.0	14.7	1.36(8)	80(3)	0.788(26)	0.105(26)	0.107(9)
KSCN	0.10	4.5	27.0	12.7	1.28(6)	–	0.888(7)	0.112(7)	0
NaI	0.40	4.5	27.0	14.5	1.02(5)	130(6)	0.626(18)	0.295(15)	0.079(4)
Na2SO4	0.22	4.5	27.0	14.6	1.49(2)	130(6)	0.670(5)	0.216(5)	0.114(3)
NaCl	0.70	2.5	27.0	13.5	1.10(6)	80(3)	0.819(23)	0.179(23)	0.002(4)
NaCl	0.10	9.0	27.0	14.0	2.30(4)	130(6)	0.856(7)	0.142(7)	0.002(1)
K2HPO4	0.10	9.5	27.0	13.6	2.15(6)	–	0.791(11)	0.209(11)	0
NaCl	0.10	10.5	27.0	13.7	2.52(9)	130(6)	0.755(15)	0.228(14)	0.017(2)
none	–	12.2	27.0	13.3	3.56(9)	130(6)	0.834(11)	0.152(11)	0.014(2)
NaCl	0.50	12.2	27.0	13.0	3.16(9)	130(6)	0.769(11)	0.210(11)	0.021(3)

^*BPTI concentration. B-values measured at other C_P values have been normalized to 14.5 mM (N_T = 3595) according to Eq. 5.

^†Uncertainty in the last position given within parentheses.

^‡The two shortest correlation times were held fixed in the fit: τ_R1 = 3.27 ns and τ_R2 = 26.3 ns at 27°C. At 4°C, these values were increased by a factor 1.994.

FIGURE 1.

¹H relaxation dispersion profile at 27°C from an aqueous solution containing 14.5 mM BPTI and 0.90 M NaCl at pH 4.5. The dispersion curve resulted from a constrained 3-Lorentzian fit according to Eqs. 1–4. The individual Lorentzian components (dashed curves) and the bulk water contribution (horizontal line) are also shown.

TABLE 2.

Results of N-Lorentzian fits to ¹H relaxation dispersion profile from a 14.5 mM BPTI solution with 0.90 M NaCl at pH 4.5 and 27°C

N	χ2*	τR1 (ns)†	τR2 (ns)†	τR3 (ns)†
1	68.0	36.8(3)
2	3.25	4.3(2)	51.8(8)
3	0.75	3.1(2)	35(3)	124(20)
3	1.03	3.27‡	26.3‡	80(3)

^*The reduced χ² should be close to unity if the model is correct and if the experimental errors are correctly estimated.

^†Uncertainty in the last position given within parentheses.

^‡These correlation times were held fixed in the fit.

The constrained fits yield, for each sample, three amplitude parameters b_n, which can be expressed as

(7)

where x_n is the fraction of BPTI molecules that belong to the n^th oligomer species or, equivalently, the weight fraction of that species. The intrinsic mean-square fluctuation amplitude β_n is proportional to the number of protons (per BPTI monomer) with residence times long enough (>τ_R,n) to sample the rotational diffusion of the oligomer but short enough (<1/(β_n τ_R,n)) to act as a relaxation sink for the observed water ¹H magnetization (Halle et al., 1999; Halle and Denisov, 2001). The fluctuation amplitude β₁ for the monomer is due to four internal water molecules and a pH-dependent number of rapidly exchanging labile BPTI protons (Venu et al., 1997). If these contributions are not the same for the decamer and the monomer, β₂ will differ from β₁. As argued below, any such differences are likely to be small.

Monomeric BPTI contains two intramolecular cavities, accommodating four internal water molecules (Wlodawer et al., 1987a) that dominate β at pH 4.5 (Venu et al., 1997). These internal water molecules are conserved in the decamer (Lubkowski and Wlodawer, 1999; Hamiaux et al., 1999). Cavities formed at the interfaces between adjacent BPTI molecules in the decamer might present long-lived hydration sites not present in the monomer, thereby making β₂ > β₁. A cavity search on the structure 1BHC (Hamiaux et al., 1999) using the program VOIDOO (Kleywegt and Jones, 1994) with 1.2 Å probe radius (Hubbard and Argos, 1995) revealed two small (30–50 ų), symmetry-related cavities in each of the five quasi-equivalent major interpentamer contact regions. In the crystal structure, no water molecules are located in these mainly nonpolar cavities. The central channel in the decamer can accommodate a few dozen water molecules, but is too wide (∼10 Å diameter) to provide the geometric constraints necessary for long-lived hydration (Denisov and Halle, 1996).

Another reason why β₂ might differ from β₁ is that labile BPTI protons contribute to different extents in monomer and decamer. This could happen if some of the involved side chains are buried at intermolecular contacts in the decamer, thereby retarding proton exchange and making β₂ < β₁. Furthermore, labile protons with residence times in the millisecond range could be in the fast-exchange limit for the monomer but not for the more slowly tumbling decamer, which would also make β₂ < β₁. At pH < 5, internal water molecules dominate β, which therefore is insensitive to moderate variations in the labile proton contribution. Moreover, most of the hydroxyl and carboxyl protons that contribute at low pH are fully exposed in the decamer. At pH > 8, ammonium and guanidinium protons make a large contribution to β, but all 110 such groups are solvent-exposed in the decamer. Calculations using known or estimated proton exchange rate constants and pK_a values (Venu et al., 1997; Denisov and Halle, 2002) show that also the second effect is negligible at the pH values studied here. (The effect could be significant in the pH range 5–8, where the labile protons in lysine and arginine side chains go from slow to fast exchange.)

These considerations justify the approximation β₂ = β₁ under the conditions of the present study. In the absence of structural information about the BPTI polymer, we assume that also β₃ = β₁. (We argue below that the polymer is a loosely associated trimer of decamers, for which we expect that β₃ = β₂.) These approximations can actually be tested with the aid of our dispersion data. Fig. 2 shows the summed amplitude B = b₁ + b₂ + b₃ for all 18 dispersions. As expected, B increases strongly with pH as base-catalyzed proton exchange brings more labile protons into the fast-exchange regime. In contrast, B is nearly invariant on addition of salt at constant pH, in particular for the NaCl series. Because the oligomer fractions x_n vary substantially with the salt concentration, as shown qualitatively by the dispersion profiles and quantitatively by the following analysis, also B = x₁β₁ + x₂β₂ + x₃β₃ should vary with salt concentration if β₂ or β₃ differ significantly from β₁. Because such a B variation is not observed, we set β₁ = β₂ = β₃ = B. The oligomer fractions, which must sum to unity, can then be obtained as

(8)

FIGURE 2.

Dependence of the summed mean-square dispersion amplitude B on (a) salt concentration at pH 4.5, and (b) pH. Panel a shows results for NaCl at 27°C (solid circles) or 4°C (open circles), CsCl (open squares), and, from left to right, KSCN, Na₂SO₄, and NaI (solid squares). Panel b shows results for no salt or 0.10 M NaCl (solid circles), 0.50 or 0.70 M NaCl (open circles), and 0.10 M K₂HPO₄ (solid square).

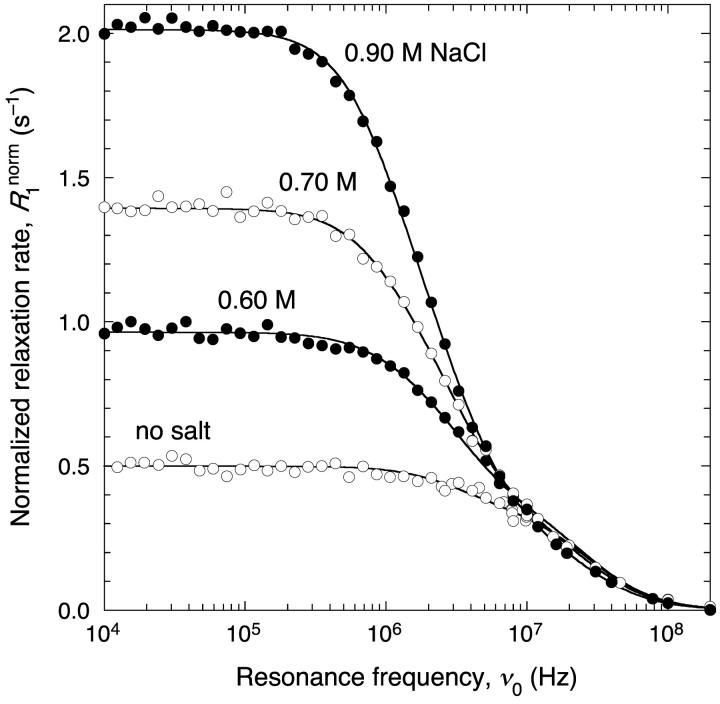
Effect of added salt on self-association

The ¹H relaxation rate from an aqueous BPTI solution is strongly enhanced at low frequencies on addition of NaCl, as seen from the dispersion profiles in Fig. 3. This observation demonstrates that added salt slows down the rotational diffusion of the BPTI molecules considerably. The data can be quantitatively described in terms of the rotational correlation times τ_R1 = 3.27 ns and τ_R2 = 26.3 ns expected for monomeric and decameric BPTI (see Materials and Methods) and a third correlation time, τ_R3 = 80 ± 3 ns, representing BPTI polymers (see Discussion).

FIGURE 3.

¹H relaxation dispersion profiles from aqueous BPTI solutions at 27°C, pH 4.5 and the indicated NaCl concentrations. The data have been normalized to 14.5 mM BPTI. The dispersion curves resulted from constrained fits according to Eqs. 1–4 with parameter values as given in Table 1. All data in Figs. 3, 5, and 8 were fitted jointly with a common τ_R3.

It is noteworthy that the salt dependence of the dispersion profile is strong even at salt concentrations where long-range electrostatic interactions are effectively screened. For example, the low-frequency ¹H relaxation rate is doubled on going from 0.6 to 0.9 M NaCl, whereas the Debye screening length only changes from 3.9 to 3.2 Å. If long-range electrostatic interactions were dominant, the dispersion profile should instead be most strongly affected at low salt concentrations. As seen from Fig. 4 a and Table 1, the decamer and polymer fractions continue to rise steeply up to the highest investigated salt concentration of 0.9 M NaCl. At this concentration, 25% of the BPTI molecules exist as decamers, whereas 10% form polymers.

FIGURE 4.

Fraction BPTI oligomers as a function of (a) salt concentration at pH 4.5 and (b) nominal net structural charge of BPTI. The shaded region is bounded from below (open symbols) by the polymer fraction x₃ and from above (solid symbols) by the sum of the decamer and polymer fractions, x₂ + x₃ = 1 − x₁. Panel a shows results for NaCl at 27°C (circles) or 4°C (squares), and for CsCl (triangles). Panel b shows results for ≤0.1 M NaCl (circles) and for 0.1 M K₂HPO₄ (squares). Sample pH was converted to BPTI charge Z with the aid of the titration curve in Fig. 7. The actual net charge per BPTI molecule in the decamer may differ due to association-induced pK_ashifts.

The finding that the decamer and polymer fractions continue to increase at high salt concentrations suggests that self-association of BPTI is promoted by weak binding of ions to specific sites or regions and not only by screening of the long-range Coulomb repulsion. It is therefore of interest to examine the dependence of self-association on ion type. Fig. 5 shows that replacement of Na⁺ by Cs⁺ leads to a moderate reduction of the dispersion amplitude. Inspection of Table 1 and Fig. 4 a shows that this reduction is caused mainly by a twofold reduction of the decamer fraction, with little difference in the polymer fraction.

FIGURE 5.

¹H relaxation dispersion profiles from aqueous BPTI solutions at 27°C, pH 4.5 and the indicated NaCl or CsCl concentrations. The data have been normalized to 14.5 mM BPTI. The dispersion curves resulted from constrained fits according to Eqs. 1–4 with parameter values as given in Table 1. All data in Figs. 3, 5, and 8 were fitted jointly with a common τ_R3.

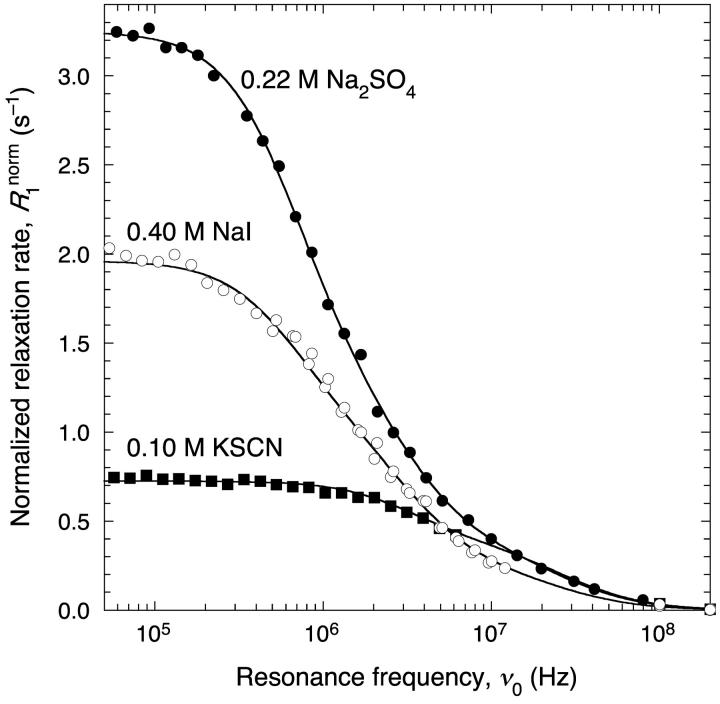
A much stronger ion-specificity is seen when the Cl⁻ ion is replaced by I⁻ or SO₄²⁻ (Fig. 6). In 0.4 M NaI, 30% of the BPTI molecules form decamers and 8% form polymers. This may be contrasted with 0.5 M NaCl, with 12% decamers and no significant amount of polymer (Table 1). The finding that I⁻ induces self-association of BPTI more strongly than Cl⁻ is consistent with I⁻ being more potent than Cl⁻ in salting out basic proteins (with a positive net charge) like BPTI (Collins and Washabaugh, 1985). The thiocyanate ion, an even more potent salting-out agent, was only examined at 0.1 M due to precipitation problems at higher KSCN concentrations. Already at this concentration, the decamer fraction is comparable to that in 0.5 M NaCl (Table 1). The sulfate ion, at the other end of the Hofmeister series (Collins and Washabaugh, 1985), was examined at 0.22 M Na₂SO₄ (Fig. 6). This corresponds to a Debye length of 3.7 Å, similar to that in 0.7 M NaCl (3.6 Å). Comparing these two solutions, we see that the decamer fraction is similar, whereas the polymer fraction is threefold higher with sulfate than with chloride (Table 1). The solubility curve of BPTI is similar for NaCl and (NH₄)₂SO₄ (Lafont et al., 1997). If Na₂SO₄ behaves as (NH₄)₂SO₄ in this regard, then our 0.22 M Na₂SO₄ sample is quite far from the solubility curve. Yet, the oligomer fractions are similar to those in 0.9 M NaCl, which is close to the solubility limit.

FIGURE 6.

¹H relaxation dispersion profiles from aqueous BPTI solutions at 27°C, pH 4.5 and the indicated salt types and concentrations. The data have been normalized to 14.5 mM BPTI. The dispersion curves resulted from constrained fits according to Eqs. 1–4 with parameter values as given in Table 1. All data in Fig. 6 were fitted jointly with a common τ_R3.

Effect of protein charge and temperature on self-association

All dispersion profiles discussed so far were recorded at pH 4.5, where the net charge Z of BPTI is +6.4. To further investigate the effect of electrostatic interactions on self-association, we made measurements from pH 2.5 to 12.2, thus varying the net charge of BPTI from +10.1 to −6.5 (Fig. 7). As expected, increasing Z to +10.1 (at pH 2.5) tends to suppress self-association even in 0.70 M NaCl (Fig. 8). The quantitative analysis shows that the effect of increased net charge is essentially to reduce the polymer fraction, whereas the decamer fraction is nearly the same, ∼20%, at pH 2.5 and 4.5 (Table 1).

FIGURE 7.

Net charge of monomeric BPTI as a function of pH, calculated from published pK_a values (Wüthrich and Wagner, 1979). The pH values of samples examined here are indicated by points.

FIGURE 8.

¹H relaxation dispersion profiles from aqueous BPTI solutions with 0.70 M NaCl at 27°C and pH 4.5 (Z = +6.4) or pH 2.5 (Z = +10.1). The data have been normalized to 14.5 mM BPTI. The dispersion curves resulted from constrained fits according to Eqs. 1–4 with parameter values as given in Table 1. All data in Figs. 3, 5, and 8 were fitted jointly with a common τ_R3.

If BPTI self-association were completely governed by long-range forces, as in the Derjaguin-Landau-Verwey-Overbeek theory (Leckband and Israelachvili, 2001), a reversal of the net protein charge should not affect self-association. Contrary to this prediction, we find (Fig. 4 b) much stronger self-association at pH 12.2 (Z = −6.5) than at pH 4.5 (Z = +6.4). This is the case in the absence of salt as well as in 0.50 M NaCl (Fig. 9). This finding points to the importance of individual charged residues in BPTI, rather than just the net charge of the protein.

FIGURE 9.

¹H relaxation dispersion profiles from aqueous BPTI solutions at 27°C with no salt or 0.50 M NaCl and at pH 4.5 (Z = +6.4) or pH 12.2 (Z = −6.5). The data have been normalized to 14.5 mM BPTI. The dispersion curves resulted from constrained fits according to Eqs. 1–4 with parameter values as given in Table 1. The pH 12.2 data in Fig. 9 and the data in Fig. 6 were fitted jointly with a common τ_R3.

We also examined self-association in 0.1 M K₂HPO₄, the salting-out agent used to produce monomeric BPTI crystals of forms I–III (Deisenhofer and Steigemann, 1975; Wlodawer et al., 1984, 1987b). The dispersion profile at pH 9.5 (data not shown) is bi-Lorentzian with 21% decamer (Table 1). An (unconstrained) mono-Lorentzian dispersion fails to describe the data (χ² = 8.8). We thus find appreciable decamer fractions (14–23%) in all samples investigated at basic pH values (9.0–12.2). In fact, we find larger decamer fractions at high pH than at low pH under otherwise comparable conditions (Table 1). In contrast, decameric crystals have so far only been grown from solutions of pH 4.5 (Hamiaux et al., 1999, 2000) or pH 7.0 (Lubkowski and Wlodawer, 1999), whereas monomeric crystals have been obtained from solutions of pH ≈ 10 (Deisenhofer and Steigemann, 1975; Wlodawer et al., 1984, 1987b). Apparently, oligomerization in solution is not simply related to the thermodynamic stability of oligomeric crystals.

In NaCl solution, the solubility of BPTI increases with decreasing temperature (Lafont et al., 1994). At given protein and NaCl concentrations, the solution will therefore be further removed from the solubility curve at low temperature. Fig. 10 shows the dispersion profiles at 4°C and pH 4.5 in the absence of salt and in 0.66 M NaCl. Apart from the trivial η/T scaling (where η is the solvent viscosity) of all correlation times (see Materials and Methods), the dispersions are very similar to the corresponding ones at 27°C. In fact, the temperature variation of the decamer and polymer fractions is hardly significant (Table 1 and Fig. 4 a).

FIGURE 10.

¹H relaxation dispersion profiles from aqueous BPTI solutions at 4°C and pH 4.5 with no salt or 0.66 M NaCl. The data have been normalized to 14.5 mM BPTI. The dispersion curves resulted from constrained fits according to Eqs. 1–4 with parameter values as given in Table 1.

Decamer lifetime

To determine the mean lifetime τ_dec of the BPTI decamer, we performed a salt-jump experiment where the NaCl concentration was changed from 0.90 to 0.45 M and the subsequent approach to oligomerization equilibrium at the new salt concentration was followed by recording R₁ at a single frequency (100 kHz) on the low-frequency plateau (Fig. 11). Within experimental accuracy, this relaxation process was single-exponential with a time constant τ_relax = 43 ± 2 min. We shall now relate the relaxation time τ_relax to the decamer lifetime τ_dec.

FIGURE 11.

The insert shows ¹H relaxation dispersion profiles recorded at 27°C from a 14.0 mM BPTI solution with 0.45 M NaCl and pH 4.5, made by mixing equal volumes of two BPTI solutions with no salt and 0.90 M NaCl. The initial dispersion profile is the average of the (concentration normalized) profiles from the original solutions and thus corresponds to the initial nonequilibrium state obtained by suddenly reducing the NaCl concentration from 0.90 to 0.45 M. The final dispersion profile was recorded one week after the salt jump. The main figure shows the time evolution of R₁, measured at 100 kHz (see dashed line in the insert). Note the change of scale at 300 min on the time axis. The curve resulted from a three-parameter fit according to Eq. 6. Omission of the t = 0 point, taken from the initial dispersion profile in the insert, had no discernable effect on the fit.

For the moment, we neglect the polymer fraction and consider only the decamer association-dissociation equilibrium 10 P ↔ P₁₀. The time-dependent relaxation rate in Fig. 11 can then be expressed as (see Eqs. 1–4):

(9)

where . All our dispersion profiles indicate that the decamer is formed cooperatively, with negligible concentrations of intermediate oligomers (dimers to 9-mers). The evolution of the decamer fraction x₂(t) is then independent of the kinetic mechanism of decamer formation, e.g., sequential association of dimers. If the deviation from the final oligomerization equilibrium is small at all times, we may linearize the rate equations (Eigen, 1964). To test this approximation, we analyzed the R₁(t) data with the initial point (open circle in Fig. 11) excluded. This had no significant effect on the derived parameters. Under these conditions, it can be shown that decays exponentially and that Eq. 9 yields

(10)

where the superscripts refer to t = 0 and t → ∞. Furthermore,

(11)

Because the polymer fraction is significant at the initial time (, from Table 1), we should really consider the two coupled equilibria 10 P ↔ P₁₀ and mP₁₀ ↔ P_10m, with m = 3 − 4 (see Discussion). The kinetic analysis then predicts a biexponential decay of R₁(t). However, if the polymer consists of weakly associated decamers (see Discussion), it should have a much shorter lifetime than the compact decamer. If this is so, then R₁(t) should exhibit a transient phase on an unobservably short timescale, followed by a much slower exponential decay with

(12)

Because is negligibly small at 0.45 M NaCl (Table 1), we can use Eq. 11 despite the initial presence of a significant polymer fraction. Taking (Table 1), we thus obtain a decamer lifetime of τ_dec = 101 ± 4 min at 27°C. This result is consistent with the lower bound on τ_dec of 10 min established by gel filtration (Hamiaux et al., 2000).

DISCUSSION

The picture of BPTI self-association derived from the present MRD data differs in important ways from what has been deduced by other methods. To resolve these differences, we reexamine relevant aspects of earlier work. We then show how our results can be rationalized in terms of the decamer crystal structure.

Translational diffusion

The MRD approach to protein self-association exploits the slowing down of rotational diffusion as monomers form stable oligomers. Oligomerization also retards translational diffusion, but the effect is smaller. Self-association of BPTI has been studied extensively by measuring the protein self-diffusion coefficient D_S by PGSE NMR (Stilbs, 1989) or the collective diffusion coefficient D_C by DLS (Berne and Pecora, 1976). A complication in such studies is that the measured diffusion coefficient may differ from D₀, the diffusion coefficient of the isolated monomer (at infinite dilution), not only because of the formation of stable oligomers but also because of other interactions (that do not give rise to stable oligomers), including hard-core repulsion (excluded volume), screened Coulomb repulsion, and hydrodynamic interaction (Wills and Georgalis, 1981; Gallagher and Woodward, 1989). At sufficiently low protein concentration C_P, the observed diffusion coefficient is predicted to vary linearly according to (X = S or C),

(13)

To remove the trivial dependence of D₀ on temperature and solvent viscosity η, a hydrodynamic radius R_H is often calculated from the Stokes-Einstein relation,

(14)

In the linear regime of Eq. 13, all effects of self-association are contained in the interaction parameter k_X, which also carries information about other interactions. If monomers associate to N-mers in a fully cooperative way (with negligible concentration of intermediate oligomers), then the leading contribution from self-association to D_X is of order . Consequently, studies of translational diffusion in the linear regime do not furnish information about cooperative self-association beyond the dimer level in any other way than via the indirect effect of self-association on the effective interoligomer interactions. In particular, if BPTI decamers assemble with strong cooperativity (as suggested by the absence of smaller oligomers, inferred from a recent SAXS study (Hamiaux et al., 2000) and from the present MRD study), then they could hardly be detected by DLS or PGSE measurements in the linear regime. Furthermore, it is important to realize that the limiting diffusion coefficient D₀, obtained by linear extrapolation of D_X to C_P = 0 within the asymptotic linear regime, always (whether or not self-association is cooperative) refers to the monomer.

PGSE studies of BPTI self-association

For BPTI in 10 mM D₂O buffer of pH 4.5 at 1°C, D_S was found to decrease linearly in the range 0.1–0.8 mM BPTI with D₀ = (7.7 ± 0.1) × 10⁻¹¹ m² s⁻¹ and k_S = −51 M⁻¹ (Pan et al., 1997). Inserting this D₀ value and the viscosity of D₂O at 1°C, η = 2.326 cP, into Eq. 14, we obtain the hydrodynamic radius R_H = 11.2 ± 0.2 Å. (In contrast, the authors of the PGSE study obtained R_H = 15.2 Å, presumably by using instead the viscosity of H₂O.) Another PGSE study, employing a different pulse sequence, reported D_S = (19.15 ± 0.45) × 10⁻¹¹ m² s⁻¹ for 0.5 mM BPTI in 50 mM buffer (95% H₂O/5% D₂O) of pH 6.2 at 25°C (Krishnan et al., 1999). Using the viscosity (0.900 cP) of this water isotope mixture at 25°C, we obtain R_H = 12.7 ± 0.3 Å. Correcting for the finite BPTI concentration with the aid of the k_S value quoted above, we get 12.3 Å.

In the only PGSE study to directly address the issue of BPTI self-association, D_S was measured as a function of temperature (from −2 to +41°C) at three BPTI concentrations (0.15, 1.5, and 4.6 mM) in D₂O with 0.15 M NaCl at pH 5.5 (Ilyina et al., 1997). These authors plotted log D_S versus 1/T and observed, for the two higher BPTI concentrations, a curvature below 10°C which they took as evidence for dimerization at low temperatures. However, this argument is based on the assumption that the viscosity of D₂O obeys the Arrhenius law quantitatively over the investigated temperature range. This is not the case: a plot of log(T/η) versus 1/T shows the same deviation from linearity as the log D_S plot. In fact, for the two higher BPTI concentrations, D_S varies linearly with T/η within the experimental accuracy, as expected in the absence of self-association (and temperature-dependent long-range interactions). Using the slopes of the D_S versus T/η plots, we find that 1/R_H varies linearly with C_P, yielding R_H = 12.6 Å (at C_P = 0) and k_S = − 34 M⁻¹.

The limiting (C_P = 0) hydrodynamic radius deduced from all reported PGSE studies of BPTI are surprisingly small: R_H = 11.2–12.6 Å. From hydrodynamic bead-model calculations (Garcia de la Torre et al., 2000) on the BPTI monomer structure 5PTI, we find a highly linear relation between R_H and the bead radius: R_H/Å = 12.45 + 1.11 a_H/Å (r = 0.9995). Clearly, the experimental R_H values cannot be rationalized for any physically reasonable bead radius. With a_H = 2.88 Å, as obtained from the rotational correlation time of the BPTI monomer (see Materials and Methods), we obtain R_H = 15.6 Å. (On the basis of experimental hydrodynamic data for a variety of proteins, a “best” value of 3 Å was obtained for a_H (Garcia de la Torre et al., 2000).) If the hydrodynamic model is accepted, we are forced to conclude that the cited PGSE data overestimate the self-diffusion coefficient of BPTI by some 20%.

In their PGSE study, Ilyina et al. (1997) also presented the variation of D_S with BPTI concentration (0.15–5.3 mM) at −2°C (pH 5.5, 0.15 M NaCl). These data reveal a significant (positive) curvature in the function D_S(C_P), which was rationalized by a monomer-dimer equilibrium model. However, this analysis attributes the concentration dependence in D_S (19% reduction of D_S over the investigated C_P range) entirely to dimerization, ignoring the concentration dependence from other interactions. The latter is presumably responsible for the interaction parameter k_S = −34 M⁻¹, derived from the linear D_S(C_P) plots obtained at higher temperatures (where dimerization is not indicated). This k_S value implies that interactions should reduce D_S by 17% over a 5 mM C_P range, leaving little room for dimerization effects. In conclusion, we feel that neither the T dependence nor the C_P dependence of D_S provides compelling evidence for self-association of BPTI. We note also that decamer formation is completely negligible at the low BPTI and salt concentrations used in the PGSE study: on the basis of our MRD data at 4°C in the absence of salt, we estimate a decamer fraction of 5 × 10⁻⁶ at C_P = 5 mM.

DLS studies of BPTI self-association

In their thorough DLS study of BPTI self-association, Gallagher and Woodward (1989) found that D_C decreases linearly over the investigated C_P range (0.5–10 mM at pH 5.5, 0.3 M KCl, 20°C). The wide extent of the linear range, also observed at other pH values and salt concentrations, led the authors to conclude that stable dimers do not form under the investigated conditions. Our MRD results indicate that the decamer fraction should have been unobservable (<0.3%) under the conditions of the DLS study. The DLS data yield a hydrodynamic radius, R_H = 14.9 ± 0.2 Å. As expected, R_H (but not k_C) was found to be independent of pH (2.6–9.9) and NaCl concentration (0.1–0.5 M). The experimental R_H value is reproduced by hydrodynamic calculations on the BPTI monomer for a reasonable bead radius of 2.20 Å (see above). With this bead radius, we calculate R_H = 30.8 Å for the decamer structure 1BHC.

Subsequent DLS studies of BPTI self-association (Veesler et al., 1996; Lafont et al., 1997) reported = (9.3 ± 0.2) × 10⁻¹¹ m² s⁻¹ and R_H = 23.1 ± 0.5 Å at pH 4.9 and 20°C under a variety of high-salt conditions (1.0–2.0 M NaCl, 0.25–0.35 M KSCN, and 1.25–1.75 M (NH₄)₂SO₄). (Since the viscosity varies by 32% among these solvents, we assume that all reported diffusion coefficients have been normalized to the viscosity of pure H₂O.) Comparing their R_H value with that (14.9 Å) obtained under low-salt conditions and attributed to the BPTI monomer (Gallagher and Woodward, 1989), the authors concluded that BPTI forms a tetramer under the investigated high-salt conditions (Lafont et al., 1997). The limiting diffusion coefficient, , determined by these authors is an apparent one, obtained by linear extrapolation of D_C values measured in a narrow range of relatively high BPTI concentrations, e.g., C_P = 7–16 mM in the case of 1.0 M NaCl (Veesler et al., 1996). At lower BPTI concentrations, D_C must approach the limiting diffusion coefficient, , of the monomer in a nonlinear way. The high-C_P extrapolation rests on the assumption that monomers do not contribute to the measured D_C (S. Veesler, personal communication).

A cumulant analysis of the DLS autocorrelation function yields the z-average diffusion coefficient (Berne and Pecora, 1976),

(15)

where x is the decamer fraction (denoted by x₂ in the foregoing MRD analysis). Two assumptions are now invoked. First, both numerator and denominator are taken to be dominated by the (second) decamer term, so that D_C = (10/9) . Second, is taken to depend linearly on C_P, as in Eq. 13. Extrapolation to C_P = 0 then yields . Because this approach simultaneously invokes a high-C_P approximation (large x) and a low-C_P approximation (linear ), it is difficult to assess its validity quantitatively. Furthermore, although the first approximation eliminates the explicit x dependence, an implicit x dependence is retained in the (linear) interaction parameter. From the reported = (9.13 ± 0.2) × 10⁻¹¹ m² s⁻¹ in 1–2 M NaCl (Veesler et al., 1996) and the monomer value, = (14.4 ± 0.2) × 10⁻¹¹ m² s⁻¹ (Gallagher and Woodward, 1989), both at 20°C, we obtain = 1.75 ± 0.05. The significant deviation of this result from the crystal structure-based hydrodynamic prediction (see above), , is presumably caused by the approximations inherent in the DLS analysis.

In another DLS study (Tanaka et al., 2002), published after the discovery of decameric BPTI crystals, D_C was reported to vary linearly with C_P (0.8–13 mM, below the solubility limit) in 1 M NaCl at pH 5.0 and 20°C. Extrapolation to C_P = 0 yielded R_H = 25.0 ± 0.6 Å, similar to the 23.1 Å obtained previously in 1 M NaCl at pH 4.9 (Veesler et al., 1996). Now, however, this was attributed to a mixture of decamers and monomers. However, if both species contribute, then D_C should not vary linearly with C_P (see Eq. 15). It was also reported that changing pH from 5.0 to 7.0 yielded a hydrodynamic radius, R_H = 15.0 ± 0.8 Å, consistent with monomers. It was thus concluded that decamers form at pH 5.0, but not at pH 7.0 (Tanaka et al., 2002). This interpretation is at variance with our MRD results, showing that the decamer fraction increases with decreasing net charge (increasing pH) and reaches a maximum at the isoelectric point (Fig. 4 b and Table 1). Moreover, it is difficult to understand how the very small change (0.2 units) in the net charge of BPTI between pH 7.0 and 5.0 (Fig. 7) could increase the decamer fraction from 0 to 80% (as implied by the R_H values).

SAS studies of BPTI self-association

Like translational (DLS, PGSE) and rotational (MRD) diffusion, small-angle scattering (SAS) of x-rays or neutrons can furnish molecular-level information about protein self-association in solution. The fundamental problem in SAS studies is to separate the form factor from the structure factor, i.e., to separate the effects on the measured scattering intensity from intraoligomer and interoligomer spatial correlations, respectively (Tardieu et al., 1999; Spinozzi et al., 2002). Under favorable conditions, usually meaning low protein concentration and high salt concentration, interoligomer correlations may be neglected. The scattering profile then provides the population-weighted average form factor, a low-resolution measure of the size and shape of the oligomer species present in solution.

Earlier SAXS data from BPTI solutions were only interpreted qualitatively as a progression from repulsive to attractive effective interactions (in the sense of the second virial coefficient) with increasing salt concentration (Veesler et al., 1996; Lafont et al., 1997). However, a recent extensive SAXS study has provided more detailed information (Hamiaux et al., 2000). This study reported scattering profiles for relatively dilute BPTI solutions (3.1 or 4.6 mM) at high concentrations (on either side of the solubility limit) of NaCl, KSCN, and (NH₄)₂SO₄ at pH 4.5 and 20°C. The scattering profiles were modeled in terms of binary mixtures of monomers, dimers, pentamers, or decamers with form factors computed from the crystal structure and under the assumption of negligible interoligomer correlations. Acceptable fits could only be obtained for monomer-decamer mixtures, the relative populations of which were thus determined.

A direct comparison with our MRD results is complicated by differences in protein and salt concentrations. The only common salt concentration is 0.1 M KSCN, where we find a decamer fraction x = 0.112 at C_P = 12.7 mM (Table 1). Assuming fully cooperative self-association, this translates into an association constant K = 4.3 × 10¹⁵ M⁻⁹, which yields x = 4 × 10⁻⁵ at C_P = 4.6 mM. Consistent with this prediction, no decamers were detected by SAXS in 0.1 M KSCN at this BPTI concentration (Hamiaux et al., 2000). The SAXS study covered the range 1.2–1.8 M NaCl with C_P = 4.6 mM, whereas our MRD data covers 0–0.9 M NaCl with C_P = 12.9–14.5 mM. To compare these two sets of data, we use the decamer fraction x to compute the stoichiometric association constant, , for a decamer formed with full cooperativity. We then calculate the standard free energy of association as ΔG° = , with the standard-state concentration C° = 1 M. Fig. 12 shows how ΔG° varies with NaCl concentration. Because the solution is not ideal (especially at low salt concentration), K cannot be expected to be fully independent of C_P. Nevertheless, Fig. 12 suggests that the MRD and SAXS data follow the same general trend. We note that the salt effect is strongest at high salt concentrations, in contrast to what would be predicted by a linear screening model of Debye-Hückel type.

FIGURE 12.

Standard free energy of association for BPTI decamers deduced from decamer populations determined by MRD at 27°C (circles, this work) or by SAXS at 20°C (squares, Hamiaux et al., 2000), both at pH 4.5. The fitted quadratic polynomial lacks physical significance. Error bars are propagated from an assumed uncertainty of ±0.03 in all decamer fractions.

In the SAXS study (Hamiaux et al., 2000), a systematic deviation was observed in the monomer-decamer fits at low scattering angles (q < 0.01 Å⁻¹). This feature might be caused by polymers and/or interoligomer correlations (giving rise to a q-dependent structure factor). Even though satisfactory fits were obtained by allowing for higher oligomers (whose stoichiometry could not be unambiguously determined), the authors, on the basis of a singular value decomposition, favored an interpretation in terms of interoligomer correlations. In the former case, and assuming that the large aggregates are formed by association of two decamers, the SAXS data yield a fraction 0.05 ± 0.01 in the range 1.2–1.8 M. In contrast, our MRD data yields a polymer fraction that increases from 0 to 0.10 in the range 0–0.9 M (Table 1). Possibly, these results could be reconciled by allowing the low-q SAXS intensity to be affected by both polymers and interoligomer correlations. Another SAXS study (Budayova-Spano et al., 2000) found from a Guinier analysis that the apparent radius of gyration, R_G, increases from 13 to 24 Å when C_P increases from 0.8 to 4.6 mM in 1.4 M NaCl at pH 4.5 and 20°C. With R_G calculated from crystal structures of the monomer (5PTI, R_G = 11.0 Å) and the decamer (1BHC, R_G = 22.9 Å) and the decamer fraction (x = 6 × 10⁻⁶ and 0.37 at C_P = 0.8 and 4.6 mM) estimated from SAXS data (Hamiaux et al., 2000), we obtain 11.0 and 21.6 Å for the apparent R_G at C_P = 0.8 and 4.6 mM. BPTI polymers, interoligomer correlations, and hydration effects may also contribute to the experimental apparent R_G.

Decamer structure, interactions, and crystallization

As a basis for the following discussion, we show in Fig. 13 the structural model 1BHC of the BPTI decamer in crystal form A (Hamiaux et al., 1999). Although the structure of the oligomer present in solution has not been unambiguously identified, our MRD study, as well as an earlier SAXS study (Hamiaux et al., 2000), strongly suggests that the crystal decamer also exists in solution. Indeed, given the intimate association of the BPTI molecules within the decamer and the weak interactions between adjacent decamers in crystal forms A, B, and C (Hamiaux et al., 1999, 2000), it seems likely that the decamer is assembled in the solution from which the crystals grow (Janin and Rodier, 1995).

FIGURE 13.

The BPTI decamer, rendered with GRASP (Nicholls et al., 1991) using the atomic coordinates from the form A crystal structure 1BHC (Hamiaux et al., 1999). The upper pentamer contains monomers A–E, with E (left) and C (right) in front, and D removed. The lower pentamer contains monomers F–J, with H (left) and J (right) in front, and I removed. The color coding represents surface electrostatic potential on a scale from −15 (red) to +15 k_BT/e (blue), calculated with dielectric constants of 4 (protein) and 80 (solvent), 0.5 M salt, and full structural charges (Z = +6). Some of the Lys-46 residues (deep blue) can be seen protruding toward the center of the channel, whereas four Asp-3 residues (light red) are visible as protrusions near the equator at the extreme left and right of the decamer.

The decamer consists of 10 quasi-equivalent BPTI monomers and is generated by orthogonal fivefold and twofold (noncrystallographic in 1BHC) symmetry operations. Each BPTI molecule makes contact with four other molecules within the decamer. There are two intrapentamer contacts (e.g., AB and AE), each burying 600 Ų of accessible (1.4 Å probe radius) surface area (ASA), and two interpentamer contacts, burying 750 Ų (AF) and 1200 Ų (AG) (Hamiaux et al., 2000). These four contact interfaces involve neither the primary binding loop (residues 13–18) that is essential for inhibition of bovine β-trypsin (Krowarsch et al., 1999), nor the nonpolar surface region thought to be responsible for the putative BPTI dimer (Zielenkiewicz et al., 1991). The largest interface (AG) involves 18 contacts (<3.5 Å) between polar atoms, including two symmetry-related ion pairs (Glu-49–Arg-20) at the rim of the contact surface (Hamiaux et al., 1999).

In terms of buried surface area and number of polar atomic contacts, the AG dimer is comparable to biologically functional heterodimers (Horton and Lewis, 1992; Lo Conte et al., 1999). For example, the BPTI-trypsin complex buries 1430 Ų with 12 hydrogen bonds (Lo Conte et al., 1999). This noncovalent complex has a standard free energy of association ΔG° = −18 kcal mol⁻¹ at pH 8.0 and 25°C (Vincent and Lazdunski, 1972). The extent and complementarity of the contact interface in the AG dimer suggests that the formation of this dimer is the first step in decamer assembly (Hamiaux et al., 2000). The AG dimers must have a high affinity for self-association to the decamer level, because neither MRD nor SAXS (Hamiaux et al., 2000) can detect a significant equilibrium dimer population.

Along the fivefold axis, the otherwise compact BPTI decamer is pierced by a channel with a uniformly high positive surface potential. In the central part of this channel, two pentagonal rings of lysine side chains (Lys-46) protrude from the cavity wall (Fig. 13). The solvent-excluded volume enclosed by these 10 lysine NZ atoms is ∼600 ų. In crystals grown in the presence of SO₄²⁻ or SCN⁻, four or five anions have been localized in this region (Lubkowski and Wlodawer, 1999; Hamiaux et al., 1999, 2000). The central third of the 45 Å-long channel also contains ten arginines (Arg-20) embedded in the cavity wall and forming tight ion pairs with Glu-49. Furthermore, the channel is lined at both ends by five arginines (Arg-17) which, together with ten additional positive charges (Lys-15 and Arg-39) exposed on the flat upper and lower external surfaces of the decamer, will attract anions to the rather narrow (6.5 Å solvent-excluded diameter) channel mouths. In total, the channel thus carries 20 positive charges that are not ion-paired. Such a high concentration of charge surrounded by a medium of low polarizability provides a strong driving force for charge neutralization by two mechanisms: sequestering of anions within the channel and deprotonation of some of the basic residues. The latter mechanism is most likely to operate on the less basic and more concentrated Lys-46 residues. A substantial pK_a shift can also be expected for Asp-50, which is located in the AG interface with merely 2.5 Å between the Asp-50 OD atoms from the two monomers. Anion sequestering within the channel is not necessarily limited to the central five binding sites discerned in the crystal structures, but may include additional ions that are not sufficiently well-localized to be crystallographically visible. (The resolution limit of the four published decamer crystal structures ranges from 2.1 to 2.8 Å.)

Decamer formation is entropically opposed by the loss of 27 translational and 27 rotational degrees of freedom. According to elementary statistical mechanics (McQuarrie, 1976), this contributes −TΔS° = 262 kcal mol⁻¹ to the standard free energy of association. This entropic penalty is diminished by 54 new internal degrees of freedom in the decamer (Tidor and Karplus, 1994), but it is clear that a substantial attractive interaction free energy is required to produce a net ΔG° of −20 to −33 kcal mol⁻¹ (Fig. 12). As with protein folding, protein association results from a small difference of many opposing enthalpic and entropic terms, including ion pairing, hydrogen bonding, van der Waals attraction, and solvation. Although it is a daunting task to quantify all these contributions (Janin, 1995), the data in Fig. 12 show that decamer formation is more favorable at high salt concentrations by ∼10 kcal mol⁻¹. Moreover, most of the salt effect comes at concentrations >0.5 M, where Debye-Hückel screening is essentially complete. This concentration dependence, as well as the dependence of ΔG° (or the decamer fraction) on ion type, points to the crucial involvement of the highly charged and narrow decamer channel. This channel allows anions to be sequestered from the external solution, thereby reducing the high internal positive charge density that would otherwise prevent decamer formation.

In the BPTI decamer, each monomer buries 1625 Ų (Hamiaux et al., 2000), or 40% of the ASA of the free BPTI molecule. Since decamer-decamer contacts are few (Hamiaux et al., 1999), we expect that BPTI buries 40–45% of its ASA in crystal form A. Although this is close to the 42.5% buried ASA in the monomeric crystal form II (Islam and Weaver, 1990), decameric and monomeric crystals differ greatly in the distribution of crystal contacts. Among the very few interdecamer contacts in crystal form A, nearly all involve Asp-3. This side chain protrudes from the external decamer surface (Fig. 13), forming ten “handles” that, in the crystal, make ion pairs with Lys-26, Lys-41, and Arg-39 residues from adjacent decamers (Hamiaux et al., 1999). As we shall now argue, this structural feature provides important clues for the interpretation of our MRD data.

According to conventional wisdom, protein crystals grow from monodisperse solutions (Rosenberger et al., 1996). This working hypothesis appeared to be supported by DLS studies of BPTI under conditions that promote crystallization of the decameric crystal forms A–C (Veesler et al., 1996; Lafont et al., 1997). However, more recent SAXS data have shown (more convincingly) that decameric BPTI crystals grow from a mixture of monomers and decamers (Hamiaux et al., 2000; Budayova-Spano et al., 2002). Under conditions (pH 9–10) that yield the monomeric crystal forms I–III, it was concluded on the basis of DLS data that only monomers are present in solution (Tanaka et al., 2002). This conclusion is incompatible with our MRD results, showing that the decamer fraction is, in fact, higher at pH 9.0–10.5 than at pH 4.5. In particular, at pH 9.5 in 0.1 M K₂HPO₄ and 13.6 mM BPTI—conditions that closely match those used to grow form II crystals (Wlodawer et al., 1984)—21% of the BPTI molecules form decamers (Table 1).

Why, then, are monomeric crystals obtained at high pH and decameric crystals at low pH? Clearly, the degree of self-association in solution does not determine the crystal form. Instead, we propose that the critical factor is the ability to form decamer-decamer contacts. At pH ≥ 9.5, Lys-26 and Lys-41 will be at least partly deprotonated, thereby preventing formation of the strong ion pairs with Asp-3 that are essential for the stability of decameric crystals (Hamiaux et al., 1999). Thus, although high pH favors decamer formation by reducing electrostatic repulsion within the decamer, the lack of appropriate ion-pairing partners prevents these decamers from associating further.

In the light of the preceding discussion, it seems likely that the polymer species detected by MRD consists of a few decamers held together by the same ion-pair contacts as are seen in the decameric crystal. Consistent with this hypothesis, we find no polymers under conditions (pH 9.5) where monomeric crystals grow and very low populations under other high pH conditions (Table 1). Furthermore, we find no polymers at pH 2.5 (even with 0.7 M NaCl), where Asp-3 is essentially protonated.

At pH 4.5, the polymer fraction increases with increasing salt concentration (see the NaCl series in Table 1). At first sight, this might be interpreted as a consequence of salt screening of the decamer charge. However, this effect is observed over a range of salt concentrations (0.5–0.9 M) where the Coulomb repulsion is effectively screened (the Debye length varies from 4.3 to 3.2 Å). Instead, we believe that the principal salt effect is exerted on the free energy of decamer formation (Fig. 12). For self-association of M decamers, the association constant K_M can be expressed in terms of the decamer (x₂) and polymer (x₃) fractions reported in Table 1 and the total BPTI concentration C_P as

(16)

Since the decamers are efficiently screened under the conditions of interest, we can regard K_M as independent of salt concentration. As shown in Fig. 14, the predicted relation is indeed obeyed by the data, and the fit yields M = 3.4 and K_M = 2.4 × 10⁷ M^−2.4. The close agreement between the aggregation number M and the ratio of the polymer and decamer correlation times, τ_R3/τ_R2 = 80/26.3 = 3.0, supports this interpretation.

FIGURE 14.

Relation between the polymer and decamer fractions at different salt concentrations (0.6–0.9 M NaCl, pH 4.5, with C_P = 14.5 mM, 27°C). The curve resulted from a fit according to Eq. 16, yielding M = 3.4.

The decamer clusters that we believe are responsible for the lowest-frequency relaxation dispersion step may be regarded as subcritical crystallization nuclei. The concentration of such clusters increases strongly with salt concentration up to 0.9 M NaCl (Fig. 14), driven by a concomitant increase in the concentration of “free” decamers. The BPTI concentration (14.5 mM) used for the measurements in Fig. 14 falls on the solubility curve for ∼1.1 M NaCl at pH 4.5 and 27°C (Lafont et al, 1994; Farnum and Zukoski, 1999). Above 0.9 M NaCl, we expect that the decamer clusters increase further in concentration and grow to the critical size required for spontaneous crystal growth.

Biological relevance

While BPTI is a valuable model system for studying protein self-association and crystallogenesis, it is not clear whether BPTI self-associates in vivo. Might the shape complementarity and favorable interactions responsible for the compactness and stability of the BPTI decamer have evolved under evolutionary pressure? To address this issue, we must consider the cellular environment of BPTI.

The in vivo synthesis of BPTI occurs in mast cells (Fritz et al., 1979), highly specialized cells found in most bovine organs and involved in a variety of allergic reactions and inflammatory conditions (Forsberg et al., 1999). Half of the mast cell volume is occupied by secretory granules, densely packed with enzymatically active proteases, other proteins, mucopolysaccharides, and histamine, all of which are released into the extracellular space in response to external stimuli (Kendall, 1988; Beil et al., 2000). Among the granule proteins is tryptase, a trypsin-like serine protease. Bovine tryptase is inhibited by BPTI and the two proteins are co-localized within the granules in equimolar amounts (Fiorucci et al., 1995). The physiological function of BPTI may thus be to control tryptase activity (Fritz et al., 1979; Fiorucci et al., 1995).

The enzymatically active form of human tryptase is a homotetramer stabilized by a 10-disaccharide segment of the sulphated glycosaminoglycan heparin, which binds to positively charged regions of the external tetramer surface (Alter et al., 1987; Sommerhoff et al., 2000). The electrophoretic mobility of bovine tryptase suggests that it forms a dodecamer (Fiorucci et al., 1998). Heparin is synthesized exclusively in mast cells and is a major constituent of the granules (Fritz et al., 1979; Lindahl et al., 1986), interacting with histamine and a variety of proteins (Alter et al., 1987; Petersen et al., 1993; Beil et al., 2000; Sommerhoff et al., 2000; Hallgren et al., 2000). By neutralizing the positive charge of basic proteins, heparin apparently allows them to pack more densely in the granule. In vitro studies have also demonstrated that heparin binds strongly to BPTI (Stoddart and Kiernan, 1973; Rivera et al., 2002), but the structure of the complex is not known.

Does the BPTI decamer occur in mast cell granules? At the intragranular pH of 5.5 (de Young et al., 1987), the decamer would be more abundant than at pH 4.5, where most of our data were recorded. The BPTI concentration in the granule is probably lower than in our solutions, but the total macromolecular volume fraction is certainly higher. Indeed, human mast cell granules sometimes exhibit a crystalline texture with a lattice spacing of order 100 Å (Whitaker-Menezes et al., 1995). Because the BPTI decamer excludes less volume to other macromolecular species than do 10 BPTI monomers, decamer formation will be entropically favored in the dense mast cell granule as compared to our solutions, a phenomenon known as macromolecular crowding (Minton, 2000; Ellis, 2001). Because the central channel of the BPTI decamer has a high positive charge density, it may be threaded by a negatively charged heparin segment. With a vdW diameter of 10–15 Å, the heparin molecule would make a good fit in the channel. Moreover, a heparin molecule could neutralize the high charge density in the channel at much lower entropy cost than small anions.

CONCLUSIONS

As demonstrated by the present study, the MRD method can provide quantitative information about protein oligomerization in solution. Because spin relaxation is induced by rotational, rather than translational, diffusion, the MRD method sensitively detects stable oligomers without the confounding influence of other interactions that can complicate the interpretation of DLS, PGSE, and SAS data.

The MRD results presented here establish, under a wide range of solution conditions, the presence of a BPTI oligomer with the rotational correlation time expected for the decamer seen in crystal forms A–C. In contrast to several previous studies, we find no evidence of dimers or other oligomers smaller than decamers. Decamer formation is thus a highly cooperative process. On the other hand, we detect a higher oligomer that appears to be a subcritical nucleation cluster of 3–5 decamers joined by specific ion-pairing interactions.

Decamer formation is opposed not only by the loss of translational and rotational degrees of freedom, but also by the high density of cationic side chains in a channel that pierces the decamer along its fivefold axis. Accordingly, the standard free energy of decamer formation decreases from −20 kcal mol⁻¹ in the absence of salt to −30 kcal mol⁻¹ at high salt concentration. This salt effect cannot be described in terms of Debye screening, but involves the ion-specific sequestering of anions within the narrow decamer channel. The stability of the decamer is reflected in its long lifetime, 101 ± 4 min at 27°C.

The decamer population increases with pH as cationic residues in the channel are deprotonated, thereby reducing the unfavorable electrostatic repulsion within the decamer. However, above the isoelectric pH, disruption of stabilizing ion pairs causes the decamer population to decrease. On the basis of previous studies, it has been proposed that high-pH monomeric crystal forms grow from a monodisperse solution of BPTI monomers, whereas low-pH decameric crystal forms grow from a polydisperse solution of monomers and decamers. Our results show that decamers are even more abundant at high pH than at low pH. We suggest that monomeric crystals are formed, not because the solution only contains monomers, but because ion pairs that stabilize decameric crystals cannot form at high pH.

The decameric crystal structure suggests several point mutations that might shed further light on the oligomerization and crystallization of BPTI. Mutations of Arg-20 and/or Glu-49, which participate in 10 stabilizing ion pairs, would presumably prevent decamer formation. Mutation of Asp-3 would not affect the decamer population in solution, but would inhibit the growth of decameric crystals.