Abstract
Image correlation spectroscopy allows sensitive measurement of the spatial distribution and aggregation state of fluorescent membrane macro molecules. When studying a single population system (i.e., aggregates of similar brightness), an accurate measure can be made of the aggregate number per observation area, but this measurement becomes much more complex in a distributed population system (i.e., bright and faint aggregates). This article describes an alternate solution that involves extraction of the bright aggregate population information. This novel development for image correlation spectroscopy, termed intensity subtraction analysis, uses sequential uniform intensity subtraction from raw confocal images. Sequential intensity subtraction results in loss of faint aggregate fluctuations that are smaller in magnitude than fluctuations due to the brightest aggregates. The resulting image has correlatable fluctuations originating from only the brightest population, permitting quantification of this population's distribution and further cross-correlation measurements. The feasibility of this technique is demonstrated using fluorescent microsphere images and biological samples. The technique is further used to examine the spatial distribution of a plasma-membrane-labeled fluorescent synthetic ganglioside, and to cross-correlate this probe with various membrane markers. The evidence provided demonstrates that bright aggregates of the fluorescent ganglioside are associated with clathrin-coated pits, membrane microvilli, and detergent-resistant membranes.
INTRODUCTION
Image correlation spectroscopy (ICS) and image cross-correlation spectroscopy (ICCS) are two fluorescence correlation techniques currently used to examine the spatial distribution of cell membrane components (Petersen et al., 1993, 1998). Like fluorescence correlation spectroscopy (FCS), the techniques of ICS and ICCS depend on the determination of the occupation number of fluorescent species within the focus of an exciting laser beam. However, unlike FCS, which holds the beam stationary, ICS and ICCS use the scanning laser of a confocal microscope (Petersen et al., 1993). The scanning laser is used to excite fluorescent fluctuations within a sample as a function of space and time rather than just as a function of time. ICS has been used extensively to measure the spatial distribution of plasma-membrane proteins (Petersen et al., 1993; Wiseman et al., 1997; Brown and Petersen, 1998; Wiseman and Petersen, 1999), and to assay the binding and fusion of Sendai virus to target cells (Rasmusson et al., 1998; Rocheleau and Petersen, 2000, 2001). ICCS provides spatial correlation with time to measure diffusion properties (Srivastava and Petersen, 1998) or cross-correlation between two different colored probes to quantify co-localization (Brown et al., 1999). These techniques can be used on both fixed and living cell preparations.
ICS analysis provides a cluster density (CD) from the occupation number and beam area defined as the number of clusters per μm2 of plasma membrane (Petersen et al., 1998). When observing two different macromolecular species tagged with red and green fluorescent labels that each exist in single populations, a CDrg can be defined as the cluster density of red-green aggregates. When the fluorescent probe exists in multiple populations, such as faint and bright aggregates, the CD becomes a mixture of these populations (Petersen, 1986), and interpretation of the CDrg becomes more complex. Aggregates that are sufficiently bright but physically smaller than the laser beam illumination area will appear as bright regions or spots within the image that have the same spatial dimensions as the beam focal area. Spot density (SD) is defined as the number of visually countable bright-beam-sized regions (spots) per μm2 of plasma membrane. If the bright aggregate population has emission intensity much brighter than the faint population, or if the faint populations are so concentrated as to be unresolvable, the SD will reflect the bright aggregate number. Since the SD reflects brighter aggregate populations which are part of the total population, a multipopulation system will generally have a SD < CD. If other information about the probe of interest is available—for example, biochemical data about the overall concentration of the probe—then information concerning each aggregate population can be extracted from the original ICS data (Brown and Petersen, 1998). Unfortunately, a visual count is sometimes ambiguous and provides no information concerning cross-correlation between two different populations. Also, additional biochemical information may be extremely difficult or impossible to attain. Applying a threshold to the image before ICS has been successfully used to count dendritic spines in brain slices (Wiseman et al. 2002), but this technique requires a relatively high signal-to-noise (≥5:1) to unambiguously set this threshold. Therefore, an alternative technique is necessary to unambiguously extract information concerning individual populations from the raw images with relatively low signal-to-noise.
This work outlines a novel development for the ICS technique termed intensity subtraction analysis (ISA). We demonstrate that by sequential subtraction of uniform intensity across a raw ICS image, fluctuations arising from the faint populations are removed leaving behind only the brightest aggregate population fluctuations. The corrected image has correlatable fluctuations originating from only the brightest aggregate population, allowing measurement of a CD for this population as well as cross-correlation analysis in multipopulation systems between the brightest aggregates of two different membrane markers. The cell biology community has been acutely interested in signaling that occurs in aggregates on the cell membrane surface, and this signaling is likely to be facilitated by co-localization within cell membrane domains and co-localization of different receptor species (Smart et al., 1999). Therefore, the ISA technique in combination with ICS and ICCS can be used to characterize bright population aggregates that are likely to be regions of cell signaling activity.
Demonstration of the ISA technique first requires proof of its validity. The focus of this work is to demonstrate its application on a static system as well as on cultured cells labeled with various fluorescent membrane probes. Previous work has shown that the fluorescent synthetic ganglioside, nitrobenzoxadiazole-GD1a (NBD-GD1a), inserts into the plasma membrane of CV1 cells and distributes into two populations (Rocheleau and Petersen, 2000). Confocal laser scanning microscope (CLSM) images of NBD-GD1a-labeled cells show a bright aggregate population distributed over a faint, possibly monomeric population. Gangliosides have been implicated in cell signaling at caveolae and detergent-resistant membrane regions (Jacobson and Dietrich, 1999). We were interested in characterizing the bright population of NBD-GD1a within the cell membrane. Since NBD-GD1a forms a multipopulation system, it was necessary to use ISA in combination with ICS and ICCS to spatially cross-correlate the bright aggregate population of NBD-GD1a with various membrane markers. Membrane structures that are likely to contain localized ganglioside concentrations include clathrin-coated pits, membrane microvilli, and detergent-resistant membranes.
MATERIALS AND METHODS
Materials
Dulbecco's Modified Eagles Medium, Dulbecco's phosphate-buffered saline with calcium and magnesium (DPBS), fetal bovine serum, penicillin-streptomycin, and 1:250 trypsin powder were obtained from Gibco (Burlington, ON). Synthetic nitrobenzoxadiazole-GD1a (NBD-GD1a) was purchased from I. Mikhalyov (CIS, Moscow, Russia). The nitrobenzoxadiazole-labeled phosphatidylethanolamine (NBD-PE), 4-(4-(dihexadecylamino)styryl)-N-methylquinolinium (DiQ) (Loew and Simpson, 1981), wheat germ agglutinin Texas Red-X (WGA-TRX), and Avidin Rhodamine Red-X were purchased from Molecular Probes (Eugene, OR). Transferrin-biotin, ConA-biotin, cholera toxin B subunit, and normal goat antibody were purchased from Sigma Chemical (St. Louis, MO).
Fluorescent microspheres sample preparation
Fluorescent microspheres samples were prepared as described previously (Petersen et al., 1993). Fluoresbrite microspheres with radii of 0.44 μm (s = 0.015 μm) were obtained from Polysciences (Warrington, PA).
Cell culture
CV1 cells were grown in Dulbecco's Modified Eagles Medium with 10% (vol/vol) fetal bovine serum and 100 U/ml penicillin/streptomycin at 37°C under humidified 5% CO2. Cells were passaged every 3–4 days and kept for a maximum of 30 passages. One day before experiments, cells were passaged 1:4 into 35-mm circular dishes containing 22-mm circular coverslips.
Cell labeling techniques
Live CV1 cells grown on coverslips in 35-mm dishes were routinely labeled with NBD-GD1a, NBD-PE, DiQ, ConA, WGA-TRX, and transferrin-biotin. The cells were washed twice with DPBS before labeling.
Lipids
NBD-GD1a and NBD-PE were premixed with DPBS from an ethanol stock solution to a final concentration of 0.2 and 1.7 μM, and were then added to the labeling dish. The DiQ probe was added directly to the cell buffer to a final concentration of 3.3 μM. Labeling with NBD-GD1a and NBD-PE was done at 37°C for 10 min and DiQ labeling was done at room temperature for 10 min. The cells were washed 3 × 1 min.
Lectins
Cells were rocked at room temperature for 20 min with 0.8 μg/ml ConA-biotin and then Avidin Rhodamine Red-X at 20 μg/ml. The cells were then washed 3 × 5 min with DPBS. For WGA labeling, cells were rocked at room temperature for 20 min with 0.2 μg/ml WGA-TRX. The cells were then washed 3 × 5 min with DPBS.
Transferrin
Dishes were placed on ice for further labeling. Cells were rocked on ice for 20 min with 0.1 μg/ml transferrin-biotin and then Avidin Rhodamine Red-X at 20 μg/ml. The cells were then washed 3 × 5 min with cold DPBS.
Cholera toxin
Cells were incubated on ice with 3 μg/ml cholera toxin B subunit in DPBS for 20 min. The cells were then washed 3 × 5 min with DPBS. The cells were incubated with Avidin Rhodamine Red-X at 10 μg/ml and then washed 3 × 5 min with DPBS.
Confocal laser scanning microscopy
CLSM images were collected on living CV1 cells immediately after labeling. Images were collected using an inverted Nikon microscope with a 60 × 1.4 NA oil immersion objective lens, using a BioRad MRC-600 CLSM. The 25-mW Ar/Kr laser was attenuated to 1 or 3% laser power for illumination. The 22-mm circular coverslips were mounted on a temperature-controlled stage (Life Science Resources, Cambridge, UK). Approximately 1.5 ml of DPBS was added to the holder and this solution was changed with new buffer at regular 20-min intervals. Cells were maintained at 10°C for no longer than 2 h to prevent internalization of surface components.
Confocal images were collected with a digital zoom factor of 10 to achieve a ∼0.03 μm per pixel resolution. These zoom-10 images were taken on flat regions of the cell far removed from the nucleus to avoid regions with autofluorescent organelles, including the endoplasmic reticulum and Golgi apparatus. In this region of the cell, the bottom and top membranes are not resolvable in the z-direction. Images were acquired in photon-counting mode to ensure linearity of the signal intensity. Multiple scans (usually 15) were added to obtain a single image taking ∼20 s per image. For each experiment a data set of 30–40 images was collected from different cells to ensure accurate determination of the cell population mean. Images were processed on a Massively Parallel Computer (MP-2, MasPar Computer, Sunnyvale, CA) using ICS programs described previously (Petersen et al., 1993; Wiseman et al. 1997).
ICS data sets provided individual ICS beam radii, intensity, corrected correlation function amplitude g(0,0), and CD values. The average and standard deviation for the image sets was calculated for the beam radius, the dark current corrected average intensity, the corrected g(0,0), and the CD. The normal probability function z-score for each image was calculated for the mean of each of these parameters, and images with any of these parameters showing values of 2 < z < −2 were rejected (Wonnacott and Wonnacott, 1990). On living cells, 2–3 out of 40 images were regularly rejected.
IMAGE CORRELATION SPECTROSCOPY
The theoretical basis of ICS and ICCS has been detailed elsewhere (Petersen et al., 1993; Srivastava and Petersen, 1998; Wiseman and Petersen, 1999). This section provides a brief outline of the theory and practice of ICS to facilitate the introduction of a further development integral to the current work.
Image correlation spectroscopy
ICS involves the analysis of fluorescence CLSM images where the scanning laser beam acts as a spatial correlator of fluorescent molecules in the sample. The normalized spatial intensity fluctuation autocorrelation function is defined as a function of spatial lag variables ξ and η:
 |
(1) |
Here, δi(x,y) and δi(x + ξ, y + η) are the relative intensity fluctuations for pixel positions (x,y) and (x + ξ, y + η), and the angular 〈brackets〉 indicate calculation of a spatial ensemble average for the image. By definition the zero lag amplitude (g(0,0)) is equal to the mean squared intensity fluctuation divided by the mean intensity squared for the image. Spurious white noise sources are not spatially correlated and contribute to the numerator of the autocorrelation function only at zero spatial lags. However, white noise contributes to the mean intensity term in the denominator of the autocorrelation function. In contrast, any real fluorescent object will be spatially correlated by the laser beam, and will contribute to both the numerator and denominator of Eq. 1. Background corrections are necessary to deal with both white noise and correlated background, as is reported elsewhere (Wiseman et al., 1997, Wiseman and Petersen, 1999).
The relative intensity fluctuations of the signal are inversely proportional to the average number of independent fluorescent particles per beam area (g(0,0) = 1/〈Np〉) in a system with monodisperse particles of uniform brightness (Elson and Webb, 1975; Magde et al., 1974). Due to this relationship and knowing the beam area from the fit of the correlation function, the cluster density (CD) value can be calculated as the number of clusters per μm2 of plasma membrane (Brown and Petersen, 1998).
In a multipopulation system with particles of different brightness (i.e., monomers, dimers etc.), the overall g(0,0) is the sum of each individual species gi(0,0) weighted by their fractional intensities (Petersen, 1986; Tompson, 1991):
 |
(2) |
where, gi(0,0) = 〈(δii)2〉/〈ii〉2. The average fluorescence intensity of the ith species is represented by 〈ii〉, and the average total intensity, 〈it〉, is a function of these species (〈it〉 = ∑〈ii〉). Brighter species are more heavily weighted in the g(0,0) due to the square intensity dependence. For example, in a bimodal system with bright and faint aggregates, if the bright aggregates are 10× as bright as the faint aggregates, there needs to be 100× more faint than bright aggregates for the faint aggregates to contribute equally to the g(0,0). Therefore, in many situations, a faint population does not significantly contribute to the g(0,0). In this case, the g(0,0) is inversely proportional to the number of bright aggregates per beam area, which allows simple interpretation of the CD value. However, if there is a significant contribution from a faint population, interpretation of the g(0,0) becomes more complex.
Image cross-correlation spectroscopy
ICCS is an extension of ICS that can determine spatial correlation between two species of macromolecules tagged with two spectrally separated fluorescent labels (Petersen et al., 1998). In the current work, dual color (green and red) CLSM images are taken for ICCS analysis. An average intensity can be calculated for the images in the red (〈ir〉) and green (〈ig〉) detection channels. Each image provides separate autocorrelation amplitudes, gr(0,0) and gg(0,0), and the normalized intensity cross-correlation function is calculated (Rigler et al., 1998). In a monomeric system, with a single population of green aggregates and a single population of red aggregates, the cross-correlation amplitude allows calculation of the average number of clusters per beam area that contain both red and green chromophores (〈Nrg〉) (Rigler et al., 1998). Therefore, it is possible to define the red-green cluster density (CDrg) as the number of clusters per μm2 that contain both labels. However, interpretation of the cross-correlation grg(0,0) value becomes much more complex when dealing with multiple-population systems composed of clusters of varying intensity.
Intensity subtraction analysis
ICS and ICCS are powerful techniques that allow the quantification of membrane distributions, but as illustrated previously, the interpretation of the values obtained with these techniques becomes more complex when dealing with multiple cluster populations. The profile of the FCS autocorrelation function can be curve-fit for multiple populations if the diffusion characteristics are different for each population. Such curve-fitting procedures are not possible with ICS or ICCS analysis since the spatial correlation is due to the scanning laser and not diffusion. For instance, as the laser scans over clusters of varying brightness the beam radius of the Gaussian profile will remain constant if the particles are physically smaller than the beam. Therefore, a novel approach to isolate information concerning ICS and ICCS populations needed to be developed.
Intensity subtraction analysis (ISA) is a novel extension of the ICS and ICCS techniques. It can be used to selectively isolate and analyze the brightest fluctuations within a confocal image and should be used when there are a large number of faint versus bright population fluctuations. The brightest intensity fluctuations are due to the largest fluorescent clusters within the sample. The ISA process involves sequential subtraction of intensity uniformly across an image to converge to an image with fluctuations originating from only the brightest population. The subtraction of intensity occurs in each pixel of the image, but if the difference is negative, the pixel value is set to zero. Since this is a spatial rather than temporal correlation (in contrast to FCS), the relative brightness of the populations in the image is only changed by subtraction of this uniform intensity.
As shown previously in Eq. 2, the g(0,0) can be broken down into intensity-weighted contributions from separate populations. Our interest was to isolate the brightest (b) fluctuation population from all the other more faint (f) populations:
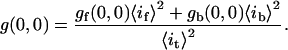 |
(3) |
The total average intensity is a function of the intensity generated by the faint population(s) (〈if〉) and the brightest population (〈ib〉). Subtraction of intensity uniformly from an image results in a new image with decreased aggregate intensities. The intensity subtracted from each population varies with the fraction of area that each occupies in the image. For example, a population that covers a large number of regions in the image will have proportionately more intensity subtracted than a population that covers only a few regions. The resulting average intensity of the subtracted image (〈iISA〉) will be a function of the original average intensities of the faint (〈if〉) and brightest populations (〈ib〉), the integer of intensity subtracted (is), and the fraction of the image area covered by each population (Ff and Fb, where [0 ≤ Ff + Fb ≤ 1]). When Ff + Fb < 1, 〈iISA〉 = (〈if〉 − Ffis) + (〈ib〉 − Fbis). When (Ff + Fb) is equal to one, 〈iISA〉 simplifies to (〈it〉 − is)—most likely due to bright aggregates distributed on a diffuse faint fluorescence background.
The intensity-subtracted image will have a new g(0,0):
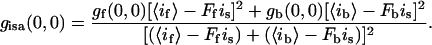 |
(4) |
Application of ISA is only necessary in images that contain a large contribution to the average intensity from the faint population(s) or when Ff > Fb. Also, the amplitude of the faint fluctuations are smaller than bright fluctuations. Therefore, as is increases, (Ff × is) will equal 〈if〉 before (Fb × is) will equal 〈ib〉. Alternatively, when (Ff × is) equals 〈if〉 then (Fb × is) will be less than 〈ib〉. This result agrees with the intuitive notion that with subsequent intensity subtraction, the contribution to the g(0,0)ISA from the faint aggregate population(s) disappears before the contribution from the brightest aggregate population.
When Ff × is = 〈if〉:
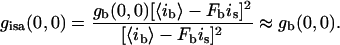 |
(5) |
Selecting the amount of intensity to subtract to achieve isolation of the brightest population is critical to this technique. Too little subtraction results in a residual contribution of faint population intensity, and too much subtraction results in decreased signal-to-noise with eventual disappearance of the brightest intensity fluctuations. Intensity subtraction initially increases the gISA(0,0) as the total average intensity decreases (refer to 〈it〉 in Eq. 3), and as the larger gb(0,0) value becomes dominant. This increase continues until the brightest population completely dominates the function (Eq. 5). Intensity subtracted beyond this point decreases the brightest population fluctuations and consequently decreases the raw gISA(0,0). The onset of this decrease is used to choose the appropriate subtraction level needed to isolate the brightest fluctuations.
A plateau in the g(0,0)ISA versus intensity-subtracted plot clearly defines the level of subtraction necessary to isolate the brightest aggregates. In biological systems there is likely to be a distribution of aggregate intensities even among the brightest aggregate population. If this distribution is so large that the dimmest bright aggregates significantly overlap with the brightest faint aggregates, there is clearly no distinction to be made, and the final ISA image will contain fluctuations from all populations. In such an image, all the correlatable fluctuations are then considered the brightest fluctuations and all that is removed using ISA is low intensity white noise background. In this situation the ISA method fails to produce a single population image, which becomes evident after normalization and comparison of the CDISA and SD values (refer to Intensity Correction and Normalization).
When a single population is recovered after intensity subtraction (refer to Intensity Correction and Normalization), the gISA(0,0) provides information about the brightest population occupation number of a multipopulation aggregate system. Furthermore, it can be used to calculate the cluster density of the brightest aggregates or the number of brightest aggregates per μm2 plasma membrane. Initial use of ISA before ICCS restricts the study to a single population, which greatly simplifies the cross-correlation analysis. The CDrg−ISA simply represents the number of red-green bright aggregates per μm2 plasma membrane. As will be demonstrated, the biological composition of these bright aggregates can be further examined through dual color labeling and ICCS.
Intensity correction and normalization
Raw ICS images contain intensity contributions from the signal of interest, nonspecific fluorescent labeling, autofluorescence, and spurious white noise sources. Each contributes to the correlation function. It is possible to correct for the additional contributions to the correlation function provided nonspecific labeling, autofluorescence, and white noise images are collected (St. Pierre and Petersen, 1992; Wiseman and Petersen, 1999). In this study, the contribution from nonspecific labeling was usually very small, making this correction of little consequence.
Intensity subtraction was done using Scion Image Release Beta 3b (Scion Image Software, Scion, MD). This program allowed sequential subtraction of intensity from the raw ICS images. Pixels with negative differences were simply registered with a value of zero intensity. Detector shot noise still contributed to these ISA-modified images. This noncorrelated intensity needed to be corrected to accurately normalize the raw g(0,0)ISA and determine an accurate CDISA (Eq. 1). The background intensity was determined using two independent methods and each method provided similar CDISA values. The first method used Scion image software to cut and paste background (noise) regions of the ISA image onto the bright (correlated signal) regions. This copying and pasting was done on all ISA images until the bright fluctuations were removed, and the average background intensity was then calculated from these modified images. The second correction method involved measurement of 20–50 background regions (away from the remaining aggregates) per image to get a mean background intensity for each image. Both methods provided similar intensity corrections, which suggests that both methods provided accurate CDISA values. It should be stressed that this measurement needed to be absolutely rigorous since it is critical to the calculation of accurate cluster densities. Importantly, the accuracy of the CDISA values can be confirmed by comparison to the spot density (SD). Failure to produce CDISA = SD indicates that either the measurement is improperly normalized or that the data set is not amenable to the ISA method. A CDISA < SD indicates that a significant number of the brightest countable population was lost during the intensity subtraction. This is likely to occur when there are few bright aggregates per image. A CDISA > SD would suggest that there was too small a separation between the brightest and faint populations for the ISA method to be effective. The resulting ISA image in these situations contains information concerning multiple populations and cannot be interpreted easily.
RESULTS AND DISCUSSION
Fluorescent sphere images and intensity subtraction analysis
CLSM images of fluorescent microsphere samples (beads) were collected (Fig. 1). These microsphere samples provided control images containing populations with a distribution of intensities. The image shown contains both bright and faint beads with the bright beads having peak intensities twice the value of the faint beads. The correlation function for this image is shown with the raw correlation function in the back and front left quadrants, while the fit to this data is in the front right quadrant (Fig. 1 B). This function has a Gaussian decay profile with a spatial extent defined by the e−2 beam radius. The g(0,0) value is extracted using the fit with extrapolation to the zero lags. In this example, the g(0,0) has contribution from both the bright and faint beads. Table 1 summarizes the average intensities (〈i〉), autocorrelation amplitude g(0,0), and CD values that are obtained from image analysis of samples composed of mixed, bright, or faint beads. The average intensity of the mixed bead image was 10.4 arbitrary units (Arb.U.), of which 4.2 Arb.U. was contributed by the bright beads and 6.2 Arb.U. was contributed by the faint beads. In this case, despite the faint beads being half as bright, they contribute more to the total average intensity of the image. The mixed bead image has a CD value of 0.81 μm−2, a SD of 0.84 μm−2, and a bright bead SD of 0.18 μm−2. The beads are all visually countable in this sample and the SD more closely reflects the CD. Because the average intensity of each population is known, it is possible to extract the individual CD values from the mixed bead image CD value. However, this is rarely possible with biological samples.
FIGURE 1.

An image composed of bright and faint fluorescent microspheres and its corresponding autocorrelation function. A 15.5 × 15.5 μm zoom-10 CLSM image of 0.44 μm diameter spheres was taken at ∼0.03 μm per pixel resolution. This image was then used to generate a second image with half-as-bright beads (Scion Image), but greater in number. This second image was merged with the first image to create the image shown (A). This image was sent for ICS analysis to obtain the correlation function shown (B). The front left and back quadrants show the raw correlation function, while the front right quadrant shows the fit to the Gaussian function.
TABLE 1.
Autocorrelation values of bead image
| Bead image | 〈i〉sub | g(0,0) | CD (/μm2) |
|---|---|---|---|
| Mixed | 10.4 | 9.3 | 0.81 |
| Bright | 4.2 | 33.2 | 0.18 |
| Faint | 6.2 | 11.8 | 0.68 |
Fig. 2 shows three separate mixed bead images (A, B, and C) and the corresponding ICS information collected after sequential intensity subtraction (i–ix). All three images have the same number of bright beads contributing the same amount of intensity to the average intensity. The individual faint beads in A are one-eighth as intense as the bright beads. The individual faint beads in B and C are one-half the intensity of the bright beads, but there are nearly 3× as many faint beads in C contributing to the average intensity. Intensity was incrementally subtracted from these images providing a g(0,0)ω2 (i–iii), intensity (iv–vi), and observed CD (vii–ix). When intensity was subtracted from A, its g(0,0)ω2 maximized after subtracting 30 intensity units (Fig. 2 i, vertical dashed line). The intensity contribution from the mixed, bright, and faint bead images is shown in Fig. 2 iv. The intensity contribution from the faint beads decreased to zero at the g(0,0)ω2 maximum. The resulting image has intensity contribution from only the bright beads, indicating the image just after the peak of the g(0,0)ω2 as the last intensity to subtract to successfully isolate intensity fluctuations from the bright bead population. Initially, the observed CD value for A was ∼0.3 μm−2 (Fig. 2 vii), which was larger than the CD for the bright beads alone (0.18 μm−2). This slowly decayed, as the contribution from the faint population diminished, and resulted in a value of 0.18 μm−2 at the g(0,0)ω2 peak maximum. Therefore, once the faint beads were fully subtracted from the image, the g(0,0) value reflected only the bright population, resulting in a CD value accurately reflecting the distribution of the bright population.
FIGURE 2.
Intensity subtraction analysis on mixed fluorescent microsphere images with varying contribution of intensity from the faint population. Images were created as in Fig. 1. All three images have the same number of bright microspheres (beads), but have varying contribution from the faint microsphere population: A contains faint microspheres one-eighth as bright as the bright microspheres; B contains the same number of faint microspheres as A, but they are only one-half as intense as the bright microspheres; and C has faint microspheres of the same intensity as B, but 3× in number. The corresponding calculated ICS parameters as a function of subtracted intensity (bottom axis) are shown: g(0,0)ω2 (i–iii), intensity (iv–vi), and CDobs (vii–ix). The intensity curves (iv–vi) show the mixed (▾), bright (○), and faint (•) microsphere contributions.
Both images B and C showed a similar increase in the g(0,0)ω2 until a maximum was reached (Fig. 2, ii and iii). The faint beads in B and C are 4× the intensity of the faint beads in A, and thus required 4× greater intensity subtraction to isolate the bright beads (120 Arb.U. in B and C vs. 30 Arb.U. in A). Again, after subtraction of enough intensity to reach the peak in the g(0,0)ω2 (Fig. 2, ii and iii), the intensity contribution from the faint beads dropped to zero (Fig. 2, v and vi), and the CD decreased to values reflecting contributions from the bright beads only (Fig. 2, viii and ix, 0.18 μm−2). The faint beads in C had the same individual intensity as the faint beads in B, but there were nearly 3× more of them contributing to a very large faint bead average intensity contribution. The g(0,0)ω2 maximized after the same amount of intensity was subtracted (120 Arb.U.), since the faint beads in images B and C had the same intensity . The initial CDobs values from each of these images further demonstrates the effect of a second population of intensity. With greater contribution from the faint population (compare A, B, and C), the observed CD value (0.3–0.4–0.8 μm−2) was increasingly greater than the CD of the bright population (0.18). However, in each situation, the fluctuations from the brightest population were successfully isolated using intensity subtraction as evidenced by the final ISA-CD values closely matching the bright bead CD value.
Fluorescently labeled cells and intensity subtraction analysis
Fig. 3 shows an ICS image of a living cell labeled with cholera toxin B subunit (A), which labels the cell in both bright and faint regions. Also shown in this figure is the g(0,0)ω2 versus intensity-subtracted plot for this image (B), and three intensity line plots (C, D, and E) taken from the pixels indicated by the white line shown in A. The intensity line plot in C shows the intensity collected from the original image. The average intensity of the original image was 22.99 Arb.U., and the dotted line in this plot indicates the dark-current contribution. Intensity was subtracted from this image and the resulting g(0,0)ω2 versus intensity-subtracted plot (B) shows a smooth variation with a maximum observed at 30 Arb.U. Also indicated are the g(0,0)ω2 values of the images from which the intensity line plots in D and E were generated. A bright spot on the line in (C) is clearly visible above the other fluctuations on this line, although the faint fluctuations are significant. The initial faint and bright fluctuations reach ∼20 and ∼60 Arb.U respectively (values calculated after subtraction of dark-current levels), which loosely corresponds to a bright:faint intensity magnitude ratio of 3:1. As intensity is subtracted, the g(0,0)ω2 increases (B) and the faint fluctuations decrease (C versus D). Beyond the g(0,0)ω2 peak maximum, the faint fluctuations are relatively insignificant compared to the remaining bright fluctuations. In fact, the remaining fluctuations are due only to the bright fluctuations and spurious noise fluctuations above the regions where the faint fluctuations once appeared. These results indicate that successive intensity subtraction and ICS analysis results in a g(0,0)ω2 versus intensity-subtracted plot that can be used to successfully isolate the brightest population in biological samples.
FIGURE 3.
Intensity subtraction analysis on live cells labeled with cholera toxin B subunit. (A) A confocal image of a live CV1 cell at 10°C labeled with cholera toxin B subunit (Materials and Methods). The image is a 512 × 512 pixel intensity map with physical dimensions of 15.5 × 15.5 μm. The line drawn across the image indicates the region from which the line plots, shown in C–E, are generated. (B) An ISA intensity plot of g(0,0)ω2 versus intensity subtracted. The two points indicated, D and E, are the subtraction levels that generated the images from which the intensity lines scans are shown in D and E. (C) Line plot measured from the original image from the line shown in A. (D) The same region plotted from the image with 26 Arb.U. subtracted from the original image. (E) The same region plotted from the image with 32 Arb.U. subtracted from the original image.
CLSM images of NBD-GD1a labeled cells
CLSM images of NBD-GD1a-labeled CV1 cells were taken at 10°C (Fig. 4). Shown are a CLSM image of a single cell (A), a z-section of a single cell (B), and a representative zoom-10 image used for ICS analysis (C). This probe has been used previously to quantify Sendai virus receptor interaction (Rocheleau and Petersen, 2000). These images demonstrate that NBD-GD1a does not label the cell uniformly, and that more brightly labeled regions appear dispersed throughout the cell membrane. From the vertical section it is apparent that most of the NBD-GD1a label appears on the plasma membrane (which outlines the cell) with the nuclear region in the center (B). Vertical sections of NBD-GD1a-labeled cells kept at 10°C reveal little or no internal labeling, and equal top and bottom membrane intensities. Fluorescence photobleaching recovery of NBD-GD1a-labeled CV1 cells have diffusion properties typical of a membrane-inserted lipid probe (Rocheleau and Petersen, 2000). By keeping the cells at 10°C and changing the buffer regularly, the ganglioside remains on the outer surface of the cells for >1–2 h. The zoom-10 image shown (C) is a typical image used for ICS analysis and demonstrates bright spotted areas dispersed across a relatively uniform background. It takes ∼20 s to collect these images, therefore, these bright population regions are stable within this timescale. These data indicate that NBD-GD1a spontaneously inserts into the plasma membrane of these cells, has surface mobility properties of a typical lipid probe, and also localizes into relatively stable bright aggregates.
FIGURE 4.

CLSM images of NBD-GD1a-labeled CV1 cells. CV1 cells were labeled with NBD-GD1a as described (Materials and Methods). Shown are images of a single cell (A), a z-section of a single cell (B), and a zoom-10 image used for ICS analysis (C). Bar in A is applicable to B.
Intensity subtraction analysis
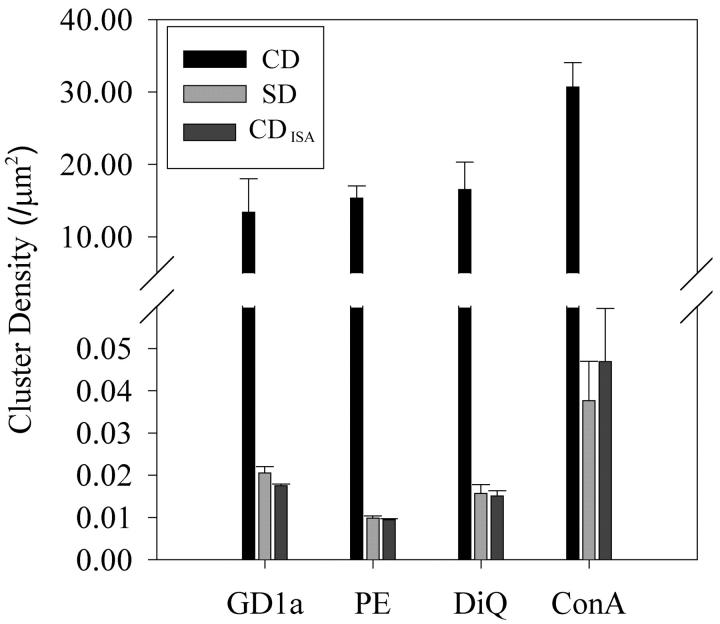
Images were collected on cells labeled with NBD-GD1a, NBD-PE, DiQ, and ConA-biotin (Fig. 5). A g(0,0)ω2 versus intensity-subtracted curve was generated that reached a maximum for each of these labeling techniques. The original and ISA images were used to measure the CD (black bar), SD (light gray bar), and CDISA (dark gray bar) values. The CD values from the original images ranged between 10 and 35 μm−2 (dark bar), and were much larger than their corresponding SD (gray bar), which indicates these probes labeled multiple populations on the cell membrane. In contrast, the SD was comparable to the CDISA (light gray versus dark gray bar). Using the SD as the actual value, the CDISA provided an average uncertainty of only 10% (absolute value of [((actual) − (experimental)) ÷ actual] × 100). Therefore, ISA before ICS analysis enabled accurate measurement of the distribution of the bright regions for each of these labels.
FIGURE 5.
Comparison of CD, SD, and CDISA values for three different labels that display multipopulation labeling. CV1 cells were labeled as described (Materials and Methods) and placed on the microscope at 10°C. Zoom-10 images were collected on NBD-GD1a (N = 180), NBD-PE (N = 170), DiQ (N = 110), and ConA-biotin (N = 120) labeled CV1 cells from at least three different sets of labeling for each label. The CD (black bar), SD (light gray bar), and CDISA was derived from these images as described (by ICS). N represents the individual number cells used to calculate the mean and standard error of the mean (error bars).
The CD values of ISA-treated images was measured for various NBD-PE and NBD-GD1a dual color labeling (Fig. 6 A). This dual color labeling involved fluorescent markers for various membrane components including: membrane topology (WGA-TRX and ConA-biotin), clathrin-coated pits (transferrin-biotin), and detergent-resistant-membrane-associated lipid (DiQ). The CDISA observed with NBD-PE was consistently ∼0.008 μm−2 from sample to sample demonstrating the reproducibility of this technique, and that there were on average only two bright NBD-PE regions per zoom-10 image. The highest cross-correlation with NBD-PE was observed with ConA-biotin labeling, but even this was not large, inasmuch as less than one-half of the NBD-PE bright regions were associated with the ConA bright regions (CDrg = 0.004 ± 0.001 μm−2). Therefore, NBD-PE exhibited few bright regions across the cell membrane and these regions did not cross-correlate strongly with any of the membrane markers used in this study.
FIGURE 6.

Analysis of NBD-PE and NBD-GD1a bright aggregate cross correlation with membrane structural markers. Cells were dual-labeled with NBD-PE or NBD-GD1a. NBD-PE samples were dual-labeled with (A) WGA-TRX, (B) ConA-biotin, (C) transferrin-biotin, or (D) DiQ. NBD-GD1a samples were dual-labeled with (A) WGA-TRX, (B) ConA-biotin, (C) Transferrin-biotin, or (D) DiQ. Also shown is dual-labeling of ConA-biotin and DiQ (E). Zoom-10 images were collected for each of these samples in two detection channels and the images were modified using ISA to isolate the bright aggregate fluctuations. Shown are the ISA-CDg (black bar), ISA-CDr (light gray bar), and ISA-CDrg (dark gray bar).
Cross-correlation between NBD-GD1a and WGA-TRX, ConA-biotin, Transferrin-biotin, or DiQ are shown, as well as cross-correlation between ConA-biotin and DiQ (Fig. 6 B). The NBD-GD1a CDISA values were consistently ∼0.17 μm−2, again demonstrating the reproducibility of this technique. It should be noted, however, that the red channel CD values for the NBD-GD1a labeled cells were larger than those for NBD-PE. It is likely that this simply represents a biological variance not accounted for in the statistics, but it is also possible that the NBD-GD1a has induced formation of more bright red aggregate regions. In either situation, the increased NBD-GD1a red-channel CD makes it more likely for overlap with the green-channel bright population, and it is unclear to what extent these “extra” aggregates may be involved in the overlap with NBD-GD1a bright aggregates. The cross-correlation observed between NBD-GD1a and these probes provided CDrg values that were consistently larger than those obtained with NBD-PE. In particular, NBD-GD1a cross-correlated well with the WGA-TRX and ConA-biotin lectins. Both lectins demonstrated greater numbers of bright population regions than NBD-GD1a. The NBD-GD1a bright regions were mainly associated with WGA-TRX (∼97%), which is not surprising inasmuch as WGA binds to neuraminic acid, an extracellular component of this ganglioside. Since WGA was able to bind to these regions, this demonstrates all of the NBD-GD1a bright regions were accessible to the membrane surface and were not internalized. The bright regions of NBD-GD1a showed a significant amount of overlap with ConA-biotin (∼66% of the bright NBD-GD1a regions overlapped with the bright ConA regions). ConA does not bind any residues on the NBD-GD1a molecule, and this overlap is likely due to co-localization within similar membrane regions rather than direct binding interaction. Lectins bind the membrane surface relatively nonspecifically and have been used as a marker for membrane protrusions such as microvilli (Friederich et al., 1989, 1993). This cell line has miniature or flaccid microvilli (Algrain et al., 1993; Friederich et al., 1989) and can be induced to form full microvilli by transfection with the protein villin (Friederich et al., 1989). The active concentration of various membrane glycoproteins onto microvilli has been shown previously for the insulin receptor (Carpentier, 1993; Carpentier and McClain, 1995), prominin (Weigmann et al., 1997), and various ion channels (Lange et al., 1998). It is therefore not unreasonable for these flaccid microvilli to have proteins and possibly lipids specifically associated with them. It is also likely that lectins are concentrated in clathrin-coated pits since membrane is constitutively internalized through these structures (Mayor et al., 1993; Hao and Maxfield, 2000).
The cross-correlation of NBD-GD1a with transferrin-biotin showed that ∼50% of the bright NBD-GD1a structures were associated with bright transferrin-biotin regions. Transferrin is a classical marker for plasma-membrane clathrin-coated pits, inasmuch as its receptor is constitutively internalized through these structures (Daro et al., 1996; Srivastava and Petersen, 1998). In this study, transferrin labeling was done on cells that were kept <10°C, leaving the coated pits at the membrane surface by inhibiting their internalization (Anderson et al., 1997a,b). Lipid internalization occurs mainly through coated pits (Mayor et al., 1993; Hao and Maxfield, 2000), so it is not surprising to find some NBD-GD1a overlap with these structures. The CDISA−rg for the cross-correlation of NBD-GD1a with transferrin had a significantly different value than that obtained for the cross-correlation of NBD-GD1a with either of the lectins providing quantitative evidence that the NBD-GD1a overlap with transferrin-biotin was due to a distinct structure. Therefore, a portion of these bright NBD-GD1a regions are associated with clathrin-coated pits.
Approximately 20% of the bright NBD-GD1a aggregates were associated with DiQ bright aggregates. DiQ lipid is a long-chain saturated acyl chain that has related structure to DiI (Loew and Simpson, 1981) and is expected to partition into detergent-resistant membranes (Korlach et al., 1999). There has been strong biochemical evidence that gangliosides are concentrated in these structures (Smart et al., 1999, Jacobson and Dietrich, 1999). These structures are believed to have very short lifetimes at physiological temperatures, but may be stabilized at lower temperatures (Jacobson and Dietrich, 1999). Fewer DiQ bright aggregates overlapped with ConA than NBD-GD1a with ConA, suggesting DiQ overlap does not include the NBD-GD1a aggregates co-localized with coated pits. It has recently been shown that microvilli are composed of a cholesterol-based lipid domain that is detergent-resistant (Lubrol, a nonionic detergent) (Roper et al., 2000). Therefore, it is likely that the overlap of NBD-GD1a and DiQ bright aggregates occurs in both microvilli and flat regions of the membrane in detergent-resistant membranes.
Image bleach and recovery
Fig. 7 shows a set of CLSM images taken on the same area of a single NBD-GD1a-labeled living cell at 10°C. High zoom images are shown before bleaching (A), immediately after bleaching (B), and after 4 min of recovery (C). The pseudocolor overlap of A and C is shown in D. NBD-GD1a distributed into multiple populations as shown previously (A). The fluorescence was easily bleached away using 5–10 scans of 0% attenuated laser power (B). After 4 min, 25% of the fluorescence intensity recovered (N = 45 image sets). The perimeter of these images have a quantitatively detectable higher average intensity than the center of the images. A multipopulation distribution of NBD-GD1a was observed after the recovery of intensity (C), with the bright population appearing in the similar regions on the surface where it was initially observed (compare A and C). However, there is some movement of these regions over the period of recovery, since precise overlap is not observed in every bright region (D). ISA combined with ICS was done on the NBD-GD1a images. The CD after recovery of 0.011 ± 0.002 μm−2 indicates that ∼63% of the bleached bright spots recovered to prebleach numbers. These data suggest a portion of the bright aggregates were stable for up to 4 min at 10°C, but also that there was an active exchange between these aggregates and the monomeric population. The bleach-recovered fraction matched well with the NBD-GD1a overlap with ConA-biotin bright aggregates, suggesting that this is likely the population recovering after the bleach. As discussed, these aggregates are thought to include both clathrin-coated pits and plasma membrane microvilli, both of which should be stable structures at 10°C.
FIGURE 7.
NBD-GD1a aggregates bleach and then recover. CV-1 cells were labeled with NBD-GD1a and imaged on a microscope at 10°C as described (Materials and Methods). Shown is a representative image bleach and recovery. An initial image is collected (A). This area was then bleached by six scans of 0% attenuated laser, after which the zoom-10 image was collected (B). Four min was allowed to pass before collection of the recovered image (C). The image in B has a large contrast stretch to verify the removal of the fluorescence in this area. The pseudocolor overlap of A and C is shown (D).
Applications for ISA
Subtraction of intensity removes information from all populations in the ICS images. We have taken advantage of the fact that the fainter populations will lose significantly more fractional intensity than the brightest population. This isolates the fluctuations from the brightest population. However, intensity subtraction also decreases the signal from the brightest population. This becomes increasingly a concern when the brightest population is only moderately brighter than the fainter populations. Therefore, every effort should be made to confirm that the method is obtaining single population CD values. In this study, we used the comparison between CDISA and SD values. To be completely rigorous, the validity of this method should be confirmed with new data sets.
ISA provides an nonarbitrary method for the isolation of the bright aggregate fluctuations in an ICS image. It allows accurate calculation of the bright aggregate cluster density. Other methods are available to obtain this same information, such as applying a threshold before ICS (Wiseman et al., 2002) or simply applying filtering techniques and counting the bright aggregates. ISA is superior to these techniques due to its nonarbitrary selection of the brightest aggregate fluctuations and its inherent sensitivity. The use of a correlation function (fit to the zero lag amplitude) to determine the subtraction level makes this technique nonarbitrary and more sensitive. Furthermore, the resulting image can be used in ICCS analysis to quantitatively examine the cross-distribution (as done in this article) or the diffusion of these bright aggregates (Srivastava and Petersen, 1998). These regions are likely the signaling centers of the cell, making them of interest to the cell biological community. Therefore, the ISA technique becomes increasingly useful with low signal-to-noise images, and when there is further interest in quantifying the cross-correlation of the brightest regions either spatially or temporally.
SUMMARY
The technique of ISA in combination with ICS was successful at isolating the density of the brightest population from a system containing two populations of microspheres with different intensity. The combined methods were also successful in measuring the surface densities of bright (clustered) populations of various membrane probes. The CD values obtained using ISA consistently agreed with the SD values (10% uncertainty). Comparison of samples labeled with the same probe from different sets of data also showed excellent reproducibility. This work dealt with the characterization of the brightest population of NBD-GD1a observed when labeling living cells. This characterization was done by spatially cross-correlating NBD-GD1a with specific membrane structure markers. All of these membrane markers labeled the surface of the cells within different-sized clusters corresponding to multiple intensity populations (CD ≫ SD). To isolate information solely from the brightest populations, it was necessary to use the novel technique of image subtraction analysis (ISA). Using this technique, the brightest population of NBD-GD1a was shown to overlap with probes that mark areas of clathrin-coated pits, microvilli, and detergent-resistant membranes. The physical mechanisms that form and maintain these aggregated domains, as well as their biological significance, warrant further study. Overall the present study demonstrates the implementation of combined ICS-ISA analysis and how this approach can be used for quantitative studies of co-localization of membrane components into cell surface domains.
Acknowledgments
The authors thank Dawn Kilkenny for proofreading this material.
This work was supported by an operating grant to N.O.P. from the Natural Sciences and Humanities Research Council of Canada.
Dr. Rocheleau's present address is Dept. of Molecular Physiology and Biophysics, Vanderbilt University, 702 Light Hall, Nashville, TN 37232.
References
- Algrain, M., O. Turunen, A. Vaheri, D. Louvard, and M. Arpin. 1993. Ezrin contains cytoskeleton and membrane binding domains accounting for its proposed role as a membrane-cytoskeletal linker. J. Cell Biol. 120:129–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson, R. G., J. L. Goldstein, and M. S. Brown. 1977a. A mutation that impairs the ability of lipoprotein receptors to localise in coated pits on the cell surface of human fibroblasts. Nature. 270:695–699. [DOI] [PubMed] [Google Scholar]
- Anderson, R. G., M. S. Brown, and J. L. Goldstein. 1977b. Role of the coated endocytic vesicle in the uptake of receptor-bound low density lipoprotein in human fibroblasts. Cell. 10:351–364. [DOI] [PubMed] [Google Scholar]
- Brown, C. M., and N. O. Petersen. 1998. An image correlation analysis of the distribution of clathrin associated adaptor protein (AP-2) at the plasma membrane. J. Cell Sci. 111:271–281. [DOI] [PubMed] [Google Scholar]
- Brown, C. M., M. G. Roth, Y. I. Henis, and N. O. Petersen. 1999. An internalization-competent influenza hemagglutinin mutant causes the redistribution of AP-2 to existing coated pits and is colocalized with AP-2 in clathrin free clusters. Biochemistry. 38:15166–15173. [DOI] [PubMed] [Google Scholar]
- Carpentier, J. L., and D. McClain. 1995. Insulin receptor kinase activation releases a constraint maintaining the receptor on microvilli. J. Biol. Chem. 270:5001–5006. [DOI] [PubMed] [Google Scholar]
- Carpentier, J. L. 1993. The journey of the insulin receptor into the cell: from cellular biology to pathophysiology. Histochemistry. 100:169–184. [DOI] [PubMed] [Google Scholar]
- Daro, E., P. van der Sluijs, T. Galli, and I. Mellman. 1996. Rab4 and cellubrevin define different early endosome populations on the pathway of transferrin receptor recycling. Proc. Natl. Acad. Sci. USA. 93:9559–9564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elson, E. L., and W. W. Webb. 1975. Concentration correlation spectroscopy: a new biophysical probe based on occupation number fluctuations. Annu. Rev. Biophys. Bioeng. 4:311–334. [DOI] [PubMed] [Google Scholar]
- Friederich, E., C. Huet, M. Arpin, and D. Louvard. 1989. Villin induces microvilli growth and actin redistribution in transfected fibroblasts. Cell. 59:461–475. [DOI] [PubMed] [Google Scholar]
- Friederich, E., T. E. Kreis, and D. Louvard. 1993. Villin-induced growth of microvilli is reversibly inhibited by cytochalasin D. J. Cell Sci. 105:765–775. [DOI] [PubMed] [Google Scholar]
- Hao, M., and F. R. Maxfield. 2000. Characterization of rapid membrane internalization and recycling. J. Biol. Chem. 275:15279–15286. [DOI] [PubMed] [Google Scholar]
- Jacobson, K., and C. Dietrich. 1999. Looking at lipid rafts? Trends Cell Biol. 9:87–91. [DOI] [PubMed] [Google Scholar]
- Korlach, J., P. Schwille, W. W. Webb, and G. W. Feigenson. 1999. Characterization of lipid bilayer phases by confocal microscopy and fluorescence correlation spectroscopy. Proc. Natl. Acad. Sci. USA. 96:8461–8466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange, K., U. Brandt, J. Gartzke, and J. Bergmann. 1998. Action of insulin on the surface morphology of hepatocytes: role of phosphatidylinositol 3-kinase in insulin-induced shape change of microvilli. Exp. Cell Res. 239:139–151. [DOI] [PubMed] [Google Scholar]
- Loew, L. M., and L. L. Simpson. 1981. Charge-shift probes of membrane potential: a probable electrochromic mechanism for p-aminostyrylpyridinium probes on a hemispherical lipid bilayer. Biophys. J. 34:353–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magde, D., E. L. Elson, and W. W. Webb. 1974. Fluorescence correlation spectroscopy. II. An experimental realization. Biopolymers. 13:29–61. [DOI] [PubMed] [Google Scholar]
- Mayor, S., J. F. Presley, and F. R. Maxfield. 1993. Sorting of membrane components from endosomes and subsequent recycling to the cell surface occurs by a bulk flow process. J. Cell Biol. 121:1257–1269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen, N. O. 1986. Scanning fluorescence correlation spectroscopy. I. Theory and simulation of aggregation measurements. Biophys. J. 49:809–815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen, N. O., P. L. Hoddelius, P. W. Wiseman, O. Seger, and K. E. Magnusson. 1993. Quantitation of membrane receptor distributions by image correlation spectroscopy: concept and application. Biophys. J. 65:1135–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen, N. O., C. Brown, A. Kaminski, J. Rocheleau, M. Srivastava, and P. W. Wiseman. 1998. Analysis of membrane protein cluster densities and sizes in situ by image correlation spectroscopy. Faraday Discuss. 111:289–305. [DOI] [PubMed] [Google Scholar]
- Rasmusson, B. J., T. D. Flanagan, S. J. Turco, R. M. Epand, and N. O. Petersen. 1998. Fusion of Sendai virus and individual host cells and inhibition of fusion by lipophosphoglycan measured with image correlation spectroscopy. Biochim. Biophys. Acta. 1404:338–352. [DOI] [PubMed] [Google Scholar]
- Rigler, R., Z. Foldes-Papp, F. J. Meyer-Almes, C. Sammet, M. Volcker, and A. Schnetz. 1998. Fluorescence cross-correlation: a new concept for polymerase chain reaction. J. Biotechnol. 63:97–109. [DOI] [PubMed] [Google Scholar]
- Rocheleau, J. V., and N. O. Petersen. 2001. The Sendai virus membrane fusion mechanism studied using image correlation spectroscopy. Eur. J. Biochem. 268:2924–2930. [DOI] [PubMed] [Google Scholar]
- Rocheleau, J. V., and N. O. Petersen. 2000. Sendai virus binds to a dispersed population of NBD-GD1a. Biosci. Rep. 20:139–155. [DOI] [PubMed] [Google Scholar]
- Roper, K., D. Corbeil, and W. B. Huttner. 2000. Retention of prominin in microvilli reveals distinct cholesterol-based lipid micro-domains in the apical plasma membrane. Nat. Cell Biol. 2:582–592. [DOI] [PubMed] [Google Scholar]
- Smart, E. J., G. A. Graf, M. A. McNiven, W. C. Sessa, J. A. Engelman, P. E. Scherer, T. Okamoto, and M. P. Lisanti. 1999. Caveolins, liquid-ordered domains, and signal transduction. Mol. Cell. Biol. 19:7289–7304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava, M., and N. O. Petersen. 1998. Diffusion of transferrin receptor clusters. Biophys. Chem. 75:201–211. [DOI] [PubMed] [Google Scholar]
- St-Pierre, P. R., and N. O. Petersen. 1992. Average density and size of microclusters of epidermal growth factor receptors on A431 cells. Biochemistry. 31:2459–2463. [DOI] [PubMed] [Google Scholar]
- Tompson, N. L. 1991. Fluorescence correlation spectroscopy. In Topics in Fluorescence Spectroscopy, Vol 1. J. R. Lakowicz, editor. Plenum Press, New York.
- Weigmann, A., D. Corbeil, A. Hellwig, and W. B. Huttner. 1997. Prominin, a novel microvilli-specific polytopic membrane protein of the apical surface of epithelial cells, is targeted to plasmalemmal protrusions of nonepithelial cells. Proc. Natl. Acad. Sci. USA. 94:12425–12430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiseman, P. W., P. Hoddelius, N. O. Petersen, and K. E. Magnusson. 1997. Aggregation of PDGF-beta receptors in human skin fibroblasts: characterization by image correlation spectroscopy (ICS). FEBS Lett. 401:43–48. [DOI] [PubMed] [Google Scholar]
- Wiseman, P. W., and N. O. Petersen. 1999. Image correlation spectroscopy. II. Optimization for ultrasensitive detection of preexisting platelet-derived growth factor-beta receptor oligomers on intact cells. Biophys. J. 76:963–977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiseman, P. W., F. Capani, J. A. Squier, and M. E. Martone. 2002. Counting dendritic spines in brain tissue slices by image correlation spectroscopy analysis. J. Microsc. 205:177–186. [DOI] [PubMed] [Google Scholar]
- Wonnacott, T. H., and R. J. Wonnacott. 1990. Introductory Statistics. John Wiley & Sons, Toronto, Canada. 109–152.