Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Jun;84(6):4102–4114. doi: 10.1016/S0006-3495(03)75135-2

Temporal Variations in Cell Migration and Traction during Fibroblast-Mediated Gel Compaction

David I Shreiber *, Victor H Barocas †, Robert T Tranquillo *,†
PMCID: PMC1302989  PMID: 12770913

Abstract

Current models used in our laboratory to assess the migration and traction of a population of cells within biopolymer gels are extended to investigate temporal changes in these parameters during compaction of mechanically constrained gels. The random cell migration coefficient, μ(t) is calculated using a windowing technique by regressing the mean-squared displacement of cells tracked at high magnification in three dimensions with a generalized least squares algorithm for a subset of experimental time intervals, and then shifting the window interval-by-interval until all time points are analyzed. The cell traction parameter, τ0(t), is determined by optimizing the solution of our anisotropic biphasic theory to tissue equivalent compaction. The windowing technique captured simulated sinusoidal and step changes in cell migration superposed on a persistent random walk in simulated cell movement. The optimization software captured simulated time dependence of compaction on cell spreading. Employment of these techniques on experimental data using rat dermal fibroblasts (RDFs) and human foreskin fibroblasts (HFFs) demonstrated that these cells exhibit different migration-traction relationships. Rat dermal fibroblast migration was negatively correlated to traction, suggesting migration was not the driving force for compaction with these cells, whereas human foreskin fibroblast migration was positively correlated to traction.

INTRODUCTION

Fibroblast migration and compaction of the extracellular matrix are fundamental in physiological processes such as tissue morphogenesis and wound healing, as well as in tissue engineering applications. Both migration and compaction are, at least in part, the result of transmission of intracellular forces from the cell to the extracellular matrix via focal adhesions. During tissue cell migration, intracellular forces, driven primarily by the dynamic assembly of cytoskeletal forms of actin and myosin, serve to push out the leading edge of a fibroblast and then retract the tail portion through a tug-of-war or towing mechanism (Lauffenburger and Horwitz, 1996; Munevar et al., 2001). (Herein we refer to the process of pseudopodial extension and retraction as “motility” and the process of cell translocation as “migration.”) This process is coordinately regulated by the spatial and temporal expression of integrins across the cell surface (Roy et al., 1999; Sheetz et al., 1998).

The mechanisms behind network compaction are less understood. Some evidence indicates that the traction exerted during cell locomotion can concomitantly compact the surrounding network (Andujar et al., 1992; Eastwood et al., 1996; Ehrlich and Rajaratnam, 1990; Kanekar et al., 2000). Other research suggests that matrix compaction is driven primarily by cells exhibiting little migration (Roy et al., 1999) but with substantial amounts of contractile proteins, such as smooth muscle actin and myosin (Arora et al., 1999; Gabbiani, 1992; Mochitate et al., 1991). A recent study by our laboratory suggests that, depending on the compliance of the system—which includes the mechanical properties of the gel as well as any mechanical restraints—either or both mechanisms of compaction may be at play (Shreiber et al., 2001). We have developed previously two algorithms that allow us to estimate separately the migration and the traction of a population of cells as time-invariant values, which facilitates statistical comparisons among experiments. We quantify cell migration by modeling cell movement as a persistent random walk analyzed with a generalized least squares regression (GLSR) algorithm (Dickinson and Tranquillo, 1993). We quantify cell traction with our anisotropic biphasic theory (ABT) of tissue equivalent mechanics, which accounts for the biomechanical feedback between cell behavior and evolving network alignment (Barocas and Tranquillo, 1997a). Moreover, we have developed an in vitro assay that enables us to collect the required data to calculate the random cell migration coefficient and the cell traction parameter for the same population of cells, thereby allowing comparisons of potential migration-traction relationships (Knapp et al., 2000). In this “isometric cell traction assay,” a cylindrical gel anchored at both ends is monitored microscopically in time-lapse with both high and low magnification so that both cell migration and the manifestation of cell traction (a necking of the gel) can be simultaneously measured.

However, characterizing the migration and traction of a population of cells assuming time invariance obviates determination of dynamic changes in the associated parameters. Frequently, the environmental cues that play significant roles in dictating cell behavior (matrix composition, exogenous and/or cell-derived soluble factors, etc.) are time varying. In these cases, identifying temporal changes in behavior can provide important clues into the kinetics of and synergies among these cues. In this paper, we refine our techniques to provide dynamic estimates of cell migration and cell traction. We use these new techniques to compare the cell migration-cell traction relationships for two kinds of fibroblasts and provide evidence that cell traction can be positively or negatively correlated with cell migration.

METHODS

Cell migration analysis

To quantify cell migration, the mean-squared displacement 〈d2(t)〉 of tracked cells (see below) was fit to a persistent random walk model with a GLSR algorithm (Dickinson and Tranquillo, 1993). Generally, 〈d2(t)〉 is calculated from position data over all experimental time, ultimately yielding a single value for the random cell migration coefficient, μ, that describes the average migration of the population of cells over the duration of the experiment. To find 〈d2(t)〉, we determine the position vector of each cell at each time point, k. The measured cell displacement over the time interval 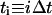Inline graphic, from position rk to rk+1 is:

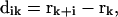graphic file with name M2.gif (1)

and the squared displacement is:

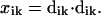graphic file with name M3.gif (2)

We consider xik to be a random variable with expected value 〈d2(t)〉, where 〈d2(t)〉 is the theoretical mean-squared displacement over ti:

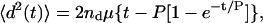graphic file with name M4.gif (3)

where nd is the number of dimensions tracked, μ is the random migration coefficient, and P is the directional persistence time for the cells.

To obtain the measured mean-squared displacement for a given time interval ti, we use the overlapping time interval sampling method (Fig. 1) and average all squared displacements xik over the cell track of that interval size:

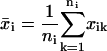graphic file with name M5.gif (4)
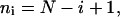graphic file with name M6.gif (5)

where N is the total number of time intervals comprising the cell track. The mean-squared displacement 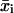Inline graphic is used to find μ and P based on Eq. 3.

FIGURE 1.

FIGURE 1

Open in a new tab

Overlapping interval method of obtaining displacement data. Each circle represents the recorded centroid position of the cell at a given time interval. In this example, the mean-squared displacement is calculated for all distances traveled over three time intervals (dashed).

We modified the calculation of 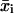Inline graphic to allow for an estimate of the temporal changes in cell migration. To introduce time dependence into the random cell migration coefficient, we found the measured mean-squared displacement over a subset, or window, of experimental time intervals of number n, beginning at the first experimental time interval, and then shifted the window of experimental time intervals up one in time. Thus, for each window of n time intervals starting at the jth time interval, we find the mean-squared displacement, 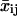Inline graphic, by averaging the squared displacements that occur within that window:

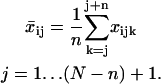graphic file with name M10.gif (6)

Each set of 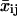Inline graphic curves is then fit to the persistent random walk model to yield a set of migration coefficients μj, of size J = (N − n) + 1 and related errors. We choose to view each μj as representative of the migration for the time at the midpoint of the interval window used. Thus, μ1 corresponds to experimental time interval n/2, μ2 to time interval (1 + n/2), and μJ to time interval N − n/2. All windows are symmetric about the operating time to ensure zero phase shift.

Analysis of simulated cell tracks

To ensure that filtering the mean-squared displacement data digitally did not introduce spurious error into the migration calculation and could detect true changes in migration, sets of simulated cell tracks obeying a persistent random walk model were created as described in Dickinson and Tranquillo (1993) and analyzed with the static (single value) and dynamic analyses described above.

To test the algorithm, 100 two-dimensional cell tracks were simulated. A single migration coefficient was calculated over all time intervals, and then temporal profiles of migration were calculated for interval windows of 11, 21, 31, 41, and 51 intervals. Odd-sized windows were used to maintain symmetry about the operating time. Similar tracks were created with a persistent random walk generated with sinusoidal and step change variations in μ as input μ(t) functions and analyzed with the same techniques.

Calculation of cell traction

The ABT was used to quantify cell traction from the compaction curves generated experimentally (see below). A detailed description of the ABT has been previously presented and will only be briefly reviewed (Barocas and Tranquillo, 1997a).

The ABT assumes that a fibrillar gel can be separated into two phases: a network phase representing the fibrillar protein (in this case collagen), and a solution phase representing the surrounding medium. The model consists of a series of conservation equations (mass and momentum for network and solution phases and cell concentration) and constitutive equations (cell alignment, network viscoelasticity, and cell spreading). The mass conservation equations for the network and solution phases are combined using total incompressibility to give one conservation equation for network volume fraction:

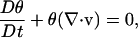graphic file with name M12.gif (7)

where θ is the volume fraction, v is the velocity of the network phase, and D/Dt denotes the substantial derivative moving with the network.

Cell proliferation, convection, and migration (as directed by contact guidance effects) were accounted for in the cell conservation equation:

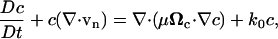graphic file with name M13.gif (8)

where c is the cell concentration, μ is the basal random cell migration coefficient, k0 is a rate constant for cell proliferation, and Ωc is the cell alignment tensor that accounts for anisotropic dispersal of cells due to contact guidance when extracellular matrix (ECM) fibrils are aligned (described below). We note that cell migration does not contribute directly to cell traction in the model, but rather is included to account for any cellular anisotropies resulting from cell migration.

The solution phase stress balance was combined with the total incompressibility equation to eliminate the solution phase velocity:

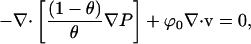graphic file with name M14.gif (9)

where P is the pressure and ϕ0 is an interstitial drag coefficient between the network and solution phases.

Finally, the solution and network phase momentum balances were combined to give the following momentum conservation equation:

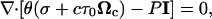graphic file with name M15.gif (10)

where σ is the network stress and τ0 is the cell traction parameter.

The cell alignment tensor Ωc was assumed to be a function solely of the collagen network alignment state. The collagen fiber orientation Ωf was determined from the local strain field (see Barocas and Tranquillo, 1997a), and Ωc was written as a monotonically increasing function of Ωf:

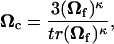graphic file with name M16.gif (11)

where κ is the cell contact guidance sensitivity parameter and the scalar prefactor ensures that Ωc = I when Ωf = I.

Both shear (Moon and Tranquillo, 1993) and compression (Knapp et al., 1997) experiments have demonstrated that the collagen network exhibits viscoelastic fluid behavior. Although it exhibits a spectrum of relaxation times (Knapp et al., 1997), for simplicity the network was modeled using a single relaxation time compressible Maxwell fluid equation, which has been shown to be of sufficient accuracy for compacting collagen up to ∼15% strain (Barocas and Tranquillo, 1997a):

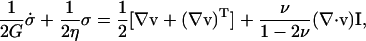graphic file with name M17.gif (12)

where G is the shear modulus, η is the shear viscosity, and ν is Poisson's ratio. The dot denotes the upper-convected derivative.

In order to account for cell spreading and development of motility from an initial, nonmotile, spherical state when the gel is formed, the cell migration and traction stress coefficients were modified accordingly with a sigmoidal dependence on time:

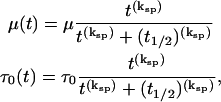graphic file with name M18.gif (13)

where ksp determines the steepness of the spreading and t1/2 is the half time for spreading.

The boundary conditions for the symmetry plane and axis for the necking cylindrical geometry of the gel in the isometric cell traction assay are as follows:

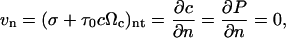graphic file with name M19.gif (14)

where n and t refer to the normal and tangent directions. The boundary conditions for the free surface are:

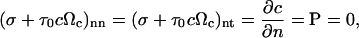graphic file with name M20.gif (15)

and, those for the platen allow neither slip nor penetration:

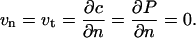graphic file with name M21.gif (16)

The parameter values used for the collagen material properties (G, η, ϕ0, and ν) were obtained from confined compression experiments of collagen gel (Knapp et al., 1997) and the cell-related parameters κ, ksp, and t1/2 were determined as described previously (Barocas and Tranquillo, 1994). The parameter values used in the fitting are shown in Table 1.

TABLE 1.

ABT parameter values

Parameter Parameter Value Reference
Shear modulus, G (dyne/cm2) 11,850 Knapp et al. (1997)
Shear viscosity, η (dyne s/cm2) 1.24 × 108 Knapp et al. (1997)
Drag coefficient, ϕ0 (dyne s/cm4) 6.4 × 106 Knapp et al. (1997)
Poisson's ratio, ν (dimensionless) 0.2 Scherer et al. (1988)
Contact guidance sensitivity parameter, κ (dimensionless) 4 Girton et al. (2002)
Cell Migration Coefficient, μ (cm2/s) 1.7 × 10−10 Barocas et al. (1995)
Cell Proliferation Coefficient, k0 (s−1) 5.3 × 10−6 Barocas et al. (1995)
Open in a new tab

To determine the cell traction parameter τ0, the system of equations was spatially discretized to generate a system of differential algebraic equations (DAE) and solved by the finite element method (FEM) (Barocas and Tranquillo, 1997b). The experimental gel midplane diameter as a function of time served as an objective function to find the value of the cell traction parameter τ0 that produced the optimum FEM solution to the system of equations using a DAE optimization solver, Control and Optimization of Systems (COOPT) kindly provided by Linda Petzold.

COOPT also allows the control parameter (in this case, the cell traction parameter τ0) to be represented as a piecewise quadratic function in low-dimensional vector space, yielding value, slope, and curvature at multiple points in time. To introduce time dependence, the explicit dependence of cell traction on cell spreading (Eq. 13) was removed and implicitly assumed in the time-dependent traction parameter τ0(t). Then, using gel compaction as an objective function, the optimal solution of the DAE system was found.

Simulated collagen compaction

To validate the dynamic assessment of cell traction as optimized by COOPT, a simulation was performed with prescribed τ0(t) obtained by defining values of the cell spreading parameters. A polynomial fit of the predicted midplane compaction from this simulation was then used as an objective function for dynamic assessment of the cell traction parameter τ0(t), and the output compaction was compared to the original result of the simulation.

Cell culture

Rat dermal fibroblasts (RDFs) and human foreskin fibroblasts (HFFs) were obtained using a primary explant technique (Freshney, 1987) and kept in liquid nitrogen after slow freezing. Cell lines were initiated for culture by thawing an aliquot of cells and centrifuging at 1000 rpm for 10 min at 4°C. The pellet of cells was resuspended in Dulbecco's modified Eagle's medium (DMEM supplemented with penicillin-streptomycin (pen-strep) (1% v/v) and L-glutamine (1% v/v)) (Gibco Laboratories, Grand Island, NY). Cells were plated on 60 × 15 mm petri dishes using 5 ml of DMEM with 10% fetal bovine serum (FBS) (HyClone Laboratories, Logan, UT), 1% pen-strep, and 1% L-glutamine and kept in a humidified CO2 incubator at 37°C. Trypsin/EDTA (Sigma Chemical Company, St. Louis, MO) was used to passage the cells once a week at a 1:4 dilution. Cells were harvested with 0.5% Trypsin/EDTA and washed twice with Medium 199 (M199) (Gibco) with Hanks' salts supplemented with 10% FBS, 1% pen-strep, and 1% L-glutamine. Cells were passed or harvested at 60–90% confluence. All experiments were conducted before the ninth passage, at which point a new culture was initiated from frozen cells.

Simultaneous cell traction and migration assay

The in vitro traction/migration assay was performed as described previously (Knapp et al., 2000). A schematic of an assay chamber is shown in Fig. 2. Briefly, the assay consisted of a cell-seeded cylindrical collagen gel (2 mg/ml type I collagen solution–20 μl 1 M HEPES buffer (Gibco), 132 μl 0.1 N NaOH (Sigma), 100 μl 10X Modified Eagle's Medium (MEM), 60 μl M199 medium, 1 μl pen-strep (5000 units of penicillin and 5000 μg streptomycin/ml in 0.85% saline), 10 μl L-Glutamine (29.2 mg/ml in 0.85% saline), and 677 μl of Vitrogen 100 (Cohesion Co., Palo Alto, CA) per ml of collagen) that was prevented from compacting axially. Two cylindrical stainless steel posts with porous polyethylene platens attached to the ends provided the axial constraint. The chambers were assembled and collagen/cell suspension was pipetted inside the polycarbonate sheath. The chambers were placed inside an incubator at 37°C to facilitate gelation. The collagen solution penetrated the porous polyethylene resulting in a firm bond between the posts and the collagen upon gelation. After gelation, a glass coverslip was attached to the bottom of the chamber with vacuum grease, and M199 with 10% FBS, 1% pen-strep, and 1% L-glutamine was added to the chamber. The polycarbonate sheath was withdrawn, and a coverslip was attached to the top of the chamber with vacuum grease. Fully assembled chambers were placed in the incubator for approximately an hour before being transferred to the automated time-lapse video microscopy system.

FIGURE 2.

FIGURE 2

Open in a new tab

Preparation of the traction/migration assay. (A) A solution of collagen monomer with uniformly dispersed polystyrene beads and dermal fibroblasts is prepared. (B) The solution is injected into a polycarbonate tube supported by stainless steel posts with porous polyethylene platens fixed to the ends. (C) After gelation, the collagen is firmly attached to porous polyethylene, and the polycarbonate sheath is slid over one of the stainless steel posts. (D) The entrapped cells are then exposed to culture medium. The attachment to the porous polyethylene provides an axial constraint resulting in compaction solely in the radial direction.

High magnification 3-D single-cell tracking

High magnification cell tracks of fibroblasts within collagen gels in assay chambers were generated as described elsewhere (Knapp et al., 2000). A Zeiss Axiovert 135 inverted light microscope (Thornwood, NY) with an automated stage and KP-M2U CCD Hitachi camera (Woodbury, NY) was coupled to a personal computer running a macro for time-lapse cell tracking programmed with KS400 image analysis software (Zeiss). Briefly, using the 40× objective, many (15–20 per chamber) individual cells were selected randomly from within the gel and their position recorded. Each cell was associated with a neighboring (within ∼400 μm) polystyrene bead. The time-lapse loop was then initiated. At the specified time interval, the cell-tracking program would move the microscope stage to the last identified cell position and execute an autofocus routine to adjust the z-position of the stage. A series of image analysis routines was used to identify the centroid of the cell. The cell position was updated and recorded, and the stage was moved automatically to the last recorded position of the next cell. The total time-lapse period was 24–48 h, and a time-lapse interval was 18–22 min. At the end of the time-lapse experiment, the cell displacement information was corrected for convection effects by subtracting the displacement of the polystyrene bead colocalized with the given cell.

Low magnification time-lapse of compacting gels

Low magnification time-lapse video microscopy to quantify gel compaction was conducted concurrently with high-magnification cell tracking. The motorized nosepiece of a Zeiss Axiovert 135 inverted microscope allowed the objective to be automatically changed from 40× to 2.5× during macro execution. A mosaic image of the gel was taken at the beginning of each time-lapse interval. Midplane diameter measurements of the gel at each time point were taken from these images and used to determine midplane compaction of the gel.

RESULTS

Simulated cell migration analysis

Simulated cell tracks obeying a persistent random walk model with time-invariant parameters (Fig. 3) were created to compare the results of the dynamic migration calculation μ(t) to the constant migration calculation μ. The simulated tracks were also used to estimate the effects of different window sizes on the fitted μ(t) (Fig. 4). In general, μ(t) fluctuated about the time-invariant coefficient value. No drift or regular patterns were observed. Just as increasing the window size of a digital filter increases the cutoff frequency and dampens high frequency noise, increasing the window size resulted in a smoother μ(t).

FIGURE 3.

FIGURE 3

Open in a new tab

Representative simulated cell tracks based on the persistent random walk model with time-invariant migration parameters (Δt = 0.4 P). Simulated cell tracks (n = 100) were created to compare the results of the GLSR analysis determining the constant random migration coefficient, μ, and migration as a function of time, μ(t).

FIGURE 4.

FIGURE 4

Open in a new tab

Effects of window size on μ(t) ± variance. Mean-squared displacement data generated from simulated cell tracks was fit to a persistent random walk model over a moving subset of 11–51 intervals to determine μ(t). The dynamic migration coefficient oscillated randomly about the migration coefficient calculated using all 100 time intervals (line, μ = 5.01 ± 0.05 μm2/min). No obvious drift can be observed. Increasing the window size decreased the cutoff frequency of the digital filter, eliminating high frequency fluctuations at larger window sizes. Error in the individual calculations generally decreased as the window size increased.

The dynamic analysis was also performed on persistent random walk tracks where migration was varied sinusoidally (Fig. 5) and as a step function (Fig. 6). In both cases, the dynamic analysis captured the fundamental changes in migration over time. As with the pure random walk tracks, increasing the window size decreased high frequency oscillations. With the sinusoidal function tested (one full period), window size had a small effect on migration amplitude but did not dramatically alter the shape of μ(t). If the frequency of the sinusoidal oscillations in migration were higher, we would expect μ(t) to be progressively damped as window size increased. This is demonstrated in the high frequency, step change in input migration, where increasing window size progressively smoothed the prediction of μ(t) relative to the step change. Interestingly, as shown in Fig. 7, the mean-squared displacement curves for the constant, sinusoidal, and step migration cases calculated traditionally with all experimental data were virtually identical, as were the resulting migration calculations. This indicates that characterizing migration as a time-averaged parameter may preclude observation of true changes in behavior.

FIGURE 5.

FIGURE 5

Open in a new tab

Effects of window size on dynamic random migration coefficient calculation for simulated cell tracks obeying a persistent random walk with sinusoidal migration (μ(t) = 5 + 0.25(sin (t/100)). Increasing window size decreases high frequency noise and does not produce a phase shift. For very large windows, the migration signal is damped.

FIGURE 6.

FIGURE 6

Open in a new tab

Effects of window size on dynamic random migration coefficient for simulated cell tracks obeying a persistent random walk with a step change in migration (μ(t) = 6, t < 50 intervals; 4, t ≥ 50 intervals). Similar to the time-invariant and sinusoidal migration inputs, increasing window size decreases high frequency changes in the migration signal. The signal is progressively smoothed as window size increases.

FIGURE 7.

FIGURE 7

Open in a new tab

Plots of mean-squared displacement (MSD) calculated over all time intervals from cell tracks generated with a persistent random walk model with time-invariant (μ = 5 μm2/min), sinusoidally varying (μ(t) = 5 + 0.25(sin (t/100))), or step (μ(t) = 6, t < 50 intervals; μ(t) = 4, t ≥ 50 intervals) random migration coefficients. The MSD for the time-varying migration input functions are nearly identical to the MSD for the time-invariant migration. Regression of this data yields values for μ that are also similar (5.01 ± 0.05 for time-invariant migration, 5.02 ± 0.05 for sinusoidal migration, and 5.00 ± 0.04 for step migration).

Although a traditional analytical derivation of the phase shift associated with the windowing technique is impossible because of the numerically derived migration coefficients, digital filters based on symmetrical windows, such as the ones employed herein, have zero phase shift. Empirically, from Figs. 5 and 6, no phase shifts were observed as a result of the dynamic analysis for either the sinusoidal or the step migration changes.

Simulated cell traction analysis

The optimization of the solution to the DAE for dynamic cell traction was validated by creating a simulated compaction profile based on preset model parameters and using the compaction profile as the objective function for a subsequent dynamic estimation of the cell traction parameter. The ABT was simulated using the values presented in Table 1, a typical cell spreading function (from Eq. 13, half time for spreading t1/2 = 4 h, steepness of spreading curve ksp = 1.6), and a constant cell traction parameter (τ0 = 0.015 dyne cm/cell). The resulting compaction profile was fit to a polynomial function, which served as the input objective function for COOPT. COOPT was then executed to determine the optimal time-varying cell traction parameter τ0(t) to produce compaction that best matches the objective function. All dependence on cell spreading was removed. Fig. 8 depicts the results of the optimization. COOPT was able to reproduce the input compaction profile accurately. Moreover, τ0(t) increased with time until it became asymptotic with the value of τ0 (0.015 dyne cm/cell) used to produce the objective function based on constant cell traction. These results demonstrate that the COOPT optimization scheme can capture time dependent changes in cell traction, such as those induced by cell spreading.

FIGURE 8.

FIGURE 8

Open in a new tab

Validation of dynamic assessment of cell traction parameter τ0(t) with COOPT. A simulation was performed to evaluate the midplane compaction predicted by the ABT based on a constant cell traction parameter, τ0 = 0.015 dyne cm/cell, where time dependence for cell traction was introduced with a sigmoidal cell spreading function (Eq. 13; open squares). The predicted compaction (open circles) was fit to a polynomial function, which served as the objective function for the optimization software. COOPT effectively optimized the solution of the ABT resulting in midplane compaction (solid line) nearly identical to the objective function. The predicted dynamic cell traction parameter (dashed line) becomes asymptotic with the constant value for τ0 used to generate the objective function and accurately captures the evolution of traction, which, for this simulation, is due to the cell spreading function.

Experimental migration analysis

From time-lapse position data for HFFs and RDFs, mean-squared displacement data was generated from the position data over all time intervals as well as for a window size of 20 time intervals (400 min), which is sufficiently greater than the typical persistence time calculated using all time intervals (20–30 min) to allow for an accurate estimate of the random cell migration coefficient, μ (Dickinson and Tranquillo, 1993; Knapp et al., 2000). The dynamic migration of the two cell types for two separate experiments are presented in Fig. 9 (HFFs) and Fig. 10 (RDFs). In general, RDFs experienced an increase in their migration during the experiment. In most cases, HFFs also experienced an increase in migration, although in some cases we have observed relatively constant migration (Fig. 9).

FIGURE 9.

FIGURE 9

Open in a new tab

Compaction/migration/traction relationships for HFFs. Corresponding plots represent the estimated quantities from two representative experiments (A–C, D–F). Each plot represents the average of three samples. The number of migration and traction points plotted has been reduced for clarity. These experiments demonstrate that for HFFs, traction and migration are positively correlated.

FIGURE 10.

FIGURE 10

Open in a new tab

Compaction/migration/traction relationships for RDFs. Corresponding plots represent the estimated quantities from two representative experiments (A–C, D–F). Each plot represents the average of three samples. The number of migration and traction points plotted has been reduced for clarity. In general, as gel compaction by RDFs plateaus and cell traction wanes, migration increases.

Experimental cell traction analysis

Experimental cell traction was estimated by optimizing the solution of the FEM to best fit the midplane compaction of the collagen gel. A representative plot of RDF compaction is shown in Fig. 11. The FEM solution was optimized for two different representations of the cell traction parameter: a single-valued coefficient τ0 where time dependence is introduced through cell spreading (Eq. 13), and an arbitrary time-dependent coefficient τ0(t). Comparisons of a representative FEM solution with the experimental compaction data along with the resulting cell traction are also displayed in Fig. 11. In general, the cell traction parameter did vary with time, and allowing the cell traction parameter to be an arbitrary function of time improved the quality of the optimized solution compared to the solution when temporal variation was introduced into cell traction by incorporating a sigmoidal function of time to account for cell spreading.

FIGURE 11.

FIGURE 11

Open in a new tab

Comparison of predicted compaction from simulations with a dynamic or constant cell traction parameter, τ0, for an experiment with RDFs. Allowing the cell traction parameter to vary with time improved the quality of the predicted midplane compaction relative to the experimental compaction. Clear time dependent trends are observed in τ0.

Combined migration and traction

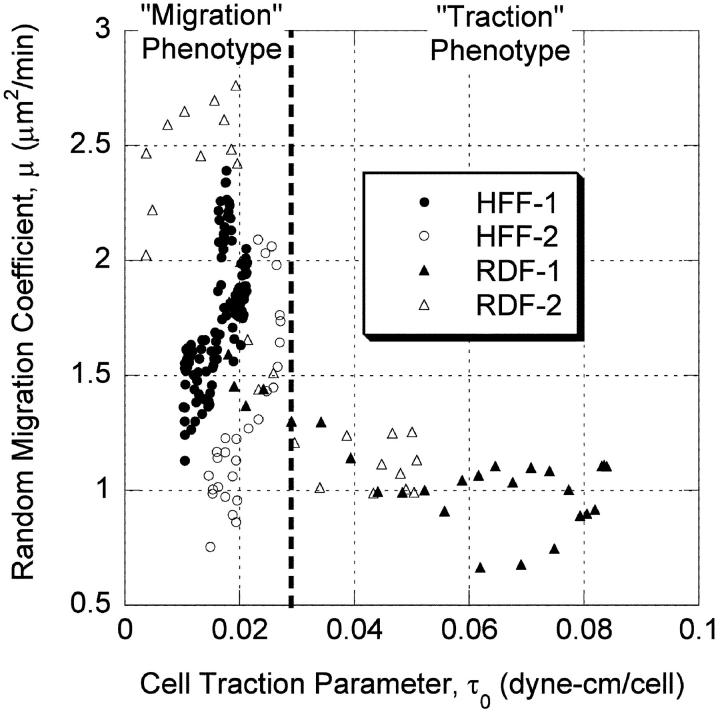
The dynamic estimates of cell migration and cell traction allow an assessment of the relationship between these two indices of cell behavior during the course of gel compaction. Migration and traction versus time data were resampled using linear interpolation to produce coincident time points, and then traction was plotted vs. migration for the different experiments (Fig. 12). In experiments with HFFs, there was a positive correlation between migration and traction (R2 = 0.43 and 0.66), whereas for RDFs, the cell migration and cell traction were negatively correlated (R2 = 0.54 and 0.72). HFF and RDF data plotted on the same axes indicate that RDFs exhibited a biphasic relationship between cell speed and traction, although this cannot be concluded for HFFs (Fig. 13).

FIGURE 12.

FIGURE 12

Open in a new tab

Traction-migration correlations for HFFs (A, B) and RDFs (C, D). Linear correlations of traction versus migration data (resampled to produce coincident time points) revealed that for both experiments with HFFs, traction was positively correlated with migration, whereas for both RDF experiments, traction was negatively correlated with migration.

DISCUSSION

We have described herein modifications to our previously published methods for determining cell migration and cell traction that provide temporal estimates of these quantities during cell-driven gel compaction. The methods were validated using results from model simulations. Comparisons of time-resolved migration and traction for two different types of dermal fibroblasts, RDFs and HFFs, indicated that these cells may produce the traction associated with gel compaction via different mechanisms. RDFs demonstrated a negative correlation between cell migration and cell traction, suggesting that these cells switch phenotypes from a high traction-producing, relatively stationary cell to a migratory cell that does not produce enough traction to continue compacting the gel. HFFs, on the other hand, generally appeared to continue to exert sufficient traction to compact the gel as they migrated, exhibiting a positive correlation between traction and migration.

Dynamic analysis of cell migration

Models of cell migration continue to be used to assess the role of surface adhesion, directional cues, and soluble factors on cell migration, and are applied to bioprocesses such as tumor invasion and tissue engineering. Most analyses are based on a persistent random walk model and quantify cell migration with time-invariant parameters (Dunn and Brown, 1987). As shown in the simulation results in Fig. 7, characterizing cell migration in this manner may lead to erroneous conclusions, especially when comparing populations of cells with time-varying migration behavior. In this simulation, three functions of cell migration with time were modeled: a constant, a sinusoidal, and a step function, all with the same time-averaged value of the random migration coefficient, μ. Analyzing the mean-squared displacement data with time-invariant analysis resulted in indistinguishable estimates of μ equal to the prescribed time-averaged value. Thus, if these were real populations of cells, we would incorrectly infer that the migration behavior of the populations was the same. Whereas these shifts in migration behavior were simulated, time-dependent shifts can occur in living cells, as shown in Fig. 9 and Fig. 10 for HFFs and RDFs in vitro. The shifts are especially clear for RDFs and indicate a switch to a migratory phenotype during the experiment. This analysis can therefore be used to quantitatively study the evolution of cell migration behavior under different experimental conditions. For example, the kinetics associated with the stimulation of migration by particular growth factors can be evaluated, or, if combined with biochemical assays to determine cytokine production by cells, synergistic or downstream signaling effects on migration can be assessed.

Recently, Bergman and Zygourakis presented a method to derive a temporal estimate of migration for leukocyte migration over different 2D substrates (Bergman and Zygourakis, 1999). In their study, experimental cell tracks were discretized into specific windows, and the mean-squared displacement and subsequent cell migration parameters were determined for each window. The analysis was presented for one window duration (an hour), and each mean-squared displacement calculation was independent. This requires a very small ratio of sampling time to experiment duration, so that a suitable number of points can be included in the mean-squared displacement calculation and enough calculations are performed to provide a meaningful assessment of temporal variations of cell migration. The analysis described herein differs in that the intervals used to calculate the mean-squared displacement overlap from point-to-point. This allows the temporal information to be extracted in cases where the ratio of the duration of the sampling window to the duration of the experiment is larger, as is the general case for high magnification tracking of cells in three dimensions.

Dynamic analysis of cell traction

The ability to assess cell traction dynamically from macroscopic images of gel compaction is very unique and involves a combination of the ABT and the novel optimization software, COOPT. Unlike most measurements of cell traction, where one end of a constrained gel is attached to a force transducer (Eastwood et al., 1996; Kolodney and Wysolmerski, 1992), we can account for the evolution of collagen fibril and cell alignment in the traction determination. As a gel becomes aligned between the points of attachment at both ends, the cells within the gel also become aligned via contact guidance. Thus, for isometric systems with an attached force transducer, the coalignment of cells with the force transducer will lead to increased force measurement, even though the cells may have been generating the same force, but in a direction perpendicular to the transducer, before network alignment (Barocas and Tranquillo, 1997b).

We are able to evaluate cell traction with this approach without contacting the gel. Therefore, we can extend the technique to study cell traction in free-floating samples. Another somewhat similar method of monitoring cell traction in a three-dimensional system involves inferring the traction from bead displacements (Roy et al., 1997), which is used more widely to study cell traction exerted on 2-D substrates (Lo et al., 2000; Munevar et al., 2001). Both methods require knowledge of the material properties of the network. One advantage of the ABT is that the material properties are scaled as the network concentration increases as a result of gel compaction (stress is multiplied by the network volume fraction in Eq. 10). Finally, we note that, as seen in Fig. 11, characterizing the cell traction parameter as a piecewise continuous function in low-dimensional vector space introduces smooth inflections in the traction for cases where gel compaction appears to occur in multiple phases.

Cell migration-cell traction relationships

The mechanisms by which tissue cells, such as fibroblasts, produce gel compaction remain debated. A strong body of evidence suggests that, in the presence of certain environmental cues, including mechanical stress (Knapp et al., 2000; Mochitate et al., 1991; Shreiber et al., 2001), elevated concentrations of TGF-β (Arora et al., 1999; Desmouliere et al., 1993; Yokozeki et al., 1997), and increased substrate stiffness (Arora et al., 1999; Shreiber et al., 2001), fibroblasts can be induced to change phenotype to a myofibroblast–one which expresses high levels of proteins commonly associated with smooth muscle cells, such as α-smooth muscle actin, desmin, and vimentin (Sappino et al., 1990; Schmitt-Graff et al., 1994). Myofibroblasts were first identified as important contributors to wound contraction (Gabbiani, 1992) and have since been implicated in fibrocontractive disorders (Desmouliere et al., 1997; Grinnell, 1994). Myofibroblasts are believed to generate traction through a smooth muscle cell-like contractile mechanism (Gabbiani and Badonnel, 1976; Mar et al., 2001).

Conversely, some have argued that the forces associated with cell migration can drive extracellular matrix compaction concomitantly. This theory is primarily based on the absence of stress fibers and focal contacts in fibroblasts during organization of collagen gels (Ehrlich and Rajaratnam, 1990). Many studies have examined the magnitude, direction, and duration of forces exerted on a substratum by cells as they migrate (Dembo and Wang, 1999; Lo et al., 2000; Roy et al., 1999; Sheetz et al., 1998). For instance, Roy et al. compared the tractional forces produced by corneal fibroblasts seeded on a collagen gel to the maintenance of tension in that gel (Roy et al., 1999). Serum-starved cells exhibited extensive pseudopodial motility but were not migrating nor exerting tractional force on the matrix. The greatest force was produced by cells stimulated to contract through the coordinated upregulation of cell adhesion and cell contractility, inferred from an increase in F-actin stress fibers, by the addition of lysophosphatidic acid (Roy et al., 1999). They also noted that substrate compliance is an important mediator of the contractile phenotype–an observation that we and others have documented as well (Arora et al., 1999; Shreiber et al., 2001).

The experimental results presented herein indicate that both mechanisms of cell-mediated gel compaction are potentially at play. With RDFs, it was clear that gel compaction was not driven by cell migration. However, with HFFs, the relationship was less obvious. Gel compaction did not plateau as quickly as with RDFs, and a more direct relationship was observed between cell migration and cell traction. In a previous study, we observed that RDFs, if stimulated to migrate with PDGF-BB, exert more traction (measured by degree of compaction) than unstimulated RDFs in free-floating collagen gels, again indicating that traction associated with cell migration can also concomitantly compact a collagen network (Shreiber et al., 2001). However, in free-floating fibrin gels, stimulating cell migration with PDGF-BB led to a decrease in cell traction, which we believe was primarily due to the increased stiffness of a fibrin gel versus a collagen gel.

It has been predicted that cell speed depends on cell traction in a biphasic manner (DiMilla et al., 1993). Our results for the RDFs are consistent with this prediction, although we did not observe the same biphasic response for HFFs—these cells never appear to enter a high traction state. However, the transient nature of the experimental conditions (e.g., the density of collagen fibrils and associated adhesion sites increases as the cell traction drives gel compaction) precludes an unambiguous comparison between our data and this theoretical prediction.

Low cell densities (1.5 × 104 cells/ml) were used in this investigation to facilitate high magnification tracking of individual cells in three dimensions as well as to limit the degree of compaction to within the limits of linear viscoelasticity. Thus, very few cell-cell contacts were observed during the course of an experiment. The formation of cell couplings has been shown to affect the contraction of fibroblast-populated collagen lattices (Ehrlich et al., 2000). Ehrlich and Rittenberg demonstrated differences in the mechanisms of compaction in free floating gels populated at high (5 × 105 cells/ml) vs. medium (5 × 104 cells/ml) cell densities (Ehrlich and Rittenberg, 2000). Whereas the compaction of medium cell density gels was modulated by interfering with traditional mediators of tractional forces (low serum, antibodies against collagen integrin subunits), the compaction of high cell density gels was dependent primarily on forces associated with cell spreading and unaffected by these mediators. Roy et al. also noted that corneal fibroblasts seeded on a compliant collagen gel were more likely to exhibit F-actin stress fibers when seeded at higher cell densities. The cell density may also affect cell migration by contact inhibition (Lee et al., 1995). We have demonstrated that increasing the number of cells increases gel compaction and decreases gel volume, which therefore increases the concentration of the cells relative to gel volume (Knapp et al., 2000).

It is not yet clear why we observed different behavior in RDFs and HFFs. Certainly, the most obvious differences between these two types of dermal fibroblasts are species and donor age. In vitro migration assays of dermal fibroblasts from different aged human donors have demonstrated that the migratory ability of these cells significantly decreases with age (Pienta and Coffey, 1990). Studies have also shown that neonatal and fetal fibroblasts are more rapidly induced into myofibroblasts during the wound healing response than adult fibroblasts (Cass et al., 1997; Darby et al., 1990). Interestingly, depending on the gestational age, myofibroblasts can disappear from the wound site (Cass et al., 1997), a phenomenon that has been correlated to scarless wound healing.

The shift in the RDF population toward a migratory one following compaction has not, to our knowledge, been documented previously. This shift in behavior would seem to represent a change away from a myofibroblastic cell that may be triggered by sensing a certain level of network stress, which may be analogous to wound contraction. Current research suggests that, during the final stages of wound healing, myofibroblasts, again, generally identified by α-smooth muscle actin expression, die through apoptosis to leave an acellular scar (Darby et al., 1990; Desmouliere et al., 1997). It is also possible, however, that some of the cells revert to a migratory phenotype, losing α-smooth muscle actin expression, and move away from the scar.

The presented techniques have been applied to characterizing dermal fibroblasts interacting with a collagen gel, but they are easily applied to other cells and polymer networks. We have previously characterized cell-matrix interactions in fibrin gels (Bromberek et al., 2002; Knapp et al., 1999; Shreiber et al., 2001), and we are currently developing biopolymer-mimetic scaffolds with immobilized functional groups for tissue engineering. Dynamic characterization of cell migration and cell traction in these systems can provide important insights into cell-scaffold interactions. The analytical techniques for cell migration are independent of the scaffold used; however, characterization of some of the material properties of the scaffold is required for analysis of cell traction.

FIGURE 13.

FIGURE 13

Open in a new tab

Traction-migration relationships for HFFs and RDFs. Open and closed circles represent two independent HFF experiments and open and closed triangles represent two independent RDF experiments. Plotting all data on the same axes reveals a biphasic correlation of migration with traction for RDFs. HFFs do not appear to enter a high traction state.

Acknowledgments

The authors thank Luca Gunther and Naomi Ferguson for their assistance with cell culture. COOPT software and support were provided by Linda Petzold and Radu Serban at UCSB.

Funding was provided by the National Institutes of Health (PO1-GM50150-03S1), the National Science Foundation (CCR 9527151), and the Materials Research Science and Engineering Center-Artificial Tissues Program (DMR-9809364).

References

  1. Andujar, M. B., M. Melin, S. Guerret, and J. A. Grimaud. 1992. Cell migration influences collagen gel contraction. J. Submicrosc. Cytol. Pathol. 24:145–154. [PubMed] [Google Scholar]
  2. Arora, P. D., N. Narani, and C. A. McCulloch. 1999. The compliance of collagen gels regulates transforming growth factor-beta induction of alpha-smooth muscle actin in fibroblasts. Am. J. Pathol. 154:871–882. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Barocas, V. H., A. G. Moon, and R. T. Tranquillo. 1995. The fibroblast-populated collagen microsphere assay of cell traction force–Part 2: Measurement of the cell traction parameter. J. Biomech. Eng. 117:161–170. [DOI] [PubMed] [Google Scholar]
  4. Barocas, V. H., and R. T. Tranquillo. 1994. Biphasic theory and in vitro assays of cell-fibril mechanical interactions in tissue-equivalent collagen gels. In Cell Mechanics and Cellular Engineering. V. C. Mow, F. Guilak, R. Tran-Son-Tay, R. M. Hochmuth, editors. Springer-Verlag, New York. 185–209.
  5. Barocas, V. H., and R. T. Tranquillo. 1997a. An anisotropic biphasic theory of tissue-equivalent mechanics: the interplay among cell traction, fibrillar network deformation, fibril alignment, and cell contact guidance. J. Biomech. Eng. 119:137–145. [DOI] [PubMed] [Google Scholar]
  6. Barocas, V. H., and R. T. Tranquillo. 1997b. A finite element solution for the anisotropic biphasic theory of tissue-equivalent mechanics: the effect of contact guidance on isometric cell traction measurement. J. Biomech. Eng. 119:261–268. [DOI] [PubMed] [Google Scholar]
  7. Bergman, A. J., and K. Zygourakis. 1999. Migration of lymphocytes on fibronectin-coated surfaces: temporal evolution of migratory parameters. Biomaterials. 20:2235–2244. [DOI] [PubMed] [Google Scholar]
  8. Bromberek, B. A., P. A. Enever, D. I. Shreiber, M. D. Caldwell, and R. T. Tranquillo. 2002. Macrophages influence a competition of contact guidance and chemotaxis for fibroblast alignment in a fibrin gel coculture assay. Exp. Cell Res. 275:230–242. [DOI] [PubMed] [Google Scholar]
  9. Cass, D. L., K. G. Sylvester, E. Y. Yang, T. M. Crombleholme, and N. S. Adzick. 1997. Myofibroblast persistence in fetal sheep wounds is associated with scar formation. J. Pediatr. Surg. 32:1017–1021. [DOI] [PubMed] [Google Scholar]
  10. Darby, I., O. Skalli, and G. Gabbiani. 1990. Alpha-smooth muscle actin is transiently expressed by myofibroblasts during experimental wound healing. Lab. Invest. 63:21–29. [PubMed] [Google Scholar]
  11. Dembo, M., and Y. L. Wang. 1999. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 76:2307–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Desmouliere, A., C. Badid, M. L. Bochaton-Piallat, and G. Gabbiani. 1997. Apoptosis during wound healing, fibrocontractive diseases and vascular wall injury. Int. J. Biochem. Cell Biol. 29:19–30. [DOI] [PubMed] [Google Scholar]
  13. Desmouliere, A., A. Geinoz, F. Gabbiani, and G. Gabbiani. 1993. Transforming growth factor-beta 1 induces alpha-smooth muscle actin expression in granulation tissue myofibroblasts and in quiescent and growing cultured fibroblasts. J. Cell Biol. 122:103–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dickinson, R. B., and R. T. Tranquillo. 1993. Optimal estimation of cell movement indices from the statistical analysis of cell tracking data. American Institute of Chemical Engineers Journal. 39:1995–2010. [Google Scholar]
  15. DiMilla, P. A., J. A. Stone, J. A. Quinn, S. M. Albeda, and D. A. Lauffenburger. 1993. Maximal migration of human smooth muscle cells on fibronectin and type IV collagen occurs at an intermediate attachment strength. J. Cell Biol. 122:729–737. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Dunn, G. A., and A. F. Brown. 1987. A unified approach to analysing cell motility. J. Cell Sci. Suppl. 8:81–102. [DOI] [PubMed] [Google Scholar]
  17. Eastwood, M., R. Porter, U. Khan, G. McGrouther, and R. Brown. 1996. Quantitative analysis of collagen gel contractile forces generated by dermal fibroblasts and the relationship to cell morphology. J. Cell. Physiol. 166:33–42. [DOI] [PubMed] [Google Scholar]
  18. Ehrlich, H. P., G. Gabbiani, and P. Meda. 2000. Cell coupling modulates the contraction of fibroblast-populated collagen lattices. J. Cell. Physiol. 184:86–92. [DOI] [PubMed] [Google Scholar]
  19. Ehrlich, H. P., and J. B. Rajaratnam. 1990. Cell locomotion forces versus cell contraction forces for collagen lattice contraction: an in vitro model of wound contraction. Tissue Cell. 22:407–417. [DOI] [PubMed] [Google Scholar]
  20. Ehrlich, H. P., and T. Rittenberg. 2000. Differences in the mechanism for high- versus moderate-density fibroblast-populated collagen lattice contraction. J. Cell. Physiol. 185:432–439. [DOI] [PubMed] [Google Scholar]
  21. Freshney, R. I. 1987. Culture of Animal Cells: A Manual of Basic Technique. New York: Alan R. Liss, Inc.
  22. Gabbiani, G. 1992. The biology of the myofibroblast. Kidney Int. 41:530–532. [DOI] [PubMed] [Google Scholar]
  23. Gabbiani, G., and M. C. Badonnel. 1976. Contractile events during inflammation. Agents Actions. 6:277–280. [DOI] [PubMed] [Google Scholar]
  24. Girton, T. S., V. H. Barocas, and R. T. Tranquillo. 2002. Confined compression of a tissue-equivalent: collagen fibril and cell alignment in response to anisotropic strain. J. Biomech. Eng. 124:568–575. [DOI] [PubMed] [Google Scholar]
  25. Grinnell, F. 1994. Fibroblasts, myofibroblasts, and wound contraction. J. Cell Biol. 124:401–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kanekar, S., T. K. Borg, L. Terracio, and W. Carver. 2000. Modulation of heart fibroblast migration and collagen gel contraction by IGF-I. Cell Adhes. Commun. 7:513–523. [DOI] [PubMed] [Google Scholar]
  27. Knapp, D. M., V. H. Barocas, A. G. Moon, K. Yoo, L. R. Petzold, and R. T. Tranquillo. 1997. Rheology of reconstituted type I collagen gel in confined compression. Journal of Rheology. 41:971–993. [Google Scholar]
  28. Knapp, D. M., E. F. Helou, and R. T. Tranquillo. 1999. A fibrin or collagen gel assay for tissue cell chemotaxis: assessment of fibroblast chemotaxis to GRGDSP. Exp. Cell Res. 247:543–553. [DOI] [PubMed] [Google Scholar]
  29. Knapp, D. M., T. T. Tower, R. T. Tranquillo, and V. H. Barocas. 2000. Estimation of cell traction and migration in an isometric cell traction assay. American Institute of Chemical Engineers Journal. 45:2628–2640. [Google Scholar]
  30. Kolodney, M. S., and R. B. Wysolmerski. 1992. Isometric contraction by fibroblasts and endothelial cells in tissue culture: A quantitative study. J. Cell Biol. 117:73–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lauffenburger, D. A., and A. F. Horwitz. 1996. Cell migration: a physically integrated molecular process. Cell. 84:359–369. [DOI] [PubMed] [Google Scholar]
  32. Lee, Y., S. Kouvroukoglou, L. V. McIntire, and K. Zygourakis. 1995. A cellular automaton model for the proliferation of migrating contact-inhibited cells. Biophys. J. 69:1284–1298. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Lo, C. M., H. B. Wang, M. Dembo, and Y. L. Wang. 2000. Cell movement is guided by the rigidity of the substrate. Biophys. J. 79:144–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Mar, P. K., P. Roy, H. L. Yin, H. D. Cavanagh, and J. V. Jester. 2001. Stress fiber formation is required for matrix reorganization in a corneal myofibroblast cell line. Exp. Eye Res. 72:455–466. [DOI] [PubMed] [Google Scholar]
  35. Mochitate, K., P. Pawelek, and F. Grinnell. 1991. Stress relaxation of contracted collagen gels: disruption of actin filament bundles, release of cell surface fibronectin, and down-regulation of DNA and protein synthesis. Exp. Cell Res. 193:198–207. [DOI] [PubMed] [Google Scholar]
  36. Moon, A. G., and R. T. Tranquillo. 1993. The fibroblast-populated collagen microsphere assay of cell traction force - Part 1. Continuum model. American Institute of Chemical Engineers Journal. 39:163–177. [Google Scholar]
  37. Munevar, S., Y. Wang, and M. Dembo. 2001. Traction force microscopy of migrating normal and H-ras transformed 3T3 fibroblasts. Biophys. J. 80:1744–1757. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Pienta, K. J., and D. S. Coffey. 1990. Characterization of the subtypes of cell motility in ageing human skin fibroblasts. Mech. Ageing Dev. 56:99–105. [DOI] [PubMed] [Google Scholar]
  39. Roy, P., W. M. Petroll, H. D. Cavanagh, C. J. Chuong, and J. V. Jester. 1997. An in vitro force measurement assay to study the early mechanical interaction between corneal fibroblasts and collagen matrix. Exp. Cell Res. 232:106–117. [DOI] [PubMed] [Google Scholar]
  40. Roy, P., W. M. Petroll, H. D. Cavanagh, and J. V. Jester. 1999. Exertion of tractional force requires the coordinated up-regulation of cell contractility and adhesion. Cell Motil. Cytoskeleton. 43:23–34. [DOI] [PubMed] [Google Scholar]
  41. Sappino, A. P., W. Schurch, and G. Gabbiani. 1990. Differentiation repertoire of fibroblastic cells: expression of cytoskeletal proteins as marker of phenotypic modulations. Lab. Invest. 63:144–161. [PubMed] [Google Scholar]
  42. Scherer, G. W., S. A. Pardenek, and R. M. Swiatek. 1988. Viscoelasticity in silica gel. Journal of Non-Crystalline Solids. 108:14–22. [Google Scholar]
  43. Schmitt-Graff, A., A. Desmouliere, and G. Gabbiani. 1994. Heterogeneity of myofibroblast phenotypic features: an example of fibroblastic cell plasticity. Virchows Arch. 425:3–24. [DOI] [PubMed] [Google Scholar]
  44. Sheetz, M. P., D. P. Felsenfeld, and C. G. Galbraith. 1998. Cell migration: regulation of force on extracellular-matrix-integrin complexes. Trends Cell Biol. 8:51–54. [DOI] [PubMed] [Google Scholar]
  45. Shreiber, D. I., P. A. J. Enever, and R. T. Tranquillo. 2001. Effects of PDGF-BB on rat dermal fibroblast behavior in mechanically stressed and unstressed collagen and fibrin gels. Exp. Cell Res. 266:155–166. [DOI] [PubMed] [Google Scholar]
  46. Yokozeki, M., K. Moriyama, H. Shimokawa, and T. Kuroda. 1997. Transforming growth factor-beta 1 modulates myofibroblastic phenotype of rat palatal fibroblasts in vitro. Exp. Cell Res. 231:328–336. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES