Unexpected Mobility Variation among Individual Secretory Vesicles Produces an Apparent Refractory Neuropeptide Pool

Abstract

Most stored neuropeptide cannot be released from nerve terminals suggesting the existence of a refractory pool of dense core vesicles (DCVs). Past fluorescence photobleaching recovery, single particle tracking and release experiments suggested that the refractory neuropeptide pool corresponds to a distinct immobile fraction of cytoplasmic DCVs. However, tracking of hundreds of individual green fluorescent protein-labeled neuropeptidergic vesicles by wide-field or evanescent-wave microscopy shows that a separate immobile fraction is not evident. Instead, the DCV diffusion coefficient (D) distribution is unusually broad and asymmetric. Furthermore, the distribution shifts with a release facilitator. This unexpected variation, which could reflect heterogeneity among vesicles or in their medium, is shown to generate the appearance of a regulated refractory neuropeptide pool.

INTRODUCTION

Neuropeptides are long-acting transmitters that influence behavior. Typically, bouts of action potentials trigger neuropeptide release (Dutton and Dyball, 1979). However, even with prolonged depolarization, only a fraction of stored neuropeptides, called the releasable pool, can be secreted (Thorn, 1966). Recent studies of exocytosis in endocrine cells have further resolved the releasable pool of dense core vesicles (DCVs) into kinetically distinct fractions (e.g. the readily releasable pool (RRP) that can be depleted quickly and the reserve pool that slowly refills the RRP). However, this type of analysis, as well as a wealth of biochemical studies, has not explicitly revealed why neuropeptide release stops with continual stimulation. This problem is further complicated by the fact that DCV handling and control of sustained release change with neuronal differentiation of PC12 cells (Ng et al., 2002a). Hence, conclusions from hormone secretion studies by endocrine cells may not apply to neuropeptide release. Yet, refractory DCVs are important because they ensure that an intense episode of activity cannot exhaust the synaptic supply of neuropeptides that can only be replaced by synthesis in the distant cell body. Thus, to understand how neuropeptide release is regulated, it is essential to ascertain the cellular basis of the refractory neuropeptide pool.

Recent imaging experiments at the ends of nerve growth factor-differentiated PC12 processes suggest that the refractory pool is equivalent to an immobile pool of undocked DCVs. First, the size of this immobile fraction measured by fluorescence photobleaching recovery (FPR) corresponds to the size of the refractory pool measured by release (Burke et al., 1997). That FPR study also indicates that DCVs are relatively immobile for many minutes consistent with the existence of a distinct pool. Furthermore, single particle tracking (SPT) reveals large differences in mobility between individual DCVs consistent with the existence of immobile and mobile fractions (Burke et al., 1997; Han et al., 1999a). Moreover, SPT shows that neuropeptidergic DCVs move by diffusion as assumed in the interpretation of FPR results (Han et al., 1999a; Abney et al., 1999). In addition, the RRP of docked and primed neuropeptidergic vesicles is small (Ng et al., 2002a), and mobile cytoplasmic DCVs are efficiently recruited to support neuropeptide release (Han et al., 1999a). This implies that immobilization of undocked DCVs must decrease the capacity for neuropeptide release. Finally, sustained neuropeptide release is proportional to DCV motion indicating that vesicle mobility is a limiting factor for secretion (Ng et al., 2002b). Thus, previous results support the conclusion that the refractory neuropeptide pool is equivalent to the immobile fraction of cytoplasmic DCVs at the ends of processes.

To gain greater insight into the nature of the refractory pool, we tracked hundreds of neuropeptidergic DCVs. Surprisingly, these measurements reveal an unusual variation in mobility between individual vesicles rather than separate mobile and immobile pools. Furthermore, a change in this variation is sufficient to explain regulation of release by a facilitator. Hence, unusual heterogeneity among vesicles, rather than the presence of a distinct immobile refractory pool, limits neuropeptide release.

MATERIALS AND METHODS

DCV diffusion theory

The observed diffusion coefficient D_obs used here is short range, involving only pairs of positions one frame apart acquired at 1 Hz. When the position of the diffusing particle (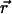) is measured at times i (=0, 1, 2, …, K) times 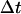(the time interval between measurements), the D_obs for a single trajectory is defined by Eq. 1:

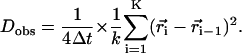(1)

These K measurements are independent, so their distribution is given by Eq. B1 of Qian et al. (1991). If the true diffusion coefficient is D, then the distribution of observed diffusion coefficients is given by Eq. 2:

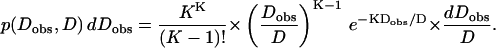(2)

This is a gamma distribution with mean D, mode D(1 − 1/K) and variance D²/K. It becomes a Gaussian for large K and is close to a Gaussian for K = 20.

The release sites studied here can be broad and flat, so to model diffusion-limited release, we assumed that the ends of processes are perfectly adsorbing infinite planes at x = ±a. Integrating a solution of the diffusion equation based on this geometry (Crank, 1975) gives total neuropeptide content as a function of time, M(t), in terms of a uniform initial concentration C_o (Eq. 3):

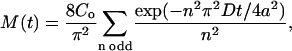(3)

where t is time and n is a series of odd numbers.

This equation assumes that all vesicles have the same D. The point of this paper is to test that assumption, and indeed to show that the vesicles have a wide range of D values. A complicating factor is that experimental measurements of D, which are necessarily based on a small number of time steps, will give a range of estimates of D for any vesicle (Eq. 2). In general, the observed distribution of diffusion coefficients must be corrected for this broadening effect, but in the following paragraphs we show here that the actual spread of D values is already so broad that this correction is unnecessary.

The true distribution of D, f(D), is convolved with the inherent broadening p(D_obs, D) resulting from measurements with small K to give rise to the observed distribution g(D_obs) as follows:

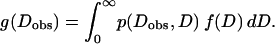(4)

Starting with an experimental g(D_obs) and the theoretical form for p(D_obs, D), the goal is to calculate f(D). If the resulting calculated f(D) closely matches the original g(D_obs), then the correction for limited K in real experiments is not necessary.

An actual calculation of f(D) is complicated by its great sensitivity to experimental noise in the observed g(D_obs). Therefore, the g(D_obs) data is first smoothed by fitting its main peak to a lognormal distribution. (The lognormal distribution approximates the main peak well, but does not have a long enough tail at high D). Then the above equation is solved for f(D) by use of a curve-fitting procedure appropriate to solve a Fredholm equation of the first kind, in this case the Tikhonov program in Matlab (Hansen, 1999) with an appropriate smoothing parameter. The result for K = 20 is that there is no appreciable difference between the calculated f(D) and the original g(D_obs), thereby proving that the spread of D values in the experimental data is almost entirely due to an actual spread of D and not an artifactual spread due to measurements with small K.

Therefore, to deduce the change in peptide content with time from DCV diffusion coefficient data, Eq. 3 was evaluated for a set of time values t with the measured diffusion coefficient D of each individual tracked secretory vesicle. Because n values must be odd, we used Eq. 3 with n = 1, 3, and 5 for the three-term model, and n = 1 for the one-term model. The results from all tracked secretory vesicles in a data set were then summed and normalized to yield the predicted time course of peptide release.

Imaging

Emerald GFP-tagged proatrial natriuretic factor was imaged at the ends of processes nerve growth gactor-treated PC12 cell as previously described (Burke et al., 1997; Han et al., 1999a,b; Ng et al., 2002a,b). Briefly, wide-field epifluorescence microscopy experiments were performed with a 60 × 1.4 numerical aperture (NA) oil immersion objective on an inverted fluorescence microscope equipped with a cooled CCD camera. To detect individual DCVs with wide-field epifluorescence microscopy, an inducible construct was used (Han et al., 1999a; Ng et al, 2002b). The time course of release for induced and continuously expressed neuropeptide are comparable (Han et al., 1999a), indicating that DCV properties are similar with the two labeling approaches. This conclusion is further supported by the similarity in motion described in this report. Total internal reflection microscopy (also called evanescent-wave microscopy) was performed with an upright microscope equipped with a trapezoidal prism and a 60 × 0.9 NA water immersion objective as described by Han et al. (1999a). Because the characteristic penetration depth for cell imaging is estimated to be 100 nm with this setup, it was possible to detect individual vesicles with steady state expression of the GFP-tagged neuropeptide. Release was inhibited with N-ethylmaleimide treatment by following the protocol of Han et al. (1999b). Controls with paraformaldehyde-fixed cells showed that noise in our SPT system produces diffusion coefficients at least an order of magnitude smaller than the smallest values measured in live cells. Tonic depolarization was induced by substituting 100 mM NaCl in the bathing medium with KCl. In some experiments, extracellular Ca²⁺ (5 mM) was also substituted with Ba²⁺. Control and experimental data were collected from parallel samples of cells on the same day to take into account batch-to-batch variation. Error bars show the standard error of the mean.

RESULTS

Unusual variation in DCV motion

Past studies support the proposal that the refractory pool consists of DCVs that diffuse ∼10-fold more slowly than the mobile cytoplasmic fraction. A diffusion coefficient (D) histogram for neuropeptidergic DCVs from single particle tracking (SPT) data has been generated to quantify neuropeptidergic DCV diffusion (Abney et al., 1999). However, the relatively small number of DCVs analyzed and the use of only three broad data bins could have prevented resolution of multiple populations of DCVs with distinct mobilities. Therefore, we examined the data acquisition requirements for discriminating between two DCV populations.

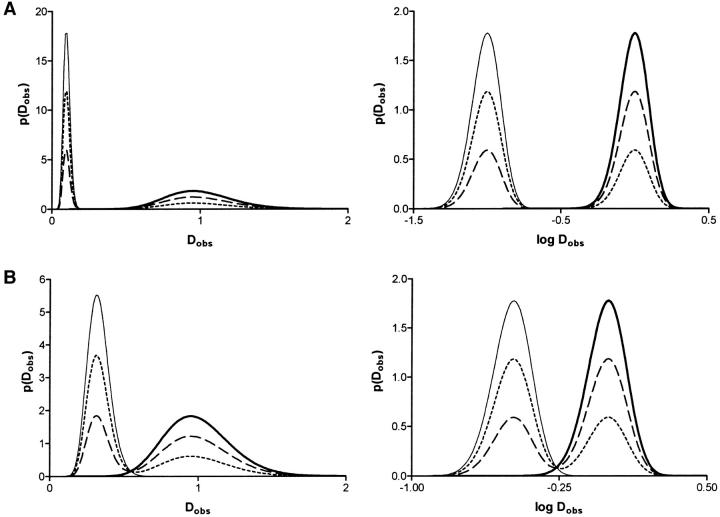
SPT measurements yield a broad distribution of D values if the number of time points in the trajectory is limited, but the distribution narrows as the number of points in the trajectory increases (Saxton, 1997). Fig. 1 A, left shows the distributions of short range diffusion coefficients predicted by Eq. 3 assuming K = 20 time points, a 10-fold difference in the D values for fast and slow DCVs, and different fractions of fast DCVs (i.e., all, 2/3, 1/3, and none). Importantly, the two populations do not overlap. When two-thirds of the DCVs belong to the slower population to approximate fluorescence photobleaching recovery results (Burke et al., 1997), the slower fraction produces an obvious narrow peak whereas the faster fraction yields a broader distribution. However, a semilogarithmic plot produces two separate peaks of comparable width (Fig. 1 A, right). When D values vary by threefold, the two fractions are closer, but are still clearly discernible (Fig. 1 B). Thus, two separate pools of DCVs that differ substantially in mobility should be evident in SPT data acquired with the methods used here.

FIGURE 1.

Expected distribution of diffusion coefficients for two populations of secretory vesicles. (A) Two populations with D values that vary by 10-fold with K = 20 measurements per vesicle. Plots are shown for different fractions (0, thin line; 1/3, short dashed line; 2/3, long dashed line; 1, thick line) of the fast population. The left graph is on a linear scale whereas the right graph is semilogarithmic. (B) Same as A except that D values for the two populations differed by threefold. The distributions f of log D_obs were obtained by transforming Eq. 2 to give f (log D_obs) = D_obs p(D_obs) (Stuart and Ord, 1994).

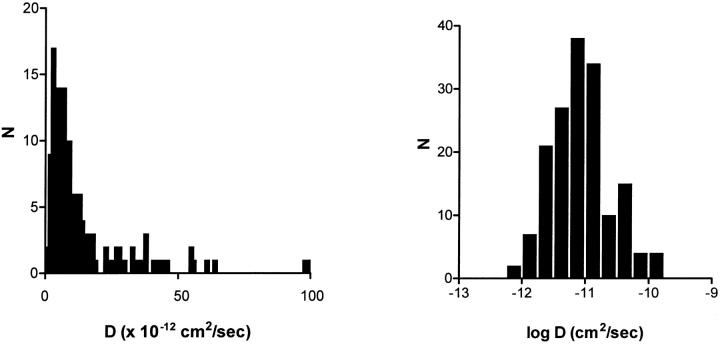
However, analysis of trajectories of DCVs at the ends of processes of differentiated PC12 cells observed by wide-field epifluorescence microscopy does not reveal the presence of two pools. For each DCV, time lapse data were collected at 1 Hz for 20 s and D values were calculated based on the mean square distance moved between successive frames. A D histogram with three broad bins of experimental data from 162 DCVs looks similar to the histogram of Abney et al. (1999) (data not shown); the only difference is that the median D is smaller probably because of the lower temperature used in these experiments (23°C vs. 37°C) and because we did not exclude very slowly moving DCVs. With finer binning (Fig. 2, left), it is evident that the D distribution that is not a simple broad Gaussian indicative of one population (p < 0.0001). Furthermore, two separate peaks that would be expected for two separate populations of immobile and mobile fraction vesicles with mobilities that differ by more than threefold are not obvious. Instead, the distribution features a narrow peak and a broad rightward shoulder. This linear plot bears some resemblance to the two fraction model (Fig. 1 A, left) indicating that the simple model approximates DCV behavior. However, the distributions are clearly different in semilogarithmic presentations. Specifically, the experimental distribution (Fig. 2, right) is extremely broad and nearly symmetric on a logarithmic scale, whereas a model with two populations yields two distinct peaks (Fig. 1, right). Hence, measured DCV mobility is not consistent with the existence of two separate pools.

FIGURE 2.

Distributions of DCV diffusion coefficients deduced by SPT performed with wide-field epifluorescence microscopy. The left plot uses linear binning whereas the right plot uses logarithmic binning. Note that wide-field microscopy samples a thick optical section.

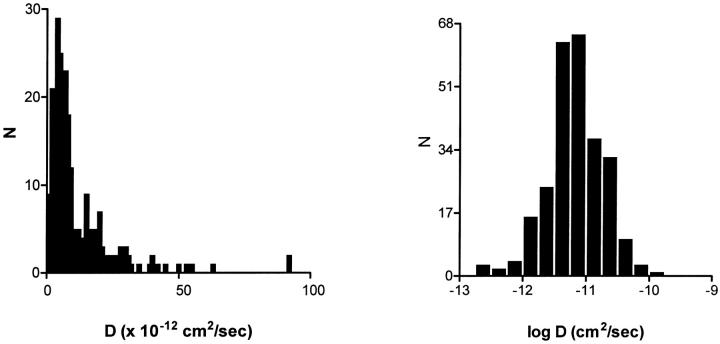
Recent total internal reflection microscopy (TIRM, also called evanescent-wave microscopy) experiments with chromaffin cells showed that DCV motion slows dramatically and smoothly during the approach to the plasma membrane of those endocrine cells (Johns et al., 2001). It is not known whether these DCV dynamics are universal (Ng et al., 2002a). To address whether such an effect influenced the D histogram obtained from the thick optical section sampled by wide-field microscopy, TIRM was used to acquire 260 DCV trajectories. TIRM preferentially illuminates vesicles that are located very close to the cell surface. Consequently, if the plasma membrane-proximal zone hinders DCV motion at the ends of processes, then the D distribution obtained with TIRM should be more dominated by slowly diffusing DCVs. However, TIRM experiments produce a similar D distribution (Fig. 3) to that found with wide-field microscopy (Fig. 2). These results imply that the variation in DCV motion is uniform throughout the release site in the preparation studied here. Therefore, the unusual D distribution for DCVs cannot be explained by a difference between membrane proximal and more distal vesicles. Instead, wherever neuropeptidergic DCVs are located, their movement does not conform to one or two conventional populations.

FIGURE 3.

Distributions of DCV diffusion coefficients deduced by SPT measured with total internal fluorescence microscopy. The left plot uses linear binning whereas the right plot uses logarithmic binning. Note that total internal reflection microscopy (also called evanescent-wave microscopy) samples a thin optical section near the cell surface.

DCV motion need not change for a long period prior to neuropeptide release

A long-lived transition in DCV motion just before release could be rate limiting, and thus, make the unusual D distribution irrelevant for the kinetics of release. Therefore, we examined movement preceding release events. Past experiments with slow episodic data acquisition suggested that initially mobile DCVs participate in neuropeptide release (Han et al., 1999a). This contrasted with the initial conclusion that it takes minutes for docked vesicles to become competent for release in chromaffin cells (Steyer et al., 1997). However, more recent chromaffin cell studies showed that this period averages ∼10 s and can be as short as 1 s at the most efficient sites of release (Oheim et al., 1998; Oheim and Stuhmer, 2000). The pause in DCV motion preceding exocytosis may reflect hindered movement near the plasma membrane as well as docking (Johns et al., 2001). Given that the former effect is not evident in our preparation and that our past experiments did not feature continual rapid data acquisition, we reexamined whether neuropeptidergic vesicle mobility is altered just before release.

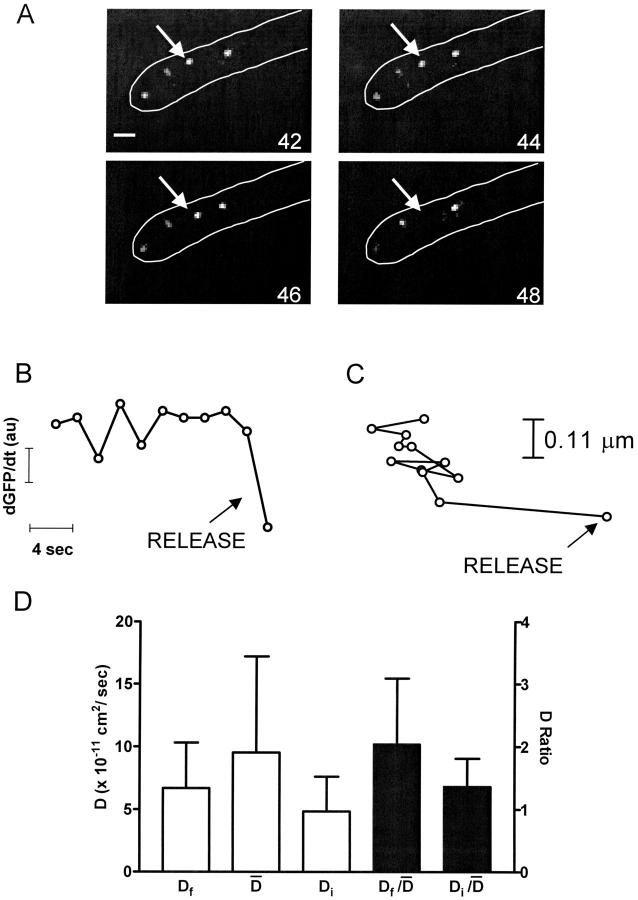
Experiments were performed similarly to (Han et al., 1999a) except that image acquisition was maintained at a rate of 0.5 Hz. Because conventional wide-field epifluorescence microscopy samples a thick optical section, in focus DCVs remained in view between neighboring frames in resting cells (i.e., it took >2 s for DCVs to move completely out of focus). In addition, DCVs never suddenly appeared within a frame reflecting rapid motion into view, and sudden complete disappearances of DCVs (Fig. 4 A) associated with sudden decreases in total neuropeptide fluorescence (Fig. 4 B) occurred only after stimulation. Since total fluorescence includes both in focus and out of focus GFP fluorescence from a depth of field far greater than the thickness of processes, these sudden decreases must reflect release (Levitan, 1998). Analysis of seven sudden decreases in fluorescence, each associated with an isolated sudden disappearance of a vesicle, showed that they were significantly larger than changes in fluorescence that occurred five frames before or after the disappearance events (p < 0.001). Thus, sudden disappearances could be correlated with sudden decreases in fluorescence indicative of release events.

FIGURE 4.

Vesicle mobility is maintained until release. (A) Wide-field fluorescence images of secretory vesicles at the end of a process outlined in white. Numbers in corners show the period in seconds since the onset of stimulation by depolarization in the presence of Ba²⁺. Bar equals 1 μm. The vesicle indicated by the arrow in the first panel moves prior to release. (B) Rate of peptide release measured as the change in total peptide fluorescence (dGFP/dt) in the region shown in A. The last 4 points correspond to the images in A. Note that the vesicle disappearance is associated with a sudden drop in peptide content indicative of release. (C) Trajectory of the DCV indicated in A. (D) Open bars show the comparison of the diffusion coefficient derived from the final trajectory step prior to release (D_f) to the mean diffusion coefficient (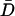) and to the diffusion coefficient for the first 14 s of tracking (D_i). The closed bars show the comparisons after normalization. N = 8. No statistically significant differences are evident.

SPT of DCVs leading up to release events showed that release was not preceded by a long-lived immobile docked state. Specifically, trajectories acquired at 0.5 Hz of DCVs with D values ranging from 6.1 × 10⁻¹² to 6.3 × 10⁻¹⁰ cm²/sec revealed no obvious slowing of motion just before exocytosis. Indeed, the example shown in Fig. 4 C shows that the final trajectory step seen on this timescale could be larger than previous steps. On average, the speed of the final trajectory step before release (D_f) was not significantly different than the average speed (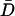) for the total time tracked (i.e., ≥56 s) or the initial speed in the first 14 s of tracking (D_i) (Fig. 4 D, open bars). To take into account the wide variation in mobility between individual DCVs, data were normalized and paired. A long-lived docked and immobile state should have been evident as a small value in the 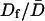ratio, but this was not found (Fig. 4 D, filled bars). These results imply that if a docked and immobile state is required for neuropeptide release, it must be routinely as short-lived (i.e., <2 s) as the most efficient sites in chromaffin cells. This result, as well as data from chromaffin cell “hot spots” (Oheim and Stuhmer, 2000), suggests that biochemical machinery involved in the late steps of exocytosis can operate quickly compared to the late phase of release.

Complex DCV motion contributes to the time course of release

Therefore, we tested whether the broad asymmetric D distribution affects the time course of neuropeptide release by generating a kinetic model based on the hypothesis that DCV motion limits sustained neuropeptide secretion. Our model utilizes the fact that neuropeptidergic DCV motion, when viewed on an individual basis, conforms to the diffusion equation in this preparation (Han et al., 1999a; Abney et al., 1999). Although the geometry used by our model (see Methods) is only a gross approximation, using a different geometry with the same limiting distance would not have a dramatic effect on the average time for a DCV to reach the membrane (Berg, 1993; see Discussion). We also posited that capture of vesicles at the cell surface is completely efficient because docking sites may be numerous and because diffusion is effective at exploring a region to find sites for binding (Berg, 1993). Therefore, it seems possible that reaching the plasma membrane will be slower than finding a docking site once a DCV is close to the cell surface. Furthermore, the impact of added distance to move to a limited number of docking sites on a geometrically complex surface can be accounted for by setting the distance a in Eq. 3 to fit the time course of release seen in our preparation. With this in mind, we set a = 3 μm. This distance is within the range found for the releasing regions used in these studies suggesting that our assumptions yield a good approximation of this experimental system.

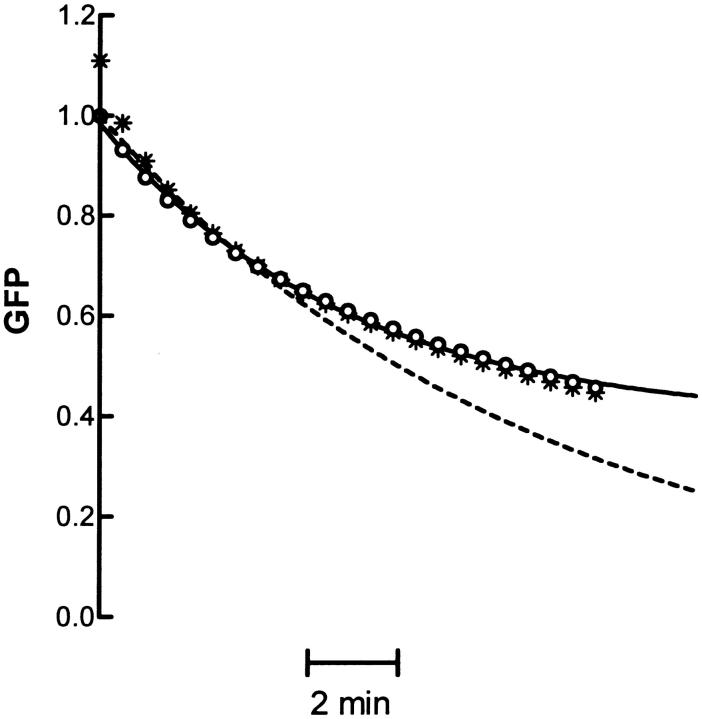
Fig. 5 shows the time course of release derived from the measured diffusion coefficients used to generate Fig. 2 with the three-term model (asterisks) or the one-term model (circles). Because the higher order terms quickly approach zero, the one-term model is sufficient for describing prolonged release. The dashed line in Fig. 5 shows the expected time course from the one-term model using only the mean diffusion coefficient from the data (1.60 × 10⁻¹¹ cm²/s).

FIGURE 5.

Model of neuropeptide release based on diffusion of secretory vesicles. The open circles show the release time course produced by using the one-term model with the data shown in Fig. 2 A. The solid line shows a fit of the open circles to a single exponential plus a constant. The dashed line shows the time course produced by the first term model for the mean D from the data in Fig. 2 A. The asterisks show the time course produced by using the three-term model.

This is a single exponential that will eventually approach zero; thus, it gives no hint of the presence of a refractory pool. However, even though the one-term model is a sum of exponentials, each derived from a single DCV, the distribution of diffusion coefficients in the primary data yields a time course that displays slowing of release at later time points (circles). The solid line in Fig. 5 shows that the model output based on experimental data can be approximated with a single exponential converging on a constant (i.e., F/F₀ = Aexp(−kt) + B, A = 0.6 and B = 0.4). A could be interpreted to represent the total releasable fraction of DCVs whereas B could be the refractory fraction. Yet, these kinetics are not the result of two distinct pools. Rather, the slowing down of release with prolonged stimulation is a consequence of the unusual distribution of DCV diffusion coefficients.

Facilitated release and secretory vesicle motion

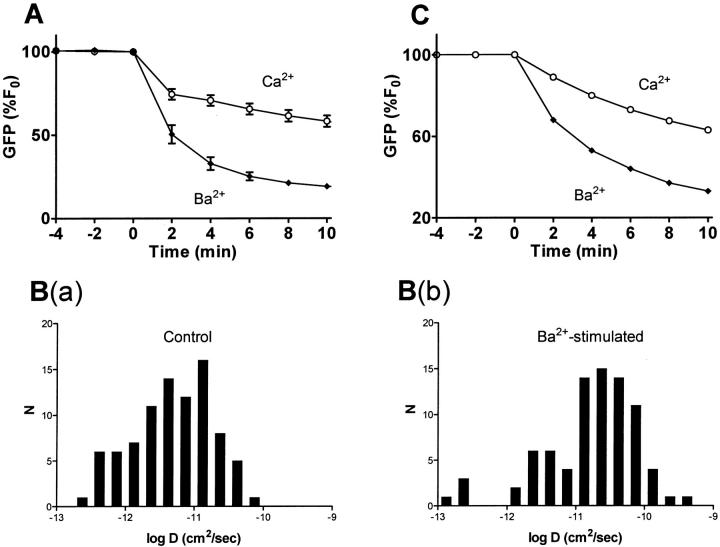
If this conclusion is correct, then apparent expansion of the releasable pool could be produced by altering the vesicle D distribution. Recently, it was concluded that an increase in mean vesicle D accounts for the greater release induced by depolarization in the presence of Ba²⁺ instead of Ca²⁺ (Fig. 6 A) in the preparation studied here (Ng et al., 2002b). However, a change in mean D on its own cannot account for the greater extent of release evoked by Ba²⁺ because the mean does not encompass the skewed variation in DCV behavior that slows release to apparently produce a refractory pool. Indeed, if the D distribution was a tight Gaussian, a shift in the mean value of D would have a kinetic effect without altering the extent of release. On the other hand, the analysis of complex DCV mobility reported here implies that a change in release at later times must involve modifying slower than average DCVs. Hence, a quantitative examination of whether facilitation is due to altered DCV mobility requires measuring the impact of Ba²⁺ on the whole D distribution and determining whether such an effect would alter release.

FIGURE 6.

A shift in the vesicle D distribution accounts for the change in release induced by Ba²⁺. (A) Comparison of observed neuropeptide release evoked by depolarization in the presence of Ca²⁺ (open circles) and Ba²⁺ (closed diamonds). N ≥ 8. (B) Diffusion coefficient histograms for vesicles under control conditions (a) and after stimulation with Ba²⁺ for 15 min (b). Secretory vesicles were tracked for 20 s at a rate of 0.5 Hz. C. Output of one-term model using the data shown in B. Note that modeled release is similar to the experimental data in A.

Such analysis indicates that regulation of DCV diffusion contributes to facilitation of release. Fig. 6 B shows semilogarithmic histograms derived from DCVs that were tracked before and after prolonged stimulation with Ba²⁺. For these experiments, cells were treated with N-ethylmaleimide to prevent exocytosis that preferentially depletes mobile DCVs (Han et al., 1999a). This treatment does not affect DCV mobility (data not shown). However, Ba²⁺ tends to shift the complex D distribution to the right (Fig. 6 B). These data were used with the one-term model to give the predicted release kinetics shown in Fig. 6 C. Notably, the change in the release time course produced by modifying the D distribution accounts for the increased release and the altered kinetics produced by Ba²⁺. Yet, this change is caused by a shift in the unusual vesicle D distribution, not an expansion of a specific pool. This further strengthens the conclusion that the time course and extent of neuropeptide release at the ends of PC12 cell processes are governed by vesicle-to-vesicle variation in mobility rather than the existence of a distinct immobile pool.

DISCUSSION

It has long been presumed that neuropeptide release is limited because of the existence of distinct pools of releasable and refractory DCVs (Thorn, 1966). However, the basis for generation of the refractory pool has been unclear. It was proposed that the refractory neuropeptide pool is a distinct immobile fraction of cytoplasmic DCVs because it is similar in size to the immobile fraction detected by FPR (Burke et al., 1997). Furthermore, SPT data are qualitatively consistent with this model (Burke et al., 1997; Han et al., 1999a; Ng et al., 2002b). This hypothesis was appealing because it incorporated the common assumptions of separate pools from the release field and two mobility fractions from FPR analysis. Yet, both of these assumptions reflect simple, but not exclusive, models to fit experimental data. In fact, more detailed SPT analysis shows that the distribution of DCV diffusion coefficients is inconsistent with the presence of two distinct pools or fractions. Instead, the distribution (when plotted linearly) is broad and asymmetric. This distribution is unusual, but is compatible with past experimental FPR and SPT results. Furthermore, modeling reveals that the unexpected variation between individual DCVs would affect the time course of neuropeptide release. This conclusion is also supported by the finding that docking can be brief. Hence, there is no reason at this point to invoke a limitation in the docking and exocytosis machinery to explain the later phases of sustained release by intact cells. Finally, facilitation of release is explained by a shift in the distribution of DCV mobilities. Therefore, the simplest interpretation of our data is that there is no distinct immobile pool. Instead, unusual variation among individual DCVs contributes to the limited capacity to secrete neuropeptides.

An important feature of our analysis is that the model used here is very simple. The fact that such an uncomplicated model can explain regulation of neuropeptide secretion is appealing because it implies that the vesicle behavior described here has obvious consequences. Yet, it is important to consider the impact of changing the model. For example, the model overestimates the density of release sites. In fact, fewer release sites would necessitate greater travel distances so that the variation in DCV mobility reported here would have an even greater effect. Also, the model could have been based on a different geometry. For example, release from a cylinder would be ∼43% quicker, but the shape of the release time course is not very different (Saxton, unpublished results). Thus, our general conclusion would not be altered because the slowest DCVs detected here would still inefficiently support release. Therefore, as long as release sites have general dimensions comparable to our model preparation, wide variation in vesicle mobility will be a significant mechanism for generating operationally refractory DCVs, and increasing DCV mobility will apparently expand the releasable pool. Although the latter was evident with Ba²⁺ in our model system, it is of interest that DCV motion has recently been found to be regulated in large Drosophila synaptic boutons (Levitan et al., 2002).

At present, there is no simple explanation for the unusual variation among DCVs. A Gaussian distribution of DCV radii in these cells (Schubert et al., 1980) would yield an asymmetric D histogram when plotted on a linear scale, if they diffused freely. But this effect is minor compared to the experimental data presented here (Saxton, unpublished results). Similarly, undersampling of rapidly diffusing DCVs in SPT experiments does not account for our data because this effect is insignificant for nearly all of the DCVs detected here (Levitan, unpublished results). We also investigated a potential explanation that was suggested by in vitro experiments with beads suspended in actin solutions that showed that inducing bundling of actin microfilaments produces D distributions that are reminiscent of those reported here (Apgar et al., 2000). If heterogeneity in actin structure affects neuropeptidergic DCV behavior in vivo, then the DCV diffusion coefficient distribution should become more normally distributed and tighter after depleting F-actin. Yet, preliminary studies suggest that depolymerizing F-actin in differentiated PC12 cell processes does not eliminate the wide distribution of DCV diffusion coefficients (Ng and Levitan, unpublished results). Given that intermediate filaments and microtubules are not thought to be abundant at these release sites, it appears that standard cytoskeletal constitutents may not generate the unexpected wide variation in DCV mobility. However, studies of coated DCV-sized (i.e., 80 nm) beads in fibroblasts suggest there is a diffusion barrier other than the three major components of the cytoskeleton (Luby-Phelps, 2000). Our results indicate that greater understanding of heterogeneities in such unidentified cytoskeletal elements and/or tethering molecules will be needed to fully account for the kinetics of neuropeptide release and the unexpected secretory vesicle behavior described here.