Na/K Pump Current and [Na]_i in Rabbit Ventricular Myocytes: Local [Na]_i Depletion and Na Buffering

Abstract

Na/K pump current (I_pump) and intracellular Na concentration ([Na]_i) were measured simultaneously in voltage-clamped rabbit ventricular myocytes, under conditions where [Na]_i is controlled mainly by membrane transport. Upon abrupt pump reactivation (after 10–12 min blockade), I_pump decays in two phases. Initially, I_pump declines with little [Na]_i change, whereas the second phase is accompanied by [Na]_i decline. Initial I_pump sag was still present at external [K] = 15 mM, but prevented by [Na]_i ∼ 100 mM. Initial I_pump sag might be explained by subsarcolemmal [Na]_i ([Na]_SL) depletion produced by rapid Na extrusion and I_pump. Brief episodes of pump blockade allowed [Na]_SL repletion, since peak postblockade I_pump exceeded I_pump at the end of previous activation (without appreciably altered global [Na]_i). The apparent K_m for [Na]_i was higher for continuous I_pump activation than peak I_pump (14.1 ± 0.2 vs. 11.2 ± 0.2 mM), whereas that based on d[Na]_i/dt matched peak I_pump (11.6 ± 0.3 mM). [Na]_SL depletion (vs. [Na]_i) could be as high as 3 mM for [Na]_i ∼ 18–20 mM. A simple diffusion model indicates that such [Na]_SL depletion requires a Na diffusion coefficient 10³- to 10⁴-fold below that expected in bulk cytoplasm (although this could be subsarcolemmal only). I_pump integrals and [Na]_i decline were used to estimate intracellular Na buffering, which is slight (1.39 ± 0.09).

INTRODUCTION

In the heart, intracellular Na concentration ([Na]_i) is very important in modulating the electrical and contractile activity. This is because [Na]_i controls the intracellular Ca and H concentration via the Na/Ca exchanger (NCX) and Na/H exchanger, respectively, and both these ions are essential factors in excitation-contraction coupling (Bers, 2001). An increase in [Na]_i shifts the balance of fluxes on the NCX to favor more Ca influx and less Ca efflux, resulting in larger Ca transients and therefore, enhanced contractility. Indeed, relatively small changes in [Na]_i can have major effects on contractile force. For example, in cardiac Purkinje fibers, force can double with ∼1 mM rise of [Na]_i (Lee and Dagostino, 1982).

The level of [Na]_i is determined by a fine balance between Na influx and efflux. While there are many Na entry pathways, the Na/K pump is the main route for Na extrusion and therefore is essential in [Na]_i regulation. The Na/K pump uses the energy derived from the hydrolysis of one ATP molecule to exchange three intracellular Na for two extracellular K ions. Not only does the pump control [Na]_i, but [Na]_i is a main regulator of the pump itself (Glitsch, 2001). This creates a feedback system, which tends to reduce the changes in [Na]_i due to variations in the Na influx produced, for example, by changes in the heart rate or by ischemia.

The aim of this article is to investigate the relationship between [Na]_i and the Na/K pump in rabbit ventricular myocytes. Generally, such studies are done by measuring the Na/K pump current (I_pump), using the whole-cell patch clamp technique, at various pipette Na concentrations and assuming that intracellular Na fully equilibrates with pipette Na (for a review, see Glitsch, 2001). However, this might not always be the case, especially when there is a net transmembrane Na flux—i.e., the cell is not in the steady state (Mathias et al., 1990). Furthermore, several reports indicate the presence of a transient I_pump component upon abrupt Na/K pump reactivation after a period of pump blockade (Bielen et al., 1991a; Su et al., 1998; Fujioka et al., 1998). Such transients could be due to either a [Na] gradient between the patch pipette and the cell or to a local, subsarcolemmal Na depletion brought about by the rapid Na extrusion upon Na/K pump activation. Here we used a different approach: we patched the cells with relatively high resistance electrodes so that [Na]_i is mainly controlled by the membrane transporters and not by the pipette solution. Thus, we could manipulate [Na]_i by changing the external conditions. The actual [Na]_i was measured simultaneously with I_pump by using the fluorescent indicator, SBFI.

Simultaneous measurements of I_pump and [Na]_i allowed us to 1), investigate whether rapid Na/K pump activation could generate intracellular Na gradients; 2), derive the [Na]_i-dependence of I_pump in single cells; and 3), determine the level of endogenous Na buffering. That Na/K pump might lower [Na]_i near sarcolemma ([Na]_SL) below the level in the bulk cytosol has been suggested by the presence of a transient I_pump component upon Na/K pump activation (Bielen et al., 1991a; Su et al., 1998; Fujioka et al., 1998) and by the increase in the amplitude of Ca transients produced by rapid Na/K pump inhibition (Terracciano, 2001; Su et al., 2001). However, [Na]_i has not been measured in these studies and one can argue that the effects are due to a change in global [Na]_i rather than to a local variation in [Na]_SL. If there is indeed a Na/K pump-dependent depletion of [Na]_SL, this could affect the activity of all Na-dependent membrane transporters, including the pump itself, with important consequences on cell contractility.

To relate quantitatively the Na fluxes to changes in the free [Na]_i, it is important to know the level of intracellular Na buffering. This is expected to be rather small but actual data are lacking. Here we determined the intracellular Na buffering as the ratio between the change in total [Na]_i, calculated from the integral of I_pump, and the change in free [Na]_i when the Na/K pump is reactivated after a period of pump inhibition.

MATERIALS AND METHODS

Myocytes isolation

The procedure for isolation of ventricular myocytes has been described previously (Bassani et al., 1994) and approved by the Loyola University Chicago animal welfare committee. Briefly, rabbits were anesthetized by IV injection of pentobarbital sodium (50–70 mg/kg) and hearts were excised quickly and placed on a Langendorff perfusion apparatus. Hearts were perfused for 5–7 min with nominally Ca-free Tyrode's solution, then perfusion proceeded with added collagenase (1 mg/ml) and albumin (0.05%) ([Ca] ≈ 36 μM) until the heart became flaccid (15–18 min). The left ventricular tissue was cut into small pieces for further incubation with 0.4 mg/ml collagenase. Incubations were stopped at 5–45 min by adding 200 μM Ca Tyrode's solution with 0.05% albumin and the tissue was filtered. The external Ca concentration was progressively increased to 2 mM. Isolated myocytes were plated on laminin-coated glass coverslips and mounted in perfusion chambers. The standard normal Tyrode's solution contained (in mM): 140 NaCl, 4 KCl, 1 MgCl₂, 10 glucose, 5 HEPES, and 2 CaCl₂ (pH = 7.4). All experiments were done at 35–37°C.

Na/K pump current measurements

Isolated ventricular myocytes were whole-cell voltage-clamped using patch electrodes made from borosilicate glass capillaries. The electrodes had a resistance of 3–5 MΩ when filled with the internal solution, resulting in a series resistance of 8–15 MΩ. After obtaining the whole-cell configuration, the cells were held at −30 mV to inactivate Na channels. Current signals were recorded using an Axopatch 200A amplifier (Axon Instruments, Foster City, CA). Membrane capacitance and series resistance were calculated from a 5-mV voltage step. The standard pipette solution contained (in mM): 10 NaCl, 20 KCl, 100 K-aspartate, 20 TEA-Cl, 10 HEPES, 5 Mg-ATP, 0.7 MgCl₂ (≈1 mM free Mg), 3 BAPTA, 1.15 CaCl₂ (≈100 nM free Ca), and 1 SBFI tetraamonium salt (pH = 7.2). In the pipette solution containing 100 mM Na, K-aspartate was replaced by equimolar concentrations of aspartic acid and NaOH. The external solution contained (in mM): 136 NaCl, 5 NiCl₂, 2 BaCl₂, 1 MgCl₂, 5 HEPES, 10 glucose, and 4 KCl (4 mM K solution) or Tris-Cl (0 mM K solution; pH = 7.4). For the 15-mM K solution, 11 mM KCl replaced 11 mM NaCl. I_pump was measured as the outward shift induced by switching from a K-free to a K-containing external solution.

[Na]_i measurements

Myocytes were loaded with SBFI (Molecular Probes, Eugene, OR) via the patch pipette. Fluorescence was elicited by illumination with a 75-W Xenon lamp. Dual excitation measurements (at 340 and 380 nm, F₃₄₀ and F₃₈₀) were performed using an Optoscan monochromator (Cairn Research, Faversham, UK). The emitted fluorescence was recorded at 535 ± 20 nm with a photomultiplier. The whole system was controlled by the Optoscan microprocessor control unit (Cairn Research). Data acquisition was done in the integration mode, where for each wavelength the signal is integrated over 20 ms. For each cell, the background signal at both wavelengths was measured on seal formation and subtracted from the signals after dye loading. In situ calibration of SBFI was done at the end of each experiment as previously described (Despa et al., 2002a). Briefly, myocytes were exposed to divalent-free solutions with 0, 10, or 20 mM extracellular [Na], in the presence of 10 μM gramicidin and 100 μM strophanthidin.

Na/K-pump-mediated Na extrusion

The Na/K pump activity can also be described in terms of the rate of Na extrusion. This was derived from the rate of [Na]_i decline (d[Na]_i/dt) upon abrupt pump reactivation after a period of pump blockade (Despa et al., 2002b). The rate of [Na]_i decline is given by:

(1)

where V is the cell volume and β is the intracellular Na buffering. J_pump is the rate (mmol/min) of the pump-mediated Na extrusion and is the dominant component of d[Na]_i/dt, whereas J_leak and J_pip represent moderate corrections for the passive Na influx from the external solution and Na exchange between the patch pipette and the cell, respectively. We have shown previously (Despa et al., 2002b) that the cell volume does not change during our Na loading/recovery protocol. Mathias and co-workers (Mathias et al., 1990) showed that Na flux between the patch pipette and the cell is given by J_pip = ρD_Na([Na]_pip – [Na]_i)/R_s, where ρ (60 Ω × cm) is the resistivity of the pipette solution, R_s is the series resistance, D_Na (600 μm²/s; Kushmerick and Podolsky, 1969) is the diffusion coefficient for Na, and [Na]_pip is Na concentration in the pipette solution. For J_leak, we used a [Na]_i-independent value of 1.1 mM/min, as previously measured in rabbit myocytes (Despa et al., 2002b). Note that J_leak may include Na influx from multiple pathways (e.g., Na/Ca exchange, Na channels, or Na/H exchange).

We calculated d[Na]_i/dt by numerical differentiation, and J_pump (transformed in units of mM/min) was determined from Eq. 1. For each cell, V was calculated from the membrane capacitance using a surface-to-volume ratio of 6.44 pF/pL cytosol (Satoh et al., 1996).

Measurement of intracellular Na buffering

This was done using the same protocol of abrupt Na/K pump activation described above. The changes of free [Na]_i were obtained from the SBFI ratio. The amount of Na pumped out of the cell via the Na/K pump was calculated from the integral of I_pump. Corrections were made for the Na exchange between the cell and the patch pipette and for the passive Na influx from the external solution. The amount of Na diffusing into the patch pipette was calculated by integrating J_pip as defined above. The transsarcolemmal Na influx was assumed constant and given by the flux that will equilibrate I_pump and J_pip at steady state. Because in our experiments [Na]_i ≈ [Na]_pip at steady state, the amount of Na that passively enters the cell was calculated from the integral of steady-state I_pump.

Statistical analysis

Data are expressed as mean ± SE. Statistical discriminations were performed using the Student's unpaired t-test. Values of p < 0.05 were considered significant.

RESULTS

Simultaneous measurements of I_pump and [Na]_i

We investigated the relationship between the Na/K pump and [Na]_i in voltage-clamped rabbit ventricular myocytes. After reaching the whole-cell configuration, the cells were Na-loaded, at E_m = −30 mV, by inhibiting the Na/K pump for 10–12 min in a K-free solution. Then, the pump was abruptly reactivated by adding back K (4 mM) and we monitored the membrane current and [Na]_i (Fig. 1). Pump reactivation resulted in a rapid outward shift in the membrane current, followed by a decay which appears to be biphasic (see Fig. 1 A; see also below) and is accompanied by a decline in [Na]_i (Fig. 1 B). Within 3–5 min, the cell reaches a steady state where both [Na]_i and the current are constant. The protocol (including the Na-loading phase) was repeated in the same myocyte, this time with the pump blocked by 200 μM strophanthidin. In the presence of strophanthidin, external K did not elicit any change in the membrane current whereas [Na]_i keeps increasing slightly (Fig. 1, right). This indicates that the outward shift in the membrane current is entirely due to activation of the Na/K pump.

FIGURE 1.

Time course of the membrane current (A) and [Na]_i (B) upon abrupt Na/K pump reactivation after a period of pump blockade. The pump was reactivated by adding back 4 mM K after perfusing the cell for 12 min in a K-free solution. When both the current and [Na]_i reached the steady state, the cell was incubated in K-free solution for another 12 min, this time in the presence of 200 μM strophanthidin. Then, the cell was perfused again with 4 mM K, in the continuous presence of strophanthidin. The myocyte was held at –30 mV throughout the experiment.

Fig. 2, A and B, show the first minute of a similar experiment (full curves are in the Inset). With this timescale, it becomes clear that, after abrupt activation, I_pump initially decays rapidly (phase a, Fig. 2 A), within 2–5 s, with little change in [Na]_i. Then, I_pump declines at a slower rate (phase b) and this is paralleled by a decrease in [Na]_i. The plot of I_pump versus [Na]_i (Fig. 2 C) emphasizes the initial I_pump sag at practically constant [Na]_i, followed by a Hill type [Na]_i-dependence of I_pump.

FIGURE 2.

I_pump decay after abrupt activation is biphasic. (A) I_pump during the first minute of an experiment similar to that shown in Fig. 1 (full curve shown in inset). (B) [Na]_i in the same experiment (full scale shown in inset). (C) The [Na]_i-dependence of I_pump indicates that initially I_pump decreases at practically constant [Na]_i (I_pump sag). The solid line represents the fit with a Hill equation I_pump = I_pump^max/(1+(K_m/[Na]_i)ⁿ). I_pump sag was excluded from the fit.

I_pump sag and local [Na]_SL depletion

I_pump is regulated by [Na]_i near the sarcolemma, [Na]_SL, as opposed to the bulk [Na]_i. If the rate of Na extrusion upon the rapid activation of the pump is faster than the diffusion of Na between the subsarcolemmal space and the bulk cytosol, this will produce a local [Na]_SL depletion, with minimal changes in the global [Na]_i as measured by SBFI. Such a decrease in [Na]_SL might reduce I_pump considerably, thus explaining the sag. However, alternative explanations are possible.

First, because Na/K pumps are located in both the external sarcolemma and the T-tubules of cardiac myocytes (McDonough et al., 1996), the I_pump sag could be caused by the depletion of external K in the T-tubules. To examine this possibility, we repeated the experiments at 15 mM external K (Fig. 3 A). This concentration is well above the K_m for binding of external K to the pump (1–2 mM, Nakao and Gadsby, 1989; Bielen et al., 1991b), therefore a possible depletion of K in the T-tubules is not expected to affect I_pump. As Fig. 3 A shows, at 15 mM [K]_o, I_pump displayed an even more prominent sag, suggesting that phase a is not a result of external K depletion. If anything, it may be enhanced by higher I_pump at near-maximal conditions for [K]_o.

FIGURE 3.

(A) Membrane current (top) and [Na]_i (bottom) upon Na/K pump reactivation with 15 mM external K. The pipette solution contained 10 mM Na. (B) I_pump (top) and the SBFI ratio (bottom) induced, in a different cell, by 4 mM K at [Na]_pip = 100 mM.

Second, rapid activation of the Na/K pump might result in local ATP depletion near the sarcolemma. This is unlikely to affect I_pump significantly because the ATP concentration for half-maximal activation of the pump is in the range of 80–150 μM (Hilgemann et al., 1991; Friedrich et al., 1996) whereas the intracellular ATP concentration is ∼5 mM. Still, a combined effect of lower ATP and increased ADP near the sarcolemma might affect the pumping capacity of the Na/K pump. To rule out such an effect, we repeated the experiments with [Na]_pip = 100 mM (Fig. 3 B). If I_pump sag is produced by an ATP depletion, it should be even more pronounced at higher [Na]_i, because the pump rate is higher and therefore more ATP is hydrolyzed. On the other hand, [Na]_SL depletion will have a minimal effect on I_pump because the pump is saturated with respect to internal Na. Fig. 3 B (top), shows that at high [Na]_pip the I_pump sag disappears, which means that I_pump sag is not due to local ATP depletion. We did not perform a careful calibration of the SBFI signal at this high [Na]_i, but a three-point calibration (0, 50, and 100 mM) indicated that [Na]_i ≈ 50 mM. This large Na gradient between the cell and the patch pipette might be why [Na]_i does not decrease upon pump activation.

To test whether local [Na]_SL depletion is indeed the cause for I_pump sag, Na-loaded myocytes were exposed to several episodes of Na/K pump inhibition/reactivation (Fig. 4). In the first experiments, the pump was repeatedly activated for 5 s and then inhibited for 20 s (Fig. 4 A). This resulted in minimal changes in [Na]_i and practically constant peak I_pump, which suggests that [Na]_SL is completely replenished within the 20-s pump inhibition interval. To allow for [Na]_i changes with this protocol, the duration of the pump activation was extended to 10 s in the next experiments (Fig. 4 B). Upon activation, I_pump decays, initially with little change in global [Na]_i ([Na]_SL depletion, see also Fig. 4 C). For each Na/K pump activation episode, the peak I_pump is higher than the I_pump at the end of the previous activation, despite a small decrease in the global [Na]_i (Fig. 4, B and C). This is because [Na]_SL was replenished during the pump inhibition, thus the [Na]_SL sensed by the pump at the moment of the peak I_pump is higher than at the end of the previous activation. Because Na influx is rather slow, we can assume that with the Na/K pump blocked, diffusion will equilibrate [Na]_i throughout the cell. This means that at the peak of I_pump, [Na]_SL = [Na]_i as measured by SBFI. Therefore, a plot of the peak I_pump versus [Na]_i (Fig. 4 D) gives a more accurate description of the Na/K pump-dependence on [Na]_SL than the continuous activation curve in Fig. 2 C.

FIGURE 4.

I_pump and [Na]_i during interrupted Na/K pump reactivation, induced by switching the external solution from 0 to 4 mM K. Myocytes were perfused for 12 min in K-free solution before the first activation of the pump and held at –30 mV throughout the experiment. (A) I_pump (top) and [Na]_i (bottom) in a cell where [Na]_i did not change appreciably (pump activations and inhibitions were 5 and 20 s, respectively). (B) I_pump (top) and [Na]_i (bottom) in a cell with longer pump activations (10 s). As more Na was extruded by the pump, [Na]_i declined and this was paralleled by a decline in the peak of I_pump. (C) I_pump and [Na]_i in the area indicated in B on an expanded scale, emphasizing I_pump sag (depletion) and the recovery after the brief pump inhibition (repletion). (D) The [Na]_i-dependence of the peak I_pump. Data were fitted with a Hill expression.

Fig. 5 A shows average data for the [Na]_i-dependence of I_pump in the presence (protocol from Figs. 1 and 2) and in the absence (protocol from Fig. 4) of [Na]_SL depletion. The points were fit with a Hill equation to derive the maximum pump current (I_pump^max), the [Na]_i for half-maximal activation of the pump (K_m), and the Hill coefficient, n (Table 1). The main effect of [Na]_SL depletion is a shift in the apparent K_m for internal Na from 11.2 mM to 14.1 mM (Table 1). Fig. 5 A can be used to estimate the amount of [Na]_SL depletion produced by the pump. For example, for an [Na]_i of 18 mM, I_pump measured in conditions that allow [Na]_SL depletion is ∼1.0 A/F. The peak I_pump versus [Na]_i curve (i.e., I_pump versus [Na]_SL) shows that a similar current occurs at [Na]_SL∼15 mM. Thus, the initial, abrupt activation of the pump lowers [Na]_SL by ∼3 mM compared to the bulk [Na]_i. This estimation is, of course, an upper limit, as it assumes that I_pump sag is entirely due to [Na]_SL depletion. For each experiment, we integrated the initial current to calculate the amount of Na that is extruded from the cell during I_pump sag. Dividing this value by Δ[Na]_SL determined as described above, we obtained a subsarcolemmal space volume of 10 ± 1% (n = 10) of the total cell volume. However, this is only a rough estimate because the subsarcolemmal space geometry and local Na buffering are not known.

FIGURE 5.

I_pump versus [Na]_i. (A) I_pump in the presence (depletion) and in the absence (peak) of [Na]_SL depletion. Solid lines are Hill expression fits (Table 1). Data in the presence of [Na]_SL depletion are averages (n = 8) where the pump is continuously activated (protocol similar to Figs. 1 and 2). Initial I_pump sag was excluded from the plot and fit. Data without [Na]_SL depletion are average of peak I_pump versus [Na]_i (n = 7) from repeated episodes of pump inhibition/reactivation. (B) Difference between the curves in A.

TABLE 1.

[Na]_i-dependence of I_pump, with (continuous activation) and without (peak) local [Na]_SL depletion and of the pump-mediated Na extrusion

	With depletion (n = 8)	Peak (n = 7)	−d[Na]i/dt (n = 12)
Vmax	1.6 ± 0.2 A/F	1.5 ± 0.2 A/F	6.1 ± 0.5 mM/min
Km (mM)	14.1 ± 0.2	11.2 ± 0.3*	11.6 ± 0.3*
n	2.3 ± 0.1	2.7 ± 0.1†	3.2 ± 0.3†

Significantly different from the continuously activated I_pump; ^*P < 0.0001; ^†P < 0.05.

Fig. 5 B shows that the difference in I_pump in Fig. 5 A (or extent of I_pump sag) is maximal around the K_m for the pump. This makes sense because the [Na]_i-dependence of I_pump is steepest there. One can also appreciate that this sag becomes negligible at low [Na]_i (where I_pump is small) and where [Na]_i ≫ K_m as shown in Fig. 3 B (because even large D[Na]_SL depletions near V_max will not reduce I_pump appreciably).

Theoretical model for radial Na diffusion in the cell

The existence of an intracellular [Na]_i gradient implies restricted diffusion with respect to the transport rate. To determine the diffusion coefficient for Na that could account for a [Na]_SL depletion of the size inferred from the I_pump measurements, we developed a simple theoretical model for the radial diffusion of Na in the cell (see Appendix). Briefly, we divided the cell, considered as a long cylinder where diffusion is everywhere radial, into small circular shell compartments. The change in [Na]_i in the compartment located immediately beneath the sarcolemma, i.e., [Na]_SL, is determined by the Na extrusion via the Na/K pump, the passive transsarcolemmal Na influx, and the Na diffusion into the next compartment. In all other compartments, the [Na]_i level is determined exclusively by Na diffusion into/from the adjacent compartments. Na extrusion via the Na/K pump was taken as a function of [Na]_SL, using the parameters obtained from the plot of the peak I_pump versus [Na]_i (Fig. 5, Table 1).

Experimental data indicate that in muscle cells D_Na = 600 μm²/s; i.e., about one-half the value measured in aqueous solutions (Kushmerick and Podolsky, 1969). However, for this diffusion coefficient the model predicts no apparent differences between [Na]_SL and bulk [Na]_i (not shown). Next, we simulated a subsarcolemmal “fuzzy” space by assuming that Na diffusion is limited in a 100- to 500-nm space beneath the sarcolemma. Fig. 6 A shows that considerable [Na]_i gradients could be induced upon abrupt Na/K pump activation if D_Na in this 400-nm subsarcolemmal space is 0.12 μm²/s (i.e., bulk D_Na/5000). In Fig. 6 A [Na]_SL decreases by more than 2 mM within the first 1–2 s of pump activation, whereas average [Na]_i that would be measured by SBFI stays almost constant (Fig. 6 A, inset). When we included interruptions in the Na/K pump activation (thus simulating the experiment shown in Fig. 4 B), the model predicted a rapid [Na]_SL repletion during each episode of pump inhibition, with simulated I_pump recovery similar to the experimental data in Fig. 4 B (not shown). The [Na]_i gradient is limited to the region with restricted Na diffusion (Fig. 6 B). Fig. 6 C shows how I_pump is expected to depend on the global [Na]_i. The model predicts an I_pump sag similar to what we observed experimentally (Fig. 2 C), followed by a Hill-type dependence on global [Na]_i. When we fitted I_pump versus global [Na]_i (excluding I_pump sag) with a Hill expression, we derived a higher K_m (14.6 mM) and a somewhat lower Hill coefficient (1.9) than the values used for I_pump versus [Na]_SL (11.2 mM and 2.7, respectively). Our experimental data (Fig. 5, Table 1) show a similar behavior.

FIGURE 6.

[Na]_i gradients predicted by a simple model assuming the existence of a subsarcolemmal space with restricted Na diffusion. (A) Time course of [Na]_i in the compartment near the sarcolemma (SL), at the center of the cell (center) and the mean [Na]_i in the cell as it would be measured by SBFI (Global). (Inset) [Na]_i changes in these regions during the first 5 s upon pump reactivation on an expanded scale. (B) The radial distribution of [Na]_i gradient at various moments after abrupt Na/K pump reactivation. (C) Predicted dependence of I_pump on the global [Na]_i. Simulations were done considering a 400-nm subsarcolemmal space where the diffusion coefficient for Na is 0.12 μm²/s. In the bulk, D_Na = 600 μm²/s. (D) Local D_Na versus the size of the subsarcolemmal space that produces a [Na]_SL depletion similar to Fig. 6 A.

The extent of [Na]_SL depletion and I_pump sag depend critically on two parameters: the size of the subsarcolemmal space and the local D_Na. Fig. 6 D shows that if we use a smaller subsarcolemmal space, the subsarcolemmal D_Na must be reduced even more dramatically to obtain results similar to Fig. 6, A and C. We also performed simulations where D_Na was reduced everywhere in the cell, not just in a limited subsarcolemmal region (not shown). To obtain a difference between [Na]_SL and the bulk [Na]_i similar to Fig. 6 A, global D_Na had to be reduced to ∼0.6 μm²/s (versus the 0.12 μm²/s for the case in Fig. 6 A). Any Na buffering at the sarcolemma (Philipson et al., 1980) would also further reduce the D_Na required to simulate our data. Thus, the upper limit of D_Na which would explain our observations is 1000× smaller than that expected.

I_pump and the rate of pump-mediated Na efflux

The rate of [Na]_i decline in the experiments shown in Figs. 1 and 2 can also be used to characterize the activity of the Na/K pump (Despa et al., 2002a,b). This provides an additional, independent, estimate to the I_pump data. The pump-mediated d[Na]_i/dt was calculated by numerical differentiation of the [Na]_i decline and corrected for the Na influx from the external solution and for the Na exchange with the patch pipette. Fig. 7 shows comparatively the [Na]_i-dependence of I_pump and of the pump-mediated Na efflux. The K_m for [Na]_i of the Na/K pump-mediated Na extrusion was 11.6 ± 0.3 mM (n = 12), which is significantly lower than the K_m derived from steadily activated I_pump (14.1 ± 0.2 mM), but similar to the value derived from peak I_pump in the absence of [Na]_SL depletion (11.2 ± 0.3 mM), in experiments with repeated Na/K pump inhibition/activation episodes.

FIGURE 7.

The [Na]_i-dependence of the Na/K pump in terms of I_pump (A) and the rate of pump-mediated [Na]_i decline (B). Data are from an experiment similar to Fig. 1, after the initial I_pump sag is excluded. The rate of [Na]_i decline was calculated by numerical differentiation and then corrected for non-pump-mediated Na fluxes between the cell and the patch pipette and external solution to derive the pump-mediated d[Na]_i/dt (see Methods).

Intracellular Na buffering

The simultaneous measurements of I_pump and [Na]_i decline during the abrupt Na/K pump activation that was described above allowed us to estimate the level of intracellular Na buffering (Fig. 8). Three processes contribute to the [Na]_i change in this protocol: 1), Na extrusion via the Na/K pump; 2), passive Na influx across sarcolemma; and 3), Na exchange with the patch pipette. Fig. 8 A shows the calculation for the net change in total [Na]_i due to Na fluxes across the sarcolemma, i.e., Na pumping out of the cell and passive Na entry. The contribution of transsarcolemmal and pipette fluxes to the change in total [Na]_i is shown in Fig. 8 B. This shows that the membrane transport is the dominant factor in controlling the [Na]_i. The change in [Na]_i estimated from these fluxes adds up to a higher level than the change in free [Na]_i measured by SBFI, indicating that some endogenous Na buffering exists (Fig. 8 C). However, this is rather slight (1.39 ± 0.09, n = 17).

FIGURE 8.

Estimation of endogenous Na buffering. (A) I_pump in a representative experiment where the Na/K pump was initially inhibited for 12 min in K-free solution and then abruptly reactivated by adding 4 mM K to the superfusing solution. The amount of Na pumped out of the cell via the Na/K pump was calculated from the integral of I_pump. To correct for the passive Na influx, this was assumed constant and given by the flux that will equilibrate I_pump at steady state (because in these experiments, [Na]_i ≈ [Na]_pip at steady state). Thus, the amount of Na that passively enters the cell was calculated from the integral of steady-state I_pump. (B) The contribution of Na fluxes across the sarcolemma and between the cell and the patch pipette to the [Na]_i change. The pipette contribution was calculated by integrating the flux ρD_Na([Na]_pip − [Na]_i)/R_sV. (C) The change in free [Na]_i as measured by SBFI versus total [Na]_i (pipette + sarcolemma in B). The calculation was done assuming a surface-to-volume ratio of 6.44 pF/pL cytosol (Satoh et al., 1996).

DISCUSSION

This article characterizes the activity of the Na/K pump, presents data suggesting that abrupt pump activation could result in local [Na]_SL depletion, and estimates the level of intracellular Na buffering in rabbit ventricular myocytes. I_pump and [Na]_i were measured simultaneously using voltage-clamp and the fluorescent indicator, SBFI, respectively. Different from most studies, voltage-clamp experiments were done under conditions that minimized the effect of cell dialysis by the patch pipette on [Na]_i while maximizing its control by the Na fluxes across sarcolemma. Thus, we selected large cells (average C_m ∼ 200 pF) and used relatively small electrodes (resulting in an R_s of 8–15 MΩ). In rabbit ventricular myocytes, [Na]_i control by the membrane transporters versus the patch pipette is also favored by the fairly large surface-to-cytosol volume ratio (6.44 pF/pL; Satoh et al., 1996). This strategy allowed us to raise [Na]_i significantly by simply blocking the Na/K pump, and then follow I_pump and [Na]_i as the cell relaxes toward steady state upon pump reactivation.

Na/K pump and intracellular [Na]_i gradients

We found that upon abrupt Na/K pump reactivation after a period of pump blockade, I_pump displays a transient peak that decays in two phases (Figs. 1 and 2). The first, rapid phase occurs with little change in [Na]_i, whereas the second phase is accompanied by a [Na]_i decline. The rapid phase is still present when the pump is reactivated by 15 mM K but disappears at high [Na]_i. This rules out external K depletion in the T-tubular system and local ATP depletion as possible explanations for the I_pump sag. The fast I_pump decay might be due to a local subsarcolemmal [Na]_i depletion produced by the pump itself. This hypothesis is supported by the behavior of I_pump when the cell is exposed to a series of Na/K pump inhibition/reactivation episodes (Fig. 4). For each pump activation episode, we observed the peak I_pump followed by the fast decay phase, whereas global [Na]_i decline had slower kinetics. Every time, the peak I_pump was higher than I_pump measured at the end of the previous activation, with limited changes in global [Na]_i. Thus, pump inhibition for a few seconds allows [Na]_SL repletion.

The presence of an [Na]_i gradient between the subsarcolemmal space and bulk cytosol in cardiac cells has been suggested by several studies (Bielen et al., 1991a; Carmeliet, 1992; Wendt-Gallitelli et al., 1993; Lipp and Niggli, 1994; Semb and Sejersted, 1996; Su et al., 1998, 2001; Terracciano, 2001). Transients in the Na/K pump current similar to those found here have been previously reported (Bielen et al., 1991a; Fujioka et al., 1998; Su et al., 1998), but [Na]_i was not measured in these studies. Our approach has the advantage that it allows for quantitative considerations (see below). Su and co-workers (Su et al., 2001) showed that abrupt Na/K pump inhibition in mouse ventricular myocytes increases the efficacy of a given Ca current to trigger sarcoplasmic reticulum Ca release. This was interpreted as a prevention of Na extrusion in the junctional cleft (between the sarcoplasmic reticulum and sarcolemma) allowing local cleft [Na]_i to rise and favor Ca entry via NCX. Abrupt Na/K pump inhibition was also shown to slow the decline of caffeine-induced Ca transients and I_NCX (Terracciano, 2001). Direct measurements of [Na]_i gradients have also been reported (Wendt-Gallitelli et al., 1993; Silverman et al., 2002). Wendt-Gallitelli et al. (1993) observed an [Na]_SL increase of up to 40 mM during stimulation in guinea-pig ventricular myocytes, with no change in the bulk [Na]_i. This steep [Na]_i gradient dissipated within minutes upon the cessation of stimulation. Silverman and co-workers (Silverman et al., 2002) found that in rabbit papillary muscle [Na]_i is higher near the sarcolemma and falls to levels equal to that in the bulk cytosol within 200–300 nm of the membrane. This [Na]_i gradient was similar whether measured in diastole or systole. However, both studies used electron probe x-ray microanalysis to measure [Na]_i and this method measures total rather than free [Na]_i. Thus, these data might reflect binding of Na in the subsarcolemmal space (Philipson et al., 1980), which could in turn alter Na diffusion.

The [Na]_SL depletion affects the experimentally determined [Na]_i-dependence of I_pump. The “true” activation curve can be obtained from the plot of the peak I_pump upon pump activation versus [Na]_i. This is because [Na]_SL is repleted during the brief episodes of pump inhibition, therefore [Na]_SL is equal to the measured global [Na]_i at the moment of pump reactivation. The main difference in the [Na]_i-dependence of I_pump measured in the presence and in the absence of [Na]_SL depletion is a shift of ∼3 mM in the apparent K_m for intracellular Na (Fig. 5). Therefore, caution has to be taken when measuring this parameter under non-steady-state conditions. Surprisingly, d[Na]_i/dt gives a closer estimate to the real K_m than does the continuously activated I_pump. These I_pump-activation curves allow us to estimate quantitatively the amount of [Na]_SL depletion. Thus, for an initial [Na]_i of 20 mM, abrupt activation of the pump could lower [Na]_SL by as much as 4 mM. When the pump is activated at 10 mM [Na]_i, the depletion is reduced to 1.3 mM, and for an initial [Na]_i of 4.5 mM, which is the resting [Na]_i level in rabbit ventricular myocytes (Despa et al., 2002a), becomes negligible (<0.2 mM). This makes sense, because at lower [Na]_i the pump rate is lower, causing less depletion. It is likely that the subsarcolemmal space is heterogeneous, thus different Na/K pumps might sense different [Na]_SL. In this context, the V_max, K_m, and n values reported here reflect average values for all the pumps in the cell.

According to our model for radial Na diffusion, [Na]_i gradients of such magnitude require that the diffusion coefficient for Na in an area extending 100–500 nm from the sarcolemma is 10³ to 10⁴ times lower than the values reported in the literature for Na diffusion into the cytoplasm (Kushmerick and Podolsky, 1969). One may expect that the mobility of ions is restricted near the sarcolemma due to interactions with the polar structures associated with the internal side of the membrane. The existence of a barrier to diffusion of Ca ions separating the bulk cytoplasm from a subsarcolemmal space has been suggested by a hysteresis between the intracellular Ca concentration and the transient inward current induced by spontaneous or caffeine-promoted Ca release from the sarcoplasmic reticulum (Trafford et al., 1995). Still, a diffusion coefficient several orders-of-magnitude lower than in the bulk cytoplasm is difficult to imagine in any simple physical sense. Although the main model predictions, including the I_pump sag and the shift in the I_pump versus [Na]_i curve, were observed experimentally, the simple geometry used, especially the absence of the T-tubular system, might affect the results. Alternatively, the I_pump sag and the change in the [Na]_i activation curve might reflect a yet-unknown regulatory mechanism, such as an external K-dependent inactivation, analogous to the Na-dependent inactivation of the Na/Ca exchanger (Hilgemann et al., 1992).

Intracellular Na buffering

The I_pump and [Na]_i decline upon Na/K pump reactivation were used to calculate the intracellular Na buffering. This seems rather slight (1.39 ± 0.09), especially when compared with other ions, such as Ca (100:1), Mg (∼100:1), or H (>1000:1). The buffering measured here represents the sum of 1), the intrinsic Na buffering in the cytoplasm; 2), the buffering by internal organelles, especially mitochondria; and 3), the buffering provided by the added SBFI. To calculate the latter, we estimated the concentration of SBFI in the cell using the expression for the flux between the patch pipette and the cell given by Mathias and co-workers (Mathias et al., 1990), a surface-to-cytosol volume ratio of 6.44 pF/pL (Satoh et al., 1996) and an average R_s and C_m of 10 MΩ and 200 pF, respectively. This resulted in an SBFI concentration of 400–500 μM at the time of I_pump and [Na]_i measurement (15–20 min postrupture). Assuming a dissociation constant of 11.3 mM (Haugland, 1996), the change in the concentration of Na bound to SBFI when the free [Na]_i decreases from 20 to 10 mM (typical in our experiments) is ∼85 μM. Thus, Na buffering by the added SBFI is negligible (∼0.085).

In the calculation of Na buffering, the mitochondrial volume was excluded from the volume available to Na, by using the surface-to-cytosol volume ratio. This assumes that [Na] in mitochondria ([Na]_m) does not change. However, in isolated heart mitochondria, [Na]_m increases linearly with external Na (Jung et al., 1992). If this is also the case in intact myocytes, then the use of the surface-to-total cell volume ratio (4.58 pF/pL; Satoh et al., 1996) is more appropriate. With this ratio, the change in [Na]_i estimated from Na fluxes becomes equal to the measured change in the free [Na]_i. Thus, the intrinsic Na buffering power in the cytoplasm is negligible (e.g., less than twofold), when compared to the powerful 10- to 1000-fold cytosolic buffering of Ca, Mg, or H (Bers, 2001).

In summary, we investigated the relationship between the Na/K pump and [Na]_i by simultaneous measurements of I_pump and [Na]_i using voltage-clamp and SBFI. Our data suggest that rapid Na extrusion upon pump activation may result in local [Na]_SL depletion. We designed a protocol that allowed us to characterize the [Na]_i-dependence of I_pump in the absence of depletion and to estimate the extent of the [Na]_SL depletion. A simple diffusion model indicated that such [Na]_SL depletion requires that Na diffusion is 10³ to 10⁴ times slower near sarcolemma versus the bulk cytoplasm. However, a fully satisfying physical explanation is lacking at this point. We also estimated the intracellular Na buffering, which was found to be rather slight (1.39 ± 0.09).

APPENDIX

We considered the cell as a long circular cylinder, with radius R, in which diffusion is everywhere radial. The model cell is divided into N small circular shell compartments of thickness Δr = R/N. [Na]_i in the compartment at the sarcolemma is affected by Na influx and efflux across sarcolemma as well as Na diffusion into the next compartment, whereas in the internal compartments a change in [Na]_i is brought about only by diffusion from the neighboring compartments. Thus, the change in [Na]_i in the outer and subsequent shells per unit time (ΔC_n/Δt) are given by

(A1)

where V_n and A_n are the volume and the area of the external surface of compartment n, D_n is the diffusion coefficient for Na in the compartment n, and J_leak and J_pump are the rates of passive Na influx and Na extrusion by the pump, respectively (in mole/time).

The Na/K-pump-mediated Na efflux is a function of [Na]_i in the compartment near the sarcolemma (C_N). According to the experimentally determined [Na]_SL-dependence of I_pump (Figs. 3 and 4, and Table 1), J_pump can be written as

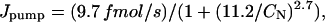where we used a surface-to-volume ratio of 6.44 pF/pL cytosol (Satoh et al., 1996) and typical values for the cell diameter (20 μm) and length (100 μm), resulting in a cytosol volume of ∼32 pL. J_leak is calculated such that the cell is at steady state for an [Na]_i of 8 mM, typical of what we observed in our measurements, thus

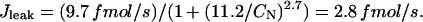Because the rate of passive Na influx is rather small (Despa et al., 2002b), we assumed that Na is uniformly distributed within the cell at the moment of Na/K pump activation. The equations system in Eq. A1 was integrated numerically with an integration step of 50 μs. Generally, 10–50 shells were sufficient for convergence. In some cases, shells were of different thickness to more readily resolve the shape near the sarcolemma.