The Convex Basis of the Left Null Space of the Stoichiometric Matrix Leads to the Definition of Metabolically Meaningful Pools

Abstract

The stoichiometric matrix, S, represents a mapping of reaction rate vectors into a space of concentration time derivatives. The left null space of the stoichiometric matrix contains the dynamic invariants: a combination of concentration variables, referred to as metabolic pools, whose total concentration does not change over time. By analogy to the traditional reaction map formed by S, a compound map can be derived from −S^T. The analogy to flux analysis of the (right) null space of S enables us to classify the metabolic pools into three categories: Type A that contains chemical elements and their combinations in the form of certain moieties, Type B that contains such moieties in addition to cofactors carrying such moieties that are internal to the network, and Type C that contains only the cofactors. A convex formulation of the basis for the left null space allows us to directly classify the metabolic pools into these three categories. Type B metabolic pools include conservation pools that form conjugates of moiety-occupied and moiety-vacant concentration states of metabolites and cofactors. Type B metabolic pools thus describe the various states of moiety exchange between the primary substrates and the cofactors that capture properties like energy and redox potential. The convex basis gives clear insight into this exchange for glycolytic pathway in human red blood cell, including the identification of high and low energy pools that form conjugates. Examples suggest that pool maps may be more appropriate for signaling pathways than flux maps. The analysis of the left null space of the stoichiometric matrix allows us to define the achievable states of the cell and their physiological relevance.

INTRODUCTION

A metabolic network can be characterized by its topological or stoichiometric features. There exists a number of analytical methods, including elementary flux modes and extreme pathway analysis, by which metabolic flux distributions are analyzed solely based on network stoichiometry (Schilling et al., 2000; Schuster and Hilgetag, 1994). Mathematically, the outcome of these analytical methods is a set of convex basis vectors that describe all the steady-state flux distributions or flux pathways in the network. The basis vectors that lie at the edge of a high-dimensional cone have been called “extreme pathways” since they represent extreme states of the network. Extreme pathways form a unique basis set for describing the flux pathways and provide a systemic definition for the topological features of the metabolic networks (Schilling et al., 2000).

Although much focus in metabolic network analysis has been directed at characterizing flux distributions, relatively few studies have dealt with the analysis of metabolite concentrations and the identification of “metabolic pools”. Metabolic pools are linear combinations of individual metabolite concentrations that do not change over time and are contained in the left null space of the stoichiometric matrix. Network characteristics and application of the left null space of connectivity matrices have been studied in other fields, including chemical networks, petri nets, and electric circuit analysis (Alberty, 1991; Clarke, 1988; Colom and Silva, 1990; Schuster and Höfer, 1991; Strang, 1988). In comparison to typical network structures studied in such fields, biochemical reaction networks are particularly different due to the extensive cofactor coupling of their reactions. These cofactors carry and transfer various chemical properties (e.g., redox, energy, chemical groups) in the network. Such couplings lead to joint edges that typically connect four nodes or metabolites and result in topologically nonlinear networks that may be challenging to study and interpret. Metabolic pools have been used as an optimization criterion for minimizing the total internal concentration of metabolites in a biochemical system (Schuster and Heinrich, 1991), to identify distinct time hierarchies in the metabolic network of human red blood cell (Schuster and Höfer, 1991). Analysis of glycolysis in the African sleeping sickness parasite, Trypanosoma brucei, has also been used for identifying of conservation relationships that may help determine suitable drug targets in the future (Cornish-Bowden and Hofmeyr, 2002). Here we study a convex representation of the left null space using the extreme pathway algorithm (Schilling et al., 1999), to introduce metabolic pools that have relevant physiological interpretations. By analogy to flux maps that represent particular flux distributions, we define “pool maps” that can be used to represent particular conserved metabolic pools. Somewhat analogous to the extreme pathways that have proved useful for flux analysis, a convex basis for the left null space ensures that the weighting of every compound in a metabolic pool is positive and thus leads to chemically interpretable combinations of concentrations. The convex representation of conservation pools allows for metabolically relevant interpretation of glycolysis and Rapoport-Leubering shunt in human red blood cell and may be more appropriate for signaling network analysis.

DEVELOPMENT OF THE CONCEPTUAL FRAMEWORK

The stoichiometric matrix as a mapping operation

The stoichiometric matrix, S, is a linear transformation between the reaction rates and the time derivative of the concentrations (Fig. 1). This transformation is expressed by the dynamic mass balance or rate equation, 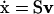, in which x is a vector of m metabolites, the dot (·) stands for time derivative, v represents a vector of n reaction rates, and S is an m × n matrix of stoichiometric coefficients (Clarke, 1980; Horn and Jackson, 1972; Reich and Sel'kov, 1981). The metabolites are therefore represented in S by the rows and the reactions by the columns. The linear transformation between v and maps the reaction rates to metabolite concentrations without the use of any kinetic parameters or information. The structural analysis of S thus does not examine the dynamic concentration states of the system explicitly but instead provides topological information about the systemic relationships among metabolites and reactions.

FIGURE 1.

The stoichiometric matrix, S, as a linear transformation between the reaction rate vectors, v, and time derivative of metabolite concentrations, dx/dt or . Each two subspaces in the domain (i.e., the null space and row space) and codomain (i.e., the left null space and column space) form orthogonal pairs with one another. The components that reside on each subspace are therefore independent from the others. (dyn, dynamic; ss, steady state; consv, conserved).

The four fundamental subspaces of S

The row space, right null space, column space, and left null space of S include all the fundamental features of the dynamic mass balance equation, (Fig. 1). They contain information about the network's dynamic properties, steady states, and time-invariant characteristics. The row space and column space of S contain the dynamics of the reaction rates and the time derivative of the concentrations, respectively, and thus comprise all the time-varying components. In comparison, the right null space of S (normally referred to as the null space) contains the steady-state (Sv = 0) flux solutions, and the left null space contains conserved concentration relationships.

Open and closed system boundary

The boundary of a metabolic network can be defined in different ways. Definition of a system's boundary partitions the reaction vector, v, into reactions that are internal to the system, v_i, and those that exchange mass with its surroundings, b_i. The vector of metabolite concentrations, x, are similarly partitioned into internal, x_i, and external, x_oi, metabolites. Thus different partitions of the stoichiometric matrix can be formed (Fig. 2). The internal stoichiometric matrix (S_int) contains only the internal reactions and metabolites, and the system is closed to the outside environment (Fig. 2 A). If the system is opened by introducing exchange reactions, the exchange stoichiometric matrix (S_exch) includes v_i and b_i, and the system becomes “open” (Fig. 2 B). The entire system becomes “closed” again if the external metabolites are explicitly accounted for in S (Fig. 2 C), and the total stoichiometric matrix (S_tot) contains all the elements external and internal to the system.

FIGURE 2.

Stoichiometric matrix and the system's boundary. (A) A system with internal reactions, v_i, and metabolites, x_i, is closed to the environment and represented by S_int. (B) When the internal metabolites are allowed to be exchanged with the environment, the stoichiometric matrix includes exchange reactions, b_i, and the system becomes “open”. (C) Once the external metabolites (x_oi) are included, the system becomes “closed” and the stoichiometric matrix contains all the reactions and metabolites, S_tot. (int, internal; exch, exchang; tot, total).

The null space of S and pathway definitions

At steady state, 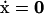, the dynamic mass balance equation becomes,

(1)

If there are linear dependencies amongst the columns of S (i.e., the reactions), a set of reactions can be identified for which the flux distribution is balanced and,

(2)

where the columns in R span the (right) null space of S. A desirable basis for the null space is one that leads to a ready physiological interpretation in a metabolic network. A unique nonnegative convex basis is useful when representing biochemical elements such as reaction rates and metabolite concentrations, since negative quantities of such elements may biologically be meaningless (Heinrich and Schuster, 1996). A unique set for the convex basis is obtained using extreme pathway analysis, in which the generating vectors are the “extreme pathways” (Schilling et al., 2000).

The left null space of S and definition of metabolic pools

If there are linear dependencies among the rows of S (i.e., the metabolites), then a matrix L exists such that,

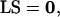(3)

where the rows of L form a basis set for the left null space of S. This relation implies that the total metabolite concentrations in certain combinations remain unchanged, 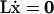, and when integrated over time results in , where a is a vector of integration constants. The individual metabolite concentrations in each conserved relationship may change over time, but their total sum will remain constant at all times, i.e., a_i = const. Each conservation quantity may be represented by ℓ_ix = a_i, in which ℓ_i is a conservation vector, i.e., a row in L. The basis vectors for the left null space define a concentration space in which the time-invariant metabolic pools reside. The size of the space in which conserved metabolites reside is constrained by the magnitude of the elements in a.

Flux and pool maps

In a connectivity matrix such as S, a row is typically taken to represent a “node” and the columns the “links” between the nodes. The stoichiometric matrix is thus shown as a reaction map in which metabolites are the nodes and reactions are the directed edges. The reaction map is the traditional way of depicting biochemical reaction networks. One can then show a particular flux map by indicating the magnitude of the steady-state reaction rates on each corresponding edge. In this manner, each vector in the null space of S can be shown as a steady-state flux map.

If the stoichiometric matrix is transposed, the rows will represent the reactions and the columns the metabolites. A metabolic network can therefore be depicted by a compound map whose nodes are the reactions and edges are the compounds (Fig. 3). The vectors of the left null space or metabolite pools can be shown as pool maps whose edges are the combinations of metabolite concentrations. The compound map is drawn using −S^T. The transpose operation allows for the conversion between the edges and nodes and the negative sign defines the substrates and products as the edges entering and leaving the reaction nodes, respectively. A closed reaction map leads to the formation of a compound map with the maximum possible conserved moieties or groupings of chemical elements that move together (e.g., amino group, P_i, etc.). Adding exchange reactions opens the system to external metabolites and leads to the disappearance of some conservation relationships (Fig. 3, right).

FIGURE 3.

Reaction maps versus compound maps. Reaction maps (left) show metabolites as nodes and reactions as directed edges. The reaction map includes both the internal and exchange fluxes, if present. In contrast, compound maps of the same systems (right) show the reactions as nodes and metabolites as directed edges. A system boundary that allows for the exchange of the internal nodes is open on a map. The compound map of an open reaction map is closed and vice versa, as it is shown by changing the network from A to B and to C.

Classification of extreme pools and pathways

Extreme pathway analysis has led to a useful classification schema of three categories of convex basis vectors for the right null space (see Fig. 4 A). These three categories correspond to through flux pathways (Type I), futile cycles coupled to cofactor use (Type II), and internal cycles (Type III). In an analogous fashion, the conservation quantities can be grouped into three basic types: Type A, B, and C (Fig. 4 B). The classification is based on grouping the metabolites into primary and secondary (Fig. 5). The primary metabolites contain the primary molecule structures that are undergoing serial transformations (e.g., the carbon backbone of glucose in glycolysis). The secondary metabolites function as cofactors and generally remain internal to the cell (e.g., ATP). Based on this classification, the three types of conservation pools correspond to: Type A pools that are composed only of the primary metabolites; Type B pools that contain both primary and secondary metabolites internal to the system; and Type C pools that are comprised only of secondary metabolites. Type B pools generally represent the conserved moieties that are exchanged from one compound to another, such as a hydroxyl or a phosphate group.

FIGURE 4.

Conserved pools and extreme pathway classifications. (A) Type I, II, and III extreme pathways correspond to through pathways, futile cycles coupled to cofactor utilization, and internal loops that are thermodynamically infeasible (Beard et al., 2002; Price et al., 2002), respectively. (B) Type A, B, and C metabolic pools correspond to the conservation of biochemical elements, metabolic moieties common to the primary and secondary metabolites, and cofactor conservation, respectively. Systems shown are presented as schematic examples of pools and flux pathways.

FIGURE 5.

Metabolic pool classification schema and structure of L. Partitioning the metabolites into primary and secondary allows for classification of metabolic pools. In the absence of the secondary and primary metabolite participation in conservation pools, the vectors are classified as Type A and C, respectively. The remaining vectors are grouped as Type B pools with both metabolite types present.

RESULTS

Study and interpretation of metabolic pools allow for the identification of metabolically meaningful conserved moieties. Systemic examination of conservation relationships using a convex representation identifies metabolic pools and delineates reaction participation in the formation of such relationships. We use nine successively more complex and biologically relevant examples to illustrate the formation and properties of conserved pools. First we examine the prototypical chemical transformations, second their combination, and third the real and skeleton representation of known pathways. This analysis should readily scale to full metabolic networks. Graphical representation of conserved pools on the compound maps is given.

Elementary chemical transformations

I. Irreversible conversion

Transformation between two compounds (comprised of two moieties, C and P) contains one conserved concentration pool (Fig. 6 I). Although such conversions are often used, they only represent simple chemical rearrangement of the molecule without any change in its elemental composition.

FIGURE 6.

Convex conservation pool representation for schematic biochemical systems. Seven example systems (I–VII) are graphically shown as reaction maps, compound maps, convex left null basis, and pool maps. Dash lines shown on the L matrix delineate metabolite and pool types.

II. Bimolecular association

The left null space of a reaction that involves the combination of two moieties, C and P, is two-dimensional spanned by two conservation quantities, a conservation of C (ℓ₁: C + CP), and a conservation of P (ℓ₂: CP + P) (Fig. 6 II).

III. A cofactor-coupled reaction

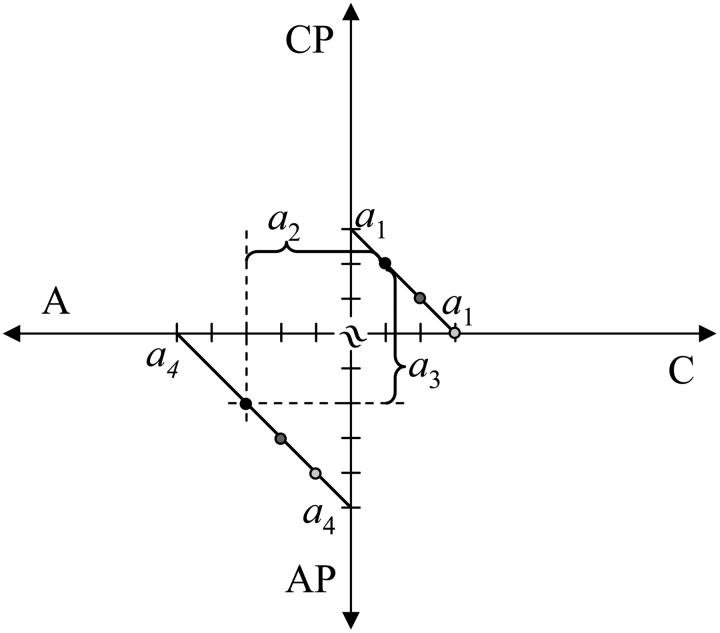
A prototypical reaction of metabolism is a reaction in which compound AP donates a moiety P to a compound C. The left null space for this transformation is three-dimensional and is spanned by three basis vectors: conservation of C (ℓ₁: C + CP), conservation of the exchanged moiety P (ℓ₂: CP + AP), and conservation of A (ℓ₄: A + AP). The convex basis is comprised of four vectors with an additional convex basis vector, ℓ₃. The fourth convex basis vector corresponds to a “vacancy” for the exchange moiety (ℓ₃: A + C) (Fig. 6 III). One can thus view ℓ₂ and ℓ₃ as a conjugate pair of occupied and nonoccupied sites for P, and in the case where P represents a high energy phosphate bond, this is a conjugate pair of high and low energy states. The convex basis thus identifies all the nonnegative conservation relationships including the energy and elemental conservations. The four convex basis vectors can be graphically depicted in two dimensions (Fig. 7). The relative values among the four metabolites are determined by the magnitude of the elements of a (Fig. 7).

FIGURE 7.

Graphical depiction of the null space for the cofactor-coupled reaction. The cofactor-coupled reaction contains four convex conservation relationships as shown in Fig. 6 III. The relative distance between the carbon and cofactor metabolites remains constant and is determined by the magnitude of the conservation quantities so C + CP = a₁, C + A = a₂, CP + AP = a₃, and A + AP = a₄. The points with the same shading (black, gray, white) correspond to an identical state depicted in two distinct two-dimensional spaces. For example, the concentration state in which C = 2, CP = 1, A = 2, and AP = 3 is depicted by the gray point and satisfies a₁ = 3, a₂ = 4, a₃ = 4, and a₄ = 5. The states represented by the white and black points also satisfy these pool sizes. The concentration solution space is the solid line shown in the two spaces. The symbol ≈ indicates that the origin is not common between the two two-dimensional spaces.

We note that the convex pool structure is related to the concept of the “charge” of a cofactor pool (Reich and Sel'kov, 1981). ℓ₂ can be partitioned into the occupied secondary cofactor (AP) and the occupied primary compound (CP). This partitioning relative to the size of the cofactor pool, given by ℓ₄ (ℓ₄: A + AP) gives the charge of the cofactor pool,

(4)

Combinations of transformations

IV. Incorporation of a moiety

Biochemical reactions often incorporate metabolic moieties or chemical elements such as H₂O and P_i. For a cofactor-coupled reaction preceding a moiety incorporating reaction, the four convex conservation vectors correspond to: conservation of primary metabolite C (ℓ₁: C + CP + CP₂), high-energy moiety conservation (ℓ₂: CP + CP₂ + AP), conservation of the stand-alone P moiety (ℓ₃: CP₂ + P), and total cofactor conservation (ℓ₄: A + AP) (Fig. 6 IV). Note also that pool maps illustrate both the conservation relationships and reaction participation in the formation of these metabolic pools. As shown in Fig. 6 IV, the conservation of P as represented in ℓ₃ occurs only through the activity of v₂. Similarly, v₁ is the only reaction participating in the conservation of the cofactor moiety A, as shown in ℓ₄ (Fig. 6 IV).

V. Multi-component cofactor coupled reactions

Cofactor coupling in biochemical networks may proceed with components of more than two elements. For example, oxidation of metabolites in dehydrogenase reactions occurs via NAD⁺ conversion to NADH and H⁺. This transformation forms more than two energy conjugates. For a two-part chemical conversion using redox potential (Fig. 6 V), the convex conservation vectors correspond to:

• Conservation of primary metabolite R (ℓ₁: RH₂ + R + R′ + R′H₂),

• Reducing power (ℓ₂: RH₂+R′H₂+NADH, and ℓ₃ : RH₂ + RH′₂ + H⁺),

• Oxidizing power (ℓ₄: R + R′ + NAD), total redox potential (ℓ₅: NAD⁺ + NADH), and

• Positive charge or total hydrogen atom (ℓ₄: NAD⁺ + H⁺).

The convex basis shows that there exist two high-energy conjugates (ℓ₂ and ℓ₃) for the low-energy oxidizing conjugate of ℓ₄. Furthermore, the basis of the left null space identifies not only the conservation of chemical elements but also the atomic charge.

Skeleton metabolic pathways

These concepts can now be used to get a glimpse of how pools form in real metabolic and signaling pathways. The symbols used in the reactions schemas below are not meant to directly indicate chemical elements.

VI. Simplified glycolysis

A few additions to schema III and IV will give the skeleton structure of glycolysis (Fig. 6 VI). The convex basis for the stoichiometric matrix for this network contains six metabolic pools, including the conservation of primary, ℓ₁, and cofactor, ℓ₆, moieties and four Type B pools that correspond to:

• High-energy conservation pool (ℓ₂: 2 C₆ + 3 C₆P + 4 C₆P₂ + 2 C₃P₁ + 2 C₃P₂ + C₃P + AP₃),

• Conservation of elemental P (ℓ₃: C₆P + 2 C₆P₂ + C₃P₁ + 2 C₃P₂ + C₃P + AP₃ + P),

• Low-energy conservation pool (ℓ₄: 2 C₆ + C₆P + C₃P + 2 C₃ + AP₂), and

• Potential to incorporate the stand-alone moiety P (ℓ₅: C₃P₂ + C₃P + C₃ + P) (Fig. 6).

ℓ₂ and ℓ₄ form energy conjugates to each other representing the high and low energy occupancy in the system. ℓ₅ corresponds to ℓ₃ in schema IV. The incorporation and exchange of phosphate thus results in four different convex basis vectors, each representing different aspects of the complex role of phosphate in energy metabolism (i.e., the high-energy phosphate and stand-alone inorganic phosphate, as shown here). The phosphate in AP₂ does not appear in the conservation of the elemental P, ℓ₃, since AP₂ interacts as a whole moiety and is never reduced to other chemical moieties in this reaction network. In addition, the pool maps readily illustrate the reaction contributions to the conservation of biochemical moieties, such as shown by the pool map of ℓ₅, which involves only v₄, v₅, and v₆.

VII. Simplified TCA cycle

The tricarboxylic acid (TCA) cycle is a circular pathway that converts a two-carbon unit into carbon dioxide and redox potential in terms of NADH. The convex basis for the left null space of the stoichiometric matrix for the simplified TCA network has five conservation moieties (Fig. 6 VII). They represent the conservation of:

• Exchanging carbon group (ℓ₁: 2 H₂C₂ + 2 H₂C₆ + HC₅ + C),

• Recycled four-carbon group that “carries” the two-carbon moiety that is degraded (ℓ₂: C₄ + H₂C₆ + HC₅),

• Hydrogen group that contains the redox inventory in the system (ℓ₃: 2 H₂C₂ + 2 H₂C₆ + HC₅ + NH), redox vacancy (ℓ₄: C + N), and

• Total cofactor pool (ℓ₅: N + NH).

The nonnegative convex representation of the left null space leads to a metabolically meaningful set of conservation relationships. The carbon in this system is represented by two pools. One is the four-carbon group that cycles through the TCA, whereas the other represents the two-carbon unit delivered by acetyl-CoA and is taken away to be oxidized into CO₂. As with the energy state of the glycolytic intermediates in the above example, the convex basis gives a conjugate pair of basis vectors that forms the redox-filled sites or the redox inventory in the system at any given time, as well as the vacant sites. Note that ℓ₃ can be partitioned into redox bound to carbon (i.e., 2 H₂C₂ + 2 H₂C₆ + HC₅) and to the cofactor (NH). This partitioning then leads to a redox charge definition analogous to Eq. 4, by rationing NH to (N + NH).

Application to real biochemical pathways

VIII. Red blood cell glycolysis and the Rapoport-Leubering shunt

Glycolysis and the Rapoport-Leubering shunt in human red blood cell consist of 20 metabolites and 13 internal, enzymatic reactions (Fig. 8 A). The conserved metabolic pools for this network were calculated by assuming that no metabolites can enter or leave the system (Fig. 8 B). The convex basis corresponds to the following conservation quantities (Fig. 8 C):

• ℓ₁, total carbon atoms: when multiplied by 3, this vector accounts for the number of carbon atoms in each compound in glycolysis. The carbon group, like the other moieties, remains conserved if the system is closed to carbon exchange with the environment.

• ℓ₂, total oxygen atom: this group corresponds to the gain or loss of an oxygen atom. This oxygen atom is incorporated in the glyceraldehydes-3-phosphate dehydrogenase (v_GAPDH) reaction as the O-[PO₃] group and is subsequently released as a part of the H₂O molecule by enolase, whereas the [−PO₃] stays on the metabolites.

• ℓ₃, total phosphate: this conservation quantity includes phosphate both in the form of a free inorganic phosphate or a phosphate moiety bound to the glycolytic intermediates, e.g., in glucose-6-phosphate. Note that ADP does not appear in this conserved relationship since its phosphate is never exchanged, whereas ATP (essentially ADP-P) appears in this set with one phosphate group that can be donated to the network.

• ℓ₄, high-energy potential release: this vector represents the potential of each carbon-containing compound to release the high-energy potential of ATP molecule. ℓ₃ forms an energy conjugate with ℓ₄ and together, they represent the total energy potential to convert adenosine group via glycolysis.

• ℓ₅, oxidized state of the metabolites pool: this pool represents the oxidized form of the metabolites in the system and thus represents the conjugate of the redox occupancy of the system.

• ℓ₆, reducing power: the carbon-containing compounds in this conserved concentration vector have the ability to release the energy of the redox potential of NAD molecule. Glucose can lead to two NADH, GA3P to one NADH, and so forth. This pool is a high redox state conjugate of ℓ₅ and is similar to ℓ₃ in schema V.

• ℓ₇, redox state of the metabolites: this pool counts the number of redox equivalents in the network. ℓ₇ also forms a redox conjugate with ℓ₅ and represents the conversion of NAD/NADH through glycolysis. This conservation pool is equivalent to ℓ₂ in schema V.

• ℓ₈, total hydrogen atom: this set represents the conservation of hydrogen atom coupled to the conversion of an NAD⁺ molecule via the v_GAPDH and v_LDH reactions. Note that the hydrogen moiety represents the positive charge on the reduced (NADH + H⁺) and oxidized NAD⁺ molecules.

• ℓ₉, total adenylate moiety: the conserved adenosine moiety and its total quantity remain constant (A_tot = ATP + ADP). The total adenosine pool shifts between the charged form (ATP) and the uncharged form (ADP).

• ℓ₁₀, total NAD moiety: the total redox potential is conserved (N_tot = NAD⁺ + NADH). The NAD moiety is thus in the oxidized form (NAD⁺) or the reduced form (NADH).

FIGURE 8.

Pool analysis of the human red blood cell glycolysis and Rapoport-Leubering shunt. (A) The reaction map of glycolysis and the Rapoport-Leubering shunt in human red blood cell contains 13 reactions and 20 metabolites. (B) The compound map of the reaction set shown in part A shows glycolytic reactions as the nodes and metabolites as the edges. (C) Pool maps of all 10 convex basis vectors in the human red blood cell glycolysis. ℓ₃ and ℓ₄ form high and low energy conjugates and ℓ₅, ℓ₆, and ℓ₇ comprise the redox conjugate set in the network. The conservation values are shown on the pool maps.

The convex basis vectors of metabolic pools include the conservation relationships and their complementary conjugates in the network. For the glycolytic network in the red blood cell, the basis set represents the conservation of the elemental groups like carbon and oxygen, cofactor groups like ATP and NADH, and their energy conjugate groups, as described.

IX. Simplified tyrosine kinase cell signaling

In the signaling pathway with a single ligand and receptor as shown in Fig. 9, seven convex basis vectors form the conserved concentration space. In this schema, all the compounds are secondary with the exception of the active ligand, L_act, the inactive ligand, L_inact, and RNA, which enter and leave the system. Conservation of the ligand is of Type B (ℓ₁: L_act + L_inact + RL + RL-P). Type C pools include the phosphate group conservation (ℓ₂: RL-P + SP + TP + DNA-TP + ATP + P), adenosine conservation (ℓ₃: ATP + ADP), transcriptional factor pool (ℓ₄: T + TP + DNA-TP + DNA-T), total DNA (ℓ₅: DNA + DNA-TP + DNA-T), STAT or signal transducers and activators of transcription pool (ℓ₆: S + SP), and the receptor conservation (ℓ₇: R + RL + RLP). Note that no Type A pool is formed in this signaling schema since most metabolites are considered to be secondary. Also, RNA does not participate in any of the conservation moieties as a result of the topology of the network (i.e., RNA is not contained in any conserved moiety in this schema).

FIGURE 9.

Schematic representation of signaling pathway (e.g., a tyrosine kinase-type signaling pathway) and its corresponding conservation pools. (A) Reaction map of the sample tyrosine kinase pathway. (B) Compound map of the tyrosine kinase pathway. (C) Metabolite pool maps of conservation pools. (L, ligand; R, receptor; LR, ligand-receptor complex; LR-P, phosphorylated ligand-receptor complex; S, signal transducers and activators of transcription (STAT); SP, phosphorylated STAT; T, transcriptional factor; TP, phosphorylated transcriptional factor; DNA-TP, active DNA-transcriptional factor complex; P, inorganic phosphate; act, active; inact, inactive).

The concentrations of the compounds involved in signaling pathways are of particular importance in translating and relating the signal to its target destination. Transformation of the signal is achieved essentially by the phosphorylation and dephosphorylation of the signaling intermediates such as STAT and the transcription factor. Thus the phosphorylation state of the signaling pathway is indicative of the signaling process, and in this schema, it is formed in two steps: 1), by the activation of the ligand-receptor complex through the active ligand (ℓ₁: L_act + L_inact + LR + LR-P), and 2), by the phosphorylation state of the intermediate compounds (ℓ₂: LR-P + SP + TP + ATP + P). In addition, the partitioning of the DNA pool into DNA and DNA-transcriptional factor complex (DNA-T) determines how much message is produced. The active pool formation in signaling pathways is directly related to the charge state of the system and is the ratio of the phosphorylated state over the total phosphorylation capacity,

(5)

where the numerator is given by ℓ₂, and the denominator is the numerator plus the summation of (LR + S + T + ADP). The conserved pools can thus be used to represent the phosphorylation state of the signaling process at a given time.

DISCUSSION

The left null space of the stoichiometric matrix contains combinations of metabolite concentrations that are time invariant. Here we have shown that: 1), a convex basis for the left null space leads to the definition of metabolically relevant pools; 2), by analogy to flux analysis of the right null space, metabolic pools can be classified into three categories; 3), by transposing the stoichiometric matrix, a compound map can be defined on which the metabolic pools may be graphically represented; 4), pool maps illustrate what reactions participate in the formation of the conservation relationships; 5), metabolic pools form high and low charge conjugates that are exchangeable and may represent the energy or redox state of cofactor pairs in the cell; and 6), metabolic as well as signaling processes can be interpreted using the conservation relationships.

The use of a convex basis for the left null space of the stoichiometric matrix allows us to generate nonnegative combinations of the concentrations and form metabolic pools. These pools can be grouped into three categories. These three pool types have analogies with the three types of extreme pathways in the convex analysis of the steady-state flux space or the null space of S (Schilling et al., 2000). The metabolic pools have chemical elements or moieties, cofactors, or the combination of the two at their core. The combination pools, Type B, form conjugate pairs, some of which are not only related to the chemical composition of the compounds but also related to occupancy and vacancy of certain properties, such as redox equivalent or a high-energy phosphate group. The Type B pools describe the exchange of elements and moieties between the primary and secondary metabolites. These pools are the most interesting as they introduce novel conservation moieties in the network.

The analysis of the concentration pools leads to consideration of −S^T that in turn leads to formulation of compound maps. In these maps, the compounds are the links and the reactions the nodes. They are complementary to the frequently used flux map, but convey different information. The conservation pools can be graphically represented on the compound map and interpreted in an analogous fashion to extreme pathways. The pool map is now a graphical representation of reaction networks and will need to be studied further. The pool and concentration quantifications are subject to experimental determination through emerging metabolomics (Fiehn, 2002) and proteomics (MacCoss and Yates, 2001).

Signaling networks are typically thought of as being different from metabolic networks. Metabolism involves the dismemberment of substrate molecules for energy and redox potential production, and for synthesis of various metabolites. The demands on metabolism are normally thought of in terms of fluxes; i.e., the cell must produce a certain amount of an amino acid to satisfy protein synthesis needs. Thus, flux maps are frequently used to describe states of metabolism. Signaling, in contrast, conveys “information”. This information is basically the transcription state of the genome. Although the result is the production of mRNA molecules (i.e., flux), it is the binding state (i.e., concentration) of the regulator sites that give the transcription state. Thus pool maps may be more appropriate than flux maps for cell-signaling pathways. Pool maps can show the activation state of a signaling molecule while its total amount is conserved. Furthermore, the conservation quantities are time invariant and thus exist in all “dynamic states” of the network, which are of interest in cell signaling.

Biochemical networks are, in general, highly nonlinear due to the cofactor coupling of the reactions. The nonlinearity of biochemical networks distinguishes their connectivity from those often studied in graph theory and requires a classification schema. In addition, a representative basis set for biochemical networks may be chosen to be nonnegative since reaction rates and concentration states with negative values may be difficult to interpret. A number of studies have been published on characterizing the left null space of transformation matrices (Alberty, 1991; Clarke, 1988; Schuster and Höfer, 1991). In biochemical networks, left null space characterization has been done with more emphasis on the dynamic and thermodynamic analysis of the network (e.g., Alberty, 1991; Clarke, 1988), and as an optimization criterion in minimizing the total internal concentrations (Schuster and Höfer, 1991). Formation of pools as a result of time-scale separation has been studied (Palsson et al., 1987), showing that effective conservation pods can be formed in different time regimes. Here we have studied pool formation in biochemical reaction networks using what we have learned from extreme pathway analysis to compute and interpret nonnegative unique convex basis for the conserved biochemical moieties. We have also presented for the first time a systemic classification schema for grouping the metabolic pools, used metabolic pool maps to graphically present the conservation vectors and identified corresponding reactions that contribute to the pool formation, and applied the pool analysis and characterization to study real metabolic and representative signaling pathways.

Complex biochemical reaction networks can now be reconstructed based on various high throughput data types. The emergence of these networks call for analysis of their topological properties. The null space of the stoichiometric matrix that describes the topology of metabolic networks and that contains the steady-state flux distributions has been analyzed in detail (Schilling et al., 1999). Here we add to our understanding of the properties of the stoichiometric matrix by studying a convex representation of its left null space. With these results in hand, we need to apply the lessons learned to large-scale biological systems.