Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Jul;85(1):27–35. doi: 10.1016/S0006-3495(03)74451-8

Simulation of F-Actin Filaments of Several Microns

Dengming Ming *, Yifei Kong †, Yinghao Wu ‡, Jianpeng Ma *,†,‡
PMCID: PMC1303062  PMID: 12829461

Abstract

Here we report the results of applying substructure synthesis method to the simulation of F-actin filaments of several microns in length. The elastic deformational modes of long F-actin filaments were generated from the vibrational modes of the 13-subunit repeat of F-actin using a hierarchical synthesis scheme. The computationally synthesized deformational modes, in the very low-frequency regime, are in good agreement with theoretical solutions for long homogeneous elastic rods, which confirmed the usefulness of substructure synthesis method. Other low-frequency modes carry rich local deformational features that are unique to F-actins. All these modes thus provide a theoretical basis set for a description of spontaneously occurring thermal deformations, such as undulations, of the filaments. The results demonstrate that substructure synthesis method, as a method for computational modal analysis, is capable of scaling up the microscopic dynamic information, obtained from atomistic simulations, to a wide range of macroscopic length scale. Moreover, the combination of substructure synthesis method and hierarchical synthesis scheme provides an effective way in dealing with complex systems of periodic repeats that are abundant in cells.

INTRODUCTION

Actins are filamentous protein complexes that are important for cell transport, cytoskeletal support, and contractile events in almost all eukaryotic cells (Chen et al., 2000). They exist in two forms. In non-ionic solutions, the dominant form is a monomeric G-actin of 41kD. In the presence of salt, however, G-actin monomers polymerize into a double-stranded helical polymer called F-actin, the functional form of actins (Oda et al., 2001). Structural information on actins (Fig. 1) includes the atomic coordinates of G-actin (Kabsch et al., 1990; McLaughlin et al., 1993; Otterbein et al., 2001; Robinson et al., 1999; Schutt et al., 1993), the Holmes model of F-actin filaments established from fiber diffraction (Holmes et al., 1990) and several related versions (Holmes et al., 1993; Lorenz et al., 1995, 1993; Tirion et al., 1995). In the Holmes model, F-actin filaments appear to be formed by two right-handed long-pitch helical strands that twist around each other with a rise of 27.5 Å and a rotation angle of –166.15° per monomer around the filament axis (Fig. 1 b). The minimum repeat of the double-stranded helix is ∼35.75 nm and contains 13 monomers (the 13-subunit repeat) and the total length of F-actin attains several microns or longer.

FIGURE 1.

FIGURE 1

Open in a new tab

Structures of actins. (a) Structure of G-actin monomer that contains 375 amino acids refined by a normal mode-based method (Tirion et al., 1995). The discontinuity of the structure in the loop region by MOLSCRIPT (Kraulis, 1991) comes from the small distortions in the original structure. (b) The Holmes model for a 13-subunit repeat of F-actin filament established from fiber diffraction (Holmes et al., 1990, 1993; Tirion et al., 1995) with two helical strands differently colored. To illustrate the overall shape, the atomic coordinates were blurred to 8-Å resolution.

There are growing lines of experimental evidence (Huxley et al., 1994; Kojima et al., 1994; Wakabayashi et al., 1994) indicating that a large portion of dynamic properties of F-actin filaments, such as those modulating operations of molecular motors, is directly related to their intrinsic elasticity. Therefore, a molecular understanding of the mechanical elastic properties of F-actin filaments is vital to elucidating their roles in motile and cytoskeletal systems.

From more than two decades of computational studies (Brooks III et al., 1988; McCammon and Harvey, 1987), it is well-established that elastic motions of molecular complexes can be well approximated by large-scale low-frequency vibrations of the structures, which also play a dominant role in complex biomolecular dynamics in general. Powerful computational methods for studying those low-frequency vibrations include harmonic modal analyses such as normal mode analysis (NMA) (Brooks et al., 1995), quasi-harmonic analysis (Janezic et al., 1995), and its related version of essential dynamics (Amadei et al., 1993). Moreover, several recently developed methods provided a broadened way of analyzing biomolecular structures. The ones most relevant to this work are the Cα-based elastic network model (Atilgan et al., 2001; Bahar et al., 1997; Tirion, 1996) that can calculate low-frequency modes based on a much simpler potential function (Doruker et al., 2002; Hinsen, 1998; Keskin et al., 2002; Li and Cui, 2002; Tama and Brooks III, 2002), and the quantized elastic deformational model (QEDM) (Ming et al., 2002a; Tama et al., 2002) that is designed to simulate biomolecules based on only low-resolution density maps (Chacon et al., 2003; Ming et al., 2002b).

To extend the computational capacity in simulating vibrational motions of very long filamentous systems such as actins, we have recently developed a new method, substructure synthesis method (SSM) (Ming et al., 2003). The essential idea is to treat a given molecular complex structure as an assemblage of substructures. The choices of substructures can be arbitrary and sometimes quite natural, for example domains, subunits, or large segments of biomolecular complexes. The motions of these substructures are first represented by a set of substructure modes obtained by methods such as NMA. Then, the entire structure is generated by linking the substructures together using a set of constraints to enforce geometric compatibility at the interfaces of adjacent substructures. The vibrational modes of the entire structure are determined from substructure modes using the Rayleigh-Ritz principle (Temple and Bickley, 1956). For periodically repeating systems, a hierarchical synthesis scheme (HSS) can be used in combination with SSM to rapidly achieve the desired complexity. Computationally, SSM gains efficiency by avoiding the full eigenvalue problem for the entire structure and only dealing with a much more desirable problem for the substructures.

In this article, we report the application of SSM-HSS to the synthesis of the vibrational modes of F-actin filaments of 4.6 microns from the modes of a single 13-subunit repeat. Our results clearly demonstrate that SSM-HSS is an effective way to scale up the microscopic dynamic information, obtained from atomistic simulations, to a wide range of macroscopic length scale.

METHODS

Outline of SSM

In SSM (Ming et al., 2003), a given structure is assumed to be composed of a set of substructures. Let us first consider a particular substructure s and assume that it moves independently of all other substructures. If us(P,t) denotes the time-dependent displacement vector of any point, P (e.g., an atom), on the substructure, the kinetic energy of substructure s in the symbolic form can be written as

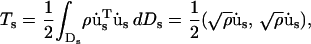graphic file with name M1.gif (1)

where Inline graphic is the inner product of Inline graphic with itself, and ρ is the mass distribution. Similarly, the potential energy can be given as

graphic file with name M4.gif (2)

where [us, us] is the energy inner product (Meirovitch, 1980) of the vector us with itself. Here, the energy inner product involves derivatives of us with respect to positional variables and integration over the entire structure. Though the mathematical forms of Eqs. 1 and 2 are written for the substructures with distributed mass and stiffness, the extension to discrete substructures is straightforward.

According to the Rayleigh-Ritz method (Temple and Bickley, 1956), the displacement us(P,t) can be expressed as a linear combination of space-dependent admissible vectors multiplied by time-dependent generalized coordinates,

graphic file with name M5.gif (3)

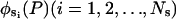where Inline graphic are admissible vectors from a complete set, which in this case are chosen to be the eigenvectors of normal modes, and Inline graphic are the time-dependent generalized normal mode coordinates. Eq. 3 can be given in the matrix form

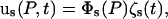graphic file with name M8.gif (4)

where Φs is a 3 × Ns matrix and ζs is an Ns-dimensional vector. Inserting Eq. 4 into Eq. 1, we obtain

graphic file with name M9.gif (5)

where

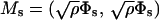graphic file with name M10.gif (6)

is an Ns × Ns matrix known as the substructure mass matrix. Correspondingly, introducing Eq. 4 into Eq. 2 gives

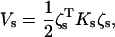graphic file with name M11.gif (7)

where

graphic file with name M12.gif (8)

is an Ns × Ns matrix termed as the substructure stiffness matrix. In the case of orthonormalized normal modes, both Ms and Ks are diagonal.

For a structure containing m substructures, s = 1,2,…m, that are assumed to move independently of one another, the combined kinetic energy of the assembled structure is

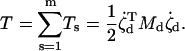graphic file with name M13.gif (9)

Here,

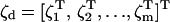graphic file with name M14.gif (10)

is an N-dimensional disjoint configuration vector, and Md is an N × N block-diagonal matrix

graphic file with name M15.gif (11)

with Inline graphic Similarly, the combined potential energy function is

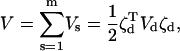graphic file with name M17.gif (12)

where Kd is also an N × N block-diagonal matrix

graphic file with name M18.gif (13)

If we assume that

graphic file with name M19.gif (14)

where ζd is a constant amplitude vector and σ(t) is a time-dependent harmonic function, we obtain the disjoint Rayleigh quotient

graphic file with name M20.gif (15)

However, in the assembled structure, the substructures are connected to each other and are subject to forces exerted by neighboring substructures at boundaries. Therefore, the boundary must satisfy certain geometric compatibility conditions to preserve the structural integrity. For example, considering two adjacent substructures r and s, we must have

graphic file with name M21.gif (16)

at every point of the boundary to connect the disjoint substructures. If there are Nc such constraints to connect substructures r and s, the system will have n = N − Nc degrees of freedom. Denoting ζ as the n-dimensional vector of independent generalized coordinates, the relation between the disjoint vector ζd and the vector ζ can be expressed as

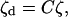graphic file with name M22.gif (17)

where C is an N × n rectangular matrix called the constraint matrix. Introducing Eq. 17 into Eq. 15 gives the Rayleigh quotient

graphic file with name M23.gif (18)

where

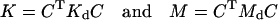graphic file with name M24.gif (19)

are the n × n stiffness and mass matrices for the assembled structure, respectively. Note that they are no longer diagonal even in the case of normal modes.

Based on the Rayleigh-Ritz principle (Temple and Bickley, 1956), one has an eigenvalue problem,

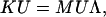graphic file with name M25.gif (20)

where U is an n × n modal matrix, and Λ is the diagonal matrix of the eigenvalues for the assembled structure. Using the transformation U′ = Φd CU, where Φd is defined in a similar way to Eq. 10 for ζd, one can obtain matrix U′, whose column vectors are the atomic displacements in the corresponding modes of the assembled structure, which can then be directly compared with the eigenvectors obtained from direct NMA of the assembled structure.

Hierarchical synthesis scheme (HSS)

To generate modes for extremely long F-actin filaments, it is computationally inefficient to synthesize them by sequentially adding a single repeating unit. A much more effective alternative is to use a hierarchical synthesis scheme. The essence lies in the fact that, to generate modes for an assembled structure from substructure modes, one only needs to utilize a set of low-frequency modes for substructures. This principle holds up at any length scale. For F-actin, since the filaments are periodic systems of a 13-subunit repeat (Holmes et al., 1993), we can first fuse two 13-subunit repeats together by SSM, and then two such products can be fused in the following cycle, and so on and so forth. With this procedure, the total length of the filament Ln after n cycles of synthesis would be Ln = 2nl0, where l0 is the length of a single 13-subunit repeat (l0 = 35.75 nm). Therefore, it only takes seven synthesis cycles to approach a length of 4.6 μm, which is close to the persistence length of actin filaments (Oosawa, 1980). This is a remarkable perspective in terms of computational efficiency. Note that if we always use the same number of lowest-frequency substructure modes, the computational cost would be the same in each cycle, regardless of the absolute length of the intermediate filaments that are used as substructures.

A word of caution regarding the errors, which do rise when only a small set of low-frequency substructure modes are used for synthesis (Ming et al., 2003). The HSS procedure gains efficiency by keeping the computational cost the same in each cycle, but it does so at the risk of losing precision of the synthesized modes as the filament elongates and the ratio of the substructure modes to the total number of degrees of freedom decreases. It is therefore preferable to employ as many substructure modes as the computational capacity allows and their number should also be significantly larger than that of the low-frequency modes one would be interested in for the final system. From our previous study (Ming et al., 2003), it is clear that the lowest-frequency modes are robust.

RESULTS

Synthesis of modes for a two 13-subunit F-actin segment

The basis of the modal synthesis of a two 13-subunit F-actin segment is the vibrational modes of a single 13-subunit repeat based on the Holmes model (Holmes et al., 1990) refined by normal mode-based method (Tirion et al., 1995). Since a 13-subunit repeat has 4875 residues, it is impossible to do an all-atom model analysis. Thus, the substructure modes were calculated by the Cα-based elastic network model (Atilgan et al., 2001), which has been shown in numerous studies to be able to reliably determine the low-frequency modes for large molecular complexes (Doruker et al., 2002; Hinsen, 1998; Keskin et al., 2002; Li and Cui, 2002; Tama and Brooks III, 2002). In our calculation, we used a 13-Å cutoff distance and 1.0 force constant (arbitrary unit, with a dimension of [energy]/[length]2). Fig. 2, a–c′, show the obtained typical deformational modes for a single 13-subunit repeat. These modes are presented together with a schematic illustration (Fig. 2 d) of the motional patterns of typical deformational modes, or waves, expected for a homogeneous elastic rod, which includes the bending (transverse), twisting (torsional), and stretching (longitudinal) modes. Clearly, the computed low-frequency modes for a single 13-subunit repeat (Fig. 2, a–c′) are consistent with the theoretical solution in Fig. 2 d. The comparison of computational results with the homogeneous elastic properties of actin filaments is justified by the fact that the experimentally measured elastic properties of F-actin filaments are consistent with those of a homogeneous elastic rod (Kojima et al., 1994; Liu and Pollack, 2002; Tsuda et al., 1996; Yasuda et al., 1996).

FIGURE 2.

FIGURE 2

FIGURE 2

Open in a new tab

Normal modes for a 13-subunit repeat of F-actin filament. The a–c′ represent the lowest-frequency modes for each type of mode: a and a′ are the bending modes (modes 7 and 10); b and b′ are the twisting modes (modes 9 and 12); and c and c′ are the stretching modes (modes 15 and 25). The two helical strands of F-actin are in different colors. Each mode is represented by two opposite end-point structures. The orientation of the filament in each mode is chosen to best illustrate that particular mode. (d) Schematic illustration of typical low-frequency normal modes (bending, twisting, and stretching) for a homogeneous elastic rod. Two lowest-frequency modes are shown for each type of mode, with the solid arrow indicating the increase of frequency.

In SSM, when two segments are fused together, the treatment of geometric boundary conditions is a key issue. As demonstrated in the previous study (Ming et al., 2003), one would have to equalize half of the boundary points during synthesis, i.e., one of the equivalent layers is sacrificed, as schematically shown in Fig. 3 a. This is a major source of errors for SSM (Ming et al., 2003). However, the errors can be asymptotically reduced and become negligible when the weight of the sacrificed points is insignificant relative to the substructure.

FIGURE 3.

FIGURE 3

FIGURE 3

Open in a new tab

(a) A schematic illustration of SSM when fusing two 3-mass-point chains together. One of the two boundary points (c and a′) is equalized (sacrificed) during synthesis. (b) Stereo pair for the interface of two substructures in the synthesis of a two 13-subunit F-actin segment showing the 15 red spheres (Cα-atoms) chosen as the boundary points by the 5-Å distance search. The subunits from different substructures are shown in different colors. For clarity, only the subunits near the interface are shown and the orientation of the filament is horizontal in the plane of the paper.

In the preparation for the synthesis of a two 13-subunit F-actin segment, to make a correct structure across the interface after synthesis, our substructure was chosen to be an entire 13-subunit repeat, plus a thin layer of points (Cα atoms) that are equivalent to those located at the boundary of the adjacent unit as boundary points. The boundary points were selected solely based on their distances to the adjacent substructure. A 5-Å distance search criterion was used which led to a total of 15 boundary points (Cα atoms) (Fig. 3 b). Therefore, the substructure contains a total of 4890 points (4875 + 15). The 15 boundary points result in 3 × 15 = 45 constraints in the synthesis. The vibrational modes were synthesized for the segment using 300 and 800 substructure modes.

The first verification of the synthesized modes is to see if they contain the characteristic modes illustrated in Fig. 2 d. In the very low-frequency regime, the deformational modes of F-actin filaments should be very similar to those of a homogeneous elastic rod. Fig. 4, a–c, shows the first bending, twisting, and stretching modes for the assembled structure using 300 substructure modes. Here the first bending mode appears in the seventh mode (the very first vibrational mode), the first twisting mode appears in the 11th mode, and the first stretching mode appears in the 17th mode. The order of these modes in terms of their frequencies is consistent with the general theory of elasticity and the stretching mode has higher stiffness. It must be noted that the amplitudes of modes in Fig. 4, a–c, are arbitrary, and the modes are primarily to show their motional directionality.

FIGURE 4.

FIGURE 4

Open in a new tab

Lowest-frequency modes from SSM synthesis of a two 13-subunit F-actin segment. (a) Bending, (b) twisting, and (c) stretching modes for F-actin. In SSM, 300 low-frequency modes from each substructure were used. Two substructures are in different colors. Each mode is represented by two opposite end-point structures. (d) Comparison of the theoretical solution of a homogeneous elastic rod (Eq. 28) with the synthesized bending mode in a. The dots represent the average positions of the bent actin filament in the lower image of a by an arbitrary sampling density, and the central tube represents the theoretical solution. Amplitudes were adjusted to achieve a best match.

More quantitatively, we studied the convergence of the first bending mode shown in Fig. 4 a by comparing it with a theoretical curve for a homogeneous elastic rod, which has the form of

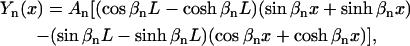graphic file with name M26.gif (21)

where L is the length of the rod, An is the amplitude of the nth mode, and βnL has a value of 4.730 when n = 2, which is the first bending mode (Meirovitch, 1967). Fig. 4 d shows the results and the agreement is excellent. Therefore, SSM successfully produced the desired modes for the F-actin filament of two 13-subunit repeats in length.

Synthesis of modes for F-actin of several microns by SSM-HSS

Vibrational analysis of long F-actin filaments will provide insightful information on the spontaneously occurring thermal deformations, such as undulations, of the filaments observed in experiments (Liu and Pollack, 2002). To demonstrate the capacity of SSM-HSS, we synthesized an F-actin filament of 4.6 μm that contains 128 13-subunit repeats. Starting from the F-actin segment composed of two 13-subunit repeats synthesized in the last section, it only took seven cycles of HSS to reach the desired length (128 = 27). This length of filament was chosen because it is close to the persistence length of F-actins reported in the literature, which varies within a range of 5–10 μm depending on the experimental methods used (Liu and Pollack, 2002). Synthesis of modes for longer filaments is straightforward. Since we are only interested in the lowest-frequency modes for the assembled structure, which can be robustly synthesized from a small set of low-frequency substructure modes (Ming et al., 2003), the synthesis was performed with 300 and 800 substructure modes for comparison purposes. We found that they are sufficient for a reasonable convergence of the synthesized modes.

The first issue in characterizing the synthesized modes is the convergence of the eigenvalues, especially as the length of the filament increases. As mentioned before, certain errors would occur for longer filaments if we use the same number of substructure modes in every synthesis cycle. Fig. 5 shows the logarithms of eigenvalues as a function of filament length using 300 and 800 substructure modes. The results are presented together with the theoretical values, which has the form of

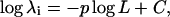graphic file with name M27.gif (22)

where λi is the eigenvalue of the ith mode of a particular type, L is the length of the filament, and integer p has a value of 4 for bending modes, and 2 for twisting and stretching modes. The constant C is related to the elastic constant and mass of the filament. Since in our calculation, the unit of eigenvalue is arbitrary and we are only interested in the trends of the curves so that the absolute value of C is irrelevant, we normalized the curves by setting the first point equal to each other. All three types of modes (bending, twisting, and stretching modes) were shown for their very lowest-frequency modes (Fig. 5) because these are the ones that can be most appropriately compared with the theoretical results. For all types of lowest-frequency modes, the trends of changes in the eigenvalues as the length of the filament increases followed those of the theoretical values. The lowest-frequency bending mode seems to be relatively insensitive to the number of substructure modes employed, while the twisting and stretching modes have better results when 800 substructure modes were used, as expected based on our previous study (Ming et al., 2003), i.e., the larger the number of substructure modes, the better the convergence of the synthesized modes. Moreover, for all types of modes, small deviations from theoretical curves were observed as the length of the filaments became longer. This is because the method loses precision as the filament elongates and the ratio of these low-frequency modes to the total number of degrees of freedom decreases (Ming et al., 2003).

FIGURE 5.

FIGURE 5

Open in a new tab

The logarithms of eigenvalues of the synthesized modes from SSM-HSS as a function of the number of the 13-subunit repeat in the F-actin filaments, presented together with the theoretical results of homogeneous elastic rods of the same length. Two cases are shown, one with 300 substructure modes (abbreviated as Submodes; left panels), and the other with 800 submodes (right panels). The very lowest-frequency modes are shown for (a) bending, (b) twisting, and (c) stretching modes. The SSM and theoretical curves were normalized in each case by setting the first point equal to each other.

The second issue is the nature of eigenvectors, which describe the patterns of deformations of F-actin filaments. From the previous study (Ming et al., 2003), the lower the frequency of a synthesized mode, the better it converges in its eigenvalue and eigenvector. Fig. 6 shows typical bending modes at a few lowest-frequencies and the patterns of motion displayed by these modes are consistent with what are expected (see Fig. 2 d). The indices of these modes in the ascending order of their frequencies are 7, 9, 11, 13, 15, 17, and 19. Each of them is accompanied by a degenerate mode (even indices). All of these modes move in a plane, a typical feature for a homogeneous elastic rod. This is in contrast to the modes for the two 13-subunit F-actin segment synthesized in the last section, among which there are many low-frequency modes, except the very lowest one for each type of mode, that have out-of-plane features. This is mostly because, as the filaments become longer, the influence of local structural features decreases and the filaments behave more and more like homogeneous elastic rods.

FIGURE 6.

FIGURE 6

Open in a new tab

The motional patterns of several lowest-frequency bending modes for the 4.6 μm F-actin filament calculated by SSM-HSS. The indices of the modes are marked. The even indices are the ones that degenerate to the displayed one. The seventh mode is the lowest-frequency mode.

Similar behavior was also observed for twisting and stretching modes, but the results are not shown here since they cannot be easily illustrated visually for the extremely long filaments due to their axial nature.

CONCLUDING DISCUSSION

We have reported the application of substructure synthesis method (SSM) (Ming et al., 2003) to the vibrational modal analysis of F-actin filaments of several microns in length. SSM is a new computational method that is capable of scaling up the microscopic dynamic information, obtained from atomistic simulations, to a wide range of macroscopic length scale. The results also demonstrated that SSM, together with HSS, can efficiently deal with periodically repeating systems, especially the extremely large filamentous ones whose elastic properties are important for their biological functions. In addition to actin, other filamentous systems in cells include tubulin, collagen, and DNA.

It should be noted that the effectiveness of SSM partially depends on the choice of boundary between substructures, which could be tricky in some cases. In systems such as viruses, the contact surface between subunits is so extensive that it would be hard to define the boundary points. In those cases, other methods may work more efficiently (Simonson and Perahia, 1992; Tama and Brooks III, 2002; Tama et al., 2000; van Vlijmen and Karplus, 2001). But for filamentous systems with long length and relatively small cross sections, SSM-HSS is more advantageous, especially in terms of the computational efficiency. In SSM-HSS, if one uses the same number of substructure modes and the same boundary points in each synthesis cycle, the computational cost in each cycle will stay the same, regardless of the length of the filament. Moreover, in contrast to the regular NMA, SSM-HSS per se does not need to calculate the Hessian matrix, except in the initial step of determining the substructure modes, which is a tremendous advantage in dealing with extremely large systems.

In our analysis, the comparison of the synthesized lowest-frequency modes and the theoretical results of homogeneous elastic rods was used to verify our synthesis results. There are two extreme regimes wherein the vibrational modes of F-actin filaments approach those of homogeneous elastic rods (the so-called wire modes). One is at long-length limit and the other is at lowest-end of vibrational frequency for a fixed length. Both regimes are captured by NMA in this article. However, this is by no means to indicate that the deformational motions of F-actin filaments are restricted to those modes. In fact, many modes, especially the ones for shorter F-actin filaments and at slightly higher frequency, carry rich local deformational features that are unique to actin molecules (ben-Avraham and Tirion, 1995). Of particular interest are the modes with wavelengths close to the physical size of an individual G-actin monomer (Galkin et al., 2002; Orlova et al., 2001), including those that have implications in the allosteric effects of local conformational changes of a single G-actin monomer on its neighboring subunits and the cooperativity among them (Egelman, 2001; Egelman and Orlova, 1995). The functional implications of these local deformational modes will be discussed elsewhere.

The synthesized vibrational modes for F-actin filaments provide a theoretical basis set by which any arbitrary elastic deformation of the filaments can then be expressed as a linear combination. They also provide a means to characterize the motions of F-actin filaments at a continuously varying length scale, i.e., from the extremely localized high-frequency motions all the way to global elastic deformational motions. In a very long scale of length, the bending motions would probably dominate, while other types of deformations such as twisting and stretching are likely to be important to short-range local deformations of the filaments (Egelman et al., 1982).

As in other cases (Brooks III et al., 1988), NMA provides a description for harmonic motions of the molecules. However, there are certain portions of molecular deformations possessing an harmonic features. Actins are not exceptions. In this regard, the harmonic basis set from NMA can be used to determine the fraction of harmonicity in the overall deformational motions. For many proteins, especially for the large molecular complexes (Go et al., 1983; Levitt et al., 1985; Li and Cui, 2002; Ma and Karplus, 1997, 1998; Seno and Go, 1990; Tama and Brooks III, 2002; Tama and Sanejouand, 2001), this fraction is always substantial.

The primary focus of this study is on the large-scale global elastic deformational motions. Therefore, in our analysis, the effects of nucleotide binding and hydrolysis were not included. However, it is likely that the nucleotide binding state of each individual G-actin monomer may alter the rigidity of the monomer and in turn affect the elasticity of the entire filaments. This will be the focus of our future work.

It is worth pointing out that the Cα-based elastic NMA (Atilgan et al., 2001) employed in our study does not provide any physically meaningful scale of stiffness of vibrational modes because of its simplified potential function (Tirion, 1996). However, SSM has correctly captured the relative trends of changes in eigenvalues as a function of the filament length. The absolute value of stiffness of the modes, if desired, can be scaled to a correct value using extra experimentally measured elastic constants (Dupuis et al., 1997; Kojima et al., 1994; Tsuda et al., 1996).

Acknowledgments

The authors thank Professor Michael F. Schmid for helpful discussions on actin simulations.

J.M. gratefully acknowledges the support from the American Heart Association, the Robert A. Welch Foundation, and the National Science Foundation Career Award (No. MCB-0237796). He is also a recipient of the Award for Distinguished Young Scholars Abroad from the National Natural Science Foundation of China.

References

  1. Amadei, A., A. B. M. Linssen, and H. J. C. Berendsen. 1993. Essential dynamics of proteins. Proteins. 17:412–425. [DOI] [PubMed] [Google Scholar]
  2. Atilgan, A. R., S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar. 2001. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 80:505–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bahar, I., A. R. Atilgan, and B. Erman. 1997. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 2:173–181. [DOI] [PubMed] [Google Scholar]
  4. ben-Avraham, D., and M. M. Tirion. 1995. Dynamic and elastic properties of F-actin: a normal-modes analysis. Biophys. J. 68:1231–1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brooks, B. R., D. Janezic, and M. Karplus. 1995. Harmonic analysis of large systems. I. Methodology. J. Comp. Chem. 16:1522–1542. [Google Scholar]
  6. Brooks III, C. L., M. Karplus, and B. M. Pettitt. 1988. Proteins: a theoretical perspective of dynamics, structure, and thermodynamics. Adv. Chem. Phys. 71:1–249. [Google Scholar]
  7. Chacon, P., F. Tama, and W. Wriggers. 2003. Mega-dalton biomolecular motion captured from electron microscopy reconstructions. J. Mol. Biol. 326:485–492. [DOI] [PubMed] [Google Scholar]
  8. Chen, H., B. W. Bernstein, and J. R. Bamburg. 2000. Regulating actin-filament dynamics in vivo. TIBS. 25:19–23. [DOI] [PubMed] [Google Scholar]
  9. Doruker, P., R. L. Jernigan, and I. Bahar. 2002. Dynamic of large proteins through hierarchical levels of coarse-grained structures. J. Comp. Chem. 23:119–127. [DOI] [PubMed] [Google Scholar]
  10. Dupuis, D. E., W. H. Guilford, J. Wu, and D. M. Warshaw. 1997. Actin filament mechanics in the laser trap. J. Muscle Res. Cell Motil. 18:17–30. [DOI] [PubMed] [Google Scholar]
  11. Egelman, E. H. 2001. Actin allostery again? Nat. Struct. Biol. 8:735–736. [DOI] [PubMed] [Google Scholar]
  12. Egelman, E. H., N. Francis, and D. J. DeRosier. 1982. F-actin is a helix with a random variable twist. Nature. 298:131–135. [DOI] [PubMed] [Google Scholar]
  13. Egelman, E. H., and A. Orlova. 1995. New insights into actin filament dynamics. Curr. Opin. Struct. Biol. 5:172–180. [DOI] [PubMed] [Google Scholar]
  14. Galkin, V. E., M. S. VanLoock, A. Orlova, and E. H. Egelman. 2002. A new internal mode in F-actin helps explain the remarkable evolutionary conservation of actin's sequence and structure. Curr. Biol. 12:570–575. [DOI] [PubMed] [Google Scholar]
  15. Go, N., T. Noguti, and T. Nishikawa. 1983. Dynamics of a small globular protein in terms of low-frequency vibrational modes. Proc. Natl. Acad. Sci. USA. 80:3696–3700. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hinsen, K. 1998. Analysis of domain motions by approximate normal mode calculations. Proteins. 33:417–429. [DOI] [PubMed] [Google Scholar]
  17. Holmes, K. C., D. Popp, W. Gebhard, and W. Kabsch. 1990. Atomic model of the actin filament. Nature. 347:44–49. [DOI] [PubMed] [Google Scholar]
  18. Holmes, K. C., M. Tirion, D. Popp, M. Lorenz, W. Kabsch, and R. A. Milligan. 1993. A comparison of the atomic model of F-actin with cryo-electron micrographs of actin and decorated actin. Adv. Exp. Med. Biol. 332:15–22. [DOI] [PubMed] [Google Scholar]
  19. Huxley, H. E., A. Stewart, H. Sosa, and T. Irving. 1994. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys. J. 67:2411–2421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Janezic, D., R. M. Venable, and B. R. Brooks. 1995. Harmonic analysis of large systems. III. Comparison with molecular dynamics. J. Comp. Chem. 16:1554–1566. [Google Scholar]
  21. Kabsch, W., H. G. Mannherz, D. Suck, E. F. Pai, and K. C. Holmes. 1990. Atomic structure of the actin: DNase I complex. Nature. 347:37–44. [DOI] [PubMed] [Google Scholar]
  22. Keskin, O., I. Bahar, D. Flatow, D. G. Covell, and R. L. Jernigan. 2002. Molecular mechanisms of chaperonin GroEL-GroES function. Biochemistry. 41:491–501. [DOI] [PubMed] [Google Scholar]
  23. Kojima, H., A. Ishijima, and T. Yanagida. 1994. Direct measurement of stiffness of single actin filaments with and without tropomyosin by in vitro nanomanipulation. Proc. Natl. Acad. Sci. USA. 91:12962–12966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kraulis, P. J. 1991. MOLSCRIPT: A program to produce both detailed and schematic plots of protein structures. J. Appl. Crystallogr. 24:946–950. [Google Scholar]
  25. Levitt, M., C. Sander, and P. S. Stern. 1985. Protein normal-mode dynamics: trypsin inhibitor, crambin, ribonuclease and lysozyme. J. Mol. Biol. 181:423–447. [DOI] [PubMed] [Google Scholar]
  26. Li, G., and Q. Cui. 2002. A coarse-grained normal mode approach for macromolecules: an efficient implementation and application to Ca2+-ATPase. Biophys. J. 83:2457–2474. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Liu, X., and G. H. Pollack. 2002. Mechanics of F-actin characterized with microfabricated cantilevers. Biophys. J. 83:2705–2715. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lorenz, M., K. J. Poole, D. Popp, G. Rosenbaum, and K. C. Holmes. 1995. An atomic model of the unregulated thin filament obtained by x-ray fiber diffraction on oriented actin-tropomyosin gels. J. Mol. Biol. 246:108–119. [DOI] [PubMed] [Google Scholar]
  29. Lorenz, M., D. Popp, and K. C. Holmes. 1993. Refinement of the F-actin model against x-ray fiber diffraction data by the use of a directed mutation algorithm. J. Mol. Biol. 234:826–836. [DOI] [PubMed] [Google Scholar]
  30. Ma, J., and M. Karplus. 1997. Ligand-induced conformational changes in ras p21: a normal mode and energy minimization analysis. J. Mol. Biol. 274:114–131. [DOI] [PubMed] [Google Scholar]
  31. Ma, J., and M. Karplus. 1998. The allosteric mechanism of the chaperonin GroEL: a dynamic analysis. Proc. Natl. Acad. Sci. USA. 95:8502–8507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. McCammon, J. A., and S. Harvey. 1987. Dynamics of Proteins and Nucleic Acids. Cambridge University Press, Cambridge, UK.
  33. McLaughlin, P. J., J. T. Gooch, H. G. Mannherz, and A. G. Weeds. 1993. Structure of gelsolin segment 1-actin complex and the mechanism of filament severing. Nature. 364:685–692. [DOI] [PubMed] [Google Scholar]
  34. Meirovitch, L. 1967. Analytical Methods in Vibrations. The Macmillan Company, London, UK.
  35. Meirovitch, L. 1980. Computational Methods in Structural Dynamics. Sijthoff & Noordhoff, Rockville, MD.
  36. Ming, D., Y. Kong, M. Lambert, Z. Huang, and J. Ma. 2002a. How to describe protein motion without amino-acid sequence and atomic coordinates. Proc. Natl. Acad. Sci. USA. 99:8620–8625. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Ming, D., Y. Kong, S. J. Wakil, J. Brink, and J. Ma. 2002b. Domain movements in human fatty acid synthase by quantized elastic deformational model. Proc. Natl. Acad. Sci. USA. 99:7895–7899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Ming, D., Y. Kong, Y. Wu, and J. Ma. 2003. Substructure synthesis method for simulating large molecular complexes. Proc. Natl. Acad. Sci. USA. 100:104–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Oda, T., K. Makino, I. Yamashita, K. Namba, and Y. Maeda. 2001. Distinct structural changes detected by x-ray fiber diffraction in stabilization of F-actin by lowering pH and increasing ionic strength. Biophys. J. 80:841–851. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Oosawa, F. 1980. The flexibility of F-actin. Biophys. Chem. 11:443–446. [DOI] [PubMed] [Google Scholar]
  41. Orlova, A., V. E. Galkin, M. S. VanLoock, E. Kim, A. Shvetsov, E. Reisler, and E. H. Egelman. 2001. Probing the structure of F-actin: cross-links constrain atomic models and modify actin dynamics. J. Mol. Biol. 312:95–106. [DOI] [PubMed] [Google Scholar]
  42. Otterbein, L. R., P. Graceffa, and R. Dominguez. 2001. The crystal structure of uncomplexed actin in the ADP state. Science. 293:708–711. [DOI] [PubMed] [Google Scholar]
  43. Robinson, R. C., M. Mejillano, V. P. Le, L. D. Burtnick, H. L. Yin, and S. Choe. 1999. Domain movement in gelsolin: a calcium-activated switch. Science. 286:1939–1942. [DOI] [PubMed] [Google Scholar]
  44. Schutt, C. E., J. C. Myslik, M. D. Rozycki, N. C. Goonesekere, and U. Lindberg. 1993. The structure of crystalline profilin-β-actin. Nature. 365:810–816. [DOI] [PubMed] [Google Scholar]
  45. Seno, Y., and N. Go. 1990. Deoxymyoglobin studied by the conformational normal mode analysis. II. The conformational change upon oxygenation. J. Mol. Biol. 216:111–126. [DOI] [PubMed] [Google Scholar]
  46. Simonson, T., and D. Perahia. 1992. Normal modes of symmetric protein assemblies. Application to the tobacco mosaic virus protein disk. Biophys. J. 61:410–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Tama, F., and C. L. Brooks III. 2002. The mechanism and pathway of pH-induced swelling in Cowpea Chlorotic Mottle virus. J. Mol. Biol. 318:733–747. [DOI] [PubMed] [Google Scholar]
  48. Tama, F., F. X. Gadea, O. Marques, and Y. H. Sanejouand. 2000. Building-block approach for determining low-frequency normal modes of macromolecules. Proteins. 41:1–7. [DOI] [PubMed] [Google Scholar]
  49. Tama, F., and Y. H. Sanejouand. 2001. Conformational change of proteins arising from normal mode calculations. Protein Eng. 14:1–6. [DOI] [PubMed] [Google Scholar]
  50. Tama, F., W. Wriggers, and C. L. Brooks. 2002. Exploring global distortions of biological macromolecules and assemblies from low-resolution structural information and elastic network theory. J. Mol. Biol. 321:297–305. [DOI] [PubMed] [Google Scholar]
  51. Temple, G., and W. G. Bickley. 1956. Rayleigh's Principle and Its Applications to Engineering. Dover, New York.
  52. Tirion, M. M. 1996. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 77:1905–1908. [DOI] [PubMed] [Google Scholar]
  53. Tirion, M. M., D. ben-Avraham, M. Lorenz, and K. C. Holmes. 1995. Normal modes as refinement parameters for the F-actin model. Biophys. J. 681:5–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Tsuda, Y., H. Yasutake, A. Ishijima, and T. Yanagida. 1996. Torsional rigidity of single actin filaments and actin-actin bond breaking force under torsion measured directly by in vitro micromanipulation. Proc. Natl. Acad. Sci. USA. 93:12937–12942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. van Vlijmen, H. W. T., and M. Karplus. 2001. Normal mode analysis of large systems with icosahedral symmetry: application to Dialanine60 in full and reduced basis set implementations. J. Chem. Phys. 115:691–698. [Google Scholar]
  56. Wakabayashi, K., Y. Sugimoto, H. Tanaka, Y. Ueno, Y. Takezawa, and Y. Amemiya. 1994. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophys. J. 67:2422–2435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Yasuda, R., H. Miyata, and K. Kinosita, Jr. 1996. Direct measurement of the torsional rigidity of single actin filaments. J. Mol. Biol. 263:227–236. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES